Confinement and Crowding Effects on Folding of a Multidomain Y‑Family DNA Polymerase

Abstract

Proteins in vivo endure highly various interactions from the luxuriant surrounding macromolecular cosolutes. Confinement and macromolecular crowding are the two major effects that should be considered while comparing the results of protein dynamics from in vitro to in vivo. However, efforts have been largely focused on single domain protein folding up to now, and the quantifications of the in vivo effects in terms of confinements and crowders on modulating the structure and dynamics as well as the physical understanding of the underlying mechanisms on multidomain protein folding are still challenging. Here we developed a topology-based model to investigate folding of a multidomain Y-family DNA polymerase (DPO4) within spherical confined space and in the presence of repulsive and attractive crowders. We uncovered that the entropic component of the thermodynamic driving force led by confinements and repulsive crowders increases the stability of folded states relative to the folding intermediates and unfolded states, while the enthalpic component of the thermodynamic driving force led by attractive crowders gives rise to the opposite effects with less stability. We found that the shapes of DPO4 conformations influenced by the confinements and the crowders are quite different even when only the entropic component of the thermodynamic driving force is considered. We uncovered that under all in vivo conditions, the folding cooperativity of DPO4 decreases compared to that in bulk. We showed that the loss of folding cooperativity can promote the sequential domain-wise folding, which was widely found in cotranslational multidomain protein folding, and effectively prohibit the backtracking led by topological frustrations during multidomain protein folding processes.

Graphical Abstract

Protein folds and performs its function in delicate and intricate cellular milieu involving various macromolecules that can collaboratively occupy as much as 40% of the cell volume.¹ Protein dynamics in vivo under such dense environments may deviate significantly from that observed in the in vitro experiments,² which are usually conducted in dilute conditions. To evaluate the results from the ideal in vitro experiments and address how they can be applicable to the in vivo circumstances, the effects of the macromolecular cosolutes, popularly termed as crowding agents, have to be quantitatively investigated.³ However, this is extremely challenging due to the high complexity of intracellular environment, which is not possible to study in full either theoretically or experimentally.⁴

For simplicity, one may first consider that the most prominent consequence led by in vivo conditions is the steric “macromolecular crowding” effect. It was claimed that the molecule is expected to exclude the other spatial neighbors due to its volume-occupancy.^5,6 The effects of excluded volume by repulsive crowders on protein dynamics have been found to profoundly modulate the thermodynamics and kinetics of protein folding,^7–9 the association¹⁰ and the stability,^11,12 as well as the enzyme activity.^13–16 The steric repulsion is entirely entropic in terms of decreasing the amount of space available to the chain,¹⁷ thus giving rise to distinct effects on different protein conformations. A nonuniform reduction of entropy during protein folding favors compact and collapsed folded states. This in general leads to an increase of folding stability.¹⁸

Significant efforts have been focused on the hard-core steric repulsion;^12,19–21 however, the interactions between the protein and the crowders can be either repulsive or attractive in reality termed as soft interactions. Recent research taking consideration of the nonspecific attractive protein-crowder interactions underlined the destabilization effect of crowders on the protein folded states.^22–24 The findings are in contrast with previous interpretations of purely steric repulsion. These features indicate that the attractive interaction serving as an enthalpic component^25–27 may play an unprecedented role on participating into the protein dynamics in vivo.²⁸

In addition to the macromolecular crowding, protein may naturally experience other types of volume restrictions in vivo, such as cotranslational folding in ribosome exit tunnel,²⁹ chaperone-assisted folding in a cavity,^30,31 and folding near/on the surfaces.³² Such confinements, which can be symbolically represented by the encapsulation of proteins within compartments, also have remarkable effects on protein folding thermodynamics and kinetics.^33,34 In an extreme case, where immobile, large, and highly populated crowders are present, the effects of macromolecular crowding on protein folding thermodynamics can be approximated by confinements.³⁴ However, quantifications of the in vivo effects in terms of crowders and confinements on modulating the structure and dynamics of protein are still challenging.

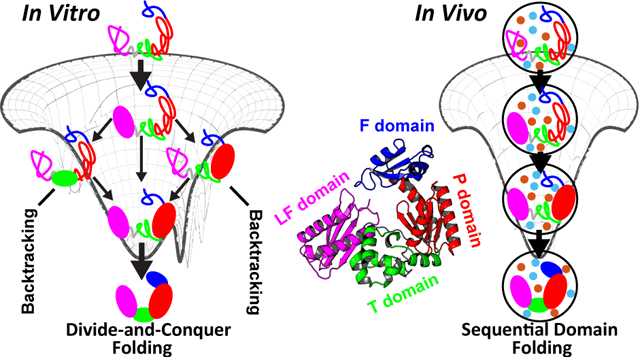
Most of the studies on protein folding have been focused on single domain proteins, despite the fact that multidomain proteins are much more prevalent in life.³⁵ Different with the single domain proteins, multidomain proteins have large domain interfaces. These exposed interaction surfaces are prone to aggregation, thus leading to a high risk of dysfunctional misfolding.³⁶ This gives rise to a folding problem at multidomain protein level: How does a domain avoid misfolding or aggregation? In vitro, a “divide-and-conquer” domain folding independently by coalescing the neighbors was observed.³⁷ Such folding picture not only eliminates the propensity of forming interfacial domain interactions during folding but also accelerates the folding process by shrinking the configurational space. In vivo, it is expected that multidomain proteins may undergo sequential domain-wise folding that is domain folds in a deterministic order.^38,39 However, it is still largely unknown how the in vivo conditions help the multidomain proteins to achieve such folding process. In vivo folding likely proceeds along with the protein synthesis and often requires the assistance from the chaperone.⁴⁰ The ribosome exit tunnel and chaperone cavity lead to confined spaces for protein folding, and the surrounding in vivo agents during protein synthesis give rise to a crowding effect. Therefore, the effects led by confinements and crowders should be explicitly considered in investigations of the cotranslational and chaperone-assisted folding. Investigations on multidomain protein folding in the presence of confined space and crowders can shed light on the understanding of the underlying mechanism of the multidomain protein folding. In addition, the presence of crowders have been found to improve enzymatic activity by inducing new compact structures that have direct functional advantages.^13–15 Multidomain proteins usually possess compact, well-folded domains, compared to extended, loosely formed domain interfaces.⁴¹ Such structural characteristic indicates that the in vivo conditions can potentially induce spatial domain rearrangement and, thus, may have more significant effects on the functional dynamics of the multidomain protein, which are mostly related to the domain movements^42–44 or local unfolding (cracking),^45,46 compared to single domain proteins.

Here we investigated the effects of confinements and crowders on folding of Y-family DNA polymerase IV (DPO4) from Sulfolobus solfatarius.⁴⁷ DPO4 is a prototype of multidomain protein,⁴⁸ of which the folding in vitro has been identified with an intermediate state.⁴⁹ Using a coarse-grained structure-based model (SBM), we examined the folding thermodynamics, cooperativity, and energy landscape of DPO4 under different environmental conditions, including confinements, repulsive, and attractive crowders. We found that the DPO4 folding mechanism preserves and the folding cooperativity decreases under all the conditions compared to that in the bulk case (“dilute” conditions). Weak confinements and repulsive crowders increase the folding stability, while the attractive crowders can completely counteract the effects. We found that DPO4 folding in bulk may encounter “backtracking”,⁵⁰ which can be subsequently eliminated by strengthening confinements or adding crowders. We suggest that, in vivo, DPO4 folding is primed to ensure high efficiency by restricting the domain folding order, reminiscent of sequential domain cotranslational folding.^38,39

2. MATERIALS AND METHODS

2.1. Coarse-Grained Structure-Based Model.

Structure-based model (SBM) is based on the energy landscape theory, which assumes protein folding occurs on a funnel-like energy landscape associated with minimal frustrations.⁵¹ SBM focuses on the interactions from the native structure and thus can significantly accelerate the folding process while still preserve the underlying molecular mechanism.^52–54 Here, we applied a C_α-level coarse-grained SBM to investigate DPO4’s folding with a typical Hamiltonian expressed as follows:⁵²

$$\begin{gathered} V_{\text{SBM}}^{\text{bulk}}=\sum _{\text{bonds}}{K}_r{\left(r-r_0\right)}^2+\sum _{\text{angles}}{K}_{\theta }{\left(\theta -{\theta }_0\right)}^2 \\ \begin{array}{l}+\sum _{\text{dihedral}}{K}_{\varphi }^{\left(n\right)}\left[1+\cos \left(n\times \left(\varphi -{\varphi }_0\right)\right)\right]\\ +\sum _{i<j-3}^{\text{native}}{\mathrm{ϵ}}_{ij}\left[5{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-6{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{10}\right]\\ +\sum _{i<j-3}^{\text{non-native}}{\mathrm{ϵ}}_{pp}{\left(\frac{{\sigma }_{pp}}{r_{ij}}\right)}^{12}\end{array} \end{gathered}$$

The SBM potential includes bond stretching, angle bending, torsional, and nonbonded interactions. The parameters K_r, K_θ, K_ϕ, ϵ_ij, and ϵ_PP weight the strength of each type of interaction. r, θ, and ϕ are the bond lengths, bending angles, and dihedral angles, with a subscript zero representing the values adopted in the native structure. Nonbonded interactions are subdivided into native interactions and nonnative interactions. For native contacts, σ_ij is the distance between beads i and j in native structure. For non-native contacts, σ_PP is equal to the diameter of the C_α bead and the associated interaction provides the excluded volume repulsion between the beads in DPO4. The native contact map is generated by Contacts of Structural Unit (CSU) software.⁵⁵ Length is in the unit of nm, and the others are in reduced units for all calculations, so K_r = 10000.0, K_θ = 20.0, $K_{\varphi }^{\left(1\right)}=1.0$, $K_{\varphi }^{\left(3\right)}=0.5$, ϵ_ij = 1.0, ϵ_PP = 1.0, and σ_PP = 0.4 nm.

2.2. SBM with Spherical Confinement.

In order to include a volume confinement in SBM, we added a spherical wall to $V_{\text{SBM}}^{\text{bulk}}$, so the Hamiltonian has the following expression:

$$V_{\text{SBM}}^{\text{confinment}}=V_{\text{SBM}}^{\text{bulk}}+V_{\text{C}}$$

V_C has a semiharmonic potential:

$$V_{\text{C}}=\{\begin{array}{cc}{K}_{\text{C}}{\left(R-R_{\text{C}}\right)}^2& R\ge R_{\text{C}}\\ 0& R<R_{\text{C}}\end{array}$$

where R is the distance of every bead to the center of the system box, and R_C is the radius of the spherical confinement. K_C controls the strength of the potential and is set to be 500.0. We calculated the radius of gyration R_g for DPO4 at native PDB structure and unfolded conformations from the simulation in bulk (no confinement or crowders), which are 2.25 nm and 5.25 nm, respectively. These two values dictate the lower and upper limit for R_C in our simulations.

2.3. SBM with Explicit Crowders.

Molecular crowders with one-bead representation were added in the system explicitly, so the Hamiltonian has the following expression:

$$V_{\text{SBM}}^{\text{crowder}}=V_{\text{SBM}}^{\text{bulk}}+V_{\text{PC}}+V_{\text{CC}}$$

where V_PC and V_CC are the potentials for protein-crowder and crowder–crowder interactions, respectively.

The volume fraction of the crowders (Φ_C) is calculated by

$${\mathrm{\Phi }}_{\text{C}}=N_{\text{C}}\frac{4}{3}\pi r_{\text{C}}^3/l^3$$

where r_C is the radius of the crowder bead, N_C is the number of crowders, and l is the length of the cubic box of the system. The crowder–crowder interaction is purely repulsive with the following expression:^56–58

$$V_{\text{CC}}={\mathrm{ϵ}}_{\text{CC}}{\left(\frac{{\sigma }_{\text{ref}}}{r_{ij}-{\sigma }_{\text{CC}}+{\sigma }_{\text{ref}}}\right)}^{12}$$

where σ_CC is the diameter of the crowder bead, which is equal to 2r_C. σ_ref = 0.6 nm is a reference diameter and ϵ_CC = 1.0. In our simulations, we set r_C = 0.8 nm.

2.3.1. Repulsive Protein-Crowder Potential.

In the first case, we applied purely repulsive potential to the protein-crowder interaction:^34,57

$$V_{\mathrm{P}\mathrm{C}}^R={\mathrm{ϵ}}_{\mathrm{P}\mathrm{C}}^R{\left(\frac{{\sigma }_{\text{ref}}}{r_{ij}-{\sigma }_{\text{PC}}+{\sigma }_{\text{ref}}}\right)}^{12}$$

where σ_PC is the sum of the radius of protein and crowder beads, which is equal to 0.5σ_PP + r_C = 1.0 nm. ${ϵ}_{PC}^R$ was set to be 1.0 throughout the simulations.

2.3.2. Lennard-Jones Like Attractive Protein-Crowder Potential.

In the second case, we used a Lennard-Jones like potential to describe protein-crowder attractive interaction:⁵⁸

$$V_{\text{PC}}^{\text{LJ}}=4{\mathrm{ϵ}}_{\text{PC}}^{\text{LJ}}\left[{\left(\frac{{\sigma }_{\text{ref}}}{r_{ij}-{\sigma }_{\text{PC}}+{\sigma }_{\text{ref}}}\right)}^{12}-{\left(\frac{{\sigma }_{\text{ref}}}{r_{ij}-{\sigma }_{\text{PC}}+{\sigma }_{\text{ref}}}\right)}^6\right]$$

We changed ${ϵ}_{\text{PC}}^{\text{LJ}}$ in practice to modulate the strength of protein-crowder interaction.

2.4. Simulation Protocol.

All the simulations were performed by Gromacs (version 4.5.7)⁵⁹ with plugin PLUMED (version 2.5),⁶⁰ which is used to implement the confinement potential. The SBM input files were generated following the standard instructions from the SMOG tool.⁶¹ All the bonds were applied by constraints through LINCS algorithm,⁶² ensuring a 0.001 time step without any simulation instability. The Langevin dynamics integrator was used and the stochastic temperature coupling was set to be 1.0, which corresponds to a friction coefficient of 1.0. All the long-range interactions were cutoff at 3.0 nm. A cubic box with length 20 nm was set up for the system. We applied different crowder concentrations Φ_C with 0.10, 0.20 and 0.30, corresponding to 373, 746, and 1119 crowders in the system, respectively.

Replica-exchange molecular dynamics (REMD) simulations were applied.⁶³ The 28 replicas for each simulation were used with the temperature ranging from 1.00 to 1.35, concentrating around the corresponding melting temperatures. Exchange frequency between neighbor replicas was set to be every 1000 steps. We found there are reasonable overall exchange probabilities, which are all higher than 0.2, guaranteeing the sampling efficiency of REMD. Finally, all the trajectories were collected, and the Weighted Histogram Analysis Method (WHAM) program was used to obtain the thermodynamic results.⁶⁴

2.5. Order, Shape Parameters, and Thermodynamic Quantities.

We used the fraction of native contacts Q to measure the native similarity of the conformation in simulations.⁶⁵ Q can be further specified to some parts of the interests. For example, Q(finger) and Q(F – T) are the measurements for the native contact sets within F domain and between F and T domain interface of DPO4, respectively. To avoid numerical discontinuity, we practically applied a step function to calculate Q with the following expression:

$$Q=\frac{1}{2}\left[1-\tanh \left(\frac{r_{ij}-\mu r_{i{j}_0}}{r_0}\right)\right]$$

where r₀ controls the slope of step function and was set to be 0.01 nm and μ was set to be 1.2 to endure a certain degree of fluctuation.

We used Δ and S suggested previously to determine the shape of the DPO4’s conformation.⁶⁶ The rotationally invariant quantities Δ and S are calculated by the inertia tensor T with components:

$$T_{\alpha \beta }=\left({\mathit{r}}_{\mathit{\alpha }}-\langle {\mathit{r}}_{\mathit{\alpha }}\rangle \right){\left({\mathit{r}}_{\mathit{\beta }}-\langle {\mathit{r}}_{\mathit{\beta }}\rangle \right)}^T$$

where r_α is a row vector that represents the αth component of the coordinate of element in the system and α, β = x, y, z.

$$\mathrm{\Delta }=\frac{3}{2}\frac{{\sum }_{k=1}^3{\left({\lambda }_k-\langle \lambda \rangle \right)}^2}{{\left(tr\mathit{T}\right)}^2}$$

where λ_k are the eigenvalues of T, corresponding to the squares of the three principal radii of gyration.

$$S=27\frac{{\prod }_{k=1}^3\left({\lambda }_k-\langle \lambda \rangle \right)}{{\left(tr\mathit{T}\right)}^3}$$

Δ and S measures the asphericity and shape of the conformation, respectively. Δ starts from the minimum value 0, which corresponds to the sphere, and the deviation indicates the extent of anisotropy. S describes the shapes from oblate (negative values) to prolate (positive values). The perfect sphere therefore has Δ = S = 0.

To describe the folding cooperativity of domain/interface coupling in DPO4 during (un)folding, we calculated the coupling magnitudes of the melting curve for each domain/interface. This is characterized by a thermodynamic coupling index (TCI) matrix.^67–69 In practice, all the melting curves ⟨Q⟩ along the temperature were fitted to a simple two-state model, from which the probability of folded states p(T) along the temperature can be obtained (Figure S1). Then the TCI matrix was calculated by comparing all the possible pairwise folding probability curves of each domain/interface with the following expression:

$$\text{TCI}\left(I,J\right)=-\ln \langle \left|\left(p^I\left(T\right)-p^J\left(T\right)\right)\right|\rangle$$

where p^I(T) and p^J(T) stand for the folding probability as a function of temperature for domain/interface I and J, respectively. We therefore expect that a higher value of TCI encodes more similarity of the pairwise (un)folding curves and thus directly corresponds to a stronger coupling and then more cooperativity. For an idea all-or-none transition, TCI will be infinity. The mean TCI is calculated by

$$\text{MTCI}=-\ln \sum _{I,J}\langle \left|\left(p^I\left(T\right)-p^J\left(T\right)\right)\right|\rangle$$

2.6. Structure of DPO4.

DPO4 is a prototype of Y-family DNA polymerase,^47,48,70 which possess a finger (F) domain for nucleotide selection, palm (P) domain for catalysis, thumb (T) domain and a unique little finger (LF) domain for DNA binding,⁷¹ associated via a flexible 15-residue-long linker between T and LF domain (Figure 1). The shape parameters of Δ and S for PDB structure are respectively 0.14 and 0.05, presenting a slightly prolate rodlike shape at native structure. We used Modeler software⁷² to add the missing residues from 34 to 39 in the F domain in PDB crystal structure⁴⁷ but completely removed the native contacts related, and the corresponding local terms were further reduced to 0.01 of the original values in $V_{\text{SBM}}^{\text{bulk}}$. Such implementations would ensure large flexibity for this region, as the absence of electron density in crystal structure is usually a sign of excessive conformation disorder.

Figure 1.

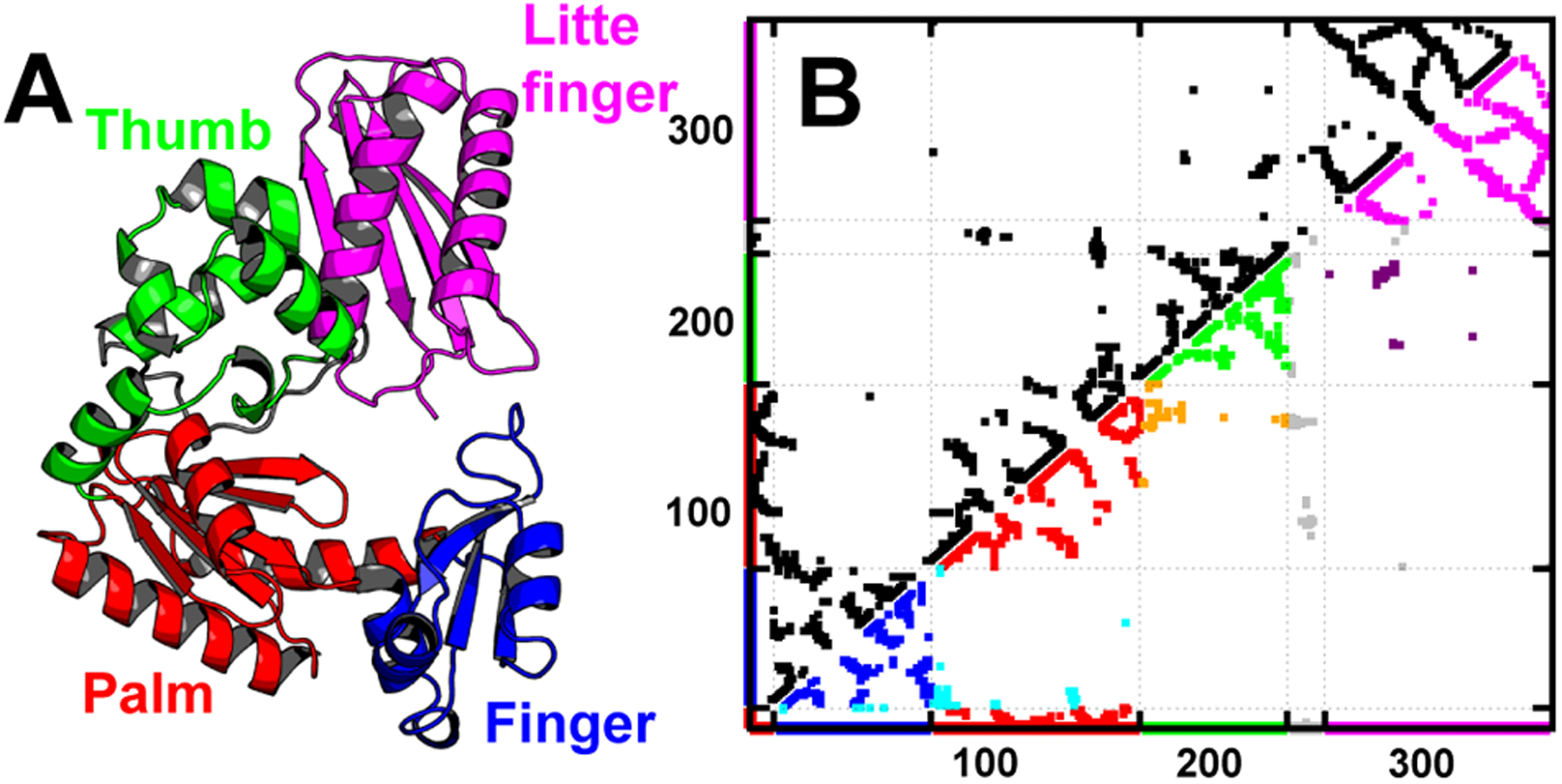
Crystal structure and native contact map of DPO4 (PDB: 2RDI).⁴⁷ (A) Different domains of DPO4 are colored with different schemes: F domain (blue, residues 11–77), P domain (red, residues 1–10 and 78–166), T domain (green, residues 167–229), LF domain (magenta, residues 245–341), and flexible linker (gray, residues 230–244). (B) The dotted points represent the native contacts generated by CSU.⁵⁵ At the bottom right, the intradomain native contacts are plotted with the color schemes used in (A) and the interfacial contacts between domains are colored cyan (F–P, between F and P domain), orange (P–T, between P and T domain), and purple (T–LF, between T and LF domain). The contacts related to the flexible linker are colored gray. Apparently, there are more intradomain contacts (population is 84.35%) than interdomain contacts (population is 9.86%), which are mostly formed by the sequential neighbor domains, in DPO4’s native structure. Flexible linker extensively forms contacts to each domain with a population of 5.79%. The details of contact formation can be found in Table S1.

3. RESULTS AND DISCUSSION

3.1. Effects of Confinements on DPO4 Folding.

We performed REMD⁶³ to explore the thermodynamics of DPO4 folding with SBM.⁵² In the absence of confinements and macromolecular crowders (in bulk), we found that the heat capacity curve of DPO4 folding has only one single prominent peak (Figure 2A) and the melting curves of typical structural parameters including fraction of native contacts Q, radius of gyration R_g, and RMSD all exhibit routinely sigmoidal behaviors (Figure S5), implying that DPO4 folding is a highly cooperative process. The free energy landscape however shows folding occurs stepwise with multiple metastable intermediate states (Figure 2B, black line), in line with our previous simulations.³⁷ Previous experiments undertaken by the circular dichroism (CD) spectroscopy identified one intermediate state during the melting of DPO4.⁴⁹ Such intermediate state was further reasoned to be the consequence of breaking the contacts formed between the P domain and linker in DPO4. From the native contact maps of the different DPO4 folding states (Figure S11), we can infer that the I₂ state found from the free energy landscape obtained in our simulations, where DPO4 exhibits the full absence of the contacts involved by the linker accompanied by partially unfolded DPO4, may correspond to the intermediate state detected by the experiments. This is also in accordance with the experimental observation that the DPO4 core, which is made up of the F, P, and T domains, starts unfolding prior to the melting of DPO4 from the intermediate state monitored by CD spectroscopy.⁴⁹ In addition, we observed the stable secondary structure formation in DPO4 preserved within a wide range of temperature prior to the high melting temperature (Figure S3), consistent with that found in CD experiments.⁴⁹ The highly consistent (un)folding process of DPO4 obtained from the experiments and simulations respectively provides an appealing manifestation that the SBM including only the interactions from native topology is capable to tackle a wide range of protein dynamics from single domain^52,73 to multidomain level⁷⁴ and is competent for our following simulations of DPO4 folding under confinements and in the presence of crowders. It is worth noting that the number of intermediates detected by CD experiment is less than that observed by our simulations. It has been known that the CD experiment only measures the ensemble-averaged secondary structure formation at one-dimensional resolution and thus may not be able to provide the precise description of the protein folding process.⁷⁵ The most accurate determination of protein unfolding mechanism relies on multiple methods that should lead to high-dimensional measurements.⁶⁷

Figure 2.

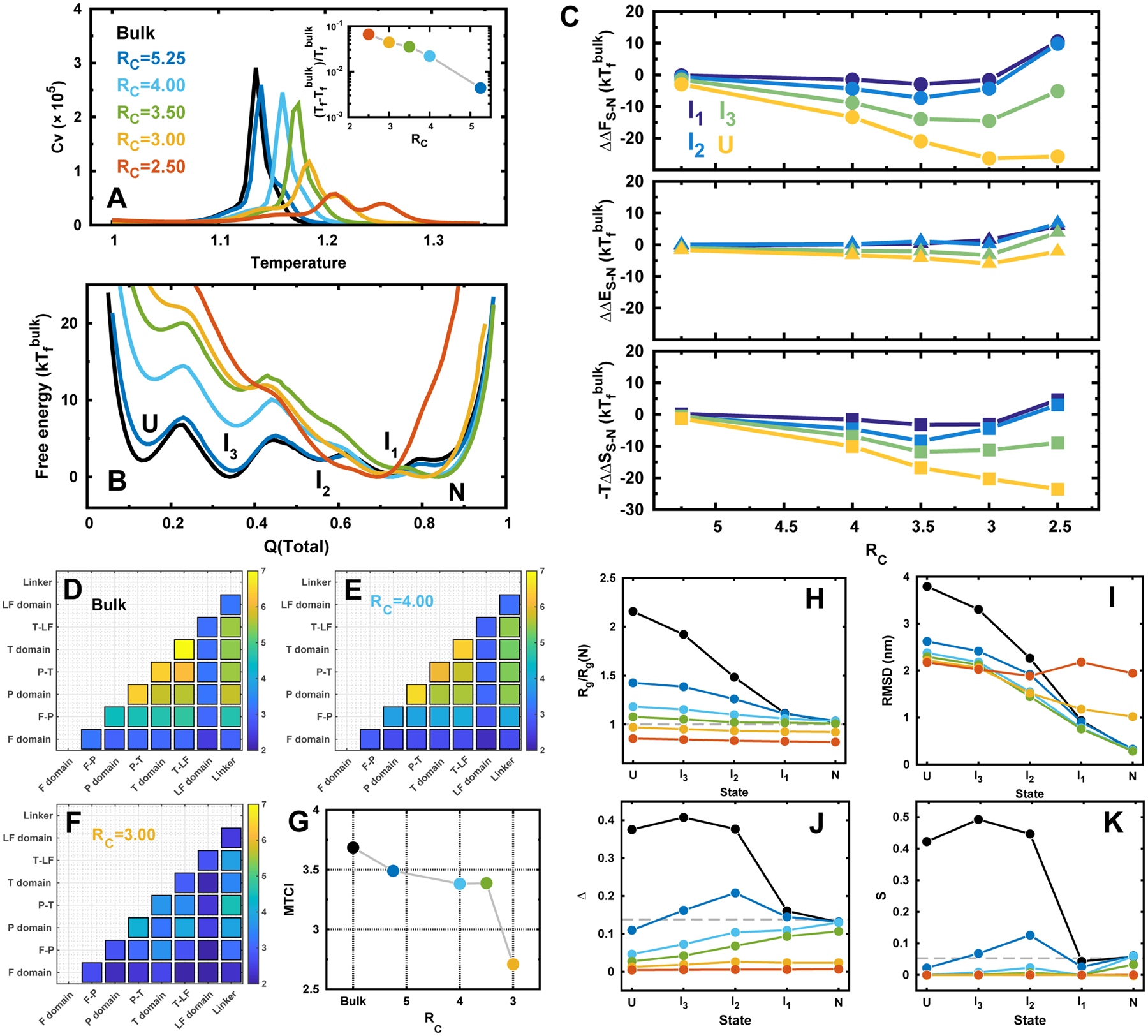
DPO4 folding in bulk and under confinements. (A) Heat capacity curves of DPO4 folding. Inset shows the folding temperature T_f changes with different confinements. Folding temperature is defined as the most prominent peak position from the heat capacity curve. R_C is the radius of spherical confinement, so a small value of R_C corresponds to a strong confinement. R_C is in the unit of nm. (B) 1D free energy landscapes along Q(total) under different confinements at the folding temperature of the bulk condition $\left(T_{\text{f}}^{\text{bulk}}\right)$. Q(total) is the fraction of total native contacts of DPO4. There are multiple states formed during the folding process indicated as “U, I₃, I₂, I₁, N”, corresponding to the unfolded states, three intermediate states, and native folded states, respectively. (C) The relative change of the differences in free energy (top), energy (middle), and entropy (bottom) for different folding states of DPO4 to that in bulk along with the different strengths of confinement. The free energy difference between the proceeding state “S” and “N”, where “S” can be any intermediate or unfolded states, is expressed as ΔF_S–N = F_N – F_S. The change of the free energy led by confinement is then expressed as ΔΔF_S–N = ΔF_S–N(R_C) – ΔF_S–N(bulk). Similar calculations were applied to the changes of difference in energy ΔΔE_S–N and entropy ΔΔS_S–N from simulation with confinement to that in bulk. (D–F) Folding cooperativity quantity TCI for DPO4 folding in bulk and under confinements. (G) MTCI along with R_C. (H–K) Structural characterizations of the folding states during DPO4 folding process under different confinements. (H) Radius of gyration R_g of each state in DPO4 folding under different confinements. R_g(N) is the R_g of PDB structure.⁴⁷ (I) RMSD to PDB structure of each state during DPO4 folding under different confinements. (J) Asphericity Δ and (K) shape S parameters of each state during DPO4 folding under different confinements. The dashed lines indicate the values at native PDB structure.

We then used a spherical wall to mimic the effects of confinement. The radius of the spherical confined space (R_C) indicates the strength of the confinement. Within spherical confined space, DPO4 folding deviates from that in bulk (Figure 2A). The folding temperature, which refers to the position of the prominent peak on the heat capacity curve, increases as the confinement strengthens (R_C decreases). The trend quantitatively resembles the previous simulations on folding of single domain proteins in the presence of various geometrical confinements with the findings that the positive shift of folding temperature has a simple power-law dependence on the confinement size.^34,76 At the same time, the height of the peak in the heat capacity curve decreases and the melting curves deviate more from sigmodial transition as the confinement strength increases (Figure S5). Taken together, our findings indicate that DPO4 folding stability increases with decreased folding cooperativity under strengthened confinement. In particular, when strong confinements are present (R_C ≤ 3.00 nm), another peak on the heat capacity curve emerges and becomes more obvious while continuing to increase the confinement strength. By monitoring the (un)folding process for individual domain/interface in DPO4 (Figure S4), we can attribute the height decrease of the peak on the heat capacity curve to the more dispersive melting curves of the domains/interfaces in the DPO4 core, which is made up by the F, P, and T domain, when confinement strength increases. The emergence of the second peak on the heat capacity curve at R_C ≤ 3.00 nm can also be explained by the distinct separation on the melting curves of the DPO4 core and the LF domain. The stability of the LF domain was found to be significantly increased by the confinement at R_C ≤ 3.00 nm, compared to the other domains/interfaces in DPO4 (Figure S4). Folding of the LF domain has led to a second peak on the heat capacity curve at the high temperature region.

From the perspective of native contact formation, the folding mechanism of DPO4 appeared not to be influenced as long as R_C > 3.00 nm, which is referred to weak confinements in the following discussions. Under such weak confinements, (1) the free energy landscapes have similar profiles associated with the same multiple states along the folding process, compared to the case without confinement (Figure 2B and Figures S6–S10); (2) the native contact maps show very similar patterns for the same state of DPO4 folding (Figure S11). The findings are further confirmed by examining the native contact evolution of each domain/interface in DPO4 along with the temperature (Figures S14 and S15), where the dependence of folding degree on temperature exhibits similar trends under weak confinements. Therefore, we conclude that the stepwise folding mechanism for DPO4 preserves under weak confinements. Nevertheless, the modest effects of confinements on modulating the domain/interface structures of DPO4 can be observed by carefully examining the native contact formation during the folding (Figure S12). When the domain/interface is largely folded/formed, the confinement tends to destabilize it as a small decrease of native contact degree can be observed and vice versa when it is unfolded/ unformed, though the overall effect is minor. In addition, by examining the conformational extension of each domain/interface in DPO4 (Figure S13), we can see the effects of confinements on collapsing the structure are more significant when the domain/interface is unfolded/unformed.

The stabilization on DPO4 at different folding states varies with different confinements (Figure 2C). The monotonic relation between the change of stability for all the folding states and confinement sizes preserves at weak confinements, where the confinements strongly destabilize more on the states when DPO4 is more unfolded (Figure 2C). While increasing the strength of the confinement to very strong magnitudes (R_C ≤ 3.00 nm), a turnover was observed. We notice that the length of the longest axis in the DPO4 PDB crystal structure is 6.71 nm, which is even longer than the diameter of the confined sphere under such circumstances, so the destabilization effect on compact folded states is in action. With strong confinements, DPO4 favors to be populated at intermediate states, as DPO4 in such intermediate states has broken the native contacts at the T–LF interface (Figure S11), which attributes to a large geometrical extension in the PDB structure. Further investigations on the stability of folded states under different confinements were performed by additional constant temperature simulations mimicking the room temperature (Figure S16). The root-mean-square fluctuation (RMSF) shows no significant change until the strong confinements are present, implying that weak confinements effectively increase folded stability by means of decreasing the stability of states possessing unfolded degrees and strong confinements destabilize the folded states. It is worth noting that the LF domain is the first segment, of which the structural fluctuations in folded states are significantly triggered when strong confinement is added (R_C = 3.00 nm in Figure S16). This is probably due to the fact that the prolate shape of DPO4 at native structure mainly attributes to the extension of the large-sized LF domain (Figure 1).

The stability change for different folding states under weak confinements (R_C > 3.00 nm) is manipulated more by entropy than energy (Figure 2C). This confirms the dominant entropic contributions in stabilizing DPO4 under weak confinements.¹⁷ It is worth noting that by strengthening the confinements within R_C ≤ 3.00 nm, most of the folding states show increase of −TΔΔS_S–N and ΔΔE_S–N. In particular when DPO4 is in I₁ or I₂, where DPO4 possesses a large degree of folding, −TΔΔS_S–N and ΔΔE_S–N can increase to be positive. This is due to the fact that the strong confinements can distort the DPO4 folded states, biasing DPO4 to the intermediate states. This effect is achieved through both entropy and energy contributions and is significant when DPO4 is in I₁ or I₂.

To see how the interplay of domain and interface in DPO4’s collaborative folding changes along with the different strengths of confinement, we extracted the melting curves of native contact formation for each domain and interface in DPO4. All the melting curves show apparently two-state transitions and thus were subsequently fitted to sigmoidal transitions, which eventually derive the folding probability curves p^I(T) (Figure S1), where I corresponds to the index of domain/interface in DPO4 and T is the temperature. TCI is calculated by comparing the difference of every domain/interface folding probability curve in DPO4 (Figure 2D–G). We can see that the core of DPO4, which corresponds to the P and T domain associated with their involved interfaces (P–T and T–LF), has the most folding cooperativity, while the F domain at N-terminus, which has the lowest stability and LF domain at C-terminus, which has the highest stability, folds quite asynchronously (Figure 2D). In the presence of confinements, the TCI matrix preserves the similar pattern (Figure 2E) until a strong confinement was applied, when all the domains/interfaces of DPO4 fold almost independently with little connection between each other (Figure 2F). The quantitative measurement of folding cooperativity of DPO4 by means of mean TCI (MTCI) clearly shows that confinement leads to less cooperative folding (Figure 2G). The sudden drop of folding cooperativity was observed at R_C = 3.0 nm, likely due to the destabilization of folded states.

By monitoring DPO4 folding process with other structural characteristics beyond the native contact formation, we found remarkable impacts of confinements on modulating DPO4’s conformation during folding process (Figure 2H–K). In bulk, DPO4 progressively increases the extension of chain with unfolding proceeding from N to U, as shown by R_g and RMSD (Figure 2H,I, black lines). Confinement shrinks the space of expanded configurations of DPO4 during folding, so the R_g and RMSD of each state become smaller than those in bulk when confinement is present. The effects become more significant when DPO4 possesses more unfolding degrees. The particular cases are under very strong confinements (R_C ≤ 3.00 nm), R_g remains constant for all the folding states and is even smaller than that of native structure, while RMSD at I₁ and N are larger than that in bulk. It indicates DPO4 is highly collapsed during the whole folding process and cannot fully fold to the native structure, though a large proportion of native contacts can be formed.

We used aspherical parameter Δ and S suggested previously to determine the shape of DPO4’s conformation.⁶⁶ We found DPO4 changes its spatial conformational geometry during folding (Figure 2J–K). In bulk, DPO4 in N and I₁ states exhibits a spherical shape with the small Δ and S; Δ and S increase sharply during DPO4 unfolding from I₁ to I₂, indicating a dramatic geometrical conformational reorganization, and DPO4 presents a rodlike shape in I₂; and unfolding of DPO4 from I₂ to I₃, and subsequently to U, does not apparently alter the geometry of DPO4’s conformations and maintains a high degree of asphericity. Confinement alters DPO4’s shape more when DPO4 possesses more unfolded degrees, especially at U states, where even a weak confinement can lead DPO4 to having more sphericity than the native structure does. The trends of monotonic decreasing Δ with folding proceeding under a certain degree of weak confinements and constant Δ and S along the folding process under strong confinements are completely different from that in bulk, implying that confinements have significantly changed the geometry of DPO4 during folding. Therefore, we conclude that although weak confinement does not change the folding mechanism and native formation of each state during DPO4 folding, the geometrical shapes of DPO4 are modulated strongly by the confinement biasing toward the collapsed spheres. Such effect may have additional impact on the folding kinetics by means of slowing down the diffusion coefficient,²⁰ which is supposed to be strongly dependent on the compactness of the protein conformation.^77,78

We investigated the folding mechanism of DPO4 by examining the evolution of intra- and interdomain native contacts during the folding process (Figure 3A). The intradomains fold closely along the diagonal line, implying that the behavior of intradomain folding is the same as the whole DPO4 folding, while the interdomains fold in a heterogeneous manner under the average behavior of DPO4 folding. This indicates in general that the intradomain folds prior to the interdomain, and folding of DPO4 can be described by folding of intradomain followed by coalescing the sequential neighbor domains. In bulk, we remarkably found that Q(inter) increases sharply at Q(total) ~ 0.4, then decreases at Q(total) ~ 0.5, and finally comes back at higher Q(total). This is a typical “backtracking” process, which has been defined as formation, breaking, and refolding of a subset of native contacts as folding proceeds.⁵⁰ In DPO4 folding, the backtracking occurs during the process from the intermediates I₃ to I₂. We plotted the free energy landscape projected onto Q(total) and Q(inter) and identified two parallel pathways from I₃ to I₂ (Figure 3B). Native contact maps of the two transition states (TS₁ and TS₂) during the two pathways show very different patterns (Figure 3C). DPO4 in TS₁ has a fully folded LF domain but partially folded P and T domains, while DPO4 in TS₂ has a fully folded P domain and partially folded T domain but an unfolded LF domain. The increase of Q(inter) attributes to the emergence of TS₂, where the P–T interface of DPO4 is largely formed because of the folded P and T domains serving as a template and are fully broken in I₃ but partially formed in I₂. In the presence of confinements, the backtracking degrades. From the free energy landscapes (Figure S10), we can see that the pathways with proceeding TS₂ gradually disappears as confinement strengthens. This indicates that the confinement stabilizes the LF domain rather than the T domain, thus in favor of pathways proceeding with TS₁. The deviation from backtracking under confinements is anticipated to faciliate the folding process through eliminating the traps on the energy landscapes.⁵⁰

Figure 3.

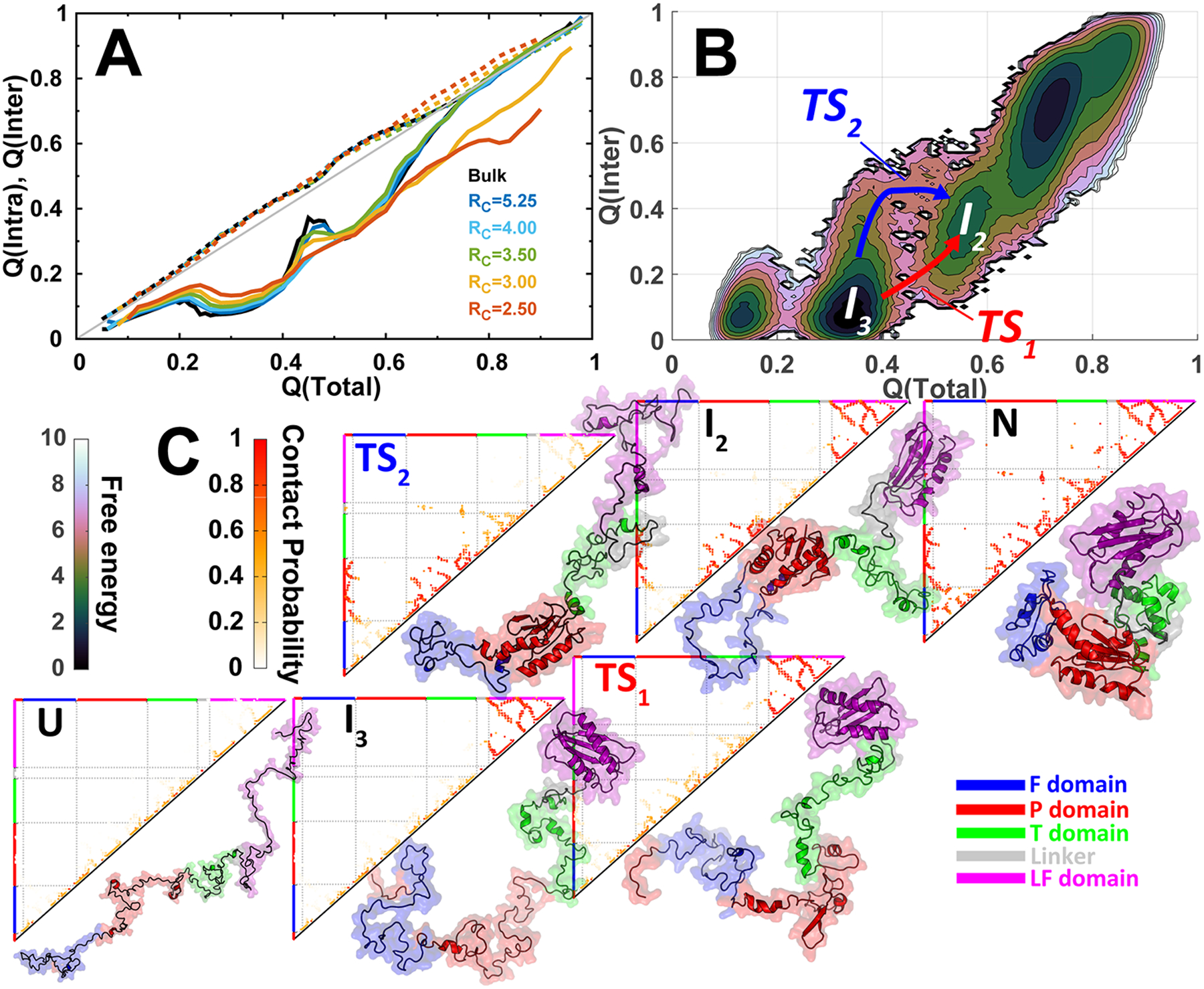
Backtracking in DPO4 folding. (A) The evolutions of native contact formation of DPO4 during folding under different confinements. Q(intra) (dashed lines) and Q(inter) (solid lines) are the fractions of intra- and interdomain contacts, respectively. (B) 2D free energy landscape projected onto Q(total) and Q(inter). Two parallel pathways are identified by proceeding through two different transition states (TS₁ and TS₂). (C) Evolutions of the native contact map in the two parallel folding pathways. Within the bottom-right triangle of each contact map panel, one representative DPO4 structure for the corresponding state is shown.

3.2. Effects of Repulsive Crowders on DPO4 Folding.

We then investigated the DPO4 folding in the presence of crowders with different concentrations Φ_C. The interactions between the residues of DPO4 and crowders were modeled purely repulsive to mimic the excluded volume effect. The influences of repulsive crowders on DPO4 folding thermodynamics are similar to that observed under weak confinements (Figure 4A–C): when more repulsive crowders are present, leading to more excluded volume in the system, the configurational space of the unfolded DPO4 to explore becomes smaller, resulting in destabilization of intermediate and unfolded states. This effect led by repulsive crowder is attributed to the entropic term, which was found to make dominant contribution to the free energy changes, in particular when the concentration of the crowder is high and the DPO4 is largely unfolded (Figure 4C). DPO4 also preserves the same folding mechanisms with multiple states on the free energy landscapes (Figure 4B and Figures S19–S23). It is worth noting that there is no backtracking observed even when a minor fraction of repulsive crowders are added (Figures S23 and S24), implying that crowder is more effective to modulate the folding pathways than what the confinement does. The stability of the folding states changed by repulsive crowders strictly follows monotonic relation with the volume fraction of crowders, and a larger degree of unfolding leads to bigger loss of stability, similar to that found in theories^9,12 and simulations⁵⁶ on single domain protein folding.

Figure 4.

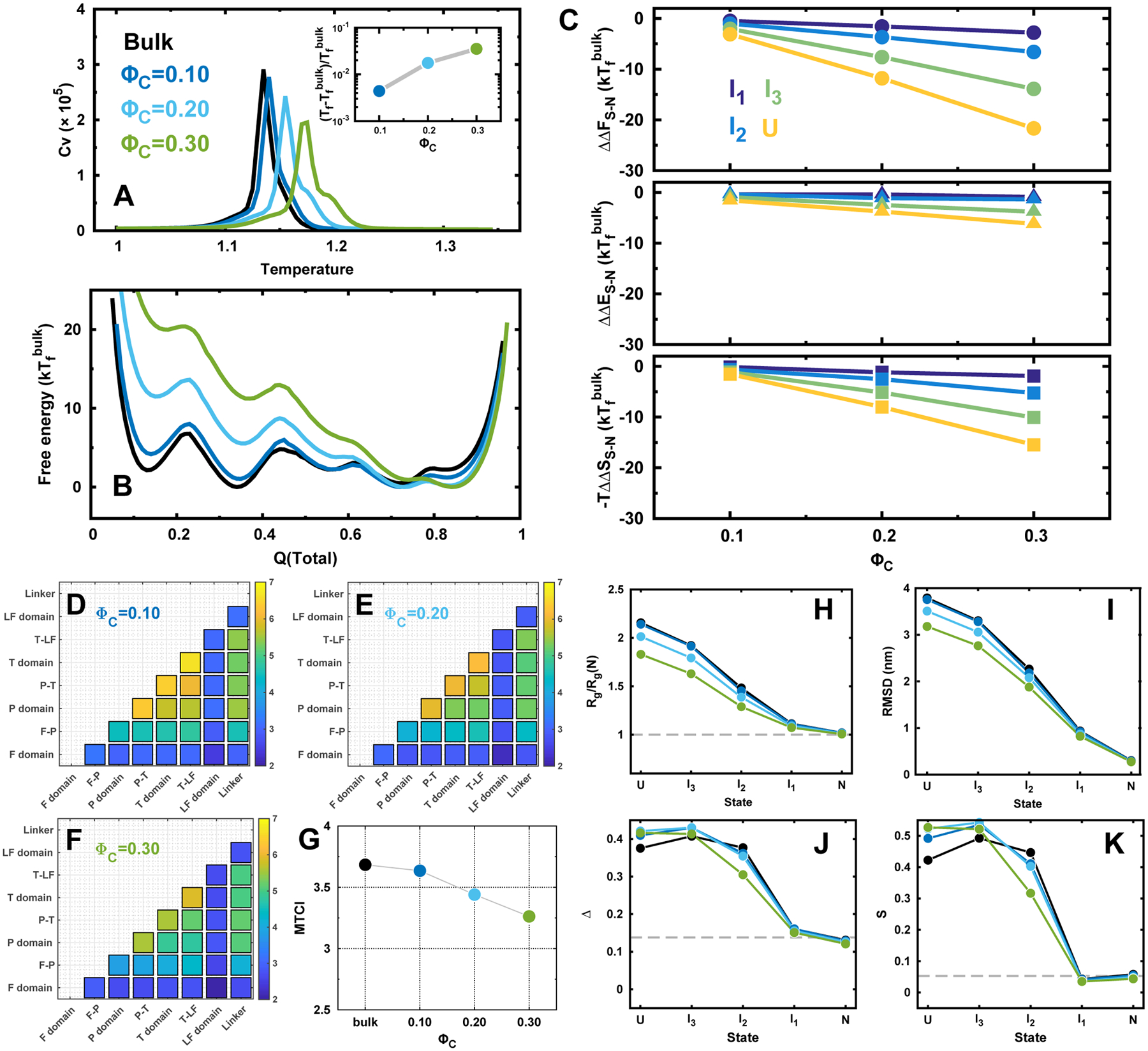
DPO4 folding in bulk and with repulsive crowders. (A) Heat capacity curves of DPO4. Inset shows the folding temperature T_f changes with different concentrations of repulsive crowders Φ_C. (B) 1D free energy landscapes along Q(total) under with different concentrations of repulsive crowders at the folding temperature of bulk condition $\left(T_{\text{f}}^{\text{bulk}}\right)$. (C) The relative change of the differences in free energy (top), energy (middle), and entropy (bottom) for different folding states of DPO4 to that in bulk along with the different concentrations of repulsive crowders. (D–G) TCI for DPO4 folding with different concentrations of repulsive crowders. (H–K) Structural characterizations of the folding states during DPO4 folding process with different concentrations of repulsive crowders.

The contact maps of DPO4 in each folding state show similar patterns as they are in bulk (Figure S25), implying that the native contact formation of each state does not change (Figure S26) and the folding mechanism remains the same. However, the conformational extension of domain/interface in DPO4 shows significant increase when it is unfolded (Figure S27) with repulsive crowders. The expanded conformation of DPO4 is probably led by the inclusion of crowders inside of the domain/interface, when they are unfolded (Figure S28). As the number of crowders located outside of the domain/interface also increases as crowder concentration Φ_C increases (Figure S29), it may make a contribution to collapsing the DPO4 conformation. The conformation of the individual domains and the interfaces in DPO4 are manipulated by these two effects from crowders at the same time.

The pattern of TCI matrix does not significantly change in DPO4 folding with repulsive crowders (Figure 4D–F). The trend of effects on DPO4 folding cooperativity along with fraction of crowders is very similar to that under confinements (Figure 4G).

The effects of repulsive crowding on R_g and RMSD of DPO4 during folding are not as significant as that shown in the confinement environment (Figure 4H–K), likely because the extended chain is able to explore the interstitial voids between crowders, while the conformation of DPO4 with the longest axis longer than R_C is strictly forbidden when confinement is applied. However, the asphericity and shape parameters show very different trends with that under confinements. As expected, crowders have little effects on modulating the geometry of DPO4 in N and I₁, where most parts of DPO4 are folded. DPO4 in I₂ is induced to be more sphere-like with both decreasing Δ and S. With more degree of unfolding in I₃ and U, DPO4 exhibits more aspheric-like shape led by crowders. The nonmonotonic observation can be explained by the different DPO4 conformations formed in different folding states. In the I₂ state, DPO4 has nonsequential folded P and LF domains, which can be pressed by the crowder surrounding as the linking segments which refer to the T domain and flexible linker are unfolded, while in I₃, only the P domain located at the C-terminus of DPO4 is folded and in the U state, DPO4 is completely unfolded. A large proportion of unfolded segments in DPO4 tends to explore all possible voids between the crowders in favor of entropy, leading to the increase of both Δ and S. At the same time, DPO4 has to endure the excluded volume effect caused by the repulsive crowders to collapse with decrease in R_g and RMSD. It is worth noting that crowders can have minor impacts on the conformations of DPO4 at N and I₁ states, where more compact and sphere-like conformations can be formed due to a substantial number of crowders surrounding the surface in the action of extruding the conformations (Figure S29). Therefore, the repulsive crowders have different impacts on modulating the conformation of DPO4 during folding compared to that led by confinements.

3.3. Effects of Attractive Crowders on DPO4 Folding.

We applied the Lennard-Jones potential between the residues in DPO4 and crowders with different strengths ${ϵ}_{\text{PC}}^{\text{LJ}}$. The attractive crowders can stabilize and destabilize protein folding as a result of competition between entropic and enthalpic thermodynamic driving forces.²⁶ This is faithfully observed in our simulations under various strengths of attractive protein-crowder interactions at a fixed concentration of the crowder Φ_C = 0.20 (Figure 5A). The folding temperature increases first when the interaction is weak (${ϵ}_{\text{PC}}^{\text{LJ}}=0.05$), then gradually decreases with the further increase of the strength, and finally becomes even lower than that in bulk. The changes on the stability of the folding states (Figure 5B,C) also depend on the strength of the protein-crowder interaction. When ${ϵ}_{\text{PC}}^{\text{LJ}}=0.05$, the effect of crowders behaves mostly entropic and the decreasing stabilities of the folding states are correlated with the degree of unfolding (Figure 5C); increasing the strength to 0.25, the magnitudes of the decreased stabilities of folding states decrease, in particular the stability of I₂ is strengthened compared to that in bulk; with strong protein-crowder attractive interaction of 0.50, all the folding states exhibit stronger stabilities than they are in bulk as the enthalpic effect is dominant (Figure 5C). It is interesting to observe that the increased free energy values of I₁, I₂, and U are almost the same. This indicates a similar compensation between entropy and enthalpy achieved by the crowders with the enthalpic effect dominating.

Figure 5.

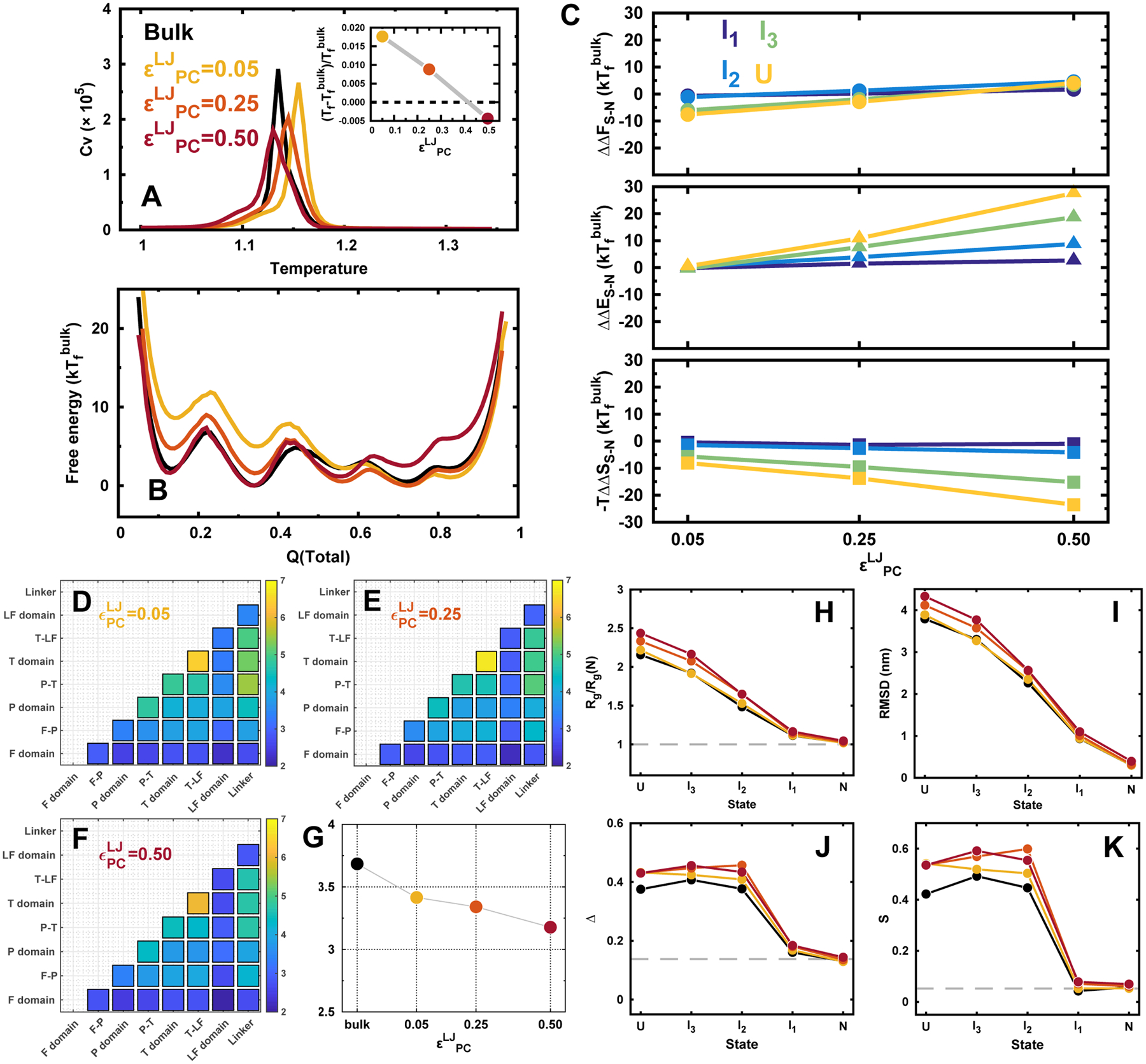
DPO4 folding with different strengths of attractive protein-crowder interaction. (A) Heat capacity curves of DPO4. Inset shows the folding temperature T_f changes with different strengths of attractive protein-crowder interaction ${ϵ}_{\text{PC}}^{\text{LJ}}$. (B) 1D free energy landscapes along Q(total) under with different strengths of attractive protein-crowder interaction at the folding temperature of bulk condition $\left(T_{\text{f}}^{\text{bulk}}\right)$. (C) The relative change of the differences in free energy (top), energy (middle), and entropy (bottom) for different folding states of DPO4 to that in bulk along with different strengths of attractive protein–crowder interaction. (D–G) TCI for DPO4 folding with different strengths of attractive protein-crowder interaction. (H–K) Structural characterizations of the folding states during the DPO4 folding process with different strengths of attractive protein–crowder interaction. The concentration of the crowder is fixed at Φ_C = 0.20 with different strengths of protein–crowder interaction.

Analyzing the folding cooperativity changes along with the strengths of protein-crowder interaction shows the similar trend with that under confinement and repulsive crowders (Figure 5D–F). However, the underlying elements that decrease the folding cooperativity are different. With very weak protein-crowder interaction, the entropic driving force dominates, the cause of loss of folding cooperativity should be the same with that led by repulsive crowders. Strengthening the attractive interactions between the protein and crowders increases the weight of the enthalpic driving force but still weakens the folding cooperativity. Interestingly, we found that the folding cooperativity is significantly reduced at ${ϵ}_{\text{PC}}^{\text{LJ}}=0.50$ even though only a minor change on folding temperature is observed (Figure 5G).

Crowders with soft interactions are shown to have distinct effects on modulating the conformations of DPO4 compared with that done by confinements and repulsive crowders (Figure 5H–K). Both R_g and RMSD increase when the protein-crowder interaction strengthens. This indicates that DPO4 is more likely expanded with attractive crowders. The effect is more apparent when DPO4 possesses more unfolding degrees such that bigger crowder accessible surface areas can be formed. The changes of asphericity and shape parameters of DPO4 with the protein-crowder interaction strength have similar trends with those of R_g and RMSD. This indicates that stronger attractive protein-crowder interaction leads to more extended, nonsphere-like conformation. It is worth noting that even when DPO4 is at compact N and I₁ states, the effects are still active but are exactly the opposite to the cases under repulsive crowders. Our results show that DPO4’s conformations during folding are more extended and aspheric under attractive crowder compared to the bulk case, due to the enthalphic effect.

In order to see the effects of the concentration of attractive crowder on DPO4 folding, we performed additional two sets of simulations at the other two values of Φ_C and Φ_C = 0.05 and 0.30 under different strengths of protein-crowder interaction. Overall, we observed a monotonic decrease (increase) of the relative stability changes for different folding states to those in bulk with increasing the crowder concentration at weak (strong) protein-crowder interaction (Figures S49–S51). Such effect on DPO4 folding led by attractive crowder with weak attractive interaction is similar to that observed by repulsive crowder, implying that the entropic contributions dominate when the attractive interaction is weak (Figure S52). In contrast, we found that attractive crowders with strong interaction modulate DPO4 folding mainly through the enthalpic contributions. These enthalpic and entropic effects led by attractive crowders on DPO4 folding can be counterbalanced at a moderate strength of protein-crowder interaction (Figures S50 and S52).

4. CONCLUSIONS

We used a coarse-grained SBM to investigate folding of a multidomain protein under different environments mimicking the in vivo conditions. SBM and other methodologies inspired from the energy landscape theory⁷⁹ were initially designed for single domain protein folding;^52,80 however, the recent successes with applications to multidomain protein folding verify their portability in tackling the more complex folding behaviors.^81,82 In addition, the highly consistent folding pictures of DPO4 obtained independently by our simulations³⁷ and experiments⁴⁹ serve as the solid bases for the current work on DPO4 folding with confinements and crowders.

The effects of in vivo conditions on protein folding have been extensively investigated by theories,^19,21,33 simulations,^{18,34,56,83,84} and experiments,^7,8,85 though small single domain or fast-folding proteins are often targeted in practical research because of their simplicity. Inspired by the previous work on single domain protein folding,¹⁸ we tried to see whether the effects of confinement and repulsive crowder on the multidomain protein DPO4 folding are transferable, as they are both entropic. In practice, we mapped the changes of folding temperature led by confinement and repulsive crowder and finally obtained a quantitative relation of $R_{\text{C}}~{\mathrm{\Phi }}_{\text{C}}^{-1/\gamma }$, where γ = 2.76 is close to 3.00, which was predicted by theory⁸⁶ and observed by simulations for single domain protein folding¹⁸ (Figure S53). Such relation between the strengths of confinement and the concentrations of repulsive crowders is effective under weak confinement (R_C > 3.0 nm) and results in a strong correlation in manipulating the stability changes for different DPO4 folding states (Figure S54). However, confinements and repulsive crowders have led to apparent discrepancy in changing of the folding cooperativity, quantified by MTCI (Figure S55). This indicates that these two in vivo conditions (confinements and repulsive crowders) are not the same in modulating the multidomain protein folding thermodynamics. In addition, the shape changes, which are computed by using the moment of inertia tensor,⁶⁶ vary distinctly for confinements and crowders. The crowders have the chance to move inside of the unfolded domain/interface to induce an extended conformation compared to that in confinement cases, which strictly prohibit the conformation across the spherical boundary. Both of the shape changes led by confinements and crowders may have impacts on folding kinetics with the fact that (1) crowders inside of the domain core have to be squeezed out to accomplish folding, reminiscence of water extrusion slowing down the protein folding from molten globule states to folded states,⁸⁷ and (2) confinements and crowders induce collapsed conformations, which exhibit slow diffusion coefficients.^20,77

As DPO4 is comprised by independently folded structural domains,⁴⁹ we quantified the cooperativity of domain/interface during folding by means of TCI. Folding in bulk presents the highest folding cooperativity. In other words, the domain/interface folds more synchronously in bulk than that in vivo conditions. The high cooperativity, however, may lead to side effects for folding, as a backtracking process during the folding was observed by the bulk simulations. The emergence of backtracking in DPO4 is mainly due to the weak refined folding order of domain/interface, so a less stable folding domain/interface has the possibility to fold prior to a more stable one during a particular folding stage. The folding order distribution was found very dispersive, and there is no dominant folding pathway in our previous kinetic simulations.³⁷ The transient folding state formed by backtracking practically has to unfold because of its thermodynamic instability compared to the other metastable intermediates, resulting in a kinetic trap.⁸⁸ It is interesting to see that the confinements and crowders can weaken the magnitude of backtracking. From cooperativity perspective, all in vivo conditions reduce the synchronous folding among domains/interfaces, of which the folding order is more clearly organized than it is in bulk. The avoidance of backtracking is capable of increasing the folding efficiency in multidomain protein folding. This is a new evidence to support the roles of in vivo conditions in restricting the folding orders that have potential implications to prohibit misfolding and aggregation, in addition to cotranslational^38,39,41 and chaperone-assisted folding.^89,90

We should note that an important point to be improved in the SBM for simulating the multidomain protein folding processes. SBM in general has completely removed the non-native interactions, leading to an efficient folding process in silico.⁵² Since the naturally occurring proteins are minimally frustrated,⁵¹ the native contacts, which are the driving forces in the SBM, determine the folding mechanism.⁵³ However, multidomain proteins usually possess extensive domain-interfaces,⁴⁰ which increase the possibility of forming non-native interactions, compared to the single domain proteins. The non-native interaction was found to trigger the multidomain protein misfolding and aggregation⁹¹ but is not present in the SBM. After the melting experiments, DPO4 was found to aggregate even under a dilute concentration.⁴⁹ This is not expected to be observed by our SBMs because of the absence of non-native interactions, which leads to a notable discrepancy between experiments and simulations. In addition, the backtracking, which was induced by purely topological frustrations in the SBM, may be more evident if non-native interactions acting as energetic frustrations at interface are present to strengthen the domain connections.⁴⁰ Further improvements of the SBM with carefully incorporating the non-native interactions should provide a more realistic and quantitative prediction on the multidomain protein folding process. We will address these issues in the future studies.

In summary, we have explored the effects of confinements and crowders on folding of a multidomain protein using a SBM. The decrease of folding cooperativity led by in vivo conditions provide new insights on the multidomain protein folding mechanism and have potential applications in protein design.