Reducing the aerosol forcing uncertainty using observational constraints on warm rain processes

Observations of cloud processes can reduce aerosol forcing uncertainty by constraining parameterizations in climate models.

Abstract

Global climate models (GCMs) disagree with other lines of evidence on the rapid adjustments of cloud cover and liquid water path to anthropogenic aerosols. Attempts to use observations to constrain the parameterizations of cloud processes in GCMs have failed to reduce the disagreement. We propose using observations sensitive to the relevant cloud processes rather than only to the atmospheric state and focusing on process realism in the absence of aerosol perturbations in addition to the process susceptibility to aerosols. We show that process-sensitive observations of precipitation can reduce the uncertainty on GCM estimates of rapid cloud adjustments to aerosols. The feasibility of an observational constraint depends on understanding the precipitation intensity spectrum in both observations and models and also on improving methods to compare the two.

INTRODUCTION

Anthropogenic aerosols affect the energy balance of the climate system by absorbing or scattering solar radiation and by changing cloud properties through their role as cloud condensation nuclei or ice-nucleating particles (1). The effect of aerosol-cloud interactions (ACIs), expressed as an aerosol-induced perturbation of the net radiative flux R of energy into the climate system, is termed effective radiative forcing of the climate by ACI (ERF_aci). ERF_aci from liquid water clouds dominates the total ERF_aci and is commonly decomposed into an instantaneous radiative forcing F_Nd due to an increase in the number of cloud droplets N_d (2) and a rapid adjustment of other cloud properties—most importantly, the liquid water path ℒ and the cloud fraction f_c—in response to the change in N_d, translated into radiative flux perturbations F_ℒ and F_fc (3, 4)

$$\begin{array}{c}{\text{ERF}}_{\text{aci}}=F_{N_{\mathrm{d}}}+F_{\mathrm{ℒ}}+F_{f_{\mathrm{c}}}=\\ (\frac{\mathrm{\partial }R}{\mathrm{\partial }\mathit{\text{ln}} N_{\mathrm{d}}}+\frac{\mathrm{\partial }R}{\mathrm{\partial }\mathrm{ℒ}}\frac{d\mathrm{ℒ}}{d\text{ln} N_{\mathrm{d}}}+\frac{\mathrm{\partial }R}{\mathrm{\partial }{f}_{\mathrm{c}}}\frac{d{f}_{\mathrm{c}}}{d\text{ln} N_{\mathrm{d}}})\mathrm{\Delta }\text{ln} N_{\mathrm{d}}\end{array}$$ (1)

where Δln N_d is the fractional anthropogenic perturbation to N_d. The instantaneous forcing cools the climate, as an increased number of proportionally smaller droplets make clouds more reflective to incoming solar radiation, constituting a negative forcing (5). Rapid cloud adjustments can increase ℒ or f_c when the smaller cloud droplet size suppresses precipitation formation in polluted conditions (6, 7), leading to a further cooling, or decrease ℒ or f_c when the smaller droplets lead to faster cloud evaporation in polluted conditions (8–11), offsetting the cooling. Aerosol-climate atmospheric general circulation models (GCMs) will continue to play an important role in climate projections for the foreseeable future despite their limited ability to represent cloud processes accurately because of the computational expense associated with running global models at higher resolution. GCMs disagree with other lines of evidence on the magnitude and even sign of ℒ and f_c changes (12, 13); this disagreement is a major reason that F_ℒ and F_fc continue to be major contributors to the ERF_aci uncertainty (14).

One reason that GCM estimates of F_ℒ and F_fc disagree with process-scale modeling and observations is an asymmetry in the treatment of positive (offsetting the cooling) rapid adjustments, which are at best implicitly represented in GCMs, and negative (enhancing the cooling) rapid adjustments, which are explicitly represented in parameterizations of the precipitation processes (text S1). Explicit representation does not guarantee physical correctness, however, and a number of long-standing problems continue to blight parameterized precipitation processes: a poor representation of cloud-scale variability and of the vertical structure of clouds, arbitrary partitioning of precipitation into “stratiform” and (intermittent) “convective,” and the use of poorly constrained process “enhancement” factors that are frequently used to tune the radiative budget of the model (15–20). This results in unrealistic precipitation statistics in the modeled climate, with compensating errors (21) in precipitation frequency and intensity. Thus, reducing the discrepancy between GCM estimates and other lines of evidence will likely require both addressing the implicitly represented processes and improving the physical realism of the explicitly represented processes.

The physical realism of a model can be improved by constraining its parameterizations to reproduce observations (22). In practice, two obstacles have impeded progress in observational constraints. The first obstacle is that a large range of possible parameterizations of the underlying processes can reproduce the state of the atmosphere—characterized by state variables such as f_c, ℒ, and radiative fluxes—but each parameterization has a different sensitivity to anthropogenic perturbations to the climate system. This problem, termed “equifinality” (23–25), limits the utility of commonly available observational datasets as constraints, since the observations are of state variables. The second obstacle is that attempts to use observations to constrain the susceptibility of cloud processes to aerosol (26, 27) instead of state variables have proven difficult (28, 29). We argue that the approaches historically taken need to be modified to overcome the obstacles to progress on observational constraints. The way to address the equifinality problem is to use observations capable of probing individual processes rather than the overall state. The way to address the susceptibility problem is to recognize that the base process behavior, i.e., the aspects of the processes independent of aerosol perturbations, deserves as much attention as the susceptibility to aerosols; precipitation suppression by aerosol can only occur in clouds that would otherwise have precipitated, so the overestimate of precipitation probability in models leads to an overestimate of precipitation suppression.

RESULTS

Precipitation processes in liquid-only clouds (“warm rain”) are the dominant mechanism for rain formation in large parts of the tropics, but their importance falls off markedly in the extratropics, particularly over land (30, 31). In many GCMs, the probability of warm rain is overestimated (16). This is also the case in the ECHAM-HAMMOZ model used in this study, shown in Fig. 1 using the fraction of rain occurrences that are due solely to warm rain processes, f_warm, as a metric (see Methods): Compared with satellite observations, the model strongly overestimates f_warm outside the tropics. Two possible modifications to the warm rain parameterization—reducing the enhancement factor and imposing an increasingly large effective radius threshold (Methods, fig. S1, and table S1)—can bring f_warm into better agreement with observations. The model bias shown in Fig. 2 is reduced over land and over extratropical ocean, albeit at the expense of a slight overcompensation in the subtropical subsidence regions, especially in the Northern Hemisphere (figs. S2 and S3). Warm rain cannot initiate without the self-collection (or autoconversion) of small cloud droplets by collision and coalescence into larger drizzle or rain drops, which can then collect further cloud droplets as they sediment through the cloud (32). Hence, the presence of warm rain is a clear indication that the autoconversion process was active in a cloud. The ideal observation with which to constrain a model would be a process rate, since this observation would be directly comparable to the process rates calculated by the process parameterizations in the model. A binary indication of process activity is equivalent to a measurement of the process rate with one bit precision, i.e., maximally coarse, but still allows for a far more specific evaluation of the model than state variables, which carry the memory of multiple processes’ contributions over many time steps. In this sense, f_warm is an observable capable of probing atmospheric processes related to ERF_aci; this is in contrast to state variables, which reflect the state of the atmosphere but not the processes that led to that state.

Fig. 1. Warm rain and warm drizzle fraction from the satellite climatology and the reference model configuration.

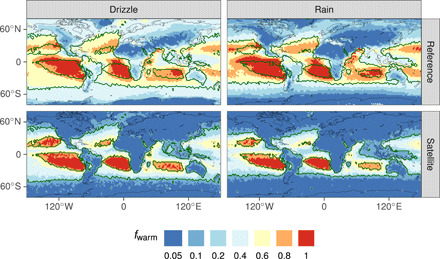
The model strongly overestimates the warm precipitation fractions over land and extratropical oceans but slightly underestimates warm drizzle over the northeastern Pacific. Dark lines indicate the 10 and 80% warm precipitation fraction contours in the satellite climatology.

Fig. 2. Change in model bias in warm precipitation fraction relative to the reference configuration.

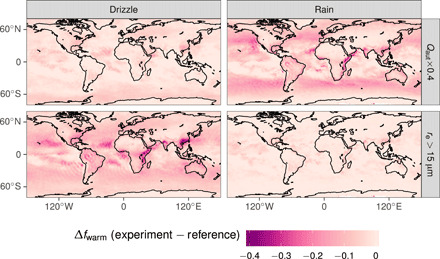
The reduced scale factor strongly decreases the warm rain fraction but leaves warm drizzle largely unaffected, whereas the r_e threshold decreases warm drizzle but leaves warm rain largely unaffected.

At this point, it is tempting to tune the model to the satellite warm rain fraction and then consider the rapid adjustments simulated by that model configuration to be the “observationally constrained” rapid adjustments (subject to caveats; text S2). However, we find that the two tuning strategies, although they both reduce the warm precipitation bias, have opposite effects on the normalized adjustment F_ℒ/F_Nd (Methods and text S3). Figure 3 shows that increasing the threshold effective radius results in a stronger normalized adjustment, whereas decreasing the scale factor results in a weaker normalized adjustment.

Fig. 3. The relationship between the (observable) bias in warm rain fraction and the (emergent) rapid adjustment under scale factor and effective radius threshold tuning strategies.

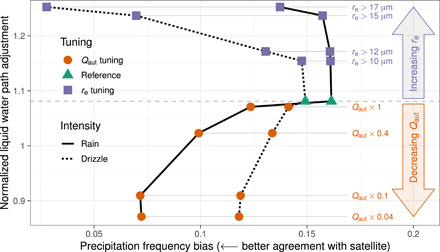
The relationship between warm rain fraction (f_warm) and normalized rapid adjustment (F_ℒ/F_Nd) is multivalued, which presents an apparent obstacle to an observational constraint. Distinguishing between rain (solid line), which responds strongly to the Q_aut scale factor tuning but weakly to the r_e threshold tuning, and drizzle (dashed line), with the opposite responses, breaks the degeneracy and removes the obstacle to formulating an observational constraint.

The source of this dichotomy becomes apparent if we consider precipitation intensity. Figure 2 shows how the warm precipitation bias reduction differs between intensity categories for the two tuning strategies. The effective radius threshold tuning mostly affects drizzle, since clouds with small effective radius correspond to low rain formation rates. By contrast, the enhancement factor tuning affects intense precipitation more strongly than drizzle, because the enhancement factor has a proportionally larger effect on high rain formation rates than on low ones. The reduced scale factor configuration weakens the normalized adjustment in accordance with our hypothesis that precipitation suppression can only occur in precipitating clouds. Geographically, the weakening is greatest in the midlatitudes (fig. S4 and text S4), where the disagreement in f_warm between satellite and the reference model is greatest, improving agreement with observational estimates (12, 33). Meanwhile, the reduced drizzle configuration leads to stronger adjustments, consistent with earlier studies (19). Inhibiting drizzle at one effective radius threshold causes the model clouds to build up condensate until they reach the higher effective radius threshold, because precipitation is such a strong sink process for cloud condensate in the model. At the higher effective radius threshold, the cloud liquid water content is more sensitive to changes in N_d—and thus, the liquid water path adjustment is stronger—because cloud liquid water content is linked to N_d via the mean droplet radius to the third power (text S4 and eqs. S4.1 to S4.3).

Parameterized precipitation initiation depends on liquid water content and N_d (see Methods). The dependence of the process rate on N_d results in process susceptibility to aerosol. Note that the range of adjustment simulated by these model configurations is large (90 % < F_ℒ/F_Nd < 125%, corresponding to −0.65 W m⁻² < F_ℒ < − 0.47 W m⁻²), even though we have only changed parameters affecting the base process behavior, not the N_d-dependent factor that explicitly encodes the susceptibility to aerosol (text S5). Similarly, a large range of normalized adjustment results from varying the parameter controlling the dependence of rain initiation on cloud liquid water content (fig. S5); this is also a modification of the base process behavior. On the other hand, varying the parameter controlling the rain initiation susceptibility to aerosol-induced N_d change (fig. S6) results in a comparatively small change in the normalized adjustment. This underscores that the aerosol-independent base process behavior is an important contributor to the global ERF_aci estimate that cannot be neglected in favor of the susceptibility to aerosol. The importance of base process behavior is well recognized in the cloud feedback community (34–38) but much less so in the ACI community (39).

DISCUSSION

Our analysis reveals that the warm rain problem in models is not one but two problems: a warm rain problem and a warm drizzle problem. In the short term, this raises new challenges both in modeling and in observations. If it were clear that a model predominantly has a warm drizzle bias or a warm rain bias, then the sign of the F_ℒ bias would also be clear. A drizzle bias (the dashed line in Fig. 3) would best be alleviated by reducing the propensity of clouds with relatively low liquid water content—and, hence, relatively small cloud droplets—to precipitate; our analysis predicts that correcting this bias would lead to a stronger F_ℒ. A rain bias (the solid line in Fig. 3), on the other hand, would best be alleviated by reducing the propensity also of warm clouds with higher liquid water content to rain; our analysis predicts that correcting this bias would lead to a weaker F_ℒ. However, diagnosing which intensity category exhibits the greater bias is not a straightforward determination due to errors and uncertainties in models, observations, and model-observation comparisons, which could easily overwhelm the small difference between the slightly higher warm rain bias and the slightly lower warm drizzle bias in our model (Fig. 3 and fig. S7). First, in observations, the challenges in classifying precipitation intensity arise because of radar sensitivity to drizzle and because large contributions to F_ℒ occur not only over ocean but also over land (40–42), where the heterogeneous surface properties substantially complicate intensity retrievals. Second, as specified earlier, longstanding structural problems cause the precipitation intensity to be biased low in models. Third, to be able to compare the modeled GCM-scale and observed satellite pixel-scale precipitation intensities, a scale- and definition-aware comparison method, ideally incorporating knowledge of the subgrid-scale variability (43), needs to be applied (44). Much work thus remains on the base precipitation process behavior, but there are known solutions for many of the problems that need to be addressed. The payoff in better process representation can therefore be realized before higher resolution models, such as global cloud-resolving models (CRMs), replace GCMs as the workhorse of climate projection. This work will also benefit other endeavors that rely on realistic precipitation intensity, such as hydrology, and it can proceed in parallel with improvements in the modeling of aerosol susceptibility.

In the longer term, these results are highly encouraging. They show that it may be possible to overcome the equifinality problem, which has dogged observational constraints on parameterizations in GCMs and is likely to bedevil parameterizations in the global CRM era as well. The hallmark of equifinality is a degeneracy in parameters, leading to the same present-day state but different sensitivities to anthropogenic perturbations. In this study, we have explored the degeneracy between two such parameters in the warm rain parameterization and found that the degeneracy can be broken by applying successively more refined observed precipitation statistics, first by discriminating between cold- and warm-cloud precipitation processes and then between rain and drizzle. The use of these variables represents a progression from observational constraints based on state variables—subject to the equifinality problem—to observational constraints based on variables probing individual processes—which, our results indicate, may be able to transcend equifinality. Present and future long-term, global active remote-sensing datasets of clouds and precipitation (45, 46) provide a gold mine of process-probing variables that may sufficiently constrain process parameterizations to allow physically realistic estimates of ERF_aci. More advanced radar capabilities, such as those under consideration for the Aerosol-Cloud Convection Precipitation mission (47), will be especially useful in formulating constraints if they retrieve rain drop size distributions, vertical air motions, and precipitation rates, while exhibiting sufficient sensitivity to distinguish between cloud, drizzle, and rain with sufficient vertical resolution to probe more deeply into the boundary layer than current sensors.

METHODS

Model results were obtained with the ECHAM-HAMMOZ model, version echam6.1-ham2.2-moz0.9 (48–52), a state-of-the-art global aerosol-climate model. The large-scale stratiform cloud scheme in this model consists of prognostic equations for cloud ice and water mixing ratio and particle number concentration (53–55). Because the convective scheme (56) uses a simple microphysics parameterization without explicit aerosol dependence, we restrict our analysis to large-scale clouds and precipitation (which includes condensate detrained from the parameterized convection).

Precipitation is treated diagnostically, i.e., precipitation is assumed to sediment out of the atmospheric column within one model time step. The rate at which the collision-coalescence “autoconversion” process converts cloud water into drizzle or rain water is parameterized on the basis of the in-cloud droplet number concentration N_d and in-cloud liquid water mixing ratio q_l as

$$Q_{\text{aut}}=\frac{\mathrm{\partial }{q}_l}{\mathrm{\partial }t}{\mid }_{\text{aut}}=1350 {\mathrm{s}}^{-1} \times \mathrm{\gamma } q_l^{\mathrm{\alpha }}{\left(\frac{N_{\mathrm{d}}}{1 {\text{cm}}^{-3}}\right)}^{-\mathrm{\beta }}$$ (2)

(57). The combination of parameters α = 2.47, β = 1.79, and γ = 1 corresponds to the original Khairoutdinov and Kogan (57) parameterization for large eddy simulations. The ECHAM-HAMMOZ parameterization uses unchanged α and β parameters and γ = 4 to account for an enhancement of the autoconversion rate due to subgrid-scale variability (43, 58–61). Apart from this enhancement factor, no information on the subgrid-scale variability in N_d or q_l is available to the parameterization. Equation 2 parameterizes adjustments to the anthropogenic increase in N_d as a decrease in removal of cloud condensate via the autoconversion process when N_d increases due to anthropogenic emissions. This leads to an increased planetary albedo through higher average q_l and, thus, ℒ; indirectly, through the relative humidity–dependent cloud cover parameterization (62), f_c increases as well. In this model, the ℒ adjustment (F_ℒ = − 0.5 W m⁻²) is the greater of the two adjustments compared with the f_c adjustment (F_fc = − 0.3 W m⁻²) (41), in line with other state-of-the-art models (40, 42). The radiative forcing F_Nd = − 0.5 W m⁻² is of similar magnitude to F_ℒ.

The observational dataset to which the model precipitation statistics are compared is the CloudSat-Calipso warm/cold rain classification of Mülmenstädt et al. (30). A further classification by intensity (“rain” versus “drizzle”) has been performed using the 2C-PRECIP-COLUMN surface precipitation flags (63, 64). The “rain certain” flag is taken as rain, and the “possible” and “probable” flags are taken as drizzle. This identification is based on the reasonable correspondence between radar reflectivity, on which the precipitation flags are based, and rain rate (65).

To enable comparison between the model behavior and satellite retrievals, the Cloud Feedback Model Intercomparison Project (CFMIP) Observational Simulator Package (COSP) (66) has been implemented into ECHAM (updated to version 1.4.1 for the present study) (67). COSP splits each grid box into n subcolumns and uses the Quickbeam (68) radar simulator to compute a radar reflectivity in each subcolumn (n = 100 in this analysis). The microphysical assumptions (size distributions of each hydrometeor type) are given by Nam and Quaas (67). In principle, the subcolumn mechanism allows COSP to be coupled to information on the subgrid variability of hydrometeors. In practice, only limited use of this capability is made so far by GCMs in general; improving this capability, especially when sophisticated knowledge of the subgrid variability of hydrometeors is available to the host model (69), has the potential to advance the state of the art notably. In ECHAM-HAMMOZ, only the vertical overlap assumption of fractional cloudiness is passed to COSP, with all hydrometeor species uniformly distributed throughout the cloudy part of the grid box.

Model columns that produce liquid precipitation at the planetary surface are classified as drizzling if their maximum radar reflectivity $Z_e^{*}$ exceeds −15 dBZ_e, and raining if their maximum radar reflectivity exceeds 0 dBZ_e. (A raining column therefore also counts as a drizzling column.) Model columns are classified as “cold” precipitation if the highest cloud layer in which the reflectivity threshold is reached contains ice, and “warm” precipitation otherwise, where a cloud layer is defined as one or more vertically contiguous model levels with nonzero cloud condensate mixing ratio. In this model, there is a reasonably close correspondence between reflectivity thresholds and surface precipitation flux (fig. S9).

The scale- and definition-aware evaluation of the modeled precipitation (44) thus accomplished can then inform choices of the parameters in the autoconversion formulation. Two possible parameters are the enhancement factor γ from Eq. 2 and a critical value r_c of the cloud droplet effective radius r_e, below which autoconversion is precluded; this parameter, introduced in the Kessler (32) scheme, traces its lineage through parameterizations (70, 71) in wide use today. We implement these parameters by modifying the Khairoutdinov and Kogan (57) scheme of Eq. 2 as follows

$$Q_{\text{aut}}=1350 {\mathrm{s}}^{-1} \times \mathrm{\gamma }{q}_l^{\mathrm{\alpha }}{\left(\frac{N_{\mathrm{d}}}{1 {\text{cm}}^{-3}}\right)}^{-\mathrm{\beta }}\mathrm{\Theta }(r_{\mathrm{e}}-r_{\mathrm{c}})$$ (3)

where Θ is the Heaviside step function. In this model, r_e is diagnosed from the volumetric-mean cloud droplet radius via a constant proportionality factor, i.e., it is a function only of q_l and N_d, not of drizzle or rain water condensate. We refer to modifications of γ as “Q_aut scaling factor tuning,” and modifications of r_c as “r_e threshold tuning.”

Because of the power-law form of the Khairoutdinov and Kogan (57) parameterization, the two tuning strategies are somewhat similar. Starting with Eq. 2 and substituting using the relationship between q_l, r_e, and N_d

$$q_l\propto r_{\mathrm{e}}^3{N}_{\mathrm{d}}$$ (4)

the autoconversion rate can be rewritten as a function of r_e and either of q_l or N_d

$$Q_{\text{aut}}\propto \{\begin{array}{c}\mathrm{\gamma }{r}_{\mathrm{e}}^{3\mathrm{\alpha }}{N}_{\mathrm{d}}^{\mathrm{\alpha }-\mathrm{\beta }}\hfill \\ \mathrm{\gamma }{r}_{\mathrm{e}}^{3\mathrm{\beta }}{q}_l^{\mathrm{\alpha }-\mathrm{\beta }}\hfill \end{array}$$ (5)

Under the limiting assumptions that r_e is uncorrelated with either q_l or N_d, we expect the autoconversion rate to scale with $r_{\mathrm{e}}^{5.5\sim 7.5}$. The large exponent of r_e effectively sets an r_e threshold, and varying the scale factor γ shifts the threshold to progressively higher r_e for progressively smaller scale factors. In the same way that γ > 1 accounts for subgrid variability of q_l in GCMs, schemes using r_e thresholds use r_c values smaller than those typically found in single clouds (19).

To establish relationships between the autoconversion process and the ERF_aci simulated by the model, we perform pairs of simulations with present-day and preindustrial aerosol and aerosol precursor emissions but an otherwise identical climate by using a fixed sea surface temperature and relaxing the large-scale flow to ERA-Interim reanalysis (72) for the years 2000–2004 (“nudging”) (73, 74). The strengths of the F_Nd forcing and the F_ℒ and F_fc adjustments are diagnosed separately using the method of partial radiative perturbations, as described in Mülmenstädt et al. (41). In model runs with modified autoconversion, no other modifications to restore the top-of-atmosphere (TOA) radiative balance are made. The nudging prevents the model state from diverging from the reference climate despite the TOA radiative imbalance, and modifying only one parameterized process simplifies attribution of the model response to that process. However, the base-state cloud amount (both f_c and ℒ) is sensitive to the autoconversion parameterization, which is a strong sink process for liquid cloud in the model. To be able to compare ERF_aci across model configurations with different base-state cloud properties, we consider the normalized adjustment F_ℒ/F_Nd instead of F_ℒ (see text S3).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/22/eaaz6433/DC1