Indirect reciprocity with simple records

Significance

Indirect reciprocity is a foundational mechanism of human cooperation, and understanding the social structures that allow it to arise continues to be a core issue in both the social sciences and evolutionary biology. This paper analyzes a model of indirect reciprocity in steady-state equilibria, where players observe only their partners’ records, and each individual’s record depends on the individual’s own past behavior alone. We show that tolerant trigger strategies based on these simple records can robustly support positive social cooperation in games with sufficient “strategic complementarity,” both in the prisoner’s dilemma and in some multiplayer public goods games, and we show that the resulting cooperative equilibria have strong stability properties.

Abstract

Indirect reciprocity is a foundational mechanism of human cooperation. Existing models of indirect reciprocity fail to robustly support social cooperation: Image-scoring models fail to provide robust incentives, while social-standing models are not informationally robust. Here we provide a model of indirect reciprocity based on simple, decentralized records: Each individual’s record depends on the individual’s own past behavior alone, and not on the individual’s partners’ past behavior or their partners’ partners’ past behavior. When social dilemmas exhibit a coordination motive (or strategic complementarity), tolerant trigger strategies based on simple records can robustly support positive social cooperation and exhibit strong stability properties. In the opposite case of strategic substitutability, positive social cooperation cannot be robustly supported. Thus, the strength of short-run coordination motives in social dilemmas determines the prospects for robust long-run cooperation.

People (and perhaps also other animals) often trust each other to cooperate even when they know they will never meet again. Such indirect reciprocity relies on individuals having some information about how their partners have behaved in the past. Existing models of indirect reciprocity fall into two paradigms. In the image-scoring paradigm, each individual carries an image that improves when the individual helps others, and (at least some) individuals help only those with good images (1, 2). In the standing paradigm, each individual carries a standing that typically improves when the individual helps others with good standing, but not when the individual helps those with bad standing, and individuals with good standing help only other good-standing individuals (3, 4).

Neither of these paradigms provides a robust explanation for social cooperation. In image-scoring models, there is no reason for an individual to help only partners with good images: Since the partner’s image does not affect one’s future payoff, helping some partners and not others is optimal only if one is completely indifferent between helping and not helping. In game-theoretic terms, individuals never have strict incentives to follow image-scoring strategies, and hence such strategies can form at best a weak equilibrium. Closely related to this point, image-scoring equilibria are unstable in several environments (5, 6). Standing models do yield strict, stable equilibria, but they fail to be informationally robust: An individual’s standing is a function of not only the individual’s past behavior, but also the individual’s past partners’ behavior, their partners’ partners’ behavior, and so on ad infinitum. In the absence of centralized record keeping or some way of physically marking bad-standing individuals, computing such a function requires information that is likely unavailable in many groups (7).

We develop a theoretical paradigm for modeling indirect reciprocity that supports positive social cooperation as a strict, stable equilibrium while relying only on simple, individualistic information: When two players meet, they observe each other’s records and nothing else, and each individual’s record depends only on the individual’s own past behavior. [Individualistic information is also called “first-order” (8–10).]

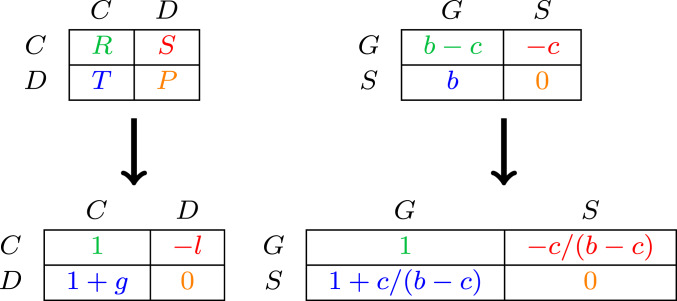
As our model of individual interaction, we use the classic prisoner’s dilemma (“PD”) with actions $C,D$ (“cooperate,” “defect”) and a standard payoff normalization, where the gain from unilateral defection, $g$, and the loss from unilateral cooperation, $l$, are both positive and satisfy the condition $g<l+1$, which means that joint payoffs are maximized by mutual cooperation (Fig. 1, Left). This canonical game can capture many two-sided interactions, such as business partnerships (11), management of public resources (12, 13), and risk sharing in developing societies (14), as well as many well-documented animal behaviors (15).

Fig. 1.

The prisoner’s dilemma. (Left) Matrices show how any prisoner’s dilemma can be represented by the standard normalization with $g=\left(T-R\right)/\left(R-P\right)$ and $l=\left(P-S\right)/\left(R-P\right)$, where $T>R>P>S$. (Right) Matrices illustrate this normalization for “donation games” in which choosing $G$ ($Give$) instead of $S$ ($Shirk$) incurs a personal cost $c$ and gives benefit $b>c$ to the opponent.

A critical feature of the PD is whether it exhibits strategic complementarity or strategic substitutability. Strategic complementarity means that the gain from playing $D$ is greater when the opponent also plays $D$. In the PD payoff matrix displayed in Fig. 1, this corresponds to the condition

$$g<l.$$

The opposite case of strategic substitutability arises when the gain from playing $D$ is greater when the opponent plays $C$: Mathematically, this occurs when

$$g>l.$$

Many previous studies of indirect reciprocity restrict attention to the “donation game” instance of the PD where $g=l$, as in Fig. 1, Right (16).* Our analysis reveals this to be a knife-edge case that obscures the distinction between strategic complementarity ($g<l$) and substitutability ($g>l$). This distinction has long been known to be of critical importance in economics (18, 19), while its implications for cooperation in the repeated prisoner’s dilemma have been noted more recently (8, 9). When a player’s record depends only on the player’s own past actions, the future reward for cooperation (or future penalty for defection) is independent of the player’s current opponent’s record. Therefore, to obtain an equilibrium where a player has a strict incentive to cooperate if and only if the opponent’s record is good, the cost of cooperation must be lower against an opponent with a good record (who cooperates) than against one with a bad record (who defects): That is, cooperation requires $g<l$.

Strategic complementarity is a common case in realistic social dilemmas. It implies that although $D$ is always selfishly optimal (a defining feature of the PD), the social dilemma nonetheless retains some aspect of a coordination game, so that playing $C$ is less costly when one’s partner also plays $C$. For example, mobbing a predator is always risky (hence costly) for each individual, but it is much less risky when others also mob (20).

In our model, each player’s record is an integer, which evolves as a function of the player’s history of plays of $C$ and $D$. We assume the system is subject to some noise, so that, whenever an individual plays $C$, with probability $\epsilon$ the individual’s record updates as if the individual had played $D$ instead.^† Here the level of noise $\epsilon \in \left(\mathrm{0,1}\right)$ can reflect either errors in recording or errors in executing the intended action.

A simple example of such a record system is the “counting $D$s” system where a player’s record is just a count of the number of times the player has defected (or cooperated and was hit by noise). More complicated record systems could also count the number of times a player cooperated and could also keep track of the time path of plays of $C$ and $D$. We analyze a fairly broad class of strategies, with the following three defining properties: 1) The set of all possible records can be partitioned into two classes, “good records” and “bad records.” 2) When two players with good records meet each other, they cooperate; if instead either partner has a bad record, both players defect. 3) The class of bad records is absorbing: Once a player obtains a bad record, the record remains bad forever. We refer to this as the class of trigger strategies.

Examples of trigger strategies include strategies where a player’s record becomes bad once the absolute number of times the player has defected crosses a threshold $K$, as well as strategies where the player’s record becomes bad the first time the fraction of times the player has defected crosses a threshold. We call strategies of the former type tolerant grim trigger strategies or $GrimK$, as they are a form of the well-known grim trigger strategies (21) with a “tolerance” of $K$ recorded plays of $D$. We will see that $GrimK$ strategies succeed in supporting cooperation for a broad range of payoff parameters. Moreover, if the payoff parameters preclude cooperation under $GrimK$ strategies, they also preclude cooperation under any other trigger strategy.

We analyze the steady-state equilibria of a system where the total population size is constant, but each individual has a geometrically distributed lifetime with survival probability $\gamma \in \left(\mathrm{0,1}\right)$. Players play the PD with random rematching every period and receive no information about their current partner other than the partner’s record. To ensure robustness, we insist that equilibrium behavior is strictly optimal at every record; in classical (normal-form) games, this implies that the equilibrium is evolutionarily stable (22, 23).

Results

Steady-State Cooperation.

We show that $GrimK$ strategies can form a strict steady-state equilibrium if and only if the PD exhibits substantial strategic complementarity, in that the gain from playing $D$ rather than $C$ is significantly greater when the opponent plays $D$: The precise condition required in the PD payoff matrix displayed in Fig. 1 is

$$g<\frac{l}{1+l}.$$

Under this condition, the tolerance level $K$ can be tuned so that $GrimK$ strategies support positive social cooperation in a steady-state equilibrium.

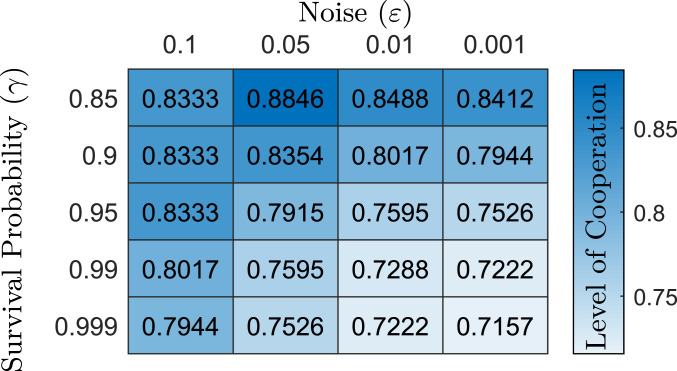
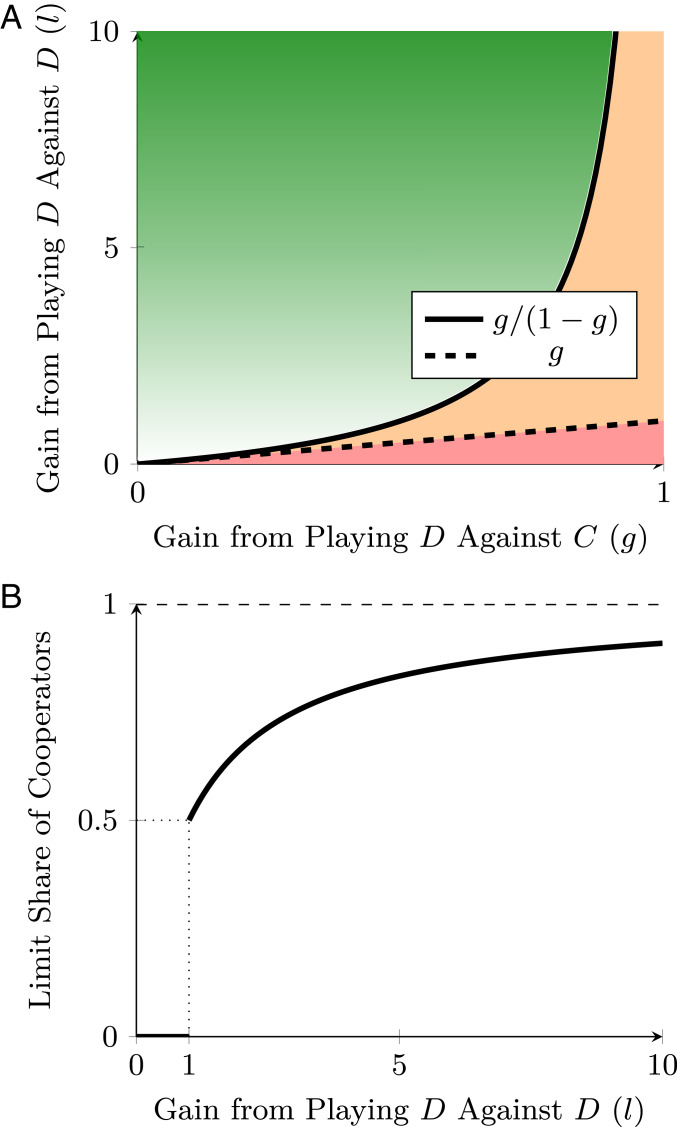
To see how to tune the threshold $K$, note that since even individuals who always try to cooperate are sometimes recorded as playing $D$ due to noise, $K$ must be large enough that the steady-state share of the population with good records is sufficiently high: With any fixed value of $K$, a population of sufficiently long-lived players would almost all have bad records. However, $K$ also cannot be too high, as otherwise an individual with a very good record (that is, with a very low number of $D$s) can safely play $D$ until the individual’s record approaches the threshold. Another constraint is that an individual with record $K-1$ who meets a partner with a bad record must not be tempted to deviate to $C$ to preserve the individual’s own good record. These constraints lead to an upper bound on the maximum share of cooperators in equilibrium. As lifetimes become long and noise becomes small, this upper bound converges to 0 whenever $g>l/\left(1+l\right)$ and to $l/\left(1+l\right)$ whenever $g<l/\left(1+l\right)$ (Fig. 2), and we show that this share of cooperators can in fact be attained in equilibrium in the $\left(\gamma ,\epsilon \right)\to \left(\mathrm{1,0}\right)$ limit. Thus, greater strategic complementarity (higher $l$ and lower $g$) not only helps support some cooperation; it also increases the maximum level of cooperation in the limit, as shown in Fig. 3.

Fig. 2.

Upper bounds on cooperation. The entries are upper bounds on the share of cooperators possible in a $GrimK$ equilibrium for various $\gamma$ and $\epsilon$ values when $g=0.5$ and $l=2.5$, with a darker shade indicating a higher value as shown in the scale at Right. As we move to the bottom right, the upper bound converges to $l/\left(1+l\right)\approx 0.7143$, which is the maximum share of cooperators sustainable in the limit, but away from the limit the upper bound can be different (the values in this table are all higher, but this is not the case for small $\gamma$ or large $\epsilon$).

Fig. 3.

Limit performance of $GrimK$ strategies. (A) In the green region ($l>g/\left(1-g\right)$), $GrimK$ strategies sustain a positive limit share of cooperators, which increases with $l$, as indicated by a deeper shade of green. In the orange region ($g<l<g/\left(1-g\right)$), the limit share of cooperators with $GrimK$ is 0, but other strategies may sustain positive cooperation in the limit. In the red region ($l\le g$), individualistic records preclude cooperation. (B) The limit share of cooperators as a function of $l$ when $g=1/2$. At $l=1$, there is a discontinuity; as $l\to \infty$, the limit share of cooperators approaches 1.

We also show that, in the $\left(\gamma ,\epsilon \right)\to \left(\mathrm{1,0}\right)$ limit, no trigger strategies can support a positive equilibrium share of cooperators if $g>l/\left(1+l\right)$, and no trigger strategies can support an equilibrium share of cooperations greater than $l/\left(1+l\right)$ if $g<l/\left(1+l\right)$. Thus, when lifetimes are long and noise is small, $GrimK$ strategies attain optimum equilibrium cooperation within the class of trigger strategies. The logic of this result is that the constraints on the performance of $GrimK$ strategies imposed by players’ incentives and the presence of noise apply equally to any strategy in the trigger class.

Stability, Convergence, and Evolutionary Properties.

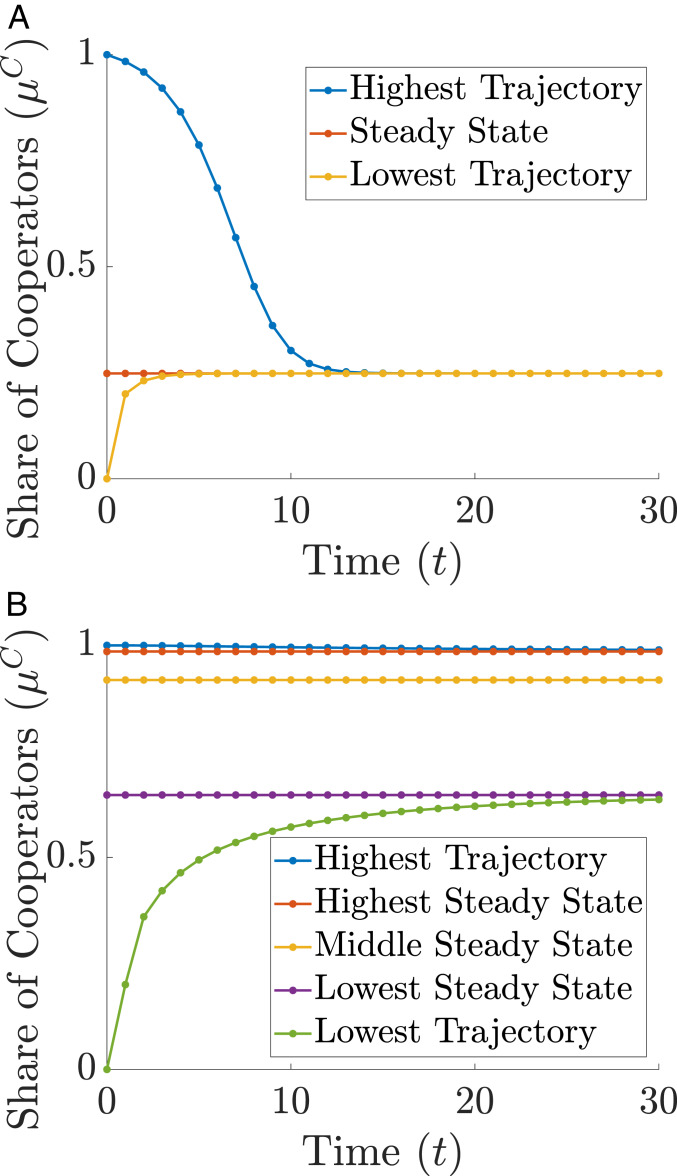
$GrimK$ strategies also satisfy desirable stability and convergence properties. These derive from an important monotonicity property of $GrimK$ strategies: When the distribution of individual records is more favorable today, the same will be true tomorrow, because players with better records both behave more cooperatively and induce more cooperative behavior from their partners. (See Methods for a precise statement.) From this observation it can be shown that, whenever the initial distribution of records is more favorable than the best steady-state record distribution, the record distribution converges to the best steady state. Similarly, whenever the initial distribution is less favorable than the worst steady state, convergence to the worst steady state obtains (Fig. 4). These additional robustness properties are not shared by more complicated, nonmonotone strategies that can sometimes support cooperation for a wider range of parameters than $GrimK$.

Fig. 4.

Convergence of the share of cooperators. A depicts trajectories for the share of cooperators when $\gamma =0.8$, $\epsilon =0.02$, and players use the $Grim1$ strategy; B does the same for the $Grim2$ strategy. In A, all trajectories converge to the unique steady state; in B, there are three steady states. Here “high” trajectories converge to the most cooperative steady state, while “low” trajectories converge to the least cooperative steady state. See Methods for details.

We also analyze evolutionary properties of $GrimK$ equilibria. When $g<l/\left(1+l\right)$, there is a sequence of $GrimK$ equilibria that are “steady-state robust to mutants” and attain the maximum limit cooperation share of $l/\left(1+l\right)$. By this we mean that, when a small fraction of players adopt some mutant $Grim{K}^{\prime }$ strategy where $K^{\prime }\hspace{0.17em}\ne \hspace{0.17em}K$, there is a steady-state distribution of records where it remains strictly optimal to play according to $GrimK$. We also perform simulations of dynamic evolution when a population playing a $GrimK$ equilibrium is infected by a mutant population playing $Grim{K}^{\prime }$ for some $K^{\prime }\hspace{0.17em}\ne \hspace{0.17em}K$ (SI Appendix, Fig. S1).

Multiplayer Public Goods Games.

Although our main analysis takes the basic unit of social interaction to be the standard two-player PD, many social interactions involve multiple players: The management of the commons and other public resources is a leading example (12, 13). In SI Appendix we establish that, when strategic complementarity is sufficiently strong, robust cooperation in the multiplayer public goods game can be supported by a simple variant of $GrimK$ strategies, wherein a player contributes to the public good if and only if all of the player’s current partners have good records. In contrast, with strategic substitutability the unique strict equilibrium involves zero contribution. As the $n$-player public good game is a generalization of the PD, this implies that individualistic records preclude cooperation in the PD with strategic substitutability, as indicated in the red region in Fig. 3A.

Discussion

We have shown how individualistic records robustly support indirect reciprocity in supermodular PD and multiplayer public goods games. To place our results in context, recall that scoring models do not provide robust incentives, while standing models compute records as a recursive function of a player’s partners’ past actions and standing, their partners’ actions and standing, and so on, and thus require more information than may typically be available. The simplicity and power of individualistic records suggest that they may be usefully adapted to specific settings where cooperation is based on indirect reciprocity, such as online rating systems (24, 25), credit ratings (10, 26), decentralized currencies (27, 28), and monitoring systems for conflict resolution (29). Individualistic records may also prove useful in modeling the role of costly punishment in the evolution of cooperation (30–33).

We interpret individualistic records and $GrimK$ strategies as both a theoretical demonstration that simple strategies can sometimes support cooperation using only first-order information and an approximation of human behavior in a range of environments. For example, when meeting a potential business partner for the first time, it is common to contact the person’s past partners and inquire about the potential partner’s past behavior, typically without delving into the past partners’ own past behavior or the past partners’ partners’ behavior. Similarly, in online marketplaces such as eBay or Airbnb, one typically rates one’s current partner’s behavior in the absence of any information about the current partner’s past partners’ behavior. Users then observe summary statistics that depend only on their current partner’s own past behavior, which is an example of individualistic (first-order) records. Moreover, if users behave honestly only with partners who have not received too many negative reviews, their behavior can be approximated by $GrimK$ strategies.

We conclude by discussing possible extensions of our analysis.

First, while we have analyzed the evolutionary stability of the $GrimK$ equilibrium, we have not analyzed how this equilibrium could first arise. In our model, it is a strict equilibrium for all agents to always defect, so that equilibrium is also an evolutionarily stable strategy. To explain how society might move from such a state to a more cooperative equilibrium such as $GrimK$, we could appeal to random mutations. Given our continuum population, this could be modeled as a deterministic drift as in ref. 34, but we do not develop that argument here.

We have also assumed that everyone shares the same assessment of each individual’s record. This “public information” assumption is known to be critical in some prior models of indirect reciprocity. In our model, allowing heterogeneous assessments of a player’s record would not change the analysis very much, so long as both partners learn their opponents’ assessments of their records before taking actions (35–37). The more complex situation where each partner’s assessment of the other’s record is private information would be interesting to study in future research.

Methods

Here we summarize the model and mathematical results; further details are provided in SI Appendix.

A Model of Social Cooperation with Individualistic Records.

Time is discrete and doubly infinite: $t\in \left\{\dots ,-2,-\mathrm{1,0,1,2},\dots \right\}$. There is a population of individuals of unit mass, each with survival probability $\gamma \in \left(\mathrm{0,1}\right)$, so each individual’s lifespan is geometrically distributed with mean $1/\left(1-\gamma \right)$. An inflow of $1-\gamma$ newborn players each period keeps the total population size constant. We thus have an infinite-horizon dynamic model with overlapping generations of players (38).

Every period, individuals randomly match in pairs to play the PD (Fig. 1). Each individual carries a record $k\in \mathbb{N}≔\left\{\mathrm{0,1,2},\dots \right\}$. Newborns have record 0. Under the counting $D$s record system, whenever an individual plays $D$, the individual’s record increases by 1, while whenever an individual plays $C$, the individual’s record remains constant with probability $1-\epsilon$ and increases by 1 with probability $\epsilon$; thus, $\epsilon \in \left(\mathrm{0,1}\right)$ measures the amount of noise in the system (39–43). More generally, a record system specifies an arbitrary next-period record as a function of the current-period record and the current-period recorded action, which equals $D$ if the individual plays $D$, equals $C$ with probability $1-\epsilon$, and equals $D$ with probability $\epsilon$ if the individual plays $C$.

When two players meet, they observe each other’s records and nothing else. A strategy is a mapping $\mathbf{s}:\mathbb{N}\times \mathbb{N}\to \left\{C,D\right\}$, with the convention that the first component of the domain is a player’s own record and the second component is the current opponent’s record. We assume that all players use the same strategy, noting that this must be the case in every strict equilibrium in a symmetric, continuum-agent model like ours. (Of course, players who have different records and/or meet opponents with different records may take different actions.)

The state of the system $\mu \in \mathrm{\Delta }\left(\mathbb{N}\right)$ describes the share of the population with each record, where ${\mu }_k\in \left[\mathrm{0,1}\right]$ denotes the share with record $k$. When all players use strategy $\mathbf{s}$, let $f_{\mathbf{s}}:\mathrm{\Delta }\left(\mathbb{N}\right)\to \mathrm{\Delta }\left(\mathbb{N}\right)$ denote the resulting update map governing the evolution of the state. (The formula for $f_{\mathbf{s}}\left(\mu \right)$ is in SI Appendix.) A steady state under strategy $\mathbf{s}$ is a state $\mu$ such that $f_{\mathbf{s}}\left(\mu \right)=\mu$.

Given a strategy $\mathbf{s}$ and state $\mu$, the expected flow payoff of a player with record $k$ is ${\pi }_k\left(\mathbf{s},\mu \right)={\sum }_{k^{\prime }}{\mu }_{k^{\prime }}u\left(\mathbf{s}\left(k,k^{\prime }\right),\mathbf{s}\left(k^{\prime },k\right)\right)$, where $u$ is the PD payoff function. Denote the probability that a player with current record $k$ has record $k^{\prime }\hspace{0.17em}t$ periods in the future by ${\varphi }_k{\left(\mathbf{s},\mu \right)}^t\left(k^{\prime }\right)$. The continuation payoff of a player with record $k$ is then $V_k\left(\mathbf{s},\mu \right)=\left(1-\gamma \right){\sum }_{t=0}^{\infty }{\gamma }^t{\sum }_{k^{\prime }}{\varphi }_k{\left(\mathbf{s},\mu \right)}^t\left(k^{\prime }\right){\pi }_{k^{\prime }}\left(\mathbf{s},\mu \right)$. Note that we have normalized continuation payoffs by $\left(1-\gamma \right)$ to express them in per-period terms. A player’s objective is to maximize the expected lifetime payoff.

A pair $\left(\mathbf{s},\mu \right)$ is an equilibrium if $\mu$ is a steady state under $\mathbf{s}$ and, for each own record $k$ and opponent’s record $k^{\prime }$, the prescribed action $\mathbf{s}\left(k,k^{\prime }\right)\in \left\{C,D\right\}$ maximizes the expected lifetime payoff from the current period onward, given by $\left(1-\gamma \right)u\left(a,\mathbf{s}\left(k^{\prime },k\right)\right)+\gamma {\sum }_{k^{″}}\left(\rho \left(k,a\right)\left[k^{″}\right]\right)V_{k^{″}}\left(\mathbf{s},\mu \right)$, over $a\in \left\{C,D\right\}$, where $\rho \left(k,a\right)\left[k^{″}\right]$ denotes the probability that a player with record $k$ who takes action $a$ acquires next-period record $k^{″}$. Note that this expression depends on the opponent’s record only through the predicted current-period opponent action, $\mathbf{s}\left(k^{\prime },k\right)$. In addition, the ratio $\left(1-\gamma \right)/\gamma$ captures the weight that players place on their current payoff relative to their continuation payoff from tomorrow on. We study limits where this ratio converges to 0, as opposed to time-average payoffs which give exactly 0 wt to any one period’s payoff, because in the latter case optimization and equilibrium impose unduly weak restrictions (44). An equilibrium is strict if the maximizer is unique for all pairs $\left(k,k^{\prime }\right)$; i.e., the optimal action is always unique. Note that this equilibrium definition allows agents to maximize over all possible strategies, as opposed to only strategies from some preselected set. We focus on strict equilibria because they are robust: They remain equilibria under “small” perturbations of the model. Note that the strategy “always defect,” i.e., $s\left(k,k\prime \right)=D$ for all $\left(k,k^{\prime }\right)$, together with any steady state is always a strict equilibrium. SI Appendix, Lemma 2 characterizes the steady states for any $GrimK$ strategy, as well as the $\gamma ,\epsilon ,g,l$ parameters for which the steady states are equilibria.

Limit Cooperation under $GrimK$ Strategies.

Under $GrimK$ strategies, a matched pair of players cooperate if and only if both records are below a prespecified cutoff $K$: That is, $s\left(k,k^{\prime }\right)=C$ if $max\left\{k,k^{\prime }\right\}<K$, and $s\left(k,k^{\prime }\right)=D$ if $max\left\{k,k^{\prime }\right\}\ge K$.

We call an individual a cooperator if the individual’s record is below $K$ and a defector otherwise. Note that individuals may be a cooperator for some periods of their life and a defector for other periods, rather than being preprogrammed to cooperate or defect for their entire life.

Given an equilibrium strategy $GrimK$, let ${\mu }^C={\sum }_{k=0}^{K-1}{\mu }_k$ denote the corresponding steady-state share of cooperators. Note that, in a steady state with cooperator share ${\mu }^C$, mutual cooperation is played in share ${\left({\mu }^C\right)}^2$ of all matches. Let ${\overline{\mu }}^C\left(\gamma ,\epsilon \right)$ be the maximal share of cooperators in any tolerant grim trigger equilibrium (allowing for every possible $K$) when the survival probability is $\gamma$ and the noise level is $\epsilon$.

SI Appendix, Theorem 1 characterizes the performance of equilibria in $GrimK$ strategies in the double limit where the survival probability approaches 1—so that players expect to live a long time and the “shadow of the future” looms large—and the noise level approaches 0—so that records are reliable enough to form the basis for incentives. [This long-lifespan/low-noise limit is the leading case of interest in theoretical analyses of indirect reciprocity (8, 45–49).] SI Appendix, Theorem 1 shows that, in the double limit $\left(\gamma ,\epsilon \right)\to \left(\mathrm{1,0}\right)$, ${\overline{\mu }}^C\left(\gamma ,\epsilon \right)$ converges to $l/\left(1+l\right)$ when $g<l/\left(1+l\right)$ and converges to 0 when $g>l/\left(1+l\right)$. The formal statement and proof of this result are contained in SI Appendix.

Barring knife-edge cases, tolerant grim trigger strategies can thus robustly support positive cooperation in the double limit $\left(\gamma ,\epsilon \right)\to \left(\mathrm{1,0}\right)$ if and only if the gain from defecting against a partner who cooperates is significantly smaller than the loss from cooperating against a partner who defects: $g<l/\left(1+l\right)$. Moreover, the maximum level of cooperation in this case is $l/\left(1+l\right)$. Here we explain the logic of this result.

We first show that $g<{\mu }^C$ in any $GrimK$ equilibrium. Newborn individuals have continuation payoff equal to the average payoff in the population, which is ${\left({\mu }^C\right)}^2$. Thus, since a newborn player plays $C$ if and only if matched with a cooperator, ${\left({\mu }^C\right)}^2=\left(1-\gamma \right){\mu }^C+\gamma {\mu }^C{V}_0^C+\gamma \left(1-{\mu }^C\right)V_0^D$, where $V_0^C$ and $V_0^D$ are the expected continuation payoffs of a newborn player after playing $C$ and $D$, respectively. Newborn players have the highest continuation payoff in the population, so $V_0^C\le V_0={\left({\mu }^C\right)}^2$. For a newborn player to prefer not to cheat a cooperative partner, it must be that $V_0^D<V_0^C-\left(1-\gamma \right)g/\gamma$, so when ${\mu }^C<1$ (as is necessarily the case with any noise),

$${\left({\mu }^C\right)}^2<\left(1-\gamma \right){\mu }^C+\gamma {\left({\mu }^C\right)}^2-\left(1-\gamma \right)\left(1-{\mu }^C\right)g.$$

This inequality can hold only if $g<{\mu }^C$.

We next show that $\gamma \left(1-\epsilon \right){\mu }^C<l/\left(1+l\right)$ in any $GrimK$ equilibrium. The continuation payoff $V_{K-1}$ of an individual with record $K-1$ satisfies $V_{K-1}=\left(1-\gamma \right){\mu }^C+\gamma \left(1-\epsilon \right){\mu }^C{V}_{K-1}$, or $V_{K-1}=\left(1-\gamma \right){\mu }^C/\left(1-\gamma \left(1-\epsilon \right){\mu }^C\right)$. A necessary condition for an individual with record $K-1$ to prefer to play $D$ against a defector partner is $\left(1-\gamma \right)\left(-l\right)+\gamma \left(1-\epsilon \right)V_{K-1}<0$, or $l>\gamma \left(1-\epsilon \right)V_{K-1}/\left(1-\gamma \right)$. Combining this inequality with the expression for $V_{K-1}$ yields $\gamma \left(1-\epsilon \right){\mu }^C<l/\left(1+l\right)$, which in the $\left(\gamma ,\epsilon \right)\to \left(\mathrm{1,0}\right)$ limit gives ${\mu }^C\le l/\left(1+l\right)$.

We have established that tolerant grim trigger strategies can support positive cooperation in the $\left(\gamma ,\epsilon \right)\to \left(\mathrm{1,0}\right)$ limit only if $g\le l/\left(1+l\right)$ and that the maximum cooperation share cannot exceed $l/\left(1+l\right)$. The proof of SI Appendix, Theorem 1 is completed by showing that when $g<l/\left(1+l\right)$, by carefully choosing the tolerance level $K$, $GrimK$ can support cooperation shares arbitrarily close to any value between $g$ and $l/\left(1+l\right)$ in equilibrium when the survival probability is close to 1 and the noise level is close to 0.

Limit Cooperation under General Trigger Strategies.

$GrimK$ strategies are an instance of the more general class of trigger strategies, which are defined by the following properties: 1) The set of all possible records can be partitioned into two classes, good records $G$ and bad records $B$. 2) Partners cooperate if and only if they both have good records: $s\left(k,k^{\prime }\right)=C$ for all pairs $\left(k,k^{\prime }\right)\in G\times G$, and $s\left(k,k^{\prime }\right)=D$ for all other pairs $\left(k,k^{\prime }\right)$. 3) The class $B$ is absorbing: If $k\in B$, then every record $k^{\prime }$ that can be reached starting at record $k$ is also in $B$.

SI Appendix, Theorem 9 shows that, in the $\left(\gamma ,\epsilon \right)\to \left(\mathrm{1,0}\right)$ double limit, the maximum steady-state share of good-record players that can be supported in any trigger strategy equilibrium converges to zero if $g>l/\left(1+l\right)$ and converges to $l/\left(1+l\right)$ if $g<l/\left(1+l\right)$. Thus, in this double limit, tolerant grim trigger strategies attain the most equilibrium cooperation that any trigger strategy can support.

The intuition for this result is that the necessary conditions $g<{\mu }^C$ and $\gamma \left(1-\epsilon \right){\mu }^C<l/\left(1+l\right)$ derived above for $GrimK$ strategies apply equally to any trigger strategy. The argument to establish the necessity of $g<{\mu }^C$ is similar to that for $GrimK$ strategies, except we must now consider the incentives of a player with whichever record $k$ yields the greatest equilibrium continuation payoff, which is no longer necessarily a newborn (i.e., we may now have $k\hspace{0.17em}\ne \hspace{0.17em}0$). The argument to establish necessity of $\gamma \left(1-\epsilon \right){\mu }^C<l/\left(1+l\right)$ is also similar to that for $GrimK$ strategies, but now we consider the incentives of any player with a “marginal” good record that will become bad if the player is recorded as playing one additional $D$, which is no longer necessarily a player who has been recorded as playing $K-1\hspace{0.17em}D$s for some fixed cutoff $K$.

Convergence of $GrimK$ Strategies.

Fix an arbitrary initial record distribution ${\mu }^0\in \mathrm{\Delta }\left(\mathbb{N}\right)$. When all individuals use $GrimK$ strategies, the population share with record $k$ at time $t$, ${\mu }_k^t$, evolves according to

$$\begin{array}{cc}\hfill {\mu }_0^{t+1}& =1-\gamma +\gamma \left(1-\epsilon \right){\mu }^{C,t}{\mu }_0^t,\hfill \\ \hfill {\mu }_k^{t+1}& =\gamma \left(1-\left(1-\epsilon \right){\mu }^{C,t}\right){\mu }_{k-1}^t+\gamma \left(1-\epsilon \right){\mu }^{C,t}{\mu }_k^t\text{for}0<k<K,\hfill \end{array}$$

where ${\mu }^{C,t}={\sum }_{k=0}^{K-1}{\mu }_k^t$.

Fixing $K$, we say that distribution $\mu$ dominates (or is more favorable than) distribution $\stackrel{\sim }{\mu }$ if, for every $k<K$, ${\sum }_{\stackrel{\sim }{k}=0}^k{\mu }_{\stackrel{\sim }{k}}\ge {\sum }_{\stackrel{\sim }{k}=0}^k{\stackrel{\sim }{\mu }}_{\stackrel{\sim }{k}}$; that is, if for every $k<K$ the share of the population with record no worse than $k$ is greater under distribution $\mu$ than under distribution $\stackrel{\sim }{\mu }$. Under the $GrimK$ strategy, let $\overline{\mu }$ denote the steady state with the largest share of cooperators, and let $\underset{\_}{\mu }$ denote the steady state with the smallest share of cooperators.

SI Appendix, Theorem 12 shows that, if the initial record distribution is more favorable than $\overline{\mu }$, then the record distribution converges to $\overline{\mu }$; similarly, if the initial record distribution is less favorable than $\underset{\_}{\mu }$, then the record distribution converges to $\underset{\_}{\mu }$. Formally, if ${\mu }^0$ dominates $\overline{\mu }$, then $\underset{t\to \infty }{lim}{\mu }^t=\overline{\mu }$; similarly, if ${\mu }^0$ is dominated by $\underset{\_}{\mu }$, then $\underset{t\to \infty }{lim}{\mu }^t=\underset{\_}{\mu }$.

In Fig. 4A the blue trajectory corresponds to the initial distribution where all players have record 0, the red trajectory is constant at the unique steady-state value ${\mu }^C\approx 0.2484$, and the yellow trajectory corresponds to the initial distribution where all players have defector records. Here all of the trajectories converge to the unique steady state. In Fig. 4B, the red trajectory is constant at the largest steady-state value ${\mu }^C\approx 0.9855$, the yellow trajectory is constant at the intermediate steady-state value ${\mu }^C\approx 0.9184$, and the purple trajectory is constant at the smallest steady-state value ${\mu }^C\approx 0.6471$. The blue trajectory corresponds to the initial distribution where all players have record 0 and converges to the largest steady-state share of cooperators. The green trajectory corresponds to the initial distribution where all players have defector records and converges to the smallest steady-state share of cooperators.

Code Availability.

All simulations and numerical calculations have been performed with MATLAB R2017b and Wolfram Mathematica 11.3.0.0. In SI Appendix, we provide the MATLAB scripts used to generate Fig. 4 as well as those to simulate evolutionary dynamics and generate SI Appendix, Fig. S1.