Statistical reprogramming of macroscopic self-assembly with dynamic boundaries

Significance

Programmable self-assembly provides valuable insights into fundamental physics and enables the design of functional materials. However, relying only on computational solutions to understand the aspects of self-assembly may overlook critical phenomena accessible through physical observation. Our work presents a control mechanism utilizing dynamic boundaries to experimentally (re)program self-assembly. We show the correlation between confinement dynamics and resulting self-assembled structures and also demonstrate the tuning of their mechanical and magnetic properties. Our approach should be scalable to different particle counts, types, and sizes. In future studies, an enlarged confinement mechanism could be used as a control method on mobile robot swarms and as a test bed to experiment with many more particles for the self-assembly processes of crystalline and amorphous materials.

Abstract

Self-assembly is a ubiquitous process that can generate complex and functional structures via local interactions among a large set of simpler components. The ability to program the self-assembly pathway of component sets elucidates fundamental physics and enables alternative competitive fabrication technologies. Reprogrammability offers further opportunities for tuning structural and material properties but requires reversible selection from multistable self-assembling patterns, which remains a challenge. Here, we show statistical reprogramming of two-dimensional (2D), noncompact self-assembled structures by the dynamic confinement of orbitally shaken and magnetically repulsive millimeter-scale particles. Under a constant shaking regime, we control the rate of radius change of an assembly arena via moving hard boundaries and select among a finite set of self-assembled patterns repeatably and reversibly. By temporarily trapping particles in topologically identified stable states, we also demonstrate 2D reprogrammable stiffness and three-dimensional (3D) magnetic clutching of the self-assembled structures. Our reprogrammable system has prospective implications for the design of granular materials in a multitude of physical scales where out-of-equilibrium self-assembly can be realized with different numbers or types of particles. Our dynamic boundary regulation may also enable robust bottom-up control strategies for novel robotic assembly applications by designing more complex spatiotemporal interactions using mobile robots.

Local interactions among a large set of simple components can generate complex (1), functional (2), and robust (3) structures through self-assembly processes in both living and nonliving systems (4). Given appropriate mobility, the components can explore a continuous energy landscape (5) and arrange into spatial and temporal configurations (6) that define the properties of the self-assembled structures in a multitude of length scales (4). The ability to program the self-assembly process (7, 8) via tuning of the interactions among the constituents (9–11) addresses fundamental physics (12–15) and has important implications for innovative fabrication technologies (2, 3, 16, 17). Similarly, the detailed specification of crystallization and annealing procedures can regulate the self-assembly process and define the physical properties of materials (18). The products of such material preparation have been appreciated in metallurgy for centuries (19) and have been the focus of more recent studies on polymers (20), granular materials (13, 21), and colloids (22, 23). The effects of boundaries on self-assembly have also been widely investigated in colloidal (12, 17, 24–27) and granular (13, 28–30) systems; however, only a few of these studies evidenced the correlation between dynamically controlled boundaries and resulting self-assemblies (17).

Restructuring materials through reversible and repeatable preparation methods allows the same constituents to be repurposed for wholly different functionalities. This remains challenging at the molecular scale due to the specificity of the assembly interactions between the constituents (31). Conversely, confined granular and colloidal systems are particularly appealing media for studying reprogrammable self-assembly processes owing to the broad space of interaction design and the direct visualization of the constituents (8). Unlike self-assembled states formed in equilibrium (14, 22), driven nonequilibrium granular matter shows reversible characteristics and thus presents an additional route toward innovative technological applications (30). Reversible and repeatable control of constituents’ positions and motion pathways is also essential for distributed robotic systems (32, 33), whereby investigations of the effect of boundaries (34, 35) and programming of magnetic interaction potentials (36–38) have recently attracted significant attention.

In this paper, we demonstrate statistical reprogrammability with dynamic boundary confinement that allows selective and reversible access to multiple stable states and tunable properties in an externally driven two-dimensional (2D) millimeter-scale granular system. Our work complements prior programmable self-assembly studies by providing the correlation between the rate of change of the dynamic boundary and the resulting self-assembled structures. We introduce macroscale control and fabrication methods inspired by the physics of self-assembly in nonequilibrium colloidal scale systems and anticipate prospective routes to promising applications, especially in robotics (32, 33, 36, 37, 39).

Our experiments were performed within a camera aperture-inspired dynamic confinement mechanism that consisted of tightly arranged and reversibly sliding leaves (i.e., hard walls). The position of the leaves generated a dodecagonal arena, whose apothem defined the arena radius $R$ (Fig. 1A). We placed $N\hspace{0.17em}=\hspace{0.17em}25$ magnetically repelling, disk-shaped particles with diameter $\rho \hspace{0.17em}=\hspace{0.17em}5\text{mm}$ (Particle Design) in the arena and confined their motion within the arena to 2D with a transparent lid. We dynamically controlled the radius of the arena and its linear rate of change over time $dR/dt=\hspace{0.17em}\dot{R}$ (i.e., confinement rate) through a geared confinement mechanism and thus regulated the free space available to the particles (Fig. 1 B and C and Movie S1). The confinement mechanism was mounted on a programmable orbital shaker, which generated the same inertial force on every point of its surface following a circular trajectory with given shaking frequency $f_r$ (40) (Fig. 1A, Orbital Shaking, and SI Appendix, section S1). The shaker transferred kinetic energy to the particles through sliding friction and inelastic collisions with the arena walls. Combined with particle–particle interactions, the driven particle trajectories covered the arena with increasing homogeneity as $f_r$ was increased (SI Appendix, section S2). A high-speed camera mounted on top of the arena allowed us to track the motion of the particles (Fig. 1C, Particle Tracking, and SI Appendix, section S1).

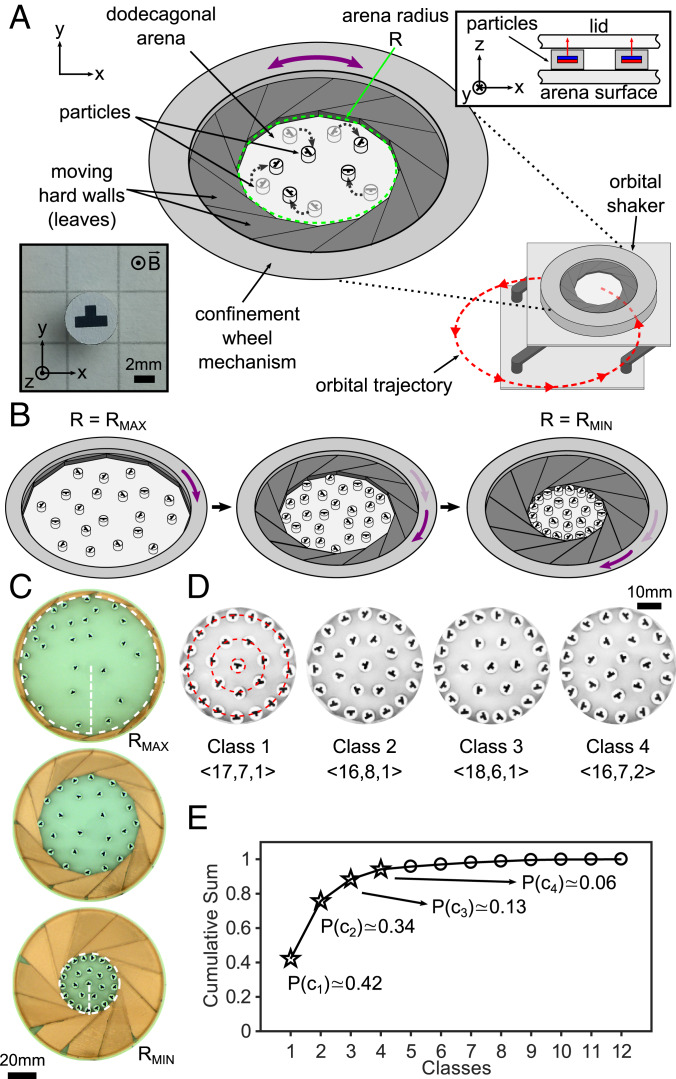
Fig. 1.

Dynamically moving hard boundaries confine mobile magnetic particles into reprogrammable 2D self-assembled patterns. (A) The confinement mechanism is mounted on a programmable orbital shaker generating a circular trajectory (shown with red arrows). The reversible rotation (purple arrow) of the confinement wheel is controlled to drive the bidirectional sliding of 12 leaves on the flat surface of the arena. The geometry and tight arrangement of the leaves maintain a dodecagonal arena shape for all values of its radius R (whose circumference is shown with green dashed line). All particles in the arena have diameter $\rho =5mm$ and host the same type of concentric, cylindrical permanent magnet. All particle magnets are oriented normally to the arena surface. A transparent top lid (Inset) seals the arena, forcing the magnetically repulsive particles to slide across the 2D domain. (B) A sample confinement process shows the change of the arena radius from $R_{MAX}=47.5\hspace{0.17em}\text{mm}$ to $R_{MIN}=20.5\hspace{0.17em}\text{mm}$. The rotation of the wheel mechanism (purple arrows) pushes the leaves toward the center of the arena. This process is reversible as the leaves are pulled back from the center when the wheel rotates in the opposite direction. (C) Snapshots of the arena captured from the top-view camera show the change of $R$ (white dashed line) from $R_{MAX}$ to $R_{MIN}$. (D) The four most frequently occurring classes of patterns self-assembling out of 25 shaken particles. The classes are labeled by the number of particles in their three-shell structure (red circles) as <#_outer, #_middle, #_inner>. (E) Cumulative distribution of the occurrence of the 12 pattern classes observed in the experiments (shown in Fig. 2C). The occurrence of the top four classes [$1/12{\displaystyle \sum _{\dot{R}}{\displaystyle \sum _{i=1}^{4}P\left(c_i\right)}}$, shown with stars] make up 95% of the total probability of all of the classes in 1,200 realizations of the programmable self-assembly experiments.

Our system was characterized by the influence of the orbital shaking frequency on the particle motion and of the dynamic confinement on the reversibility and repeatability of the self-assembly experiments. The orbital shaker platform allowed us to sweep the range of frequencies from 0 to 8.3 Hz. We showed that $f_r$ acted similarly to an effective temperature within a certain range (SI Appendix, section S3). The induced particle mobility permitted the formation of and statistical selection among several self-assembled configurations. The range of $R$ was dictated by the geometry of the confinement mechanism and could be changed from $R_{MAX}=47.5\hspace{0.17em}\text{mm}$ to $R_{MIN}=20.5\hspace{0.17em}\text{mm}$. We repeatedly compressed and decompressed the arena within these radius limits and showed the reversible transition of the particles from high-mobility to arrested states. Quantified by means of the particle-to-arena area fraction $\eta$, our experiments revealed the repeatability and reversibility of the granular system allowing reprogrammable self-assembly. Out of 1,200 experimental realizations of the process, we demonstrated the statistical reprogramming of self-assembly by regulating the arena radius with different $\dot{R}$ and by establishing a correlation between $\dot{R}$ and the occurrence probability, $P\left(c\right)$, of pattern classes $c$, that is, statistical programmability. We observed 12 distinct classes, which were identified by the topological relationship between the 25 particles when the arena was fully compressed at$R=R_{MIN}$ and their motion consequently fully arrested. Four of these classes (Fig. 1D) were observed in 95% of the realizations (Fig. 1E). Additional experimental results revealed further correlations between the dynamic boundary confinement and the programmable properties of the self-assembled structures, namely their topological stability, mechanical stiffness, and magnetic clutching.

Results

The shaking frequency $f_r$ played a critical role in defining the dynamics of the particles within the assembly arena. Static friction of the arena surface was completely dominant and prevented the particles from gaining any mobility for $f_r<3.0\hspace{0.17em}\text{Hz}$. Conversely, for $f_r>7.0\hspace{0.17em}\text{Hz}$, the motion of the particles could not be tracked smoothly due to the limit of the camera image acquisition rate. In the frequency range between 3.0 and 5.3 Hz, the interparticle magnetic repulsion force maintained a nearly fixed spacing between the particles. This interaction prevented the particles from gaining sufficient kinetic energy to cover the arena area and enforced them to follow a circular trajectory similar to that of the shaker. Only for $f_r>5.3\hspace{0.17em}\text{Hz}$ did hard interparticle collisions become prevalent, and the particles overcame the repulsive magnetic potential energy and explored the arena more homogeneously (SI Appendix, section S2). We further observed that $f_r$ acted similarly to an effective temperature in linear relation with the velocity of the particles within the 5.3- to 7.0-Hz range. The particle motion was characterized by a diffusive regime taking place in between 0.1 and 0.5 s of their trajectories (SI Appendix, sections S3 and S4). In the remainder of our experiments, we chose $f_r=6.0\hspace{0.17em}\text{Hz}$ to maintain this particle motion and corresponding arena coverage.

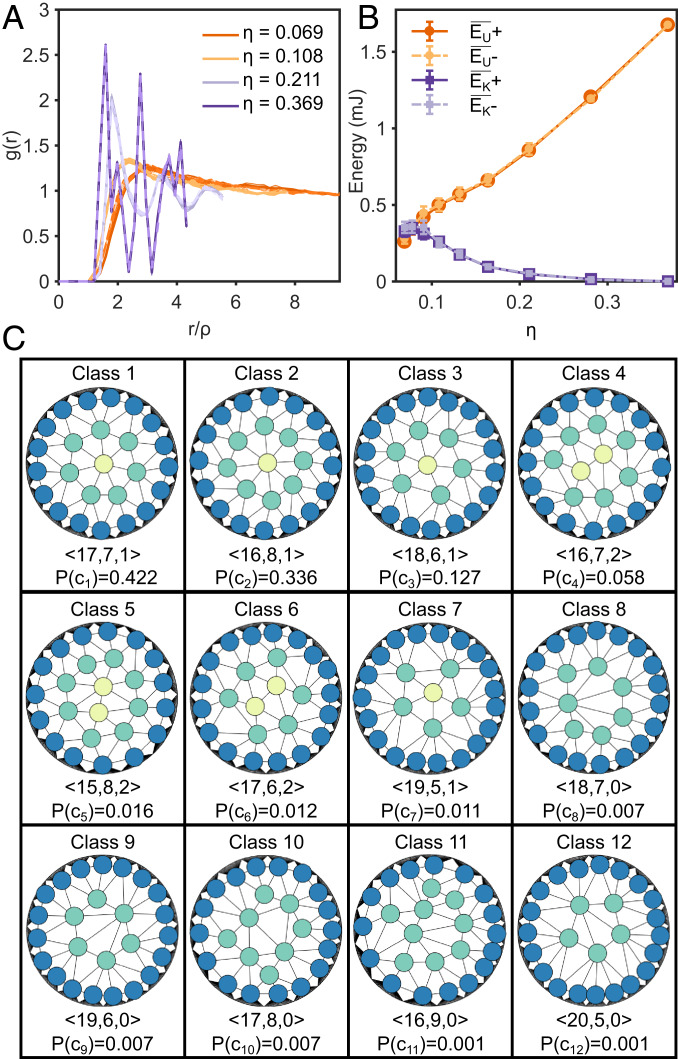
We then controlled $R$ to demonstrate the influence of the dynamic confinement on the repeatable and reversible particle behavior. We regulated $R$ to nine equally spaced values between $R_{MAX}$ and $R_{MIN}$ and showed the reversible transition of the granular system from high-mobility to arrested states (Reversible Confinement Experiments). Fig. 2A shows the radial distribution function $g\left(r\right)$ for four conditions defined by the particle-to-arena area fraction $\eta =\left(N\pi {\left(\rho /2\right)}^2\right)/\left(12\hspace{0.17em}\text{tan}\left(\pi /6\right)R^2\right)$. For $R=R_{MAX}\left({\eta }_{MIN}=\text{0}.069\right)$, the system showed a fluid-like behavior whereby particles had high mobility and lacked a persistent spatiotemporal structure. Secondary peaks emerged for smaller $R\left(\eta =\text{0}.108\right)$ and became more pronounced for larger $\eta$, evidencing the formation of persistent structures maintained by the dominant magnetic potential energy and the shaking action. For $R=R_{MIN}\left({\eta }_{MAX}=\text{0}.369\right)$, the particle motion was completely arrested, and $g\left(r\right)$ indicated the assembly of a solid-like structure with regular interparticle spacing. In the same experiments, the magnetic potential energy $E_U$, calculated through the magnetic dipole model (Energy Models and SI Appendix, section S2), increased with $\eta$ upon arena compression (Fig. 2B). At the same time, the total particle kinetic energy $E_K$ (Energy Models) progressively dropped to zero while $E_U$ dominated the particle interactions as the confinement advanced and $R$ approached $R_{MIN}$. Even though the system was being shaken with $f_r=6\text{.0}\hspace{0.17em}\text{Hz}$ throughout the compression, the particles became trapped in stiffer magnetic potential wells and their motion was arrested as the available space gradually reduced. At the smallest $R$ values, the combined friction and mutual magnetic repulsion within hard boundaries completely jammed the particles into various stable, porous, solid-like structures. When the compression was reversed and the arena decompressed, the particles reverted to a highly mobile state by accessing a larger space due to the influence of magnetic repulsion and the constant kinetic energy supply from the orbital shaker (Fig. 2 A and B). This reversible particle behavior constitutes the basis of our reprogrammable self-assembly experiments and is independent of the number of particles in the arena provided the following requirements are met: Compression and decompression are achieved without particles jamming and arresting the motion of the confinement mechanism, the particles are magnetically repulsive and preserve the 2D confinement during the process, and $f_r$ provides particles sufficient mobility.

Fig. 2.

Reversible state transitions and programmable self-assembled particle patterns by dynamic boundary confinement. (A) Confinement sampled at relevant values of the area fraction $\eta$ and described by the radial distribution function $g\left(r\right)$ (the parameter $r/\rho$ is the interparticle distance normalized with particle-diameter). Solid and dashed lines correspond to compression and decompression of the arena, respectively. Their overlap demonstrates the reversibility of the system. (B) Total magnetic potential energy $E_U$ and kinetic energy $E_K$ of 25 particles during confinement. Overlapping solid (+) and dashed lines (−), respectively, for compression and decompression of the arena reflect the reversibility of the granular confined system. (C) The complete set of pattern classes assembled out of 1,200 experiments with different confinement rates $\dot{R}$. The classes are listed in order of descending occurrence probability $P\left(c\right)$. The particles are connected by Delaunay triangles, their color highlighting the shells (outer, blue; middle, green; inner, yellow) in the patterns.

It is important to note that the particles could still relocate in the absence of shaking (i.e., for $f_r=\text{0}\hspace{0.17em}\text{Hz}$), utilizing the kinetic energy transferred by the moving boundaries during compression, but they could not explore configurations different from the initial. In this particular case, the final self-assembly patterns depended on the initial configuration of the particles before the compression started. Upon decompression from a fully compressed state, the particle system relaxed to a looser configuration within the larger accessible volume but observably retained the prior self-assembled pattern (Movie S2). This “athermal” behavior with memory prevented the sequential reconfiguration of the self-assembled patterns. These results were consistent with the observation that orbital shaking in our non-Brownian particle system produced effects similar to an effective temperature. This analogy was further reflected in the way mechanical shaking thermalized the system by obliterating the memory of initial conditions and, more generally, of prior particle configurations in all nonjammed states, as well as in the way shaking perturbed the system away from magnetic potential energy minima.

To achieve statistical programming of self-assembled particle patterns, we experimented with 12 constant $\dot{R}$ values while keeping particle count and shaking frequency fixed at 25 and 6 Hz, respectively (Statistical Programming). Out of 100 realizations of the process for each $\dot{R}$ value (1,200 realizations in total), we topologically classified 12 different self-assembled pattern classes at $R=R_{MIN}$, that is, at the end of the compression (Fig. 2C and Movies S3 and S4) using a combination of Delaunay triangulation and a shell-based heuristic template. The Delaunay triangulation identified unique connectivity between the particles while still allowing moderate flexibility in their absolute positions in the compressed arena area. A similar argument held for the heuristic template: The particles were classified based on their relative distance from the positions of the three virtual shells (Fig. 1D). The combination of these two methods offered generalizability by allowing multiple pattern configurations to be classified into a single class (Topological Pattern Classification and SI Appendix, section S6). The statistical programming was shown to be reversible upon arena decompression, which further enabled pattern reprogramming (Movie S5).

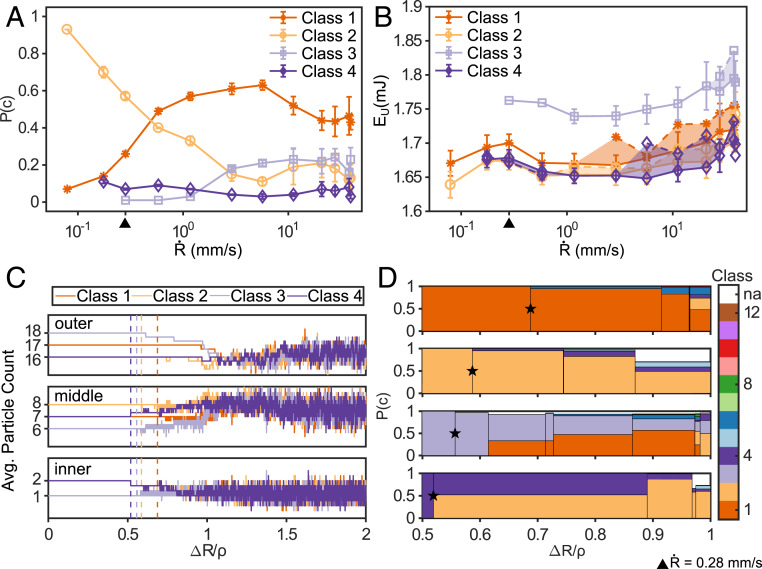
The statistical programming results reported in Fig. 3A show the correlation between $\dot{R}$ and $P\left(c_i\right)$ (i.e., the programmability of class i at the end of the compression for 100 realizations of the chosen $\dot{R}$). For the slowest $\dot{R}=\text{0}.079\hspace{0.17em}\text{mm}/\text{s}$, only classes 1 and 2 appeared, with $P\left(c_2\right)=\text{0}.93$ dominating $P\left(c_1\right)$. $P\left(c_1\right)$ was greater than $P\left(c_2\right)$ for faster confinement rates and reached its peak $P\left(c_1\right)=\text{0}.63$ for $\dot{R}=5.685\hspace{0.17em}\text{mm}/\text{s}$. While class 4 occurred infrequently throughout the $\dot{R}$ range $\left(P\left(c_4\right)\sim \text{0}.08\right)$, class 3 appeared for $\dot{R}\ge \text{0}.175\hspace{0.17em}\text{mm}/\text{s}$ and peaked at $P\left(c_3\right)\sim \text{0}.25$. These four classes (Fig. 1D) occurred across the entirety of the $\dot{R}$ range and their cumulative probability ${\displaystyle \sum _{\dot{R}}P\left(c_{i=1-4}\right)}$ averaged over the 1,200 experiments made up 95% of the total (Fig. 1E). The majority (five out of eight) of the least frequent classes appeared almost exclusively at the fastest confinement rates $\dot{R}>10\text{mm/s}$ (SI Appendix, section S7).

Fig. 3.

Programming and structural stability of the self-assembled particle patterns. (A) Programming [i.e., occurrence probability $P\left(c\right)$ within 100 realizations for each confinement rate $\left(\dot{R}\right)$ spanning from 0.079 to 39 mm/s] of the four topmost-occurring classes shown in a semilog plot. Error bars represent the number of transition states (i.e., classification mismatches) for each class. (B) Average magnetic potential energies $\left(E_U\right)$ of the top four classes versus $\dot{R}$ shown in a semilog plot. The error bars represent the variance of energies among different patterns in the same class for every value of $\dot{R}$. Shaded regions show the average $E_U$ of the transition states. (C) Average particle count on the three shells (i.e., outer, middle, and inner) during arena decompression from $R=R_{MIN}$ for each of the top four classes. Horizontal flat lines represent constant particle count. The color-coded vertical dashed lines indicate the earliest change in particle count on any shell, that is, change in the class definition. The farthest vertical line on the x axis represents the most stable class. (D) The occurrence probability of the classes during the decompression of the top four classes (subplots from top to bottom show classes from 1 to 4). Each vertical line on a subplot denotes the detection of a new class during decompression. The ratio of detected classes is represented by horizontal lines within each block using the same color code for classes. White regions, indicated by “na,” represent patterns that do not belong to the set of 12 stable classes, detected only at $R=R_{MIN}$. The black stars represent the earliest detected instability (i.e., they correspond to the dashed vertical lines in C). The $\dot{R}=0.28$ mm/s decompression rate is indicated in A, B, and D with a black triangle.

A comparison between the heuristic template- and the Delaunay triangulation-based classification hinted at the dynamic origin and possible metastability of patterns with high $E_U$. Since both classification methods allowed for moderate flexibility in absolute particle positions, seemingly different particle configurations could still be classified into the same classes (SI Appendix, section S6), which generated a variance in $E_U$ of each class. In other words, $E_U$ of a single class showed variability as particles could have different relative distances to each other while maintaining the same topological class. The relative distance between particles, and accordingly $E_U$ of each class, were influenced by the confinement rates. We observed that higher confinement rates were able to trap particles in higher energy configurations, as the particles were given less time to relax to configurations that minimized their $E_U$, that is, maximized their relative distances from each other. Fig. 3B shows the increase in average $E_U$of the top four classes corresponding to increasing $\dot{R}$. In extreme cases, particles were immobilized while switching from one shell to another. These transition states could be detected by the mismatch between the classifications, as the centroid distances to the shells remained the same while the triangulation connectivity changed (SI Appendix, section S6). The error bars in Fig. 3A represent such mismatches (i.e., the transition states), whose numbers increased with higher $\dot{R}$. These patterns also had higher $E_U$ compared to the average of the class they belonged (the shaded regions in Fig. 3B). This is further evidenced by comparing the $E_U$of all the classes; the class average energy increased when the mismatched patterns were included (SI Appendix, section S7). In our system, the confinement selected lower energy patterns for lower $\dot{R}$, that is, when the compression was slower compared to the time scale of the diffusive regime (0.1 to 0.5 s). Class 2, in particular, occurred most often in the slowest compression and was associated with the lowest energy among all patterns. Classes 6 to 12 had the highest energies (Fig. 2C) and occurred more frequently for faster compression (SI Appendix, section S7). In other words, particles were frozen into lower energy states given sufficient time to exchange neighbors and reduce $E_U$ (41).

We further investigated the topological stability of the four topmost-occurring classes, which also possessed the lowest magnetic potential energy in the most compressed state. We considered the permanence (i.e., the structural stability) of a class lost when its original particle distribution on the three-shell structure changed (e.g., from <18,6,1> to <17,7,1>). Fig. 3C shows the average number of particles on the three-shell structure while the classes were being decompressed from their frozen state at $R=R_{MIN}$ with $\dot{R}=\text{0}.28\hspace{0.17em}\text{mm}/\text{s}$ at $f_r=6\hspace{0.17em}\text{Hz}$ (Pattern Stability Analysis). The vertical dashed bars show the smallest radius for which a class first lost its stability. The permanence of the classes followed the same order as their total observation probabilities across all of the experiments (e.g., class 1 had the longest permanence; Fig. 1D). Fig. 3C also shows that particles first switched between inner and middle shells, as outer-shell particles were mostly arrested by the hard boundary walls and the magnetic repulsion from the center of the arena. For $R>R_{MIN}+1.5\hspace{0.17em}\rho$, the particle system returned to a high-mobility state and the topological definition of the classes based on the three-shell structure was lost. The subplots in Fig. 3D show the dynamic history of the top four classes and their tendency to change into different classes during the decompression. Classes 1 and 2 remained stable in a wider radius range, and they dominated the other classes [i.e., $P\left(c\right)>\text{0}.5$], whereas classes 3 and 4 had the tendency to switch to classes 1 and 2, respectively (i.e., class 3 <18,6,1> to class 1 <17,7,1>, and class 4 <16,7,2> to class 2 <16,8,1>). These results support the reversibility of our self-assembly system and hint to the existence of critical radii capable of programming certain classes with higher selection probabilities.

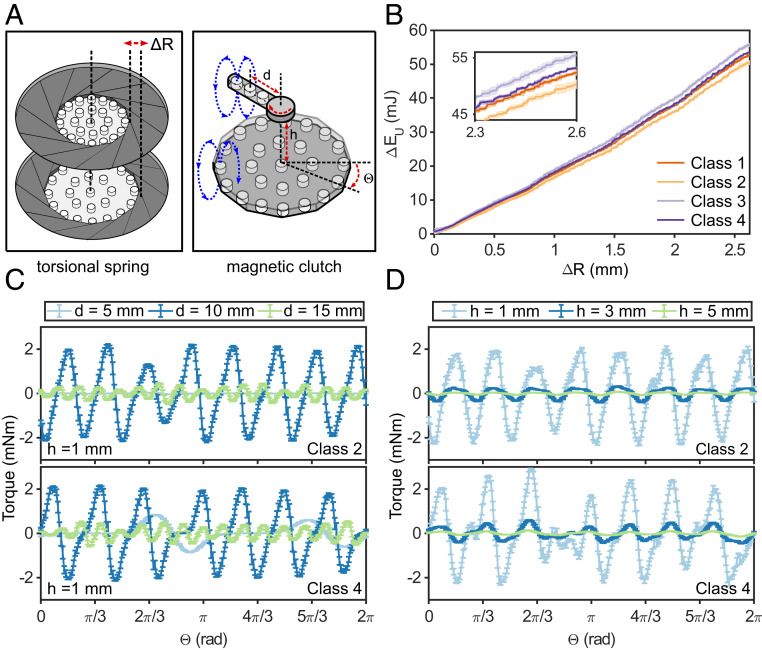
Notably, since the particles were magnetic and each particle pattern class had a different topology, programming the self-assembled particle patterns corresponded to programming the mechanical and magnetic properties of the compressed system, as demonstrated by the two different experiments sketched in Fig. 4A. Our system behaved as a 2D multistable elastic granular material with programmable stiffness (Fig. 4B). The differing slopes of $\mathrm{\Delta }{E}_U$ as a function of radial compression, $\mathrm{\Delta }R$, revealed the distinct stiffness of each pattern, with classes 2 and 3 having the lowest and highest stiffness, respectively (Quantification of Particle Pattern Stiffness and SI Appendix, section S8). Additionally, the magnetic field above and around the arrested particle patterns described a three-dimensional (3D) magnetic energy landscape suitable as a clutch mechanism for transduction. By scanning the plane over the self-assembled patterns with an auxiliary magnetic arm along the angular coordinate $\mathrm{\Theta }$ (Quantification of the Magnetic Clutch Torque), we measured unique torque profiles for each particle pattern (Fig. 4 C and D). Fig. 4C shows such profiles measured at a distance $h=1\hspace{0.17em}\text{mm}$ above the particles with arms that had magnets placed at different distances d from the center of the patterns. These torque readings correspond to a planar cross-section of the programmable 3D magnetic field over the self-assembled patterns. For $d=10\hspace{0.17em}\text{mm}$, torque readings showed eight equally distributed peaks for class 2 and seven peaks for class 4. A similar argument can be made for $d=5\hspace{0.17em}\text{mm}$, as the two particles at the inner shell of class 4 generated a fluctuating torque, unlike the single particle at the center of class 2. The magnetic clutch changed characteristics with increasing distance from the self-assembled patterns as well. Fig. 4D shows the sum of the torques measured by the rotating arm over class 2 and 4 patterns when $h$ was increasing from 1 mm to 5 mm. In both cases, the torque was decreasing but class 2 maintained its periodic torque profile, unlike class 4’s unique region in between $2\pi /3<\mathrm{\Theta }<\pi$. Unique magnetic clutch profiles for other classes are reported in SI Appendix, section S9.

Fig. 4.

Reprogrammable mechanical properties of the self-assembled patterns and transduction via their 3D magnetic profiles. (A) Sketch of the two methods used to transduce the self-assembled magnetic patterns into mechanical properties. Particle patterns behave like torsional springs against perturbations of arena radius $\mathrm{\Delta }R$ with programmable stiffness within the plane of the arena (Left). Particles generate programmable clutching, that is, magnetic gear effects, on an auxiliary arm (with magnets embedded at distance $d$ from its center) hovering (height $h$) and rotating (rotation angle $\mathrm{\Theta }$, defined positive clockwise from the x axis) over the patterns (Right). The magnetic field lines (shown with blue dashed lines) represent the interaction between magnets in the 3D space. (B) The magnetic potential difference with respect to $\mathrm{\Delta }R$ showing the planar spring effects. Class-dependent curves highlight the particle pattern-dependent difference of the self-assembled granular solids. (C) The torque generated on the magnet with different distances $d$ to the origin of the rotating arm hovering $h$ = 1 mm above class 2 and class 4 patterns showing magnetic clutch effects. (D) Sum of the torques acting on three magnets (d = 5 mm, 10 mm, and 15 mm) while the arm is rotating at different heights for class 2 and class 4. Results in C and D show the average values over three complete rotations.

Discussion

The geometry and symmetry of the self-assembled particle patterns reflected those of the boundaries of the arena (42). Alternative boundary geometries to the one we adopted are expected to induce different patterns from those we observed. This would imply that the geometrical selection of particle patterns is not just alternative but also complementary to the dynamic selection mechanism we presented. Combinations of the two mechanisms can further expand the set of reachable particle patterns that can be reprogrammed for a fixed particle count. Note that the 12 classes of particle patterns reported here did not necessarily exhaust the reachable set of all possible classes in our system; rather, they merely corresponded to the (sub)set we were able to observe when the system was fully compressed at $R=R_{MIN}$ by using 25 particles. The nonclassified patterns shown in Fig. 3D hint that there indeed appeared additional transient classes at different arena radii.

The geometry of the confinement mechanism defined the lower and upper bounds for the particle count in the experiments as moving hard walls had a finite range of motion. When $N<25$, the particles still had sufficient kinetic energy to relocate within the arena at $R=R_{MIN}$, which prevented the identification of topologically stable pattern classes (SI Appendix, section S5). In our experiments, we chose $N=25$ as it was the minimum particle number that generated topologically stable states at the end of the compression. On the other hand, $N>53$ was beyond the maximum close packing of particles within the arena at $R=R_{MIN}$. We expect the upper boundary on $N$ to be in practice even lower for high confinement rates, as this upper bound was calculated in a simulated optimization environment assuming static positions of particles (43), whereas during dynamic confinement particles might be jammed in configurations that physically arrest the moving wall mechanisms before $R_{MIN}$ is achieved. Larger particle sets than we used (i.e., $25<N<53$) might show more numerous and more complex states in the current experimental platform. For example, we would expect to witness topologies with more than three virtual rings or different transition states among the pattern classes. However, larger sets of particles within this range would expectedly require many more realizations of the process to quantify the statistical reprogrammability of longer lists of identified classes, with an increased experimental and computational effort in tracking and analysis currently outside of our capabilities. Nevertheless, since the repeatability, reversibility, and statistical (re)programmability of our system originates from the repulsive interactions between the mobile particles and the dynamic hard boundaries, and not only from our choice of $N$, we expect that experiments with $25<N<53$ would not change the claims of our work but rather only strengthen them. Moreover, an enlarged version of our platform could conceivably host much larger sets of particles to physically validate studies on defect and crystallization programming, which to date have mostly been studied in simulated environments (44, 45). Experiments of long duration or involving complex interaction potentials among nonhomogeneous or nonisotropic sets of particles, whose computational implementation would otherwise be heavy, could be physically realized using our confinement mechanism. Our mechanism can host particles with more complex interaction potentials that can be achieved either by fabricating particles with complex geometries using the 3D printer or embedding multiple magnets inside each particle, also with various orientations. These extensions suggest that our mechanism may be a test bed to reveal physical observations that may be otherwise missed during simulations of self-assembly processes.

We reported reprogrammability using a linear and unsupervised radial confinement profile; however, we expect that the determinism of pattern selection will increase by adding a visual closed-loop control system (8) that tracks the dynamic evolution of the patterns, or a nonlinear control of the arena radius. Results in Fig. 3 C and D also suggest that critical radii exist where certain classes can be programmed with higher determinism, therefore hinting toward more complex, time- and radius-asymmetric confinement profiles. Also, a closed-loop mechanism may allow for the application of machine learning methods for exploring self-assembling pathways and energy landscapes (46, 47) in a physical platform using a manageable set of particles. Besides mechanical properties that depend on the magnetic field, our approach could in principle be extended also to the tuning of optical and electromagnetic properties of functional materials that depend on the spatial configuration of their components (48).

Finally, our confinement and reprogrammable self-assembly mechanisms have potential uses also for larger-scale systems. The confinement system can be used as a transducer to convert the programmable magnetic properties of the granular assembly into variable stiffness and clutching mechanisms. These mechanisms may offer a large set of continuous and reprogrammable mechanical profiles generated by the selection of discrete granular states and may complement existing robotic actuator methods (49). Multiagent distributed robotic systems could also benefit from the dynamic boundary control scheme we presented for assembly formation once our passive particles are replaced by mobile robots (32, 34). Through the programmable boundary control, new robotic functions such as distributed sensing (33) and bioinspired collective locomotion could be generated (35).

Materials and Methods

Particle Design.

Each particle shell (diameter $\rho =5\hspace{0.17em}\text{mm}$, height $h_p=3\hspace{0.17em}\text{mm}$) was 3D-printed (Stratasys Objet 260 Connex) with stiff plastic material (Veroclear RGD810). The 3-mm (diameter) × 2-mm (height) cylindrical core at the center of each particle hosted a permanent NdFeB magnet disk of 3-mm (diameter) × 1-mm (height) size (Supermagnete, N48 grade). We placed all particles within the arena with the same vertical magnetic orientation (i.e., magnetic poles normal to the arena surface) to generate isotropic lateral magnetic repulsion force between the particles. We printed a T-shaped marker on the top surface of the particles (Fig. 1 A, Inset) to track their position and orientation with a high-speed camera (Basler Ace acA800-510uc). The marker did not induce anisotropic particle orientation in the plane of the arena.

Orbital Shaking.

The complete mechanism was mounted on top of the horizontal platform of a frequency-programmable orbital shaker (New Brunswick Innova 2300) with fixed orbital radius $L=12.6\hspace{0.17em}\text{mm}$. The orbital trajectory of every platform point $\left(x,y\right)$ is described by $x\left(t\right)=L\text{cos}\left(\omega t\right)$, $y\left(t\right)=L\text{sin}\left(\omega t\right)$ where $\omega =2\pi f_r$ (orbital radius $L$, shaker frequency $f_r$). Accordingly, the shaker applied a shearing force to all particles equally and synchronously, which scales with their mass $m\cong 0.093$ g and relates to $\ddot{x}\left(t\right)=-L{\omega }^2\text{cos}\left(\omega t\right)$ and $\ddot{y}\left(t\right)=-L{\omega }^2\text{sin}\left(\omega t\right)$.

Particle Tracking.

To track the particles during our experiments, we mounted the high-speed camera over the arena and normal to its surface and attached it to the same, noninertial frame of the programmable orbital shaker. We provided the necessary lighting conditions for the experimental setup to record 360 grayscale images per second (360 frames per second [fps]) with 600-µs shutter speed and 800 × 600 pixel² resolution. For every image, we used MATLAB’s built-in image processing functions to find the position and orientation of the particles via the high-contrast T-shaped markers. We used each particle’s position and velocity vector information to associate consecutive images to each other and track the particles continuously throughout the experiments. Additional information about particle tracking is available in SI Appendix, section S1.

Reversible Confinement Experiments.

We performed 54 experiments, resulting from three repetitions of both compression and decompression for the nine equidistant $R$ values. These values correspond to the particle-to-arena area fraction $\eta \in$ [0.069, 0.078, 0.090, 0.108, 0.132, 0.164, 0.211, 0.281, 0.369]. In all experiments, we waited for the orbital shaking to stabilize at $f_r=6\hspace{0.17em}\text{Hz}$ before proceeding. For a single compression experiment, we started with $R=R_{MAX}\left(\eta =0.069\right)$ and swept toward $R=R_{MIN}\left(\eta =0.369\right)$ with $\dot{R}=11.5\hspace{0.17em}\text{mm/s}$. After reaching each target $R$-value, we stopped the compression and video recorded the motion of the particles for 5 s at a rate of 360 fps. Conversely, for a single decompression experiment, we started with $R=R_{MIN}$ and swept toward $R\hspace{0.17em}=\hspace{0.17em}{R}_{MAX}$ with the same $\left|\dot{R}\right|$ (i.e., $\dot{R}=-11.5\hspace{0.17em}\text{mm/s}$) and repeated the recording procedure. Note that in Fig. 2A we only reported $g\left(r\right)$ for four main $\eta$ values, while Fig. 2B shows the energy results for the complete list of $\eta$. The $g\left(r\right)$ for $\eta =0.369$ in Fig. 2A corresponded to the particle configuration of a class 2 pattern and the parameter $r/\rho$ is the interparticle distance normalized with particle diameter.

Energy Models.

In our experiments, we used the magnetic potential energy and the kinetic energy of the particle system as quantitative metrics while the system was being compressed and decompressed. High-speed particle tracking allowed us to measure the particle positions, orientations, and velocities (both translational and rotational). We approximated the magnetic potential energy $E_U=-\overrightarrow{m_i}\cdot \overrightarrow{B}\left(\overrightarrow{r}\right)$, with the magnetic field $\overrightarrow{B}\left(\overrightarrow{r}\right)$ measured at a distance $\overrightarrow{r}$ from a single magnetic dipole with the moment $\overrightarrow{m_i}$:

$$\overrightarrow{B}\left(\overrightarrow{r}\right)=\frac{{\mu }_0}{4\pi {\left|\overrightarrow{r}\right|}^3}3\left(\overrightarrow{r}/\left|\overrightarrow{r}\right|\right)\left(\left(\overrightarrow{r}/\left|\overrightarrow{r}\right|\right)\cdot \overrightarrow{m_i}\right)-\overrightarrow{m_i}.$$ [1]

In our experiments, each particle had the same magnetic moment $\overrightarrow{m_i}=\left[\begin{array}{ccc}0& 0& B_{r}V/{\mu }_0\end{array}\right]$, where $B_r$ is the flux density ($B_r=1.32\hspace{0.17em}\text{T}$, 3-mm diameter, 1-mm height, N48 grade, Supermagnete; SI Appendix, Fig. S1C), $V$ the volume of the cylindrical magnet $\left(V\cong 7.07\times {10}^{-9}\hspace{0.17em}{m}^3\right)$, and ${\mu }_0$ the permeability of the vacuum $\left({\mu }_0=4\pi \times {10}^{-7}\hspace{0.17em}\text{H/m}\right)$. As the particles were confined in a 2D domain in our experiments, we assumed $\overrightarrow{r}=\left[\begin{array}{ccc}{r}_x& r_y& 0\end{array}\right]$. We calculated the total magnetic potential energy of the particle system by summing up the magnetic field in Eq. 1 for all of the 25 particles (SI Appendix, section S2).

We approximated the kinetic energy $E_K$ of the particle system by summing the translational and rotational kinetic energy of each particle $E_p$ as

$$E_p=\frac{1}{2}m\hspace{0.17em}{v}_p^2+\frac{1}{2}I{w}_p^2,$$ [2]

where m was the particle mass $\left(m\cong 0.093\hspace{0.17em}\text{g}\right)$, $v_p$ the translational velocity in meters per second, $I$ the particle moment of inertia $\left(I\cong 2.17\times {10}^{-10}\hspace{0.17em}\text{kg}\hspace{0.17em}{\text{m}}^2\right)$, and $w_p$ the rotational velocity in radians per second. We calculated the total kinetic energy of the particle system by summing up the particle energy in Eq. 2 for all of the 25 particles.

Statistical Programming.

We performed 100 repetitions for each of the 12 types of experiments. The experiment types differed by the constant value of $\dot{R}\in$ [0.079, 0.175, 0.283, 0.581, 1.172, 2.904, 5.685, 11.180, 20.810, 27.811, 37.832, 39.001] mm/s, while particle count and shaking frequency were fixed respectively at 25 and 6 Hz for all realizations. The time to change $R$ from $R_{MAX}$ to $R_{MIN}$ accordingly varied from 340 s for the lowest $\dot{R}$ to about 0.6 s for the highest (see Movies S3 and S4 for instances of two different experiment types). In the experiments, we waited for the stabilization of the shaking frequency and let the particles move for 3 s at $R=R_{MAX}$ before beginning the compression at the chosen rate. We further waited for 3 s at $R=R_{MIN}$ to register the self-assembled patterns (Fig. 2C). We did not record the complete compression sequence; instead, we recorded the image of the final emergent pattern at $R=R_{MIN}$ after waiting for 3 s.

Topological Pattern Classification.

We defined classes of self-assembled patterns based on the topology of the particles resulting from the complete arresting of their motion at $R=R_{MIN}$. We used the Delaunay triangulation method, which generates a triangular network (i.e., a topology) by connecting a set of points on a 2D plane such that no points in that set remain inside the circumcircle of any triangle. The resulting triangulation is dual to the Voronoi tessellation, wherein the vertices of the Voronoi diagram are the circumcenters of the triangles. This method afforded the representation of particle centroid positions, which existed in a continuous space, using discrete vertex edges, which we referred to as pattern classes. In this method, the relative positions of the particles to each other (i.e., the neighborhood connectivity) were more important than their absolute positions and orientations in 2D space. As long as the connectivity was preserved, particles could be relocated, reoriented, or swapped, or the whole particle assembly could be shrunk, expanded, or rotated. Thus, this topology-based classification allowed for the generalization of the patterns. With this approach, we identified 12 distinct pattern classes among the 1,200 examples of patterns observed in the experiments. In every pattern, the particles organized in a virtual three-shell structure (Figs. 1D and 2C). We described the radius of a virtual shell as the radius of the largest circle that fit the centroids of the particles residing on that shell. We referred to the radii of the three shells making up the self-assembled pattern with the minimal magnetic potential energy in the experiments as the heuristic template. Unlike the Delaunay triangulation, the heuristic template considered the absolute centroid positions of the particles concerning the three shells in Fig. 1D. We used the heuristic template in addition to the Delaunay triangulation to complete the definition of a pattern class and identify metastable patterns. Additional information about classification is available in SI Appendix, section S6.

Pattern Stability Analysis.

We selected the four topmost-occurring classes using the value of $\dot{R}$ that yielded the highest programmability for each class with $f_r=6\hspace{0.17em}\mathrm{Hz}$ (i.e., $\dot{R}=5.685\hspace{0.17em}\text{mm/s}$ for class 1, 0.079 mm/s for class 2, 39.001 mm/s for class 3, and 0.175 mm/s for class 4). After the selection, we decompressed the arena by changing $R$ from $R_{MIN}$ to $R_{MAX}$ with $\dot{R}=-\text{0}.28\hspace{0.17em}\text{mm/s}$ (i.e., the $\dot{R}$ for which all of the top four classes were selectable, shown with the black triangle in Fig. 3C). We tracked the progression of the patterns with the triangulation and the heuristic templates while the arena was expanding. We updated the three-shell radii along with the increasing $R$ of the arena. We repeated the experiments three times for each class and reported the average of the particle counts on each ring location during the decompression until $\mathrm{\Delta }R/\rho =2$ (i.e., $R=30.5\hspace{0.17em}\text{mm}$).

Quantification of Particle Pattern Stiffness.

We performed 20 experiments with 25 particles, resulting from five repetitions for each of the four most frequently occurring classes. For each class, we first selected the pattern at $R_S=R_{MIN}+\mathrm{\Delta }d$, with $\mathrm{\Delta }d=2.6\hspace{0.17em}\text{mm}$, using the $\dot{R}$ that yielded the highest $P\left(c\right)$. For $R=R_S$ the pattern of the top classes was not completely solidified and it did also not evolve into any other pattern, as the particles did not have enough space to relocate. After pattern selection, we stopped the shaking and continued the arena compression across $\mathrm{\Delta }d$ using $\dot{R}=\text{0}.079\hspace{0.17em}\text{mm/s}$ for ∼27 s. We stopped the compression at $R=R_{MIN}+0.5$mm. We waited for 3 s both before the compression started and after it ended. We recorded the particle positions for 33 s at a frame rate of 60 fps. Additional information about the pattern stiffnesses is available in SI Appendix, section S8.

Quantification of the Magnetic Clutch Torque.

We embedded the magnets inside 21-mm-radius, 5-mm-thick circular acrylic plates (Plexiglas; Evonik) at the particle positions corresponding to the self-assembled class patterns reported in Fig. 2C. We fabricated three distinct rotating arms, each housing a magnet at a distance d = 5 mm, 10 mm, and 15 mm from the axis of rotation of the arm (Fig. 4A). The rotation axis of the arm was aligned with the center of the arena. We placed the pattern disks and the rotating scanner arm in a rheometer setup (DHR-3; TA Instruments) and recorded the torque measurements. We varied the vertical gap between the pattern disk and the rotating arm from h = 1 mm to 3 mm and 5 mm. We rotated each arm three times (i.e., three complete rotations from $\mathrm{\Theta }=\text{0}-2\mathrm{\pi }$) over the pattern disks for each $h$ and reported the average torque measurements. Each line in Fig. 4D shows the sum of torques for each arm at the specific vertical gap $h$. All magnets used in the pattern disks and the rotating arms were identical to the NdFeB permanent magnets embedded inside the particles. Additional information about torques for different classes is available in the SI Appendix, section S9.

Data Availability.

All data, materials, and associated methods that support the findings of this study are shown in Materials and Methods and SI Appendix.