Adjusted Time-varying Population Attributable Hazard in Case-Control Studies

Abstract

Population attributable fraction (PAF) is a widely used measure for quantifying the disease burden associated with a modifiable exposure of interest at the population level. It has been extended to a time-varying measure, population attributable hazard (PAH) function, to provide additional information on when and how the exposure’s impact varies over time. However, like the classic PAF, the PAH is generally biased if confounders are present. In this article, we provide a natural definition of adjusted PAH to take into account the effects of confounders, and its alternative that is identifiable from case-control studies under the rare disease assumption. We propose a novel estimator, which combines the odds ratio estimator from logistic regression model, and the conditional density function estimator of the exposure and confounding variables distribution given the failure times of cases or the current times of controls from a kernel smoother. We show that the proposed estimators are consistent and asymptotically normal with variance that can be estimated empirically from the data. Simulation studies demonstrate that the proposed estimators perform well in finite sample sizes. Finally, we illustrate the method by an analysis of a case-control study of colorectal cancer. Supplementary materials for this article are available online.

1. Introduction

For evidence-based disease prevention, the population attributable fraction (PAF) has been widely used as an indispensable metric to assess the impact of modifiable exposures on disease burden in populations to help plan and prioritize public health strategies^1,2. First introduced by Levin³, the PAF is defined as the proportion of potential preventable disease cases, had the exposure been eliminated. Compared to association measures such as relative risk or rate ratio, the PAF is a more appropriate epidemiological measure for quantifying the population impact because it integrates both the strength of association between the exposure and the disease and the prevalence of the exposure. The implication, estimation, and application of the PAF have been extensively studied for various epidemiological sampling designs, see, for example, Walter⁴, Whittemore⁵, Greenland⁶, Benichou and Gail⁷, Benichou^8,9, Kooperberg and Petitti¹⁰.

PAF is a static measure, which evaluates the impact of exposure on binary disease outcome. In practice, mortality and morbidity incidences are often recorded as time-to-events. Therefore, rather than Levin’s PAF, a time-varying PAF can help researchers and policy makers better understand how the impact of risk exposure on disease varies over time, and provide guidance on the timing of actions or interventions. Recently, extensions of the PAF to right-censored failure time have been proposed, including the time-dependent population attributable hazard function (PAH)^11-13 and time-dependent population attributable disease probability^14-18. In survival analysis, the hazard function is a key concept that quantifies the impact of risk factors on the rate of developing the disease among subjects at risk at time t. Here we focus on the PAH because it directly assesses the instantaneous effect of eliminating risk factors on the hazard function.

Specifically, let T be the failure time and Z = (Z₁, …, Z_p)^T be a p-vector of time-independent risk factors, then the PAH¹¹ is defined as

$$\varphi (t)=\frac{\lambda (t)-\lambda (t\mid \mathrm{Z}=0)}{\lambda (t)},$$ (1)

where λ(t) is the hazard function for the population of interest, which is the instantaneous rate of failing at time t, that is, λ(t) = lim_δt→0 Pr(t < T ≤ t + δt)/Pr(T > t); and λ(t∣Z = 0) is the conditional hazard function given Z = 0. Estimation of λ(t) requires estimates of hazard ratios, for which methods are well established for cohort data¹⁹, and estimates of the distribution of exposure and failure time^11,15.

In the past several decades, the case-control study design is one of the most commonly used designs in epidemiological cancer research, because of its efficiency in logistic conduct, time and cost. In particular, Anderson²⁰ and Prentice and Pyke²¹ provided theoretical basis that under the rare disease assumption the relative risk of exposure on disease occurrence can be obtained from the retrospective case-control data as if they were prospectively collected under the logistic regression model. For the time-to-event outcome, the hazard ratios under the Cox proportional hazards model can also be obtained from the (time-matched) case-control data²². As a result, many case-control studies have been conducted. For example, in our motivating real data example, the Genetics and Epidemiology Colorectal Cancer Consortium (GECCO) is consisted of dozens of well-characterized case-control studies of colorectal cancer where extensive risk factor information has been collected. It is therefore important to make use of these rich data when estimating the PAH. Bruzzi et al.²³ showed that if one has the relative risk estimates, the PAF can be obtained from the distribution of exposure among the cases only. In a similar fashion, for time-varying PAH, Zhao et al.¹³ showed at any specific time t, PAH can be estimated consistently with the hazards ratio estimated from case-control data²² and the conditional distribution of exposure estimated from the cases at time t.

Confounders are nevertheless ubiquitous in observational studies. If they were not properly accounted for, the association of exposure of interest and outcome and the PAF would be biased and could be misleading in some situations^4,24. The unadjusted PAH proposed by Zhao et al.¹³ has the same issue. For instance, obesity is a potential confounder for the association between diabetes and colorectal cancer, because obese patients are more likely to have diabetes²⁵ and also more likely to develop colorectal cancer²⁶. Thus, without adjusting for obesity, the preventable effect of eliminating diabetes may be overestimated. Therefore, in order for the estimated PAH to have a meaningful interpretation, it is necessary to adjust for confounders. To this end, a natural generalization of the confounder-adjusted PAF for binary outcome⁸ to time-to-event outcome is to substitute λ(t∣Z = 0) in (1) by ${\tilde{\mathrm{E}}}_{\mathrm{U}\mid T\ge t}\{\lambda (t\mid \mathrm{Z}=0,\mathrm{U})\}$, where U are confounding variables and ${\tilde{\mathrm{E}}}_{\mathrm{U}\mid T\ge t}$ is the expectation of U given the subject at risk at time t in a ideal population where Z is eliminated at baseline. However, this quantity is not identifiable from case-control data because cases are over-sampled and the distribution of (Z, U) in the sample does not reflect the distribution in the population.

The goal of the paper is to provide an alternative adjusted PAH that approximates well to ${\tilde{\mathrm{E}}}_{\mathrm{U}\mid T\ge t}$ under the rare disease assumption, and a novel kernel-based estimator integrating the information from both cases and controls. The rest of this article is organized as follows: in Section 2, we lay out the basic formulation and the kernel-based estimator for the adjusted PAH for case-control data. We establish the large sample properties and provide asymptotic-based variance estimators. In Section 3, we present simulation studies and the performance of the proposed estimator in finite sample sizes. We show an application of the proposed estimator to a case-control study of colorectal cancer in Section 4. Finally, we provide some concluding remarks in Section 5. Some technical details are included in the appendices.

2. Formulation and Inference

2.1. Definition of Population Attributable Hazard Function Adjusting for Confounders

We first describe the data and notation. Consider a case-control study which consists of n₁ cases and n₂ controls, in total n (n = n₁ + n₂) subjects. Let Δ be the binary disease status (1: case and 0: control) and X = min(T, C) be the observed age, which is the age-at-onset i.e. failure time T if the individual is diseased (case) and age at examination i.e. censoring time C if the individual is not diseased (control). Further we denote Z a vector of time-independent covariates, which are of interest, and U a vector of time-independent confounders. We are interested in the proportion of the time-varying hazard attributed to Z while adjusting for potential confounders U.

Before we describe the PAH, we first review classic model-based adjusted PAF for binary disease status in the presence of confounders. Suppose the vector of time-independent confounders U form J levels and time-independent covariate of interest Z has I + 1 levels, then the adjusted PAF^5,23 is defined as

$$\begin{gathered} \text{PAF}=\frac{P(\Delta =1)-{\sum }_{j=1}^{J}P(\Delta =1\mid \mathrm{Z}=0,\mathrm{U}={\mathrm{u}}_j)P(\mathrm{U}={\mathrm{u}}_j)}{P(\Delta =1)} \\ =1-\sum _{j=1}^J\sum _{i=0}^I\frac{P(\mathrm{Z}={\mathrm{z}}_i,\mathrm{U}={\mathrm{u}}_j\mid \Delta =1)}{R{R}_{i\mid j}} \end{gathered}$$ (2)

where RR_i∣j = P(Δ = 1→Z = z_i, U = u_j)/P(Δ = 1∣Z = 0, U = u_j). The re-expression of the PAF in the second equation as a function of f(Z, U∣Δ) and RR indicates that both quantities can be estimated from the retrospectively collected case-control data under the rare disease assumption. As a result the adjusted PAF can also be estimated from case-control data.

Now we turn to the PAH. Let E denote the expectation with respect to the target population from which cases and controls are sampled, and $\tilde{\mathrm{E}}$ denote the expectation with respect to a ideal population in which exposure Z was eliminated at baseline. Let λ(t) be the hazard function of failure time T for the target population and λ{t∣Z = 0, U} be the hazard function of T given Z = 0 and U. In the same spirit as the adjusted PAF, we define a natural PAH of Z in the presence of U as

$${\Phi }_{adj}(t)=\frac{\lambda (t)-{\tilde{\mathrm{E}}}_{\mathrm{U}\mid T\ge t}\{\lambda (t\mid \mathrm{Z}=0,\mathrm{U})\}}{\lambda (t)},$$ (3)

which is the proportion of reduction of the hazard at time t from the current population to the ideal population that Z is eliminated at baseline, accounting for confounders U. The conditional expectation ${\tilde{\mathrm{E}}}_{\mathrm{U}\mid T\ge t}$ with respect to the ideal population is taken over U among subjects at risk at time t. Note that this can be obtained based on ${\tilde{\mathrm{E}}}_{\mathrm{U}\mid T\ge t}[\lambda \{t\mid \mathrm{Z}=0,\mathrm{U}\}]={\tilde{\mathrm{E}}}_{\mathrm{U}}[f(T=t\mid \mathrm{Z}=0,\mathrm{U})]∕{\tilde{\mathrm{E}}}_{\mathrm{U}}[\text{Pr}(T\ge t\mid \mathrm{Z}=0,\mathrm{U})]\text{if}\lambda \{t\mid \mathrm{Z},\mathrm{U}\}$ and the distribution function F_U(u) at the baseline are known, as ${\tilde{\mathrm{E}}}_{\mathrm{U}}$ is the expectation taken over U at baseline.

Comparing (3) with the adjusted PAF (2), we see that in Φ_adj(t), the probability of being diseased is replaced with the hazard function at time t, and the probability mass function of confounders is replaced with the density of confounders for subjects who are at risk at time t in the ideal population. Thus, Φ_adj(t) can be regarded as the instantaneous evaluation of the confounder-adjusted PAF at t, and measures the impact on the disease development at time t due to eliminating exposure at baseline after taking into account confounding.

However, in case-control studies where cases are over sampled, λ{t∣Z, U} and the baseline distribution function of (Z, U) are not estimable, and thus, Φ_adj(t) can not be identified. Here we provide an alternative that is identifiable from the case-control data. The definition is as follows:

$${\varphi }_{adj}(t)=\frac{\lambda (t)-{\mathrm{E}}_{\mathrm{U}\mid T\ge t}\{\lambda (t\mid \mathrm{Z}=0,\mathrm{U})\}}{\lambda (t)}.$$ (4)

It is worth noting that while E_U∣T≥t is taken with respect to the original (natural history) population conditional on {T ≥ t} in this original population, the expectation ${\tilde{\mathrm{E}}}_{\mathrm{U}\mid T\ge t}$ is conditional on {T ≥ t} with respect to an ideal population. The difference between the original and ideal populations is that at baseline subjects who have exposure in the original population are free of exposure in the ideal population. Now let f(u∣T ≥ t) and $\tilde{f}(\mathrm{u}\mid T\ge t)$ be the density functions of U conditional on T ≥ t in the original and ideal populations, respectively. Under the rare disease assumption, both density functions are approximately f(u), which implies ϕ_adj(t) ≈ Φ_adj(t).

To check the sensitivity of this approximation to the rare disease assumption, we calculated the differences of ϕ_adj(t) and Φ_adj(t) numerically under a wide range of scenarios. When the disease probability Pr(T < 70) ≤ 0.05, ϕ_adj(t) approximates well Φ_adj(t) with absolute differences below 0.05 for the vast majority scenarios. When the disease probability increases, additional parameter restrictions (e.g., log-hazard ratio for the confounder < 2 when 0.05 < Pr(T < 70) ≥ 0.1) need to be imposed for a good approximation. Appendix E shows more detailed results of the approximation of ϕ_adj(t) and Φ_adj(t). In real-data-based simulations in Section 3 and 4.2, the difference between the two is no more than several thousandths across a very wide range of t. Thus ϕ_adj(t) can be a promising alternative to Φ_adj(t) for accommodating the case-control data. We focus on ϕ_adj(t) in this article.

Assume the effects of Z and U on the hazard function of the failure time T follow the Cox proportional hazards model ²⁷,

$$\lambda (t\mid \mathrm{Z},\mathrm{U})={\lambda }_0(t)\text{exp}({\beta }^T\mathrm{Z}+{\gamma }^T\mathrm{U}),$$ (5)

where β = (β₁, ⋯, β_p)^T is a vector of regression parameters for Z, γ = (γ₁, ⋯, γ_q)^T is a vector of regression parameters for U, and λ₀(t) is the baseline hazard function. For the target population, let F_U∣T≥t(u) be the distribution function of confounders U of subjects who are disease-free at time t with the corresponding density function f_U∣T≥t(u) if U is continuous, and $\mathcal{U}$ be the space for U (i.e., Pr{U ∈ $\mathcal{U}$} = 1). Similarly we denote F_Z∣T(z∣t) and F_Z∣T(z∣t) the distribution function and the density function of Z given T = t, respectively, F_Z,U∣T≥t(z, u) and f_Z,U∣T≥t the joint distribution function and the joint density function of Z and U given T ≥t, respectively, and $\mathcal{Z}$ the space for Z.

By using the relationship λ(t) = f_T(t)/S_T(t) and applying the total probability theorem on S_T(t), we can express as ϕ_adj(t) as

$$\begin{gathered} {\varphi }_{adj}(t)=1-\frac{{\int }_{\mathcal{U}}\lambda (t\mid \mathrm{Z}=0,\mathrm{u})d{F}_{\mathrm{U}\mid T\ge t}(\mathrm{u})}{\lambda (t)} \\ =1-\frac{{\lambda }_0(t)}{\lambda (t)}{\int }_{\mathcal{U}}\text{exp}({\gamma }^T\mathrm{u})f_{\mathrm{U}\mid T\ge t}(\mathrm{u})d\mathrm{u}. \\ =1-{\left\{{\int }_{\mathcal{U}}{\int }_{\mathcal{Z}}\text{exp}({\beta }^T\mathrm{z}+{\gamma }^T\mathrm{u})f_{\mathrm{Z},\mathrm{U}\mid T\ge t}(\mathrm{z},\mathrm{u})d\mathrm{z}d\mathrm{u}\right\}}^{-1}{\int }_{\mathcal{U}}\text{exp}({\gamma }^T\mathrm{u})f_{\mathrm{U}\mid T\ge t}(\mathrm{u})d\mathrm{u}. \end{gathered}$$ (6)

The above equation explicitly show the impact of U. For example, when β = 0, ϕ_adj(t) = 0 for all t. When γ = 0, we have ϕ_adj(t) = ϕ(t) the unadjusted PAH. Furthermore, we have

$$\begin{gathered} {\int }_{\mathcal{U}}\text{exp}({\gamma }^T\mathrm{u})f_{\mathrm{U}\mid T\ge t}(\mathrm{u})d\mathrm{u}={\int }_{\mathcal{U}}\text{exp}({\gamma }^T\mathrm{u}){\int }_{\mathcal{Z}}{f}_{\mathrm{Z},\mathrm{U}\mid T\ge t}(\mathrm{z},\mathrm{u})d\mathrm{z}d\mathrm{u} \\ ={\int }_{\mathcal{U}}{\int }_{\mathcal{Z}}\text{exp}({\gamma }^T\mathrm{u}+{\beta }^T\mathrm{z})\text{exp}(-{\beta }^T\mathrm{z})f_{\mathrm{Z},\mathrm{U}\mid T\ge t}(\mathrm{z},\mathrm{u})d\mathrm{z}d\mathrm{u} \\ ={\int }_{\mathcal{U}}{\int }_{\mathcal{Z}}\frac{f_{T\mid \mathrm{Z},\mathrm{U}}(t\mid \mathrm{z},\mathrm{u})}{S(t\mid \mathrm{z},\mathrm{u}){\lambda }_0(t)}\text{exp}(-{\beta }^T\mathrm{z})f_{\mathrm{Z},\mathrm{U}\mid T\ge t}(\mathrm{z},\mathrm{u})d\mathrm{z}d\mathrm{u} \\ ={\int }_{\mathcal{U}}{\int }_{\mathcal{Z}}\frac{f_{T,\mathrm{Z},\mathrm{U}}(t,\mathrm{z},\mathrm{u})}{S(t){\lambda }_0(t)}\text{exp}(-{\beta }^T\mathrm{z})d\mathrm{z}d\mathrm{u} \\ =\frac{f_T(t)}{S(t){\lambda }_0(t)}{\int }_{\mathcal{U}}{\int }_{\mathcal{Z}}\text{exp}(-{\beta }^T\mathrm{z})f_{\mathrm{Z},\mathrm{U}\mid T}(\mathrm{z},\mathrm{u}\mid t)d\mathrm{z}d\mathrm{u} \\ =\frac{\lambda (t)}{{\lambda }_0(t)}{\int }_{\mathcal{Z}}\text{exp}(-{\beta }^T\mathrm{z})f_{\mathrm{Z}\mid T}(\mathrm{z}\mid t)d\mathrm{z}, \end{gathered}$$

and thus we can also express (6) as

$${\varphi }_{adj}(t)=1-{\int }_{\mathcal{Z}}\text{exp}(-{\beta }^T\mathrm{z})f_{\mathrm{Z}\mid T}(\mathrm{z}\mid t)d\mathrm{z}.$$ (7)

Equation (7) involves hazard ratios and conditional distribution of Z given T = t, i.e. cases who develop disease at time t. Complementary to (7), equation (6) involves hazard ratios and conditional distributions of (Z^T, U^T)^T and U given T > t, i.e., controls who are disease-free at time t.

2.2. Estimation and Large Sample Properties

Now we describe estimation of ϕ_adj(t) on the basis of (6) and (7) from case-control data. It is well established that if cases and controls are time-matched, hazard ratio parameters θ = (β^T, γ^T)^T can be consistently estimated by maximizing conditional likelihood function with logistic regression model²². For unmatched case-control studies, θ can be estimated by the convention maximum likelihood of a logistic regression model with time adjusted as a covariate. The approximation is generally not consistent, but yields little bias in practice. We denote the hazard ratio estimates by $\widehat{\theta }=({\widehat{\beta }}^T,{\widehat{\gamma }}^T)$. For ϕ_adj(t), what remains to be estimated is the conditional distribution function F_V∣T(v∣t) and F_V∣T≥t(v). Here V represents Z, U, or (Z^T, U^T)^T.

Under the random censoring assumption that the censoring time is independent of the failure time, exposures and confounders as derived in Xu and O’Quigley²⁸, we can show that F_V∣T (v∣t) equals to F(v∣T = t, T ≤ C) = P{V ≤ v∣T = t, T ≤ C}, which can be estimated from the cases, and F_V∣T≥t(v) equals to F(v∣C = t, T ≥ C) = P{V ≤ v∣C = t, T ≥ C}, a quantity that can be estimated from the controls. Therefore, either F_V∣T (v∣t) or F_V∣T≥t(v) can be estimated by its empirical estimator. However, these empirical estimators would have poor performance because of few subjects observed at time t. To improve the performance, we use a kernel smoother to estimate these distribution functions. Let

$$\begin{gathered} \phi (t)={\int }_{\mathcal{Z}}exp(-{\beta }^T\mathrm{z})f_{\mathrm{Z}\mid T}(\mathrm{z}\mid t)d\mathrm{z}, \\ \psi (t)={\int }_{\mathcal{U}}{\int }_{\mathcal{Z}}exp({\beta }^T\mathrm{z}+{\gamma }^T\mathrm{u})f_{\mathrm{Z},\mathrm{U}\mid T\ge t}(\mathrm{z},\mathrm{u})d\mathrm{z}d\mathrm{u}, \\ v(t)={\int }_{\mathcal{U}}\text{exp}({\gamma }^T\mathrm{u})f_{\mathrm{U}\mid T\ge t}(\mathrm{u})d\mathrm{u}. \end{gathered}$$

Then ϕ_adj(t) can be expressed as ϕ_adj(t) = 1 – φ(t) or ϕ_adj(t) = 1 – ψ⁻¹(t)v(t).

Consider n subjects in a case-control study. Let X_i, Δ_i, Z_i and U_i be the observed time, the censoring indicator, the exposure and confounders, respectively, for i = 1, …, n. Assume that {(X_i, Δ_i, Z_i, U_i), i = 1, …, n} are independently and identically distributed. We propose the following estimators for φ(t), ψ(t), and v(t), respectively:

$$\begin{gathered} \widehat{\phi }(t;\widehat{\beta })=\frac{{\sum }_{i=1}^n\text{exp}(-{\widehat{\beta }}^T{\mathrm{Z}}_i){\Delta }_i{K}_h(t-X_i)}{{\sum }_{i=1}^n{\Delta }_i{K}_h(t-X_i)}, \\ \widehat{\psi }(t;\widehat{\beta },\widehat{\gamma })=\frac{{\sum }_{i=1}^n\text{exp}({\widehat{\beta }}^T{\mathrm{Z}}_i+{\widehat{\gamma }}^T{\mathrm{U}}_i)(1-{\Delta }_i)K_h(t-X_i)}{{\sum }_{i=1}^n(1-{\Delta }_i)K_h(t-X_i)}, \\ \widehat{v}(t;\widehat{\gamma })=\frac{{\sum }_{i=1}^n\text{exp}({\widehat{\gamma }}^T{\mathrm{U}}_i)(1-{\Delta }_i)K_h(t-X_i)}{{\sum }_{i=1}^n(1-{\Delta }_i)K_h(t-X_i)}, \end{gathered}$$

where K_h(x) = K(x/h)/h, K(·) is a kernel function that is a weighting function that satisfies ∫ K(x)dx = 1, and h is the bandwidth that controls the spread of weighting window.

We propose two estimators for ϕ_adj(t), corresponding to equations (7) and (6), respectively:

$${\widehat{\varphi }}_{adj+}(t;\widehat{\beta })=1-\widehat{\phi }(t;\widehat{\beta }),$$ (8)

and

$${\widehat{\varphi }}_{adj-}(t;\widehat{\beta },\widehat{\gamma })=1-{\widehat{\psi }}^{-1}(t;\widehat{\beta },\widehat{\gamma })\widehat{v}(t;\widehat{\gamma }).$$ (9)

Since the kernel estimators of ${\widehat{\varphi }}_{adj+}(t;\widehat{\beta })$ and ${\widehat{\varphi }}_{adj-}(t;\widehat{\beta },\widehat{\gamma })$ are based on cases and controls separately, combining the two estimators could potentially improve the efficiency. We therefore propose a weighted estimator as follows:

$${\widehat{\varphi }}_{adjw}(t;\widehat{\beta },\widehat{\gamma })=w(t){\widehat{\varphi }}_{adj+}(t;\widehat{\beta })+\{1-w(t)\}{\widehat{\varphi }}_{adj-}(t;\widehat{\beta },\widehat{\gamma }).$$

where w(t) is a weighting function with value between 0 and 1. A natural choice of the weight is iw(t) = πq, which is proportion of cases in the sample. Then the weighted estimator is

$${\widehat{\varphi }}_{adjw}(t;\widehat{\beta },\widehat{\gamma })={\pi }_0{\widehat{\varphi }}_{adj+}(t;\widehat{\beta })+(1-{\pi }_0){\widehat{\varphi }}_{adj-}(t;\widehat{\beta },\widehat{\gamma }).$$ (10)

Next we derive the asymptotic properties of ${\widehat{\varphi }}_{adjw}(t;\widehat{\beta },\widehat{\gamma })$. Assume the number of cases n₁ and the total number of subjects n satisfy n₁/n → π₀ as n → ∞, where 0 < π₀ < 1. In addition, we assume the following regularity conditions:

A1. The time t is in a range of [0, τ] for a constant τ > 0 such that the density of failure time f_T(t), the density of censoring time f_C(t) and their survival functions, S_T(t) and S_C(t) all take positive real values on [0, τ].

A2. The density of failure time f_T(t) and the density of censoring time f_C(t) are both continuous, uniformly bounded, and have second derivatives on [0, τ].

A3. Random censoring: the censoring time C is independent of the failure time T, exposure Z and confounder U for t ∈ [0, τ].

A4. The bandwidth satisfies h = n^dh₀ for constants −1/2 < d < −1/5 and h₀ > 0.

A5. The kernel function K(·) has bounded variation and satisfies the following conditions,

$$\begin{gathered} {\int }_{-\infty }^{\infty }K(u)d\mathrm{u}=1,{\int }_{-\infty }^{\infty }{K}^2(u)d\mathrm{u}<\infty , \\ {\int }_{-\infty }^{\infty }uK(u)d\mathrm{u}=0,{\int }_{-\infty }^{\infty }{u}^{2}K(u)d\mathrm{u}<\infty . \end{gathered}$$

A6. Z and U are bounded almost surely and have uniformly bounded total variation on [0, τ].

We define the following notation.

$$\begin{gathered} B_n(t)=\frac{1}{n}\sum _{i=1}^n{\Delta }_i{K}_h(t-X_i), \\ {\mathrm{D}}_n(t;\beta )=\frac{1}{n}\sum _{i=1}^n{\Delta }_i{K}_h(t-X_i){\mathrm{Z}}_i\text{exp}(-{\beta }^T{\mathrm{Z}}_i), \\ {\overline{A}}_n(t;\beta ,\gamma )=\frac{1}{n}\sum _{i=1}^n(1-{\Delta }_i)K_h(t-X_i)\text{exp}({\beta }^T{\mathrm{Z}}_i+{\gamma }^T{\mathrm{U}}_i), \\ {\overline{B}}_n(t)=\frac{1}{n}\sum _{i=1}^n(1-{\Delta }_i)K_h(t-X_i), \\ {\overline{\mathrm{D}}}_n(t;\theta )=\frac{1}{n}\sum _{i=1}^n(1-{\Delta }_i)K_h(t-X_i){\mathrm{V}}_i\text{exp}({\theta }^T{\mathrm{V}}_i), \\ {\overline{\mathrm{G}}}_n(t;\gamma )=\frac{1}{n}\sum _{i=1}^n(1-{\Delta }_i)K_h(t-X_i){\mathrm{U}}_i\text{exp}({\gamma }^T{\mathrm{U}}_i). \end{gathered}$$

We use P₀ and E₀ to denote the probability and expectation with respect to the target population from which cases and controls are sampled. As shown in Appendix A and B, it is also useful to regard cases and controls as members of a second, hypothetical population of individuals whose disease probability is given by π₀¹³. We use P* and E* to denote the probability and expectation with respect to this hypothetical population. Let p₀ = P₀(T ≤ C), π₀ = P*(T ≤ C). Denote the limits of B_n(t), D_n(t; β), ${\overline{A}}_n(t;\beta ,\gamma )$, ${\overline{B}}_n(t)$, ${\overline{\mathrm{D}}}_n(t;\theta )$ and ${\overline{\mathrm{G}}}_n(t;\gamma )$ by B(t), D(t;β), $\overline{A}(t)$, $\overline{B}(t)$, $\overline{\mathrm{D}}(t;\theta )$ and $\overline{\mathrm{G}}(t;\gamma )$ the detailed expressions of which can be found in Appendix A. The main results, namely consistency and asymptotic normality of the proposed estimators, are summarized in the following two theorems.

Theorem 1. Consistency. Suppose assumptions A1-A6 are satisfied. Then as n → ∞, ${\widehat{\varphi }}_{adj+}(t;\widehat{\beta })$, ${\widehat{\varphi }}_{adj-}(t;\widehat{\beta },\widehat{\gamma })$ and ${\widehat{\varphi }}_{adjw}(t;\widehat{\beta },\widehat{\gamma })$ are uniformly consistent for ϕ_adj(t; β₀, γ₀) for t ∈ [0, τ], where ϕ_adj(t; β₀, γ₀) is the true value of ϕ_adj(t) defined in (4) under the Cox proportional hazards model (5).

Theorem 2. Asymptotic Normality. Suppose assumptions A1-A6 are satisfied. Then

$$\sqrt{nh}\{{\widehat{\varphi }}_{adj+}(t;\widehat{\beta })-{\varphi }_{adj}(t;{\beta }_0,{\gamma }_0)\}{\to }_{d}N(0,{\sigma }_{+}^2(t)),\text{for}t\in [0,\tau ],$$

where the limiting variance ${\sigma }_{+}^2(t)=\int K^2(u)du\int \{\text{exp}(-{\beta }_0^T\mathrm{z})-{\varphi }_{adj}(t;{\beta }_0,{\gamma }_0){\}}^{2}d{F}_{\mathrm{Z}\mid T}(\mathrm{z})/B(t)$. We also have

$$\sqrt{nh}\{{\widehat{\varphi }}_{adj-}(t;\widehat{\beta },\widehat{\gamma })-{\varphi }_{adj}(t;{\beta }_0,{\gamma }_0)\}{\to }_{d}N(0,{\sigma }_{-}^2(t)),\text{for}t\in [0,\tau ],$$

where the limiting variance ${\sigma }_{-}^2(t)=\overline{B}(t){\overline{A}}^{-2}(t)\int K^2(u)du\int \int \{\text{exp}({\gamma }_0^T\mathrm{u})-{\psi }^{-1}(t)v(t)$ $\text{exp}({\beta }_0^T\mathrm{z}+{\gamma }_0^T\mathrm{u}){\}}^2{f}_{\mathrm{Z},\mathrm{U}\mid T\ge t}(\mathrm{z},\mathrm{u})d\mathrm{z}d\mathrm{u}$. The asymptotic normality of the weighted estimator ${\widehat{\varphi }}_{adjw}(t;\widehat{\beta },\widehat{\gamma })$ then follows, that is, $\sqrt{nh}\{{\widehat{\varphi }}_{adjw}(t;\widehat{\beta },\widehat{\gamma })-{\varphi }_{adj}(t;{\beta }_0,{\gamma }_0)\}{\to }_{d}N(0,{\sigma }_w^2(t))$ for t ∈ [0, τ], where ${\sigma }_w^2(t)={\pi }_0^2{\sigma }_{+}^2(t)+(1-{\pi }_0{)}^2{\sigma }_{-}^2(t)$.

The proofs of Theorem 1 and 2 are provided in Appendix A and B.

2.3. Variance Estimation with Correction for Finite Sample

One natural estimator for ${\sigma }_{+}^2(t)$, ${\sigma }_{-}^2(t)$ or ${\sigma }_w^2(t)$, denoted as ${\widehat{\sigma }}_{+}^2(t),{\widehat{\sigma }}_{-}^2(t)$ and ${\pi }_0^2{\widehat{\sigma }}_{+}^2(t)+(1-{\pi }_0{)}^2{\widehat{\sigma }}_{-}^2(t)$, can be obtained by replacing the expectation components with the corresponding empirical estimators, and replacing parameters (β^T, γ^T) with their estimators. However, variance estimates relying solely on the asymptotic results may perform poorly due to the slow vanishing rate of $\sqrt{h}$. In fact, in real practice with finite samples, $\sqrt{h}$ might not be close to zero even with large sample size. In this case some components in $\sqrt{nh}\{{\widehat{\varphi }}_{adj+}(t;\widehat{\beta })-{\varphi }_{adj}(t;{\beta }_0,{\gamma }_0)\}$, $\sqrt{nh}\{{\widehat{\varphi }}_{adj-}(t;\widehat{\beta },\widehat{\gamma })-{\varphi }_{adj}(t;{\beta }_0,{\gamma }_0)\}$, and $\sqrt{nh}\{{\widehat{\varphi }}_{adjw}(t;\widehat{\beta },\widehat{\gamma })-{\varphi }_{adj}(t;{\beta }_0,{\gamma }_0)\}$ cannot be ignored even though their asymptotic contribution to the overall variance is negligible. Instead, we need to consider their contributions to the asymptotic results by taking the bandwidth h as a known non-zero constant. The variance estimators with finite sampling correction are

$$\begin{gathered} {\widehat{\sigma }}_{+}^{\ast 2}(t;h)={\widehat{\sigma }}_{+}^2(t)+h{\mathrm{D}}_n(t;\widehat{\beta }{)}^T{\widehat{\mathrm{I}}}^{-1}(\widehat{\beta }){\mathrm{D}}_n(t;\widehat{\beta })∕B_n^2(t) \\ +\frac{2h}{n}\sum _{i=1}^n{\Delta }_i{K}_h(t-X_i)\{1-{\widehat{\varphi }}_{adj+}(t;\widehat{\beta })-exp(-{\widehat{\beta }}^T{\mathrm{Z}}_i)\}{\widehat{\mathrm{l}}}_{\beta }(X_i{)}^T{\mathrm{D}}_n(t;\widehat{\beta })∕B_n^2(t), \\ {\widehat{\sigma }}_{-}^{\ast 2}(t;h)={\widehat{\sigma }}_{-}^2(t)+\frac{h}{n}\sum _{i=1}^n[{\widehat{\mathrm{l}}}_{\gamma }(X_i{)}^T{\overline{\mathrm{G}}}_n(t;\widehat{\gamma })-\{1-{\widehat{\varphi }}_{adj-}(t;\widehat{\beta },\widehat{\gamma })\}{\widehat{\mathrm{l}}}_{\theta }(X_i{)}^T{\overline{\mathrm{D}}}_n(t;\widehat{\theta }){]}^2∕{\overline{A}}_n^2(t;\widehat{\beta },\widehat{\gamma }) \\ +\frac{2h}{n}\sum _{i=1}^n(1-{\Delta }_i)K_h(t-X_i)\left[\text{exp}({\widehat{\gamma }}^T{\mathrm{U}}_i)-\{1-{\widehat{\varphi }}_{adj-}(t;\widehat{\beta },\widehat{\gamma })\}\text{exp}({\widehat{\beta }}^T{\mathrm{Z}}_i+{\widehat{\gamma }}^T{\mathrm{U}}_i)\right] \\ \times [{\widehat{\mathrm{l}}}_{\gamma }(X_i{)}^T{\overline{\mathrm{G}}}_n(t;\widehat{\gamma })-\{1-{\widehat{\varphi }}_{adj-}(t;\widehat{\beta },\widehat{\gamma })\}{\widehat{\mathrm{l}}}_{\theta }(X_i{)}^T{\overline{\mathrm{D}}}_n(t;\widehat{\theta })]∕{\overline{A}}_n^2(t;\widehat{\beta },\widehat{\gamma }), \\ {\widehat{\sigma }}_w^{\ast 2}(t;h)={\pi }_0^2{\widehat{\sigma }}_{+}^{\ast 2}(t;h)+(1-{\pi }_0{)}^2{\widehat{\sigma }}_{-}^{\ast 2}(t;h)+2{\pi }_0(1-{\pi }_0){\widehat{\sigma }}_{+-}^{\ast }(t;h), \end{gathered}$$

where ${\widehat{\mathrm{I}}}^{-1}(\widehat{\beta })$ is the estimated information matrix for β, ${\widehat{\mathrm{l}}}_{\beta }(X_i)$, ${\widehat{\mathrm{l}}}_{\gamma }(X_i)$ and ${\widehat{\mathrm{l}}}_{\theta }(X_i)$ are the estimated efficient influence functions for β, γ and θ, respectively, and

$$\begin{gathered} {\widehat{\sigma }}_{+-}^{\ast }(t;h)=-\{{\widehat{\sigma }}_{AF}(t;h){\overline{A}}_n^{-1}(t;\widehat{\beta },\widehat{\gamma })B_n^{-1}(t)+{\widehat{\sigma }}_{CE}(t;h){\overline{A}}_n^{-1}(t;\widehat{\beta },\widehat{\gamma })B_n^{-1}(t) \\ +{\widehat{\sigma }}_{CF}(t;h){\overline{A}}_n^{-1}(t;\widehat{\beta },\widehat{\gamma })B_n^{-1}(t)\} \\ {\widehat{\sigma }}_{AF}(t;h)=\frac{h}{n}\sum _{i=1}^n{\Delta }_i{K}_h(t-X_i)\{\widehat{\phi }(t;\widehat{\beta })-\text{exp}(-{\widehat{\beta }}^T{\mathrm{Z}}_i)\} \\ \times [{\widehat{\mathrm{l}}}_{\gamma }(X_i{)}^T{\overline{\mathrm{G}}}_n(t;\widehat{\gamma })-\{1-{\widehat{\varphi }}_{adj-}(t;\widehat{\beta },\widehat{\gamma })\}{\widehat{\mathrm{l}}}_{\theta }(X_i{)}^T{\overline{\mathrm{D}}}_n(t;\widehat{\theta })], \\ {\widehat{\sigma }}_{CE}(t;h)=\frac{h}{n}\sum _{i=1}^n(1-{\Delta }_i)K_h(t-X_i)\left[\text{exp}({\widehat{\gamma }}^T{\mathrm{U}}_i)-\{1-{\widehat{\varphi }}_{adj-}(t;\widehat{\beta },\widehat{\gamma })\}\text{exp}({\widehat{\beta }}^T{\mathrm{Z}}_i+{\widehat{\gamma }}^T{\mathrm{U}}_i)\right] \\ \times \{{\widehat{\mathrm{l}}}_{\beta }(X_i{)}^T{\mathrm{D}}_n(t;\widehat{\gamma })\}, \\ {\widehat{\sigma }}_{CF}(t;h)=\frac{h}{n}\sum _{i=1}^n\{{\widehat{\mathrm{l}}}_{\beta }(X_i{)}^T{\mathrm{D}}_n(t;\widehat{\gamma })\}[{\widehat{\mathrm{l}}}_{\gamma }(X_i{)}^T{\overline{\mathrm{G}}}_n(t;\widehat{\gamma })-\{1-{\widehat{\varphi }}_{adj-}(t;\widehat{\beta },\widehat{\gamma })\}{\widehat{\mathrm{l}}}_{\theta }(X_i{)}^T{\overline{\mathrm{D}}}_n(t;\widehat{\theta })]. \end{gathered}$$

The consistency of ${\widehat{\sigma }}_{+}^{\ast 2}(t;h)$, ${\widehat{\sigma }}_{-}^{\ast 2}(t;h)$ and ${\widehat{\sigma }}_w^{\ast 2}(t;h)$ are summarized in the following theorem with the proof and derivation of the correction terms provided in Appendix C.

Theorem 3. Suppose that assumptions A1-A6 are satisfied. Then for t ∈ [0, τ], ${\widehat{\sigma }}_{+}^{\ast 2}(t;h)$, ${\widehat{\sigma }}_{-}^{\ast 2}(t;h)$ and ${\widehat{\sigma }}_w^{\ast 2}(t;h)$ are uniformly consistent for ${\sigma }_{+}^2(t)$, ${\sigma }_{-}^2(t)$ and ${\sigma }_w^2(t)$.

Based on the variance estimator, we can construct the point-wise 100(1 – α%) confidence interval for the three estimators:

$$\begin{gathered} {\widehat{\varphi }}_{adj+}(t;\widehat{\beta })\mp z_{1-\alpha ∕2}(nh{)}^{-1∕2}{\widehat{\sigma }}_{+}^{\ast }(t;h), \\ {\widehat{\varphi }}_{adj-}(t;\widehat{\beta },\widehat{\gamma })\mp z_{1-\alpha ∕2}(nh{)}^{-1∕2}{\widehat{\sigma }}_{-}^{\ast }(t;h), \\ {\widehat{\varphi }}_{adjw}(t;\widehat{\beta },\widehat{\gamma })\mp z_{1-\alpha ∕2}(nh{)}^{-1∕2}{\widehat{\sigma }}_w^{\ast }(t;h), \end{gathered}$$ (11)

where z_1–α/2 is the 100(1 – α/2)th percentile of the standard distribution.

In practice, it is also often of interest to construct simultaneous 100(1–α)% confidence bands. Here we use the bootstrap resampling approach to construct the confidence bands^29,30. The original bootstrap method, random resampling with replacement, works well from the simulation studies. For simplicity, we only illustrate the construction of confidence band for ${\widehat{\varphi }}_{adjw}(t;\widehat{\beta },\widehat{\gamma })$. Consider a process $\sqrt{nh}\{{\widehat{\varphi }}_{adjw}(t;\widehat{\beta },\widehat{\gamma })-{\varphi }_{adjw}(t;{\beta }_0,{\gamma }_0)\}$. For each resampling, denote the resultant estimator as ${\tilde{\varphi }}_{adjw}(t;\tilde{\beta },\tilde{\gamma })$ and its corresponding variance estimator as ${\tilde{\sigma }}_w^{\ast 2}(t;h)$, calculated using the resampled data. We use the process $\sqrt{nh}\{{\tilde{\varphi }}_{adjw}(t;\tilde{\beta },\tilde{\gamma })-{\widehat{\varphi }}_{adjw}(t;\widehat{\beta },\widehat{\gamma })\}$ to approximate $\sqrt{nh}\{{\widehat{\varphi }}_{adjw}(t;\widehat{\beta },\widehat{\gamma })-{\varphi }_{adjw}(t;{\beta }_0,{\gamma }_0)\}$ by simulating a large number of realizations through random resampling with replacement. Then the critical value for 100(1–α)th percentile simultaneous confidence band can be calculated based on these simulations:

$$\text{Pr}\left\{\underset{t\in [0,\tau ]}{\text{sup}}\frac{\mid \sqrt{nh}\{{\tilde{\varphi }}_{adjw}(t;\tilde{\beta },\tilde{\gamma })-{\widehat{\varphi }}_{adjw}(t;\widehat{\beta },\widehat{\gamma })\}\mid }{{\tilde{\sigma }}_w^{\ast }(t;h)}\le {\tilde{z}}_{1-\alpha ∕2}\right\}-1-\alpha ,$$ (12)

and the resulting confidence band for the time range of [0, τ] is

$${\widehat{\varphi }}_{adjw}(t;\widehat{\beta },\widehat{\gamma })\mp {\tilde{z}}_{1-\alpha ∕2}(nh{)}^{-1∕2}{\widehat{\sigma }}_w^{\ast }(t;h).$$ (13)

2.4. Kernel and Bandwidth Selection

In the kernel estimation, the performance of the estimator depends on choices of the kernel function and the bandwidth. While the kernel function has much less impact, it is known that bandwidth choice is critical to the adequacy of the estimator. Here we use the Epanechinikov kernel given its optimization property³¹ and a “leave-one-out” least squares cross-validation approach which is a well-working approach for automatically optimizing the bandwidth^32,33. The idea is to split the data into two parts, the larger part that contains all but one subject, and the smaller part that contains one subject, then use the larger part of the data for estimation and the smaller part for evaluation of accuracy. The optimal bandwidth would minimize the average prediction squared errors. In particular, let

$$\begin{gathered} {\widehat{\varphi }}_{adj+}^{(-j)}(X_j;h)=1-\frac{{\sum }_{i=1}^{n}I(i\ne j)\text{exp}(-{\widehat{\beta }}^T{\mathrm{Z}}_i){\Delta }_i{K}_h(X_j-X_i)}{{\sum }_{i=1}^{n}I(i\ne j){\Delta }_i{K}_h(X_j-X_i)}, \\ {\widehat{\varphi }}_{adj-}^{(-j)}(X_j;h)=1-\frac{{\sum }_{i=1}^{n}I(i\ne j)\text{exp}({\widehat{\gamma }}^T{\mathrm{U}}_i)(1-{\Delta }_i)K_h(X_j-X_i)}{{\sum }_{i=1}^{n}I(i\ne j)\text{exp}({\widehat{\beta }}^T{\mathrm{Z}}_i+{\widehat{\gamma }}^T{\mathrm{U}}_i)(1-{\Delta }_i)K_h(X_j-X_i)}. \end{gathered}$$

which are the estimators of ϕ_adj(X_j) computed with all but the jth subjects. Then the cross-validation loss function is given by

$$CV(h)=\frac{1}{n}\sum _{j=1}^n{\left\{1-\text{exp}(-{\widehat{\beta }}^T{\mathrm{Z}}_j)-{\widehat{\varphi }}_{adjw}^{(-j)}(X_j;h)\right\}}^2,$$

where ${\widehat{\varphi }}_{adjw}^{(-j)}(X_j;h)$ is ${\pi }_0{\widehat{\varphi }}_{adj+}^{(-j)}(X_j;h)+(1-{\pi }_0){\widehat{\varphi }}_{adj-}(X_j;h)$ if Δ_j = 1 and ${\pi }_0{\widehat{\varphi }}_{adj+}(X_j;h)+(1-{\pi }_0){\widehat{\varphi }}_{adj-}^{(-j)}(X_j;h)$ if Δ_j = 0. A cross-validation bandwidth is obtained by minimizing CV(h) with respect to h, ${\widehat{h}}_{CV}={\text{arg min}}_{h>0}CV(h)$. In practice, this approach generally works well.

3. Simulation Studies

We conducted simulation studies to evaluate the finite sample performance of the proposed estimators for case-control data. Specifically, we first generated a large population with 100000 subjects. For each subject, we generated an exposure and a confounder. We then generated a failure time T based on the Cox model (5) with a Weibull baseline hazard λ₀(t) = (ν/η)(t/η)^ν−1, where ν and η are shape and scale parameters, respectively. We also generated an independent censoring time C. The observed time X was the minimum of T and C, and the disease status Δ = 1 if T ≤ C and Δ = 0 if T > C. We obtained the case-control sample by randomly sampling 2000 cases (Δ = 1), and 1000, 2000 or 4000 controls (Δ = 0) with time matched to the cases within five-year intervals. Thus the observed data for analysis consist of X, Z, U and Δ. We estimated (β^T, γ^T) using conventional logistic regression adjusting for age. The proposed estimators were obtained using the Epanechnikov kernel (i.e., K(x) = 0.75(1 – x²)I_∣x∣<1) and the bandwidth was selected by the proposed automatic cross-validation approach. We also obtained estimators with a range of fixed bandwidths to evaluate the performance of the automatic bandwidth selector.

We set parameters in the baseline hazard function as η = 180 or 360, and ν = 2. For generating (Z, U), we considered two scenarios. In scenario I, (Z, U) jointly follow Bernoulli distributions with the probabilities of (Z, U) being (1, 1), (1, 0), (0, 1), and (0, 0) as 0.35, 0.15, 0.15, and 0.35, respectively. In scenario II, we generated a continuous U which follows a normal distribution N(0, 0.5) and then a binary Z was generated with the probability of Z = 1 as exp(U)/{exp(U) + 1}. The log-hazard ratios of Z and U were set to be log(3) and log(1.5), respectively. Censoring time was truncated normal between 1 and 100 with standard deviation of 30, and the mean was set to yield censoring probability of 70% or 80% for η = 180, 90% or 95% for η = 360. For each simulation scenario, a total of 2000 simulated datasets were generated. It can be seen from Table 1 that ϕ_adj(t) decreases monotonically, as subjects who had the exposure experienced diseases at an earlier age, leaving fewer subjects with exposure in the older age. The performance of the proposed estimators was assessed by following summary statistics: bias, empirical standard deviation (ESD), asymptotic-based standard error (ASE), and 95% coverage rate at selected age t. In addition, we calculated the coverage rate of the 95% simultaneous confidence band calculated by bootstrap with 200 repetitions, across the range of the observed ages. Specifically, the bias was calculated by taking the absolute difference between the mean of the point estimates and the true value of ϕ_adj(t). The ESD was the empirical standard deviation of the point estimates, and ASE was the average of the standard error estimators over the 2000 simulated datasets. The 95% pointwise coverage rate was the proportion of 95% estimated confidence intervals that covered the true value ϕ_adj(t) at time t.

Table 1.

Summary statistics of the ϕ_adj(t) estimators under scenario I and II for 80% censoring and an equal number of cases and controls. Bias: absolute difference between the true value of ϕ_adj(t) and the mean of the point estimator. ESD: empirical standard deviation. ASE: mean of asymptotic-based standard error estimates. CR pointwise: coverage rate of 95% pointwise confidence intervals. CR: coverage rate of 95% simultaneous confidence bands.

	Scenario I: binary U					Scenario II: continuous U
	Age	ϕadj(t)	Φadj(t)			Age	ϕadj(t)	Φadj(t)
	30	0.509	0.507			30	0.512	0.510
	50	0.491	0.486			50	0.497	0.492
	70	0.462	0.450			70	0.473	0.463
	Age	${\widehat{\varphi }}_{adj+}$	${\widehat{\varphi }}_{adj-}$	${\widehat{\varphi }}_{adjw}$		Age	${\widehat{\varphi }}_{adj+}$	${\widehat{\varphi }}_{adj-}$	${\widehat{\varphi }}_{adjw}$
Bias	30	0.000	−0.001	0.000	Bias	30	−0.001	−0.001	0.000
	50	0.000	−0.001	0.000		50	0.000	−0.001	0.000
	70	0.001	−0.001	0.000		70	0.001	−0.002	0.000
ESD	30	0.025	0.030	0.025	ESD	30	0.027	0.032	0.026
	50	0.027	0.031	0.025		50	0.027	0.031	0.026
	70	0.030	0.043	0.028		70	0.029	0.038	0.028
ASE	30	0.027	0.029	0.026	ASE	30	0.027	0.030	0.026
	50	0.027	0.030	0.026		50	0.027	0.030	0.026
	70	0.030	0.038	0.028		70	0.029	0.036	0.027
CR(%) pointwise	30	95.7	95.5	95.4	CR(%) pointwise	30	94.8	94.0	94.3
	50	95.1	94.8	95.1		50	94.6	95.3	94.9
	70	95.4	93.5	95.4		70	94.8	93.9	94.7
CR(%)	20:70	95.2	94.1	94.8	CR(%)	20:70	93.9	93.4	94.0

Table 1 shows the summary results of the simulations under scenarios I and II for 80% censoring and an equal number of cases and controls. Results of other combinations of censoring probability and case/control ratio have similar patterns and are presented in Appendix D. We see ϕ_adj(t) approximates Φ_adj(t) very well. The bias for the proposed estimators is small under both scenarios across a wide range of ages. The ASE is close to the ESD. The estimated pointwise coverage rates are generally close to 95%, so are the simultaneous confidence bands. This indicates that the proposed estimators and the asymptotic-based variance estimators perform well. We also evaluated the proposed methods across a wide range of bandwidths and present the results in Appendix D. As expected from the bias-variance trade-off, when a small bandwidth is used, the bias tends to be smaller while the variance becomes larger, and when the bandwidth is larger, the bias tends to be greater especially at late ages, and the variance is smaller. The cross-validation selected bandwidths balance the bias and variance, yielding satisfactory estimates. As expected, ${\widehat{\varphi }}_{adjw}(t;\widehat{\beta },\widehat{\gamma })$ is more robust than either of ${\widehat{\varphi }}_{adj+}(t;\widehat{\beta })$ and ${\widehat{\varphi }}_{adj-}(t;\widehat{\beta },\widehat{\gamma })$ in terms of bias, efficiency and coverage rates.

4. An Application to a Case-Control Study of Colorectal Cancer

4.1. Real Data Analysis

We apply our proposed methods to three case-control studies from the Genetics and Epidemiology Colorectal Cancer Consortium (GECCO). GECCO consists of dozens of well-characterized (nested) case-control studies of colorectal cancer (CRC)³⁴. The broad objective of the consortium is to evaluate both lifestyle, environmental and genetic risk factors in relation to colorectal cancer risk. Key clinical and environmental data have been harmonized across all studies. Although CRC is one of the common cancers, it is still rare in the general population. As a result, the most common study design for studying CRC is the case-control study design. For illustration, the subset of the data we used includes 5498 subjects (2742 cases and 2756 controls) from three cohort-based nested case-control studies, for which controls are frequency matched on both age and gender and the risk factor information was collected at the study entry. All models are adjusted for study, age and gender. The aim of this data analysis is to estimate the adjusted PAHs of various risk factors to colorectal cancer.

In the analysis, we focus on history of diabetes (yes/no) and obesity (body mass index, BMI, >30kg/m²). Both are risk factors for colorectal cancer and obesity is a risk factor for diabetes. It is therefore of interest to examine the adjusted PAH of obesity accounting for diabetes history, and vice versa. For ever-smokers, we also examine the adjusted PAH of years-since-quit-smoking (≤ 10 years vs > 10 years) while adjusting for pack-years (≥ 22.5 vs < 22.5), and vice versa.

The descriptive statistics of risk factors as well as matching variables age and gender by case-control status are summarized in Table 2. It also includes estimates of odds ratios, classic Levin’s PAFs⁷, and the model-based adjusted PAFs for each of the risk factors³⁵, treating the outcome colorectal cancer as binary (yes/no). By study design, age and gender are balanced between cases and controls. History of diabetes, obesity, and ever smoking are more common in cases than controls. For ever-smokers, cases also have a higher average of pack-year and shorter years-since-quit-smoking. History of diabetes has the highest OR estimate of 1.57, however, the prevalence of exposure is low with 7.5% in cases and 4.7% in controls, resulting in an estimated unadjusted PAF of only 0.029 (95% confidence interval (CI): 0.016–0.043). In contrast, the odds ratio estimate for obesity is 1.17 (95% CI: 1.04–1.32) and the prevalence is 29.5% in cases and 25.7% in controls. As a result, the unadjusted PAF is 0.051 (95% CI: 0.020-0.083), which is greater than obesity. The adjusted PAF estimates are roughly the same, suggesting that both risk factors contribute to colorectal cancer risk. For ever-smokers, pack-year has an estimated unadjusted PAF of 0.153 (95% CI: 0.089-0.218) and years-since-quit-smoking has an estimate of 0.073 (95% CI: 0.024-0.121). After adjusting for pack-year, the adjusted PAF for years-since-quit-smoking is reduced roughly to half.

Table 2.

Summary statistics of risk factors by case-control status in GECCO data. Age: age at onset for cases and age at selection for controls. Years since quit smoking: <=10 years compared to >10 years since quit smoking, for ever-smokers only. Pack-year (>=22.5): for ever-smokers only.

Variables	cases	controls	OR(95% CI)	$\widehat{PAF}(95\%\text{CI})$	${\widehat{PAF}}_{adj}(95\%\text{CI})$
Age (years) (Mean, range)	70.8 (50-91)	70.9 (50-91)	-	-	-
Gender (female)	73.9%	74.2%	-	-	-
History of Diabetes	7.5%	4.7%	1.57 (1.24, 1.98)	0.029 (0.016, 0.043)	0.027 (−0.002, 0.056)
Obesity	29.5%	25.7%	1.17 (1.04, 1.32)	0.051 (0.020, 0.083)	0.043 (0.002, 0.083)
Ever smoking	55.2%	50.8%	-	-	-
Years since quit smoking	35.0%	29.9%	1.12 (0.94, 1.33)	0.073 (0.024, 0.121)	0.037 (−0.029, 0.104)
Pack-year (>=22.5)	53.9%	46.2%	1.38 (1.16, 1.63)	0.153 (0.089, 0.218)	0.150 (0.074, 0.226)

We estimated the adjusted PAH for each of the risk factors using the weighted estimator ${\widehat{\varphi }}_{adjw}(t;\widehat{\beta },\widehat{\gamma })$, because it has the most robust performance as shown in the simulation studies. The Epanechnikov kernel was used and the bandwidth was obtained by cross-validation. We fit a logistic regression model for obesity and diabetes history, and likewise for pack-year and years-since-quit-smoking in ever-smokers. As comparison, we also calculated the unadjusted PAH¹³. To test whether the constant hazard ratio hold for the underlying Cox model, an interaction term between time and the risk factor was added to the logistic model and the interaction term was not significantly different with 0 for each of the four risk factors at the 0.05 level.

It is worth noting that while obesity is a well-known confounder for the relationship between diabetes and CRC, it may not be true that diabetes is a confounder for obesity and CRC. Therefore, the PAH of obesity adjusting for diabetes need to be interpreted with caution. As diabetes may likely be on the pathway from obesity to CRC risk, such an adjusted PAH may be interpreted as the proportion of reduction of the hazard due to the direct effect of obesity with the indirect effect of obesity to CRC through diabetes unchanged. If one were to measure the impact of eliminating the total effect of obesity, adjusting for diabetes in the PAH of obesity might not be needed.

Figure 1 shows both unadjusted and adjusted PAHs for each of the four risk factors on CRC. The adjusted PAH for diabetes after adjusting for obesity is nearly unchanged compared to the unadjusted PAH, while the adjusted PAH for obesity after adjusting for diabetes is slightly lower than the unadjusted PAH and the mean difference across the age is about 0.02. The 95% confidence intervals for both adjusted PAHs of obesity and diabetes exclude 0, suggesting that despite somewhat reduced the PAH for obesity after adjusting for diabetes, both risk factors contribute to colorectal cancer risk. For ever-smokers, the PAH for pack-year after adjusting for years-since-quit-smoking is essentially the same as the unadjusted PAH. In contrast, the PAH for the years-since-quit-smoking is greatly reduced after adjusting for pack-year, and the 95% confidence intervals include 0 over time, suggesting that the PAH of years-since-quit-smoking is largely explained by pack-year.

Figure 1.

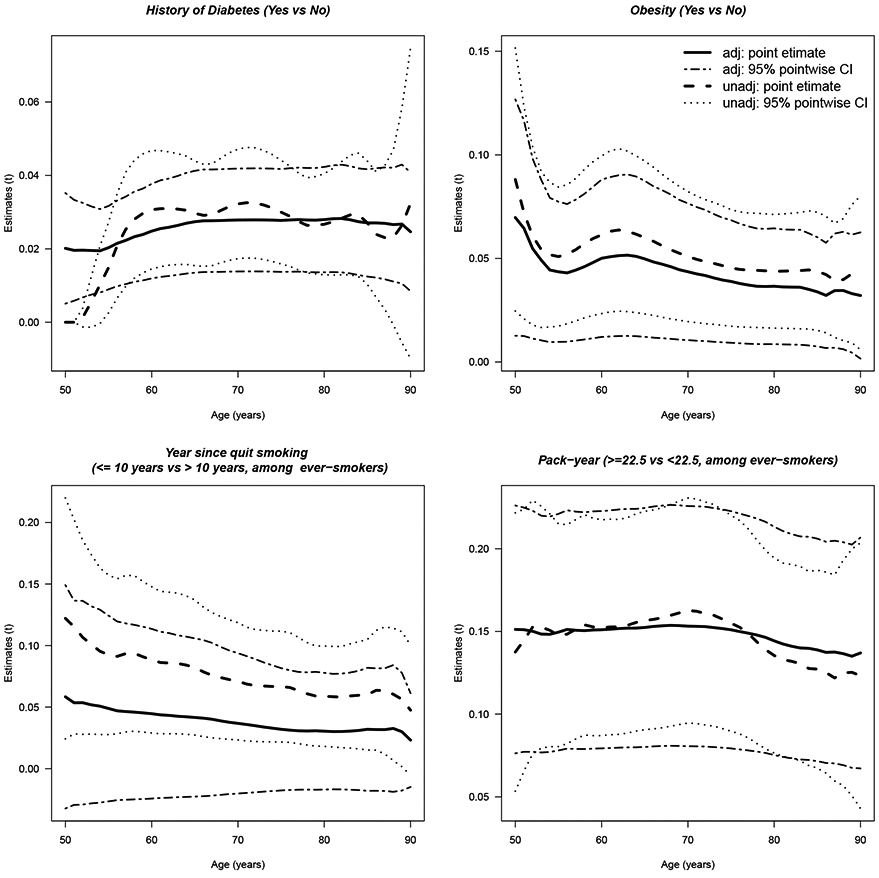
Estimates of the unadjusted and adjusted PAHs with 95% pointwise confidence intervals versus time t (age in years) for various risk factors.

The PAH for diabetes, year-since-quit-smoking and pack-years are approximately flat. The PAH for obesity decreases over time, from 8.8% at age 50 years old to 4.4% at age 80 years old, suggesting an early intervention may possibly reduce risk for early-onset colorectal cancer. Estimates of the adjusted PAHs and 95% confidence intervals at selected ages, and figures of the simultaneous confidence bands can be found in Appendix D.

4.2. Real Data Based Simulation

To assess the performance of the proposed weighted estimator for the real data, we conducted a simulation study mimicking the scenarios for diabetes and obesity as shown in the real data example. Specifically, we generated two binary covariates (diabetes and obesity) from a multinomial distribution that the probabilities of having diabetes only, obesity only and both are 4.7%, 25.7% and 2.3%, respectively, same as what we observed in the controls of the GECCO data. The failure time T was generated based on the Cox proportional hazards model with log-hazard ratios as the estimated coefficients from logistic regression for diabetes (0.45) and obesity (0.15). The baseline hazard function was chosen such that the age-specific colorectal cancer incidence rates follow the Surveillance Epidemiology and End Results Registry (SEER) registry (https://seer.cancer.gov/data/). The probability of developing colorectal cancer is 2%, which can be considered as a rare disease scenario. We generated independent right censoring time as the minimum of current age and age at death obtained from the US lifetable. We generated a large population with 300000 subjects. The case-control sample was obtained by randomly sampling 2500 cases, and 1250, 2500 or 5000 controls with age matched to the cases within five-year intervals. The estimation and inference were identical as in Section 3. A total of 2000 simulated datasets were generated.

Two exposures were considered: (1) diabetes as the exposure and obesity as the confounder; (2) obesity as the exposure and diabetes as the confounder. The same summary statistics as in Section 3 were calculated to assess the performance of the proposed estimators. The results for equal number of cases and controls are presented in Table 3, and the results for other case/control ratios are presented in Appendix D. The bias for the proposed estimators is small across a wide range of ages. The ASE approximates the ESD well. The pointwise coverage rates are close to 95%, so are the simultaneous confidence bands. Note that mild under-coverage for the scenario of diabetes as the exposure at 40 and 80 years is mainly due to relatively small sample sizes. The average sample sizes within the kernel range at 40, 60 and 80 years are 714, 1746 and 753 for the method using only cases, 795, 1887 and 828 for the method using only controls, 1523, 3657 and 1597 for the method using both cases and controls, respectively. In this situation, the kernel bandwidth selection balances between bias and variance, which may lead to moderate bias and/or somewhat imprecise estimate of standard error. For age 40, the standard error approximates the empirical standard deviation well, but the bias is not very close to 0, resulting in under-coverage; for age 80, the bias is close to 0, but the estimated standard error is a bit lower than the empirical standard deviation, also resulting in under-coverage.

Table 3.

Summary statistics of the estimators from simulated datasets based on real data for equal number of cases and controls. Bias: absolute difference between the true value of ϕ_adj(t) and the mean of the point estimator. ESD: sampling standard deviation. ASE: mean of asymptotic-based standard error estimates. CR pointwise: coverage rate of 95% pointwise confidence intervals. CR: coverage rate of 95% simultaneous confidence bands.

	Diabetes as the exposure					Obesity as the exposure
	Age	ϕadj(t)	Φadj(t)			Age	ϕadj(t)	Φadj(t)
	40	.0269	.0269			40	.0408	.0408
	60	.0266	.0266			60	.0407	.0407
	80	.0253	.0252			80	.0403	.0401
	Age	${\widehat{\varphi }}_{adj+}$	${\widehat{\varphi }}_{adj-}$	${\widehat{\varphi }}_{adjw}$		Age	${\widehat{\varphi }}_{adj+}$	${\widehat{\varphi }}_{adj-}$	${\widehat{\varphi }}_{adjw}$
Bias	40	−.0004	−.0007	−.0007	Bias	40	.0003	.0003	.0002
	60	−.0006	−.0006	−.0005		60	.0003	.0003	.0003
	80	−.0001	−.0001	−.0002		80	.0005	.0005	.0004
ESD	40	.0084	.0085	.0081	ESD	40	.0172	.0172	.0171
	60	.0074	.0074	.0074		60	.0170	.0170	.0170
	80	.0083	.0083	.0079		80	.0172	.0171	.0170
ASE	40	.0083	.0084	.0080	ASE	40	.0173	.0173	.0172
	60	.0073	.0074	.0073		60	.0171	.0171	.0171
	80	.0079	.0081	.0077		80	.0171	.0171	.0170
CR(%) pointwise	40	93.6	92.8	93.9	CR(%) pointwise	40	95.7	95.5	95.7
	60	95.0	94.9	95.4		60	95.4	95.5	95.4
	80	93.3	93.8	93.7		80	95.4	95.7	95.3
CR(%)	40:80	92.5	92.0	92.7	CR(%)	40:80	94.6	94.5	94.9

5. Discussion

In this article, we define an adjusted population attributable hazard function and propose a kernel-based estimator for the data from case-control studies. We establish the consistency and asymptotic normality of the proposed estimator, and show through extensive simulation the proposed estimator and the analytical variance estimator perform well in finite sample sizes. Our simulation also shows that the proposed estimator is robust with the proposed cross-validation bandwidth selection.

Our adjusted PAH for time-to-event outcome has connection to the adjusted PAF for binary outcome under the case-control study design. Estimation of the adjusted PAF from case-control data could be based on equation (2) where the odds ratio can be estimated by the logistic regression model to approximate relative risk (by assuming rare disease), and the density of exposure and confounders in disease can be estimated by an empirical estimator^8,23. In comparison, our estimator of the adjusted PAH is obtained by plugging in the odds ratio estimates from logistic regression model for log-hazard ratio in the Cox model and kernel estimators of the conditional density functions of exposure and confounders given T = t or T ≥ t. If a very large bandwidth is used to cover the entire time interval, the adjusted PAH becomes a flat line and approaches to the adjusted PAF proposed by Bruzzi et al.²³.

In observational studies, important assumptions underlie the unadjusted and adjusted PAFs, as well as their extensions to time-to-event. The first assumption is that removing the exposure does not change the distribution of other risk factors. It may not be true in real life, however. For example, quitting smoking may simultaneously decrease alcohol consumption due to improved health behavior, which makes interpretation of the smoking PAF for coronary deaths difficult¹. The second assumption, which is untestable, is no unmeasured confounding, i.e., measured covariates should be sufficient for confounding control³⁶. While untestable, its plausibility may be determined on a case-by-case basis using subject matter knowledge. If it is violated, the PAF and extensions need to be interpreted with caution. The third assumption is that the exposure can be eradicated perfectly by an intervention. However, complete removal of an exposure is often unrealistic. To relax this assumption, one may consider the generalized impact fraction, which is the fractional reduction of cases that would result from changing the current level of exposure in the population to some modified (partially removed) level³⁷.

Our proposed estimator was derived under the Cox proportional hazards model. In practice, the Cox model has been shown fairly robust, as long as the proportionality of the hazards functions between exposed and non-exposed is not seriously violated or could be adequately accounted for by for example, interaction between time and covariates. However, such robustness is not necessarily guaranteed. A further extension to allow for non-proportionality would be of interest. Another potential extension is that since in practice it is not uncommon that many exposures and/or confounders change with time, accommodating time-dependent exposures and/or confounders is also of importance. However, the additional methodological development for time-dependent exposures and/or confounders requires special techniques such as a marginal structural model^38,39. This is beyond the scope of the current manuscript and will be communicated in the future work.