Pathway-Level Information ExtractoR (PLIER) for gene expression data

Abstract

A major challenge in gene expression analysis is to accurately infer relevant biological insight, such as variation in cell type proportion or pathway activity, from global gene expression studies. We present a general solution for this problem that outperforms available cell proportion inference algorithms, and is more widely useful to automatically identify specific pathways that regulate gene expression. Our method improves replicability and biological insight when applied to trans-eQTL identification.

One salient feature of high dimensional molecular data structure is the presence of groups of correlated measurements. In gene expression datasets, correlation among genes commonly represents coordinated transcriptional regulation or, in studies of heterogeneous tissues, variation in cell-type proportion. Identifying the mechanisms underlying coordinated gene expression changes is crucial for interpretation. Importantly, correlated expression patterns may also be the result of various technical factors, often referred to as “batch effects” (see Leek et al. [2010] for review). The challenge is to identify and interpret biologically meaningful signatures while reducing any negative effects of technical noise. To meet these goals, we have developed Pathway-Level Information ExtractoR (PLIER). PLIER performs an unsupervised data structure deconvolution and mapping to external knowledge, reducing noise and identifying regulation in cell-type proportions or pathways.

PLIER approximates the expression pattern of every gene as a linear combination of eigengene-like latent variables (LVs). In constructing LVs, PLIER surveys a large compendium of prior knowledge (genesets) and produces a dataset deconvolution that optimizes alignment of LVs to a relevant subset of the available genesets. The method automatically finds these relevant genesets among the hundreds to thousands considered (see Fig. 1A). Technical noise reduction is also achieved during the deconvolution as technical factors are preferentially segregated into LVs that do not associate with prior information (see Supplementary Fig. 1 and 2).

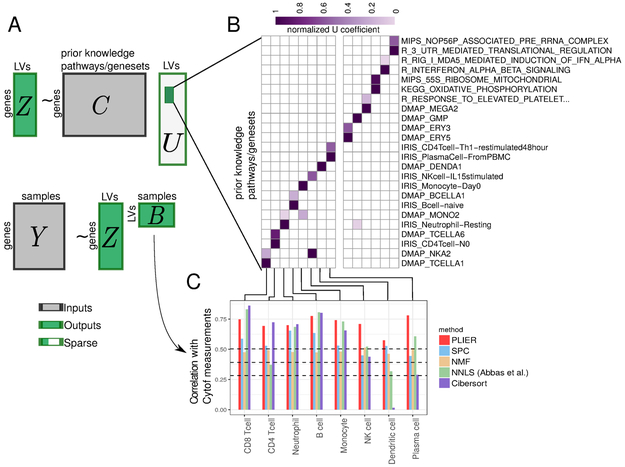
Figure 1: PLIER overview.

PLIER is a matrix factorization approach that decomposes gene expression data into a product of a small number of latent variables and their corresponding gene associations or loadings, while constraining the loadings to align with the most relevant automatically selected subset of prior knowledge. A, Given two inputs, the gene expression matrix Y and the prior knowledge (represented as binary geneset membership in matrix C), the method returns the latent variables (B), their loadings (Z), and an additional sparse matrix (U) that specifies which (if any) prior information genesets and pathways are used for each latent variable. The light gray area of U indicates the large number of zero elements of the matrix. We apply our method to a whole blood human gene expression dataset. B, The positive entries of the resulting U matrix are visualized as a heatmap, facilitating the identification of the correspondence between specific latent variables and prior biological knowledge. Since the absolute scale of the U matrix is arbitrary each column is normalized to a maximum of 1. C, We validate the latent variables mapped to specific leukocyte cell-types by comparing PLIER estimated relative cell-type proportions with direct measurements by Mass Cytometry. Dashed lines represent 0.05, 0.01, and 0.001 significance levels for Spearman rank correlation (single-tailed test). We find that the PLIER estimates are highly accurate, outperforming other matrix decomposition methods. Moreover, PLIER estimates are competitive and in 4 cases outperform both of the dedicated blood mixture deconvolution method NNLS [Abbas et al., 2009] and Cibersort [Newman et al., 2015].

We first validate the method using cell-type proportion inference because it is an important objective, other methods are available for comparative benchmarking, and predictions can be tested against a direct measurement gold standard. For this purpose, we generated a validation dataset comprising 35 human whole-blood samples assayed both by RNA-seq and direct CYTOF measurement of cell type proportion. We applied PLIER to the validation dataset using 605 pathways which included 60 cell-type markers and 555 canonical pathways from MSigDB. We produced a decomposition with 14 latent variables annotated with high confidence (AUC >0.7, FDR <0.05, see Methods for cross-validation procedure) to one or more genesets, of which 8 represented cell types also measured by the Cytof panel. The correlation between the cell type PLIER LVs and Cytof measurements in these 35 samples had a mean of 0.71 (range 0.58-0.78) (Fig. 1).

We compared PLIER against the established current methods for mixture decomposition inference. These methods either rely on low-rank matrix decomposition or reference-based approaches that fit gene expression values to cell-type specific signatures. We include the most widely used constrained matrix decomposition approaches: non-negative matrix factorization (NMF), and Sparse Principle Component Analysis (SPC) (see Methods for details). For a reference-based approach, we tested Cibersort [Newman et al., 2015] and NNLS [Abbas et al., 2009]. Both of these approaches combine a regression algorithm with a dedicated cell-type specific refernce matrix that is explicitly optimized for human blood deconvolution.

PLIER performed considerably better than other constrained matrix decomposition datasets and surprisingly outperformed the refernece-based supervised approaches on 4 out of the 8 cell-types. The excellent performance of the essentially unsupervised and general PLIER method is in part due to the capacity of PLIER to sort through many candidate genesets and find the ones most informative for the specific dataset. PLIER can be supplied with multiple and even discordant markers sets for the same cell-type and will automatically pick the one that models the data.

While PLIER shows excellent performance when benchmarked for cell type deconvolution, it is not specifically designed for this task. Instead, it is a general method for estimating pathway activity that it is applicable to a wide variety of gene expression interpretation problems.

As an example, we evaluated the usefulness of PLIER for the difficult task of genotype-quantitative trait association. Two groups of eQTLs are typically distinguished: locally acting cis-eQTLs that affect a nearby gene, and trans-eQTLs that are commonly mediated at the pathway level [Battle et al., 2014]. Many trans-eQTLs exert their effect by altering the activity of a regulatory protein, which in turn affects the expression of many downstream genes [Westra et al., 2013]. Trans-eQTLs, which provide important insight into gene regulatory networks, are difficult to detect and are less commonly identified than cis-eQTLs due to the multiple hypothesis burden of testing millions of variants by tens of thousands of genes.

We analyze the recently published DGN dataset [Battle et al., 2014], which contains whole blood RNAseq and genotype measurements from 922 individuals, to demonstrate how the PLIER framework extracts a broad spectrum of pathway effects and enables network-level eQTL discovery and interpretation. For the candidate prior information, we used a comprehensive collection of 4445 genesets comprising biochemical and transcriptional pathways (“canonical pathways” and “chemical and genetic perturbations” from MSigDB [Subramanian et al., 2005]), cell-type markers from multiple sources [Newman et al., 2015, Abbas et al., 2009, Novershtern et al., 2011] and cytokine signatures [Filiano et al., 2016]. The PLIER decomposition produced 86 LVs that have at least one matched pathway with an FDR <0.05, and were associated overall with 318 of the 4444 pathway genesets evaluated. The decomposition captured cell-type variation with a high degree of specificity, differentiating naive and memory B-cells, plasmacytoid and myeloid dendritic cells, and multiple subtypes of CD8 T-cells. PLIER also captured variation in non leukocyte cell-types such as megakaryocytes and erythrocytes, and transcriptional pathways such as Type I and Type II interferon signaling, and NKFB pathway. Overall, we find that 29 LVs were unambiguously related to cell-type, canonical pathways or cytokine signaling (see Supplementary Fig. 3 for U matrix visualization and Supplementary File 1 for a complete list of LV-geneset associations).

In order to perform eQTL analysis, we treated the PLIER LVs as quantitative traits (see Methods for details), and identified 12 LVs showing significant associations with genotypes (Table. 1, see Methods for details). In contrast to gene level trans-eQTLs, the PLIER eQTLs are pathway-level effects that capture the concerted behavior of multiple genes (Fig. 2A). The gold-standard for eQTL discovery is reproducibility in an independent dataset. As each pathway-level eQTL effect is supported by a number of gene-level effects we can directly compare the gene-level replication rates of standard (gene-centric) trans-eQTLs and pathway-centric analysis which only considers gene-level eQTLs if they also correspond to pathway-level eQTLs (see Methods for details). Using an independent dataset of human blood expression data assayed with Affymetrix microarray [Wright et al., 2014] we compared the true-postive rate, π₁, (see Methods) for gene-centric and pathway-centric eQTLs and find that the pathway-centric eQTLs are more reproducible at every p-value threshold. For example, at a cutoff that corresponds to gene-level FDR of 0.2 the gene-centric π₁ is ≈ 0.2 while for pathway-centric eQTLs it is ≈ 0.6 (see Supplementary Fig. 4 for replication across a range of cutoffs).

Table 1: Summary table of all pathway-level effects found in the DGN dataset.

Statistics were computed using Spearman rank correlation across 922 subjects with a two-sided test. False discovery rates are computed using the Benjamini-Hochberg procedure on the total number of tests (number of LVs × number of SNPs). SNP-LV associations that passed FDR<0.05 were further filtered to account for potential cis genes or mismapped cis homologs contributing to the LV estimtate (see Methods for details). In most cases pathways were named based on their geneset association captured in the U matrix. Some pathways are named based on further analysis of the expression patterns of top gene in a independent dataset of mouse immune cells, ImmGen [Heng et al,. 2008] (see Supplementary Fig. 5) and/or a the presence of a putative cis eQTL transcriptional mediator. The complete pathway utilization for these LVs can be seen in Fig.2. The expression patterns for top 15 genes driving each latent variable are plotted in Supplementary Fig. 6. Latent variables with no pathway association in PLIER decomposition (that is no positive entries in U) are starred.

LV id	LV name	snps	cis-Gene(s)	Benjamini- Hochberg FDR
44	Mega/platelet 1	rs1354034	ARHGEF3	1.707e-41
133	Mega/platelet 2	rs1354034	ARHGEF3	0.03095
120	Histones	rs1354034	ARHGEF3	0.0336191
97	Zinc fingers, pseudogenes	rs1471738	SENP7	4.011e-13
56	PLAGL1 associated, myeloid	rs9321957	PLAGL1	0.0001421
42*	IKZF1 associated, myeloid	rs10251980	IKZF1	3.39e5-61
17	NEK6 associated, myeloid	rs16927294	NEK6	0.008223
67	Neutrophils	rs13289095	PKN3,SET,ZDHHC12	0.03361
55*	NFE2 associated, erythrocyte	rs35979828	NFE2	3.538e-10
21	Interferon-gamma	rs3184504	SH2B3	0.0002198
40	NFKB/TNF	rs12100841	PPP2R3C	0.005094
16	Myeloid/ILC	rs1138358	BCL2A1,MTHFS,ST20	0.0008103

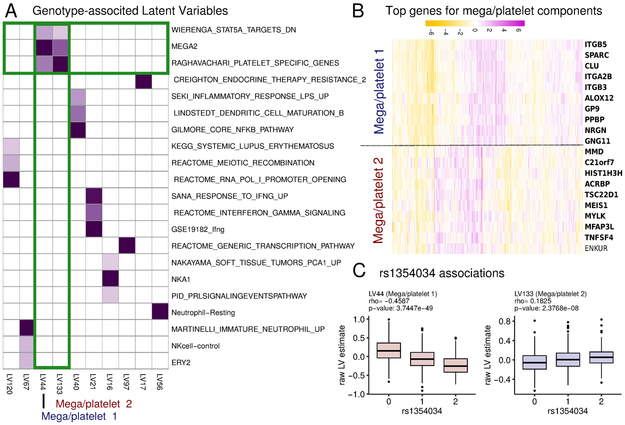
Figure 2:

A, A heatmap of a subset of the U matrix corresponding to LVs with a genotype effect (LV eQTLs). Only pathways with a cross-validation FDR of < 0.05 are shown. We find that two latent variables (LV44 and LV133) share pathway annotations (albeit with different coefficient) that suggest a relationship with megakaryocyte and platelet biology. B, Heatmap of the top genes in the loading for LV44 and LV133. Genes that are annotated to the pathways shown in panel A are in bold. C, Boxplots of the association of LV44 and LV133 with SNP rs1354034 (n=344, 429, 149 for 0, 1, 2 respectively) While the LV estimates are positively correlated, the effects of rs1354034 are opposite. These results indicate that the pathways captured by the expression patterns of LV44 and LV133 are independently regulated by the rs1354034 locus. Boxplot displays the 25th, 50th and 75th percentiles, with whiskers extending to 1.5x the interquartile range or the range of the data whichever is smallest. P-values indicate unocrrected two-tailed Spearman rank correlation test.

Besides improving the accuracy of trans-eQTL discovery, the PLIER decomposition identifies the pathway(s) associated with the LV eQTL, which can provide precise biological interpretation of the genetically regulated processes. For example, PLIER shows that SNP rs1354034 (located within gene ARHGEF3) is associated with two LVs, LV44 and LV133, that are related to megakaryocyte/platelet lineage based on their pathway association (Fig. 2A, B). In the published gene level analysis of the DGN dataset, this SNP yields the largest number of significant trans-eQTLs, however no biological interpretation was inferred (Battle and others 2014). Using PLIER, we find two of the associated LVs are annotated to platelet pathway processes, which is consistent with a known effect of this SNP on platelet number (PLT) and platelet volume (MPV) [Gieger et al., 2011]. However, our analysis further shows that the two LVs linked to this SNP are supported by different genes that show distinct expression patterns (Fig. 2B). These results suggest that the two LV eQTLS may distinguish two different processes of platelet/megakaryocyte biology. A recent hematopoetic lineage report supports this formulation. This single cell study shows that genes associated with the two LVs express at different developmental time points (Olsson et al. 2016). Specifically, mouse orthologs of MEIS1 and TSC22D1 (from LV133) are expressed in all megakaryocyte precursors, while ITGA2B (from LV44) is megakaryocyte specific, suggesting that these two LVs capture processes that are active at different times in megakaryocyte development.

LV133 and LV44 are positively correlated with each other in the DGN dataset. Notably, the effects of the rs1354034 alleles on LV133 and on LV44 go in opposite directions (Fig. 2C). Furthermore, we find that using partial correlation analysis, whereby the LVs are corrected for each other, dramatically improved the eQTL statistics (Supplementary Fig. 7). These results strongly argue that the LV44 and LV133 effects are independent.

We speculate that the independent regulation of the two LV eQTLs by the same locus results from an effect on different regulators that are modulated at different periods of megakaryocyte development. The rs1354034 SNP is known to be pleiotropic as it is linked to both MPV and PLT phenotypes, which are affected independently by other genetic variation [Gieger et al., 2011]. We hypothesize that the effects of rs1354034 on multiple LVs is reflective of its pleiotropic function. Indeed, correlation of the two LVs with SNPs known to be specifically linked to MPV or PLT alone shows divergent patterns. In addition to the association with rs1354034, the developmentally early LV133 is most strongly associated with a SNP linked to platelet number, whereas the later LV44 is most strongly associated with a SNP linked to platelet volume (Table 2). This analysis supports a model where ARGHEF3 exerts its pleiotropic affects on platelet volume and number at different developmental time points. These results demonstrate how PLIER can leverage dataset structure and external knowledge to resolve fine-grained mechanistic insight underlying complex biological processes. Additional demonstrations of how PLIER can be applied to single-cell RNAseq or cross-study concordance analysis are presented in Supplementary Note 1.

Table 2: Summary table of the associations between the two mega/platelet LVs and SNPs known to affect only one platelet phenotype.

Statistics were computed using Spearman rank correlation across 922 subjects with a two-sided test. Raw p-values are reported. A total of 80 SNPs with known platelet phenotypes were tested [Gieger et al,. 2011]. While no SNPs outside of the ARGHEF3 locus achieved genome-wide significance, some associations were significant at FDR<0.05 when we consider only the 160 (80 SNPs × 2 LVs) hypotheses that are tested (significant p-values are in bold). We find that the associations of the two mega/platelet LVs with other loci known to affect platelet biology are distinct. Our analysis suggests that the early mega/platelet LV (LV133) is more closely related to the process controlling platelet number (PLT) while the late mega/platelet LV (LV44) is related to the process controlling platelet volume (MPV).

phenotype	reported SNP	Close gene	LV44 p-value	LV 133 p- value	proxy SNP
MPV	rs10876550	COPZ1	1.1847e-05	0.69933	rs10876550
PLT	rs2911132	ERAP2	0.13817361	2.4417e-05	rs2549803

Methods

Gene expression measurements are highly correlated and this correlation structure often reflects the activity of upstream biological processes. This data structure is exploited implicitly any time a clustering is performed, as is often done with cancer datasets in order to define molecularly distinct subtypes [Network et al., 2013, Ross et al.,2000]. Likewise it is possible to analyze the structure explicitly by projecting the thousands of gene specific measurements into a smaller dimensional space that captures much of the observed variation. Principal Component Analysis, which utilizes singular value decomposition(SVD) to project the data onto orthogonal principal components (PCs) of maximal variance, is commonly applied to gene expression datasets. PCA and its higher dimensional analogs have been successfully applied to gain biological insight from complex datasets [Alter et al., 2000, Hore et al., 2016].

However SVD decompositions have several limitations. By construction PCA/SVD produces components that are orthogonal and are dense combinations of the original variables. The orthogonality implies that the components will not always correspond to specific biological variables (which are often non-orthogonal) and the loading density makes interpretation difficult.

Various alternative decomposition method that seek to improve the interpretability by imposing additional constraints have been proposed. For example, non-negative matrix factorization (NMF) has been applied to cancer gene expression decomposition yielding more intuitive results [Brunet et al., 2004]. Likewise, methods to introduce sparsity into the matrix decomposition have been proposed [Zou and Hastie, 2005, Witten et al., 2009].

However they do not make use of known biological information in their mathematically driven decompositions. We reasoned that the efficient extraction of biological insight contained in the correlated structure of the data requires using the vast information contained in biological genesets during the decomposition. To solve this problem, we develop a platform that introduces additional constraints to explicitly and iteratively optimize the decomposition using the biological knowledge represented by a compendium of prior information.

Problem Setting

Given a gene expression profile $Y\in {\mathbb{R}}^{n\times p}$, where n is the number of genes and p is the number of samples, we state the original PCA as a matrix approximation problem. Suppose n > k, p > k. We wish to find Z, B minimizing

$$\begin{gathered} \Vert Y-ZB{\Vert }_F^2 \\ \text{subject to}\text{rank}(Z)=k,\text{rank}(B)=k. \end{gathered}$$

Since gene expression measurements are highly correlated, it is reasonable to expect that the data Y can be efficiently represented in this low dimensional space. Without imposing additional constraints on Z and B, an optimal solution can be obtained from the singular value decomposition (SVD) of Y. In an SVD based decomposition, rows of B are referred to as principle components (PCs). Since PCs are necessarily orthogonal, which our method do not require, we will use the more general term latent variables (LVs).

In order to improve the interpretability of the low dimensional representation in the context of known biology, we impose additional constraints on the matrix Z. Our aim is to encourage the loadings (columns of Z) to align as much as possible with existing prior knowledge. In the most general case such prior knowledge can be expressed as a series of genesets representing biological pathways, sets of tissue- or cell-type specific markers, and coordinated transcriptional responses observed in genome wide experiments.

Given n genes and m genesets, we represent the prior knowledge as a matrix C ∈ {0,1}^n×m, so that C_ij = 1 indicates that gene i is part of the j_th geneset. Using the same notation as above, we define the revised decomposition problem based on the original formulation. We wish to find U, Z, B minimizing

$$\begin{gathered} \Vert Y-ZB{\Vert }_F^2+{\lambda }_1\Vert Z-CU{\Vert }_F^2+{\lambda }_2\Vert B{\Vert }_F^2+{\lambda }_3\Vert U{\Vert }_{L^1} \\ \text{subject to}U>0,Z>0. \end{gathered}$$

The first term of the optimization is the same as equation (1) and minimizes the overall reconstruction error. The second term specifies that Z should be “close to” sparse combinations of genesets represented by C. The third term introduces an L² penalty on B, while the fourth term is an L¹ penalty on U (applied column-wise), which ensures that only a small number of genesets represent each LV.

The parameter λ₁ keeps a balance between the proportion of prior knowledge we include and the degree to which we reconstruct the gene expression profile. We also restrict U and Z to be positive, which enforces that genes belonging to a single geneset are positively correlated with each other and the loadings are positively correlated with the prior information.

We solve the optimization problem by using block coordinate minimization, which iteratively minimizes the error on Z, U, and B. The complete method starts by initializing Z and B from the SVD decomposition and repeats the following steps until B converges.

while stopping criterion has not been reached

$$Z^{(l+1)}\leftarrow (Y{B}^{(l{)}^T}+{\lambda }_{1}C{U}^{(l+1)})(B^{(l{)}^T}+{\lambda }_{1}I{)}^{-1}$$

Set the negative part of Z^(l+1) to be zero

Solve the convex problem

$$U^{(l+1)}\leftarrow {\text{argmin}}_U\Vert Z^{(l)}-CU{\Vert }_F^2+{\lambda }_3\Vert U{\Vert }_{L^1}$$

Subject to U > 0

$$B^{(l+1)}\leftarrow (Z^{(l{)}^T}{Z}^{(l)}+{\lambda }_{2}I{)}^{-1}{Z}^{(l{)}^T}Y$$

The stopping criterion is defined as a relative change in B < 5 × 10⁻⁶, or a leveling off in the decrease of the relative change in B. While there are no convergence guarantees, in practice this algorithm converges in under a few hundred iterations.

Optimization constants

The optimization has 4 free parameters λ₁, λ₂, λ₃, and k and internal cross validation cannot be used to optimize them as the reconstruction error $\Vert Y-ZB{\Vert }_F^2$ is always minimized when λ₁ = 0. However, based on extensive testing with simulations and real data, we have set default parameters that perform well in a range of situations. For example, we find that a reasonable starting value for k can be inferred from the the number of statistically significant PCs which can be determined via permutation by the approach proposed in [Leek et al., 2007] or the simple “elbow” approach (num.pc in our package implements both). However, it is logical that the number of constrained latent variables needed to explain the data is higher, and we suggest increasing the initial k by a factor of 2. Importantly, the method is not sensitive to the exact value of k. LVs found at lower k’s persist when k is increased. It is also possible to optimze k with respect to the number of LVs with prior information above some AUC and FDR threshold, but this requires multiple runs.

A good choice for λ₁ and λ₂ can be derived from the observation that if we consider the SVD decomposition of Y as UDV^T we should have that Z ≈ UD^1/2 and B ≈ D^1/2V^T. Therefore the diagonal elements of Z^TZ and BB^T are well approximated by D which thus gives the correct range for the relevant constants. By default we set λ₂ = d_k and λ₁ = d_k/2 with the factor of 2 coming from the positivity thresholding on Z. We find that our method is robust to these choices (Supplementary Note 1). It is also possible to optimize λ₁ along with λ₂ around its default value relative to some external validation source. For example, we can check how well the LVs recovered in B correlate with an independent dataset such as clinical variables, genotype, or another set of molecular measurements.

The correct value of constant λ₃ that controls the sparsity of U is highly dataset dependent as it ultimately depends on how well the available prior information explains the data structure. We have devised an adaptive approach that works well for datasets of diverse characteristics. Specifically, we can specify the fraction of latent variables that we wish to be associated with prior information, 0.7 by default. The λ₃ constant is then periodically adjusted by binary search to meet this goal. Even though this adaptive procedure keeps the number of positive entries in U constant regardless of prior information relevance, the significance of pathway association for each LV is ultimately tested by gene-holdout cross-validation (see below).

For our dataset with matched Cytof proportions we used default PLIER parameters. For the DGN dataset we used all default parameters except that k was optimized to maximize the number of LVs with significant pathway association.

Gene-holdout Cross Validation

It is natural to ask to what extent the non-zero coefficients of U represent non-random associations between loadings (columns of Z) and prior information. In order to quantify this we design a cross validation procedure that proceeds as follows. For each pathway included in the entire prior-information compendium a random 1/5th of the positive genes are set to 0 and this new prior information matrix is used to run PLIER. Afterwards, we can test how well the gene loadings in the PLIER output matrix Z are able to recover these held-out genes. Specifically, for each LV-pathway correspondence represented as a positive value in U we compute the AUC and p-value for the recovery of that pathway in the loadings of Z using the held-out set of genes as positive labels and genes not annotated to this pathway as negative labels. We find that the cross-validation procedure produces correct AUC estimates as p-values computed from a gene-level permuted prior information geneset ( which preserves dependencies among pathways) are uniformly distributed (Supplementary Note 1).

While this procedure necessarily discards some data and may adversely effect the ability to detect small pathways we find that the benefit of having accurate statistical estimates outweighs these concerns. PLIER will run in cross-validation mode by default but we allow for cross-validation to be turned off in which case all genes belonging to each geneset are used.

Validation Data

Sample Processing

We used anonymized discard samples that the have the determination of non-human research. Blood was drawn into Tempus tubes (AB scientific) for RNA and into EDTA tubes for Cyto analysis respectively. RNA was extracted using the MagMAX™ for Stabilized Blood Tubes RNA Isolation Kit (Fisher) following the manufacturer’s protocol. Libraries were constructed using the TruSeq Stranded mRNA kit (Illumina) at the Epigenetic core at the Weil Cornell medical college.

CyTOF Sample Processing

CyTOF antibodies were either purchased pre-conjugated from Fluidigm (formerly DVS Sciences) or purchased purified and conjugated in-house using MaxPar X8 Polymer Kits (Fluidigm) according to the manufacturer’s instructions. Whole blood samples were processed within 4hrs of collection and stained by additional of a titrated panel of antibodies (table X) directly to 400uL of whole blood. After 20 minutes of incubation at room temperature, the samples were treated with 4mL of BD FACSLyse and incubated for a further 10mins. The samples were then washed and incubated in 0.125nM Ir intercalator (Fluidigm) diluted in PBS containing 2% formaldehyde, and stored at 4oC until acquisition.

Immediately prior to acquisition, samples were washed once with PBS, once with de-ionized water and then resuspended at a concentration of 1 million cells/ml in deionized water containing a 1/20 dilution of EQ 4 Element Beads (Fluidigm). The samples were acquired on a CyTOF2 (Fluidigm) at an event rate of <500 events/second.

CyTOF Data Analysis

After acquisition, the data were normalized using a bead-based normalization in the CyTOF software and uploaded to Cytobank for initial data processing. The data were gated to exclude residual normalization beads, debris, and doublets, and exported for subsequent clustering and high dimensional analyses.

Individual samples were first clustered using Phenograph [Levine et al., 2015], an agnostic clustering method that utilizes the graph-based Louvain algorithm for community detection and identifies a hierarchical structure of distinct phenotypic communities. The communities were then meta-clustered using Phenograph to group analogous populations across patients. These meta-clustered populations were then manually annotated based on similar canonical marker expression patterns consistent with known immune cell populations. These annotations are also used to generate a consistent cluster hierarchy and structure across all samples in the dataset.

RNAseq methods

The samples were sequenced SE100 to an average depth of 48.8 million reads. Quality assessment was done with FastQC [Bioinformatics, 2011]. Alignment to GenCode hg38 was done using STAR [Dobin et al., 2013]. Transcript counts are assigned using the FeatureCounts tool (subread package [Liao et al., 2013]). The final counts were filtered for genes that had 0 counts in all samples. The data was transformed to RPKM. We also created a quantile normalized count dataset by filtering all genes that had <3 counts in any samples and quantile normalizing the log transformed counts. This more stringent filtering was performed to avoid data artifacts caused by quantile normalization of low count genes. As RNA samples were processed in two separate batched both final datasets were corrected for batch difference.

Details of methods comparisons

For validation we compare the Spearman rank correlation of Cytof based proportion measurements with estimates obtained from different methods. P-values thresholds indicated on the plot are for the single tailed test. We compare performance on the validation dataset against 4 alternative approaches. Two of the approaches are matrix decomposition methods that are commonly applied to gene expression data: sparse principle component analysis (SPC), non-negative matrix factorization (MNF). The other two approaches are reference-based methods that are specifically designed to estimate human blood cell-type proportions. The methods are non-negative least-squale regressionm, NNLS (originally applied to cell-type deconvolution [Abbas et al., 2009]) and Cibersort [Newman et al. 2015]. We found that quantile normalization improved the deconvolution perfromance of matrix decomposition methods (SPC, NMF, and PLIER) but as perviously noted reference based methods (NNLS and Cibersort) performed best with raw (not log transformed) FPKMs.

For NMF we used the default algorithm and matrix norm as implemented in the NMF R package [Brunet et al., 2004]. Since NMF requires a positive matrix we used qunatile normalized log counts which achieved best performance. SPC has no restrictions on the input and in our experiments performed best on z-scored data (z-scored data are also used for PLIER). We used the SPC implementation provided in the PMA package [Witten et al., 2009]. We used the positivity constraint on the loadings matrix, which improved the results. The sparsity hyperparameters for SPC were set with cross-validation separately for each component as described in the original paper [Witten et al., 2009]. Since SPC and NMF do not assign a biological cause to the inferred latent variables, for the purpose of evaluation we report the maximum correlation for each cell-type. The number of components for SPC and NMF was set to 30 which is the same number that was used for PLIER.

For NNLS and Cibersort we used raw FPKM values which is the preferred data trasnformation for Cibersort and also performed best in our evaluations. Since NNLS and Ciberosrt are both reference based methods and can be used with any refernce/basis matrix we tried both approaches with two different references, one from Abbas et al. [2009] and LM22 from the original Cibersort publication. We found that each method performed best with its own original reference. To account for the fact that our cell-type classes are slightly different from those encoded in LM22 or the Abbas et al. [2009] reference we allowed various combinations of the estimates, for example we created an “all-Bcell” estimate by adding naive and memory B cells and picked the best correlated estimate out of the three. A similar approach was taken for other cell types.

Public Data

DGN dataset

The Depression Gene Networks (DGN) dataset is not available for public release but can be requested from National Institute of Mental Health (NIMH) following instructions in the original publication [Mostafavi et al., 2014]. The NIMH database contains several normalized versions of this data and for our study we used “trans” normalized data as described in [Battle et al., 2014]. This data is already normalized for genotype principle components and all known technical factors and no further normalizations were performed.

NESDA dataset

The NESDA (Netherlands Study of Depression and Anxiety) dataset [Wright et al., 2014] was obtained from dbGAP (phs000486.v1). Following suggestions from study authors the NESDA dataset was normalized for known technical factors and the first 3 genotype PCs using linear regression.

Prior information genesets

The generic blood cell-type marker dataset was derived from the IRIS (Immune Response In Silico) [Abbas et al., 2009] and DMAP (Differentiation Map) datasets [Novershtern et al., 2011] datasets. Many canonical marker genes (such as CD19, CD3E, CD8A) have a multimodal distribution with on high expressor group and one or more low/medium expressor ones. The highest expression group typically does not overlap with lower expression distributions and we base our marker selection metric on this observation. Genes were considered to be markers if they could be partitioned into high and medium/low expression so that the difference between minimum and maximum values respectively (the gap between these distributions) exceeds a threshold (we used 2 for IRIS and 0.7 for DMAP). Thi s procedure results in highly overlapping sets of markers for related cell-types however our method is flexible and can easily handle redundancy. The marker sets derived from the IRIS and DMAP datasets are included in the PLIER R package. For the purpose of analyzing DGN we also included cell-type markers from a recent publication [Newman et al., 2015] which covers fewer cell-types but with highly optimized marker sets. The complete prior information dataset used for DGN analysis includes cell-type markers, “canonical pathways” and “chemical and genetic perturbation” genesets from mSigDB, and a set of transcriptional signatures relevant to immune signaling described in [Filiano et al., 2016].

trans-eQTLs

For the purpose of all our analysis we define valid trans associations as gene-SNP pairs where the gene and all of its homologs (as defined by Ensembl database, Zerbino et al. [2017]) are on a different chromosome from that of the SNP.

Gene-centric eQTLs

• Compute p-value for all valid trans associations using rank correlation.

• Compute Benjamini-Hochberg false discovery rate on the total number of valid trans association test.

Pathway-centric eQTLs

Since pathway LVs are composed of multiple genes from different chromosomes all LV-SNP associations are potentially valid trans associations. The steps for computing pathway-centric eQTLs are bellow

• Step 1: Perform rank correlation tests on all LV-SNP pairs.

• Step 2: Compute Benjamini-Hochberg FDR on the entire set of pathway-level test (num. of LVs)x(num. of SNPs). Association with FDR>0.05 are not considered further.

• Step 3: Compute gene-level support for pathway-level eQTLs. Perform all valid trans association test on the subset of SNPs that passed FDR<0.05 for at least on LV in Step 2.

• Step 4: Compute Benjamini-Hochberg FDR for tests in Step 3 correcting for the total number of tests performed overall (number of tests in Step 1 plus number of tests in Step 3). We note that the p-value threshold for FDR=.2 in the PLIER-centric analysis is higher than the gene-centric analysis (4.1e-07 versus 7.7e-08). It is possible that these PLIER-centric FDRs are overly permissive due to the hierarchical nature of the tests in Step1 and Step 3, however we emphasize that we do not rely on these values for any conclusions in our analysis. They are only used to define the upper limit for associations that are checked for replication.

• Step 5: Filter pathway-level effects with low gene-level support. We defined low gene-level support as 0 genes-SNP associations that pass a gene-centric FDR of <0.2. That is any pathway-level associations has to be supported by at least one gene in gene-centric analysis at a permissive FDR. This step is designed to get rid of any spurious trans associations discovered in Step 1 that could arise due to cis genes or cis homologs contributing to the pathway-level estimate.

Replication

To assess replication in the NESDA dataset SNPs were matched based on LD using the LDlink tool with CEU population [Machiela and Chanock, 2015]. Specifically, if the exact SNP was not present in the NESDA dataset we selected the SNP with the highest LD, and if multiple SNPs had the same LD, we took the one closest in genomic coordinates. We only considered a match if the best LD was above 0.5. We asses the relationship between the NESDA replication π₁ and the p – value obtained in DGN in two different ways. On uses a consistent cutoff of λ = 0.05 so that the pi₁ estimate is simply computed as 1 minus the fraction of p-values above 0.05 divided by 0.95. We also evaluate pi₁ using the method implemented the “qvalue” Bioconductor package [Dabney and Storey, 2014]. This method selects the optimal λ for each π₁ estimate. We find that the typical value is around 0.8 though a different value may be selected at each threshold resulting in more noise in the π₁ curve.

Platelet phenotypes

The sentinel SNPs and their relevant phenotypes (MPV, PLT, or both) are supplied as the supplementary table in [Gieger et al., 2011]. Proxy SNPs were defined as above.

Data Availability

Processed gene expression and cell proportion measurements generated for this study are available through the PLIER package. The raw data can be accessed through Gene Expression Ominibus (GSE130824). The Depression Susceptibility Genes and Networks (DGN) dataset can be obtained from NIHM following instructions provided in the original publication [Mostafavi et al., 2014]. The NESDA dataset can be obtained from dbGAP (identifier: phs000486.v1).

Software Availability

The method, auxiliary functions and example datasets (including gene expression and cell proportions data used to generate Fig. 1) are compiled in the PLIER R package available at https://github.com/wgmao/PLIER. PLIER can also be used via an online interface located at http://gobie.csb.pitt.edu/PLIER/.