Abstract
Background
Cardiac MRI is limited by long acquisition times, yet faster acquisition of smaller-matrix images reduces spatial detail. Deep learning (DL) might enable both faster acquisition and higher spatial detail via super-resolution.
Purpose
To explore the feasibility of using DL to enhance spatial detail from small-matrix MRI acquisitions and evaluate its performance against that of conventional image upscaling methods.
Materials and Methods
Short-axis cine cardiac MRI examinations performed between January 2012 and December 2018 at one institution were retrospectively collected for algorithm development and testing. Convolutional neural networks (CNNs), a form of DL, were trained to perform super resolution in image space by using synthetically generated low-resolution data. There were 70%, 20%, and 10% of examinations allocated to training, validation, and test sets, respectively. CNNs were compared against bicubic interpolation and Fourier-based zero padding by calculating the structural similarity index (SSIM) between high-resolution ground truth and each upscaling method. Means and standard deviations of the SSIM were reported, and statistical significance was determined by using the Wilcoxon signed-rank test. For evaluation of clinical performance, left ventricular volumes were measured, and statistical significance was determined by using the paired Student t test.
Results
For CNN training and retrospective analysis, 400 MRI scans from 367 patients (mean age, 48 years ± 18; 214 men) were included. All CNNs outperformed zero padding and bicubic interpolation at upsampling factors from two to 64 (P < .001). CNNs outperformed zero padding on more than 99.2% of slices (9828 of 9907). In addition, 10 patients (mean age, 51 years ± 22; seven men) were prospectively recruited for super-resolution MRI. Super-resolved low-resolution images yielded left ventricular volumes comparable to those from full-resolution images (P > .05), and super-resolved full-resolution images appeared to further enhance anatomic detail.
Conclusion
Deep learning outperformed conventional upscaling methods and recovered high-frequency spatial information. Although training was performed only on short-axis cardiac MRI examinations, the proposed strategy appeared to improve quality in other imaging planes.
© RSNA, 2020
Summary
Deep learning image super resolution can consistently outperform conventional image upscaling methods and can infer high-frequency spatial detail from low-resolution inputs.
Key Results
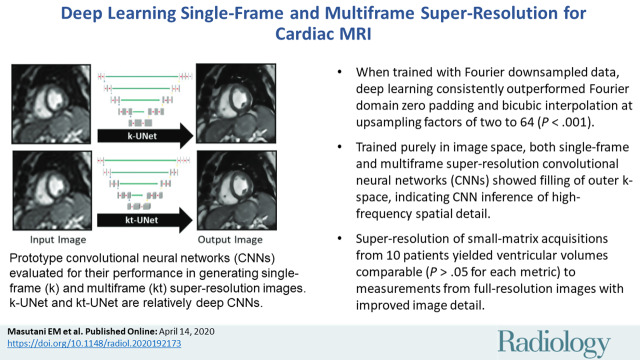
■ When trained with Fourier downsampled data, deep learning consistently outperformed Fourier domain zero padding and bicubic interpolation at upsampling factors of two to 64 (P < .001).
■ Trained purely in image space, both single-frame and multiframe super-resolution convolutional neural networks (CNNs) showed filling of outer k-space, indicating CNN inference of high-frequency spatial detail.
■ Super-resolution of small-matrix acquisitions from 10 patients yielded ventricular volumes comparable (P > .05 for each metric) to measurements from full-resolution images with improved image detail.
Introduction
Cardiac MRI is the clinical reference standard for visual and quantitative assessment of heart function (1). Specifically, cine balanced steady-state free precession (SSFP) can yield cardiac images with high myocardium–blood pool contrast for evaluation of left ventricular (LV) function (2). However, MRI suffers from long acquisition times, often requiring averaging across multiple heartbeats (3), and necessitates a trade-off among spatial resolution, temporal resolution, and scan time (4). Clinically, radiologists are forced to balance acquisition time with resolution to fit clinical needs, and certain applications such as real-time imaging may require small acquisition matrices (5). Image scaling is typically performed by using conventional upscaling methods, such as Fourier domain zero padding and bicubic interpolation (6,7). These methods, however, do not readily recover spatial detail (8), such as the myocardium–blood pool interface or delineation of papillary muscles (6).
The concept of super-resolution, or recovery of high-resolution images from low-resolution observations, has been explored since the 1980s for application in video processing (9). A few algorithms have been proposed (10) in attempts to combine information between spatially shifted and downsampled frames (11). However, based on physical arguments regarding the transformation between image space and Fourier space, multiple authors are skeptical that such methods are feasible (12–14). Peled et al (15) and Tieng et al (16) had inconsistent results when attempting to combine information from multiple intersecting imaging planes to recover spatial resolution in the white matter fiber tract and phantoms, respectively. It is largely believed that without prior knowledge, zero padding of outer k-space is the most reliable and effective method for image upscaling and therefore is widely used as the industry standard (13).
Convolutional neural networks (CNNs), a recently developed form of deep learning (DL), may have potential to overcome some of these limitations (17,18). CNNs learn relevant features from input images to predict desired outputs (18). In medical imaging, CNNs have shown potential for image classification (19), segmentation (20), and localization (1) for MRI and CT. Important to note, CNNs have a large capacity for recalling learned features and might supply a priori information and assumptions during inference (21). Our aim was to explore the feasibility of DL for enhancing spatial detail from small-matrix MRI acquisitions and evaluate its performance against that of the conventional image upscaling methods of Fourier domain zero padding and bicubic interpolation.
Materials and Methods
Prototype Neural Networks
We developed and evaluated four neural networks (18,22,23) for their ability to perform single-frame (k) and multiframe (kt) super resolution. All algorithms were developed by the lead author, a 4th-year doctoral student (E.M.M.). Two general neural network architectures were explored for feasibility in performing this task (Fig E1 [online]). The first, a relatively shallow network, is a super-resolution CNN–inspired neural network (24), which we refer to as k-SRNet (http://mmlab.ie.cuhk.edu.hk/projects/SRCNN.html). The second, a deeper, more complex network, is a modified U-Net CNN (25), which we refer to as k-UNet (https://github.com/zhixuhao/unet).
Multiframe Neural Networks
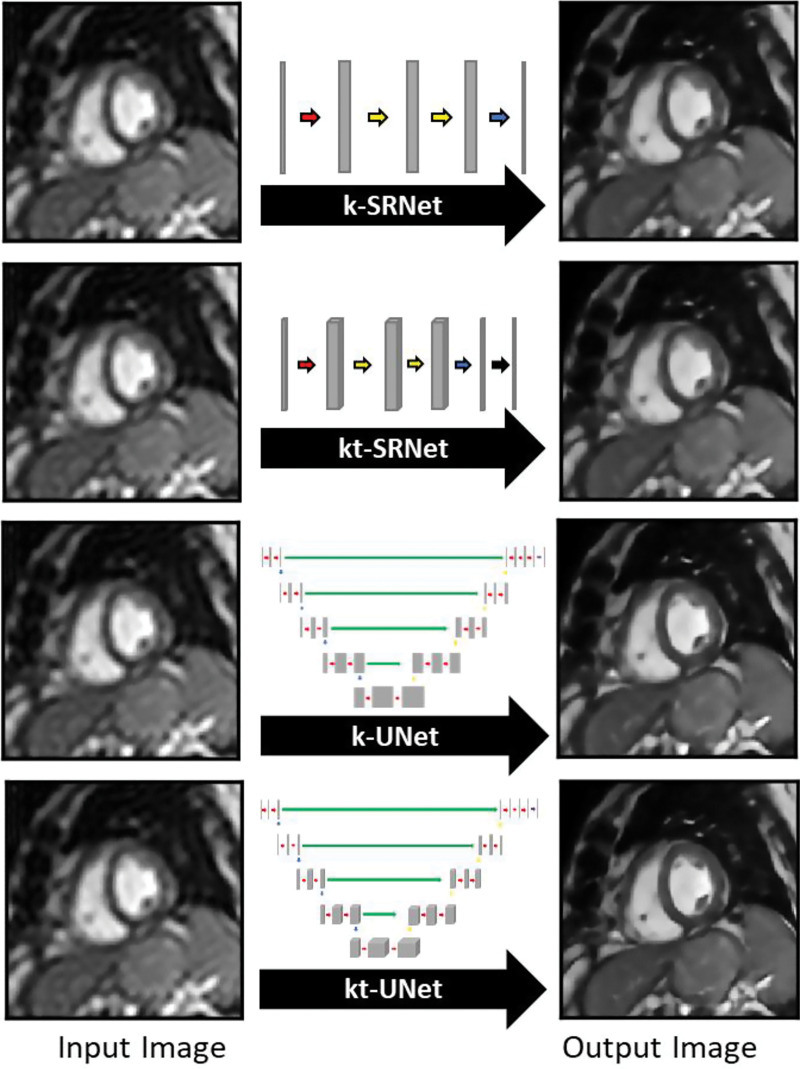
Given that additional data from neighboring time points might improve performance, we extended both architectures to incorporate three-dimensional convolutions, handling the temporal domain in the third dimension. Each input frame was combined with immediately flanking frames to generate input volumes. We refer to these spatiotemporal versions of k-SRNet and k-UNet as kt-SRNet and kt-UNet (Fig 1), respectively.
Figure 1:
Images show prototype convolutional neural networks (CNNs) evaluated for their performance in generating single-frame (k) and multiframe (kt) super-resolution images. The k-SRNet and kt-SRNet CNNs are examples of shallow networks and k-UNet and kt-UNet are relatively deep CNNs used to perform this task.
Patients and Image Data
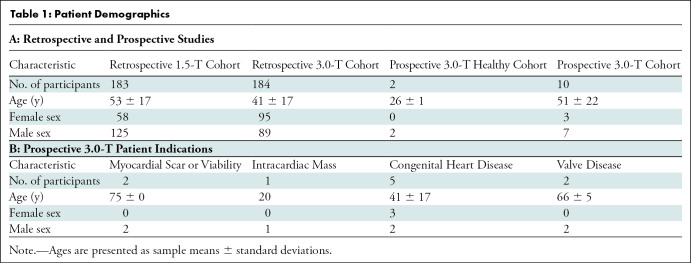
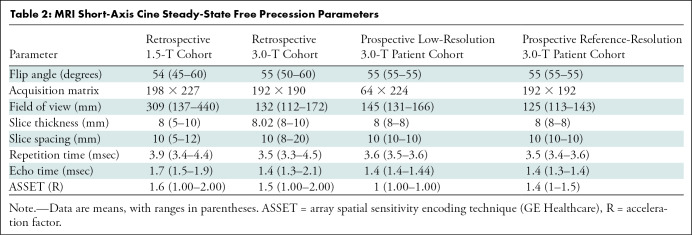
This study was compliant with the Health Insurance Portability and Accountability Act, and institutional review board approval and waiver of written informed consent were obtained. We retrospectively collected a convenience sample of short-axis (SAX) cine SSFP series from 400 clinical cardiac MRI examinations performed at our academic institution in 367 patients between January 2012 and December 2018 for algorithm development (Table 1). No exclusion criteria were applied. Of these 400 studies, 200 were performed with a 1.5-T MRI scanner (Signa HDxt; GE Healthcare, Waukesha, Wis) and 200 were performed with a 3.0-T MRI scanner (Discovery MR750 DV26; GE Healthcare) (Table 2).
Table 1:
Patient Demographics
Table 2:
MRI Short-Axis Cine Steady-State Free Precession Parameters
Synthetic Training Data
We developed a strategy for generation and use of synthetic training data to mimic the super-resolution task. Training workflow comprised two steps: (a) cropping a central 128 × 128 area of the SAX image to standardize image presentation and serve as ground truth and (b) windowing a central region of k-space to generate synthetic training data (Fig 2).
Figure 2:
Diagram shows strategy for generation of synthetic training data. Source image data were first cropped to standardize image presentation to the neural network and were windowed in Fourier space to mimic a fully sampled low-resolution acquisition. The cropped images were later used as ground truth for training, and the downsampled images were used as synthetic input images. Z-PAD = zero padding.
Fourier Downsampling
To mimic low-resolution small-matrix MRI acquisitions, we performed a process we refer to as Fourier downsampling. Each downsampling factor was simulated by retaining central windows of k-space of varying sizes. Outer portions of k-space were zero filled to a matrix size of 128 × 128. Images were transformed back to the image domain, and pixel values were scaled to 0 and 1. Each downsampling (and commensurate upsampling) factor was defined as the ratio of the k-space window area to the cropped 128 × 128 area.
Neural Network Training
SAX examinations were randomly divided and allocated to 70% (140 of 200 1.5-T examinations and 140 of 200 3-T examinations) for training, 20% (40 of 200 1.5-T examinations and 40 of 200 3.0-T examinations) for validation, and 10% (20 of 200 1.5-T examinations and 20 of 200 3.0-T examinations) for testing. We trained our networks on two workstations running Ubuntu 16.04 (Canonical, London, England) and equipped with either two Titan Xp graphics cards or one Titan V graphics card (Nvidia, Santa Clara, Calif). We used Keras 2.2.4 with TensorFlow-GPU 1.12.0 (Google, Mountain View, Calif) at the back end for all DL experiments.
Hybrid Loss Function
We chose to use a hybrid loss function based on the work of Zhao et al (26). Specifically, our loss function was the sum of L1 loss and a modified form of the multiscale structural similarity index (SSIM) loss (defined as 1 minus multiscale SSIM) (27) (Appendix E1 [online]).
Evaluation of Performance
In compliance with the Health Insurance Portability and Accountability Act and with institutional review board approval and written informed consent, we prospectively acquired SAX and four-chamber cine SSFP cardiac MRI series at 3.0 T in two healthy men and 10 clinical patients at low resolution and full resolution (Table 1). Low-resolution scans were performed with a 64 × 224 matrix (resulting in a 3.5-fold shortened scan time), and full-resolution scans were performed with a 192 × 192 matrix while leveraging the array spatial sensitivity encoding technique (ASSET; GE Healthcare). The super-resolution networks were then applied to low-resolution acquisitions and, with a tiling approach, they were also applied to full-resolution acquisitions (Appendix E1 [online]).
To evaluate the clinical utility of our strategy, we measured LV end-diastolic volume (EDV), LV end-systolic volume (ESV), LV stroke volume (SV), and LV ejection fraction (EF) in the patient cohort. One researcher (E.M.M.) performed all segmentation and volumetric analyses with software (Arterys Cardio DL, version 19.14.2; Arterys, San Francisco, Calif) under the supervision of a cardiovascular radiologist with 12 years of experience in cardiac MRI (A.H.).
Statistical Analysis
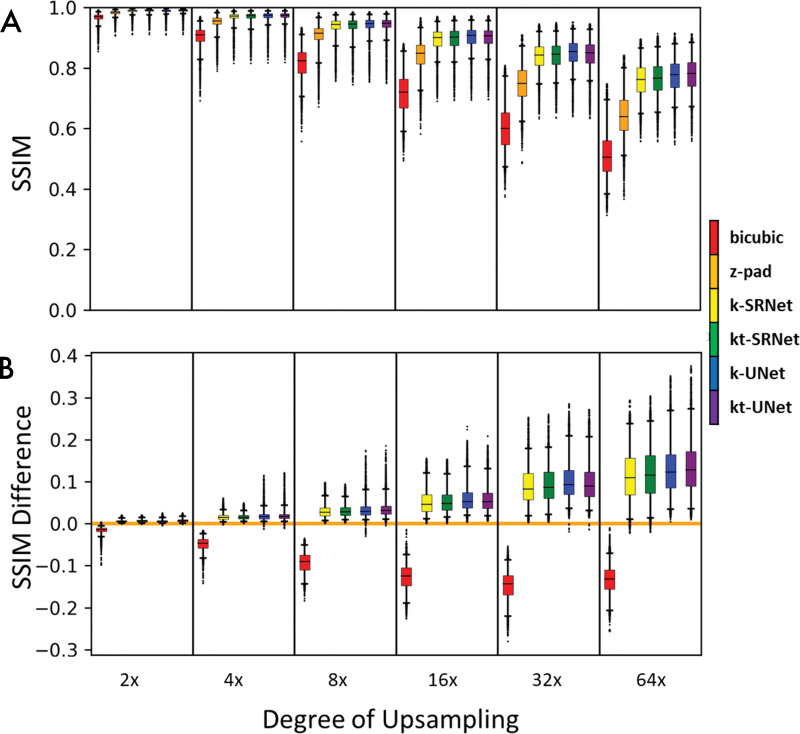
We compared CNN-based approaches and conventional methods of bicubic interpolation and zero padding by calculating the SSIM (28) between each ground truth image and its corresponding super-resolved image from each method of upscaling (Fig 3, A). We reported the mean and standard deviation of SSIM and determined statistical significance by using the Wilcoxon signed-rank test with a type I error threshold of 0.05 (P < .05). For our comparison of SSIM performance relative to zero padding (Fig 3, B), we calculated the pairwise difference of SSIM between zero padding and each super-resolution method.
Figure 3:
Box-and-whisker plots compare performance based on the structural similarity index (SSIM) for each super-resolution method across multiple upsampling factors. Boxes encapsulate interquartile ranges, whiskers demarcate the central 95% of data points, and black bars lie on the median (n = 9907 short-axis slices from testing set). A, Aggregate performance for each super-resolution method. B, Pairwise comparison of performance between each method and zero padding (z-pad). Deep learning–based methods consistently outperformed conventional methods on bulk and per-slice bases. Neural network–based methods outperformed traditional bicubic and zero padding for nearly every slice evaluated. Zero padding outperformed the bicubic method for nearly every slice evaluated. k = single frame, kt = multiframe.
To compare LV volumes from paired CNN super-resolved low-resolution acquisitions and high-resolution clinical acquisitions, we reported the mean and standard deviation of LV EDV, LV ESV, LV SV, and LV EF and determined statistical significance by using paired Student t test with a type I error threshold of 0.05 (P < .05). We used software (Python, version 3.5, Python Software Foundation, Wilmington, Del; Microsoft Excel, version 1912, Microsoft, Redmond, Wash) for all statistical analyses.
Results
Patient Characteristics
For CNN development, we retrospectively collected 200 1.5-T examinations from 183 patients (mean age, 53 years ± 17; 125 male patients) and 200 3.0-T examinations from 184 patients (41 years ± 17; 89 male patients). We prospectively collected two 3.0-T examinations from two healthy volunteers (26 years ± 1; two male patients) and 10 3.0-T examinations from 10 clinical patients (51 years ± 22; seven male patients) (Table 1). We did not exclude any of our initial 12 prospectively acquired participants.
Quantitative Differences
The SSIMs of shallow (SRNet) and deep (UNet) CNNs are shown in Table 3 and Figure 3. Mean SSIMs for zero padding ranged from 0.645 ± 0.074 at upsampling by a factor of 64 to 0.983 ± 0.007 at upsampling by a factor of two. Mean SSIMs for k-SRNet, the most poorly performing CNN, ranged from 0.760 ± 0.056 at upsampling by a factor of 64 to 0.989 ± 0.006 at upsampling by a factor of two. For all degrees of upsampling tested, every CNN outperformed conventional upscaling methods (P < .001) (Fig 3, A).
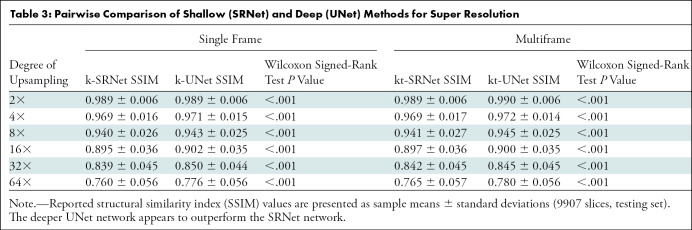
Table 3:
Pairwise Comparison of Shallow (SRNet) and Deep (UNet) Methods for Super Resolution
On a per-slice basis, every CNN consistently outperformed zero padding for nearly all input images (Fig 3, B). All four methods—k-SRNet, kt-SRNet, k-UNet, and kt-UNet—outperformed zero padding on more than 99.2% (9828 of 9907) of slices at all reported degrees of upsampling.
For synthetic test data, there were differences between SRNet and UNet (Table 3). For all degrees of upsampling, k-UNet and kt-UNet outperformed k-SRNet and kt-SRNet, respectively (P < .001). In addition, kt-SRNet outperformed k-SRNet at all degrees of upsampling (P < .001), whereas kt-UNet outperformed k-UNet at upsampling factors of two, four, eight, and 64 (P < .001). We observed average SSIM within 0.02 of all CNNs across each upsampling factor, in contrast to a widening performance gap with conventional upscaling methods with higher upsampling factors (Fig 3, A).
Qualitative Differences
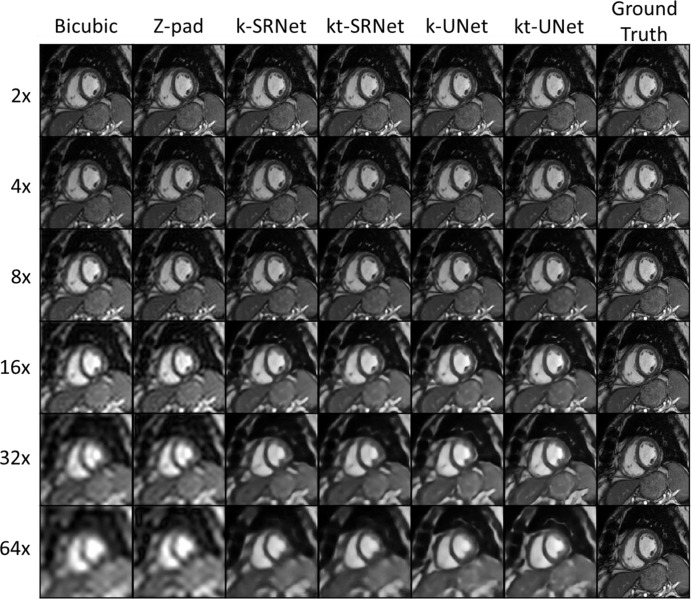
We present examples of each upsampling method in a 62-year-old man (Fig 4). At upsampling by a factor of eight, bicubic interpolation showed noticeably reduced sharpness of the right ventricular trabeculations and the myocardium–blood pool interface. At upsampling by a factor of 16, all methods showed noticeable image quality degradation, particularly with respect to papillary muscle sharpness; however, the edges of the interventricular septum were noticeably sharper in the CNN outputs. At upsampling by a factor of 32, the LV papillary muscles appeared to blend in with the LV walls in the bicubic and zero-padding outputs. The ventricular walls were noticeably blurry in bicubic and zero-padding outputs. Although there was some gross loss in texture of the blood pool and blurriness of the papillary muscles in the CNNs, the boundaries of the ventricular walls remained sharp. At upsampling by a factor of 64, the boundary between the right ventricular wall and the blood pool became severely blurred with the conventional upscaling methods; all papillary muscle detail was also lost. The ventricular walls and boundaries remained sharp in all CNNs. From upsampling factors of eight to 64, z padding shows increasingly noticeable Gibbs artifact, which is absent in CNN predictions.
Figure 4:
Representative example images in a 62-year-old man for comparison of super-resolution methods across multiple upsampling factors. Neural network–based methods had a pronounced effect at upsampling by a factor of eight or more. k = single frame, kt = multiframe, Z-pad = zero padding.
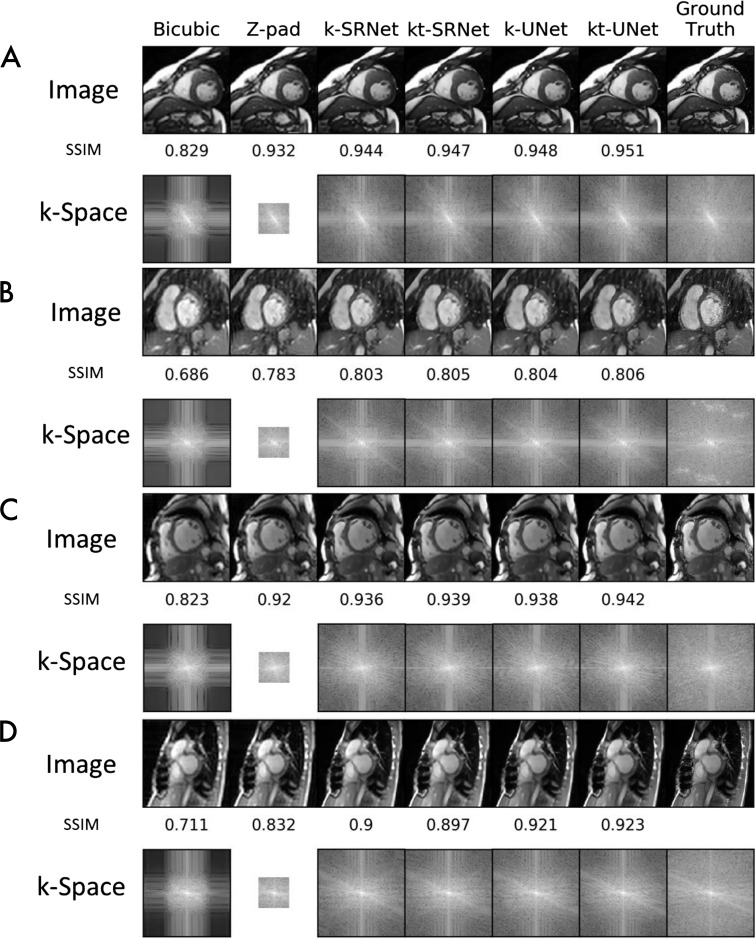
We present representative examples, upsampled by a factor of eight with each super-resolution method, in Figure 5. Each example shows the output image and corresponding k-space log plots for each method. In a 36-year-old man with hypertrophic cardiomyopathy examined at 1.5 T (Fig 5, A), only bicubic interpolation showed reduced image quality relative to ground truth. The log plots indicate that CNNs filled the outer k-space. CNNs also reduced severe radiofrequency artifacts in a 1.5-T examination in a 44-year-old woman (Fig 5, B). Both bicubic interpolation and zero padding showed reduced sharpness at the myocardium–blood pool interface and increased graininess compared with CNN outputs. The log plots showed radiofrequency artifacts in ground truth outer k-space, which were markedly reduced in CNN predictions.
Figure 5:
Example images compare super-resolution methods at upsampling by a factor of eight. Output images and corresponding log plots of k-space are shown along with the structural similarity index (SSIM) relative to ground truth. At 1.5 T, neural network methods, A, perform well in a 36-year-old male patient with hypertrophic cardiomyopathy and, B, serendipitously repair severe radiofrequency artifact in the outer k-space in a 44-year-old female patient. At 3.0 T, neural network methods, C, perform well in a 54-year-old female patient with dilated cardiomyopathy and, D, tolerate artifacts from sternal wires in a 28-year-old female patient. k = single frame, kt = multiframe, Z-pad = zero padding.
In a 54-year-old woman with dilated cardiomyopathy examined at 3.0 T (Fig 5, C), we saw loss of image sharpness with bicubic interpolation alone. The corresponding log plots indicated filling of outer k-space for all CNNs. CNNs also successfully super-resolved a 3.0-T examination with artifact from sternal wires in a 28-year-old woman (Fig 5, D). Both bicubic interpolation and zero padding showed increased blurring of the myocardium–blood pool boundary relative to CNN outputs. SSIMs of bicubic interpolation and zero padding were also markedly lower relative to CNN predictions. The log plots again indicated outer k-space filling by CNNs.
To illustrate an extreme upsampling factor, we performed super-resolved examinations upsampled by a factor of 64 at 1.5 and 3.0 T (Fig E2 [online]). All super-resolution–method outputs displayed loss of detail in right ventricular trabeculations, LV papillary muscles, and the blood pool; however, CNNs clearly demarcated the myocardium–blood pool boundary. CNNs also exhibited markedly higher SSIM.
Clinical Proof of Concept
To assess clinical feasibility of the super-resolution technique, we undertook a proof-of-concept evaluation, prospectively acquiring SAX and four-chamber SSFP images in low resolution and full resolution in two healthy participants and 10 clinical patients (Fig 6).
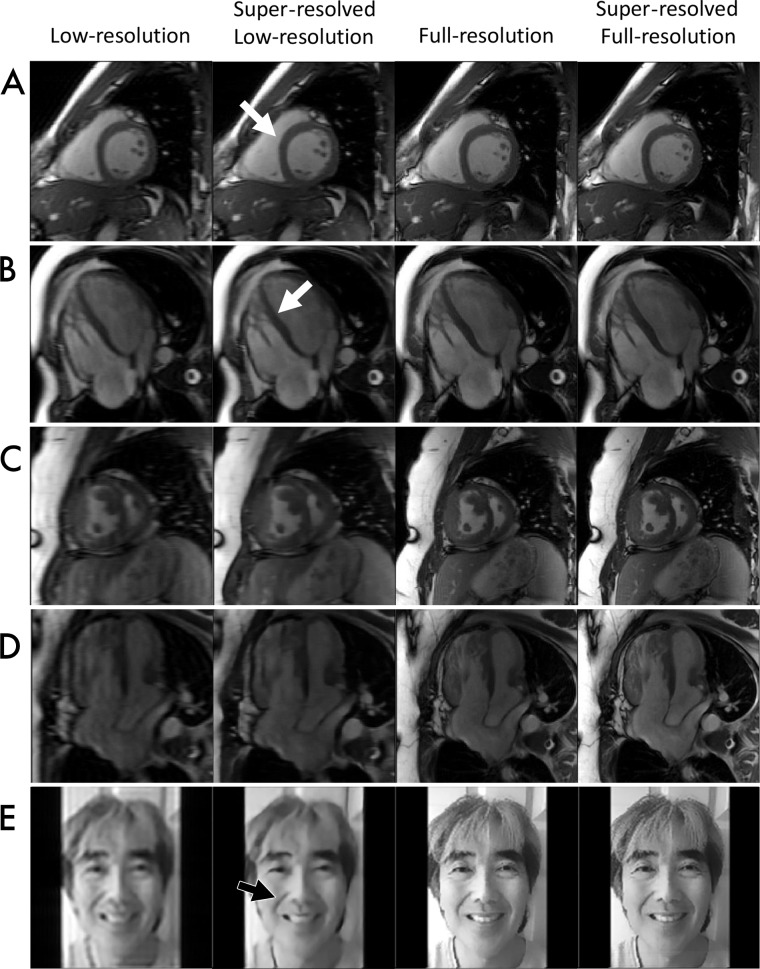
Figure 6:
Images demonstrate proof-of-concept assessment of super-resolution methods. Low-resolution input, full-resolution reference, and k-UNet super-resolved images are shown for five experiments: A, short-axis cine steady-state free precession (SSFP) in a 27-year-old healthy male volunteer at 3.0 T, B, four-chamber cine SSFP in a 26-year-old healthy male volunteer at 3.0 T, C, short-axis cine SSFP in a 36-year-old patient with transposition of the great arteries after Mustard switch, D, four-chamber cine SSFP in the same patient as in, C, and, E, photographs of a human face. The k-UNet network appears to improve myocardium–blood pool delineation, especially along the septal wall. Although trained only with short-axis images, the k-UNet network appears to generalize to long-axis images and digital photographs, sharpening details. This network also appears to further enhance detail of low-resolution images and full-resolution reference acquisitions.
In the two healthy participants, we qualitatively assessed the performance of CNNs in enhancing anatomic detail. The k-UNet successfully super-resolved 2.4-fold abbreviated 3.0-T SAX images in a healthy 27-year-old man. We noted sharpening of the myocardium–blood pool interface, right ventricular trabeculations, and LV papillary muscles (Fig 6, A). The k-UNet, trained only on SAX images, also super-resolved 2.4-fold abbreviated four-chamber acquisitions from a healthy 26-year-old man and increased sharpness of right ventricular trabeculations and the septal wall (Fig 6, B).
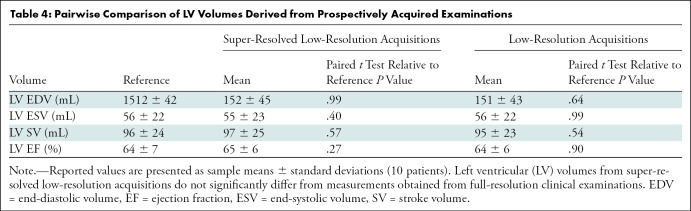
In the cohort of 10 clinical patients, we quantitatively assessed ventricular volumetry and ejection fraction. There were no significant differences between volumetric measurements obtained from super-resolved low-resolution images and full-resolution images (Table 4). On average, reference examinations yielded LV EDV of 152 mL, LV ESV of 58 mL, LV SV of 96 mL, and LV EF of 64%. On average, super-resolved low-resolution images yielded values as follows, and the differences were not significantly different: LV EDV, 152 mL (P = .99); LV ESV, 55 mL (P = .40); LV SV, 98 mL (P = .57); and LVEF, 65% (P = .27). From this cohort, we show representative super-resolved low-resolution SAX (Fig 6, C) and four-chamber (Fig 6, D) images from a 36-year-old female patient with transposition of the great arteries after Mustard atrial switch. Super resolution yielded reduced Gibbs artifact and sharpened myocardium–blood pool interfaces compared with the low-resolution input images. When applied to full-resolution input images, super resolution also achieved a similar effect, with reduced Gibbs artifact and sharpened myocardium–blood pool interfaces.
Table 4:
Pairwise Comparison of LV Volumes Derived from Prospectively Acquired Examinations
To explore whether our CNNs have applicability beyond MRI, we super-resolved a low-resolution photograph of a human face (Fig 6, E). The k-UNet removed much of the Gibbs artifact and sharpened edges. Finally, we further super-resolved high-resolution reference images using k-UNet. We observed sharper edges and less pixelation on all super-resolved high-resolution reference images.
Discussion
We have demonstrated the feasibility of convolutional neural networks (CNNs) to super-resolve cardiac MRI scans acquired at both 1.5 T and 3.0 T at a wide range of upsampling factors. We quantitatively showed that both SRNets and UNets outperform conventional upscaling methods including Fourier domain zero padding and bicubic interpolation at multiple upsampling factors as evaluated with structural similarity index (SSIM) on more than 99.2% (9828 of 9907) of slices (P < .001). Qualitatively, CNNs appeared to improve some spatial details, including the myocardium–blood pool boundary. We further showed that this approach works not only with synthetic low-resolution data, but also prospectively with patients referred clinically for cardiac MRI. Super resolution does not appear to negatively impact ventricular volumetry, achieving comparable left ventricular (LV) end-diastolic volume, LV end-systolic volume, LV stroke volume, and LV ejection fraction values between super-resolved low-resolution images and full-resolution reference images, while recovering noticeable improvement in spatial detail.
The concept of super-resolution in MRI has been explored in earlier studies, albeit without application of CNNs. These studies (9,15,16) attempted to recover in-plane high-frequency spatial information from multiple low-resolution frames but were not successful (9,12–14). Many authors have felt that spatially shifted low-resolution images do not provide informational content to resolve high-frequency detail. Unlike earlier approaches, the CNNs we explored here appeared to work even on a single image frame. In fact, the addition of multiple adjacent frames did not markedly improve performance in our study. We are uncertain why each of the CNNs we evaluated appeared to accomplish super-resolution. We speculate that this might be related to the large feature capacity of CNNs (21), which can carry learned information as prior knowledge. For this application, the learned information appears to generalize across multiple views, including the four-chamber view and, surprisingly, a photograph of a human face.
Clinically, super resolution could be used to reduce scan time, increase temporal resolution, or both. Acquisition time is, of course, proportional to the number of phase-encode lines measured (29). This results in relatively long breath holds for cardiac MRI, which cannot be tolerated by many patients. Multiple methods are now available to abbreviate acquisition, including parallel imaging (29) and compressed sensing (30). Given that we have been able to implement this as an image-space task, it is possible that CNN-based super resolution may be combined with these techniques.
Our study had some limitations. First, initial analyses of performance were based on synthetically downsampled images. Second, we sourced training data from scanners from one vendor at one institution. Clinical evaluation was limited to proof of concept, showing feasibility in 12 patients. Finally, we were able to apply super-resolution to the full-resolution image data, but ultimately there is no reference standard for this final comparison because exceedingly long breath holds would be required.
In conclusion, in this proof-of-concept study we showed that convolutional neural network (CNNs) can recover high-frequency spatial detail from low-resolution MRI scans. Each of the CNNs we evaluated (SRNet and Unet) outperformed traditional zero padding and bicubic image upscaling strategies. Further work may be required to evaluate general applicability across institutions, MRI vendors, or other pulse sequences, but these results show feasibility of super-resolution methods to improve the speed of MRI acquisition. In particular, for cardiac MRI, it is often challenging to acquire high-quality images in patients with arrhythmia. A real-time strategy that combines multiple techniques including CNN super-resolution might make this more feasible.
APPENDIX
SUPPLEMENTAL FIGURES
Acknowledgments
Acknowledgments
We gratefully acknowledge the National Institute of General Medical Sciences; National Heart, Lung, and Blood Institute; and GE Healthcare for their generous support for this work. We thank Nvidia for generously donating Titan Xp and GV100 GPUs for training the convolutional neural networks in this research and the San Diego Supercomputer Center for providing GPU-accelerated compute time. Additionally, we thank Dr Stephen Masao Masutani, the lead author’s father, for providing a photograph of his face for use in this work.
E.M.M. supported by the University of California San Diego Medical Scientist Training Program (NIH/NIHGMS T32GM007198) and the Integrative Bioengineering of Heart Vessels and Blood Training Program (NHLBI T32 HL105373). A.H. supported by a research grant from GE Healthcare.
Disclosures of Conflicts of Interest: E.M.M. Activities related to the present article: disclosed no relevant relationships. Activities not related to the present article: disclosed no relevant relationships. Other relationships: institution has filed a provisional patent for spatiotemporal resolution enhancement of biomedical images. N.B. Activities related to the present article: disclosed no relevant relationships. Activities not related to the present article: was a consultant for GE Healthcare. Other relationships: disclosed no relevant relationships. A.H. Activities related to the present article: disclosed no relevant relationships. Activities not related to the present article: is a consultant for Arterys; institution received grants from GE Healthcare, Bayer, and Arterys; institution has filed a provisional patent for spatiotemporal resolution enhancement of biomedical images; holds stock in Arterys; received travel assistance from GE Healthcare and Arterys. Other relationships: disclosed no relevant relationships.
Abbreviations:
- CNN
- convolutional neural network
- DL
- deep learning
- EDV
- end-diastolic volume
- EF
- ejection fraction
- ESV
- end-systolic volume
- k
- single frame
- kt
- multiframe
- LV
- left ventricle
- SAX
- short axis
- SSFP
- steady-state free precession
- SSIM
- structural similarity index
- SV
- stroke volume
References
- 1.Blansit K, Retson T, Masutani E, Bahrami N, Hsiao A. Deep Learning-based Prescription of MR Cardiac Imaging Planes. Radiol Artif Intell 2019;1(6):e180069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Feng L, Srichai MB, Lim RP, et al. Highly accelerated real-time cardiac cine MRI using k-t SPARSE-SENSE. Magn Reson Med 2013;70(1):64–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Xue H, Kellman P, Larocca G, Arai AE, Hansen MS. High spatial and temporal resolution retrospective cine cardiovascular magnetic resonance from shortened free breathing real-time acquisitions. J Cardiovasc Magn Reson 2013;15(1):102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wang Y, Ying L. Compressed sensing dynamic cardiac cine MRI using learned spatiotemporal dictionary. IEEE Trans Biomed Eng 2014;61(4):1109–1120. [DOI] [PubMed] [Google Scholar]
- 5.Setser RM, Fischer SE, Lorenz CH. Quantification of left ventricular function with magnetic resonance images acquired in real time. J Magn Reson Imaging 2000;12(3):430–438. [DOI] [PubMed] [Google Scholar]
- 6.Ashikaga H, Estner HL, Herzka DA, Mcveigh ER, Halperin HR. Quantitative Assessment of Single-Image Super-Resolution in Myocardial Scar Imaging. IEEE J Transl Eng Health Med 2014;2:1800512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bernstein MA, Fain SB, Riederer SJ. Effect of windowing and zero-filled reconstruction of MRI data on spatial resolution and acquisition strategy. J Magn Reson Imaging 2001;14(3):270–280. [DOI] [PubMed] [Google Scholar]
- 8.Semmlow JL, Griffel B. Biosignal and Medical Image Processing. 3rd ed. Boca Raton, Fla: CRC, 2014. [Google Scholar]
- 9.Van Reeth E, Tham IWK, Tan CH, Poh CL. Super-resolution in magnetic resonance imaging: A review. Concepts Magn Reson Part A Bridg Educ Res 2012;40A(6):306–325. [Google Scholar]
- 10.Irani M, Peleg S. Motion Analysis for Image Enhancement: Resolution, Occlusion, and Transparency. J Vis Commun Image Represent 1993;4(4):324–335. [Google Scholar]
- 11.Greenspan H. Super-Resolution in Medical Imaging. Comput J 2008;52(1):43–63. [Google Scholar]
- 12.Scheffler K. Superresolution in MRI? Magn Reson Med 2002;48(2):408; author reply 409. [DOI] [PubMed] [Google Scholar]
- 13.Greenspan H, Oz G, Kiryati N, Peled S. MRI inter-slice reconstruction using super-resolution. Magn Reson Imaging 2002;20(5):437–446. [DOI] [PubMed] [Google Scholar]
- 14.Uecker M, Sumpf TJ, Frahm J. Reply to: MRI resolution enhancement: how useful are shifted images obtained by changing the demodulation frequency? Magn Reson Med 2011;66(6):1511–1512; author reply 1513–1514. [DOI] [PubMed] [Google Scholar]
- 15.Peled S, Yeshurun Y. Superresolution in MRI: application to human white matter fiber tract visualization by diffusion tensor imaging. Magn Reson Med 2001;45(1):29–35. [DOI] [PubMed] [Google Scholar]
- 16.Tieng QM, Cowin GJ, Reutens DC, Galloway GJ, Vegh V. MRI resolution enhancement: how useful are shifted images obtained by changing the demodulation frequency? Magn Reson Med 2011;65(3):664–672. [DOI] [PubMed] [Google Scholar]
- 17.McCann MT, Jin KH, Unser M. Convolutional Neural Networks for Inverse Problems in Imaging: A Review. IEEE Signal Process Mag 2017;34(6):85–95. [Google Scholar]
- 18.Retson TA, Besser AH, Sall S, Golden D, Hsiao A. Machine Learning and Deep Neural Networks in Thoracic and Cardiovascular Imaging. J Thorac Imaging 2019;34(3):192–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bahrami N, Retson T, Blansit K, Wang K, Hsiao A. Automated selection of myocardial inversion time with a convolutional neural network: Spatial temporal ensemble myocardium inversion network (STEMI-NET). Magn Reson Med 2019;81(5):3283–3291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wang K, Mamidipalli A, Retson T, et al. Automated CT and MRI Liver Segmentation and Biometry Using a Generalized Convolutional Neural Network. Radiol Artif Intell 2019;1(2):180022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Krizhevsky A, Sutskever I, Hinton GE. ImageNet Classification with Deep Convolutional Neural Networks. 2012:1097-1105. https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks. Accessed September 17, 2019. [Google Scholar]
- 22.Chartrand G, Cheng PM, Vorontsov E, et al. Deep Learning: A Primer for Radiologists. RadioGraphics 2017;37(7):2113–2131. [DOI] [PubMed] [Google Scholar]
- 23.Zhu G, Jiang B, Tong L, Xie Y, Zaharchuk G, Wintermark M. Applications of deep learning to neuro-imaging techniques. Front Neurol 2019;10(AUG):869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dong C, Loy CC, He K, Tang X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans Pattern Anal Mach Intell 2016;38(2):295–307. [DOI] [PubMed] [Google Scholar]
- 25.Ronneberger O, Fischer P, Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In: Navab N, Hornegger J, Wells W, Frangi A, eds. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015. MICCAI 2015. Lecture Notes in Computer Science, vol 9351. Cham, Switzerland: Springer, 2015; 234–241. [Google Scholar]
- 26.Zhao H, Gallo O, Frosio I, Kautz J. Loss Functions for Image Restoration With Neural Networks. IEEE Trans Comput Imaging 2017;3(1):47–57. [Google Scholar]
- 27.Wang Z, Simoncelli EP, Bovik AC. Multiscale structural similarity for image quality assessment. In: The Thirty-Seventh Asilomar Conference on Signals, Systems & Computers, 2003, Pacific Grove, Calif, November 9–12, 2003. Piscataway, NJ: IEEE, 2003; 1398–1402. [Google Scholar]
- 28.Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process 2004;13(4):600–612. [DOI] [PubMed] [Google Scholar]
- 29.Deshmane A, Gulani V, Griswold MA, Seiberlich N. Parallel MR imaging. J Magn Reson Imaging 2012;36(1):55–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med 2007;58(6):1182–1195. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.