We synthesized a new allotrope of nitrogen, providing prospects for nitrogen-based high-energy-density materials and 2D materials.
Abstract
Group V elements in crystal structure isostructural to black phosphorus with unique puckered two-dimensional layers exhibit exciting physical and chemical phenomena. However, as the first element of group V, nitrogen has never been found in the black phosphorus structure. Here, we report the synthesis of the black phosphorus–structured nitrogen at 146 GPa and 2200 K. Metastable black phosphorus–structured nitrogen was retained after quenching it to room temperature under compression and characterized in situ during decompression to 48 GPa, using synchrotron x-ray diffraction and Raman spectroscopy. We show that the original molecular nitrogen is transformed into extended single-bonded structure through gauche and trans conformations. Raman spectroscopy shows that black phosphorus–structured nitrogen is strongly anisotropic and exhibits high Raman intensities in two Ag normal modes. Synthesis of black phosphorus–structured nitrogen provides a firm base for exploring new type of high-energy-density nitrogen and a new direction of two-dimensional nitrogen.
INTRODUCTION
The black phosphorus (BP) structure is widely adopted by group V elements, with nitrogen being the apparent exception. Unlike other group V elements, with atoms connected by single bonds that can then more readily form extended BP-structured solids, nitrogen forms diatomic N2 molecules held together by a very strong triple bond that is the strongest bond among all known molecules. To transform N2 molecules into BP-structured nitrogen, enormous energy would be required to convert the N≡N triple bond into N─N single bond. This requires extreme conditions to be applied and is very difficult to achieve. However, once BP nitrogen is formed, it would release a huge amount of energy when transforming back to N2, making it a powerful high-energy-density material (1–3). In addition, the emergence of the group V element family with two-dimensional (2D) BP crystalline structure (4–7) is of particular interest during the past 5 years. The existence of BP structure in phosphorus, arsenic, antimony, and bismuth allows the synthesis of the BP-structured 2D materials phosphorene (5), arsenene, antimonene, and bismuthine (8), which have highly anisotropic layers (Fig. 1, C to E) being “puckered” in one direction and smooth in the other direction. Obtaining BP structure in nitrogen would complete the set of BP-structured materials in group V and open up the possibility for developing nitrogen-based 2D materials.
Fig. 1. XRD characterization and illustration of the crystal structure of BP-structured nitrogen.
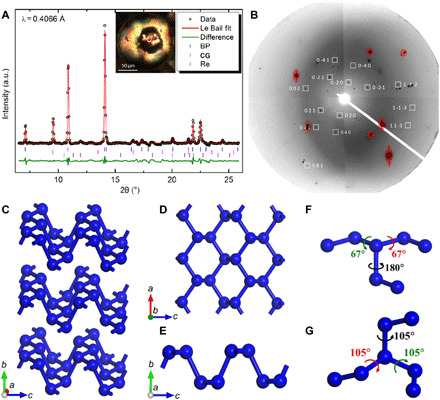
(A) Le Bail fit of XRD data at 132 GPa. Black circles, red line, and green line represent experimental data, Le Bail fitting, and residual, respectively. Blue, pink, and purple ticks mark reflections for BP-structured nitrogen, CG-nitrogen, and Re, respectively. Inset shows the microscopic image of the sample under illumination with both reflected and transmitted light, with the white circle marking the sample position being measured. BP and CG stand for BP-structured nitrogen and CG-nitrogen, respectively. (B) 2D x-ray diffraction (XRD) image from grain #2. White boxes mark the diffraction spots of BP-structured nitrogen. Numbers indicate corresponding Miller indices. Image is obtained by merging selected step scan patterns that contain BP-structured nitrogen reflections for demonstration. (C) Crystal structure of BP-structured nitrogen. (D and E) Single nitrogen layer in BP-structured nitrogen. (F and G) Dihedral angles in BP-structured nitrogen and CG-nitrogen calculated at 132 GPa, respectively. a.u., arbitrary units.
The experimental search of BP-structured nitrogen under extreme conditions, which revealed a couple of polymeric nitrogen in other crystal structures, remained unsuccessful. A series of theoretical models (including BP structure) have been proposed for polymeric nitrogen, among which “cubic gauche (CG)”–structured single-bonded nitrogen was calculated to be the thermodynamic ground state of nitrogen at high pressure (9) and was synthesized experimentally at 110 GPa and 2000 K (10). An additional single-bonded nitrogen phase in the layered polymeric (LP) structure was found to coexist with the CG-nitrogen over a similar pressure-temperature (P-T) range (11). LP-N has a crystal structure close to a previously predicted Pba2 structure (12) and exhibits interesting properties such as large Raman cross section and high stiffness. Very recently, a hexagonal layered polymeric nitrogen (HLP-N) was identified above 180 GPa (13). Despite these discoveries of single-bonded nitrogen, BP-structured nitrogen has remained elusive. Analogous to the black, white, and red phosphorus polymorphism, single-bonded nitrogen at high pressure may also have multiple polymorphs that are very close in energy, and the BP-structured nitrogen may coexist with other polymorphs and require very specific P-T conditions to synthesize and to distinguish experimentally.
In the present study using laser-heated diamond anvil cell (DAC) techniques, we conducted an in-depth search for BP-structured nitrogen in a P-T range, where other single-bonded nitrogen polymorphs have been reported. Through diagnostic probes of single-crystal x-ray diffraction (SXRD) and Raman spectroscopy, BP-structured nitrogen is observed unambiguously to coexist with CG-nitrogen at 146 GPa and >2200 K. BP-structured nitrogen and CG-nitrogen are crystallized in micrometer-sized crystals, and BP-structured, nitrogen-rich regions can be identified by XRD (Fig. 1 and Table 1) and Raman spectroscopic microprobes (Fig. 2). In addition, the newly developed high-pressure multigrain SXRD method (14) has been applied to the spotty pattern of BP-structured nitrogen (table S1) to unequivocally separate BP-structured nitrogen from CG-nitrogen. Unlike CG-nitrogen, BP-structured nitrogen has only two-thirds of the single bonds in gauche conformation with the others in trans. Notably, BP-structured nitrogen exhibits high Raman intensity as anticipated from the anisotropic nature of the layered structure.
Table 1. List of 23 reflections indexed with the BP-structured nitrogen structure at 140 GPa.
dobs and dcal represent the d-spacing of observed and calculated reflections, respectively. Dcal was obtained using unit cell parameters a = 2.1438 Å, b = 6.5554 Å, and c = 2.8534 Å.
| # | h k l | dobs (Å) | dcal (Å) | dobs-dcal (Å) |
| 1 | 0 2 0 | 3.2779 | 3.2777 | 0.0002 |
| 2 | 0 2 1 | 2.1531 | 2.1521 | 0.0010 |
| 3 | 1 1 1 | 1.6606 | 1.6582 | 0.0024 |
| 4 | 0 4 0 | 1.6383 | 1.6389 | −0.0006 |
| 5 | 0 0 2 | 1.4269 | 1.4267 | 0.0002 |
| 6 | 0 4 1 | 1.4212 | 1.4211 | 0.0001 |
| 7 | 1 3 1 | 1.3475 | 1.3486 | −0.0011 |
| 8 | 1 1 2 | 1.1678 | 1.1687 | −0.0009 |
| 9 | 2 0 0 | 1.0733 | 1.0719 | 0.0014 |
| 10 | 1 5 1 | 1.0421 | 1.0414 | 0.0007 |
| 11 | 2 2 0 | 1.0197 | 1.0188 | 0.0009 |
| 12 | 2 2 1 | 0.9597 | 0.9595 | 0.0002 |
| 13 | 0 2 3 | 0.9146 | 0.9135 | 0.0011 |
| 14 | 1 1 3 | 0.8616 | 0.8619 | −0.0003 |
| 15 | 2 4 1 | 0.8547 | 0.8558 | −0.0011 |
| 16 | 0 4 3 | 0.8230 | 0.8226 | 0.0004 |
| 17 | 0 8 1 | 0.7874 | 0.7876 | −0.0002 |
| 18 | 2 6 0 | 0.7646 | 0.7652 | −0.0006 |
| 19 | 1 7 2 | 0.7347 | 0.7354 | −0.0007 |
| 20 | 1 5 3 | 0.7245 | 0.7246 | −0.0001 |
| 21 | 0 6 3 | 0.7178 | 0.7174 | 0.0004 |
| 22 | 2 2 3 | 0.6944 | 0.6953 | −0.0009 |
| 23 | 2 8 0 | 0.6517 | 0.6510 | 0.0007 |
Fig. 2. Identification of the BP structure by Raman spectrum.
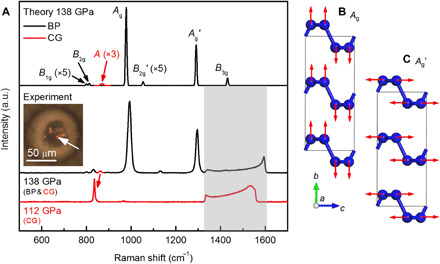
(A) Raman spectra from sample 1 measured at 138 GPa and sample 2 measured at 112 GPa compared with the superposition of two calculated spectra for BP-structured nitrogen (black) and CG-nitrogen (red) at 138 GPa. Gray shade marks the region of phonon from stressed diamond anvil, which hides B3g of BP-structured nitrogen. Inset shows photomicrograph of the sample, with the white arrow marking the sample position being measured. A mode of CG-nitrogen at 112 GPa shifts to a lower frequency compared with the spectrum at 138 GPa. Red arrow between the experiment spectra correlates the two A modes of CG-nitrogen at different pressures. (B and C) Schematic of atomic displacements of the Ag and Ag′ modes.
RESULTS AND DISCUSSION
Sample 1 was laser heated at 146 GPa. At this pressure, the sample becomes dark (fig. S1B) and can absorb the 1064-nm laser radiation directly. The temperature was increased to 2200 K at several sample positions. Once the phase transformation was complete, the heated spot immediately became transparent and ceased to absorb the laser. Both the Raman spectrum and XRD (by oscillating the DAC from −21° to 21° about the Ω axis, which is the vertical goniostat axis) measurements after laser heating at a series of sample positions indicate that the transformed regions contain a mixture of CG-nitrogen and a new phase (fig. S2). The spatial distribution of the two phases was resolved by 2D XRD contrast imaging of the entire sample using a submicrometer-focused x-ray probe, as shown in fig. S1 (C and D).
The unit cell parameters and symmetry of the BP-structured nitrogen phase were determined using SXRD with the high-pressure multigrain method, which can uniquely select the diffraction spots of a single crystal among multiple crystals and determine its corresponding orientation (14). One sample region with quite spotty XRD pattern was selected for the SXRD data collection (inset of Fig. 1A). The data were collected using 36-keV x-ray beam while rotating the DAC from −21° to 21° by a step of 0.5°. A total of 23 independent reflections covering a broad spectrum of d-spacing, from 3.28 to 0.65 Å (Table 1), were observed and indexed by the BP structure (orthorhombic in the Cmce space group), confirming unequivocally the successful synthesis of BP-structured nitrogen. The polycrystalline XRD pattern, which integrates all XRD spots and lines, collected at 132 GPa does not show any unassigned reflections other than these belonging to BP-structured nitrogen, CG-nitrogen, and Re (Fig. 1A). Individual diffraction spots were further indexed on the basis of the angles between each pair of diffraction spots in reciprocal space. Because of the weakness in intensity and scarcity of the diffraction spots (41 identified in total), a manual search and match process had to be performed. In this search, we were able to index two different grains with 19 spots (grain #1) and 14 spots (grain #2), respectively. Figure 1B shows the diffraction spots of grain #2 with corresponding indices on the raw image (see fig. S3 for grain #1 and table S1 for more details regarding the indexing). Thus, BP-structured nitrogen structure explains the XRD data both in extinction rule and angular relationships between diffraction spots in reciprocal space. The obtained unit cell parameters of BP-structured nitrogen at 140 GPa are a = 2.1438(6) Å, b = 6.5554(8) Å, and c = 2.8534(3) Å, which agree well with the calculated values using density functional theory (DFT), a = 2.1399 Å, b = 6.5577 Å, and c = 2.8255 Å. This excellent agreement supports the identified BP crystal structure in which N atoms in the puckered 2D layers are arranged in zigzag (a axis) and armchair (b axis) forms and the layers are stacked along the normal (c axis) direction (Fig. 1, C to E).
BP-structured nitrogen was also identified from the measured Raman spectrum. We synthesized a pure CG sample (sample 2) at 120 GPa as a reference (see the Supplementary Materials for details of the Raman spectrum of sample 2) and used its Raman spectrum as the reference to identify CG peaks. We are able to identify four Raman peaks uniquely belonging to BP-structured nitrogen in sample 1 at 138 GPa (Fig. 2A). Group theory analysis indicates that the BP-structured nitrogen has six Raman active modes, 2Ag (named Ag and Ag′) + B1g + 2B2g (named B2g and B2g′) + B3g. The four observed peaks at 796, 830, 993, and 1296 cm−1 can be assigned sequentially to B1g, B2g, Ag, and Ag′ modes, respectively. The calculated frequencies (799, 818, 977, and 1291 cm−1) of these modes agree very well with the measurements (Fig. 2A). B3g and B2g′ with calculated frequencies of 1431 and 1053 cm−1 are not observed. At this pressure, the B3g peak is buried by the Raman signal of the stressed diamond anvil, which moves out the diamond Raman region and becomes visible at lower pressures (fig. S4). The B2g′ has negligible theoretical intensities, i.e., <1% of the intensity of the Ag mode, and therefore not observable. A weak peak is observed at 1132 cm−1, which is not able to be assigned with either CG-nitrogen or BP-structured nitrogen and could be induced by impurities, defects, or other phases of nitrogen. The concurrent appearance of multiple orientation-dependent Raman peaks indicates that the measured sample is likely polycrystalline, given the laser spot size being ~5 μm.
The pressure dependences of XRD and Raman shift of BP-structured nitrogen were measured during decompression from 138 to 48 GPa at 300 K. The lattice parameters and unit cell volumes obtained from the XRD show an excellent agreement with the calculations (Fig. 3, A and B). A unique feature of the BP family of 2D materials is the in-plane anisotropy (15), and BP-structured nitrogen exhibits very strong in-plane anisotropic compressibility. In this range of decompression, the in-plane zigzag direction (a axis) expands 2.0% and the armchair direction (c axis) expands 7.3%, which is almost as large as the b axis, with 7.4% expansion in the layer stacking normal direction. The bulk modulus (B0) and unit cell volume (V0) at ambient pressure are obtained from fitting the second-order Birch-Murnaghan equation of state, which are B0 = 183.0 GPa and V0 = 55.66 Å3 for BP-structured nitrogen, and B0 = 254.3 GPa and V0 = 52.87 Å3 for CG-nitrogen. BP-structured nitrogen has a similar density to CG-nitrogen but becomes 1.5% denser than CG-nitrogen at the high pressure of 128 GPa, indicating pressure stabilization of BP-structured nitrogen relative to CG-nitrogen.
Fig. 3. Measured and calculated pressure-dependent evolution of unit cell volume, lattice parameters, and Raman phonons of BP-structured nitrogen.
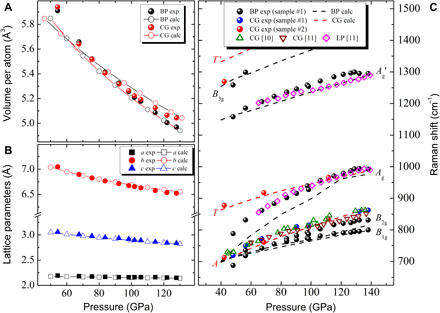
(A) Unit cell volumes of BP-structured nitrogen and CG-nitrogen. (B) Lattice parameters a, b, and c of BP-structured nitrogen. (C) Measured Raman shift compared with calculations and previously reported values (10, 11). All measurements were performed during decompression. In (C), LP stands for LP-N (11).
The measured Raman shifts of BP-structured nitrogen are compared with the calculated and previously reported experimental values (Fig. 3C). All the observed Raman peaks of BP-structured nitrogen soften under decompression with the largest softening in the Ag mode. The calculated frequencies of the B1g, B2g, and Ag′ modes are in good agreement with the measurements, while that of the Ag mode shows a notable deviation below 100 GPa. In BP-structured nitrogen, all Raman modes, except Ag, have the eigenvectors parallel to the basal plane. Ag is the only mode that vibrates perpendicular to the basal plane. The exaggerated softening in Ag indicates, possibly, an insufficient treatment of van der Waals interactions between the layers in the calculation. Raman signals from both BP-structured nitrogen and CG-nitrogen were observed down to 48 GPa, below which sample escaped due to failure of a diamond anvil. Our calculation shows that BP-structured nitrogen is not dynamically stable at ambient pressure. Auxiliary confinements, such as nanotube (16) in the case of CG-nitrogen, or doping is anticipated to preserve BP-structured nitrogen under ambient conditions.
We calculated the Raman spectra for BP-structured nitrogen and CG-nitrogen using the Placzek approximation (see the Supplementary Materials for details), which essentially reproduces the experimental spectrum of sample 1 (Fig. 2A). Phonon analysis shows that the Ag/Ag′ mode has a puckering/stretching motion of the basal plane with the eigenvector along the normal/armchair direction (Fig. 2, B and C). Both modes have a diagonal Raman tensor, i.e., (Rxx, 0, 0), (0, Ryy, 0), and (0, 0, Rzz), which is effective when the polarizations of incident and scatted radiations are collinear. The Raman tensors for both the Ag and Ag′ modes are strongly anisotropic, with a very large Rzz (armchair) compared with Rxx (zigzag) and Ryy (normal). The Rxx:Ryy:Rzz ratios are 1:1.3:8.3 for Ag and 1:0.5:13.5 for Ag′. The large intensities of the two Ag peaks therefore arise from excessively large Rzz components. As a comparison, the A mode in CG-nitrogen has an isotropic Raman tensor (Rxx = Ryy = Rzz), the magnitude of which is only 3.3% of the Rzz in Ag and 4.4% of the Rzz in Ag′, which explains the low Raman signal of CG-nitrogen in the calculated spectrum, as illustrated in Fig. 2A (the Supplementary Materials include more details regarding the calculated Raman tensors). This finding confirms that the polarizability in BP-structured nitrogen changes most rapidly along the Ag coordinate and is highly active to the incident radiation with the polarization along the armchair direction. Intuitively, this scenario makes sense since the puckering motion of the layers would be very effective in disturbing the electrons in lone pairs above and below the layers. The calculated relative dielectric constants (εr) are 6.6, 4.7, and 11.3 along the zigzag, normal, and armchair directions, respectively, showing strong anisotropy. The unique optical response is therefore expected from the anisotropy of the BP structure. However, we like to note that since the sample is mostly polycrystalline, the experimentally measured intensities of Raman peaks are influenced by the crystal orientation and, therefore, are not directly comparable to the calculated intensities.
We discuss here why the synthesis of BP-structured nitrogen is more difficult from the perspective of conformational isomerism. The buckled layer structure of BP-structured nitrogen (Fig. 1C) is formed by interconnecting the buckled honeycombs where each N atom is bonded to three neighbors. Two distinct directions define the basal plane: the armchair (c axis) and zigzag (a axis) directions (Fig. 1, D and E). The layers are stacked along the normal direction (b axis) through van der Waals interactions. The local structure of BP-structured nitrogen features sp3 hybridized N atoms, with three σ bonds and one lone pair on each atom, which is the common motif in all single-bonded N phases. Calculated band structure shows that this structure has a semiconducting ground state with a direct band gap of 1.75 eV (150 GPa). The long-range order of BP-structured nitrogen is determined by the dihedral angle within each N2N-NN2 conformer. This angle is defined as the angle by which the N2N group must be rotated about the N-N axis to be located precisely above the NN2 group. Quantum chemical calculations on isomers of X2N-NX2 (X = H, CH3, etc.) shows that the repulsion between lone-pair electrons on adjacent N atoms has a substantial impact on the preferred dihedral angle. To a first approximation, the dihedral angle can be viewed as a property of the N─N bond, which determines the crystal structures of single-bonded nitrogen allotropes (17, 18). BP-structured nitrogen has two-thirds of its bonds in global minimum gauche (DFT values at 132 GPa, ±67°) and one-third in local minimum trans conformation (180°) (Fig. 1F). The CG-nitrogen have all gauche helicity (DFT value at 132 GPa, 105°) at the same pressure (Fig. 1G). The N─N bond length in trans is 1.45 Å, notably longer than that in gauche (1.33 Å). The integrated crystal-orbital Hamilton population (ICOHP) analysis shows that the gauche bond has higher strength than the trans bond, consistent with the “shorter bond = stronger bond” paradigm. The presence of trans conformers in BP-structured nitrogen, thus, yields a higher internal energy (E) than the all-gauche CG-nitrogen. Following the same logic, the A7 structure, as another structural candidate for high-pressure nitrogen and possessed by group V element As, is formed by an all-trans helicity and therefore thermodynamically more unfavorable. A7-N has never been found in experiments and remains hypothetical.
Our success in obtaining BP-structured nitrogen demonstrates the importance of high pressure and high temperature in synthesizing novel metastable nitrogen allotropes that are energetically less favorable. The calculated enthalpies (H = E + pV) of BP-structured nitrogen and other relevant types of nitrogen phases (12, 19, 20) at the ground state show that BP-structured nitrogen never has a region of thermodynamic stability (Fig. 4A). Molecular solid (N2) and CG-nitrogen are found to be the ground-state phases below and above 56 GPa, respectively, which agrees well with previous calculations (21). However, BP-structured nitrogen is more compressible than CG-nitrogen (Fig. 3A), which means a smaller pV work term to compensate for internal energy at high pressures and a lower vibrational free energy to compensate for the enthalpy at high temperatures. To account for the temperature effects, the vibrational free energy [Fvib = −ln(Z)/β] was estimated for BP-structured nitrogen and CG-nitrogen using the harmonic approximation. The calculated finite-temperature energy (H + Fvib) shows that BP-structured nitrogen is increasingly more stable at higher temperatures at pressures above 80 GPa (Fig. 4B). The small energy deficiency in BP-structured nitrogen can be overcome with sufficient compression and laser heating, as demonstrated in our experiment. Another predicted metastable (C2/c) structure (20) in this pressure region is not observed in our experiment, which probably requires different reaction paths/conditions.
Fig. 4. Calculated enthalpies of BP-structured nitrogen under high pressure at the ground state and at high temperature.
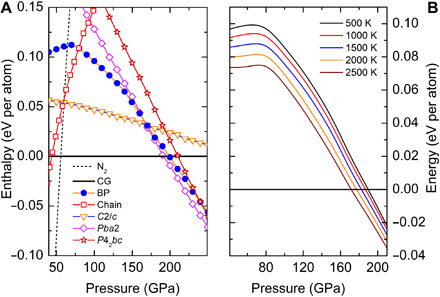
(A) Calculated enthalpies as functions of pressure for various structures of solid nitrogen with respect to CG-nitrogen. Pba2, C2/c, P42bc, and chain structures are reported in (12), (20), (13), and (19), respectively. “N2” denotes the enthalpy of the molecular solid of N2, calculated using the lowest-enthalpy structures (21) in respective pressure ranges. (B) Finite-temperature energy (H + Fvib) of BP-structured nitrogen relative to CG-nitrogen.
In summary, we synthesized the long-sought-after BP allotrope of nitrogen at high pressure and high temperature. This new phase of nitrogen exhibits large Raman intensities anticipated for the anisotropic nature of the single-bonded layered structure. This is the first confirmation of the existence of the BP structure in nitrogen, the first element in group V, which has not been found to share any crystal structure possessed by other group V elements previously. The discovery of BP-structured nitrogen opens up the possibility of searching for new high energetic materials with clean decomposition products and layer-structured 2D nitrogen.
MATERIALS AND METHODS
Symmetric DAC with beveled diamond anvils (100 μm beveled to 300 μm) were used for pressure generation. Rhenium gaskets, preindented to 20-μm thickness approximately, were used to confine the pressurized samples. Sample chambers were fabricated, with initial diameter of approximately 70 μm. A thin flake of gold was loaded near the edge of a chamber for pressure measurement (22). The diamond Raman edge (23) was also measured to check pressures. Ultrapure nitrogen gas (99.999%) commercially obtained (Airgas Inc.) was loaded into DACs at approximately 0.15 GPa using gas loaders at HPSynC and GeoSoilEnviroCARS (GSECARS), Advanced Photon Source (APS), Argonne National Laboratory (ANL). Laser heating was performed on two samples at 146 GPa (sample 1) and 120 GPa (sample 2) using ytterbium fiber lasers (1064 nm) at HPSynC and 13 IDD, respectively. Sample 1 was heated without a laser coupler at a pressure where nitrogen directly absorbs laser irradiation. Sample 2 was heated at 120 GPa, where nitrogen does not show substantial absorption of the infrared laser. Thus, a thin flake of compressed graphite powder was used as the laser coupler. SXRD measurements of sample 1 were carried out at 16-IDB of High-Pressure Collaborative Access Team (HPCAT), APS using 3 μm by 6 μm focused monochromatic beam (36 keV) and a Mar165 charge-coupled device (CCD) area detector. 2D XRD contrast imaging was performed at 34-IDE, APS using 500 nm by 500 nm focused monochromatic beam (24 keV) and a Mar165 CCD area detector. The XRD data during decompression were collected at 16-IDB using 3 μm by 6 μm focused monochromatic beam (30.5 keV) and Pilatus 1M area detector. Raman spectra during decompression were measured using a microconfocal Raman system in backscattering geometry at GSECARS, APS, with 660-nm excitation laser, 1200-cm−1 grating, and a CCD camera (24). General Structure Analysis System (GSAS) (25) was used for performing the Le Bail fit. X-ray Diffractive Imaging (XDI) was used to perform the 2D XRD contrast imaging data analysis (26). Dioptas (27) was used for XRD data reduction. Fityk (28) was used to perform peak fitting to subtract individual peak positions from the reduced XRD data and Raman spectra. EoSFit7-GUI (29) was used for fitting the EOS.
Enthalpy and phonon calculations were performed using the Vienna Ab Initio Simulation (VASP) program (30). A five-electron projector-augmented plane wave potential (31) with the Perdew-Burke-Ernzerhof functional (32) was used with a 900-eV kinetic energy cutoff. A k-spacing of 2π × 0.02 Å−1 was used for Brillouin zone sampling. Raman spectra were calculated using the Quantum ESPRESSO package (33), with norm-conserving pseudopotential and an energy cutoff of 80 rydbergs, along with a 12 × 12 × 16 k-point mesh. The crystal-orbital Hamilton population (COHP) and ICOHP analyses were performed using the LOBSTER program (34). Band structure was calculated using the Heyd-Scuseria-Ernzerhof exchange correlation function (35).
Supplementary Material
Acknowledgments
We are grateful to C.-S. Yoo for the valuable discussion and comments. Funding: We acknowledge the financial support from the National Natural Science Foundation of China (NSFC) under grant no. U1930401, and the Natural Sciences and Engineering Research Council of Canada (NSERC). The XRD experiments were performed at 16-IDB of HPCAT (sector 16), 13 IDD of GSECARS (sector 13), and 34-IDE (sector 34), APS, ANL. HPCAT operations are supported by DOE-NNSA’s Office of Experimental Sciences. GeoSoilEnviroCARS is supported by the National Science Foundation–Earth Sciences (EAR-1634415) and Department of Energy-GeoSciences (DE-FG02-94ER14466). Use of the COMPRES-GSECARS gas loading system was also supported by COMPRES under NSF Cooperative Agreement EAR-1606856. APS is a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by ANL under contract no. DE-AC02-06CH11357. Computing resources were provided by the University of Saskatchewan, WestGrid, and Compute Canada. Author contributions: H.G., Y.Y., and H.-k.M. conceived and supervised the project; A.A.A., B.W., H.G., and Y.Y. conducted the ab initio calculations and molecular dynamics simulations; L.Y. and C.J. conducted the laser heating experiments; Y.M., J.S.S., V.B.P., W.L., and G.S. developed techniques on synchrotron beamlines for laser-heated DAC and XRD measurements; B.L. and C.J. developed DAC-related techniques to achieve the experimental conditions; G.S. and L.Y. developed laser heating techniques for high-pressure, high-temperature synthesizing; V.B.P. developed high-pressure confocal Raman spectroscopy techniques; C.J. performed synchrotron XRD and Raman spectroscopy measurements; C.J., Y.Y., H.G., W.L.M., and H.K.M. performed the analysis; C.J., Y.Y., H.G., and H.K.M. wrote the manuscript in consultation with A.A.A., L.Y., B.W., B.L., Y.M., J.S.S., V.B.P., W.L., G.S., and W.L.M. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/23/eaba9206/DC1
REFERENCES AND NOTES
- 1.Goncharov A. F., Gregoryanz E., Mao H. K., Liu Z., Hemley R. J., Optical evidence for a nonmolecular phase of nitrogen above 150 GPa. Phys. Rev. Lett. 85, 1262–1265 (2000). [DOI] [PubMed] [Google Scholar]
- 2.Eremets M. I., Hemley R. J., Mao H.-k., Gregoryanz E., Semiconducting non-molecular nitrogen up to 240 GPa and its low-pressure stability. Nature 411, 170–174 (2001). [DOI] [PubMed] [Google Scholar]
- 3.Gregoryanz E., Goncharov A. F., Hemley R. J., Mao H.-k., High-pressure amorphous nitrogen. Phys. Rev. B 64, 052103 (2001). [Google Scholar]
- 4.Ling X., Wang H., Huang S., Xia F., Dresselhaus M. S., The renaissance of black phosphorus. Proc. Natl. Acad. Sci. U.S.A. 112, 4523–4530 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Carvalho A., Wang M., Zhu X., Rodin A. S., Su H., Castro Neto A. H., Phosphorene: From theory to applications. Nat. Rev. Mater. 1, 16061 (2016). [Google Scholar]
- 6.Xia F., Wang H., Hwang J. C. M., Neto A. H. C., Yang L., Black phosphorus and its isoelectronic materials. Nat. Rev. Phys. 1, 306–317 (2019). [Google Scholar]
- 7.Drozdov I. K., Alexandradinata A., Jeon S., Nadj-Perge S., Ji H., Cava R. J., Bernevig B. A., Yazdani A., One-dimensional topological edge states of bismuth bilayers. Nat. Phys. 10, 664–669 (2014). [Google Scholar]
- 8.Pumera M., Sofer Z., 2D monoelemental arsenene, antimonene, and bismuthene: Beyond black phosphorus. Adv. Mater. 29, 1605299 (2017). [DOI] [PubMed] [Google Scholar]
- 9.Mailhiot C., Yang L. H., McMahan A. K., Polymeric nitrogen. Phys. Rev. B 46, 14419–14435 (1992). [DOI] [PubMed] [Google Scholar]
- 10.Eremets M. I., Gavriliuk A. G., Trojan I. A., Dzivenko D. A., Boehler R., Single-bonded cubic form of nitrogen. Nat. Mater. 3, 558–563 (2004). [DOI] [PubMed] [Google Scholar]
- 11.Tomasino D., Kim M., Smith J., Yoo C.-S., Pressure-induced symmetry-lowering transition in dense nitrogen to layered polymeric nitrogen (LP-N) with colossal Raman intensity. Phys. Rev. Lett. 113, 205502 (2014). [DOI] [PubMed] [Google Scholar]
- 12.Ma Y., Oganov A. R., Li Z., Xie Y., Kotakoski J., Novel high pressure structures of polymeric nitrogen. Phys. Rev. Lett. 102, 065501 (2009). [DOI] [PubMed] [Google Scholar]
- 13.Laniel D., Geneste G., Weck G., Mezouar M., Loubeyre P., Hexagonal layered polymeric nitrogen phase synthesized near 250 GPa. Phys. Rev. Lett. 122, 066001 (2019). [DOI] [PubMed] [Google Scholar]
- 14.Zhang L., Yuan H., Meng Y., Mao H.-K., Development of high-pressure multigrain X-ray diffraction for exploring the Earth’s interior. Engineering 5, 441–447 (2019). [Google Scholar]
- 15.Kikegawa T., Iwasaki H., An x-ray diffraction study of lattice compression and phase transition of crystalline phosphorus. Acta Crystallogr. B39, 158–164 (1983). [Google Scholar]
- 16.Benchafia E. M., Yao Z., Yuan G., Chou T., Piao H., Wang X., Iqbal Z., Cubic gauche polymeric nitrogen under ambient conditions. Nat. Commun. 8, 930 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zahariev F., Hu A., Hooper J., Zhang F., Woo T., Layered single-bonded nonmolecular phase of nitrogen from first-principles simulation. Phys. Rev. B 72, 214108 (2005). [Google Scholar]
- 18.Adeleke A. A., Greschner M. J., Majumdar A., Wan B., Liu H., Li Z., Gou H., Yao Y., Single-bonded allotrope of nitrogen predicted at high pressure. Phys. Rev. B 96, 224104 (2017). [Google Scholar]
- 19.Mattson W. D., Sanchez-Portal D., Chiesa S., Martin R. M., Prediction of new phases of nitrogen at high pressure from first-principles simulations. Phys. Rev. Lett. 93, 125501 (2004). [DOI] [PubMed] [Google Scholar]
- 20.Oganov A. R., Glass C. W., Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 124, 244704 (2006). [DOI] [PubMed] [Google Scholar]
- 21.Pickard C. J., Needs R. J., High-pressure phases of nitrogen. Phys. Rev. Lett. 102, 125702 (2009). [DOI] [PubMed] [Google Scholar]
- 22.Anderson O. L., Isaak D. G., Yamamoto S., Anharmonicity and the equation of state for gold. J. Appl. Phys. 65, 1534 (1989). [Google Scholar]
- 23.Akahama Y., Kawamura H., Pressure calibration of diamond anvil Raman gauge to 410 GPa. J. Phys. Conf. Ser. 215, 012195 (2010). [Google Scholar]
- 24.Holtgrewe N., Greenberg E., Prescher C., Prakapenka V. B., Goncharov A. F., Advanced integrated optical spectroscopy system for diamond anvil cell studies at GSECARS. High Pressure Res. 39, 457–470 (2019). [Google Scholar]
- 25.Toby B. H., EXPGUI, a graphical user interface for GSAS. J. Appl. Crystallogr. 34, 210–213 (2001). [Google Scholar]
- 26.Hrubiak R., Smith J. S., Shen G., Multimode scanning X-ray diffraction microscopy for diamond anvil cell experiments. Rev. Sci. Instrum. 90, 025109 (2019). [DOI] [PubMed] [Google Scholar]
- 27.Prescher C., Prakapenka V. B., DIOPTAS: A program for reduction of two-dimensional X-ray diffraction data and data exploration. High Pressure Res. 35, 223–230 (2015). [Google Scholar]
- 28.Wojdyr M., Fityk: A general-purpose peak fitting program. J. Appl. Crystallogr. 43, 1126–1128 (2010). [Google Scholar]
- 29.Gonzalez-Platas J., Alvaro M., Nestola F., Angel R., EosFit7-GUI: A new graphical user interface for equation of state calculations, analyses and teaching. J. Appl. Crystallogr. 49, 1377–1382 (2016). [Google Scholar]
- 30.Kresse G., Hafner J., Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993). [DOI] [PubMed] [Google Scholar]
- 31.Kresse G., Joubert D., From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999). [Google Scholar]
- 32.Perdew J. P., Burke K., Ernzerhof M., Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]
- 33.Giannozzi P., Andreussi O., Brumme T., Bunau O., Buongiorno Nardelli M., Calandra M., Car R., Cavazzoni C., Ceresoli D., Cococcioni M., Colonna N., Carnimeo I., Corso A. D., de Gironcoli S., Delugas P., DiStasio R. A., Ferretti A., Floris A., Fratesi G., Fugallo G., Gebauer R., Gerstmann U., Giustino F., Gorni T., Jia J., Kawamura M., Ko H. Y., Kokalj A., Küçükbenli E., Lazzeri M., Marsili M., Marzari N., Mauri F., Nguyen N. L., Nguyen H. V., Otero-de-la-Roza A., Paulatto L., Poncé S., Rocca D., Sabatini R., Santra B., Schlipf M., Seitsonen A. P., Smogunov A., Timrov I., Thonhauser T., Umari P., Vast N., Wu X., Baroni S., Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 29, 465901 (2017). [DOI] [PubMed] [Google Scholar]
- 34.Maintz S., Deringer V. L., Tchougreeff A. L., Dronskowski R., LOBSTER: A tool to extract chemical bonding from plane-wave based DFT. J. Comput. Chem. 37, 1030–1035 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Heyd J., Scuseria G. E., Ernzerhof M., Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207 (2003). [Google Scholar]
- 36.Lazzeri M., Mauri F., First-principles calculation of vibrational Raman spectra in large systems: Signature of small rings in crystalline SiO2. Phys. Rev. Lett. 90, 036401 (2003). [DOI] [PubMed] [Google Scholar]
- 37.Turnbull R., Hanfland M., Binns J., Martinez-Canales M., Frost M., Marqués M., Howie R. T., Gregoryanz E., Unusually complex phase of dense nitrogen at extreme conditions. Nat. Commun. 9, 4717 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Weck G., Datchi F., Garbarino G., Ninet S., Queyroux J.-A., Plisson T., Mezouar M., Loubeyre P., Melting curve and liquid structure of nitrogen probed by X-ray diffraction to 120 GPa. Phys. Rev. Lett. 119, 235701 (2017). [DOI] [PubMed] [Google Scholar]
- 39.Gregoryanz E., Goncharov A. F., Sanloup C., Somayazulu M., Mao H. K., Hemley R. J., High P-T transformations of nitrogen to 170 GPa. J. Chem. Phys. 126, 184505 (2007). [DOI] [PubMed] [Google Scholar]
- 40.Lipp M. J., Klepeis J. P., Baer B. J., Cynn H., Evans W. J., Iota V., Yoo C.-S., Transformation of molecular nitrogen to nonmolecular phases at megabar pressures by direct laser heating. Phys. Rev. B 76, 014113 (2007). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/23/eaba9206/DC1


