Transmission dynamics of and insights from the 2018–2019 measles outbreak in New York City: A modeling study

We model the recent measles outbreak in New York City and discuss potential public health strategies to prevent future outbreaks.

Abstract

In 2018–2019, New York City experienced the largest measles outbreak in the United States in nearly three decades. To identify key contributing factors, we modeled the transmission dynamics of this outbreak. Results indicate that delayed vaccination of 1- to 4-year-olds enabled the initial spread and that increased infectious contact, likely via “measles parties,” facilitated later transmission. We found that around half of infants were susceptible by age 1 and thus had many infections. Without the implemented vaccination campaigns, numbers of infections and hospitalizations could have been >10 times higher and would predominantly affect those under 4. These results suggest that a first vaccine dose before age 1 and the second dose before age 4 could allow parents to vaccinate and protect children more effectively should a high level of vaccine hesitancy persist. Enhanced public health education is needed to reduce activities that unnecessarily expose children to measles and other infections.

INTRODUCTION

Measles is a highly contagious and severe viral disease. Thanks to an effective vaccine and high coverage of vaccination, endemic transmission of measles—i.e., continuous transmission for more than 12 months—in the United States was declared eliminated in 2000. However, because of vaccine hesitancy and declining vaccination rate, in recent years there have been an increasing number of large outbreaks following introduction of measles infection (1). Because of long-term fluctuations in vaccine coverage and infection history, population susceptibility could vary substantially by age group. This susceptibility disparity by age can further interact with age-specific social connectivity (i.e., contact rate) to shape the epidemic trajectory. As such, understanding these detailed population characteristics and their impact on transmission dynamics in the recent outbreaks is important for devising timely and effective intervention strategies.

In the fall of 2018, several New York City (NYC) residents acquired measles while traveling abroad and subsequently led to the largest measles outbreak in the United States in nearly three decades. The first case of this outbreak developed a rash on 30 September 2018, and by 3 September 2019 when the outbreak was declared over, there have been 649 confirmed cases, largely occurring in an Orthodox Jewish community (2, 3). To contain the outbreak, the NYC Department of Health and Mental Hygiene (DOHMH) launched extensive vaccination campaigns and, on 9 April 2019, ordered mandatory vaccination of all individuals living, working, or going to school in the affected zip codes. As a result, over 32,000 individuals under 19 years were vaccinated with the measles, mumps, and rubella (MMR) vaccine during October 2018 to July 2019, and the outbreak subsided (3, 4).

In this study, we model the transmission dynamics of this measles outbreak in the affected Orthodox Jewish community in NYC from 1 October 2018 to 31 July 2019, months with more than one measles cases reported. Using an age-structured model inference framework, we are able to estimate key epidemiological features, including the initial susceptibilities in five different age groups (i.e., <1, 1 to 4, 5 to 17, 18 to 49, and 50+ years) and the basic reproductive number R₀, infer key factors contributing to the spread of measles, estimate the proportions of infection attributable to each age group, and assess the impact of vaccination campaigns. We also discuss the implications of our findings to current measles vaccination policies.

RESULTS

Overview of the measles outbreak and model fit

The measles outbreak started on 30 September 2018, when a young child developed a rash. It evolved relatively slowly in the first 3 months; however, the outbreak took off quickly in early 2019, peaked in April after the city declared a public health emergence, and recorded a total of 649 cases by 31 July 2019. As shown in Fig. 1A, age-grouped incidence, estimated on the basis of health reports/alerts (3, 5), peaked first in March 2019 among 1- to 4-year-olds—the age group with the largest number of infection (275 cases or 42.8% of the total, as of 6 August 2019 at the time of this study; same as below), followed by <1-year-olds (100 cases or 15.6%) and 5- to 17-year-olds (138 cases or 21.5%) in April 2019, and 18+-year-olds (129 cases or 20.1%) in May 2019. It is also evident from Fig. 1B that infants <1 year and young children 1 to 4 years were the most affected during this outbreak.

Fig. 1. Epidemic curve.

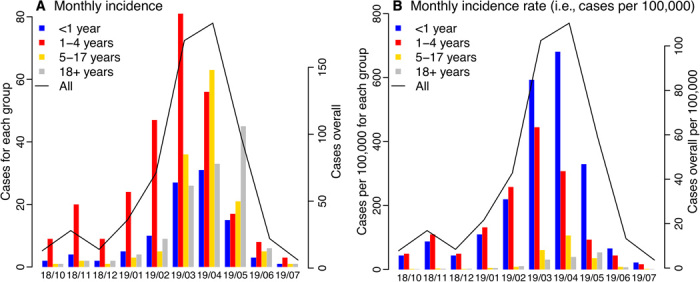
(A) Monthly incidence and (B) incidence rate (i.e., cases per 100,000 population) for all ages and by age group. The solid line (y axis on the right) shows monthly numbers for all ages, reported as of 6 August 2019. For comparison, bars (y axis on the left) show monthly numbers for <1-year-old (blue), 1- to 4-year-olds (red), 5- to 17-year-olds (yellow), and 18+-year-olds (gray), respectively, estimated on the basis of health reports. The x axis shows time in month (yy/mm).

As shown in Fig. 2 and table S1, our model inference system (see Materials and Methods) was able to recreate the overall incidence curve during October 2018 to July 2019, estimate the overall age distribution of measles cases, and recreate the estimated age-grouped incidence curves for all age groups. Note that while our model (Eq. 1) divided 18+-year-olds into two subgroups (i.e., 18 to 49 and 50+ years) given their differences in contact rates and interactions with other age groups, we present the combined results here because data were only available for the entire age group. The estimated reporting rate was around 90% throughout the study period and slightly lower in April 2019, at the peak of the outbreak [mean, 89.1%; 95% credible interval (CrI), 79.4 to 99.2%; same as below, unless stated otherwise; fig. S1].

Fig. 2. Model fit.

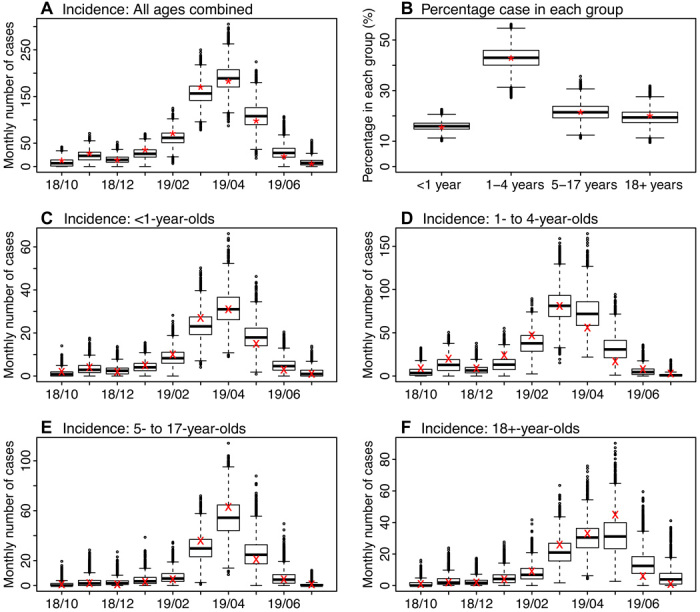
Box plots show estimates of monthly incidence for all ages (A), percentage of cases reported in each age group (B), and monthly incidence for <1-year-olds (C), 1- to 4-year-olds (D), 5- to 17-year-olds (E), and 18+-year-olds (F). Results are pooled over all 10 model inference runs (each with 10,000 and in total 100,000 model realizations). Horizontal thick lines show the median of model estimates; box edges show the 25th and 75th percentiles; whiskers show the 2.5th and 97.5th percentiles; and dots show outliers. Stars (*) in (A) and (B) show monthly incidence for all ages and the age distribution, reported as of 6 August 2019; crosses (×) in (C) to (F) show age-grouped monthly incidence estimated from health reports. The x axis shows time in month (yy/mm).

Inference of key epidemiological characteristics

The model inference system estimated that, at the beginning of the outbreak (i.e., September 2018), susceptibility was the highest in infants, at approximately 53.2% (95% CrI, 49.0 to 57.5%; Fig. 3A). This pattern was expected because maternal immunity wanes within 3 to 9 months after birth and, as a result, by their first birthday—the age eligible to receive the first dose of MMR vaccine in the United States—almost all infants have lost their maternal immunity and are susceptible to measles. Young children aged 1 to 4 years had the second highest susceptibility; approximately 24.9% (95% CrI, 20.4 to 29.7%) were susceptible. In comparison, susceptibility was lower among both 5- to 17-year-olds (6.0%; 95% CrI, 4.1 to 7.9%) and 18+-year-olds 6.0% (95% CrI, 4.4 to 7.6%; Fig. 3). These estimates were consistent with the observation that all cases recorded in October 2018 were children ranging from 11 months to 4 years (2). Sensitivity analysis on assumptions related to the vaccination campaigns showed that estimated susceptibilities were slightly higher for 5- to 17-year-olds (7.5%; 95% CrI, 5.1 to 9.9%) and 18- to 49-year-olds (7.9%; 95% CrI, 5.2,to 9.9%) if more vaccine doses were given to the Jewish Orthodox community or to 5- to 17-year-olds; however, the estimates were in general consistent with the baseline scenario (table S1).

Fig. 3. Estimated changes in population susceptibility.

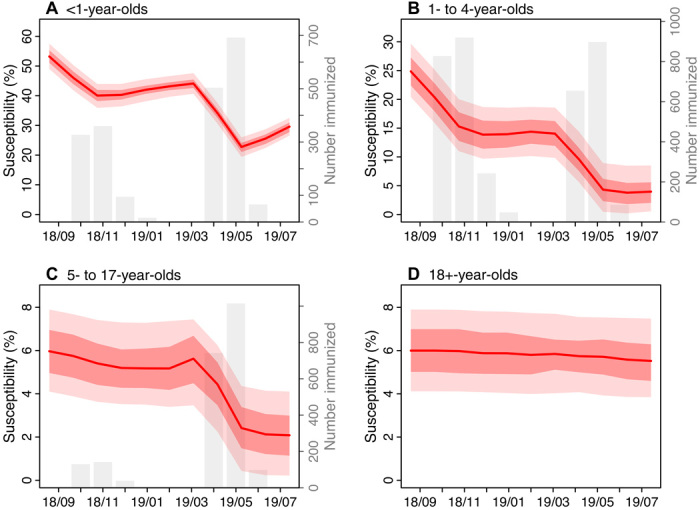
Red lines and surrounding regions (y axis on the left) show the mean and 50 and 95% CrIs of estimates pooled over all 10 model inference runs (100,000 model realizations in total) for <1-year-olds (A), 1- to 4-year-olds (B), 5- to 17-year-olds (C), and 18+-year-olds (D), respectively, at the end of each month from September 2018 to July 2019. The initial susceptibilities, estimated at the end of September 2018, were computed by adding the total numbers of individuals immunized by the vaccination campaigns in October 2018 to the posterior estimates at the end of October 2018. For comparison, the gray bars (y axis on the right) show estimated numbers of individuals immunized during the vaccination campaigns; note that the vaccination campaigns targeted individuals under 19 years and thus is not shown for 18+-year-olds.

The initial vaccination campaigns launched promptly afterward lowered susceptibility to 40.3% (95% CrI, 36.4 to 44.0%) in infants and 13.9% (95% CrI, 9.7 to 18.7%) in 1- to 4-year-olds by the end of December 2018 (Fig. 3). These efforts, along with other transmission and infection controls (2), appeared to effectively contain the outbreak at the time. The effective reproductive number (R_e) is a key epidemiological parameter reflecting the potential of an infection to cause an epidemic in a partially immune population; an epidemic is possible when R_e > 1. The estimated R_e was 1.5 (95% CrI, 0.7 to 2.9) in October 2018 and dropped to around 1 (95% CrI, 0.7 to 1.5) in December 2018 (Fig. 4B).

Fig. 4. Estimates of key model parameters.

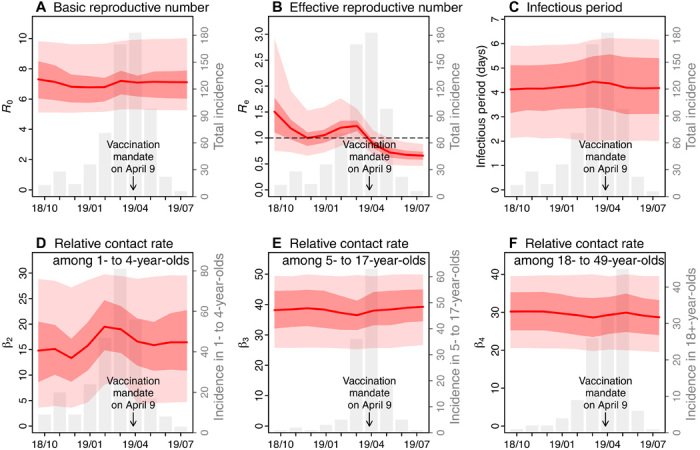
(A) the basic reproductive number, (B) the effective reproductive number, (C) infectious period, (D) relative contact rate among 1- to 4-year-olds, (E) relative contact rate among 5- to 17-year-olds, and (F) relative contact rate among 18- to 49-year-olds. Red lines and surrounding regions (y axis on the left) show the mean and 50 and 95% CrIs of estimates pooled over all 10 model inference runs (100,000 model realizations in total) made at the end of each month from October 2018 to July 2019. For comparison, the gray bars (y axis on the right) show monthly incidence for all ages (A to C) or the related age groups (D to F).

The outbreak, however, took off again in early 2019 (Fig. 1). The estimated R_e increased and remained above 1 in the first 3 months of 2019 (Fig. 4B). In a perfectly mixed model, R_e is computed as the product of the basic reproductive number R₀ and population susceptibility. In particular, the basic reproductive number R₀ measures the transmissibility of an infection in a fully susceptible population; for measles, while often reported in the range of 12 to 18, R₀ could vary from 1.4 to 770 (6). In this study, we estimated that R₀ was approximately 7 during the entire outbreak (Fig. 4A). If population susceptibility, the other factor for R_e, were to increase in a close population (i.e., without migration), it could only do so slowly as infants lose maternal immunity. Thus, these two factors alone could not explain the sudden large increase in R_e (Fig. 4B). In this study, we used an age-structured model that enables more detailed analysis of the transmission dynamics. Our model inference system detected an increase in contact rate among 1- to 4-year-olds during January to March 2019 (Fig. 4D); this increased contact rate along with the high susceptibility among 1- to 4-year-olds appeared to raise R_e above unity (Eq. 5 in Materials and Methods) and contribute to the resurge of measles in early 2019. This finding was also consistent with reports of parents hosting “measles parties” to expose unvaccinated children at the time (7) (see further analysis below in the “Estimated impact of measles parties on outbreak magnitude” section). In contrast, estimated contact rates were relatively stable for other age groups (e.g., Fig. 4, E and F, for 5- to 17-year-olds and 18- to 49-year-olds, respectively). As a result, infections increased quickly among 1- to 4-year-olds (Figs. 1 and 4D), reaching a peak of around 80 cases in March 2019. Meanwhile, infections also increased in other age groups including 5- to 17-year-olds and 18+-year-olds despite their low overall susceptibilities, due to interactions between age groups (fig. S1) and the high contact rates in these groups (Fig. 4, E and F).

The outbreak began to decline in April 2019, following more stringent public health interventions (3, 4). In particular, the model estimated that, thanks to extensive vaccination campaigns, susceptibility was reduced to 22.8% (95% CrI, 19.3 to 26.0%) in <1-year-olds, 4.3% (95% CrI, 0.5 to 8.9%) in 1- to 4-year-olds, and 2.4% (95% CrI, 0.4 to 4.4%) in 5- to 17-year-olds at the end of May 2019. Consequently, the effective reproductive number R_e dropped below 1 from April 2019 onward.

Who acquired infection from whom?

Table 1 shows the estimated proportions of infections caused by each of the five age groups based on the estimated who-acquires-infection-from-whom (WAIFW) contact matrix (Eq. 2 in Materials and Methods). Children aged 1 to 4 years not only had the largest number of infections (42.8%) but also appeared to cause the largest number of infections in other age groups. Tallied over the entire study period (October 2018 to July 2019), an estimated 51.6% (95% CrI, 39.3 to 63.1%) of the total cases were infected by 1- to 4-year-olds, compared with 25.2% (95% CrI, 15.8 to 35.5%) by 5- to 17-year-olds, 17.7% (95% CrI, 10.4 to 26.5%) by 18- to 49-year-olds, 4.5% (95% CrI, 3.0 to 6.4%) by <1-year-olds, and 1.0% (95% CrI, 0.4 to 1.8%) by 50+-year-olds. In particular, 1- to 4-year-olds caused around half of the infections in infants (44.6% or 45 cases) and the largest proportions of intergroup transmission to other age groups (ranging from 12.9% to 5- to 17-year-olds to 40.1% to 50+-year-olds; Table 1).

Table 1. Estimated proportion of infections caused by each age group.

Rows show the receiving (i.e., infectee) age groups, and columns show the sources of infection (i.e., infector age groups). The numbers are the mean (95% CrI) estimates in percentage. For instance, for <1-year-olds (top row), on average, 16.3% of cases were infected by the same age group, 44.6% by 1- to 4-year-olds, 20.9% by 5- to 17-year-olds, 15.2% by 18- to 49-year-olds, and 3% by 50+-year-olds.

Infectee age groups	Infector age groups
	<1 year	1–4 years	5–17 years	18–49 years	50+ years
<1 year	16.3 (12.3–21.0)	44.6 (35.5–53.5)	20.9 (13.9–28.4)	15.2 (9.6–21.6)	3.0 (1.4–5.0)
1–4 years	1.8 (1.0–3.0)	85.8 (77.0–91.9)	7 (3.2–12.9)	5 (2.2–9.3)	0.3 (0.1–0.6)
5–17 years	1.5 (0.9–2.4)	12.9 (6.9–21.3)	80.9 (70.4–88.4)	4.4 (2.0–8.0)	0.3 (0.1–0.5)
18–49 years	2.4 (1.5–3.7)	18.6 (10.9–28.0)	9.1 (4.8–14.9)	69.5 (56.2–80.8)	0.4 (0.2–0.8)
50+ years	15.5 (11.6–19.9)	40.1 (31.1–49.3)	19.7 (13.0–27.0)	15.6 (9.7–22.4)	9.1 (3.8–16.3)

Estimated impact of “measles parties” on outbreak magnitude

As reported above, our model inference suggests that increases in infectious contact among 1- to 4-year-olds in early 2019, likely linked to parents hosting “measles parties” to expose unvaccinated children at the time (7), could have led to the second, larger wave of the measles outbreak. To examine this impact further, we used the model and parameter estimates to simulate potential outbreaks should there be no increases in the contact rate among 1- to 4-year-olds (i.e., if there had been no measles parties) in early 2019. Figure 5 (A to E) shows the simulated outbreak outcomes. The model was able to recreate the outbreak trajectories during the first 3 months (i.e., October to December 2018) using parameters estimated for the outbreak. However, the simulated numbers of cases (Fig. 5A for all ages combined and Fig. 5, B to E, for individual age groups) were much lower than those observed in spring 2019, when setting the contact rate among 1- to 4-year-olds alone to the same level as estimated for 2018. In particular, the simulations showed that the high incidence in 1- to 4-year-olds as observed in February and March 2019 would be unlikely without the increased contact in this age group—the observed numbers were outside the 95% confidence interval (CI) of the simulated (Fig. 5C). Similarly, it would be unlikely to observe the high incidence in spring 2019 in other age groups without the increased contact among 1- to 4-year-olds (e.g., the observed numbers were outside the 95% CI of the simulated for <1 year-olds in March 2019 as shown in Fig. 5B and for 5- to 17-year-olds in April 2019 as shown in Fig. 5D). Tallied over the entire outbreak period, had there been no increased infectious contact among 1- to 4-year-olds, the total number of cases would be 152 [median; interquartile range (IQR), 12 to 492; 95% CI, 5 to 1246], less than a quarter of the observed (i.e., 642 cases reported as of 6 August 2019; Table 2 and table S2).

Fig. 5. Estimated negative impact of measles parties and positive impact of vaccination campaigns.

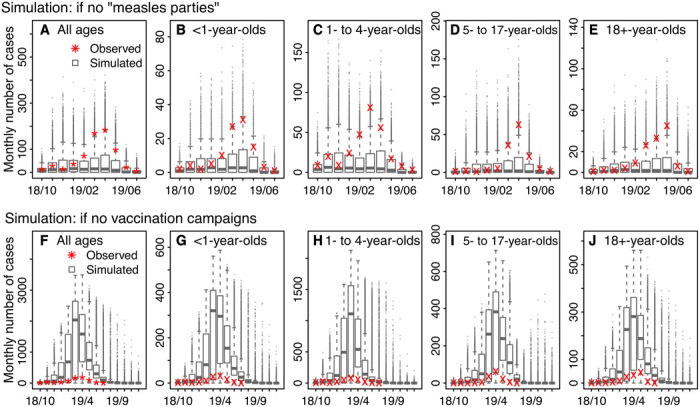
Top row: Simulated estimates of monthly incidence, should there be no measles parties, for all ages (A), <1-year-olds (B), 1- to 4-year-olds (C), 5- to 17-year-olds (D), and 18+-year-olds (E). Bottom row: Simulated estimates of monthly incidence, should there be no vaccination campaigns, for all ages (F), <1-year-olds (G), 1- to 4-year-olds (H), 5- to 17-year-olds (I), and 18+-year-olds (J). Results are pooled over 10,000 model simulations. Horizontal thick lines show the median of model estimates; box edges show the 25th and 75th percentiles; whiskers show the 2.5th and 97.5th percentiles; and dots show outliers. For comparison, stars (*) in (A) and (F) show monthly incidence for all ages, reported as of 6 August 2019; crosses (×) in (B) to (E) and (G) to (J) show age-grouped monthly incidence estimated from health reports.

Table 2. Estimated negative impact of measles parties and positive impact of vaccination campaigns during October 2018 to July 2019.

Column 2 shows the observed numbers of cases, reported as of 6 August 2019. Column 3 shows the estimated numbers of cases if there had been no measles parties. Columns 4 to 6 show the estimated total numbers of cases (fourth column), hospitalizations (fifth column), and individuals in intensive care unit (ICU) for different age groups (rows 3 to 6) and overall (last row), if there had been no vaccination campaigns. Columns 7 to 9 show the estimated numbers of cases, hospitalizations, and ICU cases averted by the vaccination campaigns. Numbers are the median (IQRs) of 10,000 simulations. See table S2 for the median and 95% CIs of the simulated estimates.

Age group	No. of cases reported	No. of cases, if no measles parties	No. if no vaccination campaigns			No. averted by vaccination campaigns
			Cases	Hospitalizations	ICU cases	Cases	Hospitalizations	ICU cases
<1	100	26 (2–81)	1302 (1062–1358)	97 (79–101)	20 (16–21)	1202 (962–1258)	89 (72–94)	18 (15–19)
1–4	275	62 (5–193)	3914 (3596–4000)	291 (267–297)	60 (55–62)	3639 (3321–3725)	271 (247–277)	56 (51–57)
5–17	138	26 (1–110)	1412 (897–1534)	105 (67–114)	22 (14–24)	1274 (759–1396)	95 (56–104)	20 (12–21)
18+	129	29 (2–102)	1141 (907–1218)	85 (67–91)	18 (14–19)	1012 (778–1089)	75 (58–81)	16 (12–17)
All	642	152 (12–492)	7810 (6480–8089)	581 (482–601)	120 (100–124)	7168 (5838–7447)	533 (434–554)	110 (90–115)

Estimated impact of vaccination campaigns

Figure 5 (F to J) shows the estimated outbreak outcomes had there been no vaccination campaigns. Without the vaccination campaigns, the model estimated that the outbreak could continue to the end of 2019 and infect a total of 7871 [median; IQR, 7104 to 8137; 95% CI, 5 to 8478] people by then or 7810 (median; IQR, 6480 to 8089; 95% CI, 5 to 8433) during the observed outbreak period (i.e., October 2018 to July 2019), compared with 642 cases reported as of 6 August 2019. In addition, these infections would largely occur in infants under 1 and young children aged 1 to 4 years. During the observed outbreak period, there would be 1302 (median; IQR, 1062 to 1358; 95% CI, 0 to 1430) infections in infants and 3914 (median; IQR, 3596 to 4000; 95% CI, 2 to 4096) infections in 1- to 4-year-olds, more than 13 times of the reported numbers in these two age groups (i.e., 100 and 275, respectively, as of 6 August 2019; Table 2 and table S2). Children aged 5 to 17 years would have the third largest number of infections, with 1412 (median; IQR, 897 to 1534; 95% CI, 1 to 1692) cases, 10 times of the reported number (i.e., 138 as of August 6, 2019).

Measles infection can lead to severe complications requiring hospitalization. According to data by 24 April 2019, among 390 individuals with measles, 29 were hospitalized, of which 6 needed intensive care (8). Assuming the same ratios among all cases, without the vaccination campaigns, during the observed outbreak period, there would have been 581 (median; IQR, 482 to 601; 95% CI, 0 to 628) hospitalizations, including 120 (median; IQR, 100 to 124; 95% CI, 0 to 130) needing intensive care, and the majority of such hospitalizations would be in young children under 4 (Table 2 and table S2).

DISCUSSION

Using a model inference system, we have reconstructed in detail the transmission dynamics of the measles outbreak in an Orthodox Jewish community in NYC during October 2018 to July 2019. We have estimated the population characteristics (e.g., age-specific susceptibilities) and epidemiological parameters (e.g., reproductive numbers) as well as subtle changes in key parameters (e.g., contact rates) that are critical to the transmission of measles. In particular, our analyses indicate that, in addition to delayed vaccination, increased infectious contact among young children likely due to “measles parties” was a key factor behind this large measles outbreak and thus should be avoided in the future. Using model simulation and the posterior estimates from the model inference system, we are also able to estimate the impact of vaccination campaigns implemented during the outbreak, including numbers of infections and hospitalizations averted, for each age group. These latter findings echo those from previous studies (9–11) and again highlight the severity of measles disease should there be no effective infection and transmission controls (in particular, vaccination).

Our analyses estimate that around a quarter of young children aged 1 to 4 in the affected community were susceptible at the onset of the outbreak, likely due to delayed vaccination. Ninety-four percent (101 of 108) of the early infections in children were unvaccinated (12). In contrast, vaccination rate remained high in older children 5 to 17 years, with an estimated 94% immune to measles. This difference may be due to better compliance with vaccination regulation at school entry or a result of vaccination campaigns in response to previous outbreaks [e.g., a large outbreak occurred in the same community in 2013 (13)]. Nevertheless, the large number of unvaccinated children under 4 was sufficient to cause many infections in late 2018, predominantly in the same age group [Fig. 1 and (2, 12, 14)]. This observation highlights the importance of vaccination compliance with both MMR vaccine doses, especially given the long lag between the two vaccine doses. In addition, recommending the second MMR dose earlier than the currently scheduled age 4 to 6 years could allow parents to fully vaccinate their children sooner and reduce the number of susceptible children overall.

Our study also reveals the intricate interplay of population dynamics and measles transmission. While the high susceptibility in children under 4 was likely responsible for the early spread of measles, our estimates suggest that the second and more severe part of the outbreak in 2019 was likely due to increased infectious contact among this age group, likely facilitated by parents hosting “measles parties” that intentionally bring unvaccinated children together and expose them to those sick with measles (7). As shown in Fig. 4, the increase in infectious contact interacting with the high susceptibility in 1- to 4-year-olds was able to raise the effective reproductive number R_e to above unity—the threshold for an epidemic to occur—and aggravate the outbreak in 2019, despite earlier public health efforts that had reduced R_e to below 1 in late 2018. Model simulations (Fig. 5, A to E) further support this finding, showing that the high incidence as observed in spring 2019 would be unlikely had there been no increases in infectious contact among 1- to 4-year-olds (i.e., if there had been no measles parties). Similar disease-related gatherings have been noted in previous measles outbreaks (15) and other disease outbreaks (16). These activities create further challenges to the control of measles spread and stress the need for enhanced public health education.

In addition, the intensified measles outbreak affected not only children with delayed vaccination but also a large number of infants under 1, who were too young to receive their first dose of MMR vaccine in the United States. At least 100 infants under 1 were infected with measles during the 10-month outbreak period, despite extensive infection and transmission control efforts, including vaccinating infants 6 months or older and postexposure prophylaxis with immune globulin given to those under 6 months (2, 14). This was largely a result of the high susceptibility in infants. Our model inference system estimates that about half of infants were susceptible by age 1 and that nearly half of the 100 infant cases were infected by 1- to 4-year-olds (Table 1). In addition, our simulations suggest that, without the vaccination campaigns, the number of infections in infants could have been over 10 times higher than observed (Table 2). These findings demonstrate the rippling effects of vaccine hesitancy beyond the risk posted to age-eligible children with delayed vaccination. These findings also suggest that administration of the first dose of routine MMR vaccine earlier than the current 1-year age limit in the United States may be necessary to protect infants should high level of vaccine hesitancy persist. Of note, the World Health Organization recommends administering the first dose of measles vaccine at 9 to 12 months of age for routine vaccination programs and as early as 6 months for settings such as during an outbreak (17).

Our model simulations, consistent with many previous studies (11, 15, 18), demonstrate the significant public health impact of vaccination in controlling measles outbreaks. Without the implemented vaccination campaigns, the severity of the measles outbreak—including number of infections, hospitalizations, and severe infections needing intensive care—could have been over 10 times worse than observed (Table 2). These estimates, however, did not include the long-term health impacts on affected individuals, particularly young children (10, 19, 20), nor the enormous economic burdens (13, 21, 22).

We note several limitations of our study. First, we did not explicitly model the impact of public health interventions other than the vaccination campaigns, because of a lack of data. During the outbreak, such efforts included prescreening patients before presence for treatment, postexposure prophylaxis, and closing schools out of vaccination compliance (2, 12, 14, 23, 24). Of note, however, here the estimated basic reproductive number R₀ was around 7, lower than the 12-to-18 range based on epidemics in the prevaccine era (25), and the estimated infectious period was around 4 days (Fig. 4C), at the lower end of the commonly used range of 4 to 6 days (26). The lower R₀ and shorter infectious period could be a result of the aforementioned public health interventions. Second, there were uncertainties in the accuracy of case reporting. Because the incidence data used here were published on 6 August 2019, a later revision of case reports, we used a relatively high but broad prior range for the reporting rate (i.e., 80 to 100%). In addition, our model inference system explicitly accounted for observational errors (Eqs. 7a and 7b). Third, because of a lack of contact data and for simplicity, we set all terms related to group 1 (i.e., <1-year-olds) in the WAIFW matrix to the same as the contact rate within the group (Eq. 2). This model formulation may have led to underestimation of the proportions of infection in <1-year-olds attributable to the same age group and/or 1- to 4-year-olds, given the likely more frequent contact within the same age group and with similar ages (i.e., 1 to 4 years here) due to more shared settings such as daycares and pediatric hospitals. Fourth, there were uncertainties regarding the settings of vaccination campaigns. Nevertheless, sensitivity analysis showed that our main estimates were robust to a wide range of assumptions (table S1). Fifth, because of data sparsity (i.e., monthly incidence was used), there were uncertainties in our parameter estimates as indicated by the wide 95% CrIs. Future studies may refine these estimates should data with finer time resolution (e.g., weekly data) become available. Last, while our analyses support that measles parties during the outbreak increased infectious contacts among young children and worsened the outbreak outcomes, we did not have detailed data to directly assess this impact. Future studies may further examine the impact of “measles parties” should relevant data become available.

In summary, using a comprehensive model inference system, we have reconstructed transmission dynamics of the recent measles outbreak in NYC in great detail. Our estimates highlight the importance of vaccination in protecting children and public health education to reduce activities that unnecessarily expose children to the risk of measles infection. Further, in light of the persistent vaccine hesitancy, revising current vaccination recommendations may allow parents to vaccinate and protect their children more effectively.

MATERIALS AND METHODS

The measles outbreak occurred predominantly among members of the Orthodox Jewish community in Williamsburg and Borough Park, two neighborhoods located in Brooklyn, NYC. As such, we focused on modeling the outbreak in this subpopulation. Estimated on the basis of the Jewish Community Study of New York (27), approximately N = 165,970 Orthodox Jews live in these two NYC neighborhoods, of which 4552 (2.7%), 18,208 (11%), 59,176 (35.7%), 60,445 (36.4%), and 23,589 (14.2%) are <1, 1 to 4, 5 to 17, 18 to 49, and 50+ years, respectively.

Estimating monthly incidence by age group

Monthly measles incidence aggregated over all ages from September 2018 to August 2019 and the age distribution of case patients over the entire outbreak were published on the NYC DOHMH website (3). Of note, one case was reported in September 2018 (i.e., the initial case), and none were reported in August 2019. In addition, the numbers of reported cases were subsequently revised by the DOHMH (often adjusted upward, presumably from retrospective case identification) and, as such, varied over time. In this study, the data used for all analyses were accessed on 6 August 2019, with a total of 642 cases reported (compared with 649 cases in the final reports). To estimate the monthly incidence for each age group, we used the age distribution of cases reported in earlier health reports/alerts (5) to apportion the total incidence for each month. For months without age information, we used estimates either from the preceding month or the following month back-calculated from the overall age distribution.

Transmission model

The transmission model used here was similar to the one described in our previous study (28). As illustrated in fig. S2, the model represents the susceptible-exposed-infectious-recovered (SEIR) disease dynamics with five age groups (i.e., <1, 1 to 4, 5 to 17, 18 to 49, and 50+ years) to account for population differences by age group (e.g., susceptibility and contact rate), routine two-dose vaccination at ages 1 and 5, and immunization during the vaccination campaigns as per Eq. 1

$$\{\begin{array}{c}\frac{{\mathit{dS}}_i}{\mathit{dt}}=-\left(\frac{S_i^{m_1}}{N_i}\right){\displaystyle \sum _{j=1}^5}{\mathrm{\beta }}_{\mathit{ij}}{I}_j^{m_2}+k(1-v)N{\mathbf{1}}_{\mathit{i}=\mathbf{1}}\\ +\frac{M}{180}{\mathbf{1}}_{\mathit{i}=\mathbf{1}}+l_{i-1}{S}_{i-1}(1-v_{i-1})-l_i{S}_i-V_i(t)\\ \frac{{\mathit{dE}}_i}{\mathit{dt}}=\left(\frac{S_i^{m_1}}{N_i}\right){\displaystyle \sum _{j=1}^5}{\mathrm{\beta }}_{\mathit{ij}}{I}_j^{m_2}-\frac{E_i}{Z}+{\mathrm{\alpha }}_i(t)+l_{i-1}{E}_{i-1}-l_i{E}_i\\ \frac{{\mathit{dI}}_i}{\mathit{dt}}=\frac{E_i}{Z}-\frac{I_i}{D}+l_{i-1}{I}_{i-1}-l_i{I}_i\\ \frac{{\mathit{dR}}_i}{\mathit{dt}}=\frac{I_i}{D}+l_{i-1}{R}_{i-1}-l_i{R}_i+l_{i-1}{S}_{i-1}{v}_{i-1}+V_i(t)\\ \frac{\mathit{dM}}{\mathit{dt}}=\mathit{kvN}-\frac{M}{180}\end{array}$$ (1)

for i = 1,..,5 (Eq. 1), where S_i, E_i, I_i, R_i, and N_i are, respectively, the numbers of susceptible, exposed (i.e., latently infected), infectious, recovered (and/or immunized) people, and population size in the i-th age group; M is the number of infants with maternal immunity, which decays exponentially with a mean duration of 180 days; and t is time in days. V_i(t) is the number of people in group i immunized by the vaccination campaigns on day t (described in detail in the next section). The exponents m₁ and m₂ describe the level of inhomogeneous mixing (29, 30), and m₁ = m₂ = 1 represents homogeneous mixing. Z and D are the latent and infectious periods, respectively.

To model the different contact rates within and between age groups, we used seven parameters for the WAIFW matrix as follows

$$\mathbf{\beta }=\left[\begin{array}{ccccc}{\mathrm{\beta }}_1& {\mathrm{\beta }}_1& {\mathrm{\beta }}_1& {\mathrm{\beta }}_1& {\mathrm{\beta }}_1\\ {\mathrm{\beta }}_1& {\mathrm{\beta }}_2& {\mathrm{\beta }}_6& {\mathrm{\beta }}_7& {\mathrm{\beta }}_1\\ {\mathrm{\beta }}_1& {\mathrm{\beta }}_6& {\mathrm{\beta }}_3& {\mathrm{\beta }}_7& {\mathrm{\beta }}_1\\ {\mathrm{\beta }}_1& {\mathrm{\beta }}_7& {\mathrm{\beta }}_7& {\mathrm{\beta }}_4& {\mathrm{\beta }}_1\\ {\mathrm{\beta }}_1& {\mathrm{\beta }}_1& {\mathrm{\beta }}_1& {\mathrm{\beta }}_1& {\mathrm{\beta }}_5\end{array}\right]$$ (2)

where β₁ to β₅ represent within-group contact for the five age groups, and β₆ and β₇ represent mixing between siblings and child-parent, respectively. For simplicity, we set all interactions with group 1 (i.e., <1 year) or group 5 (50+ years) to β₁, the lowest contact rate. For group 3 (5 to 17 years), to capture the varying contact rate following school schedules, we adjusted β₃ for each date per the school calendar in NYC as

$${\mathrm{\beta }}_3(t)=\frac{{\mathrm{\beta }}_3}{b_{\text{term}}}\cdot [1+b_1\text{term}(t)]$$ (3)

where b₁ is the amplitude of school term time forcing; term(t) is set to 1 for school days and −1 for non–school days; and b_term is the yearly average of 1 + b₁term(t) (31).

The basic reproductive number R₀, defined as the average number of secondary infections caused by a primary case patient in a naïve population, reflects the transmissibility of an infection. In an age-structured model, R₀ is computed as

$$R_0={\text{eigen}}_{\text{max}}(\mathit{n}\mathbf{\beta }D)$$ (4)

where eigen_max(·) denotes the function giving the largest eigenvalue of a matrix, and n is a diagonal matrix with elements n_i = N_i/∑N_i (i = 1, …, 5 here), i.e., the fraction of population in group i. On the basis of this relationship between R₀ and the β matrix, we reparametrized the model to include R₀ as a model parameter by setting β₁ to 1 and estimating the relative magnitude of β₂ to β₇, all scaled to R₀. In the current mass vaccination era, most people are immune via vaccination. To reflect the potential of an infection to cause an epidemic in a partially susceptible population, the effective reproductive number, R_e, accounts for population susceptibility and is computed as

$$R_{\mathrm{e}}={\text{eigen}}_{\text{max}}(\mathit{s}\mathbf{\beta }D)$$ (5)

where s is a diagonal matrix with elements s_i = S_i/N_i (i = 1, …, 5 here), i.e., the susceptibility in group i. For both R₀ and R_e, per (31), we further adjusted for the school term time forcing in group 3 (Eq. 3).

To model the demographic processes, k is the birth rate [2.7 per 1000 person-year here (27)]; v is the immunity level in mothers, approximated by the susceptibility of the child-bearing age group (i.e., 18- to 49-year-olds); N is the total population size; and 1_{i = 1} is an indicator function, with value 1 for group 1 (<1-year-olds) and 0 for all other groups. Thus, the term k(1 − v) 1_{i = 1} (first line in Eq. 1) is the number of susceptible newborns, and kvN (last line in Eq. 1) is the number of newborns with maternal immunity. The term l_i is the rate of aging for group i (i.e., the inverse of the sojourn time in each age group), with l₀ set to 0 and l₅ set to the death rate. The term v_i (for i = 1 and 2) is the percentage of susceptible 1-year-olds (entering group 2) immunized after the first vaccine dose and the percentage of susceptible 5-year-olds (entering group 3) immunized after the second vaccine dose, respectively, and v_i is set to 0 for all other age groups. In this study, for days before May 2019, we set v₁ to the vaccination rate in group 2 (approximated by 1 − S₂/N₂) times 0.9 (i.e., assuming a 90% vaccine efficacy) and v₂ to 0.7, such that for a 25% susceptibility in group 2, the immunity level among 5-year-olds would be 1 − (1 − (1 − 0.25)(0.9))(1 − 0.7) = 90%, a plausible level before the outbreak. For days afterward, we used 0.72 for v₁ and 0.9 for v₂, corresponding to a 1 − (1 − 0.72)(1 − 0.9) = 97% immunity level among 5-year-olds.

On the basis of NYC health reports/alerts (2, 12, 14), we seeded the model, via the parameter α_i(t), with three cases in group 2 (i.e., 1- to 4-year-olds)—one each with rash onset on 30 September, 15 October, and 30 October 2018, respectively—and one case each in group 3 (5- to 17-year-olds) and group 4 (18- to 49-year-olds), both during the winter recess (from 24 December 2018 to 1 January 2019).

Modeling the vaccination campaigns

To contain the outbreak, the NYC DOHMH conducted extensive vaccination campaigns and administered 31,790 doses of MMR vaccine to children under 19 years in Williamsburg and Borough Park by July 2019 (3). However, information on the age and immune status of vaccinees was not reported. In this study, per the health reports/alters (3, 12), we assumed that there were two phases of vaccination campaign: (i) October 2018 to February 2019, during which 7000 children, 90% Orthodox Jewish (15% were <1 year, 65% were 1 to 4 years, and 20% were 5 to 17 years), were vaccinated; and (ii) March to July 2019, during which 24,790 children, 60% Orthodox Jewish (10, 40, and 50%, respectively, were <1, 1 to 4, and 5 to 17 years), were vaccinated. For reference, Orthodox Jews made up for approximately 30% of the total population in the two affected neighborhoods.

For <1-year-olds, immunization could fail because of residual maternal immunity; thus, we assumed an 85% immunization success rate for group 1. For those above 1 year, some vaccinees might have received one or two doses of vaccine previously, and the higher the population susceptibility, the less likely a vaccinee would have been immune before the additional vaccine dose. As such, we assumed that the immunization success rate was twice the group-specific susceptibility for 1- to 4-year-olds and three times that for 5- to 17-year-olds or at a minimum of 25% and a maximum of 75%. That is, the vaccination campaign immunization success rate here accounted for vaccinees who had been immunized before the additional vaccine dose and thus differed from the vaccine efficacy measured among susceptibles (i.e., ~90% for one dose and 97% for two doses). We further assumed a 10-day delay in vaccine effect and computed the daily number of individuals vaccinated per a gamma distribution (mean = 30 days and SD = 21 days for phase 1, and mean = 56 and SD = 15 days for phase 2, such that it peaked ~1 week after 9 April 2019 when the city implemented a vaccination mandate). The estimated numbers matched with the reports [e.g., 1740 doses by our model versus ~1600 doses given to children under 5 as reported (32), and 1142 doses by our model versus ~1000 doses given in March 2019 as reported (7, 33)]. These daily numbers were then included in the transmission model [i.e., V_i(t) in Eq. 1]. Sensitivity to model assumptions was tested, as described below.

Estimation of model state variables and parameters

To estimate the model state variables (i.e., S_i, E_i, I_i, R_i, and M) and parameters (β₂ to β₇, R₀, b₁, D, Z, m₁, and m₂), we fit the model to the reported monthly overall incidence and the estimated monthly age-grouped incidence using a particle filter (34). Briefly, we first initialized a suite of model realizations (termed “particles,” N = 10,000 here) using Latin hypercube sampling (35) from the prior distribution of state variables and parameters (table S3). The particle filter then sequentially incorporated the monthly incidence to the model via repeated prediction-update cycles. In each cycle (i.e., each month here), the particles were stochastically integrated forward in time for a month per the model (i.e., Eq. 1; this generates the prediction). To update the model state, including all model variables and parameters, at the end of each month, the model-estimated incidence was aggregated for the month, adjusted by the reporting rate for that month (estimated simultaneously by the filter) and used to compute the likelihood of each particle (described below). The posterior of model state was then computed using Bayes’ rule (34, 36) and the particles resampled and updated—those with high posterior probabilities were retained, and those with very low posterior probabilities were discarded.

To allow for a wider observational variance than, e.g., the Poisson process, we heuristically modeled the observations using a multivariate Gaussian distribution (i.e., the likelihood function)

$${\mathit{Y}}_{\mathit{m}}\mid r,{\mathit{C}}_{\mathit{m}}~\mathcal{N}(r{\mathit{C}}_{\mathit{m}},\mathbf{\Sigma })$$ (6)

where Y_m is the vector of monthly incidence reported for month m, including the monthly incidence for individual age groups (i.e., <1, 1 to 4, 5 to 17, and 18+ years; note that 18- to 49-year-olds and 50-year-olds were combined because of a lack of data for these two groups separately) and all ages combined. Correspondingly, C_m is the vector of monthly incidence estimated by the model, and r is the reporting rate and, for simplicity, assumed the same for all ages. Σ is the covariance matrix, with the off-diagonal terms set to 0. To account for uncertainties in the estimated age-grouped incidence, the variance (Σ_ii, i = 1, …,4) for each of the four aforementioned age groups was heuristically computed as

$${\mathrm{\Sigma }}_{\mathit{ii},m}=100+\frac{{({\displaystyle {\sum }_m^{m-2}}{Y}_m/3)}^2}{3}$$ (7a)

That is, the observational variance is proportional to the average incidence in the preceding 2 months (if available) and the current month, plus a baseline constant. For the overall incidence with detailed data, a smaller variance was used

$${\mathrm{\Sigma }}_{\mathit{ii},m}=100+\frac{{({\displaystyle {\sum }_m^{m-2}}{Y}_m/3)}^2}{5}$$ (7b)

As there were great uncertainties in the susceptibilities of the younger age groups, we tested prior ranges from 5 to 45% for 1- to 4-year-olds, 4 to 25% for 5- to 17-year-olds, and 4 to 20% for 18- to 49-year-olds. For the basic reproductive number R₀, we tested prior values ranging from 5 to 12 [note that these values were lower than the oft-reported 12-to-18 range (6, 25)]. To optimize the model inference system, as in (28), we parsed these wide ranges into smaller segments and tested all combinations by permutation (5040 in total; see specific prior ranges in table S3). To account for model stochasticity, we ran the model inference system 5 times for each prior combination and 10 times for the final prior select. We then selected the optimal priors based on the model goodness of fit to the data (minimal root mean square error and maximal correlation and likelihood) over the period of October 2018 to July 2019 as well as accuracy of the one-step-ahead predictions (recall that the particle filtering process comprises sequential prediction-update cycles) for the period of October 2018 to March 2019 (i.e., before the emergency vaccination mandate). Note here that we used multiple selection criteria in addition to the likelihood, as the likelihood was relatively flat due to the large observational variances used to account for observational uncertainties. We pooled all 10 final runs (10,000 particles each run and 100,000 model realizations in total) to compute the posterior mean estimates and the 50 and 95% CrIs.

Sensitivity analysis on vaccination campaigns settings

To test the sensitivity of model results to assumptions on vaccination campaign settings, we tested the model inference system using the following alternative scenarios:

(i) For the second phase (March to July 2019), 90% (versus 60% in the baseline scenario) of the vaccine doses were given to members of the Orthodox Jewish community.

(ii) For the second phase, the age distribution of vaccinees was the same as the first phase (i.e., 15, 65, and 20%, respectively, for <1-, 1- to 4-, and 5- to 17-year-olds versus 10, 40, and 50% for the three groups in the baseline scenario).

(iii) For the second phase, 90% of the vaccine doses were given to Orthodox Jewish community, and the age distribution of vaccinees was the same as the first phase (i.e., 15, 65, and 20% for <1-, 1- to 4-, and 5- to 17-year-olds, respectively).

Because population susceptibility would be affected by the number of individuals immunized by the vaccination campaigns, we tested susceptibility ranges 5 to 45% for 1- to 4-year-olds, 4 to 25% for 5- to 17-year-olds, and 4 to 20% for 18- to 49-year-olds, divided into small segments as for the baseline scenario (140 different combinations for each alternative scenario; table S3). For simplicity, we used the same optimal prior ranges for the parameters under the baseline scenario in this sensitivity analysis.

Estimating the impact of “measles parties”

Our analysis suggested that increases in infectious contact among 1- to 4-year-olds in early 2019, likely linked to parents hosting measles parties at the time, could have led to the second, larger wave of the measles outbreak in 2019. To examine the impact of measles parties, we used the model and parameter estimates to simulate outbreak outcomes should there be no increases in infectious contact among 1- to 4-year-olds in early 2019. Specifically, we ran the model (10,000 realizations) stochastically from October 2018 to July 2019 using the posterior mean estimates of group-specific initial population susceptibilities and model parameters for each month except for the contact rate among 1- to 4-year-olds (β₂); for β₂, we used the mean posterior estimates for the first 3 months of the outbreak (i.e., October to December 2018) and the average over these 3 months for months afterward. We then computed the numbers of infections in each age group and overall from these counterfactual simulations and compared them to the reported values. Note that as the distributions of simulated outbreak outcomes were skewed (see Fig. 5), we report the median (as opposed to the mean), in addition to the IQR and 95% CI for each estimate.

Evaluating the impact of vaccination campaigns

To estimate the impact of vaccination campaigns, we generated model-simulated counterfactuals—i.e., outbreak outcomes should there be no vaccination campaigns implemented—using the posterior mean estimates of group-specific initial population susceptibilities and model parameters for each month but setting V_i(t) in Eq. 1 to 0. We ran the model (10,000 realizations) stochastically up to the end of 2019 to test how long the outbreak could last without the vaccination campaigns; for months after August 2019, parameters estimated at the end of July 2019 were used. For this simulation analysis, we also report the median, IQR, and 95% CI for each estimate.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/22/eaaz4037/DC1

View/request a protocol for this paper from Bio-protocol.