Symptom-Based Isolation Policies: Evidence from a Mathematical Model of Outbreaks of Influenza and COVID-19

Abstract

Background:

Controlling the transmission of respiratory infections such as influenza and COVID-19 is a critical public health priority. Non-pharmaceutical intervention policies such as community quarantines, closures and travel bans are often implemented in emergencies but many of them are disruptive and difficult to maintain for extended periods of time. A promising alternative recommended by the CDC for influenza is requiring individuals showing fever symptoms to remain isolated at home until they are fever-free for at least one day, but there is limited evidence to support the effectiveness of such symptom-based isolation policies.

Methods:

Here we introduce a computational model of symptom-based isolation that accounts for the timing of symptoms, viral shedding and the population structure. It was validated on outbreaks of influenza in schools and modified to account for COVID-19. It was then used to estimate the outbreak curves and the attack rates (the proportion of the population infected) under one or more days of fever-based isolation.

Results:

Using the model we find evidence that symptom-based isolation policies could reduce the attack rates of both influenza and COVID-19 outbreaks, and flatten the outbreak curves. Specifically, we found that across a range of influenza scenarios, a CDC-recommended policy of one day isolation following fever can reduce the attack rate from 27% of the population to 12%, and to 3% if the isolation is extended to two days. In COVID-19 transmission, we estimate that implementing one day post-fever isolation would reduce the attack rate from 79% to 71%, and there is possible benefit from isolation for six days. In both influenza and COVID-19, the policies are predicted to reduce the peak number of infected but not shorten the outbreak duration.

Conclusions:

Symptom-based isolation could be an important tool to control influenza and COVID-19 outbreaks in schools, and potentially other settings. We recommend that schools implement a post-fever isolation policy of two days for influenza and six days for COVID-19.

Introduction

Respiratory infections are the leading cause of death in low- or middle-income countries (LMICs) and account for an estimated four million deaths annually [1]. Before the recent emergence of SARS-CoV-2, much research focused on influenza, which causes worldwide annual epidemics of seasonal resulting in 3 to 5 million cases of severe illness, and approximately 250,000 to 500,000 deaths [2]. In the US, influenza causes on average of 226,000 hospitalizations and 3,000 to 49,000 deaths each year [3,4]. Control of influenza in children is an acute public health problem because attack rates (i.e., the proportion of the population infected) in unvaccinated children are estimated to average 12.7% [5] and exceed 30% during pandemic years [6]. Children also amplify the outbreak as they infect their peers and families, creating greater opportunities for further transmission in the community.[7,8]

For rapidly emerging outbreaks such as novel strains of influenza or SARS-CoV-2, pharmaceutical measures may be unavailable or less effective, and non-pharmaceutical intervention measures (NPIs) need to be used [9,10]. NPIs are divided by the World Health Organization into categories of personal protection, social distancing, travel and environment measures [11]. However, when the WHO systematically reviewed all studies supporting each NPI for controlling pandemic influenza, it found gaps in the evidence base for many of the measures [11]. In this study, our goal is to use a computational model to examine the policy of symptom-based isolation - a form of social distancing. Under this NPI, individuals who are showing fever due to a respiratory infection are required to remain in isolation until their symptoms subside, normally followed by an additional period of one day free of fever (or antipyretic medications or steroids). The CDC currently recommends this NPI for controlling pandemic influenza and controlling influenza in schools [12,13]. The buffer period of 1 day helps reduce transmission by keeping people in isolation when their fever symptoms temporarily subside. It also prevents transmission from viral shedding that often continues past the last episode of fever[14]. This NPI is often referred to as fever absenteeism or return-to-school policy in the context of schools.

To evaluate this NPI, our model computationally simulates outbreaks of influenza and COVID-19 in school settings, and then looks at the effect of symptom-based isolation policies. The benefit of using a model is the ability to clarify and quantify the possible effects of many different policy choices. Our work builds upon numerous previous studies that have applied mathematical models to model influenza transmission in schools (see e.g. [15–21]). Several studies also modeled non-pharmaceutical interventions such as closures but not absenteeism policies [19,21–32]). We performed a systematic analysis of studies that evaluated isolation policies by using a broad search on PubMed. We found a variety of policies involving isolation of infected individuals, particularly isolation for a fixed interval following diagnosis. For example, the large modeling consortium on pandemic influenza [18] assumed students with influenza symptoms would isolate themselves but did not examine the duration of isolation. We also found several comprehensive computational studies of school closures and isolation of infected students (e.g. [18,33]), but did not find evaluation of policies that would reduce transmission caused by infectious students returning from home. A related policy of symptom monitoring, that isolates contacts once they show symptoms, has been examined computationally and shown to be sufficient for controlling certain outbreaks [34].

Symptom-based isolation could also contribute to the control of the current COVID-19 outbreak. Currently the WHO recommends a fixed 14 days of isolation [35], but this policy may fail to contain transmission from the significant fraction of cases with extended courses of illness [36]. Indeed, evidence suggests that shedding of SARS-CoV-2 continues past the end of symptoms [37]. Therefore, symptom-based isolation for a period of time past the end of symptoms could potentially be more effective and also avoid unnecessary isolation of patients who have a faster resolution of the disease.

Despite the possible promise of this NPI for both COVID-19 and influenza, it is unclear if symptom-based isolation would be truly effective in controlling outbreaks because the CDC-recommended one day policy might not be enough to achieve a meaningful reduction in transmission, and a high rate of asymptomatic infections and partial compliance might weaken the ability to implement the policy. When the attack rate is high, transmission might occur regardless of isolation and the policy might merely create a burden on the isolated individuals and their families, without a tangible public health benefit. If the policy is proven effective, it is not known whether the CDC-recommended one day of symptom-based isolation is sufficient, and if not, how many days would be most beneficial. At the outset of our project, we hypothesized that these policies would have a small beneficial effect on reducing attack rate, delay the peak of the outbreak and reduce the height of its peak. We did not expect these policies to reduce the overall incidence because there would be many other opportunities to become infected. Furthermore, practical barriers may reduce the strictness with which the policies are enforced, which would reduce the policies’ effectiveness.

Methods

We use a deterministic compartmental dynamical model known as the Susceptible, Exposed, Infectious, Recovered (SEIR) model that tracks for each day during an outbreak the number of individuals of various cohorts and immunological states (Figure 1). This class of SEIR models has been used extensively to model influenza and COVID-19 (e.g. [15,23,38] and [39,40]), and we extended the SEIR framework in order to calculate details about the outbreak relevant to symptoms and isolation.

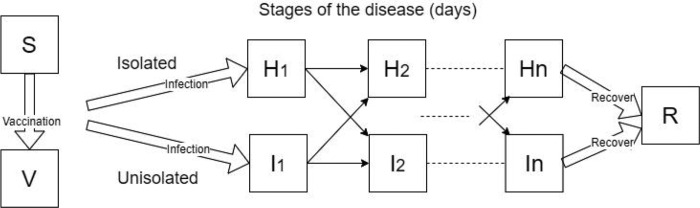
Figure 1:

Dynamics of the outbreak model and its major variables. S, susceptible, H, infected isolated, I, infected unisolated, R, recovered, and V, vaccinated (if a vaccine is available). The infectious classes (H and I) are often stratified to cohorts (shown here is the case of a single cohort), and n daily disease stages distinguished by severity of symptoms and shedding (see Appendix A). The cohort structure and other parameters are adjustable to model outbreaks in different settings and by different pathogens. Vaccination is available only for some outbreaks and has incomplete coverage and efficacy.

A relatively novel aspect of our model is the use of compartments to stratify the population by both the day of their infection, their location (un-isolated in community vs. isolated at home) and their cohort (see Appendix A for details). The day of infection determines the rate of virus shedding and the probability of symptoms, which then influences the decision to stay at home or to return. Generally, persons in the model were assumed to return to their community when their symptoms became less severe. The probability of returning was based on the stage of the illness, as well as the isolation policy. The isolation policy had a considerable effect on preventing premature return during the last days of illness, but also during the middle of the course of illness on days when symptoms temporarily waned. We allowed a vaccine to be received by some, if the vaccine is available ahead of the outbreak, attaining partial protection against the pathogen. The population was structured into cohorts representing ages in a school. In schools, students in the same grade generally have closer contacts to peers in the same grade, as opposed to the students in the other grades who also tend to be older or younger [41,42].

We considered the effect of several control policies, most importantly symptom-based isolation for one or more days, but also use of smaller class sizes and vaccination. We also evaluated stricter compliance, which could include remote monitoring, penalty for non-compliance and help in maintaining home isolation. We also considered greater symptom monitoring as could be achieved through education and providing thermometers. Further details on the model, including the equations and the parameter values are provided in Appendix A. The model was validated in several well-monitored influenza outbreaks in schools - an outbreak of 2009 pandemic influenza in a UK boarding school [43] and a US elementary school [44], as well as a seasonal influenza outbreak in a UK school in 2015 [45].

For our policy analysis, we defined a baseline scenario by using the parameters calculated for the outbreak [43] and applying the population structure of a typical school in the US (6 grades with 70 students each) [46]. We calibrated the transmission parameter of the model to give a 15% attack rate (thus matching the typical rate [5], after accounting for incomplete detection). Following calibration, we evaluated the effect symptom-based isolation policies would have on influenza and COVID-19 outbreaks. We also considered alternative scenarios with larger schools (140 students per grade), higher compliance, vaccination and others described below. For COVID-19, we calibrated the transmission parameter to give a higher 50% attack rate and used symptom and shedding rates estimated for SARS-Cov-2 (Appendix A). Because there is conflicting data on the rates of fever symptoms with this infection, we considered two scenarios: a conservative where just 50% of the cases experience and detect fever, and a higher 88% (cf. [47–49] and [50,51], respectively). To ensure that the results are robust to uncertainty parameter values, we then simulated the epidemic 500 times per scenario, with substantially different values for parameters such as the start day in the year, contact rate between cohorts and others, and reported the median and the interquartile ranges (see Appendix B for details). All modeling and statistical analysis used the RStudio Integrated Development for R. RStudio, Inc., Boston, MA.

Results

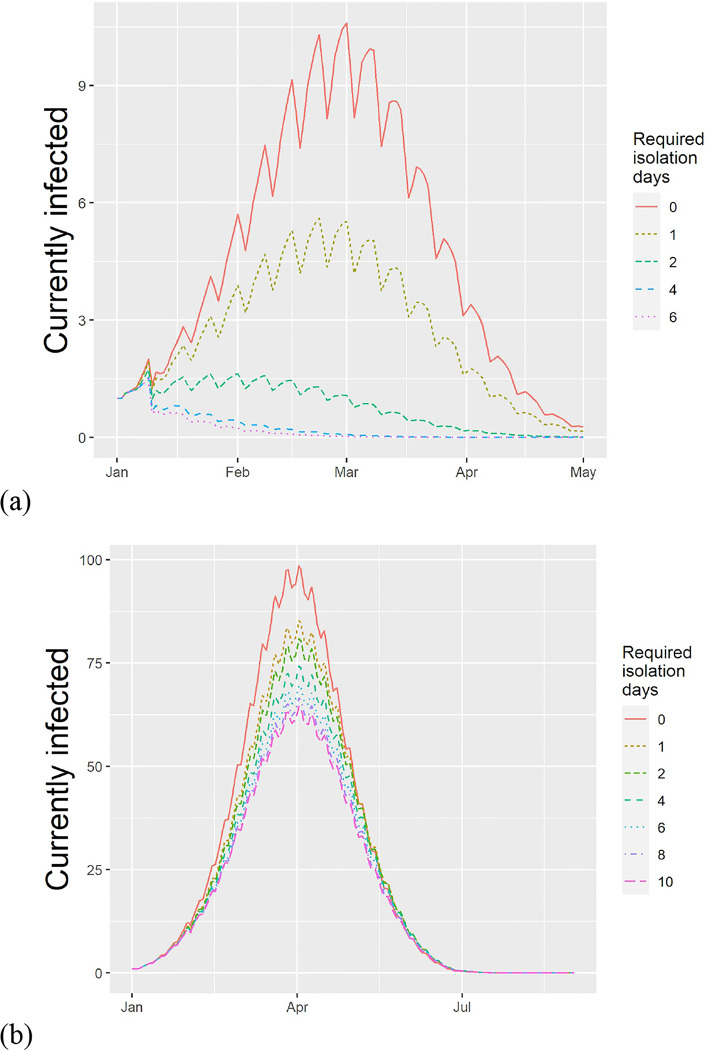
Our analysis considered the effect of symptom-based isolation policies on influenza and SARS-CoV-2 infections. The results are shown in Figure 2.

Figure 2.

Estimated effect of requiring isolation after the last fever event in a typical school experiencing an outbreak of (a) Influenza and (b) SARS-CoV-2 (at 50% rate of cases having fever symptoms). Ripples are due to weekends and school closures. Increasing the required days of isolation reduces the peak infected and the number concurrently infected.

In our baseline scenario, we predicted a median attack rate of 0.27 (Interquartile range, IQR: 0.02–0.58). Implementing a policy of one and two days of home isolation following the last episode of fever decreases the attack rate to 0.12 (0.01–0.42) and 0.03 (0–0.26), respectively (Table 1). The two-day policy substantially reduced the peak infected (23 to 2 in the median), the outbreak duration (66 to 32 in the median) and the number of person-days spent in the community (143 to 43 in the median).

Table 1.

Influenza outbreak in a school of 420 students and the effect of symptom-based isolation policies in baseline scenario with no vaccine. Median (interquartile range) of all simulations in the baseline scenario. The duration measures the interval between the first and last day with at least two infected cases, and peak date is the day from January 1st.

Isolation days	Attack rate	Peak infected	Peak date	Duration	Infected person-days isolated	Infected person-days unisolated
0	0.27 (0.02–0.58)	23 (2–79)	53 (38–60)	66 (17–81)	141 (17–339)	848 (88–1810)
1	0.12 (0.01–0.42)	7 (2–48)	53 (34–67)	61 (2–80)	111 (13–379)	342 (38–1241)
2	0.03 (0–0.26)	2 (1–23)	51 (22–67)	32 (0–76)	43 (11–302)	85 (20–659)
3	0.01 (0–0.15)	2 (1–10)	46 (18–60)	5 (0–67)	26 (10–187)	37 (13–356)
4	0.01 (0–0.09)	2 (1–6)	39 (16–67)	3 (0–61)	22 (10–145)	24 (9–193)
5	0.01 (0–0.05)	2 (1–4)	33 (13–67)	2 (0–50)	21 (10–101)	17 (8–101)
6	0.01 (0–0.04)	2 (1–4)	36 (13–67)	3 (0–46)	21 (10–96)	18 (7–85)
7	0.01 (0–0.06)	2 (1–5)	33 (13–60)	2 (0–53)	22 (11–123)	16 (6–95)
8	0 (0–0.05)	2 (1–4)	32 (14–60)	2 (0–51)	22 (11–90)	14 (6–89)
9	0 (0–0.05)	2 (1–4)	39 (15–74)	2 (0–51)	21 (11–111)	16 (6–105)

We considered a range of policies to enhance or complement symptom-based isolation (reported fully in Appendix B). The effectiveness of the two-day policy is maintained even in the presence of 80% vaccine coverage and 50% efficacy. Increasing compliance with the policy from 60% to 75% compliance had a small effect (1–2% decrease in the attack rate) and is not effective without an explicit isolation policy. Measures to increase the attention to symptoms from 67% to 84% attention reduced the attack rate to a median 5% at 0 (this and the following reflect the baseline with no isolation days). Completely cutting off transmission during weekends reduced the attack rate by 16%. Dividing the population into groups of half the normal size reduced the attack rate by 16%. The two-day isolation policy was also found to be effective for large schools.

We considered two COVID-19 outbreak scenarios, corresponding to different levels of detection of fever. The estimated attack rates were 0.79 (IQR: 0.56–0.9), 0.71 (0.43–0.86), and 0.72 (0.43–0.86) at 0, 1 and 2 days of isolation following fever in the scenario of 50% fever (Table 2). With one day of isolation the peak number of infected is reduced by 20% and the duration increases by 6 days, thus flattening the curve. No benefit was found from increasing the post-fever isolation period beyond one day. If the rate of detecting fever is a higher rate of 88%, implementing a 1 fever-free day achieves an 8% reduction in the attack rate (from 59% to 50% in the median), a 20% reduction in the peak concurrently infected and a 7 day increase in the duration of the outbreak. At this higher rate of symptom detection, increasing the isolation to 6 days achieves an attack rate of 0.43 (0.03–0.82) - a 15% reduction from no policy (see data in Appendix B).

Table 2.

COVID-19 outbreak in a school of 420 students the effect of symptom-based isolation policies. Median (interquartile range) of all simulations. The duration measures the interval between the first and last day with at least two cases. Scenario where only 50% of the cases detect fever.

Isolation days	Attack rate	Peak infected	Peak date	Duration	Infected person-days isolated	Infected person-days unisolated
0	0.79 (0.56–0.9)	148 (82–213)	87 (78–101)	139 (120–154)	1274 (692–1693)	6437 (4377–7589)
1	0.71 (0.43–0.86)	118 (58–184)	93 (79–106)	144 (128–159)	1631 (964–2015)	5406 (3350–6600)
2	0.72 (0.43–0.86)	124 (58–184)	93 (80–106)	145 (127–157)	1658 (974–2108)	5469 (3198–6604)
3	0.71 (0.45–0.86)	120 (59–181)	93 (80–106)	145 (128–158)	1702 (1005–2112)	5266 (3379–6451)
4	0.72 (0.46–0.86)	123 (63–182)	92 (80–106)	143 (128–156)	1723 (980–2180)	5459 (3536–6432)
5	0.71 (0.44–0.86)	117 (58–184)	93 (79–106)	144 (127–157)	1670 (992–2131)	5262 (3289–6522)
6	0.72 (0.43–0.85)	125 (58–180)	93 (80–106)	144 (128–157)	1709 (1016–2128)	5427 (3211–6477)
7	0.71 (0.46–0.86)	118 (65–186)	93 (80–106)	145 (128–157)	1680 (1070–2152)	5261 (3504–6507)
8	0.70 (0.42–0.86)	120 (56–186)	93 (80–106)	144 (129–157)	1676 (1012–2150)	5341 (3166–6537)
9	0.73 (0.42–0.85)	128 (56–179)	93 (80–106)	146 (128–157)	1711 (1018–2153)	5472 (3029–6449)
10	0.71 (0.45–0.85)	122 (61–183)	92 (80–106)	146 (127–156)	1687 (1023–2100)	5400 (3442–6505)

Discussion

Outbreaks of acute respiratory infections, such as influenza and the novel COVID-19, require an expansion of the available control policies. Here we used a mathematical model to examine a little-studied, non-pharmaceutical intervention policy of symptom-based isolation. We found consistent evidence in support of this policy across outbreak scenarios and settings. For influenza, a 15% and 25% reduction in the attack rate is expected with one and two days of isolation, respectively (Table 1). This indicates that the CDC-recommended policy for schools, based on a single day of isolation, could be enhanced by requiring an additional day of isolation. The result also holds in seasonal influenza in which vaccination is implemented. The isolation policy could be further strengthened with increased parental education and by reducing contacts during weekends.

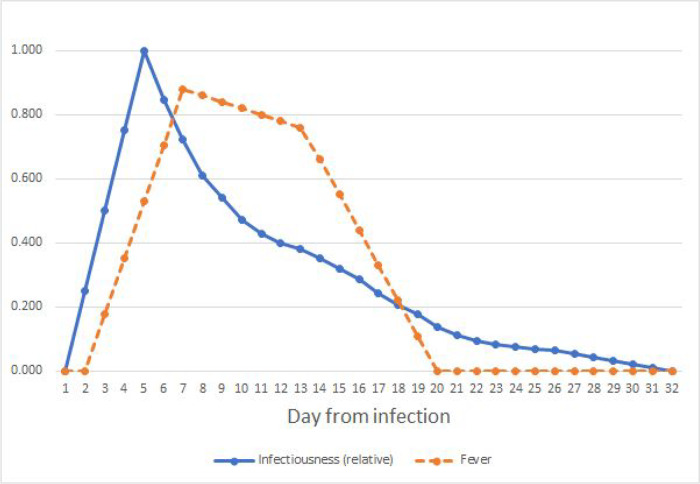
For COVID-19, we find that one day of post-fever isolation would reduce the attack rate by 8% in the conservative scenario where only 50% of the cases detect fever (Table 2). The policy is expected to achieve a 20% reduction in the peak of concurrent infections and extend the duration by 5 days. The policy is more effective if a greater proportion of cases are aware of their symptoms, and a 15% reduction is possible with six days of isolation after fever. Generally, COVID-19 is harder to control than influenza with isolation policies in part because the peak of infectiousness for SARS-CoV-2 arises before the development of fever symptoms, rather than coinciding with them (Appendix A).

Generally speaking, isolation policies, of which symptom-based isolation is a special case, are much more preferable to closures or general quarantines. Unlike the former, it allows healthy persons in the community to continue their lives. Business and critical public institutions such as schools and workplaces can remain open. Consequently, isolation of infected individuals until they recover could potentially be sustained indefinitely. It is likely that such isolation policies could be useful in the control of other acute respiratory diseases. These policies are expected to be complementary to other intervention measures, and can operate when testing resources are limited.

While our model is driven by rich sources of virological data and calibrated to several outbreaks, a few limitations are inherent in our approach. First, despite our use of multiple scenarios and hundreds of alternative simulations, the effect of any policy depends on the context where it would be applied. The details of the school or institution would matter, and therefore, we provide an online version of the model, which can be calibrated for each situation. Because our model was validated in influenza outbreaks in school settings, it should be applied to non-school settings and COVID-19 with caution. With appropriate adjustments, the model is designed to be applicable to other settings such as workplaces, prisons or even the broader community. However, such settings have important processes such as travel and complex population structures that might be less significant in the setting of schools. Lastly, symptom parameter information is based on average values, and it is expected that it will vary between patients. Future studies might attempt to evaluate symptom-based isolation policies with agent-based models (e.g. [17,52]) that can capture variability in health trajectories, the network structure of the population [53,54] and individual behavior.

Despite these limitations, our model captures essential aspects of acute respiratory outbreaks including progression through stages, the population structure and symptom trajectories.

Conclusions

In this study, we have created a model of transmission of respiratory infection and considered the effects of symptom-based isolation policies. We confirmed that such policies would be effective in controlling influenza and COVID-19 outbreaks in a variety of scenarios, and we recommend that isolation is maintained for at least two days following the last day of fever for influenza and 6 days for COVID-19. Policymakers tackling the influenza and COVID-19 outbreaks should consider implementing these policies for controlling outbreaks in schools and other settings. An online version of the model is made available for epidemiologists and policymakers as a live dashboard.

Appendix A: Model Dynamics and Parameters

We use the methodology of a multi-stage stratified SEIR model that can represent complexity of infection transmission [23,55]. Our model uses the discrete time version with daily time steps. We combine it with viral shedding and symptom data for influenza and COVID-19. The population in the model is divided into cohorts representing subpopulations in a community, school grades, office departments and the like. Each cohort is represented using its own variables, indexed by i including susceptibles, S_i, infected (explained below), and recovered R_i. Contact rates across cohorts and within them are described by a contact matrix, giving the model the ability to simulate a diverse set of institutions and communities.

In order to model the disease precisely, we stratify the infected population along three dimensions: the cohort, the degree of isolation and the stage of disease. The letters I and H distinguish infected un-isolated and thus infectious (I) from infected who are isolated and cannot transmit (H), see Table A.1. The population is further divided, so that the first subscript indicates the cohort and the second indicates the days from the person’s infection.

Table A.1.

Variables of the models. Indexi indicates the cohort (e.g. school grade, department, or communityi).

Variable	Interpretation
Si	susceptible/nai’ve persons in cohort i
Ii, d	Infected persons in cohort i on day d of infection who are not isolated
Hi, d	Similarly, but who are isolated (e.g. at home)
Ri	Recovered in cohort i

The force of infection λ_i experienced by persons in cohort i depends on the number of infected at each stage, the rate of viral shedding (s_d), and the contact matrix between all the cohorts (c_i,j). See Eqn A.1

Eqn A.1. Our modeling framework - the multi-state discrete time SEIR infection model stratified by cohort and day of infection. Variables are dependent on time t. Return rates from isolation at day r_d(p) depend on policy p, δ_1,d is the Kronecker delta function (=1 if d is 1, and otherwise zero). d_f is the final stage of infection. The parameters are listed in Table A.2

$$\begin{gathered} \Delta S_i=-b{S}_i{\lambda }_i \\ {H}_{i,d}=\left(1-r_d(p)\right)\left(H_{i,d-1}+I_{i,d-1}\right)\left(1-{\delta }_{1,d}\right) \\ {I}_{i,d}=r_d(p)\left(H_{i,d-1}+I_{i,d-1}\right)\left(1-{\delta }_{1,d}\right)+{\delta }_{1,d}b{S}_i{\lambda }_i \\ \Delta R_i=H_{i,d_f}+I_{i,d_f} \\ {\lambda }_i=\sum _j\sum _d{c}_{i,j}{s}_d{I}_{j,d} \end{gathered}$$

We model vaccination as reduction in the initially susceptible population for each cohort, which depends on the vaccination rate and the vaccine efficacy: ${\tilde{S}}_i(0)=S_i(0)-v{v}_e{S}_i(0)$. This transformation could be used to account for any resistance to infection, whether induced, or arising from genetics or prior exposure to similar pathogens.

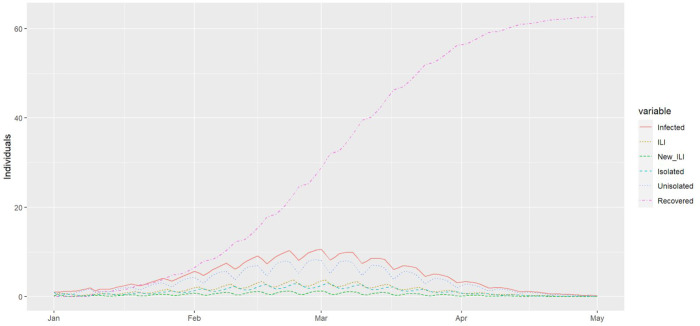
Typical outbreak curves are shown in Figure A.1.

Figure A.1.

The forecasted epidemic curve of an influenza outbreak in a typical school based on Department of Education data. Simulation is for the case with no isolation policy. Transmission is reduced during weekends resulting in visible ripples in the outbreak curves every 7 days. ILI, influenza-like illness.

Contact Rates

We assumed that persons have the most physical contact with others in their cohort. The rate of contact with other cohorts is controlled by a parameter which was varied in our sensitivity analysis. To adjust for generally higher contact rates during the winter months, we use a seasonal term cf. [56,57] which multiplies the baseline contact rate by a factor that peaks on January 1st:

$$b=b_0{b}_h(1+b_S\mathit{\text{cos}}(2\pi D/365)$$ Eqn A.2

Here D is the day of the year counting from January 1st. Like the influenza virus, SARS-CoV-2 transmission is apparently higher in cold and dry weather, but unlike influenza, it is also affected by absolute humidity [58]. Contact rates were also modified during weekends (Saturdays and Sundays) (cf. [30]), vacations and closures (see Table A.2).

Table A.2.

Summary of parameters and their interpretation. All time rate constants are in units of day ^{− 1}. Parameters are known from previous studies, set for each scenario, or calibrated to match the model to past outbreaks.

Parameter	Interpretation	Type	Range and Sources, if available
b0	Core transmission rate	Calibrated	See section on model calibration
bh	Relative contact rate during weekends	Calibrated	0 to 0.5, comparable to school closure in [18]
bc	Relative contact rate during closures, holidays or vacations	Calibrated	Generally lying around 0 to 0.5 comparable to school closure in [18]
bs	Relative seasonal amplitude of contact	Calibrated
ci, j	Relative contact rate for cohorts i and j	Input data or calibrated	Sometimes estimated from locations of cohorts in a building
L	Symptomatic rate	Input data	0.88 [59], 0.5 and 0.88 for COVID-19
p	Fraction of persons complying with policy	Calibrated	Quantifies compliance with the policy
rd	Fraction of persons return to cohort on day d after infection	Based on symptom data	See table below
sd	Shedding at day d (relative)	Input data or estimates	Proportional to log 10 titers [14]
tstart	Day of first infected case	Input data or calibration	Often reported approximately in post-outbreak investigations
v	Vaccination rate (seasonal virus)	Set during scenarios	Season flu: 60% [0.5, 0.7] [60], 0% in novel infections
ve	Vaccine efficacy (seasonal vims)	67% [0.65, 0.95]	[61,62] For novel infections with no immune response, 0%
Xi	Persons in cohort i	Set by scenario	Cohort is partitioned into fraction vve with vaccine protection and the rest
y	Fever attention	Calibrated	Fraction of persons who would return from home, of those having symptoms on the previous day

Rates of Return from Isolation and the Modeling of Policy

The values r_d express the fraction of persons returning from home on day d after they become infected when no policy is in place. It is modeled as a function of four factors: the symptoms in the previous days f_s, the symptom propensity (i.e., rate of symptomatic infections) l ∈ [0,1], the attention to symptoms y ∈ [0,1] and the compliance to policy if any p ∈ [0,1]. To be precise, in the simplest case (no isolation policy), increasing f_d−1, l or y would decrease the return rate: r_d = 1 − lyf_d−1. The introduction of the isolation policy decreases the return to school rate at day d by making the persons more attentive to the recent days of symptoms. Namely, under a one-day isolation policy, the rate is modified to:

$$r_d=1-[l(y+(1-y)p)]f_{d-1}\text{ on day }d;$$ Eqn A.3

This model ensures that the rate of symptoms lf_d−1 sets an upper bound on the effectiveness of the symptom-isolation policy. In the case of 100% compliance and 100% symptom attention, the return rate is 1 − lf_d−1 and not lower.

Under a two-day isolation policy, the rate on day d is given by replacing f_d−1 in Eqn A.3 with max(f_d−1,f_d−2), and in general, max_i=1..d−1(f_i) for longer isolation policies (see Table A.3, Table A.4).

Viral Shedding and Symptom Burden

Influenza viral shedding appears to vary by subtype, but the patterns of shedding were similar in both children and adults [63,64], and between the seasonal and p(H1N1) outbreaks [64–66], although the reproductive number appears different [65]. We allowed for some of the infections to be asymptomatic [59,63], which in our model increases the rates of return to the community and transmission, while also reducing the effectiveness of control policies. Meta-analysis of influenza studies [14] was used to determine shedding and symptom rates by disease state (see Table A.3, Table A.4).

Table A.3.

Daily symptom and shedding rates for influenza from [14]. New ILI rates is the probability of newly reporting influenza-like illness on a given day. Predicted return rates when symptom propensity is l = 0.88 and symptom attention is y = 0.5. Return rates: A = no policy, B = policy of one day of isolation with 0.5 compliance, C = policy of one day of isolation with 100% compliance. Rows are days from the time of infection.

		Symptoms					Return
Day after infection	Viral Shedding	Total Score	Fever (Systemic)	Respiratory	Nasal	New ILI Rates	A	B	C
1	1.89	0.25	0.12	0.15	0.18	0.25	1.00	1.00	1.00
2	3.00	0.67	0.93	0.66	0.79	0.50	0.92	0.91	0.90
3	2.63	0.85	0.75	0.95	0.94	0.25	0.32	0.25	0.18
4	2.16	0.67	0.60	0.91	0.91	0.00	0.45	0.40	0.34
5	1.54	0.47	0.30	0.56	0.70	0.00	0.56	0.52	0.47
6	1.07	0.18	0.17	0.56	0.47	0.00	0.78	0.76	0.73
7	0.74	0.06	0.08	0.49	0.17	0.00	0.88	0.86	0.85
8	0.30	0.06	0.07	0.36	0.02	0.00	0.94	0.93	0.93
9	0.35	0.00	0.08	0.14	0.00	0.00	0.95	0.94	0.94

Figure A.2.

Estimated SARS-CoV-2 infectiousness and symptom propensity in symptomatic cases. Infectiousness is based on [37,67,68] with linear interpolation added before day 5 and after day 28. Fever estimates are based on case reports in [69–71].

Table A.4.

Estimated symptom, shedding rates, and return rates for symptomatic persons infected with SARS-CoV-2. Asymptomatic infections are accounted for through a separate parameter. Return rates calculated for when attention is focused on fever, symptom propensity rate is l = 0.88 and symptom attention is y = 0.5. Return rates: A = no policy, B = policy of one day of isolation with 0.5 compliance, C = policy of one day of isolation with 100% compliance. Rows are days from the time of infection.

		Symptoms	Return
Day after infection	Viral Shedding	Fever (Systemic)	A	B	C
1	0.000	0	1.00	1.00	1.00
2	0.250	0	1.00	1.00	1.00
3	0.500	0.176	1.00	1.00	1.00
4	0.750	0.352	0.87	0.86	0.85
5	1.000	0.528	0.74	0.72	0.69
6	0.845	0.704	0.61	0.57	0.54
7	0.721	0.880	0.48	0.43	0.38
8	0.611	0.860	0.36	0.29	0.23
9	0.540	0.840	0.37	0.31	0.24
10	0.473	0.820	0.39	0.32	0.26
11	0.427	0.800	0.40	0.34	0.28
12	0.400	0.780	0.41	0.36	0.30
13	0.379	0.760	0.43	0.37	0.31
14	0.351	0.660	0.44	0.39	0.33
15	0.318	0.550	0.52	0.47	0.42
16	0.287	0.440	0.60	0.56	0.52
17	0.244	0.330	0.68	0.65	0.61
18	0.207	0.220	0.76	0.73	0.71
19	0.177	0.110	0.84	0.82	0.81
20	0.139	0	0.92	0.91	0.90
21	0.112	0	1.00	1.00	1.00
22	0.095	0	1.00	1.00	1.00
23	0.082	0	1.00	1.00	1.00
24	0.077	0	1.00	1.00	1.00
25	0.070	0	1.00	1.00	1.00
26	0.067	0	1.00	1.00	1.00
27	0.056	0	1.00	1.00	1.00
28	0.044	0	1.00	1.00	1.00
29	0.033	0	1.00	1.00	1.00
30	0.022	0	1.00	1.00	1.00
31	0.011	0	1.00	1.00	1.00
32	0.000	0	1.00	1.00	1.00

Model Validation

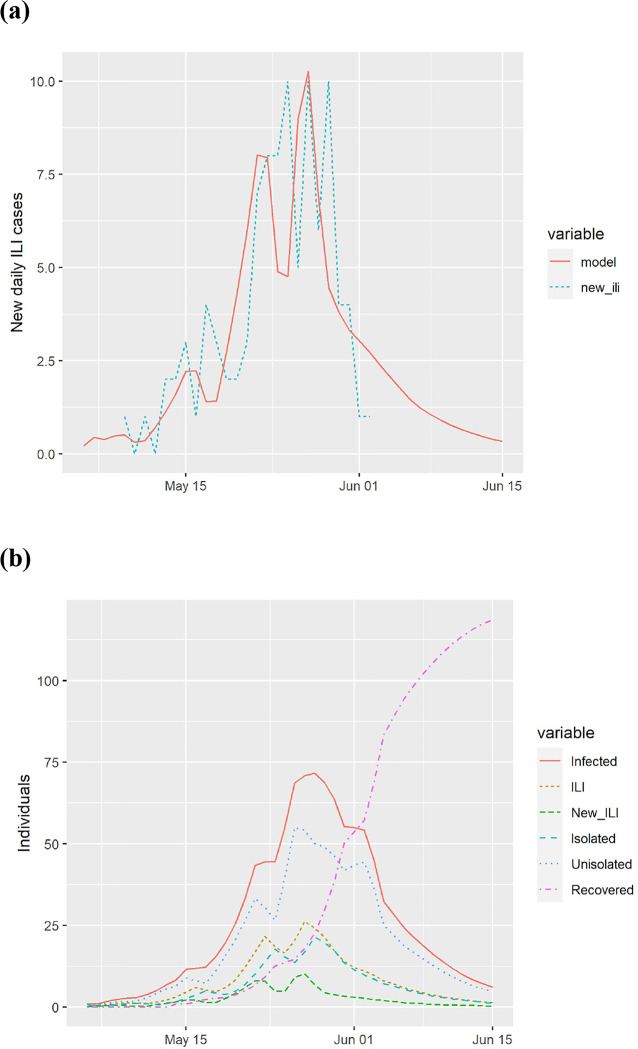
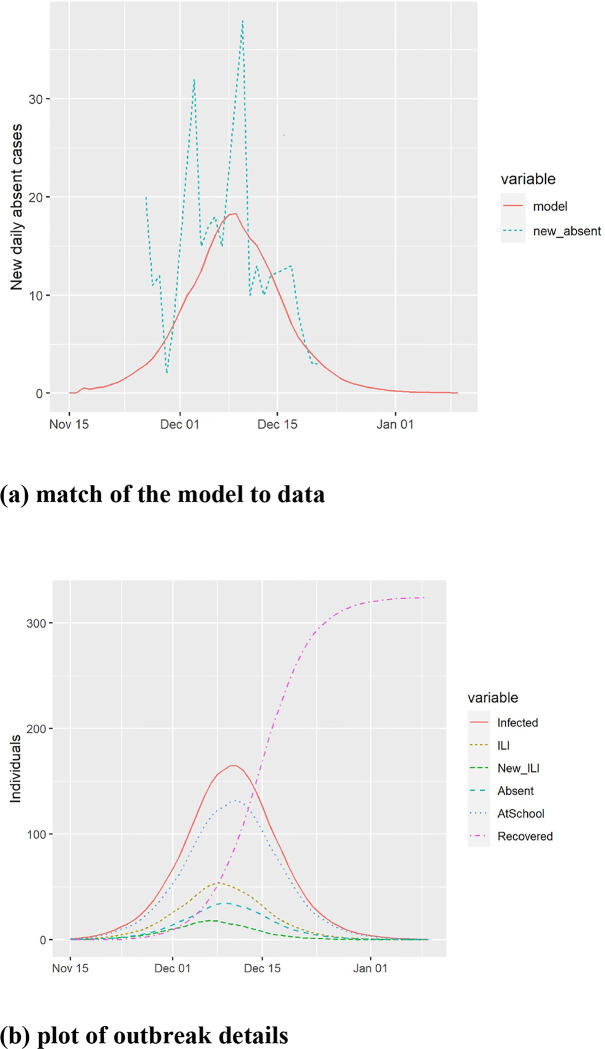
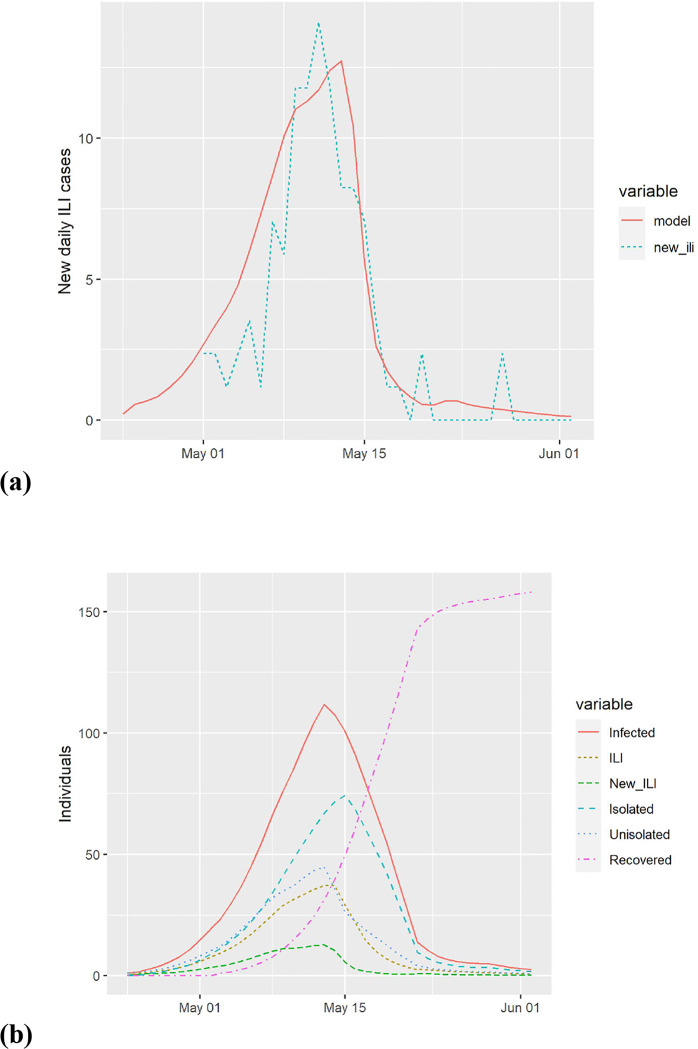
The model has been validated by comparing it to empirical data on three influenza outbreaks. The available data generally indicates the daily number of new ILI cases or the daily number of new absences, and both were also calculated from the model. In all calibrations, we found the model to give a tight fit to the data matching the attack rate, the peak date, and the overall shape, as illustrated in Figure A.3, Figure A.4, and Figure A.5.

For calibration, we need to estimate the number of individuals with influenza-like illness (ILI) and the number of newly absent. For ILI, the number of individuals with ILI at a given time t is computed by considering J_s(t) - the number of infected individuals on date t (including isolated and unisolated) who are in stage s and the rate of new ILI cases at stage s, l_s. The quantity is multiplied by l_s - the fraction of individuals that develop ILI (set at 88%, see [59]): $ILI(t)=l\sum _s{l}_s{J}_s(t)$. The symptom data indicates that influenza ILI symptoms first arise 24 hours after influenza challenge and peak around 2.5 after challenge. Accordingly, we assume that, of the population reporting ILI symptoms, ¼, ½ and ¼ first reports on day 1, 2 and 3, respectively.

We calculate the new absentees per day by considering the number of infected and the return rate. The number of isolated persons is given by: $\sum _s\left(1-r_s\right)I_s(t)$. Furthermore, the number of newly-absent (i.e. isolated) students is given by $\sum _s\prod _{q=1}^{s-1}{r}_q\left(1-r_s\right)I_s(t)$. We will use this formula in calibrating the model to absenteeism data below.

Figure A.3.

Calibration to data from a boarding school in South East England during the A(H1N1)v outbreak from May 9, 2009 through June 2, 2009, infecting 101 of the 1307 students [43]. (a) model predictions and actual new cases of influenza-like illness (ILI) and (b) estimated course of the epidemic from the model.

Figure A.4.

Calibration to absenteeism for a primary school in Thames Valley, UK during the 2012/2013 influenza season abstracted from [45]. The data shows spikes of new absences every Monday due to lack of data collection on Saturdays and Sundays. (a) model predictions and match to actual new cases of absence from school, and (b) estimated course of the epidemic from the model.

Figure A.5.

Calibration to data from an elementary school in Pennsylvania affected by the 2009 Pandemic Influenza A(H1N1). (a) model predictions and actual new cases of influenza-like illness (ILI). (b) estimated course of the epidemic from the model.

Fever policies of select schools and school districts in Metropolitan Chicago, Illinois, US is published online on our website: https://github.com/sashagutfraind/feverfighter. We also provide raw data used in the paper in the hope that it would assist other researchers.

Appendix B: Online Excel

Summary of each scenario and results available at https://github.com/sashagutfraind/feverfighter