Quantifying genetic effects on disease mediated by assayed gene expression levels

Abstract

Disease variants identified by genome-wide association studies (GWAS) tend to overlap with expression quantitative trait loci (eQTLs), but it remains unclear whether this overlap is driven by gene expression levels mediating genetic effects on disease. Here we introduce a new method, mediated expression score regression (MESC), to estimate disease heritability mediated by the cis-genetic component of gene expression levels. We applied MESC to GWAS summary statistics for 42 traits (average N = 323K) and cis-eQTL summary statistics for 48 tissues from the Genotype-Tissue Expression (GTEx) consortium. Averaging across traits, only 11±2% of heritability was mediated by assayed gene expression levels. Expression-mediated heritability was enriched in genes with evidence of selective constraint and genes with disease-appropriate annotations. Our results demonstrate that assayed bulk-tissue eQTLs, though disease relevant, cannot explain the majority of disease heritability.

Introduction

In the past decade, genome-wide association studies (GWAS) have shown that most disease-associated variants lie in noncoding regions of the genome^1–3, leading to the hypothesis that regulation of gene expression levels is the primary biological mechanism through which genetic variants affect complex traits, and motivating large scale expression quantitative trait loci (eQTL) studies^4,5. Many statistical methods have been developed to integrate eQTL data with GWAS data to gain functional insight into the genetic architecture of disease. These methods include: colocalization tests, which have shown that many genes have eQTLs that colocalize with GWAS loci^6–10; transcriptome-wide association studies, which have shown that many genes exhibit significant cis-genetic correlations between their expression and disease^11–24; and partitioning of disease heritability, which has shown that eQTLs as a whole are significantly enriched for disease heritability^25–28.

Despite these findings, it remains unclear the extent to which eQTLs from available studies capture mechanistic effects of gene expression on disease^9,29–31. In particular, eQTLs from the largest available gene expression reference panels^5,32 are measured in bulk tissues in steady-state cellular conditions, which may not reflect the specific cell types or cellular contexts in which gene expression is causal for disease^33–35. In addition, several different causal scenarios can result in similar patterns of enrichment/overlap between GWAS loci and eQTLs, summarized in Figure 1a: (1) mediation, (2) pleiotropy, and (3) linkage. Of these three scenarios, only scenario (1) is informative of the SNP’s mechanism of action on disease, but existing methods are unable to consistently distinguish scenarios (2) and (3) from scenario (1). Colocalization tests can sometimes rule out linkage as an explanation for overlap between eQTLs and disease SNPs, but cannot rule out pleiotropy^13,36. Transcriptome-wide association studies cannot rule out either pleiotropy or linkage^13,29. Among the methods that partition disease heritability, some aim to rule out linkage through fine-mapping of eQTLs²⁷, but none aim to rule out pleiotropy. Thus, it remains unclear whether enrichment/overlap between eQTLs and disease SNPs usually reflects mediation, or whether it more commonly reflects pleiotropy and/or linkage^9,29. For example, in the case of autoimmune diseases, most instances of overlap between significant disease loci and immune cell eQTLs are driven by linkage⁹, suggesting that linkage may be more prevalent than mediation³¹.

Figure 1. Schematic of MESC.

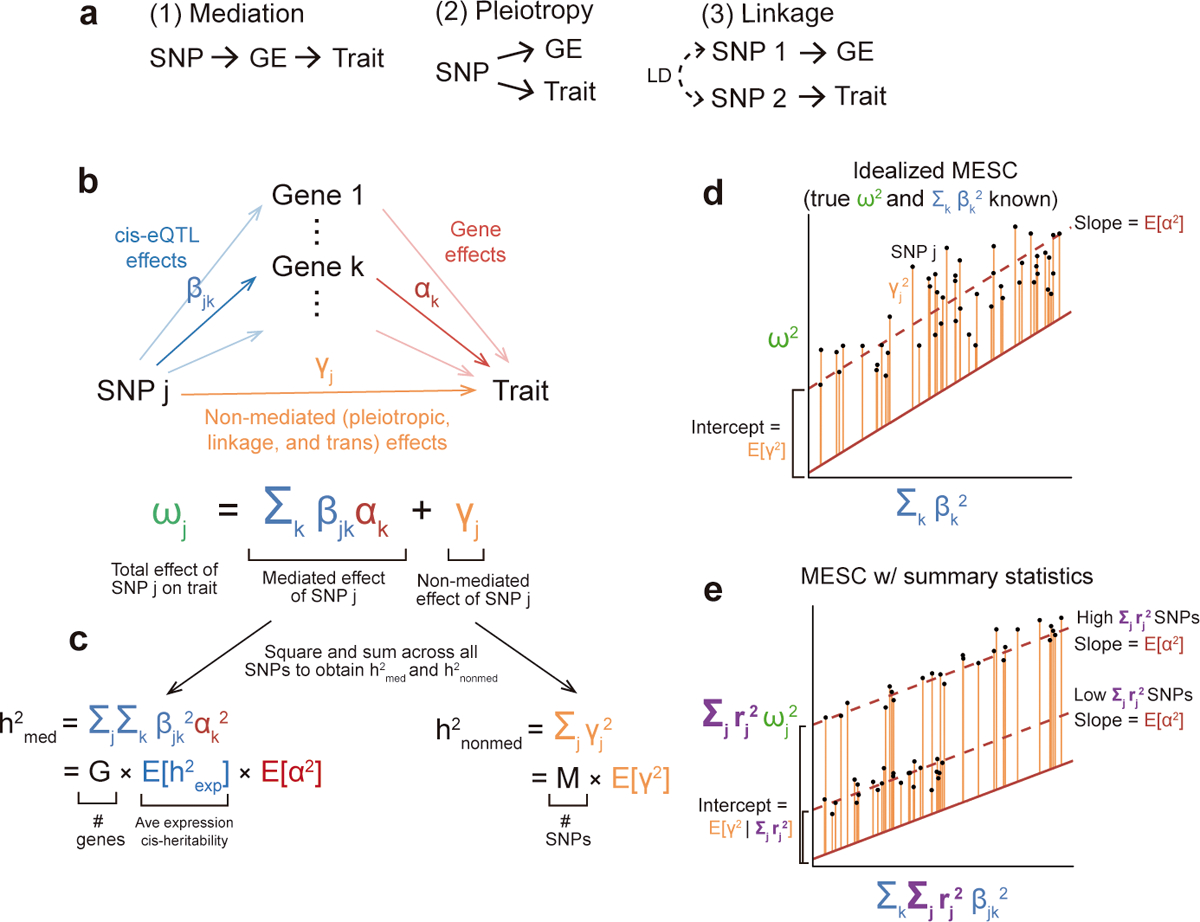
(a) Three possible causal scenarios explaining enrichment/overlap between GWAS loci and eQTLs. GE, gene expression levels. (b) SNP effect sizes are modeled as the sum of a mediated component (defined as causal cis-eQTL effect sizes β multiplied by gene-trait effect sizes α) and a non-mediated component γ. (c) Heritability mediated by the cis-genetic component of gene expression levels ($h_{med}^2$) is defined as the squared mediated component of SNP effect sizes summed across all SNPs (assuming that genotypes and phenotypes are standardized). $h_{med}^2$ can be rewritten as the product of the number of genes G, the average expression cis-heritability $E\left[h_{cis}^2\right]$, and the average gene-trait effect size E[α²] (d) The basic premise behind MESC is to regress squared GWAS effect sizes on squared eQTL effect sizes. Non-directional non-mediated effects are captured by the intercept, while directional mediated effects are captured by the slope, which equals E[α²] given appropriate effect size independence assumptions (see Methods). (e) In practice, MESC involves regressing squared GWAS summary statistics on squared eQTL summary statistics. Differences in the level of LD between SNPs are captured by an LD score covariate. In the figure, we show a simplified LD architecture with two discrete levels of LD.

In this study, we aim to quantify the proportion of disease heritability mediated in cis by assayed expression levels (scenario (1) from above). We first define expression-mediated heritability under a generative model featuring both mediated and non-mediated (including pleiotropic and linkage) effects of SNPs on the trait. This definition can accommodate assayed gene expression levels measured in a tissue or cellular context not necessarily causal for the disease. We introduce a method, mediated expression score regression (MESC), to estimate expression-mediated heritability from GWAS summary statistics, linkage disequilibrium (LD) scores, and eQTL effect sizes obtained from external expression panels. Intuitively, MESC distinguishes mediated from non-mediated effects in a set of genes via the idea that mediation (unlike pleiotropy and linkage) induces a linear relationship between the magnitude of eQTL effect sizes and disease effect sizes. We applied MESC to GWAS summary statistics for 42 diseases and complex traits and cis-eQTL data for 48 tissues from the GTEx consortium⁵ to quantify the proportion of disease heritability mediated by the expression levels of all genes as a whole, as well as by various functional gene sets.

Results

Definition of expression-mediated heritability

We briefly define heritability mediated by the cis-genetic component of gene expression levels ($h_{med}^2$). Cis-eQTL effects multiplied by gene-trait effects form an expression-mediated component of each SNP effect on trait (Figure 1b). This component is then squared and summed across all SNPs to obtain $h_{med}^2$ (Figure 1c,d). Our definition of $h_{med}^2$ additionally has two forms: $h_{med;\mathit{\text{causal}}}^2$, in which cis-eQTL effect sizes are hypothetically obtained in the causal cell types and contexts for the disease, and $h_{med;\mathit{\text{assayed}}}^2\left(T\right)$, in which cis-eQTL effect sizes are obtained in a given set of assayed tissues T (e.g. from GTEx). $h_{med;\mathit{\text{assayed}}}^2\left(T\right)$ and $h_{med;\mathit{\text{causal}}}^2$ are related by the formula $h_{med;\mathit{\text{assayed}}}^2\left(T\right)=r_g^2\left(T\right)h_{med;\mathit{\text{causal}}}^2$, where $r_g^2\left(T\right)$ is the average squared genetic correlation between expression in T and expression in the unobserved causal cell types/contexts for the disease. In practice, we only aim to estimate $h_{med;\mathit{\text{assayed}}}^2\left(T\right)$, but it is useful to conceptualize this quantity in terms of $h_{med;\mathit{\text{causal}}}^2$ since $h_{med;\mathit{\text{causal}}}^2$ has a more direct mechanistic interpretation. For brevity, we refer to $h_{med;\mathit{\text{assayed}}}^2\left(T\right)$ as simply $h_{med}^2$ for the remainder of the manuscript, where the set of tissues T is implicit.

We also define a quantity $h_{med}^2\left(D\right)$ corresponding to the heritability mediated by the expression levels of gene category D, where D can be arbitrarily defined over any set of genes (e.g. genes in a specific molecular pathway). See Methods for a more detailed definition of $h_{med}^2$ and $h_{med}^2\left(D\right)$.

Estimating expression-mediated heritability using MESC

In order to estimate $h_{med}^2$, we propose an approach that involves regressing squared GWAS summary statistics on squared cis-eQTL summary statistics summed across genes (Figure 1d). Differences in LD between SNPs are captured by conditioning on LD scores (Figure 1e). In addition, to avoid bias (see below), we stratify the regression across both gene categories D and SNP categories C. The final regression equation used to estimate $h_{med}^2$ is

$$E\left[{\chi }_k^2\right]=N\sum _c{\tau }_c{\mathcal{l}}_{k;c}+N\sum _d{\pi }_d{\mathcal{L}}_{k;d}+1$$

where ${\chi }_k^2$ is the GWAS χ² statistic of SNP k, N is the number of samples, τ_c is the per-SNP contribution to non-mediated heritability of SNPs in SNP category C, ℓ_k;c is the LD score^2,37 of SNP k with respect to SNP category C (defined as ${\mathcal{l}}_{k;c}={\sum }_{j\in C}{r}_{jk}^2$), π_d is the per-gene contribution to $h_{med}^2\left(D\right)$, and ℒ_k;d is the expression score of SNP k with respect to gene category D (defined as ${\mathcal{L}}_{k;d}={\sum }_{i\in D}{\sum }_J^M{r}_{jk}^2{\beta }_{ij}^2$). Here, r_jk refers to the LD between SNPs j and k, while β_ij refers to the causal cis-eQTL effect size of SNP j on gene i. ℒ_k;d can be conceptualized as the total expression cis-heritability of genes in D that is tagged by SNP k.

The above equation allows us to estimate π_d and τ_c via computationally efficient multiple regression of GWAS chi-square statistics against LD scores and expression scores. In order for the equation to provide unbiased estimates of $h_{med}^2$, two main effect size independence assumptions must be satisfied, of which violations can be addressed via careful partitioning of SNPs and/or genes (Methods; Supplementary Note).

Throughout this study, we present estimates of three quantities that are a function of $h_{med}^2$ and/or $h_{med}^2\left(D\right)$: (1) the proportion of heritability mediated by expression (defined as $h_{med}^2/h_g^2$), (2) the proportion of expression-mediated heritability for gene category D (defined as $h_{med}^2\left(D\right)/h_{med}^2$), and (3) the enrichment of expression-mediated heritability for D (defined as the proportion of expression-mediated heritability in D divided by the proportion of genes in D). We estimate standard errors and p-values for all quantities by jackknifing over blocks of SNPs^2,37 (Methods). We have released open source software implementing our method (https://github.com/douglasyao/mesc).

Simulations assessing calibration and bias

We performed simulations to assess the calibration and bias of MESC in estimating $h_{med}^2/h_g^2$ and its standard error from simulated complex trait and expression data under a variety of genetic architectures (Methods). We performed all simulations using real genotypes from UK Biobank³⁸ (N_GWAS = 10,000 GWAS samples; N_eQTL = 100–1000 expression samples, M = 98,499 SNPs from chromosome 1).

We evaluated the bias of MESC in estimating various values of $h_{med}^2/h_g^2$ in the following scenarios: (1) when varying expression panel sample size (Figure 2a), (2) when varying the proportion of SNPs and genes with nonzero effects (Figure 2b), (3) when simulating eQTL effect sizes in the gene expression panel that differ from those used to generate the complex trait phenotype, emulating the scenario in which assayed tissues differ from the causal tissue(s) for the disease (Figure 2c), (4) when using different methods to estimate expression scores (5 in total) (Supplementary Figure 1), (5) when varying total disease heritability (Supplementary Figure 2), and (6) when including rare variants and inducing an inverse relationship between eQTL/GWAS effect size magnitude and minor allele frequency (Supplementary Figure 3), consistent with negative selection acting on both gene expression^39,40 and complex trait^41,42. We observed that MESC produced unbiased or nearly unbiased estimates of $h_{med}^2/h_g^2$ across all simulated genetic architectures with expression panel sample size greater than 500 when using the best-performing method to estimate expression scores, LASSO with REML correction (Methods). We note that available expression panel sample sizes for individual tissues are typically smaller than 500, which necessitates meta-analysis across tissues to attain larger expression panel sample sizes (Methods). For scenario (3), we expect in theory that MESC will estimate the quantity $r_g^2\left(T\right)h_{med;\mathit{\text{causal}}}^2$ when using expression scores from a non-causal tissue with average squared genetic correlation of expression $r_g^2\left(T\right)$ with the causal tissue. Our simulation results support this theoretical expectation.

Figure 2. Simulation results.

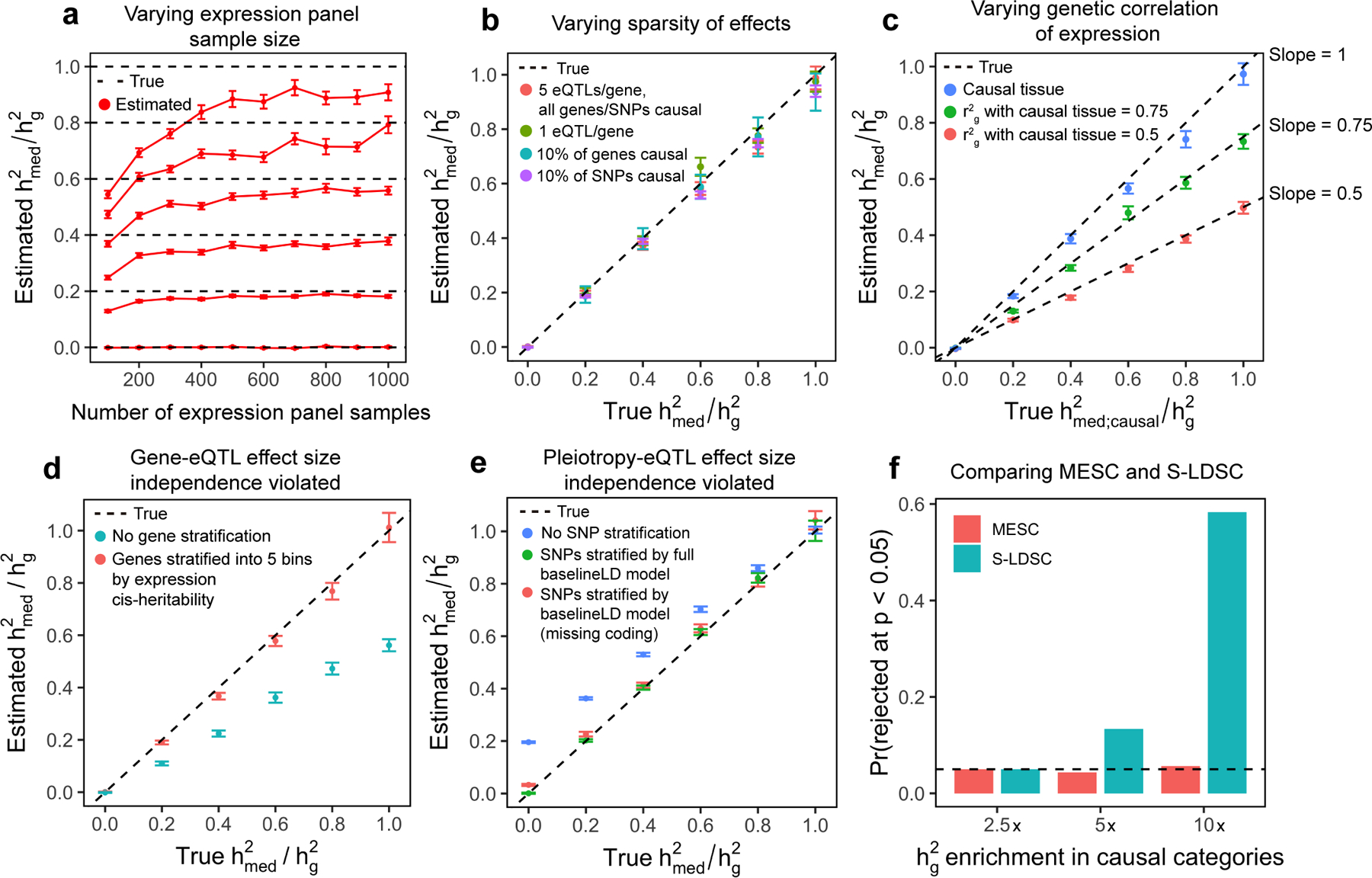
We simulated expression and complex trait architectures corresponding to various levels of $h_{med}^2/h_g^2$. GWAS sample size was fixed at 10,000 and $h_g^2$ was fixed at 0.5. Error bars represent mean standard errors across 300 simulations. (a) Impact of expression panel sample size on $h_{med}^2/h_g^2$ estimates. Expression scores were estimated from simulated expression panel samples using LASSO with REML correction. (b) Impact of sparse genetic/eQTL architectures on $h_{med}^2/h_g^2$ estimates. (c) $h_{med}^2/h_g^2$ estimates with $r_{\text{g}}^2\left(\text{T}\right)<1$. (d) $h_{med}^2/h_g^2$ estimates in the presence of a negative correlation between the magnitude of eQTL effect size and gene effect size (constituting a violation of gene-eQTL independence). Results are shown with and without stratifying genes by 5 expression cis-heritability bins. See Supplementary Figure 5 for $h_{med}^2(D)/h_g^2$ estimates of individual bins. (e) $h_{med}^2/h_g^2$ estimates when 100% of eQTL effects and non-mediated effects lie within coding regions (constituting a violation of gene-eQTL independence). Results are shown stratifying SNPs by the baselineLD model and a version of the baselineLD model with the coding annotation removed. See Supplementary Figure 6 for additional similar simulations. (f) With $h_{med}^2/h_g^2$ fixed at 0, we varied the heritability enrichment of three eQTL-enriched SNP categories (coding, TSS, and conserved regions) from 2.5x to 10x. In the figure, we show the proportion of simulations in which the null hypothesis that $h_{med}^2/h_g^2=0$ is rejected by MESC, and the proportion of simulations in which the null hypothesis of no $h_g^2$ enrichment for the set of all eQTLs is rejected by stratified LD-score regression (S-LDSC).

Next, we assessed the bias of MESC in two biologically plausible scenarios corresponding to violations of the two main effect size independence assumptions (Methods), and we assessed how well partitioning genes and SNPs ameliorated this bias. The assumptions can be summarized as: (1) gene-eQTL independence, where eQTL and gene effect size magnitude are independent within each gene category, and (2) pleiotropy-eQTL effect size independence, where eQTL and SNP non-mediated effect size magnitude are independent within each SNP category. We simulated violations of (1) by inducing a negative correlation between eQTL and gene effect size magnitude across the genome. We observed that partitioning genes into 5 bins by the magnitude of their expression heritability enabled us to obtain approximately unbiased estimates of $h_{med}^2/h_g^2$ (Figure 2d). We simulated violations of (2) by inducing enrichment of eQTLs and non-mediated effects within the same SNP categories (e.g. coding regions, transcription start sites, or conserved regions). We observed that partitioning SNPs by the baselineLD model^2,43 (a set of comprehensive functional SNP annotations) enabled us to obtain approximately unbiased estimates of $h_{med}^2/h_g^2$ (Figure 2e), even in extreme scenarios e.g. when 100% of mediated and non-mediated heritability were entirely concentrated in coding regions.

Finally, we performed simulations comparing MESC to other methods. To our knowledge, no published methods specifically aim to estimate heritability mediated by expression levels. The closest analogues are approaches that measure the genome-wide heritability enrichment of eQTLs^25–28 using GCTA⁴⁴ or stratified LD score regression (S-LDSC)^2,43. In simulations, we found that S-LDSC detected significant heritability enrichment of a SNP category corresponding to the set of all eQTLs in the absence of any mediation ($h_{med}^2/h_g^2=0$), while MESC had a well-calibrated false positive rate for detecting significantly non-zero $h_{med}^2/h_g^2$ in this scenario (Figure 2f).

In summary, we show that MESC produces approximately unbiased estimates of $h_{med}^2/h_g^2$ and well-calibrated standard errors under a wide variety of simulated genetic and gene architectures for expression panel sample sizes > 500, whereas other methods cannot distinguish mediated from non-mediated effects. See Supplementary Note for more details on simulations in this section.

Estimation of $h_{med}^2$ for 42 diseases and complex traits

We applied MESC to estimate the proportion of heritability mediated by the cis-genetic component of assayed expression levels ($h_{med}^2/h_g^2$) for 42 independent diseases and complex traits from the UK Biobank³⁸ and other publicly available datasets (average N = 323K; see Supplementary Table 1 for list of traits). In total, we produced three different types of expression scores: (1) expression scores for each individual GTEx tissue, (2) expression scores meta-analyzed within groups of GTEx tissues with common biological origin (Supplementary Table 2), and (3) expression scores meta-analyzed across all 48 GTEx tissues. Each type of expression score was used to estimate $h_{med}^2/h_g^2$ for each complex trait (Methods). To avoid biases, we partitioned genes by 5 expression cis-heritability bins and SNPs by the baselineLD model. We performed several analyses evaluating the robustness of these SNP and gene categories, finding that our estimates of $h_{med}^2/h_g^2$ were similar with other reasonable choices of SNP and gene categories but very biased when not partitioning genes or SNPs at all (Supplementary Note).

Across all 42 traits, we observed an average $h_{med}^2/h_g^2$ of 0.11 (S.E. 0.02) from the all-tissue meta-analyzed expression scores. We did not observe a relationship between $h_{med}^2/h_g^2$ and $h_g^2$ across traits (R² = 0.004) (Extended Data 1). Of the 42 traits, 26 had $h_{med}^2/h_g^2$ estimates greater than 0 at nominal significance (p-value < 0.05), with 10 reaching Bonferroni significance (p-value < 0.05 / 42). In Figure 3a, we report $h_{med}^2/h_g^2$ estimates from all-tissue and tissue-group meta-analyzed expression scores for a representative set of 10 genetically uncorrelated traits (full results in Extended Data 2 and Supplementary Table 3,4). We observed consistently lower estimates of $h_{med}^2/h_g^2$ from individual-tissue expression scores than from meta-tissue expression scores, as well as a positive correlation between tissue sample size and magnitude of individual-tissue $h_{med}^2/h_g^2$ (R² = 0.71) (Extended Data 3), suggesting downward biases in individual-tissue $h_{med}^2/h_g^2$ estimates due to low sample size.

Figure 3. Estimates of proportion of heritability mediated by expression from GTEx.

(a) Estimated proportion of heritability mediated by the cis-genetic component of assayed gene expression levels ($h_{med}^2/h_g^2$) for 10 genetically uncorrelated traits (average N = 339K). See Supplementary Note for procedure behind selecting these 10 traits and Extended Data 2 for estimates of $h_{med}^2/h_g^2$ for all 42 traits. Error bars represent jackknife standard errors. For each trait, we report the $h_{med}^2/h_g^2$ estimate for “All tissues” (expression scores meta-analyzed across all 48 GTEx tissues) and “Best tissue group” (expression scores meta-analyzed within 7 tissue groups). Here, “best” refers to the tissue group resulting in the highest estimates of $h_{med}^2/h_g^2$ compared to all other tissue groups. (b) $h_{med}^2/h_g^2$ estimates meta-analyzed across all 42 traits (average N = 323K). Error bars represent standard errors from random-effects meta-analysis. Here, “Best tissue” refers to the individual tissue resulting in the highest estimates of $h_{med}^2/h_g^2$ compared to all other tissues. BMI, body mass index; CNS, central nervous system.

As independent validation, we used cis-eQTL summary statistics from eQTLGen³² (N_eQTL = 31,684 in blood only) to estimate $h_{med}^2/h_g^2$ for the same 42 traits we analyzed above. We obtained very similar $h_{med}^2/h_g^2$ estimates as GTEx all-tissue expression for blood/immune traits and lower $h_{med}^2/h_g^2$ for non-blood/immune traits (Extended Data 4, Supplementary Table 5), consistent with the fact that that eQTLGen only captures expression levels in blood while GTEx all-tissue meta-analysis captures expression levels across diverse tissues.

Genes with low expression heritability explain more $h_{med}^2$

To investigate the relationship between expression cis-heritability ($h_{cis}^2$) and amount of complex trait heritability mediated by those genes, we looked at the proportion of $h_{med}^2$ (defined as $h_{med}^2\left(D\right)/h_{med}^2$ for gene category D) mediated by genes stratified into 10 equally-sized bins by their $h_{cis}^2$. Across 26 traits with $h_{med}^2$ significantly greater than 0, we observed an inverse relationship between meta-tissue $h_{cis}^2$ and proportion of $h_{med}^2$ across gene bins (Figure 4, Supplementary Table 6), with 32% of $h_{med}^2$ explained by the lowest 2 bins (mean meta-tissue $h_{cis}^2=0.014$) and only 3% of $h_{med}^2$ explained by the highest 2 bins (mean meta-tissue $h_{cis}^2=0.30$). This result implies that genes with less heritable expression (i.e. weaker/fewer eQTLs) have substantially larger causal effect sizes on the complex trait.

Figure 4. Low heritability genes explain more expression-mediated disease heritability.

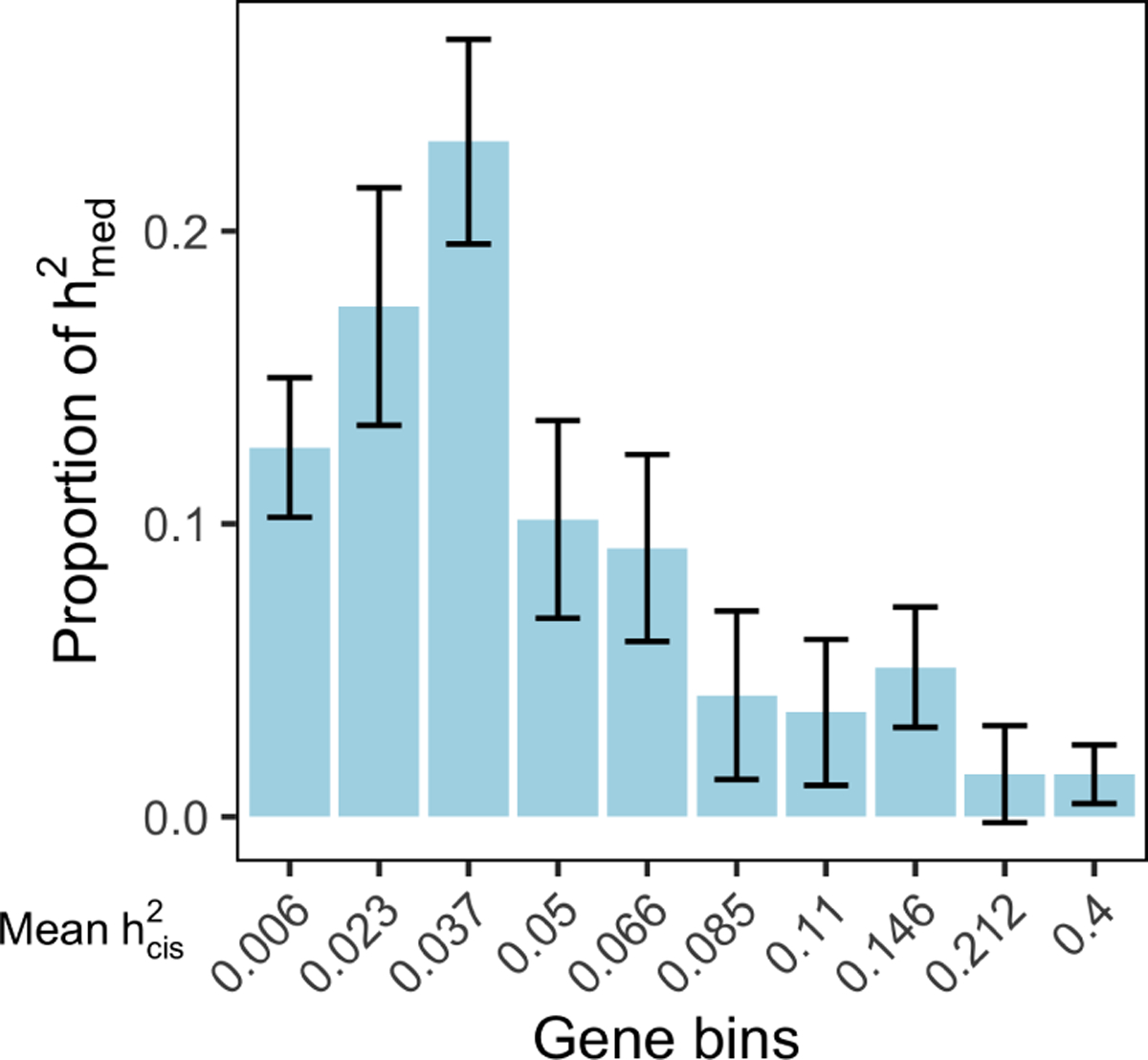
(a) Estimated proportion of expression-mediated heritability ($h_{med}^2(D)/h_{med}^2$) for 10 gene bins stratified by magnitude of expression cis-heritability. Results are meta-analyzed across 26 traits with nominally significant $h_{med}^2$. Error bars represent standard errors from random effects meta-analysis. Results for individual traits can be found in Supplementary Table 6.

We considered several reasons why genes with less heritable expression might have larger causal effects on the complex trait. One explanation is that negative selection purifies out strong eQTLs for genes with large effect on complex traits^5,45. Alternatively, genes with low meta-tissue $h_{cis}^2$ may consist of genes with tissue-specific eQTLs, which have been shown to be enriched for disease heritability^5,27,28. In support of the first explanation, we observed that the probability of being loss-of-function intolerant⁴⁶ (i.e. pLI) and the level of selection against protein-truncating variants⁴⁷ (i.e. s_het) were both inversely correlated with meta-tissue $h_{cis}^2$ (Spearman’s ρ = −0.23 and −0.21 respectively) (Extended Data 5). We did not observe strong evidence for the second hypothesis (Supplementary Note).

$h_{med}^2$ enrichment in functional gene sets

To gain insight into the distribution of expression-mediated effect sizes across various functional gene sets, we estimated $h_{med}^2$ enrichment, defined as (proportion of $h_{med}^2$) / (proportion of genes), for these gene sets. We analyzed 827 gene sets from three main sources: (1) 10 gene sets reflecting various broad metrics of gene essentiality; (2) 780 gene sets reflecting specific biological pathways, including gene sets from the KEGG⁴⁸, Reactome⁴⁹, and Gene Ontology (GO)⁵⁰ pathway databases; and (3) 37 gene sets comprising genes specifically expressed in 37 different GTEx tissues⁵¹ (Methods; see Supplementary Table 7 for list of gene sets). We restricted our analyses to large gene sets with at least 200 genes, since we observed large standard errors in $h_{med}^2$ enrichment estimates for gene sets with 200 or fewer genes (Supplementary Figure 4).

Out of 21,502 gene set-complex trait pairs (827 gene sets × 26 complex traits), we observed 226 gene set-complex trait pairs (comprising 117 unique gene sets) with FDR-significant $h_{med}^2$ enrichment (q-value < 0.05 accounting for 21,502 hypotheses tested). Significant $h_{med}^2$ enrichment estimates ranged from 1.5x to 51x across gene-set complex trait pairs. The full list of $h_{med}^2$ enrichment estimates for all 21,502 gene set-complex trait pairs is reported in Supplementary Table 8.

In Figure 5a, we show $h_{med}^2$ enrichment estimates for all 10 broadly essential gene sets meta-analyzed across 26 complex traits (individual trait results in Extended Data 6). We observed Bonferroni-significant meta-trait $h_{med}^2$ enrichment (p < 0.05 / 10) for 8 gene sets, including ExAC loss-of-function intolerant genes⁴⁶ (3.9x enrichment; p = 2.3 × 10⁻²⁵), FDA-approved drug targets⁵² (5.2x enrichment; p = 2.0 × 10⁻⁵), genes essential in mice^53–55 (4.0x enrichment; p = 1.1 × 10⁻¹⁰), and genes nearest to GWAS peaks⁵⁶ (3.9x enrichment; p = 5.0 × 10⁻⁴⁶).

Figure 5. Expression-mediated heritability enrichment estimates for functional gene sets.

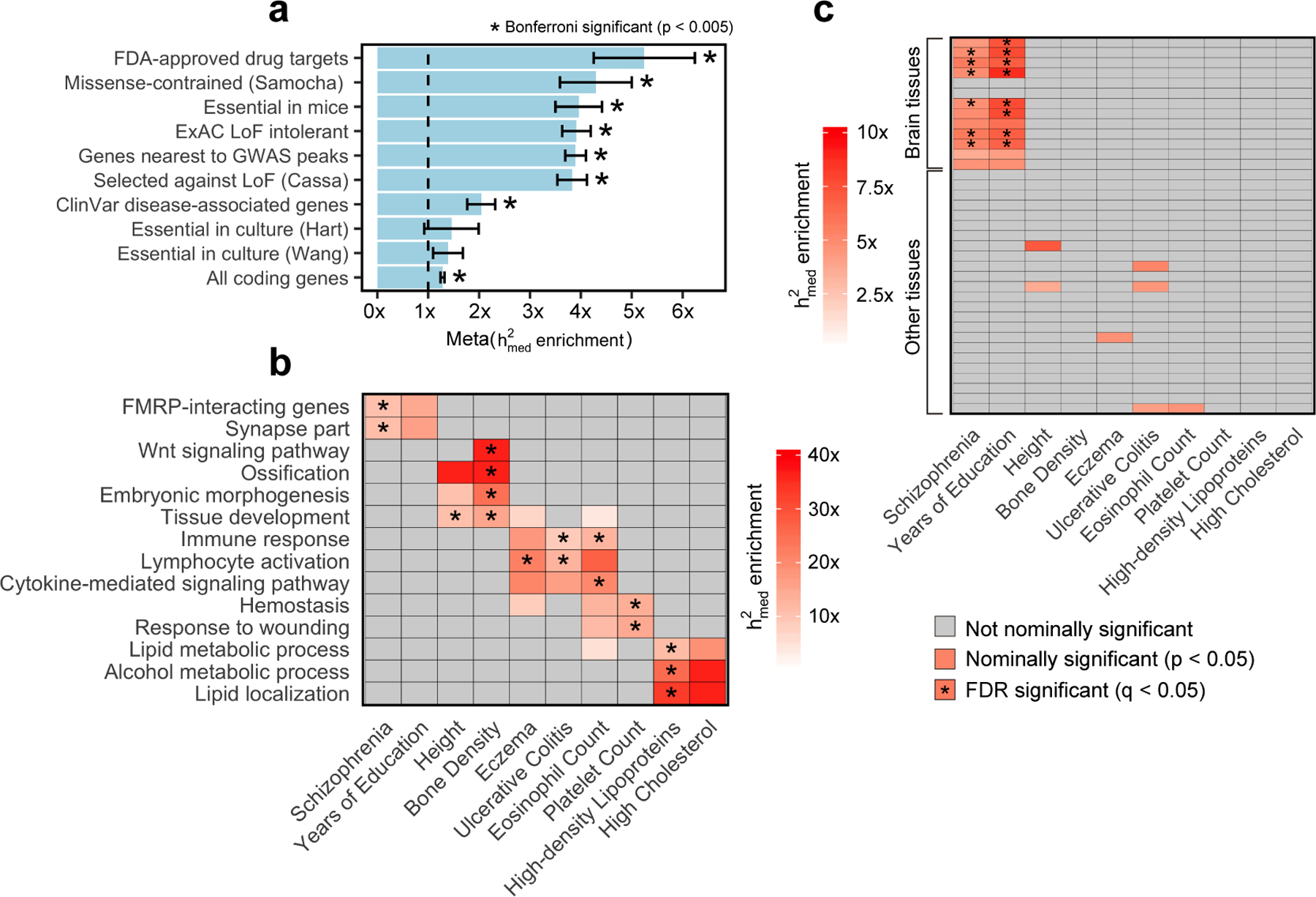
For all plots, x axis represents complex traits and y axis represents gene sets. P-values for $h_{med}^2$ enrichment are obtained using a two-tailed z-test using jackknife standard errors for $h_{med}^2$ enrichment. (a) $h_{med}^2$ enrichment estimates for 10 broadly essential gene sets meta-analyzed across 26 complex traits. $h_{med}^2$ enrichment estimates for individual traits can be found in Extended Data 6. Error bars represent standard errors from random-effects meta-analysis. (b) For ease of display, we report $h_{med}^2$ enrichment estimates for a representative set of 14 pathway-specific gene sets across 10 complex traits. $h_{med}^2$ enrichment estimates for additional complex traits and gene sets can be found in Extended Data 7 and Supplementary Table 8. (c) $h_{med}^2$ enrichment estimates for 37 gene sets corresponding to specifically expressed genes in 37 GTEx tissues. Brain tissues (13 total) are indicated as so in the figure. $h_{med}^2$ enrichment estimates for additional complex traits, with individual GTEx tissues labelled, can be found in Supplementary Figure 7. LoF, loss of function.

Of the 780 pathway gene sets, we observed that 97 had a significant $h_{med}^2$ enrichment (q-value < 0.05) in at least one of the 26 complex traits. In Figure 5b, we show the $h_{med}^2$ enrichment estimates of a representative set of 140 gene set-complex trait pairs (full results in Extended Data 7). Most gene sets exhibited highly trait-specific patterns of enrichment that were consistent with the known biology of the trait, including fragile X mental retardation protein (FMRP)-interacting genes for schizophrenia^57,58, Wnt signaling for bone density⁵⁹, and hemostasis for platelet count⁶⁰.

Finally, we investigated whether genes specifically expressed in 37 different GTEx tissues⁵¹ were enriched for $h_{med}^2$. We found significant $h_{med}^2$ enrichment (q-value < 0.05) of genes specifically expressed in brain tissues for brain-related traits (schizophrenia and years of education) (Figure 5c), demonstrating that the complex trait heritability of SNPs near genes specifically expressed in causal tissues (at least for the two traits here) is in part mediated by the expression of those genes.

Given that MESC can be used to prioritize disease-relevant gene sets based on the magnitude of their $h_{med}^2$ enrichment, it falls alongside a large class of methods that aim to perform gene set enrichment analysis from GWAS data^61–67. We compared results from MESC to two other popular gene set enrichment methods applied to the same GWAS summary statistics we analyzed, MAGMA⁶⁴ and DEPICT⁶³. We observed that MESC highlighted both broadly concordant and unique gene sets compared to these other methods (Supplementary Note; Extended Data 8; Supplementary Table 9).

Discussion

We have developed a new method, mediated expression score regression (MESC), to estimate complex trait heritability mediated by the cis-genetic component of assayed expression levels ($h_{med}^2$) from GWAS summary statistics and eQTL effect sizes estimated from an external expression panel. Our method is distinct from existing methods that identify and quantify overlap between eQTLs and GWAS hits (including colocalization tests^6–10, transcriptome-wide association studies^11–14,16, and heritability partitioning by eQTL status^25–28) in that it specifically aims to distinguish directional mediated effects from non-directional pleiotropic and linkage effects. Moreover, our polygenic approach does not require individual eQTLs or GWAS loci to be significant and is not impacted by the sparsity of eQTL effect sizes, so unlike other approaches^9–13,27 we do not exclude genes or SNPs from our analyses based on any significance thresholds. We applied our method to summary statistics for 42 traits and eQTL effect sizes estimated from 48 GTEx tissues. We show that across traits, a significant but modest proportion of complex trait heritability (0.11±0.02) is mediated by the cis-genetic component of assayed expression levels. Though many previous approaches have hypothesized that SNPs impact complex traits by directly modulating gene expression levels, our results provide concrete genome-wide evidence for this hypothesis. On the other hand, the fact that our $h_{med}^2/h_g^2$ estimates are low for most traits suggests that eQTLs estimated from steady-state expression in bulk post-mortem tissues from GTEx do not capture most of the mediated effect of complex trait heritability, motivating additional assays to better identify molecular mechanisms impacted by regulatory GWAS variants.

There are two possible explanations for our low $h_{med}^2/h_g^2$ estimates:

1. The proportion of complex trait heritability mediated by the cis-genetic component of gene expression levels is in fact high in causal cell types/contexts for the trait, but eQTL data from bulk assayed tissues from GTEx is a poor proxy for eQTL data in causal cell types/contexts, causing $h_{med}^2/h_g^2$ to be low. In other words, $h_{med;\mathit{\text{causal}}}^2$ is high, while $r_g^2\left(T\right)$ is low. Low $r_g^2\left(T\right)$ may be addressed by larger assays measuring context-specific expression^33,35 and/or single-cell expression³⁴.

2. The proportion of complex trait heritability mediated by the cis-genetic component of gene expression levels is low even in causal cell types/contexts for the trait. In particular, complex trait heritability may be mediated in ways other than through gene expression levels in cis, including through protein-coding changes, splicing, or expression levels in trans. In these scenarios, additional assays such as splicing⁶⁸, histone mark⁴, chromosome conformation⁶⁹, and trans-eQTL³² assays can potentially be informative for probing other molecular mechanisms impacted by GWAS variants. We note that much larger gene expression assays than currently available are necessary to estimate heritability mediated by gene expression levels in trans using MESC (Supplementary Note). We anticipate that MESC can be used to estimate the proportion of disease heritability mediated by future QTL studies beyond cis-eQTLs.

We considered several other explanations for our low $h_{med}^2/h_g^2$ estimates and justify that they do not apply to our analysis. Our low $h_{med}^2/h_g^2$ estimates are not related to the fact that expression cis-heritability $h_{cis}^2$ is also low, since the level of environmental/stochastic noise in gene expression measurements does not affect our $h_{med}^2/h_g^2$ estimates (Supplementary Note). Moreover, our $h_{med}^2/h_g^2$ estimates are not biased by rare variant effects on gene expression^39,40, since we only aim to estimate the proportion of common disease heritability mediated by gene expression levels (Supplementary Note).

We observed that expression scores meta-analyzed across tissues gave us higher estimates of $h_{med}^2/h_g^2$ than individual-tissue expression scores. This result is consistent with previous studies that reported higher heritability enrichment of cis-eQTLs meta-analyzed across all GTEx tissues compared to individual tissues²⁷, higher prediction accuracy for imputed expression using joint prediction from multiple tissues compared to individual tissues⁷⁰, and high cis-genetic correlations of expression between tissues overall^71,72.

We observed a strong inverse relationship between proportion of $h_{med}^2$ and expression cis-heritability across genes, suggesting that genes with low expression cis-heritability have large effects on complex traits. This result suggests that integrative association tests that prioritize genes based on probability of colocalization between eQTLs and GWAS hits^6,8,9 and/or significance of genetic correlation between expression and trait^11–13 may not detect the most mechanistically important genes, since these methods have lower power for genes with weaker eQTLs. Instead, our result suggests that genes with weaker eQTLs should be prioritized, and it motivates the implementation of larger eQTL studies and/or cell-type specific assays to more accurately detect these weak eQTLs.

There are several limitations to our method. First, our method makes the assumptions that the magnitude of eQTL effect sizes is uncorrelated with the magnitude of both gene-trait effect sizes and non-mediated effect sizes within each SNP and gene category included in the model. Although we have evaluated the robustness of our choice of SNP and gene categories in both simulations and real data, these assumptions may still be violated. Second, our method relies on the accurate estimation of expression scores from external expression panel samples. In order for our method to be well-powered, it requires large expression panel sample sizes that can only be obtained through meta-analysis across individual tissues at current sample sizes. Third, the quantity that our method estimates in practice (i.e. heritability mediated by assayed gene expression levels) can potentially be much smaller than the theoretical quantity of heritability mediated by expression levels in causal cell types/contexts if assayed gene expression levels do not adequately capture expression levels in causal cell types/contexts. Fourth, our method can only provide reliable $h_{med}^2$ enrichment estimates for large gene sets on the order of 200 or more genes, so smaller gene pathways or individual genes cannot be prioritized using our method. Fifth, our method does not capture non-additive effects of SNPs on gene expression or gene expression on trait.

Despite these limitations, our method provides a novel framework to distinguish mediated effects from pleiotropic and linkage effects and will be useful for quantifying the improvement of new molecular QTL studies over existing assays in capturing regulatory disease mechanisms. Moreover, partitioning mediated heritability can provide insight into regulatory effects mediated by specific gene sets or pathways.

Methods

Definition of $h_{med}^2$

We model trait y for N individuals as follows:

$$\text{y}=\text{X}\gamma +\text{XB}\alpha +ϵ$$ (1)

where y is an N-vector of phenotypes (standardized to mean 0 and variance 1), X is an N × Mgenotype matrix for M SNPs (standardized to mean 0 and variance 1), γ is an M vector of non-mediated SNP effect sizes on the trait (including pleiotropic, linkage, and trans-eQTL-mediated effects), B is an M × G matrix of cis-eQTL effect sizes in the causal cell types/contexts for G genes, α is a G-vector of causal gene expression effect sizes on the trait, and ϵ is an N-vector of environmental effects. We treat all variables as random. We define $h_{med;\mathit{\text{causal}}}^2$ as follows:

$$h_{med;\mathit{\text{causal}}}^2=Var\left[XB\alpha \right]$$

Under the assumption that α and β are independent of each other, we can rewrite this as follows:

$$\begin{gathered} h_{med;\mathit{\text{causal}}}^2=E_{B,\alpha }\left[Var\right[XB\alpha \mid B,\alpha \left]\left]+Va{r}_{B,\alpha }\left[E\right[XB\alpha \mid B,\alpha \right]\right] \\ =E_{B,\alpha }\left[\sum _i^G\sum _j^M{\beta }_{ij}^2{\alpha }_i^2\right] \\ =GE\left[{\alpha }^2\left]E\right[h_{cis}^2\right] \end{gathered}$$

where E[α²] is the average squared per-gene effect of expression on trait and $E\left[h_{cis}^2\right]$ is the average cis-heritability of expression across all genes. The second line above follows the first because E[XBα | B, α] = 0. We define $h_{\mathit{\text{nonmed}};\mathit{\text{causal}}}^2$ in a similar fashion:

$$\begin{gathered} h_{\mathit{\text{nonmed}};\mathit{\text{causal}}}^2=Var\left[X\gamma \right] \\ =ME\left[{\gamma }^2\right] \end{gathered}$$

where E[γ²] is the average squared per-SNP effect on trait that is not mediated by gene expression. We consider additional expression causality scenarios, such as reverse mediation, cis-by-trans mediation, and mediation by unobserved intermediaries (Supplementary Figure 8), and we justify that these scenarios do not compromise our definition of $h_{\mathit{\text{med}};\mathit{\text{causal}}}^2$ (Supplementary Note).

In practice, expression levels in causal cell types/contexts for the complex trait are likely not assayed. Given a set of assayed tissues T (which may or may not be causal for the complex trait), we define $h_{\mathit{\text{med}};\mathit{\text{assayed}}}^2(T)$ as follows:

$$h_{med;\mathit{\text{assayed}}}^2\left(T\right)=r_g^2\left(T\right)h_{med;\mathit{\text{causal}}}^2$$

while we define $h_{\mathit{\text{nonmed}};\mathit{\text{assayed}}}^2\left(T\right)$ as $h_{\mathit{\text{nonmed}};\mathit{\text{causal}}}^2+\left(1-r_g^2\left(T\right)\right)h_{med;\mathit{\text{causal}}}^2$. Here, $r_g^2\left(T\right)=\frac{1}{G}{\sum }_i^G\frac{Cov\left({\beta }_i^2,{\beta }_i{\text{'}}^2\right)}{\sqrt{Var\left({\beta }_i^2\right)Var\left({\beta }_i{\text{'}}^2\right)}}$ and denotes the average squared genetic correlation between expression in assayed tissues T vs. in causal cell types/contexts, where β_i^′ represents cis-eQTL effect sizes on gene i in T. Note that β^′ can refer to either single tissue or meta-tissue cis-eQTL effect sizes, depending on whether T contains one or multiple tissues.

Unstratified MESC

For illustrative purposes, we walk through a derivation for MESC in the idealized scenario that we know 1. the true eQTL effect sizes, β, of each SNP on each gene and 2. the true phenotypic effect sizes, ω, of each SNP on y.

Under the generative model (1), the total effect of SNP k on the complex trait is

$${\omega }_k={\sum }^{}_i^G{\beta }_{ik}{\alpha }_i+{\gamma }_k$$

Given conditional independence of α and γ given β, upon squaring ω_k we have

$$E\left[{\omega }_k^2\mid {\beta }_{1k}\dots {\beta }_{ik}\right]=\sum _i^{G}E\left[{\alpha }_i^2\mid {\beta }_{1k}\dots {\beta }_{ik}\right]{\beta }_{ik}^2+E\left[{\gamma }_k^2\mid {\beta }_{1k}\dots {\beta }_{ik}\right]$$

Assuming unconditional independence of α and γ (which requires that we make additional effect size independence assumptions involving β; see “Model assumptions”), this simplifies to

$$E\left[{\omega }_k^2\mid {\beta }_{1k}\dots {\beta }_{ik}\right]=E\left[{\alpha }^2\right]\sum _i^G{\beta }_{ik}^2+E\left[{\gamma }^2\right]$$ (2)

We use equation (2) to estimate E[α²] by regressing ω² for all SNPs on ${\sum }_i^G{\beta }_i^2$ and taking the slope, while we estimate E[γ²] by taking the intercept. See Figure 1d for a plot illustrating this approach. E[α²] can be multiplied by $GE\left[h_{cis}^2\right]$ to obtain $h_{med;\mathit{\text{causal}}}^2$, while E[γ²] can be multiplied by M to obtain $h_{\mathit{\text{nonmed}};\mathit{\text{causal}}}^2$.

When we perform this regression using eQTL effect sizes obtained from non-causal tissues T with squared genetic correlation $r_g^2\left(T\right)$ with the causal tissue(s), we obtain an estimate of the quantity $h_{med;\mathit{\text{assayed}}}^2\left(T\right)$ rather than $h_{med;\mathit{\text{causal}}}^2$ (Supplementary Note). Moreover, in practice we perform this regression using GWAS and eQTL summary statistics, in which case we account for differences in LD between SNPs with an LD score covariate (see Supplementary Note for derivation and regression equation).

Model assumptions

The two main effect size independence assumptions that are needed to derive equation (2) are:

1. Across all genes, the magnitude of gene effect sizes is uncorrelated with the magnitude of eQTL effect sizes (i.e. Cov(α², β²) = 0). We refer to this assumption as gene-eQTL effect size independence.

2. Across all SNPs, the magnitude of non-mediated SNP effect sizes is uncorrelated with the magnitude of eQTL effect sizes (i.e. Cov(γ², β²) = 0). We refer to this assumption as pleiotropy-eQTL effect size independence.

Violations of either of these two assumptions will result in biased estimates of $h_{med}^2$, where the direction of bias is the same as the direction of correlation between eQTL effect size magnitude and gene or non-mediated effect size magnitude. See Supplementary Note for a discussion of realistic scenarios in which these assumptions might be violated, as well as an illustration of how conditioning on SNP- and gene-level annotations can ameliorate any resulting bias.

Stratified MESC

In this section, we extend unstratified MESC to estimate $h_{med}^2$ partitioned over groups of genes. Note that stratified MESC can be viewed as a special form of stratified LD score regression² (Supplementary Note). Given D potentially overlapping gene categories ${\mathcal{D}}_1$, …, ${\mathcal{D}}_D$, we define $h_{med;\mathit{\text{causal}}}^2$ partitioned over gene categories as follows:

$$\begin{gathered} h_{med;\mathit{\text{causal}}}^2\left({\mathcal{D}}_d\right)=\sum _{i\in {\mathcal{D}}_d}{\alpha }_i^2\sum _j^M{\beta }_{ij}^2 \\ =\left|{\mathcal{D}}_d\right|\cdot E\left[{\alpha }_i^2\left|i\in {\mathcal{D}}_d\left]\cdot E\right[h_{i;cis}^2\right|i\in {\mathcal{D}}_d\right] \end{gathered}$$

where $h_{med;\mathit{\text{causal}}}^2\left({\mathcal{D}}_d\right)$ is the heritability mediated in cis through the expression of genes in category ${\mathcal{D}}_d$, $\left|{\mathcal{D}}_d\right|$ is the number of genes in ${\mathcal{D}}_d$, $E[{\alpha }_i^2|i\in {\mathcal{D}}_d]$ is the average squared causal effect of expression on trait for genes in ${\mathcal{D}}_d$, and $E[h_{i;cis}^2|i\in {\mathcal{D}}_d]$ is the average cis-heritability of expression of genes in ${\mathcal{D}}_d$. Similar to our definition of $h_{med;\mathit{\text{causal}}}^2$, the second line above relies on an independence assumption between α and β, namely that α_i ⊥ β_i | i∈ ${\mathcal{D}}_d$.

For gene i, we model the variance of gene effect size α_i as

$$Var\left({\alpha }_i\right)=\sum _{d:i\in {\mathcal{D}}_d}{\pi }_d$$

If gene categories ${\mathcal{D}}_d$ form a disjoint partition of the set of all genes, we have

$${\pi }_d=\frac{E\left[h_{med;\mathit{\text{causal}}}^2\left({\mathcal{D}}_d\right)\right]}{\left|{\mathcal{D}}_d\right|E[h_{i;cis}^2|i\in {\mathcal{D}}_d]}$$

On the other hand, if gene categories are overlapping, then π_d can be conceptualized as the contribution of annotation ${\mathcal{D}}_d$ to $h_{med;\mathit{\text{causal}}}^2$ conditional on contributions from all other gene categories included in the model.

Given C potentially overlapping SNP categories ${\mathcal{C}}_1$, …, ${\mathcal{C}}_C$, we define $h_{\mathit{\text{nonmed}};\mathit{\text{causal}}}^2$ partitioned over SNP categories as follows:

$$\begin{gathered} h_{\mathit{\text{nonmed}};\mathit{\text{causal}}}^2\left({\mathcal{C}}_c\right)=\sum _{j\in {\mathcal{C}}_c}{\gamma }_j^2 \\ =\left|{\mathcal{C}}_c\right|\cdot E[{\gamma }_j^2|j\in {\mathcal{C}}_c] \end{gathered}$$

where $h_{\mathit{\text{nonmed}};\mathit{\text{causal}}}^2\left({\mathcal{C}}_c\right)$ is the non-mediated heritability of SNPs in category ${\mathcal{C}}_c$, $\left|{\mathcal{C}}_c\right|$ is the number of SNPs in ${\mathcal{C}}_c$, and $E[{\gamma }_j^2|j\in {\mathcal{C}}_c]$ is the average squared non-mediated effect size of SNPs in ${\mathcal{C}}_c$.

For SNP j, we model the variance of non-mediated effect size γ_j as follows:

$$Var\left({\gamma }_j\right)={\sum }^{}_{c:j\in {\mathcal{C}}_c}{\tau }_c$$

If SNP categories ${\mathcal{C}}_c$ form a disjoint partition of the set of all SNPs, we have

$${\tau }_c=\frac{E\left[h_{\mathit{\text{nonmed}};\mathit{\text{causal}}}^2\left({\mathcal{C}}_c\right)\right]}{\left|{\mathcal{C}}_c\right|}$$

On the other hand, if SNP categories are overlapping, then τ_c can be conceptualized of as the contribution of annotation ${\mathcal{C}}_c$ to $h_{\mathit{\text{nonmed}};\mathit{\text{causal}}}^2$ conditional on contributions from all other SNP categories included in the model.

The equation for stratified MESC is

$$E\left[{\chi }_k^2\right]=N\sum _c{\tau }_c{\mathcal{l}}_{k;c}+N\sum _d{\pi }_d{\mathcal{L}}_{k;d}+1$$ (3)

where ${\chi }_k^2$ is the GWAS χ²-statistic of SNP k, N is the number of samples, ℓ_k;c is the LD score of SNP k with respect to SNP category ${\mathcal{C}}_c$ (defined as ${\mathcal{l}}_{k;c}={\sum }_{j\in {\mathcal{C}}_c}{r}_{jk}^2$), and ℒ_k;d is the expression score of SNP k with respect to gene category ${\mathcal{D}}_d$ (defined as ${\mathcal{L}}_{k;d}={\sum }_{i\in {\mathcal{D}}_d}{\sum }_j^M{r}_{jk}^2{\beta }_{ij}^2$). Here, r_jk refers to the LD between SNPs j and k. See Supplementary Note for a derivation of this equation. Analogous to unstratified MESC, when we perform this regression using expression scores in assayed tissues T rather than expression scores in causal cell types/contexts, we will estimate $h_{med;\mathit{\text{assayed}}}^2\left(T,{\mathcal{D}}_d\right)=r^2\left(T,{\mathcal{D}}_d\right)h_{med;\mathit{\text{causal}}}^2\left({\mathcal{D}}_d\right)$, where r²(T, ${\mathcal{D}}_d$) is the average squared genetic correlation of expression between T and causal cell types/contexts for genes in ${\mathcal{D}}_d$.

Estimation of expression scores

In order to carry out the regression described in equation (3), we must first estimate expression scores ℒ_k;d (where ${\mathcal{L}}_{k;d}={\sum }_{i\in \mathcal{D}}{\sum }_j^M{r}_{jk}^2{\beta }_{ij}^2$) from an external expression panel. We estimate ℒ_k;d from either eQTL summary statistics or individual-level genotypes and expression measurements, where the latter provides less noisy estimates of ℒ_k;d given that it is available. In our case, we use the first procedure to estimate expression scores from eQTLGen data (since only eQTL summary statistics are provided), whereas we used the second procedure for GTEx data.

eQTL summary statistics.

We can estimate ℒ_k;d from eQTL summary statistics using the following formula: ${\widehat{\mathcal{L}}}_{k;d}={\sum }_{i\in D}{\widehat{\beta }}_{ik\left(\mathit{\text{sumstat}}\right)}^2-\frac{\left|D\right|}{N_{exp}}$, where ${\widehat{\beta }}_{ik\left(\mathit{\text{sumstat}}\right)}^2$ is the marginal OLS eQTL effect size estimate of SNP k on gene i, |D| is the number of genes in gene category D, and N_exp is the number of expression panel samples. The right-hand side of the formula is in expectation equal to ℒ_k;d (Supplementary Note).

Individual-level genotypes and expression data.

We estimate ℒ_k;d by first using LASSO⁷³ to obtain regularized estimates of causal eQTL effect sizes (${\widehat{\beta }}_{\mathit{\text{LASSO}}}$), then multiply ${\widehat{\beta }}_{\mathit{\text{LASSO}}}^2$ by the element-wise squared LD matrix R² as follows: ${\widehat{\mathcal{L}}}_{k;d}={\sum }_{i\in D}{c}_i{\sum }_j^M{r}_{jk}^2{\widehat{\beta }}_{ij\left(\mathit{\text{LASSO}}\right)}^2$. Here, c_i is a scaling factor we apply to ${\widehat{\beta }}_{\mathit{\text{LASSO}}}$ so that $c_i{\sum }_j^M{\widehat{\beta }}_{ij\left(\mathit{\text{LASSO}}\right)}^2={\widehat{h}}_{i;cis}^2$, where ${\widehat{h}}_{i;cis}^2$ is the restricted maximum likelihood (REML) estimate of expression cis-heritability for gene i. We observed that scaling our estimates in this manner reduces noise and bias compared to unscaled estimates (Supplementary Figure 9). We obtain approximately unbiased estimates of the squared LD between two SNPs using the formula $r_{adj}^2={\widehat{r}}^2-\frac{1-{\widehat{r}}^2}{N-2}$, where ${\widehat{r}}^2$ denotes the standard biased estimator of r². We refer to this overall procedure as “LASSO with REML correction” and show that it provides the best performance in simulations compared to other methods (Supplementary Note).

Meta-analysis of expression scores

Given our method of computing expression scores from individual-level genotypes and expression data outlined above, we meta-analyze expression scores across tissues as follows. We first obtain meta-tissue expression cis-heritability ($h_{cis}^2$) estimates for each gene by averaging individual-tissue $h_{cis}^2$ estimates across tissues. We scale individual-tissue LASSO-predicted causal eQTL effect sizes to the meta-tissue $h_{cis}^2$ (see above), then average the scaled causal eQTL effect sizes across tissues. Finally, we multiply the averaged causal eQTL effect sizes by the element-wise squared LD matrix to obtain expression scores. In simulations, we show that this method of meta-analyzing expression scores produces nearly unbiased estimates of $h_{med}^2/h_g^2$ at 5 tissues × 200 samples per tissue (Supplementary Figure 10), which is comparable to the number expression panel samples in given tissue group (Supplementary Table 2).

Simulations

All simulations were conducted using genotypes from UK Biobank³⁸ restricted to HapMap 3 SNPs⁷⁴ on chromosome 1 (M = 98,499 SNPs). All simulations followed the same overall procedure outlined below in chronological order. See Supplementary Note for specific parameters used in each simulation.

1. Simulation of expression data. We simulated 1–5 eQTLs each for G = 1,000 genes, with effect sizes drawn from a normal distribution and locations randomly selected in a 1 Mb window around the gene. Total $h_{cis}^2$ was fixed at 0.05 for all simulations. We then simulated expression phenotypes for 100–1,000 expression panel samples (genotypes randomly selected from UK Biobank) using an additive generative model with normally distributed environmental noise added, representing an expression panel.

2. Simulation of GWAS data. We simulated non-mediated SNP effect sizes and gene-trait effect sizes from normal or point-normal distributions for all SNPs and genes corresponding to various levels of $h_{med}^2/h_g^2$. Total $h_g^2$ was fixed at 0.5 for all simulations (other than for Supplementary Figure 2, in which we varied $h_g^2$). Together with the eQTL effect sizes simulated in the previous step, we used these effect sizes to simulate trait phenotypes using an additive generative model with normally distributed environmental noise added for 10,000 GWAS samples (genotypes randomly selected from UK Biobank and distinct from the expression panel samples). We then produced GWAS summary statistics from this simulated data set using ordinary least squares.

3. Estimation of expression scores. We estimated expression scores from the expression panel samples using LASSO with REML correction (see “Estimation of expression scores” above). For computational ease, we did not actually use REML to predict expression cis-heritability for each gene in each simulation; we instead took the true expression cis-heritability of the gene and added noise drawn from N(0, 0.01²) to simulate REML prediction error, which is consistent with empirical standard error estimates produced by GCTA (Supplementary Figure 11).

4. Estimation of $h_{med}^2/h_g^2$. We estimated $h_{med}^2/h_g^2$ using MESC with the previously estimated expression scores, in-sample LD scores (computed from the 10,000 GWAS samples), and GWAS summary statistics.

Data and quality control

Genotypes

For MESC, we used European samples in 1000G⁷⁵ as reference SNPs to compute LD scores. Regression SNPs were obtained from HapMap 3⁷⁴. Notably, by restricting regression SNPs to HapMap 3 SNPs, we estimate common disease heritability mediated by gene expression levels (see Supplementary Note for discussion of rare vs. common variant $h_{med}^2$). SNPs with GWAS χ² statistics > max{80, 0.001N} (where N is the number of GWAS samples) and in the major histocompatibility complex (MHC) region were excluded. See Supplementary Note of ref.² for justification of these procedures.

For computing expression scores, we downloaded genotypes derived from sequencing data for GTEx v7 from the GTEx Portal (Data Availability) as described in ref.⁵. We retained SNPs that were from HapMap 3⁷⁴.

Expression data

We obtained processed and quantile normalized gene expression data for GTEx v7 from the GTEx Portal (Data Availability) as described in ref.⁵. For each tissue, the following covariates were included in all analyses: 3 genetic principal components, sex, platform, and 14–35 expression factors⁷⁶ as selected by the main GTEx analysis.

Estimation of expression scores from GTEx data

We used REML as implemented in GCTA⁴⁴ to estimate the expression cis-heritability for each gene in each individual GTEx tissue. We then used LASSO as implemented in PLINK⁷⁷ (with the LASSO tuning parameter set as the estimated expression cis-heritability of the gene) to estimate eQTL effect sizes for each gene in each individual GTEx tissue. In all procedures, we excluded gene-tissue pairs for which LASSO did not converge when predicting effect sizes. For Figure 3 and Extended Data 2, we obtained causal eQTL effect size estimates in three different ways:

Meta-analysis across all tissues.

For each gene, we averaged the expression cis-heritability estimates across all 48 tissues. Within each tissue, we scaled the LASSO-predicted eQTL effect sizes to the averaged cis-heritability value. We then averaged the scaled eQTL effect sizes for each gene across all tissues. Genes were retained if they had a LASSO-converged eQTL effect size in at least one tissue.

Meta-analysis in tissue groups.

Of the 48 tissues, we grouped together 37 of them into 7 broad tissue groups: adipose, blood/immune, cardiovascular, CNS, digestive, endocrine, and skin (Supplementary Table 2). Within each tissue group, we averaged the expression cis-heritability estimates for each gene and scaled the LASSO-predicted eQTL effect sizes to the averaged cis-heritability value. We then averaged the scaled eQTL effect sizes for each gene across the tissues for each tissue group. Genes were retained in each tissue group if they had a LASSO-converged eQTL effect size in at least one tissue within that tissue group.

Individual tissues.

For each individual tissue, we scaled the LASSO-predicted eQTL effect sizes to the within-tissue-group averaged cis-heritability estimates.

The final eQTL effect sizes were then multiplied by the element-wise squared LD matrix (estimated from 1000G⁷⁵) order to obtain expression scores (see “Estimation of expression scores”).

Set of 42 independent traits

Analogous to previous studies^27,78, we initially considered a set of 34 traits from publicly available sources and 55 traits from UK Biobank for which GWAS summary statistics had been computed using BOLT-LMM v2.3^79,80 (see Data Availability). We restricted our analysis to 47 traits with z-scores of total SNP heritability above 6 (computed using stratified LD-score regression). The 47 traits included 5 traits that were duplicated across two datasets (genetic correlation of at least 0.9). For duplicated traits, we retained the data set with the larger sample size, leaving us with a total of 42 independent traits. When meta-analyzing estimates across traits, we performed random effects meta-analysis using the R package rmeta.

BaselineLD categories

In all our analyses, we stratified SNPs by 72 functional categories specified by the baselineLD model v2.0^2,43 (Data Availability). These annotations include coding, conserved, regulatory (e.g., promoter, enhancer, histone marks, transcription factor binding sites), and LD-related annotations. The original baselineLD model v2.0 contains 76 total categories; we removed 4 categories corresponding to QTL MaxCPP annotations²⁷ because the information contained in these annotations is redundant with the eQTL effect size information contained in expression scores.

Gene set analyses

In order for us to obtain to unbiased estimates of $h_{med}^2$ enrichment for the gene sets in our analysis, we must ensure that the gene-eQTL effect size independence assumption holds within each gene set (see “Model assumptions” above). Thus, in order to capture potential correlations between the magnitude of eQTL effect sizes and gene-trait effect sizes within gene sets, we partitioned each gene set into three equally-sized bins based on the magnitude of their expression cis-heritability relative to other genes in the gene set. We then estimated $h_{med}^2(D)$ for each individual bin and aggregated these values together to estimate the overall $h_{med}^2$ enrichment of the gene set.

Broad gene sets

We obtained gene sets corresponding to all coding genes, genes near significant GWAS hits in the NHGRI GWAS catalog⁵⁶, genes essential in mice^53–55, genes essential in cultured cell lines⁸¹, genes with any disease association in ClinVar⁸², and genes that are FDA-approved drug targets⁵² from the Macarthur lab GitHub page (Data Availability). We obtained an additional gene set for genes essential in cell lines⁸³, genes depleted for protein-truncating mutations^46,47, and genes depleted for missense mutations⁸⁴ from the supplementary data of the respective papers.

Pathway gene sets

We initially considered a set of 7,246 gene sets from the “canonical pathways” and “GO gene sets” collections from the Molecular Signatures Database⁸⁵ (Data Availability), consisting of gene sets from BioCarta, Reactome, KEGG, GO, PID, and other sources. We restricted our analysis to 780 gene sets for which the number of genes with LASSO estimates of eQTL effect sizes that converged in individual GTEx tissues was at least 100 when averaged across all individual tissues. Note that this roughly corresponds to gene sets with greater than 200 total genes; see Supplementary Table 7.

Tissue specific expression gene sets

We initially considered the full set of 48 GTEx tissues. We restricted our analysis to 37 gene sets for which the focal tissue belonged to one of the 7 main tissue groups we defined in our previous analyses (Supplementary Table 2). From ref.⁵¹, we obtained the set of 10% most specifically expressed genes in each of the 37 tissues.

Data Availability

GWAS summary statistics for 42 diseases and complex traits can be found at https://data.broadinstitute.org/alkesgroup/sumstats_formatted/. Genotypes for 1000 Genomes Phase 3 data can be found at ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/release/20130502. GTEx v7 data can be found at https://www.gtexportal.org/home/datasets, though to access genotypes one is required to have an approved application. eQTLGen data can be found at https://www.eqtlgen.org/cis-eqtls.html. BaselineLD v2.0 annotations can be found at https://data.broadinstitute.org/alkesgroup/LDSCORE/. Gene sets can be found from the Macarthur lab, https://github.com/macarthur-lab/gene_lists, and Molecular Signatures Database, http://software.broadinstitute.org/gsea/msigdb/collections.jsp. S-LDSC software can be found at https://github.com/bulik/ldsc. BOLT-LMM software can be found at https://data.broadinstitute.org/alkesgroup/BOLT-LMM/downloads/.

Code Availability

Software implementing MESC can be found at https://github.com/douglasyao/mesc.

Extended Data

Extended Data Fig. 1. Relationship between $h_{med}^2/h_g^2$ and $h_g^2$.

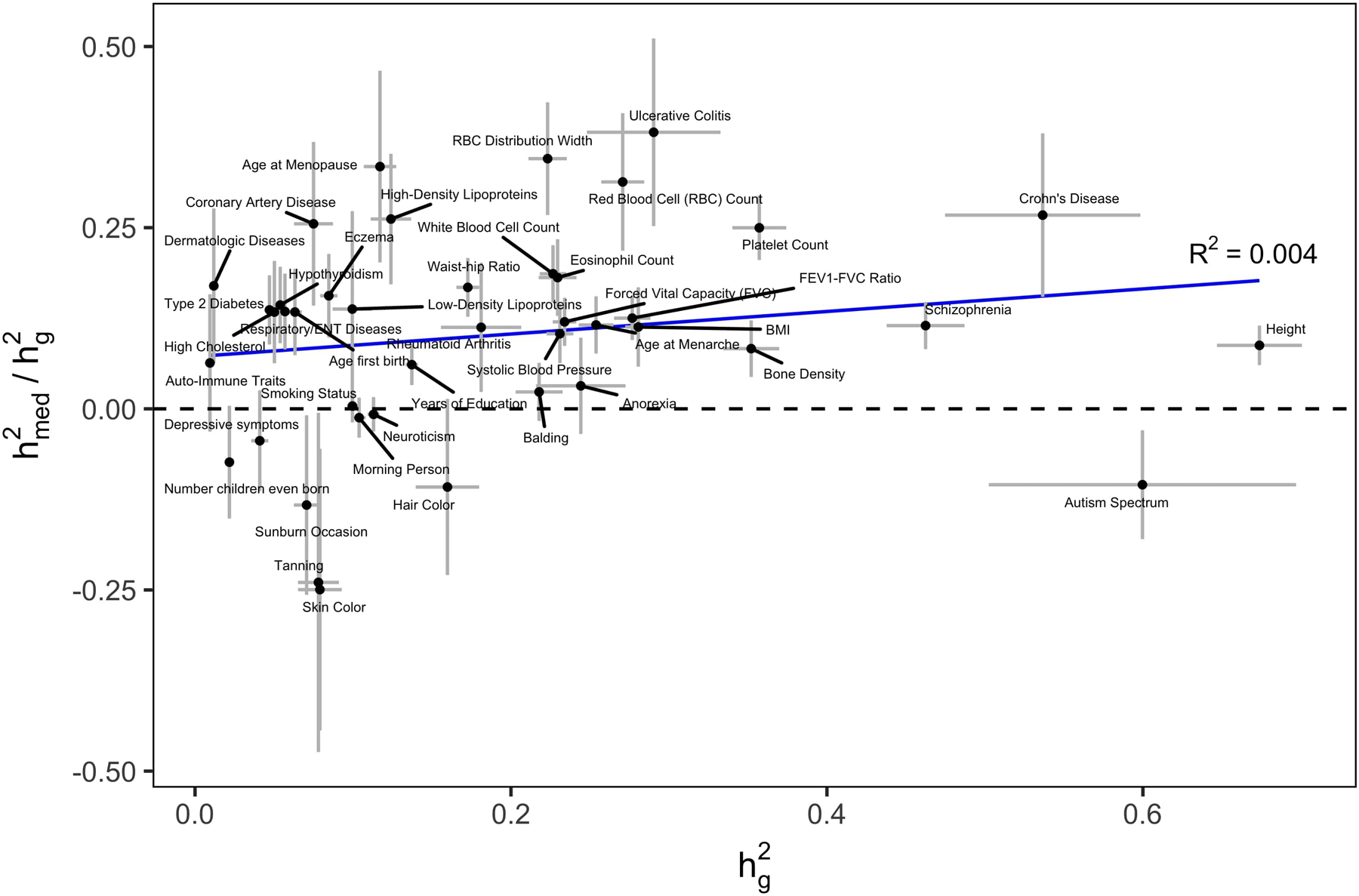
$h_{med}^2/h_g^2$ estimates were obtained using all-tissue meta-analyzed expression scores. $h_g^2$ estimates were obtained using stratified LD-score regression. Error bars represent jackknife standard errors.

Extended Data Fig. 2. $h_{med}^2/h_g^2$ estimates for all diseases and expression scores.

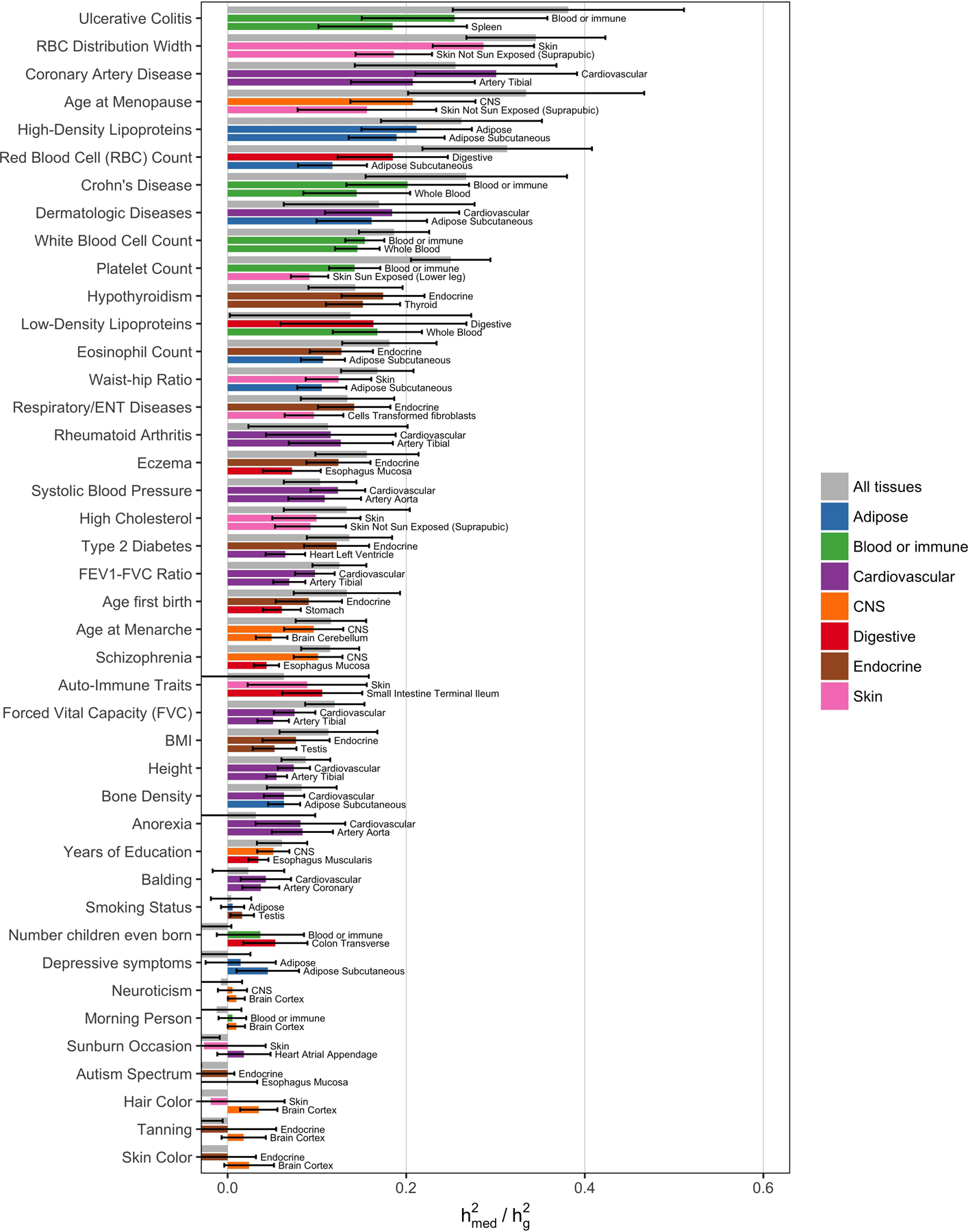
Same as Figure 3a, but containing $h_{med}^2/h_g^2$ estimates for all 42 traits from all three types of expression scores: “All tissues” (expression scores meta-analyzed across all 48 GTEx tissues), “Best tissue group” (expression scores meta-analyzed within 7 tissue groups), and “Best tissue” (expression scores computed within individual tissues). Here, “best” refers to the tissue/tissue group resulting in the highest estimates of $h_{med}^2/h_g^2$ compared to all other tissues/tissue groups. Error bars represent jackknife standard errors.

Extended Data Fig. 3. Relationship between individual tissue sample size and magnitude of $h_{med}^2/h_g^2$.

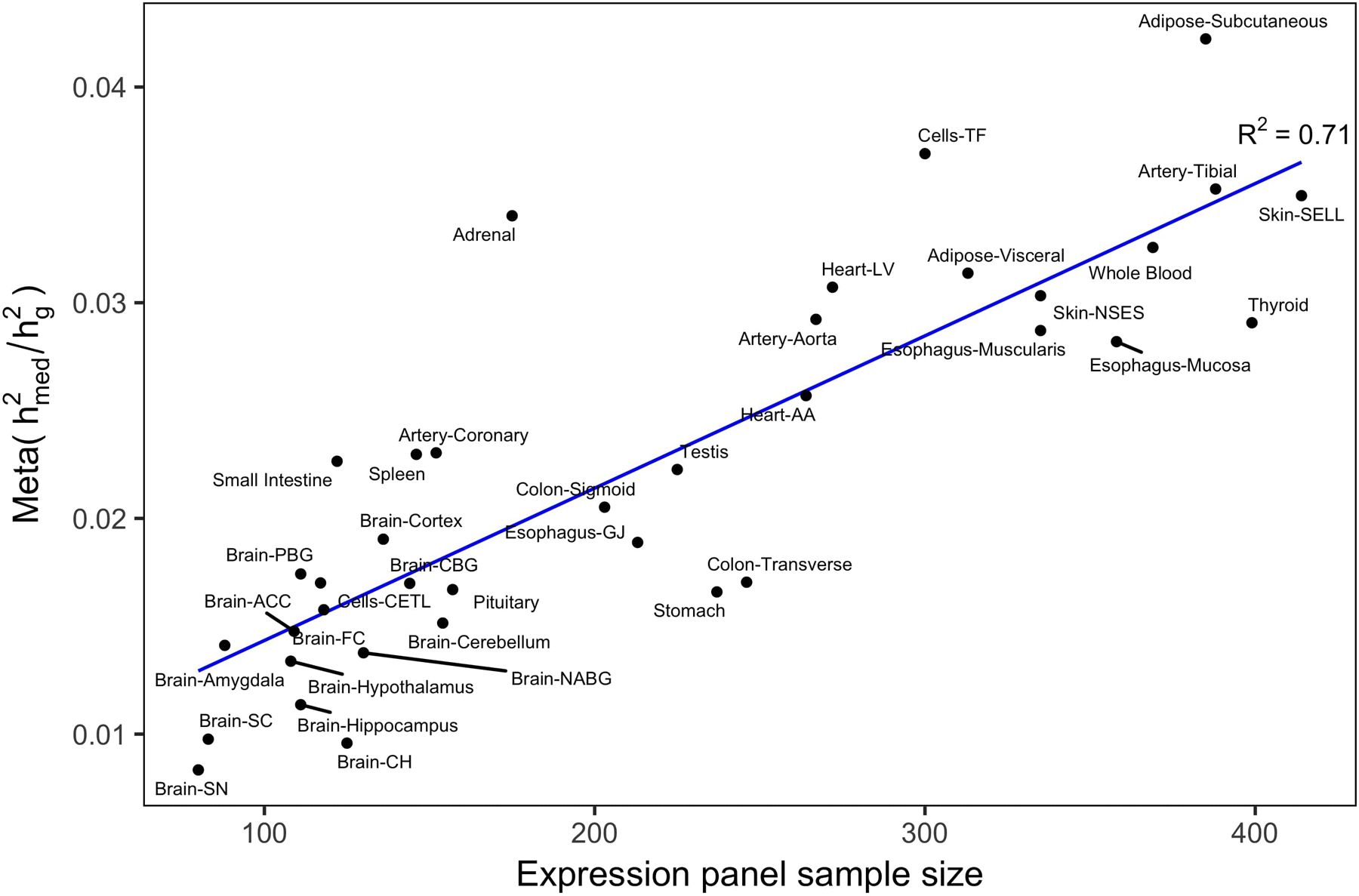
$h_{med}^2/h_g^2$ estimates from expression scores estimated in each of 48 individual GTEx tissues were meta-analyzed across 42 complex traits, then plotted against the number of samples in each tissue. We use the following abbreviations: adipose visceral, adipose visceral omentum; brain ACC, brain anterior cingulate cortex BA24; brain CBG, brain caudate basal ganglia; brain CH, brain cerebellar hemisphere; brain FC, brain frontal cortex BA9; brain NABG, brain nucleus accumbens basal ganglia; brain PBG brain putamen basal ganglia; cells CETL, cells EBV-transformed lymphocytes; cells TF, cells transformed fibroblasts; esophagus GJ, esophagus gastroesophageal junction; heart AA, heart atrial appendage; heart LV, heart left ventricle; skin NSES, skin not sun exposed suprapubic; skin SELL, skin sun exposed lower leg; small intestine, small intestine terminal ileum.

Extended Data Fig. 4. $h_{med}^2/h_g^2$ estimates for 42 diseases and complex traits using data from eQTLGen.

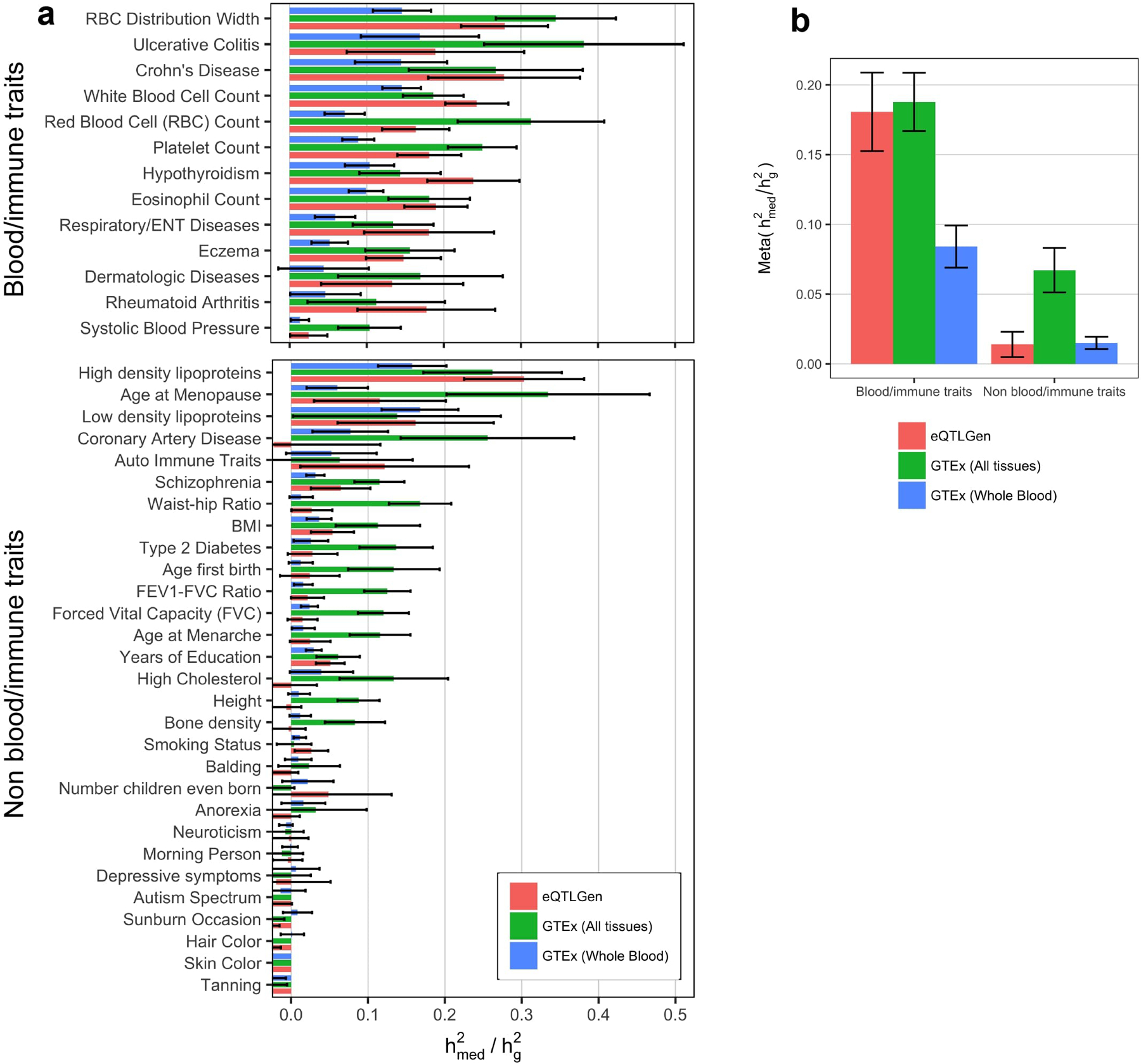
We estimated expression scores for all SNPs using cis-eQTL summary statistics from eQTLGen (N = 31,684 blood samples), then estimated $h_{med}^2/h_g^2$ using GWAS summary statistics for the same 42 traits analyzed in the main text. Expression cis-heritability estimates for eQTLGen data were obtained using LD-score regression. For sake of comparison, we also display $h_{med}^2/h_g^2$ estimates obtained from expression scores from GTEx all-tissue meta-analysis and GTEx whole blood only. (a) $h_{med}^2/h_g^2$ estimates for 42 individual traits, organized into blood/immune and non-blood/immune traits. Error bars represent jackknife standard errors. (b) Results from a meta-analyzed across traits. Error bars represent standard errors from random-effects meta-analysis. Note that low estimates of $h_{med}^2/h_g^2$ for GTEx whole blood expression scores are caused by the small sample size of the GTEx whole blood data set (N = 369).

Extended Data Fig. 5. Relationship between expression cis-heritability and metrics of gene essentiality.

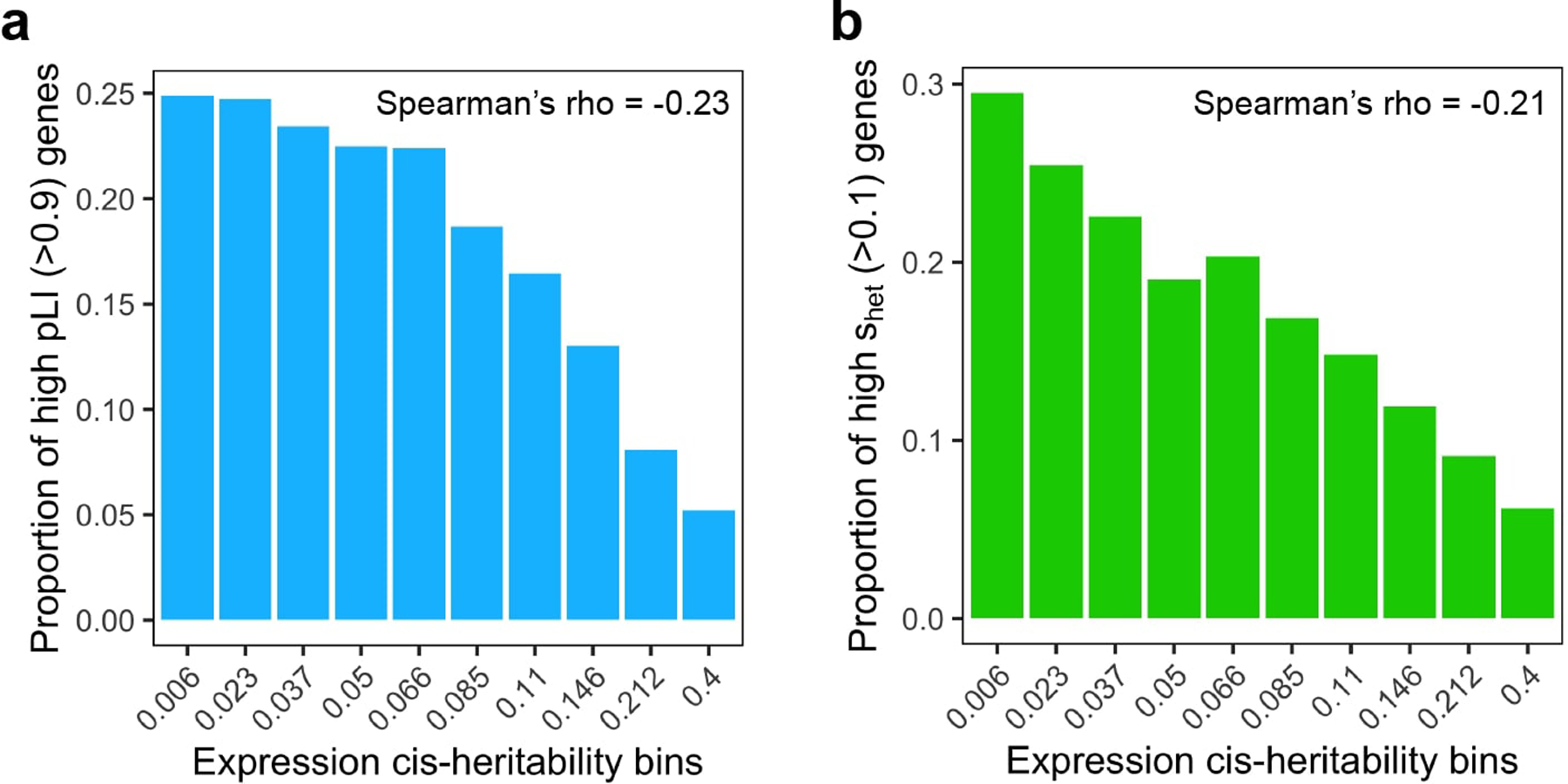
For each gene, pLI (probability of loss-of-function intolerance) was obtained from Lek et al. 2016 Nature and s_het (selection against protein-truncating variants) was obtained from Cassa et al. 2017 Nature Genetics.

Extended Data Fig. 6. $h_{med}^2$ enrichment estimates for all 10 broadly essential gene sets across all 26 complex traits.

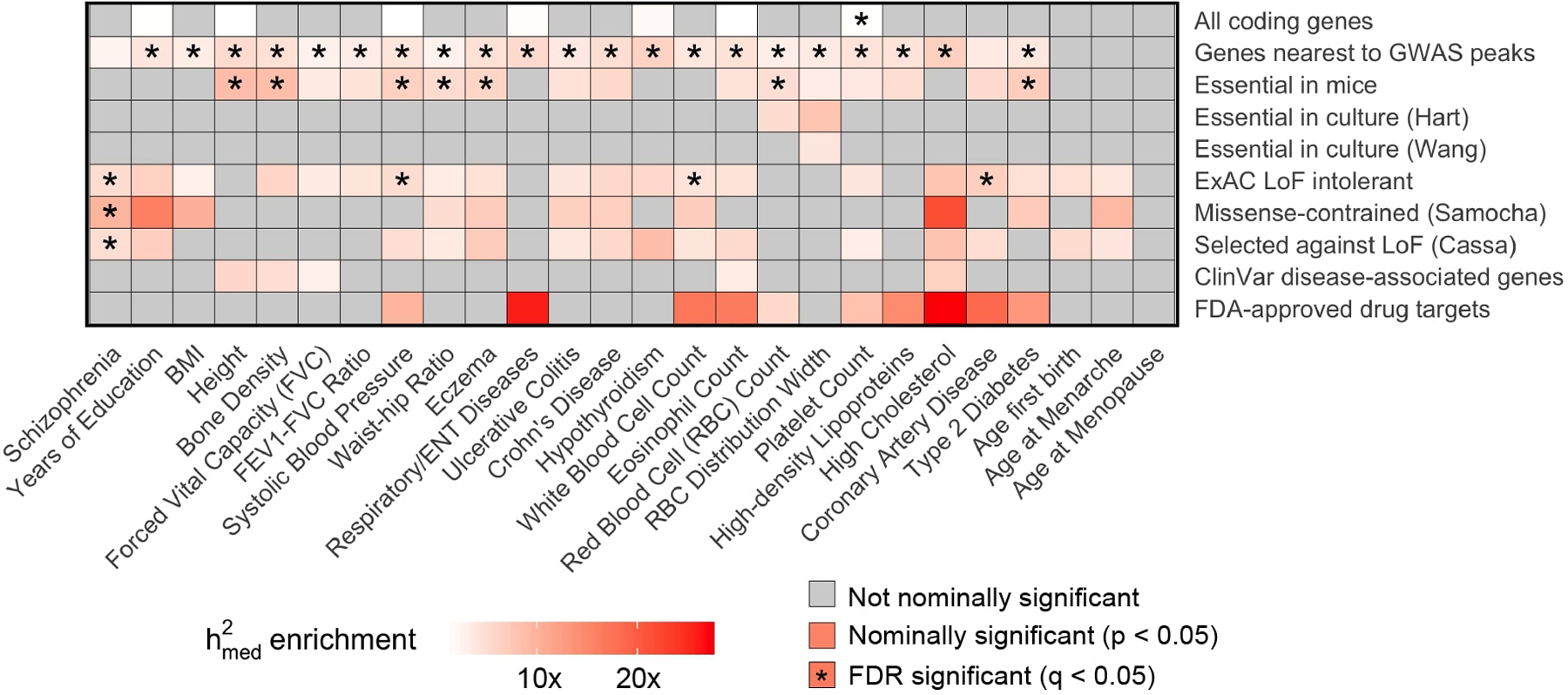
Same as Figure 5a, but showing $h_{med}^2$ enrichment estimates for individual traits rather than meta-analyzed estimates.

Extended Data Fig. 7. $h_{med}^2$ enrichment estimates for 97 pathway-specific gene sets across all 26 complex traits.

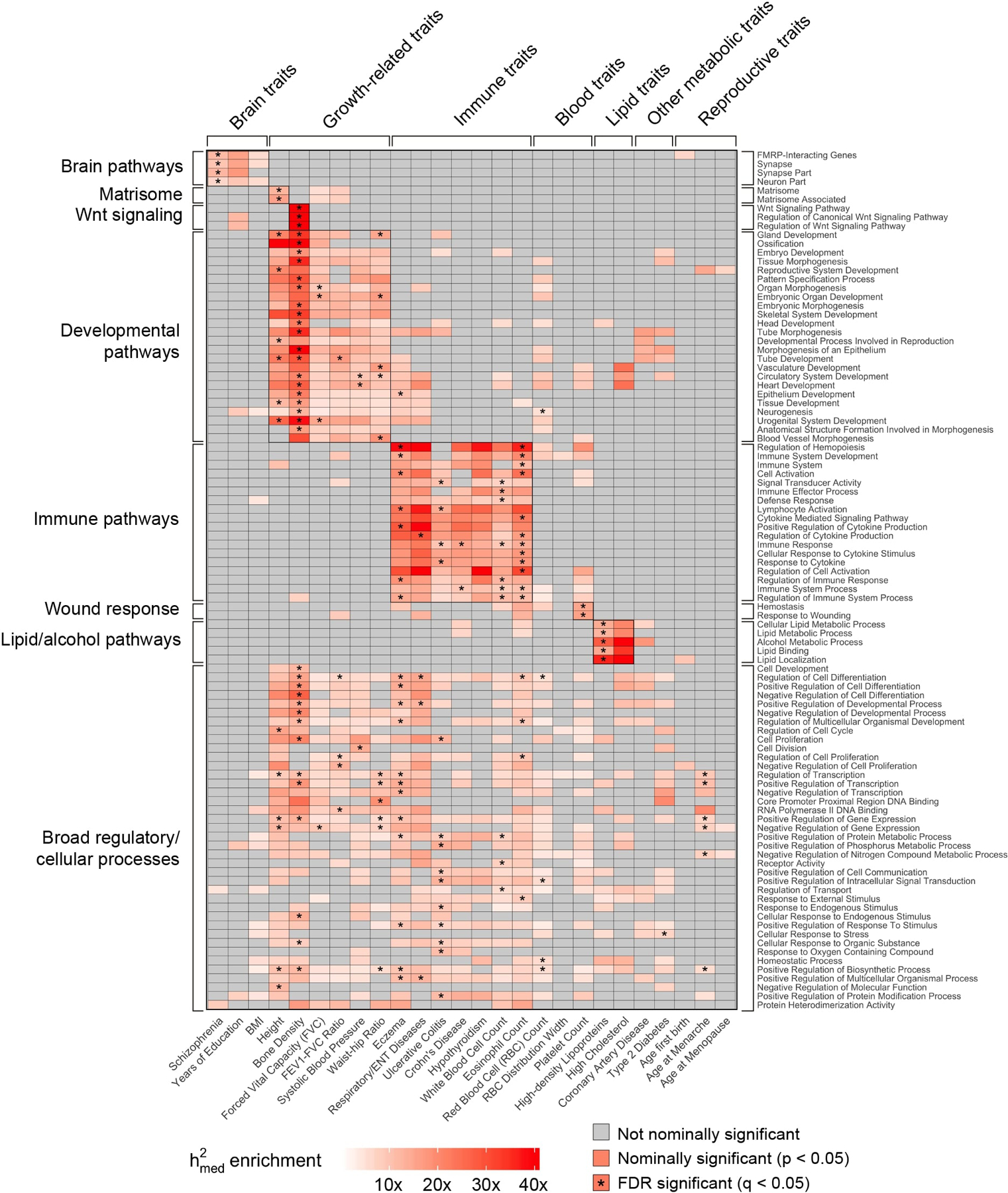
Same as Figure 5b, but plotting all pathway-specific gene sets (out of 780 total) with FDR-significant $h_{med}^2$ enrichment in at least one of the 26 complex traits. For ease of display, we grouped together related traits and gene sets.

Extended Data Fig. 8. Comparison between gene set enrichment estimates from MESC, MAGMA, and DEPICT.

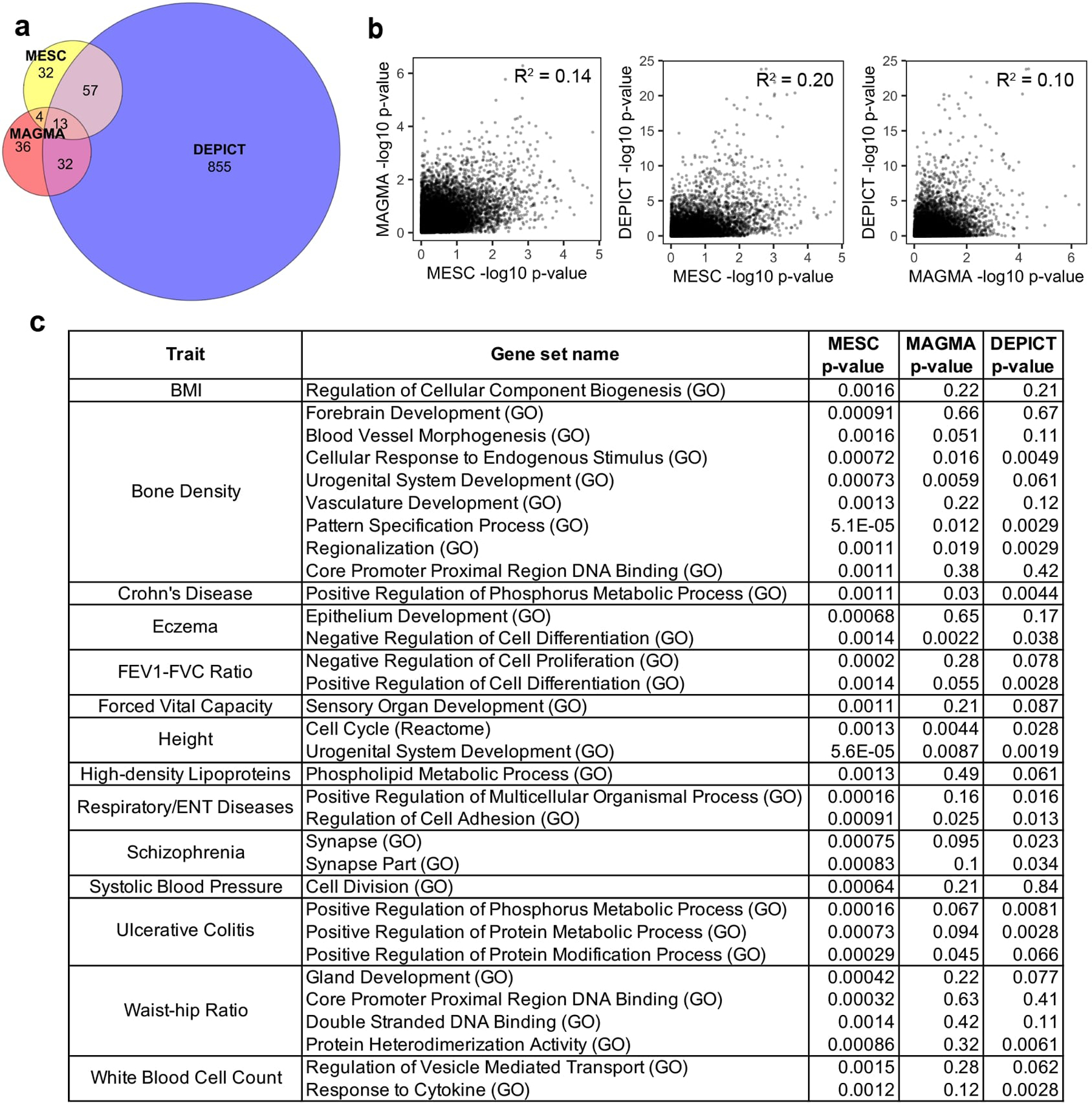
See Supplementary Note for details on these analyses. (a) Venn diagram showing the overlap between significantly enriched trait-gene set pairs (FDR < 0.05) identified by the three methods. (b) Scatterplots of -log10 enrichment p-values from MESC vs. MAGMA (left), MESC vs. DEPICT (middle), and MAGMA vs. DEPICT (right). Each point represents a trait-gene set pair. (c) List of all 32 gene sets-complex traits pairs detected as significant by MESC (FDR q-value < 0.05) that are not detected as significant by MAGMA or DEPICT. See Supplementary Table 9 for enrichment estimates for all gene set-complex traits pairs.