An investigation of the spatio-temporal parameters of gait and margins of stability throughout adulthood

Abstract

Age-related changes in the way of walking may induce changes in dynamic stability. Therefore, the relationship between age, spatio-temporal characteristics and margins of stability was examined. One hundred and five healthy adults aged between 20 and 89 years old were analysed on spatio-temporal characteristics and margins of stability using three-dimensional motion analysis. Subjects walked barefoot over a 12-m-long walkway at their preferred walking speed. Covariance among gait characteristics was reduced using a factor analysis, identifying domains of gait. The influence of age, gender, body mass index (BMI) and leg length on domains of gait and margins of stability was investigated using linear mixed models. A stepwise linear regression identified domains of gait predicting the variance in margins of stability. Four domains of gait explaining 74.17% of the variance were identified. Age had a significant influence on the medio-lateral margin of stability and the ‘variability', ‘pace' and ‘base of support' domain. BMI significantly influenced the medio-lateral margin of stability; gender and leg length had no influence on either of the margins of stability. The ‘base of support’ domain predicted 26% of the variance in the medio-lateral margin of stability. When considering the margins of stability, especially when comparing multiple groups, age, BMI and spatio-temporal parameters should be taken into account.

1. Introduction

A fundamental stage of human development is when a child takes their first few unstable steps that pave the way for an independent and stable way of walking. This stable gait may refer to a repeatable step-to-step way of walking [1], a gait resilient to external or internal disturbances [2], the ability to maintain upright balance during walking [3] or simply a gait that does not lead to falls [4]. Similarly, instability has been characterized by different measures such as step-to-step variability (e.g. standard deviation, coefficient of variation) [5], trunk stability (e.g. smoothness of trunk movement) [6] and measures based on biomechanical definitions of static and dynamic balance (e.g. local dynamic stability, margins of stability) [7,8]. Regarding gait stability, the margin of stability (MoS) expresses the deviation of the centre of mass (CoM) that an individual can handle before loss of balance occurs [7]. The MoS can be calculated in both the medio-lateral (ML) and anterior–posterior (AP) directions. Balance control during walking is more critical in the ML direction, as a negative ML MoS will result in deviation from the straight walking trajectory; a negative AP MoS, on the other hand, will interrupt forward progression. As a consequence, this will result in a crossover step or a backward step in order to prevent falling sideways or backwards, respectively [7]. These active foot placement strategies are ensured by the central nervous system [9] and are mostly driven by the distance between the centre of pressure (CoP) and the CoM extrapolated in the direction of its corresponding velocity, i.e. the extrapolated centre of mass (XCoM), at foot-off [8,10].

As walking is one of the most frequently performed physical activities in daily life [11], gait is often used as a way of quantifying physical function, quality of life and health status [12]. Previous studies have demonstrated that changes in gait performance correlate with an increased risk of falling [13], certain cognitive impairments [14] and even risk of early mortality [15]. The ability to walk safely and efficiently is an important predisposition in maintaining independence in older age [16]. However, changes in muscular, skeletal [17] and either the central [18] or peripheral [19] nervous system are related to normal ageing, which in turn may result in mobility problems and an increased risk of falling [20,21]. These age-related changes can influence gait performance; as a way to adapt to these changes compensatory strategies are observed [22]. A more cautious way of walking is commonly observed in elderly populations, characterized by a reduction in walking speed and stride length and an increase in step width [23]. To determine whether certain populations divert from the norm, spatio-temporal parameters of healthy adults are frequently used. Additionally, spatio-temporal parameters are an easy marker to investigate the influence of ageing on the walking pattern. However, much of the research focusing on the effect of ageing on gait has compared gait performances of younger adults with those of older adults or different elderly populations with each other, as indicated by the review by Herssens et al. [24]. Therefore, in order to fully understand the effects of ageing on gait performance, additional research taking the whole adult population into consideration is needed.

As the theoretical approach by Hof [10] suggests, a stable way of walking is a gait pattern where the CoP is placed at a constant distance behind and outward of the XCoM. The forward control of gait can be achieved through either adapting the step length or step time, consequently keeping the walking speed constant, and thus maintaining the forward progression. For the lateral control of gait, the straight course can be maintained through positioning the CoP (i.e. the foot) at a greater or smaller distance of the XCoM, i.e. increasing or decreasing the step width. Furthermore, several experimental studies have established an interaction between changes in spatio-temporal parameters and the MoS [7,25–28]. The results of these studies demonstrated that, indeed, through changes in step width, step length, step frequency and walking speed subjects were able to either maintain or increase their MoS in both the ML and AP direction. Although interesting, most of these studies were performed on a treadmill or focused primarily on the influence of perturbations on gait stability and not necessarily on the influence of the natural adaptations of spatio-temporal parameters that occur with ageing. Only the study of Lencioni et al. [28] investigated the relationship between spatio-temporal gait parameters and the MoS during overground walking without perturbations. Results showed that walking speed, stride length and step width were predictive for the ML stability and walking speed, stride length and cadence for the AP MoS [28]. In order to understand the mechanisms behind an increase in fall risk with increasing age more thoroughly, these adaptations need to be better described in a larger sample of healthy adults of all ages. As noted above, ageing is associated with a more cautious way of walking that involves changes in walking speed, stride length and width [23]. These changes may in their turn induce changes in dynamic stability, i.e. increase the MoS, leading to a more stable gait. However, on the other hand, these changes in spatio-temporal parameters have also been shown to be risk factors for falls in the elderly [29]. This seems paradoxical but may be explained by the elderly having already adapted to a more biomechanically stable way of walking, through slowing down and walking with shorter and wider steps [23], therefore decreasing the overall amount of additional internal or external perturbations they can manage as their residual capacity of adaptation is limited.

We thus hypothesize that the differences in spatio-temporal characteristics associated with older age are used as a strategy to increase the MoS during walking. Therefore, we examined the differences in spatio-temporal characteristics and spatial margins of stability in healthy adults aged between 20 and 89 years old. Additionally, we also sought to examine the interaction between spatio-temporal characteristics and dynamic stability measures.

2. Methods

2.1. Study design

Data on three-dimensional gait analysis in healthy adults (age 20–89) were retrospectively included in this cross-sectional study. Age-related differences in gait stability were investigated using the concepts of XCoM and MoS. The study protocol was approved by the local ethics committee (B300201316328), with data collection taking place between April 2015 and January 2016. Subjects gave written informed consent at the time of study inclusion and were aware that data could be used retrospectively for further research.

2.2. Setting

An instrumented gait analysis was performed at a movement analysis laboratory equipped with a three-dimensional motion capture system with eight cameras (Vicon T10, 100 Hz; Vicon Motion Systems Ltd, Oxford, UK; 100 fps, resolution 1 megapixel (1120 × 896)), 3 AMTI type OR 6–7 force plates (1000 fps, 46 × 50 × 8 cm) and 1 AccuGait® (1000 fps) force plate. Reflective markers were placed on anatomical landmarks on the subject's body corresponding to the full-body plug-in-gait model [30]. Subjects walked barefoot over a 12-m-long walkway at a self-selected walking speed, with the middle 6 m used for data collection. In total, a minimum of six valid walking trials (i.e. visibility of all markers, the presence of clean left and right heel strikes) were recorded. The set-up of the walkway is illustrated in the electronic supplementary material, appendix 1.

2.3. Participants

Eligibility criteria for voluntary participation were adults aged between 20 and 89 years, categorized into seven decades. Participants were excluded if they had self-reported visual impairments, antalgic gait pattern, abnormal mobility in the lower limbs or any known neurological or orthopaedic disorder that could influence motor performance and balance. Informed consent was obtained from all subjects prior to participation. In total, 114 subjects were recruited, of whom 105 subjects were included in the final analysis.

2.4. Variables of interest

2.4.1. Anthropometric measurements

For each subject, information concerning age (in years), body mass (kilograms), body height (centimetres) and leg length (millimetres) was obtained. Leg length was measured as described in the Vicon Nexus User Guide [31]: the distance was measured between the anterior superior iliac spine marker and the medial malleolus. Body mass index (BMI) was calculated based on body mass (kg) and body height (m): $\text{BMI}=\text{body}\hspace{0.17em}\text{mass}\hspace{0.17em}(\text{kg})/\text{body}\hspace{0.17em}\text{height}\hspace{0.17em}{(\text{m})}^2$.

2.4.2. Gait parameters

Walking speed (m s⁻¹), stride and step time (s), length (m), width (m); the duration of the double and single support phases (%); and cadence (steps/min) were used in order to describe the spatio-temporal characteristics of gait. We chose to analyse step time, length and width as, according to Lord et al. [32], spatial step characteristics are preferred instead of (combining them with) stride characteristics to avoid duplication and redundancy in the model. Means and standard deviations (variability) were investigated as they provide more clarity for interpretation as opposed to, for example, coefficients of variation [33]. The number of steps within one trial ranged from 1 (subject 3) to 4 steps per leg (subject 101), the total number of steps over the three trials ranged from 10 (subject 3) to 22 steps (subject 101). Walking speed was checked for excessive fluctuations between trials as described by Hof [10]. If fluctuations stayed within 20%, means and standard deviations were calculated over the total number of steps recorded in three trials. Although the total number of steps used to calculate the standard deviations seems low, it has been shown that gait variability (i.e. standard deviations) can be assessed reliably using fewer than 15 steps [34]. Gait parameters were considered as absolute.

2.4.3. Extrapolated centre of mass

The XCoM can be defined as the vector sum of the CoM position and a proportion of its velocity. During static conditions, balance can be defined as the body CoM being projected on the ground within the base of support. However, during dynamic situations this is insufficient as the velocity of the CoM should also be taken into account. Therefore, Hof et al. [8] defined XCoM as a new vector quantity in which the CoM is extrapolated in the direction of its corresponding velocity

$$\text{XCoM}=\text{CoM}+\hspace{0.17em}\frac{V_{\mathrm{CoM}}}{\sqrt{g/l}},$$

where $V_{\mathrm{CoM}}$ represents the CoM velocity, g is the acceleration of gravity (9.81 m s⁻²) and l is the pendulum length of the subject.

2.4.4. Spatial margin of stability

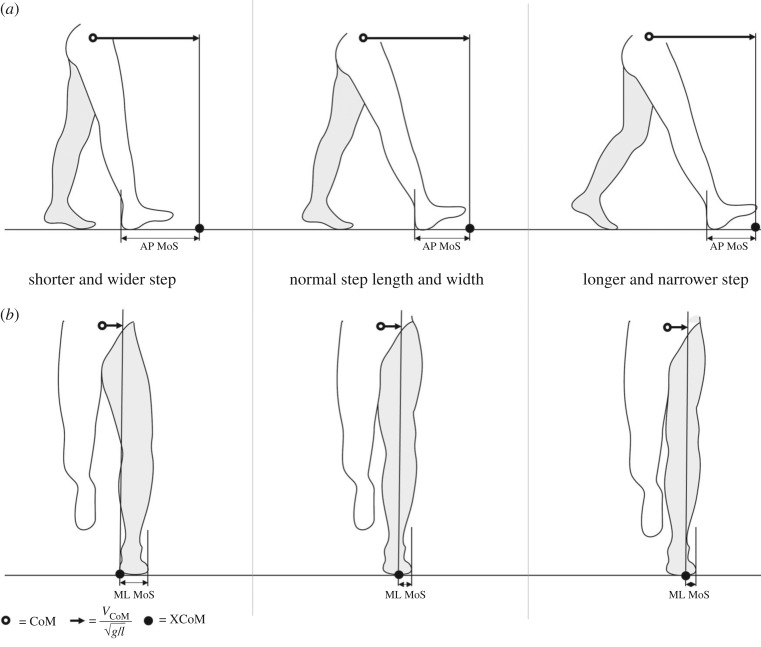
The MoS was defined in this study as the minimum distance between the CoP and the XCoM along the ML and AP axes during the single support phases. The ML axis is defined as the axis in the transverse plane, perpendicular to the walking direction derived from the CoM coordinates, and the AP axis is defined as the axis in the transversal plane, parallel to the walking direction derived from the CoM coordinates. In total, information on the MoS was available in 105 subjects, with one value of both the ML and AP MoS per leg in 15 subjects, two available values per leg in 46 subjects and three available values per leg in 44 subjects. The MoS is expressed as an absolute value (mm). A schematic of the MoS is displayed in figure 1.

Figure 1.

Schematic of the spatial margin of stability (MoS) in the anterior–posterior (AP; top row) and medio-lateral (ML; bottom row) directions. Adapted from Hak et al. [7]. (a) The AP MoS was defined as the distance in the AP direction between the extrapolated centre of mass (XCoM) and the posterior border of the leading foot at initial contact. Therefore, taking a shorter step increases the AP MoS (top left), while taking a longer step decreases the AP MoS (top right). (b) The ML MoS was defined as the minimum distance between the XCoM and the lateral border of the foot during foot contact. Therefore, a wider step results in a greater ML MoS (bottom left), while a narrower step results in a smaller ML MoS (bottom right). Although the definition from Hak et al. [7] differs from the definition used in the present study, the same principles apply.

2.5. Data measurement and calculations

Marker trajectories were labelled using the Vicon Nexus 1.8.x software. Based on the force plate data and ankle marker trajectories, events of foot-strike and foot-off were determined. The gait cycle was calculated based on the left and right heel marker trajectories.

The total body CoM was calculated using the standard Vicon clinical model (plug-in gait application for Nexus software) [30].

The .c3d files were then exported to Matlab (R2017a for Windows) and through a custom written script the MoS was calculated according to the formulae of the XCoM as described by Hof et al. [8]. Spatio-temporal parameters were calculated from the left and right ankle marker trajectories through a custom-written script in Matlab.

2.6. Statistical analysis

Statistical analysis was performed using JMP Pro® statistical software (v. 14 for Windows; SAS Institute). To describe the population, means and standard deviations were calculated for the total population as well as per decade. Q-Q plots were used to assess the normal distribution of the data and to identify outliers which were either corrected if possible or consequently removed from the dataset. Because of the large number of data points, parametric data analysis was performed.

Firstly, in order to reduce covariance among gait characteristics and to identify key variables without compromising selectivity a factor analysis was carried out [32]. The following original variables were selected: mean and standard deviation (variability) of step time, length, width and single support phase. Factor loadings were rotated by the varimax rotation with a minimum eigenvalue for extraction set at 1. Scree plots, total variance explained and rotated factor loading were investigated. If the total variance explained failed to reach 70% with the factors extracted based on the eigenvalue cut-off, factors were added until 70% variance explained was satisfied [35]. A minimum loading of 0.5 per item was considered relevant.

Secondly, the relation between MoS, spatio-temporal gait characteristics and age was modelled by means of linear mixed models. The dependent variables included the factors extracted from the factor analysis and MoS in the ML and AP directions (mm), with age (years), gender (female = 0; male = 1), BMI and leg length (mm) as fixed effects, and individuals as random effects. p-values < 0.05 were considered significant.

Lastly, by means of a stepwise forward linear regression the degree to which the identified factors predict the MoS in the ML and AP directions was investigated. Variables were entered into the model when the probability of F was less than 0.05. Variables were removed from the model when the probability of F was greater than 0.10.

3. Results

3.1. Descriptive data

Out of the available database of 114 healthy individuals, a total of 315 trials in 105 subjects were eligible for data analysis after checking for outliers and missing data. A total of 57 females and 48 males aged between 20 and 86 years (52.87 ± 19.09 years) were included in this study. Males showed an increased body mass (66.90 kg versus 84.12 kg; p < 0.0001), body height (162 cm versus 176 cm; p < 0.0001) and leg length (862 mm versus 948 mm; p < 0.0001); however, no differences were found for BMI (25.60 versus 27.01; p = 0.109). A description of the sample characteristics is presented in table 1.

Table 1.

Descriptive data of the included study sample including mean ages and anthropomorphic characteristics per decade and of the total sample. N, number of subjects; F, number of females; kg, kilograms; cm, centimetres; BMI, body mass index; mm, millimetres.

decade	N	F	age (years)		body mass (kg)		body height (cm)		BMI		leg length (mm)
			mean	s.d.	mean	s.d.	mean	s.d.	mean	s.d.	mean	s.d.
3	15	8	25.27	2.17	75.07	14.51	173.2	7.3	24.97	4.34	924	50
4	18	8	34.34	2.64	80.32	24.26	175.3	9.9	25.91	6.43	928	55
5	15	8	46.04	2.70	75.45	15.69	170.7	13.8	25.80	4.07	894	82
6	17	12	55.06	3.00	66.99	13.07	166.2	8.3	24.15	3.60	879	50
7	15	8	64.55	2.98	76.39	12.37	166.6	8.8	27.53	3.99	906	49
8	13	8	74.05	2.49	73.81	9.67	162.2	9.1	28.16	4.00	868	75
9	12	5	83.07	1.96	75.26	12.95	163.0	12.6	28.22	2.76	901	74
total	105	57	52.87	19.09	74.77	15.78	168.6	10.9	26.25	4.52	901	64

3.2. Outcome data

Descriptives of spatio-temporal characteristics and MoS per decade and for the total population can be found in tables 2 and 3.

Table 2.

Descriptive data of spatial margin of stability and gait parameters according to decade and of the total sample represented as the mean (SD). AP MoS, margin of stability in the anterior--posterior direction; ML MoS, margin of stability in the medio-lateral direction; mm, millimetres; m s⁻¹, metres per second; s, seconds; m, metres; %, percentage of gait cycle; steps/min, steps per minute.

decade	AP MoS	ML MoS	walking speed	stride time	stride length	step time	step length	step width	double support	single support	cadence
	(mm)	(mm)	(m s−1)	(s)	(m)	(s)	(m)	(m)	(%)	(%)	(steps/min)
3	349 (172)	32 (10)	1.17 (0.14)	1.12 (0.07)	1.32 (0.12)	0.56 (0.03)	0.66 (0.06)	0.17 (0.02)	21.26 (2.06)	39.47 (1.04)	107 (6)
4	305 (133)	36 (12)	1.25 (0.11)	1.06 (0.07)	1.34 (0.10)	0.53 (0.04)	0.67 (0.05)	0.18 (0.03)	19.91 (1.83)	40.11 (0.92)	113 (8)
5	287 (136)	33 (6)	1.24 (0.17)	1.03 (0.08)	1.28 (0.12)	0.52 (0.04)	0.64 (0.06)	0.18 (0.02)	20.98 (2.99)	39.48 (1.48)	117 (9)
6	263 (146)	32 (9)	1.23 (0.19)	1.04 (0.08)	1.27 (0.13)	0.52 (0.04)	0.64 (0.07)	0.17 (0.03)	20.24 (2.95)	39.93 (1.53)	117 (10)
7	268 (106)	29 (11)	1.23 (0.14)	1.04 (0.07)	1.28 (0.14)	0.52 (0.04)	0.64 (0.07)	0.17 (0.02)	20.91 (2.20)	39.57 (1.12)	116 (8)
8	283 (132)	32 (14)	1.10 (0.15)	1.06 (0.06)	1.17 (0.15)	0.53 (0.03)	0.58 (0.07)	0.17 (0.03)	23.56 (2.84)	38.26 (1.41)	114 (6)
9	294 (98)	27 (10)	1.06 (0.13)	1.08 (0.07)	1.16 (0.15)	0.54 (0.03)	0.58 (0.07)	0.18 (0.02)	23.76 (1.94)	38.14 (1.01)	112 (7)
total	293 (133)	32 (10)	1.19 (0.16)	1.06 (0.08)	1.27 (0.14)	0.53 (0.04)	0.63 (0.07)	0.17 (0.03)	21.34 (2.74)	39.37 (1.39)	114 (8)

Table 3.

Descriptive data of the standard deviations of the gait parameters according to decade and of the total sample represented as the mean (SD). m s⁻¹, metres per second; s, seconds; m, metres; %, percentage of gait cycle; steps/min, steps per minute.

decade	walking speed	stride time	stride length	step time	step length	step width	double support	single support	cadence
	(m s−1)	(s)	(m)	(s)	(m)	(m)	(%)	(%)	(steps/min)
3	0.037 (0.014)	0.024 (0.010)	0.031 (0.007)	0.018 (0.005)	0.022 (0.011)	0.027 (0.013)	1.69 (0.53)	1.31 (0.33)	3.37 (0.95)
4	0.032 (0.010)	0.018 (0.005)	0.024 (0.009)	0.015 (0.003)	0.022 (0.009)	0.023 (0.008)	1.30 (0.38)	1.21 (0.28)	3.28 (0.75)
5	0.034 (0.020)	0.019 (0.008)	0.022 (0.006)	0.014 (0.004)	0.019 (0.006)	0.022 (0.006)	1.40 (0.47)	1.16 (0.23)	3.28 (1.04)
6	0.038 (0.019)	0.019 (0.007)	0.029 (0.013)	0.014 (0.003)	0.019 (0.007)	0.024 (0.007)	1.63 (0.38)	1.24 (0.28)	3.20 (0.65)
7	0.041 (0.022)	0.020 (0.010)	0.029 (0.014)	0.016 (0.005)	0.025 (0.006)	0.026 (0.011)	1.39 (0.35)	1.24 (0.24)	3.47 (0.97)
8	0.035 (0.017)	0.021 (0.009)	0.026 (0.013)	0.016 (0.004)	0.020 (0.008)	0.025 (0.010)	1.73 (0.47)	1.39 (0.33)	3.39 (0.44)
9	0.037 (0.010)	0.022 (0.007)	0.034 (0.010)	0.019 (0.007)	0.025 (0.004)	0.030 (0.009)	1.68 (0.58)	1.50 (0.38)	3.90 (1.22)
total	0.036 (0.017)	0.020 (0.008)	0.028 (0.011)	0.016 (0.004)	0.022 (0.009)	0.025 (0.009)	1.53 (0.47)	1.28 (0.31)	3.39 (0.88)

3.3. Main results

3.3.1. Factor analysis

In total, eight variables were included in the factor analysis and clustered into four factors, depicting domains of gait. These four domains accounted for 74.17% of the variance in gait parameters. The first domain accounted for 23.15% of the variance, consisting of variability (SD) of step time, step length and single support phase and was named ‘variability'. The second domain, ‘pace', accounted for 19.94% and consisted of step length and the single support phase. ‘Base of support', the third domain, accounted for 17.34% of the total variance and consisted of step width and step time. The fourth domain, ‘base of support variability', consisted of step width variability (SD) and accounted for 13.74% of the variance. Results of the factor analysis can be found in table 4.

Table 4.

Item loadings for the four-factor rotated solution. %, percentage of gait cycle; s, seconds; m, metres; m/s, metres per second. A minimum loading of 0.5 was considered relevant. Relevant item loadings in bold.

	variability	pace	base of support	base of support variability
single support phase variability (%)	0.759	−0.080	0.055	0.106
step time variability (s)	0.759	−0.094	0.043	0.281
step length variability (m)	0.652	0.151	0.134	−0.496
step length (m)	−0.001	0.910	0.142	−0.016
single support phase (%)	−0.131	0.841	−0.362	0.015
step width (m)	−0.058	−0.004	0.894	−0.003
step time (s)	0.448	−0.143	0.642	0.039
step width variability (m)	0.231	0.041	0.049	0.872
% of variance accounted for	23.15	19.94	17.34	13.74

3.3.2. Influence of age (β₁) on stability and domains of gait

Results of the linear mixed models indicated that age had no significant influence on MoS in the AP direction (p = 0.350); however, age did seem to influence the MoS in the ML direction (p = 0.003) with increasing age inducing a decrease in ML MoS. A significant influence of age was also found on all domains of gait except for the ‘base of support variability' domain (p = 0.258). An increase in age results in an increase in the ‘variability' domain (p = 0.032) and a decrease in the ‘pace' (p = 0.0002) and ‘base of support' domains (p = 0.023). Results can be found in table 5.

Table 5.

Mixed model results of age, gender, BMI and leg length on stability and the domains of gait derived from the factor analysis. AP MoS, margin of stability in the anterior–posterior direction; ML MoS, margin of stability in the medio-lateral direction; mm, millimetres; age, years; gender, the performance of females (0) when compared with males (1); leg length = mm; *p < 0.05; **p < 0.001; ^$p < 0.0001; $Y_i=\hspace{0.17em}{\beta }_0+{\beta }_1\hspace{0.17em}\ast \hspace{0.17em}\text{age}+{\beta }_2\hspace{0.17em}\ast \hspace{0.17em}\text{gender}\hspace{0.17em}(0)\hspace{0.17em}+{\beta }_3\hspace{0.17em}\ast \hspace{0.17em}\text{BMI}+{\beta }_4\hspace{0.17em}\ast \hspace{0.17em}\text{leg length}$. Statistically significant values in the last column are indicated by italic.

parameter	β0	β1–4	95% CI	p-value
AP MoS (mm)	330.25		[−266.92 ; 927.42]	0.275
age		−0.69	[−2.14 ; 0.77]	0.350
gender (0)		−14.52	[−87.09 ; 58.05]	0.692
BMI		−3.04	[−9.07 ; 3.00]	0.320
leg length		0.10	[−0.48 ; 0.67]	0.741
ML MoS (mm)	18.08		[−21.72 ; 57.87]	0.370
age*		−0.15	[−0.25 ; −0.05]	0.003
gender (0)		−4.55	[−9.38 ; 0.29]	0.065
BMI$		1.04	[0.63 ; 1.44]	<0.0001
leg length		−0.04 × 10−1	[−0.04 ; 0.04]	0.855
variability	−3.01		[−7.34 ; 1.32]	0.171
age*		0.01	[0.01 × 10−1 ; 0.02]	0.032
gender (0)		−0.21	[−0.74 ; 0.31]	0.426
BMI		−0.48 × 10−2	[−0.49 × 10−1 ; 0.39 × 10−1]	0.828
leg length		0.29 × 10−2	[−0.12 × 10−2 ; 0.71 × 10−2]	0.165
pace	0.83		[−2.98 ; 4.64]	0.666
age**		−0.18 × 10−1	[−0.28 × 10−1 ; −0.90 × 10−2]	0.0002
gender (0)*		−0.52	[−0.98 ; −0.06]	0.027
BMI*		−0.41 × 10−1	[−0.80 × 10−1 ; −0.29 × 10−2]	0.036
leg length		0.17 × 10−2	[−0.20 × 10−2 ; 0.53 × 10−2]	0.367
base of support**	−5.67		[−8.82 ; −2.52]	0.0005
age*		−0.89 × 10−2	[−0.17 × 10−1 ; −0.13 × 10−2]	0.023
gender (0)*		−0.61	[−0.99 ; −0.23]	0.002
BMI$		0.94 × 10−1	[0.62 × 10−1 ; 0.13]	<0.0001
leg length*		0.45 × 10−2	[0.14 × 10−2 ; 0.75 × 10−2]	0.004
base of support variability	−1.61		[−6.03 ; 2.82]	0.474
age		0.62 × 10−2	[−0.46 × 10−2 ; −0.17 × 10−1]	0.258
gender (0)		0.40	[−0.14 ; 0.94]	0.146
BMI		−0.04	[−0.85 × 10−1 ; 0.46 × 10−2]	0.078
leg length		0.24 × 10−2	[−0.19 × 10−2 ; 0.66 × 10−2]	0.276

3.3.3. Influence of gender (β₂) on stability and domains of gait

Gender did not seem to influence the AP MoS (p = 0.692) or ML MoS (p = 0.065). An influence of gender was found on the ‘pace' (p = 0.027) and ‘base of support' domains (p = 0.002), with females showing a reduction in ‘pace' and ‘base of support', but not on the ‘variability' (p = 0.426) and ‘base of support variability' domains (p = 0.146). Results can be found in table 5.

3.3.4. Influence of BMI (β₃) on stability and domains of gait

A significant influence of BMI on the ML MoS was found (p < 0.0001) but not on the AP MoS (p = 0.320). An increase in BMI resulted in an increase in ML MoS and ‘base of support’ domain (p < 0.0001) and a decrease in the ‘pace' domain (p = 0.036). BMI did not seem to influence the ‘variability' (p = 0.828) and ‘base of support variability' (p = 0.078) domains. Results can be found in table 5.

3.3.5. Influence of leg length (β₄) on stability and domains of gait

Leg length only seemed to have a significant influence on the ‘base of support' domain (p = 0.004). No influence of leg length was found on both the AP (p = 0.741) and ML (p = 0.855) MoS or on the ‘variability' (p = 0.165), ‘pace’ (p = 0.367) and ‘base of support variability' (p = 0.276) domains. Results can be found in table 5.

3.3.6. Stepwise linear regression

A stepwise linear regression was used to investigate the degree to which the domains of gait resulting from the factor analysis predicted AP and ML MoS.

No significant regression equation was found for the AP MoS.

However, the test results of the stepwise linear regression using the domains of gait indicated one predictor explaining 26% of the variance in the ML MoS (R² = 0.260, F_1,103 = 2879.34, p < 0.0001). It was found that the ‘base of support' domain significantly predicted the ML MoS (β = 5.26, p < 0.0001). Figure 2 shows the linear relation between the ML MoS and the ‘base of support' domain. No additional variance in the ML MoS was explained by the remaining domains.

Figure 2.

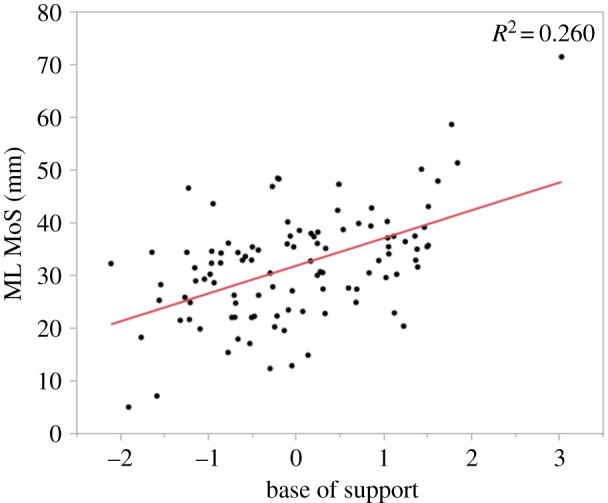
Linear relation between the medio-lateral margin of stability (ML MoS) and the ‘base of support' domain. Using a stepwise linear regression, a significant regression equation was found: $31.74+5.26\hspace{0.17em}\ast \text{ base of support}$ with an R² of 0.260 (p < 0.0001).

4. Discussion

The purpose of this study was to investigate the differences in spatial MoS in healthy adults aged between 20 and 89 years and whether these differences can be related to differences in spatio-temporal parameters of gait. The main findings of this study include: (i) eight included spatio-temporal gait characteristics loaded on four different domains of gait explaining 74.17% of the variance in gait parameters, (ii) age had a significant influence on the ML MoS but not on the AP MoS, (iii) age significantly influenced the ‘variability', ‘pace' and ‘base of support' domain, and (iv) results of the stepwise linear regression indicated a linear relation between the ‘base of support' domain and the ML MoS. Additional findings revealed that BMI had a significant influence on the ML MoS, while gender and leg length had no influence on either of the MoS values. Thus, based on the current results our hypothesis of an increase in the MoS with increasing age cannot be confirmed as no differences in the AP MoS were found and the ML MoS showed a decrease with increasing age.

4.1. Interpretation

Across the lifespan, a stable and independent gait is key for daily functioning and participation. As a result of increasing age, changes in gait emerge that can be associated with clinical phenomena such as fall risk, cognitive impairments, functional decline or even increased mortality [13–15,36]. Therefore, analysing gait provides researchers and clinicians with the opportunity to identify, understand and remediate such changes in gait. These changes can be easily identified using spatio-temporal parameters, even when the equipment to perform an instrumented gait analysis is not available [36]. However, because of the high covariance among and the broad range of available spatio-temporal parameters, there is an indication for redundancy and a need for identifying key spatio-temporal variables, i.e. domains of gait [32]. Loadings of individual spatio-temporal parameters onto these domains differ slightly depending on the spatio-temporal parameters that were added to the model. For instance, in the present study, eight spatio-temporal parameters were included in the model and yielded four domains of gait—variability, pace, base of support and base of support variability—while Kirkwood et al. [37] included 15 spatiotemporal parameters and yielded four domains of gait, i.e. rhythm, variability, support and phase. Hollman et al. [12] included 23 spatio-temporal parameters clustered into five gait domains—rhythm, phases, variability, pace and base of support. In general, mean step or stride length and walking speed tend to load upon the ‘pace' domain, whereas mean step width consistently loads onto ‘base of support' and all entered variability measures more or less cluster; hence the name ‘variability'. Verghese et al. [14] suggested that ‘pace' reflects a central gait control mechanism, being related to higher cortical mechanisms. The domain ‘base of support', also referred to as ‘postural control', is thought to be related to dynamic balance control during gait because of the consistent loading of the mean step width and its relationship to the base of support. The variability measures suggest that an individual needs to constantly adjust their steps and thus adapt their gait pattern adequately to remain stable. Therefore, gait variability has been hypothesized to represent an aspect of balance control, and even in a healthy population this seems to be a defining factor for gait stability as the ‘variability' domain accounted for 23.15% of the variance in gait stability.

Considering the influence of age on the spatial margins of stability, age had a significant influence on the ML MoS but not on the AP MoS. This suggests that with increasing age the forward progression is ensured as the AP MoS remains unchanged. Both an AP MoS that is too small or too large can result in either an interference of the forward progression or will result in an increased risk of forward loss of balance, respectively [7]. The ML MoS, on the other hand, did differ when considering age, with an increase in age indicating a decrease in the ML MoS. These results are partially in contrast to the results of Lencioni et al. [28], who also found no relationship between age and the AP MoS but found a moderate positive relation between age and the ML MoS. This difference could be related to the smaller number of participants included in the study by Lencioni et al. [28] with 34 subjects aged between 21 and 71 years.

Taking the influence of the spatio-temporal parameters on the margins of stability into consideration, the stepwise linear regression failed to yield a significant predictor for the AP MoS, while for the ML MoS the ‘base of support' domain was extracted. The lack of a significant predictor for the AP MoS also supports the notion that the forward progression is ensured with increasing age as all domains, except for the ‘base of support variability' domain, do show an influence of age. However, this may also be explained by the task constraints as all participants performed steady-state walking without any perturbations. Considering the ML MoS, the ‘base of support' domain loaded with step width and step time shows a decrease with age, thus supporting the finding of a decrease in ML stability with age. Stability in the ML direction can most effectively be regulated through modulating the relation between the lateral border of the base of support and the ML CoM position [38]. As the ML MoS is defined as the smallest distance between the CoP and the XCoM in the ML direction during the stance phase, the ML MoS can be increased or decreased by controlling the foot placement during the swing phase and taking a wider or narrower step, respectively [7,39]. This result is in line with the results of Lencioni et al. [28], who found a positive correlation between step width and ML MoS. On the other hand, using the stance leg, the CoM movement (i.e. position and acceleration) can be controlled [39,40]. Considering the inverted pendulum with regards to step time, a reduced time spent in single support results in less time for the CoM to fall to the side before the next foot is placed. This leads to a reduced excursion of the XCoM, resulting in an increased distance between the XCoM and the CoP, effectively increasing the ML MoS [9]. Taking both factors into consideration, the decrease in step time may act as a way to increase the safety margin to counter the loss of ML MoS, as a result of the decrease in step width, by spending less time on one leg. However, this decrease in step time is not sufficient to completely counter the loss of ML MoS due to a decrease in step width, therefore resulting in a decrease in ML MoS with increasing age. Moreover, Arvin et al. [41] found that even an increase in step width in older adults was not sufficient to prevent a smaller ML MoS than that in young adults. Additionally, walking with a smaller step width may minimize, or at least limit, the energetic costs of locomotion as the cost of redirecting the CoM velocity is reduced [40,42].

No influence of gender was found on the AP MoS and ML MoS although Lencioni et al. [28] did find a difference in ML MoS between males and females, with females showing a smaller ML MoS. The present results refute the suggestion that the margins of stability are sex specific, although differences between genders were found for the ‘pace' and base of support' domains. These sex-specific differences in the domains ‘pace' and ‘base of support', however, are in line with results previously described with males showing longer and wider steps [43,44]. These results may indicate that for both genders a steady forward progression without deviating from the straight walking trajectory is key, and although sex-specific differences in spatio-temporal parameters are present, they do not result in differences in dynamic stability.

Taking the influence of BMI into consideration, an increase in BMI increased the ML MoS and ‘base of support' domain while decreasing the ‘pace' domain. The increase in ML MoS with an increase in BMI may be the result of the increase in the ‘base of support' domain loaded with step width and step time. This increase in step width has also been found in obese adults [45]. A wider step increases the ML MoS as the smallest distance between the CoP and XCoM in the ML direction is increased [7]. Furthermore, a shorter single support phase in combination with an increase in step time may be induced to establish a more stable double support phase more quickly and for a longer time [46]. Another consequence of the increased step width is a reduction of the AP MoS as a wider step reduces the maximal step length a person can take [25,26,47]. Because of the increase in BMI, slower walking speeds, shorter steps and a longer double support phase are preferred in order to minimize the gross energy cost [45,48–50]. Specifically, the slower walking speed lowers the mechanical work needed to redirect the CoM [49]. The slower walking speed in combination with a shorter step length may explain the unchanged AP MoS, ensuring forward progression without increasing the risk of a backwards loss of balance [51].

Lastly, leg length only had a significant influence on the ‘base of support' domain. As the person's leg length defines the maximum feasible step a person can take [47], persons with a greater leg length are able to take wider steps while still preserving an adequate step length, thus not interfering with the AP MoS. As leg length also had no influence on the ML MoS although step width increased, the increase in step time allows the CoM to fall more to the side before the next foot is placed, reducing the distance between the XCoM and the CoP [9] and effectively counteracting the effect of an increased step width, keeping the ML MoS unchanged.

4.2. Limitations and future research

Some limitations are to be considered. All subjects participated in this study on a voluntary basis, inducing a possible selection bias with participants only being excluded through self-reported visual, neurological or orthopaedic disorders. Participants were not screened on cognitive, mental or cardiovascular impairments, which could also potentially affect gait [14,52]. Although the total amount of included participants is large, the number of participants included in each decade (n = [12;18]), and especially in decades 8 (n = 13) and 9 (n = 12), is rather limited, which may limit generalizability. Also related to the included population, mean BMI scores are increased, except for decades 3 and 6, which are at the upper limit of the norm. However, these BMI scores are in line with the BMI scores reported in the Belgian Health Interview Survey 2018 [53]. Additionally, as opposed to walking in real-life situations, the uncluttered laboratory setting creates an ‘unnatural' situation where the dynamic stability is not challenged by irregularities and unpredictable changes in environmental factors, resulting in possible small changes in the way of walking. Additionally, the walking bouts within the laboratory setting are rather short; in this case, walking bouts of maximum 12 m with only the middle 6 m used for analysis. This results in a limited number of steps compared with treadmill walking. Therefore, investigating the MoS in real-life situations outside the laboratory could be of invaluable importance. In addition, our study is one of the few that investigated the MoS in a wide range of healthy adults of different ages. For future research, more attention should be drawn to middle-aged adults as data from this age group are currently lacking. Additionally, differences in dynamic stability during walking between men and women could be an interesting subject to investigate as the ageing process may affect the way of walking differently in men and women [54]. Future studies should also strive for cooperation between multiple centres where healthy elderly reside and aim for large percentages of participation in order to increase the generalizability. Moreover, investigating the MoS in specific patient populations with impairments in motor, sensory or neural functions could also give us more insights in how stability is maintained. Another interesting topic related to understanding how humans control their gait stability is the subject of foot placement estimators (see [40] for a review) and how these relate to other strategies in order to control gait stability.

5. Conclusion

The findings of this study indicate that while the ML MoS is influenced by age, the AP MoS is not. Additionally, the ML MoS is also affected by BMI. Therefore, age and BMI should be taken into account when considering the margins of stability, especially when comparing multiple groups of subjects. As for predictability of the margins of stability, step width and step time loading on the ‘base of support' domain were predictive for the ML MoS and should be taken into account.

Ethics

The study protocol has been approved by the local ethics committee (B300201316328), with data collection taking place between April 2015 and January 2016. Subjects gave written informed consent at the time of inclusion and were aware that data could be used retrospectively for further research.

Data accessibility

The datasets are available as part of the electronic supplementary material.

Authors' contributions

N.H., W.S., L.V., V.V.R. and A.H. were involved in the conception of the study. T.v.C. and N.H. were involved in the acquisition of the data. N.H. analysed and interpreted the data and results. N.H. drafted the manuscript, T.v.C., W.S., S.T., L.V., V.V.R. and A.H. revised the manuscript for important intellectual content. All authors concurred with the content and the final version of the manuscript.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by the University of Antwerp Research Council (grant no. ID33586), the University of Antwerp and Antwerp University Hospital.