Environmental variability, reliability of information and the timing of migration

Abstract

The timing of migration and migratory steps is highly relevant for fitness. Because environmental conditions vary between years, the optimal time for migration varies accordingly. Therefore, migratory animals could clearly benefit from acquiring information as to when it is the best time to migrate in a specific year. Thus, environmental predictability and variability are fundamental characteristics of migration systems but their relationship and consequence for migratory progression has remained unexplored. We develop a simple dynamic model to identify the optimal migration behaviour in environments that differ in predictability, variability and the number of intermediate stop-over sites. Our results indicate that higher predictability along migration routes enables organisms to better time migration when phenology deviates from its long-term average and thus, increases fitness. Information is particularly valuable in highly variable environments and in the final migration-step, i.e. before the destination. Furthermore, we show that a general strategy for obtaining information in relatively uninformative but variable environments is using intermediate stop-over sites that enable migrants to better predict conditions ahead. Our study contributes to a better understanding of the relationship between animal movement and environmental predictability—an important, yet underappreciated factor that strongly influences migratory progression.

1. Introduction

Migration is an adaptation to conditions that vary seasonally or periodically between favourable, resource-rich and unfavourable or hostile [1]. Typically, there is an optimal time for migration, i.e. success/reward is highest when executed at this time [2]. Missing the optimal time incurs costs that may range from reduced reproductive success to reduced survival, e.g. [3], and this applies not only for departure from a starting site and arrival at a destination (breeding) site but also for intermediate steps on stop-over sites. In stable seasonal environments, in which the optimal time occurs invariantly at the same time of the year, natural selection would push organisms to time migration at exactly this best time [4]. In this case, a photoperiodic cue to time migration would be fully sufficient. Typically, however, there is environmental variability between years, and the optimal time cannot be predicted on the basis of photoperiod alone but requires additional (external) information [5]. If environmental variables are correlated in space or time, individuals could obtain information about environmental conditions at distant places or in the future whereas weak correlation means a low level of information only [6]. Specifically, if phenologies of successive sites are correlated, this means they may have different long-term averages for, e.g. the onset of spring, but they deviate similarly from this average in a given year: Under strong correlation, for instance, an early onset of spring at one site means spring is also earlier-than-average on the subsequent site (figure 1) while under weak correlation, the onset of spring at one site can hardly predict the onset of spring at another.

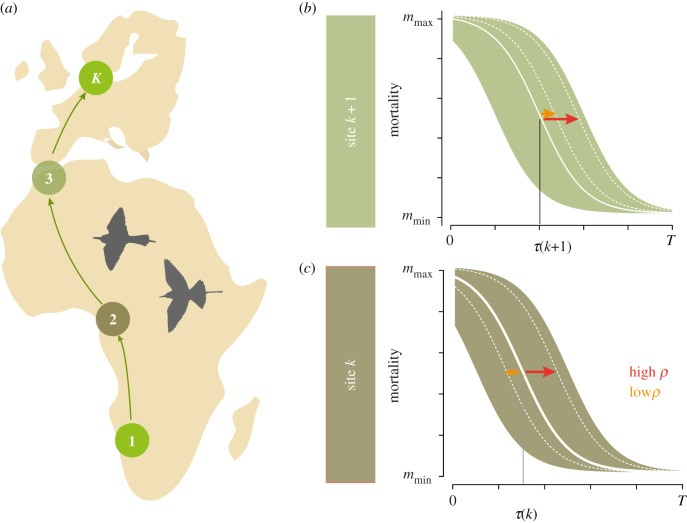
Figure 1.

Migration between a non-breeding and breeding site often involves several intermittent stop-over sites (a). We incorporated phenology on all sites as changes in mortality over time (b,c) and the onset of spring is the time when mortality decreases at its highest rate. Phenology has a long-term average (thick white line) from which it may deviate in a given year (as indicated by the arrows to dotted white lines). If phenologies of successive sites are correlated (high ρ), these deviations from the long-term averages are similar at site k and site k + 1 (red arrows) while for low correlation (low ρ, orange arrows), they can be highly dissimilar and thus, not predicted from a present site. The long-term average of onset of spring is at τ(k). (Online version in colour.)

Thus, migration systems can differ in two fundamental aspects—how variable they are between years and in how far conditions at distant sites can be predicted from the current location, i.e. environmental variability and predictability, respectively [7]. Many migrants have been shown to follow the temporal availability of resources across heterogeneous landscapes [8], e.g. green wave of spring green-up [9,10], which suggests that migrants indeed have, or can acquire, knowledge on environmental conditions at distant places. However, although it is generally acknowledged that information plays an important role for animal behaviour [11,12], the link between spatial environmental predictability and the timing of animal movements has not been systematically explored [13]. Consequently, we lack a detailed understanding of how animals should schedule migrations under different levels of information about the optimal timing, how the best migration strategy would change in environments differing in variability and which role intermediate stop-over sites could play in modifying these relationships. We address these questions with a simple model that calculates the optimal migration behaviour from a starting (wintering) to a destination (breeding) site.

2. Model description and scenarios

The migration route consists of K locations, labelled as k = 1, 2, …, K, where k = 1 marks the wintering and K the breeding site (figure 1a). Thus, K = 2 represents a non-stop migration between wintering and breeding site, and K > 2 refers to migration with one or more intermediate (stop-over) sites.

We describe phenology on sites with the ‘onset of spring’, i.e. the time when conditions become favourable and mortality decreases (figure 1b,c). The long-term average for the onset of spring at site k is τ(k) but the actual onset of spring in a given year may deviate from this average by Y(k), which is a random variable with zero mean and variance ${\sigma }^2(k)$, i.e. $E\{Y(k)\}=0$ and $\text{Var}\{Y(k)\}={\sigma }^2(k)$. Thus, in a given year, the actual onset of spring is at time $\tau (k)-Y(k)$.

We assume that conditions at neighbouring sites (e.g. k and k + 1, k < K) are correlated, i.e. the joint distribution of Y(k) and Y(k + 1) is a bivariate normal distribution with correlation coefficient ρ(k). This correlation coefficient shows to what extent the onset of spring on site k predicts the onset of spring on site k + 1. Given the value of Y(k) we assume that values at later sites are conditionally independent of the values at previous sites (the Markov property). With this assumption, the product of all ρ(k) (i.e. $\rho ={\prod }_{k=1}^{K-1}\rho (k)$) is the correlation between Y(1) and Y(K) and hence indicates the expected predictability across the entire migration landscape, i.e. the predictability of conditions at the breeding site from conditions at the wintering site.

(a). Decision making on the migratory journey

Individuals start migration at the wintering site (k = 1), subsequently move to following sites and if surviving the journey, finally arrive at the breeding site K. We allow no skipping of sites but assume that travel time between sites is negligible compared to time spent on sites. On arrival at site k, an animal immediately observes its phenological stage, i.e. by how much the actual onset of spring deviates from its long-term average. More formally, the animal observes y, i.e. the actual value of Y(k) for that year. It then decides when to leave this site and move on to the next site k + 1. The migration strategy of an animal is specified by a function L of two variables, where L(y,k) is the target time at which to leave site k when the deviation from the average onset of spring at this location is y. The animal leaves the site immediately if it arrives after this target time, otherwise remaining there until the target time is reached. Thus, if the animal arrives at site k at time t and the deviation in the onset of spring at this site is y, the animal leaves the site at time $\text{max}\{t,L(y,k)\}$.

(b). The optimization criterion

We describe the consequences of arriving at site k at a specific time by assuming that site k is characterized by a mortality rate, which depends on the time of year and the advancement of spring at that site. Specifically, if the onset of spring on a site deviates by Y(k) = y then the mortality rate at location k at time of year t is M(t + y, k) (for k = 1,2, …, K) for which we use the following function:

$$M(t+y,k)=m_{\min }+\frac{m_{\max }}{1+{\text{e}}^{-0.05(-(t+y-\tau (k)))}},$$

that is mortality decreases sigmoidally from a maximum value (m_max + m_min) to the minimum value of m_min, except for the starting site, where we kept mortality at m_min throughout; we used m_max = 0.005 and m_min = 0.0001. The inflection point of the mortality function is at t = τ(k) – y, which characterizes when mortality decreases at the fastest pace, i.e. when spring starts (figure 1b,c).

Let $S(k)=1-M(t+y,k)$ denote the probability that an individual survives while at location k. We do not consider mortality during movement between sites, assuming that mortality during movement is low compared to mortality on sites and constant for all movement episodes. Thus, $s=S(1)S(2)\cdots S(K-1)$ is the probability that an animal survives the entire journey. If the animal survives the journey to the breeding site K, it starts (preparations for) reproduction immediately after arrival. Its terminal reward there is then given by a function of the onset of spring at this site and the time of arrival t at the site R(y,t). We assume that $R(y,\hspace{0.17em}t)=F(t+y,\tau (K),R_{\mathrm{wide}})+R_{\mathrm{future}}{\prod }_{n=t}^Q(1-M(n+y,K))$, where $F(t+y,\tau (K),R_{\mathrm{wide}})$ is a bell-shaped function of t + y centred at τ(K) with a spread of $R_{\mathrm{wide}}$, which gives the value of an offspring born at time t in a year when spring is advanced by y. The second part ${\prod }_{n=t}^Q(1-M(n+y,K))$ gives the probability of survival until the end of season, Q (Q = day 100) weighed by the expected future reproductive success, $R_{\mathrm{future}}$. We used $R_{\mathrm{future}}$ = 1 and $R_{\mathrm{wide}}=30.$

The payoff (reproductive value) for the strategy L is then

$$E_L\{sR(Y(K),T(K))\},$$

where the random variable Y(K) is the deviation of spring at site K (see above) and the random variable T(K) is the time of arrival at the site, and E_L{·} denotes the expectation given strategy L. An optimal strategy maximizes this payoff.

For model details, dynamic programming equations and R-code, see the electronic supplementary material, S1 and [14].

(c). Scenarios

To explore the interplay between predictability, environmental variability and the timing of migration, we systematically varied the correlation (landscape ρ) across the entire migration landscape, the number of intermediate sites (K), and environmental (year-to-year) variability (σ²) and analysed their effects on migration times, i.e. departure and arrival dates, spread of arrival dates and fitness, i.e. reproductive values.

We varied the correlation across the entire migration landscape ρ between ρ = 0.0 and ρ = 1, i.e. from completely unpredictable to perfectly predictable. Unless stated otherwise, we set ρ(k) = ρ₀ for all k, i.e. the same ρ(k) for all sites, such that the landscape ρ is given by ρ = ρ₀^K−1. We varied the number of sites, K, to include from zero to nine intermediate sites (i.e. K = 2, …, 11) while keeping the landscape ρ constant. Please note that the latter required changes in ρ₀ such that for a given landscape ρ, sites in landscapes with more intermediate sites are more ‘informative’ (i.e. they have a higher ρ₀) than landscapes with fewer sites. Alternatively, we could have kept ρ₀ constant when adding sites but this would have changed the landscape ρ, making it less straightforward to compare landscapes with different numbers of intermediate sites. For the relationship between landscape ρ and ρ₀, see the electronic supplementary material, figure S1.

We also varied environmental year-to-year variability σ²(k), between 1 and 10, i.e. from a nearly invariable environment in which spring starts at almost the same day every year to highly variable environments with great variation in the onset of spring; again, we used σ(k) = σ(k + 1) for all k.

Finally, for identifying the importance of information at specific places, we lowered ρ(k) on one specific site in a five-site migration landscape while using the same ρ(k) on all other sites. This lower correlation at one place could be interpreted as an ‘information barrier’, and we varied the specific location of this barrier.

3. Results

(a). Value of information under varying degrees of environmental variability in non-stop migrations

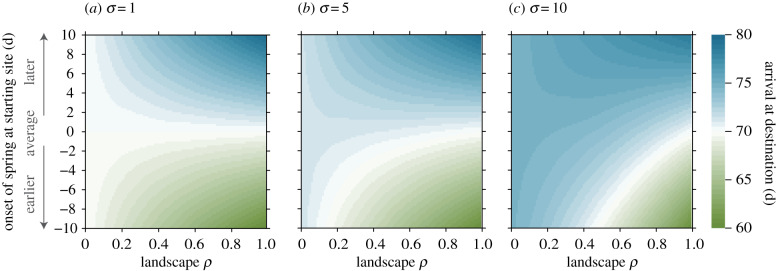
The correlation between sites, and thus, the level of predictability, clearly influenced migration timing but this strongly depended on the overall variability of environment and the deviation in the onset of spring from its long-term average at the starting site (figure 2). For high landscape ρ, migrants responded to deviations in the onset of spring directly and proportionally, i.e. they could accurately predict when spring starts at the destination site and departed from the starting site accordingly. For instance, if spring started 10 days earlier than the long-term average, then migrants also departed 10 days earlier (day 60), so as to arrive at the breeding site at the start of spring in that year (day 70, figure 2a).

Figure 2.

Arrival at the destination site (days, colour shades) changes with landscape ρ (x-axis), with how much the onset of spring deviated from its long-term average at the wintering site (y-axis) and with environmental variability (increasing σ in a–c) in a migration landscape with no intermediate decision points (K = 2): with high landscape ρ, migrants adjust departure from starting site (and arrival at destination) to deviations from the average onset of spring, i.e. they depart as many days earlier (green shades) as spring is advanced or as many days later (blue shades) as spring is delayed. However, under lower landscape ρ migrants cannot predict when spring starts at the destination site and therefore, their best choice is to depart at the time when spring starts on average at the destination site (white areas, day 70). Increasing environmental variability (b,c) modifies this pattern. In variable environments, the actual onset of spring can deviate greatly from its long-term average. Because arriving at a site before spring has started poses a significant mortality risk, the best migrants can do in environments that are highly variable AND hardly predictable is to migrate late (large blue areas in c) and so ensure survival but possibly miss out on this year's reproduction. (Online version in colour.)

However, a lower correlation between sites makes it harder for migrants to predict conditions at the breeding site from conditions at the starting site. For instance, if individuals experience an extreme deviation from the average onset of spring at the wintering site, they have no reliable information as to whether this is also the case at the breeding site. Consequently, departure from the starting site becomes more and more independent of the onset of spring, even if the actual onset of spring strongly deviates from its long-term average, and in the extreme case of no predictability (landscape ρ ≈ 0.0), migrants depart on a fixed day (figure 2a).

Increasing environmental variability modified this relationship between predictability and timing of migration (figure 2a–c): in relatively constant environments (figure 2a), large deviations from the average onset of spring are unlikely but such deviations are no exception anymore under high environmental variability (figure 2c). Consequently, arrivals become increasingly later already at intermediate landscape ρ and indicate that migrants avoid arriving at the breeding site before spring has started as this would increase mortality. Thus, migrants jeopardize reproductive success but play it safe when it comes to survival—an intuitively reasonable strategy in highly variable environments with low predictability.

This pattern is also reflected in reproductive values (figure 3a): the highest reproductive values are reached under high predictability (high landscape ρ) or low environmental variability (low σ), while reproductive values are low for highly variable environments or those with low predictability.

Figure 3.

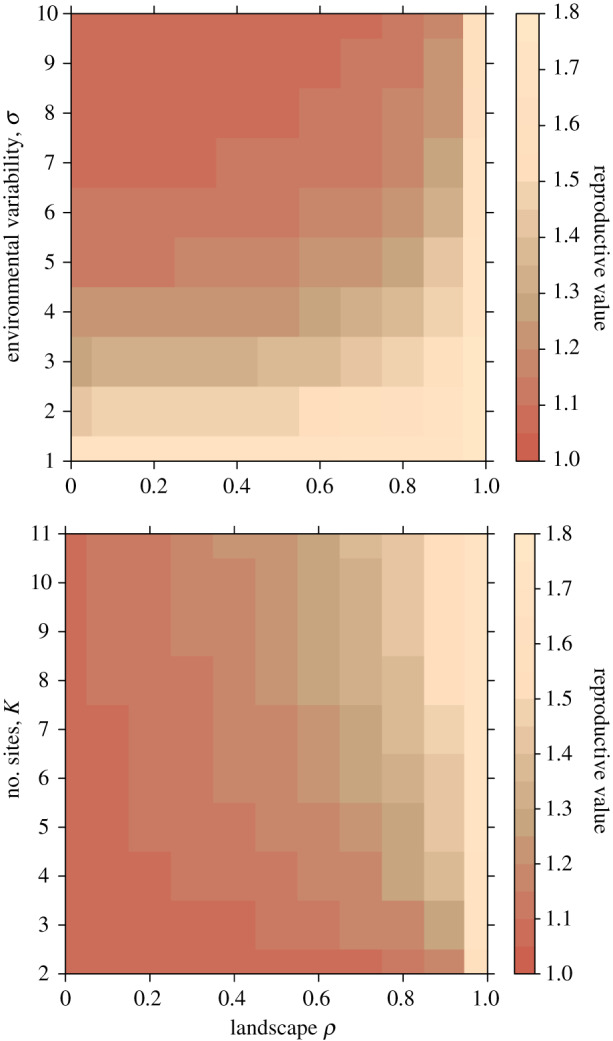
Reproductive values as dependent on landscape ρ and (a) environmental variability (using K = 2, for other values of K, see the electronic supplementary material, figure S2) and (b) number of sites, K (using σ² = 10, for comparison to other values of σ², see the electronic supplementary material, figure S2). (Online version in colour.)

(b). From non-stop migration to many intermediate steps

Adding intermediate sites between starting site and destination changed migration from non-stop (skip) to ‘jump’ and ‘hop’ migrations. As we kept the correlation across the migration landscape the same, adding intermediate sites changed the pairwise correlation between sites, ρ₀ (see ‘Scenarios’). The ρ₀ differ little from landscape ρ for very low or very high landscape ρ (electronic supplementary material, figure S1) but ρ₀ is significantly larger than landscape ρ at low to intermediate landscape ρ, and when there are many intermediate sites, suggesting that intermediate sites can be valuable when predictability is intermediate.

The value of intermediate sites is reflected in fitness-consequences: the lowest reproductive values result in landscapes with no predictability (landscape ρ ∼ 0.0) but also when there are no intermediate sites (K = 2) (figure 3b). For a specific landscape ρ, the addition of intermediate sites increases reproductive values, and this effect is more pronounced at intermediate ρ. However, there is also a saturation effect—adding a few sites increases reproductive values much more under low K but less so when there are already some intermediate sites. The effect of additional sites increasing reproductive values depends on environmental variability. In less variable environments (low σ), adding intermediate sites has hardly any effect because the onsets of spring occur at their long-term averages; yet, the more variable an environment is, the more helpful are intermediate sites in predicting conditions ahead (electronic supplementary material, figure S2).

The number of intermediate sites has consequences for the timing of departure from the starting site, staging at intermediate sites and arrival times at the breeding site (figure 4). At low to intermediate landscape ρ, migrants depart increasingly earlier from the starting site when there are more intermediate sites and stay increasingly longer on intermediate sites as they successively obtain information on sites ahead and, if required, wait for the onset of spring on the successive site. Ultimately, this leads to a larger spread in arrivals between years with more sites at intermediate landscape ρ. By contrast, for non-stop migrations, for very low or very high landscape ρ, arrivals at the breeding site occur within a very confined period.

Figure 4.

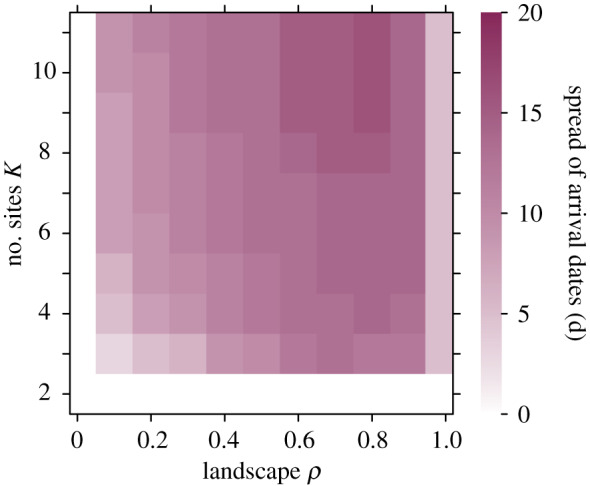
Temporal spread of arrival dates at the destination site as dependent on landscape ρ and the number of sites. Intensity of colours indicates the length of periods (days) over which around 80% of arrivals occur, i.e. lighter colours show a more confined arrival period and darker colours spread-out arrivals. Arrivals are almost invariably at the same day at extreme values for landscape ρ (e.g. ρ = 0 or ρ = 1) and for non-stop migrations (K = 2), and for these, increasing ρ or K has no effect. By contrast, for values of landscape ρ between these extremes, increasing the number of sites leads to a more spread-out arrival. (Online version in colour.)

(c). Importance of predictability on specific sites

Introducing an ‘information barrier’—a much lower predictability between two sites than between the others—showed that information is not equally valuable at all sites: ρ(k) on sites close to the destination was generally more important than ρ(k) at earlier sites (figure 5). Particularly, a barrier on the penultimate site was highly influential for departure and arrival times—it delayed departure from the starting site and advanced arrival at the last site—and was clearly detrimental for fitness (reduced reproductive values), while no such effects appeared when a barrier was inserted between any of the earlier sites.

Figure 5.

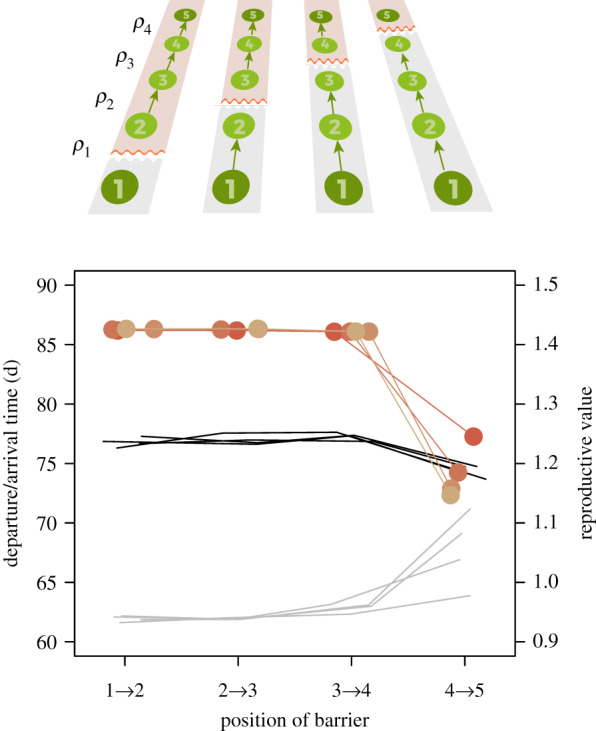
If there are gaps in predictability, i.e. the correlation between two specific sites is lower than the correlation between other sites, the position of such barriers appears to be crucial for departure from starting site (grey lines) and arrival at destination (black lines) as well as for reproductive values (coral-red dots and lines): while barriers hardly matter early in migration, they can substantially reduce reproductive values when they occur close to the destination. Line colours from light to dark coral-red depict barriers with a ρ(k) of 0.7, 0.5, 0.3 and 0.1, respectively, compared to ρ between all other sites of 0.9. (Online version in colour.)

4. Discussion

Our model has important implications for understanding the timing of migration in environments that differ in variability and predictability. Generally, we predict that information on distant conditions is particularly important in variable environments and before the ‘final’ stages (i.e. those with the strongest fitness-consequences). Furthermore, we suggest that using intermediate sites is a strategy for obtaining information in variable environments or in those that are relatively uninformative. These predictions have implications that particularly concern environmental predictability along major migration routes and their consequences for the timing of migration, the capacity of migrants to respond to changes in phenology and the use of intermediate sites as sources of information. Although some of these predictions and implications remain to be fully scrutinized in future investigations, several are already supported by earlier studies (see below).

Our model makes a few important assumptions: first, if the onset of spring in one site is predictive of that on the next site, then the relationship between the onsets of spring on the sites is specified by the joint probability distribution. For simplicity, we assumed that this joint distribution is bivariate normal and thus, specified by their means, variances and correlation [4] but, of course, other joint distributions are possible.

Second, we assume that mortality decreases in spring and thus, that arrival before the onset of spring poses a significant mortality risk. A lower survival has indeed been found for early-arriving individuals in long-distance migrant birds [3] but the relationship between the timing of arrival (in the breeding grounds) and survival has only been investigated in a few studies and even less for the timing of stop-over site use. We think that this relationship will certainly apply to temperate or Arctic regions, i.e. regions with a strong seasonality [7], where resources only become available in the course of the season but will perhaps be less pronounced in tropical or subtropical regions.

Thus, although we think that these assumptions are generally justified, deviations in specific empirical migration systems might exist and could be incorporated in an adjusted model.

(a). Predictability in real environments

Environmental variables are often spatially and temporally correlated and thus, conditions at distant places can, in principle, be predicted from afar. The strength of correlations typically decreases with distance, i.e. the closer two sites are, the better can conditions be predicted [6]. Applied to migrations, this means that for short-distance migrants, correlations between wintering and breeding sites are expected to be stronger than for long-distance migrants [15]. Consequently, short-distance migrants are better able to predict phenology on breeding sites from their wintering sites and thus, have a higher capacity for ‘correctly’ timing migrations under phenological deviations from long-term averages [16]. By contrast, wintering and breeding grounds of long-distance migrants are much farther apart and typically far less or not correlated. In such cases and in support of our predictions for no-correlation, long-distance migrants depart on a fixed day irrespective of the deviations from the average onset of spring in the wintering site, e.g. [17], and often fail to adequately respond to phenological changes [16,18,19]. However, when long-distance migrants approach their breeding sites, they should be increasingly better able to predict the advancement of spring and adjust migratory progression as correlations become stronger with the remaining shorter distance. Indeed, such behaviour has been found in Palaearctic-African migratory birds that adjust migration speed or migratory progression in the Mediterranean in response to the advancement of spring in Europe [20,21].

However, correlations are rarely only distance-dependent but vary between habitats [22], ecosystems and topographies. Locations within one climatic zone or regions that are under the influence of large-scale climatic phenomena, e.g. Southern Oscillation, North-Atlantic Oscillation [23], are probably more similar and thus, more predictable, than landscapes that are separated by physical barriers like mountain ranges, deserts or stretches of the sea that interrupt existing correlations [23]. Migrants often avoid crossing barriers and use detours instead, i.e. they deliberately fly, walk or swim longer distances than the shortest possible route [24]. Although reasons for taking such detours have been brought forward [25], another reason could be that making detours (or using additional stop-overs, see below) can be beneficial if such a longer route provides more information than a shorter one and yields clear fitness benefits by syncing the timing of arrival with local phenology. However, if barriers cannot be avoided, e.g. for birds migrating from sub-Saharan non-breeding to European breeding grounds, and migrants cannot predict conditions ‘behind’ the barrier, they migrate on a fixed day, using an invariable cue such as photoperiod [5]. Once behind the barrier, information may become available and migrants may wait out the progress of the season and adjust arrival to local phenology [26].

Although most studies that investigate the consequences of climatic/phenological changes on migrants implicitly assume a relationship between migration distance and predictability, a formal quantification of climatic connectivity and thus, predictability, across major migration routes (similar to [27]) is still lacking. Calculating predictability across the world would allow us to compare major migration routes with regard to their environmental information content and the possibility for migrants to predict phenology on distant sites [13]. Repeating such analyses over the past decades could identify whether uneven climate changes have altered existing correlations and whether these changed correlations could be one causative factor in the population trends of migrants [28]. Furthermore, such analyses could also identify environments in which memory of resource phenology would be expected to be a successful strategy [29,30].

(b). Intermediate sites as information sources

Similar to making detours, using intermediate sites can be important for obtaining information on conditions ahead. Indeed, many migrants use intermediate staging sites even if it was energetically possible to migrate non-stop (e.g. in ungulates [31] or birds [32–34]). According to our results, we predict that migrants with at least a few stop-over sites should be less affected by changes in phenology than those migrating non-stop [35]. This seems to be empirically supported in, e.g. Arctic-breeding geese, of which many populations and species cope with climate change very well [36]; yet, non-stop migrating Brent geese (Branta bernicla hrota) arrive at their Arctic-breeding sites out of sync with local phenology (phenological mismatch), and consequently, are one of the few goose species with currently declining populations [37]. Of course, how many stop-over sites are ultimately used will be governed by refuelling needs but also by a trade-off between the benefit of obtaining information and the costs of staging, e.g. a higher predation risk because of unfamiliarity in a novel environment [38] or the morphological adjustments from locomotion to digestion [39].

If—as we predict—stop-over sites are also used for obtaining information, they might be ‘strategically chosen’ and located at places where information is advantageous or where they increase predictability. For instance, although purely speculative at this point, shorebirds show a variety of skip, jump or hop migration patterns [34,40,41] that differ between populations at different geographical places and may be shaped by the need for acquiring information.

However, we also found that information is not equally important across all sites—information becomes particularly valuable close to the destination. Thus, we expect migrants to use stop-over sites close to breeding locations to assess the progress of spring at their breeding sites. Such a pattern has indeed been found in birds migrating from African non-breeding to European breeding sites and stopping over in the Mediterranean. For instance, semi-collared flycatchers (Ficedula semitorquata) stayed three times longer (15 days instead of 5) in the Mediterranean basin in a year with a cold spell in Europe before proceeding to eastern Bulgarian breeding sites [21].

Our results contribute to a better understanding of the relationship between environmental predictability and the timing of movements [13], showing how different levels of information shape migration strategies and how environments differing in variability and number of stop-over sites modify these. Such a better understanding of the relationship between information and movement is important for assessing the consequences of large-scale climatic changes that may shift phenologies [35], change environmental variability and disrupt existing correlations [4], including changes in correlations from human structures and activities, e.g. supplemental feeding or sensory pollution through anthropogenic light and noise [42,43].

(c). Beyond migration: information and the timing of life-history transitions

A variety of life-history transitions exist that are conceptually similar to migration in that they are escapes from seasonally or periodically varying conditions and that their success also highly depends on timing, e.g. timing of flowering in plants determines expected fruit set [44,45], emergence-time from hibernation determines reproductive success in bats [46] and timing of diapause stages in killifish influences survival [47]. Similar to the predictions that we derived for the timing and success of migrations, we predict several general patterns for the timing of other transitions. First, in more variable environments, we expect ‘safe’ strategies, i.e. strategies that enhance long-term fitness, even at the expense of short-term fitness benefits, particularly in longer-lived organisms with more than one reproductive bout. Such safe strategies might include to react only to very strong, reliable cues—those with high predictability. For instance, the different levels of spring predictability across North America, Europe and East Asia explained the differences in leaf-unfolding strategies in their woody floras: in regions with high variability, woody species have higher winter chilling requirements and need longer periods above a certain temperature threshold to start to leaf-out compared to species in regions with lower variability [48].

Second, in more variable environments, we expect transitions with more intermediate stages—which provide flexibility in the timing of life-history stages [49]. An interesting example is the diversity of annual cycles and the number of intermediate stages in killifish (Cyprinodontiformes), which live in ephemeral aquatic habitats that range from stable and predictable to stochastic and unpredictable [47]. Depending on the predictability and uncertainty of their specific environment, killifish can enter up to three diapause stages before hatching and thereby, halt development at multiple points, which favours hatching at an appropriate time and complete development as false-starts are largely avoided.

Thus, the role of information in the timing of transitions under environmental variability seems to be an over-arching phenomenon across species and taxa. Naturally, various strategies exist for obtaining and using information depending on specific environments and species. However, using intermediate stages is such a general strategy as well as basing decisions on strong, reliable environmental signals before the transition that bears the strongest fitness-consequences.

Data accessibility

This article has no additional data.

Authors' contributions

S.B., J.M.M. and Z.B. conceived the idea, J.M.M. developed the model, Z.B. developed the programming code, S.B. ran and analysed scenarios. S.B. wrote the manuscript with input from the co-authors.

Competing interests

We declare we have no competing interests.

Funding

Z.B. was financed by the Higher Education Institutional Excellence Program (NKFIH-1150-6/2019) of the Ministry of Innovation and Technology in Hungary, within the framework of the FIKP-DE Behavioral Ecology Research Group thematic program of the University of Debrecen. S.B. received funding through the 2017–2018 Belmont Forum and BiodivERsA joint call, under the BiodivScen ERA-Net COFUND programme from the Swiss National Science Foundation (grant no. SNF 31BD30_184120), the Belgian Federal Science Policy Office (grant no. BelSPO BR/185/A1/GloBAM-BE), the Netherlands Organisation for Scientific Research (grant no. NWO E10008), the Academy of Finland (grant no. aka 326315) and the National Science Foundation (grant no. NSF 1927743).