Variability in electrophysiological properties and conducting obstacles controls re-entry risk in heterogeneous ischaemic tissue

Abstract

Ischaemia, in which inadequate blood supply compromises and eventually kills regions of cardiac tissue, can cause many types of arrhythmia, some life-threatening. A significant component of this is the effects of the resulting hypoxia, and concomitant hyperklaemia and acidosis, on the electrophysiological properties of myocytes. Clinical and experimental data have also shown that regions of structural heterogeneity (fibrosis, necrosis, fibro-fatty infiltration) can act as triggers for arrhythmias under acute ischaemic conditions. Mechanistic models have successfully captured these effects in silico. However, the relative significance of these separate facets of the condition, and how sensitive arrhythmic risk is to the extents of each, is far less explored. In this work, we use partitioned Gaussian process emulation and new metrics for source-sink mismatch that rely on simulations of bifurcating cardiac fibres to interrogate a model of heterogeneous ischaemic tissue. Re-entries were most sensitive to the level of hypoxia and the fraction of non-excitable tissue. In addition, our results reveal both protective and pro-arrhythmic effects of hyperklaemia, and present the levels of hyperklaemia, hypoxia and percentage of non-excitable tissue that pose the highest arrhythmic risks.

This article is part of the theme issue ‘Uncertainty quantification in cardiac and cardiovascular modelling and simulation’.

1. Introduction

The sheer diversity of cardiac diseases, and the functional or anatomical changes that they cause, and especially their multifaceted interactions, make it very difficult to understand how their specific manifestation will impact on the delicate electrical signalling process that controls the heart. Nevertheless, the particular combination of ischaemia and micro-structural heterogeneity is highly correlated with dangerous arrhythmias, as seen in conditions such as hypertrophic cardiomyopathy [1], hypertensive heart disease [2], myocardial infarction [3] and arrhythmogenic right ventricular cardiomyopathy [4]. Variant and unstable angina also produce regions of injury that are highly heterogeneous due to obstruction by fibrotic, necrotic and adipose tissue [5,6], and the recurrence of ischaemia in these conditions is also associated with ventricular arrhythmia [7].

Ischaemia, a lack of sufficient oxygen due to restricted bloodflow to cells, triggers a number of self-protective measures in cardiac myocytes. Hypoxia triggers the activation of previously dormant ion channels to conserve energy [8], cell surroundings are acidified [9], and increased potassium ion efflux combined with the lack of bloodflow results in their accumulation in the extracellular space, hyperklaemia [10]. However, although these measures may increase cell survival, they simultaneously cause a multitude of disruptions to typical electrophysiological behaviour [11], with pro-arrhythmic consequences [12,13]. This leads to a delicate balance between protection of ischaemic tissue and the maintenance of healthy electrical signalling that must be treated with care. Further complicating the issue is variability, intersubject or otherwise, that presents itself in cardiac ischaemia as it does in most (if not all) physiological and biological systems [14]. These matters have significantly hampered efforts to treat the arrhythmogenic consequences of ischaemia, through what might otherwise appear to be compelling pharmacological targets [8].

Given the difficulties of exploring ischaemia’s pro-arrhythmic effects in the experimental setting, computational studies have proven very important in furthering understanding [15]. Furthermore, due to the ease of control over physiological properties in silico, computational approaches are particularly well suited to studies of variability [16], motivating the development of techniques in cardiac modelling that explicitly take it into account [17,18]. The electrophysiological manifestation of ischaemia in in silico populations of cells exhibiting variability has been thoroughly considered [19–21], although such an approach has apparently not been extended to tissue in the ischaemia context. Analyses of how changes in severity of individual components of ischaemia (hyperklaemia, hypoxia and acidosis) affect spiral wave stability [22] and the dynamics of fibrillation in realistic ventricular anatomies [23,24] have consistently implicated hyperklaemia as a critical stabilizing factor.

Less considered, however, is how variation in the severity of ischaemia (and its constituent electrophysiological impacts) controls the initiation of arrhythmia. Although many computational studies have demonstrated mechanisms of arrhythmia initiation due to ischaemia/infarction (for example [25–28]), the sensitivity of these mechanisms to different manifestations of the condition is far less clear. Studies that have considered the issue have suggested that for macro re-entry through an ischaemic region, hyperklaemia is most critical [29], whereas for re-entries residing within heterogeneous tissue, hypoxia is most important [30]. Understanding these dependencies in detail is critical for informing anti-arrhythmic treatment.

In this study, we focus on the latter mechanism, namely ‘micro’ re-entries formed within heavily heterogeneous tissue [31]. Such a phenomenon has been observed in both atrial [32] and ventricular [33] preparations, as well as clinically [34,35]. These re-entries can then serve as points of focal activation, potentially triggering arrhythmia through premature ventricular complexes or ectopic beating originating from ischaemic regions of the heart [36–38]. We concentrate on re-entries initiated by a single stimulus [39], that is without requiring a carefully timed premature systole or fast pacing. Making use of an optimized cardiac simulator leveraging graphical processing units [40], we generate a relatively large amount of data regarding the effects of hypoxia, hyperklaemia and acidosis upon re-entry initiation in heterogeneous ischaemic tissue. Making use of our recent method for partitioned emulation [41], we then carry out an exhaustive analysis of how these different components of ischaemia govern the propensity for such re-entries, informing the dependence on different manifestations of the condition (or similarly in computational studies, different choices regarding how it is modelled).

2. Methods

(a). Modelling ischaemia at cellular level

Acute ischaemia was modelled by modifying the reduced ten Tusscher (TT3) model of human ventricular myocytes [42] to incorporate the primary electrophysiological impacts of hypoxia, hyperklaemia and acidosis, in the fashion established in the literature [11,30,43]. Briefly, hypoxia was incorporated by a reduction in the intracellular concentration of adenosine triphosphate (ATP), which affects the cell model through activation of an additional outward potassium current $I_{K(\mathrm{ATP})}$ and modulation of the conductance of I_Ca,L. Hyperklaemia was incorporated by increasing the extracellular concentration of potassium, [K⁺]_o. Acidosis was incorporated by reducing the conductance of the L-type calcium and fast inward sodium currents (g_CaL and g_Na, respectively), shifting the Nernst equilibrium potential for sodium, V_mod, and decreasing the intracellular potassium concentration, [K⁺]_i .

Variability in ischaemic remodelling was explored through parameters representing the separate extents of the components of ischaemia, θ_hypox, θ_hyper and θ_acid. These were linked to the parameters of the ionic model by deciding upon a set of reference values representing significantly progressed ischaemia, defining these as a 100% contribution of that component (k = 1), and varying the ionic model parameters linearly over the ranges quoted in table 1. A set of 1000 different combinations of these three parameters was selected via Latin hypercube sampling [45], for which information was generated via direct simulation in the fashion described below.

Table 1.

Implementation of variable ischaemic remodelling. Ionic model parameters modified in ischaemia were allowed to vary uniformly in a range from a set of base values to values a little beyond an established set of ‘ischaemic values’ taken from literature [44]. The multiple electrophysiological impacts of pH changes in the cardiac myocyte were varied together, according to a single parameter representing the extent of acidosis, θ_acid.

parameter	model parameter	base value (θ = 0)	ischaemic value (θ = 1)
θhypox ∈ [0, 1.25]	${[\mathrm{ATP}]}_{\mathrm{i}}$	5.4 mM	2.6 mM
θhyper ∈ [0, 1.25]	[K+]o	5.4 mM	10 mM
θacid ∈ [0, 1.25]	Vmod	0.0 mV	3.4 mV
	[K+]i	138.3 mM	125.0 mM
	$g_{Na\hspace{0.17em}(\mathrm{factor})}$	1.00	0.75
	$g_{Ca,L\hspace{0.17em}(\mathrm{factor})}$	1.00	0.75

(b). Cardiac fibre simulations

In order to explore the electrophysiological impacts of ischaemic remodelling separate from the effects of structural tissue heterogeneity we later consider, we first simulated action potential (AP) propagation along one-dimensional fibres of tissue. This was modelled using the monodomain model,

$$\begin{array}{rl}& \chi C_m\frac{\mathrm{\partial }V}{\mathrm{\partial }t}=\mathrm{\nabla }(\sigma \mathrm{\nabla }V)-\chi I_{\text{ion}}(V,\mathbf{\text{s}})\\ \text{and}& \frac{\mathrm{\partial }\mathbf{\text{s}}}{\mathrm{\partial }t}=\mathbf{\text{f}}(V,\mathbf{\text{s}}),\end{array}\}$$ 2.1

with V the membrane potential, σ = 5.336 × 10⁻⁵ mS μm⁻¹ the conductivity tensor, χ = 0.14 μm⁻¹ the surface-to-volume ratio and C_m = 100 pF μm⁻² the tissue capacitance. The ionic model determines the flow of ions in/out of the cell, I_ion, in terms of a set of state variables s updated by a set of strongly nonlinear functions f. The specific definitions of these terms is given by the ischaemia-modified TT3 model described above.

Equation (2.1) was integrated using an efficient GPU-based parallel cardiac solver [40]. Although this particular solver can handle non-uniform and non-conforming adaptive meshes, here a regular mesh of a single layer of hexahedral volumes with side length 100 μm was used. A semi-implicit finite volume discretization was used, with the Rush–Larsen method used to integrate the ordinary differential equations for the state variables [46]. Both methods used a time discretization of Δt = 0.02 ms. Fibre was paced at 1 Hz until rest state (membrane potential and state variables) changed by less than 1%. Properties of the AP and its propagation were then measured, including wavelength (WL, calculated as the product of AP duration, APD, and conduction velocity, CV), rest potential V_rest and AP amplitude.

Re-entries can form in heterogeneous tissue due to the phenomenon of source/sink mismatch, in which conduction block is caused by an imbalance between the number of excited cells at the wavefront (the source of depolarizing current) and the number of cells awaiting excitation just beyond it (the sink for current) [47]. This effect can produce unidirectional block without repolarization heterogeneity, thus permitting re-entry from only a single stimulus, as we use here. We, therefore, sought to investigate the effects of ischaemic remodelling on the susceptibility to this effect in a manner divorced from the complexly heterogeneous tissue formed by diffuse fibrosis in those simulations.

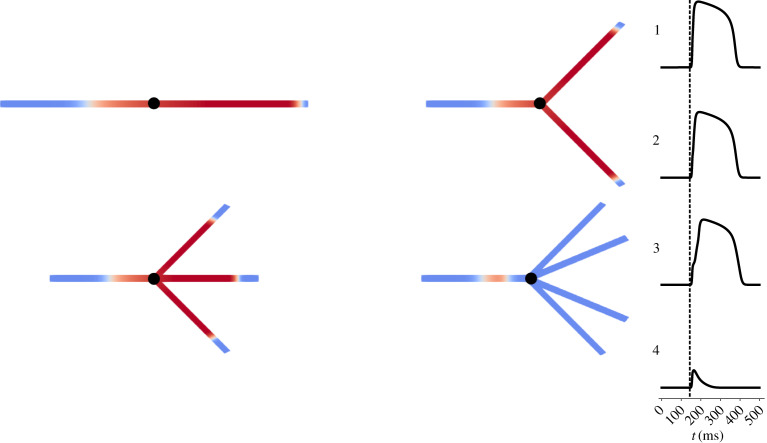
To achieve this, we subjected APs propagating in one-dimensional fibres to different levels of source/sink mismatch using a fixed set of meshes, in which the fibre split into multiple identical fibres as shown in figure 1. Depending on the severity of the reduction in excitability due to electrical remodelling, propagation differentially succeeded or failed for the cases of bifurcation, trifurcation and quadrifurcation, as well as exhibiting variable amounts of activation delay in the cases of successful propagation. This information was then combined into a single measure that quantified the susceptibility to conduction block, S, calculated as

$$S=1-\frac{1}{2}({\text{e}}^{-{\alpha }_2({\tau }_2-{\tau }_1)}+{\text{e}}^{-{\alpha }_3({\tau }_3-{\tau }_1)}),{\alpha }_m=\ln 2/\hspace{0.17em}\overline{({\tau }_m-{\tau }_1)}.$$ 2.2

Here, τ_m is the delay in activation for a fibre that splits in m directions, with failure to propagate represented by a delay value of infinity. Delays were scaled using the average delay for each scenario (subtracting ‘delay’ values for the first scenario representing the standard time required for conduction), $\overline{({\tau }_m-{\tau }_1)}$, and only the bifurcating and trifurcating cases in calculating this metric were used as these proved most indicative of the actual susceptibility to conduction block observed in the simulations of tissue slices with diffuse fibrosis. Success or failure of propagation for each mesh and combination of parameters was also noted, for use by the partitioned emulator (described subsequently).

Figure 1.

Tissue fibres with splits inducing variable extents of source/sink mismatch. A schematic demonstration of the meshes used to determine basic electrophysiological properties and the sensitivity to conduction block for different manifestations of ischaemic remodelling. In each case, an initial 2 cm cable allows excitation to reach a steady travelling pulse, which then encounters a split into some number of identical cables, also 2 cm in length. Note that the meshes pictured only represent an illustration of the graph structure, and that in each case the fibre splits into a number of geometrically equivalent fibres despite how the diagrams appear. An example simulation is shown, with failure to propagate through a quadrificated fibre and successful propagation in the other three scenarios. Time courses are plotted at the point marked in black, showing also the delay in activation experienced in the trifurcated fibre. (Online version in colour.)

(c). Simulations in heterogeneous ischaemic tissue

The potential for arrhythmia induction was tested in a two-dimensional (4 cm × 4 cm) slice of tissue, with ischaemic remodelling alongside structural heterogeneity. This heterogeneity was created by selecting 100 μm × 100 μm areas of active tissue at random, replacing them with inert, non-conducting tissue. This resulted in tortuous paths of conduction, as has been observed in cases of ischaemia that generate fractionated electrograms [48].

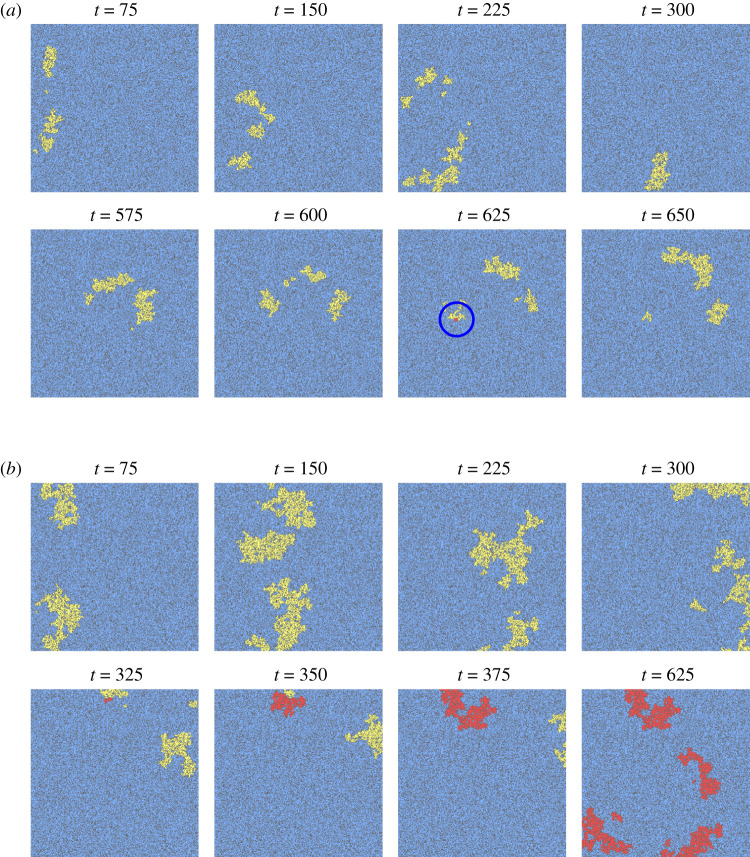
Of the 1000 combinations of parameters (θ_hypox, θ_hyper, θ_acid) simulated in one-dimensional fibres, 200 that successfully propagated were selected to be tested for re-entry in heterogeneous two-dimensional tissue. Three unique realizations of scar tissue with three different proportions of fibrotic sites, ϕ = 33%, 36% or 39% were simulated for each, resulting in 1800 tissue simulations in total. These values for ϕ were chosen by considering the levels of diffuse fibrosis for which micro-re-entries had been observed under hypoxic conditions in our previous work [49]. Two such simulations are presented as an example in figure 2, one that demonstrates a minor re-entry event that quickly terminates due to further conduction block, and another that initiates a sustained micro-re-entry potentially capable of acting as an ectopic pacemaker.

Figure 2.

Two simulations of a single wave of excitation passing through ischaemic tissue, one of which develops into a sustained re-entry. Fibrosis is coloured in dark grey, with unexcited tissue in blue, and tissue with membrane potential above rest in yellow (first activation), or red (subsequent activations). (a) An unidirectional block event does allow a small number of sites to be multiply activated (blue circle), but low excitability results in further conduction blocks that terminate the re-entry (local re-entry in table 2). (b) When tissue excitability is higher, the re-entry that begins to form persists and proceeds to repeatedly re-activate the tissue (sustained re-entry in table 2). Parameters used were (a) θ_hypox = 0.8283, θ_hyper = 0.6742, θ_acid = 0.0599 and (b) θ_hypox = 0.8098, θ_hyper = 0.0253, θ_acid = 0.7024. Diffuse fibrosis had proportion ϕ = 0.39 in both cases. (Online version in colour.)

Tissue simulations were run until all activity died out, or a simulation time of t = 1000 ms was reached. Re-entry was detected by considering the proportion of multiply activated sites, with re-entries further classified as local, transient or sustained according to the criteria presented in table 2. Simulations that did not exhibit re-entry were classified as either propagating or non-propagating, according to whether excitation successfully penetrated into the fibrotic tissue. For each simulation, the number of conduction block events was determined by searching for neighbouring sites that exhibited a difference in activation times above a threshold (5 ms). Additionally, the wavelength (WL) at all activated sites was estimated by finding the closest site that was repolarizing at the moment of activation. WL values reported for simulations in fibrotic tissue slices are the mean of these values, discounting any sites where WL could not be measured (for example, if no repolarization events had occurred yet) as well as those falling within the leftmost 30% of the tissue to prevent corruption due to the effect of the stimulus.

Table 2.

Classification of the broad behaviour observed in the simulations of excitation in ischaemic tissue with fibrosis.

classification	criteria
non-propagating	excitation failed to propagate 75% of the way into the tissue, or failed to propagate in a one-dimensional cable
propagating	excitation successfully propagated 75% of the way into the tissue, and less than 0.1% of activated sites recorded a second activation
local re-entry	excitation successfully propagated halfway into the tissue, and between 0.1% and 2.5% of activated sites recorded a second activation
transient re-entry	more than 2.5% of activated sites recorded a second activation, but excitation did not persist until t = 1000 ms
sustained re-entry	more than 2.5% of activated sites recorded a second activation, and excitation persisted until t = 1000 ms

(d). Emulation for simulator interrogation

Gaussian process (GP) emulation, very popular in fields such as engineering design [50], replaces simulations of prohibitive runtime with the predictions of a statistical model, fit to a provided set of training data [51]. Here, we use GP emulation to avoid the computational cost of running simulations to steady state in fibres, and then connect these predictions to the simulations of re-entry induction in two-dimensional, heterogeneous tissue. Specifically, a separate emulator was constructed for each of the different AP properties (APD, CV and so on), including the block susceptibility S (2.2), using the values of these quantities for the simulated 1000 parameter combinations as training and test data. These emulators provide very rapid prediction of these quantities for other combinations of parameter values, used both to carry out a global sensitivity analysis and to make predictions regarding parameter values that pose a risk of re-entry in heterogeneous tissue.

GPs are a type of non-parametric regression, assuming no set form for the response surface of each quantity of interest. This desirable property gives GP emulation the flexibility to predict the outputs of many different types of simulation, as well as enabling uncertainty quantification that does not make the assumption of linearity invoked by many other types of sensitivity analysis [17]. However, a type of structure is imposed by the choice of a GP’s covariance function, which typically (including here) enforces the property that small variations in parameter values result in relatively small variations in the value of the predicted quantity. This is not quite appropriate in this setting, however. There exists a critical threshold of excitability, below which propagation fails and quantities of interest cannot be calculated. The block susceptibility (2.2) can also show rapid variation, when the threshold for propagation failure occurs in one of the split fibre scenarios (figure 1) and the corresponding delay jumps to infinity. For these reasons, we make use of the partitioned GP emulation technique presented recently by some of the authors [41], in which the distinct regions of the parameter space separated by these transitions are emulated separately.

The separate regions were identified by noting how many of the four split fibre scenarios exhibited conduction block for each set of parameters simulated. These observations then served as the training data for a basic multi-class classifier based on support vector machines (created using Matlab’s fitcecoc function). This classifier, here denoted $\mathcal{C}(\mathit{\theta })$, then selects which GP emulator to use to predict the quantities of interest at that location in parameter space. Mathematically, this can be described

$$y_{\text{pred}}(\mathit{\theta })=\sum _{i=0}^4{\mathbb{1}}_{\mathcal{C}(\mathit{\theta })=i}\hspace{0.17em}{\mathbf{\text{K}}}_i^{\ast T}{\mathbf{\text{K}}}_i^{-1}{\mathbf{\text{y}}}_i.$$ 2.3

That is, a prediction for a quantity of interest y_pred for a set of parameters θ is generated by first evaluating the classifier model, then taking the mean value of the GP trained to the set of data falling within that classification, y_i, which has covariance matrix between training data points K_i and covariance between training data points and prediction point(s) K*_i. Elements of these matrices are defined by the GP’s covariance function, here the Matern-3/2 covariance with automatic relevance determination (further details in electronic supplementary material, also see [51]). GP training was carried out by the Matlab function fitrgp.

Our approach to emulation treated each quantity of interest independently, ignoring correlations between them. Although more complex methods that explicitly take these correlations into account do exist [52], we note that if a set of independent GPs successly learn the functions y_j = f_j(θ) defining the response surfaces for each individual quantity of interest, then these GPs have also necessarily learned the correlation between those quantities. Expressed a different way, although the emulators are constructed assuming no covariance between quantities of interest, the covariance as predicted by the functions learned by these GPs,

$$\text{Cov}(y_i,y_j)={\int }_{\mathit{\theta }}{f}_i(\mathit{\theta })f_j(\mathit{\theta })\hspace{0.17em}\text{d}\mathit{\theta }-{\int }_{\mathit{\theta }}{f}_i(\mathit{\theta })\hspace{0.17em}\text{d}\mathit{\theta }{\int }_{\mathit{\theta }}{f}_j(\mathit{\theta })\hspace{0.17em}\text{d}\mathit{\theta },$$

will not necessarily be zero.

We use emulators to take very large numbers of Monte Carlo samples, improving the calculation of sensitivity indices, namely Sobol indices and their corresponding main effects [41,53,54]. The main effect of a parameter θ_i on a quantity of interest y provides information on how that quantity depends on that parameter after variance due to the changes in the other parameters is removed (averaged out). It is calculated by

$$y_{\text{me}}({\theta }_i)={\int }_{{\theta }_{\sim i}}y({\theta }_1,{\theta }_2,\dots )\hspace{0.17em}\text{d}{y}_{{\theta }_{\sim i}}\approx \frac{1}{N}\sum _{j=1}^{N}y({\xi }_{1j},{\xi }_{2j},\dots ,{\theta }_i,\dots ,{\xi }_{nj}),$$ 2.4

with θ_∼i denoting the set of parameters other than θ_i and ξ_mj denoting the jth sample value for parameter θ_m used in approximating the integral via Monte Carlo integration. Here, we again use Latin hypercube sampling as a space-filling design to select these sample points uniformly across the domain of integration. The main effects are functions of a single variable (the parameter for which sensitivity is being considered), and may be plotted by repeating the calculations (2.4) for a series of values of that parameter across its range of interest.

3. Results

(a). Potential for micro re-entry induction in heterogeneous ischaemic tissue

Significant (transient or sustained) re-entries were not commonly observed, with only 2.5% of the 1800 simulations considered resulting in sustained re-entry, and a further 0.5% in transient re-entry. Figure 3 shows these data, including parameter combinations for which propagation was assumed to fail in heterogeneous tissue because it also failed in the less demanding case of a single cardiac fibre. The highest level of diffuse fibrosis strongly facilitated re-entry, with 70.4% of the observed re-entries (any type) having ϕ = 0.39. This is further evidence for the importance of tortuous paths created by fibrosis near the percolation threshold [30,39]. High levels of hypoxia were also very strongly associated with re-entry, with all but two re-entries having θ_hypox > 0.7. Weak values of hyperklaemia could also be associated with re-entry, but this is predominantly due to the propensity for propagation to fail altogether as hyperklaemia worsened. Acidosis appears to be the least important component of ischaemia. Re-entries that rapidly terminated (‘local’ re-entries) were typically observed close to the boundary where propagation begins to fail. No obvious distinction in terms of the parameters could be drawn between transient and sustained re-entries.

Figure 3.

Parameter combinations and levels of diffuse fibrosis (ϕ) for which re-entries were observed. Visualized are the projections of the data onto the two-parameter planes labelled, with a very slight jitter applied to the data in order to visualize the multiple results observed for each combination of ischaemic remodelling parameters and fibrosis levels. Crosses indicate parameter combinations for which propagation failed in heterogeneous fibrotic tissue (dark grey) or along a tissue fibre (light grey). Other markers represent simulations for which propagation was successful, leading to either no significant re-entry (blue dots) or a re-entry (diamonds) either local (green), transient (magenta) or sustained (red). High amounts of diffuse fibrosis and of hypoxia are both clearly linked to re-entry, whereas the dependence on hyperklaemia and acidosis is more complex. No obvious factor separates transient from sustained re-entries. (Online version in colour.)

(b). Wavelength and block susceptibility are informative of re-entry risk in ischaemic tissue

Micro-re-entry formulation in the heterogeneous tissue simulated depends critically and non-trivially on the precise realization of fibrotic obstacles. This poses a significant obstacle to understanding the effect of uncertainty in the parameters, as performing enough simulations to ‘average out’ the effect of structural heterogeneities is not plausible. Furthermore, previous studies considering micro-re-entry in similar tissue have seen very low but non-zero incidence rates of re-entry for a given manifestation of ischaemia and proportion of fibrosis [49]. Although we attempted to use emulation to predict how quantities of interest from the two-dimensional simulations (such as WL, and the extent of conduction blocks) depended on the components of ischaemia, noise in these measures introduced by the variability in the structural heterogeneity rendered this not successful.

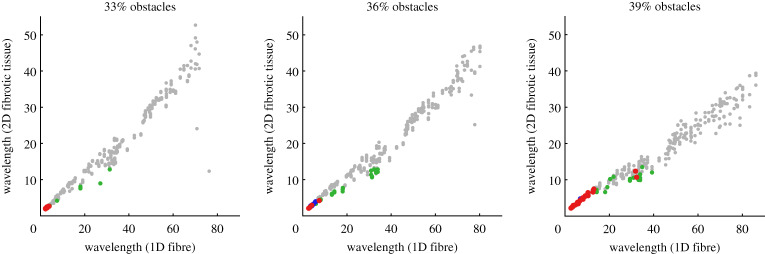
Instead, we consider how these critical features determining vulnerability to re-entry relate to analogous quantities measured in the one-dimensional simulations. WLs measured in a tissue fibre for different sets of electrophysiological parameters were found to relate strongly to mean WLs estimated for APs travelling through complex heterogeneous tissue in the two-dimensional simulations with the same parameters. This is especially pronounced when the observations for different extents of fibrosis ϕ are considered separately (figure 4). However, WLs estimated in obstructed tissue are consistently shorter than in cardiac fibres, owing to the combination of tortuous paths taken by excitation and the macroscopic estimation technique we use. More importantly, a short WL is seen to be a critical component of re-entry, with only very short WLs ever permitting transient or sustained re-entry for ϕ = 0.33 or 0.36. As the percolation threshold is approached (ϕ = 0.39), lengths of potential re-entrant paths become much longer, and the range of WLs that permit re-entry is larger. A very small number of cases with a WL greater than 3 cm in fibre resulted in re-entry, distinct from the remaining re-entries that all had WL less than 0.75 cm.

Figure 4.

Wavelength in fibre as a predictor of wavelength in scarred tissue, and of micro-re-entry risk. Each point corresponds to a different simulation in tissue with obstructions (three per set of parameters θ), for which the WL in a one-dimensional fibre of tissue with those parameters was also calculated. Points in grey, green, blue and red indicate no re-entry, local re-entry, transient re-entry, and sustained re-entry, respectively (definitions in table 2). Wavelengths in scarred tissue are lower than those measured in a one-dimensional fibre, due to the use of a macroscopic estimation technique that cannot track path length. Nevertheless, wavelengths calculated in simple fibre simulations are highly predictive, with an extremely clear correlation. Micro-re-entry initiation is seen to depend critically on a small wavelength, but with a threshold dependent on the proportion of obstacles due to its effect on path length. (Online version in colour.)

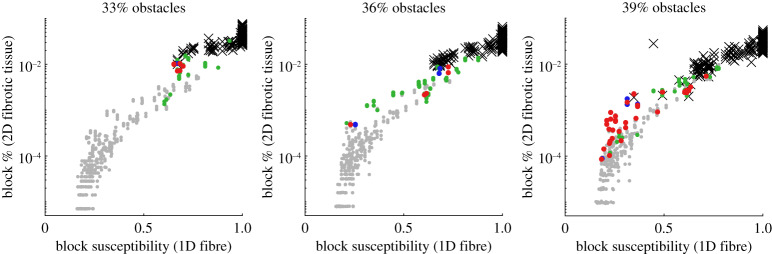
Our metric for susceptibility to conduction block S, calculated (2.2) using the results of AP propagation in the set of fibre split scenarios (figure 1), was seen to be highly correlated to the frequency of conduction block events observed in the simulations of obstructed, ischaemic tissue with the same electrophysiological parameters (figure 5). This correlation was strongest after the fourth one-dimensional fibre splitting scenario (quadrifurcation) was removed (as has been done in the provided form (2.2) for calculation of S), presumably because this represented an extent of imposed source/sink mismatch not typically realized in our heterogeneous two-dimensional structures. For each proportion of obstacles, there is seen to be a critical value of S beyond which propagation is certain to fail in the two-dimensional tissue. This threshold value lowers as the fraction of obstacles increases, owing to a reduced number of viable paths and thus greater risk of propagation failure. Only a very small window of S values close to where two-dimensional simulations started to block appears to permit re-entry for the lowest proportion of obstacles (ϕ = 0.33). On the other hand, the highest obstacle proportion (ϕ = 0.39) permits re-entry almost regardless of S, so long as susceptibility to block is not so strong as to cause propagation through afflicted tissue to fail completely.

Figure 5.

Our measure of block susceptibility, S, as a predictor of conduction block frequency in scarred tissue and risk of micro-re-entry. Each point corresponds to a different simulation in tissue with obstructions (three per set of parameters θ), for which the S value was also calculated using a set of one-dimensional simulations in different fibre split scenarios. Points in grey, green, blue and red indicate no re-entry, local re-entry, transient re-entry, and sustained re-entry, respectively, while black crosses indicate a failure to propagate (definitions in table 2). Susceptibility S measured in one-dimensional fibres correlates very strongly with the observed frequency of conduction block events in fibrotic two-dimensional tissue. Critical thresholds of susceptibility beyond which propagation consistently fails are seen, but depend on the proportion of obstacles. Furthermore, the windows of susceptibility that permit re-entry successively widen as the number of obstacles increases. Note that conduction block frequency in 2D is plotted on a logarithmic scale. (Online version in colour.)

(c). Emulation captures complex dependencies upon the components of ischaemia

With the relevance to re-entry risk of AP properties measured in tissue fibres now established, we explore how these properties depend on the individual components of ischaemia. Although many of these impacts have been previously explored (e.g. [11,43]), our far more exhaustive interrogation of the dynamics allows us to go beyond linear considerations of sensitivity. Furthermore, using our block susceptibility metric S, we are able to investigate how hypoxia, hyperklaemia and acidosis combine to determine the sensitivity to conduction block using a metric shown to relate to the amount of block observed in complexly heterogeneous tissue.

Using only 800 of the 1000 points of data from the one-dimensional fibre simulations as training data, the remaining 200 then serve as test data to validate our emulators’ predictions. After applying our partitioning approach to deal with parameter combinations that failed to propagate excitation, as well as rapid transitions in the block sensitivity, the emulators for all of the quantities of interest were found to serve as good surrogates for the actual dynamics (electronic supplementary material, figure S1). Importantly, there is no obvious bias towards under- or over-estimation in the emulator predictions. Additionally, a plot of the emulator predictions against the data for the two most important quantities of interest (WL and S) shows that their dependence on one another is also well replicated by their respective emulators (electronic supplementary material, figure S2).

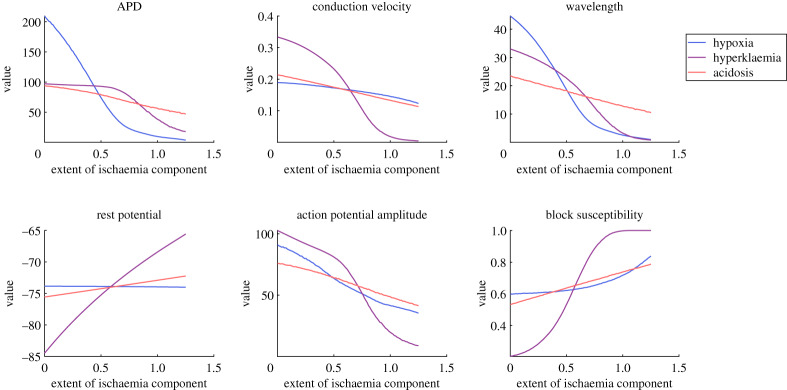
Using these emulators, we then constructed the main effects of hypoxia, hyperklaemia and acidosis via equation (2.4), shown in figure 6. These were calculated using the full range of the parameters, and thus included regions of the parameter space where ischaemia grew strong enough to completely block propagation and quantities such as APD or CV could not be measured. These undefined values were treated as zero for the purposes of equation (2.4), following the logic that quantities such as APD and CV are essentially zero when propagation fails. Although this may induce a small bias, we additionally varied the parameters over a smaller range that avoided any undefined values (electronic supplementary material, figure S3), observing almost the same set of dependencies on the ischaemia components that we now discuss.

Figure 6.

Main effects of the different components of ischaemia on excitation and its propagation in a cardiac fibre. Plotted trends represent the effect of that parameter on the quantity of interest, accommodating for variation in the remaining parameters by averaging over its effects. Such a nonlinear approach nevertheless largely confirms the common understanding of the condition, namely the importance of hypoxia in APD shortening and hyperklaemia in decreased excitability. Block susceptibility is seen to depend most critically on hyperklaemia, and neither conduction velocity nor action potential amplitude serve as adequate substitute measures. (Online version in colour.)

The basic information provided by the main effects agrees with that previously established using simpler considerations of sensitivity [11,43], with hypoxia serving as the primary determinant of APD, albeit with a saturating effect for particularly low ${[\mathrm{ATP}]}_{\mathrm{i}}$ values. Hyperklaemia shows most control over CV, APA and V_rest, while acidosis exhibits only a minor effect (in the expected direction) on all of the measured quantities. A stronger effect of decreased pH in acute ischaemia has been seen to become apparent in the later stages of its progression (stage 1b) [43], here somewhat equivalent to 1 ≤ θ_acid ≤ 2.

Our conduction block measure S was found to depend most strongly on hyperklaemia, and less so on acidosis, owing to their relative contributions to tissue excitability. However, S exhibits a less obvious dependence on the extent of hypoxia. For weak hypoxia, the APD persists long enough to drive neighbouring tissue over the depolarization threshold, and thus changes in hypoxia level show little effect on excitability. However, when hypoxia is strong, APDs are short enough that they can potentially fail to provide sufficient source current. This results in a much stronger dependence of S on the level of hypoxia, and thus an overall nonlinear trend.

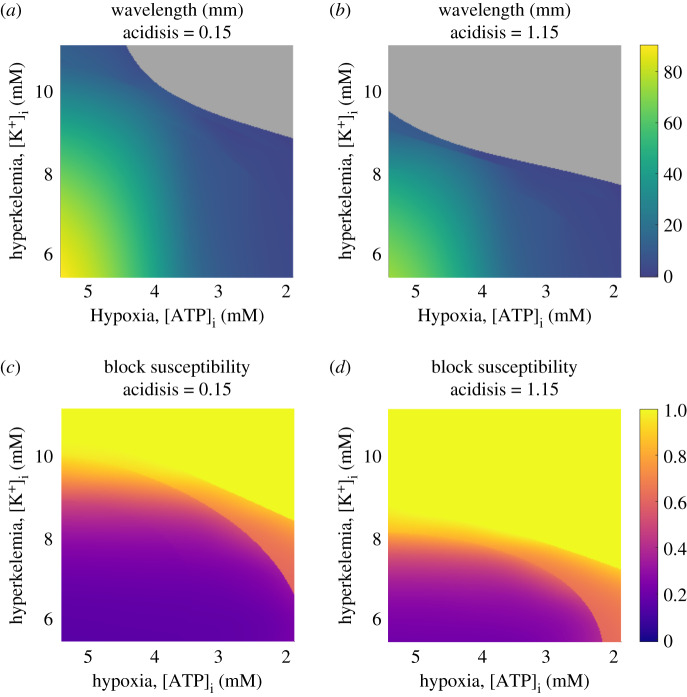
Our simulations in obstructed tissue slices demonstrated the importance of WL and propensity for conduction block as informing the risk of re-entry initiation, and we have also demonstrated the strong relation between these measures in two dimensions with the WL and S values calculated in cardiac fibres. In figure 7, we show how these two quantities depend on the different components of ischaemia, via two-dimensional slices through the parameter space for fixed values of the least important component (acidosis). As was also implied by the main effects, WL is seen to depend most strongly on hypoxia (decreased APD), but also decreases in response to increasing hyperklaemia (decreased CV) and acidosis (decreased APD and CV). The less pronounced effect of hypoxia as excitability weakens is also observed, with hypoxia and hyperklaemia demonstrating similar levels of effect in the case of strong acidosis. All three parameters play a role in determining whether propagation along a tissue fibre will succeed (grey regions in figure 7), with hyperklaemia playing the most critical role. We also note that despite the use of discontinuous emulators, the predicted surfaces of WL values are quite smooth, indicating that the emulation has correctly matched emulator predictions across partition boundaries in order to correctly capture the response surface of this smoothly varying quantity.

Figure 7.

Precise dependence of the key properties for arrhythmia risk upon the most important components of ischaemia, hypoxia and hyperklaemia. Shown are the predictions of the partitioned emulators, along two slices through the three-dimensional parameter space using fixed (low and high) extents of acidosis. Grey regions mark those where the emulator predicts no wavelength as excitation is expected not to propagate. (a,b) For low acidosis, wavelength depends most strongly on hypoxia, but in the high acidosis case, both hypoxia and hyperklaemia have similar levels of effect. Even after ischaemic remodelling worsens and the wavelength is significantly decreased, large regions of the parameter space still permit propagation at low wavelength values. (c,d) Susceptibility to block depends most critically on hyperklaemia, and to a lesser extent on hypoxia. Increased acidosis compensates weakly for both of the other components. Sharp transitions in S value correspond to critical excitability thresholds where excitation begins to fail to propagate through one of the split fibre scenarios, and are not an artefact. Recall that S = 1 denotes a failure to propagate in the bifurcated fibre, but may still permit propagation in a regular fibre (compare to regions in grey). (Online version in colour.)

By contrast, the susceptibility to block does not vary smoothly. Transitional regions in the parameter space are clearly evident, where the value of S jumps at the moment propagation fails in either the bifurcated or trifurcated fibre. Similar to the conditions for conduction failure in a traditional fibre, block in the split fibres is modulated most strongly by hyperklaemia, as the primary determinant of tissue excitability. When hypoxia is weak, increasing hyperklaemia (or acidosis, but with a weaker effect) results in increased activation delay (smooth transition in S values in figure 7). When hypoxia is strong and source current becomes limited, propagation simply either succeeds or fails, resulting in sharp transitions in S.

(d). Emulation identifies the types of ischaemic remodelling at risk of re-entry

For the 200 parameter combinations trialled in obstructed tissue slices, three realizations of obstacle patterning were used at each of the three obstacle proportions ϕ we have considered. This proved sufficient for identifying a moderate number of re-entries across the parameter space, but it would be too computationally demanding to generate enough data to fully explore the parameter space, and/or to thoroughly investigate each combination of parameters across many different pattern realizations. Given the complexity of the underlying dynamics that we have demonstrated (for example, sharp transitions in our measure of block susceptibility), and the insufficient data, it would also be naive to try to use the parameter values for which re-entry was observed to predict other manifestations of ischaemia that might be prone to re-entry.

Instead, we seek to predict other combinations of parameters that may permit re-entry in a manner that takes these dynamics into account. We have demonstrated that WL and S values measured in tissue fibres are strongly related to the analogous quantities in heterogeneous two-dimensional tissue, and that these measures inform the potential for re-entry formulation (figures 4 and 5). Given that our emulators successfully predict the dependence of WL in a tissue fibre and S on the parameters, we now use those emulator predictions to suggest further manifestations of ischaemia for which the electrophysiological dynamics are expected to permit re-entry.

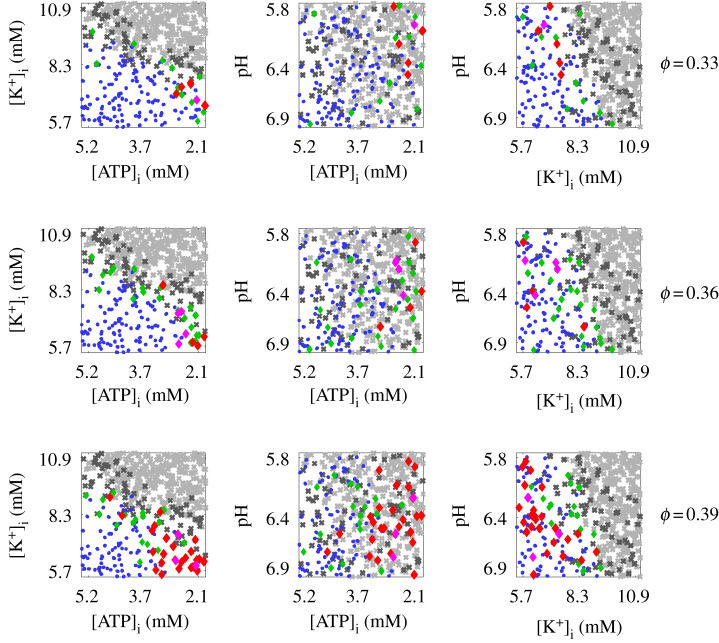
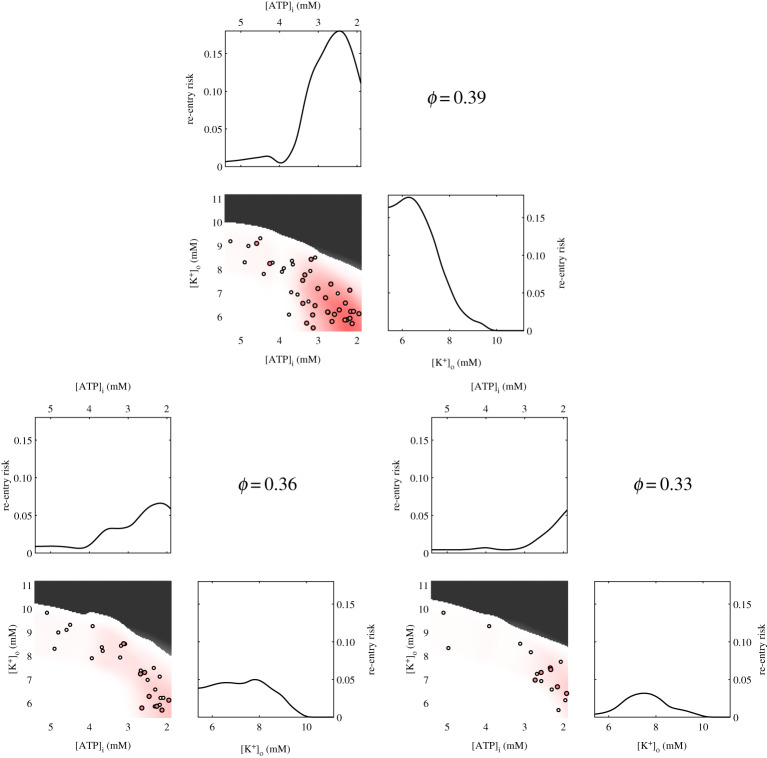
Specifically, we estimate the risk throughout the $(\text{WL},S)$ space by using a GP fit to the WL and S values for the observations from tissue simulations of re-entry, normal propagation or failed conduction (the categories in table 2). Transient and sustained re-entries are assigned a risk value of one, local re-entries are assigned a risk value of 0.2, and all other observations imply a risk value of zero, and risk is averaged over the three observations for each combination of parameter values and ϕ. The results of this process are shown in electronic supplementary material, figures S4–S6, and further details are provided in the electronic supplementary material. This approach is rather like a smoothing of the data that allows observations of re-entry to also imply re-entry is likely for nearby combinations of WL and S, but in a manner such that observations of no re-entry also correctly serve to lower the risk (a risk value of unity then implies that all configurations of structural heterogeneity with that proportion of obstacles will produce transient or sustained re-entries). Figure 8 visualizes the relative levels of risk of re-entry associated with combinations of the two most important parameters (hypoxia and hyperklaemia) for the different values of ϕ. Visualizations of the other pairs of parameters are also provided in electronic supplementary material, figures S7–S9.

Figure 8.

Manifestations of ischaemic remodelling with the potential for re-entry. Shown are the marginals for re-entry risk obtained by integrating over the two remaining parameters, and a heat map of the dependence on the two most important parameters (extent of hypoxia and hyperklaemia), averaging over the third, acidosis. Depth of red indicates extent of risk. Grey marks regions predicted to block, with no significant risk predicted. For reference, the tissue simulation data showing transient or sustained re-entry (red circles) and local re-entry (white circles) is projected onto the same parameter space. (Online version in colour.)

Near the percolation threshold (ϕ = 0.39), re-entry depends on at least a moderate amount of hypoxia, owing to the requirement for a sufficiently low WL. As the proportion of obstacles decreases, the length of potential re-entrant paths becomes shorter and the threshold amount of hypoxia required for re-entry shifts higher. Although acidosis has minor effects on both WL and S, re-entry is predicted to be permissible for any extent of acidosis, regardless of ϕ (electronic supplementary material, figures S7–S9). Acidosis simply acts to slightly shift the permissible values of the two more sensitive parameters (predominantly hyperklaemia).

As the primary determinant of the amount of conduction block, hyperklaemia tends to act in a protective manner, precluding propagation through occluded tissue altogether when excitability is sufficiently reduced. However, the maximum permissible values for [K⁺]_o actually increase as ϕ increases, due to the relaxed restriction on WL values that permit re-entry. For the lowest obstacle density (ϕ = 0.33), [K⁺]_o values permitting re-entry are shifted away from control, as some extent of functional block is now required to compensate for the reduced number of obstacles and hence generate sufficiently tortuous paths of activation.

4. Discussion

Our study used a large number of simulations in two-dimensional slices of heterogeneous ischaemic tissue to investigate for the first time how the potential for re-entry initiation depends on both the precise extents of the components of ischaemic remodelling and the extent of non-conductive tissue. This addresses questions about intersubject variability in different manifestations of ischaemia, as well as uncertainty in the selection of parameter values used to represent the condition in silico. Furthermore, although we did not incorporate the dynamic progress of electrical remodelling in ischaemia [43] into our simulations, this process can be interpreted as a curve traced through the space of parameter values we have explored.

We have demonstrated that measurements taken from simulations in cardiac fibres (including a novel measure of susceptibility to block, S) are predictive of overall behaviour in heterogeneous ischaemic tissue, and then used these measurements to separate out the electrophysiological and structural effects on the potential for re-entry. A sophisticated emulation technique was used to predict the dependence of key properties of APs and their propagation on the different components of ischaemia, allowing us to conduct a nonlinear sensitivity analysis by calculating the main effects to a high degree of accuracy. Many of these effects were linear, and in agreement with previous studies [11,43], however, we have also demonstrated different patterns of behaviour for low and high extents of hypoxia, and quantified the relative importance of the three primary electrophysiological components of ischaemia on the susceptibility to conduction block (in both simple fibres and strongly heterogeneous tissue).

Our emulation also allowed us to generate plausible parameter maps of re-entry risk in heterogeneous tissue, as well as the likelihoods of successful/blocked propagation in such tissue. Our results implicate WL as the most critical component of re-entry formulation, given that even cases with a low frequency of block (and low S) still often exhibited the unidirectional block event(s) required for re-entry initiation. Only for the lowest ϕ value was a decrease in excitability seen to clearly increase propensity for re-entry, as this proportion of obstacles was no longer guaranteed to generate the required block through structural effects. On the other hand, block susceptibility does directly inform at which point re-entries will fail to develop due to a complete inability to propagate through the heterogeneous tissue. As such, high amounts of hyperklaemia, in fact, protect against re-entries situated in regions of heavily damaged tissue.

There are also several limitations to our study, that we address here in detail. Firstly, concerns of computational feasibility allowed us to only simulate a small number of realizations for each combination of ischaemia parameters and obstacle proportion ϕ. Our use of emulation to predict further regions of interest in the parameter space partially alleviates this issue, but more robust conclusions could, of course, be obtained with access to richer data. Variability introduced by different micro-scale realizations of obstruction is important—for example, our patient-specific study considering this used 500 biventricular meshes each with their own unique pattern of obstructions in order to thoroughly examine the effects of structural variability on re-entry dynamics [30].

We selected the reduced ten Tusscher et al. (TT3) ionic model for the human ventricular AP, which has been used in related studies both in reduced [49] and original [28] form. It is well established that predictions can change significantly between models, and in a context-dependent manner [55–57]. We have not explored to what extent our conclusions are model-independent. Additionally, some experimental and computational studies have suggested that acidosis may play an important role in intracellular calcium handling, potentially generating pro-arrhythmic delayed afterdepolarization events [58,59]. The simplifications adopted by the TT3 model prevent it from capturing these dynamics, and our results may underestimate the impact of acidosis during acute ischaemia.

In fact, the effects of ischaemia sit across multiple types of physics and multiple spatial scales that we have not taken into account. Hypoxia has been co-observed with oxidative stress, and this combination involves multiple scales of cellular metabolism and leads to further reduction of AP [60]. Recent studies have also explored the effects of the immune system during ischaemia, with a particular focus on macrophages and their coupling to myocytes [61], although there is no consensus on the most suitable approach. Fluid accumulates during ischaemia, and this myocardial oedema is also known to be pro-arrhythmic [62]. A recent study proposed a hydro-mechanical model describing oedema formation [63], although the mechanisms by which oedema affects cardiac electrophysiology remain to be further studied. Our study and its conclusions thus speak only to the electrical remodelling that occurs in direct response to ischaemia.

5. Conclusion

Our simulations exploring re-entry initiation in variably ischaemic tissue with structural heterogeneity make clear the complexity of the dynamics that underlie arrhythmic risk. Efforts to directly use this data to predict vulnerability to re-entry within a region of ischaemia, or the metrics we found to be predictive (macroscopic wavelength and frequency of conduction block events) proved unsuccessful, owing to the complex uncertainties that result from the combination of electrophysiological and structural variability. Instead, we have formulated an informative metric that can be calculated in simple simulations of cardiac fibres with fixed spatial structures, thus separating out the electrophysiological effects. Partitioned emulation was then able to predict the dependence of key electrophysiological properties upon the different components of ischaemia.

Through a sensitivity analysis making use of our emulator, we saw agreement with established knowledge regarding the basic impacts of hypoxia, hyperklaemia and acidosis but extended this by considering susceptibility to conduction block, via a metric we demonstrated to relate directly to the frequency of block events in complex two-dimensional structures. We additionally identified the subtle effects of different levels of hypoxia on this susceptibility to block. We then used the predictions of our emulator to identify manifestations of ischaemia that are expected to support re-entry, for different levels of obstruction in tissue. Excitation wavelength, along with the amount of obstruction emerged as the primary determinants of re-entrant risk. Susceptibility to conduction block could protect tissue by preventing excitation propagation, but at intermediate levels could compensate for lower amounts of structural heterogeneity, created re-entrant paths of sufficient length through functional block. In terms of the components of acute ischaemia, hypoxia and hyperklaemia both prove very important, with hypoxia the primary determinant of wavelength and playing the clearest role. Acidosis had only a minor effect, acting similarly to a weaker type of hyperklaemia in this context.

Data accessibility

Code to reproduce the results is available at https://github.com/betalawson.

Authors' contributions

B.A.J.L., R.S.O., L.A.B. and P.A.A.S. developed the codes and performed the simulations. B.A.J.L., R.W.S. and K.B. drafted the manuscript and analysed the data. B.A.J.L., R.W.d.S., K.B. and R.S.O. conceived and designed the study. All authors read and approved the manuscript.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by the Brazilian Government via CAPES, CNPq, FAPEMIG, UFSJ and UFJF, and by the Australian Government via Endeavour Research Leadership Award from the Department of Education, and ARC(CE-140100049). R.W.S. thanks the Isaac Newton Institute for Mathematical Sciences for support and hospitality during the ‘Fickle Heart’ programme.