A semiautomatic approach for prostate segmentation in MR images using local texture classification and statistical shape modeling

Abstract

Segmentation of the prostate in magnetic resonance (MR) images has many applications in image-guided treatment planning and procedures such as biopsy and focal therapy. However, manual delineation of the prostate boundary is a time-consuming task with high inter-observer variation. In this study, we proposed a semiautomated, three-dimensional (3D) prostate segmentation technique for T2-weighted MR images based on shape and texture analysis. The prostate gland shape is usually globular with a smoothly curved surface that could be accurately modeled and reconstructed if the locations of a limited number of well-distributed surface points are known. For a training image set, we used an inter-subject correspondence between the prostate surface points to model the prostate shape variation based on a statistical point distribution modeling. We also studied the local texture difference between prostate and non-prostate tissues close to the prostate surface. To segment a new image, we used the learned prostate shape and texture characteristics to search for the prostate border close to an initially estimated prostate surface. We used 23 MR images for training, and 14 images for testing the algorithm performance. We compared the results to two sets of experts’ manual reference segmentations. The measured mean ± standard deviation of error values for the whole gland were 1.4 ± 0.4 mm, 8.5 ± 2.0 mm, and 86 ± 3% in terms of mean absolute distance (MAD), Hausdorff distance (HDist), and Dice similarity coefficient (DSC). The average measured differences between the two experts on the same datasets were 1.5 mm (MAD), 9.0 mm (HDist), and 83% (DSC). The proposed algorithm illustrated a fast, accurate, and robust performance for 3D prostate segmentation. The accuracy of the algorithm is within the inter-expert variability observed in manual segmentation and comparable to the best performance results reported in the literature.

1. INTRODUCTION

Prostate cancer (PCa) is the most commonly diagnosed cancer among men in the United States [1]. It is the third leading cause of death from cancer with an estimated 26,730 deaths in 2017 [1]. Magnetic resonance imaging (MRI), due to its high image contrast for soft tissue structures, is one of the imaging modalities used in PCa diagnosis, staging, and treatment [2, 3]. T2-weighted MRI is superior to other MRI sequences for anatomy visualization [3]. Contouring of the prostate gland on T2-weighted MR images could assist with MRI-guided procedures used for PCa diagnosis and management [4]. However, manual delineation of the prostate border is a time-consuming task with high inter-observer variability [5, 6]. One solution to address these issues is to use computer-assisted segmentation algorithms.

There are several automatic, and semiautomatic segmentation techniques have been investigated and developed to perform prostate MRI segmentation faster and more reproducible compared to manual contouring [7–17]. Korsager et al. [10] presented an automatic segmentation algorithm based on atlas registration combined with intensity and shape information in a graph cut segmentation framework. Mahapatra and Buhmann [11] used a supervoxel-based image representation for segmentation of the prostate using supervoxel classification followed by a graph cut-based segmentation. Tian et al. [15, 16] also presented a superpixel-based segmentation algorithm for T2-weighted prostate MRI using 3D graph-cut for energy function minimization. Shahedi et al. [12, 13] developed a semiautomatic and an automatic segmentation algorithm for prostate segmentation based on local appearance and shape characteristics of the prostate border in endorectal T2-weighted MRI. Cheng et al. [8] developed deep-learning methods for segmentation of the prostate in T2-weighted MRI. They tested both a patch-based convolutional neural network and holistically nested networks for segmentation. Jia et al. [9] presented a coarse-to-fine segmentation technique based on atlas registration and deep learning.

There have also been some studies published for validation of the segmentation algorithms designed for prostate MRI [6, 18, 19]. Martin et al. [19] have presented a three-phase study to validate prostate segmentation on MR images. They compared a semi-automatic and an automatic segmentation approach to fully manual contouring regarding segmentation time and accuracy. They reported up to 49% relative timesaving for using automatic or semiautomatic segmentation compared to manual segmentation. Shahedi et al. [6] have conducted a multi-observer user study to investigate the prostate MRI segmentation repeatability and operation time after manual editing. They measured the required editing time to yield clinically acceptable MRI prostate segmentation and the inter-observer variability of computer-assisted segmentation after manual editing. They used multiple error metrics for segmentation accuracy evaluation. In 2012, the Medical Image Computing and Computer-Assisted Intervention (MICCAI) conference held a Prostate MRI segmentation (PROMISE12) challenge to compare the performance of the 11 segmentation algorithms involved in the challenge. All the algorithms were tested on the same dataset and evaluated using Dice similarity coefficient [20] (DSC), mean absolute distance (MAD), 95% Hausdorff distance [21] (HDist), and absolute relative volume difference (|ΔV%|) [18]. The results of these studies support this idea that for a more thorough evaluation of the algorithms more than one error metric might be required to quantify the segmentation accuracy.

Moreover, for a more comprehensive evaluation, the performance of each algorithm should be compared to the inter-expert observer variation in manual prostate border delineation. There are some published results in the literature about the inter-observer variation in the manual segmentation of the prostate in T2-weighted MRI [5,13]. Therefore, it is useful for a deeper understanding of the algorithm performance to take inter-observer variability into account for evaluation.

In this study, we present a learning-based semiautomatic algorithm for 3D segmentation of the prostate gland on T2-weighted MR images, based on the smooth globular shape of the prostate and the local image texture near the surface of the prostate. To evaluate the performance of the algorithm, we compare the algorithm segmentation with expert reference segmentation using a set of error metrics that measure surface distances, regional overlap errors, and volume differences. The main contributions of this work are: (1) A novel learning-based semiautomatic algorithm for segmentation of the prostate on MR images. (2) A local texture classification close to an estimated prostate surface to decrease the negative effects of image texture distortion caused by, e.g., cancer tumors. (3) A novel shape model developed based on the smooth globular prostate gland shape.

2. METHODS

2.1. Materials

Our MRI dataset contained 43, transverse T2-weighted MR images from 43 patients, which were acquired by 1.5 T and 3.0 T with three Siemens Magnetom imaging systems: Aera, Trio Tim, and Avanto. No endorectal coil was used for the data acquisition. The repetition time (TR) varies from 1000 ms to 7500 ms and echo time (TE) varies from 91 ms to 120 ms. The field of view for each image was 256 × 256 to 320 × 320 voxels with 0.625 mm, 0.875, or 1.0 mm in-plane voxel size and 1.0 mm to 6.0 mm slice spacing. We resampled all the images using Lanczos resampling (windowed sinc interpolation) to make the voxels isotropic. For each image, the prostate was manually contoured by two experienced radiologists.

2.2. Semiautomatic Segmentation

The proposed learning-based segmentation algorithm consists of training and test parts. Figure 1 shows the schematic block diagram of each part. The training and test components are explained in detail in sections 2.2.1 and 2.2.2, respectively.

Figure 1.

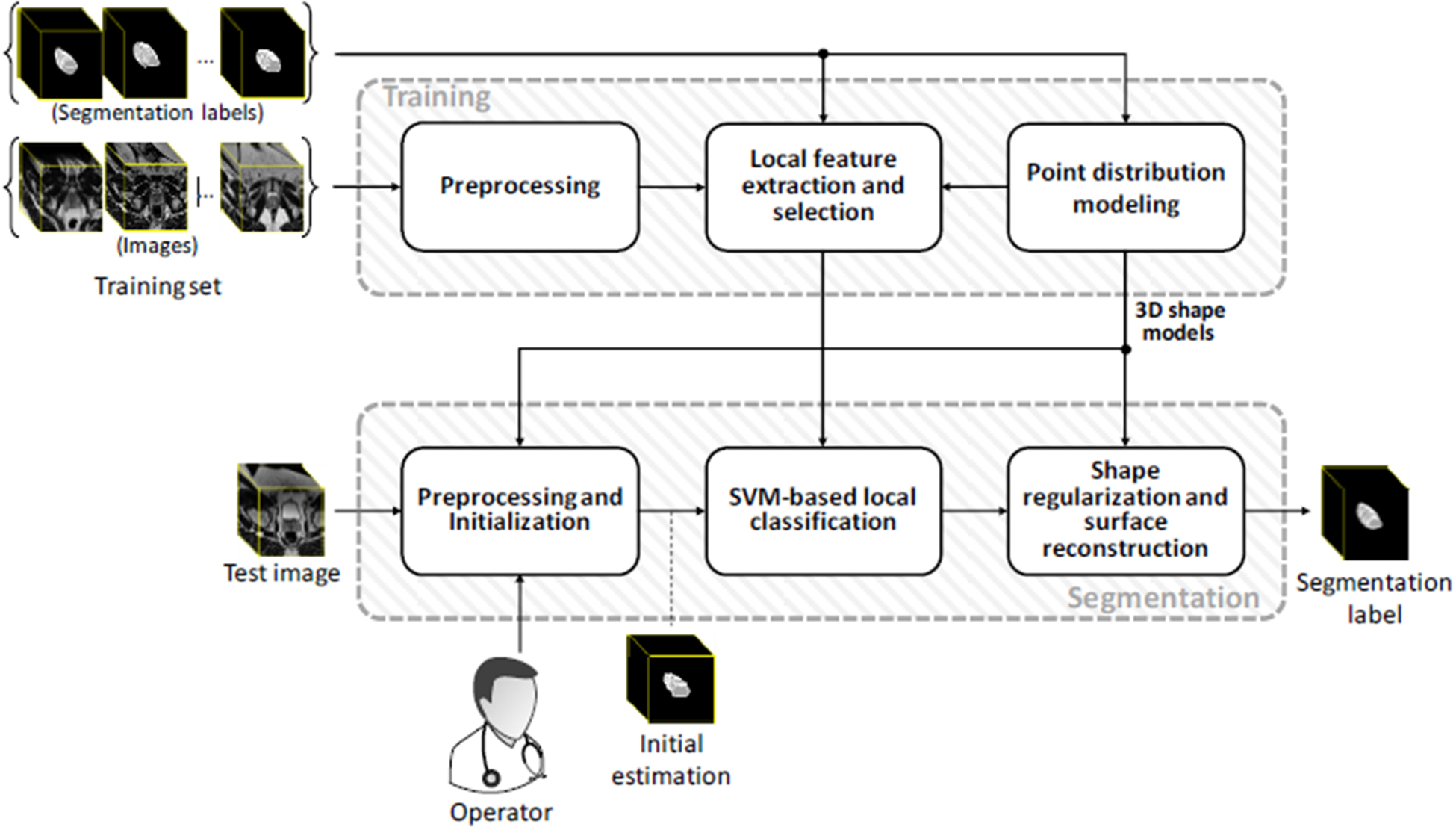
The schematic framework of the proposed segmentation method.

2.2.1. Training

We used a set of training images to extract a set of image texture features from the prostate surface area within each sector of the spherical space, separately. Then we selected the most discriminative features to train one classifier per sector. We also used the manual segmentation labels of the training image set to build two shape models for prostate; a low-density (LD) and a high-density (HD) point distribution model (PDM). These shape models were used for shape regularization and surface reconstruction at the final steps of the segmentation.

Preprocessing:

We rotated all of the training images about their inferior-superior axes to align the anteroposterior symmetry axes of the patients parallel to the anteroposterior axes of the images. The image intensities of MR images are highly related to the imaging setting and can vary from one scan to another. Therefore, to reduce the inter-scan inconsistency while preserving the image texture, we applied an intensity normalization that was limited to the window and level adjustment within the prostate region. The intensities of the other regions were adjusted accordingly. To decrease the effect of image noise we applied a 2D 3×3 median filter to all the 2D axial slices.

Shape modeling:

For a point distribution shape modeling we need to represent any shape in the training set as a series of surface landmarks. To select the landmarks on each prostate surface, we defined N equally spaced rays in 3D space, emanating from the centroid point of the prostate gland. Then we selected the N contact points between the rays and the surface of the prostate as the landmark set. Considering the centroid as the origin of the spherical coordinate system, we assumed all the landmarks with the same elevation and azimuth angles across the training set corresponding to each other. In our model each prostate shape is represented by the N surface point cloud plus the centroid point, yielding a set of N+1 points in total. Finally, all the shapes were aligned (translating, rotating and scaling) to a reference shape, using generalized 3D Procrustes analysis [22] and the mean square distance error metric. We built an LD PDM with N=86 and an HD PDM with N = 2056 equally spaced casted rays.

Local feature extraction:

For each of the 86 rays (R_i, i = 1,2,3,…,86) casted from the prostate centroid point (x_c, y_c, z_c) we selected a set of points (p_i) on the ray within a defined range around the corresponding prostate border landmark:

$${\mathit{p}}_{\mathit{i}}=\{(x,y,z)|r_{min}<r<r_{max},\theta ={\theta }_i\phi ={\phi }_i\},$$ (1)

where r, θ, and φ are radial, elevation, and azimuth coordinates of point (x, y, z) in a spherical coordinate system, respectively. r_min = r_b – d and r_max = r_b + d are the radial coordinates of the first and the last selected points on the ray, respectively, where r_b is the radius of the border landmark on the ray and d is the distance of the first and the last selected points from the border landmark. To keep our texture analysis limited to the local image textures near the prostate border, d should be relatively small compared to the gland dimensions (in this paper we defined d = 5 mm). θ_i and φ_i are, respectively, elevation and azimuth angles of points on the ith ray (R_i). θ_i and φ_i have constant values for all the points on the ray. Figure 2a illustrates the details.

Figure 2.

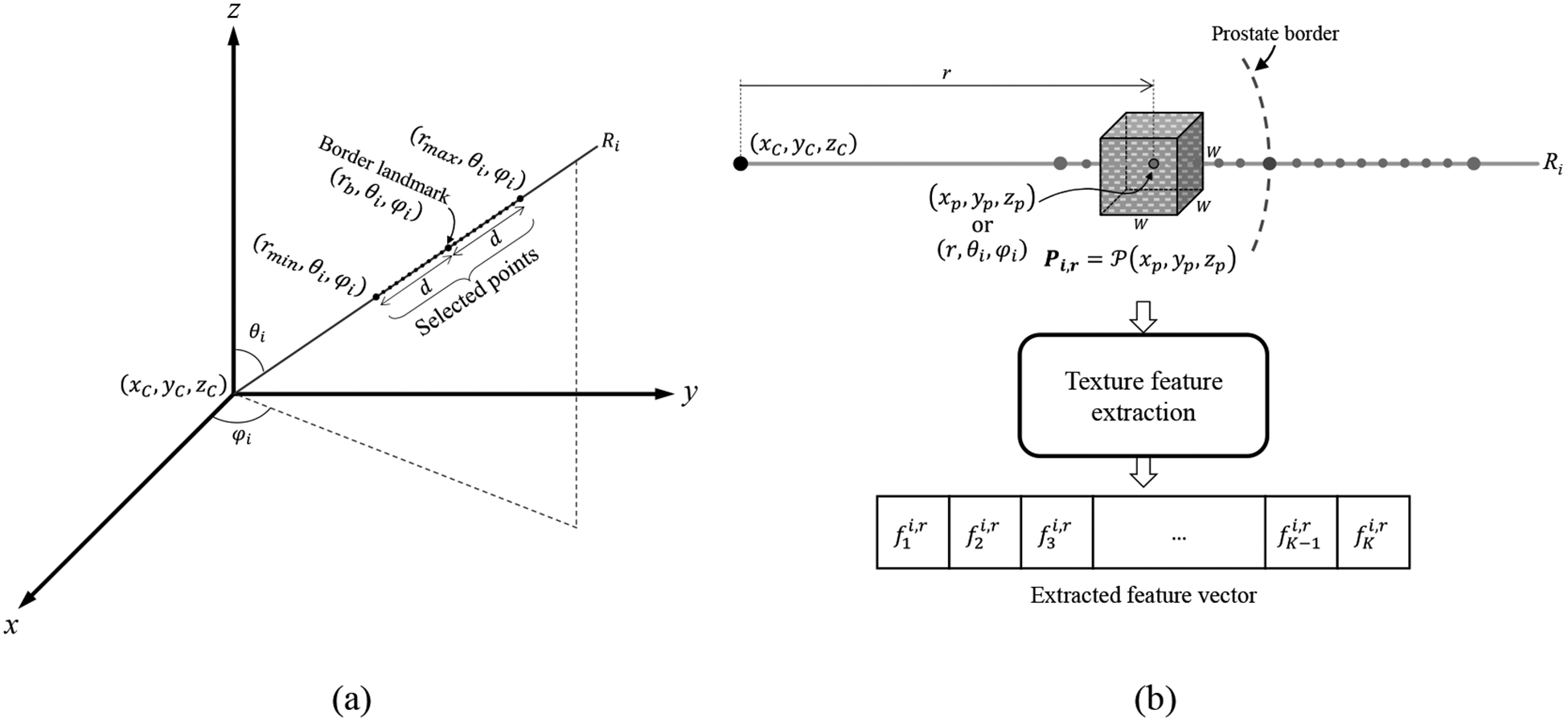
(a) A schematic illustration of the selected points on a sample ray (Ri) used for feature extraction. (b) A sample cubic image patch (P) centered on the ray point (x_p, y_p, z_p) and extraction of a vector of K = 67 texture features of the image patch.

We extracted the texture features within 3D cubic image patches centered on the selected points on the rays; see Figure 2b. For any (x_p, y_p z_p) point of the 3D image on ray R_i with spherical coordinates of (r,θ_i,φ_i) we defined the patch P_i,r of size W × W × W = (2D + 1) × (2D + 1) × (2D + 1) as:

$${\mathit{P}}_{\mathit{i},\mathit{r}}=\mathcal{P}(x_p,y_p,z_p)=\{(x,y,z)|x_p-D<x<x_p+D,y_p-D<y<y_p+D,z_p-D<z<z_p+D\}.$$ (2)

To have image patches that are small relative to the prostate gland size but large enough to contain 3D image patterns for texture analysis, we chose the fixed value of 5 mm for parameter D in this study.

For each of the selected cubic patches, we calculated a vector of 67 texture features that are listed in Table I. We assigned “prostate” or “one” label to those patches centered at a point inside the prostate gland, and “non-prostate” or “zero” to those patches centered at a point outside the prostate. For each patch, we also calculated the percentage of the patch voxels that are within the prostate (L_p).

Table I.

List of tested texture features and their descriptions.

Feature	# of features	Description
First-order features	10	Intensity of the voxel at the patch center, mean (μp), median (mP), standard deviation (σp), minimum, maximum, skewness [23], kurtosis [23], energy [23], and entropy [23] of a 3D patch intensity histogram. The first-order texture features are measured based on the histogram of the image, therefore the 2D implementations could be easily generalized for 3D input patches.
Histogram of oriented gradients (HOG)24	8	The distribution of intensity gradients. In this study, we formed HOG as a histogram of eight, 2D orientation bins. To obtain HOG for 3D patches, we calculated one histogram per 2D axial slice and measured the average of all the corresponding HOG bins to form one, eight-bin HOG.
Histogram of Local binary patterns (LBP)25	8	We calculated LBP in 3D within a 3×3×3 mask and formed one, eight-bin histogram per image patch.
Grey-level co-occurrence, matrices- based26 (GLCM)-based features	32	We defined GLCM for a 3D patch as the average of the GLCMs of all the 2D axial patch slices related to the same 2D pixel neighboring. In this study we measured GLCM-based features based on four 2D offsets, i.e. (−1,0), (0,−1), (1,−1), (−1,−1). The features consist of entropy, energy, contrast [23], homogeneity [27], inverse different moment [23], correlation [23], cluster shade [27], and cluster prominence [27] of the four GLCMs.
Mean gradient angle	1	For a 3D patch, we measure mean gradient angle as the average of mean gradient angles of all the 2D axial slices.
Edge-based features	8	We formed an eight-bin histogram of edge directions for a 3D patch. The edges are detected using Sobel operator [28] as an edge detector for all the 2D slices.
Total	67

Ray and feature selection:

We collected the feature vectors of all the image patches for all the 86 rays across the training images. Then for each of the 67 features, we made a set of feature values collected from all the similarly directed rays across the training set. We applied the two-tailed t-test [29] to detect the features with statistically significant differences (α=0.01) between prostate and non-prostate means (hereafter called “discriminative features”). For each of the discriminative features, we defined two threshold values (T_b and T_p); T_b was the feature value that all of the values below/above it belong to non-prostate patches and T_p was the feature value that all the values above/below it belong to prostate patches (see Figure 3).

Figure 3.

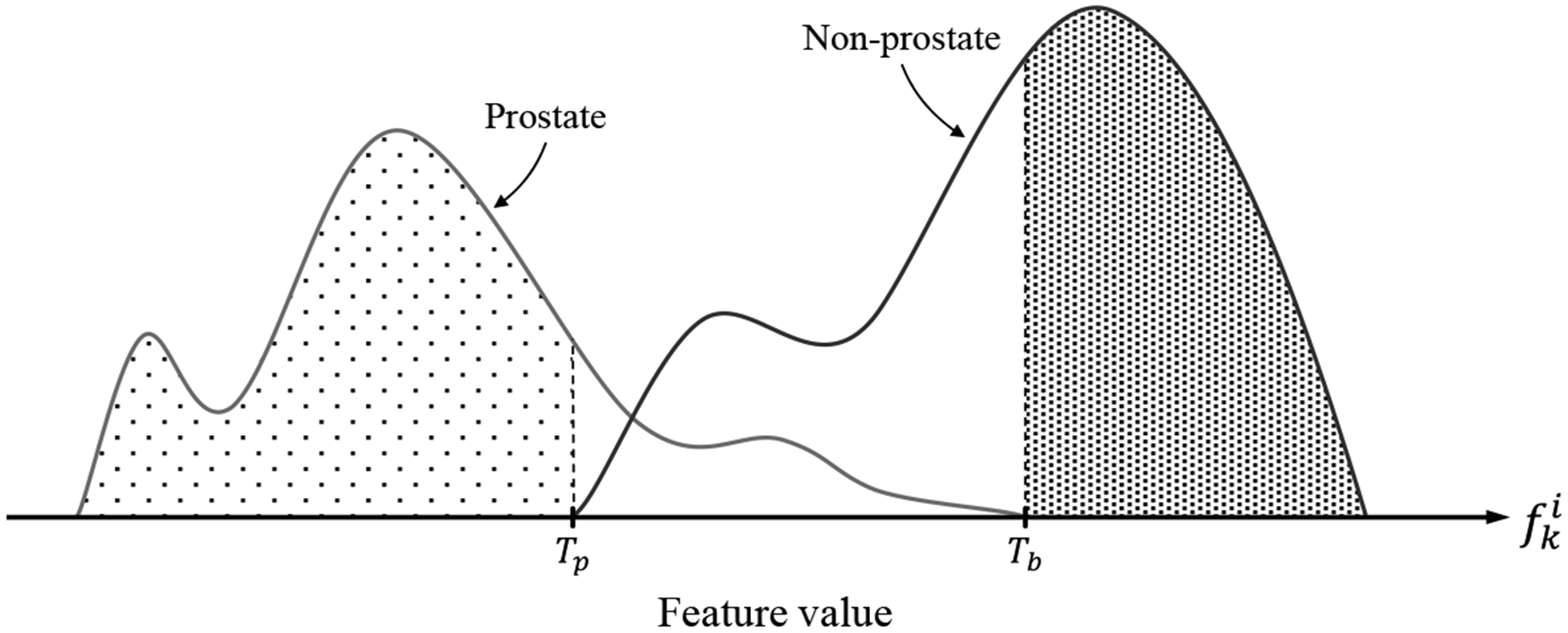
Histograms of feature values extracted from prostate and non-prostate image patches. T_b is the threshold level that all of the feature values above that belong to non-prostate patches, and T_p is the threshold level that the feature values below that belong to prostate patches. The feature values between T_b and T_p belong to either prostate or non-prostate patches.

To select a feature, we measured the monotonic correlation between each discriminative feature and L_p using Spearman’s rank-order correlation (ρ). For each ray, those discriminative features with high (ρ > 0.65) and statistically significant (p < 0.001) correlation coefficients were selected to be used for training a support vector machine [30] (SVM) classifier. The SVM classifier was used to classify between the prostate and non-prostate patches. Those rays with at least one selected feature were used for SVM training.

2.2.2. Testing

Preprocessing:

We applied a preprocessing to the test image similar to that used for the training images; i.e., anteroposterior symmetry axis alignment, image intensity normalization, and median filtering. For image intensity normalization we used initially estimated prostate surface explained below.

Manual initialization:

The operator first selected two points on the prostate tissues at the inferior-most slice (apex) and the superior-most slice (base). Then the operator selected 12 points on the prostate border on three, equally spaced axial slices between the defined apex and base slices; four points per slice, approximately at four, different sides (right, left, anterior, and posterior). Therefore, the total number of manually selected points (anchor points) is 14. We used the centroid of the anchor point set as an approximation for the prostate center. Similar to the training section we casted 86, equally spaced rays emanating from the centroid.

Initially estimated prostate surface:

We first find the nearest plausible shape in the LD model generated during training to the manually selected anchor points. For this purpose, we first used the casted rays to determine the 14 points in the LD PDM correspond to the anchor points. Then we used 3D thin-plate spline (TPS) analysis [31] and warp the model mean shape to the 14 anchor points to estimate the 72 missing points between the anchor points. This process yielded to a set of 86 points. To extract the representative PDM parameters for the point set, we aligned the estimated shape to the model mean shape using 3D Procrustes analysis. To find the nearest plausible shape within the model, we restricted each parameter to the range of $\left[-\sqrt{3}{\lambda }_k,\sqrt{3}{\lambda }_k\right]$ in which λ_k is the kth eigenvalue of the model that corresponds to kth parameter.

Local classification:

For each of the selected rays during training, we have a trained linear kernel SVM classifier that classifies patches to prostate and non-prostate ones, using the selected discriminative features for the ray. We searched for the prostate surface point on each of the test rays $(R_i^S)$ around the estimated surface point within the range of $\left[{\widehat{r}}_o-d_S,{\widehat{r}}_o+d_S\right]$ where ${\widehat{r}}_o$ is is the radial coordinate of the surface point in the spherical coordinate system, and d_s is the distance of the start and stop search points from the estimated surface point (Figure 4a). We selected a set of cubic image patches centered at the ray points within the defined search range. We measured the features for each patch and applied the corresponding threshold levels (T_b and T_p) obtained from the training section to the feature values to make obtained from the training section to the feature values to make the search range on the ray narrower. Then we apply the SVM classifier to the remaining unclassified image patches and classify them into prostate and non-prostate (Figure 4b). We shifted the initially estimated surface point to the boundary of prostate and non-prostate points after removing potentially singular labels within the search range (Figure 4c). Applying this process to all the selected rays yielded a set of candidate surface points.

Figure 4.

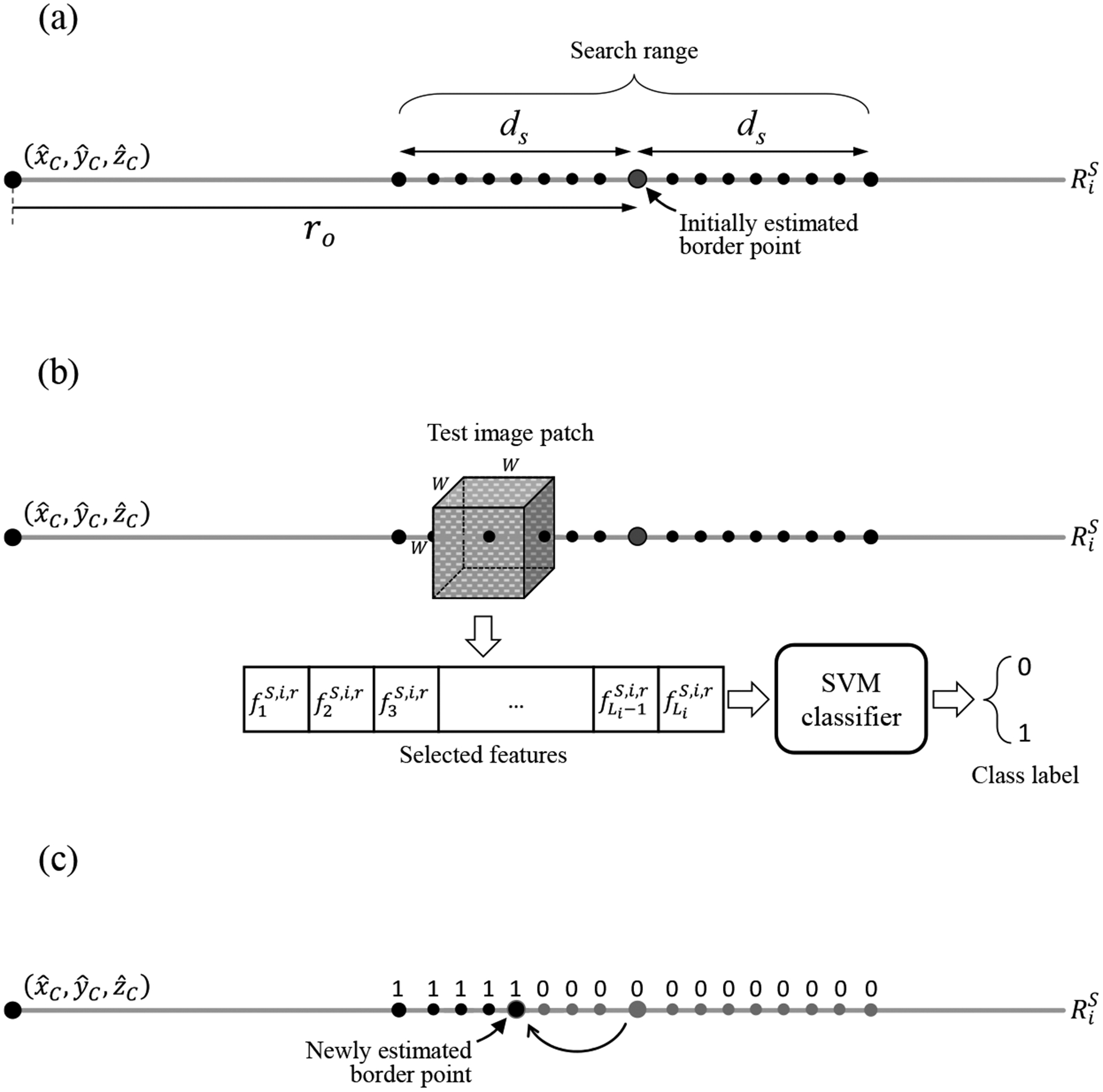
Local classification process. (a) Selected search points on a sample test ray $(R_i^S)$. $({\widehat{x}}_C,{\widehat{y}}_C,{\widehat{z}}_C)$ is the estimated prostate center point. (b) A sample cubic image patch centered at one of the ray points within the defined search range. The patch is classified based on an extracted vector of texture features containing the features selected for the test ray during training. (c) A new border point is estimated after classification of all the search points.

Shape regularization and surface reconstruction:

To regularize the segmentation, we first found surface points for those rays that were excluded during classification by using TPS warping of the LD mean shape to the estimated points. Then we applied the HD shape model to the estimated surface points followed by a scattered data interpolation [³²] to build a continuous surface out of the candidate surface points as the final segmentation label.

2.3. Evaluation

We evaluated our segmentation algorithm by comparing the segmentation results against an expert observer’s manual segmentations as the reference. We used a set of different types of error metrics containing DSC, precision rate (PR), recall or sensitivity rate (SR), MAD, HDist, and volume difference (ΔV). See references [13, 20, 21] for more details about metric calculations. In this paper, when we compared two manual references with each other, we reported the absolute value of the volume difference (|ΔV|). We applied the mentioned error metrics to the entire prostate gland, as well as three separate regions of interest (ROI), i.e., superior-most third (base subregion), the inferior-most third (apex subregion), and the middle third (mid-gland subregion) of the prostate.

3. RESULTS

3.1. Implementation details

We implemented the proposed segmentation algorithm no MATLAB 9.2.0 platform using a 64-bit Windows 7 desktop with a 3.0 GHz Intel Xeon central processing unit (CPU) and with 64 GB memory. To speed up the execution, we used MATLAB parallel computing toolbox to develop a parallel implementation of the algorithm. We ran the code on 12 CPU cores.

We used one of the manual segmentation reference (reference #1) for training the algorithm. We randomly selected two third of the images, i.e., 29 images, for training the algorithm. The remaining 14 images were used for testing the algorithm.

For feature extraction during training, we set d to 5 mm and for the search range during test, we set d_s to 7 mm. We also used patch size of 11 × 11 × 11 mm.

3.2. Inter-expert observer variability in manual segmentation

We compared the manual segmentation labels of the two expert observers to each other using our segmentation error metrics to measure the inter-expert observer variation in manual prostate border delineation. Table II shows the results.

Table II.

The average and range of inter-expert observer variability in manual prostate segmentation across the whole and the test dataset. Mean ± standard deviation of difference observed between two experts based on our metrics. Since both segmentation labels in each of the pairwise comparisons were from expert observers (i.e., lack of reference for MAD and signed ΔV calculation), the bilateral MAD (MAD_b) and absolute volume difference (|ΔV|) are reported in this Table. N_pat and N_Img are the number of patients and the number of test images, respectively.

ROI	NPat	NImg	MADb (mm)	HDist (mm)	DSC (%)	|ΔV| (cm3)	|ΔV| (%)
Whole Gland	14	14	1.5 ± 0.6	9.0 ± 3.1	83 ± 8	4.7 ± 3.9	22 ± 19
Apex			1.5 ± 0.6	7.7 ± 2.6	79 ± 11	1.8 ± 1.4	28 ± 24
Mid-Gland			1.3 ± 0.4	6.7 ± 1.8	89 ± 5	1.5 ± 0.6	17 ± 11
Base			1.8 ± 0.9	7.9 ± 3.1	79 ± 11	2.4 ± 1.8	31 ± 24

3.3. Segmentation algorithm accuracy and computation time

We applied the proposed segmentation algorithm to 14 test images using the first reference segmentation (reference #1) for both initialization and evaluation of the algorithm. Table III shows the quantitative results of the algorithm accuracy based on the error metrics. We did not detect any statistically significant (based on one-tailed t-tests; p < 0.05) error increase when the results of the table are compared to the difference between two experts reported in Table II. Figure 5 shows the qualitative segmentation results for three sample cases on five 2D slices per patient. Figure 6 illustrates the segmentation results for the same three sample cases in 3D. The average measured segmentation Execution time was 30 ± 9 s. per 3D image. We compared the segmentation performance of our algorithm to some of the most recent segmentation algorithms presented in the literature in Table IV.

Table III.

Quantitative segmentation accuracy of the proposed algorithm. Mean ± standard deviation of the error metrics for different ROIs. Twenty-nine images were used for training the algorithm. N_pat and N_Img are the number of patients and the number of test images, respectively.

ROI	NPat	NImg	MAD (mm)	HDist (mm)	DSC (%)	SR (%)	PR (%)	ΔV (cm3)	ΔV (%)
Whole Gland	14	14	1.4 ± 0.4	8.5 ± 2.0	86 ± 3	80 ± 6	93 ± 3	−3.7 ± 3.1	−17 ± 11
Apex			1.5 ± 0.6	7.6 ± 2.1	82 ± 6	76 ± 10	92 ± 6	−1.3 ± 1.8	−23 ± 20
Mid-Gland			1.3 ± 0.4	6.9 ± 2.2	90 ± 3	87 ± 7	93 ± 5	−1.0 ± 1.4	−9 ± 13
Base			1.3 ± 0.4	6.9 ± 2.1	84 ± 3	76 ± 6	94 ± 4	−1.5 ± 1.1	−24 ± 11

Figure 5.

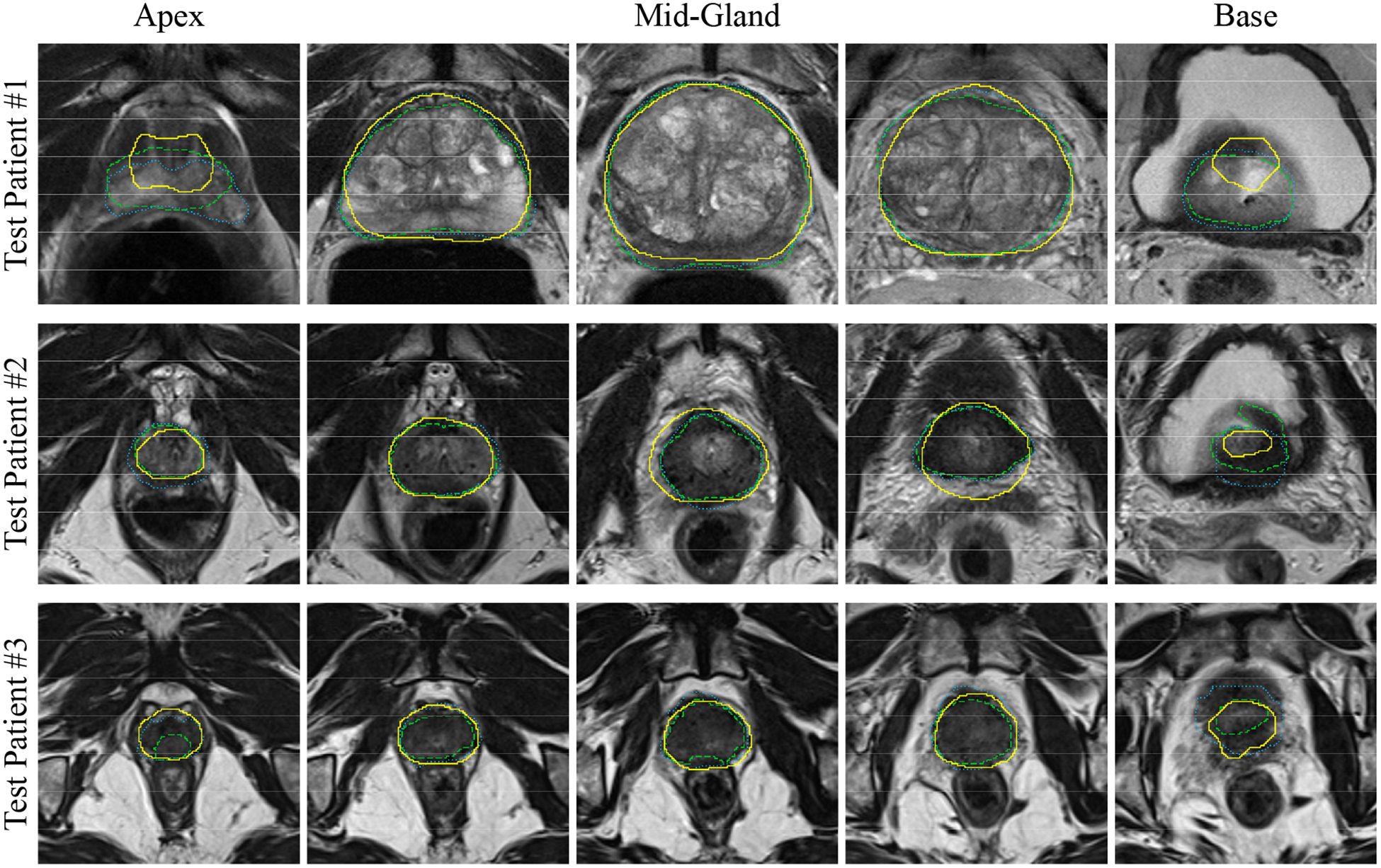
Qualitative segmentation results on five, 2D axial slices for three sample prostates. Each row shows the results for one patient. For each case, the left image is the inferior-most (apex) slices, and the right image is the superior-most (base) slice. The algorithm segmentation is shown with solid yellow contours; reference #1 is shown with dotted, blue contours; and the reference #2 is shown with dashed, green contours.

Figure 6.

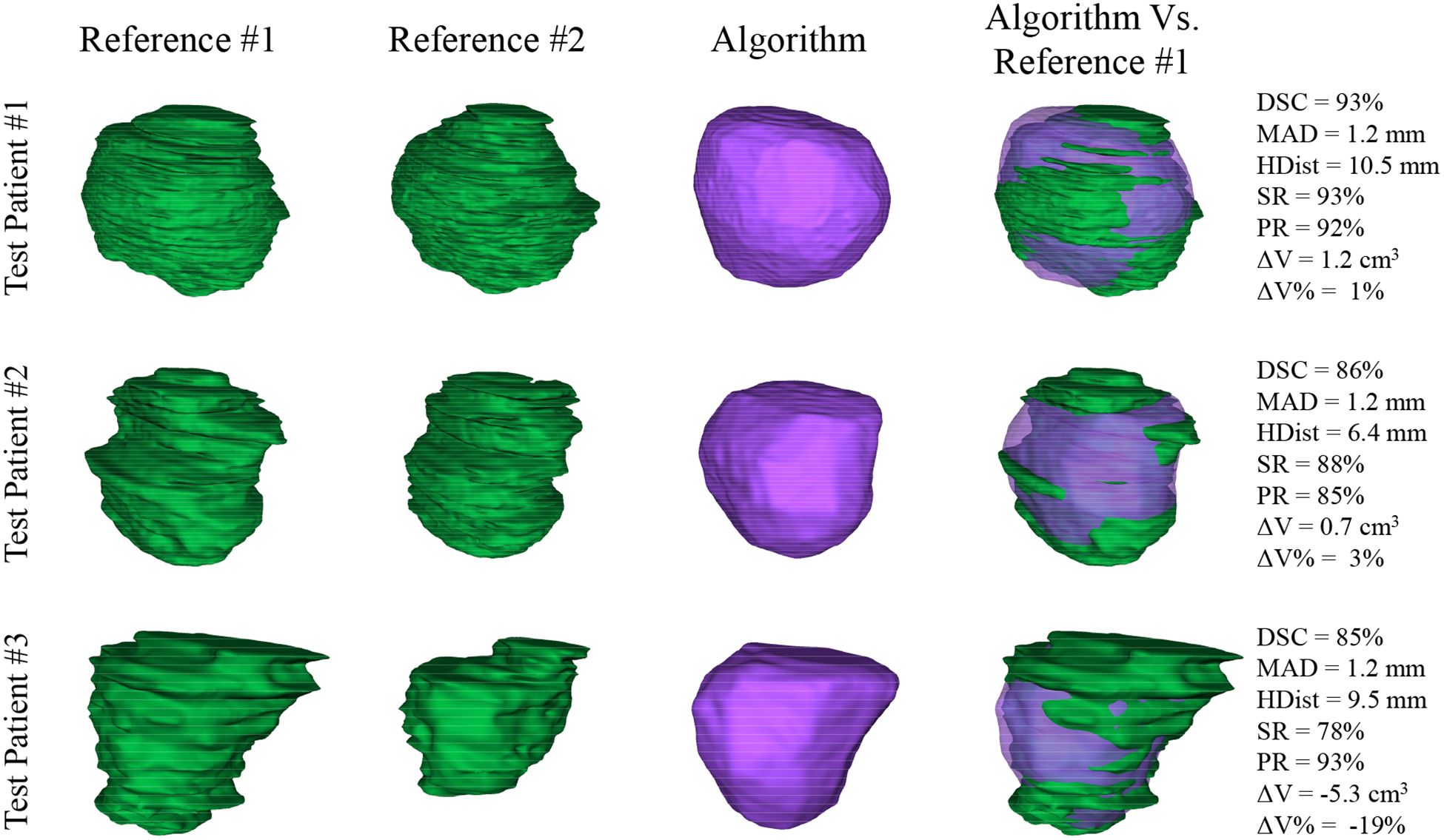
Qualitative and quantitative segmentation results in 3D for the three, sample prostates shown in Figure 5. First two left columns show the manual segmentations by two radiologists in green, the third column shows the algorithm segmentation results in purple, and the fifth column compares the algorithm segmentation against the reference #1 (first column) along with the error metric values mentioned on the right.

Table IV.

Comparison of the proposed segmentation method to previous work where applicable. Mean ± standard deviation of the segmentation error metrics for the whole prostate gland.

Method	Year	Semiautomatic / Automatic	No. test images	DSC (%)	MAD (mm)	HDist (mm)	ΔV (cm3)	ΔV (%)	Execution Time (min)
Proposed algorithm	2018	Semiautomatic	14	86 ± 3	1.4 ± 0.4	8.5 ± 2.0	−3.7 ± 3.1	−17 ± 11	0.5 ± 0.15
Jia et al. [9]	2017	Automatic	-	91 ± 4	1.6 ± 0.4	4.6 ± 1.8	-	-	~40
Tian et al. [16]	2017	Semiautomatic	43	87 ± 2	2.1 ± 0.4	9.9 ± 1.8	-	−5 ± 8	0.67
Cheng at al. [7]	2017	Automatic	250	90 ± 3	-	13.5 ± 7.9	-	-	0.05
Shahedi et al. [12]	2017	Automatic	42	71 ± 11	3.2 ± 1.2	-	−3.6 ± 10.4	−8 ± 20	0.28 ± 0.07
Tian et al. [15]	2016	Semiautomatic	43	89 ± 2	1.7 ± 0.4	8.7 ± 2.7	-	1 ± 8	0.58
Korsager et al. [10]	2015	Semiautomatic	67	88	1.5	-	-	12	> 1
Tian et al. [14]	2015	Automatic	12	83 ± 4	-	9.3 ± 2.6	-	-	4
Mahapatra and Buhmann [11]	2014	Automatic	30	81 ± 5	-	5.9 ± 2.1	-	-	20 to 25
Shahedi et al. [13]	2014	Semiautomatic	42	82 ± 4	2.0 ± 0.5	-	−4.6 ± 7.2	−12 ± 14	1.88
Liao et al. [33]	2013	Automatic	66	88 ± 3	1.8 ± 0.9	7.7 ± 2.1	-	-	2.9
Toth et al. [34]	2012	Semiautomatic	108	88 ± 5	1.5 ± 0.8	-	-	-	2.57

To record the operator interaction time for initialization of the algorithm, we asked a radiologist to select the anchor points on all the test images. The average recorded time for selecting apex and base slices were 14 ± 4 s. The average recorded time for selecting the 12 anchor points were 13 ± 2 s. In total, the average operator interaction time (selecting apex and base slices, and the 12 anchor points) were 27 ± 5 s.

4. DISCUSSION AND CONCLUSIONS

4.1. Inter-expert observer variability in manual segmentation

Pairwise comparisons between our two, manual reference segmentations (Table II) show a high inter-observer variation in the manual segmentation of the prostate in MRI that is consistent with the reported variation in references [5] and [13]. We observed that the disagreement between the expert observers for the whole prostate gland segmentation was ranging from 71% to 94% in terms of DSC, from 0.8 mm to 2.7 mm in terms of MAD, from 4.4 mm to 14.8 mm in terms of HDist, and up to 14.7 cm³ (58%) in terms of absolute volume difference. This disagreement is lower in the mid-gland region and higher for the prostate apex and base. The variation in manual prostate segmentation between expert observers makes it challenging to evaluate the segmentation algorithms based on a single-observer reference segmentation. It also limits the higher meaningful segmentation accuracy can be achieved for an algorithm to the measured inter-observer variation. Therefore, any segmentation for which the error value reaches the inter-observer disagreement level might be as accurate as an expert segmentation. The inter-observer variation, furthermore, challenges the comparison between two, segmentation algorithms based on the reported segmentation error metrics when each has been tested on a different image dataset with a different reference segmentation.

4.2. Segmentation algorithm accuracy and computation time

Concerning the inter-observer variation in manual segmentation, there is no “gold standard” defined for prostate segmentation algorithm validation in MR images. Therefore, for a computer-assisted segmentation method, the best reasonable and measurable segmentation accuracy compared to a manual reference segmentation will be the highest observed variation range between every two experts in manual segmentation. For the proposed algorithm, a comparison between corresponding mean values of Table II and Table III shows that the algorithm reached the observed variation ranged in terms of all the metrics and all the ROIs. The results reported based on our test dataset suggest that there is no room left for improvement of the algorithm regarding the measured error metrics.

Comparing the proposed algorithm to some of the recently published work listed in Table IV, the metric values show that the performance of the proposed method was within the reported metric values. Our algorithm outperformed the other algorithms in terms of MAD. The performance of the algorithm based on MAD and DSC is comparable to the best-ranked results reported in reference [18], and the HDist error metrics are within the reported ranges. Although the proposed algorithm’s performance in terms of volume difference is close to the higher bound of the reported error range in reference [18], the measured error values are still within the range, and it reached the inter-observer variability level we have observed in manual segmentation on the same test dataset. Table III shows that we measured PR (i.e., the proportion of the segmentation label that covers the reference) of 92% and more for the proposed segmentation method at different ROIs. However, the SR values (i.e., the proportion of the reference that is covered by the segmentation label) are 80% or less. This observation suggests that on average, our algorithm under-segment the prostate. The negative volume difference values also support this finding.

The main part of the proposed segmentation algorithm is run on a set of rays, and the algorithm execution on each ray is completely independent of the others. Hence, the segmentation part is computationally parallelizable that makes the algorithm capable for computation speed up. A parallel implementation on an unoptimized MATLAB research platform, using 12 CPU cores yields to about 30 s. of the computation time per 3D image. The average operator interaction time was 27 s. per subject. The total segmentation time including the operator interaction time was about one min per 3D image which is substantially less than fully manual segmentation time reported in the literature (i.e., about 5 to 20 minutes per 3D image) [6, 19, 35].

4.3. Limitations

This study should be considered in the context of its strengths and limitations. For texture extraction, we used a fixed patch size of 11 × 11 × 11 voxels. Optimization on the size of the image patches might improve the performance of the segmentation algorithm in terms of time and accuracy. For this study, we assumed that prostate has a globular, smooth shape. However, in some cases, the prostate shape could be irregular (e.g., in prostates with median lobe hyperplasia), and the shape irregularity can affect the performance of the algorithm. The small test dataset size (14 test images) is another limitation of this study.

4.4. Conclusions

In this paper, we have proposed a semiautomatic, learning-based technique for 3D segmentation of the prostate on T2-weighted MR images. Our algorithm is trained based on local texture characteristics and shape variation of the prostate in MRI. The algorithm is initialized with a set of points manually selected by the operator. To have a better understanding of the algorithm performance, we evaluated our segmentation method against manual reference segmentations using a set of error metrics including region overlap-, surface-, and volume-based error metrics. We reported the error metrics for the whole gland as well as for the three subregions of the prostate (i.e., apex, mid-gland, and base subregions). We also evaluated our method robustness to changing the operator and reference. The quantitative evaluation of the proposed algorithm shows that our segmentation method achieved a segmentation accuracy within the variation range observed in manual segmentation and comparable to the recently presented work with better accuracy in terms of MAD compared to the previous work.