Low-dimensional Dynamics of Two Coupled Biological Oscillators

Abstract

The circadian clock and the cell cycle are two biological oscillatory processes that coexist within individual cells. These two oscillators were found to interact, which can lead to their synchronization. Here, we develop a method to identify a low-dimensional stochastic model of the coupled system directly from time-lapse imaging in single cells. In particular, we infer the coupling and non-linear dynamics of the two oscillators from thousands of mouse and human single-cell fluorescence microscopy traces. This coupling predicts multiple phase-locked states showing different degrees of robustness against molecular fluctuations inherent to cellular-scale biological oscillators. For the 1:1 state, the predicted phase-shifts upon period perturbations were validated experimentally. Moreover, the phase–locked states are temperature-independent and evolutionarily conserved from mouse to human, hinting at a common underlying dynamical mechanism. Finally, we detect a signature of the coupled dynamics in a physiological context, explaining why tissues with different proliferation states exhibited shifted circadian clock phases.

The circadian clock and the cell cycle are two periodic processes that cohabit in many types of living cells. In single mammalian cells, circadian clocks consist of autonomous feedback loop oscillators ticking with an average period of about 24h¹, and controlling many downstream cellular processes². In conditions of high proliferation such as those found in cultured cells or certain tissues, the cell cycle progresses essentially continuously and can thus be abstracted as an oscillator with an average period matching the cell doubling time. Both processes fluctuate due to intra-cell molecular noise, as well as external fluctuations. While the precision of the circadian period is typically about 15% in fibroblast cells¹, the cell cycle can be more variable depending on the conditions and cell lines^3,4. Interestingly, previous work showed that the two cycles can mutually interact¹, which may then lead, as theory predicts, to synchronized dynamics^5,6 and important physiological consequences such as cell-cycle synchrony during liver regeneration⁷. In tissue-culture cells, which are amenable to systematic microscopy analysis, it was found that the phase dynamics of two oscillators shows phase-locking^5,6, defined by a rational rotation number p:q such that p cycles of one oscillator are completed while the other completes q.

Concerning the nature of those interactions, the influence of the circadian clock on cell-cycle progression and division timing has been analyzed in several systems^7–13. In contrast, we showed in mouse fibroblasts that the cell cycle strongly influences the circadian oscillator⁵, which was also investigated theoretically and linked with DNA replication in bacteria¹⁴. In addition, human cells can switch between a state of high cell proliferation with a damped circadian oscillator, to a state of low proliferation but robust circadian rhythms, depending on molecular interactions and activities of cell cycle and clock regulators¹⁵.

Here, we exploit the fact that the two coupled cycles evolve on a low dimensional and compact manifold (the flat torus) to fully characterize their dynamics. In particular, starting from a generic stochastic model for the interacting phases combined with fluorescence microscopy recordings from thousands of individual cells, we obtained a data-driven reconstruction of the coupling function describing how the cell cycle influences the circadian oscillator. This coupling phase-locks the two oscillators in a temperature-independent manner, and only few of the deterministically predicted phase-locked states were stable against inherent fluctuations. Moreover, we established that the coupling between the two oscillators is conserved from mouse to human, and can override systemic synchronization signals such as temperature cycles. Finally, we showed in a physiological context how such coupling explains why mammalian tissues with different cell proliferation rates have shifted circadian phases.

Modeling the dynamics of two coupled biological oscillators

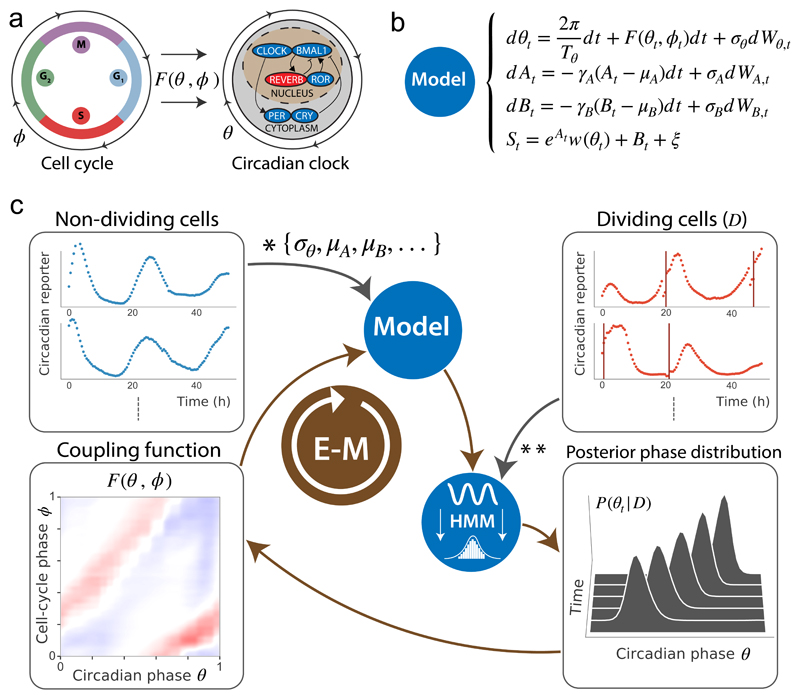
To study the phase dynamics of the circadian and cell cycle oscillators, we reconstructed a stochastic dynamic model of the two coupled oscillators from single-cell time-lapse microscopy traces of a fluorescent Rev-erbα-YFP circadian reporter^1,5. Our approach consists in explicitly modeling the measured fluorescent signals, using a set of stochastic ordinary differential equations (SODEs) whose parameters are estimated by maximizing the probability of observing the data over the entire set of cell traces (Methods). We here present the key components of the model (detailed in Supplementary Information).

Phase model

First, we represent the phase dynamics of the circadian oscillator (θ = 0 corresponds to peaks of fluorescence) and cell cycle (ϕ = 0 is the cytokinesis) [0,2π)×[0,2π) on a torus. Since we showed previously that the influence of the clock on the cell cycle was negligible in NIH3T3 cells⁵, we here model only how the cell-cycle progression influences the instantaneous circadian phase velocity ω_θ using a general coupling function F(θ,ϕ) (Fig. 1a). To account for circadian phase fluctuations and variability in circadian period length known to be present in single cells^1,16, we added a phase diffusion term σ_θ dW_t. For the cell-cycle phase, we assumed a piecewise linear and deterministic phase progression in between two successive divisions. The SODEs for the phases read:

$$\{\begin{array}{lll}d\theta \hfill & =\hfill & \frac{2\pi }{T_{\theta }}dt+F\left(\theta ,\varphi \right)dt+{\sigma }_{\theta }d{W}_t\hfill \\ d\varphi \hfill & =\hfill & \frac{2\pi }{T_{\varphi }^i}dt\hfill \end{array}$$ (1)

Here, T_θ represents the intrinsic circadian period, while the term $T_{\varphi }^i$ represents the i^th cell-cycle interval between two successive divisions.

Figure 1. Reconstructing the phase dynamics and coupling of two biological oscillators.

(a) In mouse fibroblasts, the cell cycle (left) can influence the circadian oscillator (right) according to a coupling function F(θ, ϕ), where ϕ denotes the cell cycle and θ the circadian oscillator phases. (b) Stochastic model for the signal S_t using diffusion-drift SODEs for the circadian phase θ_t, amplitude A_t and background B_t fluctuations, as well as a function W(θ) linking the phase θ_t to the measured observations, and F(θ, ϕ) (c) Fluorescence microscopy traces (Rev-erbα-YFP circadian reporter) are recorded for non-dividing and dividing cells (top left and top right boxes). Coupling-independent parameters (*) are estimated from non-dividing cells while dividing cells are necessary to infer F(θ, ϕ) (**). The optimization problem is solved by converting the model to a HMM in which θ_t, A_t and B_t are latent variables. The HMM is used on traces to compute posterior probabilities of circadian phases (bottom right box), while the cell-cycle phase is retrieved using linear interpolation between successive divisions (top right box, vertical orange lines). An iterative EM algorithm then yields the converged F(θ, ϕ) (bottom left box).

Model of the signal

We linked the circadian phase with the measured time traces through a 2π-periodic function w(θ). In addition, as suggested by typical data traces (Supplementary Fig. 1a), we considered amplitude (A_t) and baseline (B_t) fluctuations, which for simplicity we modeled as independent from θ_t, an assumption that was supported a posteriori (Supplementary Information). The full model for the observed signal S_t thus reads:

$$S_t=e^{A_t}w\left({\theta }_t\right)+B_t+\xi$$ (2)

where ξ is a normally distributed random variable (measurement noise) and A_t,B_t are Ornstein-Uhlenbeck processes varying more slowly than the phase distortion caused by F(θ,ϕ), i.e., on timescales on the order of the circadian period (Supplementary Information).

Inference of phases & coupling function

From this stochastic model (Equations 1&2, Fig. 1b), we built a Hidden Markov Model (HMM) to calculate posterior probabilities of the oscillator phases at each measured time point, using the forward-backward algorithm¹⁷. To estimate F(θ,ϕ), we used a maximum-likelihood approach that combines goodness of fit with sparseness and smoothness constraints, which we implemented with an Expectation-Maximization (EM) algorithm (Methods, Supplementary Information).

The successive steps of our approach are illustrated in Figure 1c. Dividing cells indicated that, typically, the circadian phase progression shows variations in phase velocity (Supplementary Fig. 1a). To validate that these variations can identify F(θ,ϕ), we generated noisy traces in silico with pre-defined F(θ,ϕ) and reconstructed the coupling function, showing excellent qualitative agreement (Supplementary Fig. 1b-c).

Influence of the cell cycle on the circadian phase

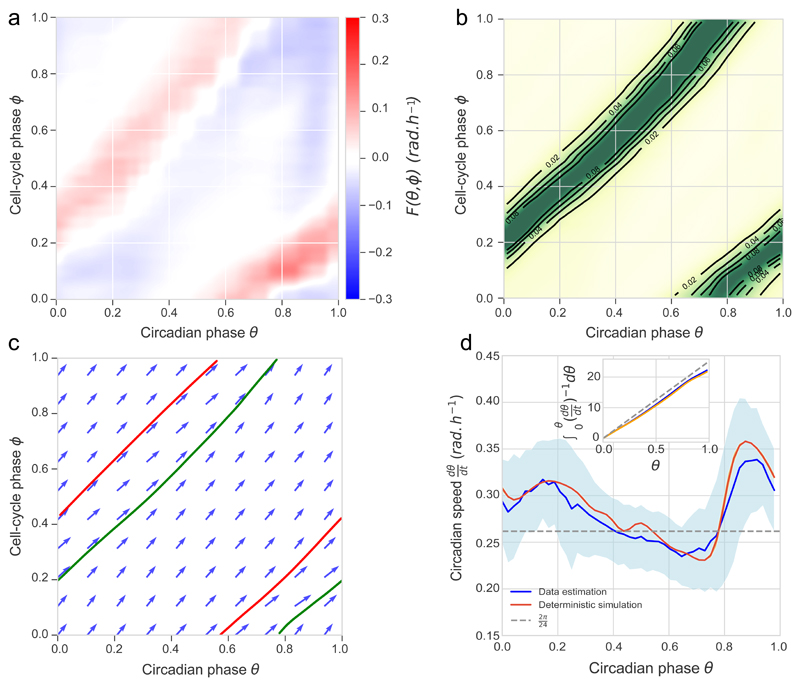
In mouse embryonic fibroblasts (NIH3T3), we showed that due to the coupling, circadian periods decrease with temperature in dividing cells, but not in quiescent cells⁵. To further understand how temperature influences the interaction between the two oscillators, we re-analyzed NIH3T3 traces (24-72h long) obtained at 34°C, 37°C, and 40°C⁵. From those, we found that both the inferred coupling functions and phase densities at the three temperatures were very similar, with almost identical 1:1 phase-locked orbits (Supplementary Fig. 2a-c). We therefore modeled the coupling as temperature-independent and re-constructed a definitive F(θ,ϕ) from traces at all temperatures (Fig. 2a, Supplementary Fig. 2d). This function shows a diffuse structure mainly composed of two juxtaposed diagonal stripes: one for phase acceleration (red), and one, less structured, for deceleration (blue). The slopes of these stripes are about one, which indicates that an approximate minimal model of the coupling would be a function F(θ,ϕ) = f (θ − ϕ). However, the phase velocity varies along the stripes and attractor (see below), which justifies using a 2D parameterization of the coupling function. The phase density for cells with fixed cell-cycle period of 22h (corresponding to the mean cell-cycle period in the full dataset) (Fig. 2b, and Movie 1) clearly suggests 1:1 phase-locking. In fact, analyzing the predicted deterministic dynamics (Equation 1, with the reconstructed F(θ,ϕ), and without the noise) shows a 1:1 attractor (Fig. 2c). Thus, in this 1:1 state, the endogenous circadian period of 24h is shortened by two hours, which results from acceleration occurring after cytokinesis (ϕ = 0) when the circadian phase is near θ ≈ 0.8 × 2π, and lasting for the entire G1 phase, until about θ ≈ 0.4 × 2π when cells typically enter S phase (ϕ ≈ 0.4 × 2π at the G1/S transition, Supplementary Information, Fig. 2d).

Figure 2. Influence of the cell cycle on the circadian phase enables 1:1 phase-locking.

(a) Coupling F(θ, ϕ) optimized on dividing single-cell traces. Due to similar results (Supplementary Fig. 2) traces from the three temperatures (n=154, 271, 302 traces at 34°C, 37°C, 40°C, resp.) are pooled. (b) Density of inferred phase traces from all the dividing traces with 22±1h cell-cycle intervals indicates a 1:1 phase-locked state. (c) Numerical integration of phase velocity field (arrows, deterministic model) yields 1:1 attractor (green line) and repeller (red line). Here, the cell-cycle period was set to 22 h. (d) Circadian phase velocity is not constant along the attractor, here for cells with 22±1h cell-cycle intervals. Data (blue line, standard deviation in light-blue shading) and deterministic simulation (orange line). Inset: integrated time along the attractor. The gray line shows constant bare phase velocity ${\omega }_{\theta }=\frac{2\pi }{24h}.$

Phase dynamics in perturbation experiments

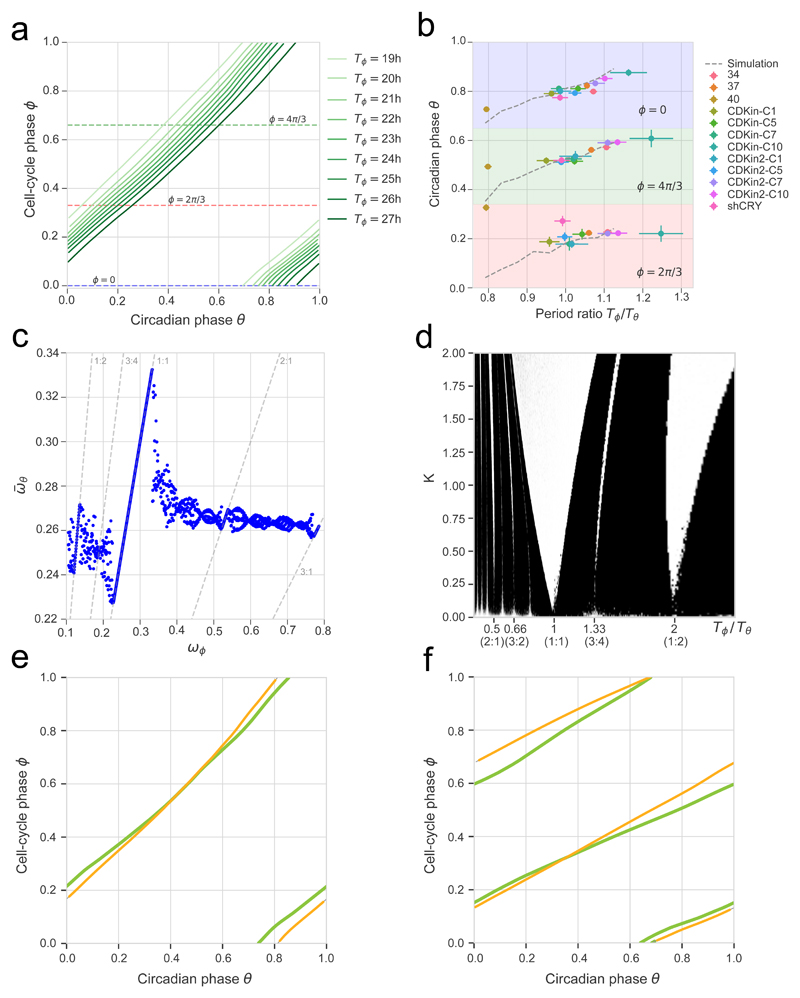
The reconstructed model allows us to simulate the circadian phase dynamics in function of the cell-cycle period, which is relevant as the cells display a significant range of cell-cycle lengths (Supplementary Fig. 3a). In the deterministic system, we find 1:1 phase-locking over a range of cell-cycle times varying from 19h to 27h, showing that the cell cycle can both globally accelerate and slow down circadian phase progression (Fig. 3a). The attractor shifts progressively to the right in the phase-space, yielding a circadian phase at division ranging from θ ≈ 0.7 × 2π at division when T_ϕ = 19h to θ ≈ 0.9 × 2π when T_ϕ = 27h. Since the attractor for different cell-cycle periods shifts, the circadian phase velocity profile also changes (Supplementary Fig. 3b). To validate the predicted shifts, we experimentally subjected cells to perturbations inducing a large variety of cell-cycle periods and compared the observed circadian phase to the model prediction at three different cell-cycle phases, revealing an excellent agreement, with no additional free parameters (Fig. 3b).

Figure 3. The coupling between the cell cycle and the circadian oscillator predicts phase shifts and phase-locking attractors in perturbation experiments.

(a) Simulated (deterministic) attractors for cell-cycle periods ranging from 19h to 27h show that the dephasing of the cell cycle and the circadian oscillator changes within the 1:1 state. Periods just outside of this range yield quasiperiodic orbits. The horizontal dashed lines indicate three different cell-cycle phases $\varphi =0,\varphi =\frac{1}{3}\times 2\pi ,\varphi =\frac{2}{3}\times 2\pi$ used in panel (b). (b) Predictions from a) (dashed grey lines) against independent experimental data collected from 12 perturbation experiments (colored symbols, see legend, notation explained in Methods). (c) Multiple phased-locked states are predicted, recognizable by rational relationships between the frequencies of the entraining cell cycle and the entrained circadian oscillator, interspersed by quasiperiodic intervals. (d) Arnold tongues showing multiple phase-locked states in function of cell-cycle periods and coupling strength (K=1 corresponds to the experimentally found coupling). Stable zones (white tongues) reveal attractors interspersed by quasi-periodicity. Although there are only two wider phased-locked state (1:1 and 1:2), several other p:q states are found. (e-f) Representative single-cell traces (data in yellow) evolving near predicted attractors (green lines). A cell with T_ϕ = 24h (e) and one with T_ϕ = 48h (f) near the 1:1 and 1:2 orbits, respectively.

The simulations also clearly revealed multiple phase-locked states (1:2, 1:1, 2:1, 3:1, etc, p:q indicating the number of cell cycles p and the number of clock cycles q), represented as Arnold tongues (Fig. 3c, and Movie 2 for an animated phase-space representation). We identified cell data trajectories following almost perfectly the deterministic attractors, both in the 1:1 and 1:2 phase-locking states (Fig. 3e and 3f, respectively); however, cells showing other p:q states were rarely observed.

Fluctuations extend 1:1 phase-locking asymmetrically

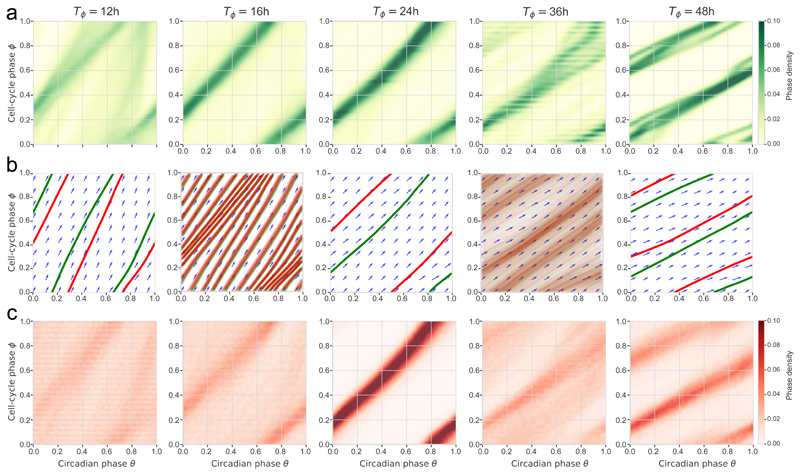
To understand the differences between the simulated deterministic system and observed cell traces, we simulated the stochastic dynamics (Equation 1). We then compared measured data trajectories stratified by cell-cycle periods (Fig. 4a) with deterministic (Fig. 4b) and stochastic simulations (Fig. 4c). This revealed that data agree better with stochastic than deterministic simulations, indicating that the phase fluctuations qualitatively change the phase portrait. One striking observation is the increased range of 1:1 phase-locking in the noisy system, however asymmetrically, since this occurs for shorter, but not for longer cell-cycle periods. Indeed, while 1:2 phase-locking is observed in the data and the noisy simulations, the deterministically predicted 2:1 state is replaced in the data and stochastic system by 1:1-like orbits. Consistently, spectral analysis revealed significant differences between deterministic and stochastic simulations (Supplementary Fig. 4a-b, Movie 3); in addition, the coupling, specifically in the 1:1 state, was able to efficiently filter the noise (Supplementary Fig. 4b, right).

Figure 4. Single-cell data and stochastic simulations reveal robust 1:1 and 1:2 phase-locked states.

(a) Phase-space densities from the experimental traces stratified by cell-cycle periods (±1h for each reference period); n=16, 223, 303, 54, 4 cell traces in the T=12, 16, 24, 36, 48 h panels, resp. (b) Vector fields and simulated (deterministic) trajectories for the different cell-cycle periods. Attractors are shown in green (forward time integration) and repellers (backward integration) in red (see also Movie 2). (c) Phase-space densities obtained from stochastic simulations of the model match better with the data compared to b).

Evolutionarily conserved phase-locking

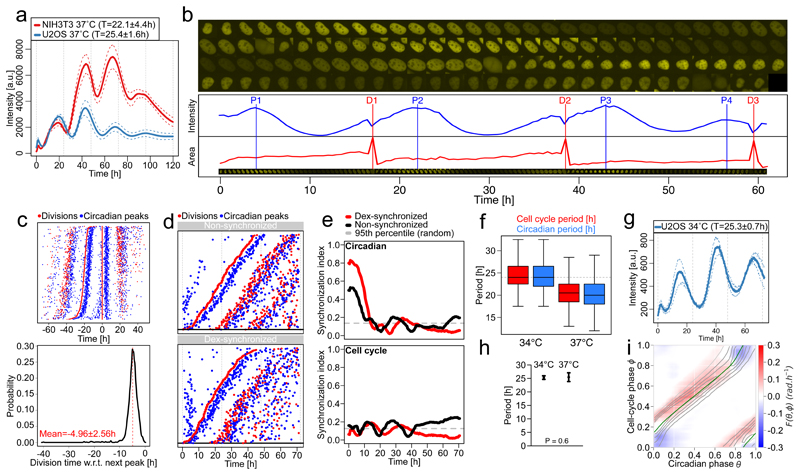
Most studies investigating the interaction between the cell cycle and the circadian oscillators in mammals are from rodent models^1,5–8,18. To test if the above phase-locked dynamics are conserved in human U2OS cells, an established circadian oscillator model^19,20, we engineered a U2OS cell line termed U2OS-Dual expressing a dual circadian fluorescent (Rev-erbα-YFP) and luminescent (Bmal1-luc) reporter system. U2OS-Dual cells possess a functional circadian clock behaving similarly to NIH3T3 cells also expressing a Bmal1-Luc luminescent reporter²¹ (Fig. 5a). We scrutinize the relation between the two cell lines by comparing their behavior in different conditions: at 34°C and 37°C for cells with synchronized and non-synchronized circadian cycles⁵ (Fig. 5b-g).

Figure 5. Conserved influence of the cell cycle on the circadian clock in human U2OS osteosarcoma cell.

(a) Mean luminescence intensities (±SD, n=3) from non-dividing NIH3T3 and U2OS cells grown at 37°C expressing a Bmal1-Luc reporter. Values in the legend correspond to the mean periods ±SD. (b) Semi-automated segmentation and tracking of U2OS cell lines expressing the Rev-erbα-YFP circadian fluorescent reporter. Red vertical lines represent cell divisions (cytokinesis) and blue vertical lines show Rev-erbα-YFP signal peaks. (c) Top: stack of divisions (red) and Rev-erbα-YFP peaks (blue) for single U2OS traces centered on divisions. Bottom: distribution of the time of division relative to the next Rev-erbα-YFP peaks (in read mean±SD, n=1298). (d) Divisions and Rev-erbα-YFP peaks from single non-synchronized (top), and dexamethasone (dex)-synchronized (bottom) U2OS traces ordered on the first division. (e) Synchronization index (SI) from non-synchronized (black) and dex-synchronized (red) traces for the circadian phase (top) and cell-cycle phase (bottom) estimated as in Bieler et al. ⁵. The circadian SI from non-synchronized cells is relatively high due to plating. Dashed gray lines show 95^th percentiles of the SI for randomly shuffled traces. (f) Cell-cycle and circadian periods for U2OS cells grown at 34°C and 37°C (n > 90 for all distributions). (g) Mean luminescence intensities (±SD, n=3) for non-dividing U2OS cells grown at 34°C expressing a Bmal1-Luc reporter. Values in the legend correspond to the mean periods ±SD. (h) Mean and standard deviation of the circadian period for non-dividing U2OS cells grown at 34°C and 37°C (n=8 at 34 and n=9 at 37, two-sided Wilcoxon’s test). (i) Coupling function F(θ, ϕ) optimized on n=551 dividing U2OS traces grown at 37°C, superimposed with the attractor (T_ϕ = 22h) obtained from deterministic simulations (green line).

Similarly to NIH3T3 cells, the division events of non-synchronized U2OS-Dual cells grown at 37°C occurred 4.96 ± 2.6 h before a peak in the circadian fluorescent signal (Fig. 5c), indicating that the cell cycle and the circadian clock interact. To investigate the directionality of this interaction, we tested, like in NIH3T3 cells⁵, whether the circadian clock phase could influence cell-cycle progression by resetting the circadian oscillator using dexamethasone (dex), a circadian resetting cue²² that does not perturb the cell cycle¹. We found the expected resetting effect of dex on the circadian phase by the density of peaks in reporter levels during the first 10h of recording, but with unnoticeable effects on the timing of the first division (Fig. 5d). However, the circadian peak following the first division occurred systematically around 5h after the division in both conditions, suggesting that cell division in U2OS can reset circadian phases and overwrite dex synchronization. Synchronization of the circadian clocks for dex- vs non- treated cells was expectedly higher for dex and gradually decreased to reach the level of the untreated cells (Fig. 5e), contrasting with the generally lower synchronization of cell divisions in both conditions. To then test if the cell cycle could influence the circadian clock, we lengthened the cell-cycle period by growing cells at 34°C and compared with 37°C. Interestingly, cells at 34°C showed a longer circadian period compared to 37°C (Fig. 5f), unlike the temperature compensated circadian periods (~25h) in non-dividing cells (Fig. 5a, g-h).

Thus, similarly to mouse NIH3T3 cells, the coupling directionality is predominantly from the cell cycle to the circadian clock. In fact, the reconstructed coupling function for U2OS-Dual cells grown at 37°C (Fig. 5i) is structurally similar to that obtained in mouse fibroblasts (Fig. 2a), with the ensuing dynamics also showing a 1:1 attractor.

Dividing cells lose circadian temperature entrainment

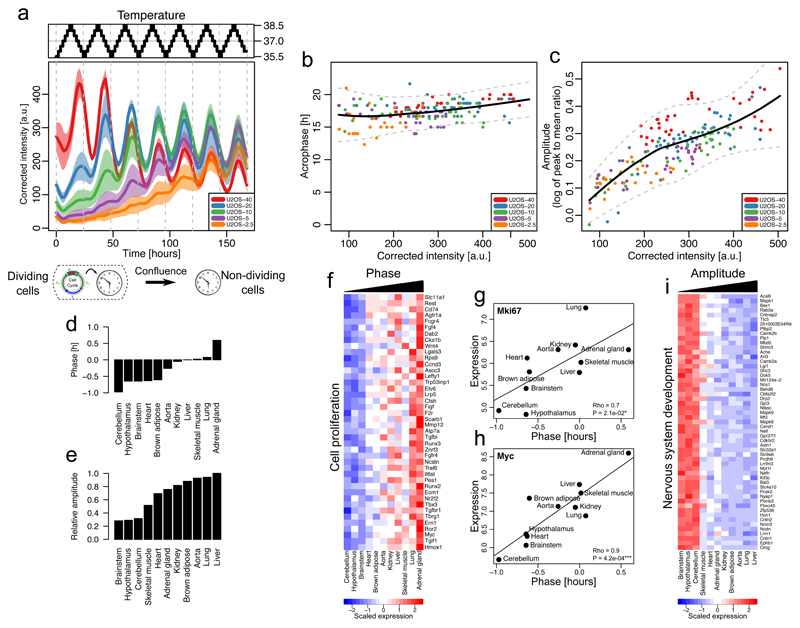
In mammals, circadian clocks in tissues are synchronized by multiple systemic signals²³. In fact, temperature oscillations mimicking those physiologically observed can phase-lock circadian oscillators in non-dividing (contact-inhibited) NIH3T3 cells in vitro²⁴. To study how the found interactions influence temperature entrainment, we applied temperature cycles (24h period ranging from 35.5°C to 38.5°C) to U2OS cells growing at different rates (plated at different densities) and monitored population-wide Bmal1-luc signals (Fig. 6a). We found that, independently of initial densities, as the populations reach confluency, the phases and amplitudes become stationary, showing 1:1 entrainment (Fig. 6b, c and Supplementary Fig. 5a). During the initial transients, emerging circadian oscillations in non-confluent cells showed phases that were already stationary, at least once cell numbers were sufficiently high to obtain reliable signals.

Figure 6. Temperature cycles do not entrain circadian oscillators in dividing cells and proliferation genes are associated with tissue-specific circadian phases.

(a) Corrected and averaged Bmal1-Luc intensities and 95% confidence intervals (n=6) from U2OS-Dual cells plated at different initial densities and subjected to a temperature entrainment (top). (b) Acrophases (times of the local peaks in luminescence) of the Bmal1-Luc signal in function of the reporter intensity for the cells in a). Loess fit (black) and 95% confidence intervals (gray). (c) Amplitude (log of peak to mean ratio) of the Bmal1-Luc oscillations in function of the reporter intensity for the cells in a). Loess fit (black) and 95% confidence intervals (gray). (d-e) Circadian phases (d) and amplitudes (e) of different mouse tissues obtained in ref²⁷, relative to liver. (f) Expression levels of genes positively associated with phases from d) and linked to cell proliferation. (g-h) Correlations between Mki67(g) and Myc (h) mRNA expression and circadian phases across mouse tissues (Pearson’s correlation, two-sided P-values from t-distribution with n-2 degrees of freedom). (i) Expression levels of genes negatively associated with amplitudes and linked to nervous system development.

As cell confluence increases, the proportions of cells which stop cycling (exit to G0) increases²⁵. We therefore hypothesized that the observed phase and amplitude profiles in Bmal1-luc signals (Fig. 6b, c) originate from a mixture of two populations: an increasing population of non-dividing cells (G0) showing ‘normal’ entrainment properties, and dividing cells. We considered three scenarios for the dividing cells: i) the circadian oscillators in dividing cells adopt the same circadian profile as non-dividing entrained cells; ii) are not entrained; or iii) are entrained, but with a different phase compared to non-dividing cells (Supplementary Fig. 5b). These scenarios can be distinguished by the predicted phase and amplitude profiles (Supplementary Fig. 5c). Clearly, the measured profiles for U2OS-Dual cells favored the second scenario, suggesting that circadian oscillators in dividing cells do not entrain to the applied temperature cycles.

Proliferation is associated with tissue-specific circadian phases

The above findings suggest that phases or amplitudes of circadian clocks in organs in vivo might be influenced by the proliferation state of cells in the tissue. To test this, we investigated circadian clock parameters in different mouse tissues using a study of mRNA levels in twelve adult (6 weeks old males) mouse tissues, which revealed that clock phases span 1.5 hours between the earliest and latest tissues (Fig. 6d)^26,27, an effect which is considered large in chronobiology as even period phenotypes of core clock genes are often smaller^2,28,29. We noticed that the mean mRNA levels across tissues of many genes correlated with the phase offsets (Supplementary Table 1). However, gene functions related to cell proliferation stood out as the most strongly enriched (Fig. 6f, Supplementary Table 1). Among those genes, the levels of known markers of cell proliferation such as Mki67 or Myc were strongly correlated with the phase offsets (Fig. 6g-h, Supplementary Table 1). Amplitudes, on the other hand, were not correlated with proliferation genes, but rather with neuronal specific genes, as expected owing to the damped rhythms present in those tissues (Fig. 6i, Supplementary Table 1)²⁶. Thus, this analysis suggests that the differences in basal proliferation levels observed in normal tissues might underlie the dephasing of the circadian clock, suggesting a physiological role for the interaction of the cell cycle and circadian clocks.

Discussion

A goal in quantitative single-cell biology is to obtain data-driven and dynamical models of biological phenomena in low dimensions. In practice, the heterogeneity and complex physics underlying the emergence of biological function in non-equilibrium living systems, as well as the sparseness of available measurements pose challenges. Here, we studied a system of two coupled biological oscillators, sufficiently simple to allow data-driven model identification, yet complex enough to exhibit qualitatively distinct dynamics, i.e. p:q states and quasi-periodicity.

In the coupled cell cycle and circadian oscillator system, phase-locked states different from 1:1 have been observed¹⁰. While multiple attractors, notably 1:1 and 3:2, were found in mouse NIH3T3 cells under transient dexamethasone stimulation⁶, we here report 1:2 states for long cell-cycle times under steady, unstimulated, conditions. Unlike other deterministically predicted states, 1:2 was sufficiently robust and observed in some cells. In fact, we found that noise extended the range of the 1:1 tongue, but asymmetrically, i.e. towards decreased cell-cycle periods. This may be reminiscent of generalized Poincaré oscillators showing that the entrainment range is broader for limit cycles with low relaxation rates³⁰. Indeed, noise could decrease relaxation rates and thereby broaden Arnold tongues. In addition, for certain cell cycle periods, we observed the superposition of multiple states, both in the data and in the stochastic simulations, which were not present in the deterministic analysis (Fig. 4, see notably T=12h and T=36h). This is reminiscent of mode hopping as described in the context of an oscillatory gene circuit underlying inflammatory responses³¹, however, here the corresponding Arnold tongues do not overlap in the range of the biologically relevant coupling strength (K=1, Fig. 3d).

While we focused on the emergent dynamics in the coupled oscillator system, considerations on possible biological mechanisms are relevant for follow-up biochemical analyses. How chromosome condensation or nuclear envelope breakdown may influence the circadian clock phase progression via either transcriptional shutdown, or displacement of chromatin bound circadian repressors, respectively, was discussed previously⁵. For example, Rev-erbα transcription being so tightly locked to cell divisions (the peak accumulation of the reporter occurs 5h after mitosis) could reflect the sudden derepression of its promoter, due to displaced CRYPTOCHROME1 (CRY1) containing repressor complex following nuclear envelope breakdown³². In turn, REV-ERB-A accumulation influences clock phase by binding to promoters of multiple core clock components, including Cry1 ^33,34. More specific transcriptional activities could also play a key role in coupling the cell and circadian cycles. In fact, the circadian oscillator is exquisitely sensitive to numerous signaling pathways, impinging upon the clock by transcriptional induction of Period genes, which thus provides an efficient synchronization method²². Similarly, entrainment via temperature cycles also converges onto Period gene transcription²⁴. However, we are not aware of cell-cycle dependent transcriptional regulators, such as E2F factors, targeting clock components like the Period genes. Finally, since the regulation of protein stability is important for clock function³⁵, it is possible that phosphorylation-controlled proteolytic activities driving the cell cycle could target circadian phase regulators³⁶, thereby mediating the observed coupling.

In mammals, the circadian oscillator in the suprachiasmatic nucleus (SCN) is the pacemaker for the entire organism³⁷, driving 24h rhythms in activity, feeding, body temperature and hormone levels. In particular, the SCN can synchronize peripheral cell-autonomous circadian clocks located within organs across the body³⁸. Consistent with theory³⁹, in a physiological context of entrainment, the coupling of the cell cycle with the circadian clock can induce proliferation dependent phase-shifts, which we observed. Such phase shifts could reflect a homogenous behavior of all cells, or it could reflect heterogeneity of cell proliferation states, possibly leading to wave propagation. The phase shifts we observed in tissues were associated with low proliferation, i.e. non-pathological states of tissue homeostasis and cell renewal. For example, the liver or the adrenal gland showed a phase advance compared to fully quiescent tissues like the brain.

When cell proliferation is abnormally high such as in cancer, circadian clocks are often severely damped⁴⁰. While this absence of a robust circadian rhythm in malignant tissue states may reflect non functional circadian oscillators due to mutations in clock genes⁴¹, the damped rhythms may also reflect circadian desynchrony of otherwise functional circadian oscillators. Such desynchrony would readily follow from the coupling between the cell-cycle and circadian oscillators we highlight here, in the presence of non-coherent cell-cycle progression.

Methodologically, the new approach to reconstruct a dynamical model for the coupled oscillator system has significant advantages over previous methods, notably strong assumptions such as the sparse and localized coupling are dispensable⁵. Compared with generic model identification techniques⁴², our approach models the raw data and its noise structure explicitly. In the future, such data-driven identification of dynamical models might reveal dynamical instabilities underlying ordered states in spatially extended systems, as occurring, for instance, during somitogenesis⁴³.

Methods

Cell lines

All cell lines (U2OS-Dual, NIH3T3-Bmal1-Luc, and U2OS-PGK-Luc) were maintained in a humidified incubator at 37°C with 5% CO2 using DMEM cell culture media supplemented with 10% fetal bovine serum (FBS) and 1% penicillin-streptomycin-glutamine (PSG). One day before luminescence or fluorescence acquisitions, we replaced DMEM with FluoroBrite DMEM media supplemented with 10% FBS and 1% PSG. NIH3T3 perturbation experiments were generated in Bieler et al⁵. Briefly, they correspond to temperature changes (34, 37, and 40°C), treatment with CDK1 (RO-3306, Sigma-Aldrich) and CDK1/2 (NU-6102, Calbiochem) inhibitors at 1, 5, 7 and 10μM (CDK1in-[1,5,7,10] and CDK2in-[1,5,7,10]), and shRNA-mediated knockdown of Cry2 (shCry).

Fluorescent time-lapse microscopy

Time-lapse fluorescent microscopy for U2OS-Dual cells was performed at the biomolecular screening facility (BSF, EPFL) using an InCell Analyzer 2200 (GE healthcare). Experiments were performed at different temperature (34°C, 37°C, or 40°C) with a humidity and CO₂ (5%) control system. We used 100 ms excitation at 513/17 nm and emission at 548/22 nm to record the YFP channel. Cells were recorded by acquiring one field of view per well in a 96-well black plate (GE healthcare). We used our previously developed semi-automated pipeline for segmentation and tracking of individual cells⁵. In total, traces from n=551 U2OS cells were obtained (typically 50 cells are obtained per movie). NIH3T3 single cells trace are reanalyzed from previous work ⁵; here, we used n=2504 of those time traces. In all cases (NIH3T3 and U2OS), we followed several quality control metrics from ⁵. Briefly, we discarded all traces that left the field-of-view at some point during the acquisition. We also visually inspected all traces, using a custom-made Matlab tool, to remove traces with problematic segmentation and tracking. In addition, we only kept traces with significant circadian amplitude (peak height >0.25, rescaled signals, Supplementary Information). To minimize boundary artifacts, typically, only traces with at least 2 full cell cycles were kept. The number of cells used for specific analyses, including sub-selections of traces based on the cell-cycle intervals, are indicate in the figure captions.

Inferring the phase dynamics of two biological oscillators

Denote by D the entire set of single cells traces comprising temporal intensity measurements (∆t=30 min) from all fluorescent traces and Λ the set of model parameters, comprising the gridded coupling function F_ij. Note that all parameters are shared by all cells in D. To reconstruct the phase dynamics of our model, we seek to maximize the likelihood of the data ℒ(Λ|D), that is, we solve:

$${\mathbf{\Lambda }}^{\ast }=\text{argmax}ℒ\left(\mathbf{\Lambda }|\mathbf{\text{D}}\right)$$

In practice, we used an EM algorithm, by iteratively optimizing the function Q (Λ, Λ′) over its first argument, where Q can be written as follow:

$$Q\left(\mathbf{\Lambda },{\mathbf{\Lambda }}^{\prime }\right)=E\left[\text{log}p\left(\mathbf{\text{D}},\mathbf{\text{X}}|\mathbf{\Lambda }\right)|\mathbf{\text{X}},{\mathbf{\Lambda }}^{\prime }\right]$$

That is, Q (Λ, Λ′) corresponds to the expected value of the log-likelihood of the data with respect to the posterior probabilities of the hidden phases X (latent variables), computed using the current parameter Λ′. This process guarantees a monotonous convergence of the log-likelihood, although a global maximum is not necessarily reached⁴⁴.

To control for the many parameters F_ij, we added regularization constraints for both the smoothness and sparsity:

$$Q_p\left(\mathbf{\Lambda },{\mathbf{\Lambda }}^{\prime }\right)=Q\left(\mathbf{\Lambda },{\mathbf{\Lambda }}^{\prime }\right)-{\lambda }_1{\displaystyle \sum _{ij}{\Vert F_{ij}\Vert }^2}-{\lambda }_2{\displaystyle \sum _{ij}{F}_{ij}^2}$$

This expression is also guaranteed to converge⁴⁵.

Details about the optimization method, choice of the regularization parameters, and computation of the phase posteriors using a HMM are provided in Supplementary Information.

Long-term temperature entrainment and luminescence recording

We performed long-term temperature entrainment experiments using a Tecan plate reader Infinite F200 pro with a CO₂ and temperature modules. One day before starting the experiment, serial dilution ranging from 40,000 to 2,500 cells were seeded in 96-well white flat bottom plates (Costar 3917). To prevent media evaporation, all wells were filled with 300μl of media composed of FluoroBrite, 10% FBS, 1% PSG, and 100 nM D-luciferin (NanoLight technology) and covered with a sealing tape (Costar 6524). We set up temperature entrainment using stepwise increase (or decrease) of 0.5°C every 2 hours to produce temperature oscillating profiles going from 35.5°C to 38.5°C and back to 35.5°C again over a period of 24 hours. Intensities from all wells were recorded every 10 minutes with an integration time of 5000 milliseconds. Since temperature impacts the enzymatic activity of the luciferase⁴⁶, we corrected the signal for this systematic effect (Supplementary Information).

Association between gene expression and phase in tissues

We used the average gene expression obtained from a selected set of twelve adult (6 weeks old males) mouse tissues from the Zhang et al. dataset (GEO accession GSE54650)²⁶. For this analysis, we estimated the Pearson’s correlation between the averaged gene expression and the circadian tissue phases or amplitudes reported in ref²⁷. We selected the top 200 genes positively or negatively associated with either the phases or the amplitudes for gene ontology analysis⁴⁷ (Supplementary Table 1).