Evaluating DCA-based method performances for RNA contact prediction by a well-curated data set

Abstract

RNA molecules play many pivotal roles in a cell that are still not fully understood. Any detailed understanding of RNA function requires knowledge of its three-dimensional structure, yet experimental RNA structure resolution remains demanding. Recent advances in sequencing provide unprecedented amounts of sequence data that can be statistically analyzed by methods such as direct coupling analysis (DCA) to determine spatial proximity or contacts of specific nucleic acid pairs, which improve the quality of structure prediction. To quantify this structure prediction improvement, we here present a well curated data set of about 70 RNA structures of high resolution and compare different nucleotide–nucleotide contact prediction methods available in the literature. We observe only minor differences between the performances of the different methods. Moreover, we discuss how robust these predictions are for different contact definitions and how strongly they depend on procedures used to curate and align the families of homologous RNA sequences.

INTRODUCTION

RNA molecules play fundamental roles in a large variety of processes within cells. For example, messenger RNAs (mRNAs) carry the genetic information akin to blueprint for protein synthesis, transfer RNA (tRNA) then carry specific amino acids during protein synthesis to the site of protein elongation (Elliott and Ladomery 2016). More recently other tasks of RNA were identified, such as non-coding RNAs (ncRNAs) fulfilling fundamental roles in the control of gene expression (Wilusz et al. 2009; Cech and Steitz 2014) or small interference RNAs (siRNAs) and micro RNAs (miRNAs) that can regulate and repress the expression of target genes by interfering with the transcriptional regulation (Fire et al. 1998; Bartel 2009).

Long noncoding RNAs (lncRNAs) also contribute to these modulation mechanisms even if they are less understood. Metabolite-binding RNA structures called riboswitches that belong to the 5′ untranslated regions (5′-UTR) of the mRNA bind selectively and with high affinity to small molecules, and this binding induces major conformation rearrangements of the three-dimensional structure of the riboswitches. The two competing conformations can inhibit or activate the expression of the target gene by interfering with the translation regulation. The study of lncRNAs is of particular high interest as they are frequently involved in pathogenic mechanisms and thus can be targeted for therapeutic strategies (DiStefano 2018).

To truly understand the molecular mechanisms of lncRNAs and their function, it is important to know their three-dimensional structure. Experimental techniques to determine the 3D structure include “classical” methods such as X-ray diffraction crystallography or nuclear magnetic resonance (NMR), which provide direct structural information. Other methods do not directly provide structural information but have first to be carefully interpreted (e.g., small-angle scattering [SAXS] [Weiel et al. 2019] or fluorescence resonance energy transfer [FRET] [Reinartz et al. 2018]). Yet in spite of considerable progress of experimental techniques, the number of structurally resolved RNA structures collected in public databases (Berman et al. 2000; Narayanan et al. 2013) is still small due to experimental limitations and considerably lags the number of known RNA sequences.

Computational methods contributed substantially to deciphering how RNA structure and dynamics determine its functions (Zuker and Stiegler 1981; Aigner et al. 2012; Pucci and Schug 2019). A series of computational tools have been developed to predict RNA structures from their sequences using different approaches that can be roughly divided into fragment-based, physics-based, and comparative modeling (Das and Baker 2007; Ding et al. 2008; Parisien and Major 2008; Flores and Altman 2010; Rother et al. 2011; Popenda et al. 2012; Zhao et al. 2012; Cheng et al. 2015; De Leonardis et al. 2015; Krokhotin et al. 2015; Biesiada et al. 2016; Boniecki et al. 2016; Zhao et al. 2017). Their performances are improving as one can see from the results of the three RNA-puzzle rounds (Cruz et al. 2012; Miao et al. 2015, 2017), where a set of experimentally resolved 3D structures has been blindly predicted.

Recent investigations (De Leonardis et al. 2015; Weinreb et al. 2016; Wang et al. 2017) have shown that the performances of these methods can be substantially improved by using information extracted from multiple sequence alignment (MSA) of families of homologous RNAs. Improvements are achieved by identifying top-ranked site-pairs with stronger coevolutionary signals and using them as distance constraints in modeling tools.

Thanks to the advancement of next-generation sequencing technologies, the huge and increasing amount of sequence data available can be fully exploited to study and model RNA structures. In this article, we set up a manually curated data set of about 70 RNA structures with a high resolution and evaluate the performances of different contact prediction methods on this set. Moreover, we analyze the impact on their performances of important features such as the effective number of homologous RNA sequences that are available, the nucleotide–nucleotide contact definition and the procedure used to construct, align and curate the MSA.

RESULTS

Assessing the performance of DCA-based methods

In this section we compare the performance of the prediction methods tested, namely the mean-field of pydca (Zerihun et al. 2020), EVcouplings (Weinreb et al. 2016), Boltzmann learning (Cuturello et al. 2020), GREMLIN (Kamisetty et al. 2013), CCMpred (Seemayer et al. 2014), and PSICOV (Jones et al. 2012). In Figure 1A we report the positive predicted values (PPVs) on the data set D as a function of the number of contacts. Here we are considering all contacts in the PDB structures that are distant from the sequence more than 4 nt.

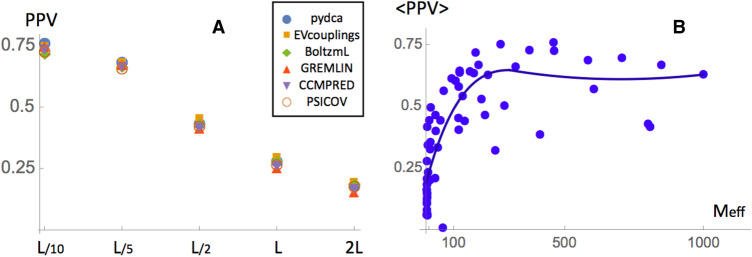
FIGURE 1.

(A) Prediction performances of the different methods analyzed in this paper measured by PPV as a function of the number of top scoring contacts. All contacts that are separated along the sequence by at least 4 nt are considered. (B) Averaged PPV of all prediction methods as a function of the effective number of sequences M_eff.

The performance based on PPV are generally quite good. We find a PPV of the order of 75% for the top L/10 contacts that goes smoothly down to 25% if one considers the top L contacts. Among all methods no statistically significant differences can be observed, as measured from the Kolmogorov–Smirnov test of the different prediction results. A slightly more accurate performance for a small number of contacts can be observed for pydca and GREMLIN for L/10 number of contacts, while at L/2 contacts the EVcouplings is a few percent more accurate than other predictors (see Table 1).

TABLE 1.

Performance of the DCA-based methods analyzed on the different data sets

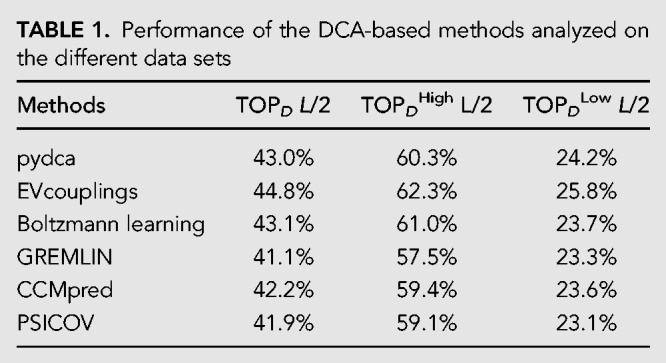
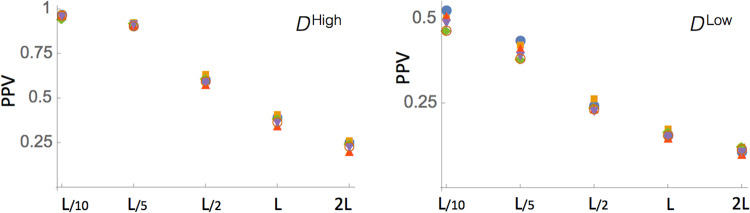
When performances are evaluated on D^High, that is, the set of PDBs associated to RFAM families with M_eff ≥ 70, we observe higher PPV equal to about 60% (at L/2) in contrast to a PPV of 26% in the D^Low set in which only families with M_eff < 70 are considered (see Table 1; Fig. 2).

FIGURE 2.

Prediction performances of the methods on the D^High and D^Low data sets. Only contacts that are separated along the sequence of at least 4 nt are considered here.

In Figure 1B we investigate how performances are related to M_eff by plotting the average PPV rate of different methods versus the M_eff of the given RFAM family. We observe a clear growth of the prediction accuracy up to M_eff values equal to about 200 while above that threshold the performance only increases slightly. Typically around M_eff ≈ 300, there is only minuscule or no further increase of accuracy for a larger number of effective sequences. For M_eff > 300, both additional information and noise are added to the MSA canceling each other. As a check of this behavior we compare the performances of pydca on the full RFAM families and on a randomly chosen subset composed of 1/3 of their entries. The ratio of their PPVs as a function of the M_eff of the reduced family subsets is plotted in Supplemental Figure S1. For subsets with a reduced M_eff < 100, the addition of information improved the method's performance as expected; above that threshold it is not trivial to find a conclusive statement due to the limited amount of data: The addition of sequences has a minor effect on the performance and can improve or decrease them.

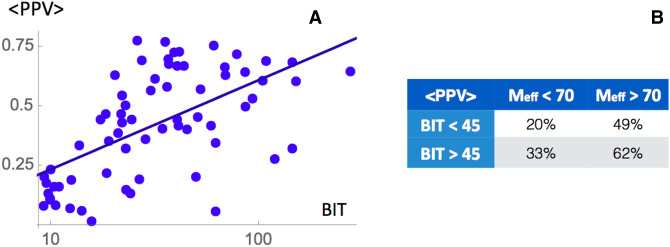
Performances are not only related to the M_eff of RFAM families but also from how well the target sequences align to them. In order to check this dependence in Figure 3A we plotted the averaged PPV as a function of the BIT value computed from Infernal, a score measuring the probability of the query sequence to match the covariance model. We observe a linear relation between these two quantities. To check the effect of both M_eff and the BIT score, we first divided each of D^High and D^Low into two subsets considering only the entries with BIT scores higher or lower than 45. Then we computed the performances in each of the four subsets and we found a stronger impact of the number of effective sequences with respect to the BIT score (Fig. 3B)

FIGURE 3.

(A) Averaged PPV of all prediction methods as a function of the BIT score value for the chosen RFAM family. (B) Table of comparison for PPV as influenced by different values of M_eff and BIT score.

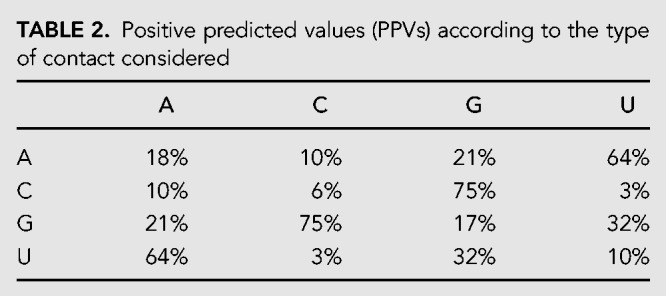
We also analyzed in detail which type of contacts are better predicted. In Table 2 we report the PPV for different nucleotide pairs and we can clearly see that C:G and A:U, which (mainly) correspond to canonical base pairs, are usually well predicted with a PPV of 75% and 65%, respectively. These larger fractions of true positives with respect to other contacts can be expected since the physical interaction between them is stronger and as a consequence also the coevolutionary signal. Note that the fact that C:G pair is more stable than A:T could be related to the slight difference between their prediction accuracy. There are, however, also noncanonical pairs that are relatively well predicted, even if to a much less extent, such as the G:U pairs with a PPV of 32%.

TABLE 2.

Positive predicted values (PPVs) according to the type of contact considered

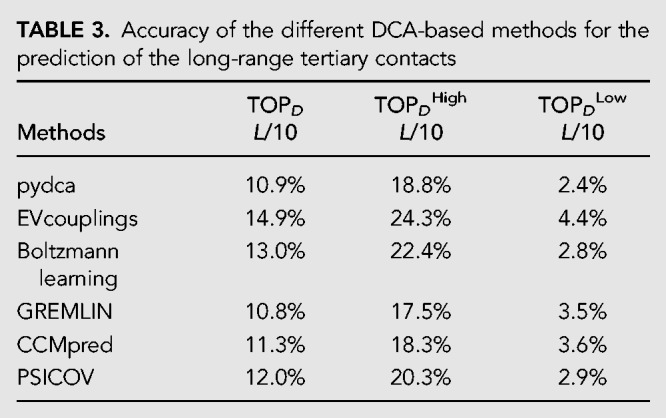
To assess more in depth the ability of the DCA methods to predict the more challenging non-WC long-range 3D contacts, which give important information regarding the three-dimensional structure of RNA molecules, we repeat the analysis shown above but exclude from the experimental RNA map all contacts that are in 5 × 5 windows centered at any WC base pairs.

In Table 3 we report the PPV for this type of contacts at L/10 numbers of contacts. We can immediately observe that the values are much smaller than in the case in which all residues are considered. There is essentially no signal in the D^Low set while for D^High the PPV is between 20% and 25% with the plmDCA method EVcouplings that reaches the best performance.

TABLE 3.

Accuracy of the different DCA-based methods for the prediction of the long-range tertiary contacts

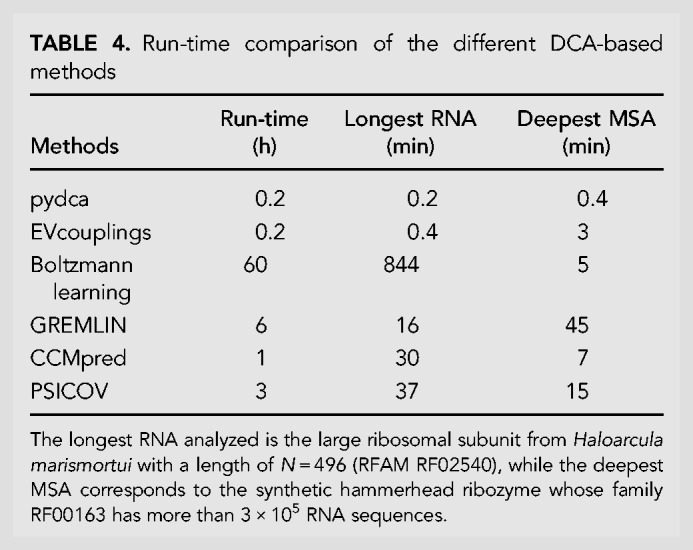
Finally, we test the computational efficiency of different methods by assessing their runtime for the complete set of RNA structures. We ran all tests on an Intel i7-7700 four-core processor using all eight threads available.

As we can see from Table 4, the mean-field DCA in pydca and EVcouplings are the fastest approaches with a global run-time for all structures of D of about 10/15 min. They are about five times faster than CCMpred, a pseudo-likelihood-based method known to be particularly performing when optimized on GPU-based architecture, and from 15 to 30 times faster than GREMLIN and PSICOV. The slowest method is the Boltzmann learning, which is about 300 times slower than mean-field DCA. Note that, as shown in Table 4, the methods tend to have two bottlenecks in terms of run-time, the first is for long RNA sequences such as the large ribosomal subunit from Haloarcula marismortui while the second one is for deep MSAs such as the family RF00163 with more than 3 × 10⁵ RNA sequences.

TABLE 4.

Run-time comparison of the different DCA-based methods

Contact type and prediction robustness

We test the robustness of the DCA-based contact predictions with respect to varying contact definitions. In Table 5, we compare the PPVs of mean-field DCA for the six different contact definitions that have been introduced in Materials and Methods.

TABLE 5.

Accuracy of the mean-field DCA for different contact definitions classified according to the distance threshold and the atoms used in the computation of the nucleotide pair distance

Regarding the type of contacts analyzed, we see that there is no substantial difference in considering different type of contact criteria N1–N9 (9.5 Å), all atoms (3.5 Å) and C1′–C1′ (9.5 Å) where the threshold distances have been taken from (Pietal et al. 2012). For this reason we took, as criteria throughout the paper, the distance between N1 atoms for purine and N9 atoms for pyrimidine that are the atoms that established the glicosylic bond with the C1′ atoms of the pentose sugar.

Not surprisingly, the PPV accuracy improves if the distance criteria are relaxed. For example, using all atoms distance from 3.5 to 9.5 we have a PPV that increases from about 40% to a value close to 60%.

RFAM family construction, sequence alignment and trimming

In this section we analyze how the preliminary steps of the computation, that is, the search for homologous sequences and the MSA curation, impact the DCA prediction of RNA contacts (Table 6). As a first step, since almost half of the RFAMs considered do not have a large enough M_eff value, we modify the E-value cutoff used to constitute the RNA families in Rfam 14.1. We did it using the cmsearch option of Infernal without modifying the covariance models of the family but choosing a large E-value threshold equal to 0.99. On the other side, since the introduction of too many sequences in a given family can introduce noise, we also repeated the same analysis but with a more stringent cutoff of 0.0001.

TABLE 6.

Impact of the MSA construction, alignment and trimming on the performances of the mean-field DCA contact prediction method

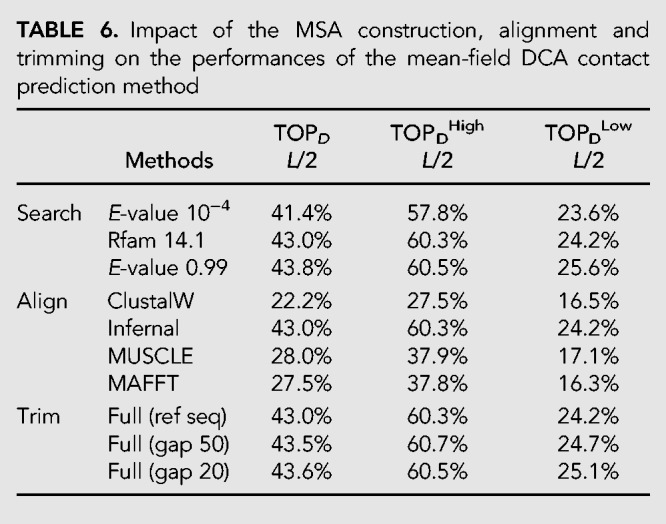
The results do not change significantly but we can observe a few trends: The enlarging of the thresholds slightly improves the contact prediction of families with M_eff less then 70 while keeping constant the prediction of the other ones. A more severe cutoff makes instead the performance predictions lower by about 2%.

The way in which the alignment is performed impacts the prediction performances more substantially. Alignments obtained via ClustalW lead to less accurate PPV with a value of about 20%. MUSCLE and MAFFT perform better than ClustalW with more or less the same accuracy (PPV values of about 30%). Finally, alignments done using Infernal improve substantially the performance with a PPV score that is about 10% above those obtained using MUSCLE and MAFFT. The higher PPV values from Infernal are, however, not surprising, as the covariance models used in Infernal are constructed from seed alignments that in turn are constructed using available information and annotations about RNA sequences such as RNA 2D structure.

Finally, the way in which the alignment is trimmed also does not change the mean-field DCA performance and usually excludes the columns in MSA that have more than 50% of gaps, which results in more accurate contact predictions.

Example of contact predictions

In order to provide an example of RNA contact prediction we analyze the aptamer domain of the adenine riboswitch from Vibrio vulnificus. Its three-dimensional structure has been deposited in the Protein Data Bank with the code 4TZX (Zhang and Ferré-D'Amaré 2014). This type of ncRNA that resides in the 5′ untranslated region of the add adenosine deaminase mRNA is one of the smallest riboswitches (with an aptamer domain of 71 residues) and it controls the translation machinery. When adenine, to which it binds, is not present, the aptamer region has a fold that prevents translation initiation. In the presence of adenine, ligand-binding allosteric effects lead to the rearrangement of the secondary structure of the aptamer region and as a consequence to the initiation of translation.

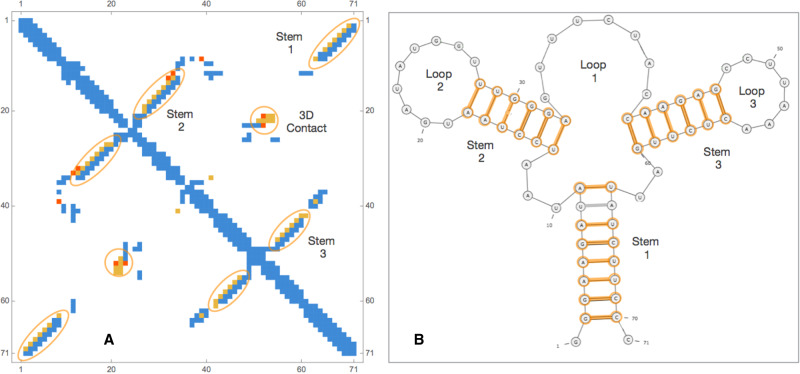
In these conditions, the structure is formed by three helices P1, P2, and P3 (see Fig. 4) and three loops. In physical space, three dimensional contacts occurring between stem–loop 2 and 3 stabilize the 3D structure.

FIGURE 4.

(A) Contact map of the adenine riboswitch from Vibrio vulnificus: in orange and red, the correctly and wrongly predicted contacts in the top 35 pairs, respectively, while in blue all other contacts from PDB structure 4TZX. In B we plot its secondary structure within orange all correctly predicted WC base pairs in the top 35 pairs.

In order to predict the contacts, we start from the RFAM RF00167 (BIT score 59.4) and realign all sequences in the family using the Infernal tool. We then applied mean-field DCA implemented in pydca and the results of contact prediction are shown in Table 7 and in Figure 4.

TABLE 7.

Predicted positive values for different number of contacts N and dfferent contact threshold definitions for the adenine riboswitch from Vibrio vulnificus

As we can see from Table 7 the PPVs are quite high as all 20 but one WC base pairs of the three stems are correctly identified in the first 35 contacts (=L/2). Moreover, there are also several 3D contacts, that is, long range contacts in the sequence that are away from any WC base pairs, predicted. For example, there are five contacts in the green circle of the contact map of Figure 4 that signal an interaction between the loops 2 and 3. In total, in the first seven 3D contacts, four of them (PPV_3D = 57%) are correctly predicted (distance threshold at 9.5 Å), but this number rises to six (PPV_3D = 86%) if the distance threshold is enlarged to 11.5 Å. As shown in a series of recent papers, the correct prediction of these 3D contacts and their use as constraints in molecular modeling tools can substantially improve the accuracy of the RNA 3D structure prediction (De Leonardis et al. 2015; Weinreb et al. 2016; Wang et al. 2017; Pucci and Schug 2019).

DISCUSSION

Coevolution between pairs of nucleotides in MSA of homologous RNAs can provide important information about the three-dimensional structure of RNA. As RNA structure and function are closely interlinked, coevolutionary methods promise to play an important role in the understanding of a wide series of RNA-based biological mechanisms.

In order to assess the accuracy of six different widely known DCA methods more precisely, we first constructed a well curated data set of about 70 RNA structures with good resolution. We then perform MSA alignment of their corresponding RFAM families and run six contact prediction tools: mean-field pydca, EVcouplings, Boltzmann Learning, GREMLIN, PSICOV and CCMpred. These tools use different DCA-approaches: mean-field DCA (pydca), pseudo-likelihood (EVcouplings, GREMLIN and CCMpred), Boltzmann learning and the sparse inverse covariance estimation (PSICOV).

We find that there are no statistically significant differences between their performances as measured by PPV. The prediction performance strongly depends on two factors: the first one is the number of effective sequences M_eff of the given RFAM family. Indeed, we show that only families that have at least M_eff of the order of about 100 lead to reliable prediction's performances.

The second is the procedure used to perform the alignment. In this regard alignments done using Infernal give much better results than those obtained with other methods, with the caveat that the Infernal covariance model is based on additional information.

We also noticed that the prediction of 3D contacts that are far in the sequence and from any WC base pairs, does not yet reach a satisfactory performance for the majority of the entries. While expected (these contacts should exhibit weaker coevolutionary signals when compared with the WC base pairs) this is also unfortunate as prediction of such long-ranged contacts can considerably boost the 3D structure prediction. Machine-learning methods could be used in this more difficult identification since these methods are constructed and optimized to detect weak signals from noisy background.

Finally, both the resolution of RNA 3D structures and the definition of contact considered do not impact significantly the methods’ performance.

In summary, improving RNA contact predictions remains a challenge. The analysis done in this paper, with the construction of a new data set of RNA structures and all tests done, provides new insights on DCA-based approaches highlighting their strong and weak points and could be a starting point for future improvements in the field.

MATERIALS AND METHODS

Data set curation

We manually curated a data set of three-dimensional RNA structures starting our analysis from the whole Protein Data Bank (Berman et al. 2000) and selecting all RNA structures that satisfied the following criteria:

• The RNA structures are not in a complex with proteins or DNAs

• Only monomeric structures are considered

• The lengths of RNA sequences are greater than 40 nucleotides

• In cases of structures with similar sequences (sequence identity (SI) between pairs of sequences ≥50%) we choose only the structures with higher resolution

• Only structures resolved via X-ray crystallography with resolution below 3.6 Å are taken into account

We associated one RNA family from the Rfam database (Kalvari et al. 2017) to each entry in the data set by choosing the family with the highest match to the sequence. This search has been done using INFERence of RNA ALignment tool (Infernal) using the BIT value as a match score (Nawrocki and Eddy 2013).

For each family we then computed the number of effective sequences M_eff via the pydca software package (Zerihun et al. 2020). This value is computed from the alignment of the given RFAM family as M_eff = $\sum _k{\omega }_k$, where ω_k is the weight of the k^th entry in the given cluster of similar sequences that is identified using a cutoff on the SI equal to 0.8 (Morcos et al. 2011).

We further split the final set D comprised by 69 RNA structures into two subsets: D^High containing 36 structures associated to RNA families with a M_eff larger than or equal to 70. The 33 remaining entries belong to D^Low set and have a MSA with M_eff < 70. The list of all entries in D with their characteristics is reported in the Supplemental Information, Table S1. The generated alignments and the PDB files for all RNA families can be found at https://github.com/KIT-MBS/RNA-dataset.

Contact definition

In order to study how the nucleotide–nucleotide contact definition influences the performance of DCA methods, we computed and compared positive predicted values (PPVs) using different criteria to construct the contact maps from PDB structures. We chose and tested six distance-based criteria to classify if a pair of nucleotides is in direct physical interaction or not:

1. Two nucleotides are in contact if the distance between the N9 atoms of a purine or the N1 of a pyrimidine is smaller than 9.5 Å.

2. Two nucleotides are in contact if the distance between their C1′ atoms is smaller than 12.0 Å.

3. Two nucleotides are in contact if the distance between two of any of their heavy atoms is smaller than 3.5, 5.5, 7.5, and 9.5 Å.

Multiple sequence alignment and curation

As the quality of the multiple sequence alignment critically impacts the accuracy of the subsequent contact prediction, we tested different methods to perform and curate such alignments. Specifically, we studied how the mean-field DCA performances change according to the method used.

1. Search. We started to verify if the construction of the RFAM families can influence the prediction performance. To do that we used either the RFAM families as given in RFAM v14.1, but we also reconstruct them using both less and more stringent E-value cutoffs equal to 0.0001 and 0.99, respectively. This search is done using the Infernal software (cmsearch) and the precomputed covariance model (CM) of the given family.

2. Align. The first methods used to perform the MSA of the RFAM families is the Infernal software (Nawrocki and Eddy 2013). Specifically, all entries of the RFAM family considered are aligned using the corresponding covariance model (CM) that is a specific profile stochastic context-free grammar that scores a combination of sequences and RNA secondary structure consensus. We also tested three other commonly used tools for the multiple sequence alignment of RNAs that are CLUSTALW (Thompson et al. 1994), MUSCLE (Edgar 2004) and MAFFT (Katoh and Standley 2013).

3. Trim. From the MSA of the given family we tested three different possibilities: in the first one only positions corresponding to the target sequence were considered for the DCA computations; in the second and the third ones, before the DCA computation we trimmed the MSA by selecting only columns that have less than 50% and 20% of gaps, respectively.

Coevolution-based methods

Different methods have been developed for the implementation of the direct coupling analysis (DCA) of RNAs. Given a family of homologous RNA sequences, these statistical models assign probabilities P(S) to each sequence S = a₁ a₂… a_L of length L using the the Boltzmann law as

$$P(S)=\frac{1}{Z}\exp (-\text{β}H),$$ (1)

where β is the inverse of the temperature usually fixed to one without loss of generality, Z the partition function and H the Hamiltonian taken of the form

$$-\text{β}H=\sum _{i=1}^L{h}_i(a_i)+\sum _{i<j}^L{J}_{ij}(a_i,a_j)$$ (2)

that contains single site terms h_i (a_i), and nucleotide pair interactions J_ij (a_i, a_j). In DCA these parameters are inferred from the input MSA using different approaches that are briefly shown here. See also Zerihun and Schug (2017) and Cocco et al. (2018) for recent reviews on the topic.

• Mean-field DCA. A mean-field approximation of the partition function is used to obtain the couplings and the single-site fields in a computationally efficient way. Within this approximation the two-body couplings J_ij (a_i, a_j) are obtained from

$$J_{ij}(a_i,a_j)=-{(C^{-1})}_{ij}(a_i,a_j),$$ (3)

where C is the matrix of correlations whose elements are given by C_ij (a_i, a_j) = f_ij (a_i, a_j) − f_i (a_i)f_j (a_j) with f_ij (a_i, a_j) and f_i (a_i) the empirical frequency counts obtained from the MSA columns. The single-site fields h_i (a_i) are obtained self-consistently from the frequencies f_i (a_i) and the couplings in Equation 3. We used the mean-field implementation in pydca (Zerihun et al. 2020).

• Boltzmann learning. In this statistical approach the parameters J_ij (a_i, a_j) and h_i (a_i) are obtained from the minimization of the negative log-likelihood

$$l=-\frac{1}{B}\sum _{b=1}^{B}Log(P(S^b)),$$ (4)

where P(S^b) with (b = 1…B) is a set of independent equilibrium configurations of the model, that is, RNA sequences that belong to a MSA. A direct way to solve the problem is to do a “brute-force” minimization starting from an initial guess for the values of the couplings and fields and using a gradient descent algorithm that uses a Markov chain Monte Carlo method for the gradient evaluation. For more details on the method and the implementation that we used, see Cuturello et al. (2020).

• We use the EVcouplings (Weinreb et al. 2016) implementation that uses a pseudo-likelihood maximization direct couplings analysis (plmDCA) (Ekeberg et al. 2013). In this method the probability in Equation 4 is substituted with the conditional probability of observing one variable a_r given the observation of the others ${\overline{a}}_r=(a_1\dots a_{r-1},a_{r+1}\dots a_L)$. Given the MSA, one has then to minimize the conditional log-likelihood

$$pl=-\frac{1}{B}\sum _{b=1}^B\sum _{r=1}^{L}Log(P(a_r^b|{\overline{a}}_r^b)),$$ (5)

with regularization to estimate the couplings and the fields. This strategy, while retaining the accuracy of the full likelihood approach, greatly increases its computational efficiency.

• GREMLIN (Kamisetty et al. 2013) uses a learning procedure that is based on the pseudo-likelihood optimization. It can incorporate prior information on predicted secondary structure and on sequence separation when it is applied on proteins. For RNA contact prediction, GREMLIN does not use any additional information with respect to MSA.

• CCMpred (Seemayer et al. 2014) is an implementation based on plmDCA similar to EVcouplings. CCMpred is computationally optimized for GPU architectures even if in this study is run on a CPU system.

• PSICOV (Jones et al. 2012) computes the elements of the so-called partial correlation coefficient matrix defined as

$${\rho }_{ij}(a_i,a_j)=\frac{J_{ij}(a_i,a_j)}{\sqrt{J_{ii}(a_i,a_i)J_{jj}(a_j,a_j)}},$$ (6)

in terms of the inverse of the covariance matrix (Eq. 3). ρ_ij encodes the correlation between any pair of amino acids or nucleotides at two sites, in terms of the frequencies at all other sites, and identifies which pairs are likely to be in direct physical contact in the native structure. The estimation of the inverse covariance matrix is done using a graphical LASSO approach and the final PSICOV score is given by $\sum _{a_i,a_j}{\rho }_{ij}(a_i,a_j)$ followed by an average product correction (APC) (Dunn et al. 2008).

SUPPLEMENTAL MATERIAL

Supplemental material is available for this article.