Abstract
Recent advances have led to the discovery of specific genetic variants that predict educational attainment. We study how these variants, summarized as a linear index—known as a polygenic score—are associated with human capital accumulation and labor market outcomes in the Health and Retirement Study (HRS). We present two main sets of results. First, we find evidence that the genetic factors measured by this score interact strongly with childhood socioeconomic status in determining educational outcomes. In particular, although the polygenic score predicts higher rates of college graduation on average, this relationship is substantially stronger for individuals who grew up in households with higher socioeconomic status relative to those who grew up in poorer households. Second, the polygenic score predicts labor earnings even after adjusting for completed education, with larger returns in more recent decades. These patterns suggest that the genetic traits that promote education might allow workers to better accommodate ongoing skill biased technological change. Consistent with this interpretation, we find a positive association between the polygenic score and nonroutine analytic tasks that have benefited from the introduction of new technologies. Nonetheless, the college premium remains a dominant determinant of earnings differences at all levels of the polygenic score. Given the role of childhood SES in predicting college attainment, this raises concerns about wasted potential arising from limited household resources.
1. Introduction
Economists generally accept that the skills rewarded in the labor market arise from a combination of endowed abilities, economic environments, and endogenous human capital investments. Endowments, environments, and investments almost certainly interact in complicated ways, transforming the distribution of abilities drawn at birth into a distribution of education, wages, and labor supply outcomes over the life-cycle.
Understanding this web of interactions and its implications for economic inequality has been a long-standing project in labor economics (Mincer 1958; Becker and Chiswick 1966; Griliches and Mason 1972). Selecting an appropriate policy response to inequality requires an accurate diagnosis of its origins. Poor households possess limited resources for human capital investment, which naturally suggests a role for redistributive policies. However, disparities in endowments might also play a part. If individuals with unfavorable endowments do not acquire more human capital for reasons unrelated to resources (e.g., lower returns to these investments), then simply relaxing resource constraints and expanding access to education may not substantially reduce inequality. However, understanding the mapping between endowments, investments, and economic outcomes is challenging: ability is notoriously difficult to measure and typical proxies (such as IQ test scores) are subject to the critique that they reflect earlier investments.
A common assumption is that genes and other biological factors at least partially determine heterogeneity in ability across individuals (e.g., Todd and Wolpin 2003). In this study we exploit recent advances in genetics to explore the relationship between a genetic index, educational attainment, and labor market outcomes in the Health and Retirement Study (HRS). Specifically, we utilize a polygenic score (a weighted sum of individual genetic markers) constructed with the results from Lee et al. (2018) to predict educational attainment.1 The markers most heavily weighted in this index are linked to early brain development, as well as processes affecting neural communication (Okbay et al. 2016; Lee et al. 2018). We interpret the polygenic score as summarizing a subset of the genetic factors that influence traits relevant for human capital accumulation.2
Pairing this score with rich longitudinal data allows us to test propositions about the role of individual endowments in shaping education and labor market outcomes. Specifically, we examine whether childhood environments interact with genetic endowments in determining educational outcomes, and whether these endowments are associated with economic outcomes beyond their relationship with completed schooling. In empirical labor economics, genetic factors and other endowments are typically subsumed into an error term, averaged out with additive fixed-effects, or relegated to a “black box” of permanent unobserved heterogeneity that must be integrated out of econometric models (Lillard and Willis 1978).3 In such approaches the structure of human capital endowments, together with the nature of their interactions with the economic environment, is assumed rather than observed.4 This may be appropriate if the goal is to reduce bias in estimation by controlling for omitted factors. However, this approach is insufficient if our goal is to learn about the structure of ability and resulting implications for policy.
A large literature uses test scores such as IQ or AFQT (Armed Forces Qualification Test) as proxies for the cognitive abilities relevant for education and labor market outcomes. However, investments and environmental factors (e.g., childhood poverty) can significantly influence these proxies, making it difficult to interpret their variation across individuals (Flynn 1987; Turkheimer et al. 2003; Todd and Wolpin 2007; Mani et al. 2013).5 Among other things, this means that two individuals with similar cognitive test scores but different childhood circumstances are unlikely to have started with the same underlying human capital endowments. Reliance on these proxies may therefore lead the analyst to misattribute observed disparities in economic outcomes to differences in ability endowments rather than earlier investments. In turn, this could lead to incorrect conclusions on the returns to human capital investments (e.g., public education, college subsidies, etc.). In contrast, even though the genetic index we study is undoubtedly correlated with parental characteristics, its use is not subject to the critique that it is the product of endogenous investments, since it is fixed at conception.6
We present two main sets of results. First, we document the association between the polygenic score and educational attainment, and demonstrate that this association differs by childhood SES. Using the HRS data, we replicate the strong relationship between the genetic score and educational attainment found in past studies (Okbay et al. 2016; Lee et al. 2018). A one-standard-deviation increase in the polygenic score predicts between 0.59 and 0.84 additional years of education, whereas variation in the score accounts for 3.4%–7.5% of the variation in years of schooling, depending on the control set. After this replication exercise, we turn to new analyses enabled by the availability of molecular genetic data for HRS respondents.7 A surprising descriptive fact emerges in the relationship between the polygenic score and retrospective measures of childhood SES. Although the polygenic score is positively correlated with childhood SES, the distribution of the score is strikingly similar across SES groups. This empirical pattern makes it possible to compare economic outcomes for a large set of individuals with similar genetic scores, but different childhood SES. We find that high childhood SES seems to reduce the association between genes and the probability of completing high school, whereas increasing the genetic gradient in the propensity to earn a college degree. These findings could reflect different patterns of substitutability and complementarity between genes and family resources in producing early versus later human capital outcomes. More broadly, these SES interactions underscore the importance of examining gene–environment interactions to understand economic inequality and the distributional consequences of interventions.
Understanding the role of endowments is particularly important in light of the large earnings premium associated with a college degree and its growth over the last several decades. Given substantial returns to schooling, we expect genetic endowments for education to unconditionally predict earnings. However, the factors that allow one to more easily acquire schooling may also permit greater economic success, even conditional on a particular level of investment (better cognitive endowments, greater persistence, etc.). This motivates our second set of new analyses that test whether—and through what mechanisms—the genetic factors associated with education independently predict better labor market outcomes. This question is particularly relevant given the sizable interactions between childhood SES and genetic endowments. Although it is certainly possible that individuals with favorable endowments realize their full earnings potential even without a college degree, it may also be the case that individuals with high polygenic scores are unable to fully compensate for the lack of a college degree in the labor market. If so, disparities in childhood SES may erect barriers to college completion and lead to the wastage of economic talent.
Using administrative records that cover the lifecycle, we find a strong relationship between the polygenic score and labor market earnings, even after controlling for completed education. The returns to these genetic endowments appear to rise over time, coinciding with the rise in income inequality after 1980. Accounting for degree and years of schooling, a one standard deviation increase in the score is associated with a 4.8% increase in earnings after 1980. These results are consistent with recent literature on income inequality showing not only an increase in the college premium, but also a rise in the residual wage variance within educational groups (Lemieux 2006). We also find a positive association between the score and the kinds of nonroutine job tasks that benefited from computerization and the development of more advanced information technologies (Autor, Levy, and Murnane 2003). This provides suggestive evidence that the endowments linked to more educational attainment may allow individuals to either better adapt to new technologies, or specialize in tasks that more strongly complement these new technologies. Nonetheless, despite returns to these endowments for those with and without a college degree, the average college premium remains large across all values of the polygenic score. Poor childhood environments appear to squander the human potential of individuals with favorable genetic endowments by preventing access to increasingly lucrative educational pathways.
This paper adds to an emerging literature examining molecular genetic associations with economic outcomes.8 However, to our knowledge, this is the first study to estimate the returns to genetic factors associated with education using micro genetic data and disaggregated measures of earnings and job tasks across cohorts. Our results therefore offer two broad contributions that link the literature on behavioral genetics to the economics literature on human capital, ability, and economic outcomes. First, our results demonstrate that several core findings obtained with proxies of cognitive ability continue to hold with a biological measure of endowments that predicts schooling and is fixed at conception. Even if genetic data offered no other insights, this would provide some evidence that test scores capture useful information on endowments, and not just post-birth investments. A second contribution, however, consists of novel results on the origin and function of heterogeneity in the earnings distribution. Our results on the rising genetic earnings premium (controlling for education) implicate genetic heterogeneity in a series of important and well-documented patterns in labor economics. In particular, the same factors associated with greater human capital accumulation also appear to be increasingly important for earnings during a period of technological and structural change in the economy.
Our results also illustrate how genetic measures can be used to generate novel insights about the importance of interactions between endowments and childhood environments in the study of economic inequality. We provide some of the first evidence using molecular genetic measures that people with favorable genetic endowments may face barriers to exploiting their potential if they are born into poor families.9 This finding relates to a larger literature exploring similar interactions using different measures of endowments, or using alternate methods to measure genetic contributions. Leibowitz (1974) is an early example of research recognizing heterogeneity in returns to ability measured by IQ. Further contributions have emphasized the consequences of such interactions for inequality. Consistent with our findings, Guo and Stearns (2002) use a twin-study design to provide evidence that resource-poor environments imply lower returns to genetic endowments. Gene–environment interactions could also explain why genetic influences on IQ are relatively strong for high-SES children, a phenomenon known as the Scarr–Rowe Hypothesis (Scarr-Salapatek 1971; Nisbett et al. 2012; Bates, Lewis, and Weiss 2013; Kirkpatrick, McGue, and Iacono 2015; Tucker-Drob and Bates 2016). This would occur if returns to genetic endowments (as measured by IQ) are stronger in resource-rich households, which is consistent with our findings on gene–environment interactions and college education.10
Our results on gene–environment interactions are also linked to work on treatment effect heterogeneity, which has emerged as an important topic in econometrics and applied work. Heckman and Vytlacil (2005) develop econometric methods for the case of heterogeneous treatment effects, either due to choices or responses. Many studies document a range of heterogeneous responses to interventions related to labor, including welfare reform (Bitler, Gelbach, and Hoynes 2006), information about payoffs to education (Wiswall and Zafar 2015) and education subsidies (Todd and Wolpin 2006). Related, Keane, Moffitt, and Runkle (1988) study how individual-level heterogeneity affects responses to economic shocks, in their case labor supply decisions over the business cycle. In our case, responses to technological shocks may in part be explained by heterogeneity in genetic endowments.
The remainder of the paper is organized as follows. In Section 2, we discuss recent developments in behavioral genetics (and their limits), focusing on techniques used to establish links between genes and economic outcomes. In Section 3, we relate the polygenic score to education and childhood SES. In Section 4, we discuss how the polygenic score relates to labor market outcomes. Section 5 concludes.
2. Genetic Data and Their Limits
In this section, we provide some basic information about the molecular genetic data we use in this study. We also discuss some problems, points of clarification and interpretational difficulties. Online Appendix A provides additional detail.11
2.1. Genetic Data and Genome-Wide Association Studies
The human genome consists of approximately 3 billion nucleotide pairs spread out over 23 chromosomes pairs. An individual possesses two copies of each chromosome, inheriting one copy from each of its parents.12 The base pairs are the “rungs on the ladder” of classic double-helix structure. Genes are subsequences of these base pairs that often contain the instructions for synthesizing proteins. There are about 50,000 genes in the human genome. At the vast majority of base pair locations in the genome (about 99%), there is no variation across individuals in the nucleotide. At the remaining locations (less than 1%), the base pair may differ across individuals. Such locations are referred to as single-nucleotide polymorphisms (SNPs, pronounced “snips”).
A major task of behavioral genetics involves determining which, if any, of these SNPs are associated with behavioral outcomes. Genome-wide association studies (GWAS) provide one tool for estimating these associations. Under the GWAS methodology, researchers scan the entire genome for SNPs that are associated with a particular phenotype (trait or outcome). Variation at a particular SNP is measured by a count variable indicating how many copies of a particular base pair molecule an individual possesses at that genetic location. These variables can take the values 0, 1, or 2 because an individual has two copies of each chromosome. The outcome of interest is typically regressed on each observed SNP count (one at a time), while also controlling for principal components of the full matrix of SNP data. As indicated by Price et al. (2006) (and discussed at length in Benjamin et al. (2012) in the context of economic outcomes) the principal components can correct for population stratification and account for genetic differences across ethnic groups. The presence of these controls limits the concern that gene-behavior associations reflect associations with specific ethnic ancestry groups as opposed to specific biological pathways. In our subsequent analysis we always control for population stratification using the first 10 principal components of the full matrix of genetic data.13
Although GWAS studies have produced a number of credible and replicable gene-outcome associations, GWAS results for educational attainment have only emerged recently. After documenting the first genome-wide significant associations for education (Rietveld et al. 2013), the Social Science and Genetics Association Consortium extended their analysis to perform an educational attainment GWAS with larger sample sizes, starting with Okbay et al. (2016) (N = 293,723), which discovered 74 SNPs with associations strong enough to be considered genome-wide significant.14 The score we study in this paper is based on results from the most recent education GWAS from this group, Lee et al. (2018), featuring a discovery sample of over 1.1 million people. Many of these SNPs were linked to biological processes known to be involved in fetal brain development. Evidence presented in Okbay et al. (2016) and Lee et al. (2018) heavily implicates cognitive mechanisms in the biological pathways that link the score to educational attainment. Lee et al. (2018) find that some of the significant SNPs tend to be expressed prenatally in brain tissues, whereas others are expressed throughout the lifecycle. This second group of SNPs tend to be found in genes that “encode proteins that carry out neurophysiological functions such as neurotransmitter secretion, the activation of ion channels and metabotropic pathways, and synaptic plasticity” (Lee et al. 2018, p. 1114).
GWAS results are often aggregated into polygenic scores for the purposes of prediction and statistical analysis. These scores are linear combinations of individual SNP count variables, weighted by their GWAS coefficients. Importantly, although HRS data are used in the published results for Lee et al. (2018), the score used here has been calculated on the basis of GWAS results without HRS data, ensuring that the score does not mechanically predict educational outcomes. We refer to the score we use as the EA score, where EA stands for “educational attainment”. Since this is the only polygenic score we examine in this paper, we use the terms “EA score”, “polygenic score”, and “genetic score” interchangeably.15
Existing work suggests that polygenic scores usefully summarize genetic information contained by some of the SNPs associated with education. Most existing studies work with earlier, less predictive polygenic scores based on the results of Rietveld et al. (2013) and Okbay et al. (2016). Conley and Domingue (2016) find evidence of changing patterns of assortative mating across cohorts on the basis of a polygenic score for education, whereas Schmitz and Conley (2017) show that genetic heterogeneity can moderate the impact of military service during the Vietnam War on subsequent educational attainment. Closer to our work, Belsky et al. (2016) use the polygenic score to predict childhood and adolescents developmental milestones and cognitive abilities. They examine a sample of 918 New Zealanders and show that a similar polygenic score not only predicts education, but also an index of adult success conditional on education. In relating genes predicting education to an aggregated measure of success in the labor market, their study provides important cross-validation to our own work, though with a different sample and a substantially different set of outcomes and research questions. Finally, Barth, Papageorge, and Thom (2019) show evidence that the EA score predicts wealth in part through financial decision-making and probabilistic thinking.
2.2. Limitations and Interpretational Challenges
We discuss five important caveats and points of clarification regarding our use of the polygenic score for education. First, the genetic variants used in the construction of this genetic score are not located on sex chromosomes. For this reason, the distribution of these variants should be identical across men and women. In our labor market analysis, we focus on males to bypass considerable issues associated with selection into employment. However, we examine both men and women when studying educational investments, the goal being to restrict the sample only when there is a compelling reason to do so. In Online Appendix B, we explore possible gender differences in how the EA score relates to years of education. There are some specifications showing larger coefficients on the EA score for men compared to women.16 An obvious direction for future research would be to study gender differences in returns and, more generally, how the genetic score interacts with female labor supply decisions and labor outcomes.
A second point is that the polygenic score we use was discovered on a sample of individuals of European ancestry. It has been shown in earlier work that a polygenic score discovered on one ethnic group is relatively less predictive if applied to other ethnic groups. A striking example is a polygenic score for height discovered on a sample of Europeans, which erroneously predicts that individuals of African ancestry are on average substantially shorter than genetic Europeans (Martin et al. 2017). It would therefore be misleading and irresponsible to use the EA score we use in this paper to analyze individuals of non-European ancestry. Thus, we limit our sample to individuals of European ancestry as categorized by the HRS. It should be noted that with this restriction, the principal components of the genetic data help to account for intra-European ethnic differences.
Third, we do not claim to estimate causal effects of particular genetic variants. Any gene-outcome association that we observe in general reflects a combination of a direct effect and an indirect effect operating through the environments that parents make for their children.17 Parents with advantageous genetic endowments (some of which they pass on to their children) are more likely to have the resources or capacity to create better environments. Indeed, Kong et al. (2018) find that parental genotypes that are not passed on to their children still predict children’s education, suggesting the operation of this indirect channel.18 Even so, an individual’s genetic make-up is not changed by human capital investments. In contrast, IQ and other cognitive test scores are subject to the critique that they reflect environmental factors, such as earlier human capital investments. Indeed, Bharadwaj, Løken, and Neilson (2013) find that variation in health care received by newborns has an impact on academic achievement years later.19 Genetic indices are not subject to this critique since they are fixed at conception. As we elaborate in what follows (see Online Appendix C and the discussion in Section 3.6), this feature of genetic endowments generates an important exclusion restriction that can be used to correctly sign gene–environment interactions. Moreover, there is strong evidence from a variety of studies showing that much of the relationship between an earlier EA score and educational attainment remains, even after controlling for family fixed effects with data on siblings (Rietveld et al. 2014; Domingue et al. 2015).20 If the relationship between the score and education merely reflected family environments, we would expect between-family variation to be much more strongly predictive of outcomes. Finally, controlling for principal components helps to alleviate the concern that we are merely capturing ethnic differences in social norms surrounding education.
A fourth limitation concerns the variation in observed outcomes that is explained by the polygenic score. Twin studies have established that roughly 25%–40% of the variation in educational attainment can be attributed to genetic endowments, suggesting that genes represent an important source of human capital endowments (Branigan, McCallum, and Freese 2013).21 In our sample of HRS respondents, we show that the polygenic score can explain up to 7.5% of the variation in educational attainment, that is, roughly 19%–30% of the total variation that other methods suggest is attributable to genes. This discrepancy is often referred to as the “missing heritability problem” (Eichler et al. 2010; Zuk et al. 2012) and may arise from a variety of causes, including limited power to detect rare variants or variants with small association sizes, failure to account for genetic interactions, and genetic variation that is not captured by SNP-level differences (e.g., copy-number polymorphic duplications). In practice, the missing heritability problem means that it is difficult to use the polygenic score to draw conclusions about the relative importance of genetic endowments versus environments in generating economic outcomes. This is a drawback of analyses using polygenic scores relative to twin-study methods.22 On the other hand, observed genetic variants allow us to more directly estimate the size and directions of gene–environment interactions (e.g., differences in gene-education gradients by childhood SES), and explicitly identify the variants involved in such interactions.
Fifth, there are interpretational challenges in using the polygenic score in economic analysis. The polygenic score is a linear index of the genetic variants that predict educational attainment. As discussed in the Introduction, we interpret the polygenic score as measuring a subset of genetically endowed abilities relevant for educational attainment, such as a facility with learning or acquiring new skills. We purposefully refrain from describing the polygenic score as ability or as a measure of cognitive ability, which is likely to be misleading and too simplistic. One reason is that the polygenic score is a single aggregate measure, which is at odds with widespread evidence that ability is best thought of as multi-dimensional with different returns depending on the economic outcome in question. In particular, there are distinct cognitive abilities associated with human capital accumulation and labor market success (e.g., attention, language, visuospatial skills, motor skills, executive function and memory) each possessing different associations with economic outcomes (Willis and Rosen 1979; Heckman 1995; Cawley et al. 1997).23 In addition, socio-emotional skills (sometimes known as noncognitive or “soft” skills) play crucial roles in education and labor outcomes (Heckman and Rubinstein 2001).24 Thus, it would make little sense to categorize an individual with a high polygenic score as “high ability” or to equate the polygenic score with cognitive ability.25 Second, it is not clear how genes generate economic outcomes, either on their own or through interactions with the environment. As discussed, pathway analyses suggest that the genes most heavily weighted in the EA score are implicated in the development of brain tissue and in processes related to neural communication. Although this strongly suggests that cognitive processes are involved, we lack a comprehensive understanding of the biological pathways at play. The EA score almost surely includes factors related to skills that are directly related to cognition and facilitate schooling, but may (or may not) be productive in other contexts, such as the labor market.26 That said, one of the benefits of examining the EA score in a rich data set such as the HRS is that it allows us to examine relationships between the EA score and several critical economic variables. Doing so provides valuable insights into how these genetic variants function over the lifecycle, which offers clues on mechanisms underlying their relationship to human capital accumulation.
3. Genes, Education, and Childhood SES
3.1. The HRS Sample and the Genetic Score
The HRS is a longitudinal panel study that follows over 20,000 Americans at least 50 years of age, as well as their spouses. Surveys began in 1992 and occur every two years. The HRS collected genetic samples from 18,994 individuals over the course of four waves (2006, 2008, 2010, 2012). Our analytic sample only includes individuals genotyped in 2006 and 2008.27 Individuals in the genotyped sample tend to be born in younger birth cohorts, since survival until at least 2006 is required for inclusion. Moreover, women and individuals with more education were more likely to agree to the collection of genetic data.
Our main analysis sample includes all genetically European individuals born before 1965 with nonmissing genetic and education data. For reasons outlined in Section 2, we restrict the sample to respondents of European ancestry since the polygenic score we use here was discovered in a sample of consisting solely of genetic Europeans.28 The resulting sample includes 8,537 individuals. Table 1 provides some basic descriptives on demographic and educational variables. The mean level of educational attainment is about 13 years, with 13% of the sample failing to graduate from high school or obtain a GED and about 25% of the sample earning at least a four year college degree. Roughly 42% of the sample is male.
Table 1.
Summary statistics—HRS sample.
| Variable | Mean | Std. | N | Variable | Mean | Std. | N |
|---|---|---|---|---|---|---|---|
| Male | 0.417 | 0.493 | 8537 | Father’s Income | 28.588 | 10.348 | 6773 |
| Birth Year: | Family SES (Childhood) | ||||||
| <1930 | 0.227 | 0.419 | 8537 | Well Off | 0.067 | 0.25 | 8537 |
| 1930–1934 | 0.152 | 0.359 | 8537 | Average | 0.645 | 0.478 | 8537 |
| 1935–1939 | 0.183 | 0.387 | 8537 | Poor | 0.273 | 0.446 | 8537 |
| 1940–1944 | 0.161 | 0.367 | 8537 | Varied | 0.013 | 0.114 | 8537 |
| 1945–1949 | 0.126 | 0.332 | 8537 | Missing | 0.001 | 0.034 | 8537 |
| 1950–1954 | 0.151 | 0.358 | 8537 | Refused | 0.000 | 0.019 | 8537 |
| Degree: | Family Moved (Childhood) | ||||||
| Education (years) | 13.161 | 2.538 | 8537 | Yes | 0.180 | 0.384 | 8537 |
| None | 0.129 | 0.335 | 8512 | No | 0.816 | 0.387 | 8537 |
| GED | 0.045 | 0.207 | 8512 | Missing | 0.004 | 0.062 | 8537 |
| High School | 0.529 | 0.499 | 8512 | Refused | 0.000 | 0.015 | 8537 |
| College (2 year) | 0.05 | 0.219 | 8512 | Fam. Asked for Help (Childhood) | |||
| College (4 year) | 0.147 | 0.354 | 8512 | Yes | 0.134 | 0.341 | 8537 |
| Masters | 0.077 | 0.267 | 8512 | No | 0.851 | 0.356 | 8537 |
| Advanced | 0.023 | 0.148 | 8512 | Missing | 0.015 | 0.12 | 8537 |
| Redo Grade | 0.14 | 0.347 | 8166 | Refused | 0.000 | 0.015 | 8537 |
| Parents’ Educ. (years) | Father Lost Job (Childhood) | ||||||
| Father | 10.229 | 3.593 | 6711 | Yes | 0.204 | 0.403 | 8537 |
| Mother | 10.672 | 3.017 | 6993 | No | 0.728 | 0.445 | 8537 |
| SSA Earnings (96,721 person-year obs.) | Never Worked | 0.006 | 0.075 | 8537 | |||
| Mean | 59,180 | Never There | 0.056 | 0.229 | 8537 | ||
| Std. Dev. | 32,851 | Missing | 0.007 | 0.084 | 8537 | ||
| 25th percentile | 34,173 | Refused | 0.000 | 0.015 | 8537 | ||
| 50th percentile | 55,295 | Health as Child | |||||
| 75th percentile | 75,005 | Excellent | 0.545 | 0.498 | 8537 | ||
| Num. Respondents | 3,140 | Very Good | 0.256 | 0.436 | 8537 | ||
| Good | 0.143 | 0.35 | 8537 | ||||
| Fair | 0.044 | 0.206 | 8537 | ||||
| Poor | 0.012 | 0.108 | 8537 | ||||
| Missing | 0 | 0.015 | 8537 | ||||
Notes: Summary statistics for the primary analytic sample, which consists of 8,537 individuals from the HRS. The sample is limited to individuals of European ancestry genotyped in the 2006 and 2008 waves. The earning data consist of 96,721 person-year observations for 3,140 men from our sample with nonmissing earnings data from the Social Security Administration Master Earnings File (MEF). These summary statistics are calculated without sampling weights. Missing values for the socioeconomic status variables include the responses “Don’t Know”, as well as cases where a response was not ascertained or the question was not asked.
Table 1 also provides descriptive statistics on parental education, as well as a series of categorical variables describing health and various aspects of the SES of the respondent during childhood. These measures include a self-reported five-point scale for health during childhood, a variable indicating the SES of the respondent’s family (Well off, Average, or Poor), as well variables indicating whether the respondent’s family suffered various negative economic shocks (moving due to hardship, asking other families for help, or experiencing an extended period of paternal unemployment or economic inactivity). We also construct a father’s income variable. To do this, we first obtain HRS survey responses on the usual occupation of the respondent’s father (when the respondent was age 16). This father occupation variable is then matched with average labor income data from the 1960 census for prime-age male workers to construct an occupation-specific income variable.29
We measure earned income using records from the Master Earnings File (MEF) of the Social Security Administration (SSA) that have been linked to the HRS.30 The MEF data span the period 1951–2013 and combine reports from employers with Internal Revenue Service (IRS) documents such as W-2 forms to provide a sum of “regular wages and salaries, tips, self-employment income, and deferred compensation” (Olsen and Hudson 2009). The earnings records are top-coded at the maximum income subject to Social Security taxes in each year. When possible, we adjust for this by replacing top-coded amounts with the average level of earnings that exceed the top-code for each year based on the Current Population Survey (CPS).31 As indicated in Table 1, the median real income for a person-year in our sample is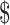 
55,295, whereas the 25th and 75th percentiles are 
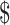;34,173 and 
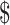75,005, respectively. Figure 1 plots average earnings for each age in our sample separately for individuals with and without a college degree. The data follow a familiar hump-shaped pattern, with earnings starting at low levels early in life, reaching a peak around age 50 for less educated individuals and closer to age 60 for more educated individuals. For less educated individuals, earnings decline as individuals age and reduce their labor supply later in life.32
Figure 1.
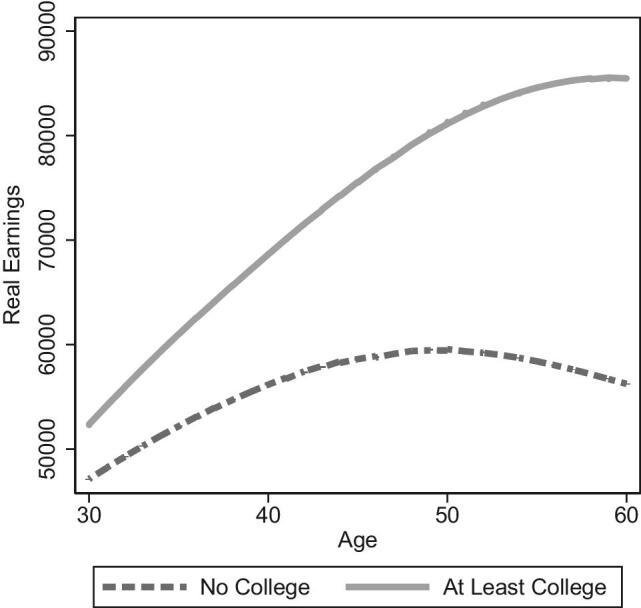
Age-earning profiles by education group. Nonparametric (lowess) estimation relating age to earnings separately for those with and without a college degree.
Turning to genetic data, Figure 2 presents a plot of the (kernel-smoothed) density of the EA score variable in our sample. Values of the score have been demeaned and rescaled to measure standard deviations relative to the mean. Figure 2 suggests that the distribution of the EA score appears to be approximately normally distributed and symmetric.33
Figure 2.
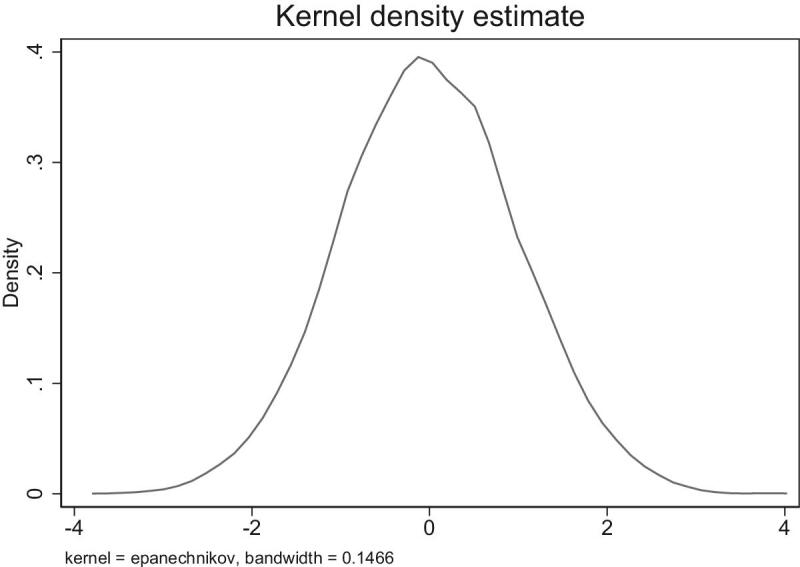
Distribution of the EA score.
Unless otherwise noted, all regressions include a full set of dummy variables for birth year, a male dummy, and interactions between the birth year and male dummies. Our basic control set also includes the first 10 principal components of the full matrix of genetic data. As noted in Section 2, these variables help to control for possible stratification of the score by ethnic ancestry group differences that exist among the broad category of individuals of European descent. To account for nonrandom selection into the genetic sample, all regressions are weighted using sampling weights that have been adjusted by the inverse probability of inclusion into the genetic sample given observables. Details on the construction of these weights are found in Online Appendix E.34
3.2. The Polygenic Score and Education
We start by replicating the basic relationship between the EA score and educational attainment found in earlier studies (Rietveld et al. 2014; Okbay et al. 2016; Lee et al. 2018). Table 2 presents estimates from regressions of years of schooling on the EA score and different control sets. The specification in column (1) only includes the score and our basic controls. A one standard deviation increase in the EA score is associated with 0.844 more years of schooling. Note that the incremental R2 associated with the genetic score in this regression is 0.075, indicating that variation in the score accounts for a large fraction of the variance in educational attainment.
Table 2.
Polygenic score and educational attainment.
| (1) | (2) | (3) | (4) | (5) | |
|---|---|---|---|---|---|
| EA Score | 0.844*** | 0.614*** | 0.610*** | 0.589*** | 0.587*** |
| (0.046) | (0.043) | (0.043) | (0.045) | (0.032) | |
| Father Educ. | 0.147*** | 0.144*** | 0.107*** | 0.109*** | |
| (0.013) | (0.013) | (0.016) | (0.013) | ||
| Mother Educ. | 0.172*** | 0.170*** | 0.149*** | 0.150*** | |
| (0.016) | (0.016) | (0.016) | (0.015) | ||
| Child Health: Very Good |
 0.141 |
 0.100 |
 0.128* |
||
| (0.126) | (0.116) | (0.070) | |||
| Child Health: Good |
 0.259** |
 0.190 |
 0.422*** |
||
| (0.127) | (0.123) | (0.090) | |||
| Child Health: Fair |
 0.197 |
 0.114 |
 0.407*** |
||
| (0.168) | (0.175) | (0.145) | |||
| Child Health: Poor |
 0.651 |
 0.549 |
 0.853 |
||
| (0.579) | (0.572) | (0.573) | |||
| Child Health: Missing | 1.561*** | 1.054 | 1.995 | ||
| (0.415) | (1.159) | (1.243) | |||
| Obs. | 8537 | 8537 | 8537 | 8537 | 8537 |
| R 2 | 0.253 | 0.361 | 0.363 | 0.380 | 0.515 |
| Child SES Measures | N | N | N | Y | Y |
| Child Region | N | N | N | N | Y |
| Religion | N | N | N | N | Y |
| Incr. R2, EA score | 0.075 | 0.038 | 0.037 | 0.034 | 0.034 |
Notes: Regressions relating educational attainment (years) to the EA score. All regressions include a full set of dummy variables for birth year, a male dummy, and a full set of interactions between the birth year and gender dummies. All specifications include the first 10 principal components of the full matrix of genetic data as controls. Some specifications include controls for parental education, childhood health, childhood SES measures, region during childhood and religion, as indicated. The last row reports the incremental R2 of the EA Score. *, **, and ***indicate statistical significance at the 10, 5 and 1 percent levels, respectively.
As discussed in Section 2, the EA score could measure biological factors that enhance an individual’s ability to acquire new skills or reduce the effort costs of learning. However, the score–education relationship could also reflect correlations between genetic factors and environments that promote education. For example, the genetic factors driving the score might affect parenting skills that encourage more schooling for one’s children, even if these factors do not affect a child’s ability to learn or acquire skill. Since the genotypes of individuals are necessarily correlated with the genotypes of their birth parents, such a scenario could generate a relationship between an individual’s EA score and their educational attainment that works purely through environmental factors. To account for such factors, we would ideally like to control for parental genotypes, since the genotype of a child is randomly assigned conditional on parental genes. Although we do not observe parental genes for respondents in the HRS, we can observe parental education, the phenotype most closely associated with these parental endowments.
In column (2) of Table 2, we again regress years of schooling on the EA score but now add separate measures for father’s education and mother’s education to our control set.35 The inclusion of parental education helps to adjust for the portion of the gene-education gradient that is driven by higher investments from more educated parents who also pass their genetic material onto their children.36 As expected, both parental education measures are positively and significantly related to a respondent’s years of schooling. However, even after controlling for parental education, the EA score still exhibits a strong association with educational attainment, with an estimated coefficient of 0.614. The incremental R2 associated with the EA score falls, but remains substantial at about 0.038. Within-family analyses in Lee et al. (2018) estimate that the associations between individual SNPs and educational attainment are, on average, approximately 40% smaller after accounting for family effects. In our sample, controlling for parental education reduces the estimated coefficient on the polygenic score by more than 25%, which accounts for a substantial fraction of the gene–environment correlation suggested by past within-family estimates. In all subsequent analyses, we control for parental education unless otherwise noted.
In column (3), we again regress years of education on the EA score, but now add a set of categorical variables reflecting self-reported health during childhood. An extensive existing literature links childhood health to SES and labor market outcomes later in life (see Currie 2009 for a review). Indeed, we find that lower self-reported health levels (relative to the Excellent reference category) exhibit a significant negative association with educational attainment. It is worth noting that these health variables have a combined incremental R2 of about 0.008 in this specification without the EA score (0.002 when parental education is included), which is substantially smaller than the incremental R2 associated with the EA score itself.37 In column (4), we add a battery of controls measuring SES during childhood. These include dummies for whether or not the individual’s family moved due to financial stress, whether the family ever asked another family for financial help, whether or not the individual’s father was ever unemployed for a significant time, and a measure for the average income of the father’s occupation in the 1960 census. Adding these controls does not significantly reduce the coefficient estimate on the EA score. In column (5), we show that our estimates are robust to the addition of dummies for the region of birth and an individual’s religious affiliation. Comparing columns (1) and (5), the entire battery of childhood socioeconomic and health controls boosts R2 by about 0.262. The incremental R2 of 0.034 associated with the EA score is nontrivial by comparison.38
Table 3 considers the relationship between the EA score and dummy variables indicating different types of highest earned degree (No Degree, Two-Year College, College, or Graduate (MA or Professional Degree)). The EA score is significantly negatively associated with having no degree and having a two-year degree, but positively associated with having a college degree or a graduate degree. Additionally, the genetic score not only predicts educational attainment, but also educational performance. Column (5) presents coefficient estimates from a specification in which the dependent variable is an indicator for whether the individual reported having to repeat a grade of schooling. The results suggest that the EA score is significantly negatively associated with the probability of repeating a grade. A one standard deviation increase in the genetic score is associated with a 4.1 percentage point reduction in the risk of ever failing a grade. Panel B of Table 3 shows that these relationships hold even when we control for parental education.39
Table 3.
Polygenic score and categorical education outcomes.
| Dep var. | No degree | Two-year coll. | College | Graduate | Redo grade |
|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | |
| Panel A: | |||||
| EA Score |
 0.068*** |
 0.008** |
0.069*** | 0.063*** |
 0.041*** |
| (0.005) | (0.004) | (0.005) | (0.004) | (0.005) | |
| Obs. | 8512 | 8512 | 8512 | 8512 | 8166 |
| R 2 | 0.201 | 0.046 | 0.082 | 0.094 | 0.085 |
| Panel B: | |||||
| EA Score |
 0.050*** |
 0.010*** |
0.051*** | 0.050*** |
 0.030*** |
| (0.005) | (0.004) | (0.005) | (0.004) | (0.005) | |
| Father Educ. |
 0.008*** |
 0.000 |
0.013*** | 0.011*** |
 0.008*** |
| (0.002) | (0.001) | (0.002) | (0.002) | (0.002) | |
| Mother Educ. |
 0.016*** |
0.004** | 0.014*** | 0.008*** |
 0.008*** |
| (0.002) | (0.002) | (0.002) | (0.002) | (0.002) | |
| Obs. | 8512 | 8512 | 8512 | 8512 | 8166 |
| R 2 | 0.251 | 0.050 | 0.120 | 0.122 | 0.098 |
Notes: Regressions relating educational attainment categories or the probability of repeating a grade to the EA score. Specifications in panel A do not include parental education. Specifications in panel B include parental education. All regressions include a full set of dummy variables for birth year, a male dummy, and a full set of interactions between the birth year and gender dummies. Additionally, every specification includes the first 10 principle components of the full matrix of genetic data. **, and ***indicate statistical significance at the 10, 5 and 1 percent levels, respectively.
Taken together, the results in Tables 2 and 3 provide support for two propositions. First, the genetic variation captured in the EA score is strongly associated with educational attainment along nearly every margin. Compared to other observables, the EA score accounts for a large fraction of the variation in educational attainment. Second, this relationship does not appear to be driven mostly by childhood environmental factors, at least those that are measurable in the HRS. After controlling for parental education, the inclusion of several controls for different aspects of childhood SES does little to attenuate the relationship between the EA score and completed education. We now take a closer look at the relationship between childhood SES and the EA score.
3.3. The Polygenic Score and Childhood SES
One aim of our subsequent analysis is to better understand how genes and the environment interact. To that end, we examine the educational outcomes of individuals with similar scores, but different childhood circumstances. Although the HRS surveys individuals at older ages, it contains a set of retrospective questions in the Demographics file that can be used to construct variables related to the SES of an individual’s household during childhood. Here, we introduce four childhood SES measures in the HRS constructed from these retrospective questions. All of the measures we construct are binary variables that take the value 1 for high childhood SES and 0 otherwise. The four variables we construct are
Father’s income: Based on respondent-provided information about father’s usual occupation, we use income data from the 1960 census to impute an annual salary/work income for each father. We calculate the median for this father’s income variable and classify individuals whose fathers earned above median incomes as experiencing high SES during childhood. The father’s occupation measures come from the Industry and Occupation Data, which contain more detailed occupation codes than the items that are publicly available from HRS.
Family well off: High SES indicates respondents who reported that their family was “pretty well off financially” or “average” from birth to age 16. Low SES indicates respondents who reported that their family was “poor”.
Move or help: The HRS asks separate questions about whether a respondent’s family ever had to move residences or ask relatives for help due to financial reasons. Since these events are similar (capturing an extraordinary household response), we combine them into a single variable. This combination increases variation in this measure since moving or asking for help are each less frequent events.40 High SES indicates respondents whose family never had to move or ask relatives for help for financial reasons. Low SES indicates respondents whose families did either move or ask relatives for help.
Father’s employment: High SES indicates respondents whose father never experienced a significant unemployment spell (“several months or more”). Low SES indicates respondents whose father did experience a significant unemployment spell, or those whose fathers were dead or never lived with them. Notice that this variable incorporates information on family structure since it takes the value 0 if the child is raised without a father.41
These SES variables have several shortcomings. For one, they are retrospective, which may lead to nonrandom measurement or reporting error. For example, an individual’s SES during adulthood could affect how they recall or report childhood circumstances. Alternatively, perceptive individuals may be more aware of their parents’ financial difficulties during childhood. If so, then any of these variables may capture unobserved skills that also lead to better economic outcomes. Moreover, the variables we use to proxy childhood SES are not exhaustive, as they do not reflect other factors affecting the level of resources available to the respondent (e.g., number of children in the household). Potential measurement problems motivate the use of several SES variables, which allows us to assess whether empirical patterns are robust across measures. Moreover, though the variable “Father’s income” is based on average income data, it is unlikely to be subject to the same types of reporting error as the other variables, since the occupation question does not require an individual to make a normative judgment about their family’s economic situation in childhood.
Despite possible measurement and reporting issues, we show that the SES variables exhibit consistent relationships with both educational attainment and the polygenic score. The first row of panel A of Table 4 reports the proportion of individuals classified as high SES using each of the four measures of childhood environments. For the three variables available directly in the HRS, between 72% and 75% of respondents report a high-SES environment, whereas the corresponding number for the imputed father’s income variable is 51%. We explore the relationship between the polygenic score and childhood environments in two ways. First, for each SES variable, panel A reports the average fraction of respondents growing up in a high-SES environment by quartiles of the EA score distribution. For example, about 70% of individuals in the first EA quartile report that their family was either “pretty well off financially” or “average” until age 16. This fraction rises to 76% for individuals in the fourth quartile—a difference of 6 percentage points that is highly statistically significant. For all four SES variables, we find that the fraction of high-SES respondents generally rises with higher EA quartiles, and that we can reject the null hypothesis of zero difference in this fraction between the fourth and first quartiles of the EA score. The largest interquartile difference in high-SES incidence appears for the father’s income variable (14 percentage points). Table 4 also presents the difference in average EA score for individuals classified as high versus low SES. Again, the largest difference appears for the father’s income: individuals with a father who earned above-median occupational income have genetic scores that are on average higher by a little under one-fifth of a standard deviation.
Table 4.
Childhood SES measures and education.
| SES measure: | Father inc. | Fam. well off | Never move or ask. | Father emp. |
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| Panel A: EA Score and Four Measures of High Family SES | ||||
| Full Sample Average | 0.510 | 0.721 | 0.746 | 0.741 |
| EA Score Quartile 1: | 0.432 | 0.699 | 0.716 | 0.713 |
| EA Score Quartile 2: | 0.487 | 0.705 | 0.741 | 0.751 |
| EA Score Quartile 3: | 0.540 | 0.719 | 0.749 | 0.717 |
| EA Score Quartile 4: | 0.572 | 0.761 | 0.776 | 0.780 |
| Q4–Q1 | 0.139 | 0.061 | 0.060 | 0.067 |
| p-value | <0.001 | 0.014 | 0.015 | 0.002 |
| Q4–Q1 (Residuals) | 0.064 | 0.004 | 0.030 | 0.037 |
| p-value | 0.007 | 0.833 | 0.174 | 0.072 |
| Δ EA Score for | ||||
| High versus Low SES | 0.196 | 0.122 | 0.143 | 0.104 |
| p-value | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
| Panel B: Dep. Var—Education | ||||
| High SES | 0.708*** | 0.592*** | 0.363** | 0.092 |
| (0.127) | (0.129) | (0.153) | (0.123) | |
| EA Score | 0.597*** | 0.610*** | 0.609*** | 0.613*** |
| (0.047) | (0.043) | (0.045) | (0.043) | |
| Obs. | 6773 | 8412 | 8385 | 8427 |
| R 2 | 0.398 | 0.370 | 0.364 | 0.361 |
Notes: Specifications relating four measures of childhood SES to education and EA score. Panel A shows how the EA score relates to family SES. The first row shows the proportion in the sample indicating high SES for each measure among those who report the measure. The following rows show the proportion indicating high SES for each measure within each EA score quartile. We also report p-values for differences between the first and fourth quartiles. We also repeat this exercise after residualizing the SES measures on our basic controls and parental education measures. For the residualized measures, we only report differences between the first and fourth quartiles of the EA score distribution, along with the associated p-values for these differences. Panel B contains coefficients on measures of high SES and EA score in regressions explaining educational attainment (years). Regressions also include a full set of dummy variables for birth year, a male dummy and a full set of interactions between the birth year and gender dummies. Additionally, every specification includes the first 10 principle components of the full matrix of genetic data, and controls for parental education. **, and ***indicate statistical significance at the 10, 5 and 1 percent levels, respectively.
Despite these strong gradients, much of the relationship between our SES measures and the EA score disappears after controlling for parental education. Table 4 reports interquartile differences in high SES indicators that have been residualized on our basic control set and measures of parental education. We find substantially less difference in SES environments across EA quartile groups. For the “Family well off” measure and the “Father’s employment” measure, the interquartile difference becomes insignificant or only marginally significant. For the “Father’s income” and “Move or help” variables, controlling for parental education attenuates the interquartile differences by at least 50%. If the polygenic score exhibits similarly modest correlations with unobserved environments or investments conditional on parental education, these results provide some reason to believe that associations between the EA score and human capital outcomes are not primarily driven by gene–environment correlations. This is similar to the point made by Altonji, Elder, and Taber (2005), who study labor market returns to Catholic schooling.42 Following this logic, adjusting for parental education bolsters the argument that differences in childhood circumstances for individuals with similar EA scores can be treated as conditionally exogenous.
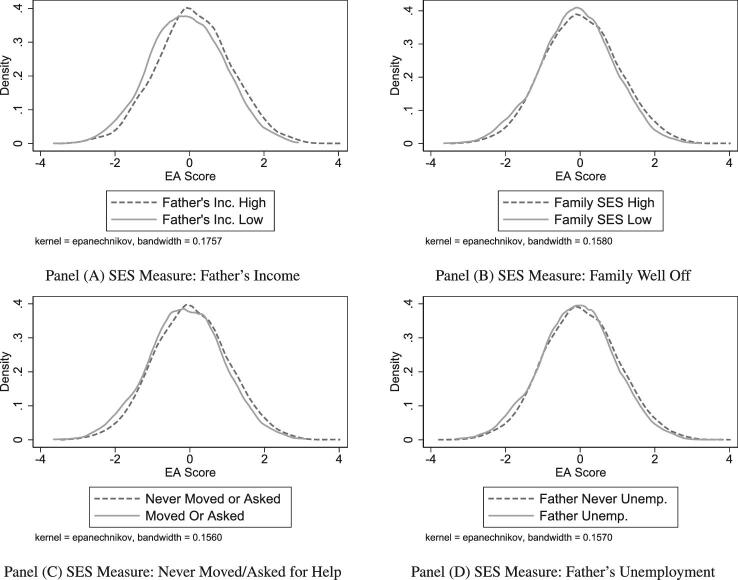
Although there are systematic relationships between the EA score and our SES measures, these mean differences appear to be modest compared to differences based on parental education or the respondent’s own educational attainment. Not only are the mean EA scores similar across SES groups, but the distribution of the EA score is nearly identical across SES groups. As a point of reference, panel A of Figure 3 plots the distribution of the EA score separately for individuals who did and did not complete a college degree, whereas panel B does the same based on mother’s education (less than 12 years vs. 12 or more). Unsurprisingly, there is a substantial rightward shift in the distribution based on completing college (mean difference of 0.67), and a smaller but substantial rightward shift based on high mother’s education (mean difference of 0.29). By contrast, Figure 4 plots the distribution of the EA score separately for high-SES and low-SES groups based on each of our four measures. In each case, we can reject the null hypothesis that the distributions are identical, but the differences in the distributions appear smaller than those based on own or parental education.43 Indeed, the distributions across SES groups are largely overlapping. This overlap is important for subsequent analyses that test for interactions between the EA score and childhood SES and thus compare educational outcomes for individuals with similar scores, but different childhood environments. Performing such an analysis would be problematic if these distributions displayed little overlap since interactions would be identified from comparisons of individuals in the tails of each distribution (e.g., comparing high-SES individuals with unusually low EA scores against low-SES individuals with unusually high EA scores). As we can see from Figure 4, the comparison of similarly scored individuals from different SES backgrounds can be made across the distribution of the EA score. Lack of this degree of overlap is why we do not treat parental income as an additional SES measure, but instead use it as a control variable.
Figure 3.
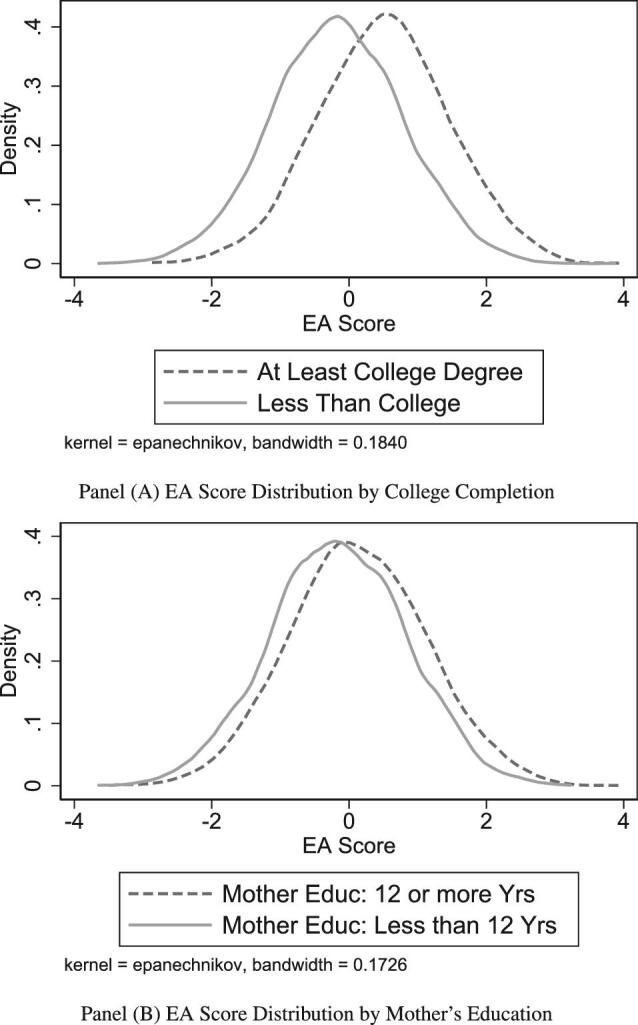
EA score distribution by own and maternal education.
Figure 4.
EA score distribution by family SES.
Panel B of Table 4 demonstrates that each of the SES measures are relevant predictors of educational attainment, with the exception of the Father’s employment variable. Controlling for the EA score, our basic controls, and parental education, we find that individuals born into high-SES households are expected to complete between 0.09 and 0.71 additional years of schooling, depending on the SES measure. Although controlling for parental education accounts for nearly all of the gene-SES gradient, these SES measures still contain explanatory power for education even after we condition on both parental education and the polygenic score.
In summary, Figures 2–4 along with Table 4 provide support for three propositions. First, both genetic endowments and childhood socioeconomic status appear to play important roles in driving educational attainment. Second, although our SES measures are certainly correlated with an individual’s polygenic score, it appears that controlling for parental education accounts for much of the gene–environment correlation that is relevant for human capital outcomes. Third, the distribution of the polygenic score is largely similar across SES groups, which suggests we can make meaningful comparisons of individuals with similar scores, but different childhood SES.
3.4. Childhood SES and the Gene-Education Gradient
A large literature explores the extent to which conditions during childhood affect completed education and later-life outcomes (Black, Devereux, and Salvanes 2005; Cunha and Heckman 2007). Of particular importance for policymakers is understanding whether changes in these conditions (e.g., increased investments in school quality) exert different influences on human capital accumulation for children with different ability endowments or accumulated skills. For example, as argued by Cunha and Heckman (2007), investments in the skills of older children from disadvantaged backgrounds might be economically inefficient if complementarities between investments and accumulated skills are sufficiently strong. Here we explore a related question—whether the effects of childhood SES on human capital accumulation differ based on levels of the endowments measured by the EA score. Our results highlight an important sign change in the interaction between childhood SES and the polygenic score in equations predicting educational attainment. We find that the relationship between the polygenic score and high school completion is weaker among individuals from high-SES backgrounds, whereas the relationship between the score and college completion is stronger for these individuals. Environments that promote human capital thus appear to be substitutes for genetic endowments in preventing extremely low education levels, but may complement these endowments in producing more advanced outcomes.
Figure 5 offers some motivating evidence of interactions between family SES and genetic endowments. We focus on our most predictive SES measure (Father’s income) and assign each individual to a quartile of the EA score distribution and a quartile of the father’s income distribution, generating 16 possible combinations of SES and EA quartile groupings. Panel A plots average rates of high school completion for each quartile combination, whereas panel B reports the same exercise for rates of college completion.44 For each quartile of father’s income, higher EA quartiles are associated with a higher probability of attaining a high school degree. Moreover, within each EA score quartile, higher levels of father’s income predict uniformly higher probabilities of completing high school, with sharper gradients for the first two EA score quartiles. In the lowest EA quartile, graduation probability ranges from approximately 58%–84%, whereas in the highest it ranges from approximately 81%–96%. Genetic endowments predict educational attainment, but childhood environments (as measured by father’s income) also matter, especially so for individuals with lower EA scores.45
Figure 5.
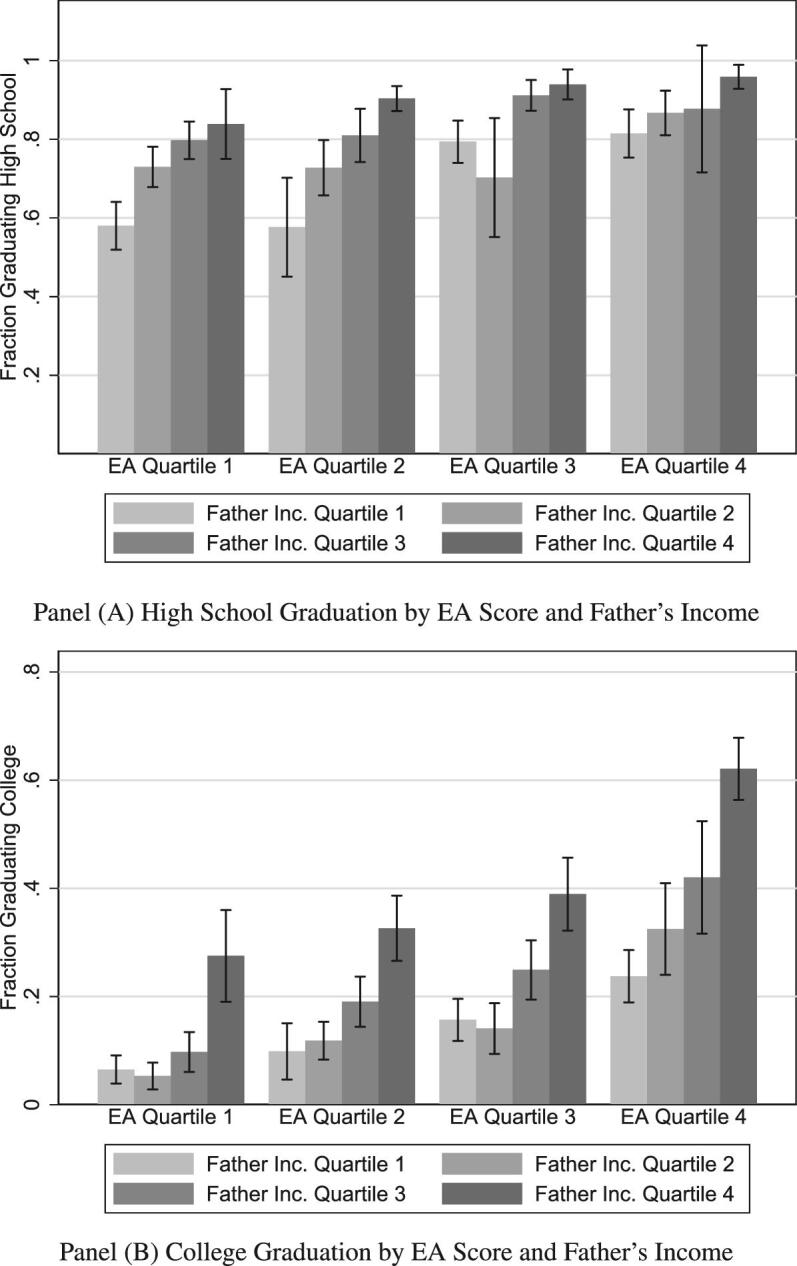
Educational attainment by father’s income and EA score. Bars are plotted with 95% confidence intervals.
Panel B of Figure 5 repeats this exercise for rates of obtaining a college degree. As with high school completion, higher EA scores are associated with higher probabilities of college graduation for each quartile of father’s income. Moreover, within each EA score quartile, father’s income predicts college graduation, especially strongly so for the top quartile. Both genetic endowments and father’s income predict higher rates of college completion. However, the differences in completion rates between above and below median income groups are much higher for individuals with high EA scores.46 One particularly striking fact that emerges from Figure 5 is that childhood SES may overwhelm genetic endowments in predicting educational attainment. In particular, panel B of Figure 5 shows that the college completion rate in the group formed by the lowest EA score quartile and the highest father’s income quartile exceeds the corresponding fraction for individuals from the highest EA score quartile and the lowest father’s income quartile, although this difference is not statistically significant.
To more formally examine whether SES moderates the relationship between the genetic score and educational attainment, we broaden our analysis to include all four SES measures and estimate regressions of the form
 |
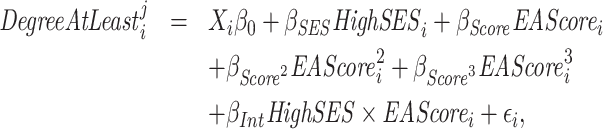(1) |
where DegreeAtLeast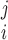
indicates whether individual i completed at least degree j, with 
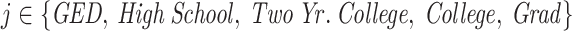. Here Xi contains our standard controls (a full set of birth year dummies, a male dummy, interactions between the birth year and male dummies, and the principle components from the full matrix of genetic data) along with the parental education controls. Note that we include a cubic in the EA score, since otherwise the 
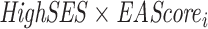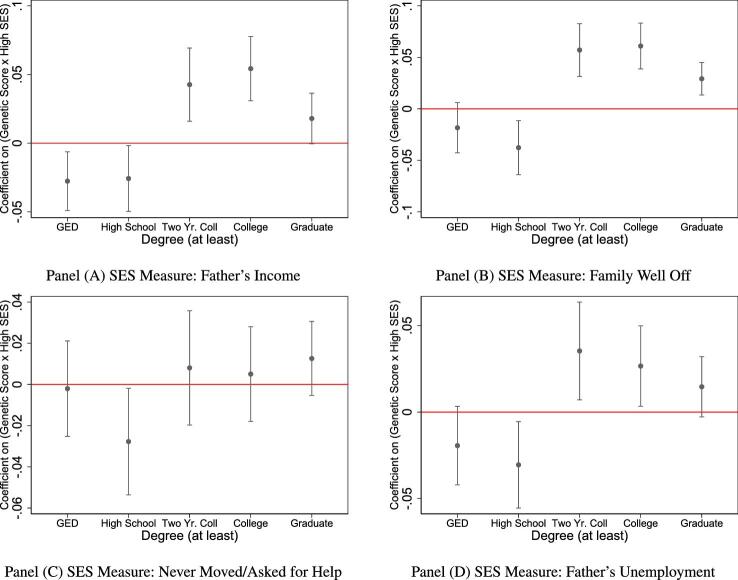
interaction could reflect nonlinearities in the relationship between education and the EA score. To further control for population stratification, we also interact the principle components with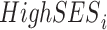 
and include them as additional controls.47 Figure 6 plots point estimates of βInt and 95% confidence intervals for different measures of SES and for different degree measures j. Each panel presents estimates for a different SES measure.48 The striking pattern that emerges is that there tends to be a significant negative interaction between SES and the score for completing at least low levels of education (high school equivalent or high school), but there tends to be a significant positive interaction for more advanced degrees (at least college or graduate school). To our knowledge, this pattern has not been shown in previous literature.49
Figure 6.
Coefficient on the interaction between EA score and high SES for different schooling categories with 95% confidence intervals.
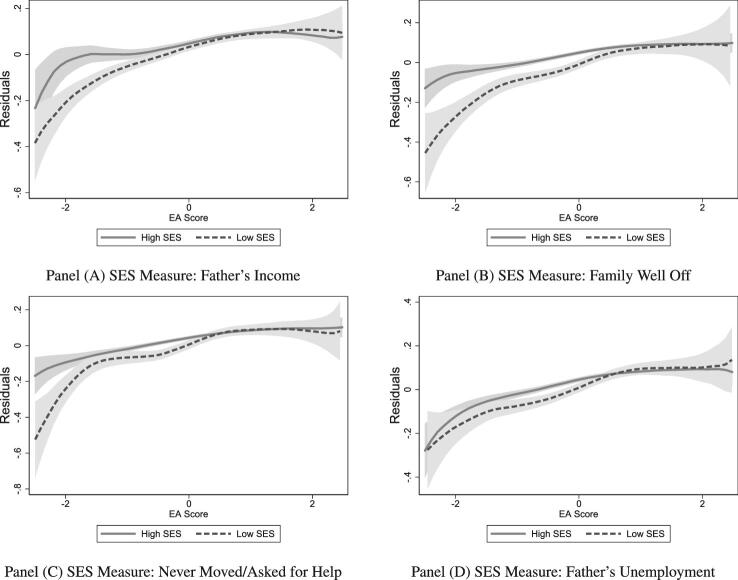
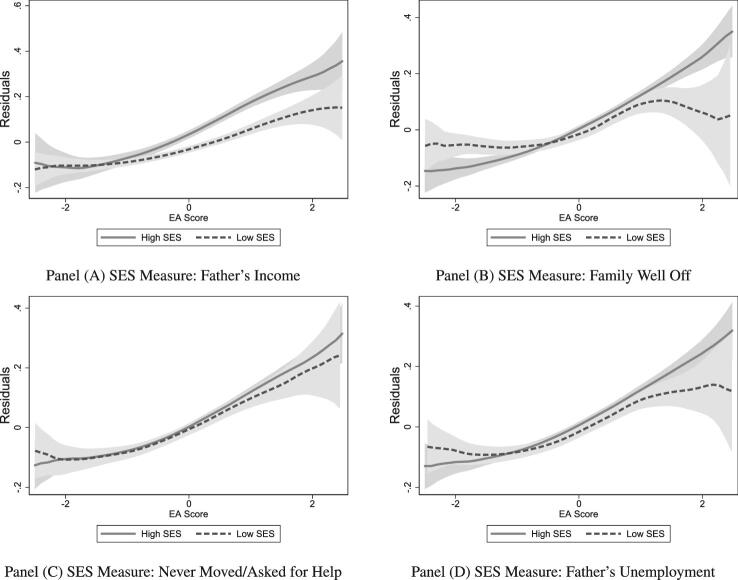
Moreover, the linear interactions presented in Figure 6 do not appear to be driven by outliers or by very specific ranges of the EA score. The continuous nature of the interaction is apparent from nonparametric (local polynomial) regressions describing the relationship between educational outcomes and the EA score for different SES groups, which are presented in Figures 7 and 8. To construct each panel of Figure 7, we regress an indicator for having at least a high school degree on a basic set of regressors: the genetic principal components, birth year dummies, a male dummy, interactions between birth year and male dummies, and controls for parental education. We then plot local polynomial regression estimates of the relationship between the EA score and these residuals separately for high- and low-SES groups. In the panels of Figure 8, we do the same, but the education outcome indicator is college degree or more. According to Figure 7, a higher polygenic score predicts higher education for both SES groups. However, the relationship is stronger for individuals who grew up in low-SES households. In contrast, Figure 8 shows that for higher educational attainment (college degree or more), the positive relationship is stronger for children who grew up in households with more resources.
Figure 7.
Nonparametric (local polynomial) estimation relating the probability of high school degree or more to EA score for high versus low SES for different measures of childhood SES. In each panel, the outcome variable is the residual from OLS regression of an indicator for completing a high school degree or more onto a set of controls and the regressor is EA score. Shaded areas depict 95% confidence intervals.
Figure 8.
Nonparametric (local polynomial) estimation relating the probability of completing a college degree or more to EA score for high versus low SES for different measures of childhood SES. In each panel, the outcome variable is the residual from OLS regression of an indicator for completing a college degree or higher onto a set of controls and the regressor is EA score. Shaded areas depict 95% confidence intervals.
3.5. Interpretation and Discussion of Mechanisms
The patterns in Figures 6–8 are consistent with human capital production functions that allow the roles of family resources and the EA score to be distinct for different outcomes at different stages of child development. Specifically, early investments in human capital (proxied by childhood family SES) may substitute for genetic endowments in preventing very low levels of educational attainment. However, these same investments could complement genetic endowments in generating higher levels of educational attainment such as college completion. It is worth mentioning that our findings on higher degrees are in line with a large literature showing that ability and investments are complements (Becker and Tomes 1986; Cunha and Heckman 2007; Aizer and Cunha 2012), as well as the literature emphasizing the importance of gene–environment interactions in producing economic outcomes. However, the idea that genetic endowments and investments might be substitutes along some dimensions merits further exploration.
Our results suggest that some features of high-SES environments are particularly helpful in preventing low-score children from dropping out of high school, and in promoting college completion among high-score children. In order for these results to have clear policy implications, it is important to understand which specific features of these environments matter for these interactions, and whether they can be manipulated by policy. For example, if father’s income matters because it allows families to afford better schooling (or reside in areas with better schools), then our results might suggest that cash transfers to poor families, or investments in better quality public schooling might be particularly useful in enabling the success of high-endowment children trapped in poor environments. However, father’s income could be serving as a proxy for other casual features of the environment (e.g., parenting style) that operate independently from school quality. Without exogenous or isolated variation in these features of the environment, it becomes difficult to draw firm conclusions about the policy-relevant mechanisms that drive these interactions.
An existing literature offers some evidence on the importance of different features of high-SES environments. For example, Belley and Lochner (2007) report stronger interactions over time between AFQT scores and family income in explaining educational attainment, which suggests that borrowing constraints play an increasingly important role as tuition costs rise. As they point out, stronger interactions between family income and AFQT scores are difficult to reconcile with a “consumption value” of education, which has also been suggested as a way to explain a positive relationship between family SES and college degrees. However, credit constraints are only one possible way that family SES could alter the returns to genetic factors.50 Interactions may also reflect physical shocks in utero or during childhood, for example, due to parental smoking. Environmental factors such as early-life stress could also induce changes in how genes are expressed (how they function in producing proteins), which is one example of an epigenetic phenomenon.51
The HRS contains only limited information on intermediate outcomes and specific human capital investments made by parents, so it is difficult to draw sharper conclusions about the role of household environments in our sample. However, the Life History file contains retrospective items that on the number of books in the respondent’s household as a child, as well as whether or not the respondent went to preschool. Existing research suggests both of these investments are linked to human capital accumulation and skill formation.52 Additionally, the Life History file also contains a question on the number of people who lived in a respondent’s household at age 10. The number of people in the household is relevant because it contains information on the number of children and other dependents in the household with claims on household resources. As noted in the literature on the quantity–quality tradeoff in fertility, poorer households may find it optimal to have more children and choose to invest less intensely in their human capital (Becker 1960; Hotz, Klerman, and Willis 1997). In results in Online Appendix B, we show that books, preschool attendance, and a lower number of individuals in the household are all associated with increased educational attainment. These measures are positively correlated with our SES measures, even after controlling for parental education. For example, regression evidence suggests that after controlling for parental education, individuals with above-median father’s income are more likely to have at least one full bookcase in the household (difference of 0.059), are more likely to have attended preschool (difference of 0.049), and are less likely to have more than five people living in the household (difference of 0.067). This provides suggestive evidence that higher SES households complement higher polygenic scores through the kinds of early childhood investments that have been highlighted in existing research. However, this evidence is merely suggestive; without exogenous variation and more complete data on rearing environments and early childhood outcomes (e.g., performance at school), we cannot rule out the possibility that these measures are simply acting as proxies for different causal mechanisms (e.g., low income and binding credit constraints at college enrollment age).
3.6. Robustness and Sensitivity
Our estimates of interactions between the polygenic score and family SES are consistent with different roles for family resources depending on the level of education, which would suggest restrictions on the production function for human capital.53 However, we cannot rule out other accounts related to measurement error or correlations between environmental factors and advantageous parental genetic endowments. For example, it could be the case that actual investment levels (which we proxy with SES) are a positive function of both observed SES and the child’s genetic endowment.54 If this is true, then SES will increasingly underestimate investment as the child’s genetic endowment grows.
To help guide our interpretation of estimates, in Online Appendix C we develop a simple econometric model that incorporates several features of our setting, including: (i) using family SES to measure human capital investments introduces measurement error; (ii) investments in children are potentially affected by children’s genetic endowments; (iii) these investments can also be affected by parents’ genetic endowments, for example, if parents’ genes lead to higher parental education, wealth or income; and (iv) children’s genetic endowments are a function of their parents’ genetic endowments.55 Using the model, we show that, under a reasonable set of assumptions, such a scenario will result in bias in the magnitude but not the sign of gene-investment interaction effects that we estimate. Therefore, the sign change in the estimated interaction between genes and investments in low versus high educational outcomes is key. It is not a necessary condition for differences in the interaction effect, but it is a sufficient condition for the existence of such differences. We also show in Online Appendix C that we cannot guarantee the identification of the interaction sign if we use a more traditional measure of ability such as IQ or cognitive test scores, which may be directly affected by investments. In other words, a key benefit of using genetic data to infer how genetic endowments interact with human capital investments is that genetic endowments are fixed and therefore not simultaneously affected by investments, even if they are correlated with them. It is also noteworthy that our pattern of interactions is robust across a number of distinct measures of SES with different patterns of correlation with the EA score. This suggests that the interactions we find do not primarily reflect correlation between parental genetic endowments and environments.56
Other factors might threaten identification of the interaction term. An omitted third factor could affect education, but exhibit a different relationship with EA score for each SES group. One possibility is that our binary childhood SES measures mask differences in how household resources rise with genetic endowments. Another possibility is that there are additional genetic factors driving education that relate to the polygenic score in different ways across SES groups. In both cases, we have not identified true complementarities, but instead have captured omitted factors. Finally, there may also be classification error that differs by group if, for example, individuals with lower polygenic scores are more likely to misclassify their childhood SES. The ideal experiment to test for these effects would involve a random assignment of resources that can be manipulated by policy (e.g., household income) to individuals with different genetic scores.
Although we cannot rule out the threats to identification rooted in selection on unobservables, the distributions of the polygenic score by SES group plotted in Figure 4, in particular the substantial overlap, help to allay some concerns. The reasoning is similar to that in Altonji, Elder, and Taber (2005). The plots demonstrate that when we divide the sample by childhood SES, the resulting groups are quite similar with regard to an important and relevant observed source of heterogeneity. Similar polygenic scores across groups provide some support for the assumption that individuals are similar on unobserved factors as well, that is, that estimated differences in returns to genetic endowments by childhood SES are not the result of selection on unobservables.57
We also acknowledge that our conclusions here are based on a fairly large number of specifications that span four different SES measures and five different educational outcomes. This raises the possibility that our results could be false positives that emerge from multiple hypothesis testing. In Online Appendix E, we adjust the p-values associated with our main hypothesis tests to account for multiple comparisons. We continue to have strong statistical evidence for multiple SES–EA score interactions even after applying these corrections.
4. Genes and Labor Outcomes
Results from the previous section suggest that low-SES environments reduce the returns to genetic endowments by lowering the probability of college attendance. This is particularly important in light of the substantial rise in the earnings premium for a college degree over the last several decades. However, earnings depend not only on completed education, but also on the returns to endowments conditional on education. High-score individuals who are shut out of college due to childhood poverty might still receive an earnings premium if the genetic endowments measured by the EA score are also associated with skills valued in the labor market. This motivates an analysis of the relationship between the score and earnings conditional on education.
The questions we ask here are related to a longstanding literature on the returns to ability. At least since Becker and Chiswick (1966), labor economists have been concerned with ability bias in estimating the relationship between schooling and various economic outcomes. If the unobserved factors that promote education also independently predict labor market success, then estimates of the return to schooling will be biased upward. This concern not only raises an econometric point; it also poses fundamental questions about the structure of heterogeneity in labor market decisions and outcomes. How and to what extent do the characteristics or traits that promote education also affect earnings over the life-cycle? Observing the EA score thus also allows us to make some progress on this larger question, demonstrating how previously unobserved factors might not only drive education, but also several other outcomes conditional on education.
4.1. The EA Score and Earnings
We begin by describing the relationship between the EA score and earnings over the life-cycle. Panel A of Figure 9 plots the relationship between age and the unconditional average earnings of men in our sample separately by terciles of the EA score. Each tercile group exhibits a classic concave age-earnings profile, with earnings rising until approximately age 55, then falling afterward. At every age, earnings are higher for individuals in higher EA terciles. To explore whether this pattern also holds conditional on education, we next regress earnings on controls for own and parental education and plot the residuals separately by EA tercile.58 Residual earnings diverge considerably as respondents age, and for most ages in the range 40–60 we can reject the null hypothesis that residual earnings are equal across the top and bottom terciles. Together both panels suggest that the EA score predicts higher earnings, this gradient is not fully explained by educational attainment, and it becomes larger as individuals age. We note that this pattern of divergence would not be fully captured by a standard fixed effects model, since fixed effects do not change over time by construction. This illustrates how observable measures, such as the EA score, can help us to better understand the structure of heterogeneity in labor outcomes. These patterns are also consistent with findings of Altonji and Pierret (2001), who demonstrate that measures of labor market ability that are presumably difficult to observe, like the AFQT, become better predictors of wages as individuals age and accumulate more experience.59
Figure 9.
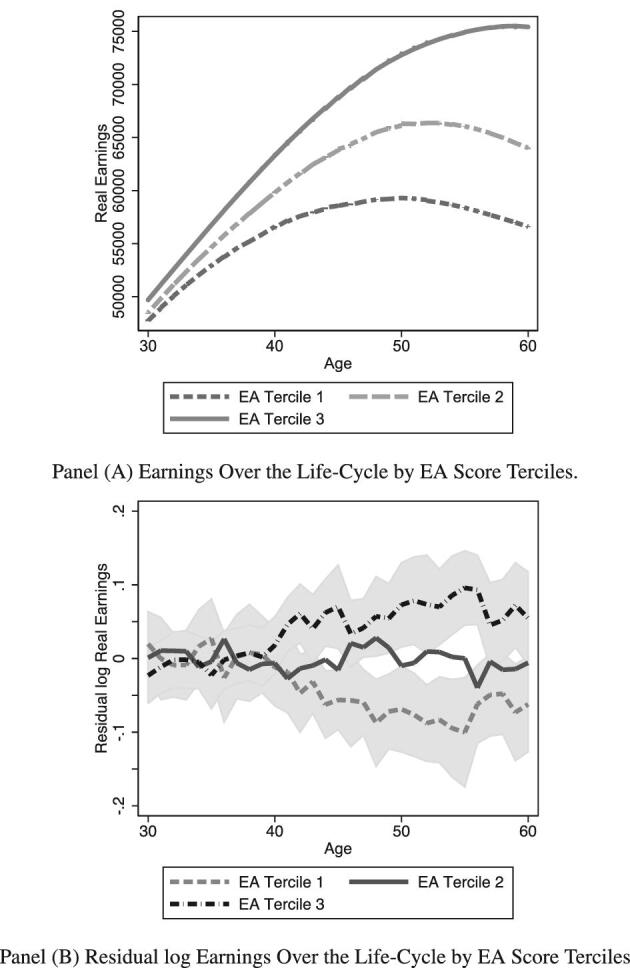
The EA score and life-cycle income. Panel A plots the nonparametric (lowess) relationship between age and earnings levels by EA tercile. Panel B plots mean residual log earnings for each age by EA score tercile. Shaded areas depict 95% confidence intervals around these means for the top and bottom terciles.
Table 5 presents more formal estimates of the relationship between the EA score and log earnings. Here we restrict the sample to all person-year observations for men aged 25–64 with at least $10,000 of annual earnings.60 Standard errors are clustered at the person level. Panel A contains our baseline specification, which regresses log earnings on the EA score and a controls set that consists of the principal components, as well as dummy variables for age, year, and birth year. As seen in column (1) of panel A, without any controls for own education a one standard deviation increase in the EA score is associated with an increase in log earnings of 0.079. In column (2) we add controls for own education (years of schooling and a full set of degree dummy variables) and parental education. Controlling for education and parental background, we estimate a coefficient on the EA score of 0.032, which remains highly significant. Thus far, we have assumed that the returns to the EA score would be the same regardless of an individual’s level of education. However, returns to the EA score might plausibly differ based on an individual’s level of completed schooling. For example, we might expect there to be larger returns to genetic endowments if formal education is a productive complement with ability in generating productive skills. Consequently, we explore whether there is any interaction between the genetic score and having at least a college degree. The results in column (3) do not allow us to reject the null hypothesis that there is no additional return for those with a college degree.61 However, we do note in robustness exercises that there appears to be a larger return for college graduates when we consider self-reported wages in the HRS as the dependent variable.62 Importantly, we find no evidence that high-EA score individuals without a college degree experience sufficient returns on their endowments to compensate for the lack of a degree. Finally, in column (4) we restrict the sample to individuals aged 40–64 and re-estimate our basic specification from column (2). We find a larger association between the EA score and earnings conditional on education for this older sample (0.041 vs. 0.032), consistent with the pattern suggested by panel B of Figure 9.
Table 5.
Polygenic score and earnings.
| Panel A: Log Earnings: | |||||
|---|---|---|---|---|---|
| Basic specifications | (1) | (2) | (3) | (4) | |
| EA Score | 0.079*** | 0.032*** | 0.025** | 0.041*** | |
| (0.009) | (0.009) | (0.010) | (0.011) | ||
| EA Score × College | 0.016 | ||||
| (0.020) | |||||
| Obs. | 96721 | 96721 | 96510 | 57469 | |
| R 2 | 0.143 | 0.189 | 0.192 | 0.150 | |
| Age Group | 25–64 | 25–64 | 25–64 | 40–64 | |
| Period | All Years | All Years | All Years | All Years | |
| Educ. Controls | N | Y | Y | Y | |
| Parent Controls | N | Y | Y | Y | |
| Panel B: Log Earnings: | |||||
| By time and cohorts | (1) | (2) | (3) | (4) | (5) |
| EA Score |
 0.010 |
0.009 | 0.018** | 0.026*** | 0.011 |
| (0.007) | (0.007) | (0.008) | (0.008) | (0.008) | |
| EA Score × Post 1980 | 0.077*** | 0.039*** | 0.043*** | ||
| (0.013) | (0.013) | (0.010) | |||
| EA Score × BY > 1942 | 0.031* | 0.009 |
 0.010 |
||
| (0.019) | (0.019) | (0.019) | |||
| College × Post 1980 | 0.276*** | 0.256*** | |||
| (0.031) | (0.024) | ||||
| College × BY > 1942 | 0.152*** | 0.041 | |||
| (0.045) | (0.044) | ||||
| Obs. | 96721 | 96510 | 96721 | 96510 | 96510 |
| R 2 | 0.194 | 0.204 | 0.192 | 0.196 | 0.206 |
| Ed. Groups | All | All | All | All | All |
| Period | All Years | All Years | All Years | All Years | All Years |
| Educ. Controls | Y | Y | Y | Y | Y |
| Parent Controls | Y | Y | Y | Y | Y |
Notes: Regressions relating the EA score to log earnings. In the first three columns of panel A, we restrict the sample to earnings records for men between the ages of 25 and 64 over the years 1951–2013. We further restrict the sample to person-years in which the respondent earned more than $10,000 in real 2010 dollars. In column (4), the sample is narrowed to cover person-years in which respondents are aged between 40 and 64. The specifications in panel B cover ages 25–64 and years 1951–2013. The dependent variable is the log of real earnings. All regressions include the first 10 principle components of the full matrix of genetic data along with a full set of dummy variables for birth year, calendar year, and age. As noted in the table, some specifications include controls for parental education (years of paternal and maternal education and dummies indicating missing values for each) and own education (years of schooling and a full set of completed degree dummies). Standard errors in all specifications are clustered at the person level. *, **, and ***indicate statistical significance at the 10, 5 and 1 percent levels, respectively.
In panel B, we examine whether the association between the score and earnings has evolved over time or across cohort groups. This is motivated by the large literature in labor economics demonstrating a rise in the return to skill and an increase in residual income inequality over the last several decades (Lemieux 2006; Autor, Katz, and Kearney 2008; Acemoglu and Autor 2011; Lochner and Shin 2014). In column (1), we interact the score with an indicator for years after 1980, when massive technological changes emerged in the work place, such as the advent of computers. We find that the coefficient on the EA score goes to zero whereas the interaction between the EA score and post-1980 is large and significant (0.077).63 However, it could be that the higher returns to the EA score after 1980 simply reflect the post-1980 increases in the college wage premium. In column (2), we include a college degree dummy interacted with the post-1980 dummy to account for this. Indeed, we find an increase of 0.276 in the log-earnings premium associated with a college degree after 1980. Adding this interaction causes a reduction in the coefficient on the EA score post-1980 interaction to 0.039, but it remains highly statistically significant. Results using the post-1980 dummy could reflect either a time or cohort interaction, since the correlation coefficient between year of birth and calendar year in our earnings sample is over 0.60. In column (3), we instead interact the genetic score with an indicator for being born after 1942 (median birth year in the wage sample). The coefficient on the interaction is close to zero. In column (4), we add an interaction between college and education being born after 1942 to the specification in column (3) and find a substantial interaction between post-1942 birth cohorts and having a college degree (0.152), but a small and insignificant interaction between the EA score and post-1942 birth cohorts. In column (5), we include all interaction terms from the specifications in columns (2) and (4). We only find statistically significant interactions between the EA score and post-1980 years, and between having a college degree and post-1980 years. This suggests that something about the labor market changed after 1980 to alter the returns that individuals experienced to the characteristics summarized by the EA score, regardless of their birth cohort.64
One limitation of the SSA data is that they do not contain information on hours worked, preventing an analysis of wages. This raises the possibility that our results on earnings could be driven by differences in labor supply instead of changes in productivity. Indeed, in Online Appendix B, we find that men with higher values of the EA score are more likely to work, and are less likely to retire in a given year. Here the self-reported earnings data in the HRS are useful, even though they are limited to observations on older men after 1990. In Online Appendix B, we find that the EA score exhibits similar associations with both the log of self-reported earnings and the log of self-reported wages in the HRS, suggesting that our earnings results are unlikely to be driven by labor supply differences.
Our earnings results suggest two key points. First, the EA score measures individual traits or characteristics that earn a premium in the labor market, above and beyond completed schooling. Second, this additional return to the EA score appears to have grown over time, and after 1980 in particular. This timing is significant because a large literature documents not only a rise in the returns to schooling beyond this point, but a rise in the returns to observable measures typically associated with labor market ability. Murnane, Willett, and Levy (1995) find that the returns to cognitive skills (measured by math test scores) were larger in the 1980s compared to the 1970s for young workers. Similarly, Gould (2002) provides evidence of a rise in the returns to intelligence based on evidence from cognitive tests scores.65
4.2. Genes, Job Tasks and Skill-Biased Technological Change
The empirical patterns demonstrated in the previous section are consistent with the ongoing rise in the returns to skill. This phenomenon is often explained by the complementarity between certain skills or abilities and the introduction of new technologies during this time period (Acemoglu 1998). Some individuals may have a greater capacity for learning how to use new technologies, either because of genetic endowments or because of past human capital investments. Such individuals may find it easier to adapt to technological shocks and use them to enhance their productivity in the workplace. If the EA score captures such an ability to learn new skills, then the rising return to genetic endowments may be a consequence of skill-biased technological change (SBTC). This suggests an interesting extension to the idea of gene–environment interactions, which are often thought of as pertaining to household environments or other investments made in human capital. Our results suggest that another environmental factor is the state of technology, which can unexpectedly shift over time, making some genetic endowments more or less productive in ways that are difficult to anticipate and plan for.
To examine whether SBTC can help to explain wage returns to ability across birth cohorts, we next consider how the EA score relates to job tasks. The literature on SBTC has implicated computerization as an important driver of rising returns to cognitive skills. In a review of the literature Katz and Autor (1999) discuss many reasons why increased access to computers shifts the demand for skilled labor. For example, it could be the case that skilled workers are “more flexible and facilitate the adoption of new technologies so that all technological change increases the relative demand for more-skilled labor” (p. 1535). Alternately, more skilled workers might be able to work more creatively with available information.
In an influential study, Autor, Levy, and Murnane (2003) link computerization and SBTC to the tasks that workers perform on the job. Specifically, Autor, Levy, and Murnane (2003) argue that computerization should substitute for the labor of workers with jobs that involve repetitive tasks that follow explicit rules or patterns (routine tasks). Conversely, computerization should complement the labor of workers who carry out nonroutine tasks that involve “problem-solving and complex communication activities”. Autor, Levy, and Murnane (2003) use the Department of Labor’s Dictionary of Occupational Titles to measure the intensity of five relevant tasks types: (i) nonroutine analytic (use of math); (ii) nonroutine interactive (direction, control and planning); (iii) routine cognitive (set limits, standards and tolerances); (iv) routine manual tasks (finger dexterity); and (v) nonroutine manual (eye, hand, and foot coordination). Examining patterns within education, occupation, and industry groups, Autor, Levy, and Murnane (2003) indeed find that computerization has been associated with a rise in nonroutine cognitive tasks, and a reduction in routine cognitive and routine manual tasks.
Data from Autor, Levy, and Murnane (2003) provide measures of how intensely every Census occupation uses the five job tasks listed previously.66 Although the public release of the HRS contains masked aggregated occupation codes, we use the detailed occupation codes available in the restricted Industry and Occupation Data file. Since a given task intensity has no natural interpretation, we standardize each intensity to have a mean of zero and a standard deviation of one. Table 6 presents estimates of the relationship between the genetic score and the task intensity for the occupation. The specification here includes all person-year observations for men between the ages of 50–64 with nonmissing occupation data. Panel A regresses the job task intensities on the principal components, and a full set of age, year, and birth year dummies. Importantly, we do not include controls for parental or own education in these specifications.
Table 6.
Polygenic score and standardized job tasks.
| Dep var. | Nonroutine | Nonroutine | Routine | Routine | Nonroutine |
|---|---|---|---|---|---|
| analytic | interactive | cognitive | manual | manual | |
| (1) | (2) | (3) | (4) | (5) | |
| Panel A: | |||||
| EA Score | 0.248*** | 0.185*** |
 0.080*** |
 0.147*** |
 0.021 |
| (0.024) | (0.022) | (0.023) | (0.022) | (0.025) | |
| Obs. | 9948 | 9948 | 9948 | 9948 | 9948 |
| R 2 | 0.104 | 0.068 | 0.028 | 0.052 | 0.032 |
| Educ. Controls | N | N | N | N | N |
| Panel B: | |||||
| EA Score | 0.073*** | 0.055** | 0.021 |
 0.009 |
0.026 |
| (0.023) | (0.022) | (0.023) | (0.022) | (0.026) | |
| Obs. | 9948 | 9948 | 9948 | 9948 | 9948 |
| R 2 | 0.286 | 0.173 | 0.094 | 0.160 | 0.048 |
| Educ. Controls | Y | Y | Y | Y | Y |
Notes: Regressions relating EA score to job tasks. In both panels, the dependent variable is job task intensity, as constructed by Autor, Levy, and Murnane (2003). We standardize each task measure by subtracting its mean and dividing by its standard deviation within our sample. All regressions include the first 10 principle components of the full matrix of genetic data, as well as a full set of dummies for birth year, calendar year and age. Specifications in panel B include controls for parental education (years of paternal and maternal education and dummies indicating missing values for each) and own education (years of schooling and a full set of completed degree dummies). In all columns the sample is restricted to men between the ages of 50 and 64. Standard errors are clustered at the person level. **, and ***indicate statistical significance at the 10, 5 and 1 percent levels, respectively.
The results in panel A suggest that the EA score is positively associated with both nonroutine analytic and interactive tasks, and negatively associated with routine tasks. We find no evidence of an association with nonroutine manual tasks. These results are consistent with the proposition that the EA score is associated with job tasks that were complemented by computerization. However, the associations in panel A may reflect the associations between completed schooling and occupation. In panel B, we repeat the specifications in panel A but now control for parental and own education. After controlling for education, we still find a positive association between the EA score and the nonroutine analytic tasks. A one-standard-deviation increase in the EA score is associated with a 0.073 standard deviation increase in nonroutine analytic task intensity, and a 0.055 standard deviation increase in nonroutine interactive task intensity. We find no statistically significant associations between the EA score and other task intensities after controlling for education.
Given the results present in Table 6, we explore whether we observe a similar relationship between the EA score and nonroutine analytic tasks across education groups. In particular, Figure 10, plots the EA score against the standardized nonroutine analytic task intensity for respondents with and without a college degree. For either education group, individuals with higher scores are more likely to be in occupations where they perform more sophisticated tasks. This may help explain patterns shown in Figure 9, which shows that higher scores predict higher earnings after adjusting for education. However, these figures also highlight one source of the college premium. Across the entire EA score distribution, individuals without a college degree are predicted to have a lower average intensity of this task than individuals with a college degree.
Figure 10.
The EA score and math task (nonroutine analytic). Nonparametric (lowess) estimation relating nonroutine analytic task intensity to the EA score separately for those with and without a college degree.
The results presented in this section add some nuance to our conclusions regarding genetic endowments and earnings. The gene-earning gradient only appears after 1980 in the SSA data. This pattern appears quite consistent with complementarities between technological change and genetic proclivity for learning. This account is bolstered by the positive association between the score and nonroutine cognitive job tasks. Yet, although individuals with high polygenic scores and across education groups profit from new technologies, the college premium remains massive. Importantly, the genetic gradients in both earnings and job tasks are roughly similar for individuals with and without a college degree. This suggests that high-EA individuals without a college degree do not find ways to easily sort into jobs with tasks that heavily complement new technologies. Genetic endowments do not compensate for a lack of a college degree in the labor market. Coupled with our earlier finding that college completion for individuals with similar scores depends in large part on childhood SES (e.g., father’s income), results in this section suggest that there may be unrealized human potential in the economy.67
5. Discussion
Recent breakthroughs in behavioral genetics—most notably the research presented in Rietveld et al. (2013), Okbay et al. (2016), and Lee et al. (2018)—allow researchers to observe genetic endowments that robustly explain educational attainment. Using HRS data, we show that up to 7.4% of the variation in educational attainment is explained by the genetic index presented in Lee et al. (2018) (the EA score). Childhood SES appears to moderate the relationship between this index and various levels of educational attainment—particularly obtaining a college degree. The endowments measured by this index also predict earnings, job tasks, and labor supply later in life. Finally, we provide novel evidence that the wage premium associated with the genetic index has risen over time. We argue that structural changes in the economy, and skill biased technological change in particular, may have contributed to a rise in the genetic gradient.
An important caveat to our results is that the genetic endowments measured by the EA score are not exogenously assigned. Individuals with higher values of the EA score necessarily have birth parents with high values of the EA score, making it difficult to determine how much of the associations we estimate arise from the biological traits linked to these genetic markers, or to the positive environments provided by their parents. Nevertheless, results from previous studies using within-family designs suggest that the majority of the associations used to construct the score remain even after controlling for family fixed effects. Controlling for parental education seems to account for much of this gene–environment correlation. Nevertheless, the associations we report conditional on education might still reflect unmeasured investments or other features of the environment that are not observed in the HRS data.
Our results suggest several interesting avenues for future research. Observed genetic heterogeneity could be incorporated into structural models that are often devised for use in ex ante policy evaluation. Such models could be used to explore long-run dynamics, such as intergenerational mobility, or to better understand how education policy can reduce inequality. The structure of heterogeneity assumed in these models is often tremendously important in driving predictions about labor market dynamics. For example, in a seminal contribution to the field, Keane and Wolpin (1997) suggest that 70% of the variability in the career paths of young men is driven by heterogeneity in unobserved factors (at age 16). When building these kinds of models, researchers face a large number of choices about how to model heterogeneity—from picking which parameters to make random, to determining the structure of correlation between unobservables. The results presented here may offer some restrictions on the structure of heterogeneity in these models. For example, our estimates offer some empirical benchmarks on how the unobservable genetic factors that drive education relate to wages and wealth, conditional on education. Our findings also point to possible differences in the education production function for high school versus college completion.
Another extension of the literature would seek to combine the polygenic score studied here with more exogenous measures of childhood SES. We believe that plausible assumptions allow us to at least sign the interaction between genetic endowments and childhood SES, even though these may be simultaneously determined by parental genes. Nevertheless, more robust inferences could be made with access to randomly assigned childhood circumstances or investments. Indeed, in any ex post evaluation of an existing policy, the genetic score can be used to detect the presence of heterogeneous effects by genetic endowments.
Another important task is to better understand the mechanisms that link the polygenic score studied here and economic outcomes. In ongoing work, we try to understand the relationship between the score, beliefs formation and the ways in which people make health and financial decisions. If the genetic underpinnings of education function through their impact on how people process new information, then this might offer clues as to how policies could be designed to better maximize the potential of individuals with disparate ability endowments. Such insights might ultimately guide the design of school curricula or the content of interventions such as job-training programs.
More broadly, a recurring theme in our empirical results is that individuals with similar abilities, but born into different socioeconomic circumstances, face diverging economic outcomes. These findings suggest an important role for policies that invest in poor children and, more generally, provide some support that such investments could mitigate inefficiently low investments in human capital (Heckman and Masterov 2007). Our findings on wasted potential complement mounting evidence from a variety of fields suggesting the misallocation or squandering of human resources. Researchers have reached this conclusion in different ways. For example, Hsieh et al. (2019) show evidence that innate talent, especially among blacks and women, is likely misallocated across occupations, and highlight the implications of misallocation for economic growth in the United States. In another study, Chetty, Henden, and Katz (2016) demonstrate that randomly assigned vouchers that move children from high-poverty to less-poor neighborhoods can improve labor market performance in the long run. This suggests that policy-relevant factors affect how well a child with a given set of endowments will eventually perform.
Supplementary Material
Acknowledgments
We thank Aysu Okbay for constructing some of the polygenic scores used in this analysis. For helpful comments and conversations, we thank Joseph Altonji, Robert Barbera, Daniel Belsky, Jonathan Beauchamp, Pietro Biroli, David Cesarini, Dora Costa, Stefanie Deluca, Jason Fletcher, Seth Gershenson, Barton Hamilton, Stephanie Heger, Erik Hurst, Steven Lehrer, Lance Lochner, Robert Moffitt, Aysu Okbay, Robert Pollak, Paul Romer, Victor Ronda, Petra Todd, and Matthew Wiswall along with participants in seminars at Johns Hopkins University, New York University, the Census Bureau, and SOLE 2016. We also thank Andrew Gray and Emma Kalish for excellent research assistance. The usual caveats apply. Research reported in this publication was supported by the National Institute on Aging of the National Institutes of Health under Award Number RF1AG055654 (Thom). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. Papageorge is a Research Fellow at IZA.
Notes
The editor in charge of this paper was Claudio Michelacci.
Footnotes
Results reported in Okbay et al. (2016) and Lee et al. (2018) represent the cutting edge in behavioral genetics relating specific genetic variants to education. We discuss these papers and the research leading up to them in Section 2, where we provide further details on the genetic data used in this project. Additional background information is in Online Appendix A.
We explicitly avoid describing the polygenic score as a measure of “ability”, since this term may be too broad and may oversimplify the complexities of genetic endowments. We also want to avoid conflating our interpretation of the polygenic score with the broader definition of “ability” as it is viewed in labor economics. For example, in Human Capital, Becker (1975) defines ability as the collection of all factors that determine persistent differences in economic outcomes given the same profile of human capital investments. More formally Becker (1975) considers earnings, Y, as a function of “unskilled ability” X, human capital investments, C, and the rate of return on investments, r: Y = X + rC (p. 62). In this framework, ability consists of all factors that influence the pair (X, r). Such factors may include genetic endowments, but are certainly not limited to genetic or other biological influences.
This point suggests that the polygenic score should capture some of the information that is contained in individual fixed effects. In results available in Online Appendix B, we show that this is the case, which provides evidence for the link between previously unobserved heterogeneity and the information contained in the polygenic score.
Considering again Becker’s formulation Y = X + rC, it is often assumed that unobserved ability enters exclusively through “unskilled ability”. (X), so that a linear fixed effects model controls for ability.
Proxies for endowments measured among children or newborns are also subject to this type of critique (Almond and Currie 2011).
As we explain throughout the paper, the genetic index is correlated with environments and investments, since parents pass on their genes in addition to shaping environments and making investments. Nevertheless, the fact that environments and investments do not change the genetic score offers an important exclusion restriction. This point is fleshed out in greater detail in Section 3.6 and is formalized in a simple econometric model provided in Online Appendix C.
According to studies that compare identical and nonidentical twins to assess the role of genetic factors in explaining behavior and outcomes, roughly 25%–40% of the variation in educational attainment can be attributed to genetic factors. Such studies treat genetic factors as unobservable and decompose the variance of education into genetic and environmental components. The incremental R2 of the EA score is substantially below the fraction of variation explained by genes in these twin studies, suggesting that the score either does not capture all genetic factors, or does so with a nontrivial amount of measurement error. We elaborate on this issue in Section 2.
For example, in a recent paper, Schmitz and Conley (2017) demonstrate that the effect of military service on educational attainment is moderated by the same polygenic score considered here. In Section 2, we discuss more papers in this line of research.
Belsky et al. (2016) study a sample of New Zealanders and track outcomes from birth through the age of 38. Their findings suggest that there may be a weaker association between genetic ability and lifetime success for high-SES households. A benefit of our analysis is that, using a richer data set, we are able to examine disaggregated measures of labor market success, including labor supply and earnings over the entire life-cycle.
Relatedly, children with high polygenic scores are more likely to grow up in resource-rich environments, meaning they enjoy higher returns to their genetic endowments compared to similarly endowed children in poorer households. Coupled with assortative mating on IQ, inequality in IQ should rise over time, which is a pattern that has been documented in Dickens and Flynn (2001).
We are grateful to Aysu Okbay for clarifying a number of questions on the description we provide in this section. However, any erroneous statements are the sole responsibility of the authors.
Most of the background information presented here on the human genome follows Beauchamp et al. (2011) and Benjamin et al. (2012).
The use of 10 principal components is standard practice in the literature (Okbay et al. 2016). Omitting the principal components, though not at all advisable as a general approach given concerns about population stratification, does not affect our results in this paper, suggesting that other controls adequately capture the type of stratification that might be more substantial or problematic in other data sets.
Many single-SNP associations from earlier genetic studies have failed to replicate. As discussed in Hewitt (2012), this problem often emerged because earlier genetic studies were underpowered to detect reasonable association sizes, and because of failures to correct for multiple hypothesis testing. Given these concerns, modern GWAS studies adopt strict conventions before considering a single-SNP association to be “genome-wide significant”. A convention benchmark for genome-wide significance is a p-value that is less than 5 × 10−8.
The polygenic score that we use is constructed using all of the SNPs that we observe, and not just those that attain genome-wide significance. This follows the practice in Okbay et al. (2016) and Lee et al. (2018). Polygenic scores based on all SNPs have performed better at predicting educational attainment in holdout samples. The score is constructed with the LDpred method (using parameters outlined in Okbay, Benjamin, and Visscher 2018), which is one way to deal with the possibility of “double-counting” given correlations between individual SNPs (Vilhjálmsson et al. 2015; Ware et al. 2017). Although the weights assigned to each SNP typically vary across methods, these weights are usually based on the strength of a SNP’s association with the outcome of interest and the joint covariance matrix of the SNPs. In a series of robustness checks presented in Online Appendix B we show that main results are qualitatively similar if we use alternative scores, for example, earlier versions discovered on smaller samples, or by using different methods to combine them. This is important as it suggests that our key results will not change qualitatively as the field advances and more genes are discovered to be genome-wide significant.
Given the argument that many gender differences could be socially constructed, Molina (2016) suggests that gender can be seen as an environmental factor and that gender differences in coefficients reflect gene-by-environment interactions.
A related identification problem is that parents can react to the genetic endowment of the child and reinforce or compensate their investments. In the literature this is called a gene–environment correlation (Plomin, DeFries, and Loehlin 1977).
See Koellinger and Harden (2018) for a further discussion of the implications of this finding.
Even birth weight, another proxy of innate endowments that has been used in prior literature, is not immune to this critique as it reflects in utero investments, for example, mother’s smoking behavior (Lien and Evans 2005), exposure to pollutants (Currie, Neidell, and Schmieder 2009), stress during pregnancy (Camacho 2008; Currie and Rossin-Slater 2013) or mothers’ own health (Costa 1998). See also Aizer and Currie (2014) for a recent discussion.
In a recent contribution, Ronda et al. (2019) use Danish data to examine within-sibling-pair differences in the EA score and educational outcomes. They find that controlling for mother’s education, which we do in our analyses, eliminates differences in within-sibling versus between-family coefficients on the EA score by 70%.
Taubman (1976) is an early contribution using data on twins, who have similar or identical genotypes, to assess the amount of variation in earnings attributable to genes.
Related, given that the polygenic score is a noisy measure of the full set of genetic endowments related to education, it would be misleading to draw conclusions about necessary or sufficient scores for economic outcomes, for example, whether above a certain threshold individuals are guaranteed to attain a college degree.
On multidimensionality, Willis and Rosen (1979) emphasize manual skill, which they distinguish from academic skill.
Later contributions to this literature include Kautz et al. (2014) and Humphries and Kosse (2017).
In Online Appendix D, we show that a measure of cognition that is available for HRS respondents is positively associated with the EA score, but only weakly so (with a correlation coefficient of roughly 0.23). Moreover, the EA score predicts education and earnings even after we control for the cognitive test score, suggesting that the EA score captures additional factors relevant to educational attainment. However, the comparison of the EA score with the cognitive test score in the HRS is difficult to interpret since the latter is meant to capture cognitive decline. A more useful exercise would be to compare the EA score with scores from tests designed to measure cognition, such as the AFQT, which is not available in the HRS.
Indeed, Papageorge, Ronda, and Zheng (2017) provide evidence that a socioemotional skill known as externalizing behavior and linked to aggression predicts higher wages despite being associated with lower educational attainment. If it has a genetic basis, it would enter negatively into the polygenic score despite its value on the labor market, further underscoring the need to interpret the polygenic score as a measure of genetic factors that influence some skills associated with educational attainment, but not as a broad measure of “ability”.
Although genetic data for the 2010 and 2012 waves are available, the polygenic score based on the results of Lee et al. (2018) and the LDpred method has only been constructed for the respondents genotyped in 2006 and 2008. In Online Appendix B, we provide further detail and show that our main results continue to hold if we use a less predictive score constructed with a different methodology for individuals from all four available waves.
As part of the genetic data release, the HRS classifies certain individuals as being of European descent based on their genetic ancestry. Polygenic scores have been publicly released for 12,090 individuals from the 2006, 2008, 2010, and 2012 waves who have been identified as having genetic European ancestry.
These retrospective childhood SES measures are discussed in greater detail in Section 3.3. We use the IPUMS release of the 1960 U.S. Census data (Ruggles et al. 2018) to estimate the average income for each father’s occupation group.
These data are found in the Respondent Cross-Year Summary Earnings file of the HRS.
We use the IPUMS release of the CPS data for the years 1962–2013 (Ruggles et al. 2018). Although the SSA data offer rich administrative records over the life-cycle, they are top-coded based on the taxable maximum for Social Security taxes in each year. This top-coded amount has changed over time, as described in Olsen and Hudson (2009). Online Appendix B provides additional details on top-coding and our correction for top-coding.
In Online Appendix B, we replicate a subset of our analyses using HRS income data. Because the HRS data contain only contemporaneous self-reported income, we cannot use them to estimate specifications related to lifetime income, which we are able to do with the SSA data. However, the HRS income data are less aggressively top-coded than the SSA data, which provides one possible advantage. The consistency of results across data sets suggests that top-coding patterns are not a significant driver of our main results.
In a formal χ2 test of normality based on skewness and kurtosis, we fail to reject the null hypothesis that the EA score is normally distributed in our sample with p-value = 0.2647.
When appropriate, we also include a cubic polynomial of the polygenic score. This is motivated by the model we develop in Online Appendix C, which is used to examine consequences of endogenous parental investments and measurement error and which guides our interpretation of estimates.
As seen in Table 1, parental education is missing for a nontrivial number of individuals. We partially address this issue by adding separate dummy variables indicating missing values of father’s and mother’s education.
Again, this is consistent with the results from Kong et al. (2018), who find that parental SNPs that are not passed on to children still predict their educational outcomes.
In results available from the authors, we experiment with specifications adding a series of more specific controls related to health during childhood. These recall questions may be less prone to measurement error than questions about self-rated health. Additional variables include indicators for measles, mumps, chicken pox, school absences, sight problems, parental smoking, asthma, diabetes, respiratory problems, speech problems, allergies, heart conditions, ear problems, epilepsy, migraines, stomach problems, blood conditions, depression, drug use, psychological conditions, concussions, disabilities, childhood smoking, learning disabilities, and other problems. When these are added to a basic regression explaining years of education (i.e., column (1) in Table 2 but excluding the EA score), they and the self-reported health scale variables have a combined incremental R2 of 0.079 (0.037 when parental education controls are added). Even when we control for these variables, we find that results on the relationship between EA score and educational attainment are consistent with the results in Table 2. For example, adding all of these childhood health dummies to the specification in the last column of Table 2 yields a point estimate of 0.523 for the coefficient on the EA score, which is within the 99% confidence interval of the estimate without these added controls (just outside of the 95% confidence interval).
It should be noted that many of these SES measures may be highly correlated with parental education. Thus the change in R2 across specifications is not necessarily a good measure of the relative importance of each new set of controls, since their relationship with education may already be reflected in the relationship between parental education and own education (Gelbach 2016). However, the aim here is not to demonstrate the relative importance of each set of controls. Rather, we are concerned with the range of explanatory power of the polygenic score as we control for additional measures of childhood circumstances. If we include the maximal set of SES controls but exclude parental education (a modified version of column (5) in Table 2), this yields an R2 of 0.470. Compared to the result in column (1), this suggests an incremental R2 of 0.217 for all SES controls when ignoring parental education. In this specification the EA score has an incremental R2 of 0.051. Much of the explanatory power of our SES variables is being picked up by parental education. Nevertheless, the incremental predictive power of the EA score is substantial in any of these comparisons.
Belsky et al. (2016) demonstrate that genetic endowments linked to completed education are associated with learning outcomes during early childhood. Using a polygenic score from an earlier GWAS, they find evidence that children with higher scores began talking earlier and, by age 7, were stronger readers.
About 18% of respondent families reported having to move, and about 14% reported asking for help. When combined, about 25% had to take at least one of these actions.
All results using this variable are robust to treating cases where the father is dead or never lived nearby as missing.
The concern is that higher wages among individuals with Catholic schooling might be selected on unobservables so that estimated returns are spurious. They argue that if the two groups are similar on observables, they are unlikely to be so selected on unobservables as to undermine estimated returns.
For each measure of childhood SES, the results of a Kolmogorov–Smirnov test suggest that we can reject the null hypothesis that the distributions of the EA score are equal for high and low SES groups with p-value < 0.01 in all cases.
This analysis is similar to the one in Belley and Lochner (2007), who study how parental income predicts educational attainment for individuals with similar cognitive test scores.
Given that polygenic scores are not well suited to decompose the variance of a trait into genetic and environmental components, these results must be interpreted with caution. It is possible that an updated score could change the relative importance of the EA score versus father’s income in predicting educational attainment.
Similar patterns emerge if we study college completion, but limit attention to individuals who graduated high school. These results are generated by the replication materials accompanying this paper.
Throughout the paper, in specifications where we interact the EA score with some other moderating variable, we also include interactions between the principle components and the moderating variable.
Regression results for this exercise, for the full sample and then separately for men and women, are found in Online Appendix B.
If we use education controls as an additional measure of SES that we interact with the polygenic score in regressions explaining educational attainment, we obtain the same patterns as we do with the SES measures considered here. Higher parental education is associated with a steeper genetic gradient for college completion and above and with a less steep gradient for lower educational outcomes. As explained earlier, we do not present this as a main result given evidence that the distributions of the polygenic score differ substantially by mother’s education, which suggests comparisons are more difficult to defend.
Cohort differences are also discussed in Galindo-Rueda and Vignoles (2005), who show that the importance of ability in explaining college degree attainment declines over time, presumably because lower-ability people are more likely to be able to pay for college in comparison to earlier cohorts. See also Lovenheim and Reynolds (2011) on changes by ability and income in post-secondary choices.
For example, Nestler (2012) discusses research showing that early-life conditions faced by mice can induce epigenetic effects that impact their behaviors and vulnerability to stress later in life.
The number of books in a household has been used in earlier literature examining the production of cognition to proxy for parental investments in their children (see, e.g., Cunha and Heckman 2008).
In related work, Todd and Wolpin (2003) suggest that typical approaches to estimating the production of cognition may be overly restrictive. Our findings are related since they suggest that ability and investments interact in complex ways (that possibly vary by schooling level) to generate educational outcomes.
Investments could rise with the child’s genetic endowment because parents target resources, or because children with high endowments also have parents with high endowments who provide more resources.
As mentioned earlier when we discuss our standard control set, the model motivates why we allow for heteroskedastic error terms and include a polynomial in the polygenic score for all specifications, which helps to control for measurement error.
Another possibility is that the interactions that we estimate arise from nonlinearities in the human capital production function. Suppose that the genetic score is related to education in a nonlinear fashion, and that SES is correlated with the genetic score. Then we could estimate significant score–SES interactions that have nothing to do with differences in the production function across SES groups. That is, an interaction between the score and observed SES may simply reflect an underlying nonlinear relationship between the score and education. As discussed earlier, we control for nonlinearities through a cubic in the EA score for all specifications examining the interaction between the EA score and childhood SES to explain educational attainment. We thank Jonathan Beauchamp for pointing out this possibility.
In results available from the authors, we assess robustness if we restrict attention to individuals who are not in the tails, that is, if we rerun regressions dropping individuals with EA scores in the top or bottom 5%. We continue to find positive and significant interactions between SES and the EA score in predicting college completion. However, we note that with this restriction many of the interaction terms become insignificant in the specifications predicting high school completion.
Specifically, we include our standard controls, years of father’s and mother’s education separately, dummies for missing values of father’s and mother’s education, years of own education, and separate dummies for each possible completed degree.
Altonji and Pierret (2001) attribute this empirical pattern to the dynamics of employer learning. Early in an individual’s work history, firms make wage offers conditional on easily observable characteristics such as educational attainment that are useful but are not sufficient to describe a worker’s true productivity. Measures like the AFQT might better capture the worker characteristics that are relevant for productivity, but firms typically have a hard time observing these proxies. However, as workers age and accumulate experience, employers learn more about worker characteristics. Consequently, as workers age, the correlation between wages and these proxies for hard-to-observe ability should increase.
The threshold of $10,000 is arbitrary, but this is chosen to restrict the sample as much as possible to full time workers and exclude those who are marginally attached the labor force.
To control for possible population stratification, we also include interaction terms between the principal components and the indicator for a college degree.
In Online Appendix B, we also show that there appear to be substantially larger wage returns to the EA score for individuals with a college degree. This difference is statistically significant when estimating an a wage equation using self-reported wage data from the HRS. When we restrict the SSA earnings data to match the years and ages of the HRS sample, we find point estimates that suggest a larger return to the EA score among college graduates, although the difference in returns between those with and without a college degree is not statistically significant.
To control for population stratification, we always include interactions between the principle components and the “Year > 1980” and “Birth Year > 1942” indicators whenever these binary variables are interacted with the EA score in panel B of Table 5.
One potential confounding factor is the sharp drop in the extent of top-coding patterns in the SSA data that occurred in the late 1970s and early 1980s. As described in Online Appendix B, the divergence in earnings between EA terciles appears to happen continuously after 1980 at a time when the top-coding scheme was relatively stable. This suggests that the post-1980 rise in the association between the EA score and earnings is unlikely to be solely due to changes in top-coding.
Further contributions to this literature include Juhn, Murphy, and Pierce (1993), Taber (2001), and Tobias (2003).
Data on the task intensities associated with each occupation can be found on David Autor’s website: http://economics.mit.edu/faculty/dautor/data/autlevmurn03. The Autor, Levy, and Murnane (2003) task intensity measurements that we use are based on the 1991 Dictionary of Occupational Titles associated with male workers.
In Online Appendix B, we conduct a similar analysis to the one used to generate Figure 5, relating quartiles of father’s income and of the EA score to the average annual earnings in adulthood. The aim is to assess whether education differences predicted by interactions between the EA score and father’s income shown in Figure 5 translate to earnings differences. We find that earnings for individuals in the lowest EA score quartile but the highest father’s income quartile have average annual earnings that are similar to individuals in the lowest father’s income quartile and the highest EA score quartile. We also find some inconclusive results on how the SES-earning gradient changes across EA score quartiles. Examining differences in average earnings between the fourth and second quartiles of father’s income suggests that the SES-earning gradient is substantially higher for individuals in the top three EA score quartiles compared to the bottom quartile. However, there is no clear pattern when examining differences in average earnings between the fourth and first quartiles of father’s income.
Contributor Information
Nicholas W Papageorge, Email: papageorge@jhu.edu, The Johns Hopkins University.
Kevin Thom, Email: kthom.work@gmail.com, Unversity of Wisconsin – Milwaukee.
References
- Acemoglu Daron. (1998). “Why Do New Technologies Complement Skills? Directed Technical Change and Wage Inequality.” Quarterly Journal of Economics, 113, 1055–1089. [Google Scholar]
- Acemoglu Daron, Autor David (2011). “Skills, Tasks and Technologies: Implications for Employment and Earnings.” Handbook of Labor Economics, 4, 1043–1171. [Google Scholar]
- Aizer Anna, Cunha Flavio (2012). “The Production of Child Human Capital: Endowments, Investments and Fertility.” Working paper, Brown University, Providence, Rhode Island. [Google Scholar]
- Aizer Anna, Currie Janet (2014). “The Intergenerational Transmission of Inequality: Maternal Disadvantage and Health at Birth.” Science, 344, 856–861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almond Douglas, Currie Janet (2011). “Killing Me Softly: The Fetal Origins Hypothesis.” Journal of Economic Perspectives, 25(3), 153–172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altonji Joseph G., Elder Todd E., Taber Christopher R. (2005). “Selection on Observed and Unobserved Variables: Assessing the Effectiveness of Catholic Schools.” Journal of Political Economy, 113, 151–184. [Google Scholar]
- Altonji Joseph G., Pierret Charles R. (2001). “Employer Learning and Statistical Discrimination.” Quarterly Journal of Economics, 116, 313–350. [Google Scholar]
- Autor David H., Katz Lawrence F., Kearney Melissa S. (2008). “Trends in US Wage Inequality: Revising the Revisionists.” Review of Economics and Statistics, 90, 300–323. [Google Scholar]
- Autor H., Frank Levy David, Murnane Richard J. (2003). “The Skill Content of Recent Technological Change: An Empirical Exploration.” Quarterly Journal of Economics, 118, 1279–1333. [Google Scholar]
- Barth Daniel, Papageorge Nicholas W., Thom Kevin (2019). “Genetic Endowments and Wealth Inequality.” Journal of Political Economy, forthcoming. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bates Timothy C., Lewis Gary J., Weiss Alexander (2013). “Childhood Socioeconomic Status Amplifies Genetic Effects on Adult Intelligence.” Psychological Science, 24, 2111–2116. [DOI] [PubMed] [Google Scholar]
- Beauchamp Jonathan P., Cesarini David, Johannesson Magnus, van der Loos Matthijs J. H. M., Koellinger Philipp D., Groenen Patrick J. F., Fowler James H., Niels Rosenquist J., Roy Thurik A., Christakis Nicholas A. (2011). “Molecular Genetics and Economics.” Journal of Economic Perspectives, 25(4), 57–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becker Gary S. (1960). “An Economic Analysis of Fertility.” In Demographic and Economic Change in Developed Countries. Columbia University Press, pp. 209–240. [Google Scholar]
- Becker Gary S., Tomes Nigel (1986). “Human Capital and the Rise and Fall of Families.” Journal of Labor Economics, 4, S1–S39. [DOI] [PubMed] [Google Scholar]
- Becker G. S. (1975). Human Capital: A Theoretical and Empirical Analysis, with Special Reference to Education. Columbia University Press. [Google Scholar]
- Becker G. S., Chiswick Barry R. (1966). “Education and the Distribution of Earnings.” American Economic Review, Proceedings, 56, 358–369. [Google Scholar]
- Belley Philippe, Lochner Lance (2007). “The Changing Role of Family Income and Ability in Determining Educational Achievement.” Journal of Human Capital, 1, 37–89. [Google Scholar]
- Belsky Daniel W., Moffitt Terrie E., Corcoran David L., Domingue Benjamin, Harrington HonaLee, Hogan Sean, Houts Renate, Ramrakha Sandhya, Sugden Karen, Williams Benjamin S., Poulton Richie, Caspi Avshalom (2016). “The Genetics of Success: How Single-Nucleotide Polymorphisms Associated with Educational Attainment Relate to Life-Course Development.” Psychological Science, 27, 957–972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamin Daniel J., Cesarini David, Chabris Christopher F., Glaeser Edward L., Laibson David I., Guðnason Vilmundur, Harris Tamara B., Launer Lenore J., Purcell Shaun, Vernon Smith Albert, et al. (2012). “The Promises and Pitfalls of Genoeconomics.” Annual Review of Economics, 4, 627–662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bharadwaj Prashant, Vellesen Løken Katrine, Neilson Christopher (2013). “Early Life Health Interventions and Academic Achievement.” American Economic Review, 103(5), 1862–1891. [PubMed] [Google Scholar]
- Bitler Marianne P., Gelbach Jonah B., Hoynes Hilary W. (2006). “What Mean Impacts Miss: Distributional Effects of Welfare Reform Experiments.” American Economic Review, 96(4), 988–1012. [Google Scholar]
- Black Sandra E., Devereux Paul J., Salvanes Kjell G. (2005). “Why the Apple Doesn’t Fall Far: Understanding Intergenerational Transmission of Human Capital.” American Economic Review, 95(1), 437–449. [Google Scholar]
- Branigan Amelia R., McCallum Kenneth J., Freese Jeremy (2013). “Variation in the Heritability of Educational Attainment: An International Meta-Analysis.” Social Forces, 92, 109–140. [Google Scholar]
- Camacho Adriana. (2008). “Stress and Birth Weight: Evidence from Terrorist Attacks.” American Economic Review, 98(2), 511–515. [PubMed] [Google Scholar]
- Cawley John, Conneely Karen, Heckman James, Vytlacil Edward (1997). “Cognitive Ability, Wages, and Meritocracy.” In Intelligence, Genes, and Success: Scientists Respond to the Bell Curve, edited by Bernie Devlin, Fienberg Stephen E., Resnick Daniel P., Roeder Kathryn. Springer, New York, pp. 179–192. [Google Scholar]
- Chetty Raj, Henden Nathaniel, Katz Lawrence F. (2016). “The Effects of Exposure to Better Neighborhoods on Children: New Evidence from the Moving to Opportunity Experiment.” American Economic Review, 106(4), 855–902. [DOI] [PubMed] [Google Scholar]
- Conley Dalton, Domingue Benjamin (2016). “The Bell Curve Revisited: Testing Controversial Hypotheses with Molecular Genetic Data.” Sociological Science, 3, 520–539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Costa Dora L. (1998). “Unequal at Birth: A Long-Term Comparison of Income and Birth Weight.” The Journal of Economic History, 58, 987–1009. [Google Scholar]
- Cunha Flavio, Heckman James (2007). “The Technology of Skill Formation.” American Economic Review, 97(2), 31–47. [Google Scholar]
- Cunha Flavio, Heckman James J. (2008). “Formulating, Identifying and Estimating the Technology of Cognitive and Noncognitive Skill Formation.” Journal of Human Resources, 43, 738–782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Currie Janet. (2009). “Healthy, Wealthy, and Wise: Socioeconomic Status, Poor Health in Childhood, and Human Capital Development.” Journal of Economic Literature, 47, 87–122. [Google Scholar]
- Currie Janet, Neidell Matthew, Schmieder Johannes F. (2009). “Air Pollution and Infant Health: Lessons from New Jersey.” Journal of Health Economics, 28, 688–703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Currie Janet, Rossin-Slater Maya (2013). “Weathering the Storm: Hurricanes and Birth Outcomes.” Journal of Health Economics, 32, 487–503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickens William T., Flynn James R. (2001). “Heritability Estimates versus Large Environmental Effects: The IQ Paradox Resolved.” Psychological Review, 108, 346–369. [DOI] [PubMed] [Google Scholar]
- Domingue Benjamin W., Belsky Daniel W., Conley Dalton, Harris Kathleen Mullan, Boardman Jason D. (2015). “Polygenic Influence on Educational Attainment.” AERA Open, 1, 1–13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eichler Evan E., Flint Jonathan, Gibson Greg, Kong Augustine, Leal Suzanne M., Moore Jason H., Nadeau Joseph H. (2010). “Missing Heritability and Strategies for Finding the Underlying Causes of Complex Disease.” Nature Reviews Genetics, 11, 446–450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flynn James R. (1987). “Massive IQ Gains in 14 Nations: What IQ Tests Really Measure.” Psychological Bulletin, 101, 171–191. [Google Scholar]
- Galindo-Rueda Fernando, Vignoles Anna (2005). “The Declining Relative Importance of Ability in Predicting Educational Attainment.” Journal of Human Resources, 40, 335–353. [Google Scholar]
- Gelbach Jonah B. (2016). “When Do Covariates Matter? And Which Ones, and How Much?” Journal of Labor Economics, 34, 509–543. [Google Scholar]
- Gould Eric D. (2002). “Rising Wage Inequality, Comparative Advantage, and the Growing Importance of General Skills in the United States.” Journal of Labor Economics, 20, 105–147. [Google Scholar]
- Griliches Zvi, Mason William M. (1972). “Education, Income, and Ability.” Journal of Political Economy, 80, S74–S103. [Google Scholar]
- Guo Guang, Stearns Elizabeth (2002). “The Social Influences on the Realization of Genetic Potential for Intellectual Development.” Social Forces, 80, 881–910. [Google Scholar]
- Heckman James J. (1995). “Lessons from the Bell Curve.” Journal of Political Economy, 103, 1091–1120. [Google Scholar]
- Heckman James J., Masterov Dimitriy V. (2007). “The Productivity Argument for Investing in Young Children.” Applied Economic Perspectives and Policy, 29, 446–493. [Google Scholar]
- Heckman James J., Rubinstein Yona (2001). “The Importance of Noncognitive Skills: Lessons from the GED Testing Program.” American Economic Review, 91(2), 145–149. [Google Scholar]
- Heckman James J., Vytlacil Edward (2005). “Structural Equations, Treatment Effects, and Econometric Policy Evaluation.” Econometrica, 73, 669–738. [Google Scholar]
- Hewitt John K. (2012). “Editorial Policy on Candidate Gene Association and Candidate Gene-by-Environment Interaction Studies of Complex Traits.” Behavior Genetics, 42, 1–2. [DOI] [PubMed] [Google Scholar]
- Hotz V. Joseph, Alex Klerman Jacob, Willis Robert J. (1997). “The Economics of Fertility in Developed Countries.” Handbook of Population and Family Economics, 1, 275–347. [Google Scholar]
- Hsieh Chang-Tai, Hurst Erik, Jones Charles I., Klenow Peter J. (2019). “The Allocation of Talent and US Economic Growth.” Econometrica, 87, 1439–1474. [Google Scholar]
- Humphries John Eric, Kosse Fabian (2017). “On the Interpretation of Non-Cognitive Skills–What Is Being Measured and Why It Matters.” Journal of Economic Behavior & Organization, 136, 174–185. [Google Scholar]
- Juhn Chinhui, Murphy Kevin M., Pierce Brooks (1993). “Wage Inequality and the Rise in Returns to Skill.” Journal of Political Economy, 101, 410–442. [Google Scholar]
- Katz Lawrence F., Autor David H. (1999). “Changes in the Wage Structure and Earnings Inequality.” Handbook of Labor Economics, 3, 1463–1555. [Google Scholar]
- Kautz Tim, Heckman James J., Diris Ron, Ter Weel Bas, Borghans Lex (2014). “Fostering and Measuring Skills: Improving Cognitive and Non-Cognitive Skills to Promote Lifetime Success.” National Bureau of Economic Research Working Paper No. 20749. [Google Scholar]
- Keane Michael, Moffitt Robert, Runkle David (1988). “Real Wages over the Business Cycle: Estimating the Impact of Heterogeneity with Micro Data.” The Journal of Political Economy, 96, 1232–1266. [Google Scholar]
- Keane M. P., Wolpin K. I. (1997). “The Career Decisions of Young Men.” Journal of Political Economy, 105, 473–522. [Google Scholar]
- Kirkpatrick Robert M., McGue Matt, Iacono William G. (2015). “Replication of a Gene–Environment Interaction Via Multimodel Inference: Additive-Genetic Variance in Adolescents’ General Cognitive Ability Increases with Family-of-Origin Socioeconomic Status.” Behavior Genetics, 45, 200–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koellinger Philipp D., Paige Harden K. (2018). “Using Nature to Understand Nurture.” Science, 359, 386–387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong Augustine, Thorleifsson Gudmar, et al. (2018). “The Nature of Nurture: Effects of Parental Genotypes.” Science, 359, 424–428. [DOI] [PubMed] [Google Scholar]
- Lee J. J., Wedow R., Okbay A., Kong E., Maghzian O., Zacher M., Nguyen-Viet T. A., Bowers P., Sidorenko J., Linnér R. K., Fontana M. A. (2018). “Gene Discovery and Polygenic Prediction from a Genome-Wide Association Study of Educational Attainment in 1.1 Million Individuals.” Nature Genetics, 50, 1112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leibowitz Arleen. (1974). “Home Investments in Children.” Journal of Political Economy, 82, S111–S131. [Google Scholar]
- Lemieux, Thomas (2006). “Increasing Residual Wage Inequality: Composition Effects, Noisy Data, or Rising Demand for Skill?” American Economic Review, 96(3), 461–498. [Google Scholar]
- Lien Diana S., William N. Evans (2005). “Estimating the Impact of Large Cigarette Tax Hikes: The Case of Maternal Smoking and Infant Birth Weight.” Journal of Human Resources, 40, 373–392. [Google Scholar]
- Lillard Lee, Willis Robert J. (1978). “Dynamic Aspects of Earnings Mobility.” Econometrica, 46, 985–1012. [Google Scholar]
- Lochner Lance, Shin Youngki (2014). “Understanding Earnings Dynamics: Identifying and Estimating the Changing Roles of Unobserved Ability, Permanent and Transitory Shocks.” National Bureau of Economic Research Working Paper No. 20068. [Google Scholar]
- Lovenheim Michael F., Lockwood Reynolds C. (2011). “Changes in Postsecondary Choices by Ability and Income: Evidence from the National Longitudinal Surveys of Youth.” Journal of Human Capital, 5, 70–109. [Google Scholar]
- Mani Anandi, Mullainathan Sendhil, Shafir Eldar, Zhao Jiaying (2013). “Poverty Impedes Cognitive Function.” Science, 341, 976–980. [DOI] [PubMed] [Google Scholar]
- Martin Alicia R., Gignoux Christopher R., Walters Raymond K., Wojcik Genevieve L., Neale Benjamin M., Gravel Simon, Daly Mark J., Bustamante Carlos D., Kenny Eimear E. (2017). “Human Demographic History Impacts Genetic Risk Prediction across Diverse Populations.” The American Journal of Human Genetics, 100, 635–649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mincer Jacob. (1958). “Investment in Human Capital and Personal Income Distribution.” Journal of Political Economy, 66, 281–302. [Google Scholar]
- Molina Teresa. (2016). “Pollution, Ability, and Gender-Specific Investment Responses to Shocks.” Working Paper, University of Hawaii, Manoa. [Google Scholar]
- Murnane Richard J., Willett John B., Levy Frank (1995). “The Growing Importance of Cognitive Skills in Wage Determination.” The Review of Economics and Statistics, 77, 251–266. [Google Scholar]
- Nestler Eric J. (2012). “Stress Makes Its Molecular Mark.” Nature, 490, 171–172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nisbett, Richard E., Joshua Aronson, Clancy Blair, William Dickens, James Flynn, Diane F. Halpern, and Eric Turkheimer (2012). “Intelligence: New Findings and Theoretical Developments.” American Psychologist, 67, 130. [DOI] [PubMed] [Google Scholar]
- Okbay Aysu, Beauchamp Jonathan P., Alan Fontana Mark, Lee James J., Pers Tune H., Rietveld Cornelius A., Turley Patrick, Chen Guo-Bo, Emilsson Valur, Meddens S. Fleur W., et al. (2016). “Genome-Wide Association Study Identifies 74 Loci Associated with Educational Attainment.” Nature, 533, 539–542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okbay Aysu, Benjamin Daniel, Visscher Peter (2018). “SSGAC Educational Attainment: GWAS and MTAG Polygenic Scores (Ver. 1.0).” SSGAC Educational Attainment: GWAS and MTAG Polygenic Scores (Ver. 1.0). [Google Scholar]
- Olsen Anya, Hudson Russell (2009). “Social Security Administration’s Master Earnings File: Background Information.” Social Security Bulletin, 69. [PubMed] [Google Scholar]
- Papageorge Nicholas W., Ronda Victor, Zheng Yu (2017). “The Economic Value of Breaking Bad: Schooling, Misbehavior and the Labor Market.” Working paper, The Johns Hopkins University. [Google Scholar]
- Plomin Robert, DeFries John C., Loehlin John C. (1977). “Genotype-Environment Interaction and Correlation in the Analysis of Human Behavior.” Psychological Bulletin, 84, 309. [PubMed] [Google Scholar]
- Price Alkes L., Patterson Nick J., Plenge Robert M., Weinblatt Michael E., Shadick Nancy A., Reich David (2006). “Principal Components Analysis Corrects for Stratification in Genome-Wide Association Studies.” Nature Genetics, 38, 904–909. [DOI] [PubMed] [Google Scholar]
- Rietveld Cornelius A., Conley Dalton, Eriksson Nicholas, Ekso Tõnu, Medland Sarah E., Vinkhuyzen Anna A. E., Yang Jian, et al. (2014). “Replicability and Robustness of Genome-Wide-Association Studies for Behavioral Traits.” Psychological Science, 25, 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rietveld Cornelius A., Medland Sarah E., Derringer Jaime, Yang Jian, Esko Tõnu, Martin Nicolas W., Westra Harm-Jan, Shakhbazov Konstantin, Abdellaoui Abdel, Agrawal Arpana, et al. (2013). “GWAS of 126,559 Individuals Identifies Genetic Variants Associated with Educational Attainment.” Science, 340, 1467–1471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ronda Victor, Agerbo Esben, Bleses Dorthe, Mortensen Preben Bo, Roshom Michael (2019). “Family Disadvantage, Gender and the Returns to Genetic Human Capital.” Working paper, Aarhus University. [Google Scholar]
- Ruggles Steven, Floor Sarah, Goeken Ronald, Grover Josiah, Meyer Erin, Pacas Jose , Sobek Matthew (2018). “IPUMS USA: Version 8.0 [dataset].” 10.18128/D010.V8.0, retrieved 1 September 2019. [DOI] [Google Scholar]
- Scarr-Salapatek Sandra. (1971). “Race, Social Class, and IQ.” Science, 174, 1285–1295. [DOI] [PubMed] [Google Scholar]
- Schmitz Lauren L., Conley Dalton (2017). “The Effect of Vietnam-Era Conscription and Genetic Potential for Educational Attainment on Schooling Outcomes.” Economics of Education Review, 61, 85–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taber Christopher R. (2001). “The Rising College Premium in the Eighties: Return to College or Return to Unobserved Ability?” Review of Economic Studies, 68, 665–691. [Google Scholar]
- Taubman Paul. (1976). “The Determinants of Earnings: Genetics, Family, and Other Environments: A Study of White Male Twins.” American Economic Review, 66(5), 858–870. [Google Scholar]
- Tobias Justin L. (2003). “Are Returns to Schooling Concentrated Among the Most Able? A Semiparametric Analysis of the Ability-Earnings Relationships.” Oxford Bulletin of Economics and Statistics, 65, 1–29. [Google Scholar]
- Todd Petra E., Wolpin Kenneth I. (2003). “On the Specification and Estimation of the Production Function for Cognitive Achievement.” The Economic Journal, 113, F3–F33. [Google Scholar]
- Todd Petra E., Wolpin Kenneth I. (2006). “Assessing the Impact of a School Subsidy Program in Mexico: Using a Social Experiment to Validate a Dynamic Behavioral Model of Child Schooling and Fertility.” American Economic Review, 96(5), 1384–1417. [DOI] [PubMed] [Google Scholar]
- Todd Petra E., Wolpin Kenneth I. (2007). “The Production of Cognitive Achievement in Children: Home, School, and Racial Test Score Gaps.” Journal of Human Capital, 1, 91–136. [Google Scholar]
- Tucker-Drob Elliot M., Bates Timothy C. (2016). “Large Cross-national Differences in Gene× Socioeconomic Status Interaction on Intelligence.” Psychological Science, 27, 138–149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turkheimer Eric, Haley Andreana, Waldron Mary, D’Onofrio Brian, Gottesman Irving I. (2003). “Socioeconomic Status Modifies Heritability of IQ in Young Children.” Psychological Science, 14, 623–628. [DOI] [PubMed] [Google Scholar]
- Vilhjálmsson Bjarni J., Yang Jian, Finucane Hilary K., Gusev Alexander, Lindström Sara, Ripke Stephan, Genovese Giulio, Loh Po-Ru, Bhatia Gaurav, Do Ron, et al. (2015). “Modeling Linkage Disequilibrium Increases Accuracy of Polygenic Risk Scores.” The American Journal of Human Genetics, 97, 576–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ware Erin B., Schmitz Lauren L., Faul Jessica D., Gard Arianna, Mitchell Colter, Smith Jennifer A., Zhao Wei, Weir David, Kardia Sharon L. R. (2017). “Heterogeneity in Polygenic Scores for Common Human Traits.” bioRxiv, 1–13. [Google Scholar]
- Willis Robert J., Rosen Sherwin (1979). “Education and Self-Selection.” Journal of Political Economy, 87, S7–S36. [Google Scholar]
- Wiswall Matthew, Zafar Basit (2015). “Determinants of College Major Choice: Identification Using an Information Experiment.” Review of Economic Studies, 82, 791–824. [Google Scholar]
- Zuk Or, Hechter Eliana, Sunyaev Shamil R., Lander Eric S. (2012). “The Mystery of Missing Heritability: Genetic Interactions Create Phantom Heritability.” Proceedings of the National Academy of Sciences, 109, 1193–1198. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.