Epidemiological control measures and predicted number of infections for SARS-CoV-2 pandemic: case study Serbia march–april 2020

Abstract

Background

In this paper, we are studying the response of the Serbian government and health authorities to the SARS-CoV-2 pandemic in the early stage of the local outbreak between Mar. 15^th and Apr. 15^th, 2020 by predictive numerical models. Such a study should be helpful to access the effectiveness of measures conducted to suppress the pandemic at a local scale.

Methods

We have performed extrapolation of the number of SARS-CoV-2 infections with the first stable set of data exploiting exponential growth (linear in logarithmic scale). Based on obtained coefficients it is performed prediction of a number of cases until the end of March. After initial exponential growth, we have changed predictive model to the generalized gamma function. Obtained results are compared with the number of infections and the prediction for the remainder of the outbreak is given.

Findings

We have found that the daily growth rate was above 21.5% at the beginning of the period, increased slightly after the introduction of the State of Emergency and the first set of strict epidemical control measures. It took about 13 days after the first set of strict measures to smooth daily growth. It seems that early government measures had an only moderate impact to reduce growth due to the social behavior of citizens and influx of diaspora returning to Serbia from highly affected areas, i.e., the exponential growth of infected persons is kept but with a reduced slope of about 14–15%. Anyway, it is demonstrated that period required that any measure has effect is up to 15 days after introduction, firstly to exponential growth with a smaller rate and after to smooth function representing the number of infected persons below exponential growth rate.

Conclusions

Obtained results are consistent with findings from other countries, i.e., initial exponential growth slows down within the presumed incubation period of 2 weeks after adopting lockdown and other non-pharmaceutical epidemiological measures. However, it is also shown that the exponential growth can continue after this period with a smaller slope. Therefore, quarantine and other social distancing measures should be adopted as soon as possible in a case of any similar outbreak since alternatives mean prolonged epidemical situation and growing costs in human life, pressure on the health system, economy, etc. For modeling the remainder of the outbreak generalized gamma function is used showing accurate results but requiring more samples and pre-processing (data filtering) concerning exponential part of the outbreak. We have estimated the number of infected persons for the remaining part of the outbreak until the end of June.

Epidemiology; Infectious disease; Public health; SARS-CoV-2, Serbia, Prediction model, Exponential growth, Generalized Gamma model.

1. Introduction

The second decade of the XXI century repeats the second decade of the XX century with global pandemic causing significant loss of human life all over the world, consequences for patients, forced change of lifestyle for a large portion of the human population, economic losses, and many other side effects. The actual SARS-CoV-2 pandemic has an outbreak at the end of 2019 in Chinese city Wuhan (province Hubei) with 11 million citizens [1]. From Jan. 23^rd Chinese government established strict quarantine rules over city Wuhan and some neighboring areas. In total, more than 68 million citizens in Hubei and neighbor regions were under strict measures [2]. Besides, entire China was affected by different epidemical and social distancing measures. Major part of measures applied on Jan. 23^rd resulting in a peak number of novel cases on Feb. 4^th. Statistics are announced daily by the National health commission of the People Republic of China [3]. Note that on Feb. 12^th China revised previous estimates of the number of cases giving a significant increase for that date. From our point of view, this is a statistical adjustment only and we can still assume that the maximal number of novel cases is on Feb. 4^th, i.e., 12 days after adopting strict quarantine and epidemiological measures. Within this interval of 12 days (a little bit shorter than the presumed incubation period of 14 days) average increase in novel cases was 25.31% while the average period required for doubling the number of patients was less than 3.1 days.

Since Chinese measures were strict but effective curbing one of the largest infective disease outbreaks in history being contained within approximately two months they can be considered as state-of-art for the SARS-CoV-2 pandemic. Therefore, all other politics in epidemical control should be compared with the Chinese efforts to get insight if it is possible to achieve similar or even better results with measures less affecting everyday life. In this paper, we are considering predicting the number of patients in Serbia based on exponential and generalized gamma models and estimating time when local epidemical control measures give benefit in the smoothing growth curve and suppressing exponential epidemic outbreak. As can be expected, predicting the second part of the outbreak by the generalized gamma function is less accurate comparing the first part modeled by the exponential growth. Anyway, the generalized gamma function model is also useful giving a good way to estimate the effect of epidemical control measures to the process dynamic.

2. Serbia and SARS-CoV-2 epidemic

In this section, we are giving basic background information on Serbia of interest for the study, i.e., information on demographics including diaspora and aging population and travel connections. In Section 2.2 basic information of the SARS-CoV-2 spread in Serbia with the timeline of key epidemical control measures conducted to contain the outbreak are given. Detailed information on the epidemical control policies performed is given in the Appendix.

2.1. Country background

Serbia is a landlocked country on the Balkan Peninsula in southeast Europe with an estimated 6.9 million citizens excluding Kosovo∗ (UN resolution 1244). Almost ¼ of the population inhabits the greater Belgrade area while about 60% is urban population. Serbia has borders with four members of the European Union (Hungary, Croatia, Bulgaria, and Romania) and four non-members (West Balkan countries) North Macedonia, Montenegro, Bosnia and Herzegovina, and Albania. The main international roads are A1 and A3 connecting West and Central with southeast Europe and further toward Asia Minor.

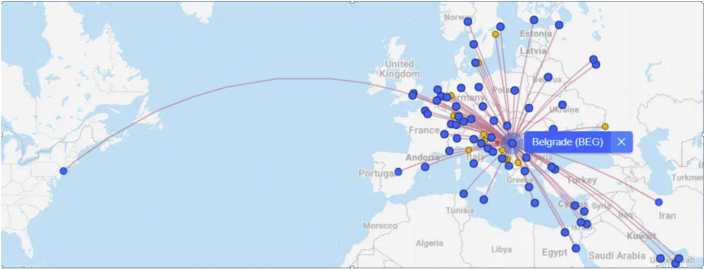
There are three international airports with the main Nikola Tesla Airport, Belgrade, serving as a hub of Air Serbia, a member of the Etihad group. Also, it is a hub for Aviolet Company with seasonal charters and WizzAir. This airport served about 6.2 million passengers in 2019 and more than 70000 aircraft. There were 79 direct connections from Belgrade to 41 countries on four continents as of Jan. 20^th, 2020 (Figure 1). Konstantin the Great airport in Niš is significantly smaller serving flights to only a dozen destinations with low flight frequency. Serbia has a large diaspora with several million persons. Census of world countries counted more than 2 million Serbs in the diaspora, but some estimates are between 5 and 7 million persons of Serbian origin worldwide. Also, more than 2 million Serbs are living in neighboring countries and Slovenia. Many international companies are operating in Serbia, most notable are Chinese but the direct spread of the SARS-CoV 2 from China to Serbia was not detected.

Figure 1.

Connections from Belgrade Airport, according to flightconnections.com.

https://www.flightconnections.com/flights-from-belgrade-beg

Serbian population is among the oldest in the world with an average age of 42.9 years and life expectancy 74.8 years. According to the Serbian statistical office, more than 19% of citizens are older than 65 that is a vulnerable category to the SARS-CoV-2.

2.2. Time-line of the epidemic in Serbia and epidemical control measures

Here, only the main events and time-line of main epidemical control measures are listed while a more detailed description is given in the Appendix.

Serbian authorities on Jan. 28^th established measures preventing the spread of SARS-CoV-2 following the same strategy previously used in the outbreaks of SARS, Ebola, MERS, Avian Flu, Swine Flu, etc. This was mainly related to the control of passengers coming from China and installing thermal cameras at some gates of the Airport Belgrade (for details see Appendix).

The number of infections is announced by the Ministry of Health and Institute for public health “Dr. Milan Jovanović Batut” (web page covid-19.rs). It is announced twice a day at 8 am and 6 pm until Mar. 23^th and after that only once per day at 3 pm. We have used these data as official (ground truth) reflecting the situation with infections in the country.

The number of tests conducted daily increased gradually. Before Mar. 23^rd it was sporadic based on symptoms, arrivals from certain geographical arrays, tracking contacts of existing cases, etc. In total, there were only 822 tests until Mar. 23^rd. However, the number increased with more cases emerging, and within the next seven days total number of tests increased to 3084 on Mar. 30^th. In the second half of April, the number of tests increased heavily so in May there were more than 6000 tests per day.

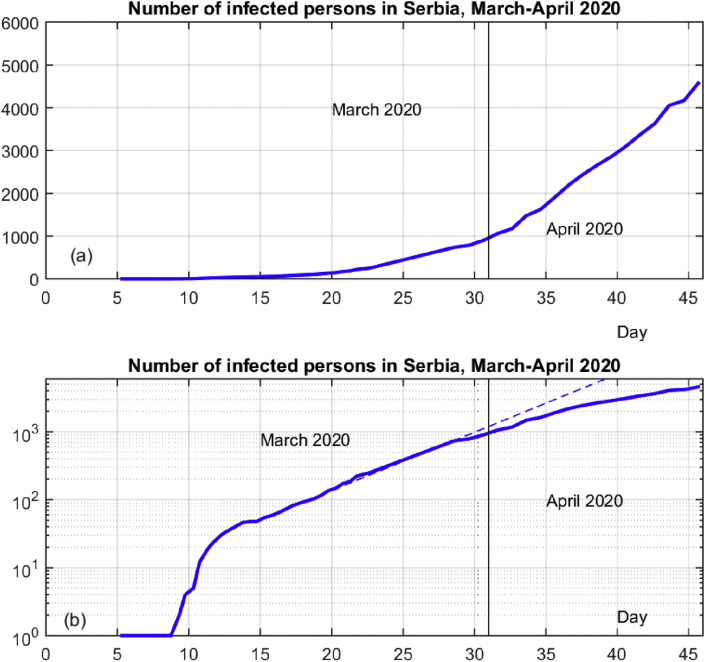
The first person infected by the SARS-CoV-2 in Serbia was announced on Mar. 6^th when the majority of neighbor countries already had infected persons. Three days later virus was confirmed to another person and after that the number of cases started gradually to increase (Figure 2).

Figure 2.

Number of infected persons in up to April 15^th, 2020, according to covid-19.rs: (a) linear; (b) logarithmic scale (dashed line represents predicted number of cases without application of quarantine measures).

The first significant growth in the number of infections was on Mar. 11^th with an increase from 5 to 19 cases within 24 h. On Mar. 15^th it was declared the State of Emergency. The time-line of main epidemical control measures conducted is (for detail see Appendix):

• -Mar. 15^th State of Emergency, closing educational institutions and local transportation, forbidden gatherings, night curfews, closing borders and establishment of mandatory self-isolation and quarantine, mandatory lockdown for persons over 65;
• -Mar. 22^nd Closing restaurants and similar establishments, hair studios and similar establishments;
• -Mar. 27^th-Mar. 30^th first long weekend curfew. Such curfews are repeated for all weekends in April, and the first weekend in May;
• -May 6^th State of Emergency is abolished.

Serious event aggravating the epidemiological situation was the return of persons from diaspora mainly from West European countries, some of them with an extremely difficult outbreak at that time. According to authorities only within 36 h before the State of Emergency more than 70000 persons returned to Serbia and in March more than 400000 citizens were coming back ranging from students at foreign universities, persons with temporal status in foreign countries, etc. Such social dynamics significantly deteriorated the epidemiological state in Serbia especially before the establishment of mandatory self-isolation or quarantine for 14 days for all arrivals.

3. Data description and importance

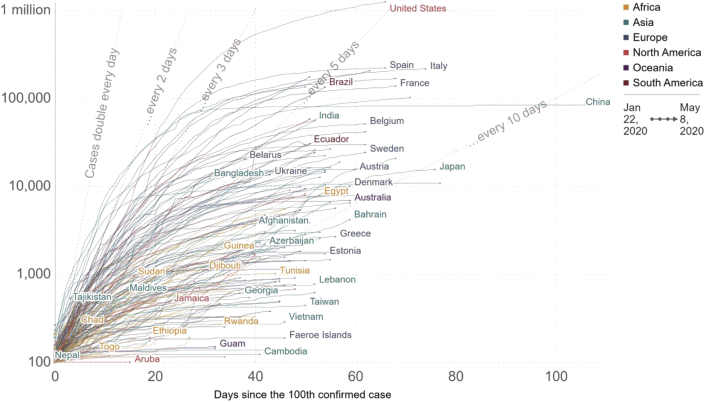
The semi-logarithmic plot of discovered infections in Serbia is shown in Figure 2(b). This is the usual behavior of many models of infective illness epidemic outbreaks [4]. After a small number in the first several day number of cases grows from 5 to 72 within 7 days from Mar. 10^th to Mar. 17^th. To compare local data with the other countries consider figure from [5] (Figure 3) where the number of infections is compared in a semi-logarithmic scale against daily growth in the number of infections from 100 detected cases up. It can be seen that a daily percentage increase is going even above 33% for some countries. To explain the importance of the daily infection growth recall study published early even before the World Health Organization announced the SARS-CoV-2 pandemic showing that the expected period of doubling the number of cases was between 4.6-6.1 (average 5.2 days) [6]. It means that it is expected daily increase in the number of cases between 12.03-16.26% (consensus 14.26%). First comments on these findings were not favorable since the majority of readers assumed that period doubling will be significantly longer.

Figure 3.

Number of infections from the day when 100 patients are diagnosed. Data provided by ourworldindata.org, European CDC, Center for Systems Science and Engineering at John Hopkins University, May. 8^th.

https://ourworldindata.org/covid-cases

However, for daily growth of 33% period doubling is only 2.43 days, for example, Spain experienced a daily increase of infections at an early stage of the epidemic (the early stage, in this case, was only several days before growing to thousands of cases and hundreds of dead) was more than 38.5% meaning period of doubling of only 2.1 days! This fact, with the severity the health conditions of many patients requiring ICU treatment and assistant ventilation, is the reason why this infection was the most serious health challenge within a lifespan. Note that at some stage in the USA period-doubling was only 1.75 days.

4. Methodology for prediction

4.1. Exponential model – first phase

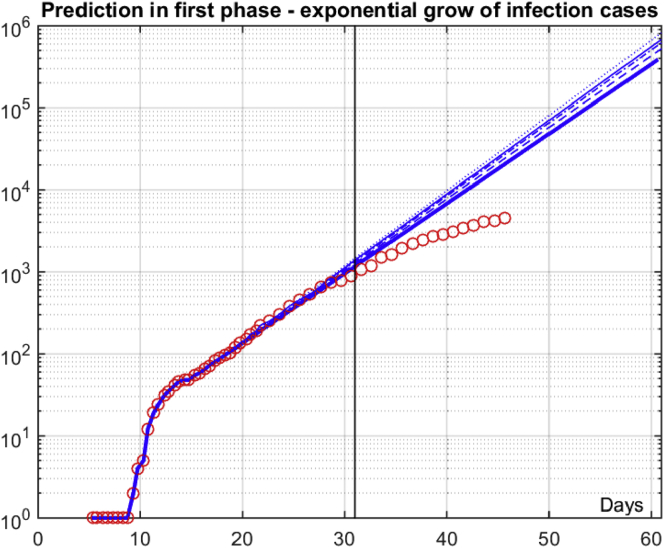
Prediction is performed only for the number of infections. The number of fatalities is significantly smaller (about 2.16% of the number of infections). Also, the response of the number of infections to control measures is faster than in the case of other potential indicators. Several first samples (between first found an infected person on Mar. 6^th and begin of clearly visible exponential growth on Mar. 15^th) are avoided. The term sample is used for the number of infections for a given instant (date). Initial prediction is performed using only five samples: two on Mar. 15^th, two on Mar. 16^th, and one on Mar. 17^th at 8 am. Within this period number of detected infections has grown from 48 to 72 with an average daily increase of 21.63% what can be considered as a moderate rate for the early stage of this infection comparing to other countries. We have decided to update prediction after three samples in a row are above or below an obtained number of infected persons (ground truth according to the Serbian authorities) in March. In total, we have revised the exponential model four times according to the above-described rule in March. Table 1 summarizes findings. Predictions are updated on Mar. 19^th, Mar. 21^st, Mar. 23^rd, and Mar. 28^th. Figure 4 gives true samples and obtained predictions. It can be seen that all predictions are in a rather narrow range between 21.5% and 23.5% for the first 14 days. However, as can be seen from Figure 4 on Mar. 28^th or 29^th the tide has been slowed down and initial exponential growth has been replaced with a more favorable function. Then, on Mar. 31^st at 15 am instead of predicted between 1029 and 1345 infected persons it was fortunately only 900. It is similar to other countries [7]: lockdown and other quarantine measures have shown the ability to smooth exponential growth within the presumed incubation period of 14 days. Average growth in exponential phase Mar. 15^th-Mar. 28^th was 21.8%. It means that all estimates of average daily growth performed within this period are consistent (see Table 1). Parameter log₁₀ (1 + Grow%) in Table 1 represents the slope of an interpolated linear function in the logarithmic scale accompanied by the standard deviation in estimation. It can be seen that there is no statistical difference between obtained results, i.e., that even a small number of available samples in the exponential growth phase can be used for reliable prediction. Therefore, it is important to stress that prediction of the exponential growth phase without effective epidemical measures is simple and estimation of daily growth rate can be reliably performed using just several samples. Of course, this holds for actual pandemic where it can be assumed that there are no persons with immunity against this agent. When some immunity in population exists or in the case when the number of infected persons approaches the number of available persons more advanced SIS or SIR models should be adopted [6, 8, 9, 10, 11].

Table 1.

Prediction and statistics for the first part of SARS-CoV-2 epidemic in Serbia.

Interval	Mar.15 18.00-Mar. 19 08.00	To Mar 21 18.00	To Mar. 22 15.00	To Mar. 28 15.00	After Mar. 28
Grow%	21.63%	22.27%	22.73%	23.52%	22.98%
log10(1+Grow%)	0.0850	0.0873	0.0890	0.0917	0.0899
StdDev	0.0425	0.0330	0.0256	0.0237	0.0128
Mar. 31st15h	1079	1170	1232	1345	1274
Mean Abs	20.02	15.22	20.31	44.02
Mean Rel	6.37%	4.80%	4.76%	6.92%
Max Abs	59.19	41.97	76.88	140.38
Mean Abs	14.48%	11.45	10.38%	18.94%
Log Mean	0.0290	0.0214	0.0209	0.0283
Log Max	0.0679	0.0528	0.0453	0.0753

Figure 4.

Predicting the number of cases in the exponential growth phase (circles – true values; solid line - prediction of Mar. 15^th, dashed line - prediction of Mar. 18^th, dash-dotted line – prediction of Mar. 21^st; dotted line – prediction on Mar. 22^nd; thick solid line – the final stage of initial exponential growth on Mar. 28^th).

Besides, we have checked the prediction accuracy of exponential daily growth. In Table 1 rows denoted with mean abs, mean rel, max abs, max rel, log mean, and log max are statistics related to the accuracy of predictions:

$$\text{Mean Abs}=\frac{1}{K}\sum _{k=1}^K\left|P_k-O_k\right|····\text{Max Abs}=\max \{\left|P_k-O_k\right|,k\in [1,K]\}$$ (1)

$$\text{Mean Rel}=\frac{1}{K}\sum _{k=1}^K\frac{\left|P_k-O_k\right|}{O_k}····\text{Max Rel}=\max \{\left|P_k-O_k\right|/O_k,k\in [1,K]\}$$ (2)

$$\text{Log}\text{Mean}=\frac{1}{K}\sum _{k=1}^K\left|{\log }_{10}{P}_k-{\log }_{10}{O}_k\right|····\text{Log}\text{Max}=\max \left\{\left|{\log }_{10}{P}_k-{\log }_{10}{O}_k\right|,k\in \left[1,K\right]\right\},$$ (3)

where P_k is a predicted number of infected persons while O_k is the true number of infected persons as announced by authorities. k = 1 hereafter is Mar. 1^st. It can be seen that accuracy gradually improves for the first three intervals (seven days in total) while after that it deteriorates a bit since it is close to the end of initial exponential daily growth. Also, it can be seen that all estimates of the number of infected persons on Mar. 31^st is above the actual number since exponential growth has been smoothed before the end of March as we already explained.

Table 2 is given for comparison of the response on epidemical measures in various countries in the early stage of the outbreak. It is considered several neighboring and close European countries. Some of these local outbreaks are already analyzed in [12, 13, 14, 15]. Date 1 corresponds to a date with the most similar measures like in the Serbian State of Emergency from Mar. 15^th. As can be seen in some countries it cannot be identified a single day with similar measures. After the description of measures, we have given date (Date 2) with the largest number of infections, followed by the length of the interval between Date 1 and Date 2. It can be seen that for the majority of countries response to epidemical measures was between 9-15 days. It took longer only in three countries. However, these three countries have good control of outbreaks with a relatively small number of infections so these results can be treated as outliers. The final column gives notes on adopted measures or related results for each of the considered countries.

Table 2.

Response to epidemical control measures in some Serbian neighboring and close countries. Date 1 corresponds to the establishment of measures that are closest to the Serbian State of Emergency, Date 2 corresponds to date with the largest number of detected infections.

Country	Date 1	Measure	Date 2	Interval	Note
Italy	Mar. 07th-08th	Lombardy lockdown	Mar. 21st	14 days	Lombardy was the main outbreak region
Croatia	Mar. 15th, 23rd, 24th	Closing schools, local transportation, border crossings	Mar. 24th	9 days	Strictest measures in the world on Mar. 24th according to the Oxford university
Romania	Mar. 16th	State of emergency (following other measures from Mar. 8th)	Apr. 01	15 days	Similar social dynamics as in Serbia
Austria	Mar. 15th-17th	Lockdown measures	Mar. 26th	9 days	Strict measures after a large outbreak in Alpine resorts
Bulgaria	Mar. 13th	State of emergency	Apr. 24th	42 days	Schools closed earlier due to the flu outbreak. A small number of cases
Czech republic	Mar. 12th	State of emergency	Mar. 26th	12 days	Strict measures early
Slovakia	Mar. 8th, Mar. 12th	Closing schools, state of emergency	Apr. 16th	35 days	Strict measures early, a small number of cases
Slovenia	Mar. 14th, Mar. 15th	Closing travel, closing schools	Mar. 27th	13 days	Strict measures after a large outbreak influenced by neighbor Italy
North Macedonia	Mar. 18th	State of emergency in the country	Apr. 16th	29 days	The first peak was on Apr. 5th, while the second is caused by an outbreak in Kumanovo

4.2. Generalized gamma model – second phase

It remains an issue of how to predict outcomes after the exponential phase. The prediction model can be changed by employing a piece-wise exponential law or a sort of combination of linear and exponential growth models. As will be seen from results, both of these models could be used reliably but an issue is number of parameters that can make prediction challenging. Namely, for each piece, we need to estimate two or three parameters and limits of intervals. Dealing with a large number of parameters could lead to significant inaccuracy. So we have decided to keep the model as simple as possible. Namely, after a period with exponential growth we have used generalized gamma function model given as [16, 17]:

$$G\left(x;c,k,\gamma \right)=c\frac{1}{\Gamma \left(k\right){\gamma }^k}{x}^k\exp (-x/\gamma )$$ (4)

where Γ() is gamma function, x is the date and $G(x;c,k,\gamma )$ is predicted the number of infected persons announced for a given date. Parameters k and γ determine the function shape. In general, larger values of these parameters correspond to larger mode (maximal number of daily infections), mean value (number of cases), and spread (duration of an outbreak). Parameter k describes also higher-order function (distribution) moments, i.e., skewness and kurtosis. For a given x, we are estimating parameters c, k, and γ for x in an interval between Mar. 15^th and x and based on that we are performing prediction, i.e., number of infected persons in forthcoming days and the cumulative number of infected persons. Estimates of c, k, and γ are updated after each sample is available. A maximum likelihood approach is applied for parameter estimation. Note that we have realized that obtained estimates are not so stable as in the case of exponential growth so estimation is performed on smoothed (filtered) data, i.e., the actual number of infections is replaced with the last five days average. In this manner, faster stabilization of prediction is ensured but as a drawback smoothing can cause a delay in recognition of reaction to epidemiological measures.

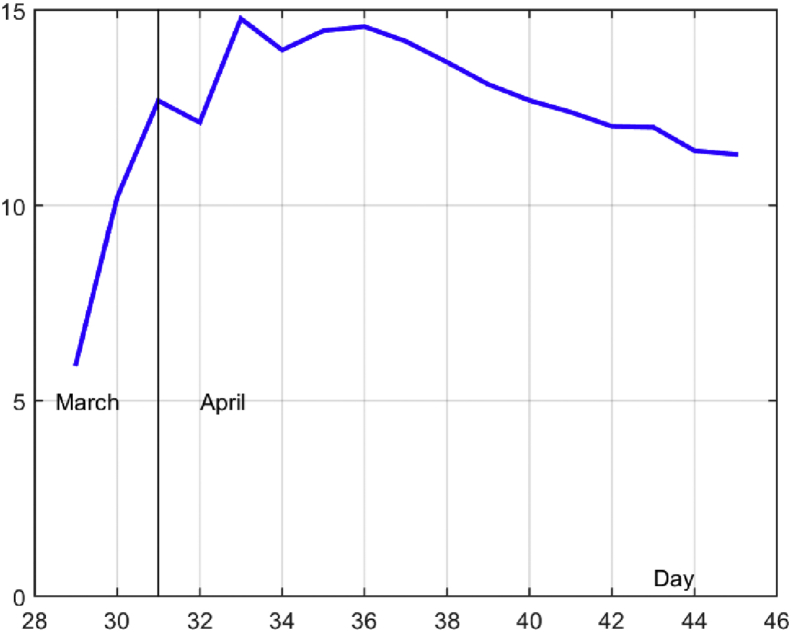
Firstly, we are interested in checking the behavior of the function after the exponential growth period concluded on Mar. 28^th. Figure 5 gives average daily growth for days after Mar. 28^th calculated as:

$$\sqrt[k-28]{O_k/O_{28}}\text{for }k>28$$ (5)

where O₂₈ is the number of cases on Mar. 28^th when initial exponential growth with an estimated daily increase of about 21.8% has been completed. It can be seen from Figure 5 that the exponential growth with attenuated growth rate of about 14% (period-doubling 5.3 days) is continued. The source of such an unfortunate response to measures adopted in the emergency decree of Mar. 15^th is unknown. It could be that some establishments continue to work like for example restaurants until Mar. 22^nd but it could be also mentioned the large influx of returnee from the diaspora. Anyway, such behavior has been noted in other countries for example in Germany [7] that partial lockdown and social distancing measures in a short term can only decrease the slope of the exponential growth but not to stop it. It is interesting that the maximum of average daily growth is achieved on day k = 33 (Apr. 2^nd), i.e., 12 days after stricter measures are adopted on Mar. 22^nd. Again, it demonstrates that it was required about 12 days before adopted measures give a visible effect. Therefore, it is simple to conclude that in the case of any similar outbreak abrupt introduction of strong measures can significantly shorten the duration of an epidemic and also alleviate other effects (loss of life, number of infected persons, a burden on health system and intensive care units, economic losses, etc.). For example, if this growth is not alleviated by other measures until the end of April the number of infected persons could reach more than 63000. Taking into account the number of citizens and the overall economic situation of the country such pressure on the health system could be critical.

Figure 5.

Average percentage of growth in the number of infections in the second phase of the outbreak (from Mar. 28^th).

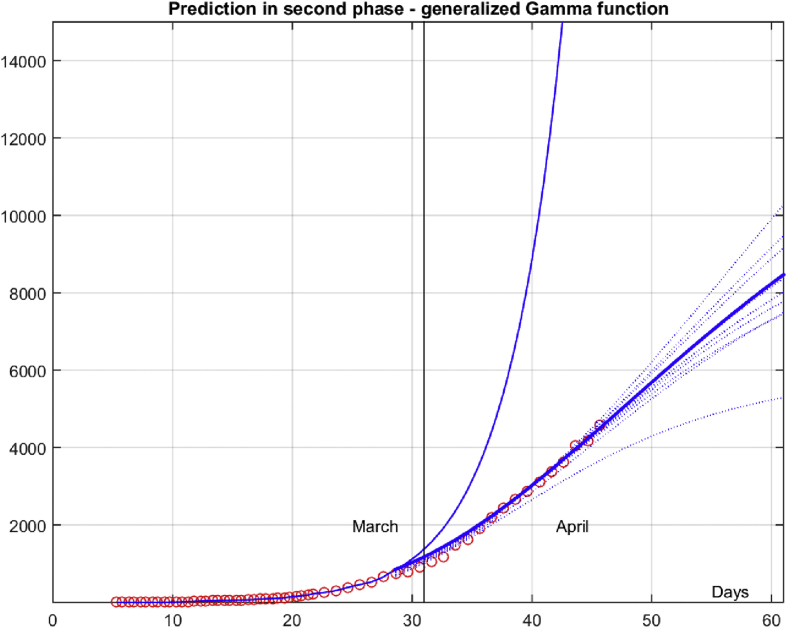
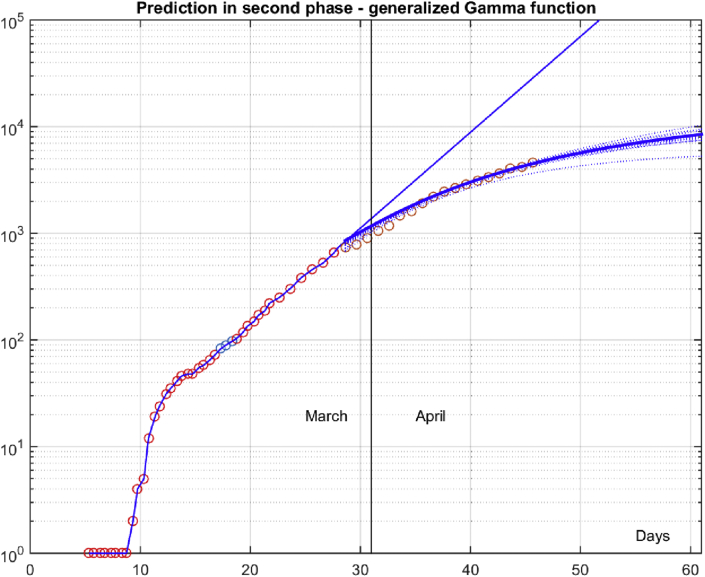
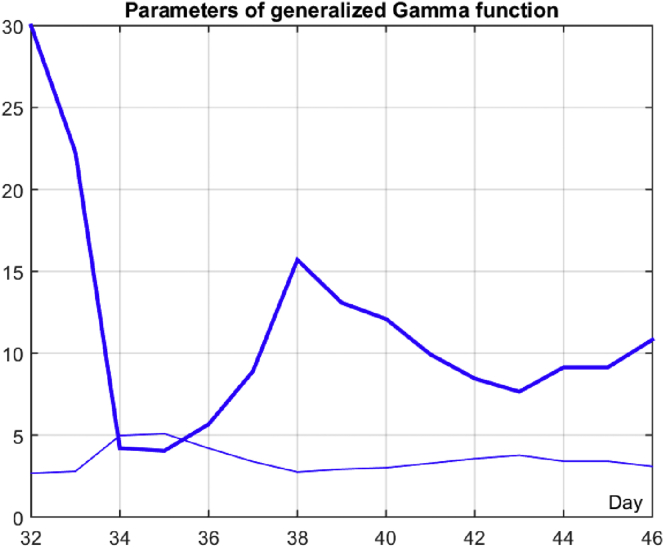
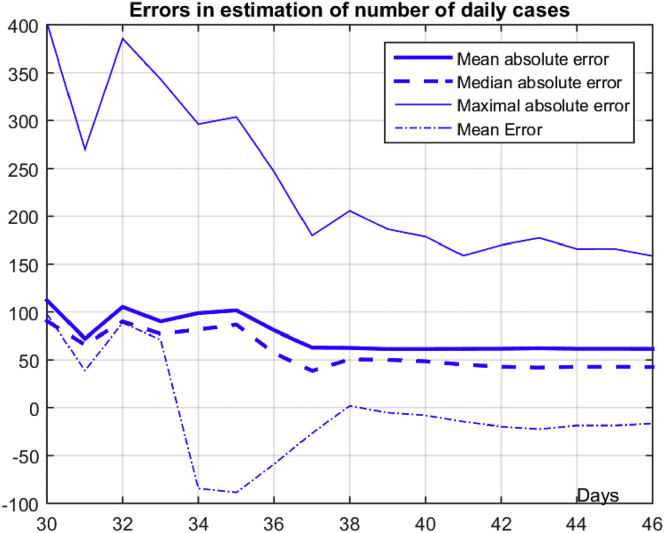
Figures 6 and 7 represent results from two stages, before Mar. 28^th with exponential growth and after with the number of cases modeled by generalized gamma model in linear and logarithmic scales. Each dotted line after Mar. 28^th represents prediction obtained based on data from Mar. 28^th to that date. The thick solid line is prediction performed on the end of the considered interval 8391 (3876 is predicted number of infections for remaining 15 days of April) obtained with (c₀,γ₀,k₀)=(401.3,10.83,3.09). Figure 8 gives estimates of two parameters describing the generalized gamma function shape and predicted number infections γ and k for various dates within an interval. Parameter k has slower changes than γ meaning that the epidemical control measures influenced more γ (duration and severity of outbreak) than k (skewness). It can be concluded that the first two sets of epidemiological control measures (Mar. 15^th and Mar. 22^nd) caused a reduction of the γ from almost 30 to less than 11. It can be seen that from date k = 38 (Apr. 7^th) obtained results become stable meaning that it was required at least 9 samples to get a reliable prediction for the generalized gamma function modeling used to estimate the second part of the outbreak. Recall that for the first interval modeled by the exponential function it was required only five samples to accurately predict the path to catastrophe if proper measures were not adopted. In addition, we have considered how accurate estimates are within interval Mar. 29^th – Apr. 15^th using estimation/prediction for the considered date. Figure 9 gives average errors (mean absolute, median absolute, max absolute, and mean) for considered estimates. It can be seen that from date k = 37 (Apr. 6^th), obtained errors are stable with a median absolute error of less than 50. Note that the mean value of error at the end of the interval is -16.7, i.e., our prediction slightly underestimates the number of cases (bias is 16.7) what influences the accuracy of the predicting number of infections. Therefore, the generalized gamma function can be used to model epidemiological outbreaks under similar conditions with acceptable accuracy for the interval when epidemiological measures become to give results in curbing infection outbreak.

Figure 6.

Modeling the second phase of outbreak in linear scale with generalized gamma function – circles – number of infections; solid line – a prediction with an exponential model obtained in the first phase; dotted lines – different predictions with generalized gamma model for the considered interval; thick line – a final prediction with generalized gamma model from Apr. 15^th.

Figure 7.

Modeling the second phase of outbreak in logarithmic scale with generalized gamma function – circles – number of infections; solid line – a prediction with an exponential model obtained in the first phase; dotted lines – different predictions with generalized gamma model for the considered interval; thick line – a final prediction with the generalized gamma model from Apr. 15^th.

Figure 8.

Estimation of generalized gamma function parameters on various dates in the interval (k=1 is Mar. 1^st) – thin line – parameter k; thick line – parameter γ

Figure 9.

Statistics of errors in modeling the number of daily infections for a considered interval with generalized gamma function up to considered date (x-axis).

4.3. Prediction of the remaining of the outbreak

We have completed the assessment on Apr. 15^th and based on obtained results it has been performed estimation for the remainder of the outbreak. It should be noted that we do not know in advance anything about any political decision nor any medical progress or change in virus behavior. Therefore, such predictions can be assumed as highly speculative. Also, as we have already explained, our final prediction on Apr. 15^th is performed on pre-filtered data with the actual number of infections replaced by the last five sample averages. Firstly, the remaining of the outbreak is predicted based on parameters c₀, k₀, and γ₀ on Apr. 15^th. It is obvious from Figure 8, that estimates of the generalized gamma function parameters change in relatively wide range before stabilizing on Apr. 7^th. Three lines are given in Figure 8. The thick line represents prediction. Two dashed lines are presenting cases when the epidemiological situation gradually improves and with parameters (γ, k) going linearly to (0.9γ₀, 0.9k₀) and if the outbreak continues more dramatically than predicted on Apr. 15^th with parameters linearly increasing toward (1.1γ₀, 1.1k₀).

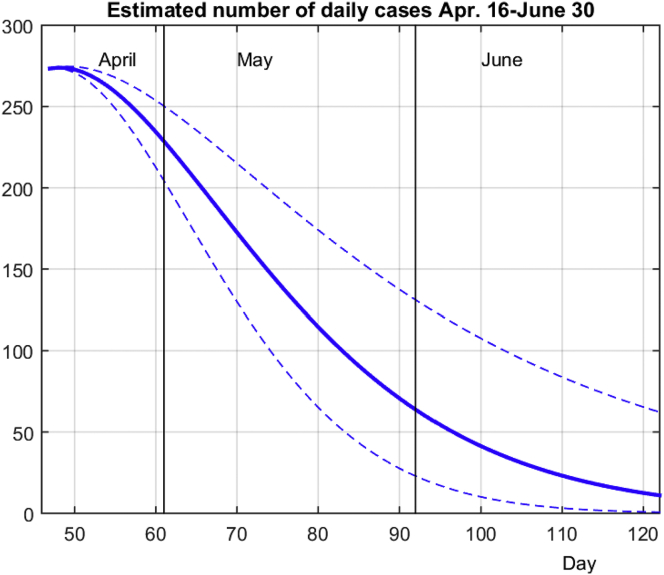
Figure 10 gives estimates of the daily number of infections in interval Apr. 15^th to June 30^th. The results are summarized in Table 3. An additional column in Table 3 gives the potential influence of bias in prediction as previously explained. An interesting point is that in the rest of April all three predictions give similar results. Our model from Apr. 15^th predicted 3876 new infections, while the other two predictions give results in the range [3731,4004]. However, there is a drastic difference in May. Our prediction gives 4200 infections with range [2855,5805]. Strict measures and their enforcement are necessary since the difference between the most favorable situation and the worst-case scenario could be substantial. Finally, the situation for June is even more emphasized (partially influenced by expected inaccuracy in extrapolation process), i.e., in the most favorable condition it could be expected that the entire outbreak is completed without novel cases at the end of June while in the worst-case scenario it could be expected about 60 (or 77 with bias) novel infections at the end of the month (more than 2700 in total in June).

Figure 10.

Predicted number of daily cases up to the end of June (thin line) and two alternative scenarios (more and less favorable) given with dashed lines.

Table 3.

Predicted number of daily infections for the rest of April, May, and June, and for last days in these months with lower and upper bounds given under the assumption of more and less favorable remaining of the outbreak. A column with bias gives what can be an influence of bias in the estimation of the generalized gamma model.

	Lower bound	Predicted	Upper bound	Bias
April 15th-30th	3731	3876	4004	+251
April 30th	204	229	251	+17
May 1st-31st	2855	4200	5805	+518
May 31st	22	64	132	+17
June 1st-30th	194	899	2738	+501
June 30th	0	11	63	+17

4.4. Assessment of the prediction accuracy

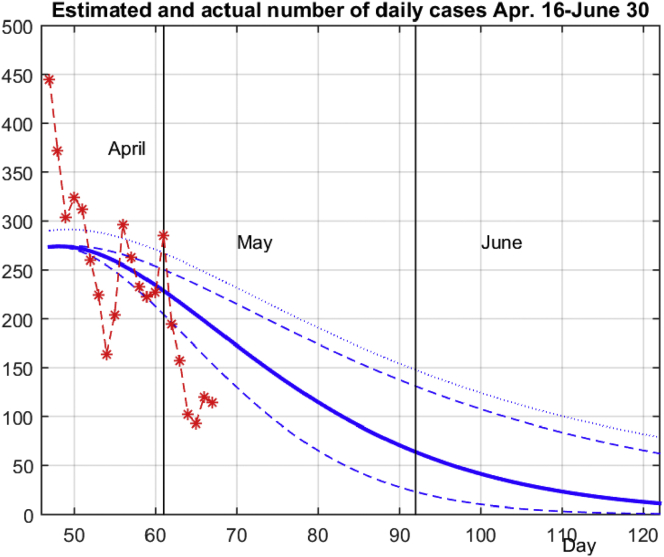
Fortunately, the paper revision is performed after the State of Emergency is abolished on May 6^th due to the favorable epidemiological situation in the country. A large portion of social distancing measures remain but the lockdown policy is abolished with partial re-establishment of local transportation, reopening of many businesses, etc. Large gatherings are still prohibited with state borders and educational institutions closed. The partial opening of kindergartens is in progress. So we are in a position to access the accuracy of a simple predictive model based on data up to Apr. 15^th. We have updated Figure 10 with novel data represented with stars in Figure 11. As can be seen, the daily number of infections significantly oscillates around prediction demonstrating that modeling the second part of the outbreak requires data preprocessing (filtering) as it is done Section 4.2. It can be seen that the daily number of infections is significantly below prediction for the first time on Apr. 23^rd (k = 54 with 164 cases). It is exactly 10 days after the second long weekend curfew, while the second drop below prediction lines is on May 4^th (k = 65 with 93 infections) that is exactly 13 days after long curfew during orthodox Easter. At first glance, it seems that these Wuhan-style curfews (widely criticized by the public) had an excellent effect on containing the SARS-CoV-2 outbreak.

Figure 11.

Predicted vs. the actual number of daily infections for an interval between Apr. 15^th and May 6^th (thin solid line with stars – daily number of infections for Apr. 16^th-May 6^th; dashed line – a prediction with upper bound increased with estimated bias).

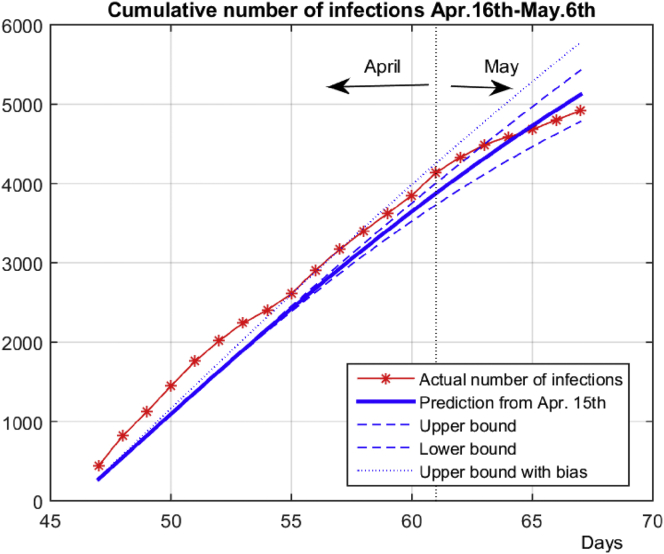
Accuracy of prediction can be accessed in a better manner from Figure 12 where the cumulative number of infections for the period between Apr. 16^th and May 6^th is given together with predictions. The developed simple predictive model gives relatively good accuracy. Obtained results are within the predicted range on May 6^th (it is within these limits for May 2^nd-6^th). However, the prediction is within wider limits when bias (dotted line) is taken into account from Apr. 23^rd toward the end of the State of Emergency. Note that relative error in prediction of the cumulative number of infections for interval Apr. 16^th-May 6^th is only 4% calculated as:

$$\frac{\left|\sum _{k=47}^{67}{O}_k-\sum _{k=47}^{67}{P}_k\right|}{\sum _{k=47}^{67}{P}_k}$$ (6)

where P_k is the predicted and O_k is the obtained number of cases for kth day, (Apr. 16^th is k = 47, while May 6^th is k = 67).

Figure 12.

Cumulative number of infections for interval Apr. 16^th-May 6^th – obtained number vs. predictions.

Finally, we have recalculated parameters of the generalized gamma model for each date in the considered interval. Obtained values of parameters (γ, k) are stabilized after Apr. 27^th with γ∈[7.23,10.62] with mean value 8.41, median 8.34, and standard deviation 0.82. The final estimate obtained on May 6^th corresponds to minimal value γ = 7.23 reflecting a significantly more favorable epidemiological situation than on Apr. 15^th what supports the abolishment of the State of Emergency. It is per Figure 12 where predicted cumulative number of infections gradually approaches toward lower prediction bound due to epidemical control measures conducted in the first half of April, i.e., long weekend curfews. Parameter k is in range k∈[3.32,4.45], with a mean value 3.95, median 3.94, and standard deviation 0.27. The final prediction is 4.45. Now we can access that during the entire interval of 36 days between Apr. 1^st and May 6^th parameter k remains within range k∈ [3, 5], i.e., skewness is relatively stable while the main effect of the epidemiological control measures is accessed in reducing parameter γ. We conclude that the long weekend curfews contributed to reducing parameter γ from γ = 10.83 (end of prediction on Apr. 15^th) toward γ = 7.23 (end of State of Emergency on May 6^th).

Taking into account the abolishment of the State of Emergency it cannot be used estimated parameters of the generalized gamma function to predict future trends in curbing the spread of infection since modeling is performed based on data obtained in the period with strict epidemiological measures.

5. Conclusion

We have modeled the SARS-CoV-2 infection outbreak in Serbia with the exponential growth model in the initial stage and generalized gamma model in the second stage. It has been shown that exponential growth can be easily estimated with just several samples and it suggests a path to catastrophe if serious epidemiological measures were not enforced timely. It is more difficult to model part of the outbreak after slowing initial exponential growth. Anyway, for the first stage we needed only five samples while for the second stage it was required data pre-processing (simple filtering) and more samples available (in our case at least 9). It is demonstrated that 12–13 days is required that epidemiological measures give some results. In the case of Serbia, initial exponential growth can be followed 13 days after the introduction of the State of Emergency and also the maximal average daily growth after this interval is achieved about 12 days after the second set of restrictions from Mar. 22^nd. Finally, we have predicted the rest of the outbreak. In the process of the paper revision, we have compared prediction with actual data up to the end of the State of Emergency on May 6^th.

Declarations

Author contribution statement

Igor Djurović: Conceived and designed the analysis; Analyzed and interpreted the data; Contributed analysis tools or data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.

Appendix. Detailed description of epidemical control measures in Serbia

On Jan. 28^th (after only 5 days of strict measures adopted in Wuhan and neighbor cities in China) it was enforced control of passengers coming from China. On Feb. 24^th government issued decree establishing stricter control of passengers coming from Italy and prohibiting organized school trips to this country (Italy is a popular destination for annual trips of high school pupils). However, this measure was light since direct air connection to Milano and Rome was kept almost intact until cutting all air connections on Mar. 15^th. Controls at the airports are light without check-ups and testing of incoming passengers. It was probably a significant mistake since, according to authorities, arrivals from West European countries were the main vectors in the early days of the outbreak in Serbia, i.e., stricter measures for passengers from these destinations could delay local outbreak probably for a week and significantly reduce further impact.

Two days later on Feb. 26^th additional controls on road and railway border-crossings were established. Additional sanitary controls were established at Airports Nikola Tesla, Belgrade, and Konstantin the Great, Niš, controlling more passengers coming from China and Italy.

On Mar. 12^th after a significant increase in the number of cases in Serbia some stricter measures are adopted. They were similar like in many other countries with slight variations in dynamics. On Mar. 12^th it was forbidden meetings of more than 100 persons in closed spaces (this number is gradually decreased), strict control of passengers from China, Korea, Iran, some regions from Italy and Switzerland, 44 smaller border crossings were closed, all persons employed in services on main transit routes were obliged to wear facemasks and gloves,… An appeal to the public to postpone and avoid family ceremonies and gatherings is largely ignored causing numerous infections, especially in Čačak and Valjevo municipalities.

Two days later after receiving dramatic news from other countries and with the emergence of more cases in Serbia, entrance to the country was forbidden for foreign citizens from China, Korea, Switzerland, Italy, Iran, Romania, Spain, Germany, France, Austria, Slovenia, and Greece. Serbian citizens returning from these countries were obliged to stay in self-isolation for 14 days.

On Mar. 15^th it was declared the State of Emergency. Some of the adopted measures were: stop of work of all educational institutions indefinitely, gradually within several decisions in forthcoming days it was enforced curfew for citizens from vulnerable categories over 65 years with the exception on Sundays between 4 am and 7 am (later this term has been changed several times) for buying necessities in selected shops, curfew for other persons for nonessential activities gradually extended from 8 pm-5 am to 5 pm-5 am and further to 3 pm-5 am on weekends, the complete lockdown on weekends going up to 60 h, state borders are closed, all non-cargo transport terminated, etc. However, with this set of measures restaurants and similar establishments remained open (with hours adjusted to curfew) until Mar. 22^nd. On Mar. 29^th curfew was extended to 3 pm-5 am over weekends, dog walk between 8 pm-9 pm of 20 min was prohibited (it is re-introduced later). Minister of health on Mar. 28^th has found that there are still too many persons on streets and officials have announced plans for stricter lockdown for cities with the most severe outbreaks (in that time Belgrade, Niš, and Valjevo, were the most critical). However, all measures were applied only to the entire country without specific measures for the most affected cities. Local outbreaks appeared city by city, region by region, from Pančevo on North toward Novi Pazar on South-West of country.

In addition to restrictive measures, it seems that the general public becomes gradually more aware of the consequences of private gatherings since a significant number of infections have been traced back from these gatherings some of them with terminal outcomes.

After the positive effects of these measures and the reduction of the number of cases, the State of Emergency is abolished on May 6^th.