Scalable Pairwise Whole-Genome Homology Mapping of Long Genomes with BubbZ

Summary

Pairwise whole-genome homology mapping is the problem of finding all pairs of homologous intervals between a pair of genomes. As the number of available whole genomes has been rising dramatically in the last few years, there has been a need for more scalable homology mappers. In this paper, we develop an algorithm (BubbZ) for computing whole-genome pairwise homology mappings, especially in the context of all-to-all comparison for multiple genomes. BubbZ is based on an algorithm for computing chains in compacted de Bruijn graphs. We evaluate BubbZ on simulated datasets, a dataset composed of 16 long mouse genomes, and a large dataset of 1,600 Salmonella genomes. We show up to approximately an order of magnitude speed improvement, compared with MashMap2 and Minimap2, while retaining similar accuracy.

Graphical Abstract

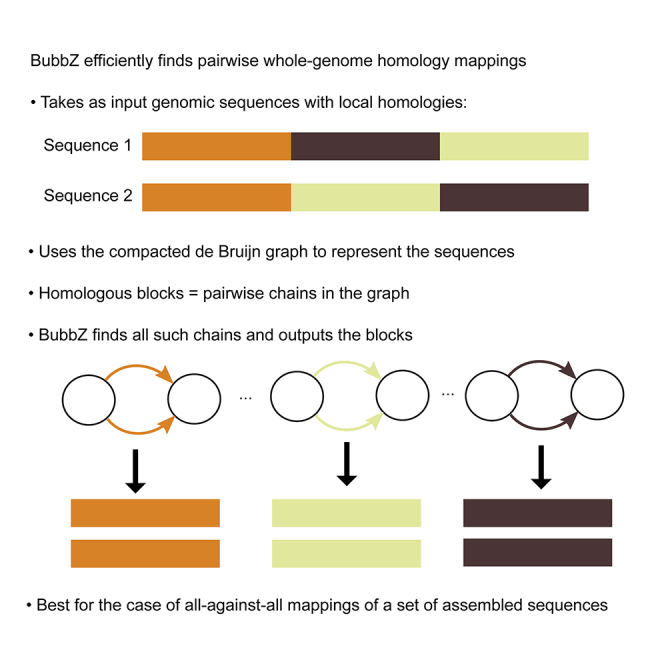
Highlights

• •BubbZ is a fast whole-genome homology mapper
• •Works by finding pairwise chains in the compacted de Bruijn graph
• •Optimized for all-against-all mappings between multiple assembled sequences
• •Tested on 16 mice and 1,600 Salmonella, offers up to an order of magnitude speed-up

Algorithms; Bioinformatics; Genomics

Introduction

Pairwise whole-genome homology mapping is the problem of finding all pairs of homologous intervals between a pair of genomes (see Dewey and Pachter (2006) for a discussion about the precise meaning of homology). Unlike local pairwise alignment, which provides base-to-base homology resolution, mapping only computes the boundaries of homologous blocks. This is, however, sufficient for many applications. For example, whole-genome homology mapping is a starting point for the analysis of genome rearrangements, which themselves are used in studies of breakpoint reuse (Pevzner and Tesler, 2003) and phylogenetics (Luo et al., 2012). It can be used as a precursor to whole-genome alignment (Dewey and Pachter, 2006, Armstrong et al., 2019) or for exploratory comparative analysis. It is also used as a tool for quality control of genome assembly (Vollger et al., 2019) and for identifying genomic duplications for the purposes of improving RNA mapping (Srivastava et al., 2019).

A straightforward solution to compute such a homology map is to do pairwise local alignment; however, alignment is a harder computational problem, requiring more resources than other more direct approaches. A related problem is locally collinear block reconstruction, where mapping blocks can have multiple instances and the overlap between them is fully resolved (Darling et al., 2004, Darling et al., 2010, Dewey, 2007, Paten et al., 2008, Pham and Pevzner, 2010, Minkin et al., 2013). Although solutions to this problem can be used to compute pairwise mappings, known methods perform poorly in regions with complex repeat structures (Minkin and Medvedev, 2019). The first direct approach to address the whole-genome homology map problem was chaining of smaller fragments using a line-sweeping approach inspired by computational geometry (Abouelhoda et al., 2008, Abouelhoda and Ohlebusch, 2005, Myers and Miller, 1995, Ohlebusch and Abouelhoda, 2006). Another approach treats sequences such as audio signals and uses cross-correlations to find homology (Grabherr et al., 2010).

However, the number of available whole genomes has been rising dramatically in the last few years, creating the need for more scalable homology mappers. Two recent tools are particularly notable in tackling this challenge; although both are known for read alignment, they also compute homology maps. Minimap2 (Li, 2018) is based on a seed-and-extend approach but using minimizers (Roberts et al., 2004) to quickly identify and reduce the number seeds. MashMap2 (Jain et al., 2018) uses a minimizer winnowing scheme to quickly identify candidates. These methods are able to compute the mapping of two mammalian-sized genomes in less than an hour. However, in a scenario where the input is a set of multiple genomes and each genome has to be mapped to every other one, even these methods can be too slow. With efforts such as the Vertebrate Genomes Project and Insect 5K promising to release thousands more genomes in the future, more scalable approaches will be needed.

The approach we take in this paper is based on the compacted de Bruijn graph. This graph provides an efficient representation of the shared k-mers between closely related genomes, whereby potentially long shared sequences are represented by small structures within the graph. Approaches based on such graphs had already proven useful to construct synteny blocks (Pham and Pevzner, 2010, Minkin et al., 2013), but recent breakthroughs in the efficiency of graph construction algorithms (Marcus et al., 2014, Chikhi et al., 2016, Baier et al., 2016, Minkin et al., 2017) make them a promising approach for homology mapping. The latest methods can construct the graph for tens of mammalian genomes in minutes rather than weeks and could construct the graph for 100 human genomes in less than a day (Minkin et al., 2017).

In this paper, we propose BubbZ, an algorithm for computing whole-genome pairwise homology mappings, especially in the context of all-to-all comparison for multiple genomes. Our algorithm is based on ideas similar to the line-sweep algorithms (Abouelhoda et al., 2008, Abouelhoda and Ohlebusch, 2005, Ohlebusch and Abouelhoda, 2006) but allows for more efficient data structures that reduce the running time. We evaluated our method on both simulated datasets and on a large dataset composed of 16 mouse genomes, as well as on a dataset consisting of 1,600 Salmonella genomes. BubbZ shows up to approximately an order of magnitude speed improvement on the datasets of hundreds of bacteria and up to three times on the mice dataset, compared with MashMap2 and Minimap2, while retaining similar accuracy.

Results

Algorithm Overview

Given a set of collection of sequences, BubbZ outputs homology information between all possible pairs of sequences in the collection. This includes homology information between a sequence and itself. Given two sequences s and t, BubbZ considers a homology, informally, to be a region of s and a region of t whose k-mer sequences are identical except for gaps of at most b k-mers (b is a parameter). BubbZ outputs the co-ordinates of all maximal homologies between s and t, except that if the regions of two homologies have the same right endpoints, only one with the most shared k-mers is output. In case of ties, BubbZ favors outputting the one with smaller gaps in t, roughly speaking. For a more precise and formal description of BubbZ, please see the Methods section.

Datasets

We evaluated BubbZ speed and accuracy on three datasets, the first based on long real mouse genomes, the second based on a large amount of short bacterial genomes, and the third containing short simulated genomes. For the long real genomes, we downloaded 16 mouse genomes from GenBank (Benson et al., 2017). These consisted of 15 different strains, assembled as part of a recent study (Lilue et al., 2018), and the mouse reference genome. The mouse reference has 377 scaffolds, whereas the other mouse strains have 2,977–7,154 scaffolds; the genomes' size fluctuates between 2.6 and 2.8 Gbp. To test the scalability of our pipeline in the number of genomes, we created four datasets from these 16 genomes. The four datasets contain genomes 1-2, 1-4, 1-8, and 1-16, respectively, with genome one being the reference genome. More details about the datasets, including accession numbers, are available as Table S1 in (Minkin and Medvedev, 2019).

The real bacterial dataset consisted of 1,600 Salmonella genomes that are a part of GenomeTrakr project (NCBI BioProject ID, 183844), a public effort to identify and track pathogens causing food-borne illness. Each genome consisted of approximately 4.6 million basepairs. As in the mouse experiment, we created four datasets containing genomes 1-200, 1-400, 1-800, and 1-1,600 genomes, respectively. Link to the ordered list of the genomes containing their RefSeq accession numbers is contained in the “Data and Code Availability” section. The goal of this dataset was to test scalability with respect to the number, rather than the length, of the genomes.

The other type of data we used were nine simulated datasets, generated as part of our earlier study (Minkin and Medvedev, 2019), and are available for download at https://github.com/medvedevgroup/SibeliaZ/blob/master/DATA.txt. Each dataset is an evolution simulation from a single ancestor genome, composed of 1,500 genes and of size approximately 1.5 Mbp; the result is ten genomes in each dataset. The datasets are distinguished by their divergence, with the evolutionary distance from the root genome to the leaves varying between 0.03 and 0.25 substitutions per site.

Evaluated Tools

We compared BubbZ against the two recent tools that are able to scale to the size of modern datasets, Minimap2 (Li, 2018) and MashMap2 (Jain et al., 2018). We ran all tools in order to produce an all-against-all mapping, including any duplications (i.e. mappings within a single genome or chromosome).

A common parameter for homology-finding tools is the minimum size of the block in the output. We tried to make the evaluated tools to generate blocks of comparable sizes but it was not possible due to the difference in the algorithmic approaches and implementations. We made BubbZ output blocks of at least 200bp. For MashMap2 we produced blocks of length at least 500bp (lowest possible setting) for bacteria and 5000bp (the default value) for mice. We used different values for MashMap2 because on the simulated bacteria dataset the default parameters produced insufficient recall. This setting is not applicable to Minimap2 because it uses alignment scores for cutoffs rather than block lengths, so we used parameters suggested by the author for all datasets.

All parameters and command lines are available at https://github.com/medvedevgroup/BubbZ/blob/master/supplementary.txt, but we highlight the important ones here. To run BubbZ, we first ran TwoPaco (Minkin et al., 2017) to construct the graph, using $k=21$for real datasets and $k=15$ for the smaller simulated ones. We then ran BubbZ using $b=300$, $m=200$, and for all datasets. The role of these parameters was explored in the context of multiple whole-genome alignment of the same datasets (Minkin and Medvedev, 2019), and we used values that were found to work best in that paper. Please refer to Minkin and Medvedev (2019) for guidance on how these parameters can be chosen and what the tradeoffs involved are.

Neither Minimap2 nor MashMap2 provide a ready-made option to compute all-against-all pairwise mappings for a collection of genomes: a user has to run the tools for each pair of genomes separately. For Minimap2 and MashMap2, we wrote a wrapper that created a separate run for each of the genome pairs; to find duplications, we also ran it on each genome separately. This wrapper can be parallelized in two ways: (1) the runs can be executed in parallel, and (2) each run can be internally parallelized by the respective tool. Assigning different amount of threads to “external” and “internal” parallelization leads to different trade-offs between running time and memory. We tried to minimize the overall running time of the mappings while keeping the peak memory usage reasonable. As we had 24 threads available, for Minimap2 and MashMap2 we decided to run six pairs of mappings simultaneously and allowed each tool to use four threads internally on the mice dataset. On the bacterial datasets, we used all 24 threads for external parallelization. For BubbZ we used all 24 threads internally because it natively supports all-against-all mappings and for TwoPaCo we used 16 threads as suggested by the documentation.

For mapping different genomes with Minimap2, we used default presets for sequences of 5% divergence. For mapping genomes against themselves, we used the parameters suggested by the author. For MashMap2 we used the default parameters, except (1) the minimum block size for bacterial genomes as described earlier, (2) that for mapping different genomes we used the orthologous filtering, whereas for computing duplications we disabled the filtering, as suggested by the authors.

Evaluation Metrics

For the smaller simulated dataset we computed both recall and precision using the mafTools package (Earl et al., 2014). This package requires an alignment for comparison, rather than just a map; we therefore took each one of the homology blocks in our output and computed an alignment of it using LAGAN (Brudno et al., 2003). To define precision and recall, mafTools views an alignment as an equivalence relation, which is the set of all equivalent position pairs participating in the true alignment. Let A denote the relation produced by an alignment algorithm, and let H denote the ground truth alignment relation (in our case, H is given by the simulator). The accuracy of A is then given as $recall\left(A\right)=1-|H\setminus A|/\left|H\right|$ and $precision\left(A\right)=1-|A\setminus H|/\left|A\right|$.

For the larger mouse dataset, there are unfortunately no ground-truth whole-genome homology maps or alignments available, making it difficult to evaluate precision. To evaluate the recall, we used an alignment of homologous protein-coding genes annotated in Ensembl. These ground-truth alignments, generated as part of our earlier study (Minkin and Medvedev, 2019) using LAGAN, are available for download at https://github.com/medvedevgroup/SibeliaZ/blob/master/DATA.txt. The alignment contains both orthologous and paralogous gene pairs, although most of the paralogous pairs come from the well-annotated mouse reference genome. For the purposes of analysis, we binned the pairs of homologous genes according to the nucleotide identity in their alignment. These alignments cover around 33% of the input genomes, i.e. 33% of base pairs in the input genome are included in the alignment. We could not compute recall using mafTools due to the computational cost of having to compute all alignments for all the homologous intervals in the output. Instead, consider all the aligned position pairs in a ground truth alignment and a homology mapping $\mathcal{C}$. We define recall as the fraction of aligned position pairs for which there exists a block in $\mathcal{C}$ covering both positions. We did not evaluate accuracy on the large bacterial dataset.

Results on the Mouse Data

The running time and memory consumption of all the tools are shown in Table 1. The pipeline consisting of TwoPaCo and BubbZ was 1.5–3 times faster than Minimap2 and 6–12 times faster than MashMap2. Starting at four genomes, we observe roughly linear scaling for BubbZ. For Minimap2 and MashMap the scaling seems superlinear, although it is difficult to make any firm conclusions given the limited number of datapoints. The linear scaling of BubbZ is consistent with the fact that only a linear number of runs is required (see Transparent Methods); however, the time of each run also grows with the size of the input. Nevertheless, we empirically found the scaling to be roughly linear.

Table 1.

Running Time (Minutes) and Memory Usage (Gigabytes, in Parenthesis) on the Mouse Data

	TwoPaCo + BubbZ			Minimap2	MashMap2
Dataset	TwoPaCo	BubbZ	Total
1–2	15 (9.3)	6 (35.2)	21 (35.2)	73 (46.5)	233 (22.3)
1–4	22 (9.4)	14 (66.5)	36 (66.5)	75 (105.4)	240 (39.7)
1–8	40 (9.3)	26 (94.9)	66 (94.9)	104 (119.2)	464 (44.7)
1–16	83 (17.8)	42 (164.2)	125 (164.2)	411 (119.6)	1,530 (45.6)

For datasets consisting of 2, 4, and 8 mice Minimap2 uses 1.3–1.6 times more memory than BubbZ, whereas for 16 mice BubbZ uses roughly 1.4 times more memory. At the same time, MashMap2 has the lowest memory usage on all datasets: it uses 1.5–3.6 times less memory than BubbZ and 2.1–2.7 times less than Minimap2. We note that for MashMap2 and Minimap2 the peak memory usage is the cumulative peak memory usage of all instances of the tool being run simultaneously by our wrapper.

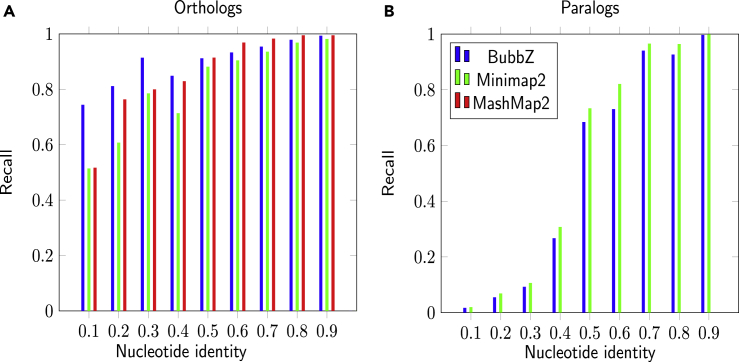
To compute the recall, we only used the dataset consisting of two genomes, because computing recall is otherwise computationally prohibitive. Figure 1 shows the recall, broken down by nucleotide identity of the gene pairs and by orthology/paralogy. Both versions of BubbZ demonstrate nearly the identical recall scores, with the exact version being marginally better. For the orthologous genes, all mappers have similar recall, although BubbZ has higher recall in genes of lower nucleotide identity. For the paralogous pairs, Minimap2 had slightly higher recall then BubbZ.

Figure 1.

Results on the Mouse Data

Recall of the position pairs belonging to pairs of protein-coding genes by BubbZ(blue), Minimap2(green), and MashMap2(red). (A) corresponds to orthologs and(B) to paralogs. MashMap2 recall on paralogs could not be computed.

Results on the Bacterial Data

The running time and memory consumption of the mapping tools on the Salmonella dataset is shown in Table 3. The total running time of TwoPaCo and BubbZ is 6–12 times smaller than of Minimap2 and 6–9 times than MashMap2. In contrast with the experiment involving the mice dataset, MashMap2 is approximately 1.3 times faster than Minimap2. Both Minimap2 and MashMap2 have comparable memory consumption ($\le 7.0$ GB); in contrast, BubbZ consumes a lot more memory due to keeping the graph for the whole dataset in memory.

Table 3.

Running Time (Minutes) and Memory Usage (Gigabytes, in Parenthesis) on the Bacterial Data

Dataset	TwoPaCo + BubbZ			Minimap2	MashMap2
	TwoPaCo	BubbZ	Total
1–200	4 (17.5)	2 (7.8)	6 (17.5)	35 (3.5)	26 (1.6)
1–400	6 (17.5)	6 (16.7)	12 (17.5)	132 (3.5)	101 (1.8)
1–800	10 (17.6)	33 (44.3)	43 (44.3)	510 (4.3)	390 (2.3)
1–1,600	19 (17.8)	257 (149.2)	276 (149.2)	2,250 (7.0)	1876 (2.3)

Results on the Simulated Data

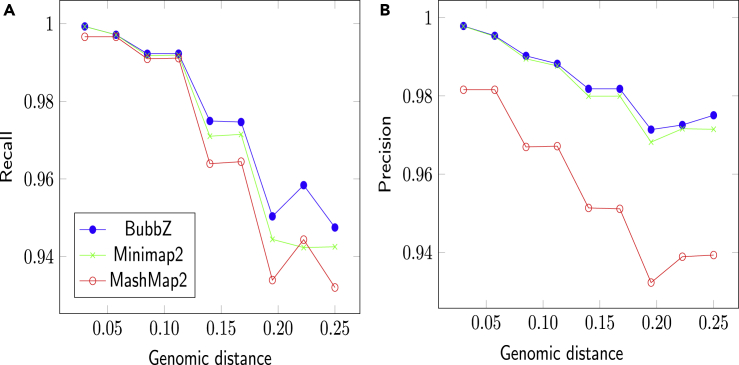
Using simulated data, we can measure the accuracy more thoroughly than we could on real data. Figure 2 shows precision and recall of the three methods, as a function of divergence between genomes. For all tools, both recall and precision decline with increase of the divergence. Both versions of BubbZ demonstrate nearly the identical recall and precision. Recall is similar for all methods, with BubbZ having slightly better values for more divergent datasets. BubbZ and Minimap2 have nearly identical precision curves, and they are substantially higher than MashMap2.

Figure 2.

Results on the Simulated Data: Accuracy as a Function of the Genomic Distance

(A) shows recall, and (B) displays precision.

Table 2 shows the running time and memory usage, although because of the small size of the datasets, it is hard to draw any conclusions about scalability in the size or number of genomes. However, this did allow us to measure how the divergence affected each of the methods. For BubbZ and MashMap2 genomic divergence did not have a significant effect on the running time, whereas Minimap2 ran slower on more divergent genomes.

Table 2.

Running Time (Seconds) and Memory Usage (Megabytes, in Parenthesis) on the Simulated Data

Dataset	TwoPaCo + BubbZ			Minimap2	MashMap2
	TwoPaCo	BubbZ	Total
0.03	7 (1,240)	1 (36)	8 (1,240)	6 (904)	3 (147)
0.06	6 (1,291)	1 (51)	7 (1,291)	8 (820)	3 (154)
0.09	6 (1,246)	1 (74)	7 (1,246)	10 (824)	3 (168)
0.11	6 (1,292)	1 (77)	7 (1,292)	10 (634)	3 (172)
0.14	6 (1,250)	2 (80)	8 (1,250)	15 (1,341)	3 (171)
0.17	6 (1,277)	2 (80)	8 (1,277)	15 (1,340)	3 (157)
0.20	6 (1,238)	2 (82)	8 (1,238)	16 (1,113)	3 (165)
0.22	5 (1,237)	2 (71)	7 (1,237)	16 (614)	4 (164)
0.25	5 (1,207)	2 (82)	7 (1,207)	16 (1,204)	3 (168)

Each dataset is labeled by its corresponding divergence.

Discussion

In this paper, we present BubbZ, a novel method for computing pairwise mapping between complete genomes. Empirical results indicate that for a large collection of bacterial genomes, our method can be up to 10 times faster than competing approaches. On closely related mammalian genomes, our method is also several times faster than competitors, while maintaining similar accuracy. Our approach for finding chains is based on the problem formulation of the sweep-line algorithms from (Ohlebusch and Abouelhoda, 2006). Those algorithms similarly defined chains and a dynamic programming formulation to find the longest chains. The main difference is that the previous work was focused on finding a single optimal chain, while we formally define the problem of finding all such non-redundant chains. In practice users are often interested in computing a set of chains that comprehensively represent homology between input genomes and are not redundant. Most practical solutions address this need by implementing heuristics that choose which chains to output. In contrast, we formally defined and solved a problem of finding all non-redundant optimal chains.

MiniMap2 also uses a chaining strategy but in a slightly different way than BubbZ. One can think of BubbZ as limiting the space of possible predecessors by restricting the gap size by a parameter b. MiniMap2, on the other hand, does not limit the gap size in its chaining algorithm. Instead, it explores at most h predecessors, where h is parameter. In some cases, it might mean that BubbZ explores more predecessors than MiniMap2, whereas in others it could be the other way around.

In addition, the approaches mentioned earlier require an efficient dynamic range-maximum-query structure (Abouelhoda et al., 2008, Abouelhoda and Ohlebusch, 2005, Ohlebusch and Abouelhoda, 2006). Although such data structures have theoretically asymptotic logarithmic query times, in practice they have a high constant due to their implementations relying on search trees with extra information. Instead of using a tree-based dynamic index, we rely on the sparseness of the compacted de Bruijn graph and use a simple BitVector-based algorithm and data structure to quickly compute optimal predecessors in the dynamic programming matrix.

Limitations of the Study

One particular limitation of our tool is its high memory usage, due to keeping in memory the graph constructed from all input genomes simultaneously. We believe that it should be possible to reduce the memory usage by developing a more efficient memory representation. One possible approach is a succinct data structure for the compacted de Bruijn graph, similar to recently published work (Almodaresi et al., 2017, Almodaresi et al., 2018, Bowe et al., 2012, Muggli et al., 2017). However, such a representation should contain extra information to permit quick mapping operations required by our algorithm. We also note that we compared BubbZ against tools that are a based on different algorithmic approaches that have different parameters. As a result, it is hard to come up with a set of parameters that result in fair comparison for all the tools. It is particular evident in our attempts to externally parallelize runs of MashMap2 and Minimap2.

Resource Availability

Lead Contact

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Ilia Minkin (ivminkin@gmail.com).

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

Our tool is open source and freely available at https://github.com/medvedevgroup/bubbz. All parameters and command lines are available at https://github.com/medvedevgroup/BubbZ/blob/master/supplementary.txt. The nine simulated datasets we used for evaluation as well as the ground-truth alignments for the mouse data are available for download at https://github.com/medvedevgroup/SibeliaZ/blob/master/DATA.txt. The ordered list of accession numbers of 1,600 Salmonella genomes is available at https://github.com/medvedevgroup/BubbZ/blob/master/salmonella_refseq.txt.

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Published: June 26, 2020