Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Apr 20;85(10):6489–6497. doi: 10.1021/acs.joc.0c00441

Modeling the Alkaline Hydrolysis of Diaryl Sulfate Diesters: A Mechanistic Study

Klaudia Szeler †, Nicholas H Williams ‡, Alvan C Hengge §,*, Shina C L Kamerlin †,*
PMCID: PMC7304899  PMID: 32309943

Abstract

graphic file with name jo0c00441_0009.jpg

Phosphate and sulfate esters have important roles in regulating cellular processes. However, while there has been substantial experimental and computational investigation of the mechanisms and the transition states involved in phosphate ester hydrolysis, there is far less work on sulfate ester hydrolysis. Here, we report a detailed computational study of the alkaline hydrolysis of diaryl sulfate diesters, using different DFT functionals as well as mixed implicit/explicit solvation with varying numbers of explicit water molecules. We consider the impact of the computational model on computed linear free-energy relationships (LFER) and the nature of the transition states (TS) involved. We obtain good qualitative agreement with experimental LFER data when using a pure implicit solvent model and excellent agreement with experimental kinetic isotope effects for all models used. Our calculations suggest that sulfate diester hydrolysis proceeds through loose transition states, with minimal bond formation to the nucleophile and bond cleavage to the leaving group already initiated. Comparison to prior work indicates that these TS are similar in nature to those for the alkaline hydrolysis of neutral arylsulfonate monoesters or charged phosphate diesters and fluorophosphates. Obtaining more detailed insights into the transition states involved assists in understanding the selectivity of enzymes that hydrolyze these reactions.

Introduction

The hydrolysis of both phosphate and sulfate esters is ubiquitous in biology and plays important roles in numerous cellular processes, including in particular the regulation of cellular signaling processes.1,2 Therefore, unsurprisingly, the enzymes that catalyze these reactions are involved in a range of human diseases, making them important drug targets.3−5 In addition, many phosphatases also possess promiscuous sulfatase activity,6 and such promiscuity is likely to be of evolutionary significance for these enzymes.7−11 While there has been substantial research focus on understanding enzymatic phosphate and sulfate hydrolysis (for reviews, see, e.g., refs (2, 6, 12), and the references cited therein), understanding the corresponding non-enzymatic hydrolysis of these compounds is also important in order to provide insights into the fundamental chemistry and the nature of the transition states involved. Here, the lion’s share of research has focused on understanding phosphoryl transfer reactions using both experimental and computational approaches, and studies of linear free-energy relationships (LFER), kinetic isotope effects (KIE), and activation entropies, complemented by computational modeling, have provided significant insights into the reactivity of these compounds (for detailed reviews, see, e.g., ref (2)).

In contrast, there has been far less research effort invested into studying non-enzymatic sulfate hydrolysis, and, in particular, while there have been a number of elegant experimental studies of sulfate ester hydrolysis, corresponding computational studies have been very limited. Both experimental11,13−22 and computational23−25 studies of sulfate monoester hydrolysis suggest that the transition states for these reactions are mechanistically similar to those of their corresponding phosphate monoesters, proceeding through concerted pathways with loose (concerted but dissociative in character) transition states, with little bond formation to the nucleophile and advanced bond cleavage to the leaving group, resulting in a SO3-like sulfuryl group. This is supported by the similar kinetic parameters,14,18 linear free-energy relationships,13−17 and kinetic isotope effects18,19 for the hydrolysis of sulfate and phosphate monoesters. In addition, studies of the pH dependence of these reactions show a broad pH-independent region between pH 4 and 1213,14,19,26 (where hydrolysis likely proceeds by S–O rather than C–O bond cleavage) and a hydrolysis rate that is accelerated under strongly acidic or basic conditions.14,27 Computational comparison of the hydrolysis of p-nitrophenyl phosphate and sulfate monoesters provides a similar mechanistic picture for these reactions,25 although the transition state for the hydrolysis of the sulfate monoester was calculated to be slightly more compact than that for the corresponding phosphate monoester. This is likely due to the fact that in contrast to the phosphate monoester dianion, the sulfate monoester is monoanionic.

In the case of sulfate diester hydrolysis, the majority of reported studies involve the reactivity of either dialkyl or aryl alkyl sulfate diesters in which the reaction proceeds by attack at carbon with C–O rather than S–O bond cleavage.28,29 In contrast, experimental work indicates that the alkaline hydrolysis of diaryl sulfate diesters proceeds through nucleophilic attack at sulfur (Figure 1),30 making it possible to compare the transition states for these reactions to those obtained in our prior work on the alkaline hydrolysis of related compounds such as sulfate and phosphate monoesters, aryl phosphate diesters, fluorophosphates, pyridinio-N-phosphonates, and neutral sulfonate monoesters.25,31−35 In all three cases, both experimental and computational works suggest that these reactions still proceed through concerted but tighter transition states than those observed in the case of phosphate and sulfate monoesters, and it would therefore not be implausible to assume that the same holds true also for neutral diaryl sulfate diesters (Figure 1). This would not be inconsistent with experimental data,30 which provides a slope, βlg, of −0.7 ± 0.2 for the alkaline hydrolysis of a series of diaryl sulfate diesters (compared to a reported value of −1.81 ± 0.09 for aryl sulfate monoesters22) and 15k and 18klg KIE of 1.0000 ± 0.0005 and 1.003 ± 0.002, respectively, for hydroxide attack on p-nitrophenyl sulfate. However, there are no experimental data pertaining to the degree of nucleophilic involvement.

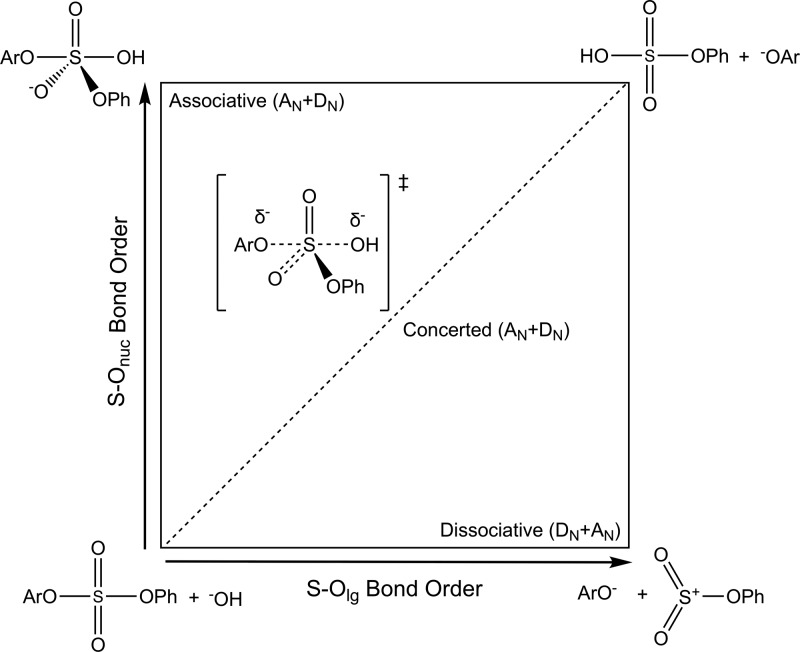
Figure 1.

Figure 1

Open in a new tab

Overview of different mechanistic possibilities for the alkaline hydrolysis of the arylsulfate diesters studied in this work, as illustrated on a More O’Ferrall–Jencks plot.36,37 Shown here are both mechanistic extremes of fully associative (AN+DN, top left) and fully dissociative (DN+AN, bottom right) pathways. The dashed line indicates a concerted (ANDN, center) pathway with concomitant bond formation to the nucleophile and bond cleavage to the leaving group; note that although we have drawn the line through the center of the plot, these transition states can potentially be either dissociative or associative in nature, depending on whether bond formation to the nucleophile precedes or follows bond formation to the leaving group. In addition, the “products” (top right) would be expected to rapidly undergo proton transfer to form PhOSO3– and ArOH (adapted with permission from ref (30) (direct link: https://pubs.acs.org/doi/abs/10.1021/jo0488309). Copyright 2004 American Chemical Society).

In the present work, we perform a detailed comparison of the alkaline hydrolysis of a series of diaryl sulfate diesters with leaving groups of varying pKa (Figure 2),30 using three different density functionals and comparing both pure implicit solvent and mixed implicit/explicit solvation for comparison to our prior work.25,34,38 We show that the slope of the calculated LFER is highly dependent both on the functional used and on the number of explicit water molecules introduced into the system but that in all cases, we are able to obtain good agreement with experimental KIE irrespective of the functional used or the number of water molecules. We also compare our calculated transition states to those obtained in our previous computational studies of related compounds25,31−35 and confirm that like other analogous compounds, the alkaline hydrolysis of sulfate diesters proceed through tighter concerted transition states than those obtained for the hydrolyses of related phosphate and sulfate monoesters.

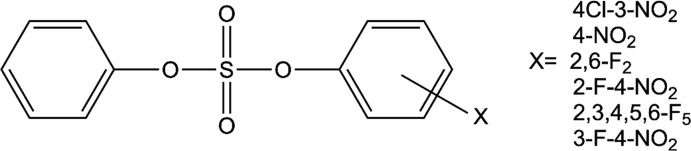
Figure 2.

Figure 2

Open in a new tab

Overview of the compounds studied in this work, based on the experimental work presented in ref (30).

Methodology

We have performed density functional theory (DFT) calculations of the alkaline hydrolysis of diaryl sulfate diesters shown in Figure 2, using the M11L,39 M062X,40 and ωB97X-D.41 All transition states were initially optimized using the M11L functional, with the final optimized structures being reoptimized using either the M062X or the ωB97X-D functionals. We note that in a small number of cases, direct reoptimization was not possible, as the transition state optimization never converged. These optimizations were therefore initiated from different starting points. Specifically, the starting structure for the final transition state for 2,3,4,5,6-pentafluoro sulfate in the presence of two explicit water molecules, optimized using the M062X functional, was the ωB97X-D-optimized transition state rather than the M11L-optimized state. In the case of the transition states for the hydrolysis of 2,6-difluoro and 2-fluoro-4-nitrophenyl sulfate, optimized with the M11L functional in the presence of eight water molecules, these structures were optimized using the transition states for 2-fluoro-4-nitrophenyl and 3-fluoro-4-nitrophenyl sulfate as starting structures, respectively. All other structures converged normally and were therefore obtained as initially described above.

Initial transition state optimizations were performed using the 6-31+G* basis set and the SMD solvation model, with the addition of between 0 and 8 explicit water molecules to the system. The water molecules were added to the system one by one in a symmetrical fashion (i.e., sequentially adding an additional water molecule to either the nucleophile or leaving group side of each optimized transition state and reoptimizing the new transition state, ensuring that each time a new water molecule is added to the system, it forms a hydrogen bonding interaction with a hydrogen bond acceptor on the sulfate diester). The water molecules were added in such a way as to saturate all possible hydrogen bonding interactions with the sulfate diester. The resulting transition states were characterized both by frequency calculations at the same level of theory and by following the intrinsic reaction coordinate (IRC)42,43 in both the reactant and product directions followed by optimization to the actual reactant and product. These structures were first optimized using an UltraFine integration grid, and the optimized stationary points were reoptimized using a SuperFine integration grid. The resulting absolute energies and Cartesian coordinates of all optimized stationary points are provided in the Supporting Information.

Bond orders, frequencies, zero-point energies, and entropies were all calculated at 313.15 K from the final optimized structures at the same level of theory, whereas the electronic energies were obtained by performing single point calculations using the larger 6-311+G** basis set. The partial charges were obtained using the CHarges from ELectrostatic Potentials using a Grid-based method (CHELPG) charge calculation scheme44 using the 6-31G* basis set, and bond orders were calculated based on the Wiberg bond index45 using natural bond orbital (NBO) analysis.46 All quantum chemical calculations were performed using Gaussian 16, Rev. B01.47 Computed rate constants for comparison to experiment were obtained by summing the electronic energies and zero-point energies and entropies, with the resulting free energies converted to rate constants using transition state theory. Finally, kinetic isotope effects were calculated using the Biegeleisen–Mayer equation48 using the frequencies in the Gaussian output files and Kinisot (“Kinetic Isotope Effects with Python”, developed by the Paton lab and available for open source download from Zenodo, DOI: 10.5281/zenodo.60082), with the 15N/14N isotopic replacement manually added to the code.

Results and Discussion

Exploring the Impact of Including Explicit Water Molecules in the Simulations

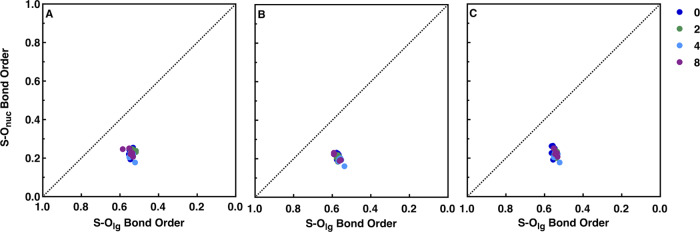
In prior work on the hydrolysis of phosphate monoester dianions and sulfate monoester monoanions, we demonstrated that the inclusion of explicit water molecules into the system (in addition to the implicit solvent model) can have a substantial impact on the energies and geometries of the resulting optimized structures and the ability to reproduce all the experimental data, including isotope effects.25 To assess whether that is also the case for neutral diaryl sulfate diesters, we performed geometry optimizations of key stationary points for the alkaline hydrolysis of 4-nitrophenyl sulfate in the presence of 0 to 8 explicit water molecules and using three different DFT functionals and examined the impact of inclusion of these water molecules on the resulting activation free energies, charge distributions, and geometries. The resulting data are shown in Figure 3, Figure S1–S3, and Tables S1–S21.

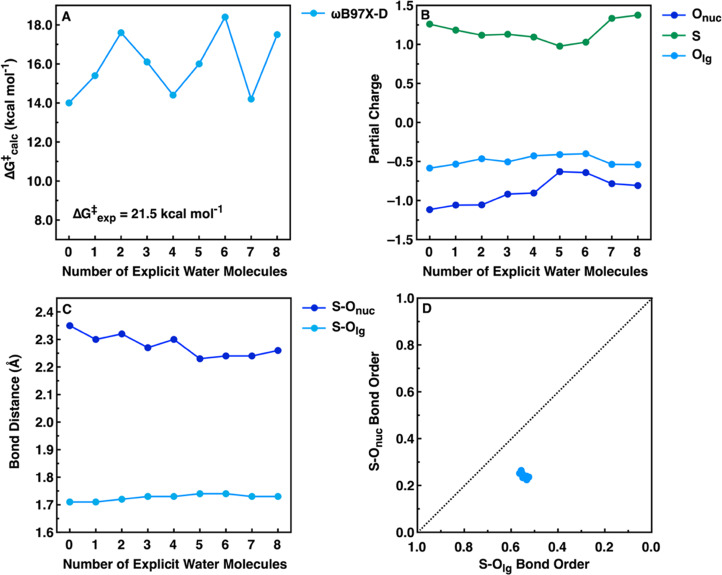
Figure 3.

Figure 3

Open in a new tab

Overview of the (A) activation free energies, (B) partial charges at the transition state, (C) S–Onuc and S–Olg distances at the transition state, and (D) S–Onuc and S–Olg bond orders at the transition state for the alkaline hydrolysis of 4-nitrophenyl sulfate with varying numbers of water molecules, obtained using the ωB97X-D41 functional, as described in the Methodology section. Note that as the transition state distances barely change with increasing numbers of water molecules (panel C), the transition states described in terms of bond orders are therefore also very similar, as can be seen from the overlap in the data in panel D. The calculated activation free energy was obtained using transition state theory at 313.15 K, based on kinetic data provided in ref (30). For the corresponding data obtained using the M11L39 and M062X40 functionals, see Figures S1 and S2, and for the corresponding raw data, see Tables S1–S21.

From these data, it can be seen that all three functionals grossly underestimate the activation free energy to the hydrolysis reaction, with the lowest energies provided by the M062X functional, the highest by the ωB97X-D functional, and the M11L functional being an intermediary between the other two functionals. This underestimation is to be expected when modeling systems involving hydroxide as a nucleophile, as discussed at length by both us and others elsewhere.33,49−51 Therefore, our focus is not on whether a functional does a good job of reproducing absolute experimental activation free energies but rather whether our models can reproduce trends in experimental observables (such as the slope of an LFER).

In terms of trends, it can be seen that there is considerable oscillation in the calculated activation free energies, depending on the number of explicit water molecules included in the system. This largely has to do with the positioning of the explicit water molecules: It is critical to introduce these water molecules symmetrically into the system, saturating all available hydrogen bond donors/acceptors to avoid accidentally over-stabilizing part of the system and obtaining potentially spurious intermediates, as discussed in detail in refs (33) and (52). However, unlike in the case of the charged species studied in most of our previous work,25,31,32,34,35,38 the diaryl sulfate diesters being studied in the present work are neutral species. This means that while the explicit water molecules interact quite nicely with the polarized transition state, the orientation of the water molecules at the reactant and product states can be quite “distorted” (for example, all water molecules clustering together and away from the sulfate diester), suggesting that the sulfate oxygen atoms are poorer hydrogen bond acceptors than the water oxygen atoms. This then leads also to a distortion in the position of the nucleophilic hydroxide ion relative to the sulfur atom, moving it away from an ideal position for in-line attack on the sulfur atom (see, e.g., Figure 4 and Figures S4 and S5), which in turn impacts the calculated activation free energies. That is, we obtain average ΔG‡calc of 12.8 ± 1.3, 10.3 ± 1.6, and 16.0 ± 1.6 using each of the M11L, M062X, and ωB97X-D functionals, indicating that our calculated energies are less sensitive to the number of explicit water molecules included in the system. Similarly, the calculated geometries are also largely independent of the number of water molecules included in the system, as can be seen from Figure S3; while there are small differences between the different density functionals, the data clusters around each functional irrespective of the number of explicit water molecules included in the system.

Figure 4.

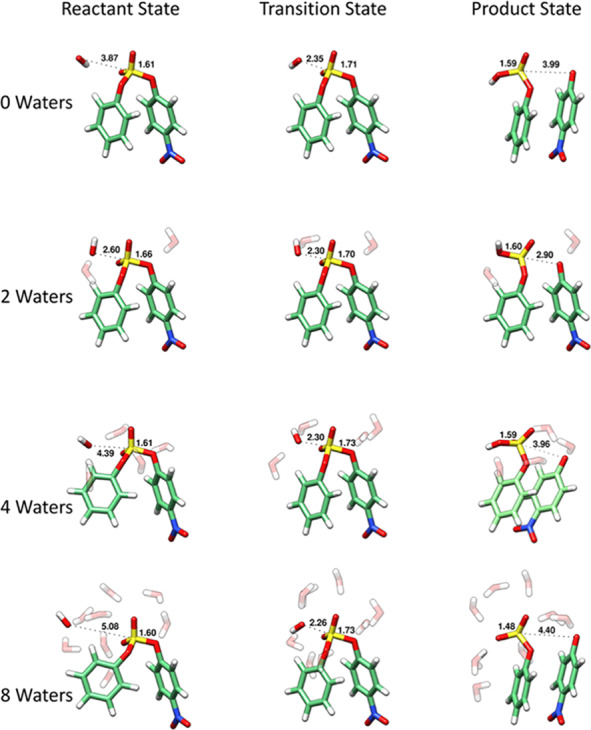
Figure 4

Open in a new tab

Representative structures of the ground, transition, and product states for the alkaline hydrolysis of 4-nitrophenyl sulfate obtained using the ωB97X-D functional,41 in the presence of varying numbers of explicit solvent molecules, as described in the Methodology section. The calculated S–Onuc and S–Olg distances are annotated for each optimized reacting state (in Å), and the corresponding data obtained using the M11L39 and M062X40 functionals is shown in Figures S4 and S5, respectively. Finally, the coordinates of all optimized stationary points are provided in the Supporting Information.

Tying in with this, as there is little change in the transition state geometry upon including additional explicit water molecules into the system, unsurprisingly, the calculated 15k and 18klg KIE are very stable irrespective of the density functional or number of explicit water molecules, and all systems give relatively good agreement with experiment (Table 1). Here, it is worth pointing out that the observed 18klg values are at the low end of those seen in any reaction with a nitrophenyl leaving group where the maximum is ∼1.03.53 While some of the calculated values shown in Table 1 are twice the experimental value, they are all at the low end of the possible ranges of values for this effect and in that regard are consistent with experiment. In addition, the negligible calculated 15k values are consistent with the experimental value of unity.

Table 1. A Comparison of Experimental and Calculated Kinetic Isotope Effects for the Alkaline Hydrolysis of 4-Nitrophenyl Phenyl Sulfate with Varying Numbers of Explicit Water Moleculesa.

  experiment
 ωB97X-D
 M11L
 M062X
water molecules 18klg 15k 18klg 15k 18klg 15k 18klg 15k
  1.003 ± 0.002 1.0000 ± 0.0005            
0     1.006 1.0012 1.003 1.0006 1.005 1.0008
1     1.006 1.0014 1.004 1.0010 1.006 1.0007
2     1.007 1.0009 1.003 1.0005 1.003 1.0010
3     1.007 1.0014 1.004 1.0005 1.004 1.0010
4     1.005 1.0007 1.003 1.0007 1.005 1.0005
5     1.006 1.0010 1.003 1.0005 1.002 1.0008
6     1.006 1.0013 1.006 1.0004 1.003 1.0007
7     1.006 1.0013 1.004 1.0006 1.005 1.0007
8     1.006 1.0013 1.005 1.0006 1.003 1.0007
Open in a new tab
a

The experimental KIE were obtained from ref (30). The computational KIE were obtained using the Biegeleisen–Mayer equation48 from vibrational frequencies calculated using the ωB97X-D,41 M11L,39 and M062X40 functionals, as described in the Methodology section.

Indeed, the only significant difference to any of the physical properties of the transition state that is observed from including the explicit water molecules is on the partial charges of the nucleophile, leaving group, and central sulfur atom: once at least ∼5 water molecules have been included into the system, the partial charge on the nucleophile oxygen becomes significantly less negative compared to that in the transition states calculated using an implicit solvent alone, illustrating the stabilization of the charge on this oxygen atom by the implicit solvent molecules (Tables S10–S12). This is coupled to a slight contraction on the S–Onuc distance upon adding at least ∼5 water molecules to the system, although the corresponding change in bond order is minimal (Tables S16–S18). However, it is clear that unlike in our previous calculations of charged systems where there was significant benefit to including additional water molecules in the system,25,34,38 here, the water molecules appear to provide minimal additional benefit in terms of describing the transition state reliably and add only to computational cost.

Calculated LFER for the Hydrolysis of Diaryl Sulfate Monoesters

Following from this, we have calculated an LFER for the alkaline hydrolysis of diaryl sulfate diesters, following the experimental work of ref (30) and based on the compounds shown in Figure 2. We have calculated these LFER using three different density functionals as described in the Methodology section and in the presence of 0, 2, 4, or 8 explicit water molecules in each case. The resulting LFER are presented in Figure 5, and the correlation between calculated and experimental activation free energies in Figure S6. The corresponding raw data is shown in Tables S22–S57. Here, it can be seen that irrespective of the functional and number of explicit water molecules included in the system, we frequently obtain very poor correlations between calculated and experimental data, with R2 values as low as 0.2 and never higher than 0.9. In addition, the slopes of the calculated LFER vary widely, with β values that range from −0.16 to −1.53 (compared to an experimental value of −0.66). This discrepancy with the experimental data is again due to the fact that while the transition states tend to be very similar irrespective of how many water molecules are included in the system, the reactant states can change quite markedly, in particular when only two or four water molecules are included in the system, in which case the water molecules sometimes do not interact with the sulfate diester but instead with each other, pulling the nucleophile away from a position suitable for in-line attack on the diester (see, e.g., Figure 4; coordinates of all stationary points are provided in the Supporting Information). Indeed, the best agreement with experiment is obtained without including explicit water molecules in the system; then, the β values range from −0.62 to −0.97 with R2 ranging from −0.58 to −0.85.

Figure 5.

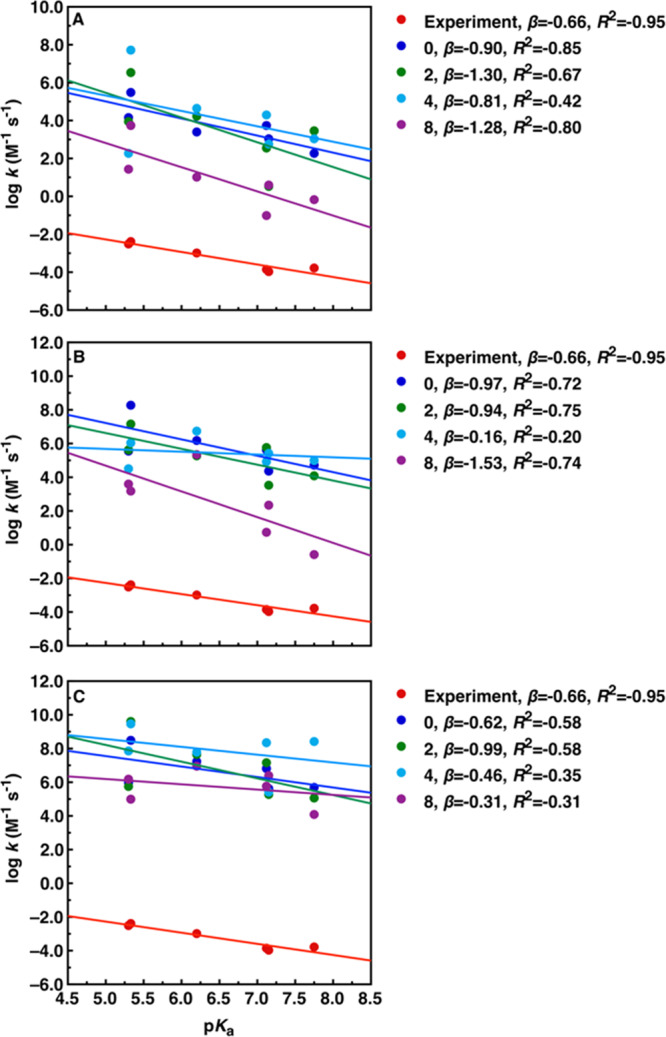
Figure 5

Open in a new tab

Comparison of calculated linear free-energy relationships for the alkaline hydrolysis of the aryl sulfate diesters studied in this work (Figure 2), in the presence of 0 (implicit solvent), 2, 4, or 8 explicit water molecules. Data was obtained using either the (A) ωB97X-D,41 (B) M11L,39 or (C) M062X40 functionals. The corresponding raw data is presented in Tables S22–S33. Experimental data was obtained from ref (30).

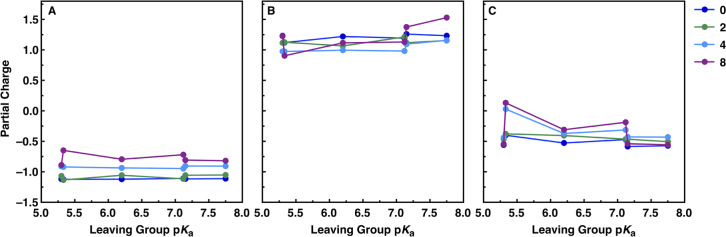
In terms of partial charges (Figure 6 and Figures S7 and S8), there are subtle overall differences in the calculated partial charges across the series, as would be expected from altering the pKa of the leaving group; however, the differences are small. It appears, in addition, that changing the functional and introducing explicit water molecules in the system change the absolute values of the calculated partial charges but have little impact on calculated trends across the series.

Figure 6.

Figure 6

Open in a new tab

Partial charges on (A) nucleophile oxygen, (B) sulfur atom, and (C) leaving group oxygen, at the transition states for the alkaline hydrolysis of the aryl sulfate diesters studied in this work (Figure 2). Partial charges were calculated using the ωB97X-D41 functional and the CHELPG charge calculation scheme44 as described in the Methodology section. The corresponding charge distributions obtained using the M11L39 and M062X40 functionals are shown in Figures S7 and S8, respectively, and the corresponding raw data is shown in Tables S58–S81.

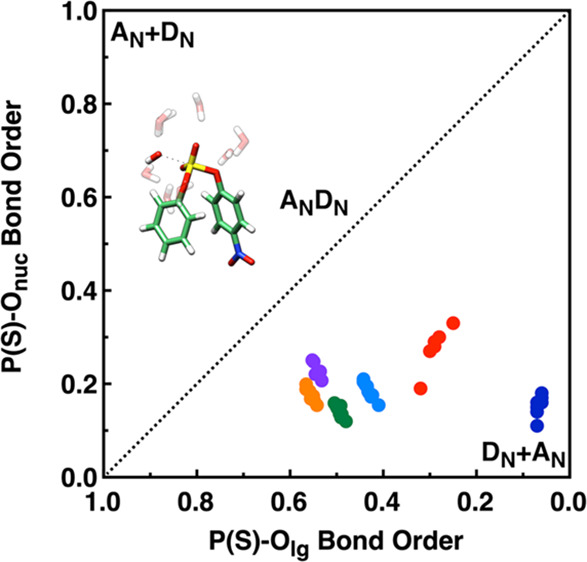
Finally, we have examined in detail the transition state geometries for the different systems, as the calculated KIE shown in Table 1 suggest that despite the problems of reliably modeling the energetics for these compounds, the transition state geometries provided by the different functionals appear to be quite reliable. As can be seen from Figure 7 and Figure S9, in all cases, we obtain dissociative but tight, concerted transition states, with partial bond cleavage to the leaving group and minimal bond formation to the incoming nucleophile. Geometric differences based on leaving group pKa are minimal and appear to primarily impact the S–Onuc bond order/distance. Comparison to other previously modeled compounds25,31−35 (Figure 8) as well as to experimental data for sulfate monoester hydrolysis suggests that these transition states are clearly more compact than those obtained for, for example, the spontaneous hydrolysis of phosphate and sulfate monoesters22,34,54 but also those obtained for the alkaline hydrolysis of phosphate diesters.31 In fact, the transition states are most similar to those we have previously obtained for the alkaline hydrolysis of aryl benezenesulfonates, which we have proposed are hydrolyzed via a similar mechanistic pathway.33 This provides validation to prior experimental data,30 which proposed that the hydrolysis proceeds through concerted (ANDN) transition states but did not provide information into the degree of bond formation at the nucleophile.

Figure 7.

Figure 7

Open in a new tab

Calculated bond orders at the transition states for the alkaline hydrolysis of the aryl sulfate diesters studied in this work (Figure 2), in the presence of 0 (implicit solvent), 2, 4, or 8 explicit water molecules. Bond orders were calculated based on the Wiberg bond index45 using natural bond orbital (NBO) analysis.46 Data was obtained using either the (A) M11L,39 (B) M062X,40 or (C) ωB97X-D41 functionals. Note that due to data similarity between different systems, it is very difficult to visualize the data with two explicit water molecules on the overlay plot; however, the corresponding raw data is presented in Tables S82–S105.

Figure 8.

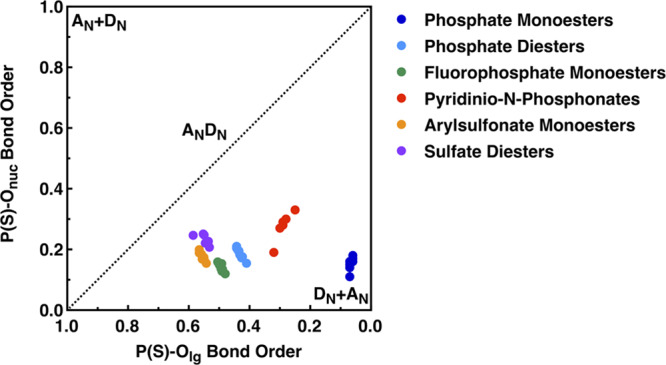
Figure 8

Open in a new tab

Comparison of the calculated bond orders at the transition states for the spontaneous hydrolysis of phosphate monoesters (dark blue), the reaction of substituted pyridinio-N-phosphonates with pyridine (red), and the alkaline hydrolysis of phosphate diesters (light blue), fluorophosphate monoesters (green), arylsulfonate monoesters (orange), and sulfate diaryl diesters (plum). In the case of the sulfate diesters, data shown is obtained in the presence of eight explicit water molecules using the ωB97X-D41 functional. All other data is from our prior work.31−35 Note that as the calculations were performed at differing levels of theory, this comparison is qualitative only. In addition, while there does not exist explicit computational data for the hydrolysis of sulfate monoester monoanions, there does exist experimental data, which suggests a Brønsted coefficient (βlg) of −1.81 for the hydrolysis of these compounds, compared to a measured βlg of −1.23 for phosphate monoester dianions.22,55 Taking into account the different effective charges in the substrates,56 the transition states for the hydrolysis of sulfate monoester monoanions and phosphate monoester dianions share a high degree of leaving group bond fission. This figure is adapted from ref (35), with permission from the Royal Society of Chemistry.

Conclusions

The present work57 provides a detailed mechanistic study of the alkaline hydrolysis of diaryl sulfate diesters using different density functionals as well as both pure implicit solvation and mixed explicit/implicit solvation with different numbers of explicit water molecules. From a methodological perspective, our prior work has focused on using mixed explicit/implicit solvation to study the attack of a neutral nucleophile (H2O) on charged electrophiles,25,34,38 whereas the current study focuses on the attack of a charged nucleophile (OH–) on neutral sulfate diesters. Prior work has shown that the introduction of explicit water molecules that introduce explicit hydrogen bonding interactions was critical when modeling nucleophilic attack on charged electrophiles. In contrast, in the present work, we obtain the best agreement with the experimentally measured LFER for the hydrolysis of these neutral compounds in pure implicit solvation; furthermore, the introduction of explicit water molecules does not significantly change the transition states involved compared to a pure implicit solvent, with stable calculated kinetic isotope effects irrespective of the number of explicit water molecules introduced. That is, we demonstrate that the reaction proceeds through concerted transition states for all compounds, without the involvement of an intermediate, as suggested by prior experimental data.30

We note that we have discussed this issue in great detail in the context of the hydrolysis of related phosphate and sulfate monoesters25 and also extensively explored whether an intermediate is feasible or not in the case of the analogous alkaline hydrolysis of arylsulfonate monoesters.33 In the case of phosphate monoester hydrolysis, multiple mechanisms are theoretically possible, including stepwise associative (AN+DN) or dissociative (DN+AN) pathways, as well as concerted ANDN pathways, and thus, it is necessary to map out a full More O’Ferrall–Jencks plot36,37 (although this can sometimes be deceptive and lead to the wrong mechanistic conclusions, as discussed in great detail in ref (25)). In the case of the associative pathway, when the nucleophile is water, phosphate hydrolysis could proceed through a substrate-assisted pathway, in which one of the non-bridging oxygen atoms of the phosphorus atoms deprotonates (and thus activates) the incoming nucleophile. In the case of sulfate ester hydrolysis, such a mechanism is a priori not viable due to the much lower pKa of the non-bridging oxygen atoms (inorganic sulfate has a first pKa of −358). This then suggests a single mechanism for nucleophilic attack, as discussed in refs (25, 33), and the question becomes whether a stable intermediate is viable or not. In the present case, in all our calculations, following the IRC from the transition state led directly to a product state with no evidence of the presence of a stable intermediate, similar to the analogous case of sulfonate monoester hydrolysis.33 This provides further support for the hydrolysis of arylsulfate diesters proceeding through a single, concerted pathway, with transition states that are dissociative in nature but still more compact than those of analogous compounds that we have studied (with the exception of arylsulfonate monoesters, see Figure 8).

Finally, the calculations provide information about the degree of nucleophilic involvement, for which no experimental data are available, and indicate that the transition states involved are slightly dissociative, with partial bond formation to the nucleophile and partial bond cleavage to the leaving group. Although still concerted, these transition states are nevertheless more compact than any obtained from our previous studies of related compounds (Figure 8) and most greatly resemble those obtained for analogous aryl sulfonates. Obtaining detailed insights into the nature of the transition states involved is an important building block to understand the chemical role of these biologically important molecules in vivo; however, this work also highlights the significant challenges involved in reliably modeling these compounds.

Acknowledgments

This work was funded by the Knut and Alice Wallenberg Foundation, through a Wallenberg Academy Fellowship to S.C.L.K. (KAW 2018.0140). All calculations were performed through a generous allocation of supercomputing time by the Swedish National Infrastructure for Computing (SNIC, 2018/2-3), on the Kebnekaise cluster at HPC2N, Umeå, and the Tetralith cluster at NSC, Linköping.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.joc.0c00441.

  • Absolute energies and additional details of relative energies, bond distances, and stationary points (PDF)

  • Cartesian coordinates of all stationary points (ZIP)

The authors declare no competing financial interest.

Supplementary Material

jo0c00441_si_001.pdf (4.8MB, pdf)
jo0c00441_si_002.zip (377.2KB, zip)

References

  1. Cleland W. W.; Hengge A. C. Enzymatic Mechanisms of Phosphate and Sulfate Transfer. Chem. Rev. 2006, 106, 3252–3278. 10.1021/cr050287o. [DOI] [PubMed] [Google Scholar]
  2. Lassila J. K.; Zalatan J. G.; Herschlag D. Biological Phosphoryl-Transfer Reactions: Understanding Mechanism and Catalysis. Annu. Rev. Biochem. 2011, 80, 669–702. 10.1146/annurev-biochem-060409-092741. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Lazo J. S.; McQueeney K. E.; Sharlow E. R. New Approaches to Difficult Drug Targets: The Phosphatase Story. SLAS Discovery 2017, 22, 1071–1083. 10.1177/2472555217721142. [DOI] [PubMed] [Google Scholar]
  4. Zhang Z. Y. Drugging the Undruggable: Therapeutic Potential of Targeting Protein Tyrosine Phosphatases. Acc. Chem. Res. 2017, 50, 122–129. 10.1021/acs.accounts.6b00537. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Gray J. L.; Delft F.; Brennan P. E. Targeting the Small GTPase Superfamily through their Regulatory Proteins. Angew. Chem., Int. Ed. 2019, 59, 6342–6366. 10.1002/anie.201900585. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Mohamed M. F.; Hollfelder F. Efficient, Crosswise Catalytic Promiscuity Among Enzymes that Catalyze Phosphoryl Transfer. Biochim Biophys. Acta. 2013, 1834, 417–424. 10.1016/j.bbapap.2012.07.015. [DOI] [PubMed] [Google Scholar]
  7. Jensen R. A. Enzyme Recruitment in Evolution of New Function. Annu. Rev. Microbiol. 1976, 30, 409–425. 10.1146/annurev.mi.30.100176.002205. [DOI] [PubMed] [Google Scholar]
  8. O’Brien P. J.; Herschlag D. Catalytic Promiscuity and the Evolution of New Enzymatic Activities. Chem. Biol. 1999, 6, R91–R105. 10.1016/S1074-5521(99)80033-7. [DOI] [PubMed] [Google Scholar]
  9. James L. C.; Tawfik D. S. Catalytic and Binding Poly-Reactivities Shared by Two Unrelated Proteins: The Potential Role of Promiscuity in Enzyme Evolution. Protein Sci. 2001, 10, 2600–2607. 10.1110/ps.ps.14601. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Khersonsky O.; Tawfik D. S. Enzyme Promiscuity: A Mechanistic and Evolutionary Perspective. Annu. Rev. Biochem. 2010, 79, 471–505. 10.1146/annurev-biochem-030409-143718. [DOI] [PubMed] [Google Scholar]
  11. van Loo B.; Bayer C. D.; Fischer G.; Jonas S.; Valkov E.; Mohamed M. F.; Vorobieva A.; Dutruel C.; Hyvönen M.; Hollfelder F. Balancing Specificity and Promiscuity in Enzyme Evolution: Multidimensional Activity Transitions in the Alkaline Phosphatase Superfamily. J. Am. Chem. Soc. 2019, 141, 370–387. 10.1021/jacs.8b10290. [DOI] [PubMed] [Google Scholar]
  12. Allen K. N.; Dunaway-Mariano D. Catalytic Scaffolds for Phosphoryl Group Transfer. Curr. Opin. Struct. Biol. 2016, 41, 172–179. 10.1016/j.sbi.2016.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Fendler E. J.; Fendler J. H. Hydrolysis of Nitrophenyl and Dinitrophenyl Sulfate Esters. J. Org. Chem. 1968, 33, 3852–3859. 10.1021/jo01274a035. [DOI] [Google Scholar]
  14. Benkovic S. J.; Benkovic P. A. Studies on Sulfate Esters. I. Nucleophilic Reactions of Amines with p-Nitrophenyl Sulfate. J. Am. Chem. Soc. 1966, 88, 5504–5511. 10.1021/ja00975a026. [DOI] [Google Scholar]
  15. Hopkins A.; Day R. A.; Williams A. Sulfate Group Transfer Between Nitrogen and Oxygen: Evidence Consistent with an Open “Exploded” Transition State. J. Am. Chem. Soc. 1983, 105, 6062–6070. 10.1021/ja00357a017. [DOI] [Google Scholar]
  16. D’Rozario P.; Smyth R. L.; Williams A. Evidence for a Single Transition State in the Intermolecular Transfer of a Sulfonyl Group Between Oxyanion Donor and Acceptors. J. Am. Chem. Soc. 1984, 106, 5027–5028. 10.1021/ja00329a078. [DOI] [Google Scholar]
  17. Bourne N.; Hopkins A.; Williams A. Single Transition State for Sulfonato Group (SO3) Transfer Between Pyridine Nucleophiles. J. Am. Chem. Soc. 1985, 107, 4327–4331. 10.1021/ja00300a042. [DOI] [Google Scholar]
  18. Hoff R. H.; Larsen P.; Hengge A. C. Isotope Effects and Medium Effects on Sulfuryl Transfer Reactions. J. Am. Chem. Soc. 2001, 123, 9338–9344. 10.1021/ja0163974. [DOI] [PubMed] [Google Scholar]
  19. Burlingham B. T.; Pratt L. M.; Davidson E. R.; Shiner V. J.; Fong J.; Widlanski T. S. 34S Isotope Effect on Sulfate Ester Hydrolysis: Mechanistic Implications. J. Am. Chem. Soc. 2003, 125, 13036–13037. 10.1021/ja0279747. [DOI] [PubMed] [Google Scholar]
  20. Denehy E.; White J. M.; Williams S. J. Ground State Structures of Sulfate Monoesters and Sulfamates Reveal Similar Reaction Coordinates for Sulfuryl and Sulfamyl Transfer. Chem. Commun. 2006, 314–316. 10.1039/B513712H. [DOI] [PubMed] [Google Scholar]
  21. Wolfenden R.; Yuan Y. Monoalkyl Sulfates as Alkylating Agents in Water, Alkylsulfatase Rate Enhancements, and the “Energy-Rich” Nature of Sulfate Half-Esters. Proc. Natl. Acad. Sci. U. S. A. 2007, 104, 83–86. 10.1073/pnas.0609644104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Edwards D. R.; Lohman D. C.; Wolfenden R. Catalytic Proficiency: The Extreme Case of S–O Cleaving Sulfatases. J. Am. Chem. Soc. 2012, 134, 525–531. 10.1021/ja208827q. [DOI] [PubMed] [Google Scholar]
  23. Kamerlin S. C. L. Theoretical Comparison of p-Nitrophenyl Phosphate and Sulfate Hydrolysis in Aqueous Solution: Implications for Enzyme-Catalyzed Sulfuryl Transfer. J. Org. Chem. 2011, 76, 9228–9238. 10.1021/jo201104v. [DOI] [PubMed] [Google Scholar]
  24. Williams S. J.; Denehy E.; Krenske E. H. Experimental and Theoretical Insights into the Mechanisms of Sulfate and Sulfamate Ester Hydrolysis and the End Products of Type I Sulfatase Inactivation by Aryl Sulfamates. J. Org. Chem. 2014, 79, 1995–2005. 10.1021/jo4026513. [DOI] [PubMed] [Google Scholar]
  25. Duarte F.; Åqvist J.; Williams N. H.; Kamerlin S. C. L. Resolving Apparent Conflicts between Theoretical and Experimental Models of Phosphate Monoester Hydrolysis. J. Am. Chem. Soc. 2015, 137, 1081–1093. 10.1021/ja5082712. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Bethell D.; Fessey R. E.; Namwindwa E.; Roberts D. W. The Hydrolysis of C12 Primary Alkyl Sulfates in Concentrated Aqueous Solutions. Part 1. General Features, Kinetic Form and Mode of Catalysis in Sodium Dodecyl Sulfate Hydrolysis. J. Chem. Soc., Perkin Trans. 2 2001, 1489–1495. 10.1039/b102957f. [DOI] [Google Scholar]
  27. Spencer B. Studies on Sulphatases. 20. Enzymic Cleavage of Aryl Hydrogen Sulphates in the Presence of H218O. Biochem. J. 1958, 69, 155–159. 10.1042/bj0690155. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Buncel E.; Raoult A.; Wiltshire J. F. Bond-Scission Processes in Sulfur Compounds. VII. Alkyl-Oxygen Scission in the Neutral and Alkalaine Methanolysis of Methyl p-Nitrophenyl Sulfate. J. Am. Chem. Soc. 1973, 95, 799–802. 10.1021/ja00784a027. [DOI] [Google Scholar]
  29. Buncel E.; Chuaqui C. Reactivity-Selectivity Correlations. 2. Reactivity of Alkyl Aryl Sulfates Toward Oxygen Nucleophiles and the Reactivity-Selectivity Principle. J. Org. Chem. 1980, 45, 2825–2830. 10.1021/jo01302a015. [DOI] [Google Scholar]
  30. Younker J. M.; Hengge A. C. A Mechanistic Study of the Alkaline Hydrolysis of Diaryl Sulfate Diesters. J. Org. Chem. 2004, 69, 9043–9048. 10.1021/jo0488309. [DOI] [PubMed] [Google Scholar]
  31. Rosta E.; Kamerlin S. C. L.; Warshel A. On the Interpretation of the Observed Linear Free Energy Relationship in Phosphate Hydrolysis: A Thorough Computational Study of Phosphate Diester Hydrolysis in Solution. Biochemistry 2008, 47, 3725–3735. 10.1021/bi702106m. [DOI] [PubMed] [Google Scholar]
  32. Alkherraz A.; Kamerlin S. C. L.; Feng G.; Sheikh Q. I.; Warshel A.; Williams N. H. Phosphate Ester Analogues as Probes for Understanding Enzyme Catalysed Phosphoryl Transfer. Faraday Discuss. 2010, 145, 281–299. 10.1039/B908398G. [DOI] [Google Scholar]
  33. Duarte F.; Geng T.; Marloie G.; Al Hussain A. O.; Williams N. H.; Kamerlin S. C. L. The Alkaline Hydrolysis of Sulfonate Esters: Challenges in Interpreting Experimental and Theoretical Data. J. Org. Chem. 2014, 79, 2816–2828. 10.1021/jo402420t. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Duarte F.; Barrozo A.; Åqvist J.; Williams N. H.; Kamerlin S. C. L. The Competing Mechanisms of Phosphate Monoester Dianion Hydrolysis. J. Am. Chem. Soc. 2016, 138, 10664–10673. 10.1021/jacs.6b06277. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Pabis A.; Williams N. H.; Kamerlin S. C. L. Simulating the Reactions of Substituted Pyridinio-N-Phosphonates with Pyridine as a Model for Biological Phosphoryl Transfer. Org. Biomol. Chem. 2017, 15, 7308–7316. 10.1039/C7OB01734K. [DOI] [PubMed] [Google Scholar]
  36. More O’Ferrall R. A. Relations Between E2 and E1cB Mechanisms of β-Elimination. J. Chem. Soc. B: Phys. Org. 1970, 274–277. 10.1039/J29700000274. [DOI] [Google Scholar]
  37. Jencks W. P. A Primer for the Bema Hapothle. An Empirical Approach to the Characterization of Changing Transition-State Structures. Chem. Rev. 1985, 85, 511–527. 10.1021/cr00070a001. [DOI] [Google Scholar]
  38. Barrozo A.; Blaha-Nelson D.; Williams N. H.; Kamerlin S. C. L. The Effect of Magnesium Ions on Triphosphate Hydrolysis. Pure Appl. Chem. 2017, 89, 715–727. 10.1515/pac-2016-1125. [DOI] [Google Scholar]
  39. Peverati R.; Truhlar D. G. M11-L: A Local Density Functional That Provides Improved Accuracy for Electronic Structure Calculations in Chemistry and Physics. J. Phys. Chem. Lett. 2012, 3, 117–124. 10.1021/jz201525m. [DOI] [PubMed] [Google Scholar]
  40. Zhao Y.; Truhlar D. G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals. Theor. Chem. Acc. 2008, 120, 215–241. 10.1007/s00214-007-0310-x. [DOI] [Google Scholar]
  41. Chai J.-D.; Head-Gordon M. Long-Range Corrected Hybrid Density Functionals with Damped Atom–Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. 10.1039/b810189b. [DOI] [PubMed] [Google Scholar]
  42. Hratchian H. P.; Schlegel H. B. Accurate Reaction Paths Using a Hessian Based Predictor-Corrector Integrator. J. Chem. Phys. 2004, 120, 9918–9924. 10.1063/1.1724823. [DOI] [PubMed] [Google Scholar]
  43. Hratchian H. P.; Schlegel H. B. Using Hessian Updating To Increase the Efficiency of a Hessian Based Predictor-Corrector Reaction Path Following Method. J. Chem. Theory Comput. 2005, 1, 61–69. 10.1021/ct0499783. [DOI] [PubMed] [Google Scholar]
  44. Breneman C. M.; Wiberg K. B. Determining Atom-Centered Monopoles from Molecular Electrostatic Potentials. The Need for High Sampling Density in Formamide Conformational Analysis. J. Comput. Chem. 1990, 11, 361–373. 10.1002/jcc.540110311. [DOI] [Google Scholar]
  45. Wiberg K. B. Application of the Pople-Santry-Segal CNDO Method to the Cyclopropylcarbinyl and Cyclobutyl Cation and to Bicyclobutane. Tetrahedron 1968, 24, 1083–1096. 10.1016/0040-4020(68)88057-3. [DOI] [Google Scholar]
  46. Foster J. P.; Weinhold F. Natural Hybrid Orbitals. J. Am. Chem. Soc. 1980, 102, 7211–7218. 10.1021/ja00544a007. [DOI] [Google Scholar]
  47. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.; Caricato M.; Marenich A. V.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratchian H. P.; Ortiz J. V.; Izmaylov A. F.; Sonnenberg J. L.; Williams; Ding F.; Lipparini F.; Egidi F.; Goings J.; Peng B.; Petrone A.; Henderson T.; Ranasinghe D.; Zakrzewski V. G.; Gao J.; Rega N.; Zheng G.; Liang W.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Throssell K.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M. J.; Heyd J. J.; Brothers E. N.; Kudin K. N.; Staroverov V. N.; Keith T. A.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A. P.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Millam J. M.; Klene M.; Adamo C.; Cammi R.; Ochterski J. W.; Martin R. L.; Morokuma K.; Farkas O.; Foresman J. B.; Fox D. J.. Gaussian 16 Rev. B.01, Gaussian, Inc.: Wallingford, CT, 2016. [Google Scholar]
  48. Bigeleisen J.; Mayer M. G. Calculation of Equilibrium Constants for Isotopic Exchange Reactions. J. Chem. Phys. 1947, 15, 261–267. 10.1063/1.1746492. [DOI] [Google Scholar]
  49. Takano Y.; Houk K. N. Benchmarking the Conductor-like Polarizable Continuum Model (CPCM) for Aqueous Solvation Free Energies of Neutral and Ionic Organic Molecules. J. Chem. Theory Comput. 2004, 1, 70–77. 10.1021/ct049977a. [DOI] [PubMed] [Google Scholar]
  50. Xie D.; Zhou Y.; Xu D.; Guo H. Solvent Effect on Concertedness of the Transition State in the Hydrolysis of p-Nitrophenyl Acetate. Org. Lett. 2005, 7, 2093–2095. 10.1021/ol0502836. [DOI] [PubMed] [Google Scholar]
  51. Zhang L.; Xie D.; Xu D.; Guo H. Supermolecule Density Functional Calculations Suggest a Key Role for Solvent in Alkaline Hydrolysis of p-Nitrophenyl Phosphate. Chem. Commun. 2007, 1638–1640. 10.1039/b617946k. [DOI] [PubMed] [Google Scholar]
  52. Babtie A. C.; Lima M. F.; Kirby A. J.; Hollfelder F. Kinetic and Computational Evidence for an Intermediate in the Hydrolysis of Sulfonate Esters. Org. Biomol. Chem. 2012, 8095–8101. 10.1039/c2ob25699a. [DOI] [PubMed] [Google Scholar]
  53. Hengge A. C. Isotope Effects in the Study of Phosphoryl and Sulfuryl Transfer Reactions. Acc. Chem. Res. 2002, 35, 105–112. 10.1021/ar000143q. [DOI] [PubMed] [Google Scholar]
  54. Abdelraheem E. M. M.; Busch H.; Hanefeld U.; Tonin F. Biocatalysis Explained: From Pharmaceutical to Bulk Chemical Production. React. Chem. Eng. 2019, 4, 1878–1894. 10.1039/C9RE00301K. [DOI] [Google Scholar]
  55. Kirby A. J.; Varvoglis A. G. The Reactivity of Phosphate Esters. Monoester Hydrolysis. J. Am. Chem. Soc. 1967, 89, 415–423. 10.1021/ja00978a044. [DOI] [Google Scholar]
  56. Williams A. Effective Charge and Leffler’s Index as Mechanistic Tools for Reactions in Solution. Acc. Chem. Res. 1984, 17, 425–430. 10.1021/ar00108a003. [DOI] [Google Scholar]
  57. Szeler K.; Williams N. H.; Hengge A. C.; Kamerlin S. C. L. Modeling the Alkaline Hydrolysis of Diaryl Sulfate Diesters: A Mechanistic Study. J. Org. Chem. 2020, 10.26434/chemrxiv.11874072. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Kolfhott I. M.Treatise on Analytical Chemistry; Interscience Encyclopedia, Inc.: New York, 1959. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jo0c00441_si_001.pdf (4.8MB, pdf)
jo0c00441_si_002.zip (377.2KB, zip)

Articles from The Journal of Organic Chemistry are provided here courtesy of American Chemical Society

RESOURCES