Further Optimization and Validation of the Classical Drude Polarizable Protein Force Field

Abstract

The CHARMM Drude-2013 polarizable force field (FF) was developed to include the explicit treatment of induced electronic polarizability, resulting in a more accurate description of the electrostatic interactions in molecular dynamics (MD) simulations. While the Drude-2013 protein FF has shown success in improving the folding properties of α-helical peptides and to reproduce experimental observables in simulations up to 1 μs, some limitations were noted regarding the stability of β-sheet structures in simulations longer than 100 ns as well as larger deviations from crystal structures in simulations of a number of proteins compared to the additive CHARMM36 protein FF. The origin of the instability has been identified and appears to be primarily due to overestimated atomic polarizabilities and induced dipole-dipole interactions on the Cβ, Cγ and Cδ side chain atoms. To resolve this and other issues, a number of aspects of the model were re-visited, resulting in Drude-2019 protein FF. Backbone parameters were optimized targeting the conformational properties of the (Ala)₅ peptide in solution along with gas phase properties of the alanine dipeptide. Dipeptides that contain N-acetylated and N’-methylamidated termini, excluding Gly, Pro and Ala, were used as models to optimize the atomic polarizabilities and Thole screening factors on selected Cβ, Cγ and Cδ carbons by targeting quantum mechanical (QM) dipole moments and molecular polarizabilities. In addition, to obtain better conformational properties, side chain χ1 and χ2 dihedral parameters were optimized targeting QM data for the respective side chain dipeptide conformations as well as PDB survey data based on the χ1, χ2 sampling from Hamiltonian replica-exchange MD simulations of (Ala)₄-X-(Ala)₄ in solution, where X is the amino acid of interest. Further improvements include optimizing nonbonded interactions between charged residues to reproduce QM interactions energies of the charged-protein model compounds and experimental osmotic pressures. Validation of the optimized Drude protein FF includes MD simulations of a collection of peptides and proteins including β-sheet structures, as well as transmembrane ion channels. Results showed that the updated Drude-2019 protein FF yields smaller overall RMS differences of proteins as compared to the additive CHARMM36m and Drude-2013 FFs as well as similar or improved agreement with experimental NMR properties, allowing for long timescale simulation studies of proteins and more complex biomolecular systems in conjunction with the remainder of the Drude polarizable FF.

Graphical Abstract

INTRODUCTION

Proteins are one of the most abundant organic molecules in biological systems. They have a variety of functions, acting as enzymes, receptors, transporters, regulatory proteins, and so on.¹ To date, many proteins serve as therapeutic targets, being important in a wide range of disease-related processes.^2–3 While proteins are polymers of the 20 amino acids arranged in a specific primary sequence, their tertiary and quaternary structures vary greatly. Therefore, a large percentage of the experimental and theoretical studies of proteins have focused on their structural and dynamical properties and relate them to their biological functions.^4–5 Among those, molecular dynamics (MD) simulations are commonly used to explore the structure and motion of proteins, with the forces required for the MD simulations typically based on classical molecular mechanics (MM),^6–7 such that a highly accurate force field (FF) is critical to ensure the accuracy of simulations.⁸ Most MD simulation studies to date have been based on nonpolarizable, additive FFs, where the partial atomic charges are fixed and the electronic polarization is treated in a mean-field manner.⁹ The widely used additive models include CHARMM,^10–13 AMBER,^14–16 OPLS,^17–18 and GROMOS.¹⁹ However, to achieve a more accurate description of the response of the charge distribution to variations in the surrounding electrostatic field, the explicit inclusion of electronic polarizability in the model is essential.²⁰

Multiple polarizable FFs have been developed for proteins, including Drude,²¹ AMOEBA,²² CHARMM fluctuating charge,^23–24 and AMBER ff02,²⁵ among others.^26–29 In the classical Drude polarizable model, explicit polarization is introduced by attaching a charged auxiliary Drude oscillator with a harmonic spring to the atomic core, which allows the induced atomic dipole to adjust in response to the surrounding electronic field.^30–31 According to equation 1, the induced atomic dipole, μ, in the presence of an electric field, E, is calculated as:

$$\mathit{\mu }=\frac{q_D^2}{k_D}E$$ Equation 1

where k_D is a harmonic spring force constant, and the atomic polarizability, α, will determine the charge of the Drude oscillator, q_D, according to equation 2.

$$\alpha =\frac{q_D^2}{k_D}$$ Equation 2

For hydrogen bond acceptors, anisotropic atomic polarizability as well as virtual particles representative of lone pairs are included to improve the treatment of nonbonded interactions.³² Induced dipole-dipole interactions for atoms within two covalent bonds (e.g. 1–2 and 1–3 relationship as defined by the atomic nuclei) are calculated explicitly with a shielding treatment proposed by Thole,³³ such that the Coulomb energy between the charge-charge interaction is damped by a Thole-like screening function, S_ij, as shown in equation 3:

$$S_{ij}\left({\text{r}}_{\text{ij}}\right)=1-\left[\left(1+\frac{\left({\mathrm{t}}_{\text{i}}+{\mathrm{t}}_{\text{j}}\right){\text{r}}_{\text{ij}}}{2{\left({\alpha }_{\text{i}}{\alpha }_{\text{j}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}}\right)\right]\text{exp}\left[\frac{-\left({\mathrm{t}}_{\text{i}}+{\mathrm{t}}_{\text{j}}\right){\text{r}}_{\text{ij}}}{{\left({\alpha }_{\text{i}}{\alpha }_{\text{j}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}}\right]$$ Equation 3

In equation 3, r_ij is the distance between atoms i and j, α_i and α_j are respective atomic polarizabilities according to equation 1, t_i and t_j are the respective atomistic Thole screening factors that dictate the degree of scaling. This is different from additive FFs where the nonbonded interactions between 1–2 and 1–3 atom pairs are excluded. Thus, the Drude model incorporates a more physically correct treatment of electronic polarizability compared with the additive FFs.

Development of the Drude polarizable force field has been ongoing since 2000, and the first generation Drude polarizable protein force field was released in 2013 (denoted as Drude-2013 FF in the following content).²¹ The Drude-2013 FF has been applied to a variety of peptides and proteins,^34–35 ions-proteins,³⁶ ligand-proteins,³⁷ with simulation times ranging from nanoseconds to a microsecond.³⁸ Results have shown that backbone and side-chain dipole moments have large variability relevant to the environment, and larger values of the dielectric constant were observed for the protein interior as compared to the additive CHARMM36 FF.³⁸ These indicate that the inclusion of explicit electronic polarizability leads to significant differences in the physical forces affecting the structure and dynamics of proteins.

While the Drude-2013 FF has shown success in reproducing experimental observables in simulations up to one microsecond, there were also some limitations. In particular, β-sheet structures in simulations longer than 100 ns displayed some instability in simulations in our laboratory (Figure 4 below) as well as in a published study³⁹. Additionally, MD simulations for a number of proteins based on the Drude-2013 model typically yielded larger RMS differences relative to crystal structures as compared to the additive CHARMM36 FF.²¹ Analysis indicates that the issue was primarily due to overestimated atomic polarizabilities and induced dipole-dipole interactions on the Cβ, Cγ and Cδ side chain atoms. To obtain more stable structures, selected aspects of the Drude-2013 FF are re-optimized in this work. This includes optimizing the backbone parameters to improve the conformational properties. Several side chain parameters were updated based on recent improvement in the parameters for molecular ions⁴⁰ and imidazole and its derivatives⁴¹ that yield more accurate hydration free energies. As an overestimation of the atomic polarizability and the treatment of induced dipole-dipole moment interactions on selected side-chain aliphatic carbons was observed in the Drude-2013 FF, selected electrostatic parameters on these atoms were optimized. Additional parametrization includes adding atom pair-specific parameters to better treat the salt-bridge interactions among the charged protein functional groups. The resulting force field was examined and validated by simulating a number of peptide and protein systems in solution and comparison with experimental crystallographic and NMR data. Optimization of polypeptide backbone parameters Compared with the additive CHARMM36 and Drude-2013 FFs, the updated protein FF, referred to as the Drude-2019 protein FF, yields more stable structural properties based on RMSD analysis over 1 μs simulations, and generally improved agreement with experimental NMR data was obtained. Accordingly, the Drude-2019 FF yields a more accurate representation proteins in various environments, making it more applicable in simulation studies of proteins as well as other complex systems in conjunction with the remainder of the Drude polarizable force field.

Figure 4.

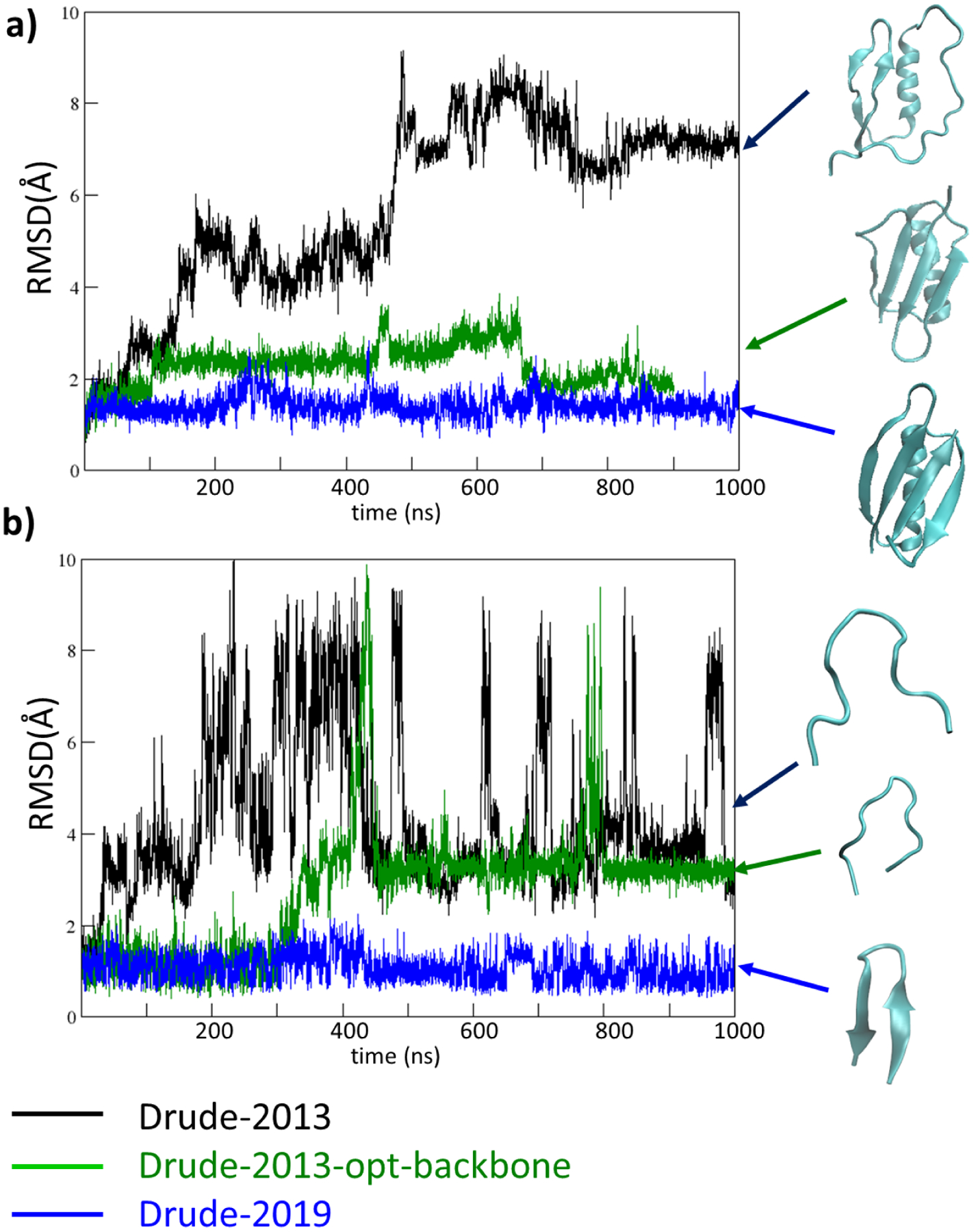
RMSD analyses based on the Cα atoms for a) protein GB3 system (PDB: 2IGD) and b) HP7 peptide (PDB: 2EVQ), using the original Drude-2013 protein FF (Drude-2013, in black), Drude-2013 with optimized backbone parameters only (Drude-2013-opt-backbone, in green), and final optimized Drude-2019 protein FF (Drude-2019, in blue). Structures obtained at the end of the simulations are shown in cyan, indicated with the corresponding colored arrows.

COMPUTATIONAL METHODS

The backbone electrostatics parameters, including partial atomic charges, atomic polarizabilities and Thole screening factors were optimized by a reweighting approach using NMR J couplings of the solvated (Ala)₅ peptide as target data^42–45. The reweighting approach allows estimation of the effects of changes in parameters on the targeted condensed phase observables by directly computing the partial derivatives of the J couplings and is effective to explore the parameter space.¹³ The conformational ensemble of (Ala)₅ used for reweighting was generated with Hamiltonian replica exchange MD simulations (H-REMD)⁴⁶ performed as described in our previous study.²¹ However, the system consisted of 12 replicas instead of 8, where the potential function was perturbed using a biasing potential grid correction energy map (bpCMAP)⁴⁷ applied to the φ, ψ backbone dihedrals with scaling factors being 0, 0.03, 0.13, 0.25, 0.35, 0.45, 0.55, 0.65, 0.75, 0.95 and 1.0 throughout the replicas. The scaling factor of 1.0 corresponds to a flat φ, ψ potential energy surface. The values of J couplings and their derivatives with respect to backbone electrostatics parameters obtained from the H-REMD simulations were then subjected to Monte Carlo simulated annealing (MCSA) to adjust the force field parameters for better agreement between computed and experimental J couplings.¹³

Treatment of the φ, ψ conformational energies of the protein backbone is performed in part using the CMAP approach, as previously described^48–49. Due to the intrinsic coupling between the backbone nonbond parameters and the CMAP potential in protein FFs, generic CMAPs had to be generated for each new version of the backbone nonbond parameters generated in the MCSA. These were generated by taking the difference between QM and MM φ, ψ PES of the gas phase N-acetylated and N’-methylamidated alanine dipeptide (ALAD) and used throughout the refinement. The MM surfaces were computed with 2D scan of the φ, ψ dihedral angles ranging from −180 to 180° in 15˚ increments for both dihedrals with no CMAP potential imposed, while the reference QM surface was computed at the MP2/6–311G(d,p)//RIMP2/CBS model chemistry by Q-CHEM.^50–51 This QM surface was obtained from our previous work.²¹ Thus, for each change of the electrostatic backbone parameters generated during MCSA, a new generic CMAP is generated and its contribution to the partial derivative of the J-couplings is computed numerically and included in the reweighting calculations. Thus, the underlying conformational properties of the peptide backbone directly reproduce the gas phase QM MP2/6–311G(d,p)//RIMP2/CBS conformational energies based on the alanine, glycine and proline dipeptides.

MCSA fitting of alpha and Thole parameters for the Cβ and Cγ atoms of the amino side chains

Dipeptides that contain N-acetylated and N’-methylamidated termini were used as models for optimization of the electrostatic parameters of selected Cβ/Cγ/Cδ atoms in the amino acid side chains. Additional optimization of Gly, Pro and Ala was not performed as instabilities were not present in these amino acids. QM single point calculation of dipole moments and molecular polarizabilities were performed at B3LYP/aug-cc-pVDZ model chemistry, as previously used for the Drude force field⁵², using the Gaussian 03 program⁵³ on a set of dipeptide conformations obtained from Zhu et. al.⁵⁴ These dipeptide conformations include varying the χ₁ and χ₂ dihedral angles by starting at −180° and −180° and incrementing them by 120° with the dipeptides constrained to three different backbone conformations (αR, β, and αL), with ϕ, ψ angles of αR (−60.0°, −45.0°), β (−120.0°, 120.0°), and αL (63.5°, 34.8°), resulting in 48 conformations for each dipeptide except the valine dipepetide, which has 12 conformations by changing χ₁ dihedral angles with the increments of 120°. A MCSA algorithm⁵⁵ was used with CHARMM^56–58 to optimize the alpha and Thole screening parameters^{21, 59–60} on the Cβ carbons for Asn, Asp, Ile, Cys, Thr, Met, Ser, Hsd, Hse, Hsp, and Trp, the Cβ and Cγ carbons for Gln, Glu, Arg, Leu) and the Cβ, Cγ, and Cδ carbons for Lys on side chains. The target data were the QM calculated total dipole moments and the x, y, and z components as well as the total molecular polarizabilities and the diagonal xx, yy, zz components, resulting in eight target values used in the MCSA for each dipeptide conformation. The scoring function for the MCSA was the root-mean-square (RMS) differences between the MM and QM dipole moments and molecular polarizabilties over all the dipeptide conformations. During the fitting, a weighting factor of 5 was assigned for αR and β backbone conformations and 1 for those from αL. In MCSA, the Drude dipole moments and molecular polarizabilities are obtained by reading the QM coordinates described above followed by relaxation of the Drude particles via a minimization by steepest-descent (SD) algorithm for 200 steps and then the adopted-basis Newton-Raphson (ABNR) algorithm to a final gradient of 10⁻⁵ kcal·mol⁻¹·Å⁻¹ with the atomic positions restrained with a force constant of 10⁷ kcal/(mol·Å²).

The molecular polarizabilities in the Drude force field are scaled to better reproduce experimental dielectric constants, with scaling factors ranging from 0.6 to 1.0^{20, 61}. As dielectric constants are not available for dipeptides, to determine their molecular polarizability scaling factors, systematic MCSA fittings were performed with five different random seeds and five different initial parameters (e.g. (Cβ_alpha, Cβ_Thole) = (−0.6, 0.6), (−0.8, 0.8), (−1.0, 1.0), (−1.2, 0.4), and (−1.2, 0.8)) to target the QM molecular polarizabilities. This procedure was repeated with the QM molecular polarizabilities scaled by 0.70, 0.80, 0.85, 0.90, 0.95 and 1.00. The resulting alpha and Thole screening parameters obtained from MCSA for dipeptides in the Drude model yield QM/Drude molecular polarizability ratios in the range of 0.7–0.8 for Glu, Met, Asp, and Cys, 0.8–0.9 for Arg, Ans, Gln, Hsd, Hse, Leu, Lys, Ser, and Thr, and 0.85–0.95 for Ile, Hsp, and Tyr. Note that the polarizabilities for remaining side chain moieties were the published scaled values ranging from 0.6–1.0 relative to the QM data. For example, 0.6 for sulfur containing groups, 0.85 for nitrogen-containing heteroaromatics and 1.0 for the aliphatics. Additionally, using the MCSA fitted parameters obtained from targeting QM molecular polarizabilities scaled by 0.85 would yield the ratio of MM/QM molecular polarizabilities around 0.85 (as shown in Table S1) except the results for Glu and Asp, which is 0.76~0.77. Accordingly, the molecular polarizability scaling factor of approximately 0.85 is considered acceptable for the resulting Drude model.

χ1 and χ2 dihedral parameter fitting

Side chain χ1 and χ2 dihedral parameters for amino acids, excluding Ala, Gly and Pro, were initially fitted to target QM potential energy surfaces for the χ1 and χ2 torsions in amino acid dipeptides, where the same set of QM surfaces of the 2D dipeptide conformations obtained from Zhu et. al were used.⁴² Here, a linear least squares (LLS) automated fitting program⁶² was used to optimize the side chain dihedral parameters. Similar to the previously reported optimization scheme,²¹ a higher weighting factor of 5 was assigned for energies from αR and β backbone conformations and 1 for those from αL conformation due to the greater sampling of the former conformations in protein structures. For neutral side chains, an energy cutoff of 12 kcal/mol was applied, while all the energies higher than the cutoff were not used to avoid the fitting being biased by these high-energy regions. For charged side chains, higher energy cutoffs of 20 kcal/mol were used for Arg and Lys and 25 kcal/mol for Asp, Glu and protonated His. Amino acids sharing the same χ1 or both χ1 and χ2 parameters (Thr/Ile/Val, Lys/Arg/Met and Tyr/Phe) were fitted together. The multiplicities (n) in the dihedral parameters were limited to the combination of 1, 2 and 3 and the phases (δ) were restricted to either 0 or 180°.

To reproduce their dihedral distributions from a crystallographic survey of the PDB,⁴² χ₁ and χ₂ dihedral parameters optimized to target the dipeptide gas phase QM surfaces were subsequently adjusted to reproduce the survey dihedral distributions using condense phase simulations. The condense phase simulation system included the 9-mer peptide (Ala)₄-X-(Ala)₄ solvated in a 32 Å cubic water box with the backbone restrained to the C7eq conformation (−82.8°, 77.9°) conformation for each type of amino acid X. Hamiltonian replica exchange with the solute scaling method (REST2) was used as described previously to enhance sampling efficiency.²¹ In REST2, four replicas were used, and the potential energy of the replica E_m computed according to equation 4, which includes the scaling of the peptide intramolecular energy (E_pp), scaling of the peptide-water interaction energy (E_pw) and the unscaled interaction energy between the water molecules (E_ww), where T₀ = 300 K for the 0^th replica and the effective T_m = 329 K, 363 K, and 400 K for the other replicas. Note that all replicas were run at the same temperature T₀, and only the 0^th replica corresponds to the desired equilibrium distribution at T₀. A 10 ns solute scaling simulation with an exchange attempt frequency of 0.1 ps⁻¹ was conducted for each (Ala)₄-X-(Ala)₄ system. Probability histograms of the χ₁ and χ₂ distributions from MD simulations were generated using a bin size of 15° and the overlap coefficient (OC) between two probability distributions and those from the crystallographic survey⁴² were calculated as shown in equation 5. To improve the OC, manual adjustment as well as the reweighting method (Figure S1) based on the condensed phase (Ala)₄-X-(Ala)₄ simulations were performed.

$$E_m=\frac{T_0}{T_m}{E}_{pp}+\sqrt{\frac{T_0}{T_m}}{E}_{pw}+E_{ww}$$ Equation 4

$$\text{OC}=\frac{{\sum }^{\text{}}{\mathit{p}}_{\mathit{m}}{\mathit{p}}_{\mathit{n}}}{\sqrt{{\sum }^{\text{}}{\mathit{p}}_{\mathit{m}}{}^{\mathbf{2}}\cdot {\sum }^{\text{}}{\mathit{p}}_{\mathit{n}}{}^{\mathbf{2}}}}$$ Equation 5

Optimization of interactions between charged protein model compounds

Atom pair-specific non-bonded parameters⁶³ were introduced targeting the QM interaction energies between charged protein model compounds. The charged protein model compounds are methylammonium (MAMM), methylguanidinium (MGUAN) and imidazolium (IMIM) that represent the positively charged side chains and termini, and acetate (ACET) that represents the negatively charged side chains and termini. In preparation of QM target data, the gas phase geometries of the monomer model compounds were optimized at the MP2/aug-cc-pVDZ level with the Gaussian 03 program.⁶⁴ Interaction energies between the positively and negatively charged model compounds were performed using the QM gas phase model compound at the MP2/cc-pVQZ model chemistry including the basis set superposition error correction of Boys and Bernardi.⁶⁵ In the MM calculation performed by CHARMM,^56–58 relaxation of the Drude particles was performed via minimization by the steepest-descent (SD) and adopted-basis Newton-Raphson (ABNR) algorithms to reach a gradient of 10⁻⁵ kcal·mol⁻¹·Å⁻¹ while the atomic positions were restrained with a force constant of 10⁷ kcal/mol/Ų. This step was performed for the individual monomers and then for the complex from which the total energies were obtained to calculate the interaction energy.

Osmotic pressure was calculated for guanidinium-acetate (GUAN-ACET) solution systems where their experimental values is available.¹³ Calculation of osmotic pressure was based on the algorithm described by Luo and Roux.⁶⁶ In this approach, the effect of ideal semipermeable membranes was modeled by two virtual walls, separating a region that contains a high concentration of the ions from a pure water region. The mean force on the virtual walls placed by the ions is directly correlated to the osmotic pressure, as defined in equation 6. Systems with given concentrations were built by randomly placing the ions within the central part of a rectangular cell box of 45×45×90 ų. The z-axis was aligned with the longest axis of the rectangular cell box with the center located at the coordinate origin (x=0, y=0 and z=0). During the simulation, the ions were constrained by the virtual walls that were defined as a half-harmonic planar restraint at z_wall = ±22.5 Å with a force constant of 10 kcal mol⁻¹Å⁻² , such that ions were kept confined in the central region of the rectangular cell box while water molecules were allowed to freely pass through these walls.

$$\langle F_{\text{wall}}\rangle =\text{k}\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$N$}\right.\right){\sum }_N{\sum }_i\left(\langle \left|z_i-z_{\text{wall}}\right|\rangle \right)$$ Equation 6

According to equation 6, the osmotic pressure was calculated as $\langle F_{\text{wall}}\rangle /A$, where A is the cross-sectional area (45² = 2025 Ų), 〈F_wall〉 is the restraint force exerted on the wall by the ions, k is the force constant, N is number of frames, and I is the index of the ions. Simulations were carried out in NAMD using the extended Lagrangian integration method implemented in NAMD.^67–68 The Langevin dynamics parameters, the treatment of Lennard-Jones (LJ) potential and electrostatic forces parameters for NAMD are the same as described for the NAMD simulations in the next paragraph. Pressure coupling using Langevin piston pressure control was applied along the z-axis while the x- and y-dimensions were fixed to maintain a constant area for each virtual wall. Following a 1 ns equilibration simulation, production simulations were carried out at each concentration for 50 ns with coordinates saved every 10 ps. The mean force was further averaged between the two half-harmonic walls. Finally, osmotic pressure values were subsequently calculated according to equation 6 using CHARMM.^56–58 Three concentrations of the guanidinium acetate solution studies were 0.3, 0.4 and 0.5 M, in which cases 16, 22 and 27 guanidinium and acetate ion pairs were included in the simulation systems, respectively.

Molecular dynamics of validation systems

Validation systems are summarized in Table 1 with their backbone 3D structures shown in Figure S2. Starting coordinates for all the peptide/protein structures were taken from the Protein Data Bank.⁶⁹ The protein coordinate and structure files were initially prepared in CHARMM additive formats using the Solvator module in the CHARMM-GUI.⁷⁰ The resulting additive coordinate and structure files were then submitted to the Drude Prepper module in the CHARMM-GUI to obtain files in Drude format. Each system was solvated in a cubic box with a 10 Å minimum distance between the edge of the box and the protein. The SWM4-NDP model⁷¹ was used for water and Na⁺ or Cl⁻ ions^72–73 were added to neutralize the systems (Table 1). Equilibrations were carried out using NAMD.^51,52 The extended Lagrangian approach with a dual-Langevin thermostat was used for integrating the equations of motion, where the temperature was maintained at 300 K for real atoms and at 1 K for Drude oscillators with thermostat friction coefficients of 5 ps⁻¹ and 20 ps⁻¹ respectively.⁵¹ SHAKE was used to fix covalent bonds involving hydrogen atoms.⁷⁴ Short-range LJ forces were potential switched to zero from 10–12 Å.⁷⁵ Electrostatic interactions were computed with the smooth particle mesh Ewald (PME) method with a real space cutoff of 12 Å, a kappa factor of 0.34 and a 6-order spline.^76–77 The Drude Hardwall constraint was set at 0.2 Å to prevent polarization catastrophe⁷⁸ and analysis was undertaken to assure that the nuclei-Drude particle distances were not reaching 0.2 Å during the simulations. Each system was equilibrated under an isothermal-isobaric (NPT) ensemble, where the pressure was set at 1 atm using Langevin piston pressure control⁷⁹ with a piston oscillation period of 200 fs and a relaxation time of 100 fs. A 100 ps equilibration was performed with a 0.5 fs time step with all heavy atom restrained using a harmonic force constant of 1 kcal/mol·Å². Following equilibration, restraints were removed and production simulations were carried out using OpenMM.^80–82 The parameters for production simulations were similar to those used in equilibration with the following differences. The simulations were carried out for 1μs with the Drude Langevin integrator using a 1 fs time step.⁶⁸ The pressure was maintained at 1 atm using the Monte Carlo barostat^83–84 with pressure changes attempted every 25 steps. The Drude Hardwall constraint was set at 0.25 Å⁷⁸. All analyses were carried out using facilities within CHARMM.^53–55 Analysis of protein secondary structures were performed using the DSSP program.⁸⁵ Dipole moment analysis of the peptide backbone included the charges on the following atoms and their Drude particles (C,O,N,H,Cα and Hα atoms, the sum of whose charges are neutral) following alignment of the non-hydrogen atoms to the corresponding atoms from the crystal structures.

Table 1.

Peptides and proteins subjected to MD simulations.^a

	Peptides/proteins	PDB	Type	Number of Ions
Amino acid < 50 aa
A)	Trp-cage	1L2Y88	α-Helix	1 Cl−
B)	IAAL-K3	1U0I89		3 Na+
C)	Crambin	1EJG90	α-Helix/β-sheet	0
D)	Cln025 (mutant of Chignolin)	2RVD91	β-sheet	2 Na+
E)	MBH12	1K4392		2 Cl−
F)	Tryptophan Zipper 4	1LE393		2 Na+
G)	HP7	2EVQ94		1 Cl−
H)	14-residue peptide	1J4M92		2 Cl−
I)	GB1 hairpin, extract from PDB: 1GB1 (residues 41–56)	1GB195		0
Amino acid > 50 aa
J)	Apo calmodulinb	1QX596	α-Helix	24 K+
K)	DNA methyltransferase 1 associated protein 1 (DMAP1)	4IEJ		1 Na+
L)	Cold-shock protein A	1MJC97	β-sheet	1 Na+
M)	Ubiquitin	1UBQ98	α-Helix/β-sheet	0
N)	Protein GB1 domain	2QMT99		0
O)	Intestinal fatty acid binding protein	1IFC100		0
P)	Hen lysozyme	6LYT101		8 Cl−
Q)	Lysozyme	135L102		0
R)	Protein GB3 domain	1P7E103		2 Na+
S)	Protein GB3 domain	2IGD		2 Na+

^aAll systems were simulated for 1 μs.

^bNa⁺ was used as the counterion for the C36m and Drude-2013 simulations with K⁺ used for the Drude-2019 simulation

Molecular dynamics simulations using the additive model were performed as well for comparison. Simulation procedures were in a similar manner as those for the Drude calculations with the following exceptions. The CHARMM36m force field¹³ was used for the protein. In equilibration using NAMD,⁵² LJ forces were force switched to zero from 10–12 Å.⁶² Pressure control was based on a Nosé–Hoover Langevin piston algorithm.^{79, 86} A 100 ps equilibration was performed with a 1 fs time step. In production using OpenMM,^66,67 the velocity Verlet integrator used a 2 fs time step, and the Andersen thermostat⁸⁷ was used.

RESULTS AND DISCUSSION

The optimization of the Drude-2013 protein force field included further adjusting selected backbone, side chain and atom pair-specific parameters (NBFIX in CHARMM^53–55). To ensure more stable protein/peptide secondary structures, including both α-helices and β-sheets, efforts have been made to optimize the backbone electrostatic parameters based on a reweighting protocol that targeted the conformational properties of the (Ala)₅ peptide in combination with a CMAP based on the alanine dipeptide that reproduces a QM gas phase 2D φ, ψ potential energy surface (PES). To achieve better reproduction of experimental hydration free energies of selected protein functional groups, parameters for histidine were updated based on recent improvements to imidazole and the 4-methylimidazole tautomers,⁴⁰ and charged moiety parameters were updated based on results for representative molecular ions.³⁹ Other improvements in the nonbond parameters included recently published improvements in NBFIX parameters between both positive and negative groups and ring systems, including cation-π interactions.¹⁰⁴ As the electrostatic parameters on the aliphatic groups, particularly with Cβ or Cγ carbons, required adjustments, a systematic parametrization of these terms was performed. Following the change of the backbone and side chain parameters, the χ1 and χ2 dihedral parameters were fitted to obtain conformational properties that better mimic those occurring in full proteins. Finally, NBFIX parameters were included between charged moieties to improve the salt-bridge interactions among protein functional groups. The resulting protein FF, referred to as Drude-2019, was applied in MD simulations of a series of peptide and protein systems to examine their stability and the ability of reproducing experimental NMR properties.

Optimization of the protein backbone electrostatic parameters

Alanine peptides have been used widely for the study of peptide conformation.^105–106 In this study, the widely studied (Ala)₅ peptide was used to optimize the peptide backbone electrostatic parameters with the CMAP adjusted to reproduce the QM gas phase alanine dipeptide 2D potential energy surface. 500 ns simulations of (Ala)₅ were performed from which the backbone dihedral distributions were obtained and used to calculate the J-coupling constants. The same χ2 calculation as performed by Best et al.¹⁰⁷ was applied to evaluate the deviation of the J-coupling constants from the experimental values. Table 2 shows the comparison of the computed J-coupling constants between the experimental data and the Drude-2013 and Drude-2019 models. With the final optimized backbone and CMAP parameters, i.e. Drude-2019 FF, the RMS is 0.85 and χ² is 5.90 (or 2.28 excluding the J ³(C,C) of residue index 2), while using the Drude-2013 FF the RMS is 0.93 and χ² is 7.41 (or 3.23 excluding the J ³(C,C) of residue index 2). Although the χ² is still larger than the values reported by other models,^22,91 the improvements associated with re-optimization of the backbone in conjunction with a CMAP that reproduces gas phase QM MP2/6–311G(d,p)//RIMP2/CBS energetics of the alanine dipeptide 2D φ, ψ PES are evident with respect to the experimental NMR values.

Table 2.

Comparison of J-coupling values (Hz) with Drude-2013/Drude-2019 FFs and experimental data (Exp)89 for the (Ala)5 peptide from 500 ns simulations.

Residue index	Type	Exp	Drude-2013	Diff2013	Drude-2019	Diff2019
2	3J(HNHA)	5.59	6.87	1.28	6.98	1.39
2	3J(HNC)	1.13	2.38	1.25	2.22	1.09
2	3J(HAC)	1.85	2.04	0.19	2.07	0.22
2	3J(CC)	0.19	2.56	2.37	2.39	2.20
2	3J(HNCB)	2.30	0.72	−1.58	0.86	−1.44
2	1J(NCA)	11.36	11.64	0.28	11.59	0.23
2	2J(NCA)	9.20	8.71	−0.49	8.71	−0.49
2	3J(HNCA)	0.67	0.84	0.17	0.82	0.15
3	3J(HNHA)	5.74	6.79	1.05	6.88	1.14
3	3J(HAC)	1.86	2.01	0.15	1.99	0.13
3	3J(HNCB)	2.24	0.99	−1.25	1.35	−0.89
3	1J(NCA)	11.26	11.56	0.30	11.45	0.19
3	2J(NCA)	8.55	8.57	0.02	8.49	−0.06
3	3J(HNCA)	0.68	0.81	0.13	0.75	0.07
4	3J(HNHA)	5.98	6.90	0.92	6.95	0.97
4	3J(HNC)	1.15	2.15	1.00	1.68	0.53
4	3J(HAC)	1.89	2.07	0.18	1.98	0.09
4	3J(HNCB)	2.14	0.96	−1.18	1.52	−0.62
4	1J(NCA)	11.25	11.52	0.27	11.25	0.00
4	2J(NCA)	8.40	8.48	0.08	8.31	−0.09
4	3J(HNCA)	0.69	0.80	0.11	0.71	0.02
5	3J(HNHA)	6.54	6.95	0.41	7.31	0.77
5	3J(HNC)	1.16	2.74	1.58	2.50	1.34
5	3J(HAC)	2.19	2.19	0.00	2.50	0.31
5	3J(HNCB)	1.96	0.24	−1.72	0.35	−1.61
5	2J (NCA)	8.27	8.40	0.13	8.01	−0.26
5	3J(HNCA)	0.73	0.86	0.13	0.77	0.04
RMS				0.93		0.85
Residue index			χ2	χ2a	χ2	χ2a
2			17.92	3.91	15.39	3.3
3			2.28	2.28	1.26	1.26
4			2.08	2.08	0.65	0.65
5			4.75	4.75	4.02	4.02
All			7.41	3.23	5.90	2.28

^aχ² computed excluding the J³(C,C) of residue index 2, which yields the largest difference.

Optimization of the protein side chain parameters

Molecular dipole moments and polarizabilities

In the original Drude-2013 protein FF, the amino acid parameters were built using parameters initially optimized targeting the model compounds that represent individual side chain functional groups and the peptide bond model compound N-methylacetamide (NMA). This led to the electrostatic parameters of the linking aliphatic carbons (e.g. Cβ and Cγ) being derived from the terminal methyl groups on the side chain model compounds. However, as the electronic response in the terminal methyl carbons (-CH₃) are different from those of the -CH₂- carbons in the proteins, this led to overestimation of the atomic polarizabilities and Thole screening factors. For example, the original Cβ derived from the methyl carbon (-CH₃) has relatively larger alpha and Thole parameters (−1.804 and 2.080 respectively), which results in higher atomic polarizability and induced dipole-dipole interactions with adjacent atoms. This is not unexpected as a higher alpha parameter will result in a larger Drude charge (q_D), yielding a larger induced atomic dipole. On the other hand, a higher Thole screening factor will result in higher values of S in equation 3, such that the Coulomb interactions will be less damped (Figure S3). This leads to larger nuclei-Drude particle distances, leading to multiple encounters with the Drude Hardwall (Figure S4). The presence of the Drude Hardwall is to avoid polarization catastrophe due to low probability displacements of the Drude that may occur during long MD simulations. However, if the Drude particles are encountering the Hardwall at a high frequency, the ensemble of the polarized states is not correct, leading to an improper electronic response and incorrect thermodynamics of the system. Therefore, to obtain a balanced electronic response it was necessary to correct the overestimation of the polarizabilities and Thole screening factors by application of MCSA fitting of electrostatic parameters for the problematic side chain aliphatic carbons targeting dipeptide dipole moments and molecular polarizabilities. Computed average difference between the Drude gas phase molecular dipole moments and the QM values as well as the average ratio of the gas phase molecular polarizabilities over the QM values are summarized in Table 3. Overall, the final electrostatic parameters obtained from the MCSA fitting of the selected Cβ, Cγ, and Cδ carbons of the dipeptides yield better agreement with the target QM molecular dipole moments and the polarizabilities, with smaller averaged dipole moment differences among all types of dipeptides (−0.04 Debye) and the averaged ratio of the MM and QM molecular polarizabilities of 0.83 being close to the target scaling of 0.85. These results indicate that the optimized model is capable of capturing polarization response more consistently over different types of dipeptides. Importantly, when these parameters were applied in MD simulations, the nuclei-Drude distances systematically stayed under the value of 0.2 Å (Figure S4), thereby correcting the inappropriate electronic response obtained with the Drude-2013 force field.

Table 3.

Average molecular dipole moment differences (MM-QM, Debye) and average molecular polarizability scaling (MM/QM) of dipeptides with different conformations, using the original Drude-2013 and optimized Drude-2019 FFs.

	Drude-2013			Drude-2019
RESI	Avg Dipole (MM-QM)	Avg Polarizablity (MM/QM)		Avg Dipole (MM-QM)	Avg Polarizablity (MM/QM)
ARG	−3.24	1.05		−0.02	0.83
ASN	−0.11	0.89		0.05	0.85
ASP	0.85	0.83		0.65	0.75
CYS	−0.30	0.78		−0.30	0.80
GLN	−0.96	1.00		−0.22	0.85
GLU	−2.70	1.00		0.51	0.75
HSD	0.61	0.86		−0.10	0.84
HSE	0.83	0.86		−0.15	0.84
HSP	0.25	0.92		0.69	0.86
ILE	−0.69	0.91		−0.57	0.85
LEU	−0.60	1.05		−0.56	0.84
LYS	−3.51	1.06		0.82	0.83
MET	−0.35	0.98		−0.24	0.81
THR	0.18	0.83		−0.09	0.84
TYR	−0.39	0.82		−0.34	0.82
TRP	−0.46	0.93		−0.33	0.84
PHE	−0.46	0.85		−0.39	0.84
SER	−0.06	0.83		−0.07	0.85
Average	−0.62±0.30	0.91±0.02		−0.04±0.10	0.83±0.01

Errors represent standard errors over the amino acids.

Side chain χ1 and χ2 dihedral parameter optimization

Re-optimization of χ1 and χ2 parameters was required due to the change in the sidechain electrostatic parameters. Proper treatment of the χ1 and χ2 conformational properties is important as they impact the conformational distribution of the polypeptide backbone.^108–110 χ1 and χ2 parameter optimization was performed by initially targeting QM potential energy surfaces for the respective side chain dipeptides. Then, these parameters together with the optimized backbone parameters were used in H-REMD simulations of (Ala)₄-X-(Ala)₄ in solution and optimized targeting the χ1 and χ2 dihedral distributions from a crystallographic survey.⁴² Presented in Table 4 are the RMSDs between the MM and QM 2D potential energy surfaces⁴² for the χ1 and χ2 torsions in the amino acid dipeptides. Table 5 shows the overlap coefficients (OC) for χ1 and χ2 distributions from the (Ala)₄-X-(Ala)₄ in the C7eq conformation with those from a crystallographic survey.⁴² Optimization of χ1 and χ2 parameters based only on the gas phase dipeptides resulted in good agreement with the target QM potential energy surfaces (Initial w/Cutoff in Table 4), with RMSDs below 2.0 except for the Glu dipeptide. However, to fit to aqueous phase conformational properties that are representative of full proteins, χ1 and χ2 parameters were further adjusted compromising the level of agreement with the target QM data (Table 4, Final/w Cutoff) leading to an increase in the RMSD from 1.43 to 1.84. Nevertheless, the final χ1 and χ2 parameters still yield improved overall agreement with the QM data as compared to Drude-2013 as well as overall better OC values, that are typically higher than 0.8 (Table 5).

Table 4.

RMSDs between the MM and QM 2D potential energy surfaces for the χ1 and χ2 torsions in amino acid (X) dipeptides capped with N-acetyl and N’-methylamide moieties using the Drude-2013 and Drude-2019 FFs. RMSD with all conformations (RMSD-ALL) and with the conformations excluding the energy cutoff (kcal/mol) regions (w/Cutoff) are shown. The RMSDs from the initial fitting results are shown in the Initial w/Cutoff column, and from the final results of Drude-2019 FF are shown in the Final w/Cutoff.

Dipeptides		Drude-2013		Drude-2019
X	Cutoff	RMSD-ALL	w/Cutoff	RMSD-ALL	w/Cutoff	Initial w/Cutoff	Final w/Cutoff
ARG	20	4.57	4.35	2.43	2.38	1.95	2.38
ASN	12	2.62	2.61	1.75	1.63	1.63	1.63
ASP	25	3.50	2.94	3.57	3.09	1.83	3.09
CYS	12	1.31	1.28	1.15	1.10	1.10	1.10
GLN	12	2.65	2.39	1.97	1.54	1.46	1.54
GLU	25	8.23	8.25	4.00	3.86	2.40	3.86
HSD	12	1.70	1.51	1.40	1.23	1.22	1.23
HSE	12	2.16	1.99	1.42	1.32	1.29	1.32
HSP	25	2.16	2.15	1.60	1.59	1.59	1.59
ILE	12	2.58	2.21	2.54	2.31	1.46	2.31
LEU	12	2.07	1.72	1.74	1.43	1.22	1.43
LYS	20	5.27	4.95	2.44	2.49	1.80	2.49
MET	12	2.43	2.30	1.89	1.49	1.39	1.49
PHE	12	1.41	1.25	1.11	1.04	1.04	1.04
SER	12	1.38	1.36	2.32	2.32	1.04	2.32
THR	12	1.86	1.72	2.14	2.18	1.28	2.46
TRP	12	1.78	1.63	1.50	1.29	1.13	1.29
TYR	12	1.55	1.31	1.33	1.06	1.06	1.06
VAL	12	1.24	1.18	1.38	1.32	1.20	1.32
Average		2.66±0.40	2.48±0.40	1.98±0.19	1.82±0.17	1.43±0.08	1.84±0.18

Errors represent standard errors over the amino acids.

Table 5.

Overlap coefficient (OC) between χ1/χ2 probability distributions of the (Ala)₄-X-(Ala)₄ condensed phase simulations and crystallographic survey, using the Drude-2013 and Drude-2019 FF. The differences of OC between the two models are shown in the Diff. OC column where the larger differences indicate improved agreement with the Drude-2019 FF.

X	Drude-201321		Drude-2019		Diff. OC
	χ1	χ2	χ1	χ2	χ1	χ2
ARG	0.82	0.85	0.96	0.97	0.14	0.12
ASN	0.82	0.61	0.84	0.91	0.02	0.30
ASP	0.65	0.79	0.82	0.93	0.17	0.14
CYS	0.87		0.87		0.00
GLN	0.92	0.60	0.95	0.88	0.03	0.28
GLU	0.68	0.81	0.85	0.80	0.17	−0.01
HSD	0.94	0.80	0.94	0.95	0.00	0.15
ILE	0.78	0.89	0.90	0.90	0.12	0.01
LEU	0.88	0.92	0.96	0.92	0.08	0.00
LYS	0.81	0.93	0.89	0.90	0.08	−0.03
MET	0.92	0.88	0.91	0.96	−0.01	0.08
PHE	0.94	0.89	0.82	0.93	−0.12	0.04
SER	0.74		0.86		0.12
THR	0.74		0.88		0.14
TRP	0.86	0.74	0.86	0.80	0.00	0.06
TYR	0.72	0.74	0.91	0.83	0.19	0.09
VAL	0.87		0.82		−0.05	0.00
Average	0.82±0.02	0.80±0.03	0.88±0.01	0.90±0.02	0.06±0.02	0.09±0.03

Errors represent standard errors over the relevant amino acids.

Optimization of interaction energies between charged protein model compounds

Salt bridges represent one of the strongest non-covalent interactions in proteins, requiring that careful attention be placed on their modeling. The optimization included introducing atom pair-specific LJ parameters (NBFIX) to target the QM interaction energies between selected model compounds with different interaction geometries (Figures 1, 2 and 3). The interaction energies with Drude-2013 FF displayed poor agreement with the QM target data (Figures 1, 2 and 3 in red), whereas the optimized Drude-2019 FF yielded significant improvement in the balance of these interaction energies (Figures 1, 2 and 3 in blue). Note that as the atom types in GUAN and MGUAN are shared together, their NBFIX parameters for the interactions with ACET must be compromised. Accordingly, emphasis was placed on obtaining better agreement with the MGUAN-ACET QM interactions Figure 2a as MGUAN is more representative of the side chain of Arg. The optimized NBFIX parameters for GUAN and ACET were also validated in osmotic pressure simulations, where their agreement with the experimental values were deemed acceptable (Table 6).

Figure 1.

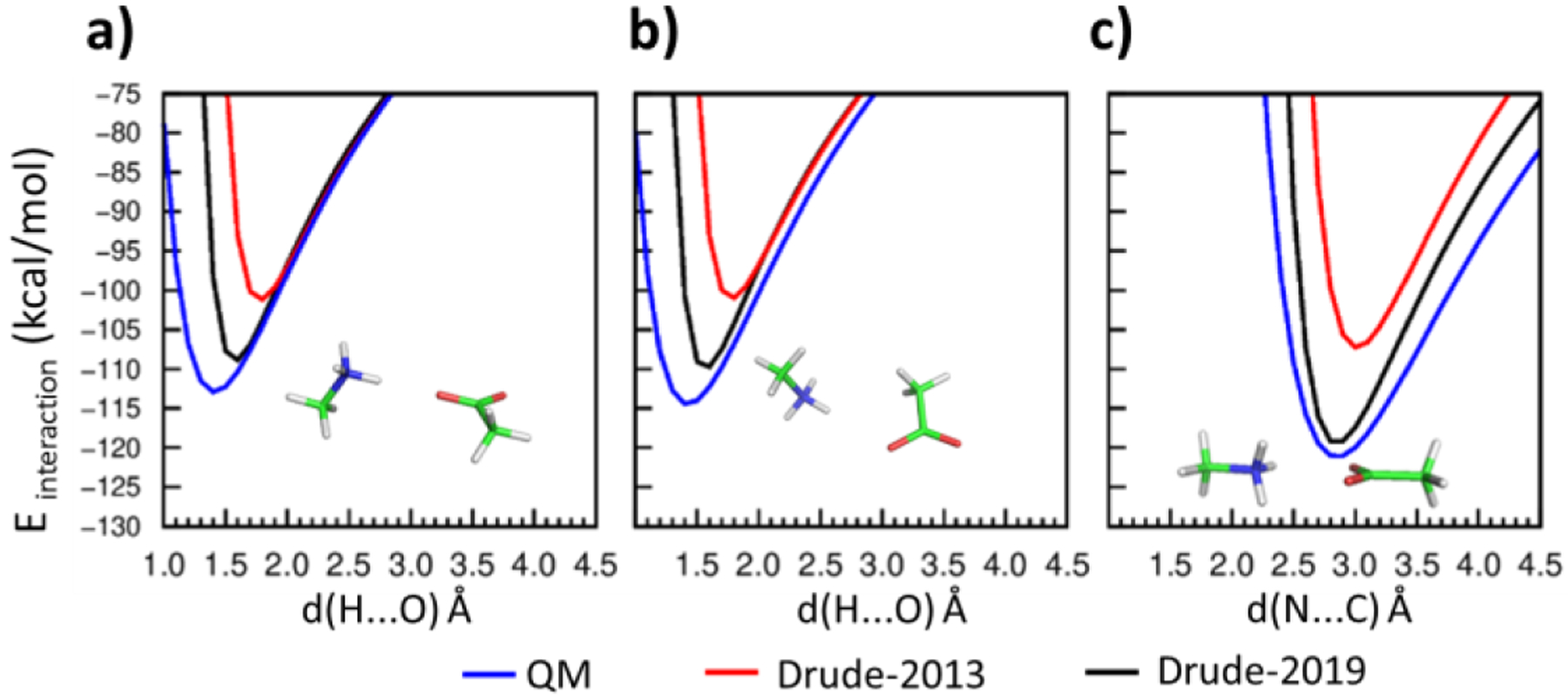
Interaction energies between methylammonium (MAMM) and acetate (ACET) in a) to c) using the QM (blue), Drude-2013 (red) and optimized Drude-2019 (black) model chemistries. Hydrogens (H) are white, carbons (C) are green, nitrogens (N) are blue, and oxygens (O) are red. Distances, d(x…y) Å, are measured between the interacting atom x and y, where x are H or N, and y are O or C.

Figure 2.

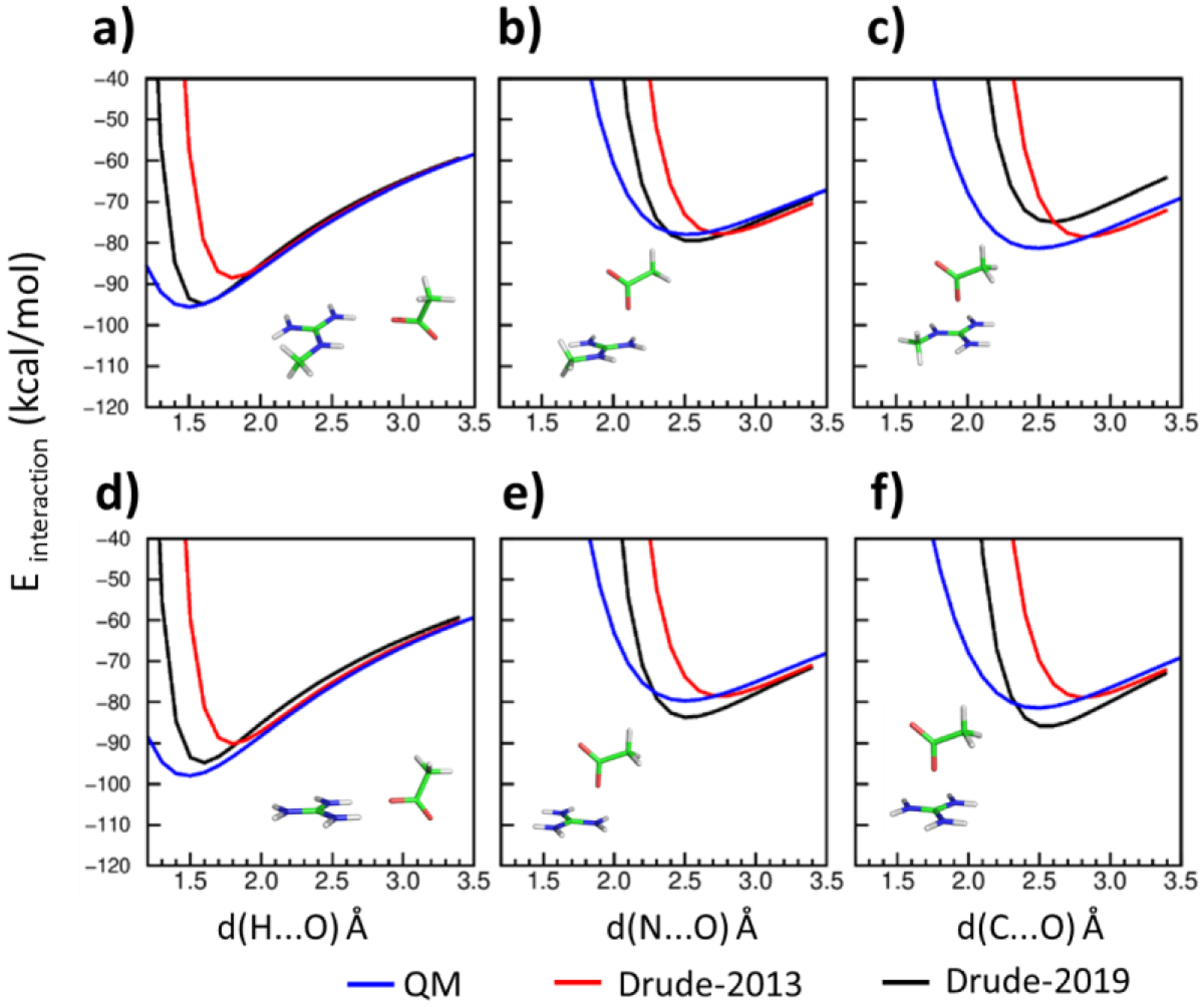
Interaction energies between methylguanidinium (MGUAN) and acetate (ACET) in a) to c) and between guanidinium (GUAN) and acetate (ACET) in d) to f) using the QM (blue), Drude-2013 (red) and optimized Drude-2019 (black) model chemistries. Hydrogens (H) are white, carbons (C) are green, nitrogens (N) are blue, and oxygens (O) are red. Distances, d(x…y) Å, are measured between the interacting atom x and y, where x are H, N or C, and y is O.

Figure 3.

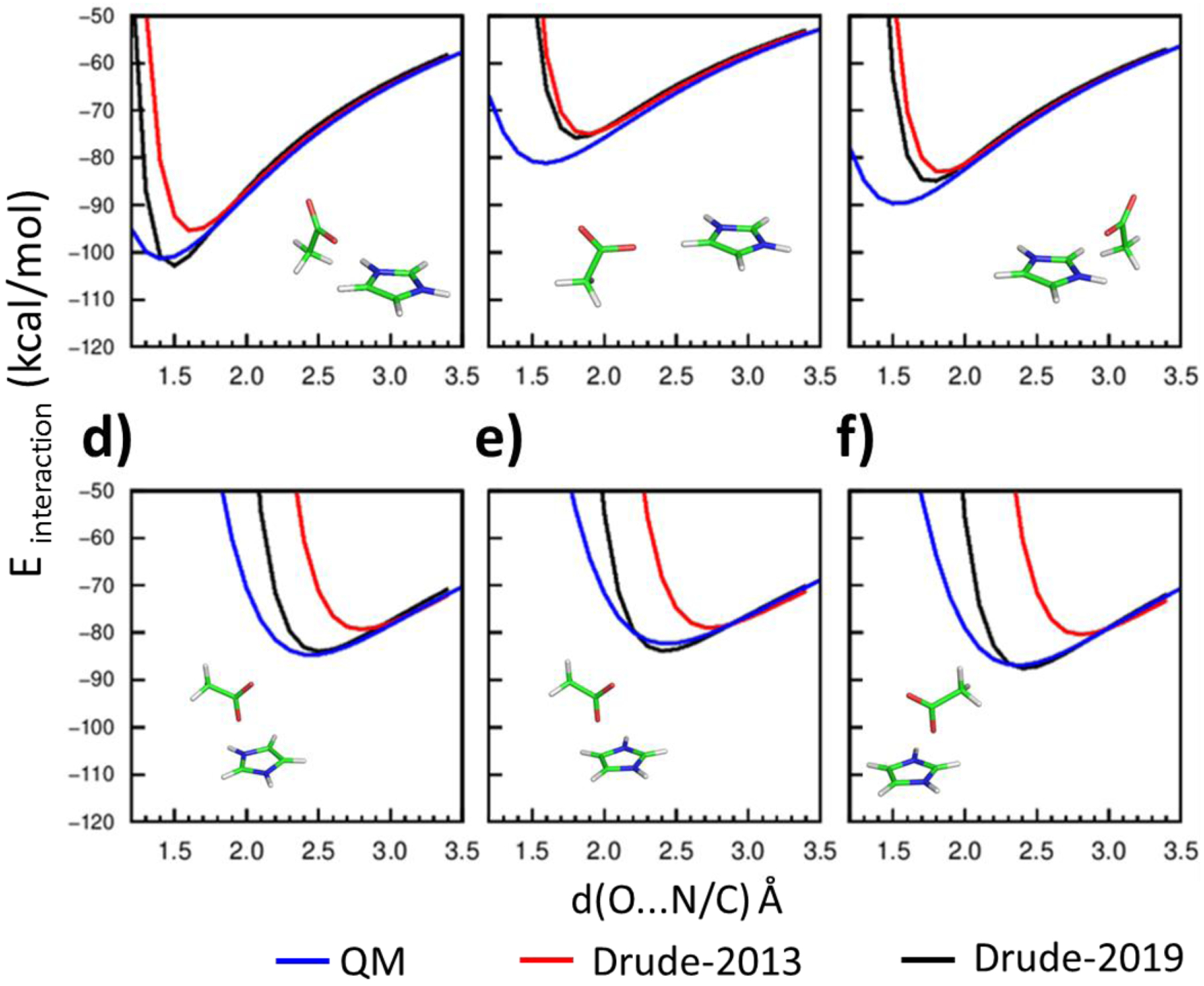
Interaction energies between imidazolium (IMIM) and acetate (ACET) with different interaction geometries of a) to f) using the QM (blue), Drude-2013 (red) and optimized Drude-2019 (black) model chemistries. Hydrogens are white, carbons (C) are green, nitrogens (N) are blue, and oxygens (O) are red. Distances, d(x…y) Å, are measured between the interacting atom x and y, where x is O and y is N or C.

Table 6.

Osmotic pressure (in Bar) for guanidinium-acetate solution at different concentrations.

Con. (M)	Exp.	Drude-2019
0.3	13.35 ± 0.12	14.06 ± 0.54
0.4	17.66 ± 0.09	18.02 ± 1.84
0.5	22.33 ± 0.08	21.66 ± 1.88

Errors represent standard errors over 5 10 ns blocks from the 50 ns production simulations.

Validation of the optimized Drude-2019 force field in peptide and protein simulations

Simulations were performed on the peptides and proteins listed in Table 1 to validate the optimized Drude-2019 FF. A majority of the peptides/proteins were small, being less than 150 amino acids (aa), as they are more computationally expedient to test the ability of the force field to maintain their folded structures as compared to larger protein systems. Additional validation calculations were performed on two membrane-bound ion channels as described below. All systems in Table 1 were run with the additive CHARMM36m (C36m) and polarizable Drude-2013 FFs along with the newly optimized Drude-2019 model. RMSD analysis was performed on all the peptides and proteins based on the backbone Cα atoms (Table 7) and on the backbone and side chain non-hydrogen atoms in Table S2–S3. The Drude-2019 FF yields overall improvements with respect to both additive C36m and Drude-2013. For the small systems with less than 50 residues the backbone RMSDs with the optimized Drude-2019 FF are consistently smaller than Drude-2013 and smaller or similar to those from the additive CHARMM36m FF. Notable are 1U0I, 1EJG, and 2EVQ which largely unfold in the C36m FF (Figure S18) but are stable with the Drude-2019 on the microsecond time scale. Similar results occur with the larger validation proteins. Systems 1QX5, 1MJC and 2IGD all show large RMSD with the additive C36m FF with the RMSD being significantly smaller with 1MJC and 2IGD with Drude-2019. 1QX5, apocalmodulin, normally binds Ca²⁺ ions and has a totally charge of −24; a small improvement is seen in both Drude models, though the RMSD values are still large, which is associated with domain motions in the protein, with those individual domains maintaining their overall structures with the polarizable FFs (Figure S19). Several other proteins including 4IEJ, 2QMT, 1IFC, 6LYT, 135L and 1P7E have smaller RMSDs with C36m as compared to Drude-2019. Thus, Drude-2019 overall maintains the folded state of both small and larger proteins as compared to C36m with the additive model showing smaller RMSD with some proteins that are stable with both the additive and polarizable FFs. While not analyzed in detail, the RMS fluctuations for the additive and Drude-2019 FFs were similar for those proteins that maintained their folded states throughout the MD simulations.

Table 7.

Average RMS differences and RMS fluctuations of the RMSD with respect to the crystal or NMR structures of the Cα atoms (values in Å)

PDB	C36m		Drude-2013		Drude-2019
	AVG	RMSF	AVG	RMSF	AVG	RMSF
Number of amino acids < 50 aa
1L2Y	1.67	0.45	5.08	1.10	1.42	0.57
1U0I	6.65	2.19	5.82	1.68	2.02	0.52
1EJG	4.15	0.15	1.54	0.33	1.28	0.13
2RVD	1.07	0.10	4.16	1.07	1.14	0.09
1K43	2.18	0.54	1.64	0.71	2.16	0.17
1LE3	0.89	0.36	5.34	1.37	1.73	0.50
2EVQ	4.37	3.31	4.50	1.80	0.96	0.32
1J4M	2.01	0.44	1.37	0.39	2.05	0.18
GB1 hairpin	2.51	0.45	7.89	2.50	7.29	2.37
AVE	2.83	0.89	4.15	1.22	2.23	0.54
SE	0.62	0.37	0.75	0.24	0.65	0.24
Number of amino acids > 50 aa
1QX5	8.50	2.35	7.91	0.61	7.22	0.58
4IEJ	1.09	0.17	3.72	0.90	2.59	0.34
1MJC	7.84	10.13	2.58	0.72	1.93	0.46
1UBQ	2.31	0.50	3.22	0.58	2.45	0.38
2QMT	0.94	0.28	2.29	0.84	1.48	0.27
1IFC	1.49	0.28	3.03	0.25	2.47	0.55
6LYT	1.36	0.27	3.74	0.98	2.08	0.44
135L	1.74	0.34	2.99	0.27	2.91	0.53
1P7E	0.73	0.20	2.26	0.42	2.00	0.20
2IGD	10.11	8.01	5.78	2.01	1.42	0.23
AVE.	3.61	2.25	3.75	0.76	2.65	0.40
SE	1.16	1.17	0.56	0.16	0.53	0.04

Averages (AVE) and standard errors (SE) are over the studied proteins.

The proteins crambin (PDB: 1EJG), ubiquitin (PDB: 1UBQ), and lysozyme (PDB: 6LYT) have also been studied using the AMOEBA protein FF.²² The reported backbone RMSDs were approximately 1, 2, and 2 Å for the three proteins, respectively, within 30 ns simulations. As seen in Table 7 and Table S2 the Drude-2019 FF yields Cα RMSDs of 1.28, 2.45, and 2.08 Å and backbone RMSDs of 1.37, 2.40, 2.05 averaged over 1 μs simulations. Thus, the new Drude-2019 yields similar RMS difference as compared to AMEOBA in simulations of significantly longer duration with Drude-2019.

Notably, the optimized Drude-2019 model in general reduces the flexibility and yields more stable β sheet structures as compared to Drude-2013. This is evidenced in simulations of the GB3 domain (PDB: 2IGD) and the stable hairpin HP7 peptide (PDB: 2EVQ) (Figure 4). In these simulations, the Drude-2013 does not yield stable structures for either protein. Simulations using a variant of Drude-2013 that only included the optimized backbone parameters, Drude-2013-opt-backbone, yielded structures closer to the experimental structures, though significant differences are evident. With the GB3 protein the hydrogen bonds within the β-hairpin structure are still disrupted (Figure S5b) leading to the larger RMS differences. These results indicate that while the updated backbone parameters facilitated the stabilization of the hydrogen bond within the β-hairpin structures, additional optimization was required. Accordingly, the optimization of the selected side chain parameters in the Drude-2019 FF leads to the simulated GB3 protein becoming more stable (Figure 4a, blue) due to the β-hairpin hydrogen bonds being maintained (Figure S5d). Similar behavior is also found in the HP7 peptide system where the optimized Drude-2019 FF significantly stabilized the β-sheet structure throughout the 1 μs simulation (Figure 4b, blue). Note that a stable simulated β-sheet structure is expected as the melting temperature of the HP7 peptide is 66°C,⁷⁸ and thus the folded state should dominate at 300 K. It should be noted that more stable β-sheet structures were obtained simply after re-optimizing the electrostatic parameters of the selected side chain aliphatic carbons (e.g. Cβ, Cγ, or Cδ, not shown). Therefore, better treatment of their atomic polarizabilities and Thole screening factors leading to lower induced dipole moments serves as an important step toward reaching the optimized Drude-2019 FF.

Further investigation into the structural properties of the optimized model involved analysis of the ϕ, ψ distributions in the larger proteins having more than 50 amino acids. Presented in Figure 5 are the ϕ, ψ inverted Boltzmann weighted distributions over the large (a.a. > 50) protein simulations reported in Table 1. Both the Drude-2013 and optimized Drude-2019 models populate regions consistent with those obtained in protein crystal structures (shown as black dots), with the location of the minima in all the models consistent with the reported survey data.²¹ Notably, the optimized Drude-2019 model exhibits a more defined β region (Figure S6, −180° < φ < −90° and 50° < ψ < 180° plus −180° < φ <−90° and −180° <ψ < −120 or 160°<φ< 180° and 110° < ψ < 180° ), while the original Drude-2013 model samples a slightly overall wider range of ϕ, ψ space.

Figure 5.

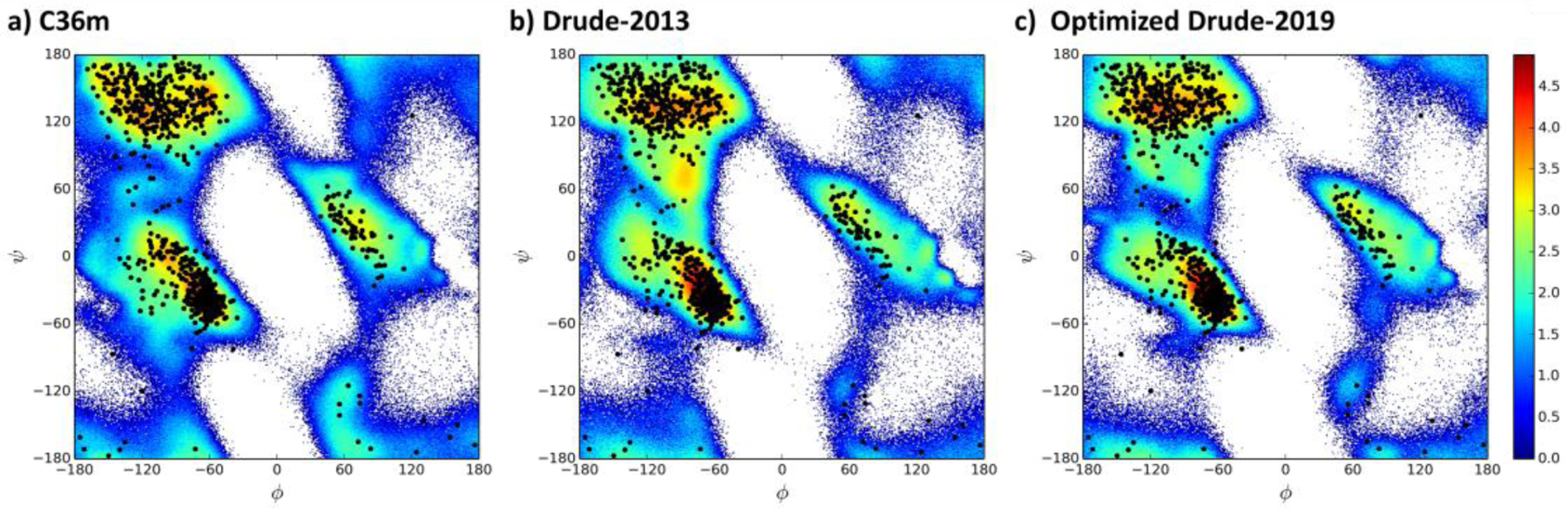
Overall ϕ, ψ distributions for the a) C36m, b) Drude-2013 and c) optimized Drude-2019 models. Results are included from PDB: 1QX5, 4IEJ, 1MJC, 1UBQ, 2QMT, 1IFC, 6LYT, 135L, 1P7E, and 2IGD. Simulation results are presented as inverted Boltzmann distributions which are free energies (FE, kcal/mol) obtained from Boltzmann weighting, FE = kTln(P), of the population, P, in 1˚x 1˚ bins summed over all the proteins where k and T are the Boltzmann constant and temperature, 298˚, respectively. Experimental data from the crystal structures are presented as black dots.

With respect to C36m, the Drude models both sample a wider region around the basin defining the extended, β-type secondary structures. This includes the region around ψ = 60–100˚ between the α-helical and extended regions (φ ~ −90˚); this region is sampled less in Drude-2019. Another region is at a lower φ values from −120 to −150˚. Importantly, these regions are sampled in the crystal structures, though it is not possible to robustly compare the amount of sampling in the simulations with the available experimental data.

NMR Analysis

NMR observables contain valuable information about the conformational properties of proteins in solution. To evaluate the behavior of the optimized Drude-2019 model in solution conditions, NMR properties from MD simulations were computed for the proteins ubiquitin (PDB: 1UBQ), protein GB1 (PDB: 2QMT), cold shock protein A (PDB: 1MJC), apocalmodulin (PDB: 1QX5), intestinal fatty acid binding protein (PDB: 1IFC), and hen lysozyme (PDB: 6LYT). These systems were selected as they served as model systems in evaluating the C36 force field.¹¹¹ The NMR properties computed in this study include the hydrogen bond scalar coupling, ^h3J_NC, which represents the coupling between N and C nuclei across N-H···O=C hydrogen bonds through space.^112–114 As their magnitudes are correlated with hydrogen bond geometries¹¹⁵ and are sensitive to hydrogen bonding network dynamics and cooperativity in proteins,^42–44 they are informative to assess the force field quality in reproducing the hydrogen bonds across backbones. A summary of the ^h3J_NC couplings is shown in Table 8. Comparison of individual calculated and experimental ^h3J_NC values are shown in Figure S7. With the optimized Drude-2019 FF, most of the correlations, average differences and RMS differences between the calculated and experimental ^h3J_NC couplings are improved as compared to the Drude-2013 FF. When compared to the C36m model, the Drude-2019 FF shows poorer agreement with respect to the correlation with the experimental data, though the average and RMS differences are similar. These results suggest that specific structural features being monitored in Drude-2019, such as those associated with specific residue types, may be problematic, with additional studies required to investigate this in more detail.

Table 8.

Correlations, Average differences and RMS differences between calculated and experimental NMR ^h3J_NC couplings with the C36m additive, original Drude-2013 and optimized Drude-2019 FF.

PDB	Correlation Coefficients			Average Differences			RMS differences
	C36m	Drude-2013	Drude-2019	C36m	Drude-2013	Drude-2019	C36m	Drude-2013	Drude-2019
1UBQ	0.84	0.39	0.65	0.01	0.10	−0.01	0.10	0.22	0.14
2QMT	0.79	0.41	0.54	−0.02	0.11	0.00	0.11	0.20	0.17
1MJC	0.67	0.51	0.66	0.21	0.14	0.07	0.24	0.22	0.16
1QX5	0.14	0.30	0.25	0.11	0.21	0.07	0.24	0.29	0.19
1IFC	0.69	0.33	0.48	0.00	0.14	0.05	0.16	0.29	0.22
AVE	0.63	0.39	0.52	0.06	0.14	0.04	0.17	0.24	0.18
SE	0.13	0.04	0.06	0.04	0.02	0.02	0.03	0.02	0.02

Averages (AVE) and standard errors (SE) are over the studied proteins.

Additional NMR analysis includes the calculation of peptide backbone N-H order parameters, S². The S² value represents the internal re-orientational motions, with the magnitude ranging from 0 to 1. Typically, the lower S² value corresponds to larger internal motions, while the higher S² value corresponds to a more rigid structure.¹¹⁶ Therefore, the calculated S² from MD simulations provides a way to measure the rigidity of each protein residue. Analysis involved comparisons of the average order parameters for each protein (Table 9) and the correlations and differences as a function of the residues in each of the proteins (Table 10). In Table 9, the calculated S² for all protein systems with Drude-2019 FF are improved versus both the additive C36m and Drude-2013 FF results, which underestimate the S² values. With C36m poor agreement is observed with 1MJC and 1QX5 associated with the instability of these proteins based on the RMSD analysis (Table 7). Concerning the simulated and experimental S² values for each residue in the proteins (Table 10), the correlations are similar for C36m and Drude-2019, with the polarizable model giving improved average and RMS differences, again due to the problematic 1MJC and 1QX5 proteins. The performance of Drude-2019 is clearly improved over Drude-2013 across the board.

Table 9.

Average backbone N-H relaxation order parameter S² in six proteins. Experimental values and calculated S² from MD simulations with the C36m, Drude-2013 and Drude-2019 FFs are listed.

PDB	Exp	C36m	Drude-2013	Drude-2019
1UBQ	0.83	0.81	0.77	0.81
2QMT	0.73	0.81	0.54	0.75
1MJC	0.82	0.35	0.60	0.68
1QX5	0.81	0.45	0.56	0.76
1IFC	0.86	0.82	0.73	0.79
6LYT	0.85	0.79	0.52	0.75
AVE	0.82	0.67	0.62	0.76
SE	0.02	0.09	0.04	0.02

Averages (AVE) and standard errors (SE) are over the studied proteins.

Table 10.

Combined RMS Differences and correlations between calculated and experimental NMR backbone N-H relaxation order parameter S² with the C36m additive, original Drude-2013 and optimized Drude-2019 FF.

PDB	Correlation Coefficients			Average Differences			RMS differences
	C36m	Drude-2013	Drude-2019	C36m	Drude-2013	Drude-2019	C36m	Drude-2013	Drude-2019
1UBQ	0.78	0.54	0.64	−0.02	−0.06	−0.02	0.10	0.13	0.09
2QMT	0.59	0.35	0.39	0.08	−0.19	0.02	0.15	0.25	0.14
1MJC	0.76	0.71	0.78	−0.47	−0.22	−0.14	0.48	0.30	0.23
1QX5	0.12	−0.03	0.43	−0.36	−0.25	−0.05	0.42	0.32	0.11
1IFC	0.11	0.01	0.01	−0.04	−0.13	−0.07	0.13	0.22	0.17
6LYT	0.65	0.45	0.42	−0.06	−0.33	−0.10	0.13	0.40	0.19
AVE	0.50	0.34	0.45	−0.15	−0.20	−0.06	0.24	0.27	0.16
SE	0.13	0.12	0.11	0.09	0.04	0.02	0.07	0.04	0.02

Averages (AVE) and standard errors (SE) are over the studied proteins.

Further analysis includes the calculation of S² order parameters_, RMS fluctuation, and secondary structures as a function of each residue (Figure S8–S13). It is possible that the lower S² values in all three FF models as compared to experiment (Table 9) is due to the residues not in helix or sheet secondary structures, as seen in the secondary structure analysis and a corresponding larger RMSF of those residues (Figure S8–S13). Notably, while in the regions of secondary structure the RMSF of Drude-2013 and Drude-2019 are similar, the Drude-2013 shows significantly large RMSF and lower S² values in the random coil regions. This suggest that the instability caused by the overestimated dipole-dipole interactions from the Drude-2013 FF could be from the more flexible residues in random coil regions (or loops). Thus. for the small peptide systems where the loop regions dominate, the impact of the instability was more obvious as reflected in the RMSD analyses (Table 7).

Validation of the optimized Drude-2019 in membrane protein simulations

Membrane proteins ion channels pose special challenges for any force field. The narrow permeation pore represents a singular environment where strong interactions between ions, water molecules and proteins play a critical role. Induced polarization associated with the permeant ions in these systems has long been thought to be important^117–118. To ascertain the accuracy of the Drude-2019 FF in the treatment of membrane-bound proteins as well as ion channels simulations were performed on bacterial potassium KcsA channel and the gramicidin A channel. The KcsA channel (~400 aa) is comprised of four identical subunits with two transmembrane α-helices (TM1 and TM2) separated by a long pore (p) loop forming a narrow pore allowing the selective permeation of K⁺ in single file. The gramicidin channel (34 aa) is formed by head-to-head dimerization of single-stranded, right-handed beta β^6.3 helices. The wealth of experimental and computational information about these proteins make them excellent prototypical model systems for investigating the relationship between structure and function of ion channels. Two high-resolution structures for the KcsA channel representing conductive (PDB: 1K4C)¹¹⁹ and inactive (PDB: 1K4D)¹¹⁹ states, were simulated. All systems were simulated with the additive C36m and the optimized Drude-2019 model for 250 ns. In addition, the 1K4C system was simulated for 100 ns using the Drude-2013 FF. RMSD analysis was performed on all the proteins based on the non-hydrogen backbone atoms for the entire proteins and, for 1K4C and 1K4D, residues defining the selectivity filters, the narrowest part of the KcsA channel formed by the highly conserved amino-acid sequence TTVGYGD.

For the KcsA channel, the conformational behavior for the whole protein with the optimized Drude-2019 FF are consistently similar with the additive C36m FF for both 1K4C and 1K4D structures. As shown in Figure 6A and 6C, the Drude-2019 FF yields backbone RMSDs of 1.67 Å (1K4C) and 1.62 Å (1K4D) averaged over the 250 ns, whereas the average backbone RMSDs using C36m FF is 1.72 Å (1K4C) and 1.64 Å (1K4D). In terms of the whole protein, Drude-2019 yields similar, even slightly smaller RMS difference as compared to C36m. From a functional point of view, the selectivity filter is critical for the selective conduction of K⁺ ions. Furthermore, this region of the KcsA channel corresponds to an atypical backbone secondary structure. Several consecutive backbone carbonyls are pointing toward the central pore axis in the conductive conformation (Figure 6B) whereas the pore is tightly constricted at its center in the non-conductive inactivated conformation (Figure 6D). The stability of these selectivity filter conformations, maintained by a combination of hydrogen bonding and packing interactions, can be very sensitive to the accuracy of the force field in MD simulations. During the 250 ns simulations using Drude-2019 FF without any restraint, the selectivity filter maintains a conformation very similar to that in the crystal structures (Figure 6B and 6D). In addition, the K⁺ ions occupancy also maintains canonical configurations in both conductive and inactive states (Figure 6B and 6D). While only simulated for 100 ns with the 1K4C structure, the Drude-2013 FF shows larger RMSD value for the filter as compared to both C36m and Drude-2019, indicating the improvements in the polarizable model associated with the additional optimization.

Figure 6.

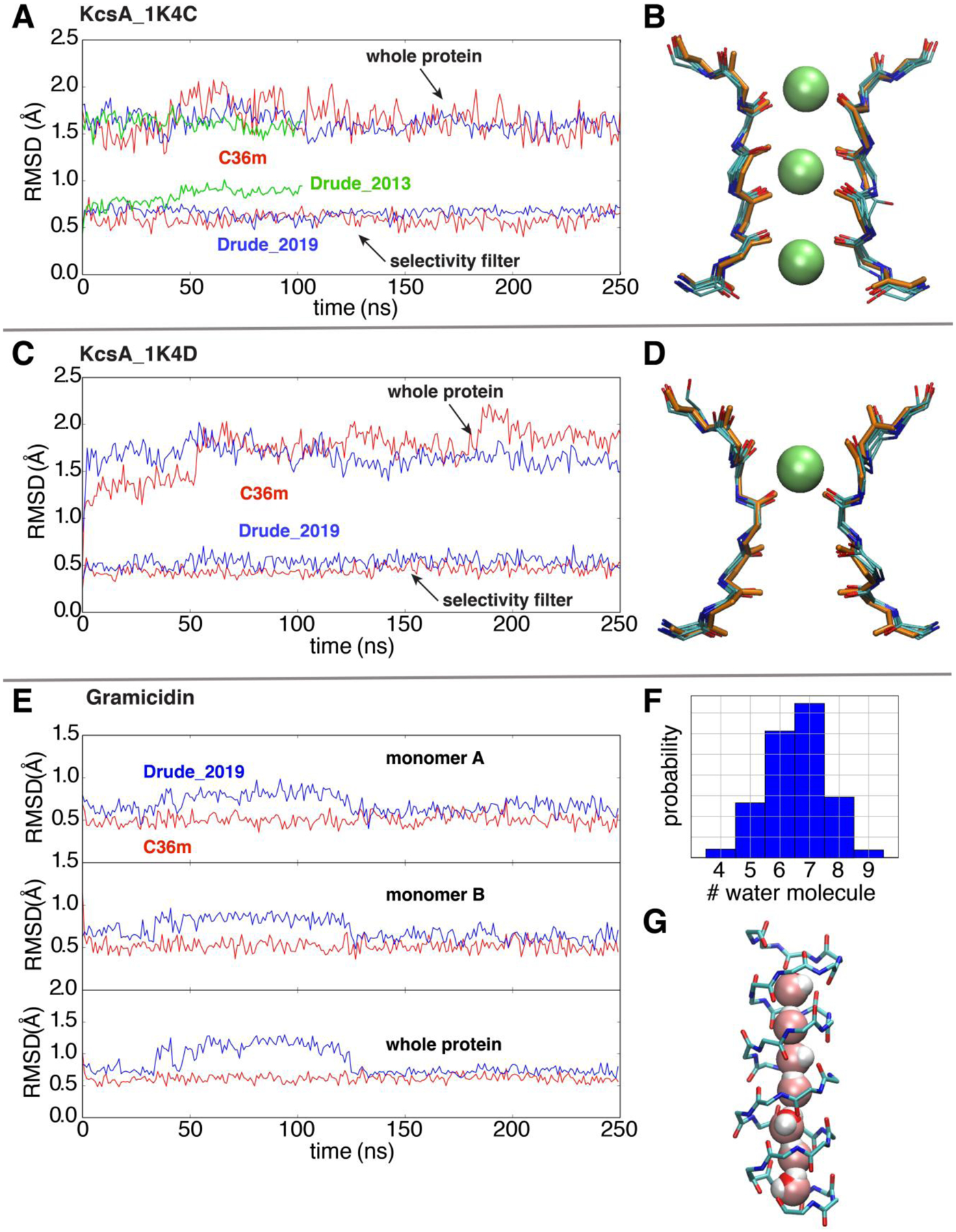
Simulations of ion channels to validate the optimized Drude 2019 FF. (A) and (C) RMSD analyses based on the backbone non-hydrogen atoms of the whole KcsA channel and the selectivity filter in simulations, respectively, using the additive C36m (red), Drude-2019 (blue) and Drude-2013 (green) FFs. The references for backbone RMSD measurements are the initial crystal structures 1K4C (conductive) and 1K4D (constricted). (B) and (D) The overlay of 5 snapshots (one frame for every 50ns in the 250ns trajectory) and the crystal structures (orange) of the selectivity filter. (E) Time series of the backbone RMSD of two monomers (top and middle) and the whole protein (bottom) of gramicidin (reference PDB: 1JNO¹²⁰). (F) The histogram of the number of water molecules in gramicidin during the whole trajectory. (G) A representative snapshot with a single-file water wire in the gramicidin A channel.

The gramicidin A channel exhibits a similar structural stability in the simulations using the Drude-2019 FF and C36m FF. Although the Drude-2019 simulation displays slightly higher RMSD than the C36m simulation in the first 130 ns, it drops to approximate 0.5 Å as in the C36m simulation in the last 120 ns (Figure 6E). Occupancy of water molecules in single-file along the narrow pore is a sensitive feature for the gramicidin channel revealed by a previous computational study¹²¹. This single-file water is also reproduced by the Drude-2019 simulation, with a complete hydrogen-bonded water chain shown as the predominant configuration in the pore region of the gramicidin channel (Figure 6F and 6G). Reproducing detailed conformational properties of the KcsA and gramicidin A channels and providing accurate water interaction energies in the simulations, the polarizable Drude-2019 FF promises to enable a more accurate description of the key functional processes for these important membrane proteins and how electronic polarizability contributes to those processes.

Analysis of variations in peptide bond dipole moments

The central motivating factor for the development of a force field that explicitly treats electronic polarizability is the presence of variations of the electronic structure as a function of environment. To illustrate this the dipole moment characteristics of peptide bonds associated with different types of secondary structure were investigated by performing MD simulations using the Drude-2019 FF for MBH12 (PDB ID: 1K43, type: β-sheet), HP7 (PDB ID: 2EVQ, type: β-sheet), and Trp-cage (PDB ID:1L2Y, type: α-Helix) at 370 K, 370 K, and 400K, respectively. This allowed for the peptides to initially sample their folded structures and then unfold to varying degrees, thereby sampling different types of secondary structure based on DSSP analysis in the same peptides.

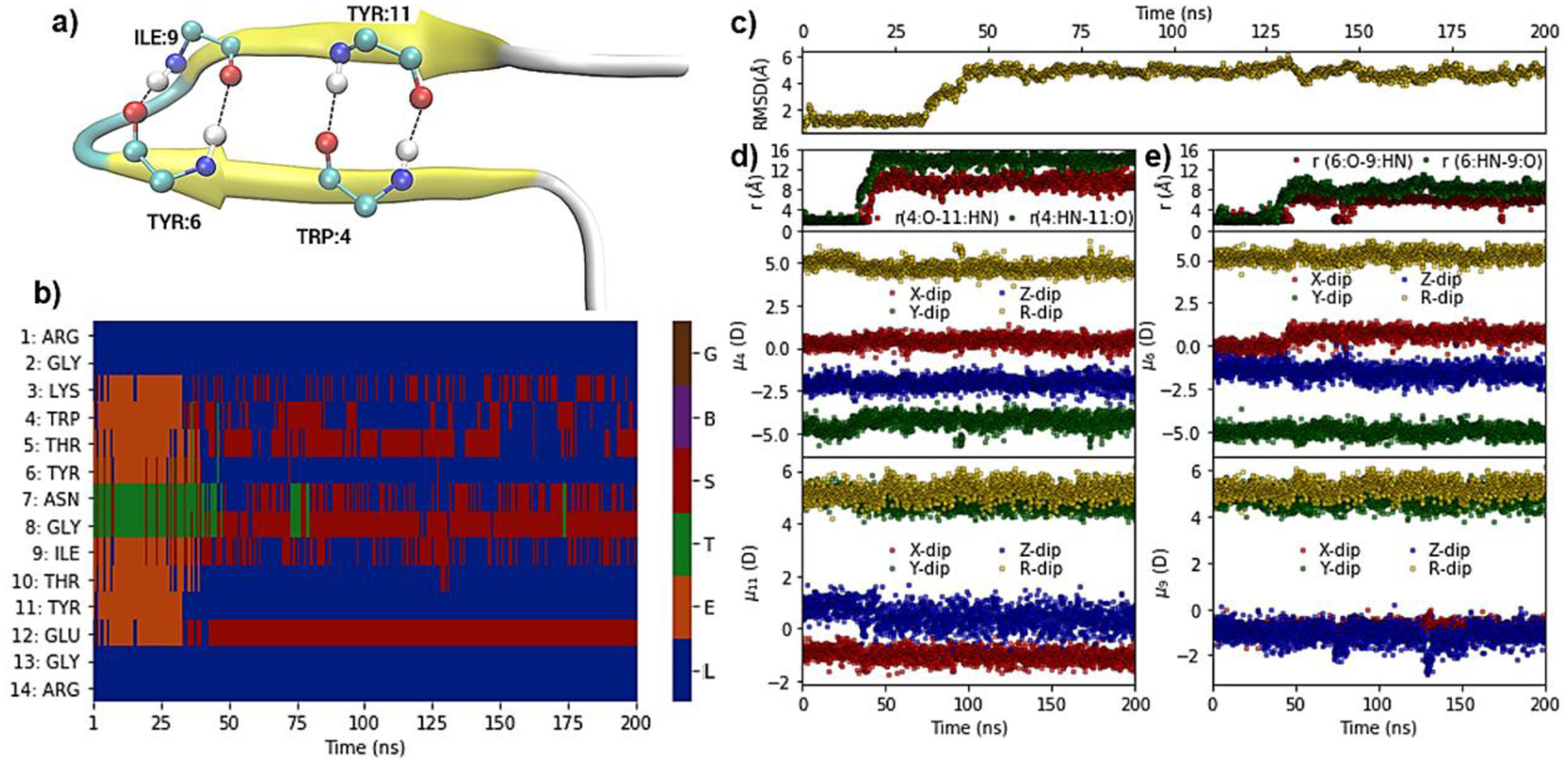
The MBH12 protein unfolded quickly at 370 K at around 30 ns as seen by RMSD values (Figure 7). The DSSP analysis highlighted the unfolding of the beta-sheet structure, which was accompanied by the loss of the H-bond interactions between the peptide bond carbonyl oxygens and nitrogen hydrogens of the THR4-TYR11 and TYR6-ILE9 residue pairs. Loss of the secondary structure is accompanied by higher fluctuation in dipole moment components and total values as may be seen in the distributions shown in Figure S17. The probability distributions of the peptide bond dipole moment components and total values for the residues in β-sheet region of the folded state (THR4-TYR11 and TYR6-ILE9) depends on the occupied secondary structure (Figure 8). When they are in the β-sheet conformation, indicated by DSSP state E, there tends to be an increase in the total dipole. However, the variations in the individual dipole components are less consistent. For example, in residue 4 there is a shift to more negative values in the x and y component while there is an shift towards more positive values in residue 11. This indicates the sensitivity of the local electronic structure to the environment in the context of both secondary structure and sequence. For HP7 the peptide unfolds after 270 ns simulations as evidenced by the RMSD analysis (Figure S14). DSSP analysis showed this to correspond to the unfolding of the β-sheet structure and the loss of the H-bond interactions between the backbones of residue pairs THR2 - THR11 and ASN4 - LYS9. This is associated with a general increase in the fluctuations of the dipole moment indicating that the peptide bond dipole moments are impacted by the type of secondary structure (Figure S14d–e). This is shown in more details in Figure S15 where the probability distribution of the peptide bond dipole components and total values for the different types of secondary structure are shown for the β-sheet sheet residues; variations in the distributions for the particular secondary structure are evident in the dipole components as well as the total dipole moments. The third system studied, the Trp-cage protein, includes a two turn α-helix. At 400 K the peptide unfolded rapidly by ~30 ns, coinciding with the loss of (i, i+4) hydrogen bond interactions between ILE4-LYS8 and GLN5-ASP9 (Figure S16). This behavior was similar to the cooperative unfolding of an amyloid helix previously reported by our lab¹²². Interestingly, partial refolding of the helix occurs at ~200ns and then again at ~450 ns with the helical content being largely maintained out to 700 ns. Analysis of the dipole components again show variations as a function of secondary structure and of sequence. In general the probability distributions of the dipole moment components showed wider distribution for the random-coil state and there tended to be a decrease in both the components and total dipole moments in the helical versus the turn or random-coil structures, with the difference typically larger with respect to the random-coil conformations (Figure S17). However, variations in behavior are again evident, with the x component of residue 5 shifted to slightly larger values in the helical state relative to random coil in contrast to the majority of the remaining residues. These results further indicate the sensitivity of the peptide bond dipole moments to both type of secondary structure and amino acid sequence, phenomena that are not accessible to additive force fields.

Figure 7.

Hydrogen-bond, structural, dipole and DSSP based secondary structure analysis of a simulation of the MBH 12 protein (PDB ID: 1K43) at 370 K. (a) Pictorial representation of crystal structure of MBH 12, with hydrogen-bond interactions between peptide bond carbonyl oxygen (O) and nitrogen hydrogen (HN) of residues TRP:4, TYR:6, ILE:9, and TYR:11. (b) Heatmap showing DSSP-defined secondary structures versus time. (c) RMSD with respect to the NMR structure for Cα atoms versus time. (d) Upper panel: Distance between TRP4:O-TYR11:HN (red) and TRP4:HN-TYR11:O atoms versus time; middle and lower panels: Dipole moment components (μ_x, μ_y, μ_z) and total dipole moment (μ_R) of peptide backbone (C,O,N,HN,Ca,Ha) for TRP4 and TYR11, respectively, versus time. (e) Upper panel: Distance of TYR6:O-ILE9:HN (red) and TYR6:HN-ILE9:O versus time; middle and lower panels: Dipole moment components (μ_x, μ_y, μ_z) and total dipole moment (μ_R) of peptide backbone for TRP4 and ILE9, respectively, versus time. The DSSP assignment codes are H: Alpha helix, B: Residue in isolated beta-bridge, E: Extended strand, participates in beta ladder, G: 3/10 helix, I: pi helix), T: hydrogen bonded turn and S: bend, while L indicates loops or irregular/random coil elements.

Figure 8.

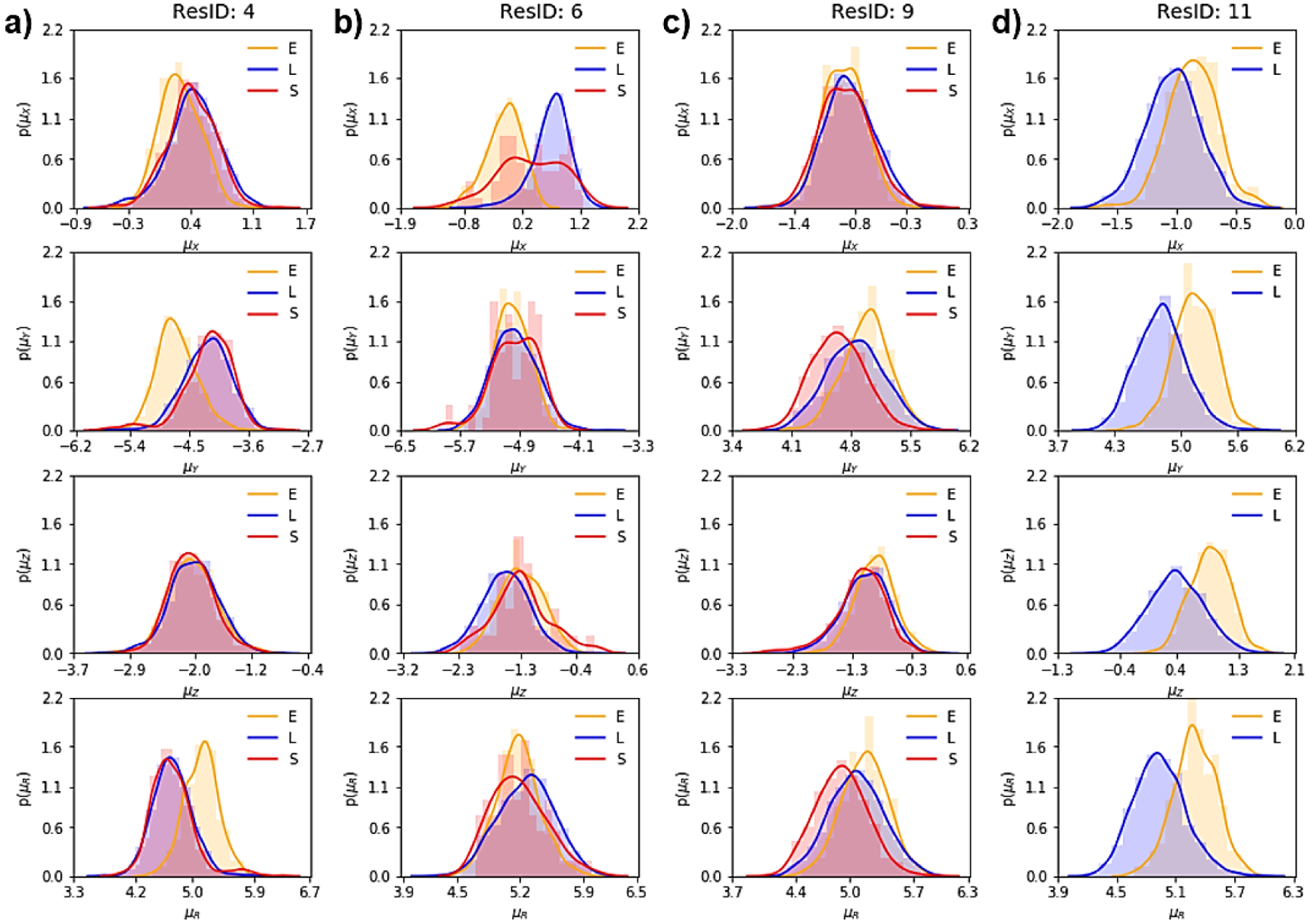
Probability density distribution, using Kernel density estimate (KDE), of dipole moment components and total values (μ_x, μ_y, μ_z and μ_R) corresponding to the sampled secondary structures for (a) Ile4, (b) Tyr6, (c) Ile9, and (d) Tyr11 from the MBH 12 simulation. The DSSP assignment codes are E: Extended strand, participates in beta ladder, S: bend, and L indicates loops and irregular/random coil elements.

CONCLUSIONS

Presented is an updated polarizable empirical FF based on the classical Drude oscillator for the modeling and simulation of peptides and proteins. The optimization included optimizing the backbone parameters, selected side-chain functional groups, electrostatic parameters of aliphatic carbons (e.g. Cβ, Cγ or Cδ), side-chain χ1 and χ2 dihedral parameters, and salt-bridge interactions among protein charged residues. The optimized backbone parameters result in better treatment of the hydrogen bond and ϕ, ψ conformational properties. The optimized charged functional groups derived from the updated molecular ion force field are expected to have more accurate water interaction energies and hydration free energies.³⁹

While the protein FF is typically constructed from small model compounds representative of the all relevant protein functionalities, we found that direct use of the electrostatic parameters of aliphatic Cβ, Cγ or Cδ carbons was not appropriate. In Drude-2013 this yielded high atomic polarizability and Thole screening factors leading to overestimation of the atomic polarization and induced dipole-dipole moment interaction resulting in the local nuclei-Drude particle distance encountering the Drude hardwall used to avoid polarization catastrophe in Drude-2013 simulations at a high frequency. This results in non-adiabatic conditions that do not yield correct ensembles. To correct this, we systematically optimized those electrostatic parameters for the linking aliphatic carbons, yielding better treatment of the electronic response. As the side chain χ1 and χ2 parameters will affect the backbone torsional conformational properties and vice versa, additional optimization of these parameters was performed, yielding better agreement with the χ1/χ2 probability distributions from a crystallographic survey. Finally, the salt-bridge interactions were investigated and optimized by introducing the atom-pair specific LJ (NBFIX) parameters for the charged functional groups.

The resulting optimized model, referred to as Drude-2019, was validated in explicit solvent MD simulations on the 1 μs time scale for a collection of peptides and proteins. Overall, the Drude-2019 model displays a reduced conformational flexibility as compared the Drude-2013 model as estimated from RMS differences with respect to crystal structures and computed NMR properties while, interestingly, the flexibility was typically slightly smaller than the additive C36m model. Such reduced flexibility could be attributed to the optimized treatment of the polarization and induced dipole-dipole interactions on the side chains. Improved agreement over the additive and Drude-2013 models was also observed in simulations of two prototypical ion channels with narrow pores, indicating the utility of the force field in more complex, heterogeneous systems.

An important outcome of the Drude-2019 force field is its ability to account for and to specifically investigate variations in electronic structure as a function of environment. Analysis of three peptides simulated at high temperatures allowing them to sample both folded and unfolded states showed the ability of the force field to model changes in the electronic structure based on the dipole moments of selected peptides bonds. Notable is the heterogeneity of the changes in the dipole moments both as a function of secondary structure and of primary sequence. These results are consistent with previous studies using the Drude FFs for lipids^{78, 123}, proteins^{21, 124}, nucleic acids^125–128 and carbohydrates,^{59, 129–131} indicating the power of the Drude, as well as other polarizable force fields in accounting for explicit changes in electronic structure as a function of environment in condensed phase macromolecular simulations.

In summary, the optimized Drude-2019 model provides a greatly improved picture of the structure and function of peptides and proteins. Since 2013, efforts have been towards the further optimization of the Drude polarizable FF, including updating the nucleic acids,^125–128 lipids,^{78, 123} carbohydrates,^{59, 129–131} and ion^{36, 132} parameters. Recent implementation of the Drude model in NAMD,^67–68 OpenMM,⁸² and GROMACS^133–134 will facilitate the application of the Drude polarizable force field in simulations up to hundreds of nanosecond or microsecond time scales. The current enhancements and capabilities will allow for wider computational studies of heterogeneous systems based on this optimized Drude-2019 model in conjunction with the remainder of the polarizable Drude FF.