Cultural evolution of conformity and anticonformity

Significance

The evolutionary dynamics of cultural variants under conformist- and anticonformist-biased transmission have implications for humans and nonhuman animals. Humans display both conformist and anticonformist biases, and models of conformist-biased transmission have been proposed to explain large-scale human cooperation. Nonhuman animals have been shown to display conformist biases in mating and foraging decisions. Here, we investigate established mathematical models of conformist and anticonformist bias with and without selection and find complex dynamics, including multiple stable polymorphic equilibria, stable cycles, and chaos. Using modifier theory, we show that evolution will reduce anticonformist bias against a culturally advantageous variant. Migration between subpopulations subject to different selection and conformity pressures can produce interesting polymorphisms or eliminate between-group differences.

Abstract

Conformist bias occurs when the probability of adopting a more common cultural variant in a population exceeds its frequency, and anticonformist bias occurs when the reverse is true. Conformist and anticonformist bias have been widely documented in humans, and conformist bias has also been observed in many nonhuman animals. Boyd and Richerson used models of conformist and anticonformist bias to explain the evolution of large-scale cooperation, and subsequent research has extended these models. We revisit Boyd and Richerson’s original analysis and show that, with conformity based on more than three role models, the evolutionary dynamics can be more complex than previously assumed. For example, we show the presence of stable cycles and chaos under strong anticonformity and the presence of new equilibria when both conformity and anticonformity act at different variant frequencies, with and without selection. We also investigate the case of population subdivision with migration and find that the common claim that conformity can maintain between-group differences is not always true. Therefore, the effect of conformity on the evolution of cooperation by group selection may be more complicated than previously stated. Finally, using Feldman and Liberman’s modifier approach, we investigate the conditions under which a rare modifier of the extent of conformity or the number of role models can invade a population. Understanding the dynamics of conformist- and anticonformist-biased transmission may have implications for research on human and nonhuman animal behavior, the evolution of cooperation, and frequency-dependent transmission in general.

Cultural transmission occurs when individuals imitate, learn, or otherwise adopt the cultural variants of other individuals. Vertical transmission occurs when offspring adopt the variants of their parents; oblique transmission occurs when offspring adopt the variants of members of their parents’ generation; and horizontal transmission occurs when offspring adopt the variants of other offspring in their generation (1). Oblique and horizontal transmission are collectively termed nonvertical transmission.

During transmission, individuals may have biases concerning which members of their population, or which variants, they copy (2). One type of bias, termed “frequency-dependent bias,” depends on a variant’s frequency in the population, irrespective of its quality or the status of those who adopt it (ref. 1, chapter 3). Frequency-dependent bias occurs when the probability that an individual in a given population acquires a cultural variant is a nontrivial function of its frequency in the current or previous generation(s) of that population (ref. 3, chapter 7; hereafter, BR ch. 7). In other words, a variant with a population frequency $x_t$ at generation $t$ is not simply adopted with probability $x_t$ by members of generation $t+1$, as would be the case with random copying, but is adopted with a probability that is a more general function of $x_t$. For example, conformist bias occurs when the probability of acquiring the more common variant(s) in the population is greater than their frequency(ies) [and therefore the probability of acquiring the less common variant(s) is less than their frequency(ies)], and anticonformist bias occurs when the opposite is true (3, 4).

Humans have been shown to display both conformist (5, 6) and anticonformist bias (7, 8). It has also been suggested that conformist bias exists in chimpanzees (9), vervet monkeys (10), songbirds (11, 12), guppies (13), and rats (14). However, the term “conformity” has been used in different ways by different researchers (15). Therefore, the extent of conformity in nonhuman animals is unclear from the above studies. Using the criterion of a biased function mentioned above, researchers have observed conformist bias in nine-spined sticklebacks (16), great tits [refs. 17 and 18; but see critique in ref. 19], and fruit flies (20). Fruit flies may also display anticonformist biases when the frequency of the common variant is very high. [Danchin et al. (20), however, did not call this “anticonformist.”]

In addition to empirical research, a great deal of theoretical research has been conducted on conformist and anticonformist biases, beginning in the fields of biology and anthropology and more recently extending to statistical physics. Early models of frequency-dependent transmission (which could include conformist or anticonformist bias, depending on the parameter values) were proposed by Cavalli-Sforza and Feldman (ref. 1, ch. 3), followed by BR (ch. 7). Further research has built upon these models by including parameters for individual learning, environmental stability, and accuracy of information (4, 21–25). Models of conformist bias have also been extended to include additional biases, such as bias for the quality of variants, prestige of the individuals who possess each variant, and success of the individuals with a variant (26–28). Conformist bias has also been used to explain the evolution of cooperation (BR and ref. 29). Walters and Kendal (30) applied conformity analysis in their epidemiological model, which incorporated transmission that was biased on both variant frequency and variant content. They showed that both affect whether a version of a cultural variant will become endemic in a population as well as its ultimate prevalence.

Agent-based models in statistical physics have been formulated in terms of conformist and anticonformist bias of “spinsons” (31). A spinson (amalgamation of “spin” and “person”) is an agent that carries either an “up” or “down” spin and performs behaviors such as conforming or anticonforming to the up vs. down spin when observing other spinsons. In terms of the Ising (32) model of ferromagnetism, conformist bias produces ferromagnetic interactions, and anticonformist bias produces antiferromagnetic interactions (31, 33). In agent-based models with conformist and anticonformist spinsons, stable “stationary concentrations” of up and down spins are possible (31, 34), or periodic cycles may arise (35).

BR (ch. 7) proposed a model of frequency-dependent transmission of a dichotomous trait. Although they characterize the transmission as vertical (BR, ch. 7, p. 207), in terms of Cavalli-Sforza and Feldman (ref. 1, ch. 3), their model combines vertical and oblique transmission. Offspring are assumed to copy a fixed number of role models in the parental generation. In general, there are $n\ge 3$ such role models, although in many subsequent treatments, $n$ is chosen to be three. With three role models and a trait with variants $A$ and $B$, which have frequencies $p$ and $1-p$ in the parental generation, the frequency $p\prime$ of $A$ in the offspring generation is

$$p\prime =p+Dp\left(1-p\right)\left(2p-1\right),$$ [1]

where the parameter $D$ is a conformity coefficient that represents the departure from unbiased transmission; $D>0$ entails a bias in favor of the variant that is more common in the sampled role models—this is conformity bias. $D<0$ is then a measure of anticonformity, or favoring the minority among the sampled role models.

Here, we investigate Boyd and Richerson’s model more closely, with and without viability selection and population subdivision with migration. We focus on the stability of the possible equilibria in the case of $n$ role models and find that with anticonformist bias, the dynamics can be quite complex; it is possible for there to be no stable isolated equilibria, in which case periodic cycles or chaos can result. We also use Feldman and Liberman’s (36) modification approach to explore the evolution of conformity in the dichotomous case.

Henrich and Boyd (4) suggested that the combination of conformist transmission and population subdivision would allow the maintenance of between-group cultural variation, because migrants would adopt the most frequent cultural variant in their destination deme. However, the interaction of cultural transmission, migration, and natural selection has not been widely explored. In this study, we examine this interaction in the context of conformist cultural transmission and find that, as in population genetic models (37), the interaction can give rise to complex evolutionary dynamics.

The Model

The basic model, due to BR, considers a population in which each individual has one of two possible cultural variants: $A$ or $B$. A set of $n\hspace{0.17em}\left(n=\mathrm{3,4},\dots \right)$ individuals from the parental generation affects the cultural trait of the offspring. The probability that an offspring is $A$ when there are $j$ role models of type $A$ is

$$Pr\left[\mathrm{offspring}\hspace{0.17em}A\hspace{0.17em}|\hspace{0.17em}j\hspace{0.17em}\mathrm{role}\hspace{0.17em}\mathrm{models}\hspace{0.17em}A\right]\hspace{0.17em}=\hspace{0.17em}\frac{j}{n}+\frac{D\left(j\right)}{n}.$$ [2]

The function $D\left(j\right)$, where $j=\mathrm{0,1,2},\dots ,n$, determines the strength of frequency-dependent bias in a set of $n$ role models, among whom $j$ are of type $A$. As pointed out by BR, the conformity coefficients $D\left(j\right)$ have the following properties:

$$D\left(0\right)=D\left(n\right)=0,$$ [3a]

$$D\left(n-j\right)=-D\left(j\right)\hspace{1em}\mathrm{f}\mathrm{o}\mathrm{r}\hspace{0.17em}j=\mathrm{0,1},\dots ,n.$$ [3b]

Eq. 3a simply means that the cultural type of the offspring coincides with that of the role models when all of the latter have the same cultural type; in these cases, there is no transmission error, and transmission is only from role models. Eq. 3b asserts transmission symmetry between the two cultural types, $A$ and $B$.

In the parental population, let $p$ be the frequency of type $A$. Then, since the $n$ role models are chosen at random, the number of $A$ role models has a binomial distribution with parameters $n$ and $p$. Since $D\left(0\right)=D\left(n\right)=0$ and

$$0<\frac{j}{n}+\frac{D\left(j\right)}{n}<1,\hspace{1em}j=\mathrm{1,2},\dots ,n-1,$$ [4a]

we must have

$$-j<D\left(j\right)<n-j,\hspace{1em}j=\mathrm{1,2},\dots ,n-1,$$ [4b]

and if $n$ is even, $D\left(\frac{n}{2}\right)=D\left(n-\frac{n}{2}\right)=-D\left(\frac{n}{2}\right)=0$. Then, $p\prime$, the frequency of $A$ in the next generation, is

$$p\prime =\sum _{j=0}^n\left[\frac{j}{n}+\frac{D\left(j\right)}{n}\right]\left(\begin{array}{c}\hfill n\hfill \\ \hfill j\hfill \end{array}\right)p^j{\left(1-p\right)}^{n-j},$$ [5]

and

$$p\prime =p+\sum _{j=0}^n\frac{D\left(j\right)}{n}\left(\begin{array}{c}\hfill n\hfill \\ \hfill j\hfill \end{array}\right)p^j{\left(1-p\right)}^{n-j}.$$ [6]

BR (box 7.4) point out that Eq. 6 can also be written in the form

$$p\prime =p+\sum _{j=k}^n\frac{D\left(j\right)}{n}\left(\begin{array}{c}\hfill n\hfill \\ \hfill j\hfill \end{array}\right)\left[p^j{\left(1-p\right)}^{n-j}-p^{n-j}{\left(1-p\right)}^j\right].$$ [7]

Throughout what follows, we take $k=\frac{n}{2}+1$ when $n$ is even and $k=\frac{n+1}{2}$ when $n$ is odd.

Let us write Eq. 7 in the form

$$p\prime =p+F_n\left(p\right),$$ [8]

then we have the following result.

Result 1.

$F_n\left(p\right)=\left(2p-1\right)G_n\left(z\right)$ where $G_n\left(z\right)$ is a polynomial in terms of $z=p\left(1-p\right)$ and $G_n\left(0\right)=0$.

The proof by induction is in SI Appendix, section A.

Equilibria and Stability without Selection.

The above model corresponds to the case where there is no selection on the cultural traits. We now explore the possible equilibria of recursion Eq. 8 and when they are stable. From Result 1, as $p\prime =p+F_n\left(p\right)$, where $F_n\left(p\right)=\left(2p-1\right)G_n\left(z\right)$ and $G_n\left(z\right)$ is a polynomial in $z=p\left(1-p\right)$ with $G_n\left(0\right)=0$, it is clear that $p^{*}=0$, $p^{*}=1$, and $p^{*}=\frac{1}{2}$ are equilibrium points. Their stability conditions are specified in Result 2, whose proof is in SI Appendix, section B.

Result 2.

• 1)If $D\left(1\right)<0$, then both $p^{*}=0$ and $p^{*}=1$ are locally stable. If $D\left(1\right)>0$, both are locally unstable.
• 2)If $-2^{n-1}<{\sum }_{j=k}^{n-1}\frac{D\left(j\right)}{n}\left(\begin{array}{c}\hfill n\hfill \\ \hfill j\hfill \end{array}\right)\left(2j-n\right)<0$, then $p^{*}=\frac{1}{2}$ is locally stable; otherwise, it is not locally stable.

Hence, if the transmission probability of a single distinct role model $\left(1/n+D\left(1\right)/n\right)$ is smaller than expected from its frequency $\left(<1/n\right)$, then fixations of both types are stable, whereas if this probability is greater than expected from its frequency $\left(>1/n\right)$, then fixations of both types are unstable and a polymorphism may exist.

Remark 1.

• 1)The stability conditions in Result 2 should be coupled with the general constraints in Eq. 4. Hence, for example, for $p^{*}=0$ and $p^{*}=1$ to be stable, we need $-1<D\left(1\right)<0$, and for them to be unstable, we need $0<D\left(1\right)<n-1$.
• 2)The conditions can be written in terms of $D\left(n-1\right)=-D\left(1\right)$. For example, $p^{*}=0$ and $p^{*}=1$ are locally stable if $D\left(n-1\right)>0$ and unstable if $D\left(n-1\right)<0$.

Comparing the stability conditions for $p^{*}=0$, $p^{*}=1$ to those of $p^{*}=\frac{1}{2}$, we see that they are not complementary. It is possible, for example, that both $p^{*}=0$ and $p^{*}=1$ are not locally stable, which entails that there is a protected polymorphism, but $p^{*}=\frac{1}{2}$ is not stable. This would suggest the existence of stable polymorphic equilibria other than $p^{*}=\frac{1}{2}$ or some kind of stable cycle or chaos. We can then explore when $p^{*}=\frac{1}{2}$ is the unique stable polymorphism and if other stable polymorphic equilibria exist. This depends on $n$, the number of role models, and the values of $D\left(j\right)$. Since $G_n\left(z\right)$ is a polynomial in $z=p\left(1-p\right)$, equilibria other than $p^{*}=\frac{1}{2}$ satisfying $G_n\left(z^{*}\right)=G_n\left[p^{*}\left(1-p^{*}\right)\right]=0$ must occur as complementary pairs whose sum is 1.

From the equilibrium equations for $n=\mathrm{3,4,5}$, for example, we see that for $n=3$ and 4, the equilibrium equations are identical (recall that if $n$ is even, $D\left(\frac{n}{2}\right)=0$):

$$p\left(1-p\right)\left(2p-1\right)=0,$$ [9]

giving rise only to $p^{*}=0$, $p^{*}=1$, $p^{*}=\frac{1}{2}$. In this case there is only one $D\left(j\right)$ involved, $D\left(1\right)=-D\left(2\right)$ for $n=3$ and $D\left(1\right)=-D\left(3\right)$ (and $D\left(2\right)=0$) for $n=4$, and the stability conditions for $p^{*}=0$, $p^{*}=1$, and $p^{*}=\frac{1}{2}$ complement each other: When $p^{*}=0$ and $p^{*}=1$ are stable, $p^{*}=\frac{1}{2}$ is not stable, and when $p^{*}=0$ and $p^{*}=1$ are not stable, $p^{*}=\frac{1}{2}$ is stable. Moreover, there is global convergence to the stable equilibria.

When $n=5$, there are two $D\left(j\right)$ s involved, $D\left(1\right)=-D\left(4\right)$ and $D\left(2\right)=-D\left(3\right)$, and the equilibrium equation is

$$p\left(1-p\right)\left(2p-1\right)\left\{D\left(4\right)-p\left(1-p\right)\left[D\left(4\right)-2D\left(3\right)\right]\right\}\hspace{0.17em}=\hspace{0.17em}0.$$ [10]

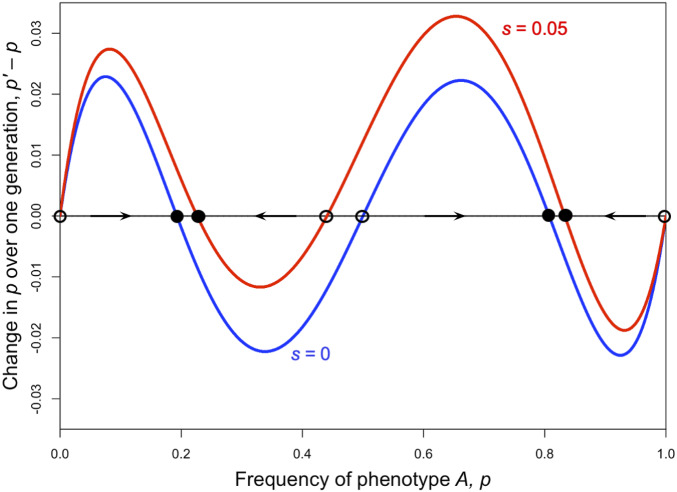
When $D\left(3\right)$ and $D\left(4\right)$ are of different signs, it is possible to have more than three equilibria. For example, when $D\left(4\right)=-0.7$ and $D\left(3\right)=1.9$, stable equilibria occur at 0.1927 and 0.8073, while 0, $\frac{1}{2}$, and 1 are unstable (blue line in Fig. 1).

Fig. 1.

Three polymorphic equilibria (two stable, one unstable) can exist with $n=5$ role models. $p\prime -p$ is plotted as a function of $p$ (Eq. 7) for $n=5$, $D\left(3\right)=1.9$, $D\left(4\right)=-0.7$, and $s=0$, shown in blue. The same plot, but with $s=0.05$ (Eq. 13), is shown in red. The black horizontal line illustrates $p=p\prime$, and the equilibria, i.e., solutions to Eq. 10, occur when the colored lines cross the black line, shown with circles. Open circles mark unstable equilibria, and filled circles mark stable equilibria. Arrows point away from unstable equilibria and toward stable equilibria. In the $s=0$ case, there are five equilibria total, with the stable ones at $\widehat{p}=0.1927$ and $1-\widehat{p}=0.8073$. In the $s=0.05$ case, there are also five equilibria, with the stable ones at $\widehat{p}=0.2263$ and 0.8331. Type $A$ is favored if $s>0$, and, in this case, the stable frequency of $A$ is higher than with $s=0$.

It is interesting to find general conditions under which $p^{*}=\frac{1}{2}$ is the only polymorphic equilibrium. This is the content of Result 3.

Result 3.

Suppose there are $n$ role models ($n\ge 3$). Then, $p^{*}=\frac{1}{2}$ is the unique polymorphic equilibrium if $D\left(j\right)$ has the same positive or negative sign for all $k\le j<n$.

Proof. From Eqs. 6 and 7, we see that $F_n\left(0\right)=F_n\left(1\right)=F_n\left(\frac{1}{2}\right)=0$. But as $2j-n\ge 1$ and

$$0<p<\frac{1}{2}\to p^{2j-n}-{\left(1-p\right)}^{2j-n}<0,$$ [11]

$$\frac{1}{2}<p<1\to p^{2j-n}-{\left(1-p\right)}^{2j-n}>0.$$ [12]

Under the assumptions of Result 3, $F_n\left(p\right)$ changes sign in $\left(\mathrm{0,1}\right)$ only at $p^{*}=\frac{1}{2}$, implying that $p^{*}=\frac{1}{2}$ is the only polymorphic equilibrium. (A special case of this is $D\left(j\right)=D$ for all $k\le j<n$.)

It might be expected that if $p^{*}=\frac{1}{2}$ is the unique polymorphic equilibrium, then either $p^{*}=0$ and $p^{*}=1$ are both stable and $p^{*}=\frac{1}{2}$ is not stable, or both $p^{*}=0$ and $p^{*}=1$ are not stable and $p^{*}=\frac{1}{2}$ is stable, since it is a protected polymorphism. In fact, when $p^{*}=0$ and $p^{*}=1$ are both stable, there is global convergence to one of them; $p^{*}=\frac{1}{2}$ is not stable, such that $\left[0,\frac{1}{2}\right)$ is the domain of attraction of $p^{*}=0$ and $\left(\frac{1}{2},1\right]$ that of $p^{*}=1$. However, when both $p^{*}=0$ and $p^{*}=1$ are not stable, then even when $p^{*}=\frac{1}{2}$ is the unique polymorphic equilibrium, it is possible that $p^{*}=\frac{1}{2}$ is not stable. For example, following Eq. B8 in SI Appendix, section B, let ${\varphi }_n=1+{\left(\frac{1}{2}\right)}^{n-2}{\sum }_{j=k}^{n-1}\frac{D\left(j\right)}{n}\left(\begin{array}{c}\hfill n\hfill \\ \hfill j\hfill \end{array}\right)\left(2j-n\right)$. From Eq. 4, the lower bound of ${\varphi }_n$ occurs when $D\left(j\right)=-j$ for all $k\le j\le n-1$, in which case all of the $D\left(j\right)$ s are negative and $p^{*}=\frac{1}{2}$ is unique by Result 3. SI Appendix, Table S1 presents the lower bounds on ${\varphi }_n$ for $n=\mathrm{3,4},\dots ,20$. The bounds on $D$, namely, $-j<D\left(j\right)<n-j$, do not provide a predictable relationship between $j$ and $D$. Changing $n$ can change the bounds on $\varphi \left(n\right)$, and if $D\left(j\right)$ is at its lower bound, then the dynamics are affected by $n$. This is shown in the third column of SI Appendix, Table S1.

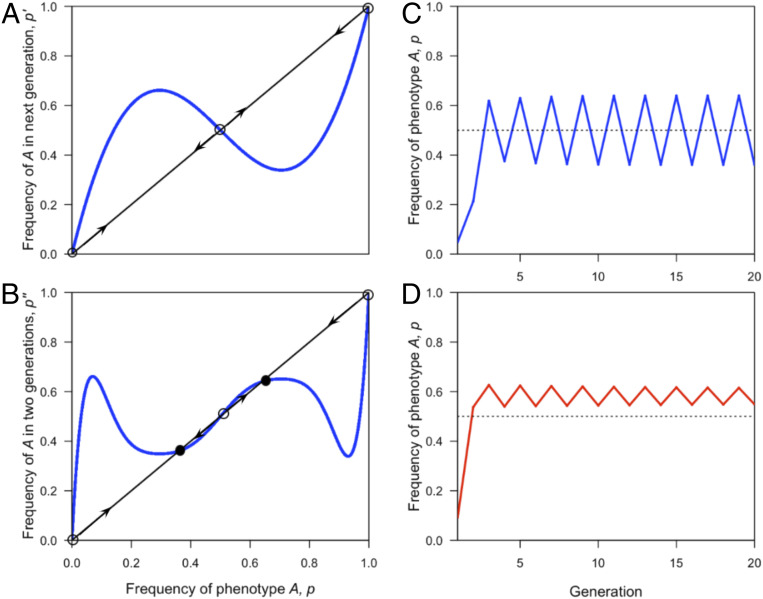
We note that unless $n=\mathrm{3,4}$, the lower bound of ${\varphi }_n$ is less than $-1$, in which case Result 2 asserts that $p^{*}=\frac{1}{2}$ is not locally stable for these values of ${\varphi }_n$. Indeed, none of the equilibria may be stable, and in this case, there can be a stable cycle, an example of which for $n=5$ is shown in Fig. 2.

Fig. 2.

Stable cycles can occur when $n=5$ role models. (A and B) $p\prime$ (A) and p^″ (B) are plotted against $p$—where $p$ is the frequency of phenotype $A$ in the current generation, $p\prime$ is its frequency in the next generation, and p^″ is its frequency in the generation after that—for $n=5$, $D\left(4\right)=-3.9$, $D\left(3\right)=-2.9$, and $s=0$, shown in blue. Open circles mark unstable equilibria, and filled circles mark stable equilibria with period 2 (i.e., the frequency returns to this point every two generations). Arrows point away from unstable equilibria and/or toward stable equilibria with period 2. (C) $p$ over time. (D) $p$ over time when the parameters are kept the same, except that $s$, the selection coefficient in favor of $A$, is changed to 1.

Equilibria and Stability with Selection.

Suppose that selection operates on $A$ and $B$ with $w_A=1+s$ and $w_B=1$ the associated fitness parameters. Thus, if $s>0$, which we shall assume throughout, type $A$ has a selective advantage. The evolution is then determined by the transformation

$$\begin{array}{cc}\hfill Wp\prime & =\left(1+s\right)\left[p+F_n\left(p\right)\right]\hfill \\ \hfill W{\left(1-p\right)}^{\prime }& =\left(1-p\right)-F_n\left(p\right),\hfill \end{array}$$ [13]

where $p$ and $p^{\prime }$ are the frequencies of type $A$ individuals in the present and the next generation, respectively. $F_n\left(p\right)$ is specified in Eqs. 6 and 7, and $W$, the normalizing factor, is

$$W=1+s\left[p+F_n\left(p\right)\right].$$ [14]

As $F_n\left(0\right)=F_n\left(1\right)=0$, it is clear from Eq. 13 that both $p^{*}=0$ and $p^{*}=1$ are equilibrium points. In order to find polymorphic equilibria, we solve the equilibrium equation

$$Wp=\left(1+s\right)\left[p+F_n\left(p\right)\right].$$ [15]

From Eqs. 6 and 7, we have $F_n\left(p\right)=p\left(1-p\right)\left(2p-1\right)H_n\left(p\right)$, where

$$\begin{array}{cc}\hfill H_n\left(p\right)& =\sum _{j=k}^{n-1}\frac{D\left(j\right)}{n}\left(\begin{array}{c}\hfill n\hfill \\ \hfill j\hfill \end{array}\right){\left[p\left(1-p\right)\right]}^{n-1-j}\hfill \\ \hfill & \hspace{1em}\times \left[\sum _{i=0}^{2j-n-1}{\left(1-p\right)}^i{p}^{2j-n-1-i}\right].\hfill \end{array}$$ [16]

Observe that

$$H_n\left(0\right)=H_n\left(1\right)=D\left(n-1\right)=-D\left(1\right).$$ [17]

We can rewrite Eq. 15 as

$$Wp=\left(1+s\right)\left[p+p\left(1-p\right)\left(2p-1\right)H_n\left(p\right)\right],$$ [18]

so either $p=0$ or

$$W=\left(1+s\right)\left[1+\left(1-p\right)\left(2p-1\right)H_n\left(p\right)\right].$$ [19]

Also, from Eq. 14,

$$W=1+s\left[p+p\left(1-p\right)\left(2p-1\right)H_n\left(p\right)\right].$$ [20]

Combining Eqs. 19 and 20, we deduce that either $p=1$ or $p$ satisfies the equation

$$Q_n\left(p\right)=\left(2p-1\right)\left[1+s\left(1-p\right)\right]H_n\left(p\right)+s=0.$$ [21]

$Q_n\left(p\right)$ is a polynomial in $p$, and from Eq. 17,

$$\begin{array}{c}\hfill Q_n\left(0\right)=s-\left(1+s\right)D\left(n-1\right),\hfill \\ \hfill Q_n\left(1\right)=s+D\left(n-1\right),\hspace{1em}{Q}_n\left(\frac{1}{2}\right)=s.\hfill \end{array}$$ [22]

To sum up, the equilibria are $p^{*}=0$, $p^{*}=1$, and possible polymorphic equilibria $p^{*}$ that lie in $\left(\mathrm{0,1}\right)$ and satisfy $Q_n\left(p^{*}\right)=0$. Before analyzing the general case with respect to stability of $p^{*}=0$, $p^{*}=1$, and the existence of polymorphic equilibria, we treat the case $n=3$, which has received a great deal of attention (3, 21, 29).

When $n=3$, we have $D\left(0\right)=D\left(3\right)=0$ and $D\left(2\right)=-D\left(1\right)$. Let $D\left(2\right)=v$; then, the transformation Eq. 13 becomes

$$W{p}^{\prime }=\left(1+s\right)\left[p+vp\left(1-p\right)\left(2p-1\right)\right],$$ [23]

with

$$W=1+s\left[p+vp\left(1-p\right)\left(2p-1\right)\right].$$ [24]

At equilibrium $p^{*}=0$, $p^{*}=1$, or there is a polymorphic equilibrium satisfying the equation

$$Q_3\left(p\right)=-2sv{p}^2+\left(3s+2\right)vp-v\left(1+s\right)+s=0.$$ (25)

Here,

$$Q_3\left(0\right)=s-v\left(1+s\right),\hspace{1em}{Q}_3\left(1\right)=s+v,\hspace{1em}{Q}_3\left(\frac{1}{2}\right)=s.$$ [26]

First, we find the local stability conditions for $p^{*}=0$ and $p^{*}=1$. The linear approximation to Eq. 23 near $p^{*}=0$ is

$$p\prime =\left(1+s\right)\left(1-v\right)p,$$ [27]

and near $p^{*}=1$

$$\left(1+s\right){\left(1-p\right)}^{\prime }=\left(1-p\right)\left(1-v\right).$$ [28]

Hence, $p^{*}=0$ is locally stable when $\left(1+s\right)\left(1-v\right)<1$ or $v\left(1+s\right)-s>0$ and unstable if $v\left(1+s\right)-s<0$. Similarly, $p^{*}=1$ is locally stable when $\frac{1-v}{1+s}<1$ or when $\left(s+v\right)>0$, and unstable if $\left(s+v\right)<0$. Comparing these stability conditions to Eq. 26, we conclude the following.

1) With $s>0$, if neither $p^{*}=0$ nor $p^{*}=1$ is stable, $v\left(1+s\right)-s<0$ and $\left(s+v\right)<0$, and then $Q_3\left(0\right)>0$ and $Q_3\left(1\right)<0$. Therefore, a polymorphic equilibrium $p^{*}$ exists such that $Q_3\left(p^{*}\right)=0$, it is unique since $Q_3\left(+\infty \right)<0$, and since $Q_3\left(\frac{1}{2}\right)=s>0$, we have $\frac{1}{2}<p^{*}<1$.

2) If both $p^{*}=0$ and $p^{*}=1$ are stable with $v\left(1+s\right)-s>0$ and $\left(s+v\right)>0$, then $Q_3\left(0\right)<0$, $Q_3\left(1\right)>0$, and as $Q_3\left(\frac{1}{2}\right)>0$ a unique polymorphism $p^{*}$ exists with $0<p^{*}<\frac{1}{2}$.

If the two fixations $p^{*}=0$ and $p^{*}=1$ are not stable, then it can be shown that the unique polymorphism $p^{*}$ is globally stable. If both $p^{*}=0$ and $p^{*}=1$ are stable, then the unique polymorphism $p^{*}$ is not stable and separates the domains of attraction to $p^{*}=0$ and $p^{*}=1$ into $\left[0,p^{*}\right)$ and $\left(p^{*},1\right]$, respectively. If $s>0$ and $-s<v<\frac{s}{1+s}$, then $p^{*}=1$ is stable and $p^{*}=0$ is not stable, in which case no polymorphic equilibrium exists and $p^{*}=1$ is globally stable. SI Appendix, Fig. S1 shows examples of all three cases.

In the case $n=3$, the stability conditions of $p^{*}=0$ and $p^{*}=1$ are related to the possible existence of polymorphic equilibria. In fact, this is the case in general. We start with the stability conditions for $p^{*}=0$ and $p^{*}=1$.

Result 4.

• 1)$p^{*}=0$ (fixation of the disfavored type) is locally stable if $-D\left(1\right)=D\left(n-1\right)>s/\left(1+s\right)$ and unstable if $-D\left(1\right)=D\left(n-1\right)<s/\left(1+s\right)$.
• 2)$p^{*}=1$ (fixation of the favored type) is locally stable if $-D\left(1\right)=D\left(n-1\right)>-s$ and unstable if $D\left(n-1\right)<-s$.
• 3)It is possible that $p^{*}=0$ and $p^{*}=1$ are both stable or both unstable. Also, $p^{*}=1$ can be stable while $p^{*}=0$ is unstable, but the opposite cannot occur. That is, if fixation of the disfavored type is unstable, then fixation of the favored type may be stable, but the opposite is not true.

Proof. Following Eqs. 13–17, the linear approximation of the frequency transformation near $p^{*}=0$ is

$$p\prime =\left(1+s\right)p\left[1-H_n\left(0\right)\right]=\left(1+s\right)p\left[1-D\left(n-1\right)\right].$$ [29]

Therefore, $p^{*}=0$ is locally stable if $\left(1+s\right)\left[1-D\left(n-1\right)\right]\hspace{0.17em}<\hspace{0.17em}1$ or if $s-\left(1+s\right)D\left(n-1\right)<0$. The linear approximation near $p^{*}=1$ is

$$\begin{array}{cc}\hfill \left(1+s\right){\left(1-p\right)}^{\prime }& =\left(1-p\right)\left[1-H_n\left(0\right)\right]\hfill \\ \hfill & =\left(1-p\right)\left[1-D\left(n-1\right)\right],\hfill \end{array}$$ [30]

and $p^{*}=1$ is locally stable if $\frac{1-D\left(n-1\right)}{1+s}<1$ or $s+D\left(n-1\right)>0$. Hence, $p^{*}=0$ and $p^{*}=1$ are both locally stable if $D\left(n-1\right)>\frac{s}{1+s}$, and both are unstable if $D\left(n-1\right)<-s$. Further, $p^{*}=0$ is not stable, while $p^{*}=1$ is locally stable if $-s<D\left(n-1\right)<\frac{s}{1+s}$. It is impossible that $p^{*}=0$ is locally stable and $p^{*}=1$ is not.

Comparing Result 4 with the values of $Q_n\left(p\right)$ at $\mathrm{0,1},\frac{1}{2}$ given in Eq. 22, we have:

Result 5.

If both $p^{*}=0$ and $p^{*}=1$ are locally stable or unstable, then there exists at least one polymorphic equilibrium $p^{*}$ with $0<p^{*}<1$.

Proof. When both $p^{*}=0$ and $p^{*}=1$ are stable or unstable, the stability conditions for $p^{*}=0$ and $p^{*}=1$ given in Result 4 imply that $Q_n\left(0\right)Q_n\left(1\right)<0$ and $Q_n\left(p\right)$ changes signs at least once for $0<p<1$. The continuity of $Q_n\left(p\right)$ implies that at least one $0<p^{*}<1$ exists such that $Q_n\left(p^{*}\right)=0$, so at least one polymorphic equilibrium exists.

Remark 2:

• 1)If only one of $p^{*}=0$ and $p^{*}=1$ is stable, then, by Result 4, it is $p^{*}=1$ that is stable and $p^{*}=0$ is not stable. In this case, $Q_n\left(p\right)>0$ for $p=0$, $p=\frac{1}{2}$, $p=1$, and it is possible that $Q_n\left(p\right)>0$ for all $0<p<1$, and no polymorphic equilibrium exists.
• 2)If $p^{*}=0$ and $p^{*}=1$ are stable, then $s-\left(1+s\right)D\left(n-1\right)<0$ and $Q_n\left(0\right)<0$. As $Q_n\left(\frac{1}{2}\right)=s>0$, in this case, there exists a polymorphic equilibrium $p^{*}$ with $0<p^{*}<\frac{1}{2}$.
• 3)The value of the mean fitness $W$ in Eq. 24 evaluated at the polymorphic equilibrium $p^{*}$ is increasing as conformity increases (positive $v$) or as anticonformity decreases ($v$ becomes less negative). An example is shown in SI Appendix, Fig. S3.
• 4)If $p^{*}=1$ and $p^{*}=0$ are unstable, then $s+D\left(n-1\right)<0$ and $Q_n\left(1\right)<0$. Again, as $Q_n\left(\frac{1}{2}\right)=s>0$, at least one polymorphic equilibrium $p^{*}$ exists with $\frac{1}{2}<p^{*}<1$.
• 5)BR stress the importance of $p=\frac{1}{2}$ in dividing the domains of attraction, even in the case where the selection coefficient $s\hspace{0.17em}\ne \hspace{0.17em}0$ (i.e., with selection). We have shown in Results 4 and 5 that it is not $p=\frac{1}{2}$, but a more complicated equilibrium in terms of $s$ and the conformity parameters that may be stable. Under some cases, there may be multiple polymorphic equilibria (red line in Fig. 1). Under some cases, there may be no stable polymorphic equilibria, and cycles may occur (Fig. 2D) or chaos. Both cycles and chaos can occur under anticonformity ($D\left(j\right)<0\hspace{0.17em}\mathrm{f}\mathrm{o}\mathrm{r}\hspace{0.17em}j\ge k$) or a combination of conformity and anticonformity (some $D\left(j\right)>0$ and some $D\left(j\right)<0$ for $j\ge k$), but not in the case of pure conformity.

These results are important for the evolution of conformity, as we now show.

Modification of Conformity

Suppose that the set of conformity coefficients is $\mathbf{D}=\left[D\left(0\right),D\left(1\right),\dots ,D\left(n\right)\right]$ and is controlled by a modifier gene with two possible alleles $M$ and $m$ in such a way that $M$ produces $\mathbf{D}$ and $m$ produces $\stackrel{\sim }{\mathbf{D}}=\left[\stackrel{\sim }{D}\left(0\right),\stackrel{\sim }{D}\left(1\right),\dots ,\stackrel{\sim }{D}\left(n\right)\right]$. Assume also that the modifier gene is selectively neutral; that is, it does not itself affect the fitnesses of the individuals carrying cultural variants $A$ and $B$.

Let $\mathbf{x}=\left(x_1,x_2,x_3,x_4\right)$ be the vector of frequencies of $MA,MB,mA,mB$, respectively. We use the notation $x_i\hspace{0.17em}\mathrm{f}\mathrm{o}\mathrm{r}\hspace{0.17em}i=\mathrm{1,2,3,4}$ for the four phenogenotypes in accordance with common notation in evolutionary genetics. Assuming that the genetic parent as well as the cultural role models are randomly drawn from the population as a whole, and if the fitness of phenotype $A$ is $w_A=1+s$ and that of $B$ is $w_B=1$, then the vector ${\mathbf{x}}^{\prime }$ of frequencies in the next generation is given by

$$\begin{array}{cc}\hfill W{x}_1^{\prime }& =\left(x_1+x_2\right)\left\{p+p\left(1-p\right)\left(2p-1\right)H_n\left(p\right)\right\}\left(1+s\right)\hfill \\ \hfill W{x}_2^{\prime }& =\left(x_1+x_2\right)\left\{1-p-p\left(1-p\right)\left(2p-1\right)H_n\left(p\right)\right\}\hfill \\ \hfill W{x}_3^{\prime }& =\left(x_3+x_4\right)\left\{p+p\left(1-p\right)\left(2p-1\right){\stackrel{\sim }{H}}_n\left(p\right)\right\}\left(1+s\right)\hfill \\ \hfill W{x}_4^{\prime }& =\left(x_3+x_4\right)\left\{1-p-p\left(1-p\right)\left(2p-1\right){\stackrel{\sim }{H}}_n\left(p\right)\right\},\hfill \end{array}$$ [31]

where $W=W\left(\mathbf{x}\right)$, the normalizing factor, is the sum of the right-hand sides of Eq. 31. Here, $p=x_1+x_3$ is the overall frequency of variant $A$, $1-p=x_2+x_4$ is the overall frequency of variant $B$, and $H_n\left(p\right)$ is defined in Eq. 16 and represents the additive effect of conformity, while ${\stackrel{\sim }{H}}_n\left(p\right)$ is a similar term with $\stackrel{\sim }{D}\left(j\right)$ instead of $D\left(j\right)$.

We assume that initially only $M$ is present, and we seek conditions under which the modifier allele $m$ will invade when introduced near a stable polymorphism where $x_3=x_4=0$. When only $M$ is present and the two fixations, $\left(\mathrm{1,0,0,0}\right)$ and $\left(\mathrm{0,1,0,0}\right)$ in type $A$ or type $B$, respectively, are not stable, assume that a polymorphic stable equilibrium ${\mathbf{x}}^{*}=\left(x_1^{*},x_2^{*},\mathrm{0,0}\right)$ exists with $x_1^{*}>\frac{1}{2}$. Using Feldman and Liberman’s (36) modification framework, we check the external stability of ${\mathbf{x}}^{*}$ when $m$ is introduced at a small frequency. Our analysis extends and rigorously generalizes BR’s treatment of the simplest conformity model.

This external stability is determined by the linear transformation ${\mathbf{L}}_{\mathrm{e}\mathrm{x}}$ given by

$$\begin{array}{cc}\hfill W^{*}{x}_3^{\prime }& =\left(x_3+x_4\right)\left[x_1^{*}+x_1^{*}\left(1-x_1^{*}\right)\left(2x_1^{*}-1\right){\stackrel{\sim }{H}}_n\left(x_1^{*}\right)\right]\left(1+s\right)\hfill \\ \hfill W^{*}{x}_4^{\prime }& =\left(x_3+x_4\right)\left[1-x_1^{*}-x_1^{*}\left(1-x_1^{*}\right)\left(2x_1^{*}-1\right){\stackrel{\sim }{H}}_n\left(x_1^{*}\right)\right],\hfill \end{array}$$ [32]

where

$$W^{*}=1+s\left[x_1^{*}+x_1^{*}\left(1-x_1^{*}\right)\left(2x_1^{*}-1\right)H_n\left(x_1^{*}\right)\right].$$ [33]

Thus, the external stability matrix ${\mathbf{L}}_{\mathrm{e}\mathrm{x}}$ specified by Eq. 32 is of the form ${\mathbf{L}}_{\mathrm{e}\mathrm{x}}=\left(\begin{array}{cc}\hfill a\hfill & \hfill a\hfill \\ \hfill b\hfill & \hfill b\hfill \end{array}\right)$ with eigenvalues ${\lambda }_1=0$ and ${\lambda }_2=a+b$, where

$$W^{*}\left(a+b\right)=1+s\left[x_1^{*}+x_1^{*}\left(1-x_1^{*}\right)\left(2x_1^{*}-1\right){\stackrel{\sim }{H}}_n\left(x_1^{*}\right)\right].$$ [34]

Hence,

$${\lambda }_2=\frac{1+s\left[x_1^{*}+x_1^{*}\left(1-x_1^{*}\right)\left(2x_1^{*}-1\right){\stackrel{\sim }{H}}_n\left(x_1^{*}\right)\right]}{1+s\left[x_1^{*}+x_1^{*}\left(1-x_1^{*}\right)\left(2x_1^{*}-1\right)H_n\left(x_1^{*}\right)\right]}.$$ [35]

${\lambda }_2$ is always positive and ${\lambda }_2>1$ if

$${\stackrel{\sim }{H}}_n\left(x_1^{*}\right)>H_n\left(x_1^{*}\right),$$ [36]

since $0<x_1^{*}<1$ and $x_1^{*}>\frac{1}{2}$.

We have thus secured the following modification result.

Result 6.

With $n$ role models, suppose that the cultural variant $A$ has selective advantage $s\hspace{0.17em}\left(s>0\right)$, the conformity coefficient $-D\left(1\right)=D\left(n-1\right)<-s$, and that $A$ and $B$ coexist at a stable equilibrium ${\mathbf{x}}^{*}=\left(x_1^{*},x_2^{*},\mathrm{0,0}\right)$, where the frequency of $A$ exceeds that of $B$ (i.e., $x_1^{*}>\frac{1}{2}$). Then, a rare modifier allele that appears near ${\mathbf{x}}^{*}$ and changes the conformity coefficients from $\mathbf{D}$ to $\stackrel{\sim }{\mathbf{D}}$ will invade if ${\stackrel{\sim }{H}}_n\left(x_1^{*}\right)>H_n\left(x_1^{*}\right)$.

Recall from Eq. 16 that

$$\begin{array}{cc}\hfill H_n\left(x_1^{*}\right)& =\sum _{j=k}^{n-1}\frac{D\left(j\right)}{n}\left(\begin{array}{c}\hfill n\hfill \\ \hfill j\hfill \end{array}\right){\left[x_1^{*}\left(1-x_1^{*}\right)\right]}^{n-1-j}\hfill \\ \hfill & \hspace{1em}\times \left[\sum _{i=0}^{2j-n-1}{\left(1-x_1^{*}\right)}^i{\left(x_1^{*}\right)}^{2j-n-1-i}\right].\hfill \end{array}$$ [37]

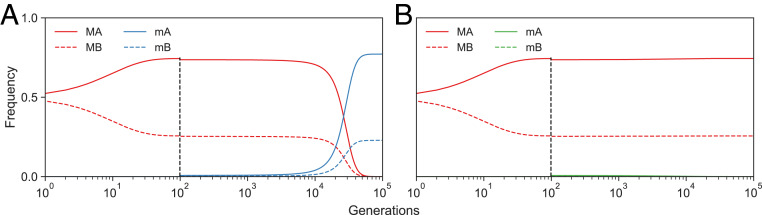
If $\stackrel{\sim }{D}\left(j\right)>D\left(j\right)$ for all $k\le j\le \left(n-1\right)$, then ${\stackrel{\sim }{H}}_n\left(x_1^{*}\right)>H_n\left(x_1^{*}\right)$, and invasion can occur. In the special case where $D\left(j\right)=D$ and $\stackrel{\sim }{D}\left(j\right)=\stackrel{\sim }{D}$ for all $k\le j\le \left(n-1\right)$, $m$ will invade if $\stackrel{\sim }{D}>D$, and as $D\left(n-1\right)=D<-s$ invasion occurs when the modifier allele $m$ reduces the transmission bias against $A$. An example with $n=3$ role models is shown in Fig. 3. In the case of $n=3$ role models, ${\stackrel{\sim }{F}}_3\left(\cdot \right)$ has the constant factor $\stackrel{\sim }{D}$, and $F_3\left(\cdot \right)$ has the factor $D$. Thus, the condition for invasion is $\stackrel{\sim }{D}>D$.

Fig. 3.

Reduction principle for anticonformity. The frequencies of phenotypes $A$ (solid lines) and $B$ (dashed lines) over time during invasions by modifier allele $m$ of a population of $M$ alleles with $n=3$ models are shown. The resident modifier allele $M$ (red lines) produces bias parameter $D=-2s=-0.2$, while the invading modifier allele $m$ (blue lines) produces $\stackrel{\sim }{D}=0.9D>D$ in A, and $\stackrel{\sim }{D}=1.1D<D$ (green lines, barely seen) in B. Modifier allele $m$ that increases the bias parameter $D$ to be less negative invades (in A), while if it decreases $D$ to make it more negative, it does not invade (in B). Invasions start at generation 10 (shown by vertical dashed lines). Here, $n=3$, the fitness of $A$ relative to $B$ is $1+s:1$, and the frequency of $m$ is initially 0.01.

Remark 3:

We can also use our analysis for the interesting case where the modifier gene controls the number of role models of any individual. Here, allele $M$ specifies that $n$ role models determine the cultural type of the offspring via the conformity coefficients $\mathbf{D}=\left[D\left(0\right),D\left(1\right),\dots ,D\left(n\right)\right]$. With the modifier allele $m$, there are $ñ$ role models with coefficients $\stackrel{\sim }{\mathbf{D}}=\left[\stackrel{\sim }{D}\left(0\right),\stackrel{\sim }{D}\left(1\right),\dots ,\stackrel{\sim }{D}\left(ñ\right)\right]$. If only $M$ is initially present and there is a stable polymorphic equilibrium ${\mathbf{x}}^{*}=\left(x_1^{*},x_2^{*},\mathrm{0,0}\right)$ with $x_1^{*}>\frac{1}{2}$, then $m$ invades when ${\stackrel{\sim }{F}}_{ñ}\left(x_1^{*}\right)>F_n\left(x_1^{*}\right)$, where ${\stackrel{\sim }{F}}_{ñ}\left(p\right)$ is defined as in Eqs. 15–18 with $n$ replaced by $ñ$, the $D\left(j\right)$’s replaced by $\stackrel{\sim }{D}\left(j\right)$’s, and $p$ replaced by $x_1^{*}$, and $k=\frac{ñ}{2}+1$ when $ñ$ is even and $k=\frac{ñ+1}{2}$ when $ñ$ is odd.

Suppose, for example, that with $M$, there are four role models for each individual, with $\mathbf{D}=\left[0,-D,0,D,0\right]$, and each carrier of $m$ has five role models with $\stackrel{\sim }{\mathbf{D}}=\left[0,-\stackrel{\sim }{D}\left(4\right),-\stackrel{\sim }{D}\left(3\right),\hspace{0.17em}\stackrel{\sim }{D}\left(3\right),\stackrel{\sim }{D}\left(4\right),0\right]$. Then, $m$ invades near ${\mathbf{x}}^{*}=\left(x_1^{*},x_2^{*},\mathrm{0,0}\right)$ with $x_1^{*}>\frac{1}{2}$ if $\left[\stackrel{\sim }{D}\left(4\right)-x_1^{*}\left(1-x_1^{*}\right)\left(\stackrel{\sim }{D}\left(4\right)-2\stackrel{\sim }{D}\left(3\right)\right)\right]>D$. Assuming that $\stackrel{\sim }{D}\left(3\right)=\stackrel{\sim }{D}\left(4\right)=\stackrel{\sim }{D}$, then $m$ invades near ${\mathbf{x}}^{*}$ if $\stackrel{\sim }{D}\left[1+x_1^{*}\left(1-x_1^{*}\right)\right]\hspace{0.17em}>D$, which is always true when $\stackrel{\sim }{D}>D$.

Population Subdivision: Selection, Migration, and Evolution of Conformity

Suppose that the population is divided into $N$ subpopulations, labeled $\mathrm{1,2},\dots ,N$, that are connected by symmetric migration at rate $\mu$. Thus, each individual has a probability $\left(1-\mu \right)$ of staying in its subpopulation and probability $\frac{\mu }{N-1}$ of migrating to any of the other $\left(N-1\right)$ subpopulations, where $0\le \mu \le 1$. All populations have the same number of role models, $n$.

In subpopulation $i\hspace{0.17em}\left(i=\mathrm{1,2},\dots ,N\right)$, type $A$ individuals have fitness $\left(1+s_i\right)$ and type $B$ individuals have fitness 1. Subpopulation $i$ has its conformity bias parameters represented by the vector ${\mathbf{D}}_i=\left[D_i\left(0\right),D_i\left(1\right),\dots ,D_i\left(n\right)\right]$. Let the vector $\mathbf{P}=\left(p_1,p_2,\dots ,p_N\right)$, where $p_i$ is the frequency of type $A$ individuals in subpopulation $i$. Then, the evolution of the $N$-deme system is described by the following transformation:

$$\begin{array}{cc}\hfill p_i^{\prime }& =\left(1-\mu \right)\frac{\left(1+s_i\right)\left[p_i+p_i\left(1-p_i\right)\left(2p_i-1\right)H_n^i\left(p_i\right)\right]}{W_i}\hfill \\ \hfill & \hspace{1em}+\frac{\mu }{N-1}\sum _{\genfrac{}{}{0ex}{}{j=1}{j\ne i}}^N\frac{\left(1+s_j\right)\left[p_j+p_j\left(1-p_j\right)\left(2p_j-1\right)H_n^j\left(p_j\right)\right]}{W_j},\hfill \end{array}$$ [38]

where from Eq. 16,

$$\begin{array}{cc}\hfill H_n^i\left(p_i\right)& =\sum _{j=k}^n\frac{D_i\left(j\right)}{n}\left(\genfrac{}{}{0ex}{}{n}{j}\right){\left[p_i\left(1-p_i\right)\right]}^{n-1-j}\hfill \\ \hfill & \hspace{1em}\times \left[\sum _{\ell =0}^{2j-n-1}{\left(1-p_i\right)}^{\ell }{p}_i^{2j-n-1-\ell }\right],\hfill \end{array}$$ [39]

and from Eq. 18

$$W_i=1+s\left[p_i+p_i\left(1-p_i\right)\left(2p_i-1\right)H_n^i\left(p_i\right)\right],$$ [40]

for $i=\mathrm{1,2},\dots ,N$. Clearly, ${\mathbf{P}}^{*}=\mathbf{0}=\left(\mathrm{0,0},\dots ,0\right)$ and ${\mathbf{P}}^{*}=\mathbf{1}=\left(\mathrm{1,1},\dots ,1\right)$ are equilibrium points denoting fixation of type $B$ or type $A$, respectively, in all $N$ subpopulations. In order to obtain conditions under which ${\mathbf{P}}^{*}=\mathbf{0}$ or ${\mathbf{P}}^{*}=\mathbf{1}$ or both are locally stable, we take the linear approximation of the transformation Eq. 38 near ${\mathbf{P}}^{*}=\mathbf{0}$ and near ${\mathbf{P}}^{*}=\mathbf{1}$. The linear approximation ${\mathbf{L}}_{\mathbf{0}}$ of Eq. 38 near ${\mathbf{P}}^{*}=\mathbf{0}$ is given by

$$\begin{array}{cc}\hfill {\epsilon }_i^{\prime }& =\left(1-\mu \right)\left(1+s_i\right)\left[1-H_n^i\left(0\right)\right]{\epsilon }_i\hfill \\ \hfill & \hspace{1em}+\frac{\mu }{N-1}\sum _{j\ne i}\left(1+s_j\right)\left[1-H_n^j\left(0\right)\right]{\epsilon }_j,\hspace{1em}i=\mathrm{1,2},\dots ,N,\hfill \end{array}$$ [41]

and ${\mathbf{L}}_{\mathbf{1}}$, the linear approximation of Eq. 38 near ${\mathbf{P}}^{*}=\mathbf{1}$, is

$${\eta }_i^{\prime }=\left(1-\mu \right)\frac{1-H_n^i\left(1\right)}{1+s_i}{\eta }_i+\frac{\mu }{N-1}\sum _{j\ne i}\frac{1-H_n^j\left(1\right)}{1+s_j}{\eta }_j,$$ [42]

where, from Eq. 17,

$$H_n^i\left(0\right)=H_n^i\left(1\right)=D_i\left(n-1\right)=-D_i\left(1\right).$$

${\mathbf{L}}_{\mathbf{0}}$ and ${\mathbf{L}}_{\mathbf{1}}$ can be represented in matrix notation as

$${\mathbf{L}}_{\mathbf{0}}=\left[\left(1-\mu \right)\mathbf{I}+\mu \mathbf{S}\right]{\mathbf{U}}_{\mathbf{0}}\hspace{1em}\mathrm{a}\mathrm{n}\mathrm{d}\hspace{1em}{\mathbf{L}}_{\mathbf{1}}=\left[\left(1-\mu \right)\mathbf{I}+\mu \mathbf{S}\right]{\mathbf{U}}_{\mathbf{1}},$$ [44]

where $\mathbf{I}$ is the identity $N\times N$ matrix, $\mathbf{S}$ is the column stochastic irreducible $N\times N$ matrix

$$\mathbf{S}=\frac{1}{N-1}\left[\begin{array}{cccc}\hfill 0\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 1\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill \cdots \hfill & \hfill 0\hfill \end{array}\right],$$ [45]

and ${\mathbf{U}}_{\mathbf{0}}$ and ${\mathbf{U}}_{\mathbf{1}}$ are $N\times N$ diagonal matrices, which we write as

$$\begin{array}{cc}\hfill {\mathbf{U}}_{\mathbf{0}}& =\text{diag}\left\{\left(1+s_1\right)\hspace{0.17em}\left[1-H_n^1\left(0\right)\right],\left(1+s_2\right)\hspace{0.17em}\left[1-H_n^2\left(0\right)\right],\dots ,\right.\hfill \\ \hfill & \hspace{1em}\dots ,\left.\left(1+s_N\right)\left[1-H_n^N\left(0\right)\right]\right\}\hfill \end{array}$$ [46]

and

$${\mathbf{U}}_{\mathbf{1}}=\text{diag}\left[\frac{1-H_n^1\left(1\right)}{1+s_1},\frac{1-H_n^2\left(1\right)}{1+s_2},\dots ,\frac{1-H_n^N\left(1\right)}{1+s_N}\right].$$ [47]

Observe that both ${\mathbf{L}}_{\mathbf{0}}$ and ${\mathbf{L}}_{\mathbf{1}}$ are positive matrices, so by the Perron–Frobenius theorem, each has a unique positive eigenvalue that is associated with a unique (up to a scalar multiplier) positive eigenvector, and this eigenvalue is its spectral radius. Fixation of $B\hspace{0.17em}\left(p^{*}=0\right)$ is stable if the spectral radius of ${\mathbf{L}}_0$ is less than one, and fixation of $A\hspace{0.17em}\left(p^{*}=1\right)$ is stable if the spectral radius of ${\mathbf{L}}_1$ is less than one. With migration rate $\mu$, let ${\rho }_{\mathbf{0}}\left(\mu \right)$ and ${\rho }_{\mathbf{1}}\left(\mu \right)$ be the spectral radii of ${\mathbf{L}}_{\mathbf{0}}$ and ${\mathbf{L}}_{\mathbf{1}}$, respectively, and recall that $H_n^i\left(0\right)=H_n^i\left(1\right)=D_i\left(n-1\right)$. Then, when $\mu =0$ (no migration) and when $\mu =\frac{N-1}{N}$ (uniform mixing), we have the following result, which is proved in SI Appendix, section C.

Result 7.

$$\mathit{(i)}\hspace{1em}\begin{array}{cc}\hfill {\rho }_{\mathbf{0}}\left(0\right)& =\underset{1\le i\le N}{max}\left\{\left(1+s_i\right)\left[1-D_i\left(n-1\right)\right]\right\}\hfill \\ \hfill {\rho }_{\mathbf{1}}\left(0\right)& =\underset{1\le i\le N}{max}\left\{\frac{1-D_i\left(n-1\right)}{1+s_i}\right\},\hfill \end{array}$$ [48]

$$\mathit{(ii)}\hspace{1em}\begin{array}{cc}\hfill {\rho }_{\mathbf{0}}\left(\frac{N-1}{N}\right)& =\frac{1}{N}\sum _{i=1}^N\left(1+s_i\right)\left[1-D_i\left(n-1\right)\right]\hfill \\ \hfill {\rho }_{\mathbf{1}}\left(\frac{N-1}{N}\right)& =\frac{1}{N}\sum _{i=1}^N\frac{1-D_i\left(n-1\right)}{1+s_i}.\hfill \end{array}$$ . [49]

The special representation for ${\mathbf{L}}_{\mathbf{0}}$ and ${\mathbf{L}}_{\mathbf{1}}$ in Eq. 44 allows us to use the following theorem due to Karlin et al. (37):

Karlin’s Theorem.

Let $\mathbf{S}$ be an arbitrary nonnegative irreducible column stochastic matrix and consider the family of matrices

$$\mathbf{M}\left(\alpha \right)=\left(1-\alpha \right)\mathbf{I}+\alpha \mathbf{S}\hspace{1em}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\hspace{1em}\alpha >0.$$ [50]

Then, for any diagonal nonscalar matrix $\mathbf{U}$ with positive terms on the diagonal, the spectral radius of $\mathbf{M}\left(\alpha \right)\mathbf{U}$ is strictly decreasing as $\alpha$ increases.

Applying Karlin’s theorem to our case, the $\mathbf{S}$ matrix in Eq. 45 is a nonnegative irreducible column stochastic matrix, and assuming that not all terms of ${\mathbf{U}}_{\mathbf{0}}$ and ${\mathbf{U}}_{\mathbf{1}}$ are the same, we have the following result:

Result 8.

${\rho }_{\mathbf{0}}\left(\mu \right)$ and ${\rho }_{\mathbf{1}}\left(\mu \right)$ are decreasing functions of $\mu$ for $0\le \mu \le 1$ and, therefore,

$${\rho }_{\mathbf{0}}\left(\frac{N-1}{N}\right)<{\rho }_{\mathbf{0}}\left(\mu \right)<{\rho }_{\mathbf{0}}\left(0\right),\hspace{1em}{\rho }_{\mathbf{1}}\left(\frac{N-1}{N}\right)<{\rho }_{\mathbf{1}}\left(\mu \right)<{\rho }_{\mathbf{1}}\left(0\right).$$ [51]

We conclude from Result 8 that for any $\mu$ in $\left(\mathrm{0,1}\right)$,

• 1)${\mathbf{P}}^{*}={\mathbf{0}}^{*}$ is stable if $\underset{1\le i\le N}{max}\left\{\left(1+s_i\right)\left[1-D_i\left(n-1\right)\right]\right\}\hspace{0.17em}<1$ and unstable if $\frac{1}{N}{\sum }_{i=1}^N\left(1+s_i\right)\left[1-D_i\left(n-1\right)\right]\hspace{0.17em}>\hspace{0.17em}1$;
• 2)${\mathbf{P}}^{*}=\mathbf{1}$ is stable if $\underset{1\le i\le N}{max}\left\{\frac{1-D_i\left(n-1\right)}{1+s_i}\right\}<1$ and unstable if $\frac{1}{N}{\sum }_{i=1}^N\frac{1-D_i\left(n-1\right)}{1+s_i}>1$.

Remark 4:

• 1)If all of the terms of ${\mathbf{U}}_{\mathbf{0}}$ (or ${\mathbf{U}}_{\mathbf{1}}$) are the same, then ${\rho }_{\mathbf{0}}\left(0\right)={\rho }_{\mathbf{0}}\left(\frac{N-1}{N}\right)={\rho }_{\mathbf{0}}\left(\mu \right)$ (or ${\rho }_{\mathbf{1}}\left(0\right)={\rho }_{\mathbf{1}}\left(\frac{N-1}{N}\right)={\rho }_{\mathbf{1}}\left(\mu \right)$) for all $0\le \mu \le 1$, so that ${\rho }_{\mathbf{0}}\left(\mu \right)$ (or ${\rho }_{\mathbf{1}}\left(\mu \right)$) is constant for all $0\le \mu \le 1$ and does not depend on $\mu$. In this case, ${\rho }_{\mathbf{0}}\left(0\right)$ and ${\rho }_{\mathbf{1}}\left(0\right)$ determine the local stability of ${\mathbf{P}}^{*}=\mathbf{0}$ and ${\mathbf{P}}^{*}=\mathbf{1}$, respectively.
• 2)The above results are sufficient conditions for the stability or instability of ${\mathbf{P}}^{*}=\mathbf{0}$ and ${\mathbf{P}}^{*}=\mathbf{1}$. The exact stability conditions are determined by ${\rho }_{\mathbf{0}}\left(\mu \right)$ and ${\rho }_{\mathbf{1}}\left(\mu \right)$.

Stability of ${\mathbf{p}}^{*}=\left(\frac{1}{2},\frac{1}{2},\dots ,\frac{1}{2}\right)$ with Migration and No Selection.

With no selection in any of the $N$ subpopulations (i.e., $s_i=0$ for all $i=\mathrm{1,2},\dots ,N$), from Eq. 38, we see that ${\mathbf{P}}^{*}=\left(\frac{1}{2},\frac{1}{2},\dots ,\frac{1}{2}\right)$ is a polymorphic equilibrium for any migration rate $0\le \mu \le 1$. Following Eq. 38, with $\mathit{\epsilon }=\left({\epsilon }_1,{\epsilon }_2,\dots ,{\epsilon }_N\right)$, the linear approximation near ${\mathbf{P}}^{*}$ is $\mathit{\epsilon }\prime ={\mathbf{L}}^{*}\mathit{\epsilon }$, which determines the local stability of ${\mathbf{P}}^{*}$. Then,

$${\epsilon }_i^{\prime }=\left(1-\mu \right)d_i{\epsilon }_i+\frac{\mu }{N-1}\sum _{j\ne i}{d}_j{\epsilon }_j,$$ [52]

where

$$d_i=1+{\left(\frac{1}{2}\right)}^{n-2}\sum _{j=k}^{n-1}\frac{D_i\left(j\right)}{n}\left(\begin{array}{c}\hfill n\hfill \\ \hfill j\hfill \end{array}\right)\left(2j-n\right),\hspace{1em}i=\mathrm{1,2},\dots ,N.$$ [53]

As before, ${\mathbf{L}}^{*}$ can be represented in matrix notation as

$${\mathbf{L}}^{*}=\left[\left(1-\mu \right)\mathbf{I}+\mu \mathbf{S}\right]{\mathbf{U}}^{*},$$ [54]

where $\mathbf{I}$ is the $N\times N$ identity matrix, $\mathbf{S}$ is the column stochastic irreducible matrix given in Eq. 45, and ${\mathbf{U}}^{*}$ is the diagonal matrix

$${\mathbf{U}}^{*}=\text{diag}\left(d_1,d_2,\dots ,d_N\right).$$ [55]

However, unlike the cases ${\mathbf{P}}^{*}=\mathbf{0}$ and ${\mathbf{P}}^{*}=\mathbf{1}$, the $d_i$’s may not be positive, in which case we cannot apply Karlin’s theorem.

Is it possible that none of the three equilibria ${\mathbf{P}}^{*}=\mathbf{0}$, ${\mathbf{P}}^{*}=\mathbf{1}$, and ${\mathbf{P}}^{*}=\left(\frac{1}{2},\frac{1}{2},\dots ,\frac{1}{2}\right)$ is stable? For one population and no selection, we found that $p^{*}=0,p^{*}=1$ can be unstable, in which case $p^{*}=\frac{1}{2}$ is the unique polymorphism, but $p^{*}=\frac{1}{2}$ may be unstable. In that case, all of the $D\left(j\right)$’s involved (for $k\le j\le n-1$) are negative, and the single $d$ (in Eq. 53 with $N=1$) that determines the stability of $p^{*}=\frac{1}{2}$ satisfied $d<-1$.

Assume now that in each of the $N$ subpopulations, $p=0$, $p=1$, and $p=\frac{1}{2}$ are not stable in the absence of migration; that is, for all $i=\mathrm{1,2},\dots ,N$ all $D_i\left(j\right)$’s (for $k\le j<n$) are negative and in Eq. 53 $d_i<-1$. Then, $-{\mathbf{L}}^{*}$ in Eq. 54, which has $-{\mathbf{U}}^{*}$ as its diagonal matrix, satisfies the requirements of Karlin’s theorem, and the spectral radii of ${\mathbf{L}}^{*}$ and $-{\mathbf{L}}^{*}$ are identical. Hence, if ${\rho }_{\frac{\mathbf{1}}{\mathbf{2}}}^{*}\left(\mu \right)$ is the spectral radius of ${\mathbf{L}}^{*}$, then it is a decreasing function of $\mu$ for $0\le \mu \le 1$. Also, as $d_i<-1$ for all $i=\mathrm{1,2},\dots ,N$,

$$\begin{array}{cc}\hfill {\rho }_{\frac{\mathbf{1}}{\mathbf{2}}}^{*}\left(0\right)& =\underset{1\le i\le N}{max}\left\{\left|d_i\right|\right\}>1\hfill \\ \hfill {\rho }_{\frac{\mathbf{1}}{\mathbf{2}}}^{*}\left(\frac{N-1}{N}\right)& =\frac{1}{N}\sum _{i=1}^n\left|d_i\right|>1.\hfill \end{array}$$ [56]

Therefore, for all $0\le \mu \le 1$, ${\rho }_{\frac{\mathbf{1}}{\mathbf{2}}}^{*}\left(\mu \right)>1$ and ${\mathbf{P}}^{*}=\left(\frac{1}{2},\frac{1}{2},\dots ,\frac{1}{2}\right)$ is unstable in the metapopulation.

Remark 5.

In the case where all $D_i\left(j\right)$’s for $i=\mathrm{1,2},\dots ,N$ and $k\le j<n$ are positive, by Result 8, both ${\mathbf{P}}^{*}=\mathbf{0}$ and ${\mathbf{P}}^{*}=\mathbf{1}$ are locally stable and in view of Eq. 53 $d_i>1$ for all $i=\mathrm{1,2},\dots ,N$. Hence, the diagonal matrix ${\mathbf{U}}^{*}$ of Eq. 55 is positive, and we can apply Karlin’s theorem, which ensures that ${\rho }_{\frac{\mathbf{1}}{\mathbf{2}}}^{*}\left(\mu \right)$, the spectral radius of ${\mathbf{L}}^{*}$, is decreasing in $\mu$ for $0\le \mu \le 1$. In addition, ${\rho }_{\frac{\mathbf{1}}{\mathbf{2}}}^{*}\left(\frac{N-1}{N}\right)=\frac{1}{N}{\sum }_{i=1}^N{d}_i>1$, which means that ${\rho }_{\frac{\mathbf{1}}{\mathbf{2}}}^{*}\left(\mu \right)>1$ for all $0\le \mu \le \frac{1}{2}$ since $\frac{N-1}{N}>\frac{1}{2}$. Therefore, with all $D_i\left(j\right)$’s positive ${\mathbf{P}}^{*}=\left(\frac{1}{2},\frac{1}{2},\dots ,\frac{1}{2}\right)$ is not stable for all $0\le \mu \le 1$.

Two Populations: Migration without Selection.

Consider two subpopulations $\left(N=2\right)$ and two cultural types $A$ and $B$ that have equal fitnesses $\left(s_1=s_2=0\right)$. We follow the evolution of $A$ and $B$ with three role models in each subpopulation $\left(n=3\right)$ and transmission bias parameters $D_1$ and $D_2$ in subpopulations 1 and 2, respectively. As before, symmetric migration between demes 1 and 2 occurs at rate $\mu$. The frequencies $p_1$ and $p_2$ of $A$ in subpopulations 1 and 2, respectively, satisfy the recursions

$$\begin{array}{cc}\hfill p_1^{\prime }& =\left[p_1+D_1{p}_1\left(1-p_1\right)\left(2p_1-1\right)\right]\left(1-\mu \right)\hfill \\ \hfill & \hspace{1em}+\left[p_2+D_2{p}_2\left(1-p_2\right)\left(2p_2-1\right)\right]\mu \hfill \end{array},$$ [57a]

$$\begin{array}{cc}\hfill p_2^{\prime }& =\left[p_2+D_2{p}_2\left(1-p_2\right)\left(2p_2-1\right)\right]\left(1-\mu \right)\hfill \\ \hfill & \hspace{1em}+\left[p_1+D_1{p}_1\left(1-p_1\right)\left(2p_1-1\right)\right]\mu .\hfill \end{array}$$ [57b]

At equilibrium $p_i^{\prime }=p_i$ for $i=\mathrm{1,2}$, and

$$\begin{array}{cc}\hfill 0& =D_1{p}_1\left(1-p_1\right)\left(2p_1-1\right)\left(1-\mu \right)-\mu p_1\hfill \\ \hfill & \hspace{1em}+\mu p_2+D_2{p}_2\left(1-p_2\right)\left(2p_2-1\right)\mu \hfill \end{array},$$ [58a]

$$\begin{array}{cc}\hfill 0& =D_2{p}_2\left(1-p_2\right)\left(2p_2-1\right)\left(1-\mu \right)-\mu p_2\hfill \\ \hfill & \hspace{1em}+\mu p_1+D_1{p}_1\left(1-p_1\right)\left(2p_1-1\right)\mu .\hfill \end{array}$$ [58b]

Adding Eq. 58 a and b, we have

$$D_1{p}_1\left(1-p_1\right)\left(2p_1-1\right)+D_2{p}_2\left(1-p_2\right)\left(2p_2-1\right)=0.$$ [59]

We will discuss two simple special cases: $D_2=-D_1$ and $D_2=D_1$.

Case 1: $D_2=-D_1$ (inverse conformity):

When $D_2=-D_1$, we have from Eq. 59

$$p_1\left(1-p_1\right)\left(2p_1-1\right)=p_2\left(1-p_2\right)\left(2p_2-1\right),$$ [60]

or

$$\left(p_2-p_1\right)\left[2\left(p_2^2+p_1{p}_2+p_1^2\right)-3\left(p_1+p_2\right)+1\right]=0.$$ [61]

Thus, at equilibrium, either $p_2=p_1$ or $p_2$ satisfies the quadratic equation

$$Q\left(p_2\right)=2p_2^2+\left(2p_1-3\right)p_2+\left(2p_1^2-3p_1+1\right)=0.$$ [62]

When $p_2=p_1$, returning to Eq. 58a, we have

$$D_1{p}_1\left(1-p_1\right)\left(2p_1-1\right)\left(1-2\mu \right)=0.$$ [63]

Assuming $D_1\hspace{0.17em}\ne \hspace{0.17em}0$ and $\mu \hspace{0.17em}\ne \hspace{0.17em}\frac{1}{2}$, we have three equilibria $\left(\mathrm{0,0}\right)$, $\left(\mathrm{1,1}\right)$, and $\left(\frac{1}{2},\frac{1}{2}\right)$. When $p_2\hspace{0.17em}\ne \hspace{0.17em}{p}_1$, we have to solve $Q\left(p_2\right)=0$, as described in SI Appendix, section D, where it is shown that two additional equilibria $\left(p_1^{*},p_2^{*}\right)$ exist, one with both $p_1^{*}$ and $p_2^{*}$ less than $\frac{1}{2}$ and one with both bigger than $\frac{1}{2}$. Simulations show that these equilibria can be stable.

Case 2: $D_2=D_1$ (equal conformity):

In SI Appendix, section E, we show that two polymorphic equilibria of the form $\left(p_1^{*},1-p_1^{*}\right)$ and $\left(1-p_1^{*},p_1^{*}\right)$, satisfying

$$p_1^{*}\left(1-p_1^{*}\right)=\frac{\mu }{D_1\left(1-2\mu \right)},$$ [64]

exist if $\mu <\frac{1}{6}$. These are stable if $\mu <\frac{1}{8}$. An example is illustrated in SI Appendix, Fig. S4.

Observe that as $D_2=D_1>0$ in this case, when $D_1>\frac{6\mu }{1-2\mu }$, $\left(\mathrm{0,0}\right)$ and $\left(\mathrm{1,1}\right)$ are locally stable, but $\left(\frac{1}{2},\frac{1}{2}\right)$ is not. Here, we have an interesting case where the two fixations are stable as well as two polymorphic equilibria.

Two Populations with Migration and Identical Selection.

Suppose $A$ and $B$ have relative fitnesses $1+s:1$ and that the population is divided into two subpopulations labeled 1 and 2 that are connected by symmetric migration at rate $\mu >0$. The value of $s$ is the same in the two subpopulations. Each population has $n=3$ role models, and in subpopulations 1 and 2, the conformity coefficients are $D_1$ and $D_2$. Then, writing $p_1$ and $p_2$ for the frequencies of $A$ in populations 1 and 2, respectively, the recursions are

$$\begin{array}{cc}\hfill p_1^{\prime }& =\frac{\left(1-\mu \right)\left\{\left(1+s\right)\left[p_1+D_1{p}_1\left(1-p_1\right)\left(2p_1-1\right)\right]\right\}}{W_1}\hfill \\ \hfill & \hspace{1em}+\frac{\mu \left\{\left(1+s\right)\left[p_2+D_2{p}_2\left(1-p_2\right)\left(2p_2-1\right)\right]\right\}}{W_2}\hfill \\ \hfill p_2^{\prime }& =\frac{\mu \left\{\left(1+s\right)\left[p_1+D_1{p}_1\left(1-p_1\right)\left(2p_1-1\right)\right]\right\}}{W_1}\hfill \\ \hfill & \hspace{1em}+\frac{\left(1-\mu \right)\left\{\left(1+s\right)\left[p_2+D_2{p}_2\left(1-p_2\right)\left(2p_2-1\right)\right]\right\}}{W_2},\hfill \end{array}$$ [65]

where $W_1=1+s\left[p_1+D_1{p}_1\left(1-p_1\right)\left(2p_1-1\right)\right]$, $W_2=1+s\left[p_2+D_2{p}_2\left(1-p_2\right)\left(2p_2-1\right)\right]$.

We check the local stability conditions for the two fixation states $\left(p_1,p_2\right)=\left(\mathrm{0,0}\right)$ and $\left(\mathrm{1,1}\right)$. Near fixation on $B$, with the frequency of $A$ small in both populations, we have the local stability matrix

$${\mathbf{S}}_0=\left[\begin{array}{cc}\hfill \left(1-\mu \right)\left(1+s\right)\left(1-D_1\right)\hfill & \hfill \mu \left(1+s\right)\left(1-D_2\right)\hfill \\ \hfill \mu \left(1+s\right)\left(1-D_1\right)\hfill & \hfill \left(1-\mu \right)\left(1+s\right)\left(1-D_2\right)\hfill \end{array}\right],$$ [66]

which gives the characteristic polynomial

$$\begin{array}{cc}\hfill P_0\left(\lambda \right)& ={\lambda }^2-\lambda \left(1+s\right)\left(1-\mu \right)\left(2-D_1-D_2\right)\hfill \\ \hfill & \hspace{1em}+{\left(1+s\right)}^2\left(1-2\mu \right)\left(1-D_1\right)\left(1-D_2\right).\hfill \end{array}$$ [67]

Since $D_1,D_2<1$ and $\mu <\frac{1}{2}$, we have $P_0\left(0\right)>0$.

In the same way, near the fixation $\left(\mathrm{1,1}\right)$, the local stability matrix is

$${\mathbf{S}}_1=\left[\begin{array}{cc}\hfill \frac{\left(1-\mu \right)\left(1-D_1\right)}{1+s}\hfill & \hfill \frac{\mu \left(1-D_2\right)}{1+s}\hfill \\ \hfill \frac{\mu \left(1-D_1\right)}{1+s}\hfill & \hfill \frac{\left(1-\mu \right)\left(1-D_2\right)}{1+s}\hfill \end{array}\right],$$ [68]

$$\begin{array}{cc}\hfill P_1\left(\lambda \right)& ={\lambda }^2-\lambda \frac{\left(1-\mu \right)\left(2-D_1-D_2\right)}{1+s}\hfill \\ \hfill & \hspace{1em}+\frac{\left(1-2\mu \right)\left(1-D_1\right)\left(1-D_2\right)}{{\left(1+s\right)}^2},\hfill \end{array}$$ [69]

and again, since $D_1,D_2<1$ and $\mu <\frac{1}{2}$, $P_1\left(0\right)>0$.

Result 4 gives the conditions for existence and global stability of the possible equilibria in each subpopulation in the absence of migration to the other subpopulation. How does migration interfere with these rules? Consider first stability of the fixation of phenotype $B$, the point $\left(\mathrm{0,0}\right)$. We have $P_0^{\prime }\left(0\right)=-\left(1+s\right)\left(1-\mu \right)\left(2-D_1-D_2\right)<0$. Also,

$$\begin{array}{cc}\hfill P_0\left(1\right)& =\left[D_1\left(1+s\right)-s\right]\left[D_2\left(1+s\right)-s\right]\hfill \\ \hfill & \hspace{1em}+\mu \left\{\left(1+s\right)\left(1-D_1\right)\left[D_2\left(1+s\right)-s\right]\right.\hfill \\ \hfill & \hspace{1em}+\left.\left(1+s\right)\left(1-D_2\right)\left[D_1\left(1+s\right)-s\right]\right\},\hfill \end{array}$$ [70]

and

$$P_0^{\prime }\left(1\right)=2-2\left(1+s\right)\left(1-\mu \right)+\left(D_1+D_2\right)\left(1+s\right)\left(1-\mu \right).$$ [71]

If $p_1=0$ and $p_2=0$ are stable in the absence of migration, then we have $D_1+D_2>2s/\left(1+s\right)$ and $P_0^{\prime }\left(1\right)>2\mu >0$. Hence, $\left(\mathrm{0,0}\right)$ is locally stable if $D_1,D_2>s/\left(1+s\right)$, since $P_0\left(1\right)>0$ and $P_0^{\prime }\left(1\right)>0$.

In SI Appendix, section F, we discuss some interesting examples of how migration, selection, and conformity interact to produce different dynamics in the case of two populations.

Conformity and Between-Group Differences.

The role of conformist transmission in maintaining between-group differences is often emphasized (3, 38, 39). For example, Henrich (ref. 40, p. 23) states, “As stochastic forces …introduce random variation between groups, conformist transmission will act to maintain this group-level variation—variation that would otherwise be depleted by migration between groups, natural selection and payoff-biased forms of cultural transmission.” Henrich and Boyd (ref. 4, p. 231) state, “Conformist transmission generates a population-level process that creates and maintains group boundaries and cultural differences through time.” Boyd and Richerson (ref. 41, p. 3790) state that “if [conformity] is strong compared with migration, then variation among groups can be maintained.”

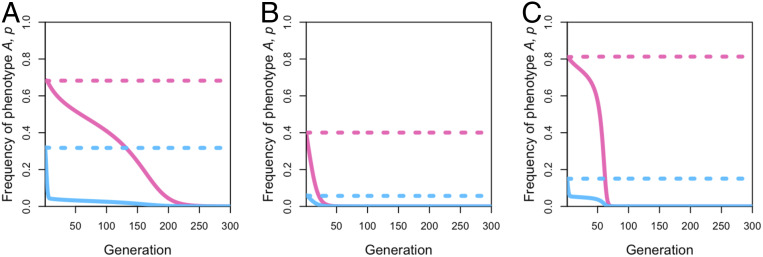
While it is true that, under some conditions, biased transmission can create or sustain between-group differences, under other conditions, conformist transmission can actually eliminate between-group differences. Suppose that there are two populations with migration between them and that there is a stable between-group difference in the frequency of variant $A$ (Fig. 4, dashed lines). This between-group difference may be caused by selection (e.g., selection favoring variant $A$ in population 1 and favoring variant $B$ in population 2) (Fig. 4A), the effects of conformity and anticonformity (Fig. 4B), or some combined effect of selection and transmission biases (Fig. 4C), together with migration. We can include conformity if it is not initially present, or increase the conformity coefficient if conformity is initially present. Fig. 4 shows that, in doing so for the simplest three-role-model case of conformity with two populations, these between-population differences can be eliminated.

Fig. 4.

Adding or increasing conformity can eliminate between-group differences. There are two populations with migration between them at rate $\mu =0.05$. An initial stable between-group difference exists, shown in a dashed line, either due to differences in selection (A), conformity in one population and anticonformity in the other (B), or conformity favoring different variants in each population (C). Adding or increasing conformity to population(s) can eliminate these differences by eliminating the polymorphisms, shown in a solid line. Specifically, the dashed line in A has $D_1=D_2=0$, $s_1=0.1$, $s_2=-0.09090909$, and initial frequencies $p_1=0.68$ (pink) and $p_2=0.32$ (blue). The solid line in A has all parameters kept the same, except that $D_1=0.1$ and $D_2=0.9$; this addition of conformity eliminates the previous between-group difference. In B, the dashed line has parameters $D_1=-0.4$, $D_2=0.4$, $s_1=s_2=0$, and initial frequencies $p_1=0.40$ (pink) and $p_2=0.06$ (blue). The solid line in B has all parameters kept the same, except that the anticonformity in population 1 is switched to conformity at $D_1=0.1$; this addition of conformity again eliminates the between-group differences. The dashed line in C has parameters $D_1=D_2=0.4$, $s_1=s_2=-0.01$, and initial $p_1=0.81$ (pink) and $p_2=0.15$ (blue). The solid line shows that increasing the extent of conformity in one of the populations can eliminate this difference by eliminating the polymorphism; the parameters are the same, except that $D_2=0.9$.

Discussion

Empirical findings regarding conformist transmission have been described in various ways. Whiten et al. (9) showed that naive chimpanzees matched “the predominant approach of their companions” in a food-producing task. Kendal et al. [ref. 13; see also Lachlan et al. (42)] described a feeding behavior in guppies where the fish chose to copy demonstrators rather than use their individual experience if the latter was “too costly to use.” Although that study showed that the fish relied on “social information,” the role of frequency dependence in their learning process is not at all clear.

A form of frequency-dependent copying was, however, observed in the Drosophila mate-choice experiments of Danchin et al. (20), and other studies (16, 17). Danchin et al. found that observer females disproportionately preferred males of the phenotype chosen most commonly by demonstrator females at certain frequencies and suggest that this has the hallmarks of conformist cultural transmission.

The results of simulation studies that explore the evolution of conformity appear to depend sensitively on the precise design of the simulations. Kandler and Laland (43) used a measure called “adaptation level” of a cultural variant at a given time and spatial location. Variants with a higher adaptation level at time $t$ and location $x$ are adopted then and there at a higher rate. They find “a positive relationship between the level of conformity necessary to maximize adaptation levels and the rate of dispersal.” This suggests that there should be a relationship between the rate of migration and the evolution of conformist transmission. However, it is not clear that the results of Kandler and Laland (43) support the proposition of BR, p. 220, that in spatially varying environments conformist transmission “can serve as a simple, generally applicable rule that increases the probability that individuals acquire traits that are favored in the local habitat.”

Lachlan et al. (12) developed a lattice-based simulation of interactions among neighbors based on bird-song-related contests in which the winner gained some of the losers’ resources. Each individual possessed a variant of a dichotomous cultural trait. Two strategies for contests were examined; enforcers chose opponents at random from among neighbors with a different variant, while tolerators selected opponents at random. The enforcer strategy, which is regarded as a conformity-enforcing behavior, was more successful, provided that there was a negative correlation between the number of contests and likelihood of winning.

These examples of simulation studies incorporate many parameters and are difficult to analyze in the form of recursion systems. It is, therefore, difficult to relate them directly to the conformity coefficient, $D$, and the number of role models, $n$, that define the dynamics we have explored here.

Most formal models for evolutionary dynamics under conformist transmission have a generalized logistic structure that gives rise to the S-shaped dynamics seen in many models for the adoption and spread of innovations [e.g., Rogers (44)]. In the context of cultural evolution, the simplest depiction of this mode of transmission allows oblique transmission to follow random vertical transmission of a variant $A$ at frequency $p$, resulting in the recursion (ref. 1, p. 133).

$$p^{\prime }=p+p\left(1-p\right)\varphi \left(p\right).$$ [72]

The simplest case takes $\varphi \left(p\right)=D$, say, where the constant $D$ is the rate of conversion to variant $A$ of offspring that did not obtain variant $A$ by vertical transmission. [Note: Cavalli-Sforza and Feldman (1) use $f$ instead of $D$ to denote the constant.]

Exactly the same recursion is reproduced by Henrich (ref. 26, equation 3) as formalizing “biased cultural transmission” using “basic replicator dynamics.” Henrich (ref. 26, equation 6) modifies Cavalli-Sforza and Feldman’s (1) model by changing the first term so that the recursion becomes $p^{\prime }=\alpha +\beta p+Dp\left(1-p\right)$, where $\alpha$ and $\beta$ define properties of “environmental learning.” Here, neither $\widehat{p}=0$ nor $\widehat{p}=1$ are equilibria, and, depending on the signs and magnitudes of $\alpha$, $\beta$, and $D$, a polymorphic equilibrium may exist.

The model of conformist transmission in BR (ch. 7) takes the formulation in Eq. 72 above and assumes $\varphi \left(p\right)=D\left(2p-1\right)$. If $D>0$, this forces $p$ to increase over time if initially $p>\frac{1}{2}$ and to decrease over time if initially $p<\frac{1}{2}$. In this case, there is a transmission bias toward majority type, while if $D<0$, this bias is toward the minority type; these are called “conformist” and “anticonformist” bias, respectively.

If the number of role models is greater than four, however, the simple dynamics of recursion 1 may become much more complicated with $\varphi \left(p\right)=\left(2p-1\right)H_n\left(p\right)$. With five role models, for example, two conformity coefficients analogous to $D$ in Eq. 10 are required, and, depending on their signs and magnitudes, more polymorphic equilibria than the single point $p=\frac{1}{2}$ may exist and be stable. Thus, it is possible that none of the equilibria that characterize the three-role-model system may be stable when there are more role models. In addition, cycling or even chaos may emerge as the conformity parameters change.

Complex dynamics have been observed in different versions of BR’s original conformity model. Kendal et al. (24) track individual learners and social learners whose fitness depends on their level of conformity. In their model, as in that of Efferson et al. (23), they use a single conformity coefficient, $D$, to weight the frequency-dependent bias. They compute the probability of conforming (in the context of a dichotomous trait) from the binomial distribution. In their analysis, they do not observe multiple isolated stable equilibria, but in some cases, they do see cycles and chaos in the dynamics. Walters and Kendal (30) incorporated a form of frequency-dependent transmission closely related to the usual conformity case with three role models in a susceptible–infected–susceptible epidemic model with cultural transmission. For some parameters, they observed a bistable situation in which for strong enough conformity, both one fixation state and a polymorphism could be stable, depending on the initial variant frequency.

The model studied here assumes that $n$ is fixed, and the degree of conformity depends on how many of each type $\left(A,B\right)$ are sampled from these $n$ role models. If $n$ itself represented a random sample from a population of, say, $N$ potential role models, the model would be quite different. It would also be different if individuals with prestige or some measure of success were copied at a rate greater than just their likelihood of being $A$ or $B$ among the $n$ role models. Some aspects of this kind of model are discussed by Fogarty et al. (28).

With selection and conformist transmission, $p=\frac{1}{2}$ no longer plays the important role it has in the absence of selection. In the three-role-model case with selection coefficient $s>0$, if $D>s/\left(1+s\right)$, both fixations on phenotypes $A$ and $B$ are stable, and an unstable polymorphism separates their domains of attraction. If $s/\left(1+s\right)>D>-s$, this polymorphism disappears, and only fixation on phenotype $A$, whose fitness is $1+s$ relative to 1 for phenotype $B$, can occur. Finally, if $D<-s$, the unique polymorphic equilibrium is stable. Result 4 addresses the case of more than three role models.

Although conformist transmission, as a case of frequency-dependent cultural transmission (45), can affect the evolution of cultural traits, the evolution of the propensity to conform is also an important issue in cultural evolution. We treat this issue as analogous to the evolution of genetic transmission in the purely biological context, where recombination and mutation are included under the rubric of transmission, and their evolution is usually studied by using modifier theory (36).

Our application of modifier theory to the evolution of the conformity coefficients and the number of role models whose variant frequencies form the basis for conformity follows the logic of modifier theory in population genetics. This formal theory does not track mean fitness or some other utility function that depends on conformity. The evolution of conformity is determined by the dynamics of the modifier alleles $M$ and $m$.

Our function $H_n\left(p\right)$ in Eq. 37 determines whether a modifier of conformity can invade a population. In approaching this problem, it is essential that the invading modifier allele arises near a stable polymorphism; if the population happens to be fixed on $A$ or $B$ ($x_1^{*}=1$ or $x_1^{*}=0$), one might make an argument in terms of the mean fitness Eq. 14. This would essentially be a group-selection approach, one that has largely been used in verbal (nonmathematical) arguments about the evolution of conformity. Our modifier approach fits within Eshel and Feldman’s (46) paradigm of evolutionary genetic stability. With an arbitrary number of role models ($n$), $H_n\left(p\right)$ takes the role of $D$ in the simplest analysis (BR, p. 108), and if all of the conformity parameters $D\left(j\right)$ are the same, i.e., $D\left(j\right)=D$ for all $j$, then $D<-s$ (i.e., anticonformism) is necessary for existence of a stable polymorphism. A modifier then invades if it reduces anticonformism; i.e., if it makes $D$ less negative. Under many conditions, the common phenotype will be the one favored by selection, and, therefore, anticonformity can be regarded as a process that increases phenotypic variation. Therefore, selection for reduction of anticonformity is in accordance with the reduction principle (47).

The interaction between conformist transmission and population subdivision has been a focus of attention. Boyd and Richerson (41, p. 3790) state that “if [conformity] is strong compared with migration, then variation among groups can be maintained.” Mesoudi (48, p. 1) finds that “surprisingly little conformist acculturation is required to maintain realistic amounts of between-group cultural diversity.” Examples from Fig. 4 show that conformity can also eliminate between-group differences. Part of the difficulty in reconciling different explanations of the interaction between conformity and migration lies in the variety of assumptions underlying the models.

We have attempted to be precise about the migration analysis that gives Result 8 and conditions for stability of the fixation states and possible polymorphisms. Thus, if the conformity parameters in all populations are sufficiently negative, none of $\left(\mathrm{0,0},\dots ,0\right)$, $\left(\mathrm{1,1},\dots ,1\right)$, or $\left(\frac{1}{2},\frac{1}{2},\dots ,\frac{1}{2}\right)$ are stable. If these parameters are all positive, then $\left(\frac{1}{2},\frac{1}{2},\dots ,\frac{1}{2}\right)$ is not stable, but the two fixation states are.

Our detailed analysis of the two-population case without selection illustrates how complex the relationship between migration and conformist transmission can be. If the conformity coefficients are the same in both populations, two polymorphic equilibria other than $\left(\frac{1}{2},\frac{1}{2}\right)$, as well as the fixation states $\left(\mathrm{0,0}\right)$ and $\left(\mathrm{1,1}\right)$, can be stable if the migration rate is less than $\frac{1}{8}$ and the conformity coefficient is large enough (Eq. 64). However, if this coefficient is small enough, only the fixation states are stable.

Thus the claim that “conformist transmission generates a population-level process that creates and maintains group boundaries and cultural differences through time” (ref. 4, p. 231) is not always true.

Data Availability.

All additional methods are in SI Appendix. There are no additional data.