Self-assembled plasmonics for angle-independent structural color displays with actively addressed black states

Significance

Functional nanomaterials will enable the next generation of displays, detectors, and photovoltaic devices by interacting with light at subwavelength length scales. However, performance and practical integration with current electronic systems remain a scientific and engineering challenge. Here, we report the wafer-scale self-assembly/growth of nanoparticles which reproduce the cyan, magenta, and yellow color space. We explore the physics of the optical resonances and the advantageous properties they manifest for color filter technology, such as angle insensitivity and high saturation. The versatile formation process then enables integration with commercial devices to realize a hybrid, nanoparticle–liquid crystal reflective display.

Abstract

Nanostructured plasmonic materials can lead to the extremely compact pixels and color filters needed for next-generation displays by interacting with light at fundamentally small length scales. However, previous demonstrations suffer from severe angle sensitivity, lack of saturated color, and absence of black/gray states and/or are impractical to integrate with actively addressed electronics. Here, we report a vivid self-assembled nanostructured system which overcomes these challenges via the multidimensional hybridization of plasmonic resonances. By exploiting the thin-film growth mechanisms of aluminum during ultrahigh vacuum physical vapor deposition, dense arrays of particles are created in near-field proximity to a mirror. The sub-10-nm gaps between adjacent particles and mirror lead to strong multidimensional coupling of localized plasmonic modes, resulting in a singular resonance with negligible angular dispersion and ∼98% absorption of incident light at a desired wavelength. The process is compatible with arbitrarily structured substrates and can produce wafer-scale, diffusive, angle-independent, and flexible plasmonic materials. We then demonstrate the unique capabilities of the strongly coupled plasmonic system via integration with an actively addressed reflective liquid crystal display with control over black states. The hybrid display is readily programmed to display images and video.

The demand for higher-resolution displays is omnipresent—especially for the next generation of near-eye, virtual/augmented reality, and three-dimensional displays in which form factor and/or additional functionalities place constraints on pixel size. The integration of nanostructured optical materials into system-level display electronics will meet this need by simultaneously interacting with light at subwavelength length scales and allowing spatiotemporal control over said interactions. Coupled with increased photostability and the potential to engineer the polarization, phase, and amplitude of light, optical nanostructures can improve current displays and lead to novel forms. Several examples of nanostructure-integrated displays have been demonstrated, in which metallic nanostructures generate color (1–3) and are then combined with liquid crystal modes (4, 5), electroactive polymers (6–9), or phase-change materials (10) to modulate the amplitude of reflected/transmitted light. Alternatively, the plasmonic resonances of these metallic nanostructures can be tuned via liquid crystal orientation (11, 12) (our previous work) or reversible chemical reactions (9, 13–17) to result in novel color-changing surfaces. However, for such plasmonic displays to be competitive and relevant in the context of current display technology, they must meet rigorous consumer standards in color quality and angular performance while simultaneously meeting requirements for active addressing and manufacturability.

Here, we overcome these challenges and demonstrate an actively addressed plasmonic display with angle-independent diffuse color enabled by multidirectional resonance hybridization. Vividly colored surfaces originate from a dense array of aluminum nanoparticles in the near-field proximity of a mirror. Formed through a large area, highly reproducible self-assembling technique, the <10-nm gaps between particles and mirror result in strong lateral and vertical hybridization of plasmonic modes and manifest a single, angle- and polarization-insensitive resonance with ∼98% absorption at a desired wavelength. The large-area formation process is compatible with, and takes on the scattering properties of, arbitrarily structured substrates and can result in diffusive, angle-independent, and flexible plasmonic color surfaces. We demonstrate the potential of such a nanostructured optical system through its integration into addressable optoelectronic devices, namely, a commercial 80° mixed-mode twisted nematic (MTN) reflective liquid crystal display (LCD). The resulting high-aperture-ratio monochrome display is capable of 1-bit grayscale control (limited by the thin-film transistor [TFT] which was harvested from a Sharp memory display) and the portrayal of images and video. Our approach demonstrates several key advancements over our previous work in color quality, angle independence, large-scale fabrication, and system-level electronics integration that when combined lead to a plasmonic display with actively addressed black states. Together, these efforts represent a significant step toward the integration of plasmonic nanostructures into display and consumer product technologies.

Results

Self-Assembled Aluminum Plasmonic Surface.

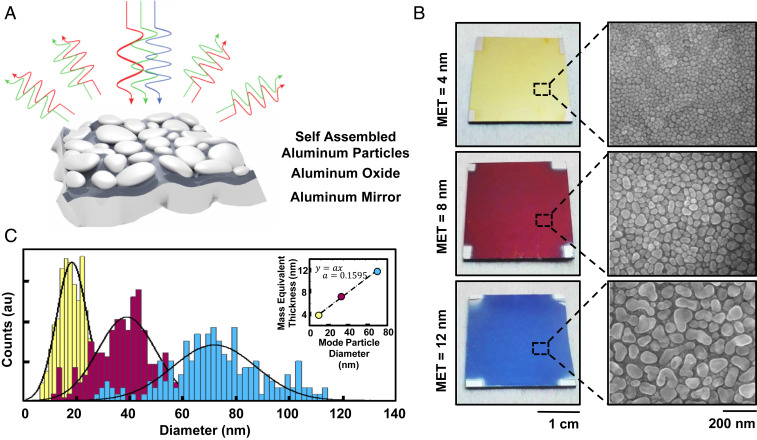
The plasmonic system consists of a dense array of aluminum nanoparticles formed on top of an oxide-coated aluminum backplane, an illustration of which is shown in Fig. 1A. Ambient white light excites resonances within the structure which are predominantly confined to the gaps between particles. These resonances demonstrate a high degree of angle independence and their spectral location is a function of the size distribution of the aluminum particles, the surrounding refractive index, and the optical distance from each other and the mirror. Light which is not absorbed by the surface is reflected to result in a perceived color. The fundamental physics of this gap-plasmon mode is discussed in the sections below.

Fig. 1.

Self-assembled plasmonic system and particle statistics. (A) Schematic of self-assembled aluminum particles atop an oxide spacer and aluminum mirror. Wavelength of plasmon resonance scales with particle size. (B) Camera images and scanning electron microscope images of three sampled surfaces corresponding to yellow, magenta, and cyan. (C) Histogram of particle sizes obtained from the SEM images shown in B. Radii for particles are calculated assuming an area equivalent sphere.

The particles form through a temperature- and pressure-dependent thin film growth mechanism in an ultrahigh vacuum electron beam evaporator, and understanding this growth mechanism is vital in designing and controlling attributes of the surface. Island formation during physical vapor deposition has been extensively studied (18–20) and is generally categorized into three modes (21): Frank–van der Merwe (layer by layer), Volmer–Weber (island), and Stranski–Krastanov (layer and island). Aluminum exhibits the Volmer–Weber growth mode (22) which is initiated by the adsorption of atoms to the surface of the substrate. The energetic molecules are free to diffuse along the surface until they settle on a site with a local energy minimum. Subsequent aluminum atoms adsorb, diffuse, and condense about these low-energy sites in a process termed nucleation. As this continues, particles anchored at adjacent nucleation sites grow and form grain boundaries, or, if energetically favorable, coalesce to form larger particles. The shape of the combined particles depends on the equilibrium condition between the aluminum’s free energy and interfacial stress with the substrate. The cumulative result of this process at three mass equivalent thicknesses (MET) (4, 8, and 12 nm) can be seen in Fig. 1B, resulting in yellow, magenta, and cyan sample colors, respectively. Scanning electron micrographs (SEMs) of the samples show an increase in particle size as a function of material deposited. Interestingly, the fill fraction of particles on the surface remains near unity for all samples, which indicates a high number of nucleation sites in the initial phase of deposition. From the SEM images, we obtain histograms of particle size using the Gwyddion software package (23) and approximate the area of each particle with an equivalent circular area. The distributions are shown in Fig. 1C and indicate that the spread of particle diameters increases within a sample as deposition continues. This is also seen qualitatively from the SEM images that the rather circular particles of the yellow sample become more irregular as lateral particle size increases. We attribute this to the interfacial energy of aluminum to the aluminum oxide substrate at odds with the aluminum particle surface energy, preventing the aluminum from reforming into symmetric oblate ellipsoids. Despite this increasing irregularity, the particle distributions are isotropic and show no preferred particle elongation direction.

Color Space and Origin of Plasmonic Color.

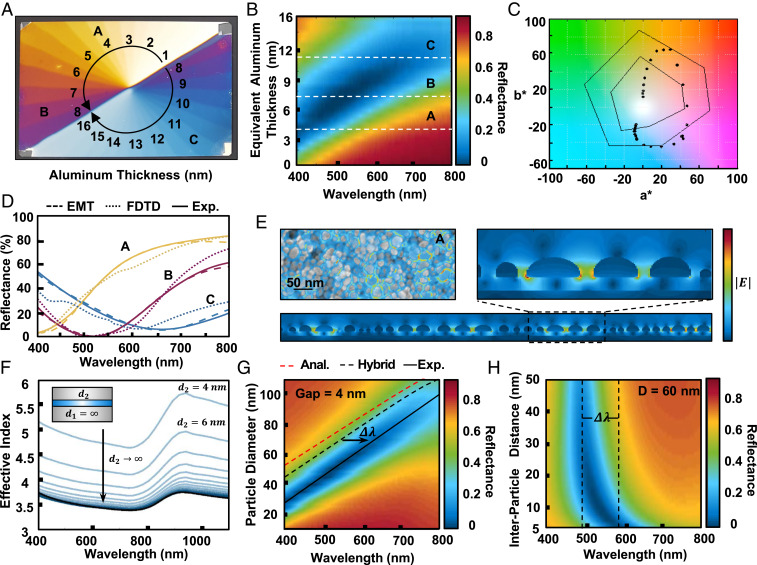
To show the range of color achievable with such a system, we sweep over the thickness of aluminum deposited on a single sample by adapting a partial (half) shutter and rotatable stage. We rotate the sample roughly 11° every 0.5-nm Al deposition for a total of 8 nm over 180° and then statically deposit another 8 nm on top. This method results in the vivid sample and corresponding spectra shown in Fig. 2 A and B. As the deposition begins, the white mirror-like reflectance of the sample turns yellow as the plasmon resonance red-shifts from the ultraviolet (UV) to visible spectrum. The pronounced, near-100% absorption resonance continues to shift through the visible regime, creating a standard subtractive color palette. The dashed white lines of Fig. 2B correspond to the yellow (A), magenta (B), and cyan (C) samples of Fig. 2A and the SEM images of Fig. 1B. The color quality or contrast of the reflective colors is quantified in Fig. 2C as represented in the CIELAB color space. The more vivid a color, the further it is from the origin—while near the center resides unsaturated mixtures of light culminating in the white point. Black dots on the graph represent the color of the plasmonic surface and are obtained by applying the standard CIE chromaticity function conversion of the spectra in Fig. 2B. To provide context to this color quality, we overlay two color-quality standards used in the commercial printing industry: ISO 12647-3 for the inner hexagon representing newsprint and SWOP coated 1, ISO-standard on grade 1 high-quality photo paper for the outer hexagon in Fig. 2C. We find that the color generated by the plasmonic surface exceeds a fair portion of the newsprint color space and reaches that of the high-quality photo paper for certain colors. However, the singular subtractive resonance of the surface prohibits the creation of green and color mixing techniques must be employed—just as in conventional CMYK (cyan, magenta, yellow, and key [black]) printing. We address this limitation and propose methods to achieve green and expand the color space within sections below.

Fig. 2.

Particle size-dependent plasmonic color and quality. (A) Camera image of a 1- × 2-in. sample in which the amount of aluminum deposited is azimuthally varied. This changes the size of particles and results in the reflectance spectra seen in B. White dotted lines indicate thicknesses corresponding to 4, 7.5, and 11 MET. (C) The CIELAB space diagram where black dots indicate values for the surface color in A and B. Black outlines indicate print industry standards ISO 12647-3 for the inner hexagon and SWOP coated 1, ISO-standard on grade 1 high-quality photo paper for the outer hexagon. (D) Reflectance measurements of the surface compared to discrete dipole approximation theory and finite difference time domain modeling. (E) Field profiles obtained through FDTD at resonance showing field confinement in the gaps between particles. (F) Finite element method modeling of an MIM system as a function of top metal thickness. (G) FDTD simulations predicting resonance location as a function of particle diameter. The dotted red line shows the MIM model resonance location, while the dotted black line shows the hybrid MIM model taking into account finite film thickness. The solid black line indicates the experimentally observed location. (H) FDTD simulations over interparticle distance in which the shift in resonance location from the MIM model and experiment is found to be due to near-field coupling of adjacent particles.

The island formation is a statistical process which greatly depends on the temperature of the substrate and pressure of the chamber at the time of evaporation. We find that surfaces deposited within 25 to 100 °C and 10⁻⁶ to 10⁻⁷ torr result in colored surfaces; however, they are relatively unsaturated. Alternatively, the color vibrancy appears to increase with lower pressures (10⁻⁷ to 10⁻⁹ torr) and hotter substrates (100 to 150 °C). We attribute these differences to changes in contact angle between the aluminum particles and that of the aluminum oxide spacer—therefore modifying the plasmon resonance strength and coupling efficiency. A detailed exploration of the temperature and rate parameter space on the resulting color for a constant oxide thickness of 10 nm is given in SI Appendix, Fig. S1. The thickness of this oxide layer also influences the coupling and overall strength of the resonance. SI Appendix, Fig. S2 shows finite-difference time-domain (FDTD) simulations over oxide thickness and that while the optimal value for maximum absorption depends slightly on particle size, a thickness of 10 nm results in the greatest average absorption across all particle diameters. Furthermore, the surface is highly insensitive to polarization due to the lateral isotropic distribution of particles and particle shapes. SI Appendix, Fig. S3 shows images of the swept plasmonic surfaces for unpolarized and two orthogonal linearly polarized states. This is highly important for integration into optoelectronic devices which utilize the polarization of light such as LCDs.

To understand the fundamental resonance mechanisms involved in the particle system, we employ analytical modeling techniques based on effective medium and metal–insulator–metal (MIM) waveguide theories. The predictions of these models are then compared with experimental and FDTD simulated reflection spectra of the three selected particle distributions, yellow (A), magenta (B), and cyan (C), shown in Fig. 2D. Due to the highly dense and subwavelength nature of the particle films, we first apply a stratified effective medium theory (EMT) where an effective polarizability is obtained for the particle film assuming the fundamental shape of oblate ellipsoids (24–26). Size distributions and depolarization terms are included to account for the inhomogeneous linewidth broadening and particle-to-particle near-field coupling, respectively. Once this singular layer is approximated, Fresnel equations are then applied to find the total reflectance coming from the combined multilayer stack comprised of particle film, oxide spacer, and back mirror. SI Appendix, Fig. S4 shows experimental and EMT reflection spectra of the aluminum particle films in the absence of a mirror, as an intermediary to that of the mirror-coupled system. Alternative models which account for truncated spheroids (27), near-field interactions at material interfaces (28–30), and higher-order multipolar resonances (31) can all be implemented, but each is constrained by respective assumptions and limitations on particle shape, coverage, surrounding media, and so on. We find that the EMT model employed here adequately matches that of the experimental spectra (Fig. 2D) with the use of a single fitting parameter that approximates the cumulative depolarization of particles imparted by particle–particle and particle–mirror near-field coupling.

To further validate the EMT method and visually identify resonance mechanisms, FDTD simulation is performed on the system obtained directly from the SEM image of the experimental samples in Fig. 1B. This brute-force approach—of importing particle surfaces and extrapolating into large simulation volumes—accounts for particle distributions and near-field coupling effects and gives a unique perspective on field localization within a randomly distributed particle media. Reflectance spectra are shown in Fig. 2D and compared to the experiment and the EMT model. While the spectra are close, the SEM images only give an accurate x–y profile of the particle shape and location. Hence, in FDTD the out-of-plane profile is approximated as a cropped oblate ellipsoid which contributed as one source of spectral differences. Many particles are also required to accurately represent the dispersion of particles and the broad resonances they create. Here, we use surfaces with 1,372, 1,659, and 1,539 particles or equivalently a total surface area of 10.76, 2.983, and 0.662 μm² for cyan (C), magenta (B), and yellow (A) samples, respectively. Fig. 2E shows the FDTD predicted field for the A sample in the x–y plane as well as in the x–z plane at the resonant wavelength of 400 nm. From these we see that the field is highly confined to the edges of the particles and within particle–particle gaps. Further, results of the full-wave simulations for A, B, and C—including decompositions of field—are provided in SI Appendix, Fig. S5. The field surrounding the particles is characteristic of gap surface plasmons but which occur at wavelengths not predicted in previous reports. To elucidate the relation of the dense particle system with that of gap surface plasmons, we modify an alternative model which first determines the dispersion of an MIM waveguide (32, 33). The following relation is commonly used:

$$\text{tanh}\left(\frac{\sqrt{{\beta }^2-k_0^2{\epsilon }_d}{t}_d}{2}\right)=\frac{-{\epsilon }_d\sqrt{{\beta }^2-k_0^2{\epsilon }_m}}{{\epsilon }_m\sqrt{{\beta }^2-k_0^2{\epsilon }_d}},$$

where $\beta$ is the propagation constant,$t_d$ is the thickness of the insulator, and ${\epsilon }_d$ and ${\epsilon }_m$ are the dielectric constants of the insulator and metal, respectively. This equation assumes two infinite metal regions surrounding a dielectric gap of finite thickness. The particles and thin films used in MIM resonators, however, cannot be approximated as infinite if their thickness is comparable to their skin depth. We perform finite-difference eigenmode simulations (Mode Solutions; Lumerical) to quantify the impact of this approximation on the effective index of a mode propagating parallel to the surface, within the dielectric gap, as a function of top metal thickness, d₂. Here, aluminum is used as the metal and 10 nm of aluminum oxide used as the spacer. The thickness, d₁, of the bottom metal is 150 nm—well beyond the skin depth of the material—and can therefore be safely approximated as infinite within the visible domain. Fig. 2F shows the results of these simulations and that the index of the mode varies greatly for top film thicknesses less than 20 nm. As the film thickness increases, the index approaches that of the infinite case and closely matches that obtained analytically, represented by the black line. Once the effective index is attained as a function of film thickness, we apply the condition for constructive interference for such a propagating mode (32, 34):

$$W\left(\frac{2\pi }{{\lambda }_{res}}\right)n_{eff}=m\pi -\varphi ,$$

where $W$ is the mean diameter of Al particles on the top layer, $n_{eff}$ the effective index of the propagating mode, $m$ the mode order, and $\varphi$ a phase term due to reflection at the particle boundary. Using the first order (m = 1) and assuming zero reflective phase, the combination of these relations allows us to predict the resonant wavelength, ${\lambda }_{res}$, for a given particle diameter. Due to the close packing nature of the particle arrays, we approximate the particle height as the MET of the deposited film and relate this to particle diameter through the particle distributions of Fig. 1. The results of this approach are represented by the dashed black line in Fig. 2G and can be compared to the red dashed line of the infinite metal MIM case and the solid black line of experiment—all of which are overlaid atop a sweep of FDTD simulations. For these FDTD simulations, a single particle is assumed within square periodic boundary conditions. This simplification of the surface as a perfectly ordered square array neglects the impact of size distributions but accounts for particle−particle and particle−mirror coupling, allowing us to isolate the impacts of various physical parameters and greatly reducing simulation requirements. The resonances also have a narrower full width at half maximum (FWHM) than experimental results due to the lack of inhomogeneous broadening. Using an interparticle gap of 4 nm, which we obtain through SEM images, the location of the plasmon resonance red-shifts linearly with particle diameter—a result in close agreement with the experimental spectra shown in Fig. 2D. In comparing the results of Fig. 2G, we find a discrepancy in the predicted resonance location obtained through the analytical and hybrid MIM models and that of experiment. Accounting for the finite thickness of the MIM resonators produces an averaged corrective shift of 40 nm but differs still from the experimental case by a wavelength of $\mathrm{\Delta }\text{λ}=90\hspace{0.17em}\text{nm}$. We attribute this to the near-field coupling that occurs between particles and subsequent hybridization of plasmonic modes which is not considered in the analytical MIM model. This hybridization can be understood as the splitting of energy levels within the system into parallel and antiparallel resonances on adjacent particles (35, 36). The in-phase resonance becomes a blue-shifted nonradiative mode whereas the out-of-phase resonance red-shifts and can be excited via external light. The strength of this splitting and, therefore, amplitude of the red or blue shift depends greatly on the interparticle distance and has been termed the plasmonic ruler effect in previous literature (37–39). This idea stems from classical electromagnetic theory, where the interaction energy between two radiating dipoles is given by

$$U=\frac{1}{4\pi {\epsilon }_0}\frac{{\left|\mu \right|}^2}{n_m^2{S}^3}\kappa ,$$

where ${\left|\mu \right|}^2$ is the squared modulus of the transition dipole moment, $n_m$ is the refractive index of the surrounding medium, S is the dipole–dipole separation, and the orientation factor $\kappa =\cos {\alpha }_{12}-3\cos {\alpha }_{1S}\cos {\alpha }_{2S}$, where ${\alpha }_{12}$, ${\alpha }_{1S}$, and ${\alpha }_{2S}$ represent the angles between the two dipoles and the vector connecting them. Fig. 2H shows a series of FDTD simulations by changing this interparticle distance while keeping a constant particle diameter. As the interparticle distance increases, we observe the characteristic $1/r^3$ decay in interaction energy and blue shift of the resonance wavelength. This value asymptotically approaches that of the infinitely spaced particle case but becomes negligible beyond 40 nm. The resonance shift, $\mathrm{\Delta }\text{λ}$, from the infinite interparticle case to the experimentally obtained distance of 4 nm closely matches that obtained through Fig. 2G and confirms that the near-field coupling plays a pivotal role in defining the resonance location and ultimately color of the plasmonic surfaces. If this gap were to decrease to zero (signifying touching particles), the electron confinement and therefore plasmonic resonance would cease to exist. Through these models and simulations we show how the system can be understood through different theoretical starting points. Whether beginning with the optical properties of a single particle, extending to an effective optical film and then the effects of mirror coupling, or beginning with a combined MIM system, obtaining resonance relations through constructive interference conditions, and then accounting for hybridization due to the close packed nature of the film, we show that they are consistent.

Angle-Independent, Diffuse, and Flexible Plasmonic Color.

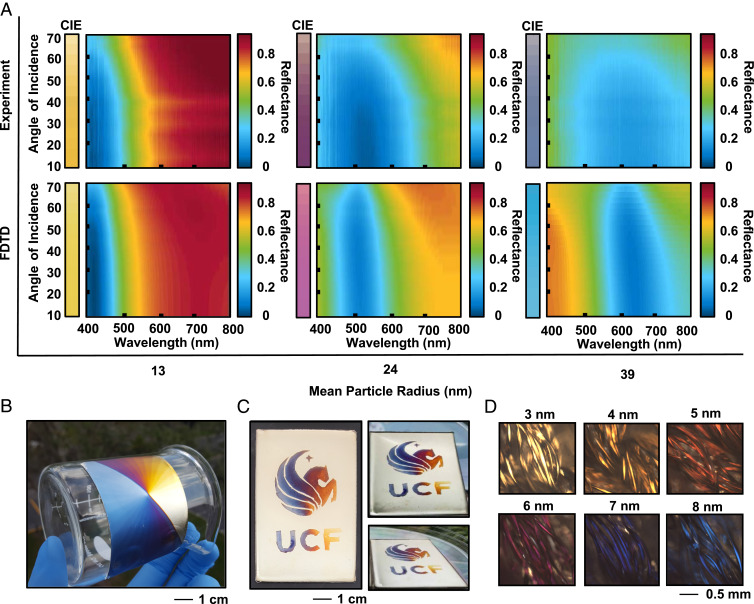
Grating coupled or Fabry–Perot-based nanostructure modes (40–42) can produce narrow and high amplitude reflectance. However, the color observed is inherently dependent on the angle of incident light. For display and consumer product coloration this can be undesirable and has limited such structural color from several practical applications. In Fig. 3A we demonstrate a key advantage of the subwavelength, localized gap plasmon resonance of the aluminum island nanostructure and address the need for high-contrast color in addition to angle insensitivity. Utilizing an integrating sphere with a rotatable mount (RTC-060-SF; Labsphere) and a spectrometer (HR 2000+; Ocean Optics), we show experimental spectra of the three selected samples (yellow [A], magenta [B], and cyan [C]) in the top row of Fig. 3). Past an incident angle of 60°, the amplitude of the resonance gradually decreases but maintains its spectral location. This invariance of the aluminum island plasmonic system to excitation angle is validated via FDTD simulations and shown in the bottom row of Fig. 3 for three particle radii, 13, 24, and 39 nm, corresponding to yellow, magenta, and cyan samples, respectively. These radii are obtained by the mean of the particle distributions of Fig. 1B. We approximate the particle system as a perfectly periodic square array to perform the large number of angle-dependent simulations. The FDTD-predicted resonances based on periodic arrangements are narrower than the experimental case due to the lack of inhomogeneous broadening of the actual aperiodic particle arrangement. The resulting simulations closely match in resonance location, as well as the qualitative behavior of the resonance as a function of angle. To further quantify the impact of these results on the color perceived from the surface, the CIE-predicted color as a function of angle is presented in a bar adjacent to each dataset.

Fig. 3.

Angle-independent, diffuse, and flexible plasmonic color. (A) Top experimental row is obtained through angle-resolved reflectance measurements using an integrating sphere and fiber optic coupled spectrometer. The bottom row consists of FDTD simulations using a perfectly periodic square array of particles. Adjacent to each dataset is the projected color of the surface obtained using the CIE chromaticity matching functions. (B) Fabrication performed on a thin, flexible layer of PDMS (2 × 3 in.) and (C) masked fabrication of the aluminum particles in the form of the UCF Pegasus logo (2 × 3 in. sample). (D) Microscope images of the surface fabricated on a 100% polyethylene terephthalate fabric.

In addition to the angle insensitivity of the plasmonic system, the ability to form them at low temperatures allows uniform implementation on a wide selection of substrates. This is in contrast to the annealing techniques commonly employed to generate similar particle island films (43–45). This fabrication flexibility also allows the system to take on the scattering attributes of the substrate and leads to a demonstration of engineerable, diffuse plasmonic color. Fig. 3B shows the color space of the plasmonic system fabricated on a flexible polydimethylsiloxane (PDMS) substrate attached to a curved surface. Interestingly, the deposition of a thick aluminum mirror on the PDMS creates microcorrugations on the surface, which results in a shimmering semidiffuse effect on the reflected color. This potentially opens opportunities to a large range of consumer products and further research including dynamic, stretchable, and tunable systems. Stencils or conventional photolithography lift-off techniques can also be employed to pattern the plasmonic surface. By placing a physical mask on the substrate and rotating during particle deposition, we recreate the “UCF” Pegasus logo in Fig. 3C. The accompanying images are taken at increasing angles to reaffirm the system’s angular invariance. Finally, we show the ability to form the plasmonic system on fibers and fabrics. Microscope camera images of the surface formed on a 100% polyester fabric (TexVantage Polyester; Texwipe) are presented in Fig. 3D. The images are at 15× magnification and span the same subtractive color gamut produced on alternative substrates. Due to the anisotropic nature of electron beam evaporation, only a portion of the fibers are coated with the plasmonic surface, which can lead to poor angular response. However, implementation of angled depositions along with stage rotation can greatly reduce these effects.

To quantify the impact of an extreme diffuse substrate on the plasmonic resonance and resulting color, we measure the integrated diffuse reflectance of a plasmonic surface on sandblasted glass in SI Appendix, Fig. S6. The surface of the glass is jagged and contains random microstructures more than 100 μm in height. The result is an extremely diffuse, matte, and paper-like finish compared to the specular mirror finish when formed on optically smooth surfaces. The summation of these advantageous attributes makes the plasmonic particle system a promising candidate for new multifunctional materials with stretchable, flexible, angle-independent, and diffuse color properties which can find use in displays and biosensing applications (46).

Liquid Crystal Integration, Gray States, and Active Addressing.

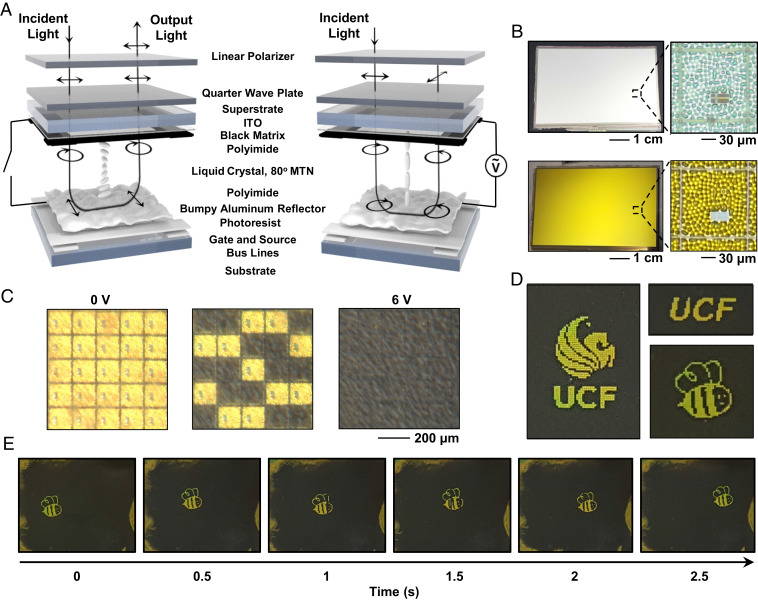
The combination of angle insensitivity and substrate versatility allows the plasmonic particle system to be readily integrated with various optoelectronic devices. Here, we leverage decades of research and engineering within the LCD industry to quickly compose and evaluate novel types of reflective hybrid displays. A pixel schematic of the reflective display can be seen in Fig. 4A, in which light passes through a circular polarizer (linear polarizer and quarter-wave plate), LC layer and is incident upon a bumpy aluminum reflector. The display uses the 80° MTN LC cell (47). This reflective LC mode is chosen as it has high angle tolerances of more than 50^o (48). In the OFF state of the device, the twist, birefringence, and cell gap of the cell are designed so light hits the aluminum reflector in a linearly polarized state. Light is then reflected back through the LC, regains its circular state, and passes again through the circular polarizer—resulting in a bright state. In the voltage ON state of the device, the LC aligns to the vertical field created by the top indium tin oxide (ITO) film and bottom aluminum reflector. The vertically aligned LC does not influence the polarization state of the propagating circularly polarized light. Upon reflection, the light changes hand and again passes through the LC unaffected. The light is then absorbed by the circular polarizer—resulting in a black state.

Fig. 4.

Active addressing and LCD integration. (A) Schematic illustration and working principle of the 80° mixed–twisted–nematic reflective display. (B) Camera image of the 2.7-in. diagonal display before and after particle coating. Microscope images depict single pixels. (C) Microscope images of the completed display and demonstration of individual pixel control. (D) Camera images of the display showing various logos and symbols. (E) Time series of the “bee” as it has a sinusoidal trajectory across the active region of the display. The functional display can be seen in Movie S1.

To increase the surface area of active portions of the display, various electronics (capacitors, transistors, and electrical lines) are designed beneath the bumpy aluminum reflector. To integrate the display with plasmonic nanostructures, a TFT backplane (Sharp Memory Display, LS027B7DH01A; Sharp) is harvested by mechanical separation from the ITO-coated superstrate and subsequently removed from the LC and polyimide alignment layers through an isopropanol rinse and plasma etching, respectively. The surface is then coated with 10 nm of Al₂O₃ through atomic layer deposition and 5 nm mass equivalent thickness of the self-assembled aluminum particles to produce a solid yellow color. Fig. 4B shows the TFT backplane before and after the particle deposition process. The microstructural modulation of the aluminum surface is engineered to result in a paper-like, diffuse white surface. Only a system with angle-insensitive resonances and which can be formed on complex surfaces can accomplish these stringent requirements. SI Appendix, Fig. S7 emphasizes this by comparing the color of a bumpy aluminum reflector with angle-insensitive and angle-dependent plasmonic resonances. By leaving the original polyimide alignment layer on the bumpy aluminum mirror and coating with particles, angle-dependent Fabry–Perot resonances are introduced that result in color profiles directly related to the vertical gradients of the surface. Once the desired angle-independent color(s) are formed on the surface, a reassembly process follows where the TFT backplane with particles are coated with a polyimide alignment layer, rubbed horizontally to the long axis of the display and rejoined with the top superstrate. This polyimide layer is necessary to create the 80° twist within the LC cell and through planarization also guarantees the plasmonic surface morphology does not negatively impact the optical performance of the local LC. The polyimide layer also has a small impact (∼10-nm shift) on the color of the surface as the strong vertical and lateral hybridization of the particles result in a system comparatively insensitive to external refractive index. After aligning the pixel array and black matrix of the respective substrates, the device is UV-cured. Conveniently, the polymer spacers implemented in the commercial display remain adhered to the ITO substrate and assure a controlled cell gap between 3 and 3.5 μm in the reassembled device. Once this cell gap is confirmed optically through spectrometer measurements (HR 2000+; Ocean Optics), an appropriate LC (in this case, ZLI 1800, Δn = 0.07) is chosen to maximize the bright state of the display across all visible wavelengths. To evaluate this, we use the transfer matrix approach and numerically simulate the reflectance spectrum from the cell as a function of birefringence and cell gap (47). SI Appendix, Fig. S8 shows the simulated reflection spectra for the 80° MTN LCD given a birefringence of 0.07. The finished devices can then be interfaced and controlled through a computer or microprocessor, as shown in SI Appendix, Fig. S9. Fig. 4C shows a microscope image of the assembled and functioning display for various states. As outlined above, the OFF state allows the passage of light in and out of the cell and the imaging of the 100- × 100-μm pixel array. As voltage is applied to arbitrary pixels, they progressively turn dark and demonstrate active control over black states and patterns. When the maximum voltage is applied (6 V), the pixels turn black with a contrast ratio comparable to that of the unmodified commercial display (14:1). Reflectance measurements and contrast ratio of a nonaddressed plasmonic device are given in SI Appendix, Fig. S10, as well as images at a viewing angle of 50°—past which the dark state is compromised by the LC mode. The maximum reflectance of the hybrid plasmonic display is 15% and given by the multiplication of the reflectance of its individual components—the MTN LC mode (including polarizers), the bumpy reflector, and the plasmonic surface. This is very close to the 17.5% reported for the unmodified commercial reflective display (LS027B7DH01A; Sharp). The total reflection for MTN LC display is largely limited due to the double pass of the optical path through circular polarizers. Alternatively, the plasmonic surface can be implemented with polarizer-absent LC modes, such as guest-host dye-doped LC (commonly used in smart windows), to achieve maximum reflectance values exceeding 50% (49).

Finally, arbitrary images and video are displayed in Fig. 4D with the UCF Pegasus logo and a “bee” imaged through a cellphone camera (Galaxy S5; Samsung). A time sequence of the “bee” flying in a sinusoidal trajectory across the active area is shown in Fig. 4E and video of the bee can be seen in Movie S1. The refresh rate of the device is 1 Hz, which is determined by the ultralow-power in-pixel electronics designed into the original Sharp Memory display. A quicker refresh rate can be realized by using a reflective TFT designed for video—the limiting factor being the response time of the 80° MTN mode, which has been previously shown to be ∼66 Hz (47). While the demonstration shown here is in monochrome (which is due to our limitations in salvaging commercial TFT backplanes) multicolored subpixels are well within the realm of possibility via conventional UV lithography if implemented during the original fabrication process.

Discussion

This work demonstrates a relatively large CMY color gamut (CMYK in conjunction with LC) compared to other plasmonic color schemes; however, we believe this can be further improved through an exploration of aluminum thin-film growth mechanisms. Given a singular Gaussian absorption peak, the ideal resonance width to maximize CMY color saturation is ∼75 nm (FWHM) and changes based on the resonance location. This is due to the subtractive nature of the color as opposed to the additive color of light-generating systems like light-emitting diodes. While a sharp peak in the spectra is desired for additive color, a narrow and deep absorption dip (<75 nm FWHM) still results in an unsaturated color close to the white point. For this reason, independent control over the resonance location and width is highly desirable. We have shown that the resonance location depends directly on the mean particle size, which we control through the amount of deposited material. The width of the resonance, however, depends on several factors from the geometry of the system to the dispersion of the underlying plasmonic material. A main contributing factor is the inhomogeneous resonance linewidth broadening due to variations in particle size and shape. Above, we have seen that as more material is deposited and islands begin to coalesce the distribution of particle size increases. The reflectance spectrum of a distribution of particles can be understood as the geometrical mean of the spectra arising from its individual components. Therefore, templated self-assembling methods which exhibit order may allow control over the distribution and size of particles as they coalesce (50, 51). Alternatively, modifications to the formation process of the particles through higher growth temperatures (52, 53), alloys (54), applied voltage (19), or barrier oxides can be explored to increase surface tension and allow coalescing particles to reach more uniform equilibrium states.

Another approach to widen the color space of the plasmonic surface is the addition of multiple layers of aluminum particles and oxides (55, 56). From the color space of the surface, expanding the quality of the subtractive colors (yellow, magenta, and cyan) is achievable and should be pursued, however, the creation of green would drastically improve the plasmonic surface color span. By coating a cyan sample with an aluminum oxide layer and then depositing smaller particles which produce yellow a range of greens is achievable and is the subject of ongoing research.

In conclusion, we have demonstrated a plasmonic system which exhibits multidirectional hybridization of plasmonic modes between adjacent particles and their mirror images via a large-area, highly reproducible self-assembling technique. The hybridized modes are largely angle-insensitive and allow uniform color formation on nearly arbitrary surfaces—taking on the scattering properties of the underlying substrates and resulting in diffusive, angle-independent, and flexible plasmonic color surfaces. We then demonstrate the potential and novelty of such a color-generation mechanism by exploring its integration into an actively addressed reflective LCD which can produce black states, arbitrary images, and video. As plasmonic structures are pushed to ever-more-stringent requirements and integrated into commercial devices, we foresee advances in their fundamental understanding as well as smaller, higher-resolution electrooptic devices and novel display elements.

Methods

Fabrication of the Self-Assembled Plasmonic System.

The 150-nm Al mirrors are deposited on glass using a Thermionics electron beam evaporation system. Deposition is performed at ∼5 × 10⁻⁶ T at a rate of ∼0.1 nm⋅s⁻¹ and room temperature. The aluminum oxide layer is deposited by atomic layer deposition (Savannah 2; Cambridge Nanotech) at 100 °C using pulses of trimethylaluminum and water. The aluminum particles are then evaporated in an AJA electron beam evaporator at ∼5 × 10⁻⁸ T, 100 °C, and ∼0.05 nm⋅s⁻¹.

LC Cell Formation.

The plasmonic reflective LCD is fabricated using a commercially available Sharp Memory Display (LS027B7DH01A; Sharp). The displays are separated using a belt sander with careful attention not to break electrical lines. The ITO and TFT substrates are then cleaned with isopropyl alcohol and dried. The TFT substrate is oxygen-plasma-etched for 10 min in a Plasma Etch system at 40 W. Atomic layer deposition deposits 10 nm aluminum oxide followed by 5 nm aluminum via electron beam evaporation using the processes described above. The now-colored TFT is spun-coated with polyimide and baked at 220 °C for 2 h. After rubbing, the substrates are reassembled using NOA UV glue. Once UV-cured, the LC-plasmonic device is infiltrated with LC (ZLI 1800; ZLI). The finished device is then controlled through a programmed microprocessor and circuit in accordance to the Sharp Memory Display product description and Adafruit Arduino guides.

Optical Measurements and Images.

Reflection spectra are collected using a 4×, 0.07 numerical aperture objective, beam splitter and fiber coupled to spectrometer (HR 2000+; Ocean Optics). Reflection spectra are normalized to an aluminum mirror with 96% reflectivity and a linear polarizer. Angular measurements are performed with a integrating sphere (RTC-060-SF; Labsphere) with a fiber optic link to the Ocean Optics spectrometer.

Finite Difference Time Domain Modeling.

Reflection spectra are calculated using experimental parameters with a commercial FDTD software package (Lumerical FDTD; Lumerical Solutions Inc.). The wavelength-dependent refractive index of aluminum and aluminum oxide is taken from Palik (57).

Code and Materials Availability.

All data needed to support the conclusions presented in this paper are available in the paper and/or SI Appendix.