Liquid network connectivity regulates the stability and composition of biomolecular condensates with many components

Significance

LLPS plays an important role in the spatiotemporal organization of the numerous molecular constituents of living cells, via formation of biomolecular condensates. Our simulations provide predictive rules governing the stability and composition of multicomponent biomolecular condensates. Biomolecules that increase the molecular connectivity of condensates are present in higher concentrations because connectivity is positively correlated with stability. Greater connectivity within highly multicomponent condensates manifests in higher critical temperatures in the phase diagrams of accessible systems involving just a few components. Hence, composition of highly multicomponent condensates can be predicted from the critical points of reduced-component mixtures. Our findings expand the mechanisms relating phase behavior of multicomponent intracellular mixtures to critical parameters (temperature, pH, salt concentration, etc.) of the constituent biomolecules.

Abstract

One of the key mechanisms used by cells to control the spatiotemporal organization of their many components is the formation and dissolution of biomolecular condensates through liquid–liquid phase separation (LLPS). Using a minimal coarse-grained model that allows us to simulate thousands of interacting multivalent proteins, we investigate the physical parameters dictating the stability and composition of multicomponent biomolecular condensates. We demonstrate that the molecular connectivity of the condensed-liquid network—i.e., the number of weak attractive protein–protein interactions per unit of volume—determines the stability (e.g., in temperature, pH, salt concentration) of multicomponent condensates, where stability is positively correlated with connectivity. While the connectivity of scaffolds (biomolecules essential for LLPS) dominates the phase landscape, introduction of clients (species recruited via scaffold–client interactions) fine-tunes it by transforming the scaffold–scaffold bond network. Whereas low-valency clients that compete for scaffold–scaffold binding sites decrease connectivity and stability, those that bind to alternate scaffold sites not required for LLPS or that have higher-than-scaffold valencies form additional scaffold–client–scaffold bridges increasing stability. Proteins that establish more connections (via increased valencies, promiscuous binding, and topologies that enable multivalent interactions) support the stability of and are enriched within multicomponent condensates. Importantly, proteins that increase the connectivity of multicomponent condensates have higher critical points as pure systems or, if pure LLPS is unfeasible, as binary scaffold–client mixtures. Hence, critical points of accessible systems (i.e., with just a few components) might serve as a unified thermodynamic parameter to predict the composition of multicomponent condensates.

Eukaryotic cells contain a large number—estimated at a few thousand (1)—of different components that are generally heterogeneously distributed in space (2–4). The molecular complexity of cellular mixtures is imparted mainly by the protein and RNA composition. There are around 6 million different human protein species and posttranslational modifications (5), and the estimated number of RNAs is in the tens to hundreds of thousands (6, 7). Spatiotemporal organization of this large number of components is crucial for the functioning of living cells. This is because compartmentalization enables the formation of curated reactive volumes that selectively concentrate and exclude specific molecules, allowing the coordinated control of thousands of simultaneous chemical reactions that are required to maintain biological function (8).

Cell compartmentalization is achieved through the formation of two main types of organelles. In addition to the formation of the well-known membrane-bound organelles (2), membraneless organelles (3, 9)—also known as biomolecular condensates (8, 10), cellular bodies (11), or otherwise (8)—are ubiquitous within the cell interior. Biomolecular condensates account for numerous highly diverse domains, both inside the cytoplasm [e.g., P granules (12) and RNA granules/bodies (13–15)] and in the cell nucleus [e.g., Cajal bodies (16), nucleoli (17), heterochromatin domains (18, 19), the transport channels in the nuclear pore complex (20), and possibly superenhancers (21, 22)]. The catalog of biomolecular condensates is constantly increasing (23) and unexpected biological roles beyond compartmentalization—such as the ability of condensates to exert mechanical forces to induce chromatin reorganization (24, 25) or to act as molecular sensors of intracellular and extracellular changes (26)—keep emerging.

The importance of biomolecular condensates for cellular function is driving the effort to characterize their biophysical properties, both in vitro and in vivo (23). Although this goal is far from being achieved, several important concepts have emerged. The accumulated evidence suggests that biomolecular condensates are condensed-phase domains that exhibit liquid-like properties (e.g., they are spherical; can fuse, flow, and grow; and display wetting of surfaces) (12, 17, 27). These organelles form via spontaneous liquid–liquid phase separation (LLPS). LLPS is a thermodynamic process in which multicomponent cellular mixtures minimize their free energy by demixing into a phase where the concentration of certain proteins and nucleic acids is greatly enhanced over their concentrations elsewhere in the cell (28–33).

While the number of possible components of a biomolecular condensate is potentially very large (ranging from tens to hundreds of different types of biomolecules) (34–37), only a fraction of these molecules seem to be essential for their integrity (29, 38, 39). Based on this distinction, Banani et al. (11) proposed two broad categories to classify biomolecules inside condensates: “scaffolds” and “clients” (for an excellent review on this subject see ref. 36). Scaffolds are defined as groups of biomolecules that self-associate through multivalent interactions and subsequently drive LLPS. In contrast, clients are biomolecules that are dispensable for the formation of condensates but are recruited through their interactions with the scaffold biomolecules (11).

The ability of protein scaffolds to drive LLPS depends strongly on their valency (defined as the number of sites or domains they possess for interactions with other biomolecules) (11, 23, 28, 36, 40), which in turn is dictated by the amino acid sequence, the protein conformational landscape, and the microenvironment. High valencies facilitate multiple protein–protein (11, 28, 40), protein–RNA (15), or protein–DNA (18, 19) interactions. Other crucial factors include the scaffold–client stoichiometry (11), and the ability of biomolecules to bind weakly to one another through nonspecific and promiscuous binding sites (e.g., via charge–charge, dipole–dipole, $\pi$–$\pi$, and cation–$\pi$ interactions) (23, 27, 41, 42).

Multivalency is ubiquitous in the cell and the number of different molecules that can act as scaffolds is large (36). These include multidomain folded proteins [with repeating (28) or varying domains (18, 19)], proteins mainly formed by intrinsically disordered regions (IDRs) with multiple binding motifs (29–32, 40), proteins combining both well-folded domains and IDRs (18, 19, 29, 43), and the combination of RNA-binding proteins and their complementary RNA strands (44–46). Furthermore, a scaffold may constitute a single type of multivalent protein [e.g., the fused in sarcoma (FUS) protein (43) or the heterochromatin protein 1 (HP1) (18, 19)] or a mixture of two or more multivalent biomolecules [e.g., the combination of the high-valency engineered proteins poly-SUMO and poly-SIM (11) or the mixture of LAF-1 and RNA found in P granules (29)]. Examples of clients include the set of low-valency (one to three repeats) versions of poly-SUMO and poly-SIM and the small RNAs that dissolve into liquid drops of Ddx4 proteins (47).

Deciphering the physical determinants of LLPS of intracellular mixtures is needed to fully understand, and eventually control, how a cell organizes its contents in space and time. Missing information includes the dependence of molecular mechanisms of condensate formation on varying conditions, the fundamental physical mechanisms that explain the connection between multivalency and the stability and composition of condensates with many components, and the molecular link between condensate compositional diversity and stability. A key challenge in obtaining such information, either by experiment or by simulation, is the difficulty in relating the microscopic properties of proteins and nucleic acids, and the nature of their interactions, to the macroscopic characteristics of multicomponent biomolecular condensates including density, composition, and stability.

In the present work, we combine the simplicity of a minimal coarse-grained protein model with the efficiency of molecular dynamics (MD) simulations of continuous potentials, enabling many long simulations on large systems (48). With this approach we are able to compute the phase diagrams of systems containing thousands of interacting proteins and many different components. Our approach allows us to link microscopic properties of the constituent biomolecules to the stability and composition of the condensates, and to elucidate the physical mechanisms leading to the observed behavior, thereby attaining a thermodynamic description of intracellular LLPS.

Results and Discussion

Minimal Coarse-Grained Model for Protein LLPS.

Based on the dependence of intracellular LLPS on multivalency, stoichiometry, and weak biomolecular interactions, we developed a minimal coarse-grained model that allows us to simulate multicomponent mixtures of thousands of interacting multivalent proteins, while varying all of these features (48). Although atomistic descriptions are needed to investigate the microscopic determinants of LLPS—such as the impact of chemical modifications, specific intermolecular interactions, and conformational dynamics—due to the exponential scaling of the search space with protein size (49), sampling the formation of protein condensates atomistically is currently unfeasible. Atomistic simulations of relevant systems for understanding protein LLPS are scarce and have been limited to aggregates of $\sim$10 to 20 small proteins (e.g., a 56-residue peptide) that are formed prior to simulation (50).

Sequence-dependent protein coarse-grained models (noteworthy examples are those described in refs. 51–53) can simulate condensates containing $\sim$100 copies of the same protein for up to 10 $\mathrm{\mu }$s and are ideal for identifying the dependency of LLPS on amino acid sequence. However, as we move from single-component protein condensates to multicomponent systems, important finite-size effects (e.g., those related to the relative number of copies of each component in the system) arise, creating the need to consider much larger numbers of proteins in the simulation setup. Hence, to investigate multicomponent condensates, minimal models that significantly reduce the degrees of freedom but retain essential physicochemical information are mandatory (54).

A notable approach to investigate LLPS is the “stickers-and-spacers” lattice-based model, which represents multivalent proteins as heteropolymers composed of stickers (LLPS-binding motifs) and spacers (regions in between stickers). This model has been successfully used to generate phase diagrams of multicomponent systems (55, 56), and predict and rationalize the phase behavior of proteins (40, 56). Patchy-particle models represent another class of important minimal models that have been successfully employed to investigate the phase behavior of biomolecules and colloids. These models have been extensively validated to study the phase behavior of DNA constructs (57) and proteins (58–62), and to assess the role of multivalency in phase transitions (48, 63, 64). Therefore, they are ideal for investigating the phase behavior of multicomponent protein mixtures.

Accordingly, our model represents each multivalent protein as a “patchy particle”: a sphere with a few anisotropic attractive patches on its surface (Fig. 1). Each attractive patch allows the protein to engage in one orientationally specific interaction with another protein, accounting for generic features of protein–protein interactions, such as electrostatics, hydrogen bonding, and hydrophobic attraction. Although our model represents proteins as sticky spheres, it adequately captures the way in which intrinsically disordered proteins interconnect (see Dominant Role of Protein Multivalency in LLPS). In what follows, we define the valency of our proteins as the number of patches on their surface.

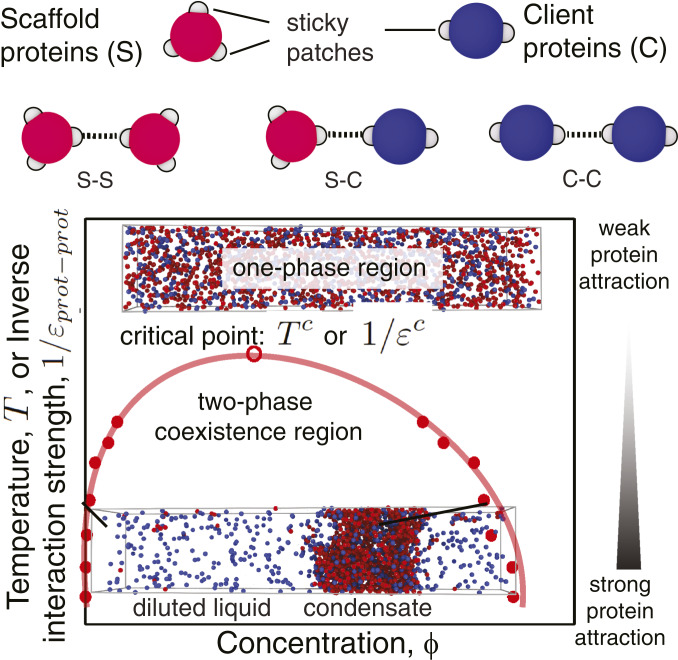
Fig. 1.

Graphical illustration of the minimal coarse-grained protein model used in this work (Top) and a representation of a typical phase diagram as a function of the (inverse) interaction strength (Bottom). Proteins (scaffolds and clients) are represented as hard-sphere cores (red for scaffolds and blue for clients) with attractive sites on their surface (gray patches). Each patch allows the protein to engage in one weak attractive protein–protein interaction. The phase diagrams explore the space of (inverse) protein–protein interaction strengths ($1/{\epsilon }_{prot-prot}$; vertical axis) or equivalently temperature ($T$, since $T\propto 1/{\epsilon }_{prot-prot}$) versus volume fractions ($\varphi$; horizontal axis). For a given value of $1/{\epsilon }_{prot-prot}$, if two phases are detected, we measure the volume fractions ($\varphi$) of the proteins in the different phases and use this information to plot a coexistence curve. The volume fraction is defined as the fraction of the volume of a phase ($V$) that is occupied by proteins: ${\varphi }_i=N_i{V}_i/V=C_i{V}_i$, where $V_i$ is the volume of the hard core of protein of type $i$ and $N_i$ is the total number of proteins of type $i$ in a given phase. $C_i$ is the number density of proteins of type $i$ in that phase. The coexistence curve (shown in red) is useful when assessing the propensity of a protein to phase separate because it shows for what values of the protein–protein interaction strength (vertical axis) and for what protein concentration (horizontal axis) demixing will occur. The region above the coexistence curve is the “one-phase region,” where protein–protein interactions are too weak to sustain phase separation (top snapshot of a well-mixed homogeneous phase). The region below the coexistence curve, the “two-phase coexistence region,” represents stronger protein–protein interactions that favor demixing into a condensed (protein-enriched) and a diluted (protein-depleted) liquid phase (bottom snapshot of a demixed system). The maximum in the coexistence curve is known as the critical point ($T^c$ or $1/{\epsilon }^c$): For interaction strengths lower than the critical value, liquid–liquid phase separation is no longer observed. If, in a simulation, the interaction strength exceeds the critical value, liquid–liquid phase separation occurs spontaneously.

To evaluate phase diagrams, we perform MD simulations, exploiting our continuous patchy-particle potential (48), which permits long and large simulations. We use the direct coexistence method that involves simulating two different phases—the condensed (protein-enriched) liquid in contact with the diluted (protein-depleted) liquid—in the same simulation box separated by an interface (65–67) (SI Appendix, section III). Strictly speaking, because our solvent is represented implicitly, the direct coexistence is that of a liquid (protein-enriched phase) and a vapor (protein-depleted phase).

Simulations and mean-field theory have demonstrated that systems with many different interacting components that exhibit a sufficiently broad distribution of weak intermolecular interactions undergo LLPS easily (4). Indeed, such systems demix into various different coexisting liquid phases with similar densities but different compositions, where the selection of specific phases is controlled by the differences in intermolecular interactions among components (4). Our model focuses on the proteins that are enriched upon phase separation; i.e., we do not compute the density of “spectator” proteins and other biomolecules that are not actively involved in LLPS. However, we expect that the overall volume fraction of proteins (including spectator molecules) is likely to be similar inside and outside the droplets.

Our phase diagrams allow us to determine the conditions under which LLPS takes place (Fig. 1). The most important parameter controlling the phase diagram of simple molecular mixtures is the temperature (T) (48, 58, 63). However, cells typically operate in a narrow temperature range. It is therefore more relevant to consider the effect of varying the strength of the inverse protein–protein interaction ($1/{\epsilon }_{prot-prot}$) at a fixed temperature.

Dominant Role of Protein Multivalency in LLPS.

Biomolecular condensates are stabilized by chemically diverse weak protein–protein interactions, which are determined by the specific nature (e.g., hydrophobicity, aromaticity, and charge) and patterning of amino acids, and affected by intracellular conditions (e.g., temperature, pH, and ion concentration) (32, 40, 68, 69). Importantly, regardless of the exact chemical nature of the protein–protein interactions, experiments suggest that the ability of proteins to undergo LLPS increases with valency (11, 28, 30, 32, 40, 55, 56). Indeed, tightly integrated experiments and simulations recently demonstrated that the critical temperature of prion-like domain proteins rises as the protein valence is artificially increased (40). Previously, in vitro experiments had revealed the inhibition of LLPS under conditions that likely reduce the protein valency, e.g., via introduction of posttranslational modifications or replacement of proteins by their mutants (28, 32, 70, 71).

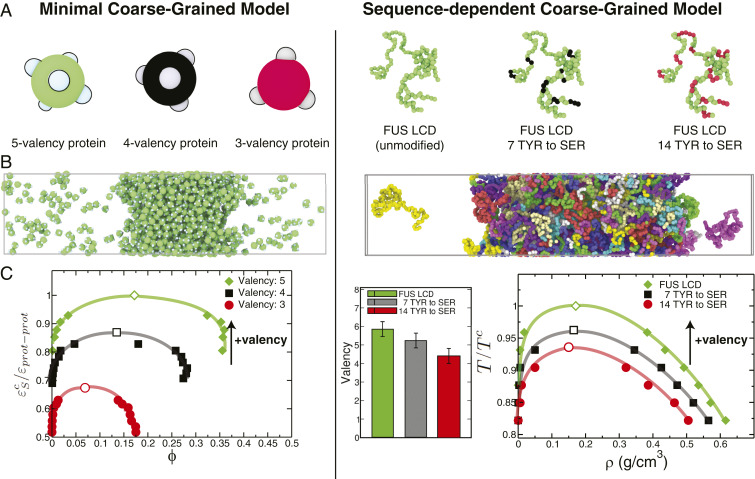
To decipher whether modulation of LLPS by protein modifications can indeed be explained by changes in protein valency, we focus on the phase behavior of the low-complexity domain (LCD) of FUS (70, 71)—a 163-residue-long tyrosine- and arginine-rich segment that phase separates when unmodified. Phase separation of FUS LCD is inhibited by phosphorylation and tyrosine-to-serine mutations (70, 71). We begin by employing the sequence-dependent residue-resolution protein model of Dignon et al. (52) to compute the phase diagrams of FUS LCD (80 chains) and two variants with 7 and 14 tyrosine-to-serine mutations, respectively (SI Appendix, sections IV–VI). Consistent with experiments (71), these simulations (Fig. 2 A–C, Right) confirm that the liquid–liquid coexistence region of FUS LCD shrinks with increasing number of tyrosine-to-serine mutations. Further, by computing the average valency of FUS LCD within the condensed phase (SI Appendix, section V), we observe that these LLPS-destabilizing mutations limit the formation of protein intermolecular contacts (SI Appendix, Table S6) and, subsequently, reduce the protein valency from $\sim$6 to $\sim$4.

Fig. 2.

Impact of protein valency modulation in their phase behavior as predicted by the minimal coarse-grained protein model used in this work (A–C, Left) and the realistic residue-resolution sequence-dependent protein model of Dignon et al. (52) (A–C, Right). (A, Left) Schematic illustration of proteins with three different valencies (green, 5-valency; black, 4-valency; and red, 3-valency) modeled as patchy particles. (A, Right) The low-complexity domain (residues 1 to 163) of the human FUS protein (green, unmodified FUS LCD), FUS LCD with 7 of its tyrosine (TYR) residues mutated to serine (SER) (green with black spheres highlighting the mutated TYR) and with 14 of its TYR residues mutated to SER (green with red spheres highlighting the mutated TYR). (B) Simulation snapshots illustrating the coexistence of condensed and diluted liquid phases. (C, Left) Phase diagrams (inverse protein–protein interaction strengths, $1/{\epsilon }_{prot-prot}$, versus volume fraction, $\varphi$) for the three minimal proteins. (C, Right) Average valency (SI Appendix, section V) and liquid–liquid phase diagrams (temperature, $T$, versus density, $\rho$) for the three FUS LCD proteins studied. The vertical axes in C have been normalized by the critical point of the highest-valency protein in each set (Left, $1/{\epsilon }_{\mathrm{S}}^c$ for the 5-valency protein; Right, $T^c$ for the unmodified FUS LCD). The black arrows indicate the direction toward which the critical parameters ($1/{\epsilon }_{prot-prot}^c$ or $T^c$) move upon an increase in valency. Error bars in the phase diagrams are of the same size as or smaller than the symbols. Typical statistical uncertainties are provided in SI Appendix, Table S5.

Despite its simplicity, our minimal coarse-grained model captures this dominant role of valency in protein LLPS. We observe that the liquid–liquid phase diagrams of proteins are most strongly influenced by changes in the valency (SI Appendix, Fig. S1 and Table S1), with the region in the phase diagram where LLPS occurs shrinking significantly as the protein valency drops from 5 to 3 (Fig. 2 A–C, Left), and disappearing completely for proteins with a valency of 2 (SI Appendix, Fig. S1), in agreement with previous simulations (48, 63, 64). Thus, these results suggest that a minimal model that accounts for the dominant role of valency is a reasonable approximation to investigate the phase behavior of multicomponent mixtures of proteins with different valencies.

Our sequence-dependent and minimal coarse-grained simulations further explain the dominant role of valency in protein phase behavior: Valency dictates the average number of intermolecular connections per unit of volume that proteins can establish within the condensed-liquid network—the “liquid network connectivity” (SI Appendix, Tables S7 and S8). Higher valencies result in more densely connected liquid networks (SI Appendix, Tables S7 and S8) and, as a result, more stable condensates (Fig. 2).

Formation of the dense-liquid phase occurs only when proteins are able to interconnect with one another, forming a dynamic percolated network (SI Appendix, Fig. S1). We thus find that LLPS occurs when the biomolecules in the condensed phase can form a percolating cluster, where all proteins are connected to at least one other protein. Proteins with a valency of 2 cannot form percolated structures (rather, they form linear chains) and, therefore, cannot undergo LLPS on their own (SI Appendix, section I and Fig. S1C). In addition, for the system to be liquid-like rather than gel-like, the interactions among biomolecules must be weak and transient (29, 33, 72). We note that gels are also characterized by a percolated structure, but exhibit local rigidity due to the prevalence of long-lived bonds (33, 73). Weak interactions allow proteins to dynamically switch their interaction to other neighbors (i.e., bind/unbind on short timescales). Because the attractive molecular connections are weak, having a high number of them per unit of volume (i.e., high connectivity) becomes critical to compensate for the entropy loss upon demixing and stabilize biomolecular condensates; hence, there is the dominance of multivalency in protein LLPS.

Having confirmed that our minimal model reproduces well the modulation of protein liquid–liquid phase diagrams by multivalency, in the rest of this work we employ this minimal model to simulate systems containing thousands of proteins, multiple components (i.e., proteins with different valencies), and long timescales to assess both equilibrium properties and the mechanism of formation of multicomponent condensates.

Modulation of Stability of Biomolecular Condensates Formed by Scaffolds and Different Types of Clients.

To elucidate the essential physical chemistry governing the formation of phase-separated cellular compartments, which contain many components (36), experimental approaches are generally based on the reconstitution of minimal in vitro representations—using just one or two essential biomolecules (i.e., the scaffolds) (23). It is then highly desirable to have rules predicting how the stability and physical properties of simplified biomolecular condensates change upon adding more components, thereby approaching the conditions for condensates inside cells. Accordingly, we employed our minimal model in a series of computer experiments to investigate how the phase diagrams of pure scaffold systems change upon addition of clients with different characteristics. Throughout this work, scaffolds represent a single type of protein or group of different proteins that can phase separate on their own via homotypic or heterotypic scaffold–scaffold interactions. Clients, on the contrary, are considered as proteins that do not undergo LLPS on their own under any conditions, either because they are divalent or because they do not self-interact (i.e., no attractive client–client interactions). We prepared systems where the scaffolds are trivalent proteins and vary the valency of the clients—comparing clients with a lower-than-scaffold valency of 2 that cannot undergo LLPS on their own (SI Appendix, section I) with clients that have a higher-than-scaffold valency of 4 (and do not self-interact). We also varied the stoichiometry of the scaffold–client mixtures and the scaffold–client binding affinity. In addition, we probed the effects of the client-binding mode, i.e., binding to scaffolds at sites also used for scaffold–scaffold interactions versus binding at alternative scaffold sites.

When comparing the phase diagrams of the various client–scaffold mixtures with those of the pure scaffold system, we observe that introducing low-valency clients that are strong competitors for scaffold–scaffold binding sites always reduces the stability of condensates (Fig. 3A). Such destabilization is strongly influenced by stoichiometry: It is marginal when the scaffolds are in excess (6.5% reduction in the critical value of the inverse interaction strength, the weakest protein–protein interaction energy that still favors LLPS) and becomes significant (a 21% reduction) when the clients are in surplus. In contrast, regardless of stoichiometry, adding poorly competing clients (i.e., clients that bind with low affinity to the scaffold–scaffold binding sites) has a negligible effect on the condensate stability (Fig. 3B). This difference is consistent with the high-affinity clients being present at much higher concentrations inside the condensates (SI Appendix, section II and Fig. S3B). These trends are in excellent agreement with experiments showing inhibition of LLPS in the (SH3)₅–PRM(N-WASP)₈ system (two high-valency proteins that undergo LLPS when mixed together) due to an excess of PRM(H)₁, which is a high-affinity monovalent competitor for (SH3)₅ (28), and only a moderate suppression of (SH3)₅–PRM₅ LLPS by lysozyme, a low-affinity monovalent client (74).

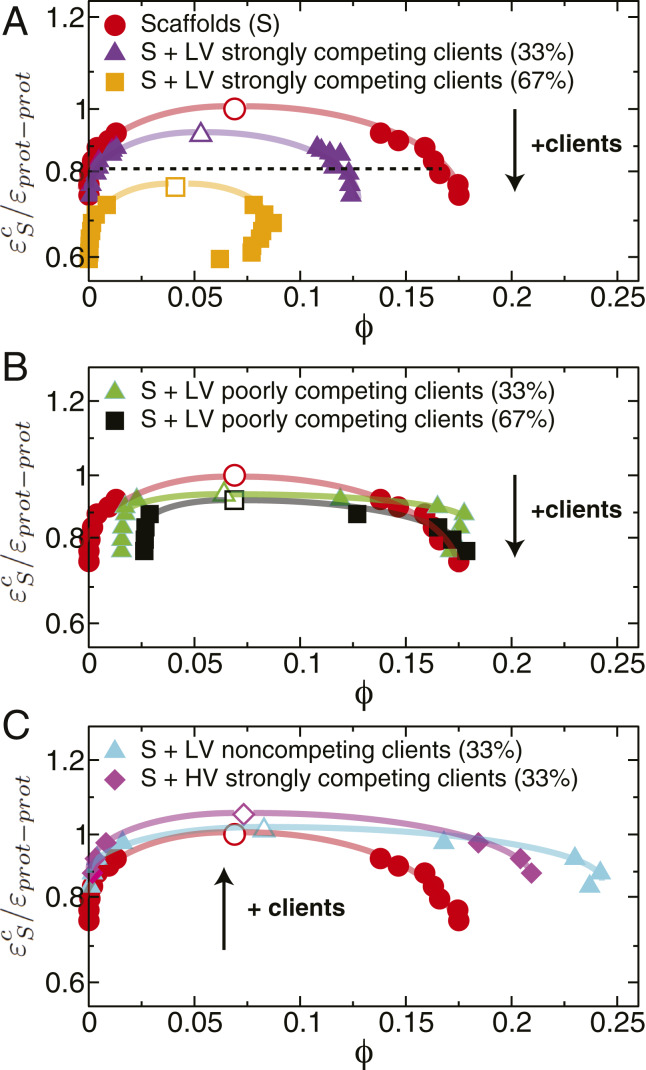
Fig. 3.

Modulation of stability of biomolecular condensates formed by scaffolds (valency of 3) and different types of clients assessed through liquid–liquid phase diagrams. Clients are either low-valency proteins (LV), i.e., valency of 2, or higher-than-scaffold valency proteins (HV), i.e., valency of 4. The lines joining the data points in the phase diagrams are shown as a visual guide to facilitate comparison of the coexistence regions. The values on the vertical axes of the phase diagrams have been normalized (for comparison purposes) by dividing over the critical point of the pure scaffold system (i.e., $1/{\epsilon }_{\mathrm{S}}^c$ for the 3-valency pure system). (A) Destabilization of liquid-drop formation by adding LV strongly competing clients to the condensate. Throughout, we define strongly competing clients as those that bind to scaffolds at the same sites, and with the same strength, as in scaffold–scaffold interactions. We compare two cases: 67% scaffold proteins (purple triangles) with 33% high-affinity clients versus 33% scaffolds (orange squares) and 67% clients. The dotted line illustrates the constant value of the inverse interaction strength used in Fig. 4 to evaluate the molecular mechanism of condensate formation. (B) Negligible change in the stability of a biomolecular condensate by addition of LV poorly competing clients. Poorly competing clients are defined as those that bind to scaffolds with one-half of the strength of the scaffold self-interactions, while using the same binding sites as those used for scaffold–scaffold interactions. We compare 67% scaffolds (green triangles) with 33% clients versus 33% scaffolds (black squares) with 67% clients. Note that the diluted-liquid branch exhibits higher densities as the proportion of poorly competing clients increases because clients are predominantly excluded from the condensate and, therefore, concentrated in the diluted phase (SI Appendix, Fig. S3). (C) Increase in condensate stability by addition of clients in two scenarios. First, a moderate increase in condensate stability is observed upon addition of 33$\%$ LV noncompeting clients (cyan triangles). These clients bind to scaffolds with the same strength as the scaffolds’ self-interactions but use alternate binding sites in the scaffold exclusively devoted to scaffold–client interactions. Second, a significant increase in stability of the condensate is observed upon addition of 33% strongly competing clients with higher-than-scaffold valencies (magenta diamonds). The black arrows indicate the direction toward which the critical parameters $1/{\epsilon }_{prot-prot}^c$ move upon the addition of clients. Error bars in the phase diagrams are of the same size as or smaller than the symbols. Typical statistical uncertainties are provided in SI Appendix, Table S5. Numerical values of the critical points are given in SI Appendix, Table S2.

In other words, LLPS is significantly suppressed upon client addition when 1) clients possess lower-than-scaffold valencies, 2) clients bind to scaffolds via the same sites used for scaffold self-assembly, and 3) the scaffold–client binding affinity is high. These three conditions lead to replacement of some scaffold–scaffold interactions (high–high valency) with scaffold–client ones (high–low valency) in the condensate, which reduces the density of favorable interconnections in the condensed-liquid network. Indeed, if we focus on a fixed value of $1/{\epsilon }_{prot-prot}$ (shown by a dashed line in Fig. 3A) and compare the average number of connections per unit volume in the condensate for the pure-scaffold system (valency of 3) with that of the mixed scaffold–client system (with 33% of strongly competing 2-valency clients), we notice a marked decrease ($\sim$37%) in the connectivity of the condensed-liquid network when clients are present (SI Appendix, Table S8). A reduced number of attractive protein–protein associations decreases the stability of the condensate because it results in modest gains in enthalpy that eventually become insufficient to compensate for the entropy loss upon demixing.

The next question we address is whether there are conditions under which recruitment of clients can increase the stability of a condensate. In Fig. 3C, we analyze the case in which scaffolds recruit low-valency clients that do not compete for scaffold–scaffold binding sites, but instead bind with high affinity to scaffolds via two additional sites specific for scaffold–client interactions. We find that recruitment of clients via sites not used for scaffold–scaffold interactions can increase the stability of condensates (widen the coexistence region) if clients have a valency of 2 or higher. This is because clients that are at least divalent and bind to alternate scaffold sites, rather than disrupt scaffold–scaffold connections, can facilitate new connections between distant scaffolds (i.e., scaffold$\cdots$client$\cdots$scaffold). In this case, connections per unit of volume (estimated at the same fixed value of $1/{\epsilon }_{prot-prot}$ used above) are 75$\%$ more abundant than in the pure scaffold system (SI Appendix, Table S8).

An alternative mechanism to increase the stability of a biomolecular condensate is through recruitment of clients that have higher-than-scaffold valencies (Fig. 3C, magenta diamonds) and, thereby, enhance the molecular connectivity. Such an increase is limited to scaffold–client ratios that provide sufficient free scaffold sites for client recruitment. Promotion of LLPS by high-valency clients was observed for the (SH3)₅–PRM₅ mixture upon addition of heparin—a highly negatively charged polymer that has a higher valency than the scaffolds and binds with high affinity to PRM₅ (74).

Molecular Mechanism of Condensate Formation and Client Recruitment.

In addition to providing full phase diagrams, our simulations allow us to probe the spatial reorganization of individual scaffold and client molecules over time. To this end, we prepared a well-mixed scaffold–client system (Fig. 4A) at a protein–protein interaction strength that favors phase separation, and monitor how phase separation proceeds (Fig. 4 B and C) to the final equilibrium state (Fig. 4D) by defining two order parameters (definitions in SI Appendix, section III). One parameter is a “condensation” order parameter [$Q^X\left(L\right)$], which we compute independently for scaffolds ($X=S$) and clients ($X=C$) as a function of their position in the simulation box (in the direction of the largest box dimension, $L$). $Q^X\left(L\right)=0$ indicates a well-mixed state (as in Fig. 4A), and an increasingly positive value of $Q^X\left(L\right)$ signals the formation of protein condensation clusters (Fig. 4B). The ratio of the integrals of $Q^S\left(L\right)$ over $Q^C\left(L\right)$ with respect to the largest box dimension defines a second order parameter, ${\chi }_{S/C}$, that probes the change in relative abundance of scaffolds and clients inside the condensation clusters.

Fig. 4.

Mechanism of formation of a condensate composed of scaffolds and clients (67% 3-valency scaffolds + 33% 2-valency high-affinity clients) at a value of the normalized inverse interaction strength equal to 0.85 (dashed line in Fig. 3A). Each panel gives a plot of the condensation order parameter for scaffolds (red), $Q^S\left(L\right)$, and clients (blue), $Q^C\left(L\right)$, versus the direction of the largest dimension, $L$, of the simulation box, as well as the value of the relative enrichment of scaffolds over clients in the newly formed condensates ${\chi }_{S/C}$. Simulation snapshots (scaffolds as red spheres and clients as blue spheres) for the different stages of the condensate-formation process are also provided: (A) initial well-mixed configuration, (B) nucleation, (C) growth, and (D) equilibrium condensate.

Starting from a well-mixed fluid (Fig. 4A; ${\chi }_{S/C}\sim 1$), we observe that, as time progresses, the concentration of the scaffolds in various regions of the simulation box increases locally (${\chi }_{S/C}$ increases to 2.22), signaling the formation of nuclei rich in scaffolds (Fig. 4B; the nucleation stage) that will eventually give rise to the condensate (Fig. 4D). After nucleation, the scaffold-rich nuclei increase in size and fuse (Fig. 4C; growth stage), while the condensate begins to sequester clients from the dilute phase (${\chi }_{S/C}$ drops to 2.08). The scaffolds continue to recruit clients until an equilibrium condensate (Fig. 4D) is formed (${\chi }_{S/C}$ decreases further to 1.28). The “scaffolds and clients” model (11) proposes that scaffolds self-associate first and subsequently recruit low-affinity, low-valency clients to excess scaffold sites that are free for binding. Our results support this mechanism and demonstrate that it also holds for clients that bind with high affinity to the scaffolds. Indeed, as long as clients are unable to undergo LLPS on their own, their phase separation will be dependent on the prior nucleation of scaffolds.

Biomolecular Condensates with Many Components.

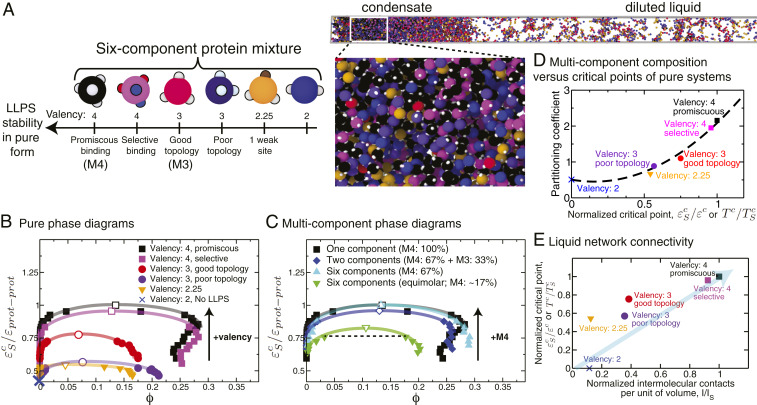
To investigate the properties of biomolecular condensates as a function of their compositional diversity, we prepared multicomponent mixtures that included six different types of proteins with different intrinsic abilities to phase separate (Fig. 5 A and B) and that bind to each other with high affinity. Fig. 5C shows that as long as the proteins with the highest single-component critical point (in inverse interaction strength $1/{\epsilon }_{prot-prot}^c$ or temperature $T^c\propto {\epsilon }_{prot-prot}^c$) are in excess, the coexistence curves of a binary (blue diamonds in Fig. 5C) and a six-component (cyan triangles in Fig. 5C) mixture nearly coincide with that of the pure high-critical-point protein (i.e., the 4-valency promiscuous proteins in our example; black squares in Fig. 5C). The curve of the binary mixtures lies slightly below that of the six-component mixture, likely because, besides the high-critical-point proteins, the latter includes a fraction of additional proteins (4-valency, selective) that are better at interconnecting the liquid network than the proteins added (3-valency, good topology) to the binary mixture. Notably, when we significantly reduce the proportion of high-critical-point proteins (to reach equal concentrations of all species), the stability of the condensate decreases substantially (green triangles in Fig. 5C). Hence, the phase behavior of a multicomponent condensate is dominated by the microscopic properties and stoichiometry of the proteins with the higher critical points. Importantly, for a constant concentration of high-critical-point proteins, we expect the phase landscape to be robust against an increase in compositional diversity; i.e., the coexistence curve is marginally altered as the system swaps its other components for a more diverse composition.

Fig. 5.

Phase behavior of biomolecular condensates with up to six different types of phase-separating proteins. (A, Left) Cartoon illustrating types of proteins in the mixtures: two types of 4-valency proteins (promiscuous, which we term “M4,” and selective), two types of 3-valency proteins (good, which we term “M3,” and poor topology), a 3-valency protein with one binding site partially deactivated (1/4; 2.25-valency), and a 2-valency protein. The 4-valency promiscuous protein has the largest coexistence region and highest critical temperature and dominates the phase behavior of the mixture. (A, Right) Simulation snapshot showing liquid–liquid coexistence of a six-component equimolar mixture. (B) Phase diagrams of the single-component protein systems showing how the critical point varies with the protein characteristics. The vertical axes in all of the phase diagrams represent the inverse interaction strength normalized by the critical value of the single-component scaffold ($1/{\epsilon }_{\mathrm{S}}^c$ for the 4-valency promiscuous protein). Note that because 2-valency proteins do not undergo LLPS on their own, a coexistence curve is not shown for such a system. The black arrow indicates the direction of change of the critical parameter $1/{\epsilon }_{prot-prot}^c$ as the valency increases. Numerical values of these single-component critical points are given in SI Appendix, Table S2. (C) Phase diagram of a six-component mixture at two different mixing concentrations versus a binary mixture. The binary mixture (blue diamonds) contains 67% 4-valency promiscuous proteins and 33% 3-valency good-topology proteins. The first six-component mixture (cyan triangles) contains 67% 4-valency promiscuous proteins and 33% remaining proteins at equal concentrations (6.6% each). The second six-component mixture (green inverted triangles) is an equimolar mixture, i.e., formed by equal concentrations of all proteins (16.6% each). The black arrow indicates the direction of change of the critical parameter $1/{\epsilon }_{prot-prot}^c$ as the concentration of the highest-valency protein in the mixture (in this case M4) increases. Numerical values of the critical points for these systems are given in SI Appendix, Tables S2 and S3. (D) Partitioning coefficient as a function of the normalized critical point (critical inverse interaction energy of each protein in pure form divided over the highest critical value among the set (that for the 4-valency proteins) or, equivalently, critical temperatures of each protein in pure form divided over the highest critical temperature among the set). The partitioning coefficients (defined here as the natural logarithm of the ratio of concentration of a protein in the condensate versus the diluted liquid) were calculated for the equimolar mixture at a constant value of the normalized inverse interaction energy (0.75) depicted by a dotted line in C. (E) Normalized critical points for the proteins in pure form (as defined as in D) plotted as a function of the normalized number of intermolecular protein–protein contacts per unit volume ($I/I_S$) calculated for each independent system in pure form at a constant value of ${\epsilon }_S/{\epsilon }_{prot-prot}=0.8$ and finite pressure (SI Appendix, section VIII). The normalization was done by dividing over the highest number of contacts established by a protein in the mixture (the 4-valency protein). Error bars in the phase diagrams are of the same size as or smaller than the symbols. Typical statistical uncertainties are provided in SI Appendix, Table S5.

In experiments, partitioning coefficients, defined as the ratio of concentration of a protein in the condensate versus the diluted liquid, are measured to assess the extent to which proteins are enriched or depleted in condensates (11, 47, 75). Fig. 5D reveals a strong correlation between the partitioning coefficient of species in an equimolar multicomponent mixture (with equal intermolecular binding strengths among all components) and the respective single-component critical temperatures (or, equivalently, the critical value of the inverse interaction strength).

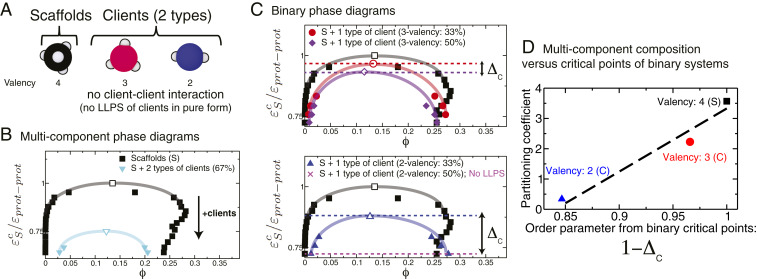
As discussed above, multicomponent condensates can also include species that do not undergo LLPS on their own (a.k.a. clients) and for which estimating critical points in pure form is unfeasible. We investigate these type of systems by evaluating an equimolar multicomponent mixture formed by the same high-valency protein as before (4-valency proteins, which act as scaffolds) and two types of client proteins that exhibit interactions only with the scaffolds (3-valency and 2-valency client proteins; Fig. 6A). As expected, the coexistence region for the mixture shrinks significantly with respect to that of the pure scaffold system due to the depletion of scaffolds (Fig. 6B). Moreover, our simulations reveal that a similar predictive rule—like that postulated above for mixtures of phase-separating proteins—can also be obtained for these scaffold–client multicomponent condensates. Clients that cause the least disruption to the overall connectivity of the multicomponent condensate are expected to be preferentially partitioned into the condensate. Here, we assess the effect of each client on the scaffold connectivity (and, thus, the overall condensate composition) independently. This is achieved by measuring critical points of binary mixtures containing only the scaffolds and one type of client and repeating this measurement for different scaffold–client mixing ratios (Fig. 6C). Adding a small number of clients that marginally disrupt the connectivity (i.e., 3-valency clients) yields binary mixtures (i.e., where the scaffolds are in excess) with critical points that lie close to that of the pure scaffold system and that decrease only moderately as more clients are added to the mixture (Fig. 6C, Top). In contrast, adding clients that substantially disrupt the connectivity (i.e., 2-valency clients) gives rise to much lower binary critical points (with excess scaffolds) that decrease substantially (and can even lead to LLPS inhibition) as more clients are added (Fig. 6C, Bottom). Strikingly, the partitioning coefficient of each client in the multicomponent condensate and an order parameter that quantifies the variation in the critical points of the binary mixtures ($1-{\mathrm{\Delta }}_c$) (Fig. 6 C and D) are positively correlated too. Since this procedure captures the effect of clients in disrupting connectivity of the condensate, it is expected to hold independently of the valencies of the clients and of the binding affinities and binding strengths between clients and scaffolds.

Fig. 6.

Phase behavior of biomolecular condensates with one type of scaffold and two types of client proteins that do not undergo LLPS in pure form. (A) The scaffold is a 4-valency protein that self-interacts and drives LLPS. The two types of clients are 3-valency and 2-valency proteins that exhibit only scaffold–client interactions (no client–client interactions) and can phase separate only when mixed with the scaffolds. (B) Phase diagram of the equimolar multicomponent mixture versus that of the pure scaffold. The black arrow indicates the direction toward which the critical parameter $1/{\epsilon }_{prot-prot}^c$ moves upon addition of clients. Numerical values of the critical points of these systems are given in SI Appendix, Table S4. (C) Phase diagrams of binary mixtures consisting of the scaffolds and one type of client each (Top, 3-valency clients; Bottom, 2-valency clients) at two different scaffold–client ratios (33$\%$ and 50$\%$ clients). For each type of client, we define the parameter ${\mathrm{\Delta }}_c$ as the difference in the normalized critical points of the binary scaffold–client mixture at two client concentrations, i.e., ${\mathrm{\Delta }}_c={\epsilon }_S^c/\left({\epsilon }_{\mathrm{L}\mathrm{o}\mathrm{w}}^c-{\epsilon }_{\mathrm{H}\mathrm{i}\mathrm{g}\mathrm{h}}^c\right)$, where the subscripts Low and High indicate that the critical point is taken from the low (e.g., 33$\%$) and high (e.g., 50$\%$) client concentrations, respectively. For systems where increasing the client concentrations results in LLPS inhibition (e.g., scaffold–client mixture with 50$\%$ of 2-valency clients), we define ${\mathrm{\Delta }}_c$ instead as ${\mathrm{\Delta }}_c={\epsilon }_S^c/\left({\epsilon }_{\mathrm{L}\mathrm{o}\mathrm{w}}^c-{\epsilon }_{\mathrm{L}\mathrm{o}\mathrm{w}}^{min}\right)$, where ${\epsilon }_{\mathrm{L}\mathrm{o}\mathrm{w}}^{min}$ is the lowest temperature or largest protein–protein interaction strength that we can explore without observing gelation. Consistent with this definition, ${\mathrm{\Delta }}_c$ for the scaffolds is always equal to zero. The horizontal dashed lines indicate the values of ${\epsilon }_S^c{/\epsilon }_{Low}^c$ (red) and ${\epsilon }_S^c/{\epsilon }_{\mathrm{H}\mathrm{i}\mathrm{g}\mathrm{h}}^c$ (purple) for the 3-valency clients, and ${\epsilon }_S^c{/\epsilon }_{Low}^c$ (blue) and ${\epsilon }_S^c{/\epsilon }_{Low}^{min}$ (magenta) for the 2-valency clients. The double-headed arrows illustrate the values of ${\mathrm{\Delta }}_c$. (D) Partitioning coefficient of the different species in the equimolar mixture versus the order parameter $1-{\mathrm{\Delta }}_c$ determined from the critical points of the different binary mixtures. Error bars in the phase diagrams are of the same size as or smaller than the symbols. Typical statistical uncertainties are provided in SI Appendix, Table S5.

These results suggest that proteins with higher single-component critical temperature or with higher binary scaffold–client critical temperatures are able to form more connections inside the condensed phase and are generally more concentrated in the condensate. Hence, we can predict the composition of a multicomponent condensate by estimating the critical parameters (temperature, pH, salt concentration, etc.) of the different components in pure form or, when they cannot phase separate on their own, in binary scaffold–client mixtures.

The available simulations (48, 63, 64) and our work show that the critical point of a system rises as the number of possible of intermolecular connections per unit of volume in the condensed-liquid network increases (Fig. 5E and SI Appendix, Table S3). We, therefore, suggest that the key physical factor governing the stability and composition of a biomolecular condensate with many components is the overall ability of the different components to enhance the molecular connectivity of the condensate. Higher connectivity can be achieved through a higher valency, through an optimal topology [i.e., an angular distribution of patches that favors network formation (48)], or by binding promiscuously rather than selectively.

Conclusions

Our simulations indicate that the dominant physical determinant governing the stability of biomolecular condensates in general—and of those with many components in particular—is the ability of the components to enhance the connectivity (i.e., average number of attractive intermolecular interactions per unit volume) of the percolating condensed-liquid network. Valency plays the dominant role in modulating protein LLPS because it determines the density of intermolecular connections that biomolecules can form to stabilize the condensed liquid.

High molecular connectivity is crucial for the stability of condensates because scaffold–scaffold interactions are required to be weak and transient for the condensate to be liquid-like. A system will generally experience a loss in the total number of available microstates upon demixing (entropy loss), but dynamic formation and rupture of a large number of weak attractive scaffold–scaffold interactions at small intermolecular separation (enthalpy gain) can compensate for such loss, making LLPS thermodynamically favorable; higher connectivity implies a higher enthalpic gain. In vivo, posttranslational chemical modifications or replacement of scaffolds by their variants can result in an increase/decrease of the valency of and/or the interaction strength of scaffolds, suggesting that modulation of scaffold valency is one of the key mechanisms used by cells to dynamically control the stability of their phase-separated condensates.

Besides varying the properties of scaffolds, an alternative way of fine-tuning the stability of multicomponent biomolecular condensates is by introducing clients. Consistent with the work of Banani et al. (11), our simulations demonstrate that multicomponent condensates nucleate by forming clusters of pure scaffolds (sustained by scaffold–scaffold interactions) and subsequently recruit clients as they grow. We find that recruitment of low-valency clients to condensates via scaffold–client interactions can significantly transform condensate stability. Low-valency clients that bind with high affinity to scaffolds and compete for scaffold–scaffold binding sites (strongly competing clients) can induce substantial LLPS destabilization, which is enhanced as the client concentration rises. This is because strongly competing low-valency clients reduce the number of scaffold–scaffold interconnections per unit volume. In contrast, low-valency clients that bind to scaffolds through sites not used for scaffold–scaffold interactions (noncompeting clients) can notably increase the stability of condensates if they create new scaffold–client–scaffold bridges and effectively increase the density of connections within the condensate. Similarly, introduction of clients with higher valencies than the scaffolds increases the scaffold connectivity and condensate stability. Hence, we suggest that a general mechanism that could be employed by cells to modulate the stability of their liquid compartments is the introduction of clients or the activation/enhancement of scaffold–client interactions by means of posttranslational modifications. Introducing high-affinity low-valency clients that compete for scaffold–scaffold interactions triggers condensate dissolution, whereas adding clients that bind to alternate sites on scaffolds or have higher-than-scaffold valencies favors compartmentalization.

As we increase the number of components of a biomolecular condensate, we see that the same rules apply; i.e., the physical determinant of the stability of a biomolecular condensate with many components is its intermolecular connectivity. Because of this, the concentration and valency of the scaffolds play a major role. Indeed, the phase diagrams of multicomponent condensates with an excess of scaffolds (e.g., 67$\%$) are dominated by the properties (e.g., valency, topology, and scaffold–scaffold binding affinity) of the scaffolds. As long as the scaffold concentration remains constant, substituting one of the additional protein components for a multitude of different proteins (i.e., increasing the compositional diversity) has a minor effect. However, if the compositional diversity of the condensate is increased at the expense of the scaffold concentration, the condensate stability can be reduced significantly.

The ability of biomolecules to form favorable interconnections also determines their composition inside multicomponent condensates. That is, species that can increase the connectivity of the condensate are present in higher concentrations. Indeed, for scaffolds, which can phase separate on their own, we find a clear correlation between their partitioning coefficients in a multicomponent mixture and their single-component critical points. Similarly, for clients, we can correlate their partitioning coefficients in multicomponent mixtures with the critical points of simple binary scaffold–client mixtures. Therefore, the critical points of highly simplified systems (i.e., either single-component systems or binary mixtures) can be considered as a thermodynamic parameter for predicting the relative composition of the different species in a condensate with many components. In other words, we propose that in experiments one can predict the relative concentration of proteins of interest within highly multicomponent condensates by measuring critical points of much simpler systems (i.e., composed of one or two types of components). Proteins yielding higher critical points in the experiments of reduced systems would be expected to appear at higher concentrations in the multicomponent condensate. These ideas present opportunities for developing models that can predict critical points of inaccessible highly multicomponent condensates from those of easily measured reduced-component systems.

Taken together our work identifies thermodynamic and molecular features that shift the equilibrium between formation and dissolution of multicomponent biomolecular condensates. Our findings expand the current mechanistic picture relating phase behavior of multicomponent intracellular mixtures to the microscopic properties of the constituent biomolecules, and are useful for understanding—and eventually controlling—regulation and misregulation of LLPS inside cells.

Materials and Methods

Full details of the minimal multivalent protein model, the direct coexistence simulation method, the analyses, and simulation details are provided in SI Appendix.

Data Availability.

All relevant data are provided in this paper and in SI Appendix.