Summary
A common phenomenon in cancer syndromes is for an individual to have multiple primary cancers (MPC) at different sites during his/her lifetime. Patients with Li-Fraumeni syndrome (LFS), a rare pediatric cancer syndrome mainly caused by germline TP53 mutations, are known to have a higher probability of developing a second primary cancer than those with other cancer syndromes. In this context, it is desirable to model the development of MPC to enable better clinical management of LFS. Here, we propose a Bayesian recurrent event model based on a non-homogeneous Poisson process in order to obtain penetrance estimates for MPC related to LFS. We employed a familywise likelihood that facilitates using genetic information inherited through the family pedigree and properly adjusted for the ascertainment bias that was inevitable in studies of rare diseases by using an inverse probability weighting scheme. We applied the proposed method to data on LFS, using a family cohort collected through pediatric sarcoma patients at MD Anderson Cancer Center from 1944 to 1982. Both internal and external validation studies showed that the proposed model provides reliable penetrance estimates for MPC in LFS, which, to the best of our knowledge, have not been reported in the LFS literature.
Keywords: Age-at-onset penetrance, Familywise likelihood, Li-Fraumeni syndrome, Multiple primary cancers, Recurrent event model
1. Introduction
A second primary cancer develops independently at different sites and involves different histology than the original primary cancer; it is not caused by extension, recurrence, or metastasis of the original cancer (Hayat and others, 2007). Multiple primary cancers (MPC) is a term for the development of primary cancers more than once in a given patient over the follow-up time. The occurrence of MPC is becoming more common due to advances in cancer treatment and related medical technologies, which enable more people to survive certain cancers. The National Cancer Institute estimated that the US population in 2005 included around 11 million cancer survivors, which was more than triple the number in 1970 (Curtis and others, 2006). Furthermore, surviving a given cancer does not necessarily suggest a decreased risk of developing another cancer. For example, van Eggermond and others (2014) reported that the risk of developing a second primary cancer among survivors of Hodgkin’s lymphoma is 4.7-fold more than that among the general population. The risk of developing MPC varies by genetic susceptibility factors as well. For example, Li-Fraumeni syndrome (LFS), a rare pediatric disease involving higher risk of developing MPC, is associated with germline mutation in the tumor suppressor gene TP53 (Malkin and others, 1990; Eeles, 1994).
Penetrance is defined as the probability of actually experiencing clinical symptoms of a particular trait (phenotype) given the status of the genetic variants (genotype) that may cause the trait. Penetrance plays a crucial role in many genetic epidemiology studies as it characterizes the association of a germline mutation with disease outcomes (Khoury and others, 1988). For example, penetrance is an essential quantity for disease risk assessment, which involves identifying the at-risk individuals and providing prompt disease prevention strategies. To be more specific, popular risk assessment models often require penetrance estimates as inputs (Domchek and others, 2003; Chen and Parmigiani, 2007).
The data that motivated our study is a family cohort of LFS collected through probands with pediatric sarcoma treated at MD Anderson Cancer Center (MDACC) from January 1944 to December 1982 and their extended relatives (Strong and Williams, 1987; Bondy and others, 1992; Lustbader and others, 1992; Hwang and others, 2003; Wu and others, 2006). We use “proband” to denote the affected individual who seeks medical assistance, and based on whom the family data are then gathered for inclusion in datasets (Bennett, 2011). In the LFS application, the MPC-specific penetrance is defined as
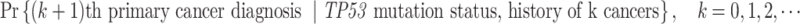 |
(1.1) |
If an individual currently has no cancer history (i.e., 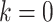 ), then the MPC-specific penetrance (1.1) becomes
), then the MPC-specific penetrance (1.1) becomes 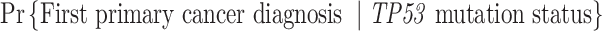 , which has been estimated previously by Wu and others (2010) ignoring MPC. It shall, therefore, lead to more accurate cancer risk assessment in LFS for both cancer survivors and no-cancer-history individuals by utilizing more detailed individual cancer histories with MPC.
, which has been estimated previously by Wu and others (2010) ignoring MPC. It shall, therefore, lead to more accurate cancer risk assessment in LFS for both cancer survivors and no-cancer-history individuals by utilizing more detailed individual cancer histories with MPC.
Few attempts have been made to account for MPC in penetrance estimation. Wang and others (2010) used Bayes rule to calculate multiple primary melanoma (MPM)-specific penetrance, based on penetrance estimates for TP53 mutation carriers, the ratio of MPM patients among carriers and non-carriers, and the ratio of MPM and patients with single primary melanoma (SPM) among carriers. However, that estimation did not account for age and other factors that may contribute to variations observed in patients with SPM and MPM, and relied on previous population estimates of penetrance and relative risk.
MPC can naturally be regarded as recurrent events, which have been extensively studied in statistics (Cook and Lawless, 2007). However, the MPC-specific penetrance estimation from LFS data is more challenging than estimations that use the conventional recurrent event model due to the following reasons. Most individuals (74%) in the LFS family data have unknown TP53 genotypes, and the LFS data are collected through high-risk probands, e.g., those diagnosed with pediatric sarcoma at MDACC, resulting in ascertainment biases. Such bias is inevitable in the study of rare diseases such as LFS as they require an enrichment of cases to achieve a sufficient sample size.
Shin and others (2018) recently investigated both of the aforementioned problems for the LFS data under a competing risk framework to provide a set of cancer-specific penetrance estimates. In particular, they defined the familywise likelihood by averaging the individual likelihoods within the family over the missing genotypes, which is possible since the exact distribution of missing genotypes is available according to the Mendelian law of inheritance. The familywise likelihood can minimize the efficiency loss since the missing genetic information is taken into account in its calculation. They also proposed to use the ascertainment-corrected joint (ACJ) likelihood (Iversen and Chen, 2005) to correct the ascertainment bias for the LFS data.
In this article, we propose a Bayesian semiparametric recurrent event model based on a non-homogeneous Poisson process (NHPP) (Brown and others, 2005; Cook and Lawless, 2007; Weinberg and others, 2007) in order to reflect the age-dependent and time-varying nature of the cancer occurrence rate in LFS. Our preliminary analysis justifies the NHPP model for the LFS data. We develop what we call the ascertainment-corrected familywise likelihood for the proposed NHPP model and estimate the parameters using a Markov chain Monte Carlo (MCMC) algorithm. Then, we provide a set of MPC-specific penetrances for LFS, which, to the best of our knowledge, have never been reported in the literature.
The rest of this article is organized as follows. In Section 2, we introduce the LFS family data that motivate this study. In Section 2.2, we provide an explorative analysis for the data to justify our approach. In Section 3, we propose a semiparametric recurrent event model for MPC based on NHPP. In Section 4, we describe in detail how to construct the familywise likelihood, including the ascertainment bias correction. We provide the posterior updating scheme via MCMC in Section 5. We describe a simulation study in Section 6. In Section 7, we apply the proposed method to the LFS data and obtain the estimated age-at-onset MPC-specific penetrances. We also carry out both internal and external validation analyses. Our final discussion follows in Section 8.
2. Preliminary analysis of the LFS data
2.1. LFS data summary
The pediatric sarcoma cohort data from MDACC consists of 189 unrelated families, with 17 of them being TP53 mutation positive families in which there is at least one TP53 mutation carrier, and 172 being negative ones with no carrier (Appendix G in supplementary material available at Biostatistics online). The TP53 status was determined by PCR of TP53 exonic regions. Ascertainment is carried out through identification of a proband who has a diagnosis of pediatric sarcoma and who introduces his/her family into the data collection. After a family was ascertained, family members were contacted regularly and continually recruited into the study over 1944–1982. Blood samples from members of the family were collected whenever available. The genetic testing of TP53 was performed on these blood samples, which constitutes the genotype data. Among a total of 3706 individuals, 964 of them had TP53 testing results. The age at the diagnosis of each invasive primary tumor for each individual was recorded. The follow-up periods for each family ranges from 22 years to 62 years starting from the ascertainment date of probands. Among 570 individuals with a history of cancer, a total of 52 had been diagnosed with more than one primary cancer (Table 1). Further details on data collection and germline mutation testing can be found in Hwang and others (2003) and Peng and others (2017).
Table 1.
Number of primary cancers in the LFS dataset
| Number of primary cancers | Gender | Wildtype | Mutation | Unknown |
|---|---|---|---|---|
| 0 | Male | 300 | 10 | 1294 |
| Female | 344 | 8 | 1214 | |
| 1 | Male | 100 | 24 | 123 |
| Female | 118 | 21 | 96 | |
| 2 | Male | 3 | 9 | 6 |
| Female | 3 | 11 | 5 | |
| 3 | Male | 0 | 3 | 0 |
| Female | 0 | 3 | 4 | |
| 4 | Male | 0 | 2 | 0 |
| Female | 0 | 1 | 0 | |
| 5 | Male | 0 | 0 | 0 |
| Female | 0 | 2 | 0 | |
| 7 | Male | 0 | 0 | 0 |
| Female | 0 | 2 | 0 | |
| Total number of individuals | 868 | 96 | 2742 | |
| Total number of cancer patients | 224 | 78 | 234 | |
| Total number of MPC patients | 6 | 33 | 15 | |
2.2. Exploratory analysis
We first carry out a preliminary analysis of the LFS data to propose a model that correctly reflects the nature of the data. For simplicity in this analysis, we ignore the family structure. Let 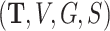 be a set of data given for an arbitrary individual. For an individual who experiences
be a set of data given for an arbitrary individual. For an individual who experiences 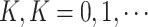 primary cancers,
primary cancers, 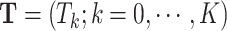 denotes the individual’s age at diagnosis of the
denotes the individual’s age at diagnosis of the 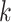 th primary cancer, with
th primary cancer, with 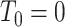 ;
; 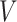 is the censored age at which the individual is lost to follow-up, which is assumed to be independent of all
is the censored age at which the individual is lost to follow-up, which is assumed to be independent of all 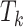 ’s;
’s; 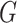 denotes the genotype variable, coded as 1 for germline mutation and 0 for wildtype, with a large number of missing values as shown in Table 1; and
denotes the genotype variable, coded as 1 for germline mutation and 0 for wildtype, with a large number of missing values as shown in Table 1; and 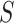 denotes sex, coded as 1 for male and 0 for female.
denotes sex, coded as 1 for male and 0 for female.
In the analysis of MPC, a primary objective is to model the time to the next cancer given the current cancer history. We let 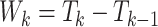 denote the
denote the 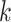 th gap time between two adjacent primary cancers, where
th gap time between two adjacent primary cancers, where 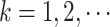 . In analyzing the serial gap times
. In analyzing the serial gap times  , the censoring time
, the censoring time 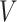 , although independent of
, although independent of 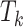 , can be dependent on
, can be dependent on 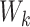 when the
when the 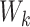 ’s are not independent (Lin and others, 1999). This is often referred to as dependent censoring in the literature. Dependent censoring makes it inappropriate to fit marginal models for the
’s are not independent (Lin and others, 1999). This is often referred to as dependent censoring in the literature. Dependent censoring makes it inappropriate to fit marginal models for the 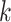 th gap times
th gap times 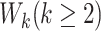 . For example, Cook and Lawless (2007) showed that ignoring dependent censoring can lead to underestimation of the survival functions of the second and subsequent gap times.
. For example, Cook and Lawless (2007) showed that ignoring dependent censoring can lead to underestimation of the survival functions of the second and subsequent gap times.
To check the dependent censoring, we compute the correlation between 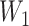 and
and 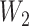 using Kendall’s
using Kendall’s 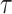 . Table 1 shows that values of
. Table 1 shows that values of 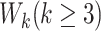 are rarely observed in the LFS data, and we therefore, exclude them from the analysis. Noting that both
are rarely observed in the LFS data, and we therefore, exclude them from the analysis. Noting that both 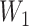 and
and 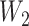 can be censored, we use the inverse probability-of-censoring weighted (IPCW) estimates of Kendall’s
can be censored, we use the inverse probability-of-censoring weighted (IPCW) estimates of Kendall’s 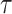 after adjusting for the induced dependent censoring issue (Lakhal-Chaieb and others, 2010). In the analysis, we exclude probands who are the index person for family ascertainment. More details about IPCW estimates of Kendall’s
after adjusting for the induced dependent censoring issue (Lakhal-Chaieb and others, 2010). In the analysis, we exclude probands who are the index person for family ascertainment. More details about IPCW estimates of Kendall’s 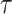 can be found in Appendix A (supplementary material available at Biostatistics online). Finally, the estimated IPCW Kendall’s
can be found in Appendix A (supplementary material available at Biostatistics online). Finally, the estimated IPCW Kendall’s 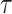 =
= 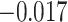 (jackknife estimation of the standard error = 0.005), which indicates a statistically significant, but very weak correlation between the two gap times within individuals. We have further calculated Kendall’s
(jackknife estimation of the standard error = 0.005), which indicates a statistically significant, but very weak correlation between the two gap times within individuals. We have further calculated Kendall’s  within subgroups of mutation carriers and non-carriers. Neither of the subgroup
within subgroups of mutation carriers and non-carriers. Neither of the subgroup 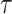 estimates was significantly different from zero.
estimates was significantly different from zero.
We computed Kaplan–Meier estimates of survival functions 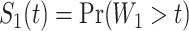 and
and 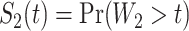 , stratified by genotype (Appendix G in the supplementary material available at Biostatistics online). The risk set used for calculating
, stratified by genotype (Appendix G in the supplementary material available at Biostatistics online). The risk set used for calculating 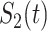 considers only patients with a single primary cancer (SPC) and MPC starting from the first cancer, while
considers only patients with a single primary cancer (SPC) and MPC starting from the first cancer, while 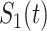 includes all individuals. For both TP53 mutation carriers and non-carriers or untested individuals, the lengths of the first and second gap times are not identically distributed, with the first gap time significantly longer than the second one. This suggests a time trend in the process where the rate of event occurrence increases with age. Moreover, the mutation carriers appear to have different length distributions for wildtype and untested individuals. This empirical difference in successive survival also suggests the importance of providing subgroup-specific and MPC-specific penetrance.
includes all individuals. For both TP53 mutation carriers and non-carriers or untested individuals, the lengths of the first and second gap times are not identically distributed, with the first gap time significantly longer than the second one. This suggests a time trend in the process where the rate of event occurrence increases with age. Moreover, the mutation carriers appear to have different length distributions for wildtype and untested individuals. This empirical difference in successive survival also suggests the importance of providing subgroup-specific and MPC-specific penetrance.
3. Model
3.1. Semiparametric recurrent event model for MPC
Viewing the MPC as recurrent events that occur over time, we employ a counting process to model the MPC.
Let 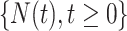 be the number of primary cancers that an individual experiences by age
be the number of primary cancers that an individual experiences by age 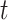 . The intensity function
. The intensity function 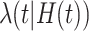 that characterizes the counting process
that characterizes the counting process 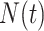 is defined as
is defined as
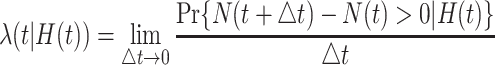 |
(3.1) |
where 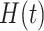 denotes the event history up to time
denotes the event history up to time 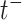 , i.e.,
, i.e., 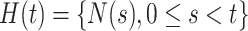 , with
, with  being a time infinitesimally before
being a time infinitesimally before 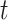 (Cook and Lawless, 2007; Ning and others, 2015).
(Cook and Lawless, 2007; Ning and others, 2015).
For the LFS data, we incorporate a covariate 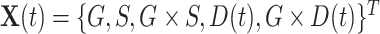 into the Poisson process model, where
into the Poisson process model, where 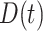 is a time-dependent, but periodically fixed MPC variable that is coded as 1 if
is a time-dependent, but periodically fixed MPC variable that is coded as 1 if 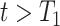 and 0 otherwise. We propose the following multiplicative model for the conditional intensity function given
and 0 otherwise. We propose the following multiplicative model for the conditional intensity function given 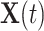 as
as
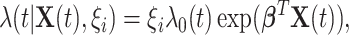 |
(3.2) |
where 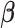 denotes the coefficient parameter that controls effect of covariate
denotes the coefficient parameter that controls effect of covariate 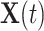 on the intensity and
on the intensity and 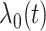 is a baseline intensity function. Here,
is a baseline intensity function. Here, 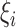 is the
is the 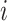 th family-specific frailty used to account for the within-family correlation induced by non-genetic factors that are not included in
th family-specific frailty used to account for the within-family correlation induced by non-genetic factors that are not included in 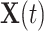 . We remark that
. We remark that 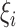 allows us to relax the assumption that the disease histories are conditionally independent given the genotypes. We consider the gamma frailty model that assumes
allows us to relax the assumption that the disease histories are conditionally independent given the genotypes. We consider the gamma frailty model that assumes 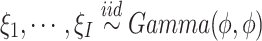 , where
, where 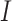 denotes the number of families. The gamma frailty model has been used as a canonical choice (Duchateau and Janssen, 2007) due to the mathematical convenience. Recalling that
denotes the number of families. The gamma frailty model has been used as a canonical choice (Duchateau and Janssen, 2007) due to the mathematical convenience. Recalling that 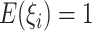 and
and 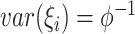 , a large value of
, a large value of 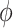 indicates that the within-family correlation is negligible, and we can drop the frailty term to obtain a more parsimonious model.
indicates that the within-family correlation is negligible, and we can drop the frailty term to obtain a more parsimonious model.
There are several choices for the baseline intensity function. Constant or polynomial baseline intensity can be used due to its simplicity, but it may be too restrictive in practice. As an alternative, the piecewise constant model has been widely used due to its flexibility. However, the selection of knot points may be subjective, and it always produces a non-smooth function estimate, which is not desired in some applications. We propose to employ Bernstein polynomials to approximate the cumulative baseline intensity function, 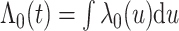 , which is monotonically increasing. Bernstein polynomials are widely used in Bayesian nonparametric function estimation with shape constraints. Assuming
, which is monotonically increasing. Bernstein polynomials are widely used in Bayesian nonparametric function estimation with shape constraints. Assuming 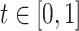 without loss of generality, Bernstein polynomials of degree
without loss of generality, Bernstein polynomials of degree 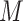 for
for 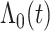 are
are 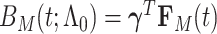 , where the parameter vector
, where the parameter vector 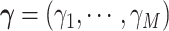 with
with 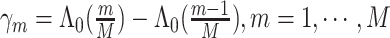 and
and 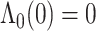 ; and
; and 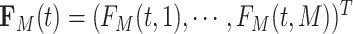 , with
, with 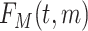 being the beta distribution function with parameters
being the beta distribution function with parameters 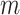 and
and 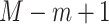 evaluated at
evaluated at 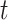 (Curtis and Ghosh, 2011). We restrict
(Curtis and Ghosh, 2011). We restrict 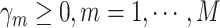 to have
to have 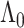 monotonically increasing. The Bernstein-polynomial model for
monotonically increasing. The Bernstein-polynomial model for 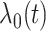 is then obtained by
is then obtained by
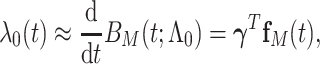 |
(3.3) |
where 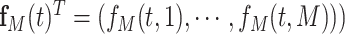 denotes the beta density with parameters
denotes the beta density with parameters 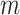 and
and 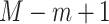 evaluated at
evaluated at 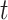 .
.
A large value of 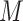 provides more flexibility to model the shape of baseline rate function, but at the cost of increased computations. Gelfand and Mallick (1995) empirically showed that a relatively small value of
provides more flexibility to model the shape of baseline rate function, but at the cost of increased computations. Gelfand and Mallick (1995) empirically showed that a relatively small value of 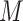 works well in practice, and we assume
works well in practice, and we assume 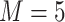 in the upcoming analyses.
in the upcoming analyses.
Finally, the proposed semi-parametric model for the intensity function of NHPP is given by
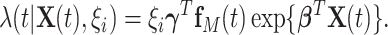 |
3.2. MPC-specific penetrance
The MPC-specific age-at-onset penetrance defined in (1.1) is equivalently rewritten as
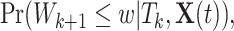 |
(3.4) |
which is identical to 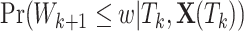 since
since 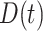 is periodically fixed. The MPC-specific penetrance (3.4) is then obtained by marginalizing out the random frailty
is periodically fixed. The MPC-specific penetrance (3.4) is then obtained by marginalizing out the random frailty 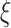 as follows:
as follows:
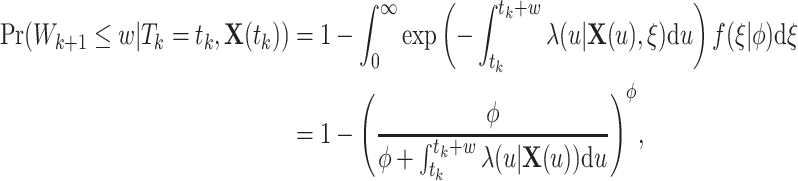 |
where 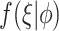 is the gamma density function of the frailty
is the gamma density function of the frailty 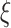 given
given 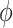 , and
, and  .
.
4. Computing likelihood
In this work, the computing likelihood is not trivial due to a large number of missing genotypes and the ascertainment bias. In this section, we propose an ascertainment-bias-corrected familywise likelihood to tackle these issues.
Let 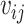 and
and 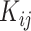 denote the censoring time and the total number of primary cancers developed for individual
denote the censoring time and the total number of primary cancers developed for individual 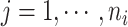 from family
from family 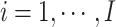 , respectively. Suppose we are given a set of data
, respectively. Suppose we are given a set of data 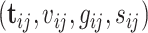 , where
, where 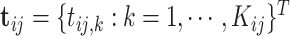 and
and 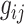 and
and 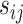 are the observed genotype and sex, respectively. Given the data, we can easily define the observed version of
are the observed genotype and sex, respectively. Given the data, we can easily define the observed version of 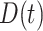 denoted by
denoted by 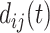 as 1 if
as 1 if 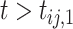 and 0 otherwise, and
and 0 otherwise, and 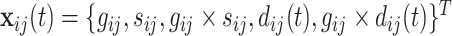 .
.
4.1. Individual likelihood
Let 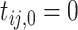 and
and 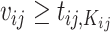 , conditioning on
, conditioning on 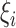 , the likelihood contribution of the
, the likelihood contribution of the 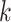 th event since the
th event since the 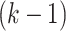 th event is
th event is
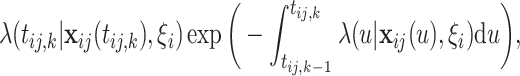 |
(4.1) |
Let 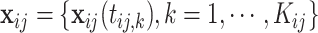 and
and 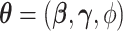 denote the parameter vectors of interest. Given
denote the parameter vectors of interest. Given 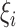 , the likelihood of the
, the likelihood of the 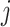 th individual of the
th individual of the 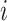 th family with primary cancer events
th family with primary cancer events 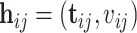 , denoted by
, denoted by 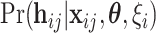 is
is
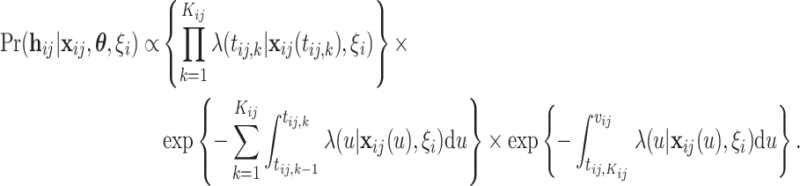 |
(4.2) |
4.2. Familywise likelihood
Tentatively assuming that the covariates 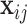 are completely observed for every individual, the likelihood for the
are completely observed for every individual, the likelihood for the 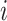 th family is simply given by
th family is simply given by 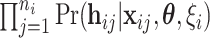 . However, in the LFS data, most individuals have not undergone testing for their TP53 mutation status. For simplicity, we partition the covariate vector
. However, in the LFS data, most individuals have not undergone testing for their TP53 mutation status. For simplicity, we partition the covariate vector 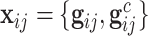 , where
, where 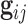 and
and 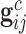 denote the covariates that are related and unrelated to the genotype
denote the covariates that are related and unrelated to the genotype 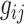 , respectively. Let
, respectively. Let  ,
, 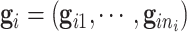 and
and 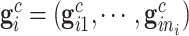 . Due to a large number of family members without genotype information,
. Due to a large number of family members without genotype information,  , we further introduce
, we further introduce  and
and 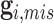 to respectively denote the observed and missing parts of genotype vector
to respectively denote the observed and missing parts of genotype vector 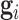 , i.e.,
, i.e., 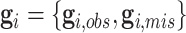 . The familywise likelihood for the
. The familywise likelihood for the 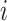 th family is naturally defined by
th family is naturally defined by
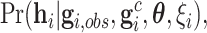 |
(4.3) |
while its evaluation is not trivial since 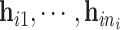 are correlated through
are correlated through 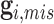 .
.
To tackle this issue, we employ Elston–Stewart’s peeling algorithm to recursively calculate (4.3) (Elston and Stewart, 1971; Lange and Elston, 1975; Fernando and others, 1993). Let us suppress the conditional arguments in (4.3) except 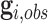 for simplicity. The peeling algorithm is developed to evaluate the pedigree likelihood
for simplicity. The peeling algorithm is developed to evaluate the pedigree likelihood 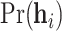 , not
, not 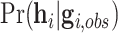 , accounting for the probability distribution of genotype configurations of all family members (e.g.,
, accounting for the probability distribution of genotype configurations of all family members (e.g., 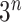 genotype configurations for one gene and
genotype configurations for one gene and 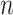 family members). It proceeds by recursively partitioning a large family into smaller ones. An illustrative example of the peeling algorithm for the familywise likelihood evaluation is given in Appendix B (supplementary material available at Biostatistics online). Notice that if there is no genotype observed, i.e.,
family members). It proceeds by recursively partitioning a large family into smaller ones. An illustrative example of the peeling algorithm for the familywise likelihood evaluation is given in Appendix B (supplementary material available at Biostatistics online). Notice that if there is no genotype observed, i.e., 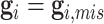 , then (4.3) can be evaluated by directly applying the peeling algorithm. We have made slight modification on the peeling algorithm to include known genotype information of some family members in our data (Shin and others, 2018).
, then (4.3) can be evaluated by directly applying the peeling algorithm. We have made slight modification on the peeling algorithm to include known genotype information of some family members in our data (Shin and others, 2018).
4.3. Ascertainment bias correction
Ascertainment bias is inevitable in studies of rare diseases like LFS because the datasets are usually collected from a high-risk population. For example, our LFS dataset is ascertained through probands diagnosed at LFS primary cancers such as pediatric sarcoma at MD Anderson Cancer Center, and therefore, has oversampled LFS primary cancer patients. Such ascertainment must be properly adjusted to generalize the corresponding results to the population, for which the familywise likelihood (4.3) alone is not sufficient.
We propose to use an ACJ likelihood (Kraft and Thomas, 2000; Iversen and Chen, 2005). Introducing an ascertainment indicator variable 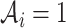 that takes 1 if the
that takes 1 if the 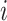 th family is ascertained and 0 otherwise, the ACJ likelihood for the
th family is ascertained and 0 otherwise, the ACJ likelihood for the 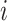 th family is given by
th family is given by
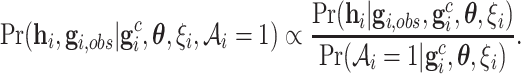 |
(4.4) |
That is, the ACJ likelihood corrects the ascertainment bias by inverse-probability weighting (4.3) by the corresponding ascertainment probability. Now, the ascertainment probability, the denominator in (4.4), is the likelihood contribution of the proband, computed as follows:
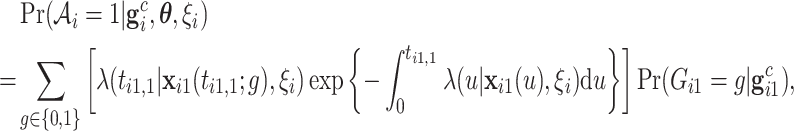 |
(4.5) |
where 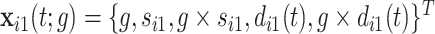 for the proband in family
for the proband in family  . Notice this likelihood is marginalized over genotype since the genotype information for the proband is not available when the ascertainment decision is made. In general, the covariate specific prevalence
. Notice this likelihood is marginalized over genotype since the genotype information for the proband is not available when the ascertainment decision is made. In general, the covariate specific prevalence 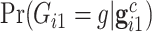 is assumed to be known. In our LFS application, we assume the TP53 mutation prevalence is independent of all non-genetic variables, and therefore, the conditional prevalence is equal to the unconditional prevalence
is assumed to be known. In our LFS application, we assume the TP53 mutation prevalence is independent of all non-genetic variables, and therefore, the conditional prevalence is equal to the unconditional prevalence 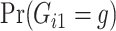 for a general population, which can be calculated from the mutated allele frequency denoted by
for a general population, which can be calculated from the mutated allele frequency denoted by 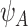 :
: 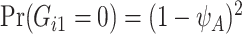 and
and 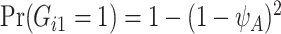 . Here,
. Here, 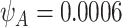 for TP53 mutations in the Western population (Lalloo and others, 2003).
for TP53 mutations in the Western population (Lalloo and others, 2003).
Finally, the ACJ familywise likelihood for the LFS data is then given by
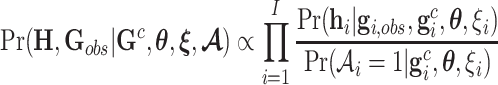 |
where 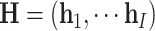 ,
, 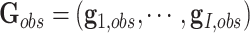 ,
, 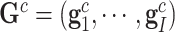 , and
, and 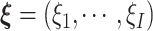 , and
, and 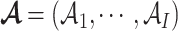 .
.
5. Posterior sampling through MCMC
We set an independent normal prior for 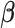 where
where 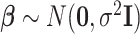 where
where 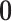 and
and 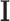 denote a zero vector and an identity matrix, respectively, and
denote a zero vector and an identity matrix, respectively, and 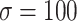 for vague priors. We assign nonnegative flat priors for
for vague priors. We assign nonnegative flat priors for 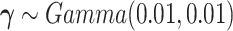 for the baseline intensity. We assume a gamma prior for
for the baseline intensity. We assume a gamma prior for 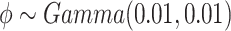 . The joint posterior distribution of
. The joint posterior distribution of 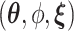 is
is
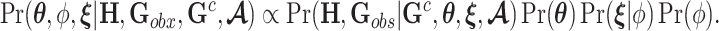 |
(5.1) |
where 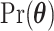 and
and 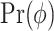 denote prior distributions, and
denote prior distributions, and 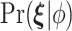 is a frailty density that we assume to follow gamma distribution. We use a random walk Metropolis-Hastings-within-Gibbs algorithm to generate 100 000 posterior estimates in total, with the first 5000 as burn-in. Details about the algorithm steps, R code and convergence diagnostics can be found in the Appendix C (supplementary material available at Biostatistics online).
is a frailty density that we assume to follow gamma distribution. We use a random walk Metropolis-Hastings-within-Gibbs algorithm to generate 100 000 posterior estimates in total, with the first 5000 as burn-in. Details about the algorithm steps, R code and convergence diagnostics can be found in the Appendix C (supplementary material available at Biostatistics online).
6. Simulation study
We simulated family history data containing patients with single and MPC as follows:
- (1) We first simulated the genotype of the proband by
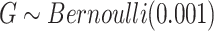 , based on which we generated the first and second gap times,
, based on which we generated the first and second gap times, 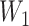 and
and 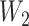 , from the exponential distribution with the rate parameter being
, from the exponential distribution with the rate parameter being
where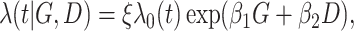
(6.1) 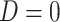 for
for 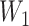 and
and 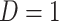 for
for 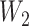 . We set a constant baseline
. We set a constant baseline 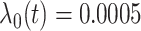 , and
, and 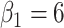 and
and 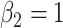 . We simulated
. We simulated 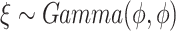 with
with 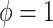 . The two gap times were then compared to censoring time generated by
. The two gap times were then compared to censoring time generated by 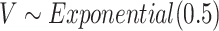 to determine the event indicator. To mimic the ascertainment procedure, for the family data simulation, we retained only the probands with at least one primary cancer observed.
to determine the event indicator. To mimic the ascertainment procedure, for the family data simulation, we retained only the probands with at least one primary cancer observed. (2) Given the proband’s data, we generated his/her family data for three generations. The complete pedigree structure for the simulation is depicted in Appendix G (supplementary material available at Biostatistics online). We set the genotype of all family members as
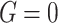 if the proband was a non-carrier. If the proband was a TP53 mutation carrier, one of his/her parents was randomly set as a carrier, and the proband’s siblings and offsprings were set independently as carriers with a probability of 0.5. The offspring of the proband’s siblings were also randomly set as carriers with a probability of 0.5 if the proband’s siblings were carriers. To mimic the scenario of the rate of a rare mutation such as that of the TP53 gene, all family members with non-blood relationships with the proband were set as non-carriers.
if the proband was a non-carrier. If the proband was a TP53 mutation carrier, one of his/her parents was randomly set as a carrier, and the proband’s siblings and offsprings were set independently as carriers with a probability of 0.5. The offspring of the proband’s siblings were also randomly set as carriers with a probability of 0.5 if the proband’s siblings were carriers. To mimic the scenario of the rate of a rare mutation such as that of the TP53 gene, all family members with non-blood relationships with the proband were set as non-carriers.(3) We simulated the first two gap times and the cancer event indicators for the probands’ relatives as we did for the probands. We simulated a total of 100 such families, each of which had 30 family members. To mimic the real scenario in which genotype data are not available for a majority of family members, we randomly removed 70% of the genotype information from non-proband family members.
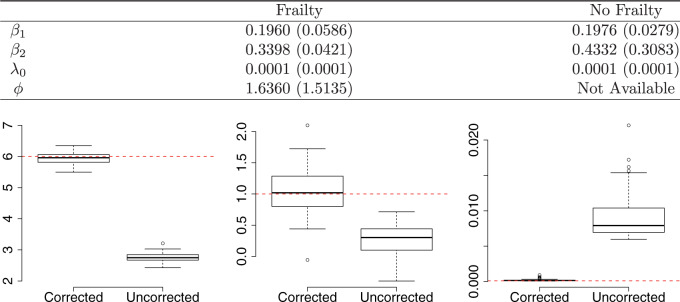
We applied the proposed methods to the simulated data. We generated 5000 posterior samples from the MCMC algorithm, with the first 1000 as burn-in, and checked that the MCMC chains converged well. Simulation results based on 100 independent repetitions are summarized in Figure 1. The proposed method can successfully recover the true parameters. See the top panel for the comparison to a model without frailty, in terms of the root mean squared error and absolute bias, and the bottom panel for the comparison to a model without ascertainment bias correction.
Fig. 1.
Simulation results: The top panel reports root mean squared errors and absolute biases (in parenthesis) of the estimates from the models with and without frailty term. The bottom panel shows boxplots of the estimates from 100 independent repetitions with the corresponding true values depicted in dashed line. The truths for the simulation data are: 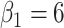 ,
, 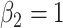 , and
, and 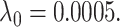
7. Case study
We applied our method to the LFS data (Section 2.2) and estimated the parameters using the MCMC algorithm as described in Section 5. We performed cross-validation, in which we compared our prediction of the 5-year risk of developing the next cancer given the individual’s cancer history and genotype information with the observed outcome, based on our penetrance estimates. We also compared our penetrance results with population estimates and the results in previous studies on TP53 penetrance.
7.1. Model fitting
We fit our model to the LFS data up to the second cancer event due to the limited number of individuals with three or more primary cancers in the dataset (Table 1). Our model contains three relevant covariates: genotype, sex, and cancer status at time 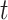 , respectively denoted by
, respectively denoted by 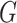 ,
, 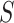 , and
, and 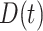 . We also included two interaction effects on genotype.
. We also included two interaction effects on genotype.
We applied the proposed method to the entire dataset to obtain penetrance estimates for SPCs and MPCs given the TP53 mutation status. We first conducted a sensitivity analysis, which showed that the penetrance estimates are not overly sensitive to the choice of priors. The results of the sensitivity analysis are provided in Appendix D (supplementary material available at Biostatistics online).
We then computed the deviance information criterion (DIC) to identify the best set of covariates. We compare five different combinations of 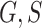 , and
, and 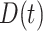 . We observe that the simplest model with
. We observe that the simplest model with 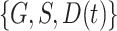 achieves the minimum DIC value. However, we decided to select the second best model in terms of the DIC, with
achieves the minimum DIC value. However, we decided to select the second best model in terms of the DIC, with 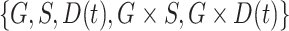 as our final model since it has been reported that cancer status has different effects on cancer risk for mutation carriers and non-carriers (van Eggermond and others, 2014; Mai and others, 2016). All posterior estimates of the model generated from the MCMC algorithm converged well and had reasonable acceptance ratios. See Appendix G (supplementary material available at Biostatistics online) for the model comparison results.
as our final model since it has been reported that cancer status has different effects on cancer risk for mutation carriers and non-carriers (van Eggermond and others, 2014; Mai and others, 2016). All posterior estimates of the model generated from the MCMC algorithm converged well and had reasonable acceptance ratios. See Appendix G (supplementary material available at Biostatistics online) for the model comparison results.
Table 2 contains summaries of the posterior estimates for both the frailty and no-frailty models. We observe that the variance of frailty, 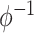 , is estimated to be quite small, which indicates that the no-frailty model may be preferred. It turns out that both models produce nearly identical penetrance estimates (Appendix E in the supplementary material available at Biostatistics online), and we decide to use the no-frailty model to analyze the LFS data. The genotype has dominant effects on increasing cancer risk, both through a main effect and through interaction with the cancer history, as expected from the exploratory analysis (Section 2.2).
, is estimated to be quite small, which indicates that the no-frailty model may be preferred. It turns out that both models produce nearly identical penetrance estimates (Appendix E in the supplementary material available at Biostatistics online), and we decide to use the no-frailty model to analyze the LFS data. The genotype has dominant effects on increasing cancer risk, both through a main effect and through interaction with the cancer history, as expected from the exploratory analysis (Section 2.2).
Table 2.
Summary of posterior estimates
| Coefficient | Frailty | No frailty | ||||||
|---|---|---|---|---|---|---|---|---|
| Median | SD | 2.5% | 97.5% | Median | SD | 2.5% | 97.5% | |
|
3.516 | 0.256 | 3.068 | 3.953 | 3.288 | 0.223 | 2.871 | 3.687 |
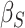
|
0.027 | 0.115 |
 0.189 0.189 |
0.232 | 0.027 | 0.118 |
 0.187 0.187 |
0.241 |
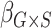
|
 0.332 0.332 |
0.246 |
 0.809 0.809 |
0.139 |
 0.354 0.354 |
0.239 |
 0.817 0.817 |
0.106 |
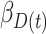
|
 0.380 0.380 |
0.363 |
 1.152 1.152 |
0.259 |
 0.197 0.197 |
0.336 |
 0.929 0.929 |
0.389 |
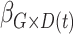
|
0.716 | 0.429 |
 0.070 0.070 |
1.601 | 0.700 | 0.402 |
 0.033 0.033 |
1.548 |
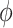
|
5.883 | 1.695 | 3.427 | 9.855 | Not available | |||
SD, standard deviation
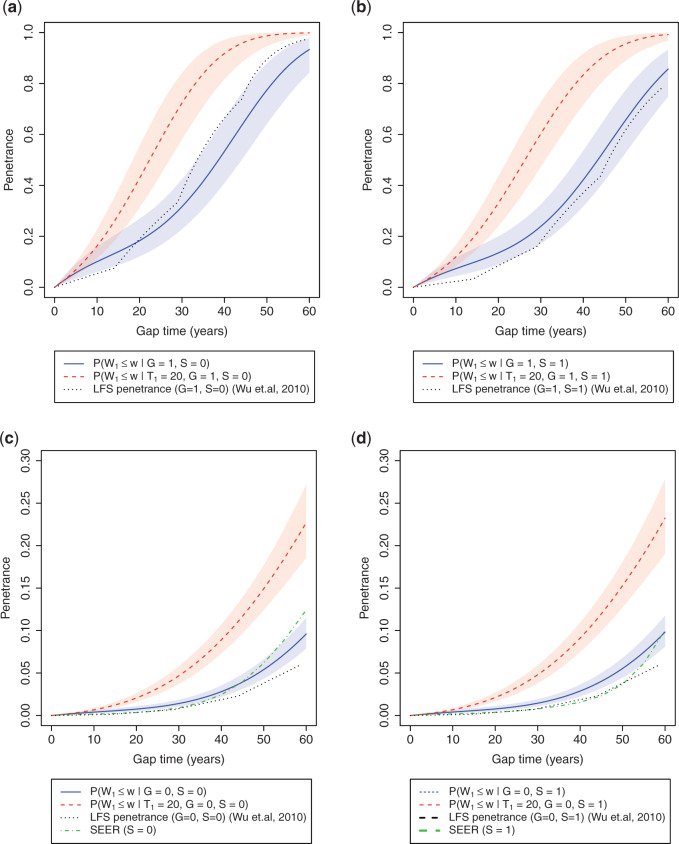
Figure 2 compares penetrance estimates at different ages for females and males, respectively, stratified by genotype. As expected, TP53 mutation has a clear effect on the increase of cancer risk, especially when the individual has a recent history of cancer. For an individual without a TP53 mutation, a history of cancer also has a positive effect on increasing the risk of developing subsequent cancer.
Fig. 2.
Age-at-onset penetrances of SPC and MPC for (a) female mutation carriers, (b) male mutation carriers, (c) female non-carriers, and (d) male non-carriers. The shaded area is the 95% credible bands. Note the y-axis scales between carriers and non-carriers are different. Notations: 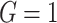 , mutation carriers;
, mutation carriers; 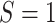 , male;
, male; 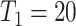 , the first primary cancer diagnosed at age 20. “LFS penetrance” denotes an estimate for
, the first primary cancer diagnosed at age 20. “LFS penetrance” denotes an estimate for 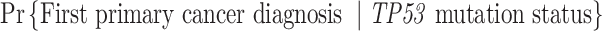 that was previously published using a subset of our LFS dataset without considering the onset of multiple primary cancers.
that was previously published using a subset of our LFS dataset without considering the onset of multiple primary cancers.
Wu and others (2010) estimated TP53 penetrance for the first primary cancer only from six pediatric sarcoma families, a subset of our LFS dataset. Figure 2 shows that, for mutation carriers, this age-at-onset TP53 penetrance estimate aligns with those for SPC in our model but is slightly increased at an older age. Such consistency with a published analysis validates the performance of our model in real data. Another validation is when we compared our estimates for non-carriers to population estimates from the Surveillance, Epidemiology, and End (SEER) Results program (LAG and others, 2008), they also align well (Figure 2c and d, more consistent in males than in females).
7.2. Cancer risk prediction
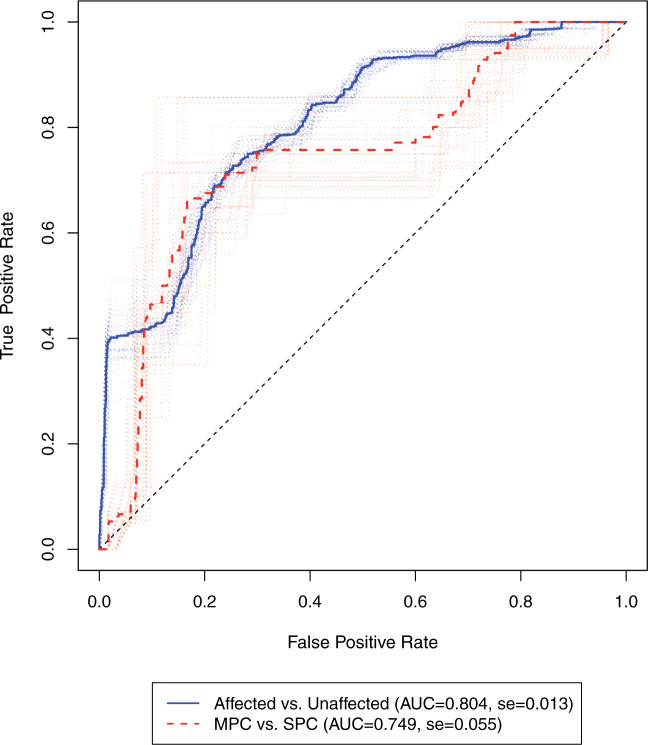
We assessed the ability of our model to predict cancer risk using 10-fold cross-validation. We randomly split the 189 families into 10 portions and repeatedly fit our model to the nine portions of all the families to estimate the penetrance, based on which we made predictions using the remaining one portion of the data. The individuals used for prediction are those who have known genotype information. We removed the probands because they were not randomly selected for genotype testing. We rolled back five years from the age of diagnosis of cancer or the censoring age. Based on the rolled-back time, we then calculated a 5-year cumulative cancer risk. We made two types of risk predictions that are of clinical interest. In the first scenario, we predicted the 5-year risk of developing a cancer given that the individual has no history of cancer (affected versus unaffected). In the second scenario, we predicted the risk of developing the next cancer when the individual had developed cancer previously (SPC versus MPC). We combined these results with those from the 10-fold cross-validation together and evaluated them using the receiver operating characteristic (ROC) curves. To assess the variation in prediction caused by data partitioning, we performed random splits for cross-validation 25 times. Figure 3 shows the risk prediction results from each random split. The median area under the ROC curve (AUC) is 0.804 for predicting the status of being affected by cancer versus the status of not being affected by cancer, given that the individual has no history of cancer. The median AUC is 0.749 for predicting the status of the next cancer when the subject has had one primary cancer. The validation showed that the model performance is robust to random splits in cross-validation.
Fig. 3.
ROC of the 5-year risk of developing the second primary cancer in the LFS dataset. The dotted lines denote the ROC curves for 25 random splits of the data, each undergone a 10-fold cross-validation. The solid lines denote the median ROC curves. Affected vs. Unaffected, prediction of developing a cancer given that the individual has no history of cancer; MPC versus SPC, prediction of developing the next cancer given that the individual has had one primary cancer (SPC). Sample size: n(Affected) = 116, n(Unaffected) = 661, n(MPC) = 29, n(SPC) = 87. se, standard error.
8. Discussions
To our knowledge, this is the first attempt to estimate MPC-specific penetrance for TP53 germline mutation to include family members with unknown genotype information, which will, in turn, substantially improve the sample size and power of a study. In our LFS study, the increases in the number of cancer patients used in the analysis are 48% (from 27 to 40) for MPCs, and 89% (from 274 to 518) for the control group of SPCs. We developed a novel NHPP and incorporated it with a familywise likelihood so that it can model MPC events in the context of a family, while properly accounting for age effects and time-varying cancer status. We applied a Bayesian framework to estimate the unknown parameters in the model. We also adjusted for ascertainment bias in the likelihood calculation so that our penetrance estimates can be compared to those generated from the general population. Our new method provides a flexible framework for the penetrance estimation of MPC data, and shows reasonable predictive performance of cancer risk. As the number of patients with MPC continues to rise in the general population, our method will be useful to predict subsequent cancers and to assist in clinical management of the disease.
Some possible extensions remain. First, we restricted our analysis up to the second primary cancer because of the limited power in the LFS dataset. This makes our penetrance estimation unsuitable for individuals with a history of more than two cancers. It is straightforward to extend our model to account for three or more cancers if we have such cases for each subpopulation.
Second, the occurrence of primary cancers may depend on other factors such as cancer treatment. For example, radiotherapy can damage normal cells in tumor-adjacent areas and is associated with excessive incidence of secondary solid cancers (Inskip and Curtis, 2007). Our model can include additional covariates to adjust for such dependency between successive events. However, the availability of reliable data on radiotherapy is scarce and we have shown here that the current model can have reasonable predictive performance even without incorporating treatment factors.
Third, because the correlation between the first two gap times in the real data is very small, the recurrent event model we used in this study does not explicitly consider such an association. For future datasets that exhibit a stronger level of correlation between the gap times, we would expect the predictive performance for the second or subsequent primary cancers to be improved by properly utilizing such correlation information (i.e., through Bayesian parametric copula models for sequential gap time analyses (Meyer and Romeo, 2015)).
Finally, in MPC studies, there usually exist multiple types of cancer. In our LFS study, even though our genetic background is simple, TP53 germline mutations, the presentation of cancer outcomes is diverse. LFS is characterized by occurrence of many different cancer types, such as sarcoma, breast cancer and lung cancer. Patients with MPC are thus subject to the competing risk of multiple types of cancer. In our current model, we pool together all cancer types and do not address the onset of second primary cancer at any specific site. As we collect more datasets on LFS from multiple clinics to increase our sample size, future work will include extending our methodology to provide MPC-specific and cancer-specific penetrance estimation.
9. Software
Finally, we provide an illustration of our method in Appendix F (supplementary material available at Biostatistics online). The associated example dataset and results, and all of the source code, are available at http://github.com/wwylab/MPC.
Supplementary Material
Acknowledgements
Conflict of Interest: None declared.
Funding
Cancer Prevention Research Institute of Texas (RP130090) to J.L. and W.W. U.S. National Institutes of Health (P01CA34936) to J.B. and L.C.S; (1R01CA174206, 1R01 CA183793, and P30 CA016672) to W.W; (1R01CA193878) to J.N.
References
- Bennett R. L. (2011). The Practical Guide to the Genetic Family History. New Jersey: John Wiley & Sons. [Google Scholar]
- Bondy M. L., Lustbader E. D., Strom S. S., Strong L. C. and Chakravarti A. (1992). Segregation analysis of 159 soft tissue sarcoma kindreds: comparison of fixed and sequential sampling schemes. Genetic Epidemiology 9, 291–304. [DOI] [PubMed] [Google Scholar]
- Brown L., Gans N., Mandelbaum A., Sakov A., Shen H., Zeltyn S. and Zhao L. (2005). Statistical analysis of a telephone call center: a queueing-science perspective. Journal of the American Statistical Association 100, 36–50. [Google Scholar]
- Chen S. and Parmigiani G. (2007). Meta-analysis of BRCA1 and BRCA2 penetrance. Journal of Clinical Oncology 25, 1329–1333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cook R. J. and Lawless J. F. (2007). The Statistical Analysis of Recurrent Events. New York: Springer Science & Business Media. [Google Scholar]
- Curtis M. S. and Ghosh S. K. (2011). A variable selection approach to monotonic regression with Bernstein polynomials. Journal of Applied Statistics 38, 961–976. [Google Scholar]
- Curtis R. E., Freedman D. M., Ron E., Ries L. A. G., Hacker D. G., Edwards B. K., Tucker M. A. and Fraumeni J. F. Jr (2006). New malignancies among cancer survivors: SEER Cancer Registries, 1973–2000 Bethesda, MD: National Cancer Institute; (2006). [Google Scholar]
- Domchek S. M., Eisen A., Calzone K., Stopfer J., Blackwood A. and Weber B. L. (2003). Application of breast cancer risk prediction models in clinical practice. Journal of Clinical Oncology 21, 593–601. [DOI] [PubMed] [Google Scholar]
- Duchateau L. and Janssen P. (2007). The Frailty Model. New York: Springer Science & Business Media. [Google Scholar]
- Eeles R. A. (1994). Germline mutations in the TP53 gene. Cancer Surveys 25, 101–124. [PubMed] [Google Scholar]
- Elston R. C. and Stewart J. (1971). A general model for the genetic analysis of pedigree data. Human Heredity 21, 523–542. [DOI] [PubMed] [Google Scholar]
- Fernando R. L., Stricker C. and Elston R. C. (1993). An efficient algorithm to compute the posterior genotypic distribution for every member of a pedigree without loops. Theoretical and Applied Genetics 87, 89–93. [DOI] [PubMed] [Google Scholar]
- Gelfand A. E. and Mallick B. K. (1995). Bayesian analysis of proportional hazards models built from monotone functions. Biometrics 51, 843–852. [PubMed] [Google Scholar]
- Hayat M. J., Howlader N., Reichman M. E. and Edwards B. K. (2007). Cancer statistics, trends, and multiple primary cancer analyses from the Surveillance, Epidemiology, and End Results (SEER) program. The Oncologist 12, 20–37. [DOI] [PubMed] [Google Scholar]
- Hwang S.-J., Lozano G., Amos C. I. and Strong L. C. (2003). Germline p53 mutations in a cohort with childhood sarcoma: sex differences in cancer risk. The American Journal of Human Genetics 72, 975–983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inskip P. D. and Curtis R. E. (2007). New malignancies following childhood cancer in the united states, 1973–2002. International Journal of Cancer 121, 2233–2240. [DOI] [PubMed] [Google Scholar]
- Iversen E. S. and Chen S. (2005). Population-calibrated gene characterization: estimating age at onset distributions associated with cancer genes. Journal of the American Statistical Association 100, 399–409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khoury M. J., Flanders W. D., Beaty T. H., Optiz J. M. and Reynolds J. F. (1988). Penetrance in the presence of genetic susceptibility to environmental factors. American Journal of Medical Genetics 29, 397–403. [DOI] [PubMed] [Google Scholar]
- Kraft P. and Thomas D. C. (2000). Bias and efficiency in family-based gene-characterization studies: conditional, prospective, retrospective, and joint likelihoods. American Journal of Human Genetics 66, 1119–1131. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
Lakhal-Chaieb L., Cook R. J. and Lin X. (2010). Inverse probability of censoring weighted estimates of Kendall’s
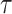 for gap time analyses. Biometrics 66, 1145–1152. [DOI] [PMC free article] [PubMed] [Google Scholar]
for gap time analyses. Biometrics 66, 1145–1152. [DOI] [PMC free article] [PubMed] [Google Scholar] - Lalloo F., Varley J., Ellis D., Moran A., O’Dair L., Pharoah P., Evans D. G. R.; Early Onset Breast Cancer Study Group (2003). Prediction of pathogenic mutations in patients with early-onset breast cancer by family history. The Lancet 361, 1101–1102. [DOI] [PubMed] [Google Scholar]
- Lange K. and Elston R. C. (1975). Extensions to pedigree analysis. Human Heredity 25, 95–105. [DOI] [PubMed] [Google Scholar]
- Lin D. Y., Sun W. and Ying Z. (1999). Nonparametric estimation of the gap time distribution for serial events with censored data. Biometrika 86, 59–70. [Google Scholar]
- Lustbader E. D., Williams W. R., Bondy M. L., Strom S. and Strong L. C. (1992). Segregation analysis of cancer in families of childhood soft-tissue-sarcoma patients. American Journal of Human Genetics 51, 344. [PMC free article] [PubMed] [Google Scholar]
- Mai P. L., Best A. F., Peters J. A., DeCastro R. M., Khincha P. P., Loud J. T., Bremer R. C., Rosenberg P. S. and Savage S. A. (2016). Risks of first and subsequent cancers among TP53 mutation carriers in the national cancer institute Li-Fraumeni syndrome cohort. Cancer 122, 3673–3681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malkin D., Li F. P., Strong L. C., Fraumeni J. F., Nelson C. E., Kim D. H., Kassel J., Gryka M. A., Bischoff F. Z., Tainsky M. A.. and others (1990). Germ line p53 mutations in a familial syndrome of breast cancer, sarcomas, and other neoplasms. Science 250, 1233–1238. [DOI] [PubMed] [Google Scholar]
- Meyer R. and Romeo J. S. (2015). Bayesian semiparametric analysis of recurrent failure time data using copulas. Biometrical Journal 57, 982–1001. [DOI] [PubMed] [Google Scholar]
- Ning J., Chen Y., Cai C., Huang X. and Wang M.-C. (2015). On the dependence structure of bivariate recurrent event processes: inference and estimation. Biometrika 102, 345–358. [Google Scholar]
- Peng G., Bojadzieva J., Ballinger M. L., Li J., Blackford A. L., Mai P. L., Savage S. A., Thomas D. M., Strong L. C. and Wang W. (2017). Estimating TP53 mutation carrier probability in families with Li–Fraumeni syndrome using LFSPRO. Cancer Epidemiology and Prevention Biomarkers 26, 837–844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ries L. A. G., Melbert D., Krapcho M., Stinchcomb D. G., Howlader N., Horner M. J., Mariotto A., Miller B. A., Feuer E. J., Altekruse S. F., Lewis D. R., Clegg L., Eisner M. P., Reichman M., Edwards B. K. (eds). SEER Cancer Statistics Review, 1975–2005, National Cancer Institute; Bethesda, MD, https://seer.cancer.gov/csr/1975_2005/, based on November2007SEER data submission, posted to the SEER web site, 2008. [Google Scholar]
- Shin S. J., Yuan Y., Strong L. C., Bojadzieva J., and Wang W. (2018). Bayesian semiparametric estimation of cancer-specific age-at-onset penetrance with application to Li-Fraumeni syndrome. Journal of the American Statistical Association. DOI: 10.1080/01621459.2018.1482749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strong L. C. and Williams W. R. (1987). The genetic implications of long-term survival of childhood cancer: a conceptual framework. Journal of Pediatric Hematology/Oncology 9, 99–103. [DOI] [PubMed] [Google Scholar]
- van Eggermond A. M., Schaapveld M., Lugtenburg P. J., Krol A. D. G., De Boer J. P., Zijlstra J., Raemaekers J. M. M., Kremer L. C. M., Roesink J. M., Louwman M. W. J.. and others (2014). Risk of multiple primary malignancies following treatment of Hodgkin lymphoma. Blood, 124, 319–327. [DOI] [PubMed] [Google Scholar]
- Wang W., Niendorf K. B., Patel D., Blackford A., Marroni F., Sober A. J., Parmigiani G. and Tsao H. (2010). Estimating CDKN2A carrier probability and personalizing cancer risk assessments in hereditary melanoma using MelaPRO. Cancer Research 70, 552–559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinberg J., Brown L. D. and Stroud J. R. (2007). Bayesian forecasting of an inhomogeneous Poisson process with applications to call center data. Journal of the American Statistical Association 102, 1185–1198. [Google Scholar]
- Wu C.-C., Shete S., Amos C. I. and Strong L. C. (2006). Joint effects of germ-line p53 mutation and sex on cancer risk in Li-Fraumeni syndrome. Cancer Research 66, 8287–8292. [DOI] [PubMed] [Google Scholar]
- Wu C.-C., Strong L. C. and Shete S. (2010). Effects of measured susceptibility genes on cancer risk in family studies. Human Genetics 127, 349–357. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.