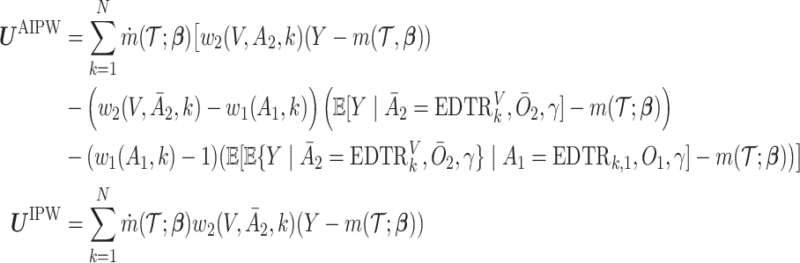Summary
Sequential, multiple assignment, randomized trial (SMART) designs have become increasingly popular in the field of precision medicine by providing a means for comparing more than two sequences of treatments tailored to the individual patient, i.e., dynamic treatment regime (DTR). The construction of evidence-based DTRs promises a replacement to ad hoc one-size-fits-all decisions pervasive in patient care. However, there are substantial statistical challenges in sizing SMART designs due to the correlation structure between the DTRs embedded in the design (EDTR). Since a primary goal of SMARTs is the construction of an optimal EDTR, investigators are interested in sizing SMARTs based on the ability to screen out EDTRs inferior to the optimal EDTR by a given amount which cannot be done using existing methods. In this article, we fill this gap by developing a rigorous power analysis framework that leverages the multiple comparisons with the best methodology. Our method employs Monte Carlo simulation to compute the number of individuals to enroll in an arbitrary SMART. We evaluate our method through extensive simulation studies. We illustrate our method by retrospectively computing the power in the Extending Treatment Effectiveness of Naltrexone (EXTEND) trial. An R package implementing our methodology is available to download from the Comprehensive R Archive Network.
Keywords: Embedded dynamic treatment regime (EDTR), Monte Carlo, Multiple comparisons with the best, Power, Sample size, Sequential multiple assignment randomized trial (SMART)
1. Introduction
Sequential, multiple assignment, randomized trial (SMART) designs have gained considerable attention in the field of precision medicine by providing an empirically rigorous experimental approach for comparing more than two sequences of treatments tailored to the individual patient, i.e., dynamic treatment regime (DTR) (Lavori and others, 2000; Murphy, 2005; Lei and others, 2012). A DTR is a treatment algorithm implemented through a sequence of decision rules which dynamically adjusts treatments and dosages to a patient’s unique changing need and circumstances (Murphy and others, 2001; Murphy, 2003; Robins, 2004; Nahum-Shani and others, 2012; Chakraborty and Moodie, 2013; Chakraborty and Murphy, 2014; Laber and others, 2014). SMARTs are motivated by scientific questions concerning the construction of an effective DTR. The sequential randomization in a SMART gives rise to several DTRs which are embedded in the SMART by design (EDTR). Many SMARTs are designed to compare more than two EDTRs and identify those showing greatest potential for improving a primary clinical outcome. The construction of evidence-based EDTRs promises an alternative to ad hoc one-size-fits-all decisions pervasive in patient care (Chakraborty, 2011).
The advent of SMART designs poses interesting statistical challenges in the planning phase of the trials. In particular, determining an appropriate sample size of individuals to enroll becomes analytically difficult due to the correlation structure between the EDTRs. Previous work includes sizing pilot SMARTs (small scale versions of a SMART) so that each sequence of treatments has a pre-specified number of individuals with some probability by the end of the trial (Almirall and others, 2012; Gunlicks-Stoessel and others, 2016; Kim and others, 2016). The central questions motivating this work are feasibility of the investigators to carry out the trial and acceptability of the treatments by patients. These methods do not provide a means to size SMARTs for comparing EDTRs in terms of a primary clinical outcome.
Alternatively, Crivello and others (2007a) proposed a new objective for SMART sample size planning. The question they address is how many individuals need to be enrolled so that the best EDTR has the largest sample estimate with a given probability (Crivello and others, 2007b). Such an approach based on estimation alone fails to account for the fact that some EDTRs may be statistically indistinguishable from the true best EDTR for the given data in which case they should not necessarily be excluded as suboptimal. Our approach goes one step further than Crivello’s by providing a means to size SMARTs in order to construct narrow confidence intervals which not only tell which is the best EDTR, but also provide the ability to screen out inferior EDTRs. Crivello and others (2007a) also discussed sizing SMARTs to attain a specified power for testing hypotheses which compare only two treatments or two EDTRs as opposed to comparing all EDTRs. The work of Crivello and others (2007a) focused mainly on a particular common two-stage SMART design whereas our method is applicable to arbitrary SMART designs.
More recently, Ogbagaber and others (2016) proposed two methods for sizing a SMART. Their first approach is to choose the sample size in order to achieve a specified power for a global chi-squared test of equality of EDTR outcomes. Their second approach is to choose the sample size in order to detect pairwise differences between EDTR outcomes while adjusting for a specified number of pairwise comparisons using the Bonferroni correction. Their second approach sizes a SMART so that for each pairwise comparison, a difference can be detected with a specified probability 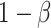 . Our approach offers an alternative which requires a smaller sample size to achieve the same power.
. Our approach offers an alternative which requires a smaller sample size to achieve the same power.
One of the main goals motivating SMARTs is to identify the optimal EDTR. It follows that investigators are interested in sizing SMARTs based on the ability to screen out EDTRs which are inferior to the optimal EDTR by a clinically meaningful amount while including the best EDTR with a specified probability. In this article, we develop a rigorous power analysis framework that leverages the multiple comparisons with the best (MCB) methodology (Hsu, 1981, 1984, 1996). The main justification for using MCB to adjust for multiple comparisons is that it involves fewer comparisons compared to other methods and thus, it yields greater power for the same sample size with all else being equal (Ertefaie and others, 2015).
In Section 2, we give a brief overview of SMARTs, notation, and background on estimation and MCB. In Section 3, we present our power analysis framework. In Section 4, we look at the sensitivity of the power to the covariance matrix of EDTR outcomes. In Section 5, we demonstrate the validity of our method through extensive simulation studies. In Section 6, we apply our method to retrospectively compute the power in the Extending Treatment Effectiveness of Naltrexone (EXTEND) trial. In Section 7, we discuss how to choose the covariance matrix of EDTR outcomes for sample size calculations. In Sections 8 and 9, we give concluding remarks. In the supplementary material available at Biostatistics online, we provide additional details about our simulation study, a comparison with the method presented in Ogbagaber and others (2016), and additional simulation studies for power analysis when data from a pilot SMART is available. The R package “smartsizer” is available to download from the Comprehensive R Archive Network.
2. Preliminaries
2.1. Sequential multiple assignment randomized trials (SMART)
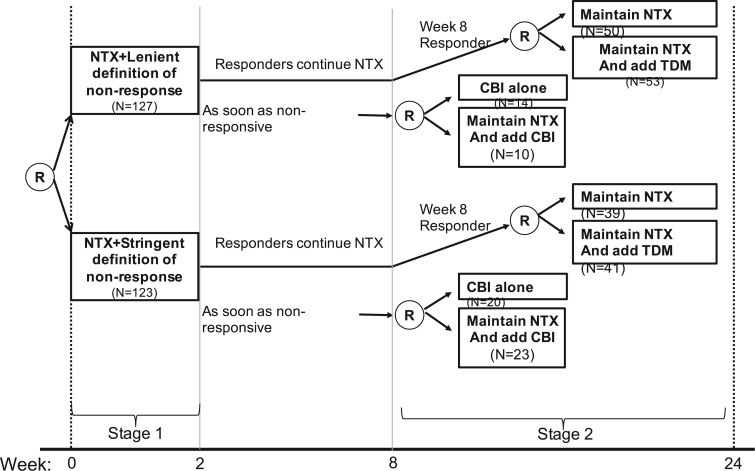
In a SMART, individuals proceed through multiple stages of randomization such that some or all individuals may be randomized more than once. Additionally, treatment assignment is often tailored to the individuals’ ongoing response status (Nahum-Shani and others, 2012). For example, in the Extending Treatment Effectiveness of Naltrexone (EXTEND) trial (see Figure 1 for the study design and Nahum-Shani and others, 2017 for more details about this study), individuals were initially randomized to two different criteria of non-response: lenient or stringent. Specifically, all individuals received the same fixed dosage of naltrexone (NTX)—a medication that blocks some of the pleasurable effects resulting from alcohol consumption. After the first 2 weeks, individuals were evaluated weekly to assess response status. Individuals assigned to the lenient criterion were classified as non-responders as soon as they had five or more heavy drinking days during the first 8 weeks of the study, whereas those assigned to the stringent criterion were classified as non-responders as soon as they had two or more heavy drinking days during the first eight weeks. As soon as participants were classified as non-responders, they transitioned to the second stage where they were randomized to two subsequent rescue tactics: switch to combined behavioral intervention (CBI) or add CBI to NTX (NTX + CBI). At week 8, individuals who did not meet their assigned non-response criterion were classified as responders and re-randomized to two subsequent maintenance interventions: add telephone disease management (TDM) to NTX (NTX + TDM) or continue NTX alone. Note that the stage-2 treatment options in the SMART are tailored to the individuals’ early response status. This leads to a total of eight EDTRs. For example, one of these EDTRs recommends to start the treatment with NTX and monitor drinking behaviors weekly using the lenient criterion (i.e., 5 or more heavy drinking days) to classify the individual as a non-responder. As soon as the individual is classified as a non-responder, add CBI (NTX + CBI); if at week 8 the individual is classified as a responder, add TDM (NTX + TDM). A primary goal motivating many SMARTs is the determination of optimal EDTR. For example, determining an optimal EDTR in the EXTEND may guide in evaluating a patient’s initial response to NTX and in selecting the best subsequent treatment. We develop our power analysis framework with this goal in mind.
Fig. 1.
This diagram shows the structure of the EXTEND trial.
One important challenge for power analysis in SMART designs is the correlation of EDTR outcomes. The correlation arises, in part, due to overlapping interventions in distinct EDTRs and because patients’ treatment histories may be consistent with more than a single EDTR. For example, patients in distinct EDTRs of the EXTEND trial all receive NTX. Also, patients who are classified as responders in stage 2 and subsequently randomized to NTX will be consistent with two EDTRs: one where non-responders are offered CBI and one where non-responders are offered NTX + CBI. In Sections 4 and 5, we will discuss the dependence of power on the covariance. We provide guidelines on choosing the covariance matrix in Section 7.
2.2. Notation
We focus on notation for two-stage SMART designs, but the methods in this paper are applicable to an arbitrary SMART. We use the same notation as in Ertefaie and others (2015). Let 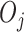 and
and 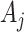 denote the observed covariates and treatment assignment, respectively, at stage
denote the observed covariates and treatment assignment, respectively, at stage 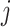 . Let
. Let 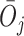 and
and 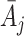 denote the covariate and treatment histories up to and including stage
denote the covariate and treatment histories up to and including stage 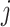 , respectively. Let
, respectively. Let 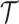 the treatment trajectory be the vector of counterfactual treatment assignments for an individual. For example, in a two-stage SMART with stage-2 treatment tailored to response status,
the treatment trajectory be the vector of counterfactual treatment assignments for an individual. For example, in a two-stage SMART with stage-2 treatment tailored to response status, 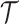 may be of the form
may be of the form 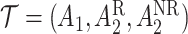 where
where 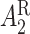 is the stage-2 treatment assignment had the individual responded and
is the stage-2 treatment assignment had the individual responded and 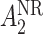 is the stage-2 treatment assignment had the individual not responded. The reason these are counterfactual treatment assignments is that for an individual who responds to the stage-1 treatment,
is the stage-2 treatment assignment had the individual not responded. The reason these are counterfactual treatment assignments is that for an individual who responds to the stage-1 treatment, 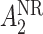 would be unobserved. Hence, the treatment history
would be unobserved. Hence, the treatment history 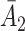 would be
would be 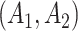 while the treatment trajectory
while the treatment trajectory  would be
would be 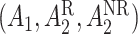 and would include the unobserved counterfactual. Let
and would include the unobserved counterfactual. Let 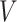 be the embedded tailoring variable for the stage-2 treatment. For example, in EXTEND,
be the embedded tailoring variable for the stage-2 treatment. For example, in EXTEND, 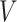 is the indicator of response to the stage-1 treatment. Let
is the indicator of response to the stage-1 treatment. Let 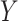 denotes the continuous observed outcome of an individual at the end of the study. Let the
denotes the continuous observed outcome of an individual at the end of the study. Let the 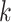 th EDTR be denoted by
th EDTR be denoted by 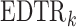 . Let
. Let 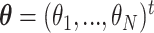 be the true mean outcome vector of EDTRs where
be the true mean outcome vector of EDTRs where 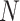 is the total number of EDTRs. Let
is the total number of EDTRs. Let 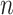 denote the sample size.
denote the sample size.
2.3. Estimation
We summarize the estimation procedures inverse probability weighting (IPW) and augmented inverse probability weighting (AIPW) introduced in Ertefaie and others (2015) for a two-stage SMART, but the method can be extended to arbitrary SMART designs. In order to perform estimation with IPW/AIPW, a marginal structural model (MSM) must be specified. A MSM models the response as a function of the counterfactual random treatment assignments in the treatment trajectory vector 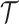 , while ignoring non-treatment covariates. For example, in a two-stage SMART, a MSM is:
, while ignoring non-treatment covariates. For example, in a two-stage SMART, a MSM is: 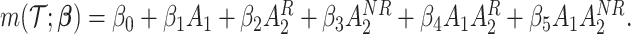 Subsequently, the IPW and AIPW estimators
Subsequently, the IPW and AIPW estimators 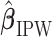 and
and 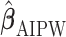 for
for 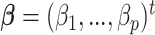 may be obtained by solving the following respective estimating equations:
may be obtained by solving the following respective estimating equations:
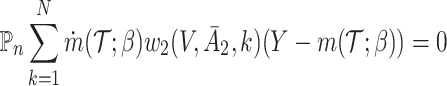 |
(IPW) |
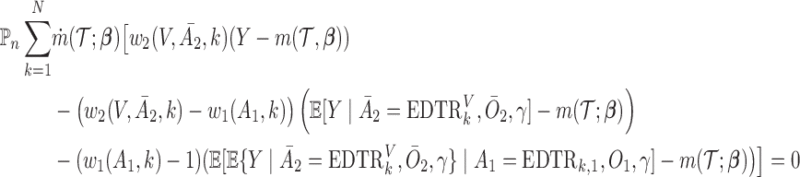 |
(AIPW) |
where 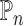 denotes the empirical average,
denotes the empirical average, 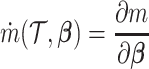 ,
, 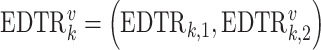 is the
is the  th EDTR for
th EDTR for  ,
, 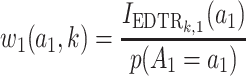 for
for 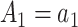 , and
, and 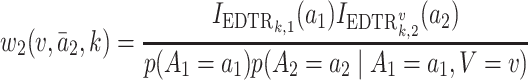 for
for  and
and 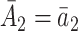 .
.
Then, the EDTR outcome estimators are 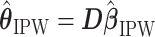 and
and 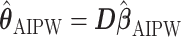 where
where 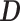 is a
is a 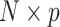 matrix with
matrix with 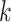 th row of
th row of 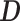 corresponding to the
corresponding to the 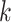 th EDTR contrast and
th EDTR contrast and 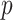 is the number of parameters in the MSM. AIPW is doubly robust in the sense that it will still provide unbiased estimates of the MSM coefficients
is the number of parameters in the MSM. AIPW is doubly robust in the sense that it will still provide unbiased estimates of the MSM coefficients 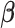 when either the conditional means or the treatment assignment probabilities are correctly specified. The following theorem from Ertefaie and others (2015) is included for the sake of completeness.
when either the conditional means or the treatment assignment probabilities are correctly specified. The following theorem from Ertefaie and others (2015) is included for the sake of completeness.
Theorem 2.1
Let
denote IPW or AIPW. Let
. Then, under standard regulatory assumptions,
where
and
with
The asymptotic variance
may be estimated consistently by replacing the expectations with expectations with respect to the empirical measure and
with its estimate
and may be denoted as
.
We will see the sample size needed in a SMART is a function of the asymptotic covariance matrix 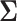 of the EDTR outcomes
of the EDTR outcomes 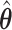 . This is because the amount of variation in EDTR outcomes and the correlation between EDTRs determines how easy it is to screen out inferior EDTRs. Identifying the optimal EDTRs and excluding inferior EDTRs may be viewed as the multiple testing problem. In the next section, we discuss how the MCB procedure (Hsu, 1981, 1984, 1996) can be used to address scientific questions concerning the optimal EDTR.
. This is because the amount of variation in EDTR outcomes and the correlation between EDTRs determines how easy it is to screen out inferior EDTRs. Identifying the optimal EDTRs and excluding inferior EDTRs may be viewed as the multiple testing problem. In the next section, we discuss how the MCB procedure (Hsu, 1981, 1984, 1996) can be used to address scientific questions concerning the optimal EDTR.
2.4. Determining a set of best EDTRs using multiple comparison with the best (MCB)
The MCB procedure permits identification of a confidence set of EDTRs which cannot be statistically distinguished from the true best EDTR for the given data while adjusting for multiple comparisons. In particular, 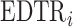 is considered statistically indistinguishable from the best EDTR for the available data if and only if
is considered statistically indistinguishable from the best EDTR for the available data if and only if 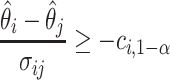 for all
for all 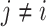 where
where 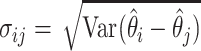 and
and 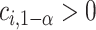 is chosen so that the set of best EDTRs includes the best EDTR with at least a specified probability
is chosen so that the set of best EDTRs includes the best EDTR with at least a specified probability  . Then, the set of best can be written as
. Then, the set of best can be written as 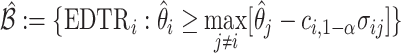 where
where 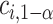 depends on
depends on 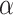 and the covariance matrix
and the covariance matrix 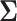 . The above
. The above 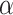 represents the type I error rate for excluding the best EDTR from
represents the type I error rate for excluding the best EDTR from 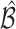 . To control the type I error rate, it suffices to consider the situation in which the true mean outcomes are all equal. Then, a sufficient condition for the type I error rate to be at most
. To control the type I error rate, it suffices to consider the situation in which the true mean outcomes are all equal. Then, a sufficient condition for the type I error rate to be at most 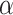 is to choose
is to choose 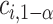 so that the set of best includes each EDTR with probability at least
so that the set of best includes each EDTR with probability at least  :
: 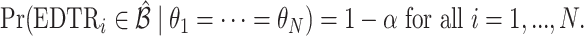 It is sufficient for
It is sufficient for 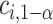 to satisfy:
to satisfy:
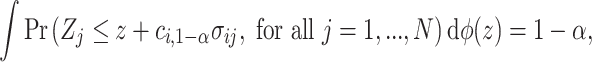 |
(2.1) |
where 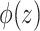 is the marginal cdf of
is the marginal cdf of 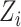 and
and 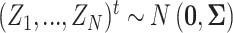 . Observe that
. Observe that 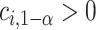 is a function of
is a function of 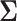 and
and 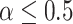 , but not of the sample size
, but not of the sample size 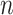 . The integral in (2.1) is analytically intractable, but the
. The integral in (2.1) is analytically intractable, but the 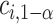 may be determined using Monte Carlo methods.
may be determined using Monte Carlo methods.
It is important to note that while EDTRs included in the set of best are statistically indistinguishable for the given data, this does not mean that the EDTRs are equivalent in efficacy. This is because SMART designs may not have enough individuals in each EDTR to justify the interpretation of equivalence without an unrealistically large sample size. Our method sizes SMARTs for screening out EDTRs inferior to the best and does not size for testing equivalence.
The MCB procedure has an important advantage over other procedures which adjust for multiple comparisons: MCB provides a set with fewer EDTRs since fewer comparisons yields increased power to exclude inferior EDTRs from the set of best. Specifically, for a SMART design where N is the number of EDTRs, the MCB procedure involves only  comparisons whereas, for example, all pairwise multiple comparison procedures entail
comparisons whereas, for example, all pairwise multiple comparison procedures entail 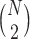 comparisons.
comparisons.
In the next section, we introduce our Monte Carlo simulation based approach to compute the number of individuals to enroll in a SMART to achieve a specified power to exclude EDTRs inferior by a specified amount from the set of best.
3. Methods
Let 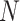 be the index of the best EDTR,
be the index of the best EDTR, 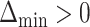 be the minimum detectable difference between the mean best EDTR outcome and the other mean EDTR outcomes,
be the minimum detectable difference between the mean best EDTR outcome and the other mean EDTR outcomes, 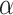 be the type I error rate, and
be the type I error rate, and 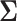 be the asymptotic covariance matrix of
be the asymptotic covariance matrix of 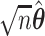 where
where 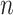 is the sample size. Furthermore, let
is the sample size. Furthermore, let 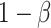 denote the desired power to exclude EDTRs with true outcome
denote the desired power to exclude EDTRs with true outcome 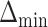 or more away from that of the true best outcome. Let
or more away from that of the true best outcome. Let 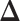 be the vector of differences between the mean best EDTR outcome and all other mean EDTR outcomes. So,
be the vector of differences between the mean best EDTR outcome and all other mean EDTR outcomes. So, 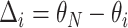 for all
for all 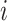 . We also refer to
. We also refer to 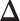 as the vector of effect sizes and
as the vector of effect sizes and 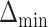 as the minimum detectable effect size, but this terminology should not be confused with a standardized effect size such as Cohen’s d.
as the minimum detectable effect size, but this terminology should not be confused with a standardized effect size such as Cohen’s d.
We wish to exclude all 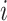 from the set of best for which
from the set of best for which 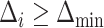 . We have that
. We have that
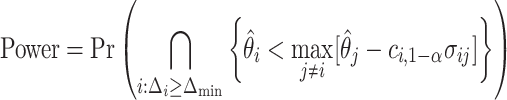 |
(3.2) |
However, the 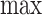 operator makes (3.2) analytically and computationally complicated, so we will instead bound the RHS of the following inequality:
operator makes (3.2) analytically and computationally complicated, so we will instead bound the RHS of the following inequality:
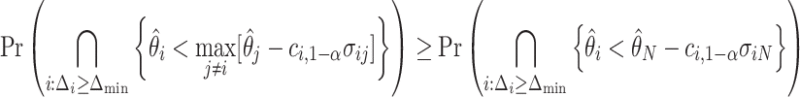 |
(3.3) |
Theoretically, the bound obtained using (3.3) may be conservative, but it is often beneficial to be conservative when conducting sample size calculations because of unpredictable circumstances such as loss to follow up, patient dropout, and/or highly skewed responses. Since the normal distribution is a location-scale family, the power only depends on the vector of mean differences 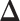 and not on
and not on  . Henceforth, we write
. Henceforth, we write 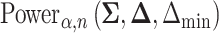 for the RHS of (3.3). It follows that
for the RHS of (3.3). It follows that
 |
(3.4) |
where 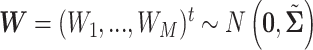 and
and 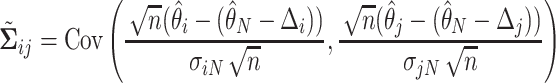 , and
, and  is the number of indices
is the number of indices 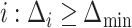 . Note that
. Note that  and
and 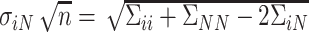 do not depend on the sample size
do not depend on the sample size 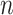 since
since 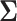 does not depend on
does not depend on 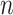 . If the effect sizes
. If the effect sizes 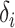 which are standardized by the standard deviation of the difference are specified instead of
which are standardized by the standard deviation of the difference are specified instead of 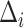 , then
, then 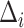 may be replaced by
may be replaced by 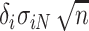 . Note that
. Note that 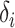 is not the same as Cohen’s d which is standardized by the pooled standard deviation rather than the standard deviation of the difference. It follows that the power may be computed by simulating normal random variables and substituting the probability in (3.4) with the empirical mean
is not the same as Cohen’s d which is standardized by the pooled standard deviation rather than the standard deviation of the difference. It follows that the power may be computed by simulating normal random variables and substituting the probability in (3.4) with the empirical mean 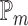 of the indicator variable as is shown in Algorithm 1.
of the indicator variable as is shown in Algorithm 1.
Recall the main point of this article is to assist investigators in choosing the sample size for a SMART. To this end, we will derive a method for finding the minimum 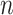 such that
such that 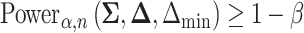 . We proceed by rewriting the RHS of (3.3):
. We proceed by rewriting the RHS of (3.3):
 |
(3.5) |
where  ,
,  ,
,  is the number of indices
is the number of indices 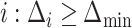 , and
, and 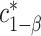 is the
is the 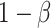 equicoordinate quantile for the probability in (3.5). It follows from (3.5) that
equicoordinate quantile for the probability in (3.5). It follows from (3.5) that 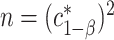 . Here, we write the quantile
. Here, we write the quantile 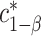 with an asterisk to distinguish it from the quantile
with an asterisk to distinguish it from the quantile 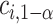 which controls the type I error rate
which controls the type I error rate 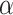 . The constant
. The constant 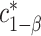 may be computed using Monte Carlo simulation to find the inverse of equation (3.5) after first computing the
may be computed using Monte Carlo simulation to find the inverse of equation (3.5) after first computing the 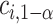 ’s as is shown in Algorithm 2. The above procedure works because the
’s as is shown in Algorithm 2. The above procedure works because the 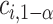 ’s do not change with
’s do not change with 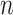 , so the distribution of
, so the distribution of 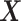 is constant as a function of
is constant as a function of 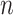 . Our approach for computing
. Our approach for computing 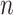 is an extension of the sample size computation method in the appendix of Hsu (1996) to the SMART setting when
is an extension of the sample size computation method in the appendix of Hsu (1996) to the SMART setting when 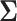 is known. Algorithms 1 and 2 are implemented in an R package “smartsizer” available at the Comprehensive R Archive Network.
is known. Algorithms 1 and 2 are implemented in an R package “smartsizer” available at the Comprehensive R Archive Network.
Algorithm 1
SMART power computation
Given
, compute
for
.
Given
and
, generate
for
, where
,
is the number of Monte Carlo repetitions, and
is the number of indices
.
Compute the Monte Carlo probability
for some
In the next section, we will explore the sensitivity of the power to the covariance matrix.
4. Sensitivity of power to 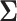
We now examine how sensitive the power is to the choice of 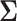 . We will address the case in which
. We will address the case in which 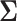 is unknown in Section 5. For simplicity, we consider the most conservative case in which the effect sizes are all equal:
is unknown in Section 5. For simplicity, we consider the most conservative case in which the effect sizes are all equal: 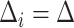 for all
for all 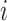 . In Figure 2, we evaluated the power over a grid of values for
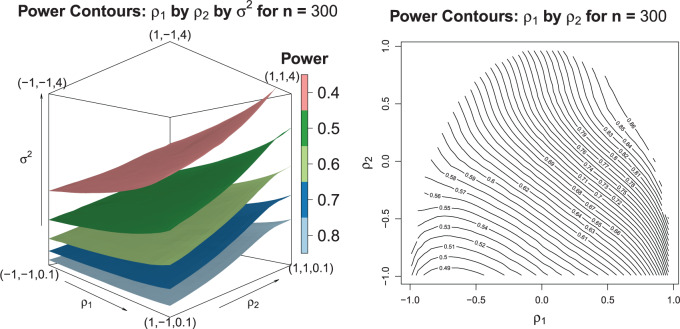
. In Figure 2, we evaluated the power over a grid of values for 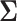 using Equation (3.4) and Algorithm 1. These plots suggest the trend that higher correlations and lower variances tend to yield higher power which means that in order to obtain conservative power estimates, larger variances, and smaller correlations should be used. Furthermore, the correlation between best and non-best EDTRs appears to have a greater influence on power than the correlation between two inferior EDTRs as we see in the left-hand plot of Figure 2. We discuss this further in Section 7.
using Equation (3.4) and Algorithm 1. These plots suggest the trend that higher correlations and lower variances tend to yield higher power which means that in order to obtain conservative power estimates, larger variances, and smaller correlations should be used. Furthermore, the correlation between best and non-best EDTRs appears to have a greater influence on power than the correlation between two inferior EDTRs as we see in the left-hand plot of Figure 2. We discuss this further in Section 7.
Fig. 2.
The left-hand plot shows the 3D contours of the power (denoted by shade/color) as a function of 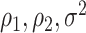 where
where  and the fourth EDTR is best.
and the fourth EDTR is best. 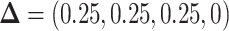 and
and 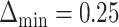 . The right-hand plot shows power contours over the correlations where
. The right-hand plot shows power contours over the correlations where 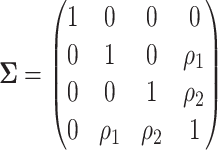 . Note that the power appears monotone with respect to
. Note that the power appears monotone with respect to  and
and 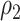 . The finger-shaped boundary is due to the feasible region of values for
. The finger-shaped boundary is due to the feasible region of values for 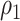 and
and 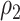 such that
such that 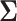 is positive definite. The sequence of contour curves in the left-hand plot in ascending order from
is positive definite. The sequence of contour curves in the left-hand plot in ascending order from  to
to 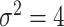 corresponds to the order of the power key from 0.8 to 0.4.
corresponds to the order of the power key from 0.8 to 0.4.
It is analytically difficult to prove monotonicity for a general 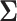 structure. However, it can be proven the power is a monotone non-decreasing function of the correlation and a monotone non-increasing function of the variance for an exchangeable covariance matrix. We conjecture this property is true in general for
structure. However, it can be proven the power is a monotone non-decreasing function of the correlation and a monotone non-increasing function of the variance for an exchangeable covariance matrix. We conjecture this property is true in general for 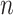 sufficiently large. To confirm that a conservative estimate of power is obtained, one may compute the power for different values of the correlation and variance and confirm the monotone trend when using a non-exchangeable covariance matrix.
sufficiently large. To confirm that a conservative estimate of power is obtained, one may compute the power for different values of the correlation and variance and confirm the monotone trend when using a non-exchangeable covariance matrix.
Theorem 4.1
Let
be exchangeable:
where
and
. The power is an increasing function of
and a decreasing function of
.
Algorithm 2
SMART sample size computation
Given
, compute
for
.
Given
and
, generate
for
where
,
is the number of Monte Carlo repetitions, and
is the number of indices
.
Find the
equicoordinate quantile
of the simulated
for each
.
The sample size is
.
5. Simulation study
We have explored how the power changes in terms of a known covariance matrix. In this section, we present simulation studies for two different SMART designs in which we evaluate the assumption of a known covariance matrix. In practice, the true covariance matrix is estimated consistently by some 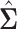 (see Section 2.3 for more details). The designs and generating models are based on those discussed in Ertefaie and others (2015). For each SMART, we simulated 1000 datasets across a grid of sample sizes
(see Section 2.3 for more details). The designs and generating models are based on those discussed in Ertefaie and others (2015). For each SMART, we simulated 1000 datasets across a grid of sample sizes 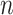 . We computed the sets of best EDTRs using the estimates
. We computed the sets of best EDTRs using the estimates 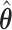 and
and 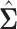 obtained using the AIPW estimation method after correctly specifying an appropriate MSM and conditional means (see Appendix A and the Tables and Figures of the supplementary material available at Biostatistics online for more details).
obtained using the AIPW estimation method after correctly specifying an appropriate MSM and conditional means (see Appendix A and the Tables and Figures of the supplementary material available at Biostatistics online for more details).
5.1. SMART simulation design 1
In SMART simulation design 1, the stage-2 randomization is tailored based on response to the stage-1 treatment assignment. Individuals are considered responders if and only if 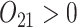 where
where 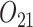 is an intermediate outcome. Non-responders to the stage-1 treatment are subsequently re-randomized to one of the two intervention options while responders continue on the initial treatment assignment. We generated 1000 data sets for each sample size
is an intermediate outcome. Non-responders to the stage-1 treatment are subsequently re-randomized to one of the two intervention options while responders continue on the initial treatment assignment. We generated 1000 data sets for each sample size 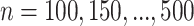 according to the following scheme:
according to the following scheme:
- (a) Generate
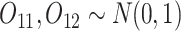 (baseline covariates)
(baseline covariates) - (b) Generate
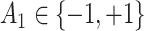 from a Bernoulli distribution with probability
from a Bernoulli distribution with probability 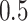 (stage-1 treatment option indicator)
(stage-1 treatment option indicator)
- (a) Generate
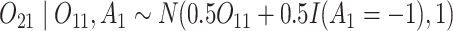 and
and 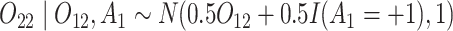 (intermediate outcomes)
(intermediate outcomes) - (b) Generate
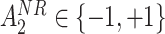 from a Bernoulli distribution with probability
from a Bernoulli distribution with probability 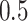 (stage-2 treatment option indicator for non-responders)
(stage-2 treatment option indicator for non-responders)
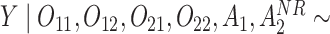 Normal with unit variance and mean equal to
Normal with unit variance and mean equal to
where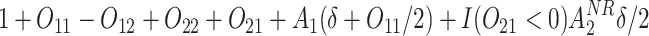
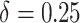
The true 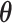 is
is 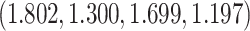 . Note the first EDTR is the best. The vector of effect sizes
. Note the first EDTR is the best. The vector of effect sizes 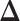 is
is 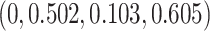 and the minimum detectable effect size
and the minimum detectable effect size 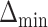 was set to
was set to 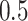 . We computed the set of best EDTRs using MCB for each data set and sample size
. We computed the set of best EDTRs using MCB for each data set and sample size 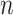 . The empirical power was calculated as the fraction of datasets which excluded all EDTRs with true mean outcome
. The empirical power was calculated as the fraction of datasets which excluded all EDTRs with true mean outcome 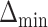 or more away from the best EDTR (in this case EDTRs 2 and 4), for each
or more away from the best EDTR (in this case EDTRs 2 and 4), for each 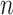 . The true covariance matrix
. The true covariance matrix 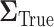 for this SMART was estimated using AIPW by averaging the estimated covariance matrix of 1000 simulated datasets each of 10000 individuals:
for this SMART was estimated using AIPW by averaging the estimated covariance matrix of 1000 simulated datasets each of 10000 individuals:
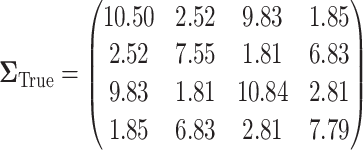 |
(5.6) |
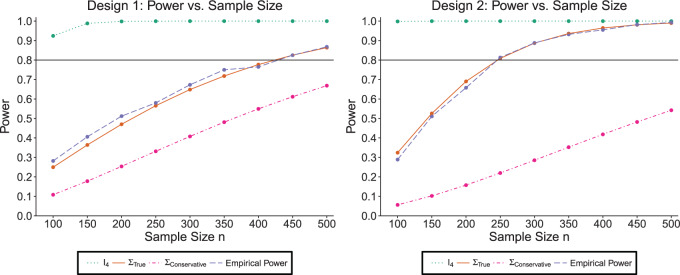
5.1.1. SMART simulation design 1: results
The simulation results are summarized in the plot on the left-hand side of Figure 3. The plot shows the sample size is sensitive to the choice of 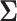 . Choosing
. Choosing 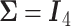 will greatly underestimate the required sample size, predicting 72 individuals compared to the true 423 individuals needed to achieve
will greatly underestimate the required sample size, predicting 72 individuals compared to the true 423 individuals needed to achieve 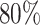 power. We also looked at the power for a covariance matrix
power. We also looked at the power for a covariance matrix 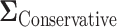 which yields a conservative estimate of power.
which yields a conservative estimate of power. 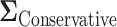 had variances chosen to be equal to the true variances and correlations chosen to be equal to zero to achieve a lower bound on the power. The minimum sample size to achieve
had variances chosen to be equal to the true variances and correlations chosen to be equal to zero to achieve a lower bound on the power. The minimum sample size to achieve 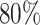 power for the conservative covariance matrix was
power for the conservative covariance matrix was 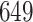 .
.
Fig. 3.
The plots shows the power as a function of the sample size n with a horizontal line where the power is 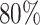 . The plot shows the power curves for
. The plot shows the power curves for 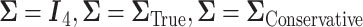 , and the empirical power curve.
, and the empirical power curve.
5.2. SMART simulation design 2
In SMART simulation design 2, stage-2 randomization depends on both prior treatment and intermediate outcomes. In particular, individuals are randomized at stage-2 if and only if they are non-responders whose stage-1 treatment option corresponded to 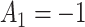 (call this condition B). Individuals are considered responders if and only if
(call this condition B). Individuals are considered responders if and only if 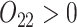 where
where 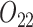 is an intermediate outcome. We generated 1000 data sets for each sample size
is an intermediate outcome. We generated 1000 data sets for each sample size 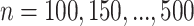 according to the following scheme:
according to the following scheme:
- (a) Generate
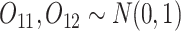 (baseline covariates)
(baseline covariates) - (b) Generate
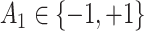 from a Bernoulli distribution with probability
from a Bernoulli distribution with probability 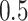 (stage-1 treatment option indicator)
(stage-1 treatment option indicator)
- (a) Generate
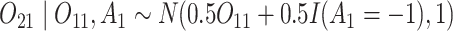 and
and 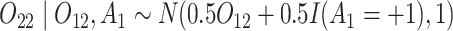 (intermediate outcomes)
(intermediate outcomes) - (b) Generate
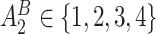 from a Multinomial distribution with probability
from a Multinomial distribution with probability 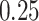 (stage-2 treatment option indicator for individuals satisfying condition B)
(stage-2 treatment option indicator for individuals satisfying condition B)
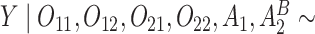 Normal with unit variance and mean equal to
Normal with unit variance and mean equal to 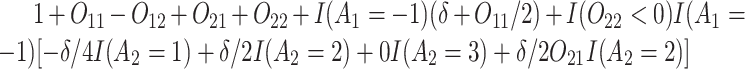 where
where 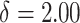
The true 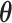 value is
value is 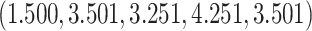 . The vector of effect sizes
. The vector of effect sizes  is
is 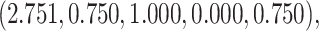 and the minimum detectable effect size
and the minimum detectable effect size  was set to
was set to 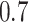 . The set of best was computed for each data set. For each sample size, the empirical power is the fraction of
. The set of best was computed for each data set. For each sample size, the empirical power is the fraction of 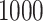 data sets which exclude EDTRs 1, 2, 3, and 5. The true covariance matrix
data sets which exclude EDTRs 1, 2, 3, and 5. The true covariance matrix 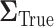 for this SMART was estimated using AIPW by averaging the estimated covariance matrices of 1000 simulated datasets each of 10000 individuals:
for this SMART was estimated using AIPW by averaging the estimated covariance matrices of 1000 simulated datasets each of 10000 individuals:
 |
(5.7) |
5.2.1. SMART simulation design 2: results
Our simulation results are summarized in the plot on the right-hand side of Figure 3. The power plot shows the predicted power is similar to the empirical power when assuming the correct 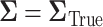 . The anticipated sample size is 246 individuals for
. The anticipated sample size is 246 individuals for  . Choosing
. Choosing 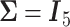 yields overestimated power for each sample size, predicting 40 individuals necessary to achieve 80% power. Conversely, choosing a conservative covariance matrix
yields overestimated power for each sample size, predicting 40 individuals necessary to achieve 80% power. Conversely, choosing a conservative covariance matrix 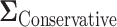 underestimates the power. The
underestimates the power. The 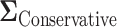 is a diagonal matrix with variances set to the true variances and the correlation set to
is a diagonal matrix with variances set to the true variances and the correlation set to 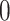 . The sample size for the conservative covariance matrix is
. The sample size for the conservative covariance matrix is 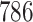 to achieve 80% power. The loss of power when assuming the conservative covariance matrix compared with the true covariance is due to there being a high correlation between EDTR outcomes.
to achieve 80% power. The loss of power when assuming the conservative covariance matrix compared with the true covariance is due to there being a high correlation between EDTR outcomes.
6. Illustration: EXTEND retrospective power calculation
In this section, we examine how much power there was to distinguish between EDTRs 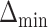 away from the best in the EXTEND trial. Please see Section 2.1 for more details about EXTEND and Figure 1 for a diagram depicting the trial. The true sample size was 250. The outcome of interest was the Penn Alcohol Craving Scale (PACS) and lower PACS were considered better outcomes. The covariance matrix
away from the best in the EXTEND trial. Please see Section 2.1 for more details about EXTEND and Figure 1 for a diagram depicting the trial. The true sample size was 250. The outcome of interest was the Penn Alcohol Craving Scale (PACS) and lower PACS were considered better outcomes. The covariance matrix 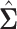 and the vector of EDTR outcomes
and the vector of EDTR outcomes 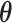 were estimated using both IPW and AIPW. See Table 1 for the mean EDTR outcome estimates. The covariance matrices are:
were estimated using both IPW and AIPW. See Table 1 for the mean EDTR outcome estimates. The covariance matrices are:
 |
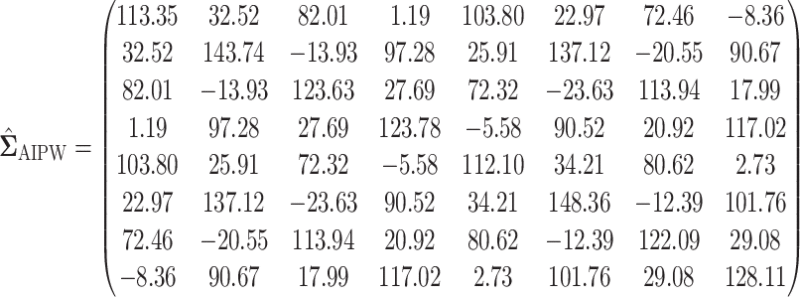 |
Table 1.
Extend trial: EDTR outcome estimates and standard errors
|
|
|
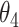
|
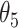
|
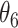
|
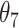
|
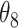
|
||
|---|---|---|---|---|---|---|---|---|---|
| IPW | Estimate | 7.56 | 9.53 | 8.05 | 10.02 | 7.71 | 9.68 | 8.19 | 10.17 |
| SD | 0.76 | 0.81 | 0.71 | 0.83 | 0.74 | 0.80 | 0.69 | 0.82 | |
| AIPW | Estimate | 7.65 | 9.44 | 7.83 | 9.62 | 8.06 | 9.85 | 8.24 | 10.03 |
| SD | 0.67 | 0.76 | 0.70 | 0.70 | 0.67 | 0.77 | 0.70 | 0.72 |
The EDTR outcome vectors 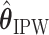 and
and 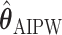 are summarized in Table 1. The vector of effect sizes for IPW is
are summarized in Table 1. The vector of effect sizes for IPW is 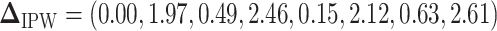 and for AIPW is
and for AIPW is 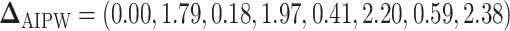 . The set of best when performing estimation using AIPW excluded EDTRs 6 and 8. The set of best when using IPW failed to exclude any of the inferior EDTRs. In order to evaluate the power there was to exclude EDTRs 6 and 8, we set the minimum detectable effect size
. The set of best when performing estimation using AIPW excluded EDTRs 6 and 8. The set of best when using IPW failed to exclude any of the inferior EDTRs. In order to evaluate the power there was to exclude EDTRs 6 and 8, we set the minimum detectable effect size 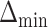 to
to 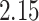 .
.
At an 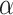 level of
level of 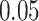 , the power to exclude all EDTRs inferior to the best by
, the power to exclude all EDTRs inferior to the best by 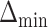 or more was
or more was 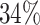 for IPW and
for IPW and 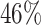 for AIPW. AIPW yields greater power than IPW because AIPW yields smaller standard errors compared with IPW (Ertefaie and others, 2015). Our method estimates that a total of
for AIPW. AIPW yields greater power than IPW because AIPW yields smaller standard errors compared with IPW (Ertefaie and others, 2015). Our method estimates that a total of 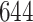 individuals would need to be enrolled to achieve a power of
individuals would need to be enrolled to achieve a power of 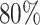 using IPW and a total of
using IPW and a total of 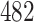 individuals would need to be enrolled when using AIPW.
individuals would need to be enrolled when using AIPW.
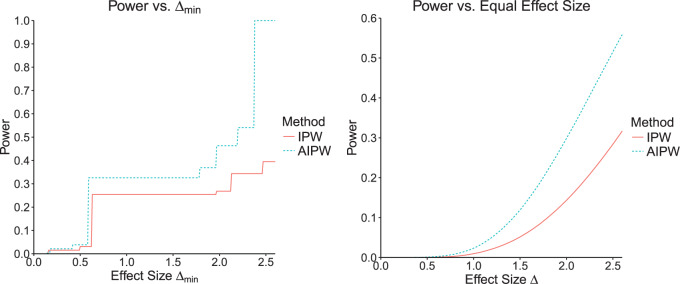
In the left-hand plot of Figure 4, we computed the power over a grid of 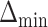 values to see how the power changes as a function of effect size. In the right-hand side of Figure 4, we show how the power changes as a function of a uniform effect size. Specifically, we assume EDTR 1 is the best and set the effect sizes of EDTRs 2, 3,..., 8 to be equal. We then vary this uniform effect size. In this case, we ignore the actual effect sizes of the true EDTR estimates
values to see how the power changes as a function of effect size. In the right-hand side of Figure 4, we show how the power changes as a function of a uniform effect size. Specifically, we assume EDTR 1 is the best and set the effect sizes of EDTRs 2, 3,..., 8 to be equal. We then vary this uniform effect size. In this case, we ignore the actual effect sizes of the true EDTR estimates 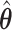 . We see the trend that AIPW yields greater power when compared with IPW.
. We see the trend that AIPW yields greater power when compared with IPW.
Fig. 4.
The left-hand plot shows the power as a function of 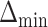 in the EXTEND trial when performing estimation with IPW and AIPW, respectively. The right-hand side of the plot shows the power as a function of the uniform effect size in the EXTEND trial when performing estimation with IPW and AIPW, respectively.
in the EXTEND trial when performing estimation with IPW and AIPW, respectively. The right-hand side of the plot shows the power as a function of the uniform effect size in the EXTEND trial when performing estimation with IPW and AIPW, respectively.
7. Guidelines for choosing the covariance matrix 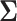
We saw in Sections 4 and 5 that the power is sensitive to 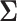 . However, the dependence of power on the covariance matrix is not unique to MCB. We argue this is a necessary feature of power analysis in SMART designs because it entails comparisons of correlated EDTR outcomes. We demonstrate the sensitivity of the power to the covariance matrix when sizing a SMART to detect differences in pairwise comparisons in Appendix B of the supplementary material available at Biostatistics online.
. However, the dependence of power on the covariance matrix is not unique to MCB. We argue this is a necessary feature of power analysis in SMART designs because it entails comparisons of correlated EDTR outcomes. We demonstrate the sensitivity of the power to the covariance matrix when sizing a SMART to detect differences in pairwise comparisons in Appendix B of the supplementary material available at Biostatistics online.
We focus on how to choose the covariance when the variances can be estimated (or an upper-bound given). We consider the situation in which the correlations are unknown in the absence of pilot SMART data and the situation in which pilot SMART data are available to estimate the correlations. In the absence of information about the correlation between EDTR outcomes, it is reasonable to assume all correlations are equal. Figure 2 illustrates that the correlation between the best EDTR and the non-best EDTR outcomes has a greater impact on power than the correlation between two non-best EDTR outcomes. Therefore, the correlation between the best EDTR and second best EDTR is important while the other correlations do not have as great an impact on the power, so we may make the working assumption that the correlations are equal. For example, the conservative covariance matrices in the simulation studies have equal correlations. Theorem 4.1 shows that the power for an exchangeable matrix is a monotone increasing function of the common correlation and a decreasing function of the variances. A similar monotone trend can be seen in Figure 2 for non-exchangeable covariance matrices. Specifically, larger variances and smaller correlations are more conservative. This is rather intuitive as if there is less variation, then it will be easier to distinguish between EDTRs.
When only an upper bound can be obtained for the variance of EDTR outcomes, one may assume a conservative exchangeable covariance matrix in which the diagonal elements are all equal to the upper bound on the variance and the correlation is set to the smallest plausible value. Information about the variances of outcomes for each EDTR may be obtained from prior non-SMART studies that provide the variation in outcomes for the treatments embedded in each EDTR. In this case, one may assume a matrix in which the diagonal elements equal the known variances and the correlation is set to the smallest plausible value. If a negative correlation between EDTR outcomes is implausible, a diagonal matrix may be chosen to obtain a conservative power estimate. For a covariance matrix in which the correlations are equal, the minimum negative correlation is bounded below by 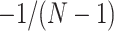 for the covariance matrix to be positive definite (Tong, 2012).
for the covariance matrix to be positive definite (Tong, 2012).
As an alternative to sizing SMARTs based off a conservative covariance matrix, we propose conducting a pilot SMART to estimate the correlations in 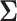 in order to fine-tune power calculations. In addition to assisting in sample size calculations, pilot SMARTs are able to answer questions about the feasibility of the investigators to carry out the SMART and acceptability of the treatments by patients (Almirall and others, 2012; Gunlicks-Stoessel and others, 2016; Kim and others, 2016). If estimates of the variances of each EDTR outcome are known (by choosing the largest plausible values based off knowledge of the variance of response to treatments embedded in the EDTRs), the pilot SMART may be used to estimate the correlations by first estimating the full covariance matrix using AIPW and then transforming to a correlation matrix. The covariance matrix with given variances may then be obtained by left and right multiplying the correlation matrix by the square root of the diagonal matrix whose elements consist of the variances of EDTR outcomes. We propose the following algorithm: (i) conduct a pilot SMART; (ii) bootstrap
in order to fine-tune power calculations. In addition to assisting in sample size calculations, pilot SMARTs are able to answer questions about the feasibility of the investigators to carry out the SMART and acceptability of the treatments by patients (Almirall and others, 2012; Gunlicks-Stoessel and others, 2016; Kim and others, 2016). If estimates of the variances of each EDTR outcome are known (by choosing the largest plausible values based off knowledge of the variance of response to treatments embedded in the EDTRs), the pilot SMART may be used to estimate the correlations by first estimating the full covariance matrix using AIPW and then transforming to a correlation matrix. The covariance matrix with given variances may then be obtained by left and right multiplying the correlation matrix by the square root of the diagonal matrix whose elements consist of the variances of EDTR outcomes. We propose the following algorithm: (i) conduct a pilot SMART; (ii) bootstrap 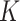 times to obtain
times to obtain 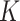 estimates of the covariance matrix using an estimation procedure such as AIPW; (iii) transform the covariance matrix estimates to correlation matrices and then use the variances of EDTR outcomes obtained from prior study data to transform back to covariance matrices; (iv) compute the sample size for each bootstrapped covariance matrix and choose the maximum sample size (or 97.5th percentile, for example). When planning the pilot SMART, it is necessary to choose the pilot SMART sample size sufficiently large so that there are patients in each EDTR in order for the covariance to be estimated. It is the subject of future work to develop methods for sizing pilot SMARTs to estimate the unknown covariance matrix to a specified accuracy. For now, we refer readers to Kim and others (2016) and Almirall and others (2012) for sizing a pilot SMART. In Appendix B of the supplementary materials available at Biostatistics online, we demonstrate the above algorithm for two simulated pilot SMARTs with
estimates of the covariance matrix using an estimation procedure such as AIPW; (iii) transform the covariance matrix estimates to correlation matrices and then use the variances of EDTR outcomes obtained from prior study data to transform back to covariance matrices; (iv) compute the sample size for each bootstrapped covariance matrix and choose the maximum sample size (or 97.5th percentile, for example). When planning the pilot SMART, it is necessary to choose the pilot SMART sample size sufficiently large so that there are patients in each EDTR in order for the covariance to be estimated. It is the subject of future work to develop methods for sizing pilot SMARTs to estimate the unknown covariance matrix to a specified accuracy. For now, we refer readers to Kim and others (2016) and Almirall and others (2012) for sizing a pilot SMART. In Appendix B of the supplementary materials available at Biostatistics online, we demonstrate the above algorithm for two simulated pilot SMARTs with 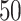 individuals.
individuals.
8. Final comments
If practitioners size a SMART using MCB, the study may be underpowered for conducting all pairwise comparisons since MCB yields greater power compared with approaches which entail a greater number of comparisons. Such confidence intervals obtained by all pairwise comparisons might not be sufficiently narrow. An important point is that MCB does not provide a p-value, so practitioners may wish to apply a method such as the global test for equality of EDTR outcomes (Ogbagaber and others, 2016). Sizing a SMART based off our method may overpower such an approach.
9. Discussion
One important goal of SMARTs is determination of an optimal EDTR. It is hence crucial to enroll a sufficient sample size to be able to detect the best EDTR and exclude EDTRs inferior to the best one by a clinically meaningful quantity. We introduced a novel method for carrying out power analyses for SMART designs which leverages multiple comparison with the best and Monte Carlo simulation. We saw the power is sensitive to the covariance matrix and have provided guidelines for choosing it. We illustrated our method on the EXTEND SMART to see how much power there was to exclude inferior EDTRs from the set of best and the necessary sample size to achieve 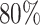 power.
power.
Other work has focused on estimating the optimal DTR (not embedded DTR) based on tailoring variables not embedded in the SMART. Such methods include Q-learning (Watkins, 1989; Chakraborty and Moodie, 2013; Ertefaie and others, 2016). These analyses are exploratory in nature and are typically not the primary goal of SMARTs. Future work will involve developing methods for sizing a SMART for such exploratory aims (Laber and others, 2016; Kidwell and others, 2018).
Software
The R package smartsizer implementing Algorithms 1 and 2 is available to download at the Comprehensive R Archive Network (https://cran.r-project.org/web/packages/smartsizer/). The R code used in this manuscript is also available to download at https://github.com/wilart/SMART-Sizer-Paper.
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
Funding
The NIAAA (R01 AA019092, R01 AA014851, RC1 AA019092, and P01 AA016821) (in part) and also R01 DA039901 (NIH/NIDA) and K24 DA029062 (NIDA, national institute on drug abuse). The project described in this publication was partially supported by the University of Rochester CTSA award number UL1 TR002001 from the National Center for Advancing Translational Sciences of the National Institutes of Health. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
References
- Almirall, D., Compton, S. N., Gunlicks-Stoessel, M., Duan, N. and Murphy, S. A. (2012). Designing a pilot sequential multiple assignment randomized trial for developing an adaptive treatment strategy. Statistics in Medicine 31, 1887–1902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chakraborty, B. (2011). Dynamic treatment regimes for managing chronic health conditions: a statistical perspective. American Journal of Public Health 101, 40–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chakraborty, B. and Moodie, E. E. (2013). Statistical Methods for Dynamic Treatment Regimes. New York: Springer. [Google Scholar]
- Chakraborty, B. and Murphy, S. A. (2014). Dynamic treatment regimes. Annual Review of Statistics and its Application 1, 447–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crivello, A. I., Levy, J. A. and Murphy, S. A. (2007a). Evaluation of sample size formulae for developing adaptive treatment strategies using a smart design. Technical Report No. 07-81 University Park, PA: The Pennsylvania State University, The Methodology Center. [Google Scholar]
- Crivello, A. I., Levy, J. A. and Murphy, S. A. (2007b). Statistical methodology for a smart design in the development of adaptive treatment strategies. Technical Report No. 07-82. University Park, PA: The Pennsylvania State University, The Methodology Center. [Google Scholar]
- Ertefaie, A., Shortreed, S. and Chakraborty, B. (2016). Q-learning residual analysis: application to the effectiveness of sequences of antipsychotic medications for patients with schizophrenia. Statistics in Medicine 35, 2221–2234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ertefaie, A., Wu, T., Lynch, K. G. and Nahum-Shani, I. (2015). Identifying a set that contains the best dynamic treatment regimes. Biostatistics 17, 135–148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gunlicks-Stoessel, M., Mufson, L., Westervelt, A., Almirall, D. and Murphy, S. (2016). A pilot smart for developing an adaptive treatment strategy for adolescent depression. Journal of Clinical Child & Adolescent Psychology 45, 480–494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsu, J. C. (1981). Simultaneous confidence intervals for all distances from the “best”. The Annals of Statistics 9, 1026–1034. [Google Scholar]
- Hsu, J. C. (1984). Constrained simultaneous confidence intervals for multiple comparisons with the best. Annals of Statistics 12, 1136–1144. [Google Scholar]
- Hsu, J. C. (1996). Multiple Comparisons: Theory and Methods. London: CRC Press. [Google Scholar]
- Kidwell, K. M., Seewald, N. J., Tran, Q., Kasari, C. and Almirall, D. (2018). Design and analysis considerations for comparing dynamic treatment regimens with binary outcomes from sequential multiple assignment randomized trials. Journal of Applied Statistics 45, 1628–1651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim, H., Ionides, E. and Almirall, D. (2016). A sample size calculator for smart pilot studies. SIAM Undergraduate Research Online. DOI: 10.1137/15S014058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laber, E. B., Lizotte, D. J., Qian, M., Pelham, W. E. and Murphy, S. A. (2014). Dynamic treatment regimes: technical challenges and applications. Electronic Journal of Statistics 8, 1225–1272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laber, E. B., Zhao, Y., Regh, T., Davidian, M., Tsiatis, A., Stanford, J. B., Zeng, D., Song, R. and Kosorok, M. R. (2016). Using pilot data to size a two-arm randomized trial to find a nearly optimal personalized treatment strategy. Statistics in Medicine 35, 1245–1256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavori, P. W., Dawson, R. and Rush, A. J. (2000). Flexible treatment strategies in chronic disease: clinical and research implications. Biological Psychiatry 48, 605–614. [DOI] [PubMed] [Google Scholar]
- Lei, H., Nahum-Shani, I., Lynch, K. G., Oslin, D. and Murphy, S. A. (2012). A SMART design for building individualized treatment sequences. Annual Review of Clinical Psychology 8, 21–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy, S. A. (2003). Optimal dynamic treatment regimes. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 65, 331–355. [Google Scholar]
- Murphy, S. A. (2005). An experimental design for the development of adaptive treatment strategies. Statistics in Medicine 24, 1455–1481. [DOI] [PubMed] [Google Scholar]
- Murphy, S. A., van der Laan, M. J., Robins, J. M.. and Conduct Problems Prevention Research Group (2001). Marginal mean models for dynamic regimes. Journal of the American Statistical Association 96, 1410–1423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nahum-Shani, I., Ertefaie, A., Lu, X., Lynch, K. G., McKay, J. R., Oslin, D. W. and Almirall, D. (2017). A smart data analysis method for constructing adaptive treatment strategies for substance use disorders. Addiction 112, 901–909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nahum-Shani, I., Qian, M., Almirall, D., Pelham, W. E., Gnagy, B., Fabiano, G. A., Waxmonsky, J. G., Yu, J. and Murphy, S. A. (2012). Experimental design and primary data analysis methods for comparing adaptive interventions. Psychological Methods 17, 457–477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogbagaber, S. B., Karp, J. and Wahed, A. S. (2016). Design of sequentially randomized trials for testing adaptive treatment strategies. Statistics in Medicine 35, 840–858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robins, J. M. (2004). Optimal structural nested models for optimal sequential decisions. In: Proceedings of the Second Seattle Symposium in Biostatistics. New York, NY: Springer, pp. 189–326. [Google Scholar]
- Tong, Y. L. (2012). The Multivariate Normal Distribution. Springer Series in Statistics. New York: Springer. [Google Scholar]
- Watkins, C. J. C. H. (1989). Learning from delayed rewards [Ph.D. Thesis]. Cambridge: King’s College. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.