Summary
Despite the wide application of dynamic models in infectious disease epidemiology, the particular modeling of variability in the different model components is often subjective rather than the result of a thorough model selection process. This is in part because inference for a stochastic transmission model can be difficult since the likelihood is often intractable due to partial observability. In this work, we address the question of adequate inclusion of variability by demonstrating a systematic approach for model selection and parameter inference for dynamic epidemic models. For this, we perform inference for six partially observed Markov process models, which assume the same underlying transmission dynamics, but differ with respect to the amount of variability they allow for. The inference framework for the stochastic transmission models is provided by iterated filtering methods, which are readily implemented in the R package pomp by King and others (2016, Statistical inference for partially observed Markov processes via the R package pomp. Journal of Statistical Software69, 1–43). We illustrate our approach on German rotavirus surveillance data from 2001 to 2008, discuss practical difficulties of the methods used and calculate a model based estimate for the basic reproduction number 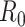 using these data.
using these data.
Keywords: Iterated filtering, Model selection, Parameter inference, Partially observed Markov process, Rotavirus surveillance data, Seasonal age-stratified SIRS model
1. Introduction
Infectious disease outbreaks are often observed in the form of uni- or multivariate time series, e.g. as the number of newly reported cases aggregated over some time period. In order to estimate the relationship between variables, a classical statistical approach is the use of time series analysis of the incident cases, e.g. as in Finkenstädt and others (2002), Held and others (2006). These models are useful for prediction and forecasting, however, they teach us little about the dynamics of the disease spread, which are crucial if one wants to, e.g. assess the risk of emerging pathogens or evaluate the impact of control measures such as vaccination. Hence, another popular approach are transmission models, i.e. dynamic models which reflect the mechanisms of disease spread between individuals explicitly (Anderson and May, 1991; Keeling and Rohani, 2008; Diekmann and others, 2013). However, despite their wide application in infectious disease epidemiology, the choice between a stochastic and a deterministic transmission model for a specific data set is often subjective and based on expert knowledge or non-generalizable, ad hoc preferences (Sun and others, 2015). Additionally, in case of a stochastic transmission model the corresponding likelihood function is, except for the simplest cases, intractable. This makes inference for this type of models complicated which in turn makes a thorough analysis for model selection and parameter inference difficult. As it becomes more common to include the results of dynamic models as part of data analysis in infectious disease epidemiology, this challenge becomes increasingly interesting for, for example, public health authorities. Hence, the objective of this article is to demonstrate the application of an inference framework which facilitates (i) model selection for both, deterministic and stochastic transmission models and (ii) parameter inference and quantification of the uncertainties of the estimates based on the observed data. The idea of our work is similar to the one in Sun and others (2015), however, the inference method and area of application are different: we use iterated filtering methods to perform inference and demonstrate our approach on an age-structured model for rotavirus transmission in Germany. In our work, we consider a simplified version of the SIRS-type model used in Weidemann and others (2013) who analyzed the same data in a different context, including fewer disease states and fewer age classes but accounting for seasonality, age-structure and, in particular, more variability.
A convenient framework to answer infectious disease epidemiology related questions in a model based and data driven way are partially observed Markov processes (POMP). This model class consists of two model components: (i) an unobserved Markovian transmission process, which can be either continuous or discrete in time and in our application operates on the population level describing the dynamics of disease spread and (ii) an observation model, which relates the data collected at discrete points in time to the transmission model. In our work, we compare three different transmission models, which all assume the same underlying disease mechanisms but differ with respect to the amount of stochasticity they allow for. Namely, we compare a set of ordinary differential equations (ODEs), a continuous time Markov chain (CTMC), which is purely driven by demographic stochasticity, and an overdispersed CTMC which allows for variability beyond demographic noise by stochastic transmission rates (Bretó and others, 2009; He and others, 2009). All three approaches have their advantages and shortcomings. Models based on a deterministic transmission model component are preferably used when the population size is large and since they assume no randomness in the transmission, analysis and inference is easier and hence very popular among practitioners. However, these models explain any discrepancy between the deterministic model and the data by observation noise since this is the only element where stochasticity enters. In observed data in turn, we see fluctuations, which are clearly not due to variation in data collection alone but, e.g. due to environmental changes, different genotypes or variability in social behavior such as super spreaders etc. Most of these possible sources of variability are in part not sufficiently understood or not measurable in any way. Hence, stochastic variation in the transmission model is potentially an essential element to capture in order to quantify these influences. However, inference is more complicated than in the deterministic case, because the likelihood is often a complex and high dimensional integral resulting from integrating out stochasticity or missing state information.
With increasing computational power, simulation-based methods to solve those high dimensional integrals gained more and more attention. In this work, we use iterated filtering (Ionides and others, 2015) for maximum likelihood estimation in partially observed epidemic models, which takes advantage of the fact that it is relatively easy to generate samples from the Markov process compared with evaluating its transition probabilities. The method is, among others, conveniently implemented in the R package pomp (King and others, 2016), which spans a wide collection of inference tools for both deterministic and stochastic underlying transmission models. Other likelihood- and simulation-based inference methods for POMP models are simulated moments (Kendall and others, 1999), nonlinear forecasting (Sugihara and May, 1990), synthetic likelihood (Wood, 2010), or Bayesian approaches such as approximate Bayesian computations (Toni and others, 2009) and particle MCMC (Andrieu and others, 2010).
Since the package was developed fairly recently, we also comment on our experiences with the package and discuss its scientific as well as practical use. We base our criteria for model selection on Akaike Information Criterion (AIC) and coverage, i.e. how often the data is covered by the 95% point wise in-sample prediction interval evaluated at the best choice of parameters. The reasoning behind this choice is that we are interested in a relative measure assessing the trade-off between goodness-of-fit and complexity of the models on the one hand, and in an absolute measure of how well the models actually deal with variability in the data on the other hand. Our analysis will show for the particular data set at hand, to obtain the lowest AIC and best coverage it is important to include variability in the form of overdispersion into both model components. In Section 2, we give a short overview of rotavirus disease and the German rotavirus surveillance data. In Section 3, we present three different but related transmission models for the data. We explain how the transmission models are connected to the data via an observation component and formulate an expression for the basic reproduction number 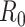 . In Section 4, we present the inference framework and give some details concerning implementation. We perform a simulation study to demonstrate the suitability of the inference method for each of the models in Section 5. In Section 6, we apply our methods to data introduced in 2 and compare the findings to the approach used in Weidemann and others (2013). Section 7 ends the article with a discussion.
. In Section 4, we present the inference framework and give some details concerning implementation. We perform a simulation study to demonstrate the suitability of the inference method for each of the models in Section 5. In Section 6, we apply our methods to data introduced in 2 and compare the findings to the approach used in Weidemann and others (2013). Section 7 ends the article with a discussion.
2. Motivating example: rotavirus disease
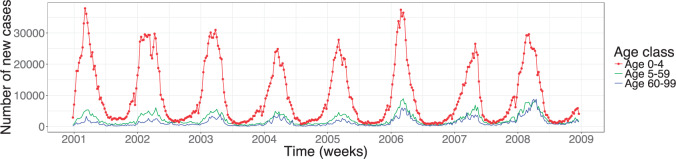
Rotavirus disease is a childhood disease and the primary cause for gastroenteritis in infants and young children, while adults are rarely infected (Grimmwood and Lambert, 2009). By the age of five nearly every child has been infected with the virus at least once (CDC, 2017). The virus spreads by direct transmission on the faecal oral route. The incubation time of rotavirus is around 2 days, while severe symptoms last for approximately 4–8 days (CDC, 2017). Reinfection is possible because neither natural infection with rotavirus nor rotavirus vaccination provides full protection from future infections. The data, we analyze is the weekly reported number of new, laboratory-confirmed rotavirus cases among children younger than 5 years of age, individuals between age 5–59 and elderly aged 60–99 years from 2001 to 2008 in Germany. After 2008, a significant impact on the rotavirus incidence by the increasing vaccination coverage is observed (Weidemann and others, 2013). The data are available through SurvStat@RKI (RKI, 2017) and were previously analyzed in Weidemann and others (2013) as part of advising the German standing board of vaccination (STIKO) about the possible impact of a recommendation of rotavirus vaccination for children. Such modeling questions are typical in a public health context—mathematical modeling with SIRS-type models of rotavirus has already been carried out for different countries, cf. e.g. Atkins and others (2012); Weidemann and others (2013); Martinez and others (2016) and references therein. One problem with the available routine surveillance data is under-reporting, however, since our focus is on methodological insights, we use the results from Weidemann and others (2013) and simply scale up the available data with the inferred under-reporting factors. The time series depicted in Figure 1 shows the scaled up data for the three age groups. The case report data clearly shows seasonal variation of rotavirus.
Fig. 1.
Weekly number of new rotavirus cases among the three aggregated age groups of 0–4, 5–59, and 60–99 years of age in Germany between 2001–2008. The values we used for scaling up are the median estimates of the under-reporting parameter from the averaged posterior distribution inferred in Weidemann and others (2013), namely 4.3% in the former western federal states (WFS) and 19.0% in the former eastern federal states (EFS) between 2001 and 2004 and 6.3% in WFS and 24.1% in EFS from 2005 onward. This sudden increase in reporting behavior is due to a nationwide change in the reimbursement of hospitalized rotavirus cases from January 2005.
3. Methods
We formulate three different transmission models, which assume the same transmission mechanisms but differ with respect to the amount of variability they allow for. The three different models are (i) a CTMC with demographic noise, (ii) an overdispersed CTMC with demographic noise and stochastic transmission rates, and (iii) a deterministic transmission model. Additionally, we investigate the role of overdispersion in the observation model, leading to two distinct models one of which allows for overdispersion and one that does not. By combining the three transmission models with the two observation models we obtain six different models for rotavirus infection, cf. Table A.1 in the supplementary material available at Biostatistics online, where Model DtSt contains the least stochasticity and Model St+St+ the most. We finish this section by deriving an expression for the basic reproduction number 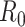 based on the transmission dynamics assumed here.
based on the transmission dynamics assumed here.
3.1. Transmission models
3.1.1. CTMC with demographic noise.
We assume that the transmission model is a Markov process where individuals move between compartments at random times, as described in detail below. The schematic representation of our model is given in the flow diagram of Figure 2. We consider a model that subdivides the population into three age classes, i.e. age 0–4, age 5–59, and age 60–99 years, identified by the indices 1, 2, and 3, respectively. We choose this age stratification, because the disease burden is highest for young children, very low for children over 5 years of age and rises again later in life. The variables 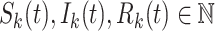 with
with 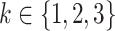 count the number of susceptible, infectious, and recovered in each of the three age groups at time
count the number of susceptible, infectious, and recovered in each of the three age groups at time 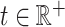 . Concerning the rates, young children “age” with a rate
. Concerning the rates, young children “age” with a rate 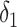 into the second age class and individuals of age 5–59 “age” with a rate
into the second age class and individuals of age 5–59 “age” with a rate 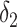 into the class of elderly (age 60 +). The vector
into the class of elderly (age 60 +). The vector 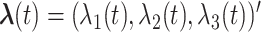 is called the force of infection and is the per capita rate at which susceptible individuals get infected, which depends on the number of currently infected individuals
is called the force of infection and is the per capita rate at which susceptible individuals get infected, which depends on the number of currently infected individuals 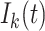 . Susceptible individuals can become infected by transmission from an infectious individual in one of the three age groups. The recovery rate
. Susceptible individuals can become infected by transmission from an infectious individual in one of the three age groups. The recovery rate 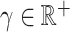 is assumed to be independent of age. We also assume that waning of immunity is independent of age and immunity from infection lasts for a limited, exponentially distributed period with mean
is assumed to be independent of age. We also assume that waning of immunity is independent of age and immunity from infection lasts for a limited, exponentially distributed period with mean 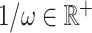 after which the individual is again fully susceptible; for a discussion of those assumptions cf. Section 7. To account for demographics, we assume that the average population size,
after which the individual is again fully susceptible; for a discussion of those assumptions cf. Section 7. To account for demographics, we assume that the average population size, 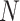 , is constant, which implies that the birth rate,
, is constant, which implies that the birth rate, 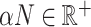 , equals the overall death rate. Furthermore, it is assumed that death can only occur in the last age class with rate
, equals the overall death rate. Furthermore, it is assumed that death can only occur in the last age class with rate 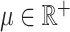 independent of the health status of the individual. This seems reasonable because in developed countries 90 % of the mortality comes from individuals older than 60 years, hence, premature death can be ignored for our purposes (Atkins and others, 2012). In the following, the notation is adopted from King and others (2016). We let
independent of the health status of the individual. This seems reasonable because in developed countries 90 % of the mortality comes from individuals older than 60 years, hence, premature death can be ignored for our purposes (Atkins and others, 2012). In the following, the notation is adopted from King and others (2016). We let 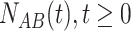 denote a stochastic counting process counting the number of individuals which have moved from compartment A to compartment B during the time interval
denote a stochastic counting process counting the number of individuals which have moved from compartment A to compartment B during the time interval 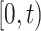 with
with 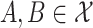 , where
, where 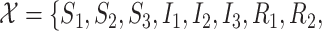
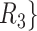 contains all compartments of our model. Furthermore,
contains all compartments of our model. Furthermore, 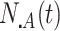 counts the number of births and
counts the number of births and 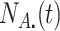 counts the number of deaths in the respective compartment up until time
counts the number of deaths in the respective compartment up until time 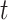 . The infinitesimal increment probabilities of a jump between compartments connected by an arrow (Figure 2) fully specify the continuous time Markov process describing disease transmission. Let
. The infinitesimal increment probabilities of a jump between compartments connected by an arrow (Figure 2) fully specify the continuous time Markov process describing disease transmission. Let 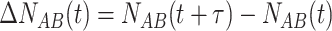 count the number of individuals changing compartment in an infinitesimal time interval
count the number of individuals changing compartment in an infinitesimal time interval 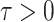 . Then we define for the model depicted in Figure 2 the following system of transition probabilities:
. Then we define for the model depicted in Figure 2 the following system of transition probabilities:
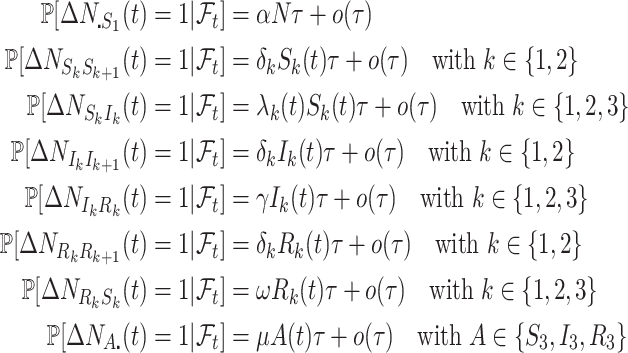 |
(3.1) |
with the filtration 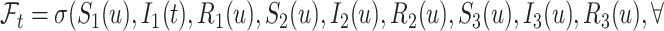
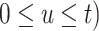 denoting the history of the process until time
denoting the history of the process until time 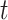 ; cf. Appendix A.1 of the supplementary material available at Biostatistics online for how transition rates and the state variables are related. A consequence of this model formulation is that we assume that the waiting time of each individual within each compartment is exponentially distributed given the current state; we discuss how this assumption can be relaxed in Section 7. The number of newly infected individuals in age class
; cf. Appendix A.1 of the supplementary material available at Biostatistics online for how transition rates and the state variables are related. A consequence of this model formulation is that we assume that the waiting time of each individual within each compartment is exponentially distributed given the current state; we discuss how this assumption can be relaxed in Section 7. The number of newly infected individuals in age class  accumulated in each observation time period
accumulated in each observation time period 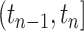 is then given as
is then given as
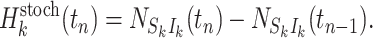 |
(3.2) |
Fig. 2.
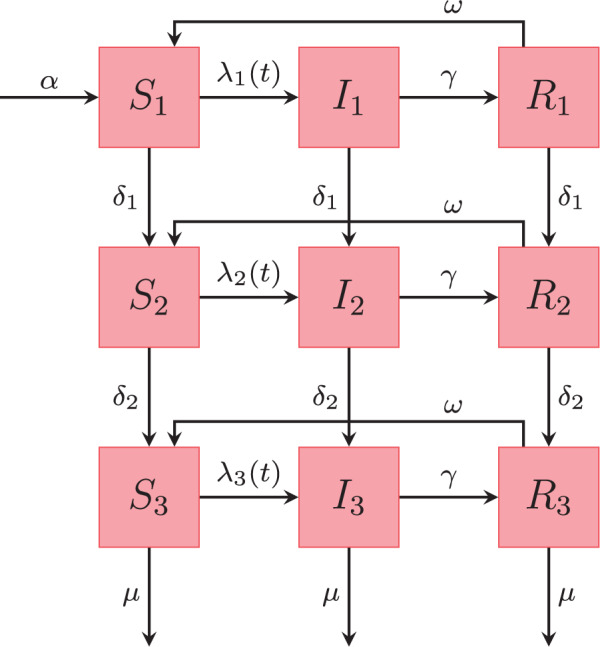
Schematic representation of the states in our SIRS model with three age classes. The rates on the arrows are explained in the text. Table 1 provides a list of notation, specifying which parameters are estimated in this work, and which are assumed known from the literature.
The force of infection, written in vector notation, consists of the following components
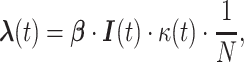 |
(3.3) |
where 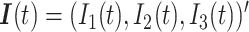 . Disease transmission is represented in a transmission-matrix
. Disease transmission is represented in a transmission-matrix 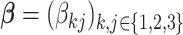 where the parameter
where the parameter 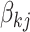 denotes the average number of infectious contacts of infected individuals of age group
denotes the average number of infectious contacts of infected individuals of age group 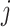 with susceptible individuals of age group
with susceptible individuals of age group 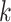 per time unit and hence is the product of contact rates and transmission probability. Our modeling should account for the possibility that individuals in each age class
per time unit and hence is the product of contact rates and transmission probability. Our modeling should account for the possibility that individuals in each age class 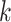 could have a different immune status due to age and hence having differing susceptibility to the disease, so we assume
could have a different immune status due to age and hence having differing susceptibility to the disease, so we assume 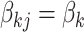 for all
for all 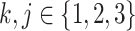 . Furthermore, motivated by the rotavirus application, we introduce a seasonal periodic forcing to account for the clear seasonal pattern in the data. In contrast to
. Furthermore, motivated by the rotavirus application, we introduce a seasonal periodic forcing to account for the clear seasonal pattern in the data. In contrast to 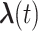 which is state dependent, the seasonal forcing function
which is state dependent, the seasonal forcing function 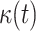 is assumed to be purely time dependent, i.e. it has the same effect in all age groups. We let
is assumed to be purely time dependent, i.e. it has the same effect in all age groups. We let
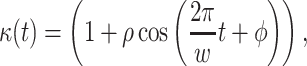 |
(3.4) |
where 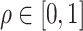 denotes the amplitude of the forcing,
denotes the amplitude of the forcing, 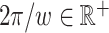 denotes the period of the forcing (e.g. if the time unit is weeks, then
denotes the period of the forcing (e.g. if the time unit is weeks, then 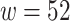 ) and
) and 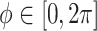 denotes the phase shift parameter. Note that with the choice of forcing in Equation (3.4) the parameter
denotes the phase shift parameter. Note that with the choice of forcing in Equation (3.4) the parameter 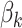 denotes the baseline transmission rate of an individual of age group
denotes the baseline transmission rate of an individual of age group 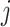 with age group
with age group 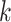 which varies between
which varies between 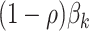 and
and 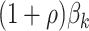 during the year (Keeling and Rohani, 2008).
during the year (Keeling and Rohani, 2008).
3.1.2. Overdispersed CTMC with demographic noise and stochastic transmission rates.
Including sufficient stochasticity in a model as a way to capture drivers and phenomena not covered otherwise by the model (e.g. late season peak) is essential if one wants the model to fit the data, e.g. to explain the data well (Bretó and others, 2009). So far, we have accounted for stochasticity in the underlying system by assuming that individuals move between classes at random times. However, for the transmission model in Section 3.1.1 the role of randomness diminishes as the population size increases. The same occurs by modeling disease spread via stochastic differential equations (Fuchs, 2013). One way to introduce variability, which is independent of population size, is to assume stochastic fluctuations in the transmission rates. In this work, we follow the approach of Bretó and others (2009) and introduce a time continuous stochastic process, 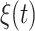 , which fluctuates around the value one and is multiplied onto the transmission rate. It can be shown that by choosing the corresponding integrated noise process,
, which fluctuates around the value one and is multiplied onto the transmission rate. It can be shown that by choosing the corresponding integrated noise process, 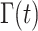 , in a way such that its increments are independent, stationary, non-negative, and unbiased the Markov property is retained (Bretó and others, 2009). One convenient example for a process which satisfies these conditions is a Lévy process with
, in a way such that its increments are independent, stationary, non-negative, and unbiased the Markov property is retained (Bretó and others, 2009). One convenient example for a process which satisfies these conditions is a Lévy process with 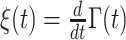 , where marginally
, where marginally 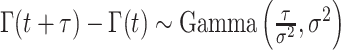 and where
and where 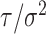 denotes the shape and
denotes the shape and 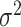 the age-independent scale parameter with corresponding mean
the age-independent scale parameter with corresponding mean 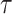 and variance
and variance 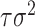 . Note that the integral of
. Note that the integral of 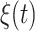 over a time interval is well defined even though the sample paths of
over a time interval is well defined even though the sample paths of 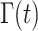 are not formally differentiable (Bretó and others, 2009). We build this into the model as defined in Equation (3.1) and Equation (A.1) of the supplementary material available at Biostatistics online by modifying Equation (3.3) as
are not formally differentiable (Bretó and others, 2009). We build this into the model as defined in Equation (3.1) and Equation (A.1) of the supplementary material available at Biostatistics online by modifying Equation (3.3) as
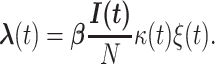 |
(3.5) |
A consequence of this construction is that the variability of the distribution of the transmission process for a given time 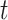 becomes larger compared with the case when there is no extra-demographic noise, hence we call the CTMC overdispersed. This form of overdispersion has been used in previous studies of infectious diseases, for example, measles (He and others, 2009), malaria (Bhadra and others, 2011), or rotavirus (Martinez and others, 2016).
becomes larger compared with the case when there is no extra-demographic noise, hence we call the CTMC overdispersed. This form of overdispersion has been used in previous studies of infectious diseases, for example, measles (He and others, 2009), malaria (Bhadra and others, 2011), or rotavirus (Martinez and others, 2016).
3.1.3. Deterministic transmission model.
Calculating the expected values of the equations in (A.1) in Appendix A.1 of the supplementary material available at Biostatistics online with the aid of (3.1), dividing by 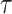 , and taking the limit as
, and taking the limit as 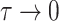 , we obtain the underlying deterministic form of the model
, we obtain the underlying deterministic form of the model
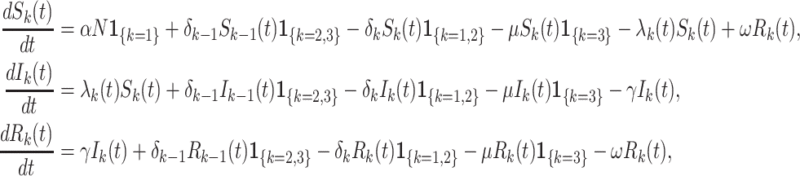 |
(3.6) |
for 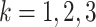 , the force of infection as in (3.3) and initial values satisfying
, the force of infection as in (3.3) and initial values satisfying 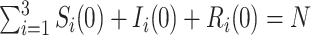 . Note that for the deterministic model, the state variables are continuous rather than integer valued. The number of newly infected individuals in age class
. Note that for the deterministic model, the state variables are continuous rather than integer valued. The number of newly infected individuals in age class 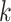 accumulated in each observation time unit
accumulated in each observation time unit 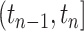 ,
, 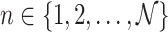 is then given as
is then given as
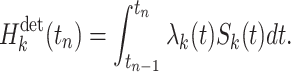 |
(3.7) |
3.2. Observation models
To incorporate the count nature of the observations a natural first assumption would be to model the reported cases as realizations of a Poisson distributed random variable with a given time dependent mean to account for errors in classification of cases, including false positives. However, the data at hand suggests that the sample variance is larger than the sample mean, i.e. there is indication of overdispersion in the data. Another choice in this case is the negative binomial distribution which allows for additional variance. Hence, let the number of recorded cases 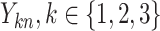 within a given reporting interval
within a given reporting interval 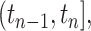
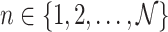 be either
be either
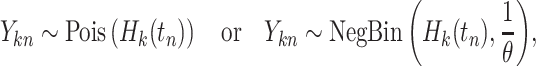 |
(3.8) |
with 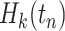 being the true number of accumulated incidences in age class
being the true number of accumulated incidences in age class 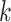 per time unit
per time unit 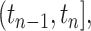 in the model, cf. Equation (3.2) for the stochastic models and (3.7) for the deterministic model. Here
in the model, cf. Equation (3.2) for the stochastic models and (3.7) for the deterministic model. Here 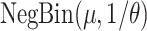 denotes the negative binomial distribution with mean
denotes the negative binomial distribution with mean 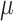 and variance
and variance 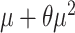 . To reduce the number of parameters, the same dispersion parameter
. To reduce the number of parameters, the same dispersion parameter 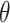 for all age classes is chosen as in Weidemann and others (2013).
for all age classes is chosen as in Weidemann and others (2013).
3.3. Calculation of 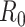
An important mathematical characteristic of an epidemic model is its basic reproduction number 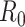 ; we apply the theory of Diekmann and others (2013), Chapter 7, in the following.
; we apply the theory of Diekmann and others (2013), Chapter 7, in the following. 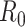 is the expected number of new infections by a typical infectee during the early stage of an epidemic when everyone is susceptible. We can calculate the basic reproduction number
is the expected number of new infections by a typical infectee during the early stage of an epidemic when everyone is susceptible. We can calculate the basic reproduction number 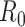 for the deterministic transmission model which is, also, representative for the stochastic transmission model, because it approaches the deterministic system for a large population size
for the deterministic transmission model which is, also, representative for the stochastic transmission model, because it approaches the deterministic system for a large population size 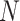 . Hence, let
. Hence, let 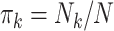 denote the community fraction of age class
denote the community fraction of age class 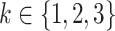 in the population and
in the population and 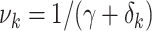 for
for 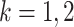 and
and 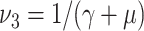 the average length an individual of type
the average length an individual of type 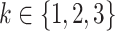 stays in the infectious compartment. With the seasonal forcing function chosen as in Equation (3.4) the expected number of
stays in the infectious compartment. With the seasonal forcing function chosen as in Equation (3.4) the expected number of 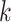 individuals a
individuals a 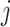 individual infects if everyone is susceptible is
individual infects if everyone is susceptible is 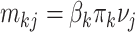 , which represents a yearly average. The basic reproduction number
, which represents a yearly average. The basic reproduction number 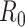 can then be calculated as the largest eigenvalue of the matrix
can then be calculated as the largest eigenvalue of the matrix 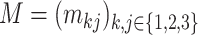 . It follows with “proportionate mixing” that
. It follows with “proportionate mixing” that  where we denote
where we denote 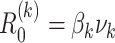 as the age-specific basic reproduction number for age group
as the age-specific basic reproduction number for age group 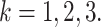 Since
Since 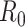 is a yearly average here, its interpretation as a threshold value for an epidemic changes slightly. Only if the yearly range does not cover the value one it can be interpreted in the traditional way.
is a yearly average here, its interpretation as a threshold value for an epidemic changes slightly. Only if the yearly range does not cover the value one it can be interpreted in the traditional way.
4. Inference and implementation
We describe the general procedures of how to perform likelihood-based inference for a POMP for both a deterministic and a stochastic underlying transmission model. Since we use the R package pomp we give details on the implementation and provide the code at Stocks (2017).
4.1. Likelihood of a POMP
Let 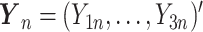 with
with 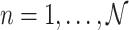 denote the random variables counting the new cases at time
denote the random variables counting the new cases at time 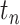 in each of the three age-classes. These depend on the state of the continuous time transmission process
in each of the three age-classes. These depend on the state of the continuous time transmission process 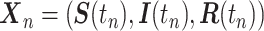 at that time where, e.g.
at that time where, e.g. 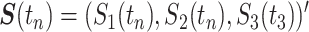 . Furthermore, we let
. Furthermore, we let 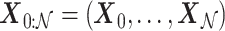 and denote the parameter vector by
and denote the parameter vector by 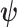 . The joint density of the states and the observations is then defined as the product of the one-step transmission density,
. The joint density of the states and the observations is then defined as the product of the one-step transmission density, 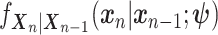 , the observation density,
, the observation density, 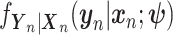 , and the initial density
, and the initial density 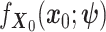 as
as
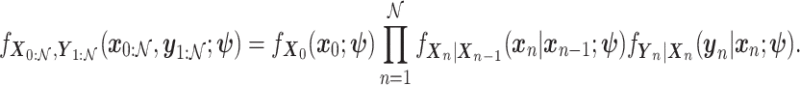 |
The likelihood of the parameter vector is then given as the marginal density for a sequence of observations, 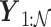 , evaluated at the data,
, evaluated at the data, 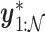 , as
, as
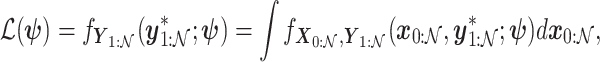 |
(4.1) |
see, e.g. King and Ionides (2017). Note that for our model this is a high-dimensional integral of dimension 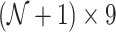 , which, except for the simplest cases, cannot be reduced analytically, see Section 4.1.2.
, which, except for the simplest cases, cannot be reduced analytically, see Section 4.1.2.
4.1.1. Maximum likelihood estimation for deterministic transmission model.
Inference for partially observed dynamical systems with a deterministic underlying transmission model is relatively straightforward, because Equation (4.1) is computable. Indeed 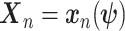 is a known function of
is a known function of 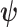 for each
for each 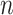 if the initial values of the system are fixed and known, cf. Section 4.2. Hence, the integral over
if the initial values of the system are fixed and known, cf. Section 4.2. Hence, the integral over 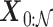 in Equation (4.1) is over a function which only has a single point mass, i.e.
in Equation (4.1) is over a function which only has a single point mass, i.e. 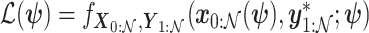 . The solution of the ODE system can be calculated numerically with, e.g. Runge–Kutta methods. Given this solution, maximum likelihood estimation boils down to a classical numerical optimization problem for a nonlinear function of the parameter vector. Maximum likelihood estimation for partially observed dynamical systems with a deterministic underlying transmission model is, e.g. implemented in the traj.match function in the R package pomp (King and others, 2016), which accesses R’s optim function. For further implementational details see Appendix B.1 of the supplementary material available at Biostatistics online. To determine a 95% confidence interval (CI) for the obtained estimates we calculate the profile log-likelihood for each parameter of interest and invert Wilks’ (likelihood ratio) test to get the desired intervals (Held and Sabanés Bové, 2013). To construct a 95% pointwise prediction interval for model realizations we calculate the 2.5% as well as the 97.5% quantile of the respective observation distribution (Equation 3.8) at each observation time
. The solution of the ODE system can be calculated numerically with, e.g. Runge–Kutta methods. Given this solution, maximum likelihood estimation boils down to a classical numerical optimization problem for a nonlinear function of the parameter vector. Maximum likelihood estimation for partially observed dynamical systems with a deterministic underlying transmission model is, e.g. implemented in the traj.match function in the R package pomp (King and others, 2016), which accesses R’s optim function. For further implementational details see Appendix B.1 of the supplementary material available at Biostatistics online. To determine a 95% confidence interval (CI) for the obtained estimates we calculate the profile log-likelihood for each parameter of interest and invert Wilks’ (likelihood ratio) test to get the desired intervals (Held and Sabanés Bové, 2013). To construct a 95% pointwise prediction interval for model realizations we calculate the 2.5% as well as the 97.5% quantile of the respective observation distribution (Equation 3.8) at each observation time 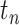 with mean
with mean 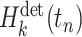 (Equation 3.7) evaluated at the MLE and hence ignoring uncertainty in the parameters.
(Equation 3.7) evaluated at the MLE and hence ignoring uncertainty in the parameters.
4.1.2. Maximum likelihood estimation for stochastic transmission model.
For a partially observed stochastic transmission model the likelihood is not tractable, because knowledge of the parameters does not uniquely determine the solution of the transmission model and marginal likelihoods are very computationally demanding. Iterated filtering is a simulation-based method to find the maximum likelihood estimate, cf. Ionides and others (2015) and references therein. It explores the parameter space by adding noise to the parameters of interest and at each iteration approximates the likelihood of the perturbed model by evaluating the particle filter (Doucet and others, 2001). Particle filtering methods return a stochastic estimate of the log-likelihood marginalized over the latent states using re-sampling techniques which make them more efficient than standard Monte Carlo methods. The iterated filtering algorithm is implemented in the mif2 function in the R package pomp (King and others, 2016). All algorithm specific parameters are reported in Appendix B.2 of the supplementary material available at Biostatistics online. For an application oriented introduction to iterated filtering methods see Stocks, 2017. To obtain 95% CIs for the parameters we construct a Monte Carlo error adjusted profile log-likelihood (Ionides and others, 2017) of each parameter and use Wilks’ test. For each observation, a 95% prediction interval is computed based on 1000 realizations of the model evaluated at the MLE. Note that these are in-sample prediction intervals because all observations where used to fit the model.
4.2. Initial values and starting values
Optimally, all parameters of a model can be inferred from the data. However, our investigations showed that the inference algorithms are very sensitive to starting values of parameters as well as initial values of the system and fail if those values are chosen completely at random. We discuss in detail how to overcome this practical issue in Appendix C of the supplementary material available at Biostatistics online. Based on this analysis we estimate the two seasonality parameters 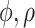 , the age-specific susceptibilities
, the age-specific susceptibilities 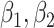 , and
, and 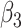 and the overdispersion parameters
and the overdispersion parameters 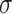 and
and 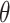 in the following.
in the following.
5. Simulation study
We perform a simulation study to demonstrate the suitability of the inference method for each of the models presented in Table A.1 of the supplementary material available at Biostatistics online. As proof of concept, we generate one realization of each model with parameters chosen as the periodic equilibrium of the deterministic model (cf. Appendix C of the supplementary material available at Biostatistics online), which we then treat as data to estimate parameters from. All other parameters are fixed at biological plausible values shown in Table 1. After the inference we compare the obtained estimates to the true parameters which serves as validation of our implementation, the results can be found in Table D.2 in the supplementary material available at Biostatistics online. For all models the estimated parameters are in good accordance with the true parameters. As an example, Figure D.1 in the supplementary material available at Biostatistics online shows the simulated data from Model DtSt , together with pointwise 95% prediction intervals obtained from the model evaluated at the MLE for the solution of the ODE. To provide evidence that the results are also consistent for more than one model realization we carry out a small additional study, the results of which can be found in Appendix D of the supplementary material available at Biostatistics online, cf. Figures D.2 and D.3. In order to check if observation noise and transmission noise are distinguishable and how the estimation results change under model misspecification we carry out a robustness study. For this we generate one realization of each model and fit the obtained realizations to every model respectively. We find that both noise components
, together with pointwise 95% prediction intervals obtained from the model evaluated at the MLE for the solution of the ODE. To provide evidence that the results are also consistent for more than one model realization we carry out a small additional study, the results of which can be found in Appendix D of the supplementary material available at Biostatistics online, cf. Figures D.2 and D.3. In order to check if observation noise and transmission noise are distinguishable and how the estimation results change under model misspecification we carry out a robustness study. For this we generate one realization of each model and fit the obtained realizations to every model respectively. We find that both noise components 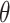 and
and 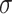 are indeed distinguishable from each other and parameters are estimated correctly even under model misspecification. However, Models St+St and StSt give a substantial amount of filtering failures in every iteration when fitting model realizations from models with overdispersion, for an example, cf. Figure D.4 in the supplementary material available at Biostatistics online. A filtering failure occurs if at some observation time point all suggested particles are too unlikely, i.e. the probability of each particle given the observation is below a certain threshold which generally implies that the model and data are inconsistent (King and Ionides, 2017). Even when doubling the number of particles the problem persists. This means that those two models fit data from other models (hence under the type of model misspecification we investigated) very poorly. We, therefore, conclude that for inference for stochastic transmission models, overdispersion in the observation model is an important ingredient in order to get robust results also under model misspecification. As a consequence, we exclude those two models from our comparative analysis. To investigate the performance of model selection, we calculate the AIC for each model fit, cf. Table D.3 of the supplementary material available at Biostatistics online. We find that for each realization, the respective true model always has the lowest AIC which confirms the correctness of our methods. To ensure that the AIC is a reasonable choice for the problem at hand we investigate in a small simulation study tailored to our specific model setting (SIRS in endemic state) how well the AIC can detect potential misspecifications in the transmission model. We find that for this particular case the AIC can explicitly discriminate between forms that directly affect the transmission event, for details, cf. Section D.2 of the supplementary material available at Biostatistics online.
are indeed distinguishable from each other and parameters are estimated correctly even under model misspecification. However, Models St+St and StSt give a substantial amount of filtering failures in every iteration when fitting model realizations from models with overdispersion, for an example, cf. Figure D.4 in the supplementary material available at Biostatistics online. A filtering failure occurs if at some observation time point all suggested particles are too unlikely, i.e. the probability of each particle given the observation is below a certain threshold which generally implies that the model and data are inconsistent (King and Ionides, 2017). Even when doubling the number of particles the problem persists. This means that those two models fit data from other models (hence under the type of model misspecification we investigated) very poorly. We, therefore, conclude that for inference for stochastic transmission models, overdispersion in the observation model is an important ingredient in order to get robust results also under model misspecification. As a consequence, we exclude those two models from our comparative analysis. To investigate the performance of model selection, we calculate the AIC for each model fit, cf. Table D.3 of the supplementary material available at Biostatistics online. We find that for each realization, the respective true model always has the lowest AIC which confirms the correctness of our methods. To ensure that the AIC is a reasonable choice for the problem at hand we investigate in a small simulation study tailored to our specific model setting (SIRS in endemic state) how well the AIC can detect potential misspecifications in the transmission model. We find that for this particular case the AIC can explicitly discriminate between forms that directly affect the transmission event, for details, cf. Section D.2 of the supplementary material available at Biostatistics online.
Table 1.
Full list of notation and parameter values used
| Parameter | Explanation | Value | Unit |
|---|---|---|---|
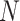
|
Population size |
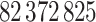
|
individuals |
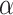
|
Individual birth rate |
|
week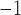
|
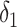
|
Aging from age group 1 (age 0–4) to 2 (age 5–59) |
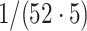
|
week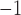
|
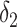
|
Aging from age group 2 (age 5–59) to 3 (age 60+) |
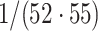
|
week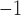
|
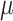
|
Death rate (from age group 3 (age 60+) ) |
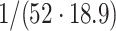
|
week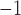
|
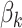
|
Susceptibility of age group 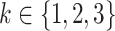
|
To be estimated | individuals/week |
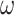
|
Immunity waning rate |
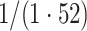
|
week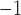
|
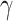
|
Recovery rate |

|
week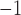
|
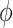
|
Phase shift of the seasonal forcing | To be estimated | 1 |
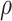
|
Amplitude of the seasonal forcing | To be estimated | 1 |
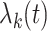
|
Force of infection of age group 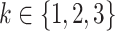
|
Defined by Eqn. (3.3) | individuals/week |
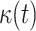
|
Seasonal forcing function | Defined by Eqn. (3.4) | 1 |
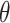
|
Overdispersion parameter | To be estimated | 1 |
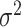
|
Scale parameter of the 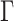 -noise -noise |
To be estimated | 1 |
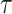
|
Time step | To be estimated | week |
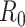
|
Basic reproduction number | To be estimated | individuals |
The inverse of the yearly birth rate equals the sum of the inverses of the yearly aging and death rates which add up to 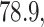 which is the total life expectancy at birth in Germany averaged between the years 2001 and 2008, taken from The World Bank (2016). The averaged population size
which is the total life expectancy at birth in Germany averaged between the years 2001 and 2008, taken from The World Bank (2016). The averaged population size 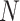 in Germany during that time period is taken from Statistisches Bundesamt (2016) and the reporting interval is 1 week. As in Atkins and others (2012), we assume that all individuals are immune against rotavirus for an average of one year. A more detailed discussion on the choice of this assumption can be found in Section 7.
in Germany during that time period is taken from Statistisches Bundesamt (2016) and the reporting interval is 1 week. As in Atkins and others (2012), we assume that all individuals are immune against rotavirus for an average of one year. A more detailed discussion on the choice of this assumption can be found in Section 7.
6. Rotavirus infection application results
Parameter estimates, CIs as well as model diagnostics for the four models are given in Table 2. We report in the column “coverage” how often the actual data is covered by the pointwise 95% prediction interval of the respective model. For the stochastic transmission models StSt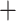 and St
and St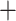 St
St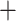 we also report how often the 95% prediction interval of the stochastic transmission model covers the data in order to investigate how much the observation noise additionally contributes to explaining the data. We find that matching Model DtSt to the data coincides well with the equilibrium results for the susceptibility parameters of the deterministic model without seasonality (cf. Equations C.5 in Appendix C.2 of the supplementary material available at Biostatistics online), although, this model obviously neither has an observation model nor a seasonal forcing component. However, the 95% prediction interval only covers 8.8% of the observed data and, hence, the model only poorly explains the variation in the data as is also reflected in a low log-likelihood value, cf. Figure E.5 in the supplementary material available at Biostatistics online. Fitting the deterministic model with overdispersion (Model DtSt
we also report how often the 95% prediction interval of the stochastic transmission model covers the data in order to investigate how much the observation noise additionally contributes to explaining the data. We find that matching Model DtSt to the data coincides well with the equilibrium results for the susceptibility parameters of the deterministic model without seasonality (cf. Equations C.5 in Appendix C.2 of the supplementary material available at Biostatistics online), although, this model obviously neither has an observation model nor a seasonal forcing component. However, the 95% prediction interval only covers 8.8% of the observed data and, hence, the model only poorly explains the variation in the data as is also reflected in a low log-likelihood value, cf. Figure E.5 in the supplementary material available at Biostatistics online. Fitting the deterministic model with overdispersion (Model DtSt ) to the data improves the fit by several thousands log units. The 95% prediction interval of the estimated parameter values covers now 96.2% of the data, cf. Figure E.6 in the supplementary material available at Biostatistics online. The difference between Model DtSt
) to the data improves the fit by several thousands log units. The 95% prediction interval of the estimated parameter values covers now 96.2% of the data, cf. Figure E.6 in the supplementary material available at Biostatistics online. The difference between Model DtSt and Model St
and Model St St
St is the nature of their transmission model and we find that a stochastic transmission model improves the fit by additional 180 log units. We find that the coverage of the 95% prediction interval decreases to 90.6%, however, the coverage of the prediction interval of the transmission model is 28.9%, cf. Figure E.7 in the supplementary material available at Biostatistics online. The diagnostic plots which show how the log-likelihood of the mif2 model and the parameters evolve with each iteration can be found in Figures E.9 and E.11 in the supplementary material available at Biostatistics online. Finally, Model St
is the nature of their transmission model and we find that a stochastic transmission model improves the fit by additional 180 log units. We find that the coverage of the 95% prediction interval decreases to 90.6%, however, the coverage of the prediction interval of the transmission model is 28.9%, cf. Figure E.7 in the supplementary material available at Biostatistics online. The diagnostic plots which show how the log-likelihood of the mif2 model and the parameters evolve with each iteration can be found in Figures E.9 and E.11 in the supplementary material available at Biostatistics online. Finally, Model St St
St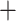 allows for additional variability by having stochastic transmission rates. It has the highest log-likelihood and lowest AIC of the four models and is hence the best suited model to explain the data. The prediction interval covers 96.5% of the data. It is interesting to note is that now the transmission model by itself is able to explain nearly all the data because its prediction interval covers 93.7%, cf. Figure 3. This indicates that the observation noise component is not as strong as the three previous models suggest. A detailed interpretation of the estimates for
allows for additional variability by having stochastic transmission rates. It has the highest log-likelihood and lowest AIC of the four models and is hence the best suited model to explain the data. The prediction interval covers 96.5% of the data. It is interesting to note is that now the transmission model by itself is able to explain nearly all the data because its prediction interval covers 93.7%, cf. Figure 3. This indicates that the observation noise component is not as strong as the three previous models suggest. A detailed interpretation of the estimates for 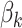 and
and 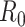 can be found in Section E.2 of the supplementary material available at Biostatistics online.
can be found in Section E.2 of the supplementary material available at Biostatistics online.
Table 2.
Inference results for the four models with maximum likelihood estimate (MLE), 95% confidence intervals (CI), basic reproduction number 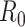 , 95% confidence interval for
, 95% confidence interval for 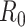 , seasonal variability of
, seasonal variability of 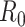 , coverage of the data by the 95% prediction interval of the full model, (coverage of the data 95% prediction interval only generated by the transmission model), log-likelihood (LL), Akaike information criterion (AIC), and standard error of the Monte Carlo approximations
, coverage of the data by the 95% prediction interval of the full model, (coverage of the data 95% prediction interval only generated by the transmission model), log-likelihood (LL), Akaike information criterion (AIC), and standard error of the Monte Carlo approximations
Model DtSt (LL:  371 713, AIC: 371 713, AIC: 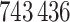 , coverage: 8.8%) , coverage: 8.8%) | |||||||
|---|---|---|---|---|---|---|---|
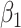
|
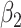
|
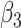
|
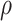
|
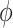
|
|||
| MLE | 12.659 | 0.237 | 0.418 | 0.151 | 0.037 | ||
| CI | [12.658, 12.659] | [0.237, 0.238] | [0.418, 0.419] | [0.151, 0.151] | [0.036, 0.038] | ||
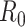 = 1.065 (1.065–1.066), seasonal range: [0.904, 1.226] = 1.065 (1.065–1.066), seasonal range: [0.904, 1.226] | |||||||
Model DtSt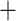 (LL: (LL:  10 383.05, AIC: 10 383.05, AIC: 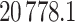 , coverage: 96.2%) , coverage: 96.2%) | |||||||
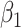
|
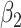
|
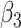
|
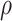
|
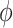
|
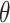
|
||
| MLE | 11.718 | 0.284 | 0.477 | 0.129 | 0.067 | 0.221 | |
| CI | [11.474, 11.956] | [0.270, 0.298] | [0.454, 0.503] | [0.125, 0.133] | [0.034, 0.100] | [0.205, 0.238] | |
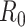 = 1.052 (1.021–1.083), seasonal range: [0.916, 1.188] = 1.052 (1.021–1.083), seasonal range: [0.916, 1.188] | |||||||
Model StSt (LL: (LL: 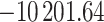 (s.e. 1.94), AIC: (s.e. 1.94), AIC: 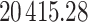 , coverage: 90.6% [only transmission model: 28.9%]) , coverage: 90.6% [only transmission model: 28.9%]) | |||||||
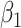
|
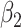
|
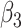
|
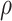
|
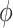
|
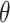
|
||
| MLE | 11.198 | 0.266 | 0.450 | 0.142 | 0.075 | 0.150 | |
| CI | [10.889, 11.326] | [0.267, 0.289] | [0.435, 0.474] | [0.138, 0.146] | [0.040, 0.109] | [0.143, 0.164] | |
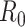 = 1.000 (0.981–1.031), seasonal range: [0.859, 1.142] = 1.000 (0.981–1.031), seasonal range: [0.859, 1.142] | |||||||
Model St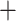 St St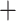 (LL: (LL: 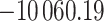 (s.e. 0.25), AIC: (s.e. 0.25), AIC: 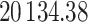 , coverage: 96.5% [only transmission model: 93.7%] ) , coverage: 96.5% [only transmission model: 93.7%] ) | |||||||
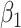
|
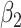
|
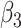
|
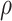
|
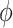
|
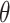
|
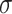
|
|
| MLE | 11.298 | 0.267 | 0.433 | 0.148 | 0.085 | 0.111 | 0.091 |
| CI | [11.131, 11.531] | [0.259, 0.278] | [0.415, 0.449] | [0.136, 0.158] | [0.006, 0.165] | [0.114, 0.127] | [0.080, 0.106] |
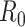 = 1.004 (0.986–1.027), seasonal range: [0.855, 1.152] = 1.004 (0.986–1.027), seasonal range: [0.855, 1.152] | |||||||
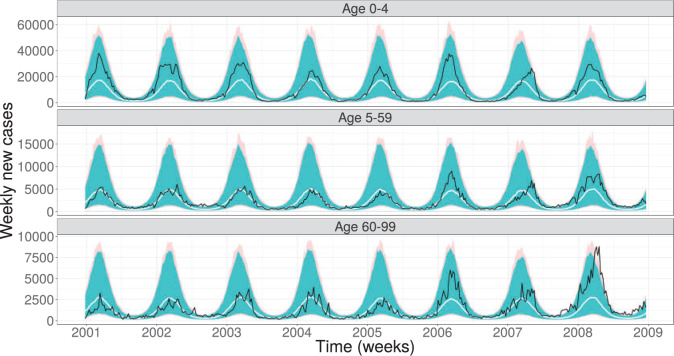
Fig. 3.
The 95% prediction interval (light shading) for 1000 realizations of Model St St
St evaluated at the maximum likelihood estimate for the rotavirus incidence data (solid back line) and the median (solid white line). Furthermore, the 95 % prediction interval of these 1000 realizations for only the transmission model is shown (darker shading).
evaluated at the maximum likelihood estimate for the rotavirus incidence data (solid back line) and the median (solid white line). Furthermore, the 95 % prediction interval of these 1000 realizations for only the transmission model is shown (darker shading).
6.1. Comparison with previous results
We find that Model St St
St explains the data very well, although the transmission component does not go into the same epidemiological detail as, e.g. the work of Atkins and others (2012) or Weidemann and others (2013). Since we analyzed the same data as in Weidemann and others (2013) with the only difference that we directly scaled the data for under-reporting, it is very insightful to compare the model fits in order to see if it is worthwhile to model disease transmission very detailed and to give recommendations to future modelers of what we consider important. In Weidemann and others (2013) a Bayesian model averaging approach was used to infer the parameters of 18 very detailed but deterministic transmission models with negative binomial distributed observations. The models included 19 age classes, three susceptibility states, maternal antibody protection, distinguishing between symptomatic and asymptomatic cases resulting in an overall number of 266 age-specific states. Moreover, the data was split into two data sets (former eastern federal states and western federal states) so a region specific analysis was carried out and time specific birth and migration rates between age classes were included. In order to compare the fit of this approach with our model on equal grounds we choose the model with the highest weight (Model 18) evaluated at the posterior mode of the fitted parameters, available at Weidemann (2017). The AIC we obtain is 20 479.2, hence, based on AIC this very complex model is competitive with Model StSt+ but is outperformed by Model St+St+ by approximately 300 AIC units. Note, that this is a conservative estimate, for details concerning the calculations, see Section E of the supplementary material available at Biostatistics online. Assuming that all region specific under-reporting rates were one (no decomposition of the expected number of incidences into the two regions) we then sampled the reported incidences according to a negative binomial observation distribution and calculated the 2.5% and 97.5% sample quantiles. The plot of these prediction intervals and the rotavirus data used in our analysis is shown in Figure E.8 in the supplementary material available at Biostatistics online. A coverage of 95.9% was obtained which is comparable to Models DtSt+ and St+St+. We conclude that a model which is simpler with respect to clinical detail in the disease transmission is sufficient in terms of fit to explain the rotavirus data as long as it accounts for overdispersion in both model components, for a discussion on this cf. Section 7.
explains the data very well, although the transmission component does not go into the same epidemiological detail as, e.g. the work of Atkins and others (2012) or Weidemann and others (2013). Since we analyzed the same data as in Weidemann and others (2013) with the only difference that we directly scaled the data for under-reporting, it is very insightful to compare the model fits in order to see if it is worthwhile to model disease transmission very detailed and to give recommendations to future modelers of what we consider important. In Weidemann and others (2013) a Bayesian model averaging approach was used to infer the parameters of 18 very detailed but deterministic transmission models with negative binomial distributed observations. The models included 19 age classes, three susceptibility states, maternal antibody protection, distinguishing between symptomatic and asymptomatic cases resulting in an overall number of 266 age-specific states. Moreover, the data was split into two data sets (former eastern federal states and western federal states) so a region specific analysis was carried out and time specific birth and migration rates between age classes were included. In order to compare the fit of this approach with our model on equal grounds we choose the model with the highest weight (Model 18) evaluated at the posterior mode of the fitted parameters, available at Weidemann (2017). The AIC we obtain is 20 479.2, hence, based on AIC this very complex model is competitive with Model StSt+ but is outperformed by Model St+St+ by approximately 300 AIC units. Note, that this is a conservative estimate, for details concerning the calculations, see Section E of the supplementary material available at Biostatistics online. Assuming that all region specific under-reporting rates were one (no decomposition of the expected number of incidences into the two regions) we then sampled the reported incidences according to a negative binomial observation distribution and calculated the 2.5% and 97.5% sample quantiles. The plot of these prediction intervals and the rotavirus data used in our analysis is shown in Figure E.8 in the supplementary material available at Biostatistics online. A coverage of 95.9% was obtained which is comparable to Models DtSt+ and St+St+. We conclude that a model which is simpler with respect to clinical detail in the disease transmission is sufficient in terms of fit to explain the rotavirus data as long as it accounts for overdispersion in both model components, for a discussion on this cf. Section 7.
7. Discussion
In this work, we demonstrated how an inference framework via iterated filtering can be applied to perform model selection and parameter estimation for POMP models in a statistical systematic way for German routine surveillance rotavirus data. We focused on the discrepancy between common epidemiological practice, which uses ODE models for large populations and more modern stochastic approaches, where statistical inference quickly becomes complicated. Furthermore, we demonstrated some practical difficulties when fitting those epidemic models to data, a task which has become increasingly important in the public health context. Although our model was focusing on rotavirus transmission in Germany, it could easily be modified to explain other infectious diseases which have comparable transmission characteristics. Based on AIC and coverage we found that for the specific data set, a POMP model which accounts for overdispersion in both the transmission model and the observational component performed best and, moreover, that the two noise components can be disentangled; He and others (2009) reached similar conclusions when modeling measles. Alternative model selection approaches would have been possible—see Gibson and others (2018) for a comprehensive overview and, e.g. Streftaris and Gibson (2012) and Lau and others (2014) for applications of such criterion for individual based epidemic models. Note also that AIC based on the marginal likelihood can have difficulties (Greven and Kneib, 2010; Gibson and others, 2018). For our 80 mio individuals model with count data response due to interval-censored observations, predictive scoring rules (Held and others, 2017) could circumvent these problems, but at the cost of many additional computations. Because simulation studies showed that AIC worked sufficiently well for our model selection setting (see Section D.2 of the supplementary material available at Biostatistics online), we did not pursue such strategies further. Throughout, we used a frequentist approach rather than a Bayesian setting for fitting the models. Bayesian approaches can be a natural choice in order to translate existing domain specific knowledge into prior distributions on unknown model parameters. However, as already stated in Bhadra (2010) and Gibson and others (2018) the choice of inference framework should be a pragmatic one and dependent on whether one wants to impose this prior knowledge on unknown parameters or not. Caution should be exercised as those prior assumptions could obscure the fact that the models reach a complexity which makes individual parameters hardly identifiable and consequently the prior plays a crucial, but sometimes unintended, role. From a technical perspective, the Bayesian analog of iterated filtering is particle MCMC, the simplest and most commonly used algorithm of which is the particle marginal Metropolis Hastings algorithm (PMMH) (Andrieu and others, 2010) also implemented in the pomp package. The conceptual difference between iterated filtering and PMMH is that iterated filtering explores simultaneously the parameter and state space in one iteration, while in PMMH in each iteration only a single noisy likelihood approximation for a parameter vector drawn at random from the proposal distribution is used (Ionides and others, 2015). Hence, for problems where filtering is a substantial computational expense, PMMH shows to perform much slower than mif2. For details, how those two methods fare against each other see Bhadra, 2010; Ionides and others, 2015. Although there exist approaches to make Bayesian inference algorithms for the class of dynamic models we consider computationally more efficient, cf. e.g. Dureau and others (2013); Murray and others (2016), the pomp package provides a convenient and flexible infrastructure for efficient simulation and a large variety of inference methods for POMP models. Using such flexible general purpose epidemic modeling software is of great interest for public health decision makers, and we hope to see such stochastic approaches in routine use of, e.g., assessing vaccination programs in the future.
The reduced complexity of our model came at the cost of neglecting some potentially important clinical details of rotavirus transmission. We did not consider maternal immunity, a latent period, premature death or immigration and we assumed that the waning immunity as well as the reporting rates, recovery rates and overdispersion parameters are age independent. Furthermore, we assumed that the population mixes homogeneously and that waiting times are exponentially distributed. The main reason for those simplifications was that the observations only carry information about time of diagnosis aggregated over one week which makes the separation of latent and infectious periods not identifiable as well as they do not contain information on how long people have been infected or who infected whom if we at the same time want to estimate the age-specific susceptibility parameters. If more was known about, e.g. age-specific recovery rates, we could have fixed the rates at those literature informed values and perform model selection, however, this data does to our knowledge not exist. Also, it would have been possible to add a latent period of known distribution, but since this would have been only be a two days shift, we decided to ignore this for simplification. To relax the homogeneously mixing assumption we could have assumed a “known” contact structure matrix as can, e.g. be obtained from the POLYMOD study (Mossong and others, 2008) and estimate the age-specific proportionality factors to this matrix, however, not the contact matrix itself. One option to enhance the exponential distribution could have been to divide the waiting period for a change in a certain compartment into several stages, yielding a gamma distribution, hence, a distribution with a more pronounced mode which is often more realistic. However, since the focus of this work was the demonstration of an inference and model selection framework we were aiming at a simple model.
In general, model complexity depends on which questions one wants to answer, e.g. more age classes or infectious states might be needed, if one was to assess vaccination strategies with our model. Nevertheless, we see from this work that, in terms of fit, simplicity has its virtues: adequate modeling of variability, can be more useful than trying to get every biological detail right, because even without this detail our model still fits the data very well. This is an important message to convey in practical public health modeling, because many transmission models tend to include overly many biological details in order to gain medical acceptance.
Supplementary Material
Acknowledgments
We thank A. A. King, F. Weidemann, N. Hens, K. Y. Leung, M. Sköld, and G. Kratzer for helpful input. Moreover, we thank three anonymous referees for constructive comments. The computations were performed on resources provided by the Swedish National Infrastructure for Computing at PDC Centre for High Performance Computing. Conflict of Interest: None declared.
Funding
This work was supported by the Swedish Research Council (2015_05182_VR for T.S. and M.H. and 2015_05015_VR for T.B.).
References
- Anderson, R. M. and May, R. M. (1991). Infectious Diseases of Humans: Dynamics and Control. Oxford: Oxford University Press. [Google Scholar]
- Andrieu, C., Doucet, A. and Holenstein, R. (2010). Particle Markov chain Monte Carlo methods. Journal of the Royal Statistical Society. Series B, Statistical Methodology 72, 269–342. [Google Scholar]
- Atkins, K. E., Shim, E., Pitzer, V. E. and Galvani, A. P. (2012). Impact of rotavirus vaccination on epidemiological dynamics in England and Wales. Vaccine 30, 552–564. [DOI] [PubMed] [Google Scholar]
- Bhadra, A. (2010). Discussion of particle Markov Chain Monte Carlo methods by C. Andrieu, A. Doucet and R. Holenstein. Journal of the Royal Statistical Society. Series B, Statistical Methodology 72, 314–315. [Google Scholar]
- Bhadra, A., Ionides, E. L., Laneri, K., Pascual, M., Bouma, M. and Dhiman, R. (2011). Malaria in northwest India: Data analysis via partially observed stochastic differential equation models driven by Lévy noise. Journal of the American Statistical Association 106, 440–451. [Google Scholar]
- Bretó, C., He, D., Ionides, E. L. and King, A. A. (2009). Time series analysis via mechanistic models. The Annals of Applied Statistics 3, 319–348. [Google Scholar]
- CDC. http://www.cdc.gov/rotavirus/about/index.html (accessed 2 October 2017). [Google Scholar]
- Diekmann, O., Heesterbeek, H. and Britton, T. (2013). Mathematical Tools for Understanding Infectious Disease Dynamics. Princeton: Princeton University Press. [Google Scholar]
- Doucet, A., de Freitas, N. and Gordon, N. (2001). Sequential Monte Carlo Methods in Practice. New York: Springer-Verlag. [Google Scholar]
- Dureau, J., Kalogeropoulos, K. and Baguelin, M. (2013). Capturing the time-varying drivers of an epidemic using stochastic dynamical systems. Biostatistics 14, 541–555. [DOI] [PubMed] [Google Scholar]
- Finkenstädt, B. F., Bjørnstad, O. N. and Grenfell, B. T. (2002). A stochastic model for extinction and recurrence of epidemics: estimation and inference for measles outbreaks. Biostatistics 3, 493–510. [DOI] [PubMed] [Google Scholar]
- Fuchs, C. (2013). Inference for Diffusion Processes. Berlin Heidelberg: Springer-Verlag. [Google Scholar]
- Gibson, G. J., Streftaris, G. and Thong, D. (2018). Comparison and assessment of epidemic models. Statistical Science 33, 19–33. [Google Scholar]
- Greven, S. and Kneib, T. (2010). On the behaviour of marginal and conditional AIC in linear mixed models. Biometrika 97, 773–789. [Google Scholar]
- Grimmwood, K. and Lambert, S. B. (2009). Rotavirus vaccines: opportunities and challenges. Human Vaccines 5, 57–69. [DOI] [PubMed] [Google Scholar]
- He, D., Ionides, E. L. and King, A. A. (2009). Plug-and-play inference for disease dynamic: measles in large and small populations as a case study. Journal of The Royal Society Interface 7, 271–283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Held, L., Hofmann, M., Höhle, M. and Schmid, V. (2006). A two-component model for counts of infectious diseases. Biostatistics 7, 422–437. [DOI] [PubMed] [Google Scholar]
- Held, L., Meyer, S. and Bracher, J. (2017). Probabilistic forecasting in infectious disease epidemiology: the 13th Armitage lecture. Statistics in Medicine 36, 3443–3460. [DOI] [PubMed] [Google Scholar]
- Held, L. and Sabanés Bové, D. (2013). Applied Statistical Inference. Berlin Heidelberg: Springer-Verlag. [Google Scholar]
- Ionides, E. L., Bretó, C., Park, J., Smith, R. A. and King, A. A. (2017). Monte Carlo profile confidence intervals for dynamic systems. Journal of The Royal Society Interface 14, 20170126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ionides, E. L., Nguyen, D., Atchadé, Y., Stoev, S. and King, A. A. (2015). Inference for dynamic and latent variable models via iterated, perturbed Bayes maps. Proceedings of the National Academy of Sciences of the United States of America 112, 719–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keeling, M. J. and Rohani, P. (2008). Modeling Infectious Diseases in Humans and Animals. Princeton: Princeton University Press. [Google Scholar]
- Kendall, B. E., Briggs, C. J., Murdoch, W. W., Turchin, P., Ellner, S. P., McCauley, E., Nisbet, R. M. and Wood, S. N. (1999). Why do populations cycle? A synthesis of statistical and mechanistic modeling approaches. Ecology 80, 1789–1805. [Google Scholar]
- King, A. A. and Ionides, E. L. (2017). Project pomp on github. http://kingaa.github.io/pomp/ (accessed 15 September 2017). [Google Scholar]
- King, A. A., Nguyen, D. and Ionides, E. L. (2016). Statistical inference for partially observed Markov processes via the R package pomp. Journal of Statistical Software 69, 1–43. [Google Scholar]
- Lau, M. S. Y., Marion, G., Streftaris, G. and Gibson, G. J. (2014). New model diagnostics for spatio-temporal systems in epidemiology and ecology. Journal of The Royal Society Interface 11, 20131093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martinez, P. P., King, A. A., Yunusd, M., Faruqued, A. S. G. and Pascual, M. (2016). Differential and enhanced response to climate forcing in diarrheal disease due to rotavirus across a megacity of the developing world. Proceedings of the National Academy of Sciences of the United States of America 113, 4092–4097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mossong, J., Hens, N., Jit, M., Beutels, P., Auranen, K., Mikolajczyk, R., Massari, M., Salmaso, S., Scalia Tomba, G., Wallinga, J.. and others (2008). Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Medicine 5, e74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray, L. M., Singh, S., Jacob, P. E. and Lee, A. (2016). Anytime Monte Carlo. https://arxiv.org/abs/1612.03319. [Google Scholar]
- RKI. Survstat. https://survstat.rki.de/ (accessed 2 October 2017).
- Statistisches Bundesamt. https://www.destatis.de (accessed 4 December 2016).
- Stocks, T. (2017a). Iterated filtering methods for Markov process epidemic models. https://arxiv.org/abs/1712.03058. [Google Scholar]
- Stocks, T. (2017b). Project pomp-astic on github. https://github.com/theresasophia/pomp-astic (accessed 2 October 2017). [Google Scholar]
- Streftaris, G. and Gibson, G. J. (2012). Non-exponential tolerance to infection in epidemic systemsmodeling, inference, and assessment. Biostatistics 13, 580–593. [DOI] [PubMed] [Google Scholar]
- Sugihara, G. and May, R. M. (1990). Nonlinear forecasting as a way of distinguishing chaos from measurement error in time series. Nature 344, 734–741. [DOI] [PubMed] [Google Scholar]
- Sun, L., Lee, C. and Hoeting, J. A. (2015). Parameter inference and model selection in deterministic and stochastic dynamical models via approximate Bayesian computation: modeling a wildlife epidemic. Environmetrics 26, 451–462. [Google Scholar]
- The World Bank (2016). http://data.worldbank.org/indicator/sp.dyn.le00.in?locations=de. [Google Scholar]
- Toni, T., Welch, D., Strelkowa, N., Ipsen, A. and Stumpf, M. P. (2009). Approximate Bayesian computation scheme for parameter inference and model selection in dynamical systems. Journal of The Royal Society Interface 6, 187–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weidemann, F. (2017). PhD project code on github. https://github.com/weidemannf/thesis_code (accessed 2 October 2017). [Google Scholar]
- Weidemann, F., Dehnert, M., Koch, J., Wichmann, O. and Höhle, M. (2013). Bayesian parameter inference for dynamic infectious disease modeling: rotavirus in Germany. Statistics in Medicine 33, 1580–1599. [DOI] [PubMed] [Google Scholar]
- Wood, S. N. (2010). Statistical inference for noisy nonlinear ecological dynamic systems. Nature 466, 1102–1104. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.