Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Mar 12;16(4):2795–2802. doi: 10.1021/acs.jctc.9b01104

Could Microwave Irradiation Cause Misfolding of Peptides?

Martin Gladovic †, Chris Oostenbrink ‡, Urban Bren †,§,*
PMCID: PMC7309322  PMID: 32163704

Abstract

graphic file with name ct9b01104_0005.jpg

Microwaves have been experimentally shown to affect the folding dynamics of peptides and proteins. Using molecular dynamics, we performed all-atom simulations of a model β-peptide in aqueous solution where individual degrees of freedom of solvent molecules were decoupled to allow for investigation at non-equilibrium microwave-irradiated conditions. An elevated rotational temperature of the water medium was found to significantly affect the conformation of the peptide due to the weakened hydrogen-bonding interactions with the surrounding solvent molecules. Cluster analysis revealed that microwave irradiation can indeed act as a promoter in the formation of new misfolded peptide structures of the hairpin type, which are generally associated with the onset of several neurodegenerative disorders such as Alzheimer’s, Parkinson’s, Huntington’s, and Creutzfeldt–Jakob diseases as well as certain cancer types such as amyloidosis.

Introduction

The tertiary structure of peptides and proteins in solution is a result of a competition between intramolecular torsional bending and nonbonding interactions, but interactions with the surrounding solvent also play an important role. Hydrogen bonds, disulfide bonds, and hydrophobic interactions all contribute to the delicate stability of the native folded structure. The thermal heating of peptides and proteins causes their structured chains to rapidly unfold and to form new, denatured conformations of the so-called random coil. It has been proposed that, apart from thermal heating, microwave (MW) irradiation can also alter the structural dynamics of biomacromolecular chains such as peptides, proteins, DNA, and RNA.1,2 Moreover, it could even lead to protein misfolding, association, and aggregation3—aberrant processes generally associated with the onset of neurodegenerative disorders such as Alzheimer’s, Parkinson’s, Huntington’s, and Creutzfeldt-Jacob’s diseases4−7 as well as with certain cancer types such as amyloidosis.8 However, experimental studies on the effects of MWs on proteins are difficult to perform in practice because of the rapid dissipation of increased rotational energy of polar species into remaining degrees of freedom via collisions with surrounding molecules.9 In addition, experiments can give little insight into the specific mechanisms that cause structural changes in the protein. On the other hand, in silico simulations can provide a useful alternative to study the non-equilibrium effects of MWs on the folding dynamics of peptides and proteins in solution.

In silico simulations of the effects of MWs on several prototypical chemical systems have already been performed. Bren et al. studied the catalytic effect of MWs on the neutral hydrolysis of the ester bond in methyl acetate. By performing a Monte Carlo simulation of the reaction with increased rotational temperatures of the reactants, they observed lowered activation free energies, signifying that MWs can indeed act as catalysts in chemical reactions.10 Later, they turned to study the effects of MWs on the solvation properties of water. An elevated rotational temperature of water molecules was found to severely hinder the hydration of polar molecules, to have a non-monotonous (ion-specific) effect on charged species, and to somewhat improve the hydration of nonpolar species.11 This has further implications on the hydration of proteins, which generally consist of different polar, nonpolar, and charged amino-acid residues. Mohorič et al. further studied the effect of MWs on the solvation properties of water. Using several popular water models, they performed molecular dynamics (MD) simulations of solutions of various cations, anions, polar molecules, and hydrophobic particles.12−15 Their results showed that upon MW irradiation, short hydrophobic chains can indeed collapse to more compact globular structures. Auerbach and co-workers16−18 provided convincing experimental evidence that in microwave-irradiated systems the rotational temperature may substantially exceed the translational one. Using quasielastic neutron scattering measurements under microwave irradiation, they (i) demonstrated the selective heating of methanol in silicalite and little to no heating of benzene in silicalite and (ii) determined the effective higher rotational and lower translational temperatures for the studied system.18 This experimental study justifies our approach to investigate the non-equilibrium microwave effects by using molecular dynamics with separate thermostats for translational and rotational motions. In the scientific literature one can also find a number of works in which the effects of microwaves are examined by non-equilibrium molecular dynamics with an explicitly included electric field of microwaves.19−21 Although it is difficult to directly compare the two approaches, they both result in the increase in kinetic energy due to the rotation of water molecules.19 The advantage of our approach lies in the clearer mechanistic picture at the molecular level, which allows even for analytical treatment of the resulting non-equilibrium microwave effects.22

In this study, we present the results of a MD simulation of structural dynamics of a model peptide23−25 in aqueous solution under MW irradiation. While this is a β-peptide whose structure was resolved with NMR in methanol, we chose it because it is one of the smallest model systems that shows reversible folding on easily accessible time scales, faster than biological peptides of similar length.26−29 We can consider continuous MW irradiation, a non-equilibrium situation where the excess rotational energy of polar molecules cannot dissipate into remaining degrees of freedom quickly enough. The resulting non-equilibrium state can therefore be described by a rotational temperature that is higher than the translational and vibrational temperature of the system.22 Such rotationally hot polar molecules were indeed observed to experience altered collision statistics under the influence of MW irradiation in an experimental setting18 and could in principle induce conformational changes of proteins.1 Due to the omnipresence of MW irradiation emitted as electromagnetic smog from mobile telephony, radars, satellites, wireless networks, microwave ovens, and GPS appliances, discerning their potential interactions with the molecules of life is of utmost importance.

Computational Methods

Nine 200 ns MD simulations of the β-heptapeptide with the sequence23−25 β-HVal-β-HAla-β-HLeu(S,S)-β-HAla(αMe)-β-HVal-β-HAla-β-HLeu in a solution of 2355 water molecules were performed in a (N,V,T) ensemble at different temperatures. These simulations were carried out using the GROMOS package of programs30 in conjunction with the GROMOS 43A1 united-atom force field31 and a GROMOS-compatible SPC water model.32 The equations of motion were integrated using the leapfrog scheme with a time step of 2 fs. The solute bond lengths were constrained by the application of the SHAKE algorithm33 using a relative geometric tolerance of 10–4, while the solvent bond lengths and angle were constrained using the SETTLE algorithm.34 The system was propagated under periodic boundary conditions based on a cubic simulation box. The volume of the box was adjusted so that the density of water molecules corresponded to 1 g/cm3. The GROMOS software allowed us to couple the translational degrees of freedom (dof) separately from the internal-rotational dof.35 The system employed three different heat baths: one for the solute’s dof and one for each of the rotational and translational dofs of the solvent. The SPC model water is a rigid molecule and therefore possesses no vibrational dofs. Using the weak-coupling thermostat36 the temperatures of all three baths were kept at 300, 400, 500, 600, or 700 K in the case of equilibrium simulations of conventional heating. In the case of non-equilibrium simulations of MW heating, only the temperature of the rotational dof of the solvent molecules was raised to 400, 500, 600, or 700 K, while the other two baths were kept at 300 K. To justify the applied temperature range, we refer to a previous study11 where the MW power of 361, 795, 1230, and 1730 W required to maintain 1 mol of water at a given elevated rotational temperature above its translational temperature of 300 K was estimated. Our selection therefore coincides well with the power of typical microwave reactors of around 1000 W.

To counter the natural phenomenon of energy dissipation in non-equilibrium simulations of condensed matter, two approaches can be taken: either the initial non-equilibrium temperature gradient is set to a somewhat higher value and the system is then pre-equilibrated to the final desired temperatures, or the simulations need to be performed with a relatively short relaxation time, τ. In our preliminary work, we found no significant differences in the peptide folding dynamics between simulations with a shorter τ and simulations with an increased rotational temperature to compensate the energy dissipation effects. Moreover, in our previous studies we have also shown that the short coupling time constants do not affect structural properties such as radial distribution functions,15 spectral properties such as calculated IR spectra,11 thermodynamic properties such as interaction energies or energy fluctuations being proportional to the square root of N,11,37 and dynamic properties such as hydrogen bond exchange.38 Therefore, to avoid the need for a complex adjusting of initial rotational temperature for each simulation, we chose to employ the approach with a shorter τ, which was set to 0.01 ps in all simulations. This albeit artificial separation of the degrees of freedom is one of the strengths of computational chemistry, which allows us the study of non-equilibrium systems at a molecular level.

Nonbonding interactions were calculated using a triple range scheme. Interactions within a short-range cutoff of 0.8 nm were calculated every step from a pair list that was updated every fifth step. At these points, interactions between 0.8 and 1.4 nm were also calculated and kept constant between the updates. A reaction field contribution was added to the electrostatic interactions, and it forces one to account for a homogeneous medium outside the long-range cutoff. System coordinates and energies were stored every 0.5 ps for further analysis. Clustering analysis was performed using the procedure previously described by Daura et al.39 Backbone (N, Cα, Cβ, C) atom positions from amino-acid residues 2–6 were compared every 5 ps and clustered using a cutoff root mean square deviation (RMSD) value of 0.1 nm. For each sampled trajectory structure, the number of structures (neighbors) with an RMSD below the cutoff value was determined. The structure with the highest number of structural neighbors was then taken as the central member of the cluster of similar structures forming a conformation. After removing the structures belonging to this first, most populated cluster from the pool of structures, the procedure was repeated to populate the second, third, and subsequent clusters. To ensure a statistically meaningful analysis of reversible peptide folding dynamics, we inspected the plots of backbone atom-positional RMSD values as a function of time and confirmed multiple transitions between the folded and unfolded states that occurred during the simulation time frame. A RMSD value of 0.1 nm from the reference structure was chosen as a cutoff between the folded and unfolded structures. Backbone atom-positional RMSD plots as a function of time for the simulations of the system at 300 K, thermal heating to 700 K, and MW heating to 700 K are included in Supporting Information Figures S1–S3.

Results and Discussion

To assess the effect of increased rotational temperature of the solvent on the properties of the peptide, we analyzed and compared the MD trajectories for the conventional and MW heating. Namely, we calculated the RMSD and RMSF values using the reference peptide structure obtained from NMR experiments,24,25 the intra- and intermolecular hydrogen bond statistics, head-to-tail distances, and radii of gyration and performed cluster analysis. These results are summarized in Table 1.

Table 1. Structural Parameters of the Peptide.

Tt/Tra (K/K) RMSDb (nm) RMSFc (nm) nHBPPd nHBPWe nHBWWf rgyrg (nm) H2Th (nm) ncl.5%i ncl.95%j
700/700 0.287 ± 0.001 0.29 ± 0.15 0.07 ± 0.03 9.43 ± 0.01 1.17 ± 0.04 0.599 ± 0.001 1.33 ± 0.01 0 2855
600/600 0.279 ± 0.002 0.28 ± 0.15 0.10 ± 0.04 9.90 ± 0.02 1.26 ± 0.05 0.599 ± 0.002 1.28 ± 0.01 0 1850
500/500 0.261 ± 0.002 0.28 ± 0.15 0.20 ± 0.07 10.40 ± 0.03 1.37 ± 0.05 0.561 ± 0.002 1.21 ± 0.01 0 742
400/400 0.243 ± 0.004 0.27 ± 0.14 0.36 ± 0.11 11.31 ± 0.04 1.52 ± 0.05 0.548 ± 0.002 1.16 ± 0.01 2 380
300/300 0.209 ± 0.008 0.24 ± 0.14 0.71 ± 0.14 12.38 ± 0.09 1.72 ± 0.06 0.526 ± 0.002 1.13 ± 0.02 4 80
300/400 0.203 ± 0.009 0.23 ± 0.13 0.84 ± 0.14 12.13 ± 0.10 1.61 ± 0.06 0.520 ± 0.002 1.11 ± 0.02 4 69
300/500 0.215 ± 0.010 0.25 ± 0.13 0.85 ± 0.16 11.85 ± 0.12 1.48 ± 0.08 0.520 ± 0.003 1.10 ± 0.02 5 72
300/600 0.186 ± 0.010 0.22 ± 0.12 1.25 ± 0.20 10.70 ± 0.11 1.35 ± 0.07 0.501 ± 0.002 1.04 ± 0.01 5 26
300/700 0.184 ± 0.012 0.22 ± 0.12 1.54 ± 0.22 10.09 ± 0.10 1.24 ± 0.07 0.493 ± 0.002 1.00 ± 0.02 5 26
Open in a new tab
a

Translational (Tt) and rotational (Tr) temperatures of the solvent during MD simulation.

b

Average trajectory root mean square deviation (RMSD) value compared to the experimentally determined peptide reference structure.24,25

c

Average trajectory root mean square fluctuations (RMSF) of the peptide backbone.

d

Average number of native structure-forming intrapeptide hydrogen bonds.

e

Average number of intermolecular hydrogen bonds between the peptide and water molecules.

f

Average number of intermolecular hydrogen bonds between the water molecules per molecule.

g

Average peptide radius of gyration.

h

Average head-to-tail distance of the peptide.

i

Number of peptide structural clusters that are stable for at least 5% of the simulation time.

j

Number of structural clusters that encompass 95% of the trajectory.

We can observe a clear correlation between conventional heating and the loss of secondary structure of the peptide. With increased equilibrium temperature, the RMSD value rises from 0.21 nm at room temperature (r.t.) to 0.29 nm at 700 K, indicating a gradual shift toward a more relaxed and flexible peptide backbone resembling the random-coil behavior. The fluctuations of individual peptide fragments also start to increase correspondingly, from 0.23 nm at r.t. to 0.29 nm at 700 K. Finally, due to the freely moving peptide, its radius of gyration increases as well, from 0.53 nm at r.t. to 0.60 nm at 700 K. The most likely molecular mechanism underlying the observed structural changes appears to be the increased kinetic energy of the peptide and solvent molecules, which gives rise to a decreased hydrogen bonding capacity under higher equilibrium temperatures. In fact, the network of intramolecular hydrogen bonds responsible for maintaining the native helical structure of the peptide dramatically weakens under conventional heating, from 0.71 hydrogen bond on average at r.t. to 0.07 hydrogen bond at 700 K, indicating an almost complete breakdown of the native structure. A hydrogen bond is throughout this work considered to be formed on a strictly geometric basis: if the distance between the hydrogen and acceptor atoms is less than 0.25 nm and the donor–hydrogen–acceptor angle is larger than 135°. The average number of intermolecular hydrogen bonds between the peptide and solvent molecules also decreases, from 12.38 at r.t. to 9.43 at 700 K. Furthermore, the hydrogen bond network between the solvent molecules is itself weakened under increased temperatures. On average, each water molecule forms 1.72 HB with the surrounding water molecules during the equilibrium simulation at 300 K. When the system is heated, this number gradually decreases and is just 1.17 in the system at 700 K. The cluster population analysis further confirms the random-coil nature of the peptide at higher equilibrium temperatures. At room temperature, we observe 4 stable structural clusters, surviving more than 5% of the total simulation time of 200 ns, and we can assign 95% of structures from the entire trajectory to just 80 different clusters. The number of stable clusters surviving more than 5% of the entire trajectory decreases to just 2 upon conventional heating of the system to 400 K, and at higher equilibrium temperatures we observe no such stable clusters. Moreover, at 700 K the number of clusters that represent 95% of all structures blows up to 2855.

The rotationally excited polar solvent molecules obtained under MW irradiation alter the structural properties of the peptide as well. Since the temperature of the peptide is kept at 300 K during these simulations and only the rotational temperature of the solvent is increased, the structural changes must be a consequence of the interactions between the peptide and solvent molecules. As was the case with conventional heating, the hydrogen bond network between the peptide and solvent indeed gets destabilized, although to a somewhat lesser extent. At an average of 10.09 hydrogen bonds at 700 K it is around 7% more stable than with equilibrium heating. On the other hand, the structure-stabilizing intramolecular hydrogen bond network of the peptide becomes significantly stronger at higher rotational temperatures, rising to an average of 1.54 hydrogen bond at 700 K. This is more than a 2-fold increase in stability over the peptide at r.t. and a 20-fold increase compared to conventional heating at the same temperature. As was the case with the thermal heating, the HB network inside the solvent is again destabilized at higher rotational temperatures. However, the average number of hydrogen bonds for a single water molecule at 700 K is now 1.24, which indicates around 6% weaker destabilization of the solvent structure than in comparison with equilibrium heating at identical temperature. This is also apparent from the analysis of the rotational correlation times of water molecules in the bulk solvent and in the first shell of solvent molecules surrounding the peptide. Panel A of Figure S4 compares the rotational relaxation times of bulk water, with conventional heating and under microwave irradiation. It can be seen that the conventional heating leads to shorter correlation times than microwave irradiation, which can be understood in the light of the additional disorder caused by the enhanced diffusion of water molecules at elevated translational temperatures. This pattern is maintained for the waters in the first solvation shell, where the rotational relaxation of water molecules is further delayed due to the presence of the peptide. This holds true for both conventional heating (panel B of Figure S4) and microwave irradiation (panel C of Figure S4).

The reinforced intramolecular hydrogen bond network of the peptide causes it to form a more rigid and compact structure. The superposition of peptide atoms over the entire time span of MD trajectories is displayed in Figure 1. For clarity, only the backbone atoms of amino-acid residues 2–6 are presented.

Figure 1.

Figure 1

Open in a new tab

Superpositions of peptide atoms over the entire time span of the trajectory (200 ns). Displayed are structures for simulations at 300 K (middle), conventional heating to 700 K (left), and microwave heating to 700 K (right). Tt/Tr are the translational (Tt) and rotational (Tr) temperatures during MD simulations.

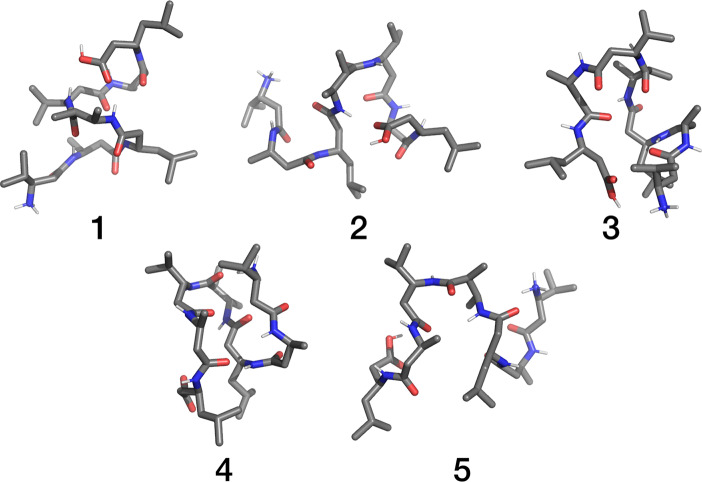
It can be clearly observed that the structure of the peptide is indeed more compact in the case of MW heating. At 700 K, its average RMSD value is 0.18 nm, a 14% decrease compared to r.t. and a 38% decrease compared to conventional heating. The peptide backbone fluctuations are also suppressed, to 0.22 nm at 700 K. This is an 8% decrease in comparison with r.t. and a 24% decrease in comparison with thermal heating. Similarly, due to the more compact peptide structure the radius of gyration decreases to 0.49 nm at 700 K, an 8% decrease compared with r.t. and an 18% decrease compared with equilibrium heating. In contrast to conventional heating, the cluster analysis shows a completely different picture with very few structural clusters even at the highest rotational temperatures. The central member structures of the most stable cluster for each simulation are provided in Supporting Information Figure S5 along with the relative lifetimes of the corresponding clusters in Supporting Information Table S1. In rotationally heated systems the most populated cluster represented between 17.7% (system at 500 K) and 32.0% (system at 600 K) of all structures in the trajectory. This is similar to the system at r.t., where the most populated cluster represented 20.6% of the trajectory, but in great contrast with the simulations of equilibrium heating, where the largest cluster’s population quickly drops from 9.6% at 400 K to just 1.1% of the trajectory at 700 K. In the system rotationally heated to 700 K only 26 clusters contain 95% of all structures. Moreover, from 500 K onward we observe a new stable cluster surviving more than 5% of the entire trajectory in addition to the original 4 at 300 K. This gives rise to the possibility of misfolding of peptides and proteins under the influence of MW irradiation. To confirm the misfolded nature of the structures at higher temperatures, we performed a combined clustering analysis40 of the trajectories at 300 K and MW heating to 700 K and evaluated the obtained central member structures and cluster population counts for the systems at the lower and higher rotational temperature. The population counts for the 10 most populated clusters are shown in Figure 2. The central member structures for the 5 most populated clusters are shown in Figure 3.

Figure 2.

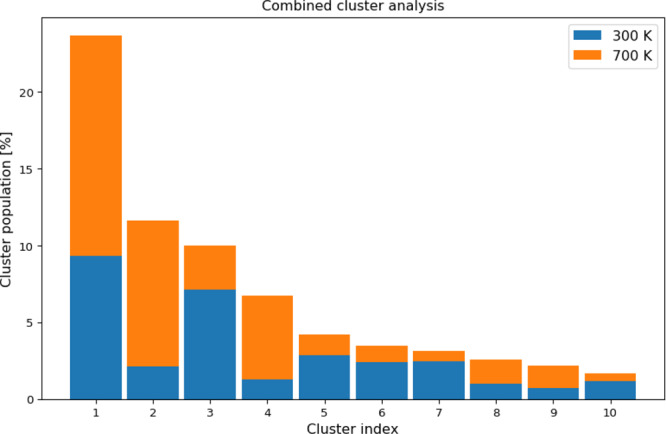
Figure 2

Open in a new tab

Clustering of the combined trajectories of the system at 300 K and rotationally heated to 700 K. The plot shows the population counts per cluster and the relative portion of structures per cluster that belong to the trajectory at lower (blue) or higher temperature (orange).

Figure 3.

Figure 3

Open in a new tab

Central members of the 5 most populated structural clusters obtained from the combined cluster analysis of the trajectories of the system at room temperature and rotationally heated to 700 K.

We observed no significantly populated clusters that were present exclusively during the room-temperature simulation or the simulation of MW heating to 700 K. However, there were some notable population shifts between the two trajectories. The most populated cluster, which encompasses almost a quarter of all structures throughout the simulation, closely resembles the experimentally determined β-helical structure. It is almost equally populated at both the lower and higher temperatures. On the contrary, the subsequent central member structures all represent either an unfolded random coil or several variants of misfolded structures. Of particular interest are clusters 2 and 4, which are mostly populated at the higher rotational temperature. Cluster 2 represents a partially folded hairpin structure, which is generally associated with fibrillation and formation of insoluble aggregates. This could have implications on the role of MWs in the etiology as well as in the design of alternative treatments of amyloid diseases.41 Clusters 3 and 5, which are somewhat less common at higher temperature, represent differently unfolded structures. In contrast, cluster 4 resembles an even more organized β-sheet structure, which is a lot less common at room temperature.

We can gain additional insight in the secondary structure of the obtained clusters by analyzing the peptide’s intramolecular hydrogen bonds. Of the 5 clusters presented in Figure 3, only cluster 1 exhibits a significant occupancy of all 5 helix-forming hydrogen bonds. In this cluster the weakest helix-forming hydrogen bond (HB1–3) was present in 6.9% of the trajectory snapshots, while the strongest was present in 86.1% of the snapshots (HB3–5). Already in cluster 2 we see a shift toward a different secondary structure, where the only helix-forming hydrogen bonds present in a significant amount of snapshots were HB1–3, HB4–6, and HB5–7. Clusters 3–5 exhibit a completely different hydrogen bond occupancy where a single helix-forming bond is present. Cluster 4 is particularly interesting because it shows a relatively strong network of hydrogen bonds, indicating a fairly stable secondary structure. Detailed results of the hydrogen bond analysis are summarized in Supporting Information Table S2.

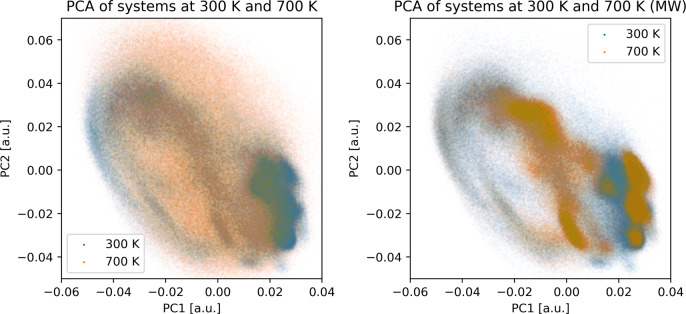
To corroborate on our findings about the newly found misfolded structural clusters, we have also performed a principal component analysis (PCA) of the combined trajectories of all 9 simulations. The comparison of the PCA results for the systems at 700 K with the simulation at 300 K as a reference is presented in Figure 4 as 2D scatter plots with the two principal components of the peptide backbone coordinates (identical atoms were considered as in the RMSD analysis; see Computational Methods). Analogous plots for the systems at 400, 500, and 600 K are also provided in Supporting Information Figure S6.

Figure 4.

Figure 4

Open in a new tab

Principal component analysis of the combined clustering of systems at equilibrium temperature of 300 K, conventionally heated to 700 K and MW heated to 700 K. The first and second principal components form the x and y axes of the scatter plots, respectively. On each plot, the trajectory at equilibrium 300 K is depicted with blue dots and the trajectory at an elevated temperature is depicted with orange dots.

The PCA shows that with conventional heating an increasing amount of unstructured conformations is observed from 400 K onward, which can be seen in the plots as a gradual and ultimately complete loss of correlation between the two principal components and the data points assuming a uniform cloud distribution. In the system conventionally heated to 700 K it is clear that there is virtually no correlation between the two components, indicating a completely disorganized structure of the peptide. In contrast, for the microwave heating the conformational distribution in the PCA plots remains largely unchanged with increasing rotational temperature, albeit with certain shifts in the conformational preferences. Even the plots for the systems at the equilibrium 300 K and rotationally heated to 700 K remain quite similar to several overlapping regions. However, there are some distinct regions where we see no population at 300 K but a significant population in the MW-irradiated system, indeed indicating newly formed misfolded structures. The cluster analysis thus confirmed the possibility of peptide misfolding under the influence of MWs.

To obtain a clearer picture of the solvent behavior in the vicinity of the β-peptide, we also analyzed the radial distributions of water molecules in the first hydration shell and compared them to the data of the bulk solvent. The corresponding radial distribution functions are provided in the Supporting Information Figure S7. We observe that the local density of water molecules in the hydration shell is reduced when compared to bulk, which follows from the simple fact that a part of the space surrounding these water molecules is occupied by the peptide. Furthermore, we observe an interesting behavior that with increasing temperatures the second solvation shell gets converted into a region of lower water density, while the subsequent region of lower water density becomes more densely occupied. This is seen for both thermal and microwave heating, but seems to be a more gradual process in the case of microwave irradiation. Similar behavior was previously reported for simulations of pure water.11

To shed light on the driving forces of the observed structural changes, we have analyzed the individual contributions to the intramolecular nonbonding energy of the peptide and also to the interactions between the peptide and solvent molecules. Resulting interaction energies are summarized in Table 2.

Table 2. Peptide–Peptide and Peptide–Water Interaction Energies.

Tt/Tra (K/K) EvdWPPb (kcal/mol) EesPPc (kcal/mol) EtotPPd (kcal/mol) EvdWPWe (kcal/mol) EesPWf (kcal/mol) EtotPWg (kcal/mol)
700/700 –51 ± 1 –510 ± 2 –561 ± 1 –151 ± 1 –572 ± 2 –723 ± 2
600/600 –62 ± 1 –513 ± 2 –575 ± 1 –165 ± 1 –589 ± 2 –753 ± 2
500/500 –80 ± 1 –517 ± 3 –597 ± 3 –175 ± 1 –600 ± 4 –775 ± 5
400/400 –97 ± 1 –508 ± 1 –605 ± 1 –184 ± 1 –640 ± 2 –824 ± 2
300/300 –114 ± 1 –518 ± 3 –632 ± 3 –192 ± 1 –656 ± 5 –848 ± 5
300/400 –114 ± 1 –528 ± 3 –642 ± 3 –194 ± 1 –639 ± 5 –833 ± 5
300/500 –114 ± 1 –529 ± 4 –642 ± 4 –194 ± 1 –632 ± 8 –826 ± 8
300/600 –114 ± 1 –555 ± 4 –669 ± 4 –194 ± 1 –574 ± 7 –768 ± 7
300/700 –114 ± 1 –568 ± 4 –682 ± 4 –195 ± 1 –538 ± 7 –732 ± 7
Open in a new tab
a

Translational (Tt) and rotational (Tr) temperatures of the solvent during simulation.

b

Intramolecular peptide interaction energy—van der Waals contribution.

c

Intramolecular peptide interaction energy—electrostatic contribution.

d

Total intramolecular peptide interaction energy.

e

Peptide–water interaction energy—van der Waals contribution.

f

Peptide–water interaction energy—electrostatic contribution.

g

Total peptide–water interaction energy.

The nonbonding energy analysis coincides with the findings of other similar studies of small designed proteins such as chignolin,42−44 which concluded that intramolecular interactions predominantly stabilize compact conformations, whereas solvent-induced interactions destabilize them. Under conventional heating, the total intramolecular nonbonding energy of the peptide increases by 71 kJ/mol when the equilibrium temperature is raised from 300 to 700 K, signifying weakened interactions within the molecule. The largest contribution to this change is due to weakened van der Waals interactions (63 kJ/mol), while the electrostatic interactions (predominantly responsible for the formation of hydrogen bonds) diminish only slightly (8 kJ/mol). At the same time, the interactions between the peptide and solvent are also weakened with an energy difference of 125 kJ/mol. Here both van der Waals and electrostatic interactions contribute significantly with 41 and 84 kJ/mol, respectively. This suggests that the change in the structural arrangement of the solvent around a peptide plays a significant role in determining the stability, rigidity, and mobility of the peptide. When the rotational temperature of the solvent was increased to 700 K under MW heating, the effect on total interaction energy between the peptide and solvent is roughly the same as with conventional heating, increasing it for 116 kJ/mol, indicating that the interactions with the solvent are significantly weakened. However, in this case almost the entire change is due to the weakened electrostatic interactions (118 kJ/mol), signifying a pronounced breakdown of the hydrogen bond network between the peptide and the surrounding solvent molecules. On the contrary, the intramolecular nonbonding interactions within the peptide have strengthened, yielding a 50 kJ/mol lower energy. This change originates almost exclusively from electrostatic interactions through the reinforcement of the intramolecular hydrogen bonds.

Conclusions

Our MD study reveals that continuous microwave irradiation through rotationally hot polar water molecules affects the conformational preferences of a small helical β-peptide. Where conventional heating leads to a complete loss of structure, the effects of microwave heating are more subtle and can be identified as a shift in conformational preferences. The rotationally heated water molecules form fewer hydrogen bonds with the peptide, consequently allowing it to maintain the intramolecular interactions leading to stable compact conformations. These changes result not only in a decreased mobility and increased compactness of natively folded structures but also lead to the formation of new, misfolded structures not present when the solution is heated conventionally. This suggests that MW irradiation could act as a promoter of peptide and protein misfolding, which is tied to the onset of several neurodegenerative disorders such as Alzheimer’s disease,4−7 Parkinson’s disease,4,5 and Huntington’s chorea,5 but also Type 2 diabetes.6 Preliminary results of a recent large-scale study have also linked MWs to several types of cancer in male rats.45 Albeit we have studied the structural dynamics of a single helical β-peptide in solution, the findings shed some light also on the general nature of peptide and protein folding. The natural next step of our research would be increasing the simulation scale to several differently folded peptides to investigate the effect of MWs on their association and aggregation.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.9b01104.

  • Backbone atom-positional RMSD plots; central member structures; relative lifetimes; additional PCA plots; radial distribution function plots; correllograms of the rotational relaxation times; relative occurrences of peptide intramolecular hydrogen bonds (PDF)

Financial support through Slovenian Research Agency Project Grant J1-6736 and Slovenian Ministry of Education, Science and Sports research program grants F4F and AB FREE is gratefully acknowledged.

The authors declare no competing financial interest.

Supplementary Material

ct9b01104_si_001.pdf (11MB, pdf)

References

  1. Bohr H.; Bohr J. Microwave-enhanced folding and denaturation of globular proteins. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 2000, 61, 4310–4314. 10.1103/PhysRevE.61.4310. [DOI] [PubMed] [Google Scholar]
  2. Edwards W. F.; Young D. D.; Deiters A. The effect of microwave irradiation on DNA hybridization.. Org. Biomol. Chem. 2009, 7, 2506–8. 10.1039/b903609a. [DOI] [PubMed] [Google Scholar]
  3. De Pomerai D. I.; Smith B.; Dawe A.; North K.; Smith T.; Archer D. B.; Duce I. R.; Jones D.; Candido E. P. M. Microwave radiation can alter protein conformation without bulk heating. FEBS Lett. 2003, 543, 93–97. 10.1016/S0014-5793(03)00413-7. [DOI] [PubMed] [Google Scholar]
  4. Irvine G. B.; El-Agnaf O. M.; Shankar G. M.; Walsh D. M. Protein aggregation in the brain: the molecular basis for Alzheimer’s and Parkinson’s diseases. Mol. Med. 2008, 14, 451–464. 10.2119/2007-00100.Irvine. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Olzscha H.; Schermann S. M.; Woerner A. C.; Pinkert S.; Hecht M. H.; Tartaglia G. G.; Vendruscolo M.; Hayer-Hartl M.; Hartl F. U.; Vabulas R. M. Amyloid-like aggregates sequester numerous metastable proteins with essential cellular functions. Cell 2011, 144, 67–78. 10.1016/j.cell.2010.11.050. [DOI] [PubMed] [Google Scholar]
  6. Ashraf G. M.; Greig N. H.; Khan T. A.; Hassan I.; Tabrez S.; Shakil S.; Sheikh I. A.; Zaidi S. K.; Akram M.; Jabir N. R.; Firoz C. K.; Naeem A.; Alhazza I. M.; Damanhouri G. A.; Kamal M. A. Protein misfolding and aggregation in Alzheimer’s disease and type 2 diabetes mellitus. CNS Neurol. Disord.: Drug Targets 2014, 13, 1280–1293. 10.2174/1871527313666140917095514. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Jouanne M.; Rault S.; Voisin-Chiret A. S. Tau protein aggregation in Alzheimer’s disease: An attractive target for the development of novel therapeutic agents. Eur. J. Med. Chem. 2017, 139, 153–167. 10.1016/j.ejmech.2017.07.070. [DOI] [PubMed] [Google Scholar]
  8. Chiti F.; Dobson C. M. Protein Misfolding, Amyloid Formation, and Human Disease: A Summary of Progress Over the Last Decade. Annu. Rev. Biochem. 2017, 86, 27–68. 10.1146/annurev-biochem-061516-045115. [DOI] [PubMed] [Google Scholar]
  9. Young D. D.; Nichols J.; Kelly R. M.; Deiters A. Microwave activation of enzymatic catalysis. J. Am. Chem. Soc. 2008, 130, 10048–10049. 10.1021/ja802404g. [DOI] [PubMed] [Google Scholar]
  10. Bren U.; Kržan A.; Mavri J. Microwave catalysis through rotationally hot reactive species. J. Phys. Chem. A 2008, 112, 166–171. 10.1021/jp709766c. [DOI] [PubMed] [Google Scholar]
  11. Bren U.; Janežič D. Individual degrees of freedom and the solvation properties of water. J. Chem. Phys. 2012, 137, 024108 10.1063/1.4732514. [DOI] [PubMed] [Google Scholar]
  12. Mohorič T.; Bren U.; Vlachy V. Effects of translational and rotational degrees of freedom on the hydration of ionic solutes as seen by the popular water models. Acta Chim. Slov. 2015, 62, 489–497. 10.17344/acsi.2014.1291. [DOI] [PubMed] [Google Scholar]
  13. Mohorič T.; Bren U.; Vlachy V. Fast rotational motion of water molecules increases ordering of hydrophobes in solutions and may cause hydrophobic chains to collapse. J. Chem. Phys. 2015, 143, 244510. 10.1063/1.4939085. [DOI] [PubMed] [Google Scholar]
  14. Mohorič T.; Bren U. Microwave irradiation affects ion pairing in aqueous solutions of alkali halide salts. J. Chem. Phys. 2017, 146, 044504 10.1063/1.4974759. [DOI] [PubMed] [Google Scholar]
  15. Mohorič T.; Bren U. How does microwave irradiation affect aqueous solutions of polar solutes?. J. Mol. Liq. 2018, 266, 218–228. 10.1016/j.molliq.2018.06.051. [DOI] [Google Scholar]
  16. Blanco C.; Auerbach S. M. Microwave-Driven Zeolite-Guest Systems Show Athermal Effects from Nonequilibrium Molecular Dynamics. J. Am. Chem. Soc. 2002, 124, 6250–6251. 10.1021/ja017839e. [DOI] [PubMed] [Google Scholar]
  17. Blanco C.; Auerbach S. M. Nonequilibrium Molecular Dynamics of Microwave-Driven Zeolite-Guest Systems: Loading Dependence of Athermal Effects. J. Phys. Chem. B 2003, 107, 2490–2499. 10.1021/jp026959l. [DOI] [PubMed] [Google Scholar]
  18. Jobic H.; Santander J. E.; Conner W. C.; Wittaker G.; Giriat G.; Harrison A.; Ollivier J.; Auerbach S. M. Experimental Evidence of Selective Heating of Molecules Adsorbed in Nanopores under Microwave Radiation. Phys. Rev. Lett. 2011, 106, 157401. 10.1103/PhysRevLett.106.157401. [DOI] [PubMed] [Google Scholar]
  19. English N. J.; MacElroy J. M. D. Molecular dynamics simulations of microwave heating of water. J. Chem. Phys. 2003, 118, 1589–1592. 10.1063/1.1538595. [DOI] [Google Scholar]
  20. Lutsko J. F. A dynamical theory of nucleation for colloids and macromolecules. J. Chem. Phys. 2012, 136, 034509 10.1063/1.3677191. [DOI] [PubMed] [Google Scholar]
  21. English N. J.; Mooney D. A. Denaturation of hen egg white lysozyme in electromagnetic fields: A molecular dynamics study. J. Chem. Phys. 2007, 126, 091105 10.1063/1.2515315. [DOI] [PubMed] [Google Scholar]
  22. Bren M.; Janežič D.; Bren U. Microwave catalysis revisited: an analytical solution. J. Phys. Chem. A 2010, 114, 4197–4202. 10.1021/jp100374x. [DOI] [PubMed] [Google Scholar]
  23. Daura X.; van Gunsteren W. F.; Rigo D.; Jaun B.; Seebach D. Studying the stability of a helical b-heptapeptide by molecular dynamics simulations. Chem. - Eur. J. 1997, 3, 1410–1417. 10.1002/chem.19970030907. [DOI] [Google Scholar]
  24. Seebach D.; Ciceri P. E.; Overhand M.; Jaun B.; Rigo D.; Oberer L.; Hommel U.; Amstutz R.; Widmer H. Probing the Helical Secondary Structure of Short-Chain β-Peptides. Helv. Chim. Acta 1996, 79, 2043–2066. 10.1002/hlca.19960790802. [DOI] [Google Scholar]
  25. Seebach D.; Overhand M.; Kühnle F. N. M.; Martinoni B.; Oberer L.; Hommel U.; Widmer H. β-Peptides: Synthesis by Arndt-Eistert homologation with concomitant peptide coupling. Structure determination by NMR and CD spectroscopy and by X-ray crystallography. Helical secondary structure of a β-hexapeptide in solution and its stability towards pe. Helv. Chim. Acta 1996, 79, 913–941. 10.1002/hlca.19960790402. [DOI] [Google Scholar]
  26. Daura X.; Jaun B.; Seebach D.; van Gunsteren W. F.; Mark A. E. Reversible peptide folding in solution by molecular dynamics simulation. J. Mol. Biol. 1998, 280, 925–932. 10.1006/jmbi.1998.1885. [DOI] [PubMed] [Google Scholar]
  27. van Gunsteren W. F.; Bürgi R.; Peter C.; Daura X. The Key to Solving the Protein-Folding Problem Lies in an Accurate Description of the Denatured State. Angew. Chem., Int. Ed. 2001, 40, 351–355. . [DOI] [PubMed] [Google Scholar]
  28. van Gunsteren W. F.; Bakowies D.; Baron R.; Chandrasekhar I.; Christen M.; Daura X.; Gee P.; Geerke D. P.; Glättli A.; Hünenberger P. H.; Kastenholz M. A.; Oostenbrink C.; Schenk M.; Trzesniak D.; van der Vegt N. F. A.; Yu H. B. Biomolecular Modeling: Goals, Problems, Perspectives. Angew. Chem., Int. Ed. 2006, 45, 4064–4092. 10.1002/anie.200502655. [DOI] [PubMed] [Google Scholar]
  29. Seebach D.; Hook D. F.; Glättli A. Helices and other secondary structures of β- and γ-peptides. Biopolymers 2006, 84, 23–37. 10.1002/bip.20391. [DOI] [PubMed] [Google Scholar]
  30. Eichenberger A. P.; Allison J. R.; Dolenc J.; Geerke D. P.; Horta B. A.; Meier K.; Oostenbrink C.; Schmid N.; Steiner D.; Wang D.; Van Gunsteren W. F. GROMOS++ software for the analysis of biomolecular simulation trajectories. J. Chem. Theory Comput. 2011, 7, 3379–3390. 10.1021/ct2003622. [DOI] [PubMed] [Google Scholar]
  31. van Gunsteren W. F.; Billeter S. R.; Eising A. A.; Hünenberger P. H.; Krüger P.; Mark A. E.; Scott W. R. P.; Tironi I. G.. Biomolecular Simulation: The GROMOS96 Manual and User Guide; Vdf Hochschulverlag AG, 1996; pp 1–1042. [Google Scholar]
  32. Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; Hermans J. In Intermol. Forces; Pullman B., Ed.; D. Reidel, 1981; pp 331–342. [Google Scholar]
  33. Ryckaert J.-P.; Ciccotti G.; Berendsen H. J. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. 10.1016/0021-9991(77)90098-5. [DOI] [Google Scholar]
  34. Miyamoto S.; Kollman P. A. Settle: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992, 13, 952–962. 10.1002/jcc.540130805. [DOI] [Google Scholar]
  35. Christen M.; Hünenberger P. H.; Bakowies D.; Baron R.; Bürgi R.; Geerke D. P.; Heinz T. N.; Kastenholz M. A.; Kräutler V.; Oostenbrink C.; Peter C.; Trzesniak D.; van Gunsteren W. F. The GROMOS software for biomolecular simulation: GROMOS05. J. Comput. Chem. 2005, 26, 1719–1751. 10.1002/jcc.20303. [DOI] [PubMed] [Google Scholar]
  36. Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; DiNola A.; Haak J. R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
  37. Mohorič T.; Hribar-Lee B.; Vlachy V. Effects of the translational and rotational degrees of freedom on the hydration of simple solutes. J. Chem. Phys. 2014, 140, 184510. 10.1063/1.4875280. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Mohorič T.; Bren U. How does microwave irradiation affect the mechanism of water reorientation?. J. Mol. Liq. 2020, 302, 112522. 10.1016/j.molliq.2020.112522. [DOI] [Google Scholar]
  39. Daura X.; van Gunsteren W. F.; Mark A. E. Foldingunfolding thermodynamics of a β-heptapeptide from equilibrium simulations. Proteins: Struct., Funct., Genet. 1999, 34, 269–280. . [DOI] [PubMed] [Google Scholar]
  40. Glättli A.; Daura X.; Seebach D.; van Gunsteren W. F. Can One Derive the Conformational Preference of a β-Peptide from Its CD Spectrum?. J. Am. Chem. Soc. 2002, 124, 12972–12978. 10.1021/ja020758d. [DOI] [PubMed] [Google Scholar]
  41. Todorova N.; Bentvelzen A.; English N. J.; Yarovsky I. Electromagnetic-field effects on structure and dynamics of amyloidogenic peptides. J. Chem. Phys. 2016, 144, 085101. 10.1063/1.4941108. [DOI] [PubMed] [Google Scholar]
  42. Pace C. N. Polar Group Burial Contributes More to Protein Stability than Nonpolar Group Burial. Biochemistry 2001, 40, 310–313. 10.1021/bi001574j. [DOI] [PubMed] [Google Scholar]
  43. Pace C. N.; Fu H.; Fryar K. L.; Landua J.; Trevino S. R.; Shirley B. A.; Hendricks M. M.; Iimura S.; Gajiwala K.; Scholtz J. M.; Grimsley G. R. Contribution of Hydrophobic Interactions to Protein Stability. J. Mol. Biol. 2011, 408, 514–528. 10.1016/j.jmb.2011.02.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Sumi T.; Koga K. Theoretical analysis on thermodynamic stability of chignolin. Sci. Rep. 2019, 9, 5186. 10.1038/s41598-019-41518-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Wyde M.; Cesta M.; Blystone C.; Elmore S.; Foster P.; Hooth M.; Kissling G.; Malarkey D.; Sills R.; Stout M.; Walker N.; Witt K.; Wolfe M.; Bucher J. Report of Partial findings from the National Toxicology Program Carcinogenesis Studies of Cell Phone Radiofrequency Radiation in Hsd: Sprague Dawley® SD rats (Whole Body Exposure). bioRxiv 2018, 055699 10.1101/055699. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ct9b01104_si_001.pdf (11MB, pdf)

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES