Simultaneous confidence corridors for mean functions in functional data analysis of imaging data

Abstract

Motivated by recent work involving the analysis of biomedical imaging data, we present a novel procedure for constructing simultaneous confidence corridors for the mean of imaging data. We propose to use flexible bivariate splines over triangulations to handle an irregular domain of the images that is common in brain imaging studies and in other biomedical imaging applications. The proposed spline estimators of the mean functions are shown to be consistent and asymptotically normal under some regularity conditions. We also provide a computationally efficient estimator of the covariance function and derive its uniform consistency. The procedure is also extended to the two-sample case in which we focus on comparing the mean functions from two populations of imaging data. Through Monte Carlo simulation studies, we examine the finite sample performance of the proposed method. Finally, the proposed method is applied to analyze brain positron emission tomography data in two different studies. One data set used in preparation of this article was obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database.

1 |. INTRODUCTION

In recent years, as digital technology advanced significantly, valuable imaging data of body structures and organs can be easily collected during routine clinical practice. This new paradigm presents new opportunities to innovate in both research and clinical settings. Medical imaging technology has revolutionized health care over the past three decades, allowing doctors to find or detect tumors and other abnormalities and evaluate the effectiveness of treatment. Functional data analysis (FDA) provides modern analytical tools for imaging data, which can be viewed as realizations of random functions. Let Ω be a two-dimensional bounded domain, and z = (z₁, z₂) be a point in Ω. The model we consider is

$$Y_i(\mathit{z})=\mu (\mathit{z})+{\eta }_i(\mathit{z})+\sigma (\mathit{z}){\epsilon }_i(\mathit{z}),i=1,\dots ,n,\mathit{z}\in \mathrm{\Omega },$$ (1)

which is one instance of the general function-on-scalar regression model. In model (1), Y_i (z) denotes the imaging measurement at location z ∈ Ω; η_i (z) is a stochastic process indexed by z, which characterizes subject-level image variations; and σ (z) is a positive deterministic function. We assume that η_i (z) and ε_i (z) are mutually independent, η_i (z) are i.i.d. copies of a L₂ stochastic process η(z) with mean zero and covariance function G_η(z, z′), ε_i (z) are i.i.d. instances of a stochastic process of ε(z) with mean zero, and covariance function Cov{ε(z), ε(z′)} = I (z = z′).

For biomedical imaging data, the objects (eg, tumor tissues, brain regions, etc) appearing in the images are typically irregularly shaped. Many smoothing methods in the literature, such as tensor product smoothing, kernel smoothing, and wavelet smoothing, suffer from the problem of “leakage” across the complex domains, that is, poor estimation over difficult regions as a result of smoothing inappropriately across boundaries of features.

In this article, we endeavor to address these challenges by applying bivariate splines over triangulations (Lai and Wang, 2013) to preserve important features (shape, smoothness) of imaging data. Spline functions defined this way offer more flexibility and varying amounts of smoothness, allowing us to better approximate the mean functions. We study the asymptotic properties of the spline estimators of μ(z) by using bivariate penalized splines (BPS) defined on triangulations and show that our estimator is consistent and asymptotically normal.

In addition, when analyzing biomedical imaging data, such as brain images, typical questions lie in estimating the mean function, μ(z), together with quantifying the estimation uncertainty and making comparisons between populations. However, making a statistically rigorous inference for imaging data is challenging, and one of the main obstacles is the complicated spatial correlation structure. The prevailing analytic technique, termed the “mass univariate” approach, involves regarding each pixel/voxel as a unit, and for each unit, making a traditional univariate statistical inference, such as a simple t test. The obvious multiple comparisons issue can be dealt with in many ways; popular approaches include the Bonferroni correction, the random field theory (Worsley et al., 2004; Adler and Taylor, 2007; Siegmund et al., 2011), and the cluster threshold-based approach (Forman et al., 1995).

However, many of the multiple testing methods are ad hoc methods, which involve setting the threshold by eye, based on the practitioner’s experience and knowledge. Our simulation study in Supporting Information Appendix A also demonstrates that those ad hoc methods heavily depend on the choice of the threshold. In this article, we propose an alternative approach that treats the imaging data as an instance of functional data, regarded as being continuously defined but observed on a regular grid. If we consider the imaging data as being functional, attention naturally turns from considering each pixel/voxel as the basic analytical unit toward analyzing the entire image simultaneous, for instance, calculating simultaneous confidence corridors (SCCs; also called “simultaneous confidence bands” or “uniform confidence band/region”). As pointed out in Choi and Reimherr (2018) and Degras (2017), conventional multiple comparison methods are less useful in the functional data setup because the infinite cardinality of the domain would lead to unbounded confidence regions.

In statistics, SCCs are vital and fundamental tools for inference on the global behavior of functions (Degras, 2017). However, they have received relatively little attention in the literature of FDA. Moreover, existing SCC work for FDA has concentrated on the one-dimensional case. For the development of SCCs for mean curves of functional data, see the simulation-based techniques (Degras, 2011; Cao et al., 2012; Zheng et al., 2014; Cao and Wang, 2018), the functional principal component (FPC) decomposition-based approach (Goldsmith et al., 2013), and the geometric approach by Choi and Reimherr (2018) in Hilbert spaces. Zhu et al. (2012) proposed SCCs for the regression coefficient functions for multivariate varying coefficient model for functional responses. Gu et al. (2014) and Chang et al. (2017) proposed the SCC for coefficient functions in the function-on-scalar regression model. However, there is scant literature on SCCs for imaging data or other more general two-dimensional (2D) functions. Although the geometric method in Choi and Reimherr (2018) can be used to construct SCCs in Hilbert spaces over rectangular domains, it doesn’t work well for objects over complex domains with arbitrary shape, which are very common in biomedical imaging studies. In addition, the geometric method is conservative because it is essentially based on a modification of Scheffé’s method.

In this article, we derive SCCs with exact coverage probability for the 2D functional mean function μ(z), z ∈ Ω, in (1) via the extreme value theory of Gaussian processes (Adler, 1990) and approximating mean functions with bivariate splines. Our simulation studies indicate that the proposed SCCs are computationally efficient and have the correct coverage probability for finite samples. We also show that the spline estimator and the accompanying SCC are asymptotically the same as if all the images are observed without noise.

Motivated by the need to statistically quantify the difference between two imaging data sets arising in medical imaging studies, we further consider two-sample inference and extend our SCC construction procedure to a two-sample problem. Specifically, we focus on constructing SCC for the difference of the mean functions from two independent samples. The comparison of mean functions is particularly useful for imaging analysis in some biomedical settings such as comparing imaging outcomes for groups randomized either to placebo or to active treatment. Any mean differences may be localized and irregularly shaped, and so an estimation method should be flexible enough to allow for such differences. The approach developed here allows comparison of treatments simultaneously across the entire domain of interest.

We organize our article as follows. Section 2 describes the BPS estimators, and establishes their asymptotic properties for imaging data. Section 3 proposes asymptotic pointwise confidence intervals and SCCs that are constructed based on the BPS estimators. In Section 4, we discuss how to estimate the unknown components involved in the SCC construction and other issues of implementation. Section 5 reports findings from a simulation study. In Section 6, we apply the proposed methods to two real brain imaging data sets. In Section 7, we conclude the article with some discussions. Proofs of the theoretical results and additional numerical results are provided in Supporting Information.

2 |. MODELS AND ESTIMATION METHOD

In practice, the functional imaging response variable, Y_i (⋅), is only measured on a regular grid of pixels, z_j ∈ Ω, j = 1, …, N. For notational simplicity, we let Y_ij = Y_i (z_j) be the imaging response of subject i at location j, and the actual data set consists of {(Y_ij, z_j)}, i = 1, …, n, j = 1, …, N, which can be modeled as

$$Y_{ij}=\mu \left({\mathit{z}}_j\right)+{\eta }_i\left({\mathit{z}}_j\right)+\sigma \left({\mathit{z}}_j\right){\epsilon }_{ij}.$$ (2)

2.1 |. Bivariate spline basis approximation over triangulations

For model (2), we first consider the estimation of the mean function, μ(⋅). Medical imaging data are typically observed on an irregular domain Ω. We approximate the mean function in (2) by the bivariate splines that are piecewise polynomial functions over a 2D triangulated domain; see Lai and Wang (2013). In the following, we briefly introduce the techniques of triangulations and describe the BPS smoothing method.

Triangulation is an effective tool for handling data distributed on irregular regions with complex boundaries and/or interior holes. In the following, we use T to denote a triangle which is a convex hull of three points that are not collinear. A collection Δ = {T₁, …, T_M} of M triangles is called a triangulation of $\mathrm{\Omega }={\cup }_{m=1}^M{T}_m$ if any nonempty intersection between a pair of triangles in Δ is either a shared vertex or a shared edge. Given a triangle T ∈ Δ, let|T| be its longest edge length, then the size of Δ is defined as |Δ| := max {|T|, T ∈ Δ}, that is, the length of the longest edge of all triangles in Δ.

For an integer r ⩾ 0, let ${\mathcal{C}}^r(\mathrm{\Omega })$ be the collection of all r-th continuously differentiable functions over Ω. Given a triangulation Δ, let ${\mathcal{S}}_d^r(\mathrm{\Delta })=\left\{s\in {\mathcal{C}}^r(\mathrm{\Omega }):{s|}_T\in {\mathbb{P}}_d(T),T\in \mathrm{\Delta }\right\}$ be a spline space of degree d and smoothness r over triangulation Δ, where s|_T is the polynomial piece of spline s restricted on triangle T, and ${\mathbb{P}}_d$ is the space of all polynomials of degree less than or equal to d. We use Bernstein basis polynomials to represent the bivariate splines. For any triangle T ∈ Δ and any fixed point z ∈ Ω, let b₁, b₂ and b₃ be the barycentric coordinates of z relative to T. Then, the Bernstein basis polynomials of degree d relative to triangle T are defined as $B_{ijk}^{T,d}(\mathit{z})={(i!j!k!)}^{-1}d!b_1^i{b}_2^j{b}_3^k$, i + j + k = d. Let ${\{B_m\}}_{m\in \mathcal{M}}$ be the set of degree-d bivariate Bernstein basis polynomials for ${\mathcal{S}}_d^r(\mathrm{\Delta })$, where $\mathcal{M}$ stands for an index set of Bernstein basis polynomials. Denote by B the evaluation matrix of Bernstein basis polynomials, where the jth row of B is given by B^Τ(z_j) = {B_m (z_j), m ∈ $\mathcal{M}$}, for j = 1, …, N. We can approximate the mean function μ(z) by μ(z) ≈ B^Τ(z)γ, where γ^Τ = (γ_m, m ∈ $\mathcal{M}$) is the spline coefficient vector. The above bivariate spline basis can be easily constructed via the R package BPST.

To define the penalized spline method, for any function g(z) and direction z_h, h = 1,2, let ${\nabla }_{z_h}^{v}g(\mathit{z})$ denote the v-th order derivative in the direction z_h at the point z. We consider the following penalized least squares problem: ${\min }_{g\in S_d^r(\mathrm{\Delta })}{\sum }_{i=1}^n{\sum }_{j=1}^N{\left\{Y_{ij}-g\left({\mathit{z}}_j\right)\right\}}^2+{\rho }_n\mathcal{E}(g)$, where $\mathcal{E}(s)={\sum }_{T\in \mathrm{\Delta }}{\int }_T{\sum }_{i+j=2}\left(\begin{array}{l}2\hfill \\ i\hfill \end{array}\right){\left({\nabla }_{z_1}^i{\nabla }_{z_2}^{j}s\right)}^{2}d{z}_{1}d{z}_2$ is the roughness penalty, and ρ_n is the roughness penalty parameter. To meet the smoothness requirement of the splines, we need to impose some linear constraints on the spline coefficients γ: Hγ = 0 to be specific. See Section B.2 of the Supplementary Material of Yu et al. (2019) for a simple example of H. Thus, we have to minimize ${\sum }_{i=1}^n{\sum }_{j=1}^N{\left\{Y_{ij}-{\mathbf{B}}^T\left({\mathit{z}}_j\right)\mathit{\gamma }\right\}}^2+{\rho }_n{\mathit{\gamma }}^T\mathbf{P}\mathit{\gamma }$, subject to Hγ = 0, where P is the block diagonal penalty matrix satisfying γ^ΤPγ = ε(Bγ).

We first remove the constraint via QR decomposition of ${\mathbf{H}}^T:{\mathbf{H}}^T=\mathbf{QR}=\left({\mathbf{Q}}_1{\mathbf{Q}}_2\right)\left(\begin{array}{l}{\mathbf{R}}_1\hfill \\ {\mathbf{R}}_2\hfill \end{array}\right)$, where Q is orthogonal and R is upper triangular, the submatrix Q₁ is the first p columns of Q, where p is the rank of H, and R₂ is a matrix of zeros. Next, we reparametrize using γ = Q₂θ for some θ, then it is guaranteed that Hγ = 0. The minimization problem is thus converted to a conventional unrestricted penalized regression problem:

$$\sum _{i=1}^n\sum _{j=1}^N{\left\{Y_{ij}-{\tilde{\mathbf{B}}}^T\left({\mathit{z}}_j\right){\mathbf{Q}}_2\mathit{\theta }\right\}}^2+{\rho }_n{\mathit{\theta }}^T{\mathbf{Q}}_2^T\mathbf{P}{\mathbf{Q}}_2\mathit{\theta },$$ (3)

where $\tilde{\mathbf{B}}(\mathit{z})={\mathbf{Q}}_2^T\mathbf{B}(\mathit{z})$. Denote ${\overline{Y}}_{\cdot ,j}=n^{-1}{\sum }_{i=1}^n{Y}_{ij}$, $\overline{\mathbf{Y}}={\left({\overline{Y}}_{\cdot ,1},\dots ,{\overline{Y}}_{\cdot ,N}\right)}^T$, U = BQ₂, and $\mathbf{D}={\mathbf{Q}}_2^T\mathbf{P}{\mathbf{Q}}_2$. Then, minimizing (3) is equivalent to minimizing

$$\begin{gathered} {\Vert \overline{\mathbf{Y}}-\mathbf{B}{\mathbf{Q}}_2\mathit{\theta }\Vert }^2+n^{-1}{\rho }_n{\mathit{\theta }}^T{\mathbf{Q}}_2^T\mathbf{P}{\mathbf{Q}}_2\mathit{\theta } \\ =\Vert \overline{\mathbf{Y}}-\mathbf{U}\mathit{\theta }{\Vert }^2+n^{-1}{\rho }_n{\mathit{\theta }}^T\mathbf{D}\mathit{\theta }, \end{gathered}$$

and the solution is given by $\widehat{\mathit{\theta }}={\left\{{\mathbf{U}}^T\mathbf{U}+n^{-1}{\rho }_n\mathbf{D}\right\}}^{-1}{\mathbf{U}}^T\overline{\mathbf{Y}}$. Thus, the estimator of γ and μ(⋅) are: $\widehat{\mathit{\gamma }}={\mathbf{Q}}_2\widehat{\mathit{\theta }}$, $\widehat{\mu }(\mathit{z})=\mathbf{B}{(\mathit{z})}^T\widehat{\mathit{\gamma }}$.

2.2 |. Functional principal component analysis

For the second component, η_i (z), in model (2), we consider a spectral decomposition of its covariance function G_η(z, z′). Denote the eigenvalue and eigenfunction sequences of the covariance operator G_η(z, z′) as ${\left\{{\lambda }_k\right\}}_{k=1}^{\infty }$ and ${\left\{{\psi }_k(\mathit{z})\right\}}_{k=1}^{\infty }$, in which ${\lambda }_1⩾{\lambda }_2⩾\cdots ⩾0,{\sum }_{k=1}^{\infty }{\lambda }_k<\infty$, and ${\left\{{\psi }_k\right\}}_{k=1}^{\infty }$ form an orthonormal basis of L₂ (Ω). It follows from spectral theory that $G_{\eta }\left(\mathit{z},{\mathit{z}}^{\prime }\right)={\sum }_{k=1}^{\infty }{\lambda }_k{\psi }_k(\mathit{z}){\psi }_k\left({\mathit{z}}^{\prime }\right)$. The ith stochastic process {η_i (z), z ∈ Ω} allows the Karhunen-Loéve L₂ representation: ${\eta }_i(\mathit{z})={\sum }_{k=1}^{\infty }{\xi }_{ik}{\varphi }_k(\mathit{z})$, where ϕ_k (z) = (λ_k)^1/2ψ_k (z), and the coefficients ξ_ik’s are uncorrelated random variables with mean 0 and E (ξ_ik ξ_ik′) = I k( = k′), referred to as the kth FPC score of the ith subject in classical functional principal component analysis (FPCA). Thus, the response measurements in (2) can be represented as follows:

$$Y_{ij}=\mu \left({\mathit{z}}_j\right)+\sum _{k=1}^{\infty }{\xi }_{ik}{\varphi }_k\left({\mathit{z}}_j\right)+\sigma \left({\mathit{z}}_j\right){\epsilon }_{ij}.$$

Next, we describe the method of estimating the FPCA: the variance-covariance function G_η(z, z′) and its eigenvalues and eigenfunctions. For any i = 1, …, n, j = 1, …, N, let ${\widehat{R}}_{ij}=Y_{ij}-\widehat{\mu }\left({\mathit{z}}_j\right)$ be the residual. We estimate η_i (z) individually by employing the bivariate spline smoothing method to ${\{({\widehat{R}}_{ij},{\mathit{z}}_j)\}}_{j=1}^N$. To be more specific, for each i = 1, …, n, we define the spline estimator of η_i (z) as ${\widehat{\eta }}_i(\mathit{z})=\arg {\min }_{g_i\in {\mathcal{S}}_d^r(\mathrm{\Delta }*)}{\sum }_{j=1}^N{\{{\widehat{R}}_{ij}-g_i\left({\mathit{z}}_j\right)\}}^2+{\rho }_n^{*}\mathcal{E}\left(g_i\right)$, where the triangulation Δ* and smoothness penalty ${\rho }_n^{*}$ may be different from those introduced in Section 2 when estimating μ(z). Next, define the estimator of G_η(z, z′) as

$${\widehat{G}}_{\eta }\left(\mathit{z},{\mathit{z}}^{\prime }\right)=n^{-1}\sum _{i=1}^n{\widehat{\eta }}_i(\mathit{z}){\widehat{\eta }}_i\left({\mathit{z}}^{\prime }\right),$$ (4)

and we estimate the eigenfunctions ψ_k (⋅) using the following eigenequations:

$${\int }_{\mathrm{\Omega }}{\widehat{G}}_{\eta }\left(\mathit{z},{\mathit{z}}^{\prime }\right){\widehat{\psi }}_k(\mathit{z})d\mathit{z}={\widehat{\lambda }}_k{\widehat{\psi }}_k\left({\mathit{z}}^{\prime }\right),$$ (5)

where ${\widehat{\psi }}_k$’s are subject to ${\int }_{\mathrm{\Omega }}{\widehat{\psi }}_k^2(\mathit{z})d\mathit{z}=1$ and ${\int }_{\mathrm{\Omega }}{\widehat{\psi }}_k(\mathit{z}){\widehat{\psi }}_{k^{\prime }}(\mathit{z})d\mathit{z}=0$ for k′ < k. If N is sufficiently large, the left hand side of can be (5) approximated by ${\sum }_{j=1}^N\widehat{G}({\mathit{z}}_j,{\mathit{z}}_{j^{\prime }}){\widehat{\psi }}_k\left({\mathit{z}}_j\right)A\left({\mathit{z}}_j\right)$, where A(z_j) is the area of the pixel z_j.

2.3 |. Theoretical properties of the estimators

We investigate the asymptotic properties of the proposed spline estimators. To discuss these properties, we introduce some notation first. For any function g over the closure of domain Ω, denote by $\Vert g{\Vert }_{L_2(\mathrm{\Omega })}^2={\int }_{\mathrm{\Omega }}{g}^2(\mathit{z})d\mathit{z}$ the regular L₂ norm of g, and by $\Vert g{\Vert }_{\infty ,\mathrm{\Omega }}={\sup }_{\mathbf{z}\in \mathrm{\Omega }}|g(\mathit{z})|$ the supremum norm of g. Let $|g{|}_{v,\infty ,\mathrm{\Omega }}={\max }_{i+j=v}{\Vert {\nabla }_{z_1}^i{\nabla }_{z_2}^{j}g\Vert }_{\infty ,\mathrm{\Omega }}$ be the maximum norms of all the υ th order derivatives of g over Ω. For notational simplicity, we suppress the subscript Ω below. Given random variables S_n for n ⩾ 1, we write S_n = O_P (b_n) if lim_c→∞ lim sup_nP (|S_n| ⩾ cb_n) = 0. Similarly, we write S_n = o_P (b_n) if lim_nP(|S_n| ⩾ cb_n) = 0, for any constant c > 0.

The following theorem provides the L₂ and uniform convergence rate of $\widehat{\mu }(\cdot )$. The detailed proofs of this theorem are given in Web Appendix B.3 of Supporting Information.

Theorem 1. Suppose Assumptions (A1) to (A4) in Web Appendix B of Supporting Information hold, and N^1/2|Δ| → ∞ as N → ∞. Then the bivariate penalized spline estimator $\widehat{\mu }(\cdot )$ is consistent and satisfies

$$\begin{gathered} \Vert \widehat{\mu }-\mu {\Vert }_{L_2}=O_P\{\frac{{\rho }_n}{nN|\mathrm{\Delta }{|}^3}\Vert \mu {\Vert }_{2,\infty } \\ +\left(1+\frac{{\rho }_n}{nN|\mathrm{\Delta }{|}^5}\right)|\mathrm{\Delta }{|}^{d+1}\Vert \mu {\Vert }_{d+1,\infty } \\ +\frac{1}{\sqrt{n}}+\frac{1}{\sqrt{nN}\left|\mathrm{\Delta }\right|}\}. \end{gathered}$$

In addition, if Assumptions (A1) to (A5) hold, we have $\Vert \widehat{\mu }-\mu {\Vert }_{\infty }=o_P\{{(n^{-1}\log (n))}^{1/2}\}$ and $\Vert \widehat{\mu }-\mu {\Vert }_{L_2}=O_P\left(n^{-1/2}\right)$.

Theorem 2 characterizes the uniform weak convergence of ${\widehat{G}}_{\eta }\left(\mathit{z},{\mathit{z}}^{\prime }\right)$ and the convergence of ${\widehat{\psi }}_k$ and ${\widehat{\lambda }}_k$.

Theorem 2. Under Assumptions (A1) to (A7) in Web Appendix B of Supporting Information, we have the following results: (a) The spline estimator ${\widehat{G}}_{\eta }\left(\mathit{z},{\mathit{z}}^{\prime }\right)$ in (4) uniformly converges to G_η(z, z′) in probability, that is, ${\sup }_{\left(\mathit{z},{\mathit{z}}^{\prime }\right)\in {\mathrm{\Omega }}^2}\left|{\widehat{G}}_{\eta }\left(\mathit{z},{\mathit{z}}^{\prime }\right)-G_{\eta }\left(\mathit{z},{\mathit{z}}^{\prime }\right)\right|=o_P(1)$; (b) $\Vert {\widehat{\psi }}_k-{\psi }_k\Vert =o_P(1)$, $|{\widehat{\lambda }}_k-{\lambda }_k|=o_P(1)$, for k = 1, …, κ.

Although, in theory, the Karhunen-Loéve representation of the covariance function consists of an infinite number of terms. In applications, it is typical to truncate the spectral decomposition to an integer chosen so as to account for some predetermined proportion of the variance. One can select the number of principal components using the Akaike information criterion (AIC; Yao et al., 2005) or Bayesian information criterion (BIC; Li et al., 2013).

3 |. SIMULTANEOUS CONFIDENCE CORRIDORS

3.1 |. One sample

Let G_η(⋅,⋅) be a positive definite function defined as $G_{\eta }\left(\mathit{z},{\mathit{z}}^{\prime }\right)={\sum }_{k=1}^{\kappa }{\lambda }_k{\psi }_k(\mathit{z}){\psi }_k\left({\mathit{z}}^{\prime }\right)$, z, z′ ∈ Ω. Denote by ζ (z), z ∈ Ω a standardized Gaussian process such that Eζ (z) = 0, Eζ² (z) = 1 with covariance function Eζ (z)ζ (z′) = G_η(z, z′){G_η(z, z)G_η(z′, z′)}^−1/2, z, z′ ∈ Ω. Denote by q_1−α the 100(1 − α)th percentile of the distribution of the absolute maximum of ζ (z), z ∈ Ω, that is P{sup_z∈Ω |ζ (z)| ⩽ q_1−α} = 1 − α, α ∈ (0,1).

Define the “oracle” estimator $\overline{\mu }(\mathit{z})=\mu (\mathit{z})+n^{-1}{\sum }_{i=1}^n{\eta }_i(\mathit{z})$, which is infeasible due to the finite pixel grid {z_j: j = 1, …, N} and the measurement error. The following theorem presents the asymptotic properties of $\overline{\mu }(\mathit{z})$ and shows that the difference between the BPS estimator $\widehat{\mu }(\mathit{z})$ and the “oracle” smoother $\overline{\mu }(\mathit{z})$ is uniformly bounded at an o_P (n^1/2) rate.

Theorem 3. Under Assumptions (A1) to (A6) in Web Appendix B of Supporting Information, for any α ∈ (0,1), as N → ∞, n → ∞,

$$\begin{gathered} P\left\{\underset{\mathbf{z}\in \mathrm{\Omega }}{\sup }{n}^{1/2}|\overline{\mu }(\mathit{z})-\mu (\mathit{z})|G_{\eta }{(\mathit{z},\mathit{z})}^{-1/2}⩽q_{1-\alpha }\right\}\to 1-\alpha , \\ \text{and}\underset{\mathit{z}\in \mathrm{\Omega }}{\sup }|\overline{\mu }(\mathit{z})-\widehat{\mu }(\mathit{z})|=o_P\left(n^{-1/2}\right). \end{gathered}$$

Based on Theorems 1 and 3, we obtain the following asymptotic SCCs for μ(z), z ∈ Ω.

Corollary 1. Under the assumptions of Theorem 3, for any α ∈ (0,1), as N → ∞, n → ∞, an asymptotic 100(1 − α)% exact SCC for μ(z) is $\widehat{\mu }(\mathit{z})\pm n^{-1/2}{q}_{1-\alpha }{G}_{\eta }{(\mathit{z},\mathit{z})}^{1/2}$.

3.2 |. Extension to two-sample case

While one-sample SCCs are of primary interest in many situations, in some brain imaging analysis, interest lies in comparing two groups, for example, patients and normal control subjects. Next, we extend our method to two-sample problems, constructing SCCs for the difference between mean functions from two independent groups, analogous to a two-sample t test.

Given two groups of imaging observations with sample sizes n₁ and n₂, respectively, defined on a common region Ω. For H = 1, 2, let $G_{H\eta }\left(\mathit{z},{\mathit{z}}^{\prime }\right)={\sum }_{k=1}^{{\kappa }_H}{\varphi }_{Hk}(\mathit{z}){\varphi }_{Hk}\left({\mathit{z}}^{\prime }\right)$ be a positive definite function and ${\widehat{\mu }}_H$ be the spline estimates for the group mean function μ_H. Let V (z, z′) = G_1η(z, z′) + τG_2η(z, z′), where $\tau ={\lim }_{n_1\to \infty }{n}_1/n_2$. Denote by W (z), z ∈ Ω, a standardized Gaussian process such that EW (z) = 0, EW² (z) = 1 with covariance E[W (z) W (z′)] = {V (z, z)}^−1/2V (z, z′){V (z′, z′)}^−1/2. Denote q_12,α the (1 − α)th quantitle of the absolute maximal distribution of W (z), z ∈ Ω.

Theorem 4. Under Assumptions (A1) to (A6) in Web Appendix B of Supporting Information, for any α ∈ (0,1), as N → ∞, n₁ → ∞,

$$\begin{gathered} P\left\{\underset{z\in \mathrm{\Omega }}{\sup }\frac{n_1^{1/2}\left|\left({\widehat{\mu }}_1-{\widehat{\mu }}_2\right)(\mathit{z})-\left({\mu }_1-{\mu }_2\right)(\mathit{z})\right|}{\sqrt{V(\mathit{z},\mathit{z})}}⩽q_{12,\alpha }\right\} \\ \to 1-\alpha . \end{gathered}$$

Theorem 4 suggests that an asymptotic 100(1 − α)% exact SCC for (μ₁ − μ₂)(z) can be constructed as $\left({\widehat{\mu }}_1-{\widehat{\mu }}_2\right)(\mathit{z})\pm n_1^{-1}{q}_{12,\alpha }{\{V(\mathit{z},\mathit{z})\}}^{1/2}$.

4 |. IMPLEMENTATION

Without loss of generality, we describe the implementation of the proposed SCCs for the one-sample case. The procedure can be similarly adopted to the two-sample mean cases.

4.1 |. Quantile estimation and smoothing parameter selection

The quantile q_1−α used to construct the SCCs in Corollary 1 cannot be obtained analytically; however, it can be approximated by numerical simulation as follows: first, we simulate ${\zeta }_b(\mathit{z})={\widehat{G}}_{\eta }^{-1/2}(\mathit{z},\mathit{z}){\sum }_{k=1}^{\kappa }{\widehat{\lambda }}_k^{1/2}{Z}_{k,b}{\widehat{\psi }}_k(\mathit{z})$, where Z_k,b are i.i.d standard normal variables with 1 ⩽ k ⩽ κ and b = 1, …, B for a preset large integer B. Then, we estimate the quantile q_1−α by the corresponding empirical quantile of these maximum values by taking the maximal absolute value for each copy of ζ_b (z). To construct the SCC for the two-sample case, denote $\widehat{V}\left(\mathit{z},{\mathit{z}}^{\prime }\right)={\widehat{G}}_{1\eta }\left(\mathit{z},{\mathit{z}}^{\prime }\right)+\tau {\widehat{G}}_{2\eta }\left(\mathit{z},{\mathit{z}}^{\prime }\right)$. We simulate ${\widehat{W}}_b(\mathit{z})={\{\widehat{V}(\mathit{z},\mathit{z})\}}^{-1/2}\left\{{\sum }_{k=1}^{{\kappa }_1}{\widehat{\lambda }}_{1k}^{1/2}{Z}_{1k,b}{\widehat{\psi }}_{1k}(\mathit{z})-{\left(n_1/n_2\right)}^{1/2}{\sum }_{k=1}^{{\kappa }_2}{\widehat{\lambda }}_{2k}^{1/2}{Z}_{2k,b}{\widehat{\psi }}_{2k}(\mathit{z})\right\}$, z ∈ Ω. Then, q_12,α can be estimated by the empirical quantile of the B simulated $||{\widehat{W}}_b|{|}_{\infty }$’s, b = 1, …, B.

Next, for a good fit of the data, it is necessary to choose a suitable value of the smoothing parameter ρ_n. A large value of ρ_n enforces a smoother fitted function with larger fitting errors, while a small ρ_n may result in overfitting of the data. Since the in-sample fitting errors cannot gauge the prediction accuracy of the fitted function, we select a criterion function that attempts to measure the out-ofsample performance of the fitted model. Minimizing the generalized cross-validation (GCV) criterion is one computationally efficient approach to selecting smoothing parameters that also has good theoretical properties. We choose the smoothing parameter by minimizing the following $\text{GCV}\left({\rho }_n\right)={\Vert \overline{\mathbf{Y}}-\mathbf{S}\left({\rho }_n\right)\overline{\mathbf{Y}}\Vert }^2/\left[N{\left\{1-\mathrm{tr}\left\{\mathbf{S}\left({\rho }_n\right)\right\}/N\right\}}^2\right]$ over a grid of values of ρ_n, where S(ρ_n) = U(U^ΤU + n⁻¹ρ_nD)⁻¹U^Τ.

4.2 |. Spline basis and triangulation selection

To construct the SCC, we need to choose the spline basis functions and triangulation used in the BPS, a notoriously difficult task for constructing nonparametric pointwise confidence intervals or simultaneous confidence bands.

When the resolution of the imaging is relatively high and the mean imaging seems to be a realization from some smooth function without sharp edges, we suggest using smooth parameter r = 1 with degree d ⩾ 4. When d ⩾ 5, the proposed spline achieves full estimation power asymptotically (Lai and Wang, 2013). It is generally believed that subject-level image variation η_is are less smooth than the mean function. Thus, we suggest considering lower order splines, such as d = 2, when estimating the η_is.

An optimal triangulation is a partition of the domain which is best according to some criterion that measures the shape, size or number of triangles. For example, a “good” triangulation usually refers to those with well-shaped triangles, no small angles or/and no obtuse angles. We suggest building the triangulated meshes using typical triangulation construction methods such as Delaunay Triangulation (De Loera et al., 2010). The Matlab code DistMesh and R package Triangulation can be used to construct the triangulation. When estimating the mean function μ(⋅), we suggest choosing the triangulation Δ_μ based on leave-images-out k-fold cross-validation (CV). In the estimation of the η_i (⋅)’s, we suggest choosing the triangulation Δ_η so as to minimize a bootstrap estimator of the coverage error of the SCCs. In Algorithm A1 in Supporting Information, we describe our selection scheme for the one-sample case, which can be extended straightforwardly to the two-sample case.

4.3 |. Variance estimation for measurement errors and SCC adjustment

For certain imaging types and modalities, our Assumptions (A2) and (A3) about the measurement errors may not be completely satisfied. We propose a modification to the SCC procedure in Section 3 to deal with images with relatively large measurement errors.

For the one-sample SCC, for any j = 1, …, N, let ${\widehat{\epsilon }}_{ij}={\widehat{R}}_{ij}-{\widehat{\eta }}_i\left({\mathit{z}}_j\right)$, and we estimate σ²(z_j) by ${\widehat{\sigma }}^2\left({\mathit{z}}_j\right)=n^{-1}{\sum }_{i=1}^n{\widehat{\epsilon }}_{ij}{\widehat{\epsilon }}_{ij}$. Next, denote $\widehat{\epsilon }(\mathit{z})={(nN)}^{-1}\tilde{\mathbf{B}}{(\mathit{z})}^T{\mathbf{\Gamma }}_{N,\rho }^{-1}{\sum }_{i=1}^n{\sum }_{j=1}^N\tilde{\mathbf{B}}\left({\mathit{z}}_j\right)\sigma \left({\mathit{z}}_j\right){\epsilon }_{ij}$. We estimate the variance-covariance function of $\widehat{\epsilon }(\mathit{z})$, ${\tilde{G}}_{\epsilon }\left(\mathit{z},{\mathit{z}}^{\prime }\right)=\text{Cov}\left\{\widehat{\epsilon }(\mathit{z}),\widehat{\epsilon }\left({\mathit{z}}^{\prime }\right)\right\}$, by

$$\begin{gathered} {\widehat{G}}_{\epsilon }\left(\mathit{z},{\mathit{z}}^{\prime }\right)=n^{-1}{N}^{-2}\tilde{\mathbf{B}}{\left(\mathit{z}\right)}^T{\mathbf{\Gamma }}_{N,\rho }^{-1}\left\{\sum _{j=1}^N\tilde{\mathbf{B}}\left({\mathit{z}}_j\right){\widehat{\sigma }}^2\left({\mathit{z}}_j\right)\tilde{\mathbf{B}}{\left({\mathit{z}}_j\right)}^T\right\} \\ \times {\mathbf{\Gamma }}_{N,\rho }^{-1}\tilde{\mathbf{B}}\left({\mathit{z}}^{\prime }\right), \end{gathered}$$

where Γ_N,ρ is given in (B.5) in Supporting Information.

Denote $\widehat{\mathrm{\Sigma }}\left(\mathit{z},{\mathit{z}}^{\prime }\right)={\widehat{G}}_{\eta }\left(\mathit{z},{\mathit{z}}^{\prime }\right)+n{\widehat{G}}_{\epsilon }\left(\mathit{z},{\mathit{z}}^{\prime }\right)$. We adjust the approximation procedure of quantile q_1−α as follows: first, we simulate

$$\begin{gathered} {\zeta }_b(\mathit{z})={\widehat{\mathrm{\Sigma }}}^{-1/2}(\mathit{z},\mathit{z})\{\sum _{k=1}^{\kappa }{\widehat{\lambda }}_k^{1/2}{\widehat{\psi }}_k(\mathit{z})Z_{k,\xi }^{(b)} \\ +N^{-1}\tilde{\mathbf{B}}{(\mathit{z})}^T{\mathbf{\Gamma }}_{N,\rho }^{-1}\sum _{j=1}^N\tilde{\mathbf{B}}\left({\mathit{z}}_j\right)\widehat{\sigma }\left({\mathit{z}}_j\right)Z_{j,\epsilon }^{(b)}\}, \end{gathered}$$

where $Z_{k,\xi }^{(b)}$ and $Z_{j,\epsilon }^{(b)}$ are i.i.d standard normal variables with 1 ⩽ k ⩽ κ, 1 ⩽ j ⩽ N; next, we estimate the quantile q_1−α by the corresponding empirical quantile of the B simulated ${\Vert {\zeta }_b\Vert }_{\infty }$; finally, we construct the SCC as $\widehat{\mu }(\mathit{z})\pm n^{-1/2}{q}_{1-\alpha }\widehat{\mathrm{\Sigma }}{(\mathit{z},\mathit{z})}^{1/2},\mathit{z}\in \mathrm{\Omega }$.

For the two-sample case, we can similarly modify the procedure by defining ${\widehat{\mathrm{\Sigma }}}_H\left(\mathit{z},z^{\prime }\right)={\widehat{G}}_{\eta ,H}+n_H{\widehat{G}}_{\epsilon ,H}$, for H = 1, 2, and $\widehat{\mathrm{\Xi }}\left(\mathit{z},{\mathit{z}}^{\prime }\right)={\widehat{\mathrm{\Sigma }}}_1\left(\mathit{z},{\mathit{z}}^{\prime }\right)+n_1/n_2{\widehat{\mathrm{\Sigma }}}_2\left(\mathit{z},{\mathit{z}}^{\prime }\right)$. Let ${\widehat{\sigma }}_H(\mathit{z})$ be the estimator of σ_H (z), for H = 1, 2. To estimate q_12,α, we simulate

$$\begin{gathered} {\widehat{W}}_b(\mathit{z})={\left\{\widehat{\mathrm{\Xi }}(\mathit{z},\mathit{z})\right\}}^{-1/2}\{\sum _{k=1}^{{\kappa }_2}{\widehat{\lambda }}_{1k}^{1/2}{Z}_{1k,\xi }^{(b)}{\widehat{\psi }}_{1k}(\mathit{z}) \\ -{\left(\frac{n_1}{n_2}\right)}^{1/2}\sum _{k=1}^{{\kappa }_2}{\widehat{\lambda }}_{2k}^{1/2}{Z}_{2k,\xi }^{(b)}{\widehat{\psi }}_{2k}(\mathit{z}) \\ +\tilde{\mathbf{B}}{\left(\mathit{z}\right)}^T{\mathbf{\Gamma }}_{N,{\rho }_1}^{-1}\frac{1}{N}\sum _{j=1}^N\tilde{\mathbf{B}}\left({\mathit{z}}_j\right){\widehat{\sigma }}_1\left({\mathit{z}}_j\right)Z_{1j,\epsilon }^{(b)} \\ -{\left(\frac{n_1}{n_2}\right)}^{1/2}\tilde{\mathbf{B}}{\left(\mathit{z}\right)}^T{\mathbf{\Gamma }}_{N,{\rho }_2}^{-1}\frac{1}{N}\sum _{j=1}^N\tilde{\mathbf{B}}\left({\mathit{z}}_j\right){\widehat{\sigma }}_2\left({\mathit{z}}_j\right)Z_{2j,\epsilon }^{(b)}\}, \end{gathered}$$

where $Z_{Hk,\xi }^{(b)}$ and $Z_{Hj,\epsilon }^{(b)}$ are i.i.d standard normal variables with 1 ⩽ k ⩽ κ_H, 1 ⩽ j ⩽ N for H = 1, 2. Then, q_12,α can be estimated by the empirical quantile of the B simulated ${\Vert {\widehat{W}}_b\Vert }_{\infty }$’s, b = 1, …, B. A modified SCC for μ₁(z) − μ₂(z) can thus be constructed as $\left({\widehat{\mu }}_1-{\widehat{\mu }}_2\right)(\mathit{z})\pm n_1^{-1/2}{q}_{12,\alpha }{\{\widehat{\mathrm{\Xi }}(\mathit{z},\mathit{z})\}}^{1/2}$.

5 |. SIMULATION STUDIES

In this section, we describe two Monte Carlo simulations to examine the finite sample performance of the proposed method.

5.1 |. One sample SCC

In this simulation study, the measurements on the images are generated from the model:

$$\begin{gathered} Y_{ij}=\mu \left({\mathit{z}}_j\right)+\sum _{k=1}^2{\lambda }_k^{1/2}{\xi }_{ij}{\psi }_k\left({\mathit{z}}_j\right)+\sigma \left({\mathit{z}}_j\right){\epsilon }_{ij},i=1,\dots ,n, \\ j=1,\dots ,N, \end{gathered}$$

where z_j = (z_1j, z_2j) ∈ Ω ⊂ [0,1]², and Ω is the same as the domain of the brain images shown in Section 6. To demonstrate the practical performance of our theoretical results, we consider the following four mean functions:

• (quadratic) μ(z) = 20{(z₁ − 0.5)² + (z₂ − 0.5)²},

• (exponential) μ(z) = 5 exp[−15{(z₁ − 0.5)² + (z₂− 0.5)²}] + 0.5,

• (cubic) μ(z) = 3.2(−z₁³ + z₂³) + 2.4,

• (sine) μ(z) = −10[sin{5π (z₁ + 0.22)} − sin {5π (z₂ − 0.18)}] + 2.8,

shown in the first column of Figures A1 to A6 in Supporting Information.

To simulate the within-image dependence, we generate ${\xi }_{ik}\stackrel{\text{i.i.d}}{\sim }N(0,1)$, for k = 1,2. For the eigenvalues, we set λ₁ = 0.5, λ₂ = 0.2. For the eigenfunctions, we let ψ₁(z) = c₁ sin(πz₁) + c₂, ψ₂ (z) = c₃ cos(πz₂) + c₄, where c₁ = 0.988, c₂ = 0.5, c₃ = 2.157, and c₄ = −0.084 to guarantee that the eigenfunctions are orthonormal. We generate heterogenous measurement errors with σ (z) = 0.25{1 − (z₁ − 0.5)² − (z₂ − 0.5)²}. We consider n = 50, 100, 200, and for each image, we consider two types of resolution: 40 × 40 and 79 × 79 with N = 921 and 3682 pixels falling inside the domain, respectively.

To apply our method, we consider three different triangulations which are also shown in the first column of Figures A1 to A6 in Supporting Information. The first triangulation (Δ₁) contains 49 triangles and 38 vertices; the second triangulation (Δ₂) contains 80 triangles and 54 vertices; while the third triangulation (Δ₃) contains 144 triangles and 87 vertices. The estimated mean function based on these three triangulations are shown in the second columns of Figures A1 to A6, and the corresponding 99% SCCs are given in the last two columns. From these figures, one can see that all three triangulations result in almost the same estimates and SCCs. One can also see that even when the number of images is moderately large, the estimation is very accurate regardless of the type of underling mean functions.

Table 1 and Table A1 in Supporting Information summarize the estimated coverage rate of the SCCs based on 1000 replications for N = 921 and 3682, respectively. The number in parenthesis represents the average width of the SCCs. These two tables also confirm that there is little difference among the three triangulations and that the coverage rate is closer to the nominal confidence level for larger values of n.

TABLE 1.

Empirical coverage rates and average widths of the simultaneous confidence corridors (N = 921)

	α = 0.10			α = 0.05			α = 0.01
n	Δ1	Δ2	Δ3	Δ1	Δ2	Δ3	Δ1	Δ2	Δ3
μ (z) = 20{(z1 − 0.5)2 + (z2 − 0.5)2}
50	0.858 (0.651)	0.860 (0.651)	0.874 (0.659)	0.928 (0.739)	0.929 (0.739)	0.935 (0.747)	0.977 (0.908)	0.981 (0.908)	0.981 (0.916)
100	0.891 (0.473)	0.893 (0.473)	0.897 (0.474)	0.944 (0.535)	0.947 (0.535)	0.949 (0.537)	0.979 (0.657)	0.979 (0.657)	0.980 (0.659)
200	0.896 (0.335)	0.897 (0.336)	0.897 (0.337)	0.942 (0.379)	0.949 (0.380)	0.948 (0.381)	0.987 (0.465)	0.988 (0.466)	0.988 (0.467)
μ (z) = 5 exp[−15{(z1 − 0.5)2 + (z2 − 0.5)2}] + 0.5
50	0.877 (0.664)	0.879 (0.666)	0.879 (0.667)	0.939 (0.752)	0.941 (0.754)	0.937 (0.755)	0.983 (0.921)	0.983 (0.923)	0.982 (0.924)
100	0.888 (0.473)	0.892 (0.474)	0.892 (0.474)	0.942 (0.535)	0.944 (0.536)	0.945 (0.537)	0.979 (0.657)	0.980 (0.658)	0.980 (0.659)
200	0.904 (0.341)	0.890 (0.336)	0.902 (0.342)	0.947 (0.385)	0.942 (0.381)	0.949 (0.386)	0.986 (0.470)	0.986 (0.466)	0.986 (0.472)
$\mu (\mathit{z})=3.2(-z_1^3+z_2^3)+2.4$
50	0.876 (0.639)	0.879 (0.639)	0.880 (0.639)	0.934 (0.727)	0.937 (0.728)	0.938 (0.728)	0.980 (0.896)	0.981 (0.896)	0.981 (0.897)
100	0.870 (0.455)	0.876 (0.455)	0.884 (0.457)	0.929 (0.517)	0.935 (0.517)	0.938 (0.519)	0.979 (0.639)	0.980 (0.640)	0.980 (0.642)
200	0.890 (0.326)	0.889 (0.325)	0.906 (0.329)	0.941 (0.370)	0.942 (0.370)	0.953 (0.373)	0.984 (0.456)	0.986 (0.456)	0.985 (0.459)
μ (z) = −10[sin {5π (z1 + 0.22)} − sin {5π (z2 − 0.18)}] + 2.8
50	0.882 (0.734)	0.869 (0.740)	0.879 (0.754)	0.937 (0.821)	0.930 (0.828)	0.939 (0.843)	0.981 (0.989)	0.976 (0.996)	0.980 (1.011)
100	0.886 (0.522)	0.901 (0.534)	0.880 (0.536)	0.938 (0.584)	0.946 (0.596)	0.935 (0.598)	0.982 (0.705)	0.983 (0.718)	0.982 (0.721)
200	0.877 (0.370)	0.891 (0.378)	0.887 (0.384)	0.937 (0.414)	0.951 (0.423)	0.947 (0.429)	0.985 (0.499)	0.986 (0.508)	0.984 (0.514)

5.2 |. Two-sample simultaneous confidence corridor

In this simulation study, we examine the power of detecting a difference in mean images based on the proposed two-sample SCC. Two group of images are generated from the model

$$Y_{H,ij}={\mu }_H\left({\mathit{z}}_j\right)+\sum _{k=1}^{\kappa }{\lambda }_k^{1/2}{\xi }_{ij}{\psi }_k\left({\mathit{z}}_j\right)+\sigma \left({\mathit{z}}_j\right){\epsilon }_{ij},H=1,2,$$

where ψ_k’s are generated as in the simulation in Section 5.1. We consider the following:

$$\begin{gathered} H_0:{\mu }_1(\mathit{z})={\mu }_2(\mathit{z}),\text{for}\text{all}\mathit{z}\in \mathrm{\Omega }\text{vs} \\ {H}_a:{\mu }_1(\mathit{z})\ne {\mu }_2(\mathit{z})\text{for}\text{some}\mathit{z}\in \mathrm{\Omega }. \end{gathered}$$ (6)

The mean functions for two groups considered here are μ₁(z) = 20{(z₁ − 0.5)² + (z₂ − 0.5)²}, and ${\mu }_2(\mathit{z})={\mu }_1(\mathit{z})+\delta (-z_1^3+z_2^3)$. The value of δ controls the difference between the two groups. The eigenvalues λ_k’s, eigenfunctions ψ_k’s and the measurement errors ε_ij’s are generated in the same way as in the simulation presented in Section 5.1, and we set σ(z) = 0.1.

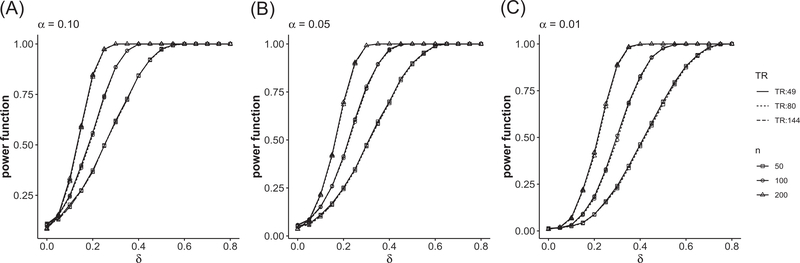
Figure 1 and Table A2 in Supporting Information summarize the estimated probability of rejecting H₀ in (6) with nominal level α = 0.10, 0.05, and 0.01. When δ = 0, the probability should be close to the nominal level, and when δ is large, the estimated power should be close to 1. From Figure 1 and Table A2, one can see even when the numbers of the images n₁ and n₂ are moderately large, the size of the test is very close to the nominal level. The estimated power increases quickly as n₁ and n₂ increase. The performance of the procedure is similar and consistent for different triangulations.

FIGURE 1.

Type I error and empirical power of two-sample tests for different α’s: (A) α = 0.10, (B) α = 0.05, and (C) α = 0.01

6 |. APPLICATIONS TO BRAIN IMAGING DATA

In this section, we implement the proposed SCCs to analyze brain imaging data. In particular, we consider data taken from positron emission tomography (PET) studies with two different settings: one using the tracer [C¹¹]WAY100635 that has an affinity for the serotonin 1 A receptor in a study of major depressive disorder (MDD); and one using the fluorodeoxyglucose tracer [F¹⁸]FDG, a glucose analog, in a study of dementia. The imaging data are naturally three-dimensional in each case, but we focus here on one strategically selected slice in each setting. For the MDD study, we select the horizontal slice which passes through the midbrain and the amygdala, two regions implicated in MDD (Parsey et al., 2010). As pointed out by Marcus et al. (2014), within the brain, the anatomical regions that are commonly affected by Alzheimer diseases are the bilateral superior medial frontal, anterior, middle cingulate and bilateral parietal cortices, while the regions such as the bilateral medial temporal lobes are usually less affected. Therefore, for the [F¹⁸]FDG study, we focus on the 48th horizontal slice of the brain since it passes through the frontal and parietal lobes. In each case, we consider the hypotheses in (6) for the difference between two mean functions.

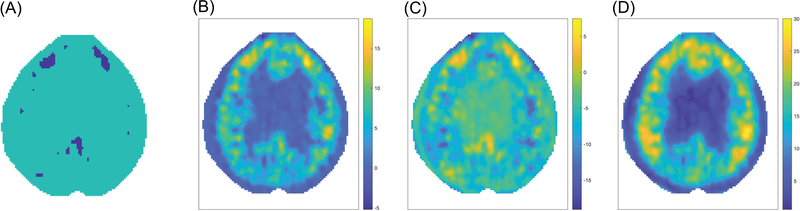
For the [C¹¹]WAY100635 data, we have 40 subjects who are classified as normal controls and 26 who have been diagnosed with MDD (Parsey et al., 2006). Figure 2 displays the results of the application of the proposed procedure to these data. The portions of the SCCs not containing zero can be seen in (A); the estimation of the mean difference betweentowards the two groups is shown in (B), and the lower and upper SCCs are shown in (C) and (D).

FIGURE 2.

Simultaneous confidence corridor (SCC) for comparison between normal control (CON) and major depressive disorder (MDD): (A) coverage of zero, (B) ${\widehat{\mu }}_{\text{MDD}}-{\widehat{\mu }}_{\text{CON}}$, (C) lower simultaneous confidence corridor (SCC), and (D) upper SCC. In (A), yellow color indicates zero falls above the upper SCC and blue color indicates zero falls beneath the lower SCC

Next, we illustrate these procedures using the PET data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI; adni.loni.usc.edu). One of the primary goals of the ADNI study is to test whether PET and some other biological markers can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD).

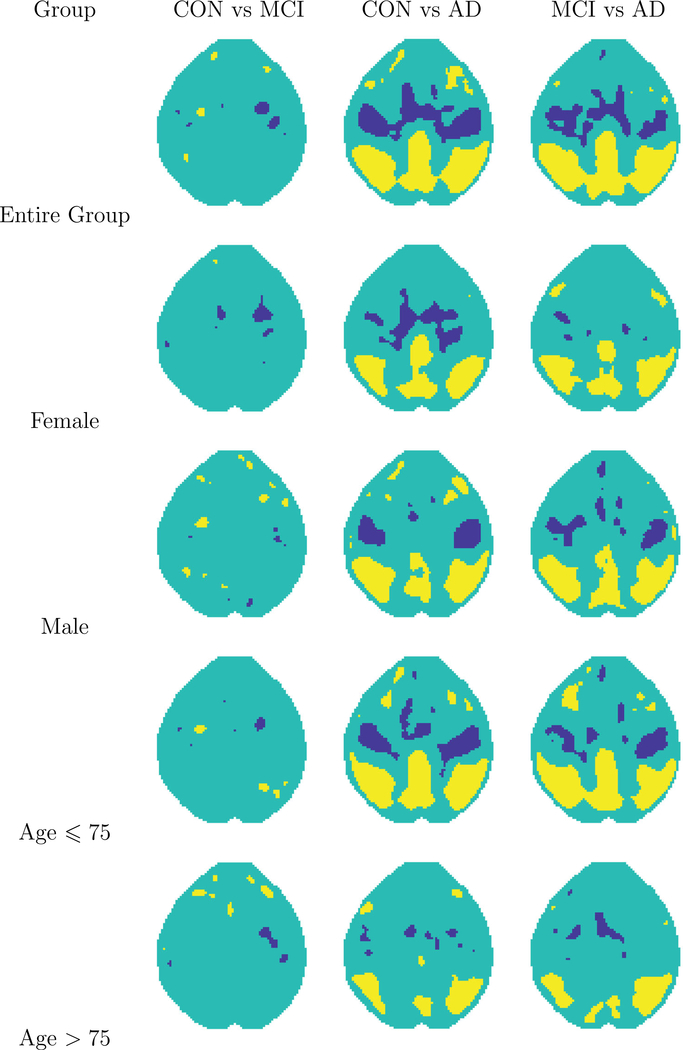
We use the proposed method in Section 4.2 to choose the triangulation and spline basis functions. Among the three triangulations (Δ₁−Δ₃) considered in simulation studies, we choose Δ₃ when estimating the mean functions, and Δ₁ when estimating the covariance functions. We use smooth parameter r = 1 with degree d = 5 for the estimation of mean function and d = 2 for the estimation of η_i’s. The first row of Figure 3 displays the areas in which zero is not contained within the 95% SCC comparing each pair of diagnostic groups. This suggests that the AD group has widespread mean differences from each of the other two groups. We also stratify the data according to sex and age, and the breakdowns of these data in terms of these variables are given in Table A1 in Supporting Information. Within each stratum, we examine the SCC for the difference between all pairs of diagnostic groups, and the results are also shown in Figure 3. The large apparent differences in the full group analysis can be seen (but to a lesser extent) in the comparisons among the males and among the relatively younger population, but are less pronounced in the other subgroup analyses.

FIGURE 3.

Coverage of zero of simultaneous confidence corridor (SCC) for pairwise comparisons among CON, mild cognitive impairment (MCI) and Alzheimer’s disease (AD). Yellow color indicates zero falls above the upper SCC and blue color indicates zero falls beneath the lower SCC

7 |. DISCUSSION

We develop SCCs for mean functions of imaging data in the functional data framework. We show that the proposed procedure has desirable statistical properties: the estimators are asymptotically efficient as if all images were observed with no error. One main advantage of our method is its computational efficiency and feasibility for large-scale imaging data. It greatly enhances the application of SCCs to imaging data in biomedical studies.

A few more issues still merit further research. For instance, the triangulation selection using the CV and wild bootstrap works well in practice, but a stronger theoretical justification for their use is still needed. In recent years, there has been a great deal of work on functional regression. It is interesting to extend the proposed methodology to functional regression models. The construction of SCCs in such models is a significant challenge and requires more in-depth investigation. Last but not least, it is also interesting to develop SCCs for large-scale longitudinal imaging data, in which accounting for the dependence within the subject as well as for the longitudinal design is crucial for making inference.