Seeing Is Believing: Experimental Spin States from Machine Learning Model Structure Predictions

Abstract

Determination of ground-state spins of open-shell transition-metal complexes is critical to understanding catalytic and materials properties but also challenging with approximate electronic structure methods. As an alternative approach, we demonstrate how structure alone can be used to guide assignment of ground-state spin from experimentally determined crystal structures of transition-metal complexes. We first identify the limits of distance-based heuristics from distributions of metal–ligand bond lengths of over 2000 unique mononuclear Fe(II)/Fe(III) transition-metal complexes. To overcome these limits, we employ artificial neural networks (ANNs) to predict spin-state-dependent metal–ligand bond lengths and classify experimental ground-state spins based on agreement of experimental structures with the ANN predictions. Although the ANN is trained on hybrid density functional theory data, we exploit the method-insensitivity of geometric properties to enable assignment of ground states for the majority (ca. 80–90%) of structures. We demonstrate the utility of the ANN by data-mining the literature for spin-crossover (SCO) complexes, which have experimentally observed temperature-dependent geometric structure changes, by correctly assigning almost all (>95%) spin states in the 46 Fe(II) SCO complex set. This approach represents a promising complement to more conventional energy-based spin-state assignment from electronic structure theory at the low cost of a machine learning model.

1. Introduction

Determination of the ground-state spins of open-shell transition-metal complexes is essential to understanding their catalytic¹⁻⁶ and materials⁷⁻¹³ properties. Nevertheless, prediction of spin-state ordering is extremely sensitive to electronic structure method choice. Correlated wave function theory methods exhibit limitations in predicting properties of open-shell transition-metal complexes¹⁴⁻¹⁷ and remain cost-prohibitive for large-scale, high-throughput screening. The need to explore large chemical spaces in materials design¹⁸⁻²³ motivates the use of computationally affordable approximate density functional theory (DFT). However, ground-state spin prediction is extremely sensitive to the nature of the DFT functional employed.²⁴⁻²⁹ Semilocal, generalized gradient approximation (GGA) DFT functionals^30,31 stabilize delocalized,^32,33 strongly covalent states,³⁴ leading to a bias for low-spin over high-spin states.^29,35−39 Hybrid functionals with an admixture of Hartree–Fock (HF) exchange approximately correct delocalization errors^40,41 and counteract^{25−27,42−46} the bias for low-spin states, but the appropriate fraction of HF exchange is strongly system-dependent.^{25−27,47−51} Divergent proposals have been made to either reduce^25,52−54 or increase^{26,41,55−57} HF exchange fractions with respect to common values (i.e., 20–25%) in order to accurately predict transition-metal complex properties. Still others have advanced meta-GGAs,^{17,27,58−60} meta-GGA hybrids,⁶¹ or double hybrid functionals⁶² as candidates to improve spin-state predictions, but such conclusions are often limited to the modest data sets over which the studies have been carried out.

The emerging area of machine learning (ML)-accelerated high-throughput computational screening^{20,21,63−75} has led to exploration of much larger chemical spaces^76,77 over which no one-size-fits-all exchange correlation functional can be expected to be predictive. Our group has developed representations^70,71 for training ML (e.g., artificial neural networks or ANNs) models to predict spin-state ordering to within sub-kilocalorie per mole accuracy of the DFT training data^70,71,78 and demonstrated the use of these models in the design of a range of spin-state-dependent catalytic⁷⁵ and materials^{63,70−73,78−80} properties. In evaluating such ML model predictions, we treated DFT as the ground truth, despite its limitations in predicting ground-state spin. One avenue we pursued to overcome challenges associated with DFT approximations is to train the ML model on a family of functionals,^63,70 providing understanding of which regions of chemical space are most sensitive^27,38 to the DFT functional. Nevertheless, this approach makes the assumption that a typical range of functional variation will include the experimental result, which cannot be guaranteed.

In comparison to energetic spin-state ordering, other properties such as the spin-state-dependent metal–ligand bond length are much less sensitive to the exchange-correlation functional.⁸¹⁻⁸³ Also in contrast to spin-state energetics, experimental bond lengths can be extracted from available databases⁸⁴ of crystal structures for a large number of transition-metal complexes. The bond length is related to spin state because high-spin (HS) states populate more antibonding states than do equivalent low-spin (LS) states, meaning that the bond length can be a sensitive indicator of the ground-state spin in midrow transition-metal complexes. While this difference can be expected to depend on the nature of the ligand as well as oxidation state and identity of the metal, we observed^27,29,70 the difference in DFT-evaluated HS and LS bond lengths for midrow complexes to be large in comparison to their change with DFT functional.

As a motivating example for this work, we first review observations from a range of transition-metal complexes for which we previously computed⁷⁰ hybrid DFT properties (i.e., B3LYP) with varied HF exchange (i.e., a_HF) fractions. This set of complexes consisted of homoleptic, mononuclear octahedral complexes with ligand strengths ranging from weak field (i.e., H₂O) to strong field (i.e., CO) in complex with d⁶ Fe(II) or d⁵ Fe(III) (Figure 1). Over these Fe(II) complexes, an increase or decrease of a_HF by 0.1 from its default value in B3LYP (a_HF = 0.2) shifts the HS–LS (here, quintet–singlet) adiabatic energetic splitting (i.e., ΔE_H-L) predictions by 10–30 kcal/mol (Figure 1). Vertical spin splitting more relevant in light-induced spin-state switching will exhibit larger exchange sensitivity.⁷⁰ This energetic variation can lead to ground-state spin reassignment: Fe(II) complexes with phen or cyano ligands that are LS at low HF exchange become HS when the admixture is increased (Figure 1). Over this same range of a_HF variation, bond lengths vary far less, and the significantly longer nature of the metal–ligand bond lengths in HS versus LS states is preserved across the spectrochemical series (Figure 1). In cases where structural data are available,⁸⁴ comparison of experimental and predicted bond lengths provides an alternative approach⁸⁵ to ground-state spin assignment⁷⁰ (Figure 1 and Supporting Information Table S1). For the phen or cyano complexes with high functional sensitivity for energetic ground-state assignment, the bond-length-based assignment strongly suggests an LS state (Figure 1). Similar observations hold for Fe(III) complexes (Supporting Information Figure S1).

Figure 1.

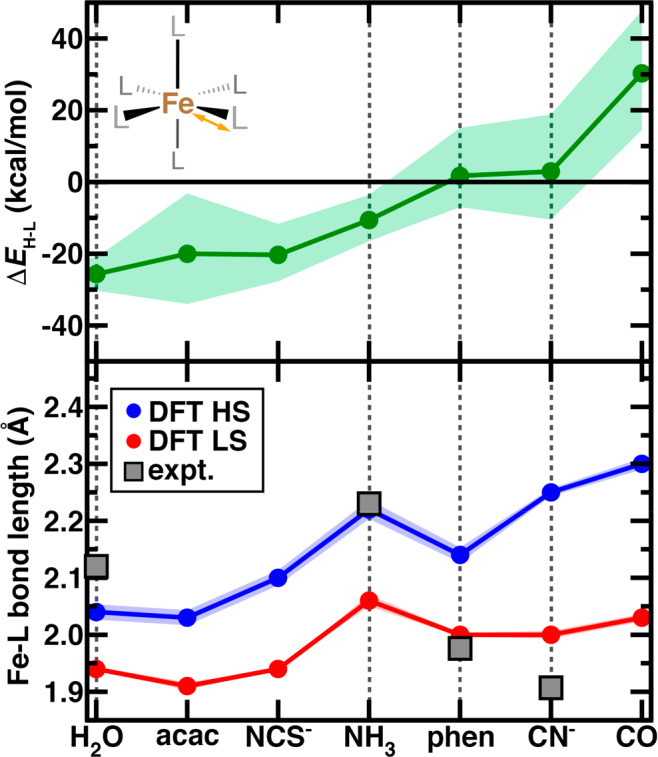
Properties of homoleptic, octahedral mononuclear Fe(II) transition-metal complexes with ligands ordered by their field strength in the spectrochemical series. A schematic of the structure is shown in inset. Properties shown are evaluated with hybrid DFT (B3LYP, a_HF = 0.2, sold lines and circle symbols) along with the range of properties evaluated at a_HF = 0.1–0.3 shown as a translucent shaded region. The high-spin to low-spin adiabatic spin splitting energy (ΔE_H-L, in kcal/mol) is shown at top, and the Fe–L bond lengths (in Å) for the HS and LS states are shown at bottom. Representative Fe–L bond lengths from crystal structures are shown as gray squares as indicated in inset legend, and vertical dotted lines are shown to enable comparison of bond-length-derived spin-state assignment (bottom) and energetic assignment (top).

In this work, we curate data sets of thousands of experimental transition-metal complex structures to demonstrate the potential of structure-based spin-state identification. We leverage an ANN previously trained⁶³ to predict spin-state dependent DFT bond lengths of midrow transition-metal complexes, exploiting the reduced method sensitivity of structural properties. Using the relative agreement between experimental and ANN-predicted HS or LS bond lengths, we develop a robust approach for ground spin state prediction, where alternatives (e.g., heuristics or DFT energetics) commonly fail. We focus our demonstration on Fe(II)/Fe(III) complexes given their widespread study, but our approach will be generally applicable for open-shell transition-metal complexes.

2. Computational Details

We employ an ANN that separately predicts equatorial and up to two unique axial metal–ligand bond lengths, which was trained on hybrid DFT bond-length data from refs (70) and (71) and first demonstrated in ref (63). The ANN consists of three fully connected layers and is trained on a revised autocorrelation (RAC) representation⁷¹ of the transition-metal complexes (Supporting Information Table S2). RACs⁷¹ are a series of products and differences on the molecular graph that do not explicitly encode geometric information, making them a suitable representation with which we can predict spin-state and oxidation-state-dependent bond lengths. The hybrid DFT training data used for these models were obtained with B3LYP⁸⁶⁻⁸⁸ using an LANL2DZ effective core potential⁸⁹ on the transition metal and 6-31G* on the remaining atoms with a developer version of TeraChem.^90,91 Following conventions in prior work, the HS or LS bond lengths predicted for d⁶ Fe(II) are quintets and closed-shell singlets, respectively, and the d⁵ Fe(III) HS and LS states are sextets and doublets, respectively. Intermediate spin states are neglected due to the higher probability of transitioning between HS and LS states experimentally.⁹² The ML model employed in this work is freely available online as part of the molSimplify⁹³ code.

3. Results and Discussion

3a. Curation of a Unique Mononuclear Transition-Metal Complex Set

We extracted a set of mononuclear octahedral Fe(II) and Fe(III) complex structures from the Cambridge Structural Database⁸⁴ (CSD) through a series of sequential steps. Overall, this procedure involved the curation of complexes with the desired coordination and oxidation state, removal of duplicates, and categorization of whether the complex was compatible with ANN-based bond length prediction. Refcodes of compounds obtained at each step of the procedure along with necessary metadata to interpret the outcomes of each step are provided in a spreadsheet in the Supporting Information. This procedure employed both the Conquest graphical interface to the CSD as well as the Python application programming interface (API), in all cases applied to the v5.40 data set with complexes from the November 2018 update.⁸⁴ The Conquest interface was used to query for structures containing an iron atom that forms exactly six bonds with p-block elements (here, the first four rows of groups 13–17, excluding boron) or hydrogen. The octahedral coordination environment was enforced by requiring a 70–90° angle for six angles between ligand-coordinating atom pairs and the iron and a 140–180° angle for three other angles. Although polymeric species were excluded, no additional filters were applied to the quality of the structures, and only compounds with a single unique, six-letter code were selected, leading to a set of 12 981 initial complexes (Table 1).

Table 1. Subsets from the CSD^a.

filtering criterion	name	all	Fe(II)	Fe(III)
Fe with 6 bonds in angle range		12 981
Fe(II) or Fe(III) with nonmetals		4862	2865	1997
Unique octahedral structures	UO	3627	2179	1448
eq plane element symmetry		2201	1558	643
eq plane bond length distortion outliers removed	AC	2037	1447	590
Same coordinating atom element	HE	1316	969	347
N and one other element	NX	580	369	211

^aDescription of filtering steps applied to obtain unique Fe(II) and Fe(III) mononuclear octahedral complexes as well as subsets for analysis, with names where appropriate.

As this query alone does not ensure we obtain only mononuclear transition-metal complexes, the CSD API was used to iterate through all components in the selected refcodes. We identified a component from the crystal structure that had a single iron center and confirmed that the deposited structure had either Fe(II) or Fe(III) in its chemical name, producing a smaller subset of 4862 complexes (Table 1). The CSD Python API was used to add missing hydrogen atoms to ∼10% (511 of 4862) of the structures and store the revised, mononuclear transition-metal complex structures in mol2 format, which preserves user- and CSD-defined connectivity in addition to the Cartesian coordinates. In 60 cases, the chemical name contained both Fe(II) and Fe(III), and these complexes were manually inspected and reassigned to the appropriate oxidation state based on the components in the full crystal structure in all but one case, where no unambiguous oxidation state could be assigned (see Supporting Information).

We next computed the molecular weights of all complexes, including the added hydrogen atoms where applicable. For any case where multiple complexes had the same molecular weight, we used the connectivity recorded in the CSD mol2 file to compute an atomic-number-weighted connectivity matrix in which the diagonal was the atomic number (i.e., Z) of that element, and the off-diagonal elements of bonded atoms i and j were Z_iZ_j. We compared the determinant of these connectivity matrices and selected a single unique complex based on having a distinct Z-weighted matrix determinant. This filtering step led to 3627 unique complexes that we refer to as the UO set, with slightly more Fe(II) cases (2179) than Fe(III) (1448, see Table 1).

In addition to this set of unique complexes, we curated a subset we refer to as ANN-compatible (AC). Specifically, our ML model for bond length prediction⁶³ was trained on complexes with a symmetric equatorial ligand field and up to two unique axial ligands. To select a subset of CSD complexes most likely to be amenable to ANN predictions, we searched for whether an equatorial plane could be identified in the transition-metal complex that contained the same metal-coordinating-atom element identities. To assign the equatorial plane (and axial positions), we performed a series of physically motivated steps designed to be repeatable across the CSD with a hierarchy of rules (Supporting Information Text S1). In brief, high-denticity (i.e., tetradentate) ligands or highest molecular weight planes were selected to be the equatorial plane first. If following this rule did not ensure the same element for the coordinating atoms in the equatorial plane but an alternative plane could be selected that did, then the equatorial plane was reassigned to that alternative plane. After this step, 2201 unique complexes could be identified as ANN-compatible (Table 1). These complexes were then filtered further to eliminate extreme outliers in which the difference of equatorial metal–ligand bond length in the equatorial plane exceeded 0.15 Å in the most symmetric plane or up to the 0.20 Å in the selected equatorial plane (i.e., where multiple planes had four identical coordinating atoms). These additional filters produced a final AC set of 2037 complexes (Table 1 and Supporting Information Figures S2 and S3). The AC constraint on the UO set eliminated a higher fraction of Fe(III) than Fe(II) complexes (60% vs 34%, Table 1). Nevertheless, overall properties of the UO and AC sets, such as the wide distribution of molecular weights of complexes in the UO set, were similar for both Fe(II) and Fe(III) complexes (Supporting Information Figures S4 and S5).

3b. Analysis of Transition-Metal Complex Structural Trends

We evaluated properties of the curated CSD data sets to identify if patterns emerged in the bond length distributions of experimental data that could enable heuristic spin-state assignment. For this analysis, we first focused on a subset of complexes in which all coordinating atoms are the same element in order to simplify effects of strongly mixed ligand fields (e.g., the trans effect^94,95), which we call the homoelemental (HE) set. A majority of all 3627 unique complexes obtained from the CSD (i.e., the UO set) satisfy this criterion, and the majority of the 2037 complexes we retained as AC are also in this HE set (Supporting Information Tables S3 and S4). This is in part due to the greater geometric symmetry in complexes with greater ligand-coordinating atom symmetry as well as the fact that fewer unique complexes contain a high number of distinct coordinating elements (Supporting Information Figures S2 and S3 and Tables S3–S6).

In total, 969 Fe(II) and 347 Fe(III) complexes comprise the HE data set (Table 1 and Supporting Information Figures S6 and S7). The coordinating elements are predominantly 2p elements (i.e., C, N, or O), but some complexes with heavier elements (i.e., P, S, or As) are also present (Supporting Information Tables S3 and S4 and Figures S6 and S7). Notably, few halide complexes are observed due to the strong negative charge (i.e., −3 or −4) on such HE complexes (Supporting Information Figures S6 and S7). Over the HE complexes, we observe significant variation in the metal–ligand bond lengths by elemental identity, some of which could be anticipated on the basis of spin-state-dependent bonding (Supporting Information Figures S6 and S7). The largest variations are between elements, following trends of the underlying covalent radii that are clearest for comparisons within a period (e.g., O: 0.62 Å vs S: 1.05 Å leads to 1.9–2.3 Å in Fe–O bonds vs 2.2–2.7 Å in Fe–S bonds, Supporting Information Figures S6 and S7 and Table S7). This observation of strong dependence on the ligand-coordinating atom identity holds across metal–ligand bond lengths if we expand to consider all 2037 AC complexes or even all 3627 UO complexes (Table 1 and Supporting Information Figures S8–S11).

Thus, we focus for our analysis on a scaled metal–ligand bond length, d_rel(Fe–X), evaluated relative to the sum of covalent radii of each ligand element, X, with iron.

1

Prior analysis⁹⁶ of experimental structures suggested that appropriate LS and HS Fe covalent radii are 1.32 and 1.52 Å, respectively (Supporting Information Table S7). We use an average value for Fe of 1.42 Å in eqn 1, which means that a d_rel(Fe–X) of 0.95 should correspond to an LS state, whereas a value of 1.05 should correspond to an HS state regardless of the ligand’s coordinating element (Supporting Information Table S7). Indeed, expected patterns in ligand-field dependence of spin-state ordering emerge when relative metal–ligand bond lengths of complexes are compared (Figure 2 and Supporting Information Figure S12). The nominally strong-field, C-coordinating Fe(II) complexes (N = 11) are well below the low-spin relative bond length cutoff (i.e., 0.95), with similar observations for the small number of pnictogen complexes (Figure 2 and Supporting Information Figure S12). Conversely, typically weak-field oxygen Fe(II) complexes (N = 45) approach or exceed the high-spin cutoff, predominantly centered around relative metal–ligand bond lengths of 1.02 (Figure 2). Interestingly, N-coordinating species (N = 902), known for their potential as spin-crossover complexes,⁹² exhibit a bimodal distribution, with one peak closer to the HS cutoff and the other closer to the LS cutoff. More surprisingly, the few S-coordinating Fe(II) complexes (N = 7) in the HE set also span a wide range of bond lengths (Figure 2).

Figure 2.

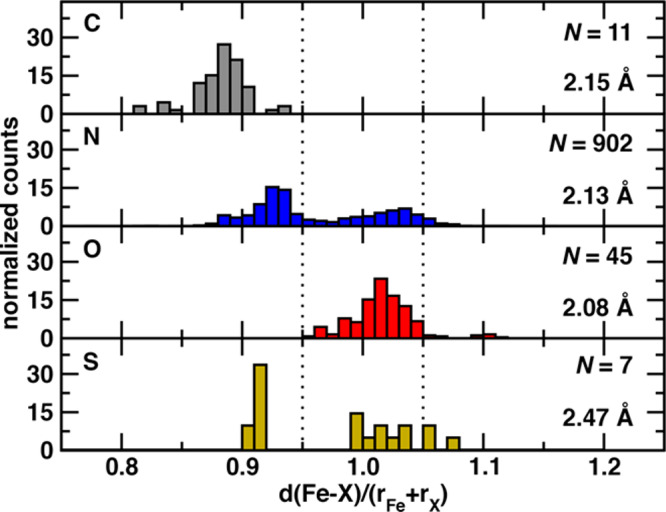
Normalized histograms of relative iron–ligand-atom bond lengths for 965 mononuclear octahedral Fe(II) complexes in the HE subset, with the coordinating element indicated in the upper left corner of each panel. Each relative Fe–X bond length is obtained with respect to the sum of covalent radii of Fe and the ligand atom, X, and the value for each element is indicated in the bottom right corner of each panel. The total number of complexes used to compute each histogram is indicated in the top right corner of each panel, and all six bond lengths in the complex are used to construct the normalized histogram. Vertical dotted lines indicate 0.95 and 1.05 relative bond length thresholds to nominally indicate LS or HS character, respectively.

Similar trends hold in Fe(III) complexes, although the increase in relative metal–ligand bond length from C-coordinating to O-coordinating species is less significant (Supporting Information Figure S12). Because of variations in available data set size, bimodal distributions are generally most evident in the larger UO or AC sets of Fe(II)/Fe(III) complexes for the specific cases of Fe–N or Fe–S bonds (Supporting Information Figures S8–S11). Overall, it appears that the multiple-peak nature of the observed relative bond-length distributions may facilitate spin-state classification, but the width and overlap of these peaks may complicate the use of heuristic cutoffs.

To identify the extent to which relative metal–ligand bond lengths can be used for spin-state classification beyond the HE set, we expanded our evaluation of structural properties to a new subset of the 2037 ANN-compatible complexes that contain up to two coordinating elements. Given the observation that relative metal–ligand bond lengths in Fe(II) N-coordinating complexes exhibit a bimodal distribution, we collected all AC Fe(II) and Fe(III) complexes that were coordinated by nitrogen and at most one other element (NX subset, Table 1 and Supporting Information Tables S8 and S9). This NX subset contains 369 Fe(II) and 211 Fe(III) complexes in which either N or the X element is the coordinating species in the equatorial plane (Table 1 and Figure 3 and Supporting Information Figure S13). On the basis of the satisfaction of heuristic cutoffs, we would expect to be confident in the classification of the ground-state spin of NX complexes as HS or LS if both d_rel(Fe–X) and d_rel(Fe–N) values are over 1.05 or under 0.95, respectively.

Figure 3.

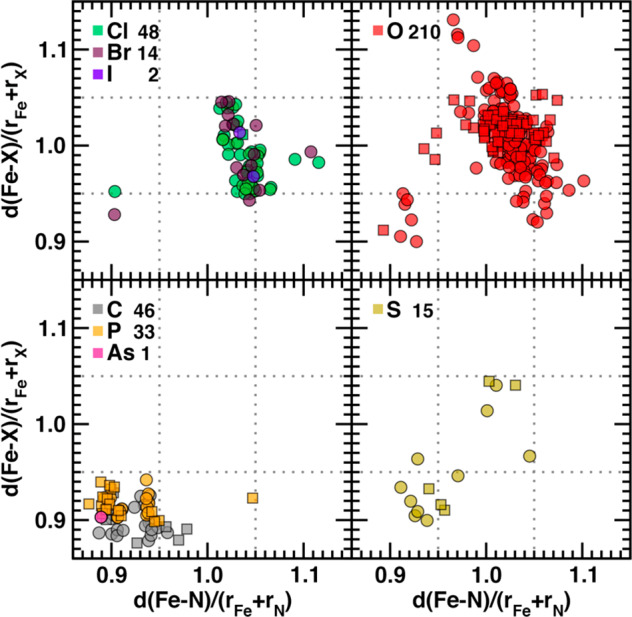
Fe–N vs Fe–X (X indicated according to inset legend) bond-length ratios computed relative to the sums of covalent radii for mononuclear octahedral Fe(II) complexes: Cl, Br, or I halides (top left), O (top right), P or As pnictogen elements, and C (bottom left), and S (bottom right). Ratios of 0.95 and 1.05 are indicated by gray dotted lines. Circle symbols indicate cases where N is the majority coordinating element (i.e., equatorial plane and up to one of the axial positions), whereas square symbols reflect the reverse cases. The Fe–N, Fe–X pair is computed from the average of all bonds of that type in the complex. The total number of cases is indicated in the legend.

Indeed, over 118 Fe(II) or Fe(III) complexes, all but one of the strong-field N/X (X = C, P, As) complexes exhibit low relative metal–ligand bond lengths for both coordinating species (Figure 3 and Supporting Information Figure S13). From this analysis, it can be concluded that structures with this combination of elements in the primary coordination sphere are unlikely to have HS ground states. For other cases, the picture is less clear. The halide-containing NX complexes exhibit a smooth variation of relative metal–ligand bond lengths that defies expectations of their role as weak-field ligands (Figure 3 and Supporting Information Figure S13). For mixtures of nitrogen coordination with other weak-field elements (e.g., O or S), a continuum of relative metal–ligand bond lengths emerges, with some structures approaching high- or low-spin thresholds but many residing between the two limits (Figure 3 and Supporting Information Figure S13). Furthermore, metal–ligand bond lengths can be relatively long for one element and short for another, confounding cutoff-based spin-state assignment (Figure 3 and Supporting Information Figure S13). The limits of cutoff-based assignment even on the NX subset thus motivates comparison to ANN predictions that can independently predict equatorial and axial bond lengths all while encoding more nonlocal information⁷¹ about the ligand chemistry’s role in metal–ligand bond length.

3c. Structure-based ANNs for Experimental Spin-State Classification

We developed a spin-state classification procedure that uses an ANN previously trained⁶³ on geometry-free representations⁷¹ for metal–ligand bond length predictions in order to overcome the limitations of heuristic cutoffs for spin-state prediction. As previously described, the ANN predicts one equatorial bond length and two independent axial bond lengths to sub-picometer accuracy on set aside test partition of the DFT data.⁶³ The assumption of high symmetry in ANN predictions mirrors that of the underlying training complexes, which had an equatorially symmetric ligand field with up to two unique axial ligands. The AC subset constrains the equatorial ligand field to contain only one coordinating element, which leads to reduced overall asymmetry with respect to the UO set (Supporting Information Figures S2, S3, and S14–S17). Nevertheless, the ligand chemistries in the AC set still may have a higher degree of asymmetry than the original training data (see Supporting Information).

To carry out spin-state classification, we developed two quantitative metrics to assign spin state based on agreement between experimental CSD values and those predicted by the ANN. If the CSD bond lengths were greater than the HS ANN prediction values or shorter than the LS ANN prediction values, then the spin state was assigned as HS or LS, respectively; otherwise, it was not assigned by this metric. One equatorial bond (eq) and two axial bonds (i.e., ax1, ax2) are compared between the CSD and ANN, but we reweighted them to reflect the four equatorial bonds in an octahedral complex and compared the difference between the CSD and HS or LS ANN predictions:

2

We also computed a reweighted root mean squared difference (RMSD) of the bond lengths between the CSD and the ANN as

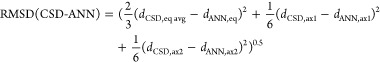3

For all complexes, we chose a spin-state assignment from the ANN prediction (i.e., HS or LS) with the lower RMSD (i.e., from eqn 3) to the CSD structural properties. For the majority of cases where both assignments were made, the two criteria led to consistent spin-state assignment. In a small number (22 Fe(II) and 11 Fe(III)) of exceptions, where two assignments were made but contradicted each other, we removed any spin-state assignment and instead labeled them as “ambiguous”. When spin states were only assigned based on the second criterion, we provided the distinguishing classification that these structures are “between” the LS and HS ANN prediction limits.

Finally, we developed a metric based on the RMSD quantities to provide an estimate of the uncertainty for the ANN-derived spin-state predictions. We computed the RMSD between the HS and LS ANN bond-length predictions with weights as in eqn 3. Our composite uncertainty score is the RMSD of the CSD to the closest ANN prediction divided by the RMSD of the two ANN spin-state predictions.

4

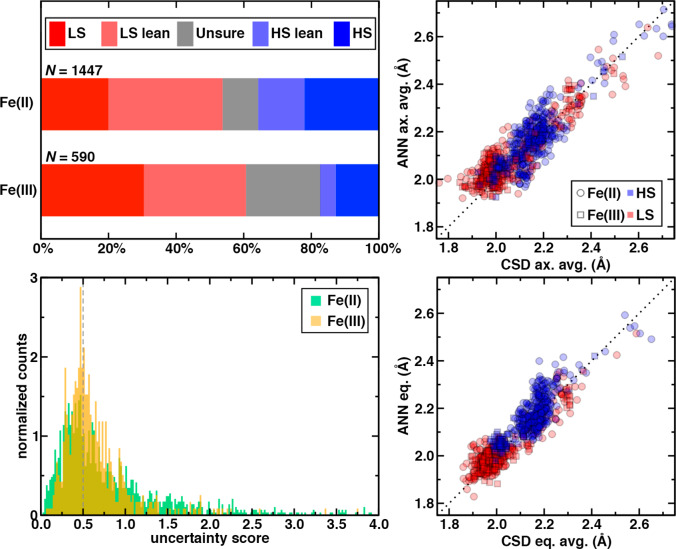
This quantity is large if CSD versus ANN agreement is poor for both candidate spin states or if the structure is relatively spin-state independent according to the ANN model. We thus selected uncertainty scores less than or equal to 0.5 as a cutoff for high confidence in ANN-derived spin-state assignments. Many Fe(II) and Fe(III) complexes have uncertainty scores below 0.5, although a long tail of high uncertainty scores is observed due to contributions from both poor ANN–CSD agreement and low spin-state sensitivity of ANN predictions (Figure 4 and see Supporting Information).

Figure 4.

(top, left) Categorization of ANN-based spin-state assignments for 1447 Fe(II) and 590 Fe(III) complexes in the AC set: confident LS (red), lean LS (pink), uncertain (gray), lean HS (light blue), and confident HS (blue). (bottom, left) Histogram of uncertainty scores for ANN predictions on Fe(II) (in green) and Fe(III) (in orange) AC complexes. The 0.5 cutoff used throughout this work is indicated as a gray dashed line. (right) Comparison of ANN and CSD bond distances (in Å) averaged over the axial bonds (top) and equatorial bonds (bottom) for Fe(II) (circles) and Fe(III) (squares) complexes on the subset of AC complexes for which spin-state assignment is confident. The LS- and HS-assigned points are shown in red and blue translucent fill, respectively. A black dotted parity line is shown on both plots.

Using the final qualitative spin-state assignment and the uncertainty score, we then classified overall spin states for structures in the AC set as definitively HS or LS if they satisfied the uncertainty score cutoff (Supporting Information Table S10). For the remaining complexes that did not satisfy the uncertainty cutoff, if the CSD value was above or below the relevant spin-derived ANN prediction, we classified these complexes as leaning LS or HS, respectively, to reflect reduced confidence (Supporting Information Table S10). Finally, both the ambiguous cases identified earlier as well as any cases both between the two ANN prediction bounds and above the uncertainty cutoff were classified as complexes with unsure spin states (Supporting Information Table S10). In total, we assign 78% of Fe(II) and 90% of Fe(III) complexes (Figure 4). A subset of 862 (602 Fe(II) and 255 Fe(III)) complexes (ca. 40% of the full set) have confident spin-state assignments (Figure 4). More complexes are expected to be LS for both Fe(II) (54% vs HS 36%) and Fe(III) (61% vs 18%), although the frequencies of confident HS and confident LS assignments are more comparable (Figure 4).

For overall structural properties of the 862-complex subset with confident ANN-derived spin-state assignments, good qualitative agreement of CSD and ANN equatorially and axially averaged bond lengths is observed (Figure 4). Since the uncertainty cutoff eliminates complexes with the poorest agreement between the CSD and ANN values, this result is not particularly surprising. However, this comparison highlights the extent to which ANN-based assignment can improve upon heuristic distance cutoffs. The distributions of ANN HS- and LS-classified bond lengths are similar, with no distinction between the axial LS or HS distributions and limited clustering of LS equatorial bond lengths at values lower than those sampled by HS-classified states (Figure 4).

We return to the HE subset of complexes for which confident spin-state assignment was obtained to determine if the significant overlap in HS and LS bond distances observed in the greater data set also hold for relative bond distances when all metal-coordinating bonds are between iron and a single element. For some elements, only a few data points remain once we isolate confident spin-state assignment, due both to their low numbers in the HE subset (e.g., Cl) as well as poor ANN performance due to their absence from ANN training data (e.g., As or P, Supporting Information Table S11). In several of these cases, only one spin state (e.g., LS As or C) that could be expected based on ligand-field arguments was assigned (Supporting Information Table S11). We therefore focus on N- or O-coordinating Fe(II) and Fe(III) complexes due to the large number of these complexes in the original HE set and the fact that they correspond to significant numbers of both HS- and LS-classified spin states after accounting for uncertainty cutoffs (Figure 5 and Supporting Information Table S11). Consistent with the greater data set, the distributions of bond lengths in Fe(II)/O or Fe(III)/O complexes overlap substantially between LS and HS complexes (Figure 5). For example, an Fe(II) complex with four dimethylformamide and two axial tetrahydrofuran ligands (CSD: CIDLIL⁹⁷) is confidently predicted (uncertainty: 0.3) by the ANN to be LS, because its CSD bond lengths (eq avg: 2.13 Å, ax avg: 2.06 Å) are much more consistent with the LS ANN prediction (eq avg: 2.11 Å, ax avg: 2.01 Å) than the HS ANN prediction (eq avg: 2.26 Å, ax avg: 2.12 Å, see Supporting Information). The CSD bond lengths for an HS-classified Fe(II) ethyl acetate complex (CSD: LIFBUX⁹⁸) are similar (eq avg: 2.12 Å, ax avg: 2.13 Å), but an HS state is confidently assigned (uncertainty: 0.25) because these bond lengths are much closer to the HS than LS ANN bond-length predictions (see Supporting Information).

Figure 5.

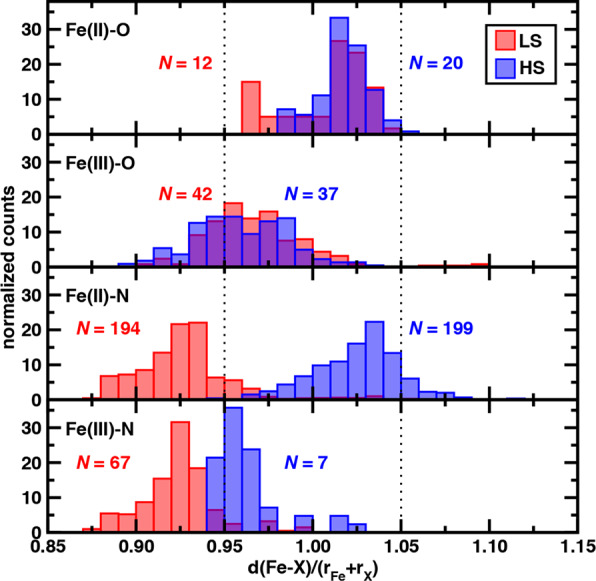
Normalized histograms of relative iron–ligand-atom bond lengths for Fe(II) and Fe(III) complexes in the HE subset with oxygen coordination (top two panes) and nitrogen coordination (bottom two panes), as indicated in insets. Only complexes for which ANN-based spin-state assignment is confident are shown, and the total count in LS (red translucent bars) and HS (blue translucent bars) are annotated in inset. Each histogram is individually normalized, and all six bond lengths in the complex are used to construct the histogram. Vertical dotted lines indicate 0.95 and 1.05 relative bond-length thresholds to nominally indicate heuristic LS or HS character, respectively.

Unlike Fe/O complexes, we observe differentiation of LS and HS bond distance distributions for Fe/N complexes (Figure 5). The greatest separation is observed for the Fe(II)/N cases, although the sample size of confident HS Fe(III) complexes is significantly smaller than for Fe(II), limiting a direct comparison of the two oxidation states (Figure 5). None of the Fe(III)/N high-spin complexes have relative bond distances above the nominal 1.05 cutoff for HS state designation, and few of the HS Fe(II)/N complexes do (Figure 5). Despite differences in the distributions, overlap is observed between the LS and HS bond lengths for both oxidation states of the Fe/N complexes (Figure 5).

To this point we have only assessed complexes based on the ANN-based spin-state classification confidence. We next consider the extent to which these classifications are consistent with ground-truth observations (e.g., experimental spectroscopy). We carry out this analysis first on representative Fe(II)/N complexes and then in greater detail in Section 3e. A representative Fe(II)/N LS complex (CSD: DOQRAC⁹⁹) consists of three acetonitrile monodentate ligands along with a tridentate macrocycle (Figure 6). Our algorithm for plane selection chooses one acetonitrile ligand and one coordination site of the tridentate macrocycle to be axial, although the range of Fe–N bond lengths across the ligands (2.09–2.15 Å) is relatively small and close to a d_rel(Fe–N) of 1.0, meaning that any cutoff-based assignment would fail (see Supporting Information Table S7). This complex is classified as LS by the ANN (uncertainty: 0.37) due to very good agreement between the CSD and the LS predictions for axial bond lengths and better agreement of the CSD with the LS ANN than HS ANN predicted average equatorial bond lengths (Figure 6). Experimental spectroscopy confirms⁹⁹ the LS assignment made by our ANN-based classification.

Figure 6.

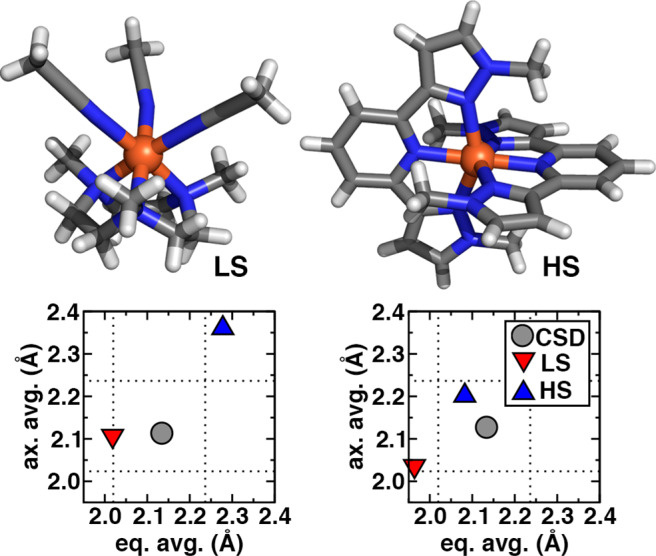
Representative LS (left) and HS (right) assignments by the ANN of two Fe(II)/N HE complexes. The structures of the complexes are shown at top (left, CSD: DOQRAC, right, CSD: VILZOH) with stick structures and the iron center shown as a sphere. Carbon atoms are in gray, nitrogen in blue, hydrogen in white, and iron in brown. The equatorially and axially averaged bond lengths (in Å) from the CSD structure (gray circle) are compared to the ANN-predicted LS (red, triangle down) and HS (blue, triangle up) values. The 95% and 105% threshold for the Fe–N bond lengths corresponding to heuristic LS and HS character are shown as dotted lines for reference.

In prior work, we⁷⁸ evaluated the ability of an ANN to predict the HS–LS adiabatic spin splitting, ΔE_H-L, of this same complex. We had observed⁷⁸ that the ΔE_H-L ANN strongly overstabilized (ΔE_H-L = −34.7 kcal/mol) the HS state with respect to ΔE_H-L from hybrid (i.e., B3LYP⁸⁶⁻⁸⁸) DFT. We rationalized this poor ΔE_H-L ANN performance by the significant dissimilarity of the CSD complex to available training data.⁷⁸ The hybrid DFT energetics predicted a weakly HS state (ΔE_H-L = −1.4 kcal/mol), inconsistent with the experimentally observed ground state, although the two states are likely nearly degenerate due to the observation of spin-crossover behavior.⁹⁹ The correct LS assignment of this complex that had challenged energy-based prediction models demonstrates that structure-based classification can provide an independent corroboration of spin-state assignment, even when training data are limited or energetics can be expected to be sensitive to the level of theory used. Our analysis of prior, energy-based spin-state assignment neglects zero point vibrational energy and the crystal field environment contributions, which could be considered in future work to more quantitatively assess the magnitude of energetic errors we observe with hybrid DFT.

For comparison, we choose a representative HS-classified Fe(II)/N complex (CSD: VILZOH¹⁰⁰) consisting of two tridentate, substituted pyridinyl ligands with bond distances (2.08–2.17 Å) relatively comparable to the CSD values in the previously described LS complex (Figure 6). A heuristic approach would fail to classify the spin state of this complex, as the relative bond lengths are intermediate (0.97–1.02) between the LS and HS cutoffs. Our approach classifies this structure as HS (uncertainty: 0.47), because the CSD bond lengths are significantly closer to the HS ANN values (eq avg, CSD: 2.13 Å vs HS ANN: 2.08 Å) than to the LS ANN values (Figure 6). Notably, the LS and HS ANN values themselves are considerably closer to each other in this case than they were in the LS complex, leading to a higher uncertainty score (Figure 6). Experimental spectroscopy¹⁰⁰ indicates that this complex has an HS ground state, confirming our ANN structure-based assignment. Interestingly, this complex is a methylated derivative of a well-known temperature-dependent, spin crossover complex (i.e., LS at low temperature). Experimental characterization showed¹⁰⁰ the methylated complex to be in an HS state at low temperature, suggesting the importance of the single addition of methyl groups three bonds away from the metal center. Such subtle effects can be expected to be easier to quantify with the structure-based ANN approach than more standard methods such as direct evaluation of ΔE_H-L with hybrid DFT or an ANN, although we had not previously evaluated ΔE_H-L for this complex.

Outside of the HE subset, even more complex relationships are observed in the relative bond distances when multiple elements are present in the primary coordination sphere, as exemplified by the NX subset (see Section 3b). We revisit NX complexes for which confident structure-based spin-state assignment was possible. We focus on the Fe(II)/N and Fe(III)/N complexes that are partly coordinated by Cl, O, or S coordinating atoms due to the significant number of these complexes in the full NX set as well as the wide range of d_rel values that are observed over these sets (see Figure 3 and Supporting Information Figure S13). Over the subset of all possible NX (X = Cl, O, or S) complexes, structure-based ANN classification is confident for 25–50% of the complexes, independent of oxidation state (Supporting Information Table S12).

Within the confidently assigned subset, the classified spin states for N/S complexes are most consistent with expectations based on heuristic cutoffs of the relative bond distances (Figure 7). All LS N/S Fe(II/III) complexes have d_rel(Fe–N) and d_rel(Fe–S) close to or below 0.95, with significantly higher values (d_rel(Fe–N) = 1.0, d_rel(Fe–S) = 1.05) for the single HS N/S Fe(II) complex (Figure 7). Mössbauer spectroscopy¹⁰¹ on the HS complex (CSD: ZERFEK¹⁰¹) corroborates the confident (uncertainty: 0.29) structure-based ANN HS classification, which was made possible by the ANN’s accurate prediction (HS ANN: 2.54 Å vs LS ANN: 2.31 Å) of elongated, equatorial Fe–S bond lengths (CSD: 2.58 Å, Figure 7).

Figure 7.

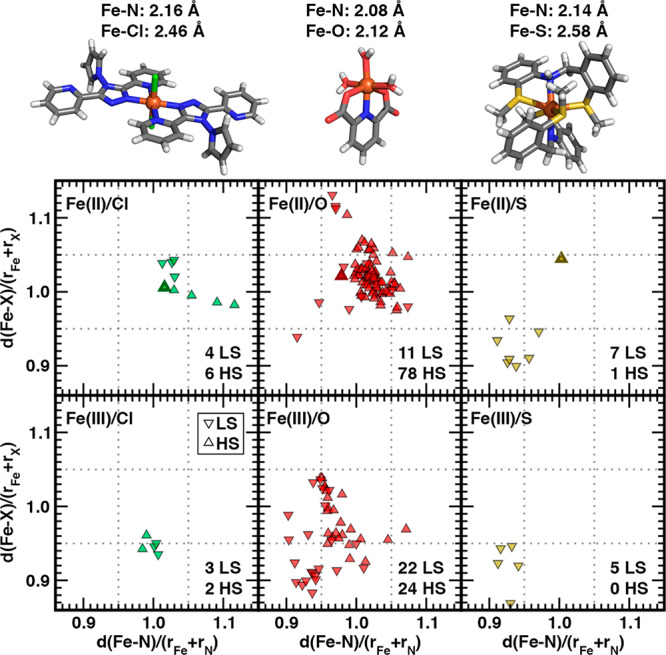
Fe–N vs Fe–X (X indicated according to inset in each pane) bond-length ratios computed relative to the sums of covalent radii for NX subset octahedral Fe(II) (top) and Fe(III) (bottom) complexes with N/Cl (left), N/O (middle), and N/S (right) coordinating atoms. Ratios of 0.95 and 1.05 are indicated by gray dotted lines. Only points for which spin-state assignment is confident are shown, and triangle down symbols indicate LS, whereas triangle up indicates HS. The total number with each spin assignment is shown in the bottom right corner of each pane. The Fe–N, Fe–X pair is computed from the average of all bonds of that type in the complex. Three representative HS Fe(II) complexes are shown at top and correspond to the only symbol that is solid filled with a dark colored border in each representative pane: N/Cl (left, CSD: POKNEJ), N/O (middle, CSD: DAQVEZ), N/S (right, CSD: ZERFEK). Structures are shown as sticks with carbon in gray, nitrogen in blue, hydrogen in white, chlorine in green, sulfur in yellow, oxygen in red, and iron in brown.

The N/Cl complexes have more ambiguous d_rel values in comparison to N/S complexes, despite a similar data set size (Figure 7). Shorter d_rel(Fe–Cl) values are observed for Fe(III) complexes regardless of spin state, likely due to stronger electrostatic attraction than in Fe(II) complexes (Figure 7). While longer d_rel(Fe–N) values (i.e., >1.05) are observed for some HS-classified Fe(II) complexes, exceptions are also apparent, and no such trend is observed in the Fe(III) complexes (Figure 7). We selected as a representative example the HS Fe(II) N/Cl complex (CSD: POKNEJ¹⁰²), which has the shortest HS d_rel(Fe–N) and a comparable d_rel(Fe–Cl), both of which are ∼1.0 (Figure 7). Susceptibility experiments¹⁰² were consistent with an HS ground state, confirming the classification by the structure-based ANN. In comparison, heuristic distance-cutoff-based assignment of this complex would not be possible, since the complex has d_rel values equidistant between the HS and LS heuristics.

For the largest N/O complex subsets, there appears to be little separation between the LS and HS d_rel values (Figure 7). The few points with short simultaneous d_rel(Fe–N) and d_rel(Fe–O) values of ∼0.95 for both are indeed classified as LS states (Figure 7). A similar classification of extreme HS points is more challenging, as LS and HS states have similarly long (>1.05) d_rel(Fe–N) values (Figure 7). Most of the points either have intermediate d_rel(Fe–N) and d_rel(Fe–O) values (i.e., close to 1.0) or have a combination of one long bond type with one short bond type (Figure 7). Thus, heuristic cutoff-based assignment of spin states would only be possible for a small fraction of N/O complexes. As a representative example HS Fe(II) N/O complex, we selected a complex (CSD: DAQVEZ¹⁰³) of a tridentate dicarboxylated pyridine ligand with water molecules in the three remaining coordination sites (Figure 7). The average Fe–N and Fe–O bond lengths are both relatively short (2.08–2.12 Å), likely due to the overriding influence of the coordinating carboxylates, but ANN-based assignment provides a confident (uncertainty: 0.16) HS classification (Figure 7 and see Supporting Information). Despite this unusual structure, magnetometry experiments on related complexes¹⁰³ are suggestive of an HS ground-state assignment, consistent with the structure-based ANN prediction. Thus, ANN structure-based spin-state classification shows promise as an alternative to energy-based or heuristic distance-based spin-state assignment across a range of complex ligand chemistries.

3d. Curation of a Spin Crossover Complex Set

Given their frequent study as candidate spin-crossover (SCO) materials, one of which we discussed in Section 3c, we curated a broad set of putative Fe(II) SCO complexes. From the original set of 2865 nonunique Fe(II) complexes, we performed a series of steps to identify the refcodes most likely to correspond to experimentally identified SCO complexes. Specifically, we focused on those deposited at multiple temperatures believed to correspond to distinct low- and high-spin states and identified by the authors in the associated publication as SCOs. The CSD refcodes containing multiple copies of the same six-letter code with a number appended were expected to represent structures diffracted at multiple temperatures. For cases where multiple refcodes were present, we reviewed every component (i.e., isolated chemical species) of the CSD crystal structure to identify the one that matched the original six-letter code Fe(II) structure based on both molecular weight and connectivity. For the 95 Fe(II) complexes that satisfied these criteria, the resulting axial and equatorial bond lengths were then saved for the highest and lowest recorded temperatures as candidate high- and low-spin geometries, respectively.

To narrow the results of this query, we carried out text search and sentiment analysis to narrow the pool of candidate SCO complexes. We mined titles and abstracts using the pybibliometrics¹⁰⁴/Scopus API package using article DOIs obtained from the CSD. For titles and abstracts, VADER¹⁰⁵ text analysis was performed on sentences containing essential keywords (i.e., “spin crossover”, “cross over”, or “sco”). We required that these keywords were not just present but had positive mentions of SCOs in their titles or abstracts, avoiding instances where the text was referring to the compound not being an SCO complex by requiring positive VADER sentiment. A large number (i.e., 626) of Fe(II) complexes were identified through the text analysis step, but only 66 complexes were identified in both the temperature-dependent bond-length extraction step and in this text analysis step.

Finally, to select an ANN-compatible subset of SCO complexes, we eliminated any cases where the change in spin state did not exhibit expected bond elongation from low- to high-spin either experimentally or predicted by our ANN. We also eliminated cases that had either low- or high-temperature structures with high equatorial plane bond distortion (>0.2 Å) as in our other data set curation steps. Finally, low- and high-temperature structures with averaged equatorial bond lengths that differed by less than 0.05 Å were also excluded because these bonds are nearly identical within the uncertainty resulting from the resolution of the X-ray diffraction experiment. After all of these steps, we obtain a final set of 46 unique complexes that both exhibit temperature-dependent equatorial bond lengths and have been positively noted as SCO complexes by their authors. Details of candidate SCO complexes eliminated at intermediate steps are provided in the Supporting Information.

3e. Analyzing Structure-based Spin State Prediction on SCO Complexes

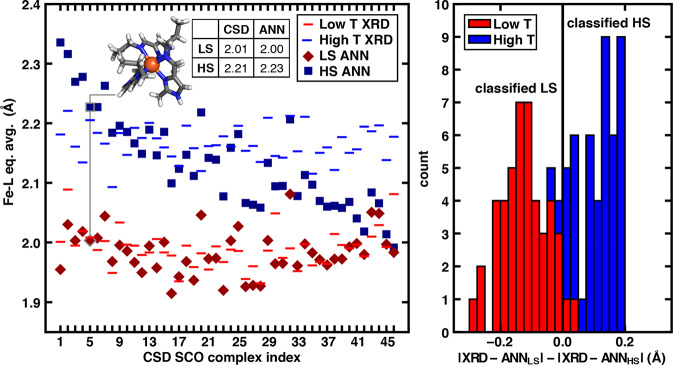
To evaluate the promise of the structure-based ANN to classify experimental spin states, we analyzed the performance of the approach over all 46 curated Fe(II) SCO complexes for which both sentiment analysis and distinguishable, multiple temperature (T) X-ray diffraction (XRD) structures were available (see Section 3d). All identified complexes belong to the HE set with nitrogen coordination, consistent with the tendency⁹² of Fe(II)/N complexes to exhibit SCO behavior. Here, we assume the low-T XRD iron–ligand bond length corresponds to the LS state and the high-T XRD iron–ligand bond length corresponds to the HS state, because the LS state is typically enthalpically favored, whereas the HS state is typically entropically favored.⁹² Given the weak separation between HS and LS axial bond lengths, we focus on the equatorially averaged bond lengths to quantify differences in the LS and HS CSD structures (see Figure 4). The difference in the equatorial bond lengths between low- and high-T XRD structures for the 46-complex SCO set is large (average: 0.18 Å, range: 0.10–0.22 Å, Figure 8 and see Supporting Information Table S13). Individual XRD bond length distributions (LS: 1.93–2.09 Å and HS: 2.09–2.22 Å) do overlap over the full set, corresponding in many cases to intermediate (i.e., between 0.97 and 1.02) d_rel(Fe–N) values (Supporting Information Table S13).

Figure 8.

(left) Fe–L equatorially averaged bond lengths (in Å) of identified CSD Fe(II)/N SCO complexes: low- and high-T XRD values (red and blue horizontal lines) are compared to predictions from the ANN for the LS (red diamond) and HS (blue square) states. An example SCO complex is shown as a stick structure in inset (CSD: BAKGUR), corresponding to the points outlined in gray and highlighted by the gray line. Atoms are colored as gray for carbon, blue for nitrogen, white for hydrogen, and brown for iron. The CSD values for the equatorially averaged bond lengths are compared to the ANN-predicted values as shown in the inset table. (right) Overlapping histograms of deviations of ANN-predicted bond lengths from XRD values (in Å) for low-T (red) and high-T (blue) XRD structures. Structures to the left of the vertical line are classified as LS, while structures to the right are classified as HS.

To perform ANN structure-based spin-state classification on this set of complexes, we compare the equatorially averaged bond lengths of the low- or high-T XRD structures to the predictions of the equatorial bond length from the LS and HS ANN. Through comparison of the expected ANN bond length to the appropriate XRD structure (i.e., LS for low-T or HS for high-T), we observe low discrepancies, especially for the LS states (avg: 0.027 Å, range: 0.00–0.097 Å, see Supporting Information Table S13). Larger disagreements observed for the HS states (avg: 0.070 Å) could be due to the fact that the DFT bond lengths are obtained at 0 K, but the high-T structures are solved at higher temperatures (HS: 160–420 K vs LS: 25–243 K), where thermal corrections to the bond lengths could be more significant (Supporting Information Table S13).

To classify spin states based on the low-T and high-T equatorial bond lengths, we select the spin state corresponding to the ANN in better agreement with the experimental structure (Supporting Information Table S13). Over the 92 low- or high-T XRD structures, 96% of structures are correctly classified by the ANN, with only two low-T and two high-T structures misclassified (Figure 8). For the small number of cases for which the ANN incorrectly classifies the spin state, incorrect classification for the LS states is due to long low-T bond lengths that are underpredicted by the LS ANN in higher denticity (i.e., tridentate in RIPZAS¹⁰⁶ or hexadentate in IMANIT¹⁰⁷) structures not present in the ANN’s training data.^70,71 The incorrect classification of high-T structures as LS in two cases occurs when the LS state has a relatively long bond length and the ANN overestimates the HS elongation, leading the high-T bond length to be closer to the LS ANN value (Figure 8 and Supporting Information Table S13).

For the remaining 88 cases, the ANN-based classification is robust when the bond length of a compound is atypical, because the ANN encodes significant information about ligand chemistry. For example, the relevant HS/LS ANN predicts the equatorial bond lengths of a homoleptic, facial isomer complex with bidentate methylimidazole/methylideneamino ligands (CSD: BAKGUR¹⁰⁸) to within 0.02 Å for both low-T (2.00 Å) and high-T (2.22 Å) XRD structures (see inset in Figure 8). The bond length in the high-T structure of a heteroleptic complex with isothiocyanate ligands (CSD: AKENAF,¹⁰⁹ high-T XRD: 2.09 Å) is comparable to that in the low-T structure of a homoleptic complex with six monodentate substituted tetrazole ligands (CSD: YAGYIP,¹¹⁰ low-T XRD: 2.09 Å), but the two structures are correctly classified as HS and LS by the ANN, respectively (Figure 8 and see Supporting Information Table S13). Thus, we expect this low-cost machine learning model approach to provide a valuable complement to experimental interpretation in spin-state assignments, particularly where energetically derived assignments from approximate electronic structure methods are challenging and time-consuming.

4. Conclusions and Summary

Given the challenges associated with predictive spin-state energetics using widely employed electronic structure methods (e.g., density functional theory), we have investigated alternative approaches to assigning the ground-state spin of experimentally characterized transition-metal complexes. For a small set of mononuclear octahedral iron complexes in the spectrochemical series, we observed that metal–ligand bond lengths were both less sensitive to method choice than spin-state energetics and also distinguishable between spin states. These observations motivated a quantitative assessment of the degree to which experimental metal–ligand bond lengths could be used for spin-state classification. From a database of experimentally characterized structures, we curated a data set of over 3600 unique, structurally characterized Fe(II)/Fe(III) mononuclear octahedral complexes. Analysis of metal–ligand bond lengths in subsets of the data suggested trends in distance distributions that could sometimes be used to assign ground-state spin. Nevertheless, intermediate bond lengths for many complexes indicated limits to purely heuristic, distance-cutoff-based spin-state assignment.

To generalize our approach, we employed an ANN trained on hybrid DFT data to predict spin-state-dependent metal–ligand bond lengths. On a 2037 complex subset of Fe(II)/Fe(III) structures compatible with the ANN, this approach led to spin-state assignments in 80–90% of all complexes. We showed how even when ANN and experimental metal–ligand bond lengths differed slightly, the use of proximity to one of the two predictions enabled confident spin-state assignment. Confident ANN ground-state spin assignments were obtained even when bond distances were paradoxical in comparison to heuristic distance cutoffs. These ANN-classified spin states were corroborated by available experimental characterization from the literature. In a representative case for which we had prior hybrid DFT energetics and ANN energetic predictions, we showed that this bond-length classification approach reversed the ground-state spin assignment in improved agreement with experiment. To generalize the approach beyond the presently ANN-compatible subset, necessary next steps would be to broaden the ANN’s training data and assess its ability to predict spin-state-dependent bond lengths in asymmetric complexes.

To develop a quantitative measure of the promise of our ANN classification approach, we screened the unique complex data set with sentiment analysis to extract known Fe(II) SCO complexes for which multiple spin states had been structurally characterized. Over these 46 SCO complexes, the bond-length-based ANN spin-state classification correctly assigned low-T and high-T XRD spin states in 96% of cases.

In brief, the chief insights and conclusions from this study were:

• Relative bond length is a valuable measure that enables distinguishing of spin-state-dependent metal–ligand chemical bonding.

• An ANN we have trained to predict DFT-level metal–ligand bond lengths can distinguish differences in bond length in differing spin states from experimental structures where any heuristic rules would fail.

• Our ANN succeeds because the RAC featurization it has learned encodes key aspects of nonlocal ligand chemistry (i.e., beyond the metal and its direct coordinating atoms).

• This structure-based approach improved upon DFT-energetics-assigned ground states and correctly predicted experimental spin states mined from the literature.

• In a set of all text-mined Fe(II) SCO complexes, we correctly assigned 96% of spin states.

Thus, our bond-length-based ANN classification approach represents a promising complement to energy-based spin-state assignment from DFT at the reduced cost of ANN model evaluation. By combining bond-length ML models with energetic models or DFT predictions, we envision improved robustness in high-throughput computational screening of challenging materials spaces.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.0c01458.

• DFT versus CSD data for Fe(II)/Fe(III) homoleptic spectrochemical complex properties; hyperparameters and training details of the bond length ANN; details of equatorial plane assignment; metrics of distortion of the eq plane, overall, and ax plane for the UO and AC sets; histogram of molecular weights in the UO and AC sets; analysis of element types and frequency in the equatorial/axial plane and overall for UO and AC complexes as well as identification of the NX subset; histograms of absolute metal–ligand distances in Fe(II)/Fe(III) HE, AC, and UO complex subsets; covalent radii used for computing relative distances; histograms of Fe(III) HE relative bond distances; pairwise relative bond distances in Fe(III) NX complexes; detailed statistics of spin-state classification in the AC set by the ANN; details of element-wise spin-state classification in the HE set by the ANN; percentage of confident spin-state assignments in representative NX complexes; spin-state classification and details of 46-complex set of SCO structures (PDF)

• Stepwise curation results of the 3627 complex UO set from the CSD as well as properties of representative subsets of data; stepwise curation results and explanation of intermediate steps of 46 Fe(II) SCO complexes from the CSD (ZIP)

Author Contributions

^§ These authors contributed equally.

The authors declare no competing financial interest.

Special Issue

Published as part of The Journal of Physical Chemistry virtual special issue “Machine Learning in Physical Chemistry”.