Deep Learning of Activation Energies

Abstract

Quantitative predictions of reaction properties, such as activation energy, have been limited due to a lack of available training data. Such predictions would be useful for computer-assisted reaction mechanism generation and organic synthesis planning. We develop a template-free deep learning model to predict the activation energy given reactant and product graphs and train the model on a new, diverse data set of gas-phase quantum chemistry reactions. We demonstrate that our model achieves accurate predictions and agrees with an intuitive understanding of chemical reactivity. With the continued generation of quantitative chemical reaction data and the development of methods that leverage such data, we expect many more methods for reactivity prediction to become available in the near future.

Activation energy is an important kinetic parameter that enables quantitative ranking of reactions for automated reaction mechanism generation and organic synthesis planning. Achieving reliable activation energy prediction is an integral step toward the complete prediction of kinetics. Machine learning, particularly deep learning, has recently emerged as a promising data-driven approach for reaction outcome prediction¹⁻⁶ and for use in organic retrosynthetic analysis.⁷⁻¹⁰ These methods leverage massive data sets of organic reactions, such as Reaxys¹¹ and Pistachio.¹² However, the methods operate on qualitative data that indicate only the major reaction product and mostly lack any information regarding reaction rates. Moreover, many of the organic chemistry reactions are not elementary. The data used by Kayala and Baldi¹ and Fooshee et al.² are an exception, but quantitative information is still missing.

Linear methods, like Evans–Polanyi relationships¹³ and group additivity models,¹⁴⁻¹⁷ have been successfully used in automated reaction mechanism generation to estimate rate constants, but they are limited in scope and applicability. New parameters have to be derived for each reaction family, and predictions far from the training data often go awry. Nonlinear decision trees provide more flexible models for the estimation of kinetics but are also most effective when they are specific to a reaction family.¹⁸ Neural networks may be a promising alternative as large data sets become more readily available.

Recently, some quantitative reaction prediction research using neural networks has become available, but it is limited in its application. Gastegger and Marquetand developed a neural network potential for a specific organic reaction involving bond breaking and formation, likely the first of its kind.¹⁹ Allison described a rate constant predictor for a specific reaction type involving reactions with OH radicals.²⁰ Choi et al. looked specifically at activation energy prediction using machine learning.²¹ However, their training data were composed of reactions in the Reaction Mechanism Generator (RMG)¹⁸ database that comprised many similar reactions such that a random test split yielded ostensibly good results. Their issue stems from the fact that the vast majority of the RMG database is composed of just two reaction families: hydrogen abstraction and addition of a radical to a multiple bond. Reactions within the same family tend to have similar kinetics. Therefore, a model trained on such data performs particularly well for the two reaction types but not well for others. Moreover, the model of Choi et al. required knowledge of the reaction enthalpy and entropy to make a prediction. Singh et al. similarly predicted reaction barriers for a small data set of dehydrogenation reactions involving dissociation of N₂ and O₂ on surfaces.²² Their model also required the reaction energy as additional input.

Our goal is to develop a deep learning model to predict activation energies across a wide range of reaction types that does not depend on any additional input and requires only a graph representation of reactants and products. Such a model would be useful as a first step in deep learning-based estimation of kinetics for automated reaction mechanism generation (e.g., in RMG¹⁸) or would allow for quantitative ranking of reaction candidates that were generated via combinatorial enumeration of potential products given a reactant.²³ Training such a model requires suitable quantitative data. We use data based on large-scale quantum chemistry calculations,²⁴ but high-throughput experimentation²⁵ is also starting to become a valuable source of new data.

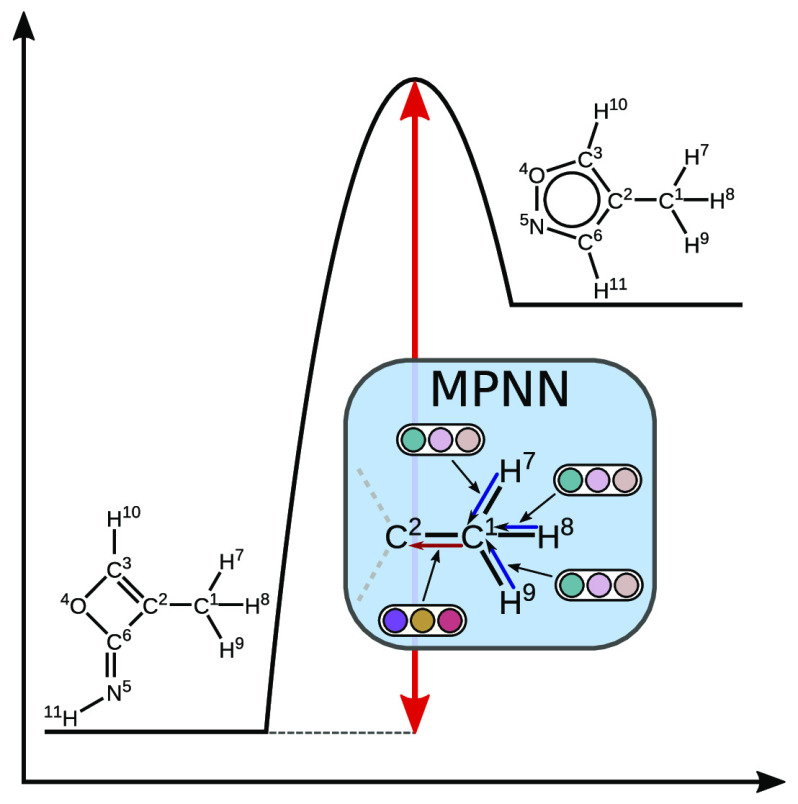
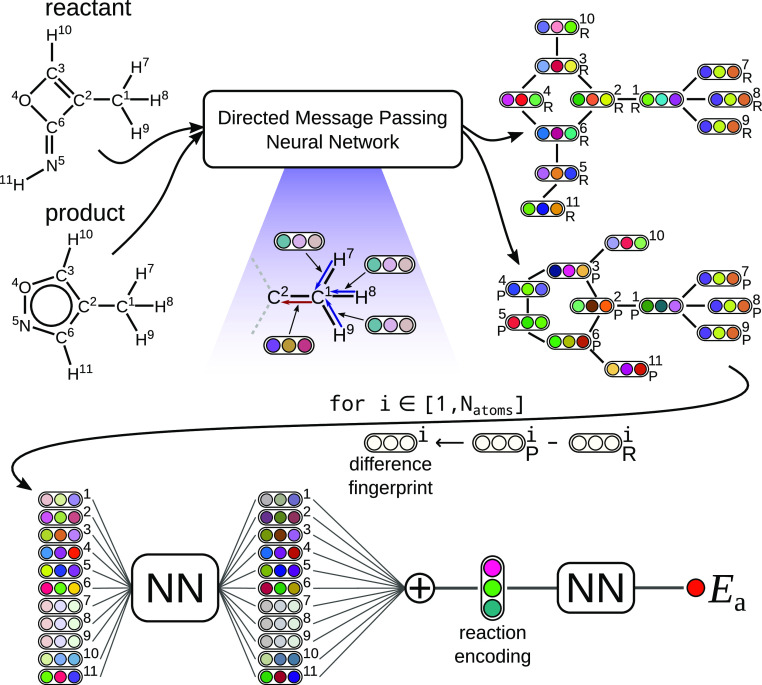
To effectively learn activation energy, we must encode the atoms involved in a reaction that change significantly in a way that they contribute most to the predicted property. To accomplish this, we extend a state-of-the-art molecular property prediction method, chemprop, developed by Yang et al.,²⁶ to work with atom-mapped reactions. Figure 1 shows a schematic of the method, while the Supporting Information provides more detail about the network, training procedure, and hyperparameter optimization. Our modified code is available on GitHub in the reaction branch of chemprop.²⁷ The code also includes the trained model in the model directory that can be directly used with the predict.py script in chemprop.

Figure 1.

Illustration of the neural network model used to predict activation energy given a chemical reaction. The difference fingerprint approach emphasizes atoms that change during the reaction.

The method of Yang et al. is a directed message passing neural network (D-MPNN) for molecular property prediction, which is a type of graph convolutional neural network.²⁸⁻³⁰ Graphs naturally represent molecules in which atoms are the vertices and bonds are the edges. The D-MPNN constructs a learned representation of a molecule by passing information between elements of the graph using messages associated with directed edges/bonds. A hidden representation for each directed bond embeds initial atom features, such as atomic number, and initial bond features, such as bond order, using a neural network. Additional neural networks iteratively update these hidden representations by incorporating the information from neighboring bonds. Afterward, we transform the hidden bond vectors into hidden atom vectors and sum them to obtain a molecular feature vector. However, such a summation would lose information about the order of atoms, which is necessary to encode reactions effectively. As shown in Figure 1, we resolve this issue by using the same D-MPNN to encode the reactant and product into the intermediate representation given by the hidden atom vectors. Because the mapping of atoms between the reactant and product is known, we calculate differences between all product and reactant atoms to yield atomic difference fingerprints. This approach is similar to the difference network described in ref (5). Next, we pass each of the fingerprints through the same neural network and aggregate them into a reaction encoding. The last step of the process is the readout phase, in which the network learns a linear combination of the elements in the reaction encoding to give an estimate of the activation energy.

The idea behind constructing difference fingerprints is to subtract out the effects of atoms that do not change significantly in the reaction and, therefore, do not contribute much to the activation energy prediction. This requires that atom-mapped reactions are available, which is often not the case, but developing methods for automatic atom mapping is an active area of research.³¹⁻³³ With large molecules, even atoms that do not change their covalent bonding environment may have large difference fingerprint magnitudes because they may strengthen van der Waals attractions between different parts of the molecule or sterically hinder certain transition states.

We train our model on a newly developed gas-phase organic chemistry data set of elementary atom-mapped reactions based on density functional theory (DFT).²⁴ These data span a diverse set of reactions with at most seven heavy atoms involving carbon, hydrogen, nitrogen, and oxygen. Reactions are available at two different levels of theory: B97-D3/def2-mSVP and ωB97X-D3/def2-TZVP. Both levels are used in a transfer learning approach similar to that in ref (34), but we measure the final model performance against the ωB97X-D3/def2-TZVP data. We augment our data by including all of the reverse reactions, as well, which essentially doubles the training data and may further help in subtracting out the effect of distant atoms. This results in a total of 33000 B97-D3/def2-mSVP and 24000 ωB97X-D3/def2-TZVP reactions. The activation energies, E_a, provided in the data set are not obtained by fitting to an Arrhenius form, but they represent the difference of transition state and reactant electronic energies, each including zero-point energy.

To assess whether the trained model can make useful predictions across a wide range of chemical reactions, the test set should contain reactions that are sufficiently different from those in the training data, i.e., out-of-domain data. To generate such a data split, we partitioned our data on the basis of the scaffold splitting technique, which has been shown to approximate time splits that are common in industry and are a better measure of generalizability than random splits.²⁶ We performed the split on the basis of the scaffold of the reactant molecule. Moreover, to obtain a less variable estimate of the model performance, we evaluated the model using 10-fold cross-validation. A split into 85% training, 5% validation, and 10% test data yields a test set mean absolute error (MAE) of 1.7 ± 0.1 kcal mol^–1 and a root-mean-square error (RMSE) of 3.4 ± 0.3 kcal mol^–1, where the indicated bounds correspond to one standard deviation evaluated across the ten folds. While this error is quite small given the diverse nature of the data, which span an activation energy range of 200 kcal mol^–1,²⁴ the true error is confounded by the accuracy of the ωB97X-D3 method used to generate the training and test data, which itself has an RMSE of 2.28 kcal mol^–1 measured against much more accurate reference data.³⁵

Because the model does not take three-dimensional structural information into account and because the training and test sets include only a single conformer for each molecule (not necessarily the most stable one), some of the error is due to conformational variations of the reactant or product structures. More accurate models could be based on the molecular geometries, which have been shown to work well for molecular property prediction and the development of neural network potentials.³⁶ Nonetheless, we do not employ such information here because it is often not readily available in applications when one wishes to rapidly predict activation energies, like in automated reaction mechanism generation.

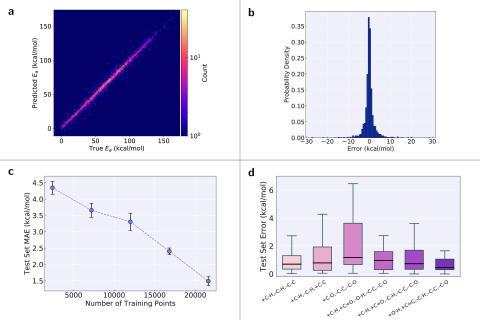
More fine-grained results are shown in Figure 2. The parity plot in Figure 2a shows that accurate predictions are made across the entire activation energy range, and this accuracy is even maintained in regions where data are sparser. Furthermore, there seems to be no systematic over- or underprediction, and large outliers are relatively infrequent. This is further shown in the error histogram in Figure 2b, which indicates that only very few reactions have errors in excess of 10 kcal mol^–1. Depending on the application, the model may be sufficiently accurate for quantitative predictions if errors slightly in excess of those of the ωB97X-D3 method are acceptable. An MAE of 1.7 kcal mol^–1 implies that rate coefficients differ by a factor of 2.4 from the true/DFT value at 1000 K on average, which is often quite acceptable. However, this error increases to a factor of 17.5 at 300 K. Moreover, entropic effects that would typically be captured in the prefactor used in Arrhenius expressions are not taken into account in this analysis and would constitute an additional source of error.

Figure 2.

Deep learning model results. (a) Parity plot of model predictions vs “true” (ωB97X-D3) data for the first fold. (b) Histogram of prediction errors (predicted minus “true”) for the first fold. (c) MAE vs the number of training data points for the deep learning model. The error bars indicate one standard deviation calculated across the ten folds. (d) Distributions of errors (outliers not shown) for the six most frequent reaction types (first fold). Each reaction type includes only the bond changes occurring in the reaction, e.g., +C–H,–C–H,–C–C means that a carbon–hydrogen bond is formed, a different carbon–hydrogen bond is broken, and a carbon–carbon single bond is broken in the reaction.

Regardless, the results show that the model is suitable for ranking a list of candidate reactions by their likelihood of occurring. This may lead to an improvement over qualitative reaction outcome prediction approaches by enabling a more quantitative ranking. However, a direct comparison is not currently possible because such approaches are generally not based on elementary reactions and involve multiple steps in solvated environments. A promising, immediate application of the model could be to enable discovery of novel reactions from species in large chemical mechanisms. Reaction candidates can be generated from each molecule in a mechanism by changing bonds systematically to enumerate potential products.²³ The deep learning model can then assess which candidates have the lowest barriers and warrant further evaluation. Such a reaction discovery process would proceed in a template-free manner, whereas conventional reaction mechanism generation software is based on templates to restrict the allowable chemistry.¹⁸

Figure 2c also shows that the model strongly benefits from additional training data, and the typical decrease in the slope of the learning curve is not yet evident. However, this is partially because hyperparameter optimization was performed on an 85:5:10 split. Optimization for the points at lower training ratios would lead to improved performance and show a more typical curve.

Unlike our model, other methods for the estimation of activation energy and kinetics, such as the decision tree estimator used in the RMG software,¹⁸ are often applicable only within a specific reaction family/template. The decision tree templates implemented in RMG are based on known reactivity accumulated over decades and manually curated into reaction rules. Conversely, the training data for the deep learning model are obtained from systematic potential energy surface exploration and contain many unexpected reactions that do not fall within the space encoded by the RMG templates. In fact, only 15% of all reactions in the data used for this study have a matching template in RMG (distribution of RMG families shown in the Supporting Information). There is no statistically significant difference between the deep learning model performance on RMG-type reactions and on non-RMG-type reactions (p ≤ 0.05), which shows that our template-free model can be applied to many reactions that do not fit into expected reaction families and may be useful for discovering new and unexpected reactions.

Figure 2d illustrates that the test set error is not the same across all reaction types (examples of each reaction type are shown in the Supporting Information), but the reasons for this are not obvious. The +C–H,–C–H,–C–C type leads to the formation of carbenes via hydrogen transfer and ring opening and has a distribution of errors similar to that of the +C–H,–C–H,+C–C type, which is its reverse. Of the most frequent reaction types, the largest errors are associated with the +C–O,–C–C,–C–O type, which is similar to the +C–H,–C–H,–C–C type but involves the transfer of a hydroxy group instead of a hydrogen or the rearrangement of a cyclic ether. The last three reaction types shown in Figure 2d generally have small errors, although the +C–H,+C=O,–C–H,–C–C,–C–O type has a tail skewed toward larger errors, potentially because of its unusual zwitterion/carbene product. Interestingly, the model generally performs poorly for reactions with three heavy atoms (shown in the Supporting Information), perhaps because the training data are dominated by larger molecules.

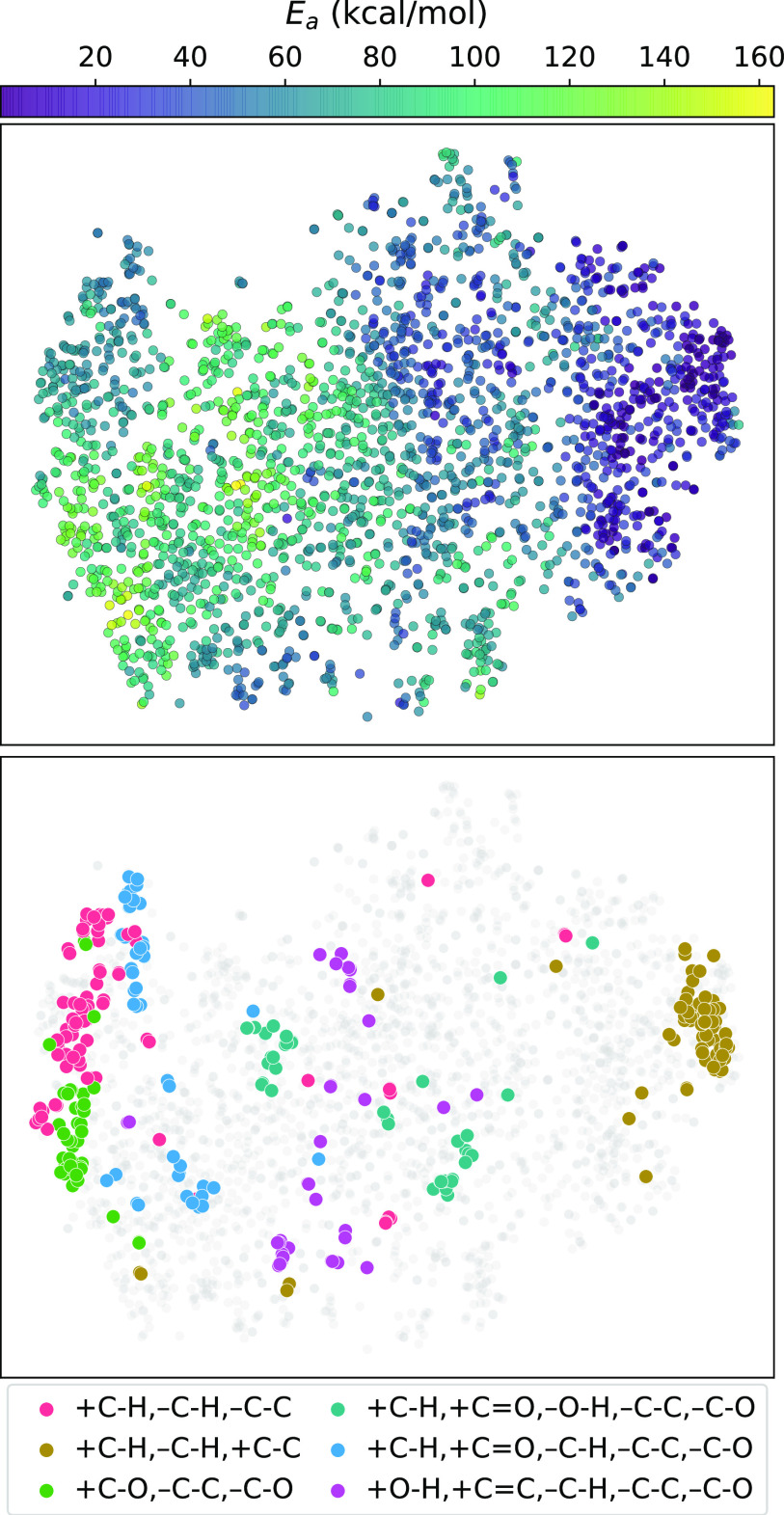
To assess whether the reaction encoding learned by the model is chemically reasonable, we embedded the encodings in two-dimensional space using t-distributed stochastic neighbor embedding (t-SNE).³⁷ The activation energy gradient in Figure 3 demonstrates that the model has learned to organize reactions it has not seen during training in a sensible manner that correlates with reactivity. Moreover, different regions in this representation of reaction space correspond to different reaction types. The six most frequent reaction types (same as those in Figure 2d) are highlighted in Figure 3. Because the reaction types are based on only the bond changes, the reactions within each type involve many different chemical functionalities; still, the model learns to cluster reactions of the same type together. The same analysis as shown here using t-SNE is conducted in the Supporting Information using principal component analysis (PCA), but the separation into reaction-type clusters is not as striking because the first two PCA components capture only 46% of the total variance.

Figure 3.

t-Distributed stochastic neighbor embedding (t-SNE) of the learned reaction encodings for the test set of the first fold. The embeddings correlate with the activation energy (top). The reactions cluster in t-SNE space on the basis of their reaction type. Shown are the six most frequent reaction types (bottom). Each reaction type includes only the bond changes occurring in the reaction, e.g., +C–H,–C–H,–C–C means that a carbon–hydrogen bond is formed, a different carbon–hydrogen bond is broken, and a carbon–carbon single bond is broken in the reaction.

To further show that the model behaves correctly when different functional groups are present, we analyzed the effects of substituting hydrogen atoms with side chains containing different functional groups and verified the model predictions using DFT. This analysis (shown in the Supporting Information) demonstrates that the model correctly identifies that a substitution of an electronegative group close to the reactive center of a reaction has a strong effect on the activation energy, whereas the substitution of any group far from the reactive center of another reaction does not affect the activation energy to any significant degree.

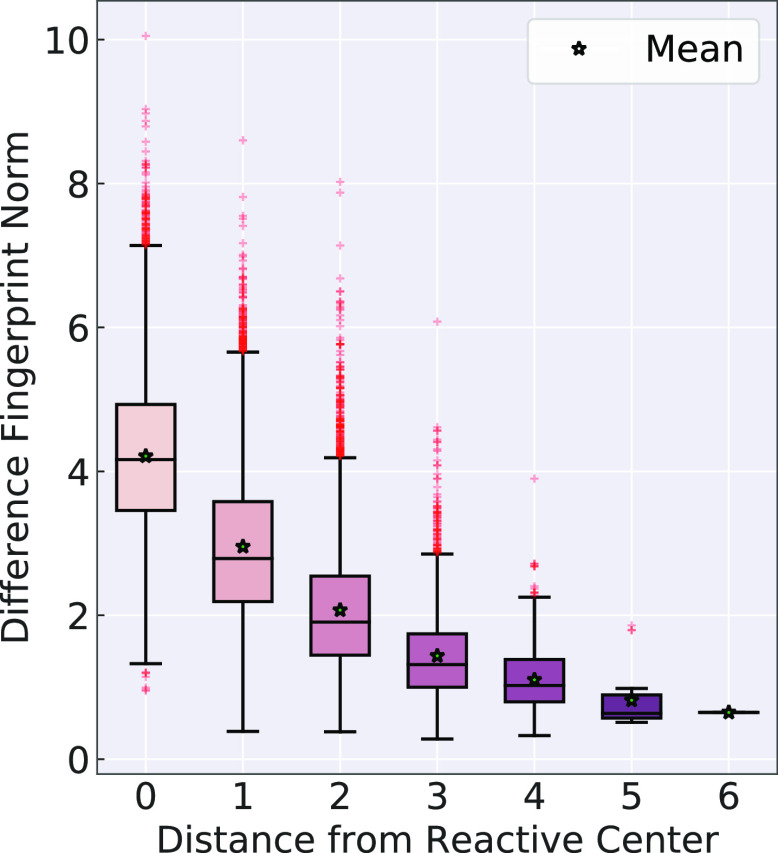
This observation also agrees with the earlier hypothesis that the difference fingerprints (recall Figure 1) should, on average, have a smaller contribution to the activation energy for atoms farther from the reactive center, although some distant atoms may influence the reactivity via electronic or steric effects. Figure 4 shows that the contribution, measured by the norm of the difference fingerprint, does indeed decrease for atoms that are farther from the reactive center.

Figure 4.

Investigation of how the difference fingerprint norm, i.e., contribution to the activation energy prediction, changes as atoms move farther from the reactive center. The reactive center is defined as those atoms that undergo bond changes in a reaction.

With quantitative data becoming more readily available through advances in high-throughput experimentation and more extensive computational resources available for data generation using, for example, quantum chemistry, quantitative predictions of reaction performance based on large training sets are becoming increasingly more feasible. Here, we have demonstrated that activation energies for a diverse set of gas-phase organic chemistry reactions can be predicted accurately using a template-free deep learning method. We expect that automated reaction mechanism generation software can strongly benefit from such a model, whether to estimate kinetics or to enable discovery of new reactivity. Further generation of large quantitative data sets will likely result in rapid development of novel machine learning algorithms suitable for predicting such quantities.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.0c00500.

• Detailed description of neural network architecture, training, and hyperparameter optimization; distribution of RMG families for reactions in the data set; example reactions for each of the six most frequent reaction types; performance based on the number of heavy atoms; principal component analysis of learned reaction encodings; and effect of substituting side chains on activation energy (PDF)

• Results of DFT calculations for side chain analysis (ZIP)

The authors declare no competing financial interest.