Abstract
We present a novel design for an ultracompact, passive light source capable of generating ultraviolet and X-ray radiation, based on the interaction of free electrons with the magnetic near-field of a ferromagnet. Our design is motivated by recent advances in the fabrication of nanostructures, which allow the confinement of large magnetic fields at the surface of ferromagnetic nanogratings. Using ab initio simulations and a complementary analytical theory, we show that highly directional, tunable, monochromatic radiation at high frequencies could be produced from relatively low-energy electrons within a tabletop design. The output frequency is tunable in the extreme ultraviolet to hard X-ray range via electron kinetic energies from 1 keV to 5 MeV and nanograting periods from 1 μm to 5 nm. The proposed radiation source can achieve the tunability and monochromaticity of current free-electron-driven sources (free-electron lasers, synchrotrons, and laser-driven undulators), yet with a significantly reduced scale, cost, and complexity. Our design could help realize the next generation of tabletop or on-chip X-ray sources.
Keywords: X-ray sources, free electrons, nanostructure, undulator, synchrotron, free-electron laser
Tabletop sources of extreme-ultraviolet and X-ray radiation are potentially useful for a wide variety of applications in medicine, engineering, and the natural sciences, ranging from medical therapy and diagnostics to X-ray imaging and spectroscopy, particle detection, and photolithography.1−4 Free-electron-driven light sources are promising schemes for realizing this goal. Synchrotrons and free-electron lasers are conventional sources that can generate high-quality, tunable radiation at extremely high brightnesses and intensities. These sources have enabled major advances in X-ray-based science, but their scope is severely limited by their large size and cost, driven by the need for kilometer-scale infrastructures to accelerate electrons to high energies.5,6 Alternative compact, cheap sources using relatively low-energy electrons are required to realize the diverse spectrum of X-ray applications intended for laboratory and clinical settings. Recently, there have been a number of proposals for compact free-electron sources relying on various spontaneous emission effects, such as Cherenkov and transition radiation sources7 and Smith-Purcell emitters,8−13 but these are limited to frequencies around the extreme ultraviolet, where the material response becomes insubstantial. Graphene plasmon-based X-ray sources have also been proposed,14,15 but they require a driving laser field and involve technical challenges such as the need to sustain intense and highly confined graphene-plasmon fields.
Here, we present a novel design for a compact, passive radiation source capable of generating ultraviolet and X-ray radiation, based on the interaction of free electrons with the magnetic near-field of a ferromagnetic material. Our design is motivated by recent advances in nanofabrication techniques of magnetic materials, which allow the confinement of large magnetic fields (∼1 T) at the surface of nanopatterned ferromagnets.16−21 We show that the near-fields of ferromagnetic nanogratings can be leveraged to produce highly directional, tunable, monochromatic radiation at short wavelengths with relatively low energy electrons in a tabletop design. Our design offers a number of advantages over other free-electron sources, bypassing the need for lengthy acceleration stages in more conventional setups and driving laser fields in other compact designs. The output wavelength is tunable via the electron energy and nanograting period, with modest output powers that are suitable for small-scale applications. The output power could be enhanced by bunching the electron beam at the wavelength scale; for instance, an electron beam with M = 10 bunches is predicted to yield power in the range 1.3 × 103 to 1.1 × 106 photons s–1 sr–1 per 1% bandwidth for an electron energy range of 20 keV to 5 MeV. In the following, we describe the concept for our compact, high-frequency radiation source. We derive analytical expressions for the frequency and intensity of radiation due to the interaction of a single electron with the source. Our expressions yield excellent predictions of the radiation output, as confirmed by our ab initio numerical simulations. We also calculate the radiation due to free-electron beams from conventional, laboratory-sized sources and discuss how the output power can be maximized by tuning the nanograting and electron beam geometries. Finally, we show how the power can be enhanced up to a factor of M2 by bunching the electron beam at the wavelength scale, where M is the number of bunches.
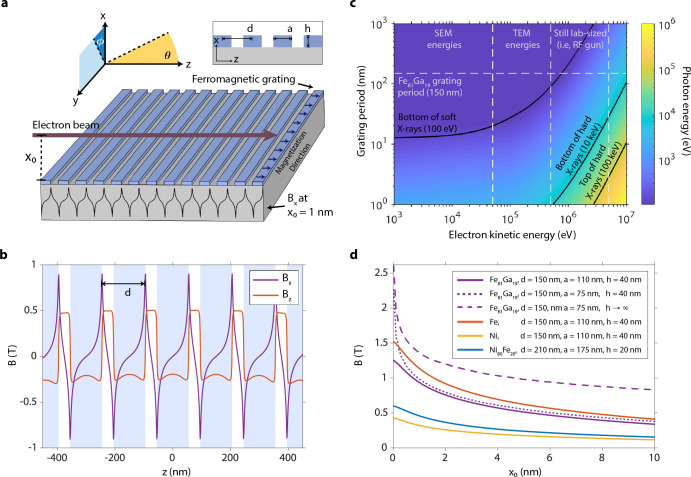
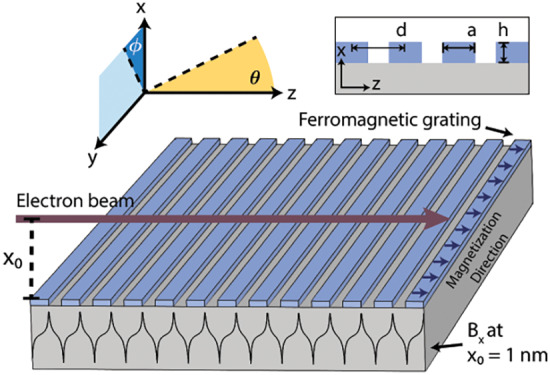
The mechanism behind the electromagnetic radiation source is illustrated in Figure 1a. The setup contains a grating with nanoscale periodicity fabricated from a ferromagnetic material. The nanograting is prepared to have a magnetization along the z direction, transverse to the nanograting stripes, by exposing the structure to an external homogeneous magnetic field. When the external magnetic field is turned off, the ferromagnetic material exhibits its saturation magnetic field due to magnetic hysteresis. The resulting field is periodic along z with the nanograting period and falls off with increasing height (x0) above the nanograting (Figure 1d). Electrons are sent parallel to the nanograting in the direction of magnetization. Interaction with the magnetic field causes electrons to oscillate primarily in the directions transverse to its unperturbed motion, which leads to the generation of high-frequency, directional radiation. The mechanism can be thought of as inverse-Compton scattering, whereby in the rest frame of the electron, a virtual photon from the magnetic field scatters off of the electron and gains energy. The same principle on a larger scale applies to undulator radiation from free-electron lasers, where the undulator period is typically a few centimeters, the magnetic field strength is 1 T, and the electron energy is 1–15 GeV. In our case, the nanoundulator period reduces to around 100 nm and the electron energy to 1 keV–5 MeV, with the field strength remaining at 1 T. Since the fundamental wavelength of radiation is proportional to d/γ2, where d is the undulator period and γ is the relativistic Lorentz factor for the electrons, our design reaches comparable frequencies to free-electron lasers with much lower initial electron energies.
Figure 1.
Compact free-electron source of high-frequency radiation. (a) Schematic of the compact radiation source, in which free electrons oscillate in the magnetic near-field of a ferromagnetic nanograting to produce high-frequency radiation. The magnetic field is periodic in z with the nanograting period and has high amplitude (∼1–2 T) toward the nanograting surface (small x0). (b) Plots of the nonzero magnetic field components at a height x0 = 1 nm above the surface, using the parameters of an Fe81Ga19 nanograting fabricated and characterized in ref (16), where μ = 1.4 × 106A/m, d = 150 nm, a = 110 nm, h = 40 nm, and N = 31. z = 0 is defined to be at the center of the nanograting. The positions of the nanograting stripes relative to the field profiles are shown in light blue. (d) The parameters of the nanograting can be tuned to produce a stronger field at the surface by taking the filling ratio a/d to 1/2 (purple, dotted line), increasing the height to period ratio h/d (purple, dashed line), and choosing a ferromagnetic material with a higher magnetization at saturation (orange line). (c) The dispersion relation of the source shows the production of high-frequency radiation ranging from extreme UV to hard X-rays that can be tuned with the nanograting period and electron kinetic energy.
An analytic formula for the magnetic field B(x, y, z) created by a nanoundulator has been previously derived.19 The expression is computed by an integration of the magnetic field produced by a magnetic dipole moment over the spatial distribution of the nanograting, assuming a constant magnetization μ in the z direction. The nanograting is taken to be infinite in the y direction and finite in the z direction. The resulting magnetic field has By(x, y, z) = 0, with Bx(x, y, z) and Bz(x, y, z) periodic in z with the nanograting period for x close to the nanograting surface (small x0). The exact profiles for Bx and Bz have dependences on five parameters of the nanograting: d, the nanograting period, a, the stripe width, h, the stripe height, N, the number of nanograting periods, and μ, the magnitude of magnetization at saturation, a function of the ferromagnetic material. In particular, the field components depend upon the ratios of the geometric parameters, and μ is a scale factor on each component. Throughout the article, all calculations are carried out for a ferromagnetic nanograting composed of Galfenol (Fe81Ga19), with μ = 1.4 × 106A/m, d = 150 nm, a = 110 nm, h = 40 nm, and N = 31 (Nd = 4.65 μm), unless stated otherwise. Such a structure was previously fabricated for a different study through magnetron sputtering onto a GaAs substrate and focused ion beam milling.16 The choice of substrate does not have practical consequences for the radiation due to inverse-Compton scattering as long as the substrate is not ferromagnetic. The choice of our reference nanograting is motivated by its relatively high magnetization, which induces a strong magnetic field, and the nanoscale period, which facilitates the production of high frequency radiation.
Figure 1b plots the components of the magnetic field induced by the reference nanograting as a function of z at a height of x0 = 1 nm. Bx and Bz are periodic along z with period d, and both components peak near fields of 1 T. Such an amplitude corresponds to the same amplitude of an electric field of intensity 0.3 TW cm–2, meaning that a laser undulator would require this level of intensity to provide a similar power per electron. As the out-of-plane distance to the nanograting (x0) increases, the magnetic field magnitude exhibits rapid decay, as illustrated in Figure 1d. Figure 1d also shows how the field magnitude can be tuned via the nanograting parameters, with plots of the field of the reference nanograting (solid purple line) against that of other structures. For instance, when the stripe width of the reference nanograting is changed from a = 110 nm to a = 75 nm, the magnitude is increased by ∼1 T at the surface of the nanograting (dotted purple line). At this width, the field is optimized with respect to a for fixed d, and the filling ratio a/d is precisely 1/2. When the height of the reference nanograting is taken from h = 40 nm to the limit where h → ∞, the field is optimized with respect to h and the magnitude is further increased (dashed purple line). In a third variation, the material of the reference nanograting is changed to Fe (orange line), which results in a slightly larger field due to the higher magnetization of Fe, μ = 1.7 × 106 A/m. For reference, we include plots for two more nanogratings composed of Ni (yellow line) and Ni80Fe20 (blue line), which have been previously fabricated for other experiments using deep ultraviolet lithography.17,18
We now turn to developing an analytical theory that describes
the
output radiation due to a single electron interacting with the magnetic
near-field of the ferromagnetic nanograting. Our theory yields an
excellent prediction of the frequency and intensity of output radiation,
as confirmed by comparisons to our ab initio numerical simulations
(see Figure 2). The
dispersion relation of the system can be derived using the law of
energy-momentum conservation. We consider an elastic collision between
an electron of rest mass m launched in the z direction with velocity v (normalized
velocity β = v/c, Lorentz
factor 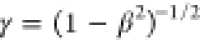 ) and a nanograting yielding
a momentum
2πℏn/d, where d is the nanograting period. The output photon has departing
angle θ with energy ℏω and momentum ℏω/c. Then ω is given by
) and a nanograting yielding
a momentum
2πℏn/d, where d is the nanograting period. The output photon has departing
angle θ with energy ℏω and momentum ℏω/c. Then ω is given by
| 1 |
where n is a positive integer.
The approximate equality neglects the effects of quantum recoil and
holds whenever 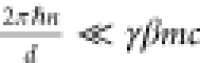 , which is always
true in the case under
study. It also assumes that the electron’s transverse velocity
oscillations due to the magnetic field are small enough such that
γ and β are approximately constant throughout the interaction,
that is, ż ≈ v and z ≈ vt + z0. This approximation can be justified as follows: we can Fourier
expand the magnetic field component Bx as
, which is always
true in the case under
study. It also assumes that the electron’s transverse velocity
oscillations due to the magnetic field are small enough such that
γ and β are approximately constant throughout the interaction,
that is, ż ≈ v and z ≈ vt + z0. This approximation can be justified as follows: we can Fourier
expand the magnetic field component Bx as 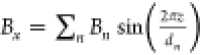 , where Bn is the amplitude and dn = d/n is the period of the nth Fourier component. The angular deflection of the electron
due to the nth Fourier component of Bx is characterized by the magnetic deflection
or undulator parameter,
, where Bn is the amplitude and dn = d/n is the period of the nth Fourier component. The angular deflection of the electron
due to the nth Fourier component of Bx is characterized by the magnetic deflection
or undulator parameter, 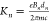 . In the case of study, Kn is at most ∼10–6, so we can neglect
the angular deflection of the electron due to Bx. In this case, the Lorentz
forces on the electron due to Bz are small, so Bz can be disregarded, and we can approximate the total magnetic field
as
. In the case of study, Kn is at most ∼10–6, so we can neglect
the angular deflection of the electron due to Bx. In this case, the Lorentz
forces on the electron due to Bz are small, so Bz can be disregarded, and we can approximate the total magnetic field
as 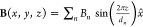 .
.
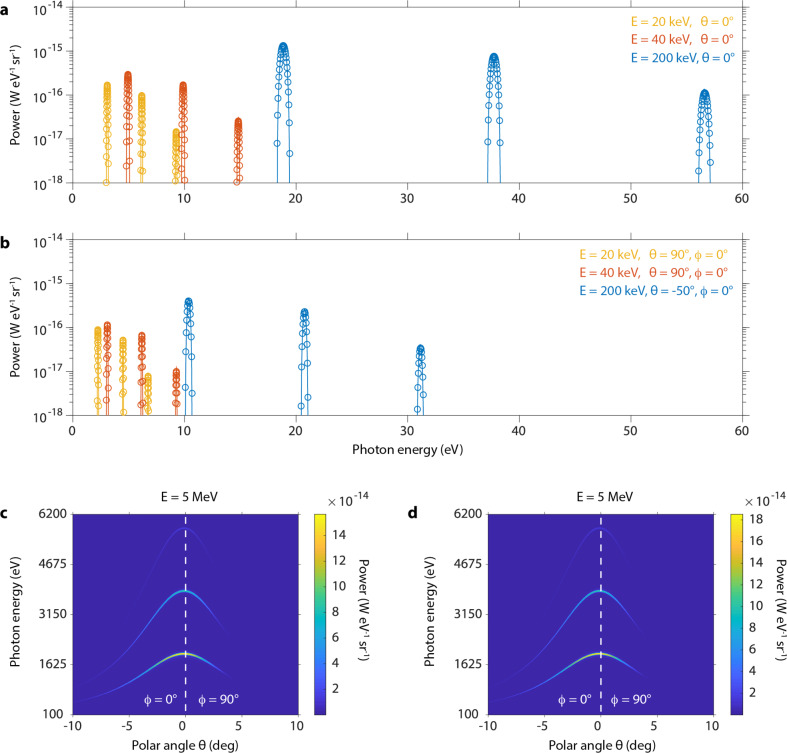
Figure 2.
Tunability of the emitted photon energy via the electron energy. (a, b) Numerical (circles) vs analytical (solid lines) results of the radiation power from a single electron in units of power per photon energy per solid angle for a variety of electron energies and fixed polar angles. Different colors represent different electron energies. The polar angles in (b) are chosen such that ϕ = 0 and θ is approximately halfway between the leftmost edge and the peak of the full angular spectrum. Numerical (c) vs analytical (d) results of the full angular spectrum of radiation power from a single electron with energy 5 MeV. All calculations are carried out using the parameters of the reference nanograting16 with a length along z of 4.65 μm and an electron launched in the z direction with initial height x0 = 1 nm above the nanograting surface.
We now derive a fully analytical expression that predicts the spectral power of emitted radiation as a function of its frequency ω, azimuthal angle ϕ, and polar angle θ. We again assume that the electron’s transverse velocity oscillations are small, and that the magnetic field can be approximated as above. Only the dominant Fourier components of the magnetic field contribute to the radiation spectrum, with each contributing to spectrally distinct peaks (see Figure 2). The spectrum of the emitted radiation as a function of its frequency ω, azimuthal angle ϕ, and polar angle θ is given by
| 2 |
where
| 3 |
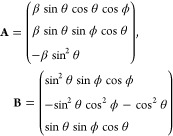 |
4 |
where 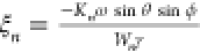 is the amplitude
of oscillation in the y direction normalized to the y component
of the wave vector
is the amplitude
of oscillation in the y direction normalized to the y component
of the wave vector  ,
, 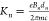 is
the magnetic deflection parameter and
is
the magnetic deflection parameter and 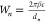 is the frequency of
oscillation due to
the nth Fourier component, e is
the electron charge, ε0 is the permittivity of free
space,
is the frequency of
oscillation due to
the nth Fourier component, e is
the electron charge, ε0 is the permittivity of free
space, 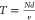 is the electron flight time, and N is the number
of nanograting periods. The full derivation
is provided in Supporting Information, Section I. Exact numerical simulations of the interaction for a range
of initial electron energies were carried out and directly compared
to the analytics. The results show excellent agreement and confirm
the validity of our analytical theory (see Figure 2).
is the electron flight time, and N is the number
of nanograting periods. The full derivation
is provided in Supporting Information, Section I. Exact numerical simulations of the interaction for a range
of initial electron energies were carried out and directly compared
to the analytics. The results show excellent agreement and confirm
the validity of our analytical theory (see Figure 2).
Figure 1c plots the dispersion relation from eq 1 (for n = 1), showing how the output radiation frequency can be tuned with the electron kinetic energy and nanograting period. Contour lines in black denote the boundaries of hard and soft X-rays, and white vertical lines separate various regimes of electron energies. The white horizontal line marks the nanograting period corresponding to the reference geometry (150 nm). The two leftmost regimes of electron energies correspond to nonrelativistic electrons from 1 to 500 keV that can be realized in conventional scanning electron microscopes (SEM) and transmission electron microscopes (TEM). These regimes are already sufficient for hard ultraviolet generation with 150 nm nanogratings, and soft X-rays can be reached with smaller periods, with 20 nm nanogratings at 50 keV, and 90 nm nanogratings at 500 keV. The next regime corresponds to electron energies from 500 keV to 5 MeV, achievable from conventional radio frequency (RF) guns (still lab-sized). At 1 MeV, soft X-rays are already achievable with 150 nm nanogratings. Hard X-rays can be reached with 11 nm nanogratings at 3 MeV and 29 nm nanogratings at 5 MeV. Current nanofabrication techniques such as electron-beam lithography can already pattern ferromagnetic materials with features as small as 10 nm,20 and sub-5 nm features have been demonstrated for metallic materials.22 With a 10 nm period, our design reaches soft and hard X-rays within a laboratory setup, circumventing the need for high energy particle accelerators and kilometer-scale infrastructures, enabling part of their capabilities at reduced scales and costs.
Next, we discuss the results of our ab initio numerical simulations for single electrons of varying energies interacting with the nanograting. The simulations compute exact radiation spectra due to the interaction by solving for electron trajectories using the Newton-Lorentz equation and taking Fourier transforms of the fields obtained from the Liénard-Wiechert potentials.14,23 We perform simulations over a range of polar angles and initial electron energies, taking the parameters of the reference nanograting. We set the length of the nanograting along z to be Nd = 4.65 μm, where N = 31. The results are displayed in Figure 2 (a and b circles), along with a comparison to our analytical formula (eq 2, solid lines), and show the production of highly directional, monoenergetic radiation. Each spectrum displays the first three harmonics of radiation generated from the dominant Fourier components of the magnetic field. There is a clear dependence of output power density on electron energy, with the scaling factor of γ2 evident from the analytics (eqs 1 and 2), as ω ∼ γ2 for on-axis peaks (θ = 0°) when β ≈ 1, and dω ∼ γ2. In Figure 2a, we plot the on-axis power per photon energy per solid angle (W eV–1 sr–1) for three different electron energies. Electrons with a kinetic energy of 40 keV, which are achievable with some SEM models, generate ultraviolet photons with on-axis peak energies of 4.96 eV (2.63% fwhm energy spread), 9.89 eV (1.32% spread), and 14.83 eV (0.81% spread). At a kinetic energy of 200 keV, achievable with a TEM, electrons produce extreme ultraviolet photons with on-axis peak energies of 18.86 eV (2.6% spread), 37.71 eV (1.19% spread), and 56.55 eV (0.80% spread). In Figure 2b, we display the same plot with different fixed polar angles θ and ϕ, showing the angular dependence of the output photon energy. We choose θ to be approximately halfway between the leftmost edge and the peak of the full angular spectrum (see Figure 2c,d). Figure 2c shows the numerical result of the full angular spectrum for an electron kinetic energy of 5 MeV, achievable with a lab-sized RF gun. The spectrum shows the generation of soft and hard X-ray photons, with on-axis peak energies of 1.91 keV (2.56% spread), 3.82 keV (1.17% spread), and 5.74 keV (0.85% spread). The radiated photons have an angular spread of ∼20° since Δθ ∼ 1/γ. In Figure 2d, we plot the analytical result for the angular spectrum from a 5 MeV electron, which shows very good agreement with Figure 2c.
We now discuss the radiation due to free-electron beams from conventional, laboratory-sized sources and show how the output power can be enhanced by tuning the nanograting and electron beam geometries. First, it is emphasized that choosing a nanograting with optimal parameters for generating a large magnetic near-field is essential, as the power scales with the field strength (eq 2). These include a ferromagnetic material with a large magnetization, a stripe width to period ratio a/d of 1/2, and a high stripe height to period ratio h/d (see Figure 1d). Other methods of enhancement include increasing the length of the nanograting along z, since the power scales with the electron interaction time T (eq 2) and vertically stacking multiple nanogratings in parallel.
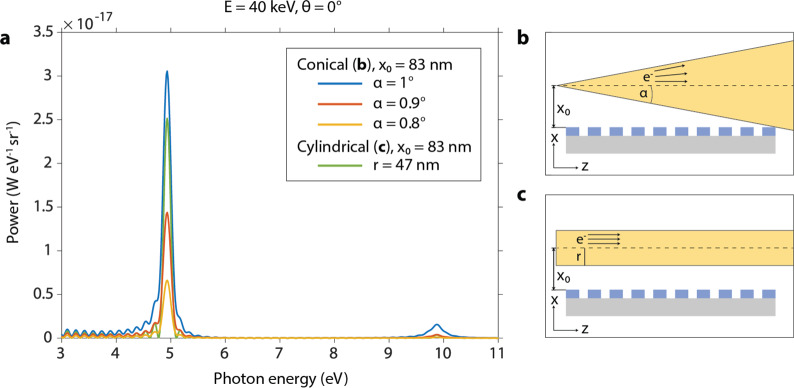
Lab-sized electron guns typically produce electron beams with a conical profile, with an outgoing half angle α (Figure 3b). Larger values of α yield higher beam currents but result in less power radiated per electron. In such a setup, the value of α should be chosen at around a few degrees to balance this trade-off. Given a fixed value of α, the initial height of the beam x0 should be chosen so that electrons graze the edge of the nanograting (see Figure 3b) to minimize distance to the surface and prevent surface collisions. Figure 3a plots the on-axis power per photon energy per solid angle for a few conical beams with differing α, obtained via numerical simulation. The electron energy is set to 40 keV and the beam brightness to 109 A cm–2 sr–1, parameters obtainable in a cold field emission SEM.24 The initial height x0 = 83 nm for all beams is chosen so that the beam with the largest half angle considered (α = 1◦) grazes the edge of the nanograting. Figure 3a shows that the conical beam with α = 1° maximizes the on-axis output power, yielding 2.3 photons s–1 sr–1 per 1% bandwidth for a photon energy of 4.96 eV, and the power drops off with decreasing α (red and yellow lines). Figure 3a also plots the on-axis power distribution for a cylindrical beam with initial height x0 = 83 nm (green line, Figure 3c), yielding similar values to the α = 1° cylindrical case. For reference, when the electron energy is 5 MeV, the α = 1° conical geometry yields an on-axis output power of 3.8 × 102 photons s–1 sr–1 per 1% bandwidth for a photon energy of 1.3 keV.
Figure 3.
Dependence of the power spectrum on electron beam geometry. (a) Numerical results of the on-axis radiation power for conical (b) and cylindrical (c) electron beam geometries in units of power per photon energy per solid angle. Conical beams with varying half angles α are considered. The initial height x0 for all geometries is chosen so that the conical beam with the largest half angle (α = 1°) grazes the edge of the nanograting, as in (b). The electron energy is set to 40 keV and the beam brightness to 109 A cm–2 sr–1. All nanograting parameters are as in Figure 2.
One of the novel features of our source is its ability to produce tunable, directional, monochromatic radiation at comparable frequencies to conventional free-electron sources while using drastically lower electron energies. One downside to using low-energy electrons is a decrease in the output power, since the power density scales with γ2 (eqs 1 and 2). The electrons used with our source typically have γ ≈ 1–10 and cannot match the output power of larger, more conventional X-ray sources, where γ ≫ 1. Additionally, low-energy (<5 keV) electron beams typically achieved in SEMs exhibit large angular divergences, thus, reducing the efficiency of the radiation process.25 Nevertheless, we proceed to point out that it is possible to enhance the output intensity substantially through the use of flat electron beams and bunched electrons.
Since the magnetic field of the nanograting drops off rapidly above the surface, using high-quality, high-brightness electron beams focused as close as possible to the source will increase the photon yield. Beams that are flattened along the y–z plane allow a greater number of electrons to lie closer to the nanograting surface and experience a stronger field.26,27 It should also be mentioned that, in addition to inverse-Compton radiation, we expect bremsstrahlung radiation to be prevalent in the system due to free electrons colliding with the nanograting. In Supporting Information, Section III, we estimate the spectral power of bremsstrahlung radiation integrated over all solid angles for a single electron of 5 MeV. We find that the energy transfer from electrons to photons is orders of magnitude more efficient for bremsstrahlung than for inverse-Compton scattering. Therefore, it is critical that bremsstrahlung radiation is minimized as much as possible, primarily by ensuring that electrons collide minimally with the nanograting. This results in a trade-off between inverse-Compton and bremsstrahlung radiation, since bringing electrons closer to the nanograting maximizes inverse-Compton radiation, but it also increases the likelihood of electron collisions and thus the production of bremsstrahlung. Further discussion of bremsstrahlung radiation in the system can be found in Supporting Information, Section III.
In addition to the enhancement methods mentioned above, the output power of inverse-Compton radiation can be enhanced orders of magnitude by prebunching the electron beam at the wavelength scale of radiation to produce coherent emission. In Supporting Information, Section II, we derive the spectral power of the emitted radiation due to a bunched electron beam interacting with the source, using ref (28). We consider a beam that is one electron thick, consisting of M equally spaced electrons along z by a distance Δz. The beam is launched parallel to the nanograting in the z direction with uniform initial velocity v. Then, the output power of radiation is given by
| 5 |
where
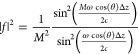 |
6 |
where f is the Fourier
transform
of the charge distribution and 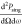 is the power due to a single electron,
given by eq 2. The power
enhancement is strongest where the bunching resonant enhancement condition
is the power due to a single electron,
given by eq 2. The power
enhancement is strongest where the bunching resonant enhancement condition 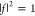 holds or where ω cos θ
=
holds or where ω cos θ
= 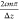 for integers m. When this
holds,
for integers m. When this
holds, 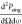 =
= 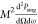 .
.
In Figure 4, we plot the enhanced power spectrum due to eq 5 for a fixed uniform beam energy of 40 keV. Figure 4a shows line cuts of the spectrum for a few values of Δz and M. On-axis peaks are enhanced when Δz = 250 nm, and peaks slightly off-axis (θ = −27°, ϕ = 0°) are enhanced when Δz = 300. The radiation power increases by 2 orders of magnitude when M goes from 1 to 10, and another 2 orders of magnitude when M goes to 100. For instance, when Δz = 250 nm, the power per solid angle of the on-axis peak at 4.96 eV goes from 1.7 × 101 photons s–1 sr–1 per 1% bandwidth to 1.6 × 103 photons s–1 sr–1 per 1% bandwidth when M = 10, and to 1.2 × 105 photons s–1 sr–1 per 1% bandwidth when M = 100. In Figure 4b, we show the full angular spectrum due to a bunched electron beam for Δz = 500 nm and M = 10. The enhancement is strongest on-axis with an angular spread of ∼24°, but occurs at off-axis angles where the bunching resonant enhancement condition holds. Additional off-axis angles can be enhanced (while keeping the on-axis peaks enhanced) by changing Δz to a higher multiple of 250 nm, as evident from the bunching resonant enhancement condition.
Figure 4.
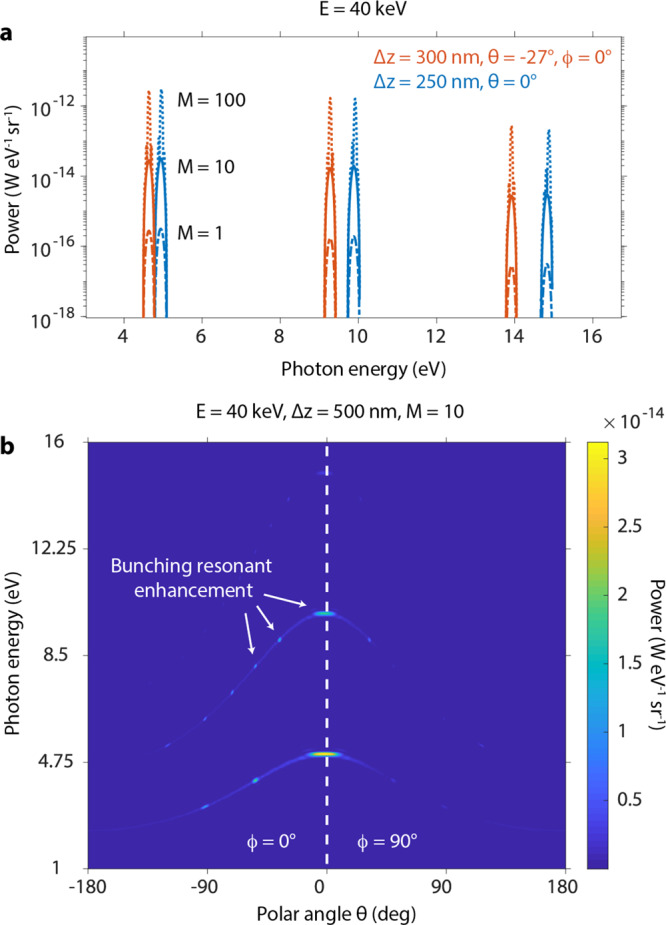
Enhanced power spectrum due to a bunched electron beam. (a, b) Radiation power in units of power per photon energy per solid angle due to a bunched electron beam with uniform energy 40 keV launched in the z direction with initial height x0 = 1 nm above the nanograting. The beam is one electron thick and consists of M electrons linearly spaced along z by a distance Δz. (a) The radiation power for varying values of Δz, M, and polar angle θ. The polar angles are chosen so that ϕ = 0° and θ lies on the enhancement occurring closest to θ = 0°. The total radiation power increases by 2 orders of magnitude for every order of magnitude increase in M, the number of bunches. (b) The full angular spectrum of radiation power for a 40 keV electron beam with Δz = 250 nm and M = 10, showing enhancement both on and off axis.
In conclusion, we have presented the concept for a compact, passive light source that produces highly directional, monochromatic radiation. The light is tunable via the ferromagnetic nanograting period and the electron energy, spanning the extreme ultraviolet to hard X-ray range. The output power can be enhanced through a number of methods, such as shaping the electron beam, bunching the beam at the wavelength scale, increasing the length of the nanograting, and stacking multiple nanogratings in parallel. The source is well suited to laboratory-scale applications with its small size, low complexity, and low cost, requiring neither large high-energy accelerators nor driving laser fields. Ferromagnetic nanogratings with feature sizes as small as 10 nm can be produced with lithographic methods. Future advances in nanofabrication could allow the patterning and mass production of ferromagnetic nanogratings at sub 5 nm scales, making even higher photon energies achievable. Further, the small scale of the source makes it suited to an on-chip device. Recent progress has been made in high-energy on-chip accelerators,29,30 which, when combined with our design, could enable an ultracompact, fully on-chip X-ray light source. Finally, an interesting topic for future research is the possibility of a nanoscale free-electron laser, in which electrons bunch coherently via self-amplified spontaneous emission, allowing for an exponential increase in radiation power.
Acknowledgments
N.R. acknowledges the support of the DOE Computational Science Graduate Fellowship (CSGF) No. DEFG02-97ER25308. L.J.W. acknowledges the support of the Agency for Science, Technology and Research (A*STAR) Advanced Manufacturing and Engineering Young Individual Research Grant (A1984c0043); and the Nanyang Assistant Professorship Start-up Grant. I.K. acknowledges the support of the Israel Science Foundation (ISF) grant no. 830/19 and the ERC starting grant NanoEP 851780 from the European Research Council. This material is based upon work supported in part by the U.S. Army Research Office through the Institute for Soldier Nanotechnologies, under Contract No. W911NF-18-2-0048, and by the Binational USA-Israel Science Foundation (BSF) 2018288.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsphotonics.0c00121.
Derivation of the spectral angular power of emitted radiation from a single electron, spectral angular power of emitted radiation from a bunched electron beam, and radiation due to brehmsstrahlung (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Sakdinawat A.; Attwood D. Nanoscale x-ray imaging. Nat. Photonics 2010, 4, 840. 10.1038/nphoton.2010.267. [DOI] [Google Scholar]
- Hitchcock A. P. Soft X-ray spectromicroscopy and ptychography. J. Electron Spectrosc. Relat. Phenom. 2015, 200, 49–63. 10.1016/j.elspec.2015.05.013. [DOI] [Google Scholar]
- Schmitz C.; Wilson D.; Rudolf D.; Wiemann C.; Plucinski L.; Riess S.; Schuck M.; Hardtdegen H.; Schneider C. M.; Tautz F. S.; Juschkin L. Compact extreme ultraviolet source for laboratory-based photoemission spectromicroscopy. Appl. Phys. Lett. 2016, 108, 234101. 10.1063/1.4953071. [DOI] [Google Scholar]
- Solak H. H. Nanolithography with coherent extreme ultraviolet light. J. Phys. D: Appl. Phys. 2006, 39, R171–R188. 10.1088/0022-3727/39/10/R01. [DOI] [Google Scholar]
- McNeil B. W. J.; Thompson N. R. X-ray free-electron lasers. Nat. Photonics 2010, 4, 814. 10.1038/nphoton.2010.239. [DOI] [Google Scholar]
- Pellegrini C.; Marinelli A.; Reiche S. The physics of x-ray free-electron lasers. Rev. Mod. Phys. 2016, 88, 015006. 10.1103/RevModPhys.88.015006. [DOI] [Google Scholar]
- Liu F.; Xiao L.; Ye Y.; Wang M.; Cui K.; Feng X.; Zhang W.; Huang Y. Integrated cherenkov radiation emitter eliminating the electron velocity threshold. Nat. Photonics 2017, 11, 289. 10.1038/nphoton.2017.45. [DOI] [Google Scholar]
- Adamo G.; MacDonald K. F.; Fu Y. H.; Wang C.-M.; Tsai D. P.; García de Abajo F. J.; Zheludev N. I. Light well: A tunable free-electron light source on a chip. Phys. Rev. Lett. 2009, 103, 113901. 10.1103/PhysRevLett.103.113901. [DOI] [PubMed] [Google Scholar]
- Massuda A.; Roques-Carmes C.; Solanki A.; Yang Y.; Kooi S. E.; Habbal F.; Kaminer I.; Soljačić M.. High-order smith-purcell radiation in silicon nanowires. Conference on Lasers and Electro-Optics; Optical Society of America, 2017; p JTh5B.8.
- Massuda A.; Roques-Carmes C.; Yang Y.; Kooi S. E.; Yang Y.; Murdia C.; Berggren K. K.; Kaminer I.; Soljačić M. Smith–purcell radiation from low-energy elec trons. ACS Photonics 2018, 5, 3513–3518. 10.1021/acsphotonics.8b00743. [DOI] [Google Scholar]
- Kaminer I.; Kooi S. E.; Shiloh R.; Zhen B.; Shen Y.; López J. J.; Remez R.; Skirlo S. A.; Yang Y.; Joannopoulos J. D.; Arie A.; Soljačić M. Spectrally and spatially resolved smith-purcell radiation in plasmonic crystals with short-range disorder. Phys. Rev. X 2017, 7, 011003. 10.1103/PhysRevX.7.011003. [DOI] [Google Scholar]
- Roques-Carmes C.; Kooi S. E.; Yang Y.; Massuda A.; Keathley P. D.; Zaidi A.; Yang Y.; Joannopoulos J. D.; Berggren K. K.; Kaminer I.; Soljacic M. Towards integrated tunable all-silicon free-electron light sources. Nat. Commun. 2019, 10, 3176. 10.1038/s41467-019-11070-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y.; Massuda A.; Roques-Carmes C.; Kooi S. E.; Christensen T.; Johnson S. G.; Joannopoulos J. D.; Miller O. D.; Kaminer I.; Soljacic M. Maximal spontaneous photon emission and energy loss from free electrons. Nat. Phys. 2018, 14, 894–899. 10.1038/s41567-018-0180-2. [DOI] [Google Scholar]
- Wong L. J.; Kaminer I.; Ilic O.; Joannopoulos J. D.; Soljacic M. Towards graphene plasmon-based free-electron infrared to x-ray sources. Nat. Photonics 2016, 10, 46. 10.1038/nphoton.2015.223. [DOI] [Google Scholar]
- Rosolen G.; Wong L. J.; Rivera N.; Maes B.; Soljacic M.; Kaminer I. Metasurface-based multi-harmonic free-electron light source. Light: Sci. Appl. 2018, 7, 64. 10.1038/s41377-018-0065-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salasyuk A. S.; Rudkovskaya A. V.; Danilov A. P.; Glavin B. A.; Kukhtaruk S. M.; Wang M.; Rushforth A. W.; Nekludova P. A.; Sokolov S. V.; Elistratov A. A.; Yakovlev D. R.; Bayer M.; Akimov A. V.; Scherbakov A. V. Generation of a localized microwave magnetic field by coherent phonons in a ferromagnetic nanograting. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 97, 060404. 10.1103/PhysRevB.97.060404. [DOI] [Google Scholar]
- Gubbiotti G.; Tacchi S.; Carlotti G.; Vavassori P.; Singh N.; Goolaup S.; Adeyeye A. O.; Stashkevich A.; Kostylev M. Magnetostatic interaction in arrays of nanometric permalloy wires: A magneto-optic kerr effect and a brillouin light scattering study. Phys. Rev. B: Condens. Matter Mater. Phys. 2005, 72, 224413. 10.1103/PhysRevB.72.224413. [DOI] [Google Scholar]
- Adeyeye A. O.; Goolaup S.; Singh N.; Jun W.; Wang C. C.; Jain S.; Tripathy D. Reversal mechanisms in ferromagnetic nanostructures. IEEE Trans. Magn. 2008, 44, 1935–1940. 10.1109/TMAG.2008.924539. [DOI] [Google Scholar]
- Buchholz D.; Drouvelis P. S.; Schmelcher P. Single electron quantum dot in a spatially periodic magnetic field. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 73, 235346. 10.1103/PhysRevB.73.235346. [DOI] [Google Scholar]
- Martın J.I; Nogues J; Liu K.; Vicent J.L; Schuller I. K Ordered magnetic nanostructures: fabrication and properties. J. Magn. Magn. Mater. 2003, 256, 449–501. 10.1016/S0304-8853(02)00898-3. [DOI] [Google Scholar]
- Luttge R. Massively parallel fabrication of repetitive nanostructures: nanolithography for nanoarrays. J. Phys. D: Appl. Phys. 2009, 42, 123001. 10.1088/0022-3727/42/12/123001. [DOI] [Google Scholar]
- Manfrinato V. R.; Stein A.; Zhang L.; Nam C.-Y.; Yager K. G.; Stach E. A.; Black C. T. Aberration-corrected electron beam lithography at the one nanometer length scale. Nano Lett. 2017, 17, 4562–4567. 10.1021/acs.nanolett.7b00514. [DOI] [PubMed] [Google Scholar]
- Wong L. J.; Hong K.-H.; Carbajo S.; Fallahi A.; Piot P.; Soljacic M.; Joannopoulos J. D.; Kärtner F. X.; Kaminer I. Laser-induced linear-field particle acceleration in free space. Sci. Rep. 2017, 7, 11159. 10.1038/s41598-017-11547-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bogner A.; Jouneau P.-H.; Thollet G.; Basset D.; Gauthier C. A history of scanning electron microscopy developments: Towards “wet-stem” imaging. Micron 2007, 38, 390–401. 10.1016/j.micron.2006.06.008. [DOI] [PubMed] [Google Scholar]
- Goldstein J.; Newbury D. E.; Joy D. C.; Lyman C. E.; Echlin P.; Lifshin E.; Sawyer L.; Michael J. R.. Scanning Electron Microscopy and X-Ray Microanalysis, 3rd ed.; Springer, 2007. [Google Scholar]
- Brinkmann R.; Derbenev Y.; Flöttmann K. A low emittance, flat-beam electron source for linear colliders. Phys. Rev. Spec. Top.--Accel. Beams 2001, 4, 053501. 10.1103/PhysRevSTAB.4.053501. [DOI] [Google Scholar]
- Piot P.; Sun Y.-E.; Kim K.-J. Photoinjector generation of a flat electron beam with transverse emittance ratio of 100. Phys. Rev. Spec. Top.--Accel. Beams 2006, 9, 031001. 10.1103/PhysRevSTAB.9.031001. [DOI] [Google Scholar]
- Sears C. M. S.; Colby E.; Ischebeck R.; McGuinness C.; Nelson J.; Noble R.; Siemann R. H.; Spencer J.; Walz D.; Plettner T.; Byer R. L. Production and characterization of attosecond electron bunch trains. Phys. Rev. Spec. Top.--Accel. Beams 2008, 11, 061301. 10.1103/PhysRevSTAB.11.061301. [DOI] [Google Scholar]
- England R. J.; Noble R. J.; Bane K.; Dowell D. H.; Ng C.-K.; Spencer J. E.; Tantawi S.; Wu Z.; Byer R. L.; Peralta E.; Soong K.; Chang C.-M.; Montazeri B.; Wolf S. J.; Cowan B.; Dawson J.; Gai W.; Hommelhoff P.; Huang Y.-C.; Jing C.; McGuinness C.; Palmer R. B.; Naranjo B.; Rosenzweig J.; Travish G.; Mizrahi A.; Schachter L.; Sears C.; Werner G. R.; Yoder R. B. Dielectric laser accelerators. Rev. Mod. Phys. 2014, 86, 1337–1389. 10.1103/RevModPhys.86.1337. [DOI] [Google Scholar]
- Peralta E. A.; Soong K.; England R. J.; Colby E. R.; Wu Z.; Montazeri B.; McGuinness C.; McNeur J.; Leedle K. J.; Walz D.; Sozer E. B.; Cowan B.; Schwartz B.; Travish G.; Byer R. L. Demonstration of electron acceleration in a laser-driven dielectric microstructure. Nature 2013, 503, 91. 10.1038/nature12664. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.