Visual Information Processing in the Ventral Division of the Mouse Lateral Geniculate Nucleus of the Thalamus

Abstract

Even though the lateral geniculate nucleus of the thalamus (LGN) is associated with form vision, that is not its sole role. Only the dorsal portion of LGN (dLGN) projects to V1. The ventral division (vLGN) connects subcortically, sending inhibitory projections to sensorimotor structures, including the superior colliculus (SC) and regions associated with certain behavioral states, such as fear (Monavarfeshani et al., 2017; Salay et al., 2018). We combined computational, physiological, and anatomical approaches to explore visual processing in vLGN of mice of both sexes, making comparisons to dLGN and SC for perspective. Compatible with past, qualitative descriptions, the receptive fields we quantified in vLGN were larger than those in dLGN, and most cells preferred bright versus dark stimuli (Harrington, 1997). Dendritic arbors spanned the length and/or width of vLGN and were often asymmetric, positioned to collect input from large but discrete territories. By contrast, arbors in dLGN are compact (Krahe et al., 2011). Consistent with spatially coarse receptive fields in vLGN, visually evoked changes in spike timing were less precise than for dLGN and SC. Notably, however, the membrane currents and spikes of some cells in vLGN displayed gamma oscillations whose phase and strength varied with stimulus pattern, as for SC (Stitt et al., 2013). Thus, vLGN can engage its targets using oscillation-based and conventional rate codes. Finally, dark shadows activate SC and drive escape responses, whereas vLGN prefers bright stimuli. Thus, one function of long-range inhibitory projections from vLGN might be to enable movement by releasing motor targets, such as SC, from suppression.

SIGNIFICANCE STATEMENT Only the dorsal lateral geniculate nucleus (dLGN) connects to cortex to serve form vision; the ventral division (vLGN) projects subcortically to sensorimotor nuclei, including the superior colliculus (SC), via long-range inhibitory connections. Here, we asked how vLGN processes visual information, making comparisons with dLGN and SC for perspective. Cells in vLGN versus dLGN had wider dendritic arbors, larger receptive fields, and fired with lower temporal precision, consistent with a modulatory role. Like SC, but not dLGN, visual stimuli entrained oscillations in vLGN, perhaps reflecting shared strategies for visuomotor processing. Finally, most neurons in vLGN preferred bright shapes, whereas dark stimuli activate SC and drive escape behaviors, suggesting that vLGN enables rapid movement by releasing target motor structures from inhibition.

Introduction

Even though the two divisions of the lateral geniculate nucleus (LGN) receive input from the eye, they are vastly different, from the level of the single cell to behavior (Monavarfeshani et al., 2017), as follows. Each subdivision has a separate developmental origin (Golding et al., 2014; Sabbagh et al., 2018). The composition of the dorsal portion of LGN (dLGN) is like that of other primary thalamic nuclei, comprising a majority of excitatory relay cells that project to cortex and a minority of inhibitory interneurons with short-range axons (Bickford, 2019). While the ratio of projection to local circuit cells is similar to that in dLGN (Gabbott and Bacon, 1994), both types of neurons are GABAergic in ventral LGN (vLGN) (Golding et al., 2014; Su et al., 2020), and the main target structures are subcortical, including many that serve sensorimotor or other behavioral roles (Monavarfeshani et al., 2017; Salay et al., 2018; Huang et al., 2019). Further, each subdivision receives input from different subsets of ganglion cells (Monavarfeshani et al., 2017), and the sizes and complexity of retinal boutons are lesser in vLGN (Hammer et al., 2014), as if scaled down to accommodate greater convergence, than in dLGN. Our goal was to understand how vLGN integrates the visual information it receives and how it communicates with downstream targets.

In highly visual animals, such as cat (Spear et al., 1977) and monkey (Babb, 1980), dLGN often dwarfs vLGN (called the pregeniculate nucleus in primate). By contrast, the two divisions are approximately the same size in rodent (Harrington, 1997), suggesting comparable importance. Thus, we chose to explore visual processing in vLGN using mouse. We studied the nucleus from two perspectives, by comparing vLGN to the principal nucleus of the form vision pathway (dLGN) and to the main station of the retinotectal pathway (superior colliculus [SC]), a sensorimotor interface. Our experimental approach involved whole-cell recording and intracellular labeling in vivo combined with standard and novel computational tools. In accord with previous accounts (Spear et al., 1977; Harrington, 1997), we found that receptive fields in vLGN were much larger, on average, than those in dLGN. The disparity in receptive field size was mirrored, and perhaps explained, by the dramatically larger breadth of dendritic arbors of cells in the ventral versus dorsal division. EPSCs were smaller and more variable in shape in vLGN than dLGN as well, indicating that cells in the ventral division integrate retinal inputs across long lengths of the dendritic arbor (Fatt and Katz, 1951).

Consistent with the spatially broad receptive fields characteristic of vLGN, spike timing with respect to the stimulus was less precise there than in SC and dLGN, and the amount of information conveyed by single spikes was lesser too. Further, roughly one-third of cells we sampled in vLGN encoded visual signals by spike timing relative to network oscillations. Oscillation phase was entrained by visual stimuli and oscillation strength waxed and waned as different sequences of natural images moved across the receptive field. Characteristics of oscillations in vLGN were closer to those recorded in SC (Brecht et al., 2001; Sridharan et al., 2011) than in dLGN (Koepsell et al., 2009; Storchi et al., 2017). Thus, although vLGN provides a spatiotemporally coarse version of visual images, it is able to engage with the intrinsic rhythms of downstream sensorimotor targets.

Materials and Methods

Experimental protocols

Preparation

Adult, pigmented, male and female mice (C57BL/6) were sedated with chlorprothixene (5 mg/kg, i.m.) after which anesthesia was initiated and maintained with urethane (0.5-1 g/kg, 10% w/v in saline, i.m.) (Niell and Stryker, 2008). After the head was cleaned and shaved, an incision was made to expose the skull so that a metal headpost could be affixed to hold the animal in place. Next, a small craniotomy centered around the LGN or SC was made. All wound margins were infiltrated with lidocaine, the brain and eyes were kept moist with saline, and body temperature was maintained at 37°C. All procedures were approved by the Institutional Animal Care and Use Committees of the University of Southern California following guidelines from the National Institutes of Health.

Recordings

Whole-cell and cell-attached recordings were made using biocytin-filled pipettes as described previously (X. Wang et al., 2007); pipette resistances were 5–20 MΩ. For whole-cell (intracellular) recordings, the membrane was held slightly below the firing threshold (in the absence of visual stimulation) to resolve subthreshold membrane currents. Neural signals were recorded with a Multiclamp 700B amplifier (Molecular Devices), digitized at 10–20 kHz using a Power 1401 data acquisition system (Cambridge Electronic Design), and stored.

Visual stimuli

Visual stimuli were generated using a ViSaGe (Cambridge Research Systems) stimulus generator and displayed on a gamma-corrected Dell U2211H LCD monitor; the refresh rate was 70 Hz and the viewing distance was 180 mm, as for a previous study of mouse dLGN (Suresh et al., 2016). The stimulus set included sparse noise, dense noise, full-field luminance steps, expanding disks, and natural movies. The sparse-noise stimulus, adapted from Jones and Palmer (1987), was individual dark or bright squares (2°–20°) shown in pseudorandom order 8 or 16 times each at 50% or 100% contrast on a 16 × 16 grid; grid spacing was 2°–5° (Suresh et al., 2016); dense noise was also as described previously (Suresh et al., 2016). Dark or bright expanding disks were stepped from 0° to 40° (Zhao et al., 2014) or 5° to 100° and displayed at 50% or 100% contrast. Full-field luminance steps ranged from 50% to 100% contrast, and natural movies were displayed at a single contrast (X. Wang et al., 2007, 2011).

Histology and verification of recording site

Brains were perfused with 3% PFA, cut in coronal sections, 100 µm thick, and processed to visualize labeled cells with standard procedures (Hirsch et al., 1998). 3D reconstructions of single cells were made using Neurolucida software (MBF Bioscience). In the instances for which cells were not recovered, electrode position was estimated from stereotaxic coordinates and depth measurements (Suresh et al., 2016).

Statistical analyses

Construction and quantification of receptive fields

Receptive fields were constructed from responses to sparse noise from membrane currents or from spikes. To form On (responses to bright stimuli) and Off (responses to dark stimuli) maps of receptive fields from subthreshold responses, action potentials were removed using a median filter (medfilt2 function, MATLAB, The MathWorks) (for fuller explanation, see X. Wang et al., 2007; Suresh et al., 2016). Next, inward or outward currents evoked from each On or Off pixel on the grid were averaged and integrated during a manually selected time window (Martinez et al., 2005). For spikes, standard spike-triggered averaging of the stimulus ensemble (Schwartz et al., 2006) was used to generate spatiotemporal maps. These were displayed as smoothed 2D contour plots made from the frame (or average of nearby frames) with the peak pixel. The sizes of receptive fields were quantified using the semimajor and semiminor axes, as well as the area, of the 1σ contours of 2D Gaussian fits to the receptive field (X. Wang et al., 2007). For cells that responded to both stimulus contrasts, the map for the dominant contrast was used to determine receptive field size. The receptive fields of several cells could not be fit; for these, we report preference for stimulus contrast but not receptive field size.

Neuronal morphological analysis

The extents of the dendritic arbors were characterized in two ways. The first was classical Sholl analysis (Sholl, 1953), which measures the number of dendritic intersections at progressive distances from the soma (step size, 5 µm). To quantify the symmetry of neuronal arbors, we devised a new measure called the Arbor Isotropy Index (AII). The AII is the ratio of a neuron's actual convex hull volume (CHV), which is the total volume spanned by a given neuronal arbor, to the maximum possible CHV. Index values range from 0 to 1; low index values indicate that processes extend for different lengths along different axes, and high values indicate symmetrically distributed processes as follows:

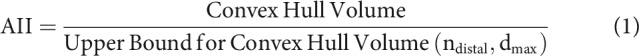where n_distal is the number of distal points anchoring the convex hull and d_max is the maximal distance of any point from the soma in the neuronal arbor.

The CHV was obtained using Neurolucida software. To compute the hypothetical upper limit for each neuron's CHV, we created a synthetic arbor that had the same number of distal points as the neuronal CHV but with each point placed at the maximum distance from the soma. To meet the challenge of computing the maximal possible CHV in 3D, we chose a well-studied approach, the Thomson problem (Thomson, 1904), (optimized using the lbfgs function, MATLAB Poblano toolbox, Sandia National Laboratories). We ran the optimization process repeatedly, using different initial values, and then selected the configuration that generated the maximal CHV.

Temporal precision and information content of neuronal responses

To quantify the temporal precision of neuronal responses across stimulus repetitions, we used a reliability measure (Schreiber et al., 2003) that reflects the correlation between pairs of filtered spike trains (R_corr), as follows:

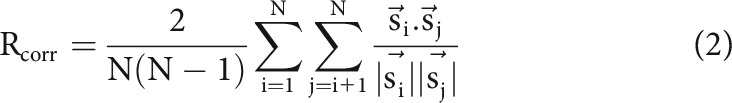where N and ${\overrightarrow{\mathrm{s}}}_{\mathrm{i}}$ indicate the number of stimulus repetitions and the filtered spike trains for individual repetitions, respectively. Note, ${\overrightarrow{\mathrm{s}}}_{\mathrm{i}}$ is computed as the convolution of the binary spike train with a Gaussian filter set to have a standard deviation of 10 ms.

Neuronal information was calculated in bits per spike as described by Brenner et al. (2000). This information measure (I) is defined as follows:

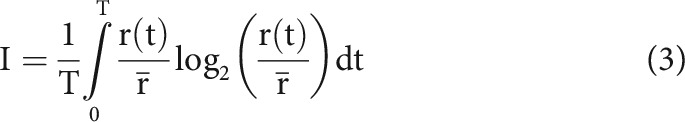where T, t, r(t), and $\overline{\mathrm{r}}$ indicate stimulus duration, time, average firing rate as a function of time, and average firing rate throughout the stimulus, respectively. Data limitations (finite number of repetitions of finite length) and narrow time bins can lead to artificially high information values, so we used the linear extrapolation method to address this issue (Brenner et al., 2000; Koepsell et al., 2009).

To estimate lower bounds for temporal precision and information content within a given spike train, we created artificial spike trains based on a homogeneous Poisson process with constant firing rate. We then ran simulations that spanned the range of physiological firing rates.

Model fitting and comparison of temporal precision and information across populations of cells

Both the reliability and information measures are systematically influenced by mean firing rate. Thus, one cannot compare these measures across cells or populations without taking the mean spike rate into account. To address this issue, we were able to devise simple models, with only a single free parameter, that capture the relationship between each of the measures (reliability, information) and mean firing rate, as follows:

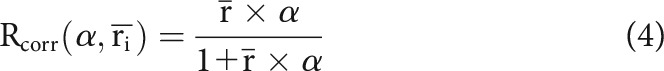where $\overline{r}$ and α indicate average firing rate and the free parameter (α), respectively. For each mean firing rate, the distribution of data points was modeled as a Gaussian centered around the value of the fitting curve; the width of the Gaussian was set to be the same for all firing rates. To fit these models, we used maximum likelihood (L) estimation, as follows:

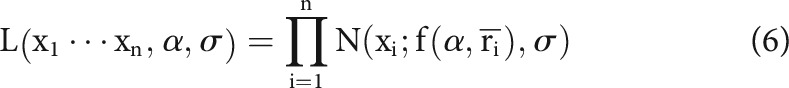where N(x; μ, σ) is the normal probability density function, f(α, $\overline{\mathrm{r}}$) is the fitting function (Eqs. 4, 5) for the mean, and x_i denotes a measurement (either reliability or information) and n is the number of data points. Optimization was performed using a gradient descent approach with a line search strategy.

We used these models to compare response properties across populations of cells from vLGN to dLGN or SC. To determine whether response properties differ significantly across nuclei, we compared joint versus separate models. The joint model used the same set of fitting parameters to describe two populations, whereas the separate model optimized individual parameter sets for each population. Rather than just using the likelihood to compare the joint versus separate models, we used the Akaike information criterion (AIC) (Akaike, 1974) to account for the differences in complexities between the two models as follows:

where k represents the number of free parameters and $\widehat{\mathrm{L}}$ the maximum likelihood value for this model. The model with the lower AIC was defined as the better model.

Quantifying oscillatory neuronal activity

To quantify the strength of oscillations in spike trains and membrane currents, we used the oscillation score method (Mureşan et al., 2008). This score is based on the Fourier transform of the smoothed autocorrelation function in which the central peak and the segment corresponding to the refractory period are removed. Then, to calculate the oscillation score, the frequency with the highest amplitude in the range of interest (the gamma band, 25-100 Hz) is selected, and its amplitude normalized by the averaged amplitude across frequencies. The oscillation score, along with the confidence score (the consistency of the oscillation score across stimulus repetitions), is used to test the significance of oscillatory activity. Significant oscillations were defined as having oscillation scores >5 and confidence scores >0.65. We excluded responses without a clear peak in the gamma range; the lack of a gamma peak may have been due to data limitations (<200 spikes total) in some cases.

To analyze oscillatory activity in membrane currents, we performed a Fourier transform of spike-subtracted membrane currents. Because the amplitude of the frequency components of the resulting spectra obeyed a power law, we needed to adapt the oscillation score method, as this method assumes little to no general trend in the Fourier transform. Hence, we plotted amplitude versus frequency using logarithmic axes to yield a linear trend that could be fit with a line in the logarithmic domain. It was then possible to use the resulting fit to normalize the spectrum so that we could discern the frequency with the highest amplitude and proceed to compute the oscillation score. Using a sliding window, we characterized oscillation strength before, during, and after stimulus onset and determined significance by bootstrapping with resampled datasets matched in size to the original dataset. Thresholds for the oscillation score were determined from the 200 ms window preceding stimulus onset and by using Bonferroni correction (for the number of samples in the window analyzed) at a significance level of 0.01.

To compute the distribution of oscillation phases in the membrane currents at which spikes occurred, we convolved the membrane currents with a complex Morlet waveform and computed the phase of this complex signal to estimate the phase of the intracellular signal, as we have done previously for studies of cat (see Koepsell et al., 2009). The oscillation frequency derived from membrane currents was the frequency parameter and the period of that frequency was the temporal width parameter for the Morlet waveform.

To determine whether the stimulus entrained oscillations, we first computed oscillation phase over time for each repetition. Then, we fit the cross-trial distribution of phases with a von Mises function to obtain a concentration parameter (see Koepsell et al., 2009). In order to determine the statistical significance of entrainment, we compared the width of phase distributions obtained from each biological dataset to a simulated distribution of concentration parameter values computed for phases drawn randomly from a range of 0° to 360°. The threshold for significance was determined as above, α = 0.01 with Bonferroni correction. The latency for entrainment was taken as the time from stimulus onset to the initial significant peak value of the concentration parameter.

Linear encoding model for the oscillation score

To investigate how the oscillations we recorded reflected local (within the receptive field) versus full-field changes in the stimulus, we performed the following analysis. The image features used were the average intensity of the full image or the average intensity of the image patch inside the receptive field (determined from a rectangular kernel tightly enclosing the 1σ contour of the fit made to the receptive field map obtained with sparse noise). We reasoned that if changes in the movie influence the oscillation score, then one should be able to use image features to predict changes in the oscillation score. Thus, we modeled the oscillation score as the weighted average of the image features computed from the preceding 214 ms movie segment. Then, the model parameters were estimated using ridge regression (ridge function, MATLAB, The MathWorks) for regularization. The model parameters were then used to predict the oscillation score.

To estimate model performance, we used leave-one-out cross-validation (one stimulus repetition is reserved for testing and all other trials are used for training, with the process repeated to leave out each trial). We then calculated the Pearson correlation between the oscillation scores that the model predicted and those obtained directly from recordings. The mean correlation across trials was calculated for a wide range of values of the ridge parameter, and the value that gave the maximum mean correlation was selected for each model. This entire analysis was done separately for the mean contrast of the full image and within the region demarcated by the receptive field. Finally, to provide a practical upper bound for model performance, we calculated the average correlation between the oscillation scores of individual repetitions and the average oscillation score across trials.

Additional statistics

In addition to the analyses described above, statistical variation for a given data set is reported as mean ± SEM, unless otherwise noted as mean ± SD. Significance values were calculated using a Wilcoxon rank sum test unless otherwise noted.

Results

Here, we used an interdisciplinary approach to study the mouse vLGN, including extracellular and whole-cell recording in vivo, anatomy, and computational tools. Further, to gain a functional perspective, we compared the results from vLGN to those obtained in dLGN and SC, subcortical structures that receive direct retinal input and are part of either the form vision (geniculostriate) or the visuomotor (retinotectal) pathways. Our dataset includes 39 visually responsive neurons from vLGN (or adjacent intergeniculate leaflet [IGL]). Unless otherwise noted, we included the few cells we identified in IGL with those from vLGN in the population statistics as no differences emerged in anatomical measures, synaptic physiology, receptive field size, temporal precision, or oscillatory activity. The remaining sample includes 11 neurons from superficial SC and 59 from dLGN that were part of an earlier study (Suresh et al., 2016). We were unable to test all cells with all stimuli. Also, although all the cells we labeled in our studies of dLGN and vLGN resembled projection cells, our sample may have included local circuit cells.

Comparison of receptive field structure and scale in dLGN versus vLGN

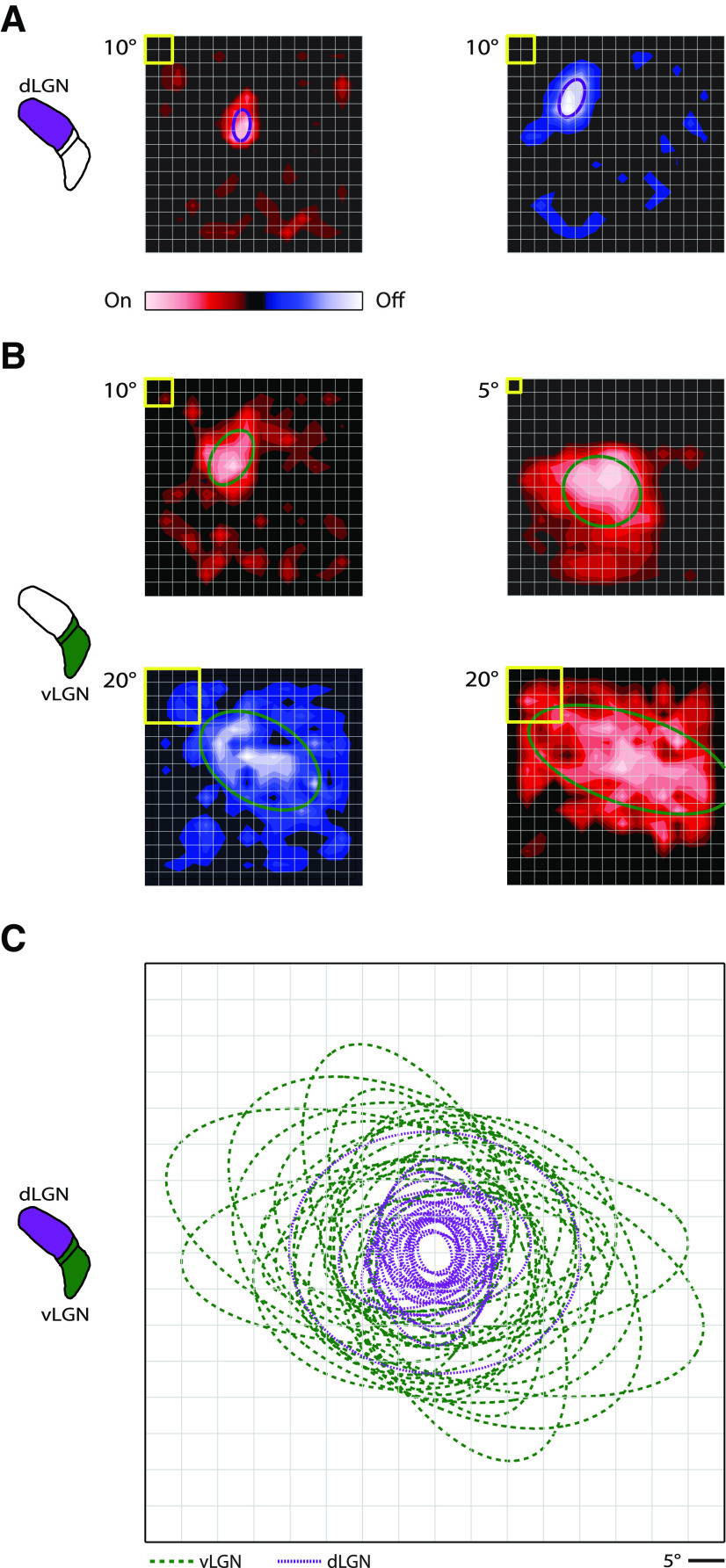
While receptive fields in dLGN have been quantified for several taxonomic orders (primate, carnivore, and rodent) (Bullier and Norton, 1979; Shapley and Lennie, 1985; Piscopo et al., 2013; Suresh et al., 2016), there are only scant and qualitative descriptions of receptive fields (Spear et al., 1977; Sumitomo et al., 1979) or overall luminance preference (see, e.g., Thankachan and Rusak, 2005) in vLGN. Thus, we used a sparse-noise stimulus to map On and Off components of neural receptive fields in murine vLGN and quantified their sizes with 2D Gaussian fits. Then we compared receptive fields in vLGN with those in dLGN. Typically, neural receptive fields in dLGN were smaller (Fig. 1A) (see Suresh et al., 2016) than those in vLGN (Fig. 1B); receptive fields are shown as contour plots with an overlay representing the 1σ contour of the Gaussian fit. Even in vLGN, however, there was a range of spatial extents from smaller to larger (Fig. 1B). To visualize population differences, the 1σ fits of maps for all cells in vLGN (green) and the same number of (randomly selected) cells in dLGN (purple) were aligned at their centers and superimposed (Fig. 1C). To quantify differences between receptive fields in the dLGN versus vLGN, we used two measures. First, we compared the average of the extent of the semimajor and semiminor axes obtained from the Gaussian fits: vLGN, 33.99 ± 2.05°; dLGN, 13.63 ± 1.35°, p = 2.3 × 10⁻⁸, n = 25 for each subdivision. Second, we compared the area (°)²: vLGN, 897.83 ± 102.24; dLGN, 173.75 ± 41.51, p = 2.3 × 10⁻⁸, n = 25 for each subdivision. Both measures show that receptive field size in vLGN is significantly larger than in dLGN.

Figure 1.

Receptive field structure in dLGN and vLGN. A, Contour plots of two sample receptive fields from dLGN derived from membrane currents of an On-center (red, left) and Off-center relay cell (blue, right). The stimulus was sparse noise. Yellow box at top left corner of each contour plot indicates stimulus size. Overlays are 1σ contours from 2D Gaussian fits of the receptive fields. B, Sample receptive fields in vLGN for three On cells (top left, top right, bottom right) and an Off cell (bottom left); conventions as in A. C, Plot of the 1σ contours for receptive fields of relay cells in dLGN (purple, dotted lines) and cells in vLGN/IGL (green, dashed lines); the contours are aligned at each receptive field center.

Most of the cells we mapped in vLGN preferred bright stimuli. All in all, there were 17 On, 3 Off, and 4 On-Off (3 On-dominant, 1 Off-dominant) cells. Four remaining cells were inhibited rather than excited by the presentation of visual stimuli; 3 of these were inhibited by bright stimuli, and an additional cell was inhibited by bright or dark stimuli. The receptive fields of some of these cells appear in subsequent figures.

Neuronal morphologies in different divisions of the LGN

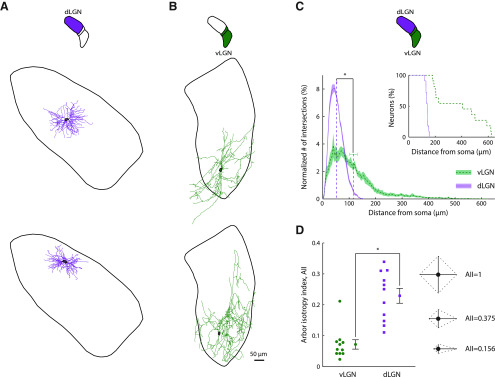
The large size of receptive fields in vLGN suggested that single cells were able to pool input arriving from broad retinal territories. By labeling and reconstructing cells in vLGN, we were able to show that the dendritic arbors were wide-ranging. Of the 8 cells we labeled well, 4 had dendrites that spanned the full mediolateral extent of the nucleus and another spanned the entire dorsoventral axis. Furthermore, 6 cells had processes that spread outside of vLGN or IGL. In dLGN, by contrast, previous work, including our own, had shown that the dendritic arbors of all subtypes of relay cells are compact (Dhande et al., 2011; Krahe et al., 2011; Suresh et al., 2016). Reconstructions for 2 sample cells each from dLGN (Fig. 2A) and vLGN (Fig. 2B) illustrate the difference in arbor size between subnuclei.

Figure 2.

Morphological differences between neurons in dLGN versus vLGN. A, Reconstructions of a Y (top) and an X relay cell (bottom) in dLGN projected in the coronal plane. Somas are outlined in black, and the contour surrounding each cell indicates the boundary of dLGN at the location of the soma. B, Drawings of two different cells in vLGN; conventions as in A. C, Plot of the distribution of processes as a function of distance from the soma computed using Sholl analysis for dLGN (purple, dotted line) and vLGN (green, dashed line). The values for each neuron were normalized before calculating population statistics. Shading represents the SEM. Dashed vertical lines indicate the mean distance from the soma for each LGN subdivision. Horizontal error bars indicate the SEM. Top right, Inset, Plot of the percentage of neurons that had processes that reached the distances indicated along the abscissa. Arbors of all neurons in vLGN extended farther than those of relay cells in dLGN. D, Left, Plot of AII values in vLGN (green dots) and dLGN (purple squares) and (right) a graphical depiction of the AII in 2D. For a neuron with four dendrites of equal length along four cardinal directions, the AII value is 1, with progressively smaller values when the relative lengths of dendrites extending along each axis differ as illustrated. Dashed lines indicate the convex hull. For reference, the AII values for the four neurons illustrated in this figure were as follows: A, top, 0.339; A, bottom, 0.279; B, top, 0.042; B, bottom, 0.042.

Next, we placed cells in a template vLGN, as we had done previously for dLGN (Suresh et al., 2016) and measured the ratio of the distance of the soma from the lateral border to the full extent of the nucleus at a given anteroposterior position; these values were as follows: 0.61, 0.53, 0.53, 0.49, 0.45, 0.13, 0.13, and 0.05. From this analysis, it seems likely that the somas of most or all of our labeled cells lay in the retinorecipient (lateral) zone of vLGN, which occupies more territory than the medial zone in mouse (Monavarfeshani et al., 2017; Sabbagh et al., 2018). In addition, labeled neurons resembled projection cells, which are multipolar and begin to branch near the soma, versus local interneurons, which are typically bipolar and branch distally (Brauer and Schober, 1982; Gabbott and Bacon, 1994). It remains possible, however, that some unlabeled cells in our sample were local interneurons or were visually responsive cells that lay in the medial zone (Thankachan and Rusak, 2005). We also filled 3 cells in IGL; their arbors spanned the leaflet, and their statistics are pooled with vLGN in the analyses described below.

In order to quantify the difference between the extent of neuronal processes in each subnucleus, we first used Sholl analysis (Sholl, 1953), which counts how many processes intersect each of a series of concentric rings centered on the soma. Dendrites in vLGN sampled distances as far as 600 µm from the soma, whereas arbors of relay cells in dLGN rarely extended beyond 150 µm. The average intersection distance for neurons in vLGN was roughly double that for cells in dLGN: vLGN, 116.1 ± 14.8 µm; dLGN, 52.7 ± 1.3 µm, p = 8.2 × 10⁻⁵, n = 11 for each subdivision (the cells in dLGN were randomly selected from the larger dataset). Histograms of the results of the Sholl analysis for each neuron were normalized before calculating population statistics (Fig. 2C). A companion plot shows the percentage of neurons with processes that reached a given distance from the soma (Fig. 2C, inset). Overall, arbors of relay cells in dLGN tended to have similar diameters, whereas there was considerable variation among cells in vLGN.

Further, the arbors of cells in vLGN had a markedly asymmetric appearance. Previous studies of dendritic anisotropies in dLGN used Sholl-based methods that assigns dendrites into two perpendicular planes (Krahe et al., 2011). This work showed that arbors in dLGN core are compact, with a degree of variation in radial symmetry that recalls the division between Y cells and a subset of X cells in cat (cat X cells arbors vary widely in shape, so this cell class is defined by diverse criteria) (Friedlander et al., 1981; Humphrey and Weller, 1988; Krahe et al., 2011); separate analysis restricted to the perimeter of the dLGN identified a third, W-like, class of cells for which dendrites preferred one hemisphere over the other. We wished to measure anisotropies in vLGN in 3D (Sholl analysis is limited to 2D) without having to group dendrites into specified planes. Thus, we devised an index that took all three dimensions into account and that was free of assumptions about the trajectory of the dendritic arbor. We call the new measure the AII (see Materials and Methods). The value of the index is 1 for perfect symmetry and decreases as the preference for particular axes grows stronger. A 2D graphical depiction of how the AII reflects directional biases in arbors is provided for 3 sample configurations, shown to the right of the population data in Figure 2D. As per our initial impression, values for vLGN were significantly lower than for dLGN: vLGN, 0.072 ± 0.015; dLGN, 0.229 ± 0.024, p = 3.0 × 10⁻⁴, n = 11 for each subdivision (the cells in dLGN were randomly selected from the larger dataset published in Suresh et al. (2016); this dataset did not include interneurons. One might have thought that the narrow profile of IGL would have enforced greater arbor asymmetry than the boundaries of the (far larger) subdivisions of LGN. This was not the case, however, because dendrites of cells in IGL spread into neighboring structures.

Synaptic physiology in different divisions of the LGN

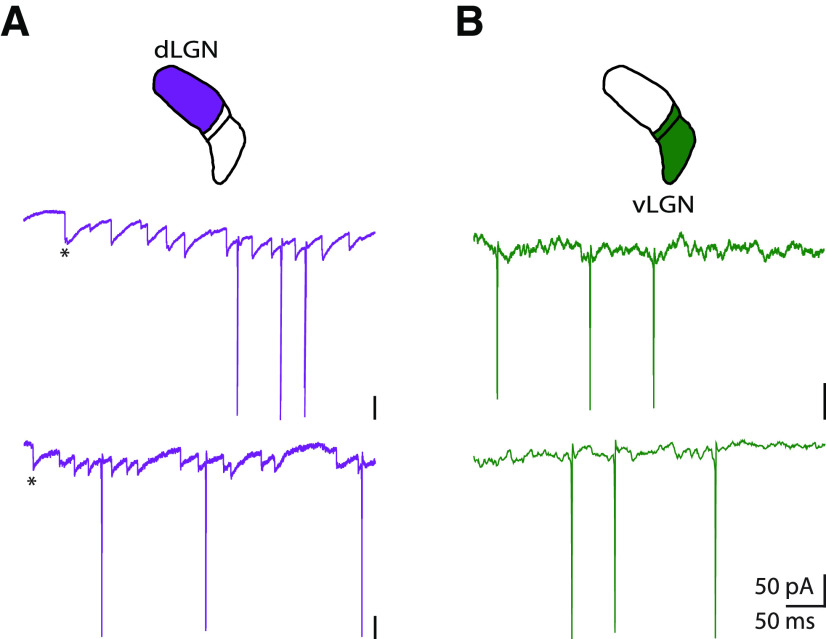
Given that receptive fields were larger and dendritic arbors wider in the vLGN versus dLGN, we asked whether there werecommensurate differences in synaptic physiology. To explore this possibility, we assessed recordings of membrane currents. Sample recordings from dLGN and vLGN reveal differences in the pattern of EPSCs in each subdivision (Fig. 3). In dLGN, intracellular currents recorded from relay cells were dominated by trains of sharp, unitary EPSCs that can be distinguished by eye (Fig. 3A) and easily labeled using machine learning tools, such as a support vector machine, as we have published previously (Suresh et al., 2016). These EPSCs almost certainly come from retinal inputs (X. Wang et al., 2007, 2011; Koepsell et al., 2009; Suresh et al., 2016), which are large and proximal (Hamos et al., 1987; Morgan et al., 2016). The recordings from vLGN were more complicated, however. Localizing individual EPSCs in the recordings from vLGN was challenging because events, when visible, were small, slow, or overlapping, as seen for 2 representative cells in Figure 3B. This difference in synaptic physiology is consistent with the idea that neurons in vLGN pool a larger number of inputs than in dLGN (Turrigiano et al., 1998) and receive retinal inputs over long lengths of dendrites (Fatt and Katz, 1951; Bloomfield et al., 1987). While we have illustrated results from only 2 cells in each nucleus, these are characteristic of the entire sample as can be seen in additional figures in this manuscript and in our previous study of dLGN (Suresh et al., 2016).

Figure 3.

The shapes of membrane currents recorded from dLGN and vLGN. Membrane currents recorded from (A) two cells in dLGN (purple) and (B) two cells in vLGN (green). Retinogeniculate EPSCs (*first EPSC) are easily visible in traces from relay cells in dLGN. By contrast, individual synaptic events are difficult to discern in records from vLGN.

Receptive field structure and response timing in vLGN, SC, and dLGN

Unlike dLGN, which innervates cortex, vLGN projects subcortically, with a main target, SC, a hub for sensorimotor behaviors (Monavarfeshani et al., 2017; Cang et al., 2018). SC projects back to vLGN in turn (Harrington, 1997). To understand how vLGN might interact with visuomotor brainstem regions, we compared receptive field structure and spike timing in vLGN to that in the superficial (retinorecipient) SC. For this analysis, receptive fields were estimated from spike-triggered averages made using sparse noise, and their sizes quantified with 2D Gaussian fits (while receptive fields had been mapped previously in the mouse SC(L. Wang et al., 2010; Gale and Murphy, 2014; Ellis et al., 2016), it was important to collect a dataset with a standardized stimulus). The receptive fields in vLGN were larger than those in the superficial SC as illustrated in Figure 4A, C. The 2D extent was as follows: vLGN, 32.48 ± 2.47°, n = 24 cells; SC, 15.45 ± 1.96°, n = 11 cells, p = 3.5 × 10⁻⁵; mean area in (°)²: vLGN, 853.70 ± 160.10, n = 24 cells; SC, 176.30 ± 35.85, n = 11 cells, p = 1.3 × 10⁻⁵.

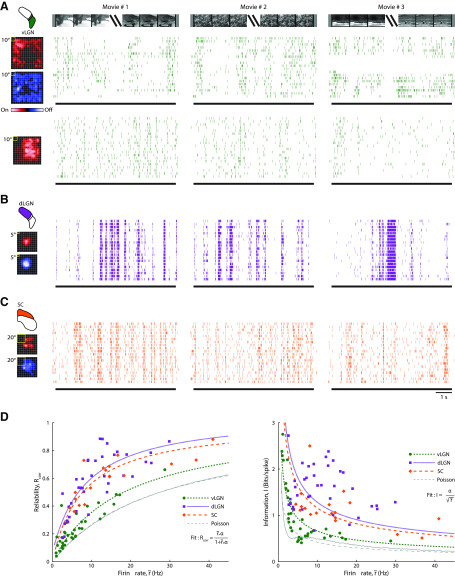
Figure 4.

Temporal precision and information content of spike trains evoked by natural scene movies for vLGN, dLGN, and SC. Responses of (A) two cells in vLGN (green), (B) one cell in dLGN (purple), and (C) one cell in the superficial SC (orange) to three different natural movies. Receptive fields (spike-triggered averages) made with sparse noise are shown to the left of raster plots showing spiking responses to repeated stimulus trials for each movie for each cell. D, Left, Scatter plot of the correlation-based reliability measure against spike rate. Each point was calculated from a given cell's response to one of the three movies. Green dots represent vLGN. Purple squares represent dLGN. Orange diamonds represent SC. Various styles of broken lines indicate best fits, as indicated in the legend. Green short dashes represent vLGN. Purple dotted lines indicate dLGN. Orange long dashes indicate SC. See legend for the fitting function used. Thin gray line indicates results from a simulation with homogenous Poisson spike trains; gray dashed line indicates the corresponding fit. Right, Plot of bits per spike against firing rate; conventions as for D (left).

Our next question was whether or not the size of receptive fields and the degree of temporal precision in a given area covary. That is, since small receptive fields often correlate with high visual acuity, we wondered whether they might also correlate with high temporal precision (i.e., reliability across trials). Temporal precision has implications for the amount of information conveyed within spike trains (de Ruyter van Steveninck et al., 1997; Brenner et al., 2002; Schreiber et al., 2003). Hence, after mapping each receptive field, we recorded responses to natural scene movies. Since natural images share 1/f statistics (they are dominated by low spatial frequencies) (Field, 1987), these movie stimuli mimic the statistics of the animal's environment. Sample receptive fields and raster plots of responses to repeated presentations of three different movies illustrate the approach for vLGN (Fig. 4A), dLGN (Fig. 4B), and SC (Fig. 4C). Although the level of temporal precision changed throughout the stimulus and from cell to cell, at the population level, the spike trains recorded from SC and dLGN seemed more reliable than for vLGN.

In order to quantify potential differences in temporal precision across structures, we used a correlation-based reliability measure (Schreiber et al., 2003) (see Materials and Methods). This measure reflects differences in spike timing from one stimulus trial to another; values range between 0 and 1, with 1 indicating maximal precision. Because the measure is influenced by firing rate, we chose to plot index values against this parameter. The resulting scatterplot (Fig. 4D, left) indicated that cells in SC (orange) and dLGN (purple) fire more reliably than those in vLGN (green) at a given spike rate. Each marker in the plot represents an index value computed for an individual cell's response to a single movie stimulus (maximal number of points per cell is 3).

To perform a statistical comparison across populations, we used an approach that models the reliability score as a function of firing rate. We optimized the fit for the distribution of points for each brain structure using maximum likelihood estimation (Fig. 4D, left, dashed lines) (see Materials and Methods). The fits for SC (orange) and dLGN (purple) lay above that for vLGN (green), indicating a higher degree of temporal precision in both dLGN and SC than in vLGN. Finally, all neural responses were more reliable than simulated, homogeneous Poisson spike trains (Fig. 4D, left, gray dashed line).

We next used the AIC (Akaike, 1974) to determine whether the results from SC and dLGN were significantly different from those in vLGN. This criterion takes into account the likelihood of data given a particular statistical model, as well as model complexity. It is a standard tool to compare the relative performance of statistical models; lower values correlate with better model quality. We began by comparing vLGN with SC. A model that used separate parameter sets (separate model) for fitting SC and vLGN data performed better than a model with shared parameters (joint model) for fitting both datasets. The AIC for the separate model was −123.4 and for the joint model was −82.1 (vLGN, n = 37 responses; SC, n = 18 responses). This means that the increase in the logarithm of the likelihood for the model that fit both datasets separately was greater than the penalty introduced by adding the free parameters required to fit this model. When we restricted the analysis to datasets from responses to a single movie only (the movie we used was of snow monkeys, see Movie 1, Fig. 4); the difference between the separate versus joint model was similar; the value for the separate model was −67.6 and that for the joint model was −46.4 (vLGN, n = 25 cells; SC, n = 10 cells).

To address any biases that might have been introduced by differences in firing rates across nuclei, we performed additional tests. First, we analyzed a subset of data in which firing rates were similar for both regions (4.4-28.7 Hz in this case). Again, the separate model outperformed the joint model, the AIC values were −85.6 and −39.7, respectively (vLGN, n = 19 responses; SC, n = 15 responses). Second, we calculated statistics for reliability; these were also significantly higher in SC (0.560 ± 0.035, n = 15) than in vLGN (0.318 ± 0.030, n = 1); p = 1.2 × 10⁻⁴.

We performed the same analysis to compare vLGN with dLGN; the responses from dLGN were more reliable. For the data from all movies, the AIC values were −137.0 for the separate model and −97.3 for the joint model (n = 37 responses for each LGN subdivision). For a single movie, the criterion value was −83.1 for the separate model and −63.5 for the joint model (n = 25 responses for both LGN subdivisions). For the dataset associated with the range of firing rates common to both subdivisions (2.5-28.7 Hz in this case), the criterion value was −130.2 for the separate model and −79.4 for the joint model (vLGN, n = 28 responses; dLGN, n = 36 responses). The difference in reliability between vLGN (0.270 ± 0.025, n = 28) and dLGN (0.503 ± 0.033, n = 36) was significant (p = 8.2 × 10⁻⁶).

Information in spikes of vLGN, SC, and dLGN

In general, the amount of information that a single spike contributes decreases as firing rate increases, and we quantified this relationship for our data. We computed the information in bits per spike (Brenner et al., 2002) (see Materials and Methods), using the dataset obtained with natural movies. The results (Fig. 4D, right) show that the amount of information per spike was usually higher for SC than vLGN for comparable firing rates. We modeled bits per spike as a function of firing rate and plotted the fits of these results as dashed lines (Fig. 4D, right). The curves for SC lay above those for vLGN. The AIC value was 45.4 for the separate model and 68.2 for the joint model (vLGN, n = 37 responses; SC, n = 18 responses). When we split the datasets into responses for individual movies, the differences in the AIC were similar. The value for the separate model was 32.6, and for the joint model 50.0 (vLGN, n = 25 responses; SC, n = 10 responses).

We next recalculated these values using firing rates for which there was substantial overlap between SC and vLGN (4.4–28.7 Hz). Again, the criterion value (10.9) for the separate model was better than that (49.2) for the joint model (vLGN, n = 19; SC, n = 15). Values of bits per spike, independent of firing rate, were higher in SC (1.245 ± 0.100, n = 15 responses) than in vLGN (0.567 ± 0.028, n = 19 responses); p = 1.0 × 10⁻⁶. For reference, we calculated information in bits per spike from simulated Poisson spike trains (Fig. 4D, right, dashed gray lines); in almost all cases, values from biological spike trains were higher.

We repeated the analyses for the two divisions of the LGN. As expected, values for dLGN were higher than vLGN at comparable firing rates (Fig. 4D, right). The AIC value was 101.8 for the separate model and 155.2 for the joint model (n = 37 responses for both subnuclei). For a single movie type, the criterion values for separate and joint models were 67.0 and 100.1 respectively (n = 25 for both structures). For the dataset associated with the overlapping range of firing rates (2.5–28.7 Hz), the criterion was 62.9 for the separate model and 140.8 for the joint model (vLGN, n = 28 responses; dLGN, n = 36 responses). The information in bits per spike was as follows: vLGN, 0.689 ± 0.043, n = 28; dLGN, 1.581 ± 0.079, n = 36; p = 2.98 × 10⁻¹⁰. Thus, single spikes in vLGN convey less information about the stimulus than those in dLGN or SC.

Oscillatory neural responses in vLGN and SC

Neurons can encode information about the stimulus in two ways: changes in spike rate with respect to an extrinsic signal(i.e., the stimulus) and spike timing with respect to intrinsically generated rhythms, such as oscillations (Koepsell et al., 2010). The analyses that we illustrated in Figure 4 pertain to the rate code. However, there was reason to explore potential roles of oscillations in vLGN. Visually evoked oscillations are reported in SC (Brecht et al., 2004; Sridharan et al., 2011; Stitt et al., 2013). Further, in earlier work, we (Koepsell et al., 2009, 2010) and others (Saleem et al., 2017; Storchi et al., 2017) showed that some cells in dLGN use both rate and oscillation-based coding schemes. There is, however, a difference between oscillation-based coding in dLGN and SC. In dLGN, oscillations typically reflect ongoing activity in the retina and their phase is rarely, if ever, entrained by visual stimuli (Saleem et al., 2017; Storchi et al., 2017). By contrast, oscillations in SC are evoked and entrained by visual stimuli and, hence, seem to be generated by local, extraretinal, networks (Brecht et al., 2004; Sridharan et al., 2011; Stitt et al., 2013).

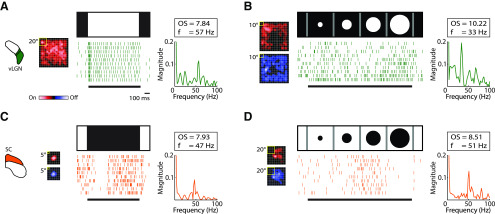
We often recorded visually evoked oscillations from vLGN that resembled those reported in SC. Full-field stimuli evoked oscillations in the spike trains of 9 cells (6 of 19 On cells and 3 of 7 Off [or On inhibited] cells), as illustrated in Figure 5A. Bright, but not dark, expanding discs evoked oscillations in 2 of 3 cells (Fig. 5B). By contrast, in SC, either full-field dark stimuli (Fig. 5C) or expanding (e.g. looming) (Fig. 5D) dark discs drove oscillations. Here, oscillation frequency, strength, and significance were computed using the oscillation score method (Mureşan et al., 2008) (see Materials and Methods). We might have underestimated the percentage of oscillating spike trains in our sample because of data limitations. For example, there may have been instances in which the number of spikes recorded from a given cell was insufficient to generate a significant oscillation score.

Figure 5.

Visually evoked oscillatory spike trains in vLGN and SC. Examples of oscillatory spike trains in vLGN (green [A]) and SC (orange [C]) evoked by a full-field stimulus. Receptive fields are shown to the left of spike rasters of responses to repeated trials of the stimulus that is depicted above each raster plot. Plots of oscillation strength against frequency are shown to the right of the rasters, with insets containing values for the oscillation score (OS) and frequency (f). B, D, Same as in A, C, except the stimulus was an expanding spot, as indicated in the figure. Spot size was stepped from 5° to 100° for vLGN and from 0° to 40° for SC.

Oscillatory membrane currents in response to visual stimulation in vLGN

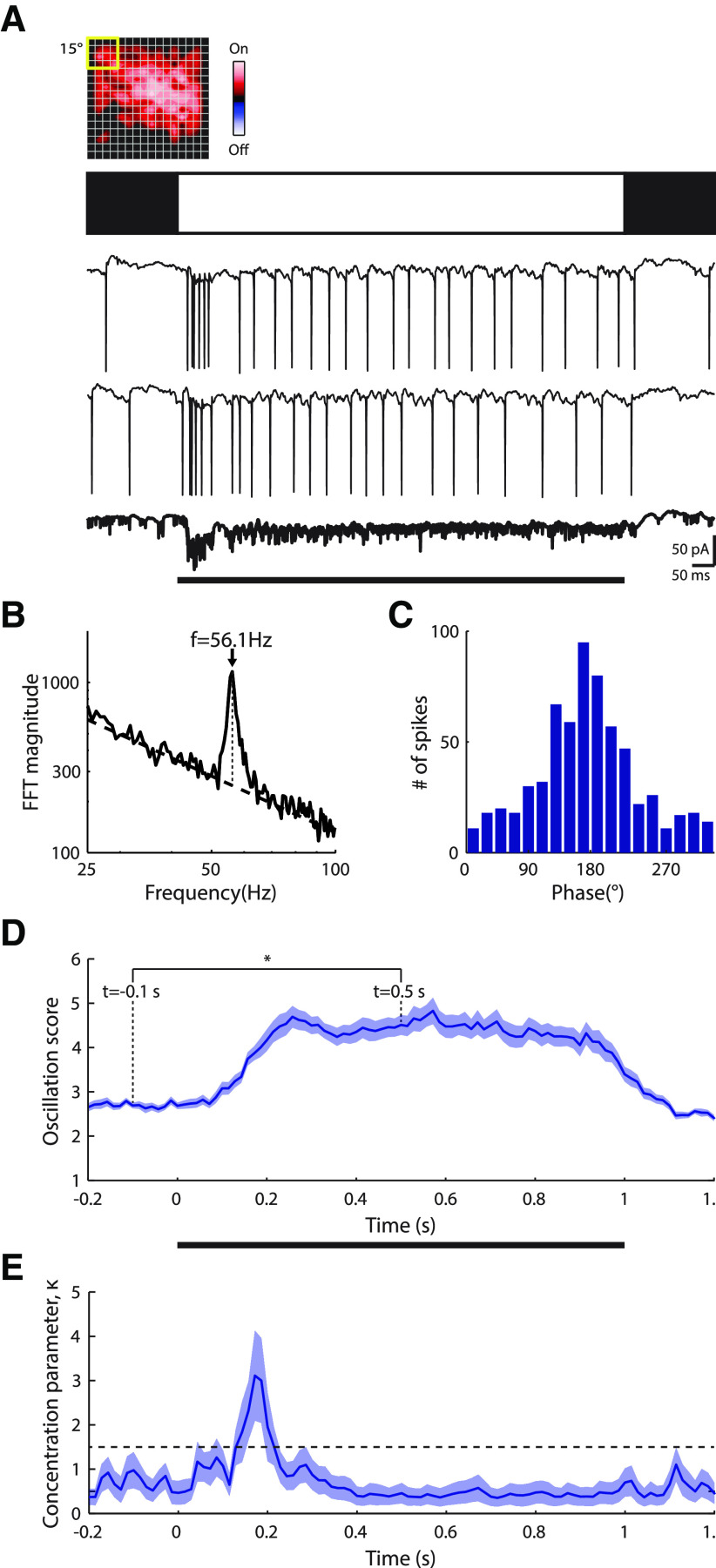
It was natural to assume that oscillatory activity recorded in spike trains reflected oscillations in underlying membrane currents. To test this assumption, we obtained whole-cell patch recordings, such as those shown in Figure 6A, and modified the oscillation score method for subthreshold responses (see Materials and Methods). Our modified analysis revealed oscillatory membrane currents similar in frequency to that observed for spike trains (Fig. 6B). Thus, we calculated phase coherence between membrane currents and spikes using a concentration parameter; higher values indicate greater coherence (Koepsell et al., 2009) (see Materials and Methods). Our results show that spikes phase-lock to membrane oscillations faithfully (Fig. 6C). The concentration parameter for this cell was 1.15, similar to the population average of cells with oscillating membranecurrents and that fired a sufficient number of spikes (≥100 spikes) to compute the concentration parameter (1.29 ± 0.48, mean ± SD, n = 11 cells).

Figure 6.

Flash-evoked gamma band oscillatory currents for a sample ON cell in vLGN. A, Top, Contour plot of the receptive field; conventions as in Figure 1. Middle, Icon depicting a full-field bright stimulus. Bottom, Two individual responses to the stimulus, and the average across trials, bolded and at 2× gain. B, Illustration of how the oscillation score analysis was adapted for membrane currents. The oscillation frequency is computed by taking the frequency that has the highest amplitude (dotted vertical line) with respect to the linear trend (dashed line) in the spectrum (plotted on a logarithmic scale). The oscillation score is then computed as the relative spectrum amplitude, normalized by the trend, at the oscillation frequency. C, Histogram of phase coherence between intracellular currents and spikes during the stimulus reveals temporal locking between synaptic input and neural output. D, Plot of the mean ± SEM of the oscillation score of membrane currents over time across trials; values were calculated using a 204.8 ms sliding window (n = 25 repetitions). *p < 0.01. E, Plot of the mean ± SD of the phase concentration parameter (κ) over time (computed by bootstrapping with resampled datasets matched in size to the original dataset). Dashed horizontal line indicates the threshold for significant entrainment (α = 0.01).

Because intracellular responses provide a sensitive measure of neural response, we used these to explore the evolution and duration of visually evoked oscillations. Oscillation strength lagged the initial neuronal response, likely because it took time for the network dynamics to change state (Fig. 6D). During the stimulus, the oscillation score remained high overall and then began a steady decline to baseline after the stimulus ended. Thus, oscillations, once engaged, were maintained throughout stimulus duration. This example was from an On cell, and the responses displayed were evoked by a full-field bright stimulus. Various full-field or expanding-disk stimuli evoked significant (see Materials and Methods) oscillatory membrane currents in 18 of 29 cells, including On-inhibited and On-Off cells.

The nature of the information that the oscillations convey depends, in part, on how strongly they are entrained by the stimulus. Thus, we asked whether oscillations phase-lock to stimulus onset and found that this was most often the case. After stimulus onset, the phase of membrane currents across repetitions began to synchronize (see Materials and Methods), as illustrated in Figure 6E. We observed significant entrainment for 13 of the 18 cells (72%) that oscillated in response to the full-field or expanding-disk stimuli; the mean latency of entrainment was 98 ± 63 ms (mean ± SD); n = 13. Last, because we hyperpolarized cells slightly to visualize membrane currents, firing rates were too low to provide sufficient data for a parallel analysis with spikes.

Oscillatory membrane currents during naturalistic stimulation

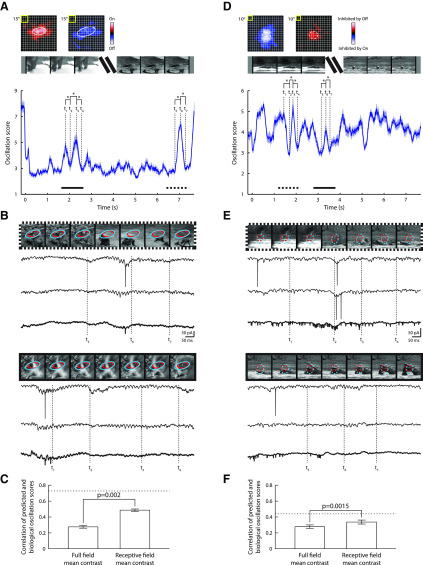
Simple flashed stimuli evoke strong responses but are far from the spatiotemporal patterns the animal experiences in the environment. Thus, we investigated the potential role of oscillations for vision by making whole-cell recordings during the presentation of natural movies. Oscillation strength in membrane currents waxed and waned during specific stimulus sequences; we quantified those changes using the oscillation score (Fig. 7). Figure 7A plots receptive field maps (obtained using sparse noise) for a single cell above a graph of oscillation strength over time made from responses to a movie. Certain transitions in the image sequence, either abrupt variations (segment indicated by the dotted horizontal line, Fig. 7A) or smooth gradual ones (segment indicated by the solid horizontal line, Fig. 7A), preceded changes in oscillation strength. Example membrane responses to each of the different sample sequences are shown in Figure 7B, where markers (t_1-7) indicate corresponding time points in the plot of oscillation score. We wondered whether the oscillations were driven locally from the portion of the image falling within the receptive field, or globally, by the entire visible image. Thus, we modeled the oscillation score either as a linear function of average stimulus intensity for the entire image, or as the portion within the receptive field. These models were fit using ridge regression, and the fitted models were used to generate an oscillation score waveform. The correlation between this prediction and the oscillation scores from individual repetitions spared for testing was calculated, along with realistic upper bounds of performance (see Materials and Methods), (Fig. 7C). This analysis suggested that stimulus features in the receptive field had more predictive power for oscillations than features pooled across the full field. Overall, this simple model was able to achieve performances close to the realistic upper bound. A similar analysis for a second cell is also illustrated (Fig. 7D–F).

Figure 7.

Changes in the strength of membrane oscillations during the presentation of natural scene movies in vLGN. A, On and Off maps of the receptive field of an On-Off cell and an illustration of the stimulus are shown above the oscillation score computed continuously from membrane currents recorded during the movie (n = 10 repetitions). Solid curve indicates the mean. Shading represents the SEM. The 1 s segments of the curves marked by the dotted and solid horizontal lines correspond to responses illustrated in B, as do the vertical dashed lines labeledt_1-7. *p < 0.01. B, Top, Image sequences (every 10th frame of the movie) for the interval marked by the dotted line in A, with the position of the On and Off receptive field maps, indicated by overlays, shown above sample membrane currents (two individual traces with the average of all trials bolded at 2× gain). Bottom, Same as for the top panel but for the interval marked by the solid line. C, Bar plots of correlations between predicted oscillation scores (made using ridge regression analysis) and oscillation scores computed from the biological data for the mean contrast of the full field, or the mean contrast of the image patch that contained the receptive field. Error bars indicate mean ± SEM. Dashed line represents a heuristic upper bound for model performance. D–F, Same analyses for a second cell (n = 20 repetitions).

Discussion

To learn about the role of vLGN in visual processing, we compared it with dLGN, which projects to cortex to serve form vision, and the superficial SC, a subcortical hub for sensorimotor processing that is reciprocally connected with vLGN. Compatible with past studies in different species (Spear et al., 1977; Sumitomo et al., 1979; Harrington, 1997), receptive fields in vLGN were larger than those in the other two structures. To address the basis of the difference in receptive field size, we labeled individual neurons in both divisions of LGN. The length and volume of the dendritic arbors were far larger in vLGN than dLGN, and thus able to sample a wider distribution of inputs. Also, the arbors of cells in vLGN usually extended along a preferred direction, consistent with the presence of sublaminae within this subnucleus (Monavarfeshani et al., 2017). EPSCs recorded from vLGN were smaller and more variably shaped than those from dLGN (Suresh et al., 2016), supporting the view that cells in vLGN collect greater numbers of retinal inputs along the dendritic length (Hammer et al., 2014). In addition to quantifying spatial receptive fields, we analyzed temporal properties of sensory integration. Consistent with differences in receptive field size across nuclei (Grubb and Thompson, 2004; L. Wang et al., 2010; Piscopo et al., 2013; Gale and Murphy, 2014; Suresh et al., 2016), neurons in SC and dLGN fired with greater temporal precision than those in vLGN. Further, some cells in vLGN responded to visual images with gamma-band oscillations whose phase could be entrained by the stimulus and whose strength was modulated by changes in visual patterns moving across the receptive field. Stimulus-entrained oscillations also occur in SC (Brecht et al., 2001; Stitt et al., 2013), suggesting that vLGN can engage its targets using both oscillation-based and rate-based codes. Several cells in IGL are included in the vLGN dataset since values for all properties we measured in these related structures were similar. Finally, we highlight that neurons in vLGN usually prefer large bright shapes (consistent with the scarcity of Off retinal afferents) (Monavarfeshani et al., 2017), whereas expanding dark stimuli activate the tectum and drive escape behaviors. Thus, among other functions, vLGN might be able to gate rapid movement by releasing its targets from inhibition and then reset inhibitory tone and restore stability.

Structure-function relationships in LGN

Our quantitative results showing that receptive fields in vLGN are significantly larger than those in dLGN are consistent with qualitative descriptions from earlier studies in cat and rodent (Spear et al., 1977; Sumitomo et al., 1979; Harrington, 1997). To explore the structural basis of this difference in receptive field size, we labeled and reconstructed single cells in each main division of the LGN. The dendritic arbors of cells in vLGN (our sample was likely located in the retinorecipient zone), and associated IGL, were large and spanned the length and/or width of the nucleus. The arbors in dLGN, by contrast, were relatively compact. In addition, dendritic arbors in vLGN often extended along certain subsets of directions, a feature we quantified by developing a new measure of directional symmetry in 3D. These results provide two insights. First, the anisotropy of the arbors complements the idea that different types of ganglion cells preferentially target specific zones within vLGN (Monavarfeshani et al., 2017). Second, cells in vLGN are positioned to aggregate input from ganglion cells at a wider range of retinotopic distances than are sampled by relay cells in dLGN. This greater convergence might explain why cells in vLGN have receptive fields larger than those of presynaptic ganglion cells (Monavarfeshani et al., 2017). Last, local circuit neurons are small and scarce (Gabbott and Bacon, 1994; Charalambakis et al., 2019; Su et al., 2020), and we do not seem to have labeled them; thus, we cannot speak to potential differences in response properties between these cells in the two divisions of the LGN.

The notion of greater convergence in the vLGN versus dLGN fits with differences in the synaptic physiology, anatomy, and receptive field size between the two subdivisions. A corollary of the principle of synaptic scaling (Turrigiano et al., 1998) holds that individual inputs grow weaker as their total number increases. Accordingly, ultrastructural studies and work in vitro show that retinal boutons are smaller and retinogeniculate EPSCs are weaker in the vLGN versus dLGN (Hammer et al., 2014; Monavarfeshani et al., 2017). These differences are reflected in our in vivo finding that individual EPSCs have stereotyped large, sharp profiles in dLGN but smaller, blended, and variable shapes in vLGN (and IGL). The placement of retinal inputs might also contribute to differences in EPSC shape across LGN subdivisions. Retinal inputs concentrate on the proximal dendrites of projection neurons in dLGN but may be distributed across the length of dendrites in vLGN (Stelzner et al., 1976). Filtering along the dendritic cable would yield a varied complement of EPSC size and shape at the soma (Fatt and Katz, 1951; Bloomfield et al., 1987) in vLGN.

Temporal processing in vLGN versus the main subcortical nuclei in the sensorimotor (SC) and form vision (dLGN) pathways

We asked whether or not differences in the spatial scale of receptive fields paralleled differences in temporal precision. Thus, we compared spike trains recorded from vLGN, where receptive fields are usually large, with those from cells in dLGN and superficial SC, where receptive fields are usually smaller (Grubb and Thompson, 2004; L. Wang et al., 2010; Piscopo et al., 2013; Gale and Murphy, 2014; Suresh et al., 2016). Specifically, we used a correlation-based method (Schreiber et al., 2003) to explore the temporal precision of responses to natural movies. Overall, spike trains in vLGN were not as precise as in dLGN and SC. Consequently, the amount of information each spike carried in vLGN was lesser than in the other two nuclei. These differences in temporal precision are consistent with the idea that vLGN modulates rather than instructs downstream targets.

Neurons can encode information by changes in spike timing with respect to the stimulus, as above, or by spike timing with respect to network oscillations. Neural oscillations serve diverse functions, such as increasing the amount of information that spike trains convey, resolving stimulus features and context, and routing information from one structure to another (Koepsell et al., 2010; Storchi et al., 2017). Oscillations take different forms. Some, as in retina (Castelo-Branco et al., 1998; Ishikane et al., 1999; Koepsell et al., 2010), are ongoing and are modulated rather than evoked by the stimulus (Saleem et al., 2017; Storchi et al., 2017). Other types are produced only after a stimulus activates a network (Sridharan et al., 2011). Both ongoing and entrained forms of gamma oscillations, though often studied in anesthetized animals, have also been recorded in awake animals (Brecht et al., 2001; Saleem et al., 2017; Storchi et al., 2017).

We recorded stimulus-evoked oscillations from a subset of cells in vLGN. These changes in oscillation strength could be evoked by gradual changes in the image, as would be caused by object motion, or by abrupt changes, as would result from self-motion. Further, our analysis suggested that the oscillations are driven by stimuli falling within the receptive field and are, thus, induced by local stimulus features. Interestingly, visually evoked oscillations are also seen in the subcortical motor structures that connect with vLGN, including SC (Brecht et al., 2001; Sridharan et al., 2011; Stitt et al., 2013). Thus, communications between vLGN and partner structures involve both rate-based and oscillation-based codes.

Potential functional roles of vLGN

The vLGN is positioned to play a role in visuomotor integration given its dense interconnections with subcortical structures associated with sensorimotor functions (Monavarfeshani et al., 2017). It also resembles motor structures, such as the basal ganglia (Nelson and Kreitzer, 2014) in that it contacts remote structures via GABAergic synapses (Monavarfeshani et al., 2017). The logic for these long-range inhibitory projections is that the mechanism by which they excite their targets, (release from inhibition) is less likely than direct excitation to overstimulate (Whittington and Traub, 2003) and cause unwanted movements (Nelson and Kreitzer, 2014).

Large bright stimuli evoke activity in most cells in vLGN, whereas large dark stimuli evoke excitation in SC (Cang et al., 2018). This reverse preference for stimulus contrast between structures is interesting in the context of the sensorimotor behaviors, such as the escape response, which involves tectal neurons that are excited by looming dark stimuli (Gandhi and Katnani, 2011; Cang and Feldheim, 2013; Zhao et al., 2014). The inhibition vLGN provides in ambient conditions would be reduced as a predator cast a shadow, disinhibiting SC to allow rapid flight. This idea is also consistent with other roles proposed for vLGN, including involvement with behavioral states such as fear (Salay et al., 2018) and anxiety (Huang et al., 2019).

In sum, our and others' results suggest that vLGN does not convey the type of detailed spatial and temporal information that dLGN provides to cortex or that SC provides to its targets, but rather is wired to provide an express route for information blended from diverse sources to coordinate and modulate activity in downstream sensorimotor structures.