Flexible low-voltage high-frequency organic thin-film transistors

Optimized materials and device design lead to record static and dynamic performance of organic thin-film transistors.

Abstract

The primary driver for the development of organic thin-film transistors (TFTs) over the past few decades has been the prospect of electronics applications on unconventional substrates requiring low-temperature processing. A key requirement for many such applications is high-frequency switching or amplification at the low operating voltages provided by lithium-ion batteries (~3 V). To date, however, most organic-TFT technologies show limited dynamic performance unless high operating voltages are applied to mitigate high contact resistances and large parasitic capacitances. Here, we present flexible low-voltage organic TFTs with record static and dynamic performance, including contact resistance as small as 10 Ω·cm, on/off current ratios as large as 10¹⁰, subthreshold swing as small as 59 mV/decade, signal delays below 80 ns in inverters and ring oscillators, and transit frequencies as high as 21 MHz, all while using an inverted coplanar TFT structure that can be readily adapted to industry-standard lithographic techniques.

INTRODUCTION

Flexible electronics (1–3) are currently a $20-billion-per-year industry driven mainly by the recent trend of manufacturing active-matrix organic light-emitting diode (AMOLED) smartphone displays on polyimide substrates. Of the 600 million AMOLED displays manufactured in 2018, approximately 60% were made on polyimide rather than glass, and this share is projected to further increase (4). Among the many challenges associated with this transition was to reduce the process temperature of the thin-film transistor (TFT) technology based on low-temperature polycrystalline silicon (LTPS) from 550° to 450°C to make it compatible with polyimide substrates without compromising TFT characteristics (5). Further progress toward fully bendable and rollable active-matrix displays on a wider range of polymeric substrates has incentivized the search for an alternative TFT technology that has a lower-thermal-budget process compared with LTPS. Amorphous metal oxide TFTs, such as those based on indium gallium zinc oxide (IGZO), have already seen some market success and typically outperform organic TFTs in terms of charge-carrier mobility and dynamic performance. However, process temperatures above 150°C are often still required, whereas organic TFTs can often be fabricated at temperatures below 100°C (6). The most critical issue preventing the adoption of organic TFTs in high-frequency, low-voltage applications such as mobile AMOLED displays is that the contact resistance between the source and drain contacts and the organic semiconductor (R_C) is often very high when compared to IGZO and LTPS TFTs (7). The fundamental reason that a small contact resistance is so critical for high-frequency TFT applications is that as the channel length (L) is reduced to increase the maximum operation frequency, the TFT enters a contact-limited regime where the contact resistance constitutes a substantial portion of the total resistance of the TFT. This effectively nullifies any potential benefits of, e.g., increasing the intrinsic carrier mobility (μ₀) in the organic-semiconductor channel. Channel-width-normalized contact resistances (R_CW) of organic TFTs typically fall into the range of 10² to 10⁵ Ω·cm. Several factors contribute to the contact resistance, including the TFT architecture (8–12), the semiconductor thin-film morphology at the contact interface (9, 13), and the energetic injection barrier arising from the mismatch between the work function of the contact metal and the organic-semiconductor transport levels. Effective barrier heights of several 100 meV or more are often observed (8, 14). Despite substantial efforts to improve charge injection in organic TFTs via various methods over the past 20 years, only a handful of reports have shown contact resistances below 100 Ω·cm (Fig. 1D). Excepting the electrolyte-gated polymer TFTs presented by Braga et al. (15) (denoted by a star in Fig. 1D), the lowest contact resistance reported for organic TFTs so far (29 Ω·cm) was achieved in inverted coplanar TFTs by using a very thin gate dielectric and gold source and drain contacts modified with a chemisorbed layer of pentafluorobenzenethiol (PFBT) (12). The improvement in contact resistance over comparable inverted staggered TFTs (56 Ω·cm) was attributed primarily to a stronger influence of the electric field imposed by the applied potentials in the coplanar device architecture (11). The lowest contact resistance reported for staggered organic TFTs (46.9 Ω·cm) was achieved by using a bilayer of highly crystalline organic semiconductor monolayers in combination with contact doping using 2,3,5,6-tetrafluoro-7,7,8,8-tetracyanoquinodimethane (F₄-TCNQ) (16). Both of these results, while representing a substantial advance in the quest for low contact resistance in organic TFTs, are still larger by at least an order of magnitude compared to IGZO TFTs (17) and several orders of magnitude compared to silicon transistors (18).

Fig. 1. Flexible organic transistors with small contact resistance and high-frequency performance.

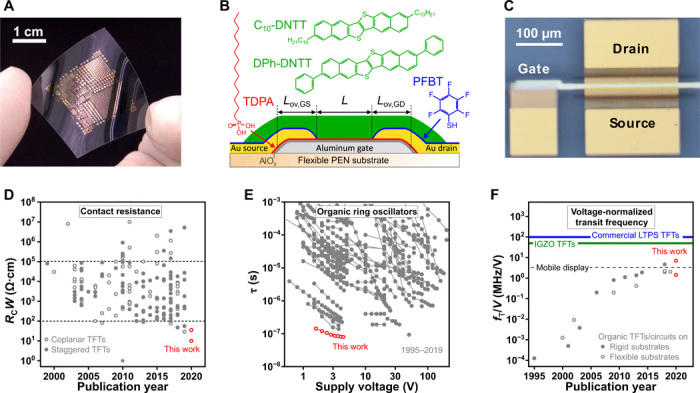
(A) Photograph of organic TFTs and circuits fabricated at a maximum process temperature of 100°C on a flexible, transparent PEN substrate. (B) Schematic cross section of the TFTs and chemical structures of the organic materials used in their fabrication: n-tetradecylphosphonic acid (TDPA) used for the self-assembled monolayer (SAM) in the hybrid aluminum oxide/SAM gate dielectric, PFBT used to treat the gold source and drain contacts to reduce the contact resistance and the small-molecule organic semiconductors DPh-DNTT and C₁₀-DNTT. (C) Photograph of a TFT having a channel length of 8 μm, a total gate-to-contact overlap of 4 μm, and a channel width of 200 μm. (D) Literature overview of the width-normalized contact resistance (R_CW) in organic TFTs. The dotted lines at 10² and 10⁵ Ω·cm indicate the typical range of contact resistances reported for organic TFTs. (E) Literature overview of the signal propagation delay per stage (τ) of organic TFT–based ring oscillators as a function of supply voltage. (F) Literature overview of the highest voltage-normalized transit frequencies (f_T/V) of organic TFTs fabricated on rigid and flexible substrates. The solid horizontal lines indicate the voltage-normalized transit frequencies of LTPS TFTs used in smartphone displays and of state-of-the-art low-temperature–processed IGZO TFTs; the dashed line indicates approximately the minimum requirement for mobile displays (3 MHz V⁻¹). For references, see table S1. (A and C) Photo credit: James W. Borchert, Max Planck Institute for Solid State Research.

Here, we further demonstrate the capabilities of our previously reported method for fabricating low-voltage organic TFTs with record low contact resistance (12) to enhance the static and dynamic performance characteristics of both individual TFTs and circuits. The TFTs and circuits were fabricated on flexible polyethylene naphthalate (PEN) sheets using high-resolution silicon stencil masks (see Fig. 1, A to C), to pattern all device layers (19–21). The small-molecule organic semiconductors 2,9-didecyl-dinaphtho[2,3-b:2′,3′-f]thieno[3,2-b]thiophene (C₁₀-DNTT) or 2,9-diphenyl-dinaphtho[2,3-b:2′,3′-f]thieno[3,2-b]thiophene (DPh-DNTT) were used as the active layer (22). Transmission line method (TLM) analysis of the transfer characteristics of the TFTs in the linear regime of operation indicates a width-normalized contact resistance of 35 Ω·cm, in close agreement with our previous report for similarly fabricated TFTs (12). By combining this low contact resistance with a small channel length and small gate-to-contact overlaps, the TFTs and circuits show record static and dynamic performance by several metrics. The TFTs show on/off current ratios as high as 10¹⁰ and subthreshold swings as small as (59 ± 2) mV/decade, within measurement error of the theoretical limit of 58.6 mV/decade at the temperature at which the measurements were conducted (292 K). Biased-load inverters switch with rise and fall time constants as short as 19 and 56 ns, respectively. An 11-stage ring oscillator operates with a signal propagation delay per stage of 79 ns at a supply voltage of 4.4 V. The dynamic performance of individual TFTs, including the unity-current gain (transit) frequency, was measured using two-port network analysis of a set of TFTs operated in the saturation regime. By analyzing the channel-length dependence of the transit frequency, a width-normalized contact resistance of (10 ± 2) Ω·cm was determined; the fact that this value is smaller than the contact resistance determined by TLM in the linear regime is related to the non-Ohmic nature of the contact resistance. Last, a transit frequency as high as 21 MHz was measured at gate-source and drain-source voltages of −3 V, corresponding to a record voltage-normalized transit frequency of 7 MHz/V. These characteristics represent important proof of concepts for the development of low-power flexible circuits using organic TFTs and for applications in flexible AMOLED displays (23–25). A literature overview and comparison to our results are provided for the contact resistance, ring oscillator stage delay, and voltage-normalized transit frequency in Fig. 1 (D to F).

RESULTS AND DISCUSSION

Static TFT performance

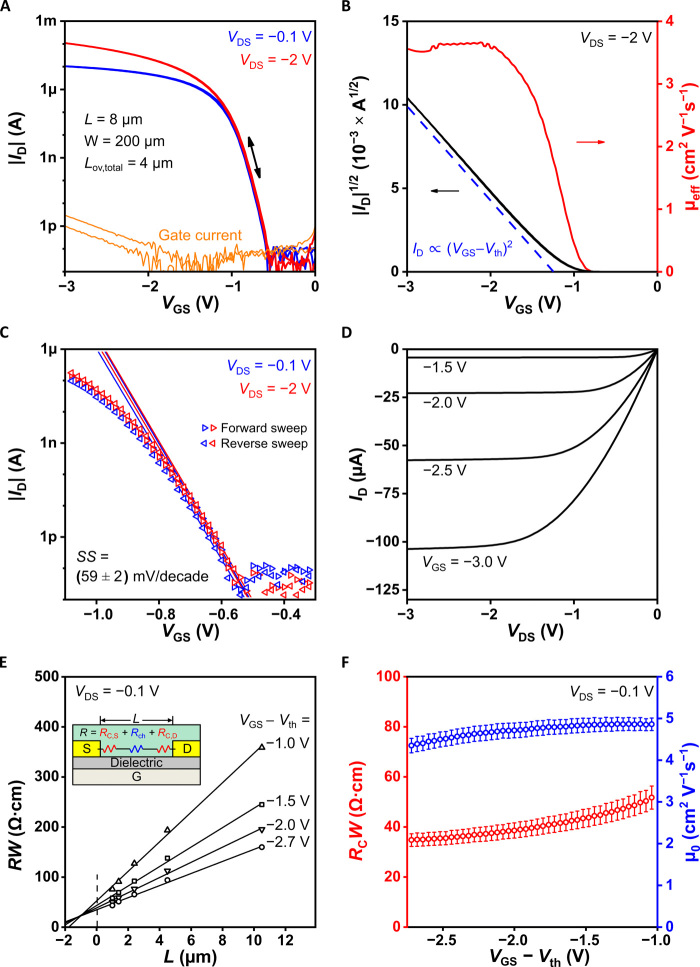
The static performance characteristics of DPh-DNTT TFTs fabricated on flexible PEN substrates are summarized in Fig. 2. Figure 2A shows the transfer characteristics of a DPh-DNTT TFT with a channel length of 8 μm, a total gate-to-contact overlap (L_ov,total = L_ov,GS + L_ov,GD) of 4 μm, and a channel width of 200 μm. The transfer curves show negligible hysteresis and a gate-leakage current of less than 10 pA over the gate-source voltage (V_GS) measurement range. When measured in the saturation regime, i.e., with a drain-source voltage of −2 V, the drain current shows a nearly ideal quadratic dependence on the gate-overdrive voltage (the difference between the gate-source voltage and the threshold voltage), an on/off current ratio of 10¹⁰, and a nearly gate voltage–independent effective carrier mobility (μ_eff) of ~3.6 cm² V⁻¹ s⁻¹ (see Fig. 2B). The subthreshold swing is determined to be (59 ± 2) mV/decade by fitting the exponential region of the drain current between V_GS = −0.5 V and −0.8 V (see Fig. 2C). We note that for the measurement temperature of 292 K, this is within the measurement error of the theoretical minimum (58.6 mV/decade) given as ln(10)kT/q where k is the Boltzmann constant and q is the elementary charge. The output characteristics show the expected linear and saturation behavior (see Fig. 2D). The reproducibility of the fabrication process is illustrated in fig. S2, where the measured transfer characteristics of 10 nominally identical DPh-DNTT TFTs with a channel length of 1.5 μm are shown. Figure S3 shows a comparison of the transfer and output characteristics of TFTs based on DPh-DNTT and C₁₀-DNTT, illustrating the fact that similar TFT performance can be obtained with multiple semiconductors.

Fig. 2. Static transistor characteristics.

(A) Measured transfer characteristics of a DPh-DNTT TFT fabricated on a PEN substrate having a channel length (L) of 8 μm, a total gate-to-contact overlap (L_ov,total = L_ov,GS + L_ov,DS) of 4 μm, and a channel width (W) of 200 μm. (B) Square root of the absolute drain current and effective charge-carrier mobility (μ_eff) calculated from the transfer characteristics measured at a drain-source voltage (V_DS) of −2 V as a function of the gate-source voltage (V_GS). The blue dashed line is a guide to the eye, indicating the ideal quadratic dependence of the drain current in the saturation regime on the gate-overdrive voltage (V_GS-V_th). (C) Extraction of the subthreshold swing (SS) from the forward and reverse sweeps of the transfer curves. The average subthreshold swing of (59 ± 2) mV/decade is within measurement error of the limit set by the thermal voltage at the measurement temperature (T) of 292 K. The threshold voltage (V_th), defined here as the gate-source voltage at which the drain current is 100 pA, is (−0.75 ± 0.01) V. (D) Measured output characteristics of the same TFT. (E) TLM analysis of the linear transfer characteristics of flexible DPh-DNTT TFTs with channel lengths ranging from 1 to 10.5 μm for four different gate-overdrive voltages. (F) Channel width–normalized contact resistance (R_CW) and intrinsic channel mobility (μ₀) extracted from the TLM analysis and plotted as a function of the gate-overdrive voltage.

The TLM analysis of the transfer characteristics of DPh-DNTT TFTs with a channel width of 50 μm and channel lengths ranging from 1.0 to 10.5 μm in the linear regime shows a width-normalized contact resistance of 35 Ω·cm and an intrinsic channel mobility (μ₀) of 4.3 cm² V⁻¹ s⁻¹ at a gate-overdrive voltage of −2.5 V (see Fig. 2, E and F). These results are similar to those in our previous report (12), confirming the good reproducibility of the fabrication process.

Static and dynamic circuit characteristics

The performance characteristics of an inverter based on DPh-DNTT TFTs and of an 11-stage ring oscillator based on C₁₀-DNTT TFTs, both fabricated on flexible PEN substrates, are summarized in Figs. 3 and 4, respectively. The critical dimensions of the TFTs are identical in both circuits (channel length, 1 μm; total gate-to-contact overlap, 4 μm), and both circuits use the biased-load design (26). An advantage of this design over single-power-rail designs is that the gate-source voltage of the load TFT can be kept above the threshold voltage at all times, facilitating more rapid discharging of the output node through the load TFT when the output node is switched from the high state (output voltage near the supply voltage) to the low state (output voltage near 0 V). As a result, the characteristic fall time and thus the total switching delay of biased-load circuits can be shorter than those of unipolar circuits without such an additional power supply. An additional advantage of the biased-load design is that it creates the possibility to tune the trip voltage (i.e., the input voltage at which the transition at the output occurs) independent of the supply voltage. To illustrate this, in Fig. 3 (A and B), we show transfer curves of the inverter. In Fig. 3A, the transfer curve is measured for a supply voltage (V_DD) of 2 V and a bias voltage (V_bias) of −1 V, i.e., with the load TFT biased slightly above the threshold voltage. Figure 3B shows transfer curves of the same inverter measured for a supply voltage of 1 V and at bias voltages ranging from −1 to 0 V, illustrating that the trip voltage (indicated in Fig. 3B by open circles) can be tuned over a range of approximately 15% of the supply voltage.

Fig. 3. Static and dynamic inverter characteristics.

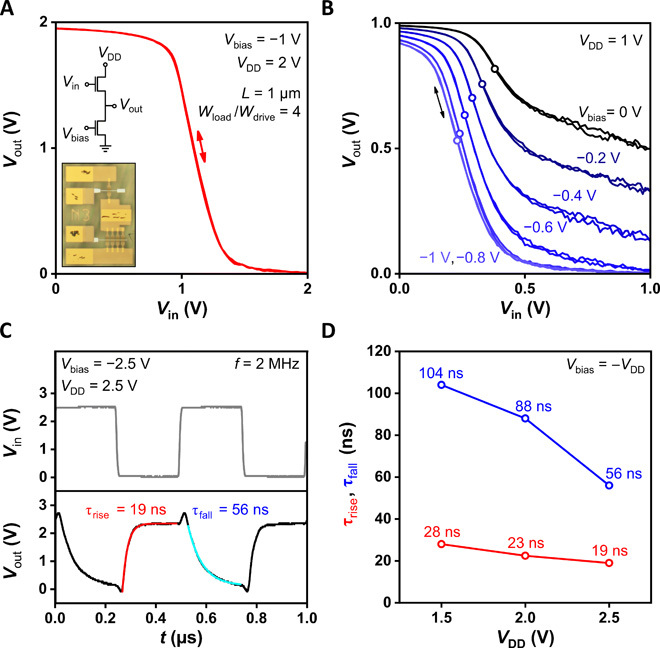
(A) Static transfer characteristics of an inverter based on two DPh-DNTT TFTs in a biased-load circuit design fabricated on a flexible PEN substrate for a supply voltage (V_DD) of 2 V and bias voltage (V_bias) of −1 V. The TFTs have a channel length (L) of 1 μm and a total gate-to-contact overlap of 4 μm. The insets show the circuit diagram and a photograph of the inverter. Photo credit: James W. Borchert, Max Planck Institute for Solid State Research. (B) Static transfer characteristics of the same inverter for bias voltages ranging from −1 to 0 V. The open circles indicate the trip voltage. (C) Dynamic characteristics of the inverter in response to a square-wave input signal with a frequency of 2 MHz, a duty cycle of 50%, and an amplitude of 2.5 V. Characteristic rise and fall time constants of the switching delays (τ_rise, τ_fall) were determined by fitting simple exponential functions to the measured output waveform. (D) Rise and fall time constants measured for supply voltages (V_DD) of 1.5, 2.0, and 2.5 V. The amplitude of the square-wave input signal was identical to the supply voltage, and V_bias = −V_DD for each measurement.

Fig. 4. Dynamic circuit characteristics.

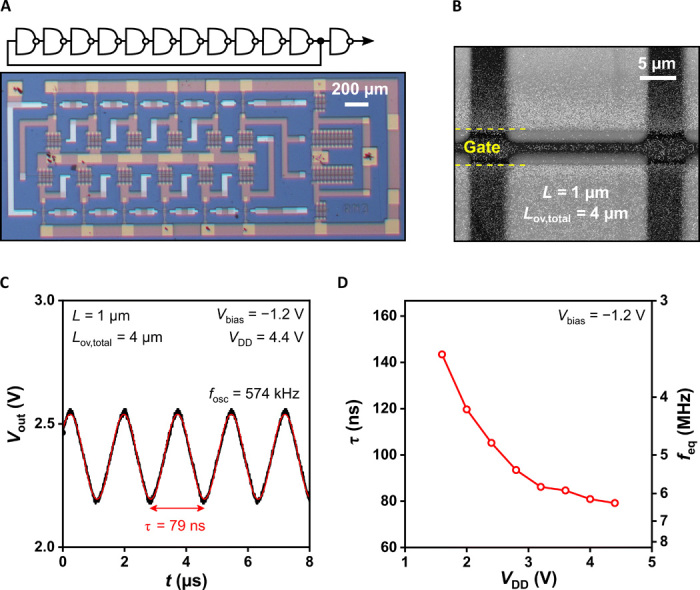
(A) Circuit diagram and photograph of an 11-stage ring oscillator based on biased-load inverters fabricated on a PEN substrate. Photo credit: James W. Borchert, Max Planck Institute for Solid State Research. (B) SEM micrograph of the channel region of an individual C₁₀-DNTT TFT in the ring oscillator. All TFTs in the circuit have a channel length (L) of 1 μm and a total gate-to-contact overlap (L_ov,total) of 4 μm. (C) Measured output signal of the ring oscillator operated with a supply voltage (V_DD) of 4.4 V. A signal-propagation delay per stage (τ) of 79 ns is determined by fitting a sine wave to the output signal. (D) Stage delay and equivalent frequency (f_eq = 1/2τ) plotted as a function of the supply voltage.

The dynamic performance of the inverter was evaluated by applying a square-wave input signal with a frequency (f) of 2 MHz and an amplitude (V_in) of 1.5, 2.0, or 2.5 V (and adjusting the supply and bias voltages so that V_DD = −V_bias = V_in for all measurements). The characteristic rise and fall time constants (τ_rise and τ_fall) of the switching events were determined by fitting simple exponential functions to the measured output-voltage transitions. The smallest time constants (19 and 56 ns) were observed for a supply voltage of 2.5 V (see Fig. 3C). The dependence of the time constants on the supply voltage is shown in Fig. 3D.

The results from an 11-stage ring oscillator based on C₁₀-DNTT TFTs are summarized in Fig. 4. Figure 4 (A to C) show the schematic and a photograph of the circuit, a scanning electron microscopy (SEM) image of the channel region of one of the TFTs, and the measured output signal of the ring oscillator. The signal-propagation delay (τ), which was determined by fitting a sine wave to the measured output signal, is 143 ns per stage for a supply voltage of 1.6 V and 79 ns per stage for a supply voltage of 4.4 V (see Fig. 4D). This is the smallest signal delay reported to date for an organic TFT–based ring oscillator at a supply voltage of less than 50 V (see Fig. 1E) (27). From the signal-propagation delay, an equivalent frequency (f_eq = 1/2τ) can be calculated that provides an estimate of the average frequency at which the TFTs are switching in the ring oscillator and which can be used to approximate the TFTs’ transit frequency (f_T) to within a factor of about 2 (7). For a supply voltage of 4.4 V, we obtain an equivalent frequency of 6.3 MHz, corresponding to a supply voltage–normalized equivalent frequency of 1.4 MHz V⁻¹.

Two-port network analysis

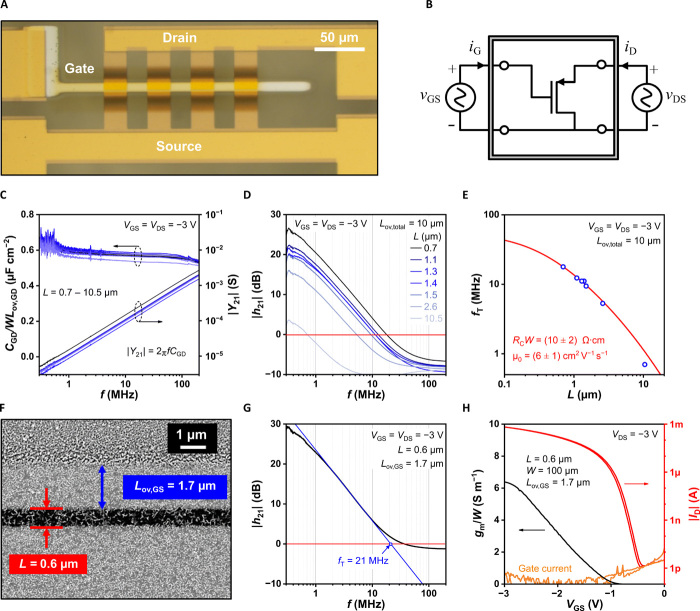
While the dynamic performance of a ring oscillator provides a measure of the average switching frequency of the TFTs used in the circuit, more detailed information about the dynamic properties of individual TFTs can be provided by two-port network analysis (2). In particular, scattering-parameter (S-parameter) measurements are attractive for their capability of unambiguously assessing the high-frequency characteristics of organic TFTs (28, 29). These measurements can, e.g., provide access to the various contributions to the total gate capacitance (C_G) by converting the S-parameters to admittance (Y) parameters (30) and enable measurement of the unity-current-gain cutoff (or transit) frequency (f_T) of individual TFTs (28). Using this method, we performed detailed dynamic characterization of DPh-DNTT TFTs with channel lengths ranging from 0.6 to 10.5 μm, a total gate-to-contact overlap of 10 μm, and a channel width of 100 μm (see Fig. 5A). All measurements were performed with constant gate-source and drain-source voltages of −3 V, superimposed with a small-amplitude component (see Fig. 5B). To assess the high-frequency characteristics of the gate dielectric, we evaluated the gate-drain capacitance (C_GD) from the Y parameters by noting that under saturation conditions, |Y₂₁| = 2πfC_GD according to the Meyer model (see Fig. 5C) (2, 31). In all TFTs that were measured, the area-normalized gate-drain capacitance was found to be constant with frequency (with a decrease of less than 20% up to the maximum measurement frequency of 200 MHz) and closely corresponds to the value expected for the unit-area gate-dielectric capacitance (C_diel) of 0.7 μF cm⁻² (31).

Fig. 5. Two-port network analysis of flexible organic transistors.

(A) Photograph of an organic TFT designed for two-port network analysis fabricated on a PEN substrate. All TFTs considered here have a total gate-to-contact overlap (L_ov,total) of 10 μm and a channel width (W) of 100 μm. Photo credit: James W. Borchert, Max Planck Institute for Solid State Research. (B) Circuit diagram of a two-port network with a TFT as the device under test. (C) Drain component of the total gate capacitance (C_GD) normalized by the gate-to-drain overlap area (WL_ov,GD) and plotted as a function of the measurement frequency (f) for all of the TFTs in the two-port network analysis. The gate-drain capacitance C_GD was calculated from the measured admittance parameters (|Y₂₁| = 2πfC_GD). (D) Magnitude of the small-signal current gain (|h₂₁|) of TFTs with channel lengths (L) ranging from 0.7 to 10.5 μm and with nominally identical gate-to-source and gate-to-drain overlaps (L_ov,GS = L_ov,GD) plotted as a function of the measurement frequency. The transit frequencies (f_T) are determined as the frequency at which |h₂₁| = 0 dB (red line). (E) Transit frequency (f_T) plotted as a function of the channel length (L). The red line is a fit of Eq. 1 to the measurement data (blue circles), yielding a width-normalized contact resistance (R_CW) of (10 ± 2) Ω·cm and an intrinsic channel mobility (μ₀) of (6 ± 1) cm² V⁻¹ s⁻¹. (F) SEM micrograph of the channel region of an asymmetric DPh-DNTT TFT with a channel length (L) of 0.6 μm, a gate-to-source overlap (L_ov,GS) of 1.7 μm, and a gate-to-drain overlap (L_ov,GD) of 8.3 μm. (G) Measured small-signal current gain (|h₂₁|) of the same TFT plotted as a function of the measurement frequency, indicating a transit frequency (f_T) of 21 MHz. (H) Measured transfer characteristics and transconductance (g_m) plotted as a function of the gate-source voltage of the same TFT.

To obtain the transit frequency (f_T), the S-parameters were used to calculate the hybrid parameter corresponding to the small-signal current gain (|h₂₁| = |i_D|/|i_G|) (see Fig. 5, D and G). In Fig. 5D, since the gate-to-contact overlaps were approximately equivalent for all TFTs, it was possible to determine the transit frequency directly as the frequency at which |h₂₁| = 0 dB. The transit frequencies determined for this set of TFTs ranged from 17.8 MHz for a channel length of 0.7 μm to 0.7 MHz for a channel length of 10.5 μm. The dependence of the transit frequency on the channel length (L), the width-normalized contact resistance (R_CW), and the intrinsic channel mobility (μ₀) is derived as (see section S1)

$$f_{\mathrm{T}}=\frac{{\mathrm{\mu }}_0(V_{\text{GS}}-V_{\text{th}})}{2\mathrm{\pi }(L+\frac{1}{2}{\mathrm{\mu }}_0{C}_{\text{diel}}{R}_{\mathrm{C}}W(V_{\text{GS}}-V_{\text{th}}))(L_{\text{ov},\text{total}}+\frac{2}{3}L)}$$ (1)

Since the unit-area gate-dielectric capacitance (C_diel) and the total gate-to-contact overlap (L_ov,total) are nominally identical for all TFTs considered here, the contact resistance and the intrinsic channel mobility can be extracted by fitting Eq. 1 to the empirical dependence of the transit frequency on the channel length, considering R_CW and μ₀ as free parameters. Figure 5E shows that an excellent fit to the experimental data is achieved with R_CW = (10 ± 2) Ω·cm and μ₀ = (6 ± 1) cm² V⁻¹ s⁻¹. There is a notable discrepancy between the contact resistance determined using the TLM (35 Ω·cm; see Fig. 2F) and the transit frequency method shown in Fig. 5E. This discrepancy is likely due to the fact that the lateral electric fields applied in the S-parameter measurements are substantially larger than the fields applied during TLM. It is not uncommon for the contact resistance of organic TFTs to show lateral-field dependence (32). This effect could be caused by various nonidealities of the metal-organic semiconductor interface, such as diffusion-limited charge injection and image-force lowering (33, 34).

Parasitic fringe-capacitance effects can arise in field-effect transistors when the semiconductor layer extends beyond the edges of the device (35). While operating a TFT in the saturation regime, these effects are isolated to the source side of the TFT, so that reducing the gate-to-source overlap (L_ov,GS) while keeping the total gate-to-contact overlap (L_ov,total) and the channel length constant will lead to a smaller total gate capacitance and thus a higher transit frequency (36). By fabricating an asymmetric TFT with a smaller L_ov,GS of 1.7 μm (L_ov,total = 10 μm) and a channel length of 0.6 μm, a transit frequency of 21 MHz at V_GS = V_DS = −3 V was obtained, compared to 17.8 MHz for a TFT with symmetric gate-to-contact overlaps (see Fig. 5, F to H). This is to our knowledge the highest transit frequency reported to date for an organic transistor fabricated on a flexible substrate. Normalized to the supply voltage (7 MHz V⁻¹), it is the highest voltage-normalized transit frequency reported to date for any organic transistors (see Fig. 1F and table S1) (16, 37, 38). In addition, the TFT shows a channel width–normalized transconductance (g_m/W) up to 6.4 S/m, a subthreshold slope of 66 mV/decade, and an effective carrier mobility of 2.7 cm² V⁻¹ s⁻¹, all records for submicron-channel-length organic TFTs. These results demonstrate that it is possible to fabricate organic TFTs on flexible substrates with static and dynamic performance parameters suitable for high-frequency mobile electronic applications and approaching those of industry-standard LTPS TFTs (5) and high-performance IGZO TFTs (6), all while using a TFT architecture amenable to existing industry-standard fabrication processes.

MATERIALS AND METHODS

Fabrication of organic TFTs and circuits with small critical dimensions

Stencil lithography based on high-resolution silicon stencil masks enables the fabrication of organic TFTs and circuits on flexible substrates with small critical dimensions and excellent reproducibility (20, 21). This approach was used to fabricate all organic TFTs (see fig. S1) and circuits presented in this work on 125-μm-thick PEN sheets (Teonex Q65 PEN; provided by W. A. MacDonald, DuPont Teijin Films, Wilton, UK). Separate masks were used to pattern the interconnects, gate electrodes, source and drain contacts, and organic semiconductor layers. The masks were aligned manually using an optical microscope. To enable low-voltage TFT operation, a hybrid gate dielectric with a total thickness of approximately 6 nm was prepared by exposing the aluminum gate electrodes to oxygen plasma (Oxford Instruments, 30 sccm oxygen, 10 mTorr, 200 W, 30 s) and subsequently immersing the substrate into a 1 mM 2-propanol solution of n-tetradecylphosphonic acid (TDPA; PCI Synthesis, Newburyport, MA, USA) to allow a self-assembled monolayer (SAM) to form on the aluminum oxide surface (39). The area-normalized gate dielectric capacitance (C_diel) of this hybrid aluminum oxide/SAM gate dielectric is typically between 0.5 and 0.7 μF cm⁻². Gold source and drain contacts were then deposited by thermal evaporation in vacuum, and the substrates were subsequently immersed into a 10 mM solution of PFBT (Santa Cruz Biotechnology, Heidelberg, Germany) in ethanol (nondenatured) or 2-propanol for 30 min. The PFBT forms a chemisorbed monolayer that substantially improves the contact resistance for the organic semiconductors used in this work. Last, the small-molecule semiconductors 2,9-didecyl-dinaphtho[2,3-b:2′,3′-f]thieno[3,2-b]thiophene (C₁₀-DNTT) or 2,9-diphenyl-dinaphtho[2,3-b:2′,3′-f]thieno[3,2-b]thiophene (DPh-DNTT) were used as the active layer in the channel region of the TFTs (Nippon Kayaku, provided by K. Ikeda). The organic semiconductors were deposited by thermal sublimation in vacuum (base pressure of 10⁻⁶ mbar) at a substrate temperature of 80°C for C₁₀-DNTT or 90°C for DPh-DNTT.

Electrical measurements and morphological characterization

All electrical measurements were performed at room temperature (T = 292 K) in ambient air. Static transfer and output characteristics were measured using an Agilent 4156 C Semiconductor Parameter Analyzer. A Keysight 33500B function generator, a Tektronix TDS1000 oscilloscope, and a GGB Industries Picoprobe 19C high-impedance probe were used to assess the dynamic performance of the inverters and ring oscillators. S-parameter measurements were performed using a Keysight N5231A Vector Network Analyzer and Cascade Microtech GS-SG |Z| high-frequency probes. Complete details about the measurement approach for extracting the transit frequency of organic TFTs from S-parameter measurements can be found in (2) and (29). SEM and atomic force microscopy measurements were used for morphological characterization of the organic-semiconductor layers and to measure the critical TFT dimensions. The quality of the PFBT monolayers on gold surfaces was assessed using polarization-modulated infrared reflectance-absorbance spectroscopy (IRRAS). For this measurement, a gold film was deposited onto a silicon substrate with an area of approximately 1 cm² and treated with a PFBT monolayer according to the procedure outlined above. In addition, stock PFBT was characterized by IRRAS to compare to the PFBT monolayer. The results show that a clean monolayer of PFBT is formed on the surface, and the results are in good agreement with similar experiments reported previously (see fig. S1) (40).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/21/eaaz5156/DC1