Protein Binding Pocket Optimization for Virtual High-Throughput Screening (vHTS) Drug Discovery

Abstract

The virtual high-throughput screening (vHTS) approach has been widely used for large database screening to identify potential lead compounds for drug discovery. Due to its high computational demands, docking that allows receptor flexibility has been a challenging problem for virtual screening. Therefore, the selection of protein target conformations is crucial to produce useful vHTS results. Since only a single protein structure is used to screen large databases in most vHTS studies, the main challenge is to reduce false negative rates in selecting compounds for in vitro tests. False negatives are most likely to occur when using apo structures or homology models of protein targets due to the small volume of the binding pocket formed by incorrect side-chain conformations. Even holo protein structures can exhibit high false negative rates due to ligand-induced fit effects, since the shape of the binding pocket highly depends on its bound ligand. To reduce false negative rates and improve success rates for vHTS in drug discovery, we have developed a new Monte Carlo-based approach that optimizes the binding pocket of protein targets. This newly developed Monte Carlo pocket optimization (MCPO) approach was assessed on several datasets showing promising results. The binding pocket optimization approach could be a useful tool for vHTS-based drug discovery, especially in cases when only apo structures or homology models are available.

Introduction

In computational chemistry, molecular docking is a powerful approach used to predict the binding affinities of ligands and discover novel drugs as well as optimize already available drugs. The principle of docking is to identify the low (free) energy binding models of a small molecule within the active site of a macromolecule. The earliest docking methods were based on the lock and key assumption originally proposed by Fischer.¹ In early versions of docking programs, such as DOCK,² both ligand and receptor were treated as rigid bodies and their affinity was derived from the fit between their two shapes. Yet in reality, both receptors and ligands are flexible. Later work by Koshland³ suggested that a ligand and its receptor undertake complementary conformational changes. When considering only a small number of ligands rather than a library, flexibility of the protein can be accounted to some degree and is being utilized in some docking programs such as Autodock,⁴ Autodock FR,⁵ Glide,⁶ Gold,⁷ and ICM.⁸ Docking that allows receptor flexibility is a challenging task for virtual screening of large databases, due to its computational expense. Thus, target flexibility remains less exploited in high-throughput virtual screening.⁹ The main challenge of virtual screening in selecting compounds for in vitro confirmation is reduction in false negative and positive rates rather than identification of nanomolar or low micromolar binders.¹⁰ This is because once a compound showing activity is identified, medicinal chemistry approaches and/or more accurate, but computationally expensive, calculations can be utilized to identify stronger binders.

For virtual screening applications, two paradigms have emerged to model protein flexibility in docking screens. The simplest methods consider protein flexibility implicitly by allowing a small degree of overlap between the ligand and receptor. This is done through softening the van der Waals interactions of the receptor in docking calculations. Although this method is straightforward to implement with little computational cost, it accounts for only small conformational changes.¹¹⁻¹³ Due to the increasing complexity, only a small number of degrees of freedom can be considered. An alternative approach focuses on averaging multiple conformations together. Although this can reduce the number of conformational states of the side chains, it results in a non-physical average of energies, in turn, reducing predictive success. Furthermore, this method has been shown to increase false positive rates.⁹ There are other schemes that can explicitly sample protein side chains using Monte Carlo methods or using rotamer libraries to identify plausible configurations of side chains. These methods are well regarded in the literature producing accurate ligand binding poses, but their implementation does come with a significant cost in computational efficiency.^6,14−16

In general, properly modeling receptor flexibility during the docking process imparts a large computational cost and complexity due to the need to address the high dimensionality of the conformational space and the complexity of the energy function. A typical binding site might involve 10 to 20 amino acids with total degrees of freedom several times greater than what is typically considered in a standard docking scheme.¹⁷⁻²⁰ When larger protein movements are considered, such as backbone rearrangements that can affect several side chains, the complexity of the conformational space increases further. This kind of computational sampling imposes a high cost when computing the energy of the system. It is necessary to distinguish between different configurations in similar low-energy states to identify correct poses. These demands on both the energy function and the conformational space sampling result in an optimization problem in the presence of a ligand. A more feasible approach is to greatly restrict the conformational space sampled by considering only protein side chains for sampling.^18,20

Limiting the sampling to specific side chains within the binding pocket reduces the conformational space involved and allows for exhaustive sampling of side-chain conformations and has been used with some success.^14,21−26 But these kinds of methods are hampered in their ability to be scaled up for screening large libraries potentially of the order of millions of compounds.

In addressing the problems with the computational efficiency of flexible receptor docking, one scheme has dominated high-throughput virtual screening: ensemble docking.²⁷ Multiple receptor conformations or ensemble docking can take advantage of using different explicit configurations of the ligand binding site to maximize hits. Significant improvement can be made if selections of conformers are drawn from protein–ligand complexes with dissimilar ligands or can accommodate diverse binding conformations.^28,29 However, this kind of scheme has some drawbacks. Although ensemble docking has been useful to address some of the conformational sampling challenges in virtual screening, the performance of ensemble docking is highly dependent on the scoring function and target structures. Large errors can be introduced if the ensembles are used for docking inadequately.³⁰ These kinds of limitations can exacerbate the false positive rates of ensemble docking and scale with the number of receptor conformations used. To minimize these errors, the minimum number of conformers needs to be used.

In the current study, we addressed problems of conformational sampling and the increased chances of false negatives in virtual ligand screening. We have developed a method that samples the conformation of binding pocket side chains. Figure 1 shows that potential drug candidates (medium or large size) could be rejected by apo structures due to relatively small binding pockets to fit into. Even for holo structures, drug candidates (large or dissimilar in shape) could be rejected due to the induced fit effect of binding pocket that is highly dependent on the bound ligands. However, by optimizing binding site residues to maximize the volume of the binding pocket, enabling it to accommodate ligands of various sizes and shapes, potential false negative ones can be accommodated. This newly developed Monte Carlo pocket optimization (MCPO) approach was assessed on several test sets and has shown promising results. The binding pocket optimization approach could be a useful tool to improve the success rate of virtual high-throughput screening (vHTS) for drug discovery with a minimal additional computational cost.

Figure 1.

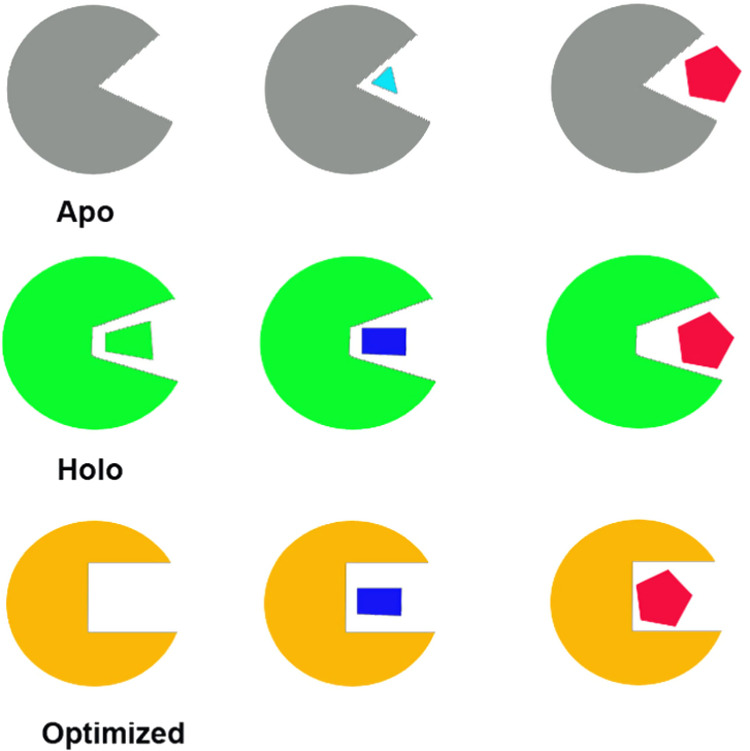
Virtual high-throughput screening (vHTS) using different protein structures. Apo: only small ligands can be docked in; Holo: only similar or smaller ligands can be docked in; Optimized: all potential (small, medium, large) ligands can be docked in.

Results and Discussion

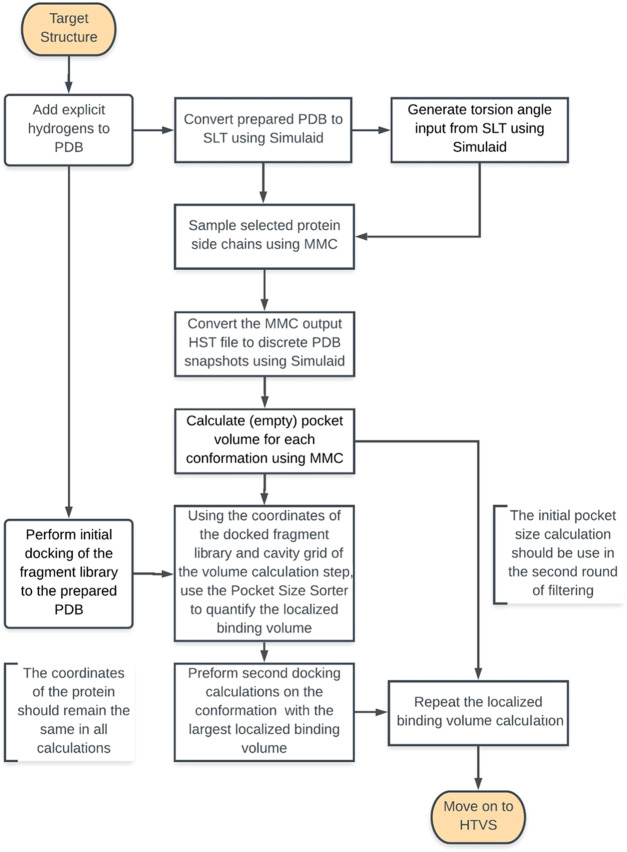
The workflow for MCPO is shown in Figure 2, and described in detail in the Computational Methods section. This methodology relies on the optimization of the binding volume via a two-step approach, Monte Carlo torsional angle sampling of the binding site residues and binding site pocket volume calculation and selection. While traditional induced fit methodologies work by sampling the possible ligand and binding site configurations, this methodology decouples these steps, thereby enabling the time-consuming part to be performed once, at the outset of the vHTS. Pocket volume calculation typically works by inserting a virtual particle with a known small radius into a cavity on the protein. Since the radius of these particles is known, so is the volume. A summation of the volume of each probe point within a given cavity would approximate the volume of the cavity. Because the volume of the pocket is directly proportional to the number of virtual or probe particles, we can filter the binding site based on the number of particles that exist within a given cavity.³¹ Typically, the entire volume of the cavity is not available for ligand binding due to the presence of highly flexible side chains such as methionines, lysines, and arginines.^31,32 This methodology attempts to minimize the volume that is occupied by these side chains and maximize the volume of the pocket that can accommodate a small molecule. To define this localized binding volume, we employ a fragment library of relatively low molecular weights under 150 Dalton. By docking this library into a given pocket configuration, we can define a region of volume that would accept a ligand’s presence. Using low-molecular-weight fragments reduces the possibly of a side-chain clash that would prevent the docking of larger fragments. We define the localized binding volume using a small radius from each atom of the docked fragments. To maximize the volume that these fragments can occupy, we count the number of probe points that can occupy this expanded localized volume across all sampled configurations. This process is then repeated a second time to further maximize the localized binding volume and account for the side-chain conformation that would cause a clash in the initial configuration.

Figure 2.

Workflow for binding pocket optimization. Sampling is done to generate multiple binding site configurations. Fragment docking is able to define the volume available for small-molecule binding. Pockets are filtered based on maximizing the volume that fragments can occupy in the initial configuration. The docking and filtering steps are repeated a second time to eliminate any side-chain clashes.

Assessment of the MCPO Approach on a Pilot Dataset

The initial cross-docking set contained a small dataset (three apo/holo protein pairs) with known ligand-induced side-chain changes. In each member of this set, at least one side chain prevented the cross-docking of ligands from the holo structure. These side chains were selected for torsional angle sampling. The optimized pocket configuration based on maximizing the localized binding volume was selected for cross-docking experiments. The cross-docking results of the side-chain sampling are shown in Table 1. The initial cross-docking experiments were not able to reproduce the poses seen in the holo structures, when ligands were directly docked into the apo structure. In each apo crystal structure, there is at least one protein side chain that extends into the volume that would normally be occupied by the ligand in the holo structures. The pocket refinement procedure was able to clear the clashes between the residue side chains and ligand in the apo conformations.

Table 1. Cross-Docking Results of Apo Structures before and after Pocket Optimizations.

target	receptor (PDBID)	ligand (PDBID)	docking RMSD (in Å) before MCPO	docking RMSD (in Å) after MCPO
coagulation factor Xa	1FAX	1LPG	10.90	1.15
antibody DB3	1DBA	1DBB	4.19	0.88
cyclin-dependent kinase 2	4EK3	1YKR	4.11	0.79

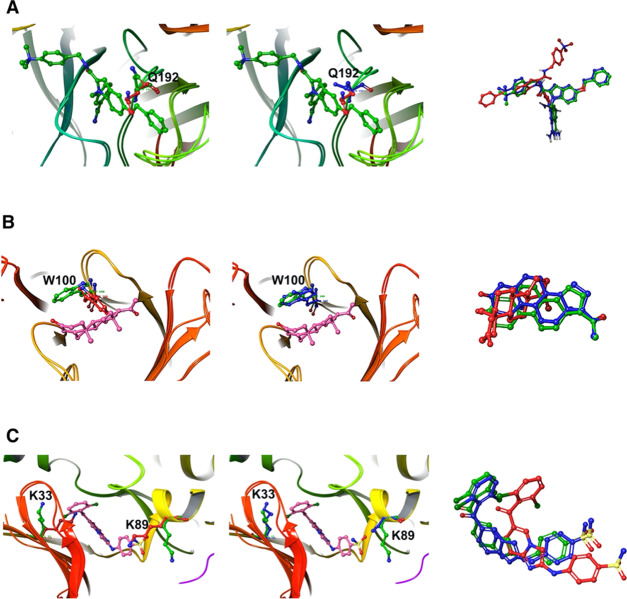
In the simplest case, we considered the two crystal structures of the blood clotting factor Xa (PDB: 1FAX and 1LPG). The primary differences between the apo (1FAX) and holo (1LPG) structures are shown in Figure 3A. Gln192 oriented into the pocket in the apo structure. Upon ligand binding, this residue underwent a rotamer change and cleared the ligand binding volume. This was not accompanied by any backbone movements. In this case, the Monte Carlo torsional angle sampling was able to rotate the residue and clear it from the localized binding volume. Figure 3A shows the resulting sampled structure in comparison to the apo configuration. The MCPO calculated pocket in the binding site of coagulation factor Xa is shown in Figure 4.

Figure 3.

Docking poses of (A) 1FAX/1LPG, (B) 1DBB/1DBA, and (C) 4EK3/1YKR before and after pocket optimization. Left: overlapping of apo (residues in red) and holo (residues in green) structures; middle: apo after pocket optimization (residues in blue) and holo (residues in green) structures; right: ligands (holo in green, docked apo in red, docked apo after pocket optimization in blue).

Figure 4.

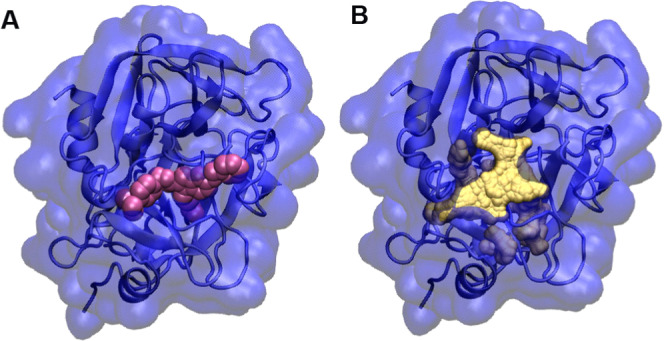
Example of pocket volume calculation for coagulation factor Xa. (A) Coagulation factor Xa in complex with a compound IMA (pink); (B) calculated pocket (yellow) in the binding site of coagulation factor Xa.

Similar to the previous case, in the monoclonal anti-progesterone antibody DB3 (PDB: 1DBA and 1DBB) a single amino acid side chain caused the failure of the cross-docking. Trp100 protruded into the center of the pocket and caused similar problems to Gln192 of clotting factor Xa in the apo configuration. Figure 3B shows the binding site alignment between the apo (1DBA) and holo (1DBB) configurations. The torsion-angle sampling could effectively clear the bulky side chain from the localized volume around the ligand. This allowed for the correct cross-docking of the ligand into the pocket. Figure 3B shows the sampled conformation of the pocket relative to the holo structure.

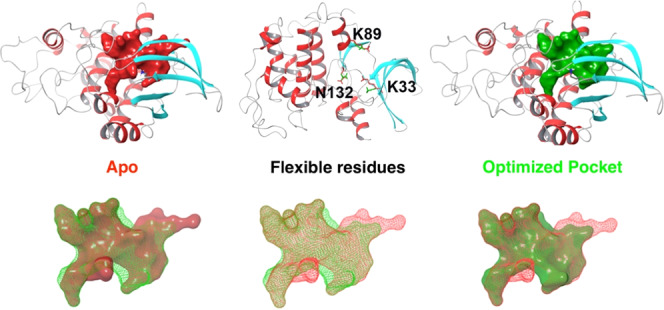
Cyclin-dependent kinase 2 (4EK3 and 1YKR) is an example used by AutoDock FR.⁵ In the apo (4EK3), two residues Lys33 and Lys89 protruded into the binding pocket and prevented ligand binding. The aligned binding sites of apo and holo (1YKR) are shown in Figure 3C. Torsional sampling and pocket optimization of these two residues opened the pocket to a similar size to the holo structure conformation, which allowed the binding of the ligand without any clashes. Figure 3C shows the docked ligand in apo (before and after pocket optimization) conformations compared to the holo conformation.

While these three are relatively simple cases requiring only one or two side chains to be sampled, this kind of methodology can be expanded further to sample a large number of residues given sufficient Monte Carlo sampling steps. We further evaluated this methodology in the context of two additional datasets by evaluating the cross-docking success rate.

Assessment of the MCPO Approach on the SEQ17 Dataset

The SEQ17 dataset (seventeen apo/holo protein pairs) was designed to specifically test the flexible docking algorithm employed in Autodock FR.⁵ The SEQ17 dataset was chosen specifically due to a large number of residues needed to be refined in each protein for successful redocking. With the protein pocket optimization scheme, we were able to successfully redock 35% of the dataset, which is comparable to ADFR (AutoDock Flexible Receptor) results (35%) and much better than rigid docking (RCD, 6%). Table 2 details the root-mean-square deviation (RMSD) calculations for this dataset. In these cases, the failed cross-docking could be primarily attributed to small backbone rearrangements within loops. In the case of 1HCL and the cross-docking of the ligand from 1AQ1, there was some rearrangement of a loop within the binding site. In the holo position, the ligand conflicted with the backbone carbonyls of Asp145. To resolve this kind of steric clash, a loop sampling protocol, which MMC is capable of doing, has to be used to maximize the localized binding volume. There were similar problems with the redocking of the ligand of 2A9K into the optimized pocket of 2A78. In this case, the docked ligand’s position was inverted relative to the holo structure. The loop that incorporated Phe183 underwent a small backbone change in which Phe183 was shifted out of the pocket.

Table 2. SEQ17 Cross-Docking Results of Apo and Pocket-Optimized Apo Conformations with Multiple Modified Receptor Side Chains^a.

		ADFR				docking after MCPO
systems		RCD (1)		FCD (5)		sampled (6)
holo	apo	RMSD	rank	RMSD	rank	RMSD	rank
1k4h	1pud	6.26		2.06	1	0.62	1
3jrx	2hjw	7.97		2.26	1	0.69	1
1it8	1iq8	1.26	1	0.64	1	0.83	1
2h8h	1fmk	6.9		1.36	1	1.11	1
1yxt	1xqz	5.83		5.15		1.6	1
1rbp	1brq	3.48		3.72		2.13	1
3erk	1erk	8.25		3.66	14 (0.77)	8.47	2 (2.50)
1ikg	3pte	6.94		3.46		3.48
1zg3	1zhf	8.03		3.92		4.1
1c1h	1doz	5.62		5.41	14 (2.42)	4.39
1qkj	2bgt	3.51		3.52	3 (1.85)	4.49
1aq1	1hcl	7.46		3.97	2 (2.26)	5.8
1z6p	2gpn	4.25	9 (1.86)	4.28	2 (2.04)	6.4
2a9k	2a78	5.37		4.87		6.7
1br5	1rtc	8.89		5.28		6.8
1lnm	1kxo	7.52		8.01	3 (2.28)	7.98
1gx9	1bsq			2.13	1	-

^aRCD: rigid receptor docking; FCD: flexible receptor docking; and MCPO: Monte Carlo pocket optimization.

Assessment of the MCPO Approach on the CDK2 Dataset

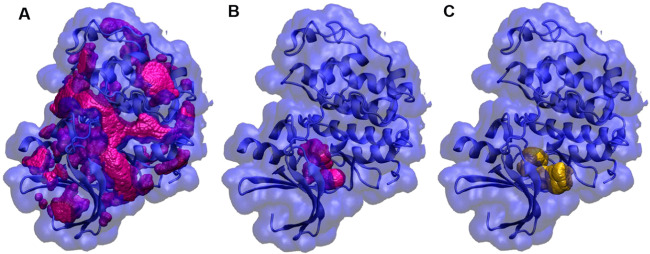
Similarly, the CDK2 cross-docking set (52 apo/holo protein pairs) was built to evaluate the performance of Autodock FR against a diverse set of ligands.⁵ To make the optimized pocket selection unbiased from ligands, we docked all of the fragments in the Glide diverse fragment dataset (less than 150 Dalton molecular weight, 397 fragments) into the CDK2 binding site. We found that the second-round docking was helpful to select the largest binding pocket (Figure 5). The results of the CDK2 cross-docking are shown in Table 3. From the results, 52% of ligands (27 out of 52) showed correct binding poses within 2.5 Å using the pocket-optimized structure, better than ADFR, which predicted 42% (22 out 52) of correct binding poses of ligands.

Figure 5.

Binding pocket optimization of the CDK2 crystal structure (PDB: 4EK3) based on docked fragments. (A) All pockets (magenta) of CDK2 were identified by the MMC program; (B) optimized binding pocket (magenta, 15 004 probes) based on the first-round fragment docking; and (C) optimized binding pocket (yellow, 18 123 probes) based on the second-round fragment docking.

Table 3. CDK2 Cross-Docking Results of Refined Apo Conformations with Multiple Modified Receptor Side Chains Compared to ADFR Results^a.

	ADFR				docking after MCPO
	RCD (12)		FC12 (22)		8 (27)
systems	RMSD	rank	RMSD	rank	RMSD	rank
2R3I	1.90	1	1.49	1	0.00	1
1JVP	4.48	2 (2.3)	4.86	2 (1.06)	0.00	1
2CCH	8.83		8.07		0.00	1
4FKG	0.78	1	1.01	1	0.51	1
2R3Q	2.04	1	1.58	1	0.57	1
4FKL	13.47		4.32		0.59	1
4EK4	0.41	1	10.21	7 (0.45)	0.65	1
4EK8	8.94		2.07	1	0.69	1
4EK5	10.36	2 (0.81)	0.79	1	0.88	1
2B53	2.23	1	2.89	19 (1.95)	1.29	1
2BTS	8.48		0.37	1	1.54	1
4FKQ	14.73	5 (1.84)	1.33	1	1.62	1
2B52	3.81	2 (2.04)	3.67	2 (1.74)	1.69	1
4FKS	11.53		0.82	1	1.76	1
1H1S	5.32	2 (2.04)	1.62	1	1.79	1
2A4L	10.23	9 (1.80)	1.18	1	2.06	1
4FKO	2.20	1	1.55	1	2.08	1
2BKZ	2.53		2.22	1	2.09	1
1Y8Y	1.67	1	1.16	1	2.13	1
2W17	5.96		0.95	1	2.16	1
1H1R	1.67	1	3.31	3 (2.06)	2.16	1
2C6I	7.75		7.38	2 (1.58)	2.17	1
4FKU	6.29		2.15	1	2.19	1
4FKW	8.24		2.19	1	2.25	1
4FKP	6.13		0.90	1	2.25	1
3DDQ	5.28		5.93	2 (2.4)	2.25	1
2B55	5.38	4 (1.92)	4.07	2 (1.46)	2.45	1
4FKT	11.06		1.69	1	2.71
4FKV	6.46		0.78	1	2.96
4FKR	1.65	1	0.92	1	2.97
4FKI	1.58	1	10.55	9 (2.12)	3.31
2WIH	7.02		6.69	4 (1.29)	3.44
2V0D	13.01		9.38		4.12
2BTR	8.36		6.10	2 (1.12)	4.28
2EXM	9.66		8.83	2 (2.29)	4.56
2FVD	8.34		7.82		4.57
1YKR	5.96		0.34	1	4.80
2UZO	5.49		4.78		5.02
4FKJ	14.26	3 (1.49)	7.46	9 (1.38)	5.18
1H1P	5.56		6.20		5.22
3EZV	7.03		5.40		5.59
2R3F	1.69	1	3.07	2 (1.65)	5.92
2W05	5.88		1.33	1	6.29
2DUV	4.33		4.58	14 (1.54)	6.31
1PYE	3.08		4.46		6.49
2J9M	1.56	1	4.87	7 (1.3)	6.53
1H1Q	5.40	3 (1.65)	5.28	7 (1.96)	6.81
3EZR	7.59		5.25		7.25
1VYW	14.00	6 (1.63)	10.22	4 (1.5)	9.2
4EK6	14	2 (2.39)	9.84	5 (2.36)	9.21
2G9X	4.98		1.70	1	9.68
2BPM	13.09	4 (1.68)	7.42	18 (1.47)	9.72

^aRCD: rigid receptor docking; FCD: flexible receptor docking; and MCPO: Monte Carlo pocket optimization.

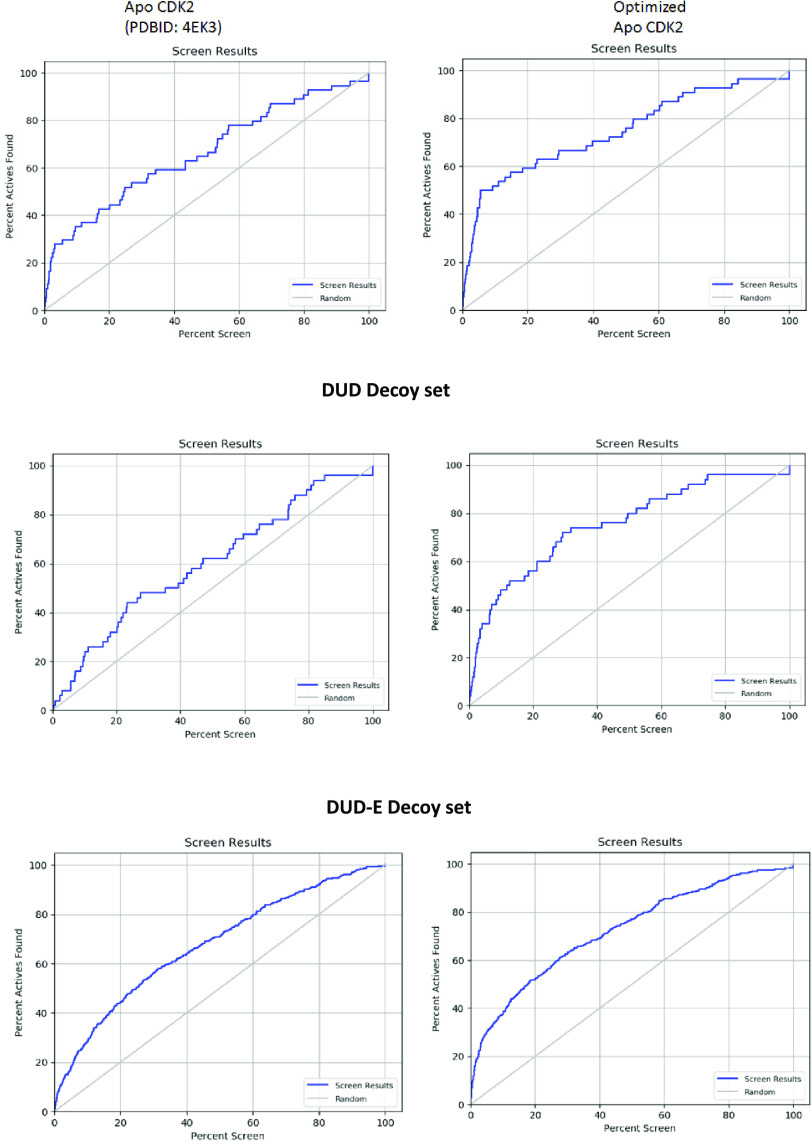
We have expanded this dataset using the Schrödinger 1000 drug-like decoy dataset with an average molecular weight of 360 Dalton. The resulting dataset consisted of 1052 compounds of which 52 were known active ligands. This resulted in about 20 decoys per active ligand. We have further expanded enrichment studies with the CDK2-specific subsets of the DUD and DUD-E libraries.^33,34 Enrichment factor calculations were also performed to quantify the improvement in the ability of the optimized structure to return active hits (Figure 6 and Table 4). Initial enrichment studies were conducted using the Schrödinger decoy set with an average molecular weight of 360 Dalton. With this decoy set, the optimized structure was able to return ∼20% greater hits in the top 1% of the screen when compared to the unoptimized structure. Similarly, the optimized structure could return more diverse hits than the apo structure. This behavior was carried forward when examining more diverse datasets. In the original directory of useful decoys, there was more than 2-fold increases in returning active hits and a 9-fold increase in returning diverse hits when compared to the unoptimized structure. Similarly, in the newer enhanced version of the directory of useful decoys, there is nearly a 2-fold increase in the returned active compounds in the top 1% of the scored dataset. There is also a 2-fold increase in the diversity of the active compounds reported (Table 4). This suggests that this methodology of pocket refinement can be used to return a greater number of active molecules in virtual screening applications when compared to an apo structure.

Figure 6.

Enrichment factor results for the apo structure (PDBID: 4EK3) and the optimized apo structure.

Table 4. Summary of Calculated Enrichment Factor Results for Various Decoy Sets.

decoy set	structure	EF1%	DEF1%	EF5%	DEF5%	ROC
Schrodinger 360MW	apo CDK2 (4EK3)	8.9	8.7	5.5	5.5	0.67
	optimized CDK2	12.0	12.0	8.5	8.5	0.76
DUD	apo CDK2 (4EK3)	4.0	1.1	1.6	2.3	0.60
	optimized CDK2	10	9.9	6.8	6.8	0.76
DUD-E	apo CDK2 (4EK3)	7.2	7.1	3.5	2.8	0.68
	optimized CDK2	12.0	12.0	6.2	6.1	0.73

Discussion

In this paper, we introduce a new method for implementing receptor flexibility in high-throughput virtual screening workflows. By clearing the localized binding volume that a majority of fragments are able to bind to, we are able to reproduce existing crystal structure poses as well as return a far greater amount of hits with a virtual screen that uses the apo structure alone.

The SEQ17 dataset consists of 17 receptors in which substantial side-chain torsional rotations were required to achieve the holo conformation. In this dataset, we correctly reported 35% lowest ranked docking poses for the dataset suggesting broad applicability on par with flexible receptor methods such as Autodock FR. The primary application of Autodock FR is as a comprehensive solution for simultaneously sampling binding site side chains and ligand torsional angles. Although this methodology works well, it is unsuitable for larger virtual screening workflows due to the added computational cost. The methodology described in this paper does not add to the computational cost of the docking step making it more attractive for virtual screening applications.

While Glide has been well studied in virtual high-throughput screening applications with the ability of ensemble docking, there are two major drawbacks. Additional conformations increase the chance of a false positive in virtual screening applications.^27,35 Furthermore, the increased number of conformers increases linearly the time required for screening. Barril and Morley investigated the effects of multiple receptor conformations on virtual screening.³⁶ Their results demonstrated that in the best-case scenario when choosing the best-performing structures, the maximum enrichment factors for CDK2 were 8.7 for a single conformation and 13 for two receptor conformations. When more conformations were included in the virtual screening, the enrichment factor tended to decrease sharply. Furthermore, this multiconformational screening strategy has been shown to only improve enrichment factors for the top 10% of ranked results in a screen. When screening millions of compounds, the resulting subsets can range in the thousands of hits for a given library. Thus, the top 10% is impractical to screen experimentally. A more practical subset would be the top 1% of results. In this case, multiple receptor conformations tend to decrease the enrichment factors due to the average conformation including more false positives in top ranking poses. We were able to generate a single receptor conformation for CDK2 similar to that of a multiconformational virtual screen (Figure 6 and Table 4).

More recent work in ensemble-based virtual screening suggests that molecular dynamics simulations are able to reproduce a majority of the binding poses for ligands even when using sub-microsecond simulations. However, clustering protein configurations does not suggest which structures are favored by ligand binding.^27,37−39 The only method of identifying these conformations is to run parallel simulations with the protein of interest in complex with a known ligand. Unfortunately, this would also bias the result of a virtual screen to those compounds that favor the same set of protein conformations. This results in the identification of structurally or chemically similar compounds and necessitates a wide variety of known ligands for ensemble docking to be used successfully.

It has been suggested that a large subset of protein structures from a single molecular dynamics simulation is required to correctly identify possible ligands, on the order of tens to hundreds of conformations.^27,37 This further results in 10–100-fold increases in the required computational resources to screen through a single target. Ensemble docking repeats the screening of the entire library against each conformation. Our methodology is able to a priori identify one binding site configuration that can bind a diverse range of ligands and maximize the number and diversity of possible active compounds in a virtual screen.

Last but not the least, recent studies showed that protein binding pockets underwent dynamic changes during molecular dynamics simulations. Developing appropriate computational tools is highly desired to take into account protein binding pocket dynamics for structure-based drug discovery.⁴⁰ A computational approach, mkgridXf, developed by Monet et al, can be used to identify sites in a consistent way on an ensemble of structures such as MD trajectories.⁴¹ In combination with this approach, our methodology can be applied to the protein structures from MD trajectories to optimize the protein binding pocket. In this case, both protein backbone and side-chain flexibility in the binding site can be optimized to fully mimic the induced fit effect of ligands. In combination with MD simulations and high-level binding free energy calculations, our methodology could further improve vHTS performance. Future work will be pursued in this direction.

Conclusions

Protein receptor flexibility is important to be considered for molecular docking and vHTS. However, accounting for protein flexibility or using multiple receptor conformations is time-consuming for vHTS of large databases. Here, we have developed a Monte Carlo-based computational approach to optimize binding pocket of protein targets for vHTS drug discovery. The approach starts with sampling torsional angles of binding site residue side chains, followed by binding pocket volume calculations. The sampled structure with the largest binding pocket is selected for rigid receptor docking or vHTS studies. We assessed this approach on several examples, which were previously used by flexible receptor docking program validations and we have obtained promising results. We also applied the approach to the SEQ17 and CDK2 datasets and showed comparable or even better results compared with flexible receptor docking. In all cases, the performance of structures after the pocket optimization was significantly superior to results using apo structures for docking simulations and matched or surpassed results using flexible target dockings (that are inherently much slower). Thus, this binding pocket optimization approach could be a useful tool for vHTS-based drug discovery, especially in cases where only apo structures or homology models are available for virtual screening studies.

Computational Methods

Structure Preparation

Structures used in this study were retrieved from the Protein Database (PDB). The crystal structures were processed with Maestro, included in the Schrödinger 2017-1 package. The missing side chains were predicted by Prime. The crystallographic waters, ions, cofactors, and, in the case of multimeric proteins, monomers not containing the binding site were removed. Hydrogen atoms, formal charges, and bond orders were added to the remaining structures using the Protein Preparation Wizard within Maestro. Only apo structures were used in docking experiments.

Pocket Optimization

The workflow for this pocket optimization is shown in Figure 2. The program MMC⁴²⁻⁴⁶ (https://mezeim01.u.hpc.mssm.edu/mmc/) was used to sample binding pocket configurations.⁴² MMC can define voids within a static protein structure. The volume of these voids itself does not inform the volume available for small-molecule binding, as side chains may fragment this volume resulting in clashes. To minimize the chances of rejecting a possible active ligand, we can use small fragments to define a subset of the pocket volume where ligands are most likely to bind when a clash is present. This is referred to as the localized binding volume within the pocket. By sampling side-chain configurations in conjunction with the binding volume of the static configuration, we can identify a pocket configuration that minimizes side-chain clashes with the localized binding volume. We can then repeat the fragment docking to the newly defined region, which is most likely to allow for some reorientation of the side chains. This localized volume can then be used in a second set of selection calculations to identify a configuration where the side-chain clashes are resolved.

Side chains of selected residues underwent torsional rotation sampling at 998K to ensure that sampling of side-chain torsional angles occurs well above the potential energy surface. The interactions between solute atoms used a spherical cutoff of 17.00 Å (typically used for both Monte Carlo and dynamical calculations when considering electrostatics), based on the central atom of the corresponding residue. The protein was parametrized with the CHARMM36 force field⁴⁷ (for an example of an input file used in these refinements, see the Supporting Information).

Pocket torsional angle sampling was followed by pocket-size calculations.⁴³ The pockets were defined with a grid-based procedure that employs a filter using circular variance⁴⁸ involving the following steps:

• (1)A 250 × 250 × 250 grid was overlaid to the protein in a rectangle that encompassed it.
• (2)Grid points that would conflict with a protein atom were removed. Conflict is defined as being closer to a protein atom than 1.25 + 0.9*σ/2 where σ is the Lennard-Jones diameter of that atom
• (3)The remaining grid points were clustered into connected sets (each grid point has at most six connections).
• (4)Small clusters were internal cavities
• (5)By far the largest cluster was formed by the grid points surrounding the protein. For these points, their circular variance CV_g with respect to the protein was calculated. The circular variance is between zero and one, and the larger it is, the closer that point is to the center of the protein.
• (6)Grid points with CV_g < 0.6 were dropped and the remaining grid points were clustered again—each new cluster represented a pocket on the protein’s surface.

The volume of each pocket and cavity is proportional to the number of grid points forming it (an example input file for pocket-size calculations is shown in the Supporting Information) (Figure 4). A CV_g value of less than 0.6 is representative of a particular probe point being located with the bulk solvent. Values greater than 0.6 indicate that a particular probe point is closer to the center of the protein and is more likely to be either along the protein surface or in the interior.

Fragment docking into the apo structure is able to define a subset of the pocket volume that a diverse set of chemotypes can occupy by considering the set of docked fragments as a single ligand. The volume of a docked fragment is defined by the number of grid points it covers. Grid points covered are those that are within 1.75 Å from the docked fragment’s coordinates. The value of 1.75 Å was chosen as the cutoff primarily due to being the upper range for van der Waals radius for heavy atoms typically used for small-molecule design. Both carbon and chlorine have approximate van der Waals radius of 1.75 Å. Other heavy atoms such as nitrogen and oxygen have approximate van der Waals radius of 1.2 Å. Using these cutoffs allows for sufficient expansion of the localized binding volume such that the volume occupied by any potential side-chain clashes can be identified. If we consider the fragment library, the volume that this fragment library occupies would be about the same volume of a larger small molecule. This volume is obtained as the union of the volumes of all fragments.

The individual pocket configurations that the MC run generated were rank-ordered by the overlap between the empty pocket space and the space occupied by the combined fragments as defined above. This resulted in a pocket structure that is closer to potential holo structures. The second round used this conformation instead of the apo structure used in the first to arrive at a new choice that is more holo-like. The holo ligand was docked into this configuration. RMSD calculations were carried out using the binding site of the holo ligand as the reference.

Preparation of Ligands

The prepared holo structures were aligned to the respective apo structures using the binding site alignment tool included in the Schrödinger 2017-1 package (Schrödinger, LLC). This gave their approximate coordinates in the apo structure and gave reference coordinates for RMSD calculations. Ligands were extracted from the holo structures and prepared using the LigPrep software. Explicit hydrogens were added to each structure. Ionization states were generated for pH of 7.00 ± 2.00. Up to eight tautomeric forms were generated for each ligand. Chirality of the ligands was preserved due to the already known binding conformations.

Docking

Receptor (water molecules were removed) grids for docking were generated using Glide. The van der Waals radius scaling was set to 1.00 with a partial charge cutoff of 0.25. The binding region was defined by a 10×10×10 Å grid box centered on the coordinates of the aligned ligands for the pilot and SEQ17 test sets and the center of mass among the binding site residues for the CDK2 test set. These receptor grids were used with the Glide standard precision (SP) docking. The van der Waals radii of the ligand were scaled by 0.8 with a partial charge cutoff of 0.15. Nitrogen inversion and ring conformations were both sampled during the docking calculations. The OPLS3 force field was used for grid generation and ligand treatment. The top five output poses per ligand were used. Energy scoring was conducted after a post-docking minimization step of the Glide docking workflow. Lowest energy poses were used for RMSD calculations. Penalties were applied for non-cis–trans amide bonds. These are the default setting for GLIDE.

In the case of the CDK2 dataset, rather than utilizing one ligand to optimize the binding pocket, the Glide diverse fragment dataset was used. This fragment set is composed of 441 unique small fragments with molecular weights in the range of 32 to 226 Dalton. Each fragment includes up to 7 ionization/tautomerization variants giving a total library size of 667 fragments. Only one pose was generated for each fragment. An upper limit of 150 Dalton molecular weight was used to define the fragments that would be included in the pocket filtration step (Figure 5). This was done primarily to characterize the binding pocket with a large variety of chemotypes and sterically diverse small molecules. The fragments can adequately describe the available binding volume for a small molecule when the pocket is blocked via unfavorable side-chain orientation.

Datasets

We performed protein pocket optimization and docking experiments across three different datasets. The pilot dataset, which contains flexible receptor docking examples from GOLD, GLIDE, and AutoDock FR, was first used to validate the ability of this method to resolve single side-chain steric clashes when used with rigid protein docking schemes (Figure 3 and Table 1). The SEQ17 dataset, which contains apo–holo pairs from a diverse set of receptors, was built specifically to test the ability of Autodock FR to modify receptor side-chain conformations.⁵ In our application, we sampled several protein side chains and validated the iterative docking and filtering process. The CDK2 dataset (the cyclin-dependent kinase 2 catalytic domain dataset) represents a high-throughput virtual screening-like benchmark to evaluate the performance of a single receptor conformation to return a diverse set of active compounds.

Once Glide docking was completed, RMSD calculations were performed using the crystal structure ligand coordinates as the reference.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c00522.

• Two examples of input files for torsional angle sampling and pocket-size calculations used by the MMC program; example input file for torsional angle sampling (Section S1); example input file for pocket-size calculations (Section S2) (PDF)

The authors declare no competing financial interest.