Beyond Beer's Law: Revisiting the Lorentz‐Lorenz Equation

Abstract

In this contribution we show how the Lorentz‐Lorenz and the Clausius‐Mosotti equations are related to Beer's law. Accordingly, the linear concentration dependence of absorbance is a consequence of neglecting the difference between the local and the applied electric field. Additionally, it is necessary to assume that the absorption index and the related refractive index change is small. By connecting the Lorentz‐Lorenz equations with dispersion theory, it becomes obvious that the oscillators are coupled via the local field. We investigate this coupling with numerical examples and show that, as a consequence, the integrated absorbance of a single band is in general no longer linearly depending on the concentration. In practice, the deviations from Beer's law usually do not set in before the density reaches about one tenth of that of condensed matter. For solutions, the Lorentz‐Lorenz equations predict a strong coupling also between the oscillators of solute and solvent. In particular, in the infrared spectral region, the absorption coefficients are prognosticated to be much higher due to this coupling compared to those in the gas phase.

Lorentz‐Lorenz equation revisited: The local field of Lorentz shifts the oscillator position to lower wavenumber and leads to coupling. Therefore, absorbance is no longer depending linearly on concentration.

In today's curricula, the Lorentz‐Lorenz and the Clausius‐Mosotti equations are well‐known in the context of the determination of dipole moments.1 Their quintessence is the establishment of a relation between the externally applied electric field and the local electric field around a molecule, a unit cell or an atom. In contemporary textbooks the information that the local fields also play a major role in dispersion theory, as shown among others by Max Planck2 and Hendrik Antoon Lorentz,3 is often no longer discussed. This is of interest, because the concentration dependence of absorbance, i. e. Beer's law, can be derived from dispersion theory.4 In fact, the derivation of quantities like the molar refractivity, the molar polarization and absorbance is based on the same formalism,5 which we will shortly introduce in the following.

Accordingly, the macroscopic polarization $\overrightarrow{P}$ is related to the microscopic dipole moment $\overrightarrow{p}$ by:

$${\displaystyle \overrightarrow{P}=N·\overrightarrow{p}}$$ (1)

In Equation (1), N is the number of dipole moments per unit volume and $\overrightarrow{p}$ is the microscopic dipole moment characterized by Equation (2):

$${\displaystyle \overrightarrow{p}=\alpha ·{\overrightarrow{E}}_{loc}}$$ (2)

wherein α is the molecular polarizability and ${\overrightarrow{E}}_{loc}$ the local electric field. This local electric field is in general not the same as the applied electric field, since at the location of the atom or molecule all fields generated by all the other atoms or molecules, as a reaction to the change of the microscopic dipole moment, will have to be taken into account. On the other hand, the macroscopic polarization $\overrightarrow{P}$ is connected with the applied electric field $\overrightarrow{E}$ , if scalar media characterized by a scalar dielectric function are assumed, according to:

$${\displaystyle \overrightarrow{P}={ϵ}_0\left({ϵ}_r-1\right)\overrightarrow{E}={ϵ}_0\chi \overrightarrow{E}}$$ (3)

In Equation (3), ${ϵ}_r$ is the relative dielectric function, ${ϵ}_0$ the vacuum permittivity and $\chi$ the electric susceptibility. Equating Equations (1) and (3) with help of Equation (2) leads to [Eq. (4)]:

$${\displaystyle N·\alpha ·{\overrightarrow{E}}_{loc}={ϵ}_0\left({ϵ}_r-1\right)\overrightarrow{E}}$$ (4)

To continue, it is necessary to find the relation between ${\overrightarrow{E}}_{loc}$ and $\overrightarrow{E}$ . If we assume a so‐called “local field of Lorentz” ${\overrightarrow{E}}_L$ , the local electric field consists of two parts, the originally applied field and ${\overrightarrow{E}}_L$ [Eq. (5)]:

$${\displaystyle {\overrightarrow{E}}_{loc}=\overrightarrow{E}+{\overrightarrow{E}}_L}$$ (5)

For the derivation of ${\overrightarrow{E}}_L$ , it is usually assumed that it in turn consists of two parts, one exerted by the neighbors at the location of the atom or molecule in question, which is virtually removed from its location, since its own contribution does not belong to ${\overrightarrow{E}}_L$ . Furthermore, distant molecules or atoms contribute to the local field like a uniformly polarized medium. If the field inside a cavity around the removed molecule or atom containing only neighboring moieties is calculated, one finds for an isotropic medium that the effect by these cancels out and the local field is given by Equation (6):6, 7

$${\displaystyle {\overrightarrow{E}}_{loc}=\overrightarrow{E}+\frac{1}{3{ϵ}_0}\overrightarrow{P}}$$ (6)

Therefore, using Equations (1) and (2) we obtain [Eq. (7)]:

$${\displaystyle \overrightarrow{P}=N·\alpha ·\left(\overrightarrow{E}+\frac{1}{3{ϵ}_0}\overrightarrow{P}\right)}$$ (7)

or, equivalently:

$${\displaystyle \overrightarrow{P}=\frac{N·\alpha }{1-\frac{N·\alpha }{3{ϵ}_0}}·\overrightarrow{E}}$$ (8)

From Equation (8) together with Equation (3) we arrive at [Eq. (9)]:

$${\displaystyle {ϵ}_r=1+\frac{N·\alpha }{{ϵ}_0-\frac{1}{3}N·\alpha }=\frac{1+\frac{2}{3}\frac{N·\alpha }{{ϵ}_0}}{1-\frac{1}{3}\frac{N·\alpha }{{ϵ}_0}}}$$ (9)

which can also be written as [Eq. (10)]:

$${\displaystyle \frac{{ϵ}_r-1}{{ϵ}_r+2}=\frac{1}{3}\frac{N·\alpha }{{ϵ}_0}}$$ (10)

At this point we depart from the derivation of the Lorentz‐Lorenz relation. Instead we realize that the number of dipole moments per unit volume N can also be written as molar concentration c with N=c ⋅ N_A, where N_A is Avogadro's constant. Furthermore, we use a result from Maxwell's wave equation according to which ${ϵ}_r={\widehat{n}}^2$ and obtain Equation (11):

$${\displaystyle \frac{{\widehat{n}}^2-1}{{\widehat{n}}^2+2}=\frac{1}{3}c\frac{N_A·\widehat{\alpha }}{{ϵ}_0}}$$ (11)

Note that here we have introduced a complex relative dielectric function and a complex index of refraction $\widehat{n}=n+ik$ , where k is the index of absorption. For the following, we consider matter generally as absorbing, consequently the polarizability becomes also a complex quantity.

For diluted gases, $\widehat{n}$ is not very different from unity: ${\widehat{n}}^2+2\approx 3$ . This allows to provide approximations [Eq. (12)]:

$${\displaystyle \widehat{n}\left(\tilde{\nu }\right)=\sqrt{1+c\frac{N_A·\widehat{\alpha }\left(\tilde{\nu }\right)}{{ϵ}_0}}\approx 1+c\frac{N_A·\widehat{\alpha }\left(\tilde{\nu }\right)}{2{ϵ}_0}}$$ (12)

This first approximation also results, if in Equation (4) ${\overrightarrow{E}}_{loc}\approx \overrightarrow{E}$ is assumed,5 therefore both assumptions are equivalent. If we focus on the index of absorption, the second approximation reads [Eq. (13)]:

$${\displaystyle k\left(\tilde{\nu }\right)=c\frac{N_A·\alpha {}^{\text{'}\text{'}}\left(\tilde{\nu }\right)}{2{ϵ}_0}}$$ (13)

which leads to Beer's law, in which A is the absorbance, $ϵ{}^{*}\left(\tilde{\nu }\right)$ the molar attenuation constant, d the sample thickness and $\alpha {}^{\text{'}\text{'}}$ the imaginary part of the polarizability [Eq. (14)]:

$${\displaystyle \mathrm{A}\left(\tilde{\nu }\right)={\underbrace{\frac{2\pi lge{N}_A·\tilde{\nu }·\alpha {}^{\text{'}\text{'}}\left(\tilde{\nu }\right)}{{ϵ}_0}}}_{ϵ{}^{*}\left(\tilde{\nu }\right)}·c·d}$$ (14)

To study the consequences of a local electric field different from the applied field, it is of advantage to use the frequency dispersion of $\widehat{\alpha }\left(\tilde{\nu }\right)$ which results from dispersion theory. Accordingly, if we assume a single oscillator, the molar polarizability $\widehat{\alpha }{}^{*}\left(\tilde{\nu }\right)=N_A·\widehat{\alpha }\left(\tilde{\nu }\right)/{ϵ}_0$ can be expressed as Equation (15):

$${\displaystyle \widehat{\alpha }{}^{*}\left(\tilde{\nu }\right)=\frac{S{{}^{*}}^2}{{\tilde{\nu }}_0^2-{\tilde{\nu }}^2-i\tilde{\nu }\gamma }}$$ (15)

wherein $S{}^{*}$ is the molar oscillator strength, ${\tilde{\nu }}_0$ the resonance position and γ the damping constant. If this expression is put into eqn. (10) taking into account N=c ⋅ N_A, the result is [Eq. (16)]:8

$${\displaystyle \frac{{ϵ}_r-1}{{ϵ}_r+2}=1-\frac{3}{{ϵ}_r+2}=\frac{1}{3}c\frac{S{{}^{*}}^2}{{\tilde{\nu }}_0^2-{\tilde{\nu }}^2-i\tilde{\nu }\gamma }\to {ϵ}_r-1=3\left(\frac{1}{1-c\frac{S{{}^{*}}^2}{{\tilde{\nu }}_0^2-{\tilde{\nu }}^2-i\tilde{\nu }\gamma }}-1\right)=\frac{3c\frac{S{{}^{*}}^2}{{\tilde{\nu }}_0^2-{\tilde{\nu }}^2-i\tilde{\nu }\gamma }}{1-c\frac{S{{}^{*}}^2}{{\tilde{\nu }}_0^2-{\tilde{\nu }}^2-i\tilde{\nu }\gamma }}\to {ϵ}_r-1=3c\frac{S{{}^{*}}^2}{\left({\tilde{\nu }}_0^2-cS{}^{*}2\right)-{\tilde{\nu }}^2-i\tilde{\nu }\gamma }}$$ (16)

This can be brought into the typical form of dispersion relations, featuring a Lorentz‐oscillator:

$${\displaystyle {ϵ}_r=1+c\frac{S{{}^{*}}^2}{\left({\tilde{\nu }}_0^2-\frac{c}{3}S{{}^{*}}^2\right)-{\tilde{\nu }}^2-i\tilde{\nu }\gamma }\to {ϵ}_r=1+c\frac{S{{}^{*}}^2}{\tilde{\nu }{{}^{\text{'}}}_0^2-{\tilde{\nu }}^2-i\tilde{\nu }\gamma }}$$ (17)

Equation (17) can also be derived directly assuming a damped harmonic oscillator driven by the local electric field.2, 3 From this result it seems that the only change introduced by the local electric field, enhanced relative to the applied electric field, is to redshift the oscillator position. With the exception of few textbooks,6, 7, 9 this is the usual conclusion drawn. In fact, as has been shown by Herzfeld and Wolf,8 even if there are local field effects and more than one oscillator, and the dispersion of the molar polarizability is correspondingly expressed as sum of all contributions of the different oscillators

$${\displaystyle \widehat{\alpha }{}^{*}\left(\tilde{\nu }\right)=\sum _i\frac{S_i{{}^{*}}^2}{{\tilde{\nu }}_{0i}^2-{\tilde{\nu }}^2-i\tilde{\nu }{\gamma }_i}}$$ (18)

it is still possible to express the dielectric function in its usual form:

$${\displaystyle {ϵ}_r=1+\sum _i\frac{S{{}^{\text{'}}}_i^2}{\tilde{\nu }{{}^{\text{'}}}_{0i}^2-{\tilde{\nu }}^2-i\tilde{\nu }{\gamma }_i}}$$ (19)

Under these circumstances, however, some important changes occur. While the oscillators of the individual molecules are still uncoupled in Equation (18), the local electric field leads to the fact that this is no longer the case for the oscillators assumed in eqn. (19). Oscillator strength and oscillator position in this equation are not individual properties, but influenced by any other oscillator – very much as this is also the case for the inverse dielectric function, for which the local electric field is different from the applied electric field, too.10 In other words, an oscillator located in the UV will alter the strength and the position of an oscillator in the infrared and vice versa in Equation (19).

This is certainly not a new insight per se,7 but it has some important consequences for the concentration dependence of the peak and integrated value of the absorbance, which seemingly have not been investigated until now.

One of these consequences is that focusing on an oscillator as it appears in Equation (19), the value of the squared oscillator strength is no longer proportional to the concentration. This also means that in general even the integrated absorbance of this band no longer depends linearly on the concentration. A consequence for gases is that under compression and for higher densities deviations from Beer's law are inevitable. The only question is at which point they set in.

Note that the model makes no difference between different kinds of oscillators from the same or different molecules. Therefore, it enables to calculate the indices of refraction of mixtures. Henceforth, based on the same model it should be possible to calculate absorbances of mixtures with j different kinds of molecules each featuring i oscillators [Eq. (20)]:

$${\displaystyle \widehat{\alpha }\left(\tilde{\nu }\right)=\sum _j{c}_j\sum _i\frac{S_{ji}{{}^{*}}^2}{{\tilde{\nu }}_{0ji}^2-{\tilde{\nu }}^2-i\tilde{\nu }{\gamma }_{ji}}}$$ (20)

As a consequence, all oscillators of all components in a mixture would mutually couple.

In the following we will investigate these conclusions in some more detail. In Ref. [4], we investigated the absorbance and its concentration dependence based on a single oscillator in the infrared with the following parameter, S*²=4900 l/(mol cm²), ${\tilde{\nu }}_0=$ 1700 cm⁻¹ and γ=20 cm⁻¹. A further assumption was that the concentration of the neat substance is 50 mol/l. Since every molecule has absorptions in the UV‐Vis, we now have to complete our assumptions with a second oscillator located in this spectral region. For this oscillator we assume the parameters S ^*2=1.25 ⋅ 10⁸ l/(cm²), ${\tilde{\nu }}_0=$ 6 ⋅ 10⁴ cm⁻¹ and γ=2 ⋅ 10³ cm⁻¹. These assumptions lead to an index of refraction of about 1.5 in the transparency region between UV‐Vis and IR spectral region, if a local field of Lorentz is assumed (without the additional local field, the index of refraction would be less than 1.3!). Furthermore, we will also consider a solution of the hypothetic substance in a hypothetic solvent which has a single oscillator located in the UV‐Vis region with the parameters S*²=2.5 ⋅ 10⁸ l/(mol cm²), ${\tilde{\nu }}_0=$ 1.2 ⋅ 10⁵ cm⁻¹ and γ=2 ⋅ 10³ cm⁻¹. These parameters lead to the same index of refraction in the transparency region as those of the UV‐Vis oscillator of the hypothetic solute. The oscillators have been used to calculate the absorbance according to Equation (21)

$${\displaystyle \mathrm{A}\left(\tilde{\nu }\right)=\frac{4\pi \tilde{\nu }}{ln10}\mathrm{k}\left(\tilde{\nu }\right)d}$$ (21)

in the infrared spectral range (Figure 1) and in the UV‐Vis (Figure 2).

Figure 1.

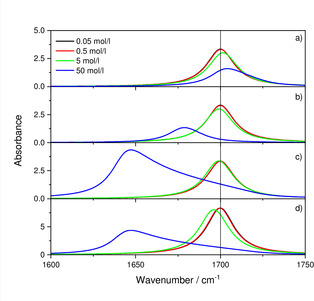
Absorbance for different concentrations of 0.05, 0.5, 5 and 50 mol/l of the hypothetical substance assuming c ⋅ d=5 ⋅ 10³ cm ⋅ mol/l. a) conventional dispersion formula. b) conventional dispersion formula assuming additionally a redshift according to $\tilde{\nu }{{}^{\text{'}}}_{0i}=\sqrt{{\tilde{\nu }}_{0i}^2-\frac{c}{3}{S}_i{}^{*}2}$ . c) Lorentz‐Lorenz formula [Eq. (10)] in combination with Equation (18). d) Same as c) but with hypothetical solvent (please note the change concerning the range of the y‐axis for d).

Figure 2.

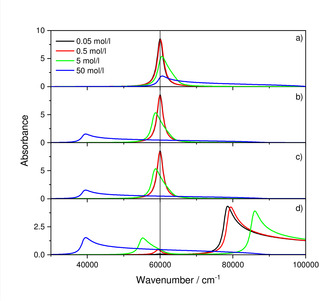
Absorbance for different concentrations of 0.05, 0.5, 5 and 50 mol/l of the hypothetical material assuming c ⋅ d=50 cm ⋅ mol/l: a) conventional dispersion formula, b) conventional dispersion formula assuming additionally a redshift according to $\tilde{\nu }{{}^{\text{'}}}_{0i}=\sqrt{{\tilde{\nu }}_{0i}^2-\frac{c}{3}{S}_i{{}^{*}}^2}$ , c) Lorentz‐Lorenz formula [Eq. (10)] in combination with (18), d) Same as c) but with hypothetical solvent. Note that for d), in contrast to a)–c), a constant d=10⁻⁶ cm was chosen and that the range of the y‐axis is different.

Figure 1 illustrates the changes of the absorbance spectra for four different concentrations of 0.05, 0.5, 5 and 50 mol/l, under the constraint c ⋅ d=5 ⋅ 10³ cm ⋅ mol/l. As already shown in Ref. [4], for the conventional model the absorbance stays practically the same for the two lowest concentrations. At higher concentrations the band begins to blueshift since the molar absorption coefficient is a function of the inverse index of refraction function, which has its maximum at higher wavenumbers than the index of absorption. For the graphs shown in panel b), the same model is used, except that the resonance position is shifted with increasing concentration by $\tilde{\nu }{{}^{\text{'}}}_{0i}=\sqrt{{\tilde{\nu }}_{0i}^2-\frac{c}{3}{S}_i{{}^{*}}^2}$ , i. e. the coupling between oscillators is still disregarded. Accordingly, for small concentrations blue and redshift compensate each other, and there is again virtually no difference for the two lowest concentrations before the maximum begins to redshift for higher concentrations. The same can be concluded for the full Lorentz‐Lorenz model and its influence on the two lowest concentrations in panel c). For higher concentrations, however, there is not only a redshift, which is stronger than that for b), but also an increase in the intensity compared to cases a) and b). For the case that the hypothetical substance is dissolved in a solvent with the same index of refraction function in the transparency region (panel d)), the two lowest concentrations can also not be distinguished, but their intensity is about twice as high than for the case where the hypothetical substance is suspended in vacuum (please note the change of the range of the y‐axis for panel d) in Figure 1). This factor even increases somewhat for weaker oscillators (the parameters of the infrared oscillator are approximately those of the ν₃ vibrations of oxyanions like $S{O}_3^{2-}$ or $N{O}_3^{-}$ ; note that we have subtracted the absorbance of the solvent from the spectra which otherwise would be noticeable for the two smaller concentrations in form of a baseline increasing towards the visible range). The redshift is somewhat stronger in the beginning, but since it is assumed that the hypothetical solvent has the same concentration in pure form, so that the concentration divided by 50 mol/l equals the volume fraction, there is only the hypothetical material left for the highest concentration and the spectra are enforcedly the same in c) and d).

While due to the local field of Lorentz the oscillators in the infrared are strongly affected by coupling to those in the UV‐Vis, the comparison of Figure 2b with 2c demonstrates that this coupling only weakly effects the UV‐Vis oscillators since differences between Figure 2b and 2c cannot be discerned. This is a consequence of the squared IR oscillator strength being less than 0.04 ‰ of the total oscillator strength which is mainly contributed by the UV‐Vis oscillator. Accordingly, the redshift of the UV‐Vis oscillator can be predicted to a very good approximation by $\tilde{\nu }{{}^{\text{'}}}_{0i}=\sqrt{{\tilde{\nu }}_{0i}^2-\frac{c}{3}{S}_i{{}^{*}}^2}$ , despite the coupling. Nevertheless, the spectra for the two lowest concentrations agree very well with each other (Figure 2a–c), so that absorbance scales linearly in this concentration range and Beer's law holds to a good approximation. As shown in Figure 2d, this conclusion cannot be drawn if a solvent is employed. Note that for Figure 2d the thickness d was kept constant instead of the product c ⋅ d as for a)‐c). Therefore, the absorbance is about an order of magnitude larger for c=0.5 mol, if the solvent is present, and a clear redshift by 500 cm⁻¹ can be observed, while this is not possible for the same concentration without solvent (again, as for the case presented in 2c, the band in the infrared has little influence on the UV‐Vis bands for the same reason, namely comparably weak oscillator strength). It is also interesting to note, that while the peak maximum of the band of the solute is redshifted, the oscillator of the solvent is blueshifted. Therefore, a solvent with bands close to that of the solute may cause baseline changes for higher concentrations, so that at these concentrations blank correction in the usual way, using the pure solvent, is no longer possible. This may be the reason why in practice instead of pure solvents high solute concentrations are employed for reference measurements as suggested recently.11 In general, in the case of strong coupling, it is the low wavenumber band that is red‐ and the high wavenumber band that is blueshifted (actually, the band is not blueshifted, but its redshift is reduced) and the shift is the stronger the higher the UV‐Vis oscillator strengths or, equivalently, the index of refraction of the solvent is, which was known in former times as Kundt's rule.12, 13 Note that Kundt's rule is according to the findings above only strictly applicable if there are no “chemical” changes due to the process of dissolution, i. e. the polarizabilities of both, solvent as well as solute, must not change during dissolution. In particular processes like association and dissociation are chemical changes that cannot be predicted by Kundt's rule. This also means that in more complex systems with more than one solute the probability strongly increases that Kundt's rule will not be applicable. On the other hand, for small concentrations of all solutes we do not see a reason why Kundt's rule should not be applicable as long as it is valid for every binary system of solute and solvent.

The conclusion drawn in the preceding paragraphs must be seen more as illustration of the general effects that can be expected. If one focuses in the IR spectral region, it is often possible as is known from dispersion theory to approximate the influence of the UV‐spectral region by a single oscillator, while depending on the structure of the material much more oscillator may be necessary to describe the optical properties in the IR spectral region. If one focuses on the UV‐Vis spectral region, it might even be necessary to model not only the transitions related to valence electrons, but also to take into account further electronic transitions to characterize the spectra completely, while in this case the transitions due to vibrations might be neglected.

The concentration dependence of the absorbance is, to a very good approximation, linear at 1700 cm⁻¹ until about 1 mol/l, independent of the chosen model (cf. Figure 3a). At higher concentrations the peak maximum begins to shift. Additionally, if a solvent other than vacuum is assumed, the slope is much stronger due to the intensity enhancement by coupling. The absorbance integrated over the infrared range is to a good approximation linearly depending on concentration over an even larger concentration range. In fact, without the influence of the absorption band in the UV‐Vis, the dependence would be perfectly linear,14 but due to the baseline caused by this mode, deviations occur. If this baseline remains unchanged and is thereby virtually removed, because solvent and solute cause identical baselines, which is the case for the Lorentz‐Lorenz model with solvent, a perfect linear dependence can be observed. In the UV‐Vis spectral region Beer's law breaks down without solvent above concentrations of about 0.5 mol/l and with solvent at about 0.2 mol/l. Since most of the oscillator strength is concentrated in this range, the integrated absorbance is linearly depending on the concentration except for the case with solvent. For this case, the influence of the absorption of the solvent is, due to the interaction between the oscillators of solvent and solute, no longer additive and can thus not be removed perfectly. Since Beer's law is accompanied by a twin law concerning the changes of the index of absorption,15 we have also investigated the influence of the different models on the index of refraction calculation. This may be in particular interesting for the emerging field of infrared dispersion spectroscopy.15, 16, 17, 18 The corresponding results can be found in the Supporting Information.

Figure 3.

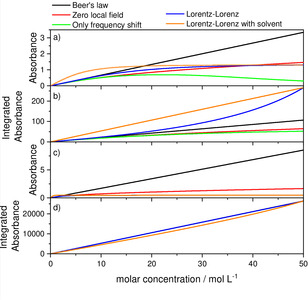
Dependence of the absorbance and the integrated absorbance from the concentration. a) Absorbance at 1700 cm⁻¹, b) integrated absorbance from 100–3000 cm⁻¹, c) absorbance at 60000 cm⁻¹, d) integrated absorbance between 30000 and 100000 cm⁻¹. d=1 micron for a) and b) and d=0.01 micron for c) and d).

Overall, we find that the different assumptions according to Beer's law vs. Lorentz‐Lorenz equation etc. are less important for concentrations below 0.5 mol/l, which are equal to densities of about 1 % of the condensed material, as long as there is no mixture with a second material which acts as solvent. In the latter case, the deviations start somewhat earlier at about 0.2 mol/l and the slope of the absorbance vs. concentration curves is much steeper. In other words, the molar absorption coefficient is much larger than without solvent. If the integrated absorbance is examined, it seems that the limits of linearity are extended by about an order of magnitude. All these considerations, however, are based on the negligence of the light's wave nature and retardation and local interference effects and electromagnetic coupling seem to start much earlier.19 For solutions, in particular also changes of chemical interactions with concentration are important. These modify, in contrast to all effects discussed so far, the atomic or molecular polarizabilities.

Close to densities of the condensed material, the Lorentz‐Lorenz equation predicts a strong nonlinear behavior, but even without local field it can no longer be stated that absorbance is proportional to the density of oscillators. Accordingly, the use of absorbance for the spectra of pure materials, which is recommended by the IUPAC, has no advantages over the use of other quantities like transmittance or reflectance.

In summary, we discussed the influence of the local field of Lorentz on the optical and IR‐optical spectra of materials in dependence of the concentration. We showed that from the Lorentz‐Lorenz equations Beer's law can be rederived assuming low oscillator densities/concentrations, so that first the local field of Lorentz becomes negligible and, secondly, the dependence of the complex index of refraction and its imaginary part, the absorption index, becomes linearly dependent on the concentration. This demonstrates that Beer's law needs no longer to be seen as an empiric law and is well‐integrated in a common theoretical fundament together with dispersion theory and the Lorentz‐Lorenz equation.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

T. G. Mayerhöfer, J. Popp, ChemPhysChem 2020, 21, 1218.