Abstract
In complex trait genetics, the ability to predict phenotype from genotype is the ultimate measure of our understanding of genetic architecture underlying the heritability of a trait. A complete understanding of the genetic basis of a trait should allow for predictive methods with accuracies approaching the trait’s heritability. The highly polygenic nature of quantitative traits and most common phenotypes has motivated the development of statistical strategies focused on combining myriad individually non-significant genetic effects. Now that predictive accuracies are improving, there is a growing interest in the practical utility of such methods for predicting risk of common diseases responsive to early therapeutic intervention. However, existing methods require individual-level genotypes or depend on accurately specifying the genetic architecture underlying each disease to be predicted. Here, we propose a polygenic risk prediction method that does not require explicitly modeling any underlying genetic architecture. We start with summary statistics in the form of SNP effect sizes from a large GWAS cohort. We then remove the correlation structure across summary statistics arising due to linkage disequilibrium and apply a piecewise linear interpolation on conditional mean effects. In both simulated and real datasets, this new non-parametric shrinkage (NPS) method can reliably allow for linkage disequilibrium in summary statistics of 5 million dense genome-wide markers and consistently improves prediction accuracy. We show that NPS improves the identification of groups at high risk for breast cancer, type 2 diabetes, inflammatory bowel disease, and coronary heart disease, all of which have available early intervention or prevention treatments.
Keywords: genome-wide association study, phenotype prediction, polygenic score, summary statistics, linkage disequilibrium, prognosis, non-parametric prediction
Introduction
In addition to improving our fundamental understanding of basic genetics, phenotypic prediction has obvious practical utility, ranging from crop and livestock applications in agriculture to estimating the genetic component of risk for common human diseases in medicine. For example, a portion of the current guideline on the treatment of blood cholesterol to reduce atherosclerotic cardiovascular risk focuses on estimating a patient’s risk of developing disease;1 in theory, genetic predictors have the potential to reveal a substantial proportion of this risk early in life (even before clinical risk factors are evident), enabling prophylactic intervention for high-risk individuals. The same logic applies to many other disease areas with available prophylactic interventions including cancers and diabetes.
The field of phenotypic prediction was conceived in plant and animal genetics (reviewed in Goddard and Hayes2 and Falke et al.3). The first approaches relied on “major genes”—allelic variants of large effect sizes readily detectable by genetic linkage or association. These efforts were quickly followed by strategies adopting polygenic models, most notably the genomic version of the Best Linear Unbiased Predictor (BLUP).4
Similarly, after the early results of human genome-wide association studies (GWASs) became available, the first risk predictors in humans were based on combining the effects of markers significantly and reproducibly associated with the trait, typically those with association statistics exceeding a genome-wide level of significance.5, 6, 7 Almost immediately, after realization that a multitude of small effect alleles play an important role in complex trait genetics,2,3,8 these methods were extended to accommodate very large (or even all) genetic markers.9, 10, 11, 12, 13, 14, 15 These methods include extensions of BLUP,9,10,16 or Bayesian approaches that extend both shrinkage techniques and random effect models.11 Newer methods benefited from allowing for classes of alleles with vastly different effect size distributions. However, these methods require individual-level genotype data that do not exist for large meta-analyses and are computationally expensive.
To leverage summary-level data from large-scale GWAS projects, an alternative approach to construct polygenic risk scores based on summary statistics has been introduced.3,12,14,17, 18, 19, 20, 21 The originally proposed version is additive over genotypes weighted by apparent effect sizes exceeding a given p value threshold. In theory, the risk predictor based on expected true genetic effects given the genetic effects observed in GWAS (conditional mean effects) can achieve the optimal accuracy of linear risk models regardless of underlying genetic architecture by properly down-weighting noise introduced by non-causal variants.22 In practice, however, implementing the conditional mean predictor poses a dilemma. The GWAS-estimated effect sizes capture genetic effects of all SNPs in linkage disequilibrium (LD), so these marginal estimates have to be first deconvoluted into genetic contribution of individual causal SNPs. Furthermore, in order to estimate the conditional mean effects, we need to know the underlying genetic architecture first, but the true architecture is unknown and difficult to model accurately. The current methods circumvent this issue by extensively sampling likely combinations of causal genetic effects under a simplified model of genetic architecture. However, these methods often ignore the correlation of sampling errors of estimated effects between SNPs in LD for the sake of computational efficiency.18,20 Such approximation can lead to a suboptimal prediction model due to double-counting of correlated sampling errors. In case of dense high-resolution GWAS data, this effect can be severe due to extensive and rank-deficient LD structures. Recent approaches account for correlated sampling errors by applying a Metropolis-Hastings technique to reject proposed states based on a full multivariate likelihood or by assuming a continuous shrinkage prior for the allelic architecture, but their prediction accuracy still depend on the convergence of high-dimensional combinatorial sampling processes, and it remains challenging to extend these models to incorporate additional complexity of true architecture.19,21
In spite of this methodological complexity, polygenic scores trained on large-scale datasets show some promise for practical applications in medical genetics. Polygenic scores have been used to analyze the UK Biobank, the largest epidemiological cohort that includes genetic data.23 Individuals with extreme values of polygenic score were shown to have a substantially elevated risk for corresponding diseases, generating enthusiasm for clinical applications of the method.
Here, we propose a novel risk prediction approach called partitioning-based non-parametric shrinkage (NPS). Without specifying a parametric model of underlying genetic architecture, we aim to estimate the conditional mean effects directly from the data. Our method accounts for both types of correlations induced by LD in GWAS summary statistics, namely the correlations of true genetic effects as well as sampling errors, by using eigenvalue decomposition of LD matrix instead of relying on a high-dimensional sampling technique. Despite growing interest in non-parametric prediction models, thus far there has been no non-parametric polygenic score that can fully allow for LD under the conditional mean effect framework.24, 25, 26, 27, 28, 29 We evaluate the performance of this new approach under a simulated genetic architecture of 5 million dense SNPs across the genome. We also test the method using real data in four disease areas: breast cancer, type 2 diabetes, inflammatory bowel disease, and coronary heart disease.
Material and Methods
Overview
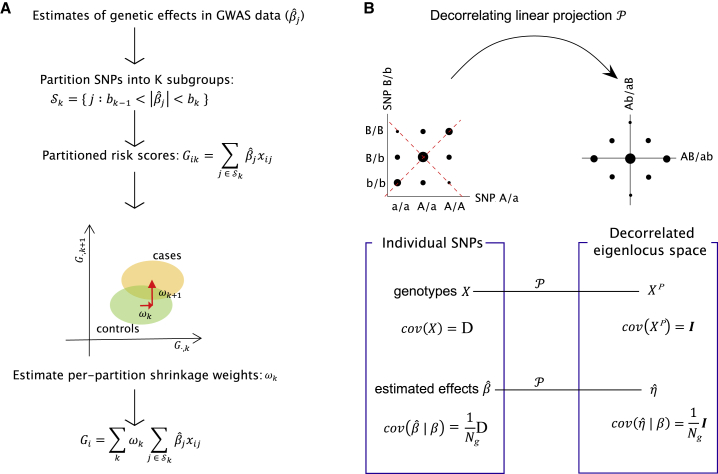
Our approach is to partition SNPs into groups and determine the relative weights based on predictive value of each partition estimated in the training data (Figure 1A). Intuitively, when there is no LD between SNPs, a partition dominated by non-causal variants will have low power to distinguish case subjects from control subjects, whereas the partition enriched with strong signals will be more informative for predicting the phenotype. This is equivalent to approximating the conditional mean effect curve by piecewise linear interpolation. Because of LD, however, we cannot apply the partitioning method directly to GWAS effect sizes. True genetic effects as well as sampling noise are correlated between adjacent SNPs. To prevent estimated genetic signals smearing across partitions, we first transform GWAS data into an orthogonal domain, which we call “eigenlocus” (Figure 1B). Specifically, we use a decorrelating linear transformation obtained by eigenvalue decomposition of the local LD matrix. Both genotypes and sampling errors are uncorrelated in the eigenlocus representation. In this representation, however, true genetic effects do not follow analytically tractable distributions except under infinitesimal and extremely polygenic architectures. Therefore, we apply our partitioning-based non-parametric shrinkage to the estimated effect sizes in the eigenlocus, and then restore them back to the original per-SNP effects.
Figure 1.
Overview of Non-Parametric Shrinkage (NPS)
(A) For unlinked markers, NPS partitions SNPs into K subgroups splitting the GWAS effect sizes () at cut-offs of . Partitioned risk scores are calculated for each partition and individual using an independent genotype-level training cohort. The per-partition shrinkage weights are determined by the separation of between training case subjects and control subjects. Estimating the per-partition shrinkage weights is a far easier problem than estimating per-SNP effects. The training sample size is small but still larger than the number of partitions, whereas for per-SNP effects, the GWAS sample size is considerably smaller than the number of markers in the genome. This procedure “shrinks” the estimated effect sizes not relying on any specific assumption about the distribution of true effect sizes.
(B) For markers in LD, genotypes and estimated effects are decorrelated first by a linear projection in non-overlapping windows of ∼2.5 Mb in length, and then NPS is applied to the data. The size of black dots indicates genotype frequencies in population. Before projection, genotypes at SNP 1 and 2 are correlated due to LD (), and thus sampling errors of estimated effects () are also correlated between adjacent SNPs. The projection neutralizes both correlation structures. The axes of projection are marked by red dashed lines. denotes the true genetic effect at SNP . is the sample size of GWAS cohort.
Decorrelating Projection
We split the genome into non-overlapping windows of SNPs each. By default, was set to 4,000 SNPs (∼2.5 Mb on average). The window size was chosen to be large enough to capture the majority of LD patterns except near the edge. For the sake of simplicity, we assume that LD is confined to each window and there exists no LD across windows. In each genomic window , let be an genotype matrix of individuals and SNPs in the window. We assume that the genotypes are standardized to the mean of 0 and variance of 1. Let be an -dimensional vector of observed effect sizes from a GWAS and be an -dimensional vector of true underlying genetic effects in window . The scales of and are defined with respect to the standardized genotypes. Then, the LD matrix is given by and can be factorized by eigenvalue decomposition into , where is an orthonormal matrix of eigenvectors and is a diagonal matrix of eigenvalues.
Now we introduce a linear decorrelating transformation , which projects summary statistics and genotypes into a decorrelated space which we call “eigenlocus space.” We call the projection an “eigenlocus projection.” is defined as the following:
By applying the eigenlocus projection on and , we obtain the estimated effect sizes and projected genotypes in this eigenlocus space as follows:
| (Equation 1) |
This projection will remove the correlation structure induced by LD in the genotypes and in the sampling error of estimated effects . Specifically, in the eigenlocus space, and follow the following multivariate normal distributions (see Appendices A and B for the derivation):
where is the sample size of GWAS from which summary statistics was obtained and is the true underlying genetic effect defined by .
Due to the rank-deficiency of LD matrix and application of regularization on (described below), the dimension of eigenlocus space can be lower than the total number of SNPs in a given window . Specifically, we set the LD between SNPs to 0 unless the absolute value of estimated LD was greater than . This is to suppress sampling noises in off-diagonal entries of LD matrix. Since the standard error of pairwise LD is approximately under no correlation, we expect that on average, only 1.7 uncorrelated SNP pairs escape the above regularization threshold in each window. In addition, projections corresponding to eigenvalues less than 0.5 were truncated for the computational efficiency since they were dominated by noises. Although we chose the window size to be large enough to capture the majority of local LD patterns, some LD structures, particularly near the edge, span across windows, which in turn yield cross-window correlations. To eliminate such correlations, we applied LD pruning in the eigenlocus space between adjacent windows. Specifically, we calculated Pearson correlations between projected genotypes belonging to neighboring windows. For the pairs with the absolute Pearson correlation > 0.3, we kept the one yielding a larger absolute effect size and eliminated the other.
By applying the above processing steps in each genomic window , we obtained -dimensional vector of estimated effect sizes and matrix of genotypes in the eigenlocus space. Here, the index indicates an individual genetic variation yielded by applying an eigenlocus projection (Equation 1) with eigenvalues . In this representation, we can operate on each genetic variation independently from each other since they are decorrelated.
Partitioning Strategy
Since the SNPs with largest effect sizes span a wide range of values but are sampled only sparsely, we cannot reliably estimate the conditional mean effect for this large-effect tail without assuming a priori parametric assumption on its distribution. This issue is particularly the case for genome-wide significant SNPs. To solve this problem, we handled the genome-wide significant SNPs as a separate partition from the rest of SNPs and treat them as fixed effect estimates. Specifically, the genome-wide significant SNPs were set aside to a special partition , for which the decorrelating projection was set to the identity matrix with eigenvalues of 1. To avoid LD across SNPs in , genome-wide significant SNPs were selected into only if the LD between them is low (r2 < 0.3). Then, we residualized the effects of SNPs in from estimated effects of the rest of SNPs in order to avoid double-counting their genetic effects.
The genetic variants which were not selected to were projected into the eigenlocus space and then grouped into 10 × 10 double-partitions on intervals of eigenvalues and absolute estimated effect sizes . This is because in the eigenlocus space, conditional mean effect depends not only on the absolute value of estimated genetic effect but also on eigenvalue of projection . The eigenvalue of projection tracks the scale of true genetic effect in the eigenlocus space (Appendix C). In total, we used 101 partitions in this study including the partition of genome-wide significant SNPs .
While fully optimizing the partitioning cut-offs can potentially improve the accuracy of prediction model, this becomes rapidly impractical as the number of partitions increases. NPS requires a large enough number of partitions to closely approximate conditional mean effects, thus the combinatorial search for optimal cut-offs is computationally intractable. Therefore, we applied the following general heuristic, which worked well across our simulation datasets. First, the partitioning cut-offs were selected on the intervals of eigenvalues, equally distributing across partitions. This partition scheme evenly distributes the tagged heritability across partitions. The partitions on eigenvalues are denoted here by , …, from the lowest to the highest. Then, each partition of eigenvalues was further partitioned on intervals of , equally distributing across partitions. This second partitioning scheme is intended to evenly distribute the overall variance in polygenic scores, namely, , across the partitions. This second partitions of are denoted by , …, from the lowest to the highest .
Estimation of Conditional Mean Effect
The predicted genetic risk scores of individual can be represented by the sum of conditional mean effects multiplied by genetic dosages across all genomic windows and genetic variations in each window. Instead of deriving conditional mean effects under a genetic architecture prior, we interpolate the conditional mean effects by fitting a linear function for each partition as follows:
| (Equation 2) |
where is an indicator function for the membership of genetic variations to partition , is the set of all genetic variations assigned to partition , and is the total number of partitions, set to 101 by default. The equation (Equation 2) can be further simplified by changing the order of summation as below:
| (Equation 3) |
where is a partitioned polygenic score of individual calculated using only genetic variations belonging to the partition . Then, becomes equivalent to the per-partition shrinkage weight. Based on Equation 3, we can estimate by fitting known phenotypes with partitioned scores across individuals in a small genotype-level training cohort.
For dichotomous phenotypes without covariates, we used a linear discriminant analysis (LDA) to estimate . The partitioned scores calculated in a training cohort form -dimensional feature space, and LDA guarantees the optimal accuracy of the classifier when case and control subgroups follow multivariate normal distributions in the feature space. Since each partition consists of a sufficient number of projected genetic variations, partitioned scores of case and control subjects, namely , follow approximately normal distributions.30 The variance of partitioned scores is approximately equal between case and control subjects since of an individual partition explains only a small fraction of phenotypic variation on the observed scale in typical GWAS data.31 Furthermore, due to the decorrelating property of eigenlocus projection, the covariance of and can be assumed to be approximately 0 between different partitions and . Although in theory, the liability thresholding effect induces slight non-zero covariance between partitions, this effect is typical small and negligible. Thus, LDA-derived shrinkage weights can be independently estimated for each partition and simplify to:
Similarly, for continuous phenotypes or the case of dichotomous traits with covariates, we can estimate per-partition shrinkage weights by applying the following linear regression model to the training data:
independently for each partition.
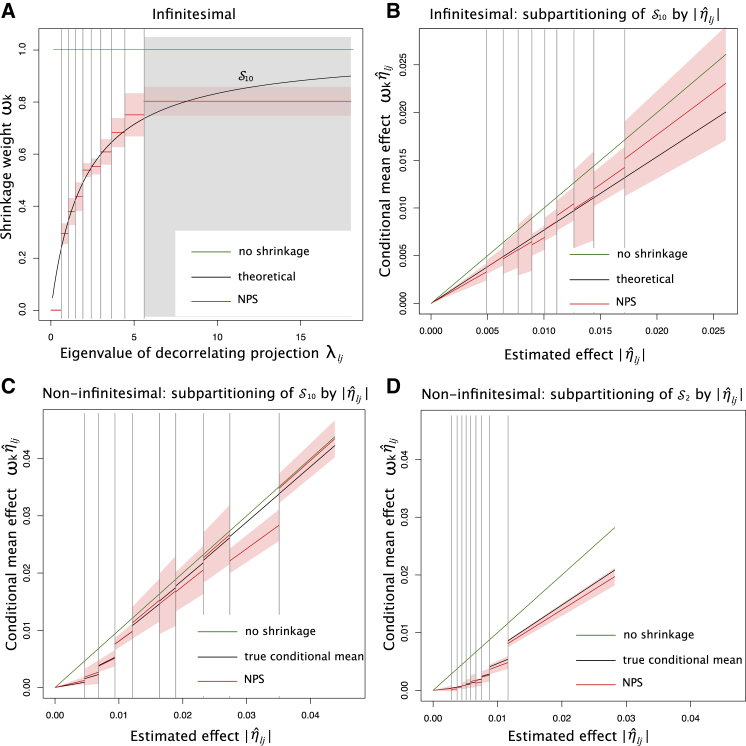
In the special case of infinitesimal genetic architecture, in which all SNPs are causal with normally distributed effect sizes, the conditional mean effects have been analytically derived and are predicted to depend only on eigenvalues ;18 therefore, we can cross-check the accuracy of our shrinkage weights estimated by NPS in simulations (Appendix D). To apply NPS, we first partitioned genetic variations in the eigenlocus space into ten subgroups on intervals of their eigenvalues as described above but without separating out the genome-wide significant SNPs (Figure 2A). The per-partition shrinkage weights trained by NPS closely tracked the theoretical optimum in most of the bins. Interestingly, in the lowest and highest partitions of eigenvalues, and , the estimated shrinkage was significantly biased away from the optimal curve. The smallest eigenvalues are too noisy to estimate with the reference LD panel. Therefore, it is correct to down-weight almost to 0. In case of partition , it spans the widest interval of eigenvalues but consists of the fewest number of SNPs. While it is ideal to apply a finer partitioning in this interval so as to better interpolate the theoretical curve, the total numbers of SNPs and independent projection vectors in the genome are the fundamental limiting factor.
Figure 2.
Per-Partition Shrinkage Weights Estimated by Non-Parametric Shrinkage (NPS) Approximate the Conditional Mean Effects in the Decorrelated Space
(A) NPS shrinkage weights (red line) compared to the theoretical optimum (black line), , under infinitesimal architecture. The partition of largest eigenvalues is marked by gray box.
(B) Conditional mean effects estimated by NPS (red line) in sub-partitions of by under infinitesimal architecture. The theoretical line (black) is the average over all in .
(C and D) Conditional mean effects estimated by NPS (red line) in sub-partitions of (C) and (D) on intervals of under non-infinitesimal architecture with the causal SNP fraction of 1%. The true conditional means (black) were estimated over 40 simulation runs.
The mean NPS shrinkage weights (red line) and their 95% CIs (red shade) were estimated from five replicates. Grey vertical lines indicate partitioning cut-offs. No shrinkage line (green) indicates . The number of markers is 101,296. The discovery GWAS size equals to . The heritability is 0.5.
In the case of infinitesimal architecture, theory predicts that per-partition shrinkage weights are independent of estimated effect sizes . To examine the robustness of NPS, we applied the general 10-by-10 double partitioning on and collected under infinitesimal simulations. In overall, the shrinkage weights estimated by double partitioning agree with the theoretical expectation. The estimated conditional mean effects, interpolated with , follow the linear trajectory (Figures 2B and S1).
For non-infinitesimal genetic architecture, we do not have an analytic derivation of conditional mean effects; therefore, we empirically estimated the conditional means using the true underlying effects and true LD structure of the population. Here, 1% of SNPs were simulated to be causal with normally distributed effect sizes. As expected, the true conditional mean dips for the lowest values of but approaches no shrinkage with increasing values of (Figures 2C and 2D). A notable difference between the partitions of largest eigenvalues and second smallest eigenvalues is that the true conditional mean is very close to no shrinkage for large in the former. This is because eigenvalues are proportional to the scale of true effects ; therefore, with large enough eigenvalues, the sampling error becomes relatively small and the estimated effect sizes more accurate. In all partitions, conditional mean effects estimated by NPS stayed very close to the true conditional means (Figure S2).
Back-Conversion from the Eigenlocus Space to Per-SNP Effects
Rewriting Equation 2 using matrix operations, we can reformulate the -dimensional vector of predicted genetic risk scores using the original SNP genotypes instead of eigenlocus genotypes as follows:
from the definition of (Equation 1). We obtain the conditional mean effects by non-parametric shrinkage in the following form:
where is an diagonal matrix with diagonal entries defined as:
with the such that
where is the partition to which the th projected genetic variation belong in the eigenlocus space. Therefore, the reweighted effects in the original per-SNP scale can be retrieved back by computing .
Application of NPS to Genome-wide Datasets
The estimated effect size at each SNP is available as summary statistics from a large discovery GWAS. As these estimated effects were represented as per-allele effects, we converted them relative to standardized genotypes by multiplying by , where is the allele frequency of each SNP in the discovery GWAS cohort.
Because the accuracy of eigenlocus projection declines near the edge of windows, the overall performance of NPS is affected by the placement of window boundaries relative to locations of strong association peaks. To alleviate such dependency, we repeated the same NPS procedure shifting by 1,000, 2,000, and 3,000 SNPs and took the average reweighted effect sizes across four NPS runs. When NPS was run in parallel on up to 88 processors (22 chromosomes × 4 window shifts), it took total computation time of 3 to 6 h for each dataset.
Simulation of Genetic Architecture with Dense Genome-wide Markers
For simulated benchmarks, we generated genetic architecture with 5 million dense genome-wide markers from the 1000 Genomes Project. We kept only SNPs with MAF > 5% and Hardy-Weinberg equilibrium test p value > 0.001. We used non-Finnish EUR panel (n = 404) to populate LD structures in simulated genetic data. Due to the limited sample size of the LD panel, we regularized the LD matrix by applying Schur product with a tapered banding matrix so that the LD smoothly tapered off to 0 starting from 150 kb up to 300 kb.32
Next, we generated genotypes across the entire genome, simulating the genome-wide patterns of LD. We assume that the standardized genotypes follow a multivariate normal distribution. Since we assume that LD travels no farther than 300 kb, as long as we simulate genotypes in blocks of length greater than 300 kb, we can simulate the entire chromosome without losing any LD patterns by utilizing a conditional multivariate normal distribution as the following. The genotypes for the first block of 1,250 SNPs (average 750 kb in length) were sampled directly out of multivariate normal distribution . From the next block, we sampled the genotypes of 1,250 SNPs each, conditional on the genotypes of previous 1,250 SNPs. When the genotype of block is and the LD matrix spanning block and is split into submatrices as the following:
then, the genotype of next block follows a conditional MVN as:
After the genotype of entire chromosome was generated in this way, the standardized genotype values were converted to allelic genotypes by taking the highest and lowest genotypes as homozygotes and the rest as heterozygotes under Hardy-Weinberg equilibrium. is the number of simulated samples and is the allele frequency of each SNP. This MVN-based simulator can efficiently generate a very large cohort with realistic LD structure across the genome and is guaranteed to produce homogeneous population without stratification.
We simulated three different sets of genetic architecture: point-normal mixture, MAF dependency, and DNase I hypersensitive sites (DHS). The point-normal mixture is a spike-and-slab architecture in which a fraction of SNPs have normally distributed causal effects for SNP as below:
where is the fraction of causal SNPs being 1%, 0.1%, or 0.01% and is a point mass at the effect size of 0. For the MAF-dependent model, we allowed the scale of causal effect sizes to vary across SNPs in proportion to with 33 as follows:
Finally, for the DHS model, we further extended the MAF-dependent point-normal architecture to exhibit clumping of causal SNPs within DHS peaks. Fifteen percent of simulated SNPs were located in the master DHS sites that we downloaded from the ENCODE project. We assumed a five-fold higher causal fraction in DHS () compared to the rest of the genome in order to simulate the enrichment of per-SNP heritability in DHS reported in the previous study.34 Specifically, was sampled from the following distribution:
In each genetic architecture, we simulated phenotypes for discovery, training, and validation populations of 100,000, 50,000, and 50,000 samples, respectively, using a liability threshold model of heritability of 0.5 and prevalence of 0.05. In the discovery population, we obtained GWAS summary statistics with Plink by testing for the association with the total liability instead of case/control status; this is computationally easier than to generate a large case/control GWAS cohort directly, and the estimated effect sizes are approximately equivalent by a common scaling factor. With the prevalence of 0.05, statistical power of quantitative trait association studies using the total liability is roughly similar to those of dichotomized case/control GWASs of same sample sizes.35 For the training dataset, we assembled a cohort of 2,500 case subjects and 2,500 control subjects by down-sampling control subjects out of the simulated population of 50,000 samples. The validation population was used to evaluate the accuracy of prediction model in terms of R2 of the liability explained and Nagelkerke’s R2 to explain case/control outcomes.
GWAS Summary Statistics
GWAS summary statistics are publicly available for phenotypes of breast cancer,36,37 inflammatory bowel disease (IBD),38 type 2 diabetes (T2D),39 and coronary artery disease (CAD).40 These GWAS summary statistics were based only on white (European) samples with an exception of CAD, for which 13% of discovery cohort comprised of non-European ancestry.
UK Biobank
UK Biobank samples were used for training and validation purposes. Case and control samples were defined as follows. Breast cancer cases were identified by ICD10 codes of diagnosis. Control subjects were selected from females who were not diagnosed with or did not self-report history of breast cancer. We excluded individuals with history of any other cancers, in situ neoplasm, or neoplasm of unknown nature or behavior from both case and control subjects. For IBD, we identified case individuals by ICD10 or self-reported disease codes of Crohn disease, ulcerative colitis, or IBD. Control subjects were randomly selected excluding participants with history of any auto-immune disorders. For T2D, case subjects were identified by ICD10 diagnosis codes or by questionnaire on history of diabetes combined with the age of diagnosis over 30. However, our T2D case subjects may include a small fraction of type 1 diabetic case subjects misdiagnosed as T2D (3.7%) as previously reported.41 For early-onset CAD, case individuals were identified by ICD10 codes of diagnosis or cause of death. The early onset was determined by the age of heart attack on the questionnaire (≤55 for men and ≤65 for women). Individuals with history of CAD were excluded from controls regardless of the age of onset. The latest CAD summary statistics include UK Biobank samples in the interim release; thus, to avoid sample overlap, we used only post-interim samples, which were identified by genotyping batch IDs. For all phenotypes, our case definition includes both prevalent and incident cases.
For genotype QC, we filtered out SNPs with MAF below 5% or INFO score less than 0.4. We also excluded tri-allelic SNPs and indels. For all phenotypes, we filtered out participants who were retracted, were not from white British ancestry, or had indication of any QC issue in UK Biobank. We included only samples that were genotyped with Axiom array. Related samples were excluded to avoid potential confounding. The samples were randomly split to training and validation cohorts. Controls were down-sampled to the case to control ratio of 1:1 to assemble training cohorts, but no down-sampling was applied to validation cohorts to keep the original case prevalence.
Partners Biobank
We used Partners Biobank42 to evaluate the accuracy of prediction models in an independent validation cohort. These genotyping data were previously generated using the MEGA-Ex array. Markers with monomorphic allele frequency, complementary alleles, less than 99.5% genotyping rate, or deviation from Hardy-Weinberg equilibrium (p < 0.05) were removed. Then, statistical imputation was conducted to infer genotypes at missing markers using Eagle v.2.4 and IMPUTE v.4 on the reference panel (1000 Genomes Phase 3). Excluding samples of non-European ancestry, a total of 16,839 samples from US white population were available for use. Participants with breast cancer, IBD, T2D, and CAD were identified using a phenotype query algorithm with the PPV parameter of 0.90.43 To obtain early-onset CAD, both case and control subjects were restricted to men with age ≤ 55 and women with age ≤ 65. Since the prevalence of early-onset CAD and T2D are sex dependent, we included the sex covariate in the genetic risk model for CAD and T2D. For all methods, the coefficient of sex covariate was estimated in the training cohort of UK Biobank.
LDPred
The accuracy of LDPred was evaluated in simulated and real datasets using the default parameter setting. The underlying causal fraction parameter was optimized using the training cohort, which is available as individual-level genotype data. Specifically, the causal SNP fractions of 1, 0.3, 0.1, 0.03, 0.01, 0.003, 0.001, 0.0003, and 0.0001 were tested in the training data, and the prediction model yielding the highest prediction R2 was selected for validation. The training genotypes were also used as a reference LD panel.
LDPred accepts only hard genotype calls as inputs at the training step. Thus, for real data we converted imputed allelic dosages to most likely genotypes after filtering out SNPs with genotype probability < 0.9. SNPs with the missing rate > 1% or deviation from Hardy-Weinberg equilibrium (p < 10−5) were also excluded. Prediction models were trained using only SNPs that passed all QC filters in both training and validation datasets, as recommended by the authors. SNPs with complementary alleles were excluded automatically by LDPred. In simulations, all genotypes were generated as hard calls, and complementary alleles were avoided; thus, the exactly same set of SNPs were used for both LDPred and NPS. In a subset of datasets, we further examined the accuracy of LDPred when it was run only with directly genotyped SNPs. In simulated datasets, we assumed that both training and validation cohorts were genotyped with Illumina HumanHap550v3 array, restricting the genotype data to 490,504 common SNPs. For UK Biobank datasets, prediction models were constrained to up to 354,110 common SNPs in UK Biobank Axiom array. In the case of validation in Partners Biobank, we did not consider running LDPred only with genotyped SNPs since too few SNPs were directly genotyped in both UK Biobank and Partners Biobank; thus, we validated LDPred only using overlapping markers in imputed data of two cohorts.
LD Pruning and Thresholding
LD Pruning and Thresholding (P+T) algorithm was evaluated using PRSice software in the default setting.44 In real data, imputed allelic dosages were converted to hard-called genotypes similarly as for LDPred. A training cohort was used as a reference LD panel and to optimize pruning and thresholding parameters. The best prediction model suggested by PRSice was evaluated in validation cohorts.
PRS-CS
PRS-CS algorithm was benchmarked using the default parameter setting.21 The optimal parameter values were optimized in training cohorts, and the highest performing model was evaluated in validation cohorts. For the reference LD panel, we used a set of simulated genotypes produced by our MVN simulator in order to accurately capture the underlying LD structure of our simulated datasets; in real data, we used the “EUR” reference LD panel provided in the software. Imputed allelic dosages were converted to hard-called genotypes similarly as recommended by the authors.
Results
Application to Simulated Data
To benchmark the accuracy of NPS, we simulated the genetic architecture using the real LD structure of 5 million dense common SNPs from the 1000 Genomes Project (Material and Methods). We considered the causal fraction of SNPs from 1% to 0.01%, dependency of heritability on minor allele frequency (MAF), and enrichment of heritability in DNase I hypersensitive sites (DHS) based on the previous literature.33,34,45 The prediction accuracy of NPS remained robust across the simulated genetic architectures (Tables 1 and S1). We measured prediction accuracy using Nagelkerke R2 and odds ratio at the highest 5% tail of the polygenic score distribution. The latter measure has been popularized by a recent study that reported that the tails of the polygenic score distribution are associated with risk that is similar to monogenic mutations.23
Table 1.
Comparison of Prediction Accuracy in Simulated Genetic Architecture
|
5% |
NPS R2NagCompared to |
||||||
|---|---|---|---|---|---|---|---|
| % Causal SNPs | Method | R2Nagelkerke | % h2Explained | Tail OR | P+T | LDPred | PRS-CS |
| 1% | P+T | 0.050 | 14.8 | 3.18 | |||
| LDPred | 0.068 | 20.6 | 3.66 | ||||
| PRS-CS | 0.075 | 22.0 | 4.02 | ||||
| NPS | 0.085 | 24.6 | 4.27 | 1.68∗ | 1.25∗ | 1.13∗ | |
| 0.1% | P+T | 0.136 | 40.8 | 6.32 | |||
| LDPred | 0.080 | 23.0 | 4.08 | ||||
| PRS-CS | 0.156 | 44.8 | 7.03 | ||||
| NPS | 0.179 | 51.2 | 8.09 | 1.31∗ | 2.22∗ | 1.14∗ | |
| 0.01% | P+T | 0.213 | 61.4 | 9.92 | |||
| LDPred | 0.153 (0.268)a | 43.8 (74.6)a | 7.66 (13.37)a | ||||
| PRS-CS | 0.228 | 65.3 | 10.35 | ||||
| NPS | 0.328 | 92.6 | 17.19 | 1.54∗ | 2.14∗ | 1.44∗ | |
Non-parametric shrinkage (NPS) is more robust and accurate compared to other methods in simulated datasets. The simulations incorporate the dependency of heritability on minor allele frequency and clumping of causal SNPs in known DHS elements. The heritability was 0.5, and the prevalence was 5%. The number of markers was 5,012,500. The GWAS sample size was 100,000. Prediction models were optimized in the training cohort of 2,500 case subjects and 2,500 control subjects. R2 of prediction was measured in the validation cohort of 50,000 samples. The h2 explained stands for the proportion of heritability on the liability scale explained by polygenic scores. The asterisk (∗) indicates a significant improvement in Nagelkerke’s R2 (paired t test; p < 0.05).
The accuracy of LDPred varies widely depending on the convergence of prediction model; thus, we report the maximum R2 in parentheses as well as the average performance.
We evaluated the performance of NPS vis-à-vis two popular methods, LDPred and P+T, as well as the newest method PRS-CS with the superior reported accuracy13,18,21 (Tables S1–S5). LDPred is the state-of-the-art Bayesian parametric method, which is similarly based on summary statistics estimated in large GWAS datasets and an independent training set with individual-level data. PRS-CS is a new sophisticated extension of the Bayesian strategy. We found that our method resulted in more accurate predictions than all three methods across a range of genome-wide simulations. PRS-CS was shown to be more accurate than P+T and LDPred on simulated data, although less accurate than NPS. The improvement over LDPred is seemingly surprising given that some of the simulated allelic architectures are the spike-and-slab allelic architecture for which LDPred is expected to be optimal as a Bayesian method. However, we found that in most simulations, LDPred adopted the infinitesimal or extremely polygenic model irrespective of the true simulated regime, pointing to the challenge of computational optimization in the parametric case (Table S3). The simulations suggest that the well-optimized parametric models are capable of generating good predictions, but NPS is much more robust and does not suffer from optimization issues. Overall, NPS improves accuracy consistently for all simulated allelic architectures for both Negelkerke R2 and odds ratios at 5% tail (Table 1).
Application to Real Data
We benchmarked the accuracy of NPS and other methods using publicly available GWAS summary statistics and training and validation cohorts assembled with UK Biobank samples (Material and Methods).36, 37, 38, 39, 40,46 For all three phenotypes except coronary artery disease, NPS showed significantly higher accuracy than LDPred or P+T (Tables 2 and S6–S9 and Figures S3–S7) and highly similar (statistically indistinguishable) accuracy compared to PRS-CS. In particular, our method and PRS-CS outperformed the other two methods by greater magnitudes with more recent GWAS summary statistics with finer resolution. For example, the latest breast cancer GWAS has twice as large sample size as the previous study and used a custom genotyping array to densely genotype known cancer susceptibility loci. The R2 of our method increased by 1.5-fold with the latest breast cancer data whereas the accuracy of LDPred did not improve at all. The R2 of P+T increased by 1.25-fold, but the gain is mainly due to the inferior accuracy with older GWAS data.
Table 2.
Accuracy of Polygenic Prediction in Real Data
| Discovery GWAS | Training (UK Biobank) | Validation (UK Biobank) | Method | R2Nag | 5% Tail OR |
|---|---|---|---|---|---|
| Breast cancer 2015 (n = ∼120,000) | n = 3,956/3,956 | n = 3,957/73,652 | P+T | 0.021 | 2.28 |
| LDPred | 0.026 | 2.42 | |||
| PRS-CS | 0.030 | 2.60 | |||
| NPS | 0.030 | 2.53 | |||
| Breast cancer 2017 (n = ∼230,000) | P+T | 0.027 | 2.37 | ||
| LDPred | 0.026 | 2.33 | |||
| PRS-CS | 0.043 | 2.96 | |||
| NPS | 0.045 | 3.01 | |||
| Inflammatory bowel disease (n = ∼35,000) | n = 2,483/2,483 | n = 2,482/157,272 | P+T | 0.028 | 3.00 |
| LDPred | 0.027 | 2.77 | |||
| PRS-CS | 0.040 | 3.67 | |||
| NPS | 0.035 | 3.60 | |||
| Type 2 diabetes (n = ∼160,000) | n = 7,298/7,298 | n = 7,298/144,020 | P+T | 0.046 | 3.04 |
| LDPred | 0.059 | 3.51 | |||
| PRS-CS | 0.066 | 3.99 | |||
| NPS | 0.065 | 3.81 | |||
| Coronary artery disease (n = ∼330,000) | n = 2,000/2,000 | n = 773/62,512 | P+T | 0.063 | 5.17 |
| LDPred | 0.078 | 5.65 | |||
| PRS-CS | 0.075 | 4.92 | |||
| NPS | 0.073 | 5.21 |
Non-parametric shrinkage (NPS) and PRS-CS outperform both pruning and thresholding (P+T) and LDPred in real data. Both training and validation cohorts were sampled from UK Biobank. The tail odds ratio (OR) stands for the odds ratios of case subjects over control subjects at the 5% tail in polygenic score distribution compared to the rest. For CAD and T2D, all prediction models were trained and validated with the sex covariate to account for the difference of disease prevalence by sex.
Since our method estimates a large number of parameters from the training data, it might be particularly vulnerable to overfitting cryptic genetic features common to both training and testing data which may result in inflated prediction accuracy. To eliminate this possibility, we benchmarked the prediction models in Partners Biobank, as an independent validation cohort (Material and Methods).42 For all phenotypes, NPS outperformed both P+T and LDPred and showed similar accuracy as PRS-CS (Tables 3 and S10–S13). NPS also has a higher odds ratio at 5% distribution tail than PRS-CS consistently for all phenotypes, although this improvement is not statistically significant (Table 3).
Table 3.
Accuracy of Polygenic Prediction in Independent Validation Cohorts
| Discovery GWAS | Training (UK Biobank) | Validation (Partners) | Method | R2Nag | 5% Tail OR |
|---|---|---|---|---|---|
| Breast cancer 2017 (n = ~230,000) | n = 3,956/3,956 | n = 754/8,324 | P+T | 0.016 | 1.56 |
| LDPred | 0.015 | 1.78 | |||
| PRS-CS | 0.034 | 2.23 | |||
| NPS | 0.034 | 2.32 | |||
| Inflammatory bowel disease (n = ~35,000) | n = 2,483/2,483 | n = 839/16,000 | P+T | 0.050 | 3.57 |
| LDPred | 0.038 | 3.07 | |||
| PRS-CS | 0.065 | 4.11 | |||
| NPS | 0.069 | 4.32 | |||
| Type 2 diabetes (n = ~160,000) | n = 7,298/7,298 | n = 2,026/14,813 | P+T | 0.038 | 2.10 |
| LDPred | 0.046 | 2.51 | |||
| PRS-CS | 0.058 | 2.80 | |||
| NPS | 0.054 | 2.97 | |||
| Coronary artery disease (n = ~330,000) | n = 2,000/2,000 | n = 268/7,107 | P+T | 0.018 | 2.72 |
| LDPred | 0.016 | 2.31 | |||
| PRS-CS | 0.027 | 3.16 | |||
| NPS | 0.025 | 4.10 |
Non-parametric shrinkage (NPS) and PRS-CS outperform both pruning and thresholding (P+T) and LDPred in completely independent validation cohorts from US white population (Partners Biobank). The same cohorts from UK Biobank was used for training prediction models (Table 2). The tail odds ratios (OR) stand for the odds ratios of cases over controls at the 5% tail in polygenic score distribution compared to the rest. For CAD and T2D, all prediction models were trained and validated with the sex covariate to account for the difference of disease prevalence by sex.
Discussion
Understanding how phenotype maps to genotype has always been a central question of basic genetics. With the explosive growth in the amount of training data, there is also a clear prospect and enthusiasm for clinical applications of polygenic risk prediction.23,47 The current reality is, however, that most large-scale GWAS datasets are available in the form of summary statistics only. Nonetheless, data on a limited number of cases are frequently available from epidemiological cohorts such as UK Biobank or from public repositories with a secured access such as dbGaP. This motivated us to develop a method that is primarily based on summary statistics but also benefits from smaller training data at the raw genotype resolution. Although we heavily rely on the training data to construct a prediction model, the requirement for out-of-sample training data is not unique for our method. Widely used thresholding-based polygenic scores and Bayesian parametric methods also need genotype-level data to optimize their model parameters.18,48 Also, our method assumes—similar to other methods—that all datasets come from a homogeneous population. It has been shown that polygenic risk models are not transferrable between populations due to differences in allele frequencies and patterns of linkage disequilibrium,49 which is a problem that should be addressed by future work in this field.
Human phenotypes vary in the degree of polygenicity,50 in the fraction of heritability attributable to low-frequency variants33 and in other aspects of allelic architecture.45,51 The optimality of a Bayesian risk predictor is not guaranteed when the true underlying genetic architecture deviates from the assumed prior. In particular, recent studies have revealed complex dependencies of heritability on minor allele frequency (MAF) and local genomic features such as regulatory landscape and intensity of background selections.33,34,45,50,51 Several studies have proposed to extend polygenic scores by incorporating additional complexity into the parametric Bayesian models, yet these methods were not applied to genome-wide sets of markers due to computational challenges.52,53 Recently, there has been a growing interest in non-parametric or semi-parametric approaches, such as those based on modeling of latent variables or kernel-based estimation of prior or marginal distributions; however, thus far they cannot leverage summary statistics or directly account for the linkage disequilibrium structure in the data.24, 25, 26, 27 To address these issues, we developed NPS, a non-parametric method that is agnostic to allelic architecture. In simulations, we show that this approach should be advantageous across a wide range of phenotypes and traits with differing underlying architectures and find that it outperforms existing prediction methods in UK Biobank for four different traits of medical interest. NPS is flexible to incorporate additional complexity of true genetic architecture. Our non-parametric approach has been recently adopted by LDPred-funct, an extension of LDPred to incorporate functional annotations.54 Finally, as demonstrated in the prediction accuracy using two different breast cancer GWAS summary statistics, with increasing size and marker density in case-control association studies across a range of diseases, our NPS method should outperform traditional parametric approaches for identifying individuals at increased risk.
Declaration of Interests
S.K. is a co-founder, chief executive officer, and a board member of Verve Therapeutics.
Acknowledgments
N.O.S. was supported in part by NIH grants K08HL114642, R01HL131961, and UM1HG008853 and by The Foundation for Barnes-Jewish Hospital. S.K. was supported by a Research Scholar award from the Massachusetts General Hospital, the Donovan Family Foundation, NIH R01HL107816, a grant from Fondation Leducq, and an investigator-initiated grant from Merck. S.R.S. was supported by NIH R35GM127131, R01MH101244, and U01HG006500. S.C., M.I., and S.R.S. were supported by a grant from the Altius Institute for Biomedical Sciences. This research has been conducted using the UK Biobank Resource under Application Number 31063.
Published: May 28, 2020
Footnotes
Supplemental Data can be found online at https://doi.org/10.1016/j.ajhg.2020.05.004.
Contributor Information
Nathan O. Stitziel, Email: nstitziel@wustl.edu.
Shamil R. Sunyaev, Email: ssunyaev@rics.bwh.harvard.edu.
Appendix A. Distribution of Projected Genotypes in the Eigenlocus Space
Let be an -dimensional genotype vector of all SNPs in genomic window and individual . We drop the subscript for genomic window for the sake of simplicity when it is clear from the context. The standardized genotype is approximated by the following multivariate normal distribution:
where is a LD matrix of the window. Since the projected genotype is derived by applying eigenlocus projection on by definition (Equation 1), also follows a multivariate normal distribution. Specifically, the distribution of is:
since and . The projected genotypes in the eigenlocus space are decorrelated with the covariance of .
Appendix B. Distribution of Effect Size Estimates in the Eigenlocus Space
In the discovery GWAS, the estimated effect sizes are calculated by linear regression as below:
where is an -dimensional phenotype vector and is the sample size of GWAS cohort. For convenience, we assume that is standardized to the mean of 0 and variance of 1. At this time, we treat genotypes as fixed variables and model the true underlying genetic effects and residuals as random. Since ,
where the residual follows an -dimensional multivariate normal distribution . In an individual window, the genetic effects explain only a small fraction of phenotypic variation, so we can assume that . The distribution of sampling noise in , namely the distribution of given , follows:
since . Since the estimated effect size in the eigenlocus space is obtained by applying on by definition (Equation 1), the distribution of given also follows a multivariate normal distribution:
since and . The sampling noise in is now decorrelated with the covariance of . Hence, the eigenlocus projection removes correlations in both genotypes and sampling noise of effect size estimates.
Appendix C. Interpretation of Eigenvalues
Let be the -dimensional vector of true genetic effect at SNPs in a genomic window. We assume that is symmetric at 0 and independent at each SNP. Then, the distribution of true genetic effects in the eigenlocus space will follow:
where and are the eigenvalue and eigenvector, respectively, projecting to by Equation 1. If we put that eigenvector is and is , the variance of true genetic effects for an eigenlocus is:
Therefore, in general, , is directly proportional to eigenvalue . In particular, when all SNPs have the same variance of per-SNP effect sizes ,
since .
Appendix D. Conditional Mean Effects under Infinitesimal Genetic Architecture in the Eigenlocus Space
Under infinitesimal genetic architecture, the conditional mean effect has been analytically derived by Vilhjalmsson et al.:18
| (Equation S1) |
where is the sample size of GWAS cohort, is the heritability of trait, is the total number of SNPs, and is the LD matrix of full rank. Then, can be factorized into with eigenvalues and eigenvectors . Since
and
we can reformulate Equation S1 as follows:
by the definition of (Equation 1). Hence,
by the definition of . Therefore, for the th eigenlocus projection defined by eigenvalue and eigenvector , the conditional mean effect is given as the following:
Thus, under infinitesimal architecture, the conditional mean effect simplifies to , where is the theoretically optimal shrinkage weight and depends only on eigenvalues as follow:
Web Resources
NPS software, https://github.com/sgchun/nps/
Supplemental Data
References
- 1.Grundy S.M., Stone N.J., Bailey A.L., Beam C., Birtcher K.K., Blumenthal R.S., Braun L.T., de Ferranti S., Faiella-Tommasino J., Forman D.E. 2018 AHA/ACC/AACVPR/AAPA/ABC/ACPM/ADA/AGS/APhA/ASPC/NLA/PCNA Guideline on the Management of Blood Cholesterol: A Report of the American College of Cardiology/American Heart Association Task Force on Clinical Practice Guidelines. Circulation. 2018;139:e1082–e1143. doi: 10.1161/CIR.0000000000000625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Goddard M.E., Hayes B.J. Mapping genes for complex traits in domestic animals and their use in breeding programmes. Nat. Rev. Genet. 2009;10:381–391. doi: 10.1038/nrg2575. [DOI] [PubMed] [Google Scholar]
- 3.Falke K.C., Glander S., He F., Hu J., de Meaux J., Schmitz G. The spectrum of mutations controlling complex traits and the genetics of fitness in plants. Curr. Opin. Genet. Dev. 2013;23:665–671. doi: 10.1016/j.gde.2013.10.006. [DOI] [PubMed] [Google Scholar]
- 4.Meuwissen T.H., Hayes B.J., Goddard M.E. Prediction of total genetic value using genome-wide dense marker maps. Genetics. 2001;157:1819–1829. doi: 10.1093/genetics/157.4.1819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ripatti S., Tikkanen E., Orho-Melander M., Havulinna A.S., Silander K., Sharma A., Guiducci C., Perola M., Jula A., Sinisalo J. A multilocus genetic risk score for coronary heart disease: case-control and prospective cohort analyses. Lancet. 2010;376:1393–1400. doi: 10.1016/S0140-6736(10)61267-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wacholder S., Hartge P., Prentice R., Garcia-Closas M., Feigelson H.S., Diver W.R., Thun M.J., Cox D.G., Hankinson S.E., Kraft P. Performance of common genetic variants in breast-cancer risk models. N. Engl. J. Med. 2010;362:986–993. doi: 10.1056/NEJMoa0907727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wray N.R., Goddard M.E., Visscher P.M. Prediction of individual genetic risk to disease from genome-wide association studies. Genome Res. 2007;17:1520–1528. doi: 10.1101/gr.6665407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yang J., Benyamin B., McEvoy B.P., Gordon S., Henders A.K., Nyholt D.R., Madden P.A., Heath A.C., Martin N.G., Montgomery G.W. Common SNPs explain a large proportion of the heritability for human height. Nat. Genet. 2010;42:565–569. doi: 10.1038/ng.608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Golan D., Rosset S. Effective genetic-risk prediction using mixed models. Am. J. Hum. Genet. 2014;95:383–393. doi: 10.1016/j.ajhg.2014.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Speed D., Balding D.J. MultiBLUP: improved SNP-based prediction for complex traits. Genome Res. 2014;24:1550–1557. doi: 10.1101/gr.169375.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhou X., Carbonetto P., Stephens M. Polygenic modeling with bayesian sparse linear mixed models. PLoS Genet. 2013;9:e1003264. doi: 10.1371/journal.pgen.1003264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chatterjee N., Wheeler B., Sampson J., Hartge P., Chanock S.J., Park J.-H. Projecting the performance of risk prediction based on polygenic analyses of genome-wide association studies. Nat. Genet. 2013;45:400–405, e1–e3. doi: 10.1038/ng.2579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Purcell S.M., Wray N.R., Stone J.L., Visscher P.M., O’Donovan M.C., Sullivan P.F., Sklar P., International Schizophrenia Consortium Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature. 2009;460:748–752. doi: 10.1038/nature08185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Stahl E.A., Wegmann D., Trynka G., Gutierrez-Achury J., Do R., Voight B.F., Kraft P., Chen R., Kallberg H.J., Kurreeman F.A., Diabetes Genetics Replication and Meta-analysis Consortium. Myocardial Infarction Genetics Consortium Bayesian inference analyses of the polygenic architecture of rheumatoid arthritis. Nat. Genet. 2012;44:483–489. doi: 10.1038/ng.2232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Abraham G., Tye-Din J.A., Bhalala O.G., Kowalczyk A., Zobel J., Inouye M. Accurate and robust genomic prediction of celiac disease using statistical learning. PLoS Genet. 2014;10:e1004137. doi: 10.1371/journal.pgen.1004137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Moser G., Lee S.H., Hayes B.J., Goddard M.E., Wray N.R., Visscher P.M. Simultaneous discovery, estimation and prediction analysis of complex traits using a bayesian mixture model. PLoS Genet. 2015;11:e1004969. doi: 10.1371/journal.pgen.1004969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Shi J., Park J.H., Duan J., Berndt S.T., Moy W., Yu K., Song L., Wheeler W., Hua X., Silverman D., MGS (Molecular Genetics of Schizophrenia) GWAS Consortium. GECCO (The Genetics and Epidemiology of Colorectal Cancer Consortium) GAME-ON/TRICL (Transdisciplinary Research in Cancer of the Lung) GWAS Consortium. PRACTICAL (PRostate cancer AssoCiation group To Investigate Cancer Associated aLterations) Consortium. PanScan Consortium. GAME-ON/ELLIPSE Consortium Winner’s Curse Correction and Variable Thresholding Improve Performance of Polygenic Risk Modeling Based on Genome-Wide Association Study Summary-Level Data. PLoS Genet. 2016;12:e1006493. doi: 10.1371/journal.pgen.1006493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Vilhjálmsson B.J., Yang J., Finucane H.K., Gusev A., Lindström S., Ripke S., Genovese G., Loh P.R., Bhatia G., Do R., Schizophrenia Working Group of the Psychiatric Genomics Consortium, Discovery, Biology, and Risk of Inherited Variants in Breast Cancer (DRIVE) study Modeling Linkage Disequilibrium Increases Accuracy of Polygenic Risk Scores. Am. J. Hum. Genet. 2015;97:576–592. doi: 10.1016/j.ajhg.2015.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zhu X., Stephens M. Bayesian large-scale multiple regression with summary statistics from genome-wide association studies. Ann. Appl. Stat. 2017;11:1561–1592. doi: 10.1214/17-aoas1046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lloyd-Jones L.R., Zeng J., Sidorenko J., Yengo L., Moser G., Kemper K.E., Wang H., Zheng Z., Magi R., Esko T. Improved polygenic prediction by Bayesian multiple regression on summary statistics. Nat. Commun. 2019;10:5086. doi: 10.1038/s41467-019-12653-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ge T., Chen C.-Y., Ni Y., Feng Y.A., Smoller J.W. Polygenic prediction via Bayesian regression and continuous shrinkage priors. Nat. Commun. 2019;10:1776. doi: 10.1038/s41467-019-09718-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Goddard M.E., Wray N.R., Verbyla K., Visscher P.M. Estimating Effects and Making Predictions from Genome-Wide Marker Data. Stat. Sci. 2009;24:517–529. [Google Scholar]
- 23.Khera A.V., Chaffin M., Aragam K.G., Haas M.E., Roselli C., Choi S.H., Natarajan P., Lander E.S., Lubitz S.A., Ellinor P.T., Kathiresan S. Genome-wide polygenic scores for common diseases identify individuals with risk equivalent to monogenic mutations. Nat. Genet. 2018;50:1219–1224. doi: 10.1038/s41588-018-0183-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zeng P., Zhou X. Non-parametric genetic prediction of complex traits with latent Dirichlet process regression models. Nat. Commun. 2017;8:456. doi: 10.1038/s41467-017-00470-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Efron B. Empirical bayes estimates for large-scale prediction problems. J. Am. Stat. Assoc. 2009;104:1015–1028. doi: 10.1198/jasa.2009.tm08523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.So H.C., Sham P.C. Improving polygenic risk prediction from summary statistics by an empirical Bayes approach. Sci. Rep. 2017;7:41262. doi: 10.1038/srep41262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gianola D., Fernando R.L., Stella A. Genomic-assisted prediction of genetic value with semiparametric procedures. Genetics. 2006;173:1761–1776. doi: 10.1534/genetics.105.049510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mak T.S.H., Porsch R.M., Choi S.W., Zhou X., Sham P.C. Polygenic scores via penalized regression on summary statistics. Genet. Epidemiol. 2017;41:469–480. doi: 10.1002/gepi.22050. [DOI] [PubMed] [Google Scholar]
- 29.Inouye M., Abraham G., Nelson C.P., Wood A.M., Sweeting M.J., Dudbridge F., Lai F.Y., Kaptoge S., Brozynska M., Wang T., UK Biobank CardioMetabolic Consortium CHD Working Group Genomic Risk Prediction of Coronary Artery Disease in 480,000 Adults: Implications for Primary Prevention. J. Am. Coll. Cardiol. 2018;72:1883–1893. doi: 10.1016/j.jacc.2018.07.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wray N.R., Yang J., Goddard M.E., Visscher P.M. The genetic interpretation of area under the ROC curve in genomic profiling. PLoS Genet. 2010;6:e1000864. doi: 10.1371/journal.pgen.1000864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Dudbridge F. Power and predictive accuracy of polygenic risk scores. PLoS Genet. 2013;9:e1003348. doi: 10.1371/journal.pgen.1003348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cai T.T., Zhang C.H., Zhou H.H. Optimal rates of convergence for covariance matrix estimation. Ann. Stat. 2010;38:2118–2144. [Google Scholar]
- 33.Speed D., Cai N., Johnson M.R., Nejentsev S., Balding D.J., UCLEB Consortium Reevaluation of SNP heritability in complex human traits. Nat. Genet. 2017;49:986–992. doi: 10.1038/ng.3865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Gusev A., Lee S.H., Trynka G., Finucane H., Vilhjálmsson B.J., Xu H., Zang C., Ripke S., Bulik-Sullivan B., Stahl E., Schizophrenia Working Group of the Psychiatric Genomics Consortium. SWE-SCZ Consortium. Schizophrenia Working Group of the Psychiatric Genomics Consortium. SWE-SCZ Consortium Partitioning heritability of regulatory and cell-type-specific variants across 11 common diseases. Am. J. Hum. Genet. 2014;95:535–552. doi: 10.1016/j.ajhg.2014.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Yang J., Wray N.R., Visscher P.M. Comparing apples and oranges: equating the power of case-control and quantitative trait association studies. Genet. Epidemiol. 2010;34:254–257. doi: 10.1002/gepi.20456. [DOI] [PubMed] [Google Scholar]
- 36.Michailidou K., Beesley J., Lindstrom S., Canisius S., Dennis J., Lush M.J., Maranian M.J., Bolla M.K., Wang Q., Shah M., BOCS. kConFab Investigators. AOCS Group. NBCS. GENICA Network Genome-wide association analysis of more than 120,000 individuals identifies 15 new susceptibility loci for breast cancer. Nat. Genet. 2015;47:373–380. doi: 10.1038/ng.3242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Michailidou K., Lindström S., Dennis J., Beesley J., Hui S., Kar S., Lemaçon A., Soucy P., Glubb D., Rostamianfar A., NBCS Collaborators. ABCTB Investigators. ConFab/AOCS Investigators Association analysis identifies 65 new breast cancer risk loci. Nature. 2017;551:92–94. doi: 10.1038/nature24284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Liu J.Z., van Sommeren S., Huang H., Ng S.C., Alberts R., Takahashi A., Ripke S., Lee J.C., Jostins L., Shah T., International Multiple Sclerosis Genetics Consortium. International IBD Genetics Consortium Association analyses identify 38 susceptibility loci for inflammatory bowel disease and highlight shared genetic risk across populations. Nat. Genet. 2015;47:979–986. doi: 10.1038/ng.3359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Scott R.A., Scott L.J., Mägi R., Marullo L., Gaulton K.J., Kaakinen M., Pervjakova N., Pers T.H., Johnson A.D., Eicher J.D., DIAbetes Genetics Replication And Meta-analysis (DIAGRAM) Consortium An Expanded Genome-Wide Association Study of Type 2 Diabetes in Europeans. Diabetes. 2017;66:2888–2902. doi: 10.2337/db16-1253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Nelson C.P., Goel A., Butterworth A.S., Kanoni S., Webb T.R., Marouli E., Zeng L., Ntalla I., Lai F.Y., Hopewell J.C., EPIC-CVD Consortium. CARDIoGRAMplusC4D. UK Biobank CardioMetabolic Consortium CHD working group Association analyses based on false discovery rate implicate new loci for coronary artery disease. Nat. Genet. 2017;49:1385–1391. doi: 10.1038/ng.3913. [DOI] [PubMed] [Google Scholar]
- 41.Thomas N.J., Jones S.E., Weedon M.N., Shields B.M., Oram R.A., Hattersley A.T. Frequency and phenotype of type 1 diabetes in the first six decades of life: a cross-sectional, genetically stratified survival analysis from UK Biobank. Lancet Diabetes Endocrinol. 2018;6:122–129. doi: 10.1016/S2213-8587(17)30362-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Karlson E.W., Boutin N.T., Hoffnagle A.G., Allen N.L. Building the Partners HealthCare Biobank at Partners Personalized Medicine: Informed Consent, Return of Research Results, Recruitment Lessons and Operational Considerations. J. Pers. Med. 2016;6:2. doi: 10.3390/jpm6010002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Gainer V.S., Cagan A., Castro V.M., Duey S., Ghosh B., Goodson A.P., Goryachev S., Metta R., Wang T.D., Wattanasin N., Murphy S.N. The Biobank Portal for Partners Personalized Medicine: A Query Tool for Working with Consented Biobank Samples, Genotypes, and Phenotypes Using i2b2. J. Pers. Med. 2016;6:6. doi: 10.3390/jpm6010011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Euesden J., Lewis C.M., O’Reilly P.F. PRSice: Polygenic Risk Score software. Bioinformatics. 2015;31:1466–1468. doi: 10.1093/bioinformatics/btu848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zeng J., de Vlaming R., Wu Y., Robinson M.R., Lloyd-Jones L.R., Yengo L., Yap C.X., Xue A., Sidorenko J., McRae A.F. Signatures of negative selection in the genetic architecture of human complex traits. Nat. Genet. 2018;50:746–753. doi: 10.1038/s41588-018-0101-4. [DOI] [PubMed] [Google Scholar]
- 46.Bycroft C., Freeman C., Petkova D., Band G., Elliott L.T., Sharp K., Motyer A., Vukcevic D., Delaneau O., O’Connell J. The UK Biobank resource with deep phenotyping and genomic data. Nature. 2018;562:203–209. doi: 10.1038/s41586-018-0579-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Riglin L., Collishaw S., Richards A., Thapar A.K., Maughan B., O’Donovan M.C., Thapar A. Schizophrenia risk alleles and neurodevelopmental outcomes in childhood: a population-based cohort study. Lancet Psychiatry. 2017;4:57–62. doi: 10.1016/S2215-0366(16)30406-0. [DOI] [PubMed] [Google Scholar]
- 48.Wray N.R., Yang J., Hayes B.J., Price A.L., Goddard M.E., Visscher P.M. Pitfalls of predicting complex traits from SNPs. Nat. Rev. Genet. 2013;14:507–515. doi: 10.1038/nrg3457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Martin A.R., Gignoux C.R., Walters R.K., Wojcik G.L., Neale B.M., Gravel S., Daly M.J., Bustamante C.D., Kenny E.E. Human Demographic History Impacts Genetic Risk Prediction across Diverse Populations. Am. J. Hum. Genet. 2017;100:635–649. doi: 10.1016/j.ajhg.2017.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Boyle E.A., Li Y.I., Pritchard J.K. An Expanded View of Complex Traits: From Polygenic to Omnigenic. Cell. 2017;169:1177–1186. doi: 10.1016/j.cell.2017.05.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Gazal S., Finucane H.K., Furlotte N.A., Loh P.R., Palamara P.F., Liu X., Schoech A., Bulik-Sullivan B., Neale B.M., Gusev A., Price A.L. Linkage disequilibrium-dependent architecture of human complex traits shows action of negative selection. Nat. Genet. 2017;49:1421–1427. doi: 10.1038/ng.3954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Hu Y., Lu Q., Powles R., Yao X., Yang C., Fang F., Xu X., Zhao H. Leveraging functional annotations in genetic risk prediction for human complex diseases. PLoS Comput. Biol. 2017;13:e1005589. doi: 10.1371/journal.pcbi.1005589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Hu Y., Lu Q., Liu W., Zhang Y., Li M., Zhao H. Joint modeling of genetically correlated diseases and functional annotations increases accuracy of polygenic risk prediction. PLoS Genet. 2017;13:e1006836. doi: 10.1371/journal.pgen.1006836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Marquez-Luna C., Gazal S., Loh P.-R., Furlotte N., Auton A., Price A.L., Márquez-Luna C., Gazal S., Loh P.-R., Kim S.S. Modeling functional enrichment improves polygenic prediction accuracy in UK Biobank and 23andMe data sets. bioRxiv. 2019 doi: 10.1101/375337. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.