Significance
Variation is rampant throughout human genomes: some of it affects disease risk, and most does not; to separate the two requires a plethora of hypothesis tests. This challenge of multiple testing—limiting false positives while maximizing power—arises in many “omics” studies and sciences. One approach is to control the false discovery rate (FDR), and a recent selective inference method for controlling FDR, adaptive P-value thresholding (AdaPT), facilitates incorporation of auxiliary information (covariates) related to each hypothesis test. How AdaPT performs on data is an open question. We apply AdaPT to results from genomic association studies and include many covariates. This adaptive search discovers a more complex and interpretable model with far greater power than classic multiple testing procedures.
Keywords: multiple hypothesis testing, false discovery rate, GWAS, eQTL, neuropsychiatric disorders
Abstract
To correct for a large number of hypothesis tests, most researchers rely on simple multiple testing corrections. Yet, new methodologies of selective inference could potentially improve power while retaining statistical guarantees, especially those that enable exploration of test statistics using auxiliary information (covariates) to weight hypothesis tests for association. We explore one such method, adaptive P-value thresholding (AdaPT), in the framework of genome-wide association studies (GWAS) and gene expression/coexpression studies, with particular emphasis on schizophrenia (SCZ). Selected SCZ GWAS association P values play the role of the primary data for AdaPT; single-nucleotide polymorphisms (SNPs) are selected because they are gene expression quantitative trait loci (eQTLs). This natural pairing of SNPs and genes allow us to map the following covariate values to these pairs: GWAS statistics from genetically correlated bipolar disorder, the effect size of SNP genotypes on gene expression, and gene–gene coexpression, captured by subnetwork (module) membership. In all, 24 covariates per SNP/gene pair were included in the AdaPT analysis using flexible gradient boosted trees. We demonstrate a substantial increase in power to detect SCZ associations using gene expression information from the developing human prefrontal cortex. We interpret these results in light of recent theories about the polygenic nature of SCZ. Importantly, our entire process for identifying enrichment and creating features with independent complementary data sources can be implemented in many different high-throughput settings to ultimately improve power.
Large-scale experiments, such as scanning the human genome for variation affecting a phenotype, typically result in a plethora of hypothesis tests. To overcome the multiple testing challenge, one needs corrections to limit false positives while maximizing power. Introduced in ref. 1, false discovery rate (FDR) control has become a popular approach to improve power for detecting weak effects by limiting the expected false discovery proportion (FDP) instead of the more classic family-wise error rate. The Benjamini–Hochberg (BH) procedure was the first method to control FDR at target level using a step-up procedure that is adaptive to the set of P values for the hypotheses of interest (1). Other methods for FDR control have led to improvements in power over BH by incorporating prior information, such as by the use of P-value weights (2). In the “omics” world—genomics, epigenomics, proteomics, and so on—the challenge of multiple testing is burgeoning, in part because our ability to characterize omics features grows continually and in part because of the realization that multiple omics are required for describing phenotypic variation. One might imagine merging complementary omics data and tests using a priori hypothesis weights to improve power; however, until recently, it was not clear how to choose these weights in a data-driven manner.
Recent methodologies have been proposed to account for covariates or auxiliary information while maintaining FDR control (3–7). We implement a selective inference approach, called adaptive P-value thresholding [AdaPT (8)], to explore prior auxiliary information while maintaining guaranteed finite-sample FDR control. A recent review compared the performance of AdaPT with other covariate-informed methods for FDR control with off-the-shelf one-dimensional and two-dimensional covariate examples (9). One of the weaknesses they ascribe to AdaPT is the unintuitive modeling framework for incorporating covariates; however, AdaPT is not a specific algorithm that one can simply apply to a dataset but rather, a metaalgorithm for marrying machine learning methods to multiple testing problems without compromising FDR control. We fully embrace AdaPT’s flexibility via gradient boosted trees in a much richer, high-dimensional setting. Our boosting implementation of AdaPT easily scales with more covariates, enabling practitioners to capture interactions and nonlinear effects from the rich resources of prior information available.
In this manuscript, we demonstrate our gradient boosted trees implementation of AdaPT on results from genome-wide association studies (GWAS), incorporating covariates constructed from independent GWAS and gene expression studies. Specifically, we apply AdaPT to GWAS for detecting single-nucleotide polymorphisms (SNPs) associated with schizophrenia (SCZ) using bipolar disorder (BD) GWAS results from an independent dataset as a covariate. Additionally, we incorporate results from the recent BrainVar study to identify a set of expression single-nucleotide polymorphisms (eSNPs) based on 176 neurotypical brains, sampled from pre- and postnatal tissue from the human dorsolateral prefrontal cortex (10). Along with the genetically correlated BD z statistics, we create additional features from this complementary data source by summarizing the associated developmental gene expression quantitative trait loci (eQTL) slopes and membership in gene coexpression networks. We demonstrate that this process of identifying an enriched set of eSNPs and applying AdaPT with covariates summarizing gene expression from the developing human prefrontal cortex yield substantial improvement in power with each additional piece of information from the BrainVar study. Furthermore, we validate the replication of our results using more recent, independent SCZ studies.
This study had two goals: to explore the use of AdaPT in a realistic high-dimensional multiomics setting and to determine what can be learned about the neurobiology of SCZ by this exploration. Our results revealed the power of incorporating auxiliary information with flexible gradient boosted trees. While each covariate independently provided at best a modest increase in power, our adaptive search discovered a more complex model with far greater power. These discoveries also led to increasing support for the polygenic basis of SCZ, complementing recent findings and suggesting that there are many physiological avenues to its underlying neurobiology. We emphasize that the process and analysis undertaken with this implementation of AdaPT can be extended to a variety of omics and other settings to utilize the rich contextual information that is often ignored by standard multiple testing corrections. We highlight this feature by analyzing two other sets of GWAS studies, type 2 diabetes (T2D) and body mass index (BMI), using results from these analyses to interpret findings from SCZ.
Results
Methodology Overview.
AdaPT is an iterative search procedure, introduced in ref. 8, for determining a set of discoveries/rejections, , with guaranteed finite-sample FDR control at target level under conditions outlined below. We apply AdaPT to the collection of P values and auxiliary information, , testing hypothesis regarding SNP i’s association with the phenotype of interest (e.g., SCZ). The covariates from some feature space, , capture information collected independently of but potentially related to whether or not the null hypothesis for is true and the effect size under the alternative. AdaPT provides a flexible framework to incrementally learn these relationships, potentially increasing the power of the testing procedure, while maintaining valid FDR control.
For each step in the AdaPT search, we first determine the rejection set , where is the rejection threshold at step that is adaptive to the covariates . This provides us with both the number of discoveries/rejections as well as a pseudoestimate for the number of false discoveries [i.e., number of P values above the “mirror estimator” of ]. These quantities are used to estimate the FDP at the current step ,
| [1] |
If , then the AdaPT search ends, and the set of discoveries is returned. Otherwise, we proceed to update the rejection threshold while satisfying two protocols: 1) the updated threshold must be more stringent , and 2) P values determining and are partially masked,
| [2] |
Under these protocols, the rejection threshold can be updated using , and . The flexibility in how this update takes place is one of AdaPT’s key strengths and allows it to easily incorporate other approaches from the multiple testing literature, such as a conditional version of the two-groups model (11) with estimates for the probability of being nonnull, , and the effect size under the alternative, .
The algorithm proceeds by sequentially updating the threshold to discard the most likely null element in the current rejection region, as measured by the conditional local false discovery rate (fdr): that is, is removed from . With the threshold updated, the AdaPT search repeats by estimating FDP and updating the rejection threshold until the target FDR level is reached: or .
This procedure guarantees finite-sample FDR control under independence of the null P values and as long as the null distribution of P values is mirror conservative (i.e., the large “mirror” counterparts are at least as likely as the small P values ). To address the assumption of independence, we select a subset of weakly correlated SNPs detailed in Data and additionally provide simulations in SI Appendix showing that AdaPT appears to maintain FDR control in relevant positive dependence settings. However, one practical limitation we encounter with the FDP estimate in Eq. 1 is observing P values exactly equal to one. While this can understandably occur with publicly available GWAS summary statistics, P values equal to one will always contribute to the estimated number of false discoveries . This nuance can lead to a failure of obtaining discoveries at a desired target , such as the reported AdaPT results by ref. 9 for multiple case studies. However, we demonstrate in SI Appendix an adjustment to the P values for T2D and BMI GWAS applications that alleviates this problem, although future work should explore modifications to the FDP estimator itself.
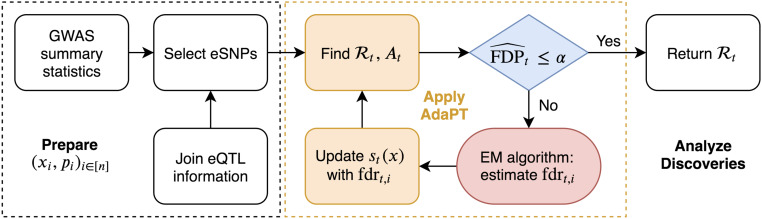
The modeling step of AdaPT estimates conditional local fdr with an expectation–maximization (EM) algorithm. In this context, we use gradient boosted trees, which construct a flexible predictive function as a weighted sum of many simple trees, fit using a gradient descent procedure that minimizes a specified objective function. The two objective functions considered correspond to estimating the probability of a test being nonnull and the distribution of the effect size for nonnull tests. The advantage of this approach to function fitting is that it is invariant to monotonic variable transformations, automatically incorporates important variable interactions, and is able to handle a large number of covariates without degrading significantly in performance due to the high dimensionality. In contrast, less effective methods might fail to capture useful information because the covariates are poorly transformed for a linear model, because the important information is only revealed through a combination of covariates, or because the important signal is simply swamped by the number of possible predictors to search through. Our choice of method gives the flexibility to include many potentially useful covariates without being overly concerned about the functional form with which they enter or their marginal utility. In our implementation, we employ the XGBoost library (12) to capitalize on its computational advantages. Fig. 1 displays the full pipeline of our implementation of AdaPT to GWAS summary statistics for SNPs using eQTL to select the SNPs under investigation.
Fig. 1.
Summary of AdaPT GWAS implementation for selected set of SNPs. SI Appendix, Fig. S1 has a summary of the AdaPT EM algorithm.
Data.
Our investigation includes AdaPT analyses of published GWAS P values, , for BMI (13), T2D (14), and SCZ (15), but we focus our presentation on SCZ results. SCZ is a highly heritable, severe neuropsychiatric disorder. It is most strongly correlated, genetically, with another severe disorder, BD (16, 17). Because of this genetic correlation, reported z statistics from BD GWAS, , can be used as informative covariates for determining the SCZ rejection threshold. As an application of our AdaPT implementation, we use the GWAS summary statistics reported in ref. 15, specifically 19,779 subjects diagnosed with either SCZ or BD with 19,423 control subjects (data are available from the Psychiatric Genomics Consortium). SCZ and BD subjects were completely independent, and independent controls were bulk matched to the sample sizes of the two case samples. Results from more recent studies in ref. 18 are used for replication analysis of our results (combined 53,555 SCZ and BD cases with 54,065 controls). However, the 2014-only studies from ref. 15 are a subset of the all-2018 studies from ref. 18. Although we do not have access to the raw genotype data, we use the fact that both papers report inverse variance-weighted fixed effects meta-analysis results (19). We then separate the summary statistics for the 2018-only studies exclusive to ref. 18, thus independent of the 2014-only studies, and create an appropriate holdout for replication analysis.
After matching alleles from both 2014-only and all-2018 studies and limiting SNPs to those with imputation score for both BD and SCZ in 2014-only (15), we obtained 1,109,226 SNPs. Rather than test all SNPs, we chose to investigate a selected subset of SNPs, eSNPs, whose genotypes are correlated with gene expression; this additional filtering step captures a set of SNPs that are more likely to be functional and not highly correlated (20). These eSNPs were identified from two sources. First, we evaluated the BrainVar study of dorsolateral prefrontal cortex samples across a developmental span (10). BrainVar included cortical tissue from 176 individuals falling into two developmental periods: prenatal, 112 individuals; and postnatal, 60 individuals. We identified = 25,076 eSNPs as any eQTL SNP–gene pairs provided by ref. 10 meeting BH for at least one of the three sample sets (prenatal, postnatal, and complete = all). These eSNPs were used for the SCZ analysis, which is a neurodevelopmental disorder, and thus, a developmental cohort seemed most appropriate for our analyses.
The second source was the Genotype-Tissue Expression (GTEx) V7 project dataset (21) with adult samples from 53 tissues. As the first winnowing step, we identified the set of GTEx eQTLs for any of the available tissues at target FDR level . Rather than use all GTEx eQTLs, however, we selected eQTL SNP–gene whose genotypes are most predictive of expression for each gene. The GTEx eSNPs were used for analysis of T2D and BMI, both of which typically onset in adults (details are in SI Appendix).
For each eSNP , we created a vector of covariates to incorporate auxiliary information collected independently of , including P values from GWAS studies of related phenotypes, and relationships inferred from gene expression studies. First, we utilize the mapping of eSNPs to genes derived from eQTLs assessed in a relevant tissue type . Although the majority of observed eSNPs have one unique cis-eQTL gene pairing, 14% of SNPs in BrainVar were eQTL for multiple genes. Let denote the set of genes whose expression is associated with eSNP and summarize the level of expression as the average absolute eQTL slope for variants in to obtain . Additionally, we account for gene coexpression networks as covariates using the modules reported in the BrainVar study, which were generated using weighted gene coexpression network analysis [WGCNA (22)]. For each of the WGCNA modules, we create an indicator variable denoting whether or not eSNP has any associated cis-eQTL genes in module .
For the eSNPs, we calculate where to capture the eSNP’s overall expression association across different epochs of the developmental span. Additionally, we use the 20 WGCNA modules (including unassigned gray) reported in ref. 10 to create indicator variables for . This culminates in a vector of 24 covariates . Although we use WGCNA modules to make use of the results from the BrainVar study, future applications could explore other approaches to account for gene set and pathway analysis (23).
AdaPT Discoveries.
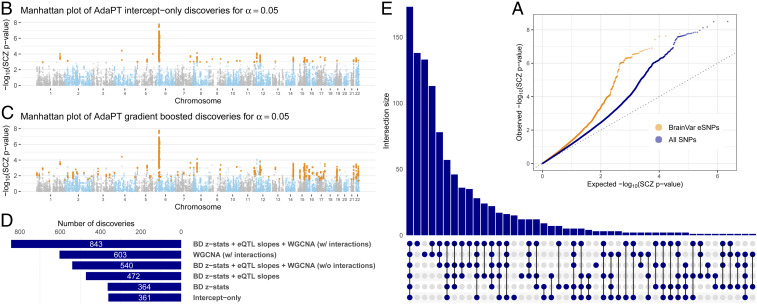
As noted elsewhere (24), eSNPs are more likely to be associated with a GWAS phenotype than are randomly chosen SNPs. This is true for the eSNP from BrainVar too, when evaluated in light of the SCZ GWAS P values (Fig. 2A). To evaluate the performance of the AdaPT search algorithm using the eSNP data, we compare the fitted full covariate model with results from its intercept-only version (Fig. 2B vs. Fig. 2C). As expected, the intercept-only analysis performs better than BH, with all 269 BH discoveries contained within the intercept-only discoveries because it incorporates an estimate for the proportion of nonnull tests. The full model rejects of the = 25,076 BrainVar eSNPs vs. 361 discoveries for the intercept-only model. For insight into AdaPT’s performance, we sequentially include 1) only the BD z statistics, then 2) eQTL slope summaries, and then 3) the WGCNA indicators (Fig. 2 D and E).
Fig. 2.
AdaPT results from analysis of SCZ P values. (A) Comparison of quantile–quantile plots revealing SCZ enrichment for both BrainVar eSNPs compared with the full set of SNPs from 2014 studies. (B and C) Manhattan plots of SCZ AdaPT discoveries (in orange) using (B) intercept-only model compared with (C) covariate-informed model at target . (D and E) Comparison of the number of discoveries at target for AdaPT with (D) varying levels of covariates and (E) their resulting discovery set intersections.
The largest number of discoveries occurs when all 24 covariates are fitted (Fig. 2D), highlighting that all three types of information together are required. Notably, only 540 associations are discovered using all covariates without interactions, fewer discoveries than only using module-based covariates with interactions. This highlights the improvement in AdaPT’s performance from modeling the interactions between covariates via gradient boosted trees. As might be expected from their counts of discoveries (Fig. 2D), the greatest overlap with the full model occurs by fitting all covariates, but without interactions, or by fitting the module-based covariates (Fig. 2E).
Additional discoveries are of little interest if they consist primarily of SNPs in linkage disequilibrium (LD) with SNPs already discovered using a simpler model, such as the logit model typically used for SCZ GWAS. For context, however, of the initial 25,076 eSNPs we analyzed, only 4 have P values , the standard GWAS threshold, and all 4 occur in the discovery sets for the AdaPT full and intercept-only models. To investigate how the AdaPT procedure performs using completely independent eSNPs, we identified the “lead” SNP in each LD block using the approach delineated in ref. 24 and compared model performance for this set of approximately independent SNPs (SI Appendix). This thinning results in roughly 3,960 eSNPs to be analyzed by the different models (Fig. 2). (Ties in q values add or subtract a few SNPs to this 3,960 count, depending on the model analyzed.) When AdaPT is fit to these independent SNPs, we obtain analogous improvements in performance compared with the larger set of SNPs (SI Appendix, Figs. S2 and S3): the full AdaPT model discovers 95 independent loci, while the intercept-only model discovers only 42 loci. Likewise, the full model is the best model, and interactions remain important. Finally, no location in the genome exerts unusual influence on the results, which is also the case for the analyses of 25,076 eSNPs.
As described previously, we performed similar analyses of T2D and BMI GWAS P values. All results for these analyses, as well as more details regarding analyses of SCZ, are available in Dataset S1 and SI Appendix.
Variable Importance and Relationships.
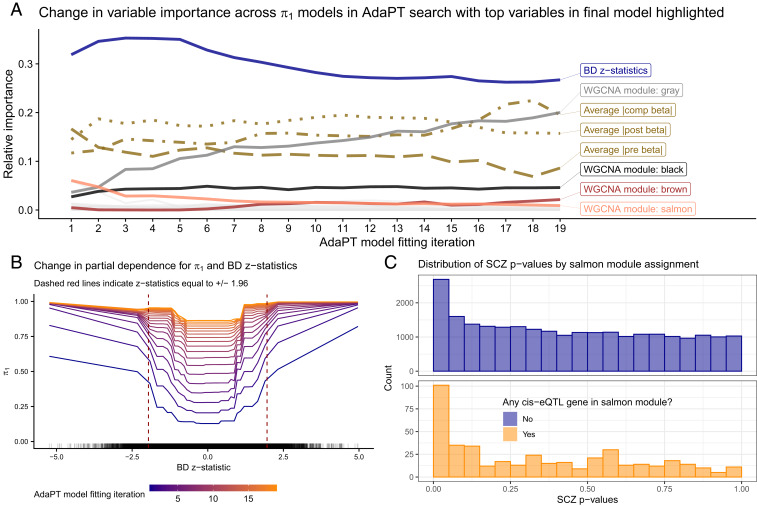
We examine the variable importance and partial dependence plots from the gradient boosted models to provide insight into the relationships between each of the covariates and SCZ associations. Fig. 3A displays the change in variable importance for the probability of being nonnull () at each model fitting iteration, with the top variables in the final model highlighted. We see that the BD z statistics are estimated as the most important for each model, but they decrease in importance in the final steps. In contrast, the unassigned gray module increases in importance throughout the AdaPT search. This change in variable importance across the AdaPT search highlights that the difference in the discriminatory power of covariates depends on the remaining masked P values.
Fig. 3.
Variable importance and relationships. (A) Change in variable importance for AdaPT estimated probability of nonnull model across the search, with top variables in final model highlighted. (B) Change in partial dependence for estimated probability of being nonnull and BD z statistics across models in AdaPT search. (C) SCZ enrichment of eSNPs based on salmon WGCNA module membership, the most important WGCNA module indicator in the first model fitting step.
Fig. 3B displays the partial dependence plot (25) at each AdaPT model fitting iteration for the estimated marginal relationship between the BD z statistics and the probability of being nonnull, evaluated at the percentiles. Because the goal of the AdaPT two-groups model (detailed in Methods) is to order the remaining masked P values, the model predicts values relative to the remaining masked P values: as the rejection threshold becomes more stringent, the masked P values are more likely nonnull (assuming there is signal). However, for each model iteration, Fig. 3B reveals an increasing likelihood for nonnull results as the BD z statistics grow in magnitude from zero, as well as a diminished impact of BD z statistics on the estimated for later model iterations. Fig. 3C displays the clear enrichment for eSNPs with cis-eQTL genes that are members of the salmon WGCNA module reported by ref. 10, which was the most important WGCNA module indicator in the first model fitting step. This differs from the unassigned gray module variable: it is predictive of SNPs that are classified as null, rather than associated with the phenotype. Taken together, Fig. 3 emphasizes the use of all covariates across different steps of the AdaPT search. SI Appendix has more analyses highlighting the advantages of accounting for interactions between covariates.
Replication in Independent Studies.
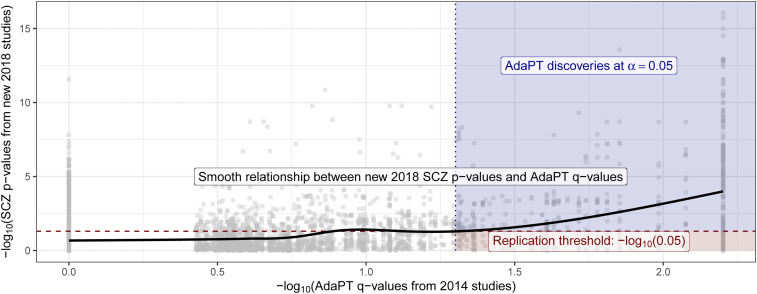
Next, we examine the replicability of the 2014-only SCZ AdaPT results using independent 2018-only studies. We find (Fig. 4) an increasing smoothing spline relationship between these sets of values, with noticeably increasing evidence indicated by the 2018-only P values for the set of AdaPT discoveries at . Additionally, of the 843 discoveries from the 2014-only studies at target FDR level , approximately 55.2% (465 eSNPs) were nominal replications for 2018 only (P values ), comparable with the replication fraction expected on the basis of power (SI Appendix has supporting simulations).
Fig. 4.
Relationship between the 2018-only P values and the resulting 2014-only q values from the AdaPT search. Black line displays smoothed relationship between SCZ P values from 2018-only studies and AdaPT q values from 2014-only studies. Blue region indicates the 2014-only AdaPT discoveries at target FDR level that are nominal replications (2018-only P values 0.05), while red region denotes 2014-only discoveries that failed to replicate (2018-only P values 0.05).
Gene Ontology Comparison.
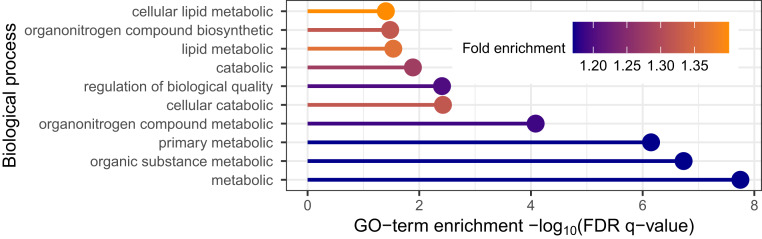
Using the SNP discoveries, which span the genome, we next sought biological insights. We applied gene ontology enrichment analysis (26, 27) to the 136 genes obtained from the eQTL variant–gene pairs associated with the 843 discoveries. This analysis produced no clear signal, yielding only a minor enrichment for biological processes related to peptide antigen assembly. Several explanations are plausible; we explore two: either AdaPT is discovering SNPs of such small effect that the discoveries are not meaningful, or SCZ is a highly complex disorder with a large number of biological processes involved. For comparison, we applied our full pipeline to GWAS summary statistics for T2D (14). This comparison is of interest because T2D is a disease with a well-understood functional basis and this is a well-powered study (74,124 T2D cases and 824,006 controls). We restricted our analysis to 176,246 eSNPs based on eQTLs obtained using GTEx data. Next, we created eQTL-based covariates using pancreas, liver, and adipose tissue samples (SI Appendix has more details). After creating a vector of covariates from GTEx, AdaPT returned 14,920 eSNPs at , resulting in 5,970 associated genes. Applying gene ontology (GO) enrichment analysis to this gene list, we discovered enrichment for biological processes related to lipid metabolic process (Fig. 5), consistent with previous literature (28). These results provide some reassurance that the lack of specificity in the SCZ results can be attributed to the complex etiology of SCZ. For comparison with the well-powered BMI GWAS (339,224 subjects), we found a lack of gene ontology enrichment in our gene discoveries (SI Appendix).
Fig. 5.
T2D gene ontology (GO) enrichment analysis results for top 10 biological processes based on positive fold enrichment.
Pipeline Results for All-2018 Studies.
In addition to applying the pipeline to SCZ P values from the 2014-only studies in ref. 15, we also modeled P values from all-2018 studies. The latter yields far more discoveries due to smaller SEs from increased study sizes, even though the covariates were the same: for , we find 2,228 discoveries at target FDR level when the pipeline was applied to the P values for the most up-to-date set of studies vs. 843 for the 2014-only studies. Notably, the intercept-only version of AdaPT returned 1,865 discoveries at , meaning the covariates contributed to 19% increase in discovery rate for all-2018 studies vs. the 134% increase (361 to 843 eSNPs) from using the covariates for the 2014-only studies. This reinforces the value of using auxiliary information in studies with lower power. Complementary to this observation, AdaPT applied to BMI GWAS with covariate informed models did not yield more discoveries than the intercept-only version (details presented in SI Appendix). Simply accounting for more auxiliary information does not guarantee an improvement in power, and the advantages thereof diminish as power increases, as witnessed by results for all-2018 studies for SCZ and the large-scale BMI GWAS. Additionally, the larger number of discoveries for the SCZ all-2018 studies, 2,228, maps onto 382 genes. Despite this increase, these genes did not reveal any clear signal from the gene ontology enrichment analysis, comporting with results from the 2014-only results.
Discussion
Our goals in this study were to explore the use of AdaPT for high-dimensional multiomics settings and investigate the neurobiology of SCZ in the process. AdaPT was used to analyze a selected set of GWAS summary statistics for SNPs, together with numerous covariates. Specifically, SNPs were selected if they were documented to affect gene expression; these SNP–gene pairs were dubbed eSNPs. Covariates for these eSNPs included GWAS test statistics from a genetically correlated phenotype, BD, which were mapped to eSNPs through SNP identity, as well as features of gene expression and coexpression networks, which were mapped to eSNPs through genes. By coupling flexible gradient boosted trees with the AdaPT procedure, relationships among eSNP GWAS test statistics and covariates were uncovered, and more SNPs were found to be associated with SCZ, while maintaining guaranteed finite-sample FDR control. The tree-based handling of covariates addresses a perceived weakness of AdaPT, namely the unintuitive modeling framework for incorporating covariates (9). Moreover, it is worth noting that the original approach implemented by ref. 8, a generalized linear model with spline bases, yields similar results (361 discoveries at target ) when applied to the univariate case of only using BD z statistics. This is an even more straightforward implementation for handling covariates without interactions. The pipeline we built should be simple to mimic for a wide variety of omics and other analyses.
The results shed light on the level of complexity underlying the neurobiology of SCZ. If the origins of SCZ arose by perturbations of one or a few pathways, we would expect to converge on those pathways as we accrue more and more genetic associations. On the other hand, if the ways to generate vulnerability to SCZ were myriad—even if there is a single ultimate cause shared across all cases—then we might expect no such convergence, at least with regards to the common variation assessed through GWAS. Gene ontology analysis of associated discovery genes from either the 2014-only or all-2018 studies reveals no enrichment for biological processes for SCZ. There are many possible explanations for these null findings, one of which is simply a lack of power or specificity of our results. However, the result stands in stark contrast to the results for T2D, for which the gene ontology analysis converges nicely on accepted pathways to T2D risk; yet, they comport with those for BMI, which is known to have myriad genetic and environmental origins. Therefore, our results are consistent with myriad pathways to vulnerability for SCZ, although it is impossible to rule out other explanations: for example, the possibility that we understand so little about brain functions that gene ontology analyses lack specificity. In any case, our results are consistent with two recent theories underlying the genetics of SCZ, namely extreme polygenicity (29) and “omnigenic” origins (30).
Although the examples considered in this manuscript pertain to omics data, this process can be adapted for a large variety of settings. We demonstrate in SI Appendix simulations showing that AdaPT appears to maintain FDR control in positive dependence settings emulating LD block structure underlying GWAS results. There is a clear need, however, for future work to explore AdaPT’s properties and computational challenges under various dependence regimes. The growing abundance of contextual information available in omics settings provides ample opportunity to improve power for detecting associations, using a flexible approach such as AdaPT, when addressing the multiple testing challenge.
Methods
Two-Groups Model.
The most critical step in the AdaPT algorithm (8) involves updating the rejection threshold . Following (8), we use a conditional version of the classic two-groups model (3, 11) where the null P values are modeled as uniform [], and we model the nonnull P-value density with a beta distribution density parametrized by , resulting in a conditional density for a beta mixture model, . In this form, we can model the nonnull probability and the effect size for nonnull hypotheses with two separate gradient boosted tree-based models. The XGBoost library (12) provides logistic and gamma regression implementations, which we use for and , respectively.
There are two categories of missing values in these regression problems: is never observed, and at each step of the search, the P values for tests are masked as . An EM algorithm can be used to estimate both and by maximizing the partially observed likelihood. We briefly restate the EM algorithm from ref. 1 and provide details in SI Appendix that reflect the approach taken in the R adaptMT package by the same authors, which differs slightly from ref. 1.
During the E step of the iteration of the EM algorithm, conditional on the partially observed data fixed at step , , we compute both and , where indicates how likely equals for nonnull hypotheses. The explicit calculations of and are available in the supplementary materials of ref. 8.
The M step consists of estimating and with separate gradient boosted trees, using pseudodatasets to handle the partially masked data. In order to fit the model for , we construct the response vector and use weights . Then, we estimate using the first predictions from a classification model using as the response variable with the covariate matrix replicated twice and weights . Similarly, for estimating , we construct a response vector with weights and again take the first predicted values using the duplicated covariate matrix.
We follow the procedure detailed in section 4.3 of ref. 8 to estimate the conditional local fdr for each and then update the rejection threshold to by removing test from .
AdaPT Gradient Boosted Trees with Cross-Validation Steps.
As a flexible approach for modeling the conditional local fdr, we use gradient boosted trees (25) via the open-source XGBoost implementation (12). Gradient boosted trees are an ensemble of many small tree models that jointly contribute to predictions. Let be an individual regression tree; then, the sum-of-trees model can be written as where is the loss function and measures the complexity of each tree such as the maximum depth, regularization, etc. Ref. 12 details the algorithms for fitting the model in an additive manner as well as determining the splits for each tree.
To tune the variety of parameters for gradient boosted trees within AdaPT, such as the number of trees and maximum depth of each tree, we use the cross-validation (CV) approach recommended in ref. 8. If we are considering different options of boosting parameters, then we evaluate each of the choices during the modeling phase of the AdaPT search. At step , we divide the data into folds, preserving the relative proportions of masked and unmasked hypotheses. Then, for each set of boosting parameters and for each fold , 1) apply EM algorithm to estimate and using parameters with data from folds ; 2) compute expected log-likelihood on holdout set using two-groups model parameters from following convergence, and compute total across folds as . Finally, we use the set of parameters in another instance of the EM algorithm to estimate and on all data.
Computational Aspects of AdaPT.
Practical decisions are necessary to implement the AdaPT search. In addition to the covariates and P values , an initial rejection threshold is required to begin the search. Rather than begin the search with a high starting threshold, such as , recommended by ref. 8, we instead begin the AdaPT search with . Our decision to lower the starting threshold is advantageous for multiple reasons. First, intuitively, this starts our search in the regime of interest for target level , whereas we would not expect to detect discoveries with larger P values using this flexible multiple testing correction. Additionally, by lowering the starting threshold, more true information is available to the gradient boosted trees at the start of the AdaPT search. For instance, with the set of BrainVar eSNPs, 21,248 true P values are immediately revealed with as compared with only 2,290 when . Simulations detailed in SI Appendix show that on average our choice for using a lower threshold results in higher power.
The most computationally intensive part of the procedure is updating the rejection threshold via the EM algorithm. Instead of updating the model for estimating at each step of the search, we reestimate every steps as recommended by ref. 8. However, the inclusion of the previously described -fold CV procedure (we use ) for tuning the gradient boosted trees obviously adds computational complexity to the AdaPT search and would be expensive to apply every time the model fitting takes place. Rather, we apply the CV step once at the beginning and then another time halfway through the search based on the similarity of simulation performance with varying number of CV steps in SI Appendix. Additionally, one needs to choose the potential model parameter choices. Technically, unique combinations can be used for both models, and , but for simplicity, we only consider matching settings for both models (i.e., both models have the same number of trees and maximum depth). As a reminder, AdaPT guarantees finite-sample FDR control regardless of potentially overfitting to the data when using the CV procedure. Simulations are provided in SI Appendix showing how extensively increasing the number of trees leads to decreasing power but maintains valid FDR control.
Code Availability.
We provide a modified version of the adaptMT R package to implement the AdaPT CV tuning steps with XGBoost models at https://github.com/ryurko/adaptMT and provide all code used to generate the manuscript’s results at https://github.com/ryurko/AdaPT-GWAS-manuscript-code.
Supplementary Material
Acknowledgments
This work was supported by National Institute of Mental Health Grant R37MH057881, Simons Foundation Grant SFARI SF575097, and NSF Grant DMS 1613202. We are grateful for help from Lambertus Klei regarding datasets and their interpretation.
Footnotes
The authors declare no competing interest.
Data deposition: A modified version of the adaptMT R package to implement the AdaPT CV tuning steps with XGBoost models is available at GitHub (https://github.com/ryurko/adaptMT). All code used to generate the manuscript’s results is also available at GitHub (https://github.com/ryurko/AdaPT-GWAS-manuscript-code).
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1918862117/-/DCSupplemental.
References
- 1.Benjamini Y., Hochberg Y., Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. Roy. Stat. Soc. B 57, 289–300 (1995). [Google Scholar]
- 2.Genovese C. R., Roeder K., Wasserman L., False discovery control with p-value weighting. Biometrika 93, 509–524 (2006). [Google Scholar]
- 3.Scott J. G., Kelly R. C., Smith M. A., Zhou P., Kass R. E., False discovery rate regression: An application to neural synchrony detection in primary visual cortex. J. Am. Stat. Assoc. 110, 459–471 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ignatiadis N., Klaus B., Zaugg J. B., Huber W., Data-driven hypothesis weighting increases detection power in genome-scale multiple testing. Nat. Methods 13, 577–580 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Boca S. M., Leek J. T., A direct approach to estimating false discovery rates conditional on covariates. PeerJ 6, e6035 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Li A., Barber R. F., Multiple testing with the structure-adaptive Benjamini–Hochberg algorithm. J. Roy. Stat. Soc. B 81, 45–74 (2019). [Google Scholar]
- 7.Zhang M. J., Xia F., Zou J., Fast and covariate-adaptive method amplifies detection power in large-scale multiple hypothesis testing. Nat. Commun. 10, 3433 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lei L., Fithian W., Adapt: An interactive procedure for multiple testing with side information. J. Roy. Stat. Soc. B 80, 649–679 (2018). [Google Scholar]
- 9.Korthauer K., et al. , A practical guide to methods controlling false discoveries in computational biology. Genome Biol. 20, 118 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Werling D. M., et al. , Whole-genome and RNA sequencing reveal variation and transcriptomic coordination in the developing human prefrontal cortex. Cell Rep. 31, 107489 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Efron B., Tibshirani R., Storey J. D., Tusher V., Empirical Bayes analysis of a microarray experiment. J. Am. Stat. Assoc. 96, 1151–1160 (2001). [Google Scholar]
- 12.Chen T., Guestrin C., “Xgboost: A scalable tree boosting system” in Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’16 (ACM, New York, NY, 2016), pp. 785–794. [Google Scholar]
- 13.Locke A. E., et al. , Genetic studies of body mass index yield new insights for obesity biology. Nature 518, 197–206 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Mahajan A., et al. , Fine-mapping type 2 diabetes loci to single-variant resolution using high-density imputation and islet-specific epigenome maps. Nat. Genet. 50, 1505–1513 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ruderfer D. M., et al. , Polygenic dissection of diagnosis and clinical dimensions of bipolar disorder and schizophrenia. Mol. Psychiatr. 19, 1017–1024 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lichtenstein P., et al. , Common genetic determinants of schizophrenia and bipolar disorder in Swedish families: A population-based study. Lancet 373, 234–239 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cross-Disorder Group of the Psychiatric Genomics Consortium , Genetic relationship between five psychiatric disorders estimated from genome-wide SNPs. Nat. Genet. 45, 984–994 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ruderfer D. M., et al. , Genomic dissection of bipolar disorder and schizophrenia, including 28 subphenotypes. Cell 173, 1705–1715.e16 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Willer C. J., Li Y., Abecasis G. R, Metal: Fast and efficient meta-analysis of genomewide association scans. Bioinformatics 26, 2190–2191 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nicolae D. L., et al. , Trait-associated SNPs are more likely to be eQTLs: Annotation to enhance discovery from GWAS. PLoS Genet. 6, 1–10 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.GTEx Consortium , The Genotype-Tissue Expression (GTEx) pilot analysis: Multitissue gene regulation in humans. Science 348, 648–660 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zhang B., Horvath S., A general framework for weighted gene co-expression network analysis a general framework for weighted gene co-expression network analysis. Stat. Appl. Genet. Mol. Biol. 4, 08 (2005). [DOI] [PubMed] [Google Scholar]
- 23.Zhu X., Stephens M., Large-scale genome-wide enrichment analyses identify new trait-associated genes and pathways across 31 human phenotypes. Nat. Commun. 9, 1–14 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Schizophrenia Working Group of the Psychiatric Genomics Consortium , Biological insights from 108 schizophrenia-associated genetic loci. Nature 511, 421–427 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Friedman J. H., Greedy function approximation: A gradient boosting machine. Ann. Stat. 29, 1189–1232 (2001). [Google Scholar]
- 26.Ashburner M., et al. , Gene ontology: Tool for the unification of biology. Nat. Genet. 25, 25–29 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.The Gene Ontology Consortium , The gene ontology resource: 20 years and still going strong. Nucleic Acids Res. 47, D330–D338 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cirillo E., et al. , From SNPs to pathways: Biological interpretation of type 2 diabetes (T2DM) genome wide association study (GWAS) results. PloS One 13, 1–19 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.O’Connor L. J., et al. , Extreme polygenicity of complex traits is explained by negative selection. Am. J. Hum. Genet. 105, 456–476 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Boyle E. A., Li Y. I., Pritchard J. K., An expanded view of complex traits: From polygenic to omnigenic. Cell 169, 1177–1186 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.