Changes in firearm mortality following the implementation of state laws regulating firearm access and use

Significance

Many US states have tried to regulate firearm storage and use to reduce the 39,000 firearms-related deaths that occur each year. Looking at three classes of laws that regulate children’s access to firearms, the carrying of a concealed firearm, and the use of a firearm in self-defense, we found that state laws restricting firearm storage and use are associated with a subsequent 11% decrease in the firearms-related death rate. In a hypothetical situation in which there are 39,000 firearms deaths nationally under the permissive combination of these three laws, we expect 4,475 (80% CI, 1,761 to 6,949) more deaths nationally than under the restrictive combination of these laws.

Abstract

Although 39,000 individuals die annually from gunshots in the US, research examining the effects of laws designed to reduce these deaths has sometimes produced inconclusive or contradictory findings. We evaluated the effects on total firearm-related deaths of three classes of gun laws: child access prevention (CAP), right-to-carry (RTC), and stand your ground (SYG) laws. The analyses exploit changes in these state-level policies from 1970 to 2016, using Bayesian methods and a modeling approach that addresses several methodological limitations of prior gun policy evaluations. CAP laws showed the strongest evidence of an association with firearm-related death rate, with a probability of 0.97 that the death rate declined at 6 y after implementation. In contrast, the probability of being associated with an increase in firearm-related deaths was 0.87 for RTC laws and 0.77 for SYG laws. The joint effects of these laws indicate that the restrictive gun policy regime (having a CAP law without an RTC or SYG law) has a 0.98 probability of being associated with a reduction in firearm-related deaths relative to the permissive policy regime. This estimated effect corresponds to an 11% reduction in firearm-related deaths relative to the permissive legal regime. Our findings suggest that a small but meaningful decrease in firearm-related deaths may be associated with the implementation of more restrictive gun policies.

In the United States, more people die of firearm injuries than car crashes, with >39,000 firearm-related deaths recorded in 2017 (1). There is a widespread consensus that firearm regulations should be designed to reduce these deaths but disagreement about which gun laws will have the desired effects (2). For instance, one survey of 35 economists who study gun policy found that two-thirds believed that laws allowing the concealed carry of firearms would reduce murder rates (3), while a separate survey of gun policy experts found the opposite, with the majority believing that placing greater restrictions on concealed-carry permits would reduce gun deaths (4). A recent survey of firearm policy experts found that those who generally favor restrictive firearm regulations estimated that “stand-your-ground” (SYG) laws cause an 5% increase in homicides, while those who generally favored permissive regulations believed that these laws cause a 10% decrease in homicides (2). Similarly, experts favoring restrictive gun policies believed that child access prevention laws (CAP) would decrease firearm suicides by 5%, while experts favoring permissive regulations believed that such laws would have no effect on firearm suicides.

Sharp disagreements about the effects of policy can persist in part because of the often-contradictory scientific evidence supporting claims about the causal effects of specific gun laws. Specifically, while several systematic reviews have found a consistent pattern of evidence regarding laws restricting the purchase of firearms, findings regarding policies designed to regulate the storage and use of firearms have generally been inconsistent (5–11). For example, some studies have concluded that SYG laws decrease violent crime (12), while others claim the opposite effect (13). Studies of right-to-carry (RTC) laws have also shown divergent results, with some studies concluding that these laws reduce violent crime (14) and others concluding that they increase it (15). Similarly, some studies have claimed that CAP laws decrease suicides among children (16), while others claim that those effects are spurious (17, 18). These conflicting conclusions occur even though many of the studies are based on similar or even identical datasets. Several systematic reviews of this literature have concluded that the estimated effects of gun laws and their statistical significance are sensitive to the choice of statistical methods, and have questioned whether the statistical methods used in the published studies are appropriate for these data (7–9, 11).

The different statistical choices made by researchers in this area make different assumptions about the underlying data, and contradictory findings may occur because many of these assumptions are inappropriate for the specific outcomes being modeled. Prior to the present study, we conducted a large-scale simulation study examining hundreds of different methods for modeling the effects of state gun laws on firearm-related deaths to identify the most appropriate statistical methods for analyzing these data (19). In these simulations, we estimated the effects of random, fictious laws on the real firearm death data used as the outcome in the present study. This allowed us to assess the validity of common statistical methods applied to these data, including their type I error rates, when there was no true effect of the fictitious law, as well as bias and statistical power when we introduced true effects. We compared models that varied in ways reflective of models in the existing literature on gun policy effects, including in terms of their model link functions, use of logarithmic transform of the outcome variable, use of population weights, inclusion of autoregressive effects, type of coding used for the law effect, inclusion of state fixed or random effects, inclusion of state-specific linear trends, use of general estimating equations, use of SE adjustments for clustering by state, and distributional assumptions of model error. These simulations identified only a handful of methods that yielded accurate type I error rates when analyzing state-level firearm death rates even when common corrections to SEs were applied, with several widely used methods having an actual type I error rate >50% when tested using a nominal α = 0.05. In addition, several methods yielded estimates that were substantially biased or had especially low statistical power.

Among all the methods we investigated, there emerged a clearly preferred method that was most appropriate for these data. It produced accurate type I error rates, minimal bias, and the highest statistical power. (For a direct comparison of the statistical properties of the various methods of effect estimation, see ref. 19). In addition, the preferred method produced estimates that were highly robust to the exclusion of important covariates, did not suffer from artifacts due to regression to the mean, and analyzes the year-over-year changes in the outcome following implementation rather than comparing the mean level of the outcome over the entire preperiod to that of the postperiod. However, this statistical method has not been used in the literature estimating the effects of state gun laws.

Having identified a more appropriate statistical approach for these time series data, the present study uses this approach to estimate the association of three classes of gun laws with changes in firearms death rates: child access prevention (CAP), right-to-carry (RTC), and stand your ground (SYG) laws. We selected these laws because they are some of the most common state regulations on firearms, have been the most widely studied laws in the existing literature yet show contrary evidence of their effects on gun deaths across studies (8), and belong to the same general class of firearm regulations (i.e., they regulate the legal storage and use of firearms, rather than who may own a firearm or how one may purchase a firearm).

Results

The model provided an excellent fit to the data. The association between the model-predicted rate of firearm deaths in a given state-year (posterior mean of predicted count ÷ population size), and the actual firearm death rate was R² = 0.94. Model predictions for the suicide and homicide subtypes of firearms deaths were similarly good fits to the data (R² = 0.91 and 0.94, respectively). This high degree of model fit reflects the low year-to-year variation in these outcomes within states, which was well captured in an AR1 autoregressive model.

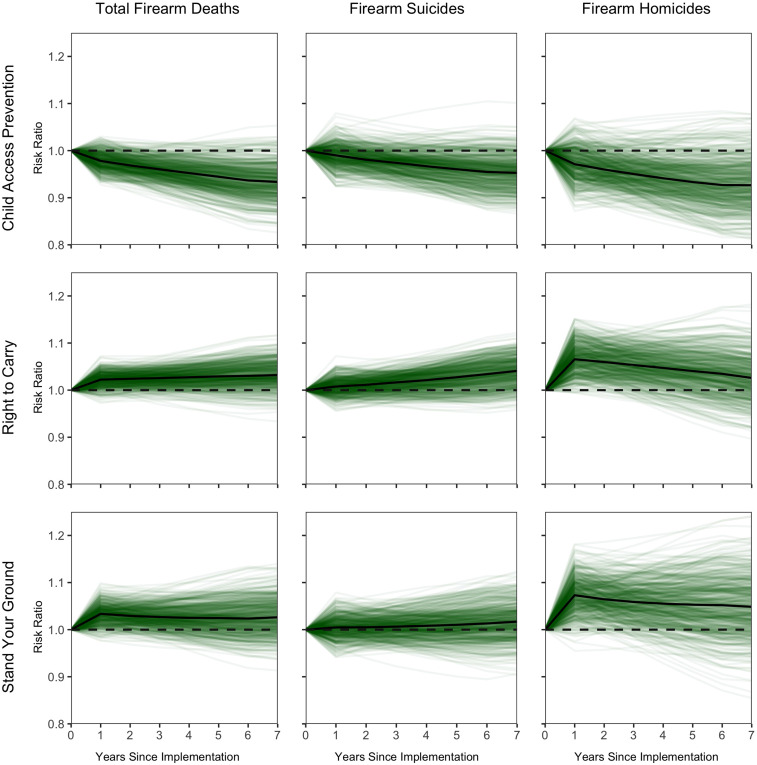
The total association of each law with firearm deaths evaluated at 6 y after implementation is presented in Table 1. The table presents the posterior median of the IRR, along with the 80% credibility interval (CI; indicating the central region containing 80% of the posterior distribution), as well as the posterior probability that each law is associated with a subsequent decrease in deaths. Fig. 1 shows the modeled phase-in of the law effects over 7 y following state implementation.

Table 1.

Effects of CAP, RTC, and SYG laws on change in state firearm death rates in the sixth year after implementation

Outcome/law	Posterior median IRR	IRR, 80% CI lower bound	IRR, 80% CI upper bound	Posterior probability of reduced deaths
Firearm deaths
CAP	0.94	0.89	0.98	0.97
RTC	1.03	1.00	1.07	0.13
SYG	1.03	0.98	1.07	0.23
Restrictive	0.89	0.82	0.95	0.98
Firearm suicides
CAP	0.95	0.91	1.00	0.90
RTC	1.03	1.00	1.07	0.10
SYG	1.01	0.97	1.06	0.33
Restrictive	0.91	0.84	0.98	0.95
Firearm homicides
CAP	0.93	0.86	1.00	0.91
RTC	1.03	0.98	1.09	0.23
SYG	1.05	0.98	1.13	0.18
Restrictive	0.85	0.76	0.96	0.95

The restrictive law refers to the effect of a restrictive combination of all three laws, relative to a permissive combination.

Fig. 1.

Posterior distribution of the effect of CAP, RTC, and SYG laws over time, by type of firearm deaths. Effects are expressed as IRR. The posterior median and 500 samples from the posterior distribution are plotted.

CAP laws mandate legal penalties for storing a handgun in a manner that allows access by a minor, which may require locked storage of firearms and/or ammunition in a large fraction of all households and vehicles. Of the three types of laws investigated, CAP laws showed the strongest evidence of association with subsequent changes in firearm death rates. Given the data, the model, and our priors, we estimate a 0.97 probability that the law is associated with a decline in firearm deaths. The estimated effect size represents a 6% decline (IRR = 0.94) in the expected firearm death rate without the law. This effect size corresponds to 2,536 (80% CI, 783 to 4,324) fewer firearm deaths nationally in 2016 had CAP laws been implemented in all states beginning in 2010 relative to having been implemented in no states. The effect size is approximately the same for firearm homicide and suicide subtypes. In addition, all outcomes showed a generally similar pattern over the 6 y following implementation with approximately one-half of the final effect manifest in the first year of implementation and the other half phasing in over the subsequent 5 y. Sensitivity analyses evaluating the effect of CAP laws on firearm suicides among minors specifically show similar or larger reductions in firearm suicides for that subpopulation (SI Appendix).

RTC laws make it easier for citizens within a state to carry concealed weapons outside of their home. RTC laws showed modest evidence of being associated with subsequent increases in firearm death rates, with a 0.87 probability of an increase in firearm deaths at 6 y after implementation. The estimated effect size represents an increase of 3% (IRR = 1.03) of the expected firearm death rate without the law, which corresponds to 1,157 (80% CI, −157 to 2,438) additional deaths nationally in 2016 had RTC laws been fully implemented in 2010 for all states relative to having been present in no states. The effect sizes in the sixth year after implementation are similar for both firearm homicides and suicides; however, the homicide and suicide effects show a different pattern over the phase-in period. The results for firearm suicides show essentially no evidence of an immediate effect of the law, but rather a gradual increase over time, with the strongest evidence in year 6, at which point the probability that there is an increase in firearm suicides is 0.90. The effect on firearm homicides, in contrast, shows the strongest evidence of harm in the first year of implementation (probability = 0.99), but over time, the posterior distribution of the effect looks more like the prior distribution, such that there is only weak evidence of harm in year 6 (probability = 0.77).

SYG laws limit the legal liability of individuals who use deadly force in self-defense outside of their own home. SYG laws showed more limited evidence of being associated with subsequent changes in firearm death rates. Given the data, the model, and our priors, there is a 0.77 probability that the law is associated with a subsequent increase in firearm deaths in the sixth year after implementation, suggesting considerable uncertainty about the direction of the effect. The estimated effect size represents an increase of 3% (incidence rate ratio [IRR] = 1.03) in the expected firearm death rate without the law. This effect size corresponds to 977 (80% CI, −747 to 2,603) additional deaths nationally in 2016 had SYG laws been implemented in all states in 2010 relative to having been implemented in no states. The estimated effects of SYG are somewhat different across firearm homicides and suicides. There is little evidence for an effect on suicide at any time point. In contrast, there is strong evidence of the law’s association with increasing homicide in the first year after implementation (probability = 0.97), but over time, the posterior distribution of the effect looks more like the prior distribution, resulting in more limited evidence of harm in year 6 (probability = 0.82).

Consistent with our findings of the individual law effects, estimation of the joint effects of these laws indicates that a restrictive policy regime (with CAP laws, but without either RTC or SYG) is associated with a subsequent decrease in deaths relative to a permissive regime (with RTC and SYG laws but without CAP). We estimate there is a 0.98 probability that the restrictive regime is associated with a subsequent decrease in firearm deaths by the sixth year after implementation. The estimated effect size represents a decrease of 11% (IRR = 0.89) relative to the expected firearm deaths under the permissive regime. Thus, in a hypothetical situation in which there are 39,000 firearm deaths nationally under a permissive combination of CAP, RTC, and SYG laws, this effect size corresponds to an expected decrease of 4,475 (80% CI, 1,761 to 6,949) deaths nationally from moving to a restrictive regime. The effect sizes for the firearm homicide and suicide subtypes are similar to each other, and the probability of a reduction in each subtype of firearm deaths in the sixth year after implementation is 0.95. The posterior median IRR for firearm suicide shows a gradual phase-in of the effect over the 6-y period, going from an IRR of 0.98 in year 1 down to 0.91. While the effect for firearm homicide shows a fast phase-in that stays stable, with all IRRs over the 6-y period falling between 0.85 and 0.86 (SI Appendix, Fig. S1).

Discussion

The estimated effect sizes are generally in line with what experts predicted for these types of marginal policy changes (2), which target firearm storage and use behaviors of only a narrow class of individuals or situations. While the IRRs are all descriptively close to 1, the magnitudes of the estimated effects are of a size considered important by policy makers and the public, with each of these policy levers potentially affecting more than 1,000 firearm deaths each year.

While the effects for individual laws are generally small with substantial uncertainty, stronger conclusions can be drawn about the overall pattern across the three laws. There are currently 18 states that have the most permissive combination of these laws (RTC and SYG laws, but no CAP law). Our findings indicate that a 11% reduction in firearm deaths in these 18 states is achievable by moving these states to the restrictive policy regime. The posterior probability that this change is associated with a decrease in firearm deaths is high (0.98).

One concern about focusing exclusively on firearm-related mortality is that it may miss unintended or second-order consequences of firearm legislation. It is likely that other outcomes of interest to some policy makers (e.g., non-firearm homicides, violent crime, economic activity) show different effects of these laws than we observed on firearm deaths. For example, it is possible that preventing firearm homicides or firearm suicides through firearms policy may fail to reduce overall homicides or suicides because perpetrators achieve the same outcomes using different lethal means. Alternatively, preventing firearm homicides and suicides may result in broader reductions in homicides and suicides, to the extent that such violence is contagious. Thus, the effect of these laws on total homicides and total suicides may diverge from the estimates that we have provided. To address this possible limitation, SI Appendix presents replications of the main analyses using total homicides and total suicides as outcomes. These analyses show a very similar pattern of findings as the analyses looking at firearm homicides and suicides. The IRRs are slightly attenuated toward 1, which is expected if the non-firearm incidents are minimally affected by the firearms laws, but the effect sizes on total suicides and homicides in terms of number of deaths are descriptively similar to what was found when predicting firearm suicide and homicide.

Although this study’s model explains 94% of the variance in firearm-related death rates over states and years, there remains the potential limitation that our observed associations represent the causal effects of omitted variables associated with the gun policies, rather than effects of the laws themselves. The current method of estimating effects is somewhat robust with respect to this type of problem; namely, the policy effects are identified through the year-over-year changes in the outcome within a large number of states that implemented these laws at different times. Thus, while it is possible for the estimates to be the result of an omitted confounding variable, that variable would need to be associated with the pattern of implementing states as well as line up with the specific implementation dates within those states.

The estimated probabilities that these policies are associated with reductions in firearm deaths reveal some uncertainty about the direction of the effects. However, when policy makers must decide whether to support or oppose such a law, it is useful for them to know whether the likelihood of a decrease in death rates following passage is a 95/5 wager rather than a 50/50 proposition. This type of information acknowledges the scientific uncertainty but still communicates the evidence that restrictive policies on firearms storage and use are likely to be followed by meaningful reductions in firearms deaths.

Materials and Methods

To estimate the effects of laws, we modeled longitudinal data from 50 states for the years 1980 to 2016. The primary outcomes for these estimates are state-level counts of annual firearm deaths from the Vital Statistics System, which contains information on coroners’ cause of death determinations for >99% of all deaths in the United States (20). We also conducted separate analyses for firearm homicides and firearm suicides. Each of the three classes of laws studied here (CAP, SYG, and RTC) contains heterogeneity in the exact text and method of implementation across states. The specific definitions used to classify CAP, SYG, and RTC laws for our analyses, as well as the dates of state implementation, are included in SI Appendix, Table S1. The analyses also include state-level time-varying demographic, economic, crime, law enforcement, and gun ownership characteristics described in SI Appendix, Table S2.

The preferred model based on the simulation analyses described above (19) was a negative binomial regression of the outcome on (a) an offset equal to the natural logarithm of the population in that state-year; (b) effects for each year in the data; (c) an autoregressive effect equal to the natural logarithm of the rate of the outcome in the prior year for a given state; (d) state characteristics included as covariates; and (e) indicators for the three classes of laws.

To correctly parametrize the effect of the three laws, we must make an assumption about how long it takes for the laws to achieve their full effects. For example, an RTC law may make it easier to get a concealed carry permit immediately on its implementation date, but it may take years for the proportion of the population with such permits to increase to a stable level. In our models, we chose the effect during the sixth year postimplementation as our primary time point for estimation of the effects. The specific coding of the laws that we use in our model allows for a nonlinear phase-in of the effect over the first 6 y after implementation, with the potential for a rapid change immediately after implementation as well a longer-term phase-in of an effect. The effect of the law is then assessed by integrating over these separate effects, through time, to estimate the total effect of the law at annual time points after implementation. Additional information about effect coding and marginal effect estimation is provided in SI Appendix.

In addition to looking at the three classes of laws individually, we also estimate their joint effects. Each of these three laws can be seen as either restricting firearm access and use or permitting firearm access and use. As such, we examine whether having a restrictive policy regime (a CAP law but no RTC or SYG laws) is associated with different firearm death rates than having a permissive policy regime (no CAP law but RTC and SYG laws).

We use Bayesian estimation of the model to assess the effect of these state laws on firearm deaths, an approach that has three advantages for our purposes. First, Bayesian methods allow us to directly estimate the probability that a given law is associated with an increase or a decrease in firearms death. These probabilities directly correspond to the likely effects of the yes/no decisions facing policymakers considering such legislation, rather than tests of a null hypothesis (21). Second, our simulations revealed that estimates of the effects of state gun policy generally lack sufficient statistical power to detect effects of the size likely to be found for common gun policies, even when these effects are of a magnitude that would be of substantial interest to policy makers (e.g., a law that would reduce firearms deaths by 1,000 deaths nationally each year) (19). Conducting significance testing with such low statistical power results in a high probability of yielding inconclusive or inaccurate results, even when there is useful information about the true effect within the available data. Using Bayesian inference generally avoids these problems in the same data when estimated with modestly informative priors (22).

Finally, we estimated the effects of the law by computing marginal effects in each year after implementation. This was done to produce unbiased treatment estimates within an autoregressive model by estimating effects of the law in a specific year that take into account both the direct effect of the law on the outcome in that year and the indirect effect of the law in the prior year that is mediated through the autoregressive term into that year. Standard maximum likelihood methods do not accurately estimate the SE for this type of marginal effect (23); however, the posterior distribution of this marginal effect can be estimated through Bayesian methods. (Details on effect estimation are provided in SI Appendix.)

All models were estimated in Stan (24). Priors for all covariates were weakly informative and centered on 0 (SI Appendix). Priors for each law’s effect were selected such that the total effect of each law evaluated at 6 y after implementation on firearm deaths was normally distributed and centered on no effect (i.e., equal likelihood that the law increased vs. decreased firearm deaths). When integrated over the coefficients for each law, the SD of the prior implied a 0.95 probability that the total effect size for each law (i.e., IRR) falls between 0.83 and 1.20. The selection of this prior is based on an earlier survey of gun policy experts showing expected gun policy effect sizes in the range described by the prior used in this study (2) (SI Appendix provides further details on the priors and results using uninformative priors.)

Data Availability.

All data are from publicly available sources, and all code used in the analyses have been posted at https://accounts.osf.io/login?service=https://osf.io/5yqx3/.