Supervised learning through physical changes in a mechanical system

Significance

Supervised learning algorithms can learn subtle features that distinguish one class of input examples from another. We explore a supervised training framework in which mechanical metamaterials physically learn to distinguish different classes of forces by exploiting plasticity and nonlinearities in the material. After a period of training with examples of forces, the material can respond correctly to previously unseen novel forces that share spatial correlation patterns with the training examples. Such generalization can allow mechanical parts of microelectronics and adaptive robotics to learn to distinguish patterns of force stimuli on the fly. Our work shows how learning and generalization are not restricted to software algorithms, but can naturally emerge from plasticity and nonlinearities in elastic materials.

Abstract

Mechanical metamaterials are usually designed to show desired responses to prescribed forces. In some applications, the desired force–response relationship is hard to specify exactly, but examples of forces and desired responses are easily available. Here, we propose a framework for supervised learning in thin, creased sheets that learn the desired force–response behavior by physically experiencing training examples and then, crucially, respond correctly (generalize) to previously unseen test forces. During training, we fold the sheet using training forces, prompting local crease stiffnesses to change in proportion to their experienced strain. We find that this learning process reshapes nonlinearities inherent in folding a sheet so as to show the correct response for previously unseen test forces. We show the relationship between training error, test error, and sheet size (model complexity) in learning sheets and compare them to counterparts in machine-learning algorithms. Our framework shows how the rugged energy landscape of disordered mechanical materials can be sculpted to show desired force–response behaviors by a local physical learning process.

The design of mechanical metamaterials usually assumes that desired force–response properties are given as a top–down specification. For example, principles of topological protection can be used to design materials where forces at specific sites lead to localized deformations (1, 2), while other principles (3) can help communicate that deformation to a specific distant site. In these examples and many others (4–8), we rationally optimize design parameters—e.g., spring constants and geometry—to achieve a specified force–response relationship.

A different approach, closely connected to supervised learning in computer science, is useful when the force–response behavior is too complex to specify in a top–down manner, but it is easy to give examples of the desired behavior. In this learning approach, the emphasis is on inferring the right force–response relationship from such training examples, with success evaluated on the ability to extrapolate the relationship to unseen test examples.

In this work, we wish to employ the advances of learning theory, but, crucially, perform the learning outside of the computer, at the level of the physical material itself. This way, we introduce a physical learning model, able to learn from (adapt to) shown examples and generalize to novel, unseen examples. The ability to generalize to show the correct response to novel test examples has fueled the success of machine learning. Such generalization would also be useful in materials when the use cases are either complex or are not fully known at the time of design. Consider applications such as micro-electro-mechanical systems, where a mechanical membrane must either complete or open an electrical circuit by deploying one of two folding responses $A$ or $B$ in response to two different sets of force patterns $S^A$ or $S^B$, respectively.

Only some examples of the force patterns in the sets $S^A,S^B$ may be known at the time of design. Further, the distinction between the force patterns in the sets $S^A,S^B$ may not be easily apparent, similarly to how pixel-intensity correlations that distinguish images of cats and dogs are nontrivial. However, much in the way a neural network can learn correlation features that distinguish cats from dogs by seeing examples, a training procedure for materials might be able to learn and respond to high-dimensional correlation features that distinguish force patterns in the sets $S^A$ and $S^B$. Crucially, the trained material could distinguish novel patterns in $S^A,S^B$ that were not used as part of the training. Finally, even when distinguishing features are known a priori, learning offers a natural way for materials to arrive at the right design parameters themselves, without need for a complex optimization algorithm on a computer.

While naturally occurring systems like neural networks (9), slime molds (10), and plant-transport networks (11) use similar ideas to adapt their response to environmental inputs, mechanical supervised learning has thus far not been used to obtain functional man-made materials. Here, we propose an approach for the supervised training of a mechanical material through repeated physical actuation. We work with a model of creased thin sheets where crease stiffnesses can change as a result of repeated folding. We assume a training set—that is, a list of force patterns and desired responses. Each training example of a force pattern is applied to the sheet; if the response is the desired one, as determined by a “supervisor,” folded creases are allowed to soften in proportion to their folding strain. If the response is incorrect, creases stiffen instead. We then test the trained sheet by applying unseen force patterns (test examples) drawn from the same underlying distribution as the training data. We study test and training errors and, thus, the sheet’s ability to generalize to novel patterns as a function of its size.

Our proposal here relies on a plastic element—namely, crease stiffness. Materials that stiffen or soften with strain have been demonstrated in several contexts (12–15), including recently in the training of mechanical metamaterials (16). We discuss how learning performance may be affected by limitations on the dynamic range of stiffness and other practical constraints in such materials. We hope our results here will provoke further work on how the frameworks of learning theory could inform the creation of new classes of designer materials.

Results

We demonstrate our results with a creased, thin, self-folding sheet (Fig. 1A), which is naturally multistable. Our analysis can be generalized to other disordered mechanical systems, such as elastic networks (16), that are also generically multistable. It was previously shown that creased sheets, such as those of self-folding origami, can be folded into exponentially many discrete folded structures from the flat, unfolded state (17, 18). Such exponential multistability can be a problem (8, 17) from an engineering standpoint, as precise controlled folding is required to obtain the desired folded structure.

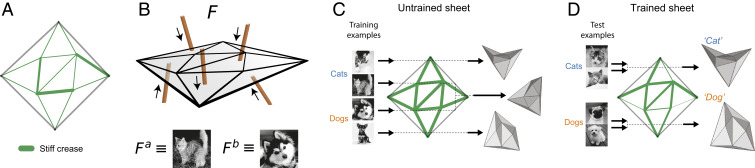
Fig. 1.

Training thin sheets to classify spatial force patterns. (A) We consider thin, stiff sheets with creases whose stiffnesses (indicated by thickness of green segments) can be changed by repeated folding. (B) Such sheets can fold in response to a discrete spatial force pattern $\mathbf{F}$ applied on the sheet. To emphasize the high-dimensional nature of $\mathbf{F}$, we draw an analogy between $\mathbf{F}$ and an image where the gray-scale value of each pixel corresponds to the force at a particular location on the sheet (SI Appendix, section 1). Particular force patterns correspond to examples of different classes (e.g., cat ${\mathbf{F}}^a$ and dog ${\mathbf{F}}^b$). (C) An untrained sheet with uniform stiffness shows random folded responses for different spatial force patterns. (D) By allowing crease stiffness to change in response to strain, we train the sheet to learn correlation features that distinguish different classes of force patterns. Consequently, the sheet classifies force patterns by showing one distinct folded response for each class.

Here, we exploit such multistability to train a classifier of input force patterns. If we apply a spatial force pattern $\mathit{F}$ on the flat sheet (Fig. 1 A and B), the sheet will fold into a particular folded structure $\mathit{\rho }\left(\mathit{F}\right)$—e.g., described by dihedral folding angles at each crease ${\rho }_i$. To emphasize the high-dimensional nature of space of force patterns, in Fig. 1 B–D, we represent each force with a gray-scale image, where pixel values are an analogy to forces at designated points on the sheet. In practice, we apply these forces as torques directly on creases (SI Appendix, section 1). The set of all force patterns $\left\{\mathit{F}\right\}$ that lead to one particular folded structure ${\mathit{\rho }}^m$, due to the dynamics of folding, is defined as the “attractor” of folded structure $m$ in the space of force patterns (color-coded regions in Fig. 2B). The complex attractor structure of force–response for a thin sheet naturally serves as a classifier of force patterns, albeit a random classifier (Fig. 1C). The goal of the training protocol is to obtain a sheet with a specific desired mapping between force patterns and folded structures (Fig. 1D).

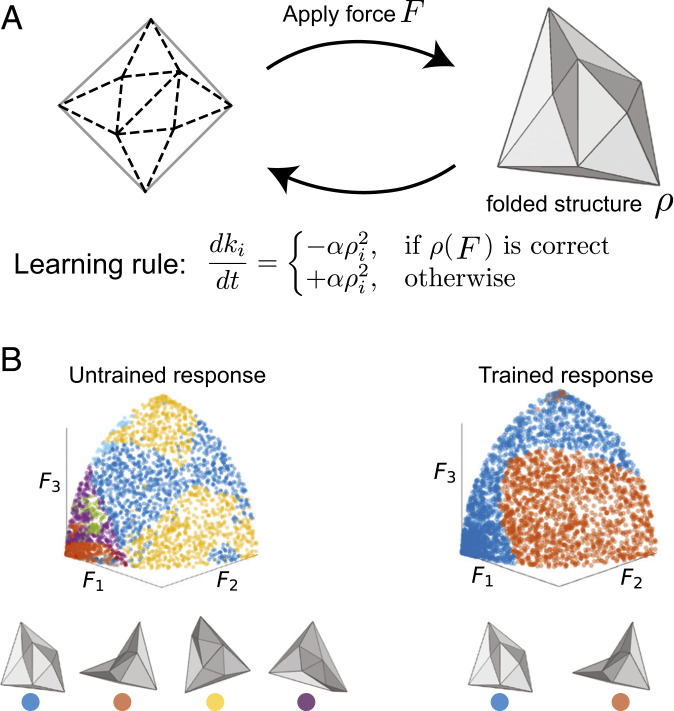
Fig. 2.

Supervised training of thin sheets. (A) A sheet with random crease geometry is folded with a training force pattern ${\mathit{F}}^a$, resulting in a folded structure $\mathit{\rho }$. The stiffness $k_i$ of each crease $i$ is modified according to a local learning rule; if the folded structure $\mathit{\rho }$ is the desired response for ${\mathit{F}}^a$, as determined by a supervisor, creases soften in proportion to their folding strain ${\rho }_i$. Otherwise, creases stiffen. (B) This rule trains the sheet to perform the desired classification of force patterns. The untrained sheet shows multiple folded structures in response to force patterns (a 2D cross-section of force pattern space is shown, with $F_1,F_2,F_3$ as three particular directions in force space; SI Appendix, section 1). The trained sheet shows only two folded responses that mimic the desired mapping of force patterns to folded structures.

The mapping between force and folded structure is controlled by local properties of the system, such as thickness or stiffness (19, 20) (SI Appendix, section 1). Previously, we found that the folded response to a given force pattern $\mathit{F}$ can be modified by changing the stiffness $k_i$ of different creases $i$ in the sheet (8). Here, we employ a “supervised learning” approach to naturally tune stiffness values $k_i$ so that the sheet classifies forces as desired. Intuitively, this is done by applying examples of force patterns to the sheet and modifying crease stiffness accordingly, in a way that reinforces the correct response and discourages incorrect folding (Fig. 2A). Such training, carried out iteratively for different force-pattern examples, has the effect of morphing the attractor structure to better approximate the desired response (Fig. 2B).

Consider two distributions of force patterns, each designated as a particular class (e.g., “cats” and “dogs”). For example, Fig. 3 A, Upper shows two classes of forces defined by: $S^{\text{dog}}=\left\{\mathit{F}|\mathit{F}\cdot {\mathit{F}}_{\text{dog}}\ge D,\mathit{F}\cdot {\mathit{F}}_{\text{dog}}>\mathit{F}\cdot {\mathit{F}}_{\text{cat}}\right\}$, and similarly for $S^{\text{cat}}$ for a threshold $D=0.6$. (In Fig. 3A, $S^{\text{dog}}$ is blue, and $S^{\text{cat}}$ is orange.)

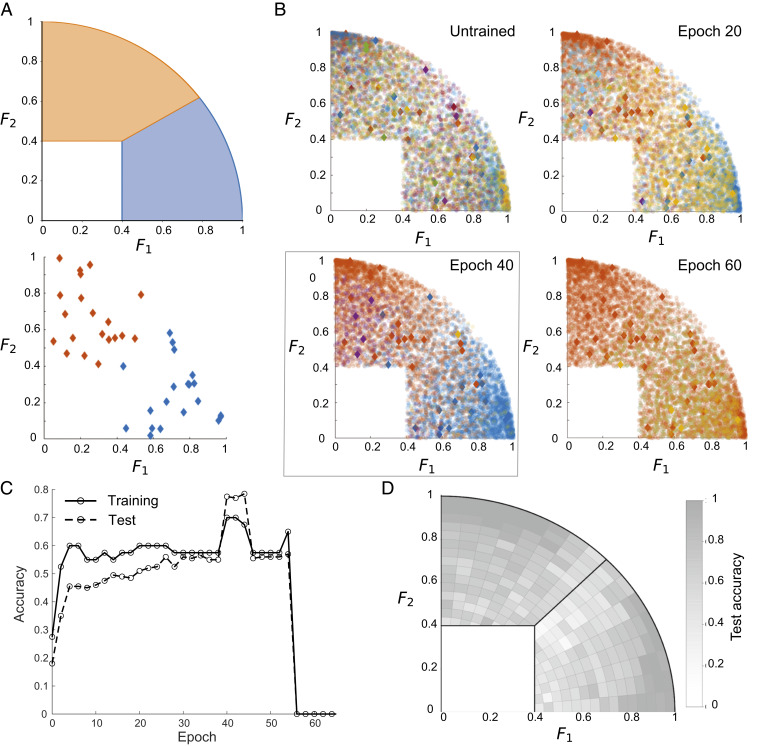
Fig. 3.

Supervised learning of cap-like force distributions. (A) We define distributions $S^{\text{dog}}$ (blue) and $S^{\text{cat}}$ (orange) of force patterns in the space of applied forces (2D projection shown). Twenty training examples (diamonds) are drawn from both distributions. (B) An untrained sheet folds into many distinct folded structures (different colors) in response to applied force patterns. As training progresses, most force patterns are classified as either blue or orange, according to the cap they belong to. When overtrained, all force patterns result in only one folded structure (orange). (C) The trained sheet reaches peak performance after $\sim 40$ epochs of supervised training (i.e., passes through the training examples). The trained sheet not only classifies the training set correctly (training accuracy), but generalizes to unseen test force patterns (test accuracy). (D) The trained sheet is highly accurate when classifying force patterns near the center of the distributions, but less accurate close to the true decision boundary between the distributions.

Assume we are given two sets of labeled force patterns as training examples ${\mathcal{F}}^{\text{dog}}=\left\{\mathit{F}\in S^{\text{dog}}\right\}$, ${\mathcal{F}}^{\text{cat}}=\left\{\mathit{F}\in S^{\text{cat}}\right\}$, each with $n$ training force patterns (in Fig. 3 A, Lower, we sample sets with $n=20$). Together, ${\mathcal{F}}^{\text{dog}}$ and ${\mathcal{F}}^{\text{cat}}$ are defined as the training set. We desire all forces in $S^{\text{dog}}$ to result in one common folded structure, while all forces in $S^{\text{cat}}$ fold the sheet to a distinct, but common, folded structure. While $S^{\text{dog}}$, $S^{\text{cat}}$ are separable in some two-dimensional (2D) projection of force space, learning is nontrivial, since the sheet must learn the two dimensions in which these distributions are separable.

A Mechanical Supervised Training Protocol.

We pick 40 forces (20 blue and 20 orange) from the dog and cat distributions to serve as the training set and apply our training algorithm described below to a thin sheet with uniformly stiff creases. In our training protocol, each of the training force patterns $\mathit{F}$ is applied to the sheet in sequence, to obtain a folded structure $\mathit{\rho }\left(\mathit{F}\right)$. A supervisor determines whether the resulting folded state $\mathit{\rho }\left(\mathit{F}\right)$ is correct or incorrect by comparing the three-dimensional geometry to that of a reference folded state ${\mathit{\rho }}_{\text{ref}}$ for that class. The reference state can be selected in several ways. Here, we average the response of the untrained sheet on training examples in each class (SI Appendix, section 2).

We then apply the following learning rule that stiffens or softens each crease in proportion to folding in that crease:

$$\frac{d{k}_i}{dt}=\left\{\begin{array}{cccc}\hfill & -\alpha {\rho }_i^r,\hfill & \hfill & \text{if}\hspace{0.17em}\mathit{\rho }\left(\mathit{F}\right)\text{is correct}\hfill \\ \hfill & +\alpha {\rho }_i^r,\hfill & \hfill & \text{otherwise},\hfill \end{array}\right.$$ [1]

for the stiffness $k_i$ of each crease $i$. $\alpha$ is a learning rate, setting how fast stiffness values $k_i$ are updated due to training examples (here, we use $\alpha =10^{-4}$). $r$ models nonlinearities in strain-based softening or stiffening of materials; we use $r=2$. Such plasticity is experimentally seen in several materials (21–23); we discuss other learning rules and experimental constraints later. As we employ a physical model of origami sheets, we note that any rule that changes the stiffness of a crease has to be local—i.e., the stiffness of a crease $i$ may not change due to the folding angle of a different crease $j$ (which crease $i$ has no information of). This is a major departure from learning rules in machine-learning algorithms, which are typically nonlocal (24, 25). For further information about this learning rule and its generalization to multiclass classification, see SI Appendix, section 2.

After each round of training, the pattern is unfolded back to the flat state. The same supervised learning step is then repeated in sequence for all training force patterns. A training epoch is defined as one pass through the entire training set.

We find that, as training proceeds, the number of observed folded structures decreases (fewer colors), and nearly all training force patterns fold the sheet into the “blue” or the “orange” labeled structures after epoch 40 (diamonds in Fig. 3B). The fraction of training force patterns that fold the sheet into the correct structure is defined as the training accuracy. This measure is an unbiased estimator of classification performance, as we choose the number of training forces to be the same in every class. Note that the different folded states of disordered sheets are typically highly distinct, even at the level of mountain–valley patterns (17, 18); hence, no special clustering algorithm is required to identify distinct structures and assign them distinct colors in Fig. 3.

However, a successfully trained sheet should correctly classify previously unseen “test” force patterns, sampled from the same distributions. We tested the trained sheet by applying such test examples drawn from the distributions $S^{\text{dog}},S^{\text{cat}}$ and recording the resulting folded structure (800 test force patterns for every class). In analogy to the training sets, the fraction of test examples yielding the correct folded structure is defined as the test accuracy. High test accuracy is observed (Fig. 3 C and D) ($\sim 80\%$ of the test examples classified correctly); thus, the sheet generalizes and is able to have the right response to novel test force patterns through the changes induced by training examples.

Heterogeneous Crease Stiffness.

Our learning rule facilitates classification by creating heterogeneous crease stiffness across the sheet (Fig. 4A). Indeed, as training proceeds, we find that the variance $\mathrm{\Delta }{k}^2$ of stiffness grows (Fig. 4B, depicting the evolution of the stiffness profile for the learning process shown in Fig. 3). If the sheet is trained beyond the optimal point, the stiffness variance still grows, but the classifier eventually fails, as seen in Fig. 3 B and C. The failure mode of overtraining is typically that all forces fold the sheet into a single folded structure, resulting in no classification. This overtraining failure is associated with a large stiffness dynamic range, rather than with too-small stiffness values.

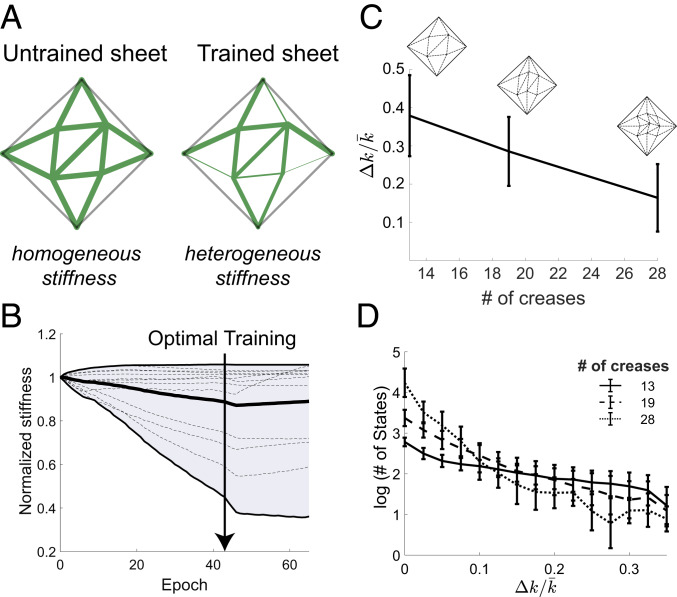
Fig. 4.

Training increases the variance of crease stiffness across the sheet. (A) Untrained sheets have a homogeneous distribution of crease stiffnesses, while trained sheets have heterogeneous stiffness profiles (width of green lines). (B) As the sheet is trained, the stiffness of different creases changes to different extents, such that the variance in stiffness values grows over training time (envelope shows the least and most stiff creases). (C) Larger sheets with more creases require smaller variance in their stiffness values for optimal training. (D) An untrained sheet starts with exponentially many available folded structures. During training, the number of available folded structures decreases exponentially with increasing stiffness variance $\mathrm{\Delta }{k}^2$, allowing the sheet to classify a few distinct classes.

We can understand this relationship between heterogeneous stiffness ($\mathrm{\Delta }k$) and training using a simple model. A heterogeneous crease stiffness profile $\mathit{k}$ with high stiffness $k_i$ in crease $i$, but no stiffness elsewhere, will lift the energy of structures $\mathit{\rho }$ with small folding ${\rho }_i$ in crease $i$ less than structures with large ${\rho }_i$. Hence, heterogeneous $\mathit{k}$ can raise the energy of select structures, reducing their attractor size, while other structures remain low in energy and grow in attractor size. If we assume that folding angles ${\mathit{\rho }}^a$ of structure $a$ are randomly distributed (verified earlier in ref. 7) and assume a random stiffness pattern with SD $\mathrm{\Delta }k$, the energies ${\sum }_i{k}_i{\rho }_i^2$ of different structures will be distributed as a Gaussian with mean $\mu =\gamma \overline{k}$ and SD $\sigma =\beta \mathrm{\Delta }k$, where $\overline{k}$ is the mean stiffness, and $\gamma ,\beta$ are some numerical parameters.

If structures above energy $E_F$ are inaccessible to folding, the number of accessible folded structures is

$$\#\left(\mathrm{\Delta }k,N\right)\sim 2^N\left[1-erf\left(\frac{\gamma \overline{k}-E_F}{\beta \mathrm{\Delta }k}\right)\right].$$ [2]

Hence, the number of surviving folded structures should decrease fast with $\mathrm{\Delta }k$. This effect is indeed observed for trained origami sheets of different sizes (Fig. 4D). From numerical exploration of the energy distributions in this model, we find that $\gamma$ is a constant, regardless of sheet size, while $\beta \sim N^{-0.5}$ shrinks with sheet size (central limit theorem). Using this form of $\beta$ in Eq. 2 predicts that the elimination of structures happens at a lower $\mathrm{\Delta }k$ for larger sheets, consistent with our results in Fig. 4 C and D.

We conclude that as the training protocol proceeds, the stiffness variance $\mathrm{\Delta }{k}^2$ grows, and the number of available folded structures decreases. The last surviving folded structures, reinforced by the learning rule of Eq. 1, classify the force distributions correctly. Thus, the learning process merges attractors of the untrained sheet such that the surviving attractors recapitulate features of the desired force-fold mapping.

Generalization and Sheet Size.

Statistical learning theory (27) suggests that two critical parameters set the quality of learning: 1) the number of training examples seen, and 2) the complexity of the learning model. An increased number of training examples usually decreases training accuracy. However, test accuracy—i.e., the response to novel examples or the ability to generalize—improves. Furthermore, the improvement of test accuracy is larger for complex models with more fitting parameters. Intuitively, complex models “overfit” details of small training sets, and thus show low test accuracy, even if training accuracy is high.

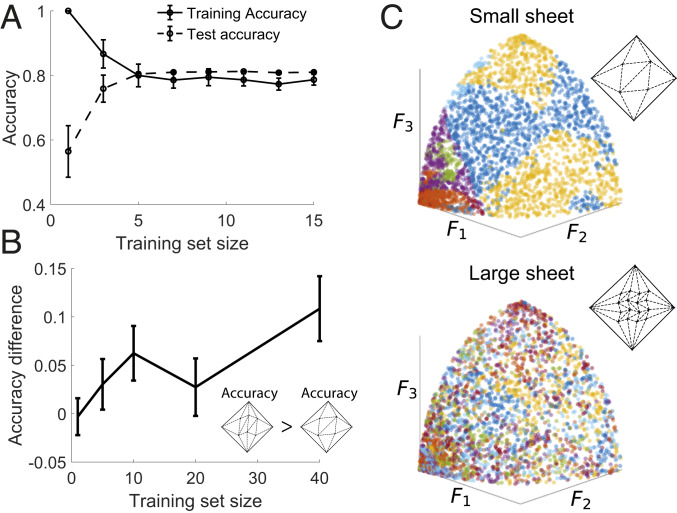
Our sheets exhibit signatures of these learning-theory results, with the size of the sheet (number of creases) playing the role of model complexity. For a sheet of fixed size, trained on the distributions of Fig. 3, we observe that increasing the number of training examples increases test accuracy and decreases training accuracy (Fig. 5A). In Fig. 5B, we find that the test accuracy of larger sheets with more creases improves more dramatically with the size of the training set, compared to smaller sheets.

Fig. 5.

Effect of training-set size and sheet size on test accuracy. (A) With fewer distinct training examples, training accuracy is high, but test accuracy is low (overfitting). Increasing the number of training examples improves test accuracy, at the expense of training accuracy. (B) Sheets with more creases show larger improvements in test accuracy with increasing number training examples, as expected of complex models with more fitting parameters. (C) A small, untrained sheet (13 creases) shows $\sim 10$ folded structures (color coded) in response to different force patterns. A larger sheet (49 creases) shows $\sim 400$ folded structures instead, each with smaller attractor regions in the space of force patterns. Consequently, larger sheets can create more flexible classification surfaces by combining smaller attractor regions; such complex models with more fitting parameters require more training examples to avoid overfitting.

These results suggest that sheets with more creases correspond to more complex classification models (e.g., a deeper neural network). For example, crease stiffnesses are the learnable parameters in our approach; hence, increasing their number amounts to using a training model with more parameters. Further, untrained sheets with more creases support exponentially more folded structures (17, 18), as shown by the color-coded force-to-folded-structure relationship in Fig. 5C. The training protocol achieves correct classification by merging different-colored regions. Thus, larger sheets can approximate more complex decision boundaries by combining the smaller regions (Fig. 5C), and thus act as more complex models to be favored when the amount of training data is large. In Discussion, we use these results to contrast memory and learning in mechanical systems.

Real-World Classification Problems.

We have shown how disordered thin sheets can classify force distributions described by one feature (Fig. 3); one may ask whether these sheets can classify data described by multiple features.

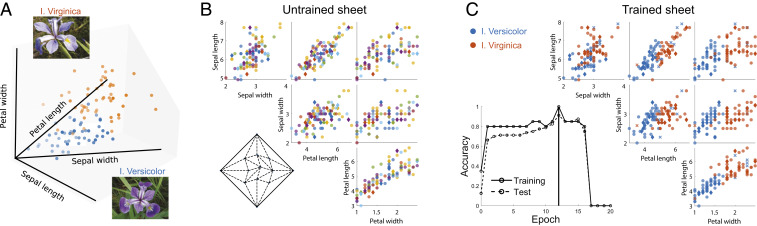
We tested our learning protocol on the classic Iris dataset (28), used extensively in the past to benchmark classification algorithms. This dataset reports four measurements—length and width of petals and sepals—for individual specimens of different Iris species. While different Iris species cannot be distinguished by any one of these properties, we wanted to test if our sheet can learn the combination of features needed to distinguish species.

We picked the two most similar species in this dataset, Iris versicolor and Iris virginica (Fig. 6A). We translated the four flower measurements to four force components applied to a sheet (SI Appendix, section 4). We then applied our training algorithm with a training set consisting of 10 examples of I. versicolor and I. virginica (diamonds in Fig. 6C). The resulting trained sheet was tested on 80 unseen examples of these species; the trained sheet was able to identify the species of $91\%$ of previously unseen specimens correctly.

Fig. 6.

Training sheets to classify Iris specimens. (A) We train a sheet to classify individual Iris specimens as one of two species based on petal and sepal lengths and widths (26). We translate these four measurements into a spatial pattern of forces applied to the sheet. (B) Folding response of an untrained (28 crease) sheet due to force patterns derived from the Iris data (shown in every cross-section). (C) The sheet is trained by using 10 random examples (diamonds) of each species from the database (26) and then tested on 80 unseen test examples (circles). Matrix shows the classification of Iris flowers at optimal training of the sheet ($91\%$ test accuracy; mistakes are denoted by x).

We have tested our training protocol on more complex, higher-dimensional distributions (SI Appendix, section 3). For example, we used the folding behavior of one thin sheet (the master) as the target behavior for another thin sheet with a distinct crease geometry. We find that the trained sheet is able to correctly predict the response of the master sheet to forces not seen during training. Thus, by using our training protocol, sheets can learn and generalize complex force-to-folded response maps from examples.

Experimental Considerations.

Our learning framework requires materials that can plastically stiffen or soften when strained repeatedly (29). Several such materials and structures are known, including shape memory polymers (30, 31), shape memory alloys (Nitinol) (32), and fluidic flexible matrix composites (33). These systems have the advantage of truly variable, user-controlled stiffness and are used for various medical applications (34). Polycarbonate multilayer sheets have been shown to produce controlled bending stiffness by more than an order of magnitude (35). Other materials can show a plastic change in stiffness in response to aging under strain, such as ethylene vinyl acetate (EVA) foam (36) and thermoplastic polyurethane (37). EVA was used recently (16) to show such behavior in a mechanical system trained for auxetic response. Another possible method, explored specifically for origami creases (20), controls the crease width (and, hence, stiffness) using photolitography (38). We conclude that several available materials and experimental methods could implement our learning rule in an experimental setting.

The specific learning rule used in this paper requires the ability to soften or stiffen, depending on the supervisor’s judgement of outcome. Such a learning rule can be implemented by materials that stiffen under strain in one condition (say, high temperature, low pH), but soften under strain in another condition.

However, the results here also hold for simpler learning rules, e.g., that only require plastic softening under strain. For example, we can modify the learning rule Eq. 1 to

$$\frac{d{k}_i}{dt}=\left\{\begin{array}{cccc}\hfill & -\alpha {\rho }_i^2,\hfill & \hfill & \text{if}\mathit{\rho }\left(\mathit{F}\right)\text{is correct}\hfill \\ \hfill & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0,\hfill & \hfill & \text{otherwise}\hfill \end{array}\right.$$ . [3]

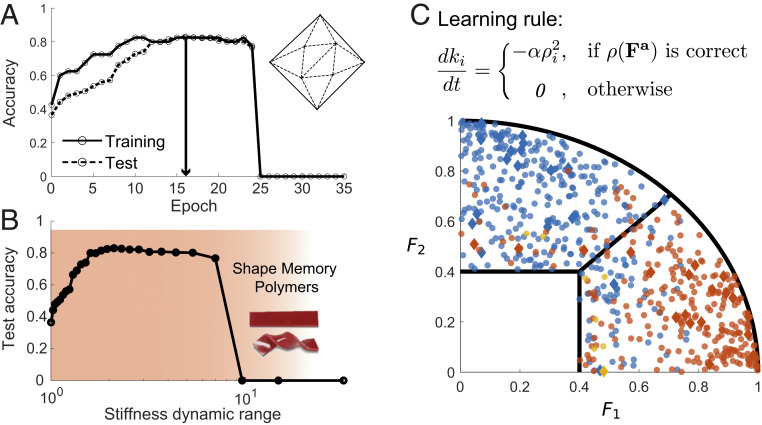
Such a rule is easily implemented with a strain-softening material with no stiffening needed. For example, if the folded outcome $\mathit{\rho }\left(\mathit{F}\right)$ is judged correct, we hold the sheet in the folded state $\mathit{\rho }\left(\mathit{F}\right)$ for a longer length of time (allowing significant softening) than when the outcome is judged incorrect (no softening). We tested this simplified learning rule for the classification problem in Fig. 3; we find similar accuracy as earlier (Fig. 7A). As discussed in SI Appendix, section 2, the softening modification itself—e.g., the specific ${\rho }^2$ form—is not essential as well. Many similar monotonic $\stackrel{.}{k}\sim f\left(\rho \right)$ would support learning in sheets.

Fig. 7.

Learning is successful, even with simplified training rules and experimentally realizable stiffness. (A) A sheet (13 crease) trained on the classification problem of Fig. 3, with a simplified, experimentally viable learning rule shown in C. (B) At peak training, the dynamic range of crease stiffness values is $\sim 2$, well within the ranges supported by existing shape memory polymers (red region) (30). (C) The trained sheet reaches peak accuracy of $80\%$ on test force examples (circles).

Another significant experimental constraint is the dynamic range of crease stiffnesses $k_i$ achievable in real materials without fracture at the creases. Fortunately, we find that for well-trained sheets, the difference in crease stiffness is moderate (Fig. 4C) and does not exceed $30\%$ of the mean stiffness value for a medium-sized (28-crease) sheet. Fig. 7B shows that our required dynamic range in stiffness is $\sim 2$, well within the range for experimentally available materials, such as shape memory polymers (30, 39). Other materials like hydrogels and polycarbonates exhibit bending stiffness that can easily adapt in a significantly larger range (35, 38), up to an order of magnitude.

Finally, another failure mode for our training protocol is overtraining. While the variance in crease stiffness $\mathrm{\Delta }{k}^2$ is critical to eliminate attractors, overtraining can result in a sheet with only one folded state. Our analysis, presented in Fig. 4, suggests that large sheets should be easier to train experimentally since the stiffness variance needed is more moderate, while the transition to overtraining does not become much more rapid.

Discussion

In this work, we have demonstrated the supervised training of a mechanical system, a thin creased sheet, to classify input force patterns. As required for learning, the trained sheet not only shows the correct response for training forces, but can generalize and show the correct response to unseen test examples of forces. We studied the relationship between training error, test error, and the size of the sheet, which plays the role of model complexity in supervised learning (27).

We can understand the promises and limitations of our physical learning approach better by considering similarities and differences with machine learning performed on computers, including for materials design (40–43).

Generalizing by Learning Features.

The core similarity is that both methods are predicated on learning “features” from training examples (e.g., in Fig. 1D, something common to cats, yet not found in dogs) and, thus, classifying never-before-seen examples correctly.

In our context, “features” are spatial correlations in forces applied to different locations on the sheet. For example, say, force patterns in class $S^A$ might exert anticorrelated forces at sheet sites $x$ and $y$, while the force patterns in $S^B$ show positive correlation at those sites. Meanwhile, all force patterns in $S^A,S^B$ might exert forces at site $z$, but those forces do not help distinguish $S^A$ from $S^B$. The sheet must learn which combinations of forces at different locations to physically respond to (e.g., at $x$ and $y$ since they distinguish $S^A$ vs. $S^B$) and which combinations to ignore (e.g., at $z$). By learning such “features,” the sheet can generalize, i.e., respond correctly to unseen patterns with the same correlations.

In this way, learning can be contrasted with memory in mechanics (44). A robust trained memory shows the correct response for all training examples (i.e., low training error), with no consideration of response to novel inputs. In contrast, we seek correct responses to unseen examples (i.e., low test error), even at some expense of training error. In this view, large sheets trained with limited training examples memorize, while smaller sheets with more training examples generalize.

Despite this similarity of our learning model to computational machine learning, it also differs significantly from machine-learning algorithms in important ways.

Physical in situ training.

The most significant difference is that our learning is not carried out on a computer, but, rather, is the result of a natural physical process that changes crease stiffness in response to crease strain. That is, our sheet changes autonomously (adapts) to physical examples of desired behaviors and, consequently, exhibits desired behaviors. Materials with such intrinsic mechanical learning can be trained by an end-user, in situ, using examples of real forces relevant to the task at hand, rather than by a designer with a theoretical specification of use cases; such behaviors are sought, e.g., in adaptive robotics (45). Thus, we envision such physical learning as offering significant benefits compared to traditional machine learning and computational design in general.

Physical plausible local training.

Physical plausibility of learning rules also constrain what can be learned; e.g., to maintain physical plausibility, we only explored a “local” learning rule where stiffness of crease $i$ is changed only by strain in crease $i$ and not creases far away. Learning models in neuroscience are often restricted to be similarly local for biological plausibility (e.g., Hebb’s rule). In contrast, artificial neural networks, trained on computers, face no such constraint; e.g., weights can be updated through back propagation to minimize a loss function, a highly nonlocal operation.

Our reliance on a physically plausible local process, instead of minimizing a loss function, might limit our capabilities compared to artificial neural networks. However, experience in neuroscience suggests that these limitations might be weaker than naively expected (46, 47). For example, our local learning rules can still learn nonlocal correlations in input forces since the sheet’s folding response to input forces is nonlocal, a property exploited by biological neural networks as well (24, 25).

Finally, unlike typical machine-learning methods, our restriction to physically plausible learning rules that soften creases in proportion to strain allows for some interpretation for “weights” (i.e., crease stiffnesses) learned. For example, if a force pattern results in an incorrectly folded structure, strongly folded creases due to this force will be stiffer than average after training. A more systematic understanding of the trade-offs between physical plausibility, interpretability, and computational power of learning rules is critical to understand the limits of learned behavior in matter.

Data Availability.

Data and Matlab codes for training origami sheets are included in Datasets S1–S4.