Bayesian Regression-Based Developmental Norms for the Benton Facial Recognition Test in Males and Females

Abstract

Face identity recognition is important for social interaction and is impaired in a range of clinical populations, including several neurodevelopmental disorders. The Benton Facial Recognition Test (BFRT; Benton & Van Allen, 1968), a widely used assessment of identity recognition, is the only standardized test of face identity perception rather than face memory that has been normed on children and adolescents. However, existing norms on the BFRT are suboptimal, with several ages not represented and no established time limit (which can lead to inflated scores by allowing individuals with prosopagnosia to use feature-matching). Here we address these issues with a large normative dataset of children and adolescents (ages 5–17, N=398) and adults (ages 18–55; N=120) who completed a time-limited version of the BFRT. Using Bayesian regression, we demonstrate that face identity perception increases asymptotically from childhood through adulthood and provide continuous norms based on age and sex that can be used to calculate standard scores. We show that our time limit of 16 seconds per item yields scores comparable to existing norms without time limits from non-prosopagnostic samples. We also find that females (N=156) score significantly higher than males (N=362), supporting the existence of a female superiority effect for face identification. Overall, these results provide more robust norms for the BFRT and promote future research on face identity perception in developmental populations.

Background

The Benton Facial Recognition Test (BFRT; Benton & Van Allen, 1968) is a standardized, commercially available neuropsychological test of face identity perception. The BFRT was first developed by neuropsychologist Arthur Benton in order to assess the face recognition abilities of brain-damaged patients who suffered from profound, isolated impairment in individual face recognition (a condition known as prosopagnosia; Benton, 1980). The BFRT is one of the most commonly used neuropsychological tests in clinical settings (Rabin, Barr, & Burton, 2005) and has also been utilized extensively to study face recognition impairment in a variety of clinical populations, including those with developmental prosopagnosia (Barton, Cherkasova, Press, Intriligator, & O’Connor, 2003; Duchaine, 2000), schizophrenia (Sachse et al., 2014; Whittaker, Deakin, & Tomenson, 2001), and autism spectrum disorder (ASD; Annaz, Karmiloff-Smith, Johnson, & Thomas, 2009; Sachse et al., 2014; Webb et al., 2012). The test requires individuals to match the identity of a photograph of a target face (presented at the top of the page) to test face(s) presented simultaneously below the target face. The BFRT consists of two phases. In the first phase, all photographs are of fully-lit, forward-oriented faces, and patients are asked to match one target face to one of six test faces. This phase is shorter (6 items) and easier, as the test and target photographs are identical. In the second phase (16 items), target faces differ from test faces in either the orientation or the lighting of the face, and patients are asked to match one target face to three of six test faces. Because it requires identity matching across changes in visual conditions, the BFRT measures an individual’s ability to form invariant representations of facial identity.

The BFRT has been widely used for decades, with considerable data on its clinical utility and sensitivity to developmental change. It has a number of desirable properties, including the lack of ceiling effects in typical populations (Benton & Van Allen, 1972) and floor effects in clinical populations in all but the youngest ages (e.g., Annaz et al., 2009; Barton et al., 2003), thus allowing accurate measurement of a very broad range of face perception skill. Because the BFRT presents the target face and test faces simultaneously, it provides an assessment of face identity perceptual skill; in fact, it is the only standardized test of face identity perception rather than face memory that has been normed in children, adolescents, and adults¹. This is an important distinction, as evidence from both neuropsychiatric patients (Tippett, Miller, & Farah, 2000; Williams, Berberovic, & Mattingley, 2007) and typical adults (Bowles et al., 2009) indicates that face memory and face identity perception are dissociable. The ability to assess identity perception independent of face memory is therefore vital to understanding which processes are disrupted for a given patient or clinical disorder.

Despite these strengths, the current implementation of the BFRT allows individuals with a clinically significant face recognition impairment to score in the normal range by using atypical face processing strategies, such as feature-matching (Duchaine, 2000; Duchaine & Nakayama, 2004). Such strategies are often time-intensive (e.g., Delvenne, Seron, Coyette, & Rossion, 2004), and the absence of a time limit on the BFRT allows patients unrestricted access to them. The use of face-matching tasks with time limits has been shown to improve sensitivity to recognition impairment (Nunn, Postma, & Pearson, 2001). Thus, the introduction of a time limit for the BFRT is an important first step to enhancing the sensitivity of the test. The utility of the BFRT is also limited by suboptimal norms, particularly for children and adolescents. Existing norms for the BFRT have not been updated since the initial publication of the instrument manual 35 years ago (Benton, Sivan, Hamsher, Varney, & Spreen, 1983). Norms for adults ages 16–74 are based on a sample of only 286 participants, with no information provided on the distribution of ages within the sample. While expected scores are available for children ages 6–14, the number of participants in each age bin is small (ranging from 19–59), and norms for ages 12 and 15 are absent (Benton, Sivan, Hamsher, & Varney, 1994). Finally, expected variability (SD) of BFRT scores is not available in the child data, preventing the calculation of standard scores. Since the BFRT is the only test of identity perception normed for children and adolescents, these flaws prevent accurate measurement with standardized scores of individual variability in face perception ability, especially in developmental samples. This is a serious challenge to the clinical assessment of face perception ability and to scientific progress in this field. The present study sought to address these limitations by providing updated norms for a time-limited version of the BFRT.

There are generally two distinct approaches to norming: traditional age binning and regression-based norming (Oosterhuis, van der Ark, & Sijtsma, 2016). The traditional approach, used for the existing BFRT norms, groups participants into discrete bins based on age and relevant demographic variables and provides expected scores separately for each bin. Although the traditional approach is the most frequently utilized (Oosterhuis et al., 2016), it has two main disadvantages. First, boundaries between age bins are defined arbitrarily. These arbitrary decisions can greatly influence the interpretation of an individual’s test performance, giving rise to abrupt shifts in standard score between bins despite little change in actual test performance (Zachary & Gorsuch, 1985). This is particularly problematic during periods of rapid development, when the expected score may increase substantially between adjacent age bins. Second, traditional norming approaches require large sample sizes to achieve precise estimates of expected score, since estimates are calculated based only on the subgroup of participants in a given age bin. In contrast, regression-based norming relies on regression models to provide continuous age-based estimates of expected score based on the entire sample. Regression-based norming thereby avoids arbitrary decisions of traditional norming while simultaneously achieving more precise score estimates for a given sample size (Oosterhuis et al., 2016). In light of these advantages, the present study selected a regression-based norming approach to provide updated norms on the BFRT.

Existing applications of regression-based norming procedures to behavioral tasks have focused on conventional ordinary least squares (OLS) regression models. These models are fast and simple to compute, familiar to a wide audience, and easy to interpret. However, OLS regression techniques require that the data adhere to a set of traditional model assumptions. This restricts the applicability of OLS regression-based norms and limits the type of information that this type of norming can capture. For example, OLS regression-based norms cannot accommodate data in which the expected variance in the dependent variable changes meaningfully over the values of a predictor (e.g., age), as this violates the assumption of homoscedasticity. Bayesian approaches, on the other hand, are flexible, allowing for nonlinear relationships between predictors and dependent variables, and they provide estimates of predictive uncertainty that may vary over values of predictors. Furthermore, they supply rich information on the distribution of possible predicted values, allowing for deeper understanding of the precision and stability of the regression model.

In addition to a need for developmental norms for the BFRT, several recent studies have provided evidence of sex differences in face recognition, with females showing better performance than males on face detection (McBain, Norton, & Chen, 2009), face perception (Bowles et al., 2009; Megreya, Bindemann, & Havard, 2011; Sommer, Hildebrandt, Kunina-Habenicht, Schacht, & Wilhelm, 2013), and face memory tasks (Bowles et al., 2009; Heisz, Pottruff, & Shore, 2013; McBain et al., 2009; Sommer et al., 2013). These findings indicate that typical performance on face recognition tasks may differ between males and females, underscoring the need for separate male and female norms for standardized face recognition tests.

In summary, the current study aimed to establish a standard time limit for the BFRT, examine sex differences in BFRT performance, and provide new Bayesian regression-based norms for the BFRT in a sample of typically-developing children, adolescents, and adults.

Method

Participants

518 typically-developing individuals completed the BFRT as part of a core phenotyping battery used across a variety of studies on autism conducted at the Yale Child Study Center and the Center for Autism Research (CAR) at the Children’s Hospital of Philadelphia. Participants were enrolled as control subjects for studies on face recognition, social cognition, and/or brain function in ASD. Participants were excluded if they had an uncorrected auditory or visual impairment, a history of traumatic brain injury, a known syndromic genetic disorder, a neurologic disorder, or history of a DSM-IV Axis I disorder or significant symptoms of an Axis I disorder based on the Child Symptom Inventory (Gadow & Sprafkin, 2002) and/or expert clinical judgment. All participants underwent a standard intelligence test selected from the following based on age and language level, as well as on the specific study protocol: Wechsler Intelligence Scales for Children – Fourth Edition (Wechsler et al., 2003), Differential Ability Scales – II (Elliott, 2007), Wechsler Abbreviated Scales of Intelligence (Wechsler, 1999), or Wechsler Preschool and Primary Scales of Intelligence – Third Edition (Wechsler, 2002). As past research has demonstrated strong concurrent validity (Pearson correlations > .80) between overall scores on these instruments in typical development (Dumont, Willis, & Elliott, 2009; D Wechsler, 1991), scores were combined into a single IQ variable for the present study. The final sample consisted of 398 children and adolescents (ages 5–17) and 120 adults (ages 18–55; see Table 1 for sample characteristics). Because the parent studies for which this normative sample was collected were focused on comparisons to autism, where there are many more males than females, the normative sample is also skewed in favor of more males.

Table 1.

Characteristics of the study sample, both within and across sexes.

	N			Chronological age (yrs)			IQ
	Yale	CAR	Total	Mean	SD	Range	Mean	SD	Range
Female	104	52	156	15.94	7.92	5–49	113.24	13.00	79–147
Male	189	173	362	14.30	6.42	6–55	113.41	15.57	72–155
Total	293	225	518	14.79	6.94	5–55	113.36	14.83	72–155

Due to differences in record-keeping across sites, race and ethnicity information was not available for participants from Yale, but was available for all participants from CAR. The sample from CAR was predominantly white (75%; N = 171), but also included black (16%; N = 35) and Asian (1%; N = 3) participants, as well as participants who were biracial/other unspecified race (7%; N = 16). With regard to ethnicity, the sample from CAR was predominantly non-Hispanic (89%; N = 200), with a minority of Hispanic participants (4%; N = 10) and participants who did not report ethnicity (7%; N = 15). Because race and ethnicity information were not available for all participants, these variables were not included in the norming analyses. Nevertheless, additional analyses were carried out to investigate possible effects of these variables on BFRT scores (see “Differences in BFRT by demographic group”).

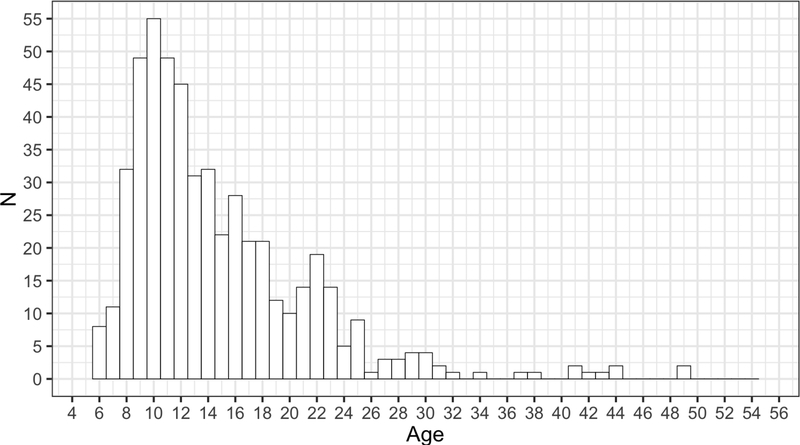
It should be noted that, though our sample has above-average intelligence (mean IQ = 113.36), IQ did not significantly predict BFRT raw score after controlling for age (b = −0.01, 95% highest density interval [−0.05, 0.03]). Moreover, previous research indicates that IQ is not correlated with face identity discrimination in typically-developing controls (Pallett, Cohen, & Dobkins, 2014). In addition, it is important to emphasize that the density of our sample sharply decreased in the older age range (starting at 33 years of age; Figure 1). Because Bayesian regression models are able to handle sparse data and provide continuous estimations of predictive uncertainty, we retained these participants in the model. However, the accuracy and utility of our norming model for individuals 33 years of age and older is limited, and additional efforts to create robust and reliable continuous norms for this age range are still needed.

Figure 1.

Histogram displaying the age distribution of the full study sample.

BFRT administration

For each trial, the experimenter instructed the participant by pointing to the reference face and saying, “Do you see this person here?” then pointing to the test faces and saying, “Find that person down here” (or “Find three pictures of that person down here” for applicable trials). The examiner prompted for answers after 12 seconds by saying, “Do you have an answer?” and at 16 seconds began to turn the page and request final answers. The participant was only given credit for responses given within the 16-second time limit. The time limit was established during extensive piloting with cases and controls before the study began, and is not prescribed by the BFRT manual. The authors’ previous experience with the BFRT indicated that typically-developing children and adults very rarely took more than 10 seconds per item, and that individuals with acquired prosopagnosia tended to engage in extensive feature-matching and only scored above chance when allowed unlimited time (often several minutes per item). Based on this experience, 16 seconds was chosen as a generous but reasonable time limit in order to make the test more sensitive and specific. This time limit is consistent with results from other research groups, who found that adults exhibit a mean response time of 10.17 seconds on BFRT items (with 16.9 seconds corresponding to the 95^th percentile of response times; Rossion & Michel, 2018) and that individuals with prosopagnosia frequently take more than one minute to respond to BFRT items (Busigny & Rossion, 2010; Delvenne et al., 2004; Duchaine, 2000).

In the current sample, 5 participants completed a short form of the BFRT (Levin, Hamsher, & Benton, 1975), and their scores were converted into long form scores using a published conversion rule (Benton et al., 1994).

Bayesian regression-based norming

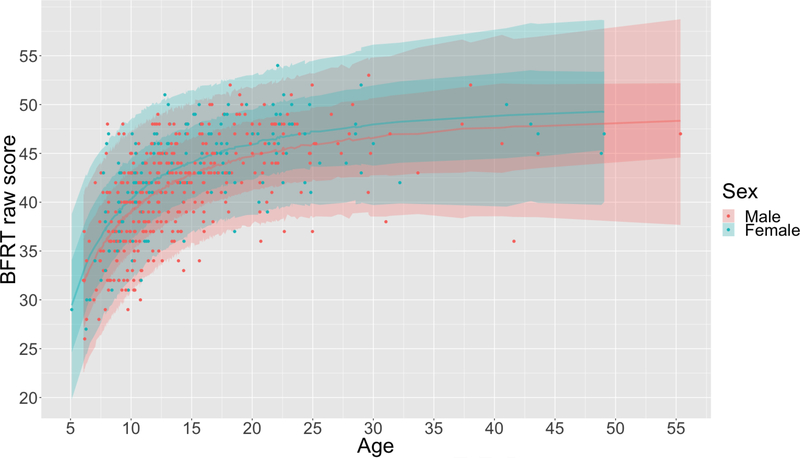
As expected, BFRT scores improved with age (Bayesian estimated ρ = .58, probability of a positive correlation > 0.999), but the relationship between age and BFRT score was nonlinear (Figure 2), making linear regression models inappropriate for norming. Previous literature utilizing regression-based norming has accounted for nonlinear relationships by including both age and age² as predictors in the regression models (Argento et al., 2016; Smerbeck et al., 2012; Van Breukelen & Vlaeyen, 2005; Van der Elst, Hurks, Wassenberg, Meijs, & Jolles, 2011; Van der Elst, Van Boxtel, Van Breukelen, & Jolles, 2006). However, quadratic models are likely to be less appropriate than other nonlinear models when modeling the development of abilities with strong maturational components. Such abilities often exhibit threshold effects (Roberts, 1986), in which initial rapid development gradually plateaus over time. These thresholded patterns of development are more accurately modeled by inverse functions (i.e., by including age⁻¹ as a predictor) rather than quadratic functions. Thus, multiple nonlinear Bayesian regressions (inverse, quadratic) were run between age and observed BFRT score and compared with a linear Bayesian model in order to determine the model of best fit. Age was centered prior to calculation of the quadratic age term to avoid multicollinearity. For all analyses, we assessed goodness of fit using the Widely Applicable Information Criterion (WAIC; Watanabe, 2010).

Figure 2.

Developmental pattern of BFRT raw scores and inverse Bayesian regression model for expected BRFT score based on age in males and females. Lines represent predicted BFRT score, while bands represent 68% (darker) and 95% (lighter) highest density intervals (HDIs) of the prediction distribution.

In contrast to OLS regression, which involves minimizing the residual sum of squares of the regression model and provides single point estimates of predicted values, Bayesian regression uses Bayes’ rule to produce a distribution of values for model parameters (i.e., posterior distributions) based on the data and the prior distributions of model parameters. Thus, Bayesian models provide probabilistic distributions for unobserved values of the dependent variable, given observed values of predictors (see Kruschke, 2014 for an introduction to Bayesian regression). In this way, Bayesian regression models yields continuous estimates of predictive uncertainty over values of predictors.

For the present study, Bayesian models were estimated using the Stan software (version 2.18.2; Stan Development Team, 2019) accessed via the brms package (version 2.8.0; Bürkner, 2017) in R (version 3.4.4). Each parameter was fit with four sampling chains, each consisting of 2000 draws from the posterior distribution; the first 1000 draws are used to tune the model parameters and subsequently discarded, while the second 1000 draws are retained in the posterior prediction distribution. Therefore, the prediction distribution contained 4000 draws of predicted values for every model parameter. As we did not have strong a priori hypotheses regarding the distribution of model parameters, prior distributions for regression coefficients were specified to be weakly informative normal distributions (N(0, 3) for age and sex; N(0, 150) for age⁻¹; following Baldwin & Larson, 2017). Prior distributions for regression intercepts were defined as half student-t distributions with three degrees of freedom and scaled to the standard deviation of the response variable (a common recommendation for non-binary parameters; Gelman, Jakulin, Pittau, & Su, 2008). With regard to modeling expected score variability, Bayesian regression conveniently allows modelling residual variance σ as a function of other predictors within a single regression model. Since we did not have a strong a priori hypothesis regarding the shape of the relationship between age and residual variance, we estimated the form of the relationship using splines (Wood, 2004).

Calculating standard scores

Following Marquand and colleagues (2016), we sought to extend a normative probability mapping approach to our behavioral data. Normative probability mapping uses Bayesian modeling to estimate the normative distribution of a response variable of interest across levels of relevant predictors. It then uses this normative model to predict the value of the response variable for a new individual based on the normative distribution. The discrepancy between the individual’s actual score and the expected score based on the normative distribution is normalized by the uncertainty of the prediction and the average degree of variation in scores in the normative population to produce a standardized z-score. That is, for each individual i, the z-score z_i is given by:

$$z_i=\frac{y_i-{\widehat{y}}_i}{\sqrt{{\sigma }_i^2+{\sigma }_n^2}},$$ (1)

where y_i is the individual’s actual score, ${\widehat{y}}_i$ is the individual’s predicted score, σ_i² is the variance of the prediction distribution (i.e., the predictive uncertainty), and σ_n² is the variance of the residuals in the normative sample. To yield interpretable, traditional standard scores with a mean of 100 and standard deviation of 15 (Groth-Marnat, 2009; Popham, 2000), these z-scores can then be rescaled via the following equation:

$$S{S}_i=z_i*\frac{15}{{\sigma }_z}+100,$$ (2)

where SS_i is the individual’s standard score, z_i is the individual’s z-score and σ_z is the standard deviation of z scores in the norming sample.

Investigating model precision, reliability, and stability

The precision of parameter coefficient estimates was assessed by examining the 95% highest density interval (HDIs) for each parameter; HDIs are the upper and lower limits containing 95% of the posterior prediction distribution for the parameter, thus describing the precision of parameter estimates. To investigate model reliability and stability, 10-fold cross-validation was conducted 10 times with random ordering of participants. This involved dividing participants into 10 equally-sized groups, or folds, and for each unique fold (1) estimating the Bayesian regression model using the 9 other folds (the training set), (2) calculating the predicted values from this training model on the data from the unique fold (the test set), (3) comparing the predicted values to the actual observed values in the test set. This was repeated 10 times with ordering of participants was randomized each time. Thus, for each of the 10 iterations of 10-fold cross validation, each individual in the norming sample was included in the test set one time, yielding one predicted value and one actual observed value for each individual in each iteration. Model performance was evaluated by computing the average Pearson correlation and root mean square error (RMSE) between the predicted values and actual values in a given iteration. This provided an index of the predictive accuracy of the model on unseen data and whether model performance was stable across different subsets of the norming sample.

Results

Raw BFRT scores and comparison to existing norms

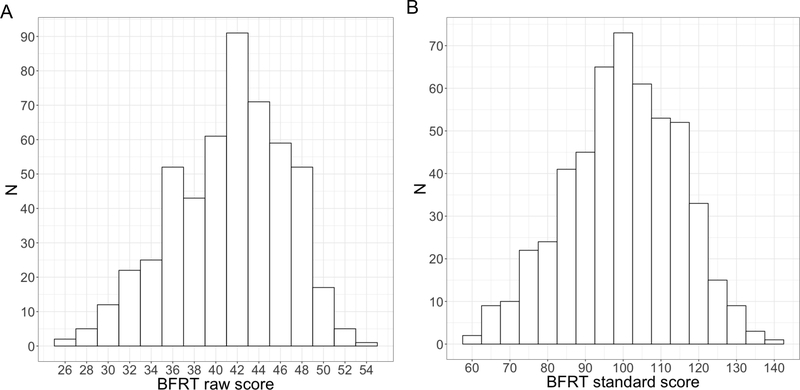
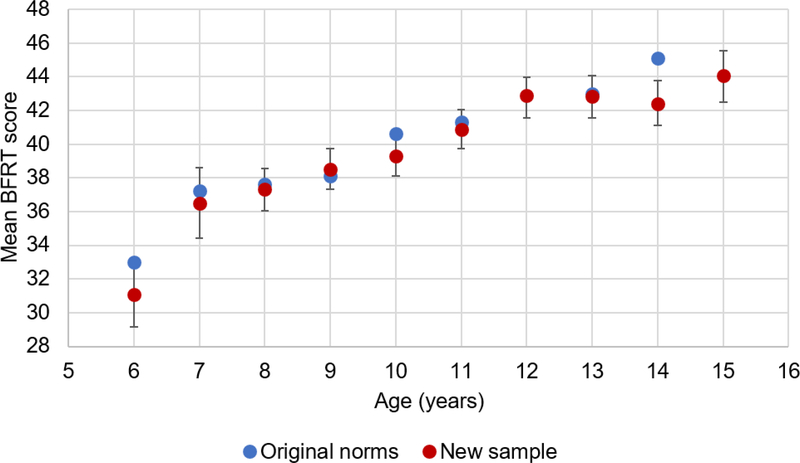
Raw BFRT scores were approximately normally distributed (Shapiro-Wilk W = .98; Figure 3), with a mean score of 41.20 for males and 43.03 for females. The addition of the 16-second time limit did not appear to significantly alter BFRT performance in typically-developing individuals, as the mean score (45.42) and standard deviation of scores (3.64) for adults in the present sample were remarkably similar to previously established norms for adults in the same age range (16 and above; mean = 45.4, SD = 3.96; Benton et al., 1994). Mean scores in the sample of children and adolescents were similarly comparable to original norms, where available (Figure 4).

Figure 3.

Distribution of BFRT scores in the norming sample. (A) Histogram of raw scores. (B) Histogram of standard scores.

Figure 4.

Comparison of BFRT scores in the new norming sample to original BFRT norms. Error bars represent bootstrapped 95% HDIs for the mean in the new norming sample (measures of score variability were not provided for original norms). Original norms did not include scores for ages 12 or 15.

Differences in raw BFRT score by demographic group

Bayesian estimation (BEST) methods for two groups were used to test whether BFRT score differed based on demographic features. BEST, implemented with the BayesianFirstAid package in R (Bååth, 2014), uses a Bayesian Markov chain Monte Carlo process to generate posterior estimates for group means and standard deviations. It provides a 95% HDI for the difference in means between two groups, reflecting the upper and lower limits containing 95% of the posterior prediction of mean difference between groups, as well as the probability that group 1 has a higher mean than group 2 (p_b); it is thus a Bayesian analogue to the t-test. BEST revealed that females in our sample scored significantly higher than males, as the 95% HDI did not include 0 (females: mean = 43.03, SD = 5.28; males: mean = 41.20, SD = 5.15; Cohen’s d = 0.35; 95% HDI [0.88, 2.90], p_b > 0.999). This is consistent with evidence of female superiority across a variety of face processing tasks (Bowles et al., 2009; Heisz et al., 2013; McBain et al., 2009; Rossion & Michel, 2018; Sommer et al., 2013). Thus, sex was coded as a dummy variable (with males as the reference group) and included as a predictor in the regression models for BFRT score.

Given that all faces included in the BFRT are white, it was also important to test the potential effects of race and ethnicity on BFRT score. Within the sample of participants with available race and ethnicity data, a preliminary Bayesian regression model for BFRT score with race as a dummy-coded variable (0 = white, 1 = black, 2 = other) was carried out to investigate whether BFRT scores differed between racial groups. The 95% HDI for the race regression coefficient was inspected to determine whether race was significantly related to BFRT scores. In this model, race did not significantly predict BFRT score, as the 95% HDI for the race parameter included 0 (95% HDI [−0.75, 1.41]). Because the “other” group was relatively small (N = 19) and heterogeneous, BEST was used to explore possible differences in BFRT score between the white and black participants specifically. Consistent with the regression analysis, no significant differences were identified (white: mean = 39.87, SD = 5.21; black: mean = 41.11, SD = 4.64; 95% HDI [−3.10, 0.50], p_b = .08). In addition, BEST was used to test the possible influence of ethnicity on BFRT score; this again found no differences between Hispanic and non-Hispanic participants (Hispanic: mean = 41.10, SD = 3.87; non-Hispanic: mean = 40.11, SD = 5.21; 95% HDI [−2.10, 4.00], p_b = .76). Thus, based on available results from a subset of our full sample, race and ethnicity did not appear to significantly influence BFRT scores, and were not considered further.

Bayesian norm model and standard scores

An inverse model was the best fit for the data based on the WAIC goodness-of-fit metric (inverse WAIC = 2900.87; linear WAIC = 2979.91; quadratic WAIC = 2925.84). Both age⁻¹ and sex were significant predictors of BFRT score, in that their 95% HDIs did not include 0. See Table 2 for results of the inverse regression model.

Table 2.

Results of inverse regression model for expected BFRT score.

Predictor	b	Lower 95% HDI limit	Upper 95% HDI limit
Intercept	50.41	49.35	51.49
Age−1	−113.59	−126.43	−101.14
Sex	1.28	0.55	2.02

Note. HDI = highest density interval.

The inverse regression model was used to generate individual z-scores for all participants in the norming sample using the formula provided in Equation 1. The average variance of the model residuals (σ_n²) was found to be 15.63, corresponding to a standard deviation of 3.95. Using these values yielded z-scores with a mean of 0 and standard deviation of 0.70. Updating the formula for conversion from z-scores to standard scores provided in Equation 2 yields the following formula:

$$S{S}_i=21.41*z_i+100$$ (3)

Computing standard scores in this fashion yielded a mean score of 99.95 and standard deviation of 15.00, consonant with the expected mean of 100 and standard deviation of 15. (See supplementary materials for an easy-to-use calculator that computes BFRT standard scores, given an individual’s age, sex, and raw score.)

Sex differences

To determine the overall effect size of the sex difference in BFRT score between males and females after controlling for the effects of age, standard scores were computed for female participants in the norming sample according to male norms. This yielded a mean standard score of 104.84 for females in the present sample (compared to 99.94 for males), reflecting a significant sex difference of a third of a standard deviation (95% HDI [2.00, 7.60], p_b > .999; Cohen’s d = 0.33).

In addition to analyzing the main effect of sex on face identity recognition ability, we also aimed to explore the developmental trajectory of sex differences in face identity recognition. While there is abundant literature supporting the existence of female superiority in identity recognition ability (e.g., McBain et al., 2009; Megreya et al., 2011), the timeline of emergence for this effect remains unclear. Some studies have found that sex differences in face memory are present in childhood (Rehnman & Herlitz, 2007), but the trajectory of sex differences in identity matching is less studied. In the present study, no significant interaction was found between age⁻¹ and sex when the interaction term was included in the overall Bayesian regression model (b = 0.85, 95% HDI [−22.72, 24.65]), indicating that sex differences are consistent across development. However, because our study was not sufficiently powered to fully investigate the developmental trajectory of sex differences, these results should be considered exploratory.

Cross-validation results

The mean Pearson correlation between predicted and actual observed BFRT scores within the 10-fold cross-validation was 0.65 (range: 0.65 – 0.66), indicating that predicted scores were consistently strongly correlated with actual scores. These correlations were nearly identical to the correlation between predicted and actual observed BFRT scores from the full model (r = 0.66). Similarly, the mean RMSE between predicted and actual BFRT scores within the 10-fold cross-validation was 3.97 (range: 3.97 – 3.98), comparable to the RMSE of 3.95 in the full model. These results demonstrate that model performance did not change substantially when it was estimated from smaller random subsets of the overall dataset, supporting the robustness of results and stability of the model.

Discussion

The present study provides new norms for a time limit-based administration of each item of the BFRT, one of the most widely used standardized tests of face identity recognition. A Bayesian regression-based approach was used to calculate standard scores with a large normative sample of children, adolescents, and adults. These continuous norms can be used to calculate age-based standard scores for individuals 5 to 55 years of age (5 to 49 for females). Analyses revealed several notable features of these norms, which merit further emphasis.

First, adult scores on the time-limited administration did not differ from the original adult norms, which could be expected from empirical data showing that adults usually respond well within the 16 second limit (Rossion & Michel, 2018). The time limit-based version of the BFRT should enhance the sensitivity of the test in special populations with real-life face recognition impairments such as prosopagnosia, some of whom have been observed in prior research to use time intensive feature-matching strategies. These strategies often (Busigny & Rossion, 2010; Delvenne et al., 2004; Duchaine, 2000), but not always (e.g., Duchaine & Nakayama, 2004), take more than 16 seconds. Nevertheless, the addition of a time limit to the BFRT is an important step toward improving measurement sensitivity for individuals who struggle to accurately and efficiently recognize facial identity day to day.

Second, there was a clear nonlinear relationship between age and face identity perception ability, with ability increasing most rapidly in early childhood. Furthermore, regression analyses showed that face identity perception ability increases monotonically with age, but the rate of change of ability gradually decreases with age, asymptotically approaching zero by middle adulthood. These findings parallel evidence that face memory improves throughout adulthood, peaking in the early 30s (Germine, Duchaine, & Nakayama, 2011; Susilo, Germine, & Duchaine, 2013). These growth patterns support the need for new age-dependent BFRT norms, the importance of including a broad age range in norm development, and the sensitivity of the BFRT to developmental change in identity perception.

Third, females scored slightly but significantly higher on the BFRT than males (Cohen’s d = 0.33). This finding is consistent with previous reports of female superiority in face identity detection, discrimination, and memory (McBain et al., 2009; Sommer et al., 2013) and with a recent large study on a computerized version of the BFRT in adults (Rossion & Michel, 2018). Collectively, these findings provide support for superior face identity recognition in females, and underscore the importance of having separate norms for males and females.

Limitations & Future Directions

The present study is among the first to apply Bayesian approaches to regression-based norming, and (to the authors’ knowledge) the first to utilize a normative probability mapping approach with behavioral data. This approach allowed for continuous estimation of the precision of predictions over values of predictors and yielded flexible, robust norms. In addition, though weakly informative priors were utilized in the present study, Bayesian modeling is also advantageous for its ability to incorporate a priori predictions about the distributions of model parameters. Researchers seeking to implement regression-based norming approaches should consider utilizing Bayesian modeling especially when working with developmental samples where there is increased possibility for heteroscedasticity and nonlinear skill growth with age.

Despite growing evidence of better face recognition ability in females relative to males, the reason for this effect remains unknown. One possible explanation is that greater early preference for faces in female infants provides more experience with faces, leading to the development of better face processing over time (Connellan, Baron-Cohen, Wheelwright, Batki, & Ahluwalia, 2000). Other potential contributing factors include both biological (e.g., differing effects of sex hormones on brain development; Knickmeyer & Baron-Cohen, 2006) and cultural (e.g., gender socialization; McClure, 2000) influences. While the present study did not find that age moderated sex differences in face recognition ability, it was not adequately powered to determine when in development these sex differences emerge. Recent research has highlighted puberty as a period when the face processing system recalibrates away from being attuned to discriminating the faces of adult caregivers toward being attuned to discriminating the faces of peers (Picci & Scherf, 2016; Scherf & Scott, 2012), and sex differences in this crucial period could potentially contribute to the female superiority effect. Further research is needed to elucidate the causes and time course of sex differences in face identity recognition.

As with any empirical study, our findings should be interpreted and applied in light of the limitations of our sample. In particular, the present study was limited in its ability to assess the effects of race on BFRT performance, as race information was only available for a subset of participants and participants were predominantly white. However, tests of the relationship between race and BFRT scores in the subset of participants for whom race information was available revealed no significant influence of race on face recognition ability. Thus, while these norms are most appropriate and well-validated for white individuals, we believe that they are still preliminarily applicable to individuals of other races. Additional investigation of the effect of race on BFRT performance including a more racially and ethnically diverse sample is needed to help address these limitations.

The addition of a standard time limit and robust norms for the BFRT across a wide age span opens the door for more accurate assessment of face identity perception in children and adolescents with briefer total time for test administration. Much of the extant literature on the developmental trajectory of face identity recognition has utilized tasks dependent on face memory (Carey, Diamond, & Woods, 1980; Dalrymple, Visconti di Oleggio Castello, Elison, & Gobbini, 2017; Germine et al., 2011; Susilo et al., 2013). Recent research has investigated the quantitative development of face recognition using tasks that exhibit ceiling effects in adults (e.g., Johnston et al., 2011) or that recruit additional higher-order cognitive processes, such as those that require participants to perform similarity judgments on morphed faces (e.g., Weigelt et al., 2014). Only a few studies to date have examined the development of face identity recognition across the lifespan using simple face-matching tasks like the BTFR, which draw on perceptual processing and not memory processing; this might be due to the lack of well-normed assessment tools for face perception skill. By accounting for typical developmental variation in identity perception ability, these new norms for the BFRT allow researchers to investigate the factors linked specifically with the development of face identity recognition ability and to examine relationships between face identity perceptual processes and memory processes.

Notably, our results regarding the asymptotic developmental trajectory of face recognition abilities are in close alignment with existing literature on the developmental timecourse of face memory (Germine et al., 2011), face identity discrimination (Weigelt et al., 2014), and simple face matching (Megreya & Bindemann, 2015), at least through middle adulthood. Across these studies, the face recognition abilities of early school-aged children improved rapidly and continued to improve throughout young adulthood, but growth slowed with age. This suggests that the BFRT appears to show the same developmental trajectory as other tasks. However, our sample did not exhibit a systematic decline in identity recognition ability after age 33, which has been previously found for both face memory and face matching (Germine et al., 2011; Megreya & Bindemann, 2015). This may be due to differences in experimental tasks, but could also be associated with the decreased sample density for older adults in the present study. As such, the norms offered for other adults (i.e., individuals over the age of 33) in the present study should be considered preliminary. Future research elucidating the expected trajectory of performance on the BFRT in later adulthood could help to both improve the normative data for the BFRT and inform understanding of the development of face recognition ability across the lifespan.

These new norms also pave the way for research on atypical development of face identity perception. Impairment in face identity recognition has been identified in a variety of neurodevelopmental disorders, including autism spectrum disorder (ASD) (Weigelt, Koldewyn, & Kanwisher, 2012; Wolf et al., 2008) and developmental prosopagnosia (Duchaine & Nakayama, 2004). Face recognition deficits are important constructs to study in these populations, as they are associated with greater social impairment and social inhibition (Parish-Morris et al., 2013; Yardley, McDermott, Pisarski, Duchaine, & Nakayama, 2008), and early impairments in face perception may contribute to the development of social interaction difficulties (Dawson, Webb, & McPartland, 2005; Schultz, 2005). Recently, researchers have argued that the face identity recognition deficits observed in ASD result from disruptions in face memory rather than identity perception (Weigelt et al., 2012), suggesting that these systems may be selectively affected by neurodevelopmental disorder. However, the absence of adequate developmental norms for simultaneous-presentation face recognition tests has limited the research on identity perception in neurodevelopmental disorders to date. The addition of new norms for the BFRT will allow researchers to control for typical developmental variation in identity perception in order to assess the degree of disorder-specific impairment. Future research should utilize these norms to examine whether face identity perception is impaired in ASD and other neurodevelopmental disorders.

It should be noted that we are not arguing that other measures of face recognition are less important than the BFRT or that the BFRT is without its limitations. There are certainly other approaches to studying face recognition that have distinct advantages over the BFRT. For example, the BFRT was not designed to assess the use of holistic face processing strategies; other tasks, such as the complete composite paradigm (Gauthier, Klaiman, & Schultz, 2009), are better suited for this purpose. Furthermore, while the BFRT avoids ceiling and floor effects in the vast majority of the population, expected scores in very young children (i.e., children less than 7 years of age) are within two standard deviations of chance. When clinical impairment is defined as scoring ≥ 2 standard deviations below the expected mean (as is often the case), this limits the utility of the BFRT from being able to discriminate between clinical impairment and typical performance in this age range. Thus, though we attempted to combat some common criticisms of the BFRT in this paper (by instituting a time limit and providing new regression-based norms), it is by no means a perfect measure. Our argument is merely that the BFRT is a simple, widely accessible, standardized test of face recognition ability that has been used extensively with neuropsychological patients and does not rely on face memory. It is thus well-suited to measure face perception ability in clinical and developmental samples.

Conclusions

The BFRT is a challenging, standardized instrument that is useful for assessing face identity perception rather than face memory. To date, the utility of the BFRT has been limited by the absence of high-quality norms for children and adolescents and by the lack of standardized protection against the use of time-intensive atypical face processing strategies. The present study supports the future use of the BFRT in both clinical and research settings by introducing a standard time limit and new regression-based norms from a large developmental sample. Results demonstrated that females significantly outperformed males on the BFRT, providing evidence of sex differences in face identity perception. These new norms can help elucidate the development and neural correlates of face identity perception in both sexes in order to better understand the face representation system and shed light on how this system functions differently among individuals with identity recognition impairment.