Protein-Protein Docking Reveals Dynamic Interactions of Tropomyosin on Actin Filaments

Abstract

Experimental approaches such as fiber diffraction and cryo-electron microscopy reconstruction have defined regulatory positions of tropomyosin on actin but have not, as yet, succeeded at determining key atomic-level contacts between these proteins or fully substantiated the dynamics of their interactions at a structural level. To overcome this deficiency, we have previously employed computational approaches to deduce global dynamics of thin filament components by energy landscape determination and molecular dynamics simulations. Still, these approaches remain computationally challenging for any complex and large macromolecular assembly like the thin filament. For example, tropomyosin cable wrapping around actin of thin filaments features both head-to-tail polymeric interactions and local twisting, both of which depart from strict superhelical symmetry. This produces a complex energy surface that is difficult to model and thus to evaluate globally. Therefore, at this stage of our understanding, assessing global molecular dynamics can prove to be inherently impractical. As an alternative, we adopted a “divide and conquer” protocol to investigate actin-tropomyosin interactions at an atomistic level. Here, we first employed unbiased protein-protein docking tools to identify binding specificity of individual tropomyosin pseudorepeat segments over the actin surface. Accordingly, tropomyosin “ligand” segments were rotated and translated over potential “target” binding sites on F-actin where the corresponding interaction energetics of billions of conformational poses were ranked by the programs PIPER and ClusPro. These data were used to assess favorable interactions and then to rebuild models of seamless and continuous tropomyosin cables over the F-actin substrate, which were optimized further by flexible fitting routines and molecular dynamics. The models generated azimuthally distinct regulatory positions for tropomyosin cables along thin filaments on actin dominated by stereo-specific head-to-tail overlap linkage. The outcomes are in good agreement with current cryo-electron microscopy topology and consistent with long-thought residue-to-residue interactions between actin and tropomyosin.

Significance

Mutations in myofibrillar proteins, including ones detected in actin and tropomyosin, are associated with cardiomyopathies and skeletal muscle disease. Their impact on muscle contraction and its regulation is uncertain because residue-by-residue level perturbations of component myofilaments are poorly defined. Absent this information, drug design and therapeutic interventions are difficult to perfect. In this study, protein-protein docking and molecular dynamics were performed to provide a comprehensive view of actin-tropomyosin interactions. Our studies provide a baseline understanding for future examination of regulatory imbalances imposed by disease-rendering mutations, potentially connecting early stage molecular insults to the development of muscle pathology.

Introduction

It is generally held that striated muscle is regulated by stepwise rearrangement of tropomyosin on the surface of actin-based thin filaments (1, 2, 3, 4). The reconfiguration of tropomyosin proceeds sequentially to block, to partially close, and then to fully open myosin-head binding sites on actin subunits, thereby controlling myosin-motor activity and hence contractility. The sequence of steps taken by tropomyosin is determined by Ca²⁺-dependent switching between Ca²⁺-free and Ca²⁺-laden troponin and additionally by the influence of myosin binding itself to actin. During muscle activation, the association of Ca²⁺ with troponin-C of the troponin complex causes troponin-I (TnI), the inhibitory subunit of troponin, to release a steric hold on tropomyosin that then facilitates TnI and tropomyosin movement away from a position on actin that had completely blocked myosin binding. Tropomyosin now can occupy a less limiting yet still partially “closed” position on actin. The closed position is permissive to weak myosin binding to actin subunits, which translates into an additional shift in tropomyosin to a more “open” position, leading to cooperative activation of the thin filament. The repositioning is accompanied by strong myosin binding and myosin-head and cross-bridge cycling on actin (1, 2, 3, 4). During relaxation, as Ca²⁺ levels drop, the process reverses. Now, to render the filament incapable of sustaining myosin binding, tropomyosin reverts with some hysteresis (5,6) to more energetically favorable closed or blocked positions, with TnI of Ca²⁺-free troponin once more buttressing tropomyosin in the blocking position to inhibit further motor activity (1, 2, 3, 4, 5, 6). The latter steps and involvement of any direct interactions between tropomyosin and myosin on actin remain poorly understood at a molecular level, whereas the blocked-to-closed transition is becoming clearer (2,3,5, 6, 7).

Please note that in the strictest sense, the terms blocked, closed, and open states refer to functional states described kinetically (2), whereas B-, C- and M-states generally refer to corresponding structural states (3). We will adhere to this nomenclature.

Tropomyosin is a coiled coil consisting of seven nonequivalent pseudorepeat modules that associate with seven successive actin subunits along thin filaments (8). Pseudorepeats consist of 39–41 residues, and each repeat can be divided further into α- and β-zones. α-zones have a somewhat more consistent amino acid sequence ready to match oppositely charged residues on actin subdomains 1 and 3, whereas β-zones are thought to bridge over the shallow aspect of actin subdomains 2 and 4 (9,10). As pointed out by Hitchcock-DeGregori, the function of tropomyosin in muscle regulation is intimately coupled to its molecular architecture, namely “tropomyosin function follows structure” (8), to which we would add that tropomyosin “form ever follows function,” satisfying a widely applicable concept first coined by Sullivan (11), but in this case, a result of evolutionary pressure and not architectural design principles. These are not just glib semantic aphorisms because as noted, the tropomyosin molecule is not a strictly canonical coiled-coil assembly with easily ascribed bioarchitecture (12). For example, it is preferentially bent to closely match the helical curvature of the actin filament, which facilitates actin binding (4,10,12, 13, 14). This bending is achieved by periodically placed noncanonical alanine residues along the elongated tropomyosin coiled coil (10). In addition, local substitution of noncanonical charged residues for buried hydrophobic amino acids appears to facilitate over- and undertwisting to more closely align coiled-coiled tropomyosin to actin filaments (12). Finally, the ends of the tropomyosin coiled coil are uniquely twisted to link head to tail to form short “four-helix bundle” junctions with adjacent molecules along thin filaments, enabling gap-free cable-like polymer formation on both sides of the actin helix (15, 16, 17, 18). As illustrated previously and in this work, tropomyosin pseudorepeats are themselves nonidentical and likely take on different characteristics, apparently linked to individualized cytoskeletal function in nonmuscle cells (18) and F-actin form-fitting requirements in muscle (4,13,14). In fact, experimental deletion of central repeat-period regions of tropomyosin, including period 4 along with its noncanonical residue Asp137, greatly reduces tropomyosin affinity for myosin-bound actin filaments but does little to tropomyosin association with myosin-free thin filaments (19,20). Conversely, deletion of internal repeats of yeast tropomyosin, yielding an ultrashort coiled coil, appears to produce unusually taut tropomyosin cables on myosin-free F-actin. Here, the cable continuity “cracks” during myosin binding, suggesting reduced dynamics (21). Such experiments underscore the need to define the basis of tropomyosin form and function reciprocity at an atomistic level.

Protein-protein docking is a well-established technique for providing insight about atomic-level interaction when high-resolution structural data are unavailable or not definitive. Computationally driven protocols have now progressed to the extent that binding proteins can be targeted to large and complex macromolecular structures (22,23). However, successful implementation of protein docking methodology is predicated on access to 1) atomic-level ligand and receptor configurations, 2) robust molecular docking programs (22,23), and in many cases, 3) biochemical and biophysical criteria to eliminate erroneous poses forbidden by experimental benchmarks (24). In the case at issue here, successful docking relies on accurate models for the thin filament F-actin “receptor” and the tropomyosin “ligand.” In an analogous case, we successfully docked well-described helical domains of troponin subunit T (TnT) to atomic models of actin-tropomyosin (24), with results in complete agreement with recent cryo-electron microscopy (cryo-EM) reconstructions (7) but now providing unparalleled residue-by-residue atomic resolution. In fact, the elegant new cryo-EM information by Yamada et al. (7) provided significant experimental structural information needed to validate our TnT docking (24) and, in this work, additionally confirms binding poses of tropomyosin on actin. Thus, we have been able to definitively ascribe residue-by-residue association of the full-length coiled coil in the troponin-free closed C-states of the thin filament.

Previous molecular dynamics studies were performed on idealized full-length tropomyosin or tropomyosin polymers on F-actin (13,14,17,25, 26, 27, 28). However, these studies may have inadvertently included local model bias in the analysis by not fully rationalizing the effects of differential local over- or undertwisting displayed by tropomyosin or its overlapping domain junction when associated with F-actin. Such a tendency is implied by the Yamada cryo-EM data (7), but the resolution there was insufficient to precisely determine residue-to-residue linkage between actin and tropomyosin. To best refine models of actin-tropomyosin interaction, we have now adopted a “divide and conquer” computational approach to assess distinctions among tropomyosin pseudorepeats and their interactions on actin filaments, employing unbiased protein-protein docking tools to identify local binding specificity of tropomyosin over the actin surface. The configuration of favorable docking poses matches electron densities cataloged by cryo-EM reconstruction very closely while providing additional atomistic detail. Indeed, our results support the view that the interaction between the tropomyosin head-to-tail overlapping domain and actin dominates the association of the rest of the complex, which then adapts to the overlap geometry and optimizes electrostatic contacts.

Materials and Methods

Protein-protein docking

To determine the position of tropomyosin on actin using a global conformational search, the programs PIPER and ClusPro (22,23) were used. However, the entire thin filament structure is too large for the docking program, so the search was conducted using a series of tropomyosin segments, each consisting of two consecutive α-zones of tropomyosin with an intervening β-zone (58 amino acids in total) docked to two actin monomers and then arranged sequentially along the long-pitch helix (three actins were used in the case of the tropomyosin overlapping domain). Here, the actin model used was from our previous work on tropomyosin-actin interactions and was initially derived from fiber diffraction studies (29). For tropomyosin, a library of ideal coiled coils was generated using published algorithms (30), with side chains defined from crystal structures (13,31) and in which each tropomyosin was rotated about its superhelical axis (pseudorotation) starting from 0 to 360° in 10° increments (with 0° as defined in (14)). Additionally, the overlapping domain (32) was grafted into each library structure and minimized. From these models, smaller tropomyosin fragments were used for docking, defined as α₁β₁α₂ (residues 8–66), α₂β₂α₃ (residues 47–105), α₃β₃α₄ (residues 86–145), α₄β₄α₅ (residues 127–184), α₅β₅α₆ (residues 165–223)_, α₆β₆α₇ (residues 205–263) segments, and N-/C-terminal overlapping domains consisting of α₁β₁α₂ (residues 1–66) and β₆α₇β₇ (residues 230–284).

Next, PIPER was used to generate large numbers (10⁹–10¹⁰) of rotated and translated tropomyosin configurations, ranking their interactions with actin according to attractive and repulsive surface complementarity as well as electrostatic, van der Waals, and hydrophobic interaction potentials. After PIPER, ClusPro was applied to ∼1000 of the lowest-energy tropomyosin-targeted actin alignments to perform a three-dimensional search for 25–50 groups of closely related “clustered” configurations, reasoning that highly populated structural arrangements most closely identified the global energy minimal of a native binding site. The highest-ranking clusters were then averaged and energy minimized. The ranking was judged according to a balanced electrostatic-van der Waals criteria (22,23). The top 10 cluster rankings for each docking based on the combination of van der Waals and electrostatic criteria were retained for further investigation, based on visual inspection of protein-protein interactions and the superimposition of the computationally created docking complexes onto the Yamada et al. (7) high-Ca²⁺ and low-Ca²⁺ cryo-EM volumes, as well as the Li et al. (14) model, with the use of Chimera (33).

Next, the docked poses were analyzed for their interaction energies with actin. First, the docked structures were minimized in NAMD (34) using the CHARMM36m force field (35) in explicit solvent containing TIP3P water and ionized with 150 mM NaCl for 5000 steps. The particle mesh Ewald method was used to calculate long-range ionic interactions. Covalent bonds involving hydrogen atoms were constrained by the SHAKE algorithm. Interaction energies were calculated using the NAMD Energy protocol of VMD (36).

Construction and refinement of tropomyosin models

Our main effort was to dock tropomyosin segments to F-actin and characterize their interactions. Once this assessment was completed, the fragments could be assembled computationally into a pseudoatomic model. Thus, after docking, the highest-ranked, energy-minimized segments were also spliced together to form a continuous tropomyosin model on F-actin by superimposing the common α-zones between two fragments and then continuing in this manner to create an entire chain. The resulting models were then subjected to molecular dynamics flexible fitting (MDFF) (37) refinement with the Yamada et al. (7) high-Ca²⁺ or low-Ca²⁺ cryo-EM volumes using secondary structure restraints and fixed troponins and actins. The model to map correlation coefficient was calculated using the ccc function of MDFF. The geometries of the atomic models were evaluated using MolProbity (38).

In addition, a model was also created starting from ideal coiled-coil structures for comparison. First, the published model of troponin T (TnT) complexed with the overlap domain of tropomyosin (24) was rigid-body fitted into the electron density map of the high-Ca²⁺ structure of the thin filament (7) using the program Chimera (33). Next, ideal coiled-coil structures of full-length tropomyosin with different pseudorotations from the tropomyosin docking library were rigid-body fitted into the same map. All pseudorotations fitted well to the map. Further analysis showed that one of these structures had its C-terminal residues positioned as indicated by the electron density map, thus starting the tropomyosin chains at a location determined by the EM data. The overlap domain was then added to this fitted ideal tropomyosin model by combining residues 12–250 of the fitted ideal coiled-coil structure and residues 251–284 from the fitted tropomyosin-TnT complex model.

Molecular dynamics flexible fitting

The models described above were then also subjected to minimization and MDFF to evaluate the constructed models further as well as to optimize their fit to the cryo-EM electron density maps (7). Dynamics were performed for 50–89 ps in NAMD (34) using the interface in VMD (36). Secondary structural restraints were used to maintain the structure of residues expected to be in helical and sheet conformations, including the junctions between fitted models in tropomyosin. With the exception of the TnT residues 89–151, which interact with tropomyosin, actin and troponin were fixed in the calculation because their positions were previously optimized in the cryo-EM map (7).

Molecular dynamics simulations in a periodic system

Once the model had been threaded into the tropomyosin overlapping domain and flexible fitting was completed, the resulting actin-tropomyosin construct was extended to a cable model in a periodic boundary system to simulate tropomyosin dynamics on an infinite filament during MD. First, the fitted model was aligned to the z axis by translating the center of mass of the system to the origin and then rotating the actin principal axis along the z axis using the orient scripts in VMD (36). Next, the actin was built out to 28 monomers by selecting the chain K actin from the model and using the actin symmetry (translating 27.52 Å and rotating −167.1318°; note that this rotation is needed to match the periodic system requirements). Then, a full tropomyosin chain was built by combining residues 1–54 of one dimer with residues 55–284 of a copy of the same dimer translated 385.28 Å and rotated 180°. This full-length tropomyosin model was used to generate three more tropomyosin dimers to give a total system size of 28 actins and four tropomyosin dimers, with two independent tropomyosin polymers on each side of the actin filament. To solvate the system, four additional tropomyosin dimers were added to each end of the system, as well as four actin monomers on either end as placeholders to exclude water placement during solvation. After addition of ions and waters with the cionize and solvate plugins in VMD (36), these placeholder molecules were removed. The box size was set at 140 × 140 × 772.56 Å using a boundary cutoff of 1.3 Å. Lastly, sodium chloride and magnesium chloride were added at concentrations of 0.15 M and 3 mM, respectively. Molecular dynamics simulations were then performed using NAMD (34) as previously carried out (14,24). In all cases, molecular dynamics was carried out using explicit solvent.

All figures were rendered with UCSF Chimera (33).

Results

Docking tropomyosin segments to F-actin

To begin, cardiac tropomyosin (αα-Tpm1.1) was divided computationally into pseudorepeat modules and then further into component α-zone segments, i.e., stretches in the repeat periods that bind to F-actin (10). Docking these fragments to F-actin using the programs PIPER and ClusPro (22,23), however, was unsatisfactory, yielding variously aberrant cross-filament interactions and little correspondence to native tropomyosin association or polarity on F-actin.

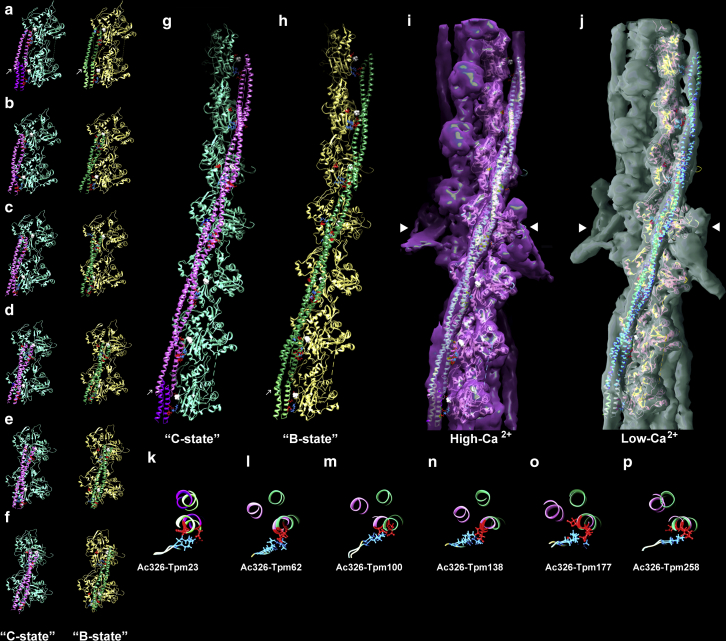
Tropomyosin was then divided computationally into a series of somewhat longer segments centered on successive tropomyosin β-zones within pseudorepeats and now flanked on both ends by their respective α-zones. This results in six overlapping α_iβ_iα_i+1 segments (i.e., α₁β₁α₂, α₂β₂α₃, α₃β₃α₄, α₄β₄α₅, α₅β₅α_6, and α₆β₆α₇) for PIPER and ClusPro docking analysis. In practice, segments α₁β₁α₂ and α₆β₆α₇ were not used because their α₁ and α₇ free ends are not configured properly when separated from the overlapping domain. Instead, a model of the overlapping N-/C-termini (i.e., β₆α₇β₇α₁β₁α₂) themselves (17,32) was docked to F-actin as part of the set of tropomyosin segments. All the tropomyosin modules contained sufficient structural information to dock along F-actin with proper orientation, polarity, and precise azimuthal positioning. The highest-scoring tropomyosin fragments docked like staples onto F-actin with easily noted electrostatic interactions between α-zone acidic amino acids and lysine residues 326 and 328 on pairs of successive actin subunits of along the filament (Table 1). The highest-ranked docking poses could be classified into three principal modes: 1) α_iβ_iα_i+1 poses with tropomyosin docked in a configuration in common with densities in the Yamada et al. high-Ca²⁺ cryo-EM reconstruction (7) (i.e., C-state like), 2) α_iβ_iα_i+1 poses with tropomyosin now docked as illustrated by the Yamada et al. low-Ca²⁺ cryo-EM reconstructions (i.e., B-state like), and 3) high-ranking overlap poses corresponding to the Yamada et al. head-to-tail tropomyosin overlap densities (Fig. 1, a–f; (7)). Very little distinction could be found among high-ranking poses for the N-/C-terminal overlap model, as if very nearly a single pose is preferred with little variance; note, this is unlike the categorization identifying two divergent high-scoring poses for the other tropomyosin fragment models examined. These trends can be best appreciated after superposition of segments of the tropomyosin poised on actin (Fig. 1, g and h), which have then been fitted to densities within the Yamada reconstructions (Fig. 1, i and j). Note the excellent correspondence of the experimental and computational models. Note also that raw PIPER and ClusPro results were used here to match the computational and cryo-EM images. Although the azimuthal position and twist of tropomyosin on F-actin in the highest-scoring poses matched those of the densities in the Yamada maps, low-scoring poses plotting to positions on the extreme outer domain as depicted in Li et al. (14) did not, nor would they, easily align to the overlapping domain.

Table 1.

Charged Residues between Tropomyosin and Actin that Closely Contact Each Other

Actin Subunit	Tpm Period	ClusPro Docking (Residue #)		MD (Residue #)
		Actin	Tpm	Actin	Tpm
7	1	326, 328	16, 20, 23	326, 328	2, 16, 20, 23
6	2	326, 328	58, 62	326, 328	58, 62
5	3	311, 326, 328	91, 96, 97, 100	326, 328	96, 100
4	4	326, 328	138, 142	326, 328	138, 142
3	5	311, 326, 328	173, 175, 177, 180, 168 (C-state only)	311, 326, 328	168, 173, 175, 177, 180
2	6	326, 328	212, 218, 219, 222	326, 328	219, 222
1	7	311, 326, 328	248, 254, 257	311, 326, 328	248, 254, 257

Residue-to-residue contacts determined for structures displayed in Figs. 1 and 3.

Figure 1.

Docking tropomyosin segments to F-actin. (a–f) Highest scoring αβα-zone tropomyosin segments dock to F-actin in one of two modes, viz. those fulfilling a C-state pose (magenta on cyan-colored actin) and those with a B-state-pose (green on tan-colored actin). Individual docking poses on actin are illustrated by (a) the overlapping domain, i.e., β₆α₇β₇α₁β₁α₂, or by (b–f) different intrachain segments (b) α₆β₆α₇, (c) α₅β₅α₆, (d) α₄β₄α₅, (e) α₃β₃α₄, and (f) α₂β₂α₃. Ribbon diagrams are shown with side chains on actin residues Asp311, Lys326, and Lys328 (red, blue, blue); side chains of tropomyosin residues that interact with actin are also indicated. Side chains of actin’s Pro333, which demarcates the inner and outer domains of actin, are highlighted with white spheres. Matching common actin subunits in the segments shown above were superposed to generate composite “single-stranded” actin-tropomyosin filaments (g and h), and then the composite filaments were fitted within respective high- and low-Ca²⁺ isosurfaces of the Yamada et al. cryo-EM reconstructions (i and j) (7), using the “Fit in Map” program in Chimera (33) to align the filaments to Electron Microscopy Data Bank (EMDB) files EMD-0729 and EMD-0728; note the excellent correspondence between data determined by the two methods. Please note that the docking in (a)–(h) and “Fit in Map” alignment to cryo-EM reconstructions in (i) and (j) did not involve any flexible fitting routines or other manipulation of respective coordinates, i.e., only “raw” PIPER/ClusPro output was evaluated. The pointed end of actin is facing up in (a)–(j); arrows mark the tropomyosin overlapping domain; arrowheads mark the troponin core domain electron density. (k–p) Transverse sections through C-state and B-state poses displayed above were made through residue Lys326 of successive actin subunits (blue), showing electrostatic contacts formed by these basic residues on actin and acidic residues along tropomyosin (red), including Glu23, Glu62, Glu100, Glu138, Glu177, and Asp258. Here, sectioned B- and C-state poses were superposed for comparison. Note that at the level of tropomyosin residues 23 and 258, which flank the tropomyosin overlapping domain, the helical chains of B-state and C-state coiled coils either lie directly over each other (at residue 23) or diverge from each other marginally (e.g., at residue 258). In contrast, at the level of residues 62, 100, 138, and 177, the outermost chains diverge from each other by a 50–60° twist like the hands on a clock moving from ∼10 o’clock to noon, whereas those positioned closest to Lys326 still coincide. A picture emerges from these results involving tropomyosin overlapping domains restrained over F-actin under these conditions, whereas the tropomyosin midpiece pivots between B- and C-states. (k–p) Sections are viewed from filament barbed to pointed ends. To see this figure in color, go online.

As the tropomyosin coiled-coil dimer wraps around the actin filament, it alternatively presents broad and narrow faces of the coiled coil to each successive actin subunit (30,39,40). Images of C- and B-state-leaning tropomyosin segments characterize the two categories further (i.e., ones with tropomyosin oriented either toward the actin inner domain (C-state-leaning poses) or its outer domain (B-state-leaning poses)) (Fig. 1, a–h). They show that electrostatic contact made between tropomyosin and actin involves just one single α-helical chain from the broad face of the coiled coil, i.e., one of the two coiled-coil α-helices associates with actin residues 326 and 328, and the second chain is oriented away from actin toward solvent (most easily appreciated in transverse sections of the filament models (Fig. 1, k–p)). Thus, the entire flat face of the coiled coil never appears to sit symmetrically, flush against residues 326 or 328. The observation indicates that two chains of the coiled coil do not share equally in the electrostatic binding to individual actin subunits along filaments. (This asymmetry becomes especially important for future actin-binding studies involving heterodimeric αβ-tropomyosin isoforms found in skeletal and smooth muscles.)

With the exception of the overlapping domain segment, transverse sections of segments having C-state-leaning poses show that tropomyosin approaches residues Lys326 and Lys328 on actin at a comparatively shallow angle (Fig. 1, k–p) and contacts actin subunits to one side of the subdomain 3 peptide loop running from Met325 to Pro333. In B-state-leaning poses, tropomyosin segments adopt a more oblique orientation, with the coiled coil facing more toward the outer domains of actin (Fig. 1, k–p). At the site of electrostatic interaction on the actin, the coiled coil itself is twisted by ∼60° relative to that seen in C-state-like segments (Fig. 1, k–p), taking on the attitude of a hinge-like motion. Superposition of B- and C-state poses in Fig. 1, k–p reinforces this characterization. It also is apparent that the coiled-coil chains closest to the actin surface typically are associated with actin subunit residues 326 and 328 and that the actin-tropomyosin residue-to-residue register is virtually the same in the two poses. Hence, a picture emerges suggesting that tropomyosin is capable of pivoting about primary contact points (Tables 1 and 2), a phenomenon also suggested by Yamada et al. (7). The reconfiguration of tropomyosin possibly reflects oscillatory motions in situ, akin to tropomyosin hinged to actin residues 326 and 328 at its point of contact with the rest of the molecule tracing an arc-like path between B- and C-like poses (Fig. 1, k–p). This angular reorientation involves an average swing of 15–18 Å at the outer tip of tropomyosin (Fig. 1) accompanied by an azimuthal shift of up to ∼6 Å between the B- and C-state-facing helices at the point of contact with actin. In marked contrast, any back and forth rocking of tropomyosin observed on actin is modest at the level of the overlapping domain (Fig. 1, k and p; Table 2).

Table 2.

Angular Pivot of Tpm between Highest-Ranking B- and C-Facing Poses

Tpm Pseudorepeat	Angular Pivot of Tpm between B- and C-Poses when Docked to F-Actin
1	0°
2	50–60°
3	50–60°
4	50–60°
5	50–60°
6	–
7	15°

Angle is measured over actin residue 326. Pivot angle at pseudorepeat 6 was not determined; its twist behavior is not revealed by the rigid-body docking protocol.

Measurement of interaction energy between tropomyosin segments and F-actin showed comparatively greater binding strength for C-state-like poses, particularly for ones including pseudorepeats 4 and 5 (Table 3). These pseudorepeats midway along the length of tropomyosin contain acidic residues 138, 139, and 142 on pseudorepeat 4 and 173, 177, and 180 on pseudorepeat 5, previously shown to be critical for actin binding (14,18,41,42). The energetics noted appears to favor C-state-leaning segments, with little obvious heightened interaction at the overlapping domain.

Table 3.

Interaction Energetics of Tropomyosin Segments Docked to F-Actin

Tpm segment	Interaction Energy Tpm for F-Actin C-State-Leaning Poses (kcal/mol)			Interaction Energy Tpm for F-Actin B-State-Facing Poses (kcal/mol)
	Electrostatic	van der Waals	Electrostatic + van der Waals	Electrostatic	van der Waals	Electrostatic + van der Waals
α2β2α3	−913	−22	−935	−1055	−11	−1066
α3β3α4	−1271	−31	−1302	−1175	−24	−1199
α4β4α5	−1219	−34	−1253	−1115	−17	−1132
α5β5α6	−1365	−58	−1423	−1086	−23	−1109
Overlap β6α7β7α1β1α2	−1132	−42	−1174	−1219	−36	−1255a
Total measured	−5900	−187	−6087	−5650	−111	−5761

Values for highest-ranked poses, i.e., in which the superhelical path of tropomyosin on F-actin target is followed. Please note that the interaction energy for pseudorepeats in the midpiece of tropomyosin is greater (more negative) for the C- versus the B-state tropomyosin, but values for the ends and the overlapping domain are the opposite, consistent with the possibility that the overlapping domain sets the initial twist of tropomyosin on actin and that TnI interactions might be important for establishing the B-state twist. In all cases, low-ranking poses representing tropomyosin delimited by the A-triad on actin (as in (14,48)) yielded poor (less negative) interaction energies (data not shown). Tabulation of values for α₁β₁α₂ and α₆β₆α₇ interactions is not measured because PIPER/ClusPro rigid-body docking protocols used do not allow for conformational twisting between α-zones at these sites and because their α₁ and α₇ are contained in overlapping structures on actin.

^aPositioning tropomyosin at the Li et al. azimuth (14) yields a 305 kcal/mol less negative value for the overlap-actin interaction.

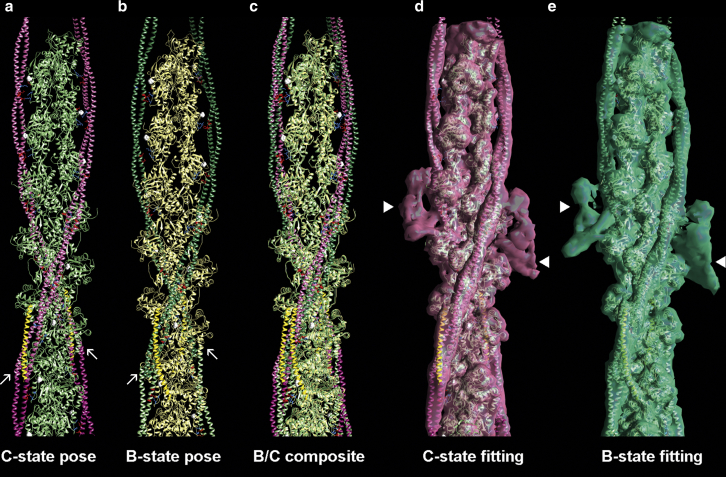
The docked segments can be spliced together to form a pseudoatomic model of tropomyosin by choosing sequentially related molecular poses in which the C- and N-termini from one segment most perfectly overlap and superpose on the next segment and finally on the overlapping domain segment (α₁β₁α₂ + α₂β₂α₃ to yield α₁β₁α₂β₂α₃, α₁β₁α₂β₂α₃ + α₃β₃α₄ to yield α₁β₁α₂β₂α₃β₃α₄, etc.) (Fig. 1, g and h). The splicing can be refined in cases in which the unbound free ends of successive fragments failed to orient precisely by flexibly fitting the merged segments to the Yamada reconstructions (7) (see Materials and Methods). As mentioned, the resulting models then form a superhelix along F-actin with residue-by-residue positional specificity characterized previously for full-length tropomyosin (14). However, despite the characteristic residue-to-residue binding contacts between actin and tropomyosin, the process does not generate a single preferred pose for assembled tropomyosin, but rather two distinctive configurations again centered on actin residues 326 and 328 with similar positional specificity to either of the B- and C-state models of Yamada et al. (7) (Fig. 1, g–j). The arrangement of tropomyosin in the two locations reinforces the notion that the tropomyosin coiled coil can pivot about sites of actin interaction, resulting in the molecule bending one way or the other about a plane orthogonal to the filament axis (Fig. 1, k–p). The raw, unrefined docking above indicates the stereospecificity of tropomyosin segment interactions with F-actin. To more faithfully display continuous tropomyosin strands, respective tropomyosin segments were also flexibly fitted to the Yamada maps, which annealed them together at their tips to form seamless cables on F-actin but without changing axial or azimuthal positioning. The refined tropomyosin cables maintained all the same residue-to-residue contacts with actin as noted above, even during MD simulation (Fig. 2).

Figure 2.

Annealing docked segments together to form a complete tropomyosin model. Respective tropomyosin segments that dock to actin in either C-state like or B-state like configurations (as displayed in Fig. 1, a–f) are shown spliced together here (a and b) and then fitted within corresponding high- and low-Ca²⁺ reconstructions of Yamada et al. (EMDB EMD-0729, EMD-0728 (7)) (d and e). The same color coding as in Fig. 1 is used, with C-state-leaning tropomyosin (magenta) in (a) and B-state-leaning tropomyosin (green) in (b) on cyan and tan actin and superposed in (c). TnT (residues Asp89 to Arg151) from our overlapping domain model (which is the same as in the Yamada model) (7,24) are included for reference and colored gold. Side chains on actin residues 311, 326, and 328, which lie in proximity to oppositely charged residues on tropomyosin, are highlighted. Actin residues 333 (white) are shown as markers delimiting inner and outer domains of actin subunits; arrows mark the tropomyosin overlapping domain; arrowheads mark the troponin core domain electron density. To see this figure in color, go online.

The Yamada C-state tropomyosin model

As indicated, Yamada et al. (7) skillfully and elegantly reconstructed the position of tropomyosin on actin of thin filaments from cryogenically preserved samples under low- and high-Ca²⁺ conditions. Alignment of moderately high-resolution tropomyosin structures (43) to the corresponding lower resolution electron densities in Yamada et al. (7) yielded PDB coordinates (Protein Data Bank, PDB): 6KN7, 6KN8 that reveal coiled-coil tropomyosin emerging from the tropomyosin overlap structure as well as the interaction of TnT1 residues 87–150 on F-actin-tropomyosin. Although the N-/C-domain tropomyosin overlapping domain structure and its interaction with TnT1 on actin is virtually identical to that described in recent molecular docking studies (24), the alignment of actin and tropomyosin proposed by Yamada et al. (7) in regions beyond this overlapping structure diverges from the generally accepted actin-tropomyosin residue-to-residue register (14,25, 26, 27, 28,39,40,44,45). Thus, the Yamada et al. alignment is inconsistent with the previously suggested periodic spacing between charged residues in tropomyosin and with interactions between α-zones and neighboring actin residues 326 and 328.

Tropomyosin was among the first proteins to be classified as a coiled coil. Lacking interruptions (staggers and stammers), it can be considered a stereotypical example of the coiled-coil motif (10,39). Coiled-coil parameters can be readily calculated using the program TWISTER (e.g., coiled-coil pitch, residues per turn) (46). Applying TWISTER to coordinates in the Yamada et al. PDB files shows that the coiled-coil pitch of tropomyosin matches those of ideal coiled coils (Table 4). This correspondence is exemplified by tropomyosin filling the helical densities in the corresponding cryo-EM maps without error. In contrast, however, TWISTER indicates that the component α-helices in the Yamada fitting appear to be compressed; therefore the rise per residue for tropomyosin specified by the deposited PDB files is significantly shorter than normal for α-helices (for example, see Table 4; (39)). The overall effect of this apparent error is an ∼10% foreshortening of the tropomyosin model contained in the EM volume. (This discrepancy leads to an artifactual ∼35 nm end-to-end length of the Yamada tropomyosin coiled coil versus the native 38.5 nm value; discussed further in Table 4.) The resulting anomalous register between actin subunits becomes most evident beyond the overlapping domain and toward the pointed end of the actin filament, likely accounting for mismatches in tropomyosin-actin residue-to-residue alignment in Yamada et al. (7). In fact, molecular dynamics performed on the actin-tropomyosin part of the Yamada model shows that pseudorepeat 5 of the tropomyosin “cracks” along one of the two coiled-coil chains during simulation, accompanied by local unwinding of pseudorepeat 6 along the opposite tropomyosin chain. These distortions in tropomyosin symmetry are associated with coiled-coil elongation during MD. This synthetic rearrangement in silico appears to generate still imperfect but more generally accepted electrostatic interactions between tropomyosin and actin subunits than ones extracted directly from the deposited PDB structures (7).

Table 4.

Measured Tropomyosin Coiled-Coil and α-Helical Parameters

	Coiled-Coil Pitch	α-Helix Residue Rise
	(Å)	(Å)
Idealized canonical tropomyosin
Stewart and McLachlan, 1975 (39)	137	1.49
Li et al., 2010 (13)	136	1.51
Crystal structure tropomyosin
Whitby and Phillips, 2000 (PDB: 1C1GAB) (43)	147	1.52
GCN4-pl Leucine Zipper
Lupas and Gruber, 2005 (PDB: 2ZTA) (56)	135	1.51
MD determination: actin-bound tropomyosin
Orzechowski et al., 2014 (AB) (17)	140	1.52
Cryo-EM determinations: actin-bound tropomyosin
Behrmann et al., 2012 (PDB: 4A7F) (44)	133	1.51
von der Ecken et al., 2015 (PDB: 3J8A) (45)	131	1.52
Yamada et al., 2020—high-Ca (PDB: 6KN8PQ) (7)	138	1.41
Yamada et al., 2020—high-Ca (PDB: 6KN8WX) (7)	138	1.41
Yamada et al., 2020—low-Ca (PDB: 6KN7PQ)	139	1.42
Yamada et al., 2020—low-Ca (PDB: 6KN7WX) (7)	139	1.42
Tropomyosin fitted to Yamada EM volume
This study	137	1.49

Coiled-coil parameters were determined for reported coordinates using the program TWISTER (46). The pitch of idealized tropomyosin coiled coils is 136–137 Å, i.e., comparable to values computed for the GCN-4 leucine zipper as well as for MD or cryo-EM models of tropomyosin linked to actin filaments (44, 45, 46,56). These coiled coils are characterized by a well-known 1.5 Å rise between residues. However, please note that although the helical rise per residue for the Whitby and Phillips 7 Å resolution crystal structure is normal, its coiled-coil pitch (∼147 Å) is longer than expected (43). Here, crystal packing forces or other factors may have caused aberrant coiled-coil undertwisting. Even though the pitch of the Whitby-Phillips structure is also longer than that attributed to tropomyosin densities in cryo-EM maps, Yamada et al. (7) used the Whitby-Phillips model (43) for atomic fitting and to generate PDB files. For flexible fitting routines to adjust the Whitby and Phillips coordinates to the Yamada EM volume, residue-to-residue spacing may have been compressed. This would produce an artifactually diminished α-helix residue rise, i.e., the 1.41–1.42 Å values computed from the Yamada PDB coordinates versus the expected value of 1.5 Å. We also note that the superhelical path described by Whitby and Phillips tropomyosin model does not accurately match the F-actin helix; thus, the bending required to meld it into filament reconstructions may have also inadvertently corrupted the model during the Yamada et al. molecular fitting routines. These or other effects could account for residue mismatches between tropomyosin and actin in PDB: 6KN8 or 6KN7 coordinates.

Building a C-state tropomyosin cable

Given the ambiguity of the Yamada actin-tropomyosin model, we sought to construct an additional tropomyosin structure de novo, designed to fill the cryo-EM volume faithfully while at the same time agreeing with standard parameters describing coiled coils and tropomyosin conformation. A full-length human Tpm1.1 tropomyosin construct was built with superhelical curvature, pitch, and residue rise per turn to match those of an idealized tropomyosin coiled-coil dimer (13,30). Here, side-chain orientations associated with Holmes-Lorenz tropomyosin structure were derived from high-resolution x-ray crystallographic solutions of tropomyosin fragments (as in Li et al. (13)). The new model was pseudorotated (30) and fitted as a rigid body into the cryo-EM density volume. The tropomyosin model was then refined further by flexible fitting routines with little obvious change in conformation or cross correlation values. The procedure worked especially well for aligning tropomyosin to the high-Ca²⁺ reconstruction. Cross correlation values for the fitting were comparable to those obtained for the Yamada model fitting discussed above.

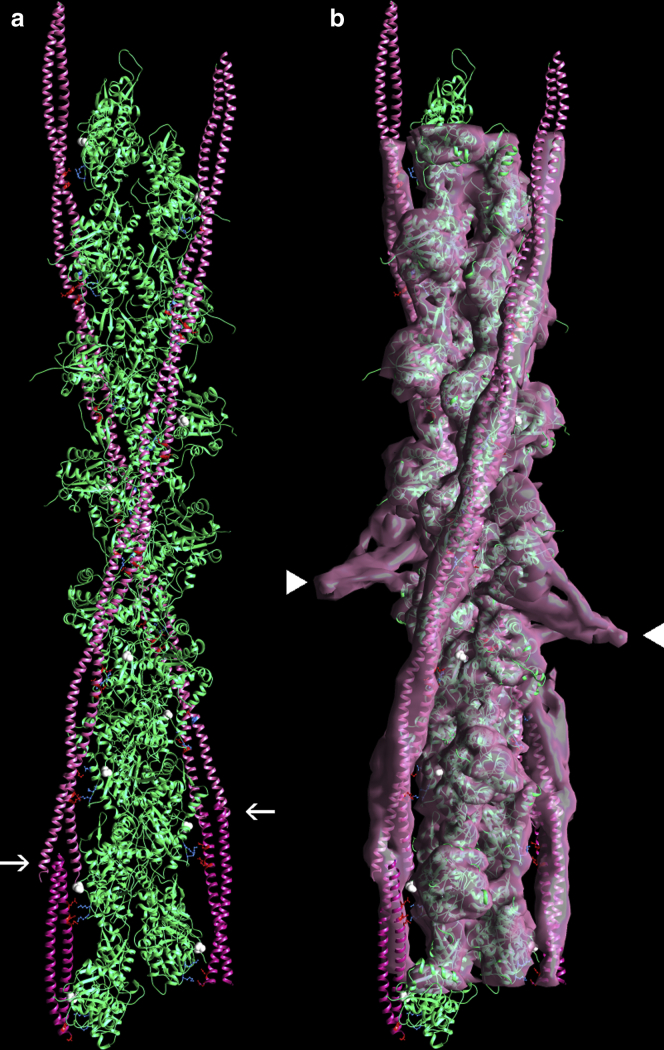
Our fitted tropomyosin structure yields proper coiled-coil and α-helical parameters (Table 4) and was threaded into the tropomyosin head-to-tail overlapping domain, common to both our (24) and the Yamada solutions, annealing tropomyosin and the overlap structure over residue 240 of tropomyosin, where they superpose. The procedure resulted in a near-perfect match of the new model to the cryo-EM volume and was refined further by flexible fitting to accommodate any localized twisting. A native 38.5 nm end-to-end tropomyosin period was now observed for the refined model, thus differing from the foreshortened 35 nm estimated value for the Yamada molecular structure of tropomyosin. Moreover, all expected electrostatic contacts between actin and tropomyosin were noted and were the same as those found in the docking study above (Table 1). These contacts and the tropomyosin chains in general remained stable during MD (Fig. 3), unlike models built from the Yamada et al. PDB coordinates.

Figure 3.

Model of actin-tropomyosin following molecular dynamics. (a) The actin-tropomyosin structure shown was started from a canonical model of tropomyosin fitted to the cryo-EM three-dimensional reconstruction (EMDB EMD-0729) and then threaded into the structure of the tropomyosin overlapping domain and troponin-T complex common to (7,24). MD was run for 30 ns. The tropomyosin coiled coil remained intact throughout simulation, and side-chain interactions noted in Table 1 also were stable during MD. Representative trajectory (a) fitted within EMD-0729 is shown (b), with the same color coding and highlighting as in Figs. 1 and 2. The trajectory snapshot was taken from the 27 to 30 ns time period of simulation and is a frame that had the lowest root mean-square deviation from the average structure over that same time period (calculated by backbone atom superimposition). PDB coordinates are provided as Data S1. To see this figure in color, go online.

Corresponding efforts to build a satisfactory atomic model of actin-tropomyosin to mimic the B-state Yamada et al. reconstruction were unsuccessful. The reduced tropomyosin resolution in the low-Ca²⁺ filament reconstruction precluded accurate assessment of actin-tropomyosin alignment. Definitive determination of tropomyosin twist in the reconstruction was obscured by the presence of C-terminal TnI density juxtaposed alongside of tropomyosin (7). In the C-state work described above, TnI-based interference did not limit modeling because there, C-terminal TnI dissociates from actin under high-Ca²⁺ C-state conditions.

Discussion

The tail wags the dog

Computational approaches to dock tropomyosin on F-actin were first performed by Lorenz and Holmes and Poole et al. (30,47) by testing the radial and azimuthal positioning of idealized models of coiled-coil tropomyosin on actin. The work was refined later by Li et al. (13,14), who incorporated amino acid side-chain data derived from newly solved crystal structures of tropomyosin fragments. Full-length tropomyosin was shown localizing over a broad energetic plateau over the surface of successive actin subunits with shallow minima centered on the so-called actin “A-triad” (48), viz. over actin residues Lys326 and Lys328 and Arg147 to the outer domain side of Pro333 protruding from the actin surface (14). Even though the fitting was done in the absence of troponin, the positioning centered tropomyosin to a myosin-blocking site despite an expected closed C-state localization suggested by biochemical data (1,2). In fact, all of the early structural studies treated tropomyosin as a rigid body without anticipating, and thus considering, relatively recent work indicating that pseudorepeats 1 and 7 of tropomyosin twist when generating an N-/C-head-to-tail overlap domain (49) and additionally that pseudodomain 4 itself is likely to twist when contacting F-actin (12,50,51). Perhaps even more significantly, neither the Lorenz-Holmes nor the Li model featured the effect of the overlap itself on the positioning of tropomyosin over actin or the added influence of TnT in stabilizing the overlap structure (7,14). Thus, the early docking studies and related energy landscape measurements failed to recognize the balancing act played out by the overlap domain and midpiece domains of tropomyosin. In our study, we began with a narrower reductionist strategy rather than with the prior holistic approach. From this vantage point, we rebuilt an actin-tropomyosin model now based on the outcomes of segment docking protocols for comparison with recent cryo-EM reconstructions of thin filaments. Indeed, the results of computational studies performed here and the cryo-EM study validate each other and suggest that once associated with the assembled thin filament, tropomyosin position on actin appears to follow the dictates of the overlap domain, viz. the tropomyosin head-to-tail complex “wags” its coiled-coil shank. In earlier modeling (17,25,26), the overlapping domain was impressed onto the main tropomyosin rod after first fitting the rod over the A-triad. In fact, when characterizing billions of docking poses, we found no preference for tropomyosin segments fitting over the A-triad of actin as previously surmised (17,25,26), whereas all high-scoring poses, including those for the overlapping domain, merged together outside of this location on actin.

Thin filament assembly

We propose that free-in-solution coiled-coil tropomyosin is configured as a Lorenz-Holmes idealized canonical superhelix (30) and, on average, is “preshaped” to the contours of the F-actin helix (4,14,15). Thus, the first tropomyosin molecules or possibly short tropomyosin oligomers that associate with F-actin are unlikely to be constrained by head-to-tail overlap configuration. We expect that at this initial stage of assembly, tropomyosin will remain canonical and thus tend to maximize electrostatic contacts along the actin surface, possibly as proposed by Li et al. (14) based on global fitting of isolated, unpolymerized tropomyosin. We posit that the broad energy landscape noted for the interaction of isolated tropomyosin on actin relates to this process (14,31). Still, even though semirigid tropomyosin is preshaped to relieve entropic barriers during assembly onto the actin filament (Gestalt-binding) (4,13,14), the initial interaction of tropomyosin and actin is extraordinarily weak (52) and thus, owing to thermal activity, transient. An estimated 10⁻³ M K_d-value for isolated, nonpolymerized tropomyosin on F-actin (52) is not compatible with effective binding in situ and therefore with regulatory function. Nevertheless, even if tropomyosin is transiently bound, as the coiled coils begin to populate the filament in higher numbers, their tandem arrangement on the actin surface will begin to support head-to-tail interaction. Once a critical distribution is reached, tropomyosin polymerization on F-actin will occur, and the corresponding on-off equilibrium from actin will change abruptly (53, 54, 55). Our results suggest that at this juncture, the overlapping domain formed then dominates binding as well as the configurational patterning of tropomyosin with the actin substrate. To be effective, the intervening shank of tropomyosin twists to constraints imposed by the overlapping domain and systemic electrostatic biases. As tropomyosin grows along the filament, it becomes topologically bound to F-actin with an exceedingly low off-rate, which is expected to parallel a narrowing of the actin-tropomyosin energy landscape discussed above. Little energetic penalty, if any, is expected by the transition from an extremely weak electrostatic or van der Waals potential to strong topological binding.

The effect of troponin

Possible excursions of tropomyosin toward charged residues Asp25, Arg28, and Arg147 on the edge of actin’s energetic plateau may be limited mechanically by the linker region of troponin-T (residues 151–198) lying across the thin filament (7). Here, the elongated linker may couple the troponin core domain and tropomyosin on one F-actin strand to tropomyosin on the opposite actin strand, thus connecting the activity of the two long-pitch actin helices together (see Fig. 7 in (7)). In addition, we anticipate that at low Ca²⁺, electrostatic attraction between tropomyosin and the C-terminal domain of TnI in the fully assembled muscle thin filament will cause the tropomyosin cable to bend in the direction of actin subdomains 1 and 2 and trap tropomyosin in a B-state leaning configuration noted above. Such behavior will block myosin cross-bridge binding, resulting in muscle relaxation. Conversely, the release of this constraint will initiate muscle activation. High-resolution cryo-EM reconstructions of TnI and tropomyosin interaction coupled together with further protein-protein docking studies are required to complete this regulatory scheme.

Summary

Key among our findings are the following:

• •Interaction energy calculations show that tropomyosin segments representing pseudorepeats 2 through 6 dock preferentially to actin in a C-state-like pose but also can link to B-state poses. In either case, the acidic residues in the tropomyosin segments associate with residues Lys326 and Lys328 on actin.
• •Consistent with results of the cryo-EM work of Yamada et al. (7), the orientations assumed by tropomyosin segments in B- and C-like poses suggest that, while centered over Lys326 and Lys328, midpiece tropomyosin pseudorepeats can pivot on actin by ∼60°. The inner aspect of the coiled coil associates closely with actin subunits, acting as a fulcrum about which the rest of tropomyosin rocks. This allows a 15–18 Å azimuthal swing at the outermost tip of tropomyosin in B- or C-state directions.
• •Azimuthal sliding of tropomyosin up to ∼6 Å is also observed in some cases. Our observations preclude significant coiled-coil rolling.
• •The overlapping domain “staples” the ends of tropomyosin onto residues Lys326 and Lys328 of actin. The four-helix bundle tilts modestly about its interaction site, but azimuthal shifting is not detected over this region. Thus, the tropomyosin overlapping domains appear to act as relatively fixed attachment points, allowing intervening pseudorepeats to flex.
• •A, to our knowledge, new paradigm emerges consistent with conclusions drawn by Yamada et al. (7), in which thin filament regulation involves this pivoting of tropomyosin, acting to either obstruct (B-state) or bend out of the way of incoming myosin heads (C-state). This account differs from the conventional view, in which the whole of the tropomyosin unit undergoes 15–25 Å azimuthal movement between B- and C-regulatory states (47).

Further advances in our understanding of thin filament regulation at an atomistic level are anticipated.

Author Contributions

W.L., M.J.R., and E.P. developed the approach taken and formulated the principal concepts presented. E.P. designed and carried out the docking studies, and E.P. and M.J.R. performed the molecular dynamics simulation and data computation; they wrote the Materials and Methods. W.L., E.P., and M.J.R. analyzed the data. W.L. wrote the manuscript. W.L. and M.J.R. prepared the figures and tables.

Editor: David Thomas.

Supporting Material

Data S1 PDB Coordinates Provided for the Reference Model of Actin-Tropomyosin Used for Molecular Dynamics Described in the Main Text

Actin-tropomyosin is presented in the PDB after fitting into the Yamada et al. high-Ca²⁺ map of the complete thin filament (7). TnT (residues 88 to 150) from Pavadai et al. (24) also shown fitted to the map. Simulation was carried out in a periodic system to emulate a tropomyosin cable on an infinitely long actin filament (as described in the main text).