Pulsed Electric Fields Can Create Pores in the Voltage Sensors of Voltage-Gated Ion Channels

Abstract

Pulsed electric fields are increasingly used in medicine to transiently increase the cell membrane permeability via electroporation to deliver therapeutic molecules into the cell. One type of event that contributes to this increase in membrane permeability is the formation of pores in the membrane lipid bilayer. However, electrophysiological measurements suggest that membrane proteins are affected as well, particularly voltage-gated ion channels (VGICs). The molecular mechanisms by which the electric field could affects these molecules remain unidentified. In this study, we used molecular dynamics simulations to unravel the molecular events that take place in different VGICs when exposing them to electric fields mimicking electroporation conditions. We show that electric fields can induce pores in the voltage-sensor domains (VSDs) of different VGICs and that these pores form more easily in some channels than in others. We demonstrate that poration is more likely in VSDs that are more hydrated and are electrostatically more favorable for the entry of ions. We further show that pores in VSDs can expand into so-called complex pores, which become stabilized by lipid headgroups. Our results suggest that such complex pores are considerably more stable than conventional lipid pores, and their formation can lead to severe unfolding of VSDs from the channel. We anticipate that such VSDs become dysfunctional and unable to respond to changes in transmembrane voltage, which is in agreement with previous electrophysiological measurements showing a decrease in the voltage-dependent transmembrane ionic currents after pulse treatment. Finally, we discuss the possibility of activation of VGICs by submicrosecond-duration pulses. Overall, our study reveals a new, to our knowledge, mechanism of electroporation through membranes containing VGICs.

Significance

Pulsed electric fields are often used for treatment of excitable cells, e.g., for gene delivery into skeletal muscles, ablation of the heart muscle, or brain tumors. Voltage-gated ion channels (VGICs) underlie generation and propagation of action potentials in these cells, and consequently are essential for their proper function. Our study reveals the molecular mechanisms by which pulsed electric fields directly affect VGICs and addresses questions that have been previously opened by electrophysiologists. We analyze the characteristics of VGICs that make them prone to electroporation, including hydration and electrostatic properties. This analysis is easily transferable to other membrane proteins, thus opening directions for future investigations. Finally, we propose a mechanism for long-lived membrane permeability after pulse treatment, which to date remains poorly understood.

Introduction

The integrity of the cell membrane, although essential for the life of any biological cell, presents a barrier that needs to be transiently disrupted to deliver therapeutic molecules into the cell. High-intensity pulsed electric fields are increasingly used in medicine to achieve such a transient increase in cell membrane permeability. Examples are cancer treatment for enhanced delivery of chemotherapeutic drugs and gene therapy techniques for intracellular delivery of genetic material (1). The applied electric field induces a phenomenon called electroporation or electropermeabilization. Thanks to insights from molecular dynamics (MD) simulations, we now understand that one type of events that takes place in the cell membrane is the formation of pores in the membrane lipid bilayer (2,3).

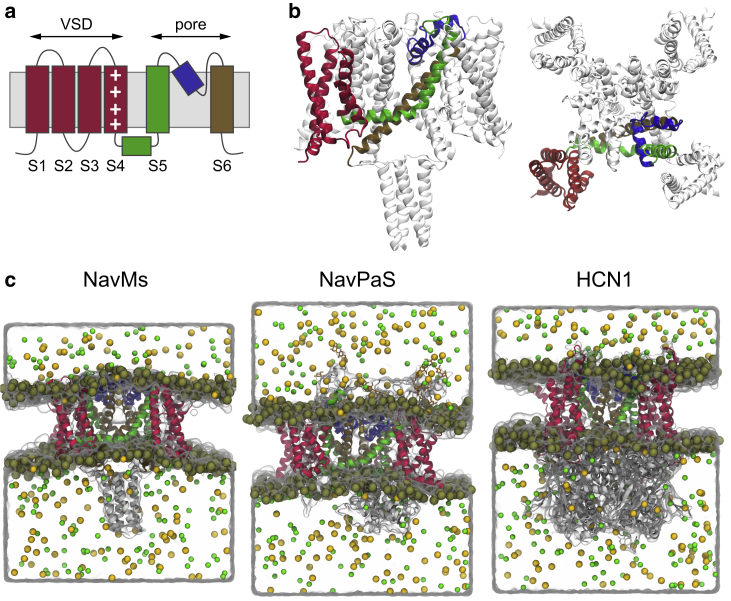
However, experimental evidence suggests that membrane proteins, particularly voltage-gated ion channels (VGICs), could be affected as well (4). VGICs are a class of transmembrane proteins that respond to changes in the transmembrane voltage (TMV) with conformational rearrangements that lead to opening or closure of an ion-selective pore. They play crucial roles in the generation and propagation of action potentials in electrically excitable cells, including neurons and muscle cells. All VGICs share a common architecture: each of the four protein domains contains six transmembrane segments (S1–S6) and a pore loop between segments S5 and S6. Segments S1–S4 act as the voltage sensor, whereas S5, S6, and the pore loop serve as the pore-forming module (Fig. 1, a and b; (5)). Segment S4 contains positively charged residues and has the ability to respond to changes in TMV. The movement of S4 then acts on S5 and S6 to open or close the channel pore depending on the direction of the electric field.

Figure 1.

Structure of the voltage-gated ion channels (VGICs) investigated in this study. (a) All VGICs share an overall architecture that includes four subunits, each containing six membrane-spanning segments denoted S1–S6. (b) Side view and extracellular view of the NavMs channel, indicating the segments of a single subunit: VSD (S1–S4) colored in red, S5 together with S4–S5 linker colored in green, pore helix colored in blue, and S6 colored in ochre. (c) Simulation box of the investigated systems: NavMs, NavPaS, and HCN1. Ion channels are shown as ribbons colored as in (a). Water molecules are represented as transparent volume, whereas phosphorus atoms of lipid headgroups, Na⁺ ions, and Cl⁻ ions are shown as gold, yellow, and green spheres, respectively. To see this figure in color, go online.

Because VGICs are sensitive to changes in TMV and because electroporative pulses induce a TMV of several hundreds of millivolts, far beyond the physiological resting voltage or voltage generated during action potentials, one can speculate that these channels become perturbed by pulsed electric fields. Indeed, by using advanced patch-clamp techniques, electrophysiologists have demonstrated that high-intensity pulses with submicrosecond duration can decrease the ionic currents mediated by different VGICs during action potentials. Nesin et al. (6) studied the effects of 300 or 600 ns pulses on Nav and Cav channels using murine pituitary (GH3) and murine neuroblastoma-rat glioma hybrid (NG108) cells. Electrophysiological measurements revealed a decrease in Nav and Cav currents for pulse amplitudes above 1.5–2 kV/cm. The results from a follow-up study (7) suggested that the decrease in Nav current was not mediated by Na⁺ leakage across the electropermeabilized membrane or downregulation of the Nav channels by a calcium-dependent mechanism. The authors thus proposed as the mechanism either an electroconformational change or a calcium-independent downregulation of the Nav channels (e.g., caused by alteration of the lipid bilayer). Decrease in Nav channel current was also observed by Yang et al. (8) when they exposed adrenal chromaffin cells to even shorter 5 ns, 50–100 kV/cm pulses. Their analysis suggested that the decrease in Nav current was not due to a change in either the steady-state inactivation or activation of the Nav channels but instead was associated with a decrease in maximal Na⁺ conductance. This decrease could be observed immediately after the pulse (within 0.5 s, earliest time measured), suggesting a direct effect of the electric field on Nav channels. No effect was observed on Kv channels, whereas a decrease in conductance could also be observed for Cav channels and/or calcium-dependent potassium channels. Although less explored, a decrease in VGIC current has been also reported when using longer millisecond pulses. Chen et al. (9,10) measured up to ∼40% decrease in Nav and delayed rectifier Kv currents after subjecting voltage-clamped frog skeletal muscle cells to hyperpolarizing 4 ms, −0.5 V pulses. In all the above-discussed studies, the effects depended on the pulse amplitude, with lower amplitude resulting in milder decrease in channel currents. Importantly, all studies also reported that the decrease was not reversible within the observation time (50 min in (10), 10–15 min in (6,8)).

Apart from decreased current through VGICs, there have been other electric-field effects observed as well. Submicrosecond pulses have been shown to activate specific VGICs (11,12). However, it remains unclear whether the electric field during such short pulses is able to directly move the VSDs or whether the channel activation is indirectly triggered by postpulse membrane depolarization, which is caused by nonselective ion leakage across the electropermeabilized membrane. Furthermore, this activation of VGICs has been found to participate in postpulse membrane depolarization (13,14) and intracellular calcium increase (15, 16, 17), both of which are important signals that can initiate cell death, proliferation, or differentiation, depending on their spatiotemporal profile (18,19). Understanding the effects of pulsed electric fields on VGICs is thus also interesting for new applications in wound healing and tissue engineering.

Electropermeabilization is associated with a complex set of events, including oxidative lipid damage, disruption of the cytoskeleton network, and its association with the plasma membrane, as well as lipid scrambling, which could all affect the function of membrane proteins (2). Yet, electrophysiological measurements suggest that pulsed electric fields induce some electroconformational change of VGICs during the pulse. However, electrophysiological measurements are not able to directly determine whether and how pulsed electric fields can affect VGICs on the molecular level. To fill this gap, we used MD simulations and unraveled the molecular events that take place in different VGICs when exposing them to an electric field that mimics electroporation conditions. Because experimental studies consistently reported a decrease in Nav current, we performed simulations of two Nav channels for which the structure had been resolved by x-ray crystallography and cryo-electron microscopy: a bacterial Nav from Magnetococcus marinus (NavMs) (20) and an eukaryotic Nav from Periplaneta americana (NavPaS) (21). Eukaryotic Nav channels are composed of a single polypeptide containing four homologous but nonidentical domains connected by intracellular linkers; bacterial Navs, on the other hand, are comprised of four identical domains, each being analogous to a single domain of their eukaryotic counterparts, and can thus be used as simple models of eukaryotic channels (22,23). In addition, we performed simulations of the human hyperpolarization-activated cyclic nucleotide-gated (HCN1) channel (24), which is a nonselective voltage-gated cation channel that is responsible for generation of rhythmic activity in heart and brain. Unlike Nav channels, HCN1 activates under hyperpolarizing TMV. The effects on HCN1 are of interest giving the rapid development of pulsed-electric-field-based cardiac ablation for treatment of heart arrhythmias (25). We found that the three tested channels, NavMs, NavPaS, and HCN1, responded differently to electric pulses, which we could relate to the channels' structural differences resulting in considerably different hydration and electrostatic profiles along their VSDs. Comparing their response thus enabled us to gain an atomistic level insight into the biophysical mechanisms governing their interaction with an electric field and to relate their propensity to be porated with their biophysical characteristics.

Methods

Systems preparation

The computational systems with NavMs (Protein Data Bank, PDB: 5HVX), NavPaS (PDB: 5X0M), and HCN1 (PDB: 5U6O) were built using the CHARMM-GUI webserver (26). Briefly, each protein was embedded into a 1-palmytoyl-2-oleoyl-phosphatidylcholine bilayer and solvated with 150 mM NaCl solution. The CHARMM36 force field (27,28) was used for proteins, lipids, and ions and the TIP3P model (29) for water. The composition of each system is reported in Table S1.

MD simulations

All simulations were performed in GROMACS 2016 (30,31). Each system was first minimized using the steepest descent algorithm. The equilibration and production run was then carried out using a leap-frog integrator with a time step of 2.0 fs, Nosé-Hoover thermostat (τ = 0.4 ps, T = 300 K) (32,33), and Parrinello-Rahman barostat (τ = 5 ps, P = 1 bar, semi-isotropic coupling) (34,35). During the first 100 ns, the protein atoms were restrained to their initial positions, after which the simulations were continued for 400–1200 ns without restraints (400 ns for NavMs, 1200 ns for NavPaS, and 700 ns for HCN1). The long-range electrostatic interactions were calculated using the particle mesh Ewald method (36), together with a Fourier grid spacing of 0.15 nm and a cutoff of 1.2 nm. A switching function was used between 0.8 and 1.2 nm to smoothly bring the short-range electrostatic interactions and the van der Waals interactions to 0 at 1.2 nm. The chemical bonds were constrained to their equilibrium values using the LINCS algorithm (37). Periodic boundary conditions were applied.

To simulate the exposure to an electric pulse, we added a force qE_z to every atom carrying a charge q (2,3). This method induces a TMV that is approximately equal to the product of the imposed electric field and the simulation box length, TMV = E_z L_z. The E_z was chosen based on the following considerations. Previous simulations on pure lipid bilayers showed that formation of a lipid pore occurs faster with increasing electric-field magnitude; to observe lipid pores within few tens of nanoseconds, simulations have been typically conducted by applying an electric field resulting in TMV above ∼3 V (38,39). Experimentally, however, the TMV that can be built on the membrane is limited because the membrane starts discharging through pores after it becomes electroporated. According to measurements performed using pulses with duration of 60 ns and longer together with voltage-sensitive dyes (40,41) and microelectrodes (42), the TMV of ∼1.5 V is the largest that a cell membrane can sustain before discharging. Thus, we chose the value of the electric field such that it resulted in a TMV of about ±1.5 V. The chosen value is a compromise between trying to observe an effect of the electric field within reasonable simulation time and at the same time staying within realistic experimental TMV values. These simulations were performed in an NVT ensemble (constant number of atoms, volume, and temperature), which kept the simulation box size constant. This ensured that the voltage applied across the membrane remained constant.

We also performed additional control simulations on the NavMs channel by using an electric field in an NPT ensemble but did not observe any considerable differences from NVT simulations that would affect the results and conclusions presented in the work (Supporting Materials and Methods, Section S4.1; Figs. S6 and S10; Table S4). In addition, we performed control simulations by applying a constant charge imbalance instead of an external electric field (Supporting Materials and Methods, Section S4.2; Fig. S7; Table S5). The charge imbalance was achieved by 1) separating the water bath into two parts by adding a vacuum layer and 2) transferring a certain number of positive and negative ions across the membrane, which created the desired initial TMV. The charge imbalance was kept constant despite the transport of ions through transmembrane pores throughout the simulation by replenishing the charge imbalance using a Monte Carlo setup (43). The box size was allowed to expand in the x and y directions by using surface-tension coupling, as described in (44).

Simulations in which we characterized the complex pores formed in VSDs, including their growth dynamics, ionic conductance, stability in the absence of an applied electric field, and perturbation of the VSD secondary structure (Figs. 8 and 9; Supporting Materials and Methods, Section S8), were carried out in the NPT ensemble.

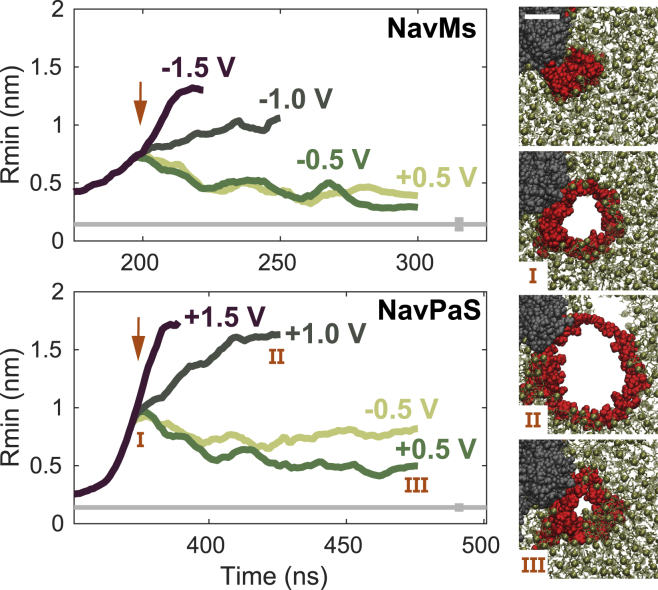
Figure 8.

Progression of the radius of complex pores in NavMs and NavPaS. Arrows mark the time at which the simulation was continued either at ±1.5 V or at a lower electric field, resulting in TMV of ±1.0 or ±0.5 V. Images on the right show extracellular views of the NavPaS complex pore at times indicated by Roman numbers. The topmost image shows the NavPaS VSD before electric-field application. Scale bar, 2 nm. VSD is shown in red, the rest of the protein in gray, and the lipids in gold. To see this figure in color, go online.

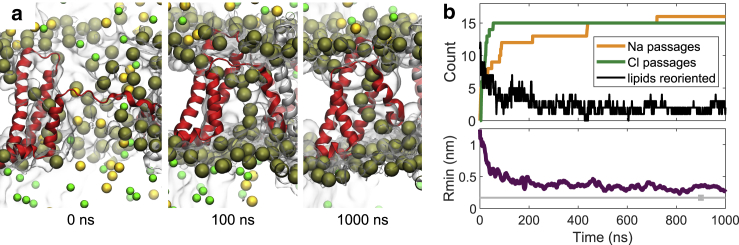
Figure 9.

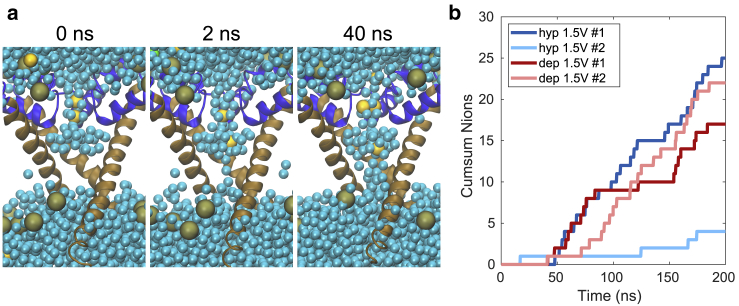
Postpulse stability of a complex pore. (a) Configuration of a complex pore in NavMs at 0, 100, and 1,000 ns after turning off the electric field. Representation of atoms is the same as in Fig. 3; water is represented as a transparent surface. (b) The cumulative sum of the number of Na⁺ and Cl⁻ that passed through the VSD pore (yellow and green line, respectively); the passage of ions is here mediated by diffusion and can occur either from intracellular to extracellular side or vice versa. The black line shows the number of lipid phosphorus atoms that are close to the VSD pore and within 0.5 nm of the z-position of the lipid bilayer’s center of mass. The number of lipids that stabilize the VSD pore decreases with time but stabilizes above zero, meaning that even at 1 μs after turning off the electric field, the VSD pore is still stabilized by lipids. The bottom graph shows the progression of the radius of the complex pore. To see this figure in color, go online.

Analysis

Trajectories were visualized with VMD (45). Ion passage through pores formed in the system was determined by a custom MATLAB (The MathWorks, Natick, MA) code based on the positions of ions extracted from the trajectories. The code is available at https://github.com/delemottelab. The radius of pores was determined by the CHAP tool (46), which uses the same concept as HOLE (47), i.e., using a Monte Carlo simulated annealing procedure to find the best route for a sphere with variable radius to squeeze through the pore cavity. Secondary structure and solvent-accessible surface area were determined with the GROMACS functions gmx do_dssp and gmx sasa, respectively. Free energy estimates for water molecules along VSDs were determined based on kernel density estimate of the probability distribution of the positions of water molecules extracted from the trajectories at 0 V (see also Supporting Materials and Methods, Section S5). To calculate electrostatic profiles along the VSDs, additional 2-ns-long simulations under an electric field were performed while keeping the position of the protein heavy atoms restrained. These short simulations were carried out starting from 10 different configurations extracted from the last 100 ns of the trajectories without applied electric field. For each of these short trajectories, we determined the three-dimensional electrostatic potential using the VMD tool PMEpot (options: ewaldfactor 0.5, grid 1.0 Å) (48). From each of the 10 three-dimensional profiles, we determined a one-dimensional (1D) electrostatic profile along the VSD by averaging the potential along a cylinder with a diameter of 0.5 nm centered at the center of mass of the VSD. Finally, we computed the average and standard deviation of the 10 1D profiles.

Results

General observations

When a cell is exposed to an electric field, the part of its membrane facing the positive electrode becomes hyperpolarized, whereas the part facing the negative electrode becomes depolarized. Thus, for each of the three investigated channels (NavMs, NavPaS, and HCN1), we generated up to 600-ns-long trajectories under hyperpolarizing and depolarizing TMV of ±1.5 V.

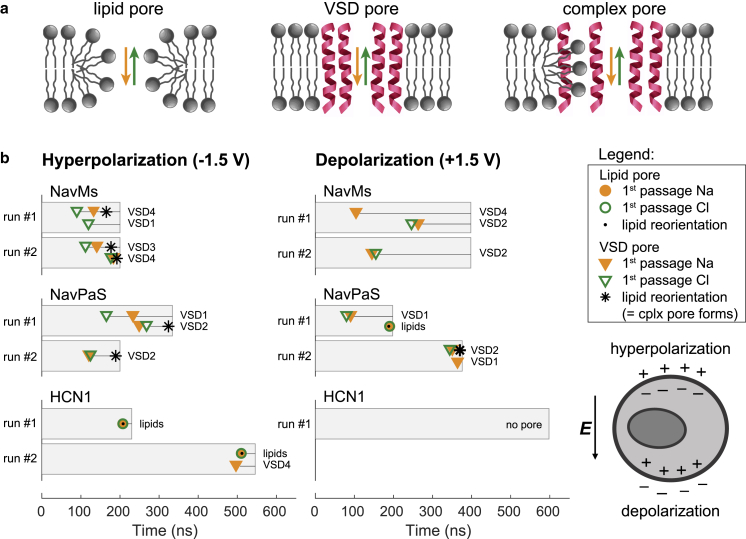
The simulations revealed that electric field promotes creation of different types of ion-conducting transmembrane aqueous pathways, which are schematically depicted in Fig. 2 a. One of possible pathways is the well-known hydrophilic lipid pore, lined by lipid headgroups, which forms in the lipid bilayer next to the protein and has been previously observed also in pure lipid bilayers (2,3). We now report that ion-conductive pathways can also form within the VSDs of VGICs, whereby two scenarios can occur: 1) A VSD becomes more hydrated and expands enough to conduct ions but not much more. As soon as the first ion passes through a VSD, we call such an ion-conductive pathway the “VSD pore.” 2) A VSD pore forms, begins to expand, and becomes stabilized by lipid headgroups. We call this pathway a “complex pore” and define it as a pore that initiates in a VSD and then induces migration of at least two lipid headgroups toward the membrane center. Field-induced expansion of such complex pore can lead to severe unfolding of the VSD. The type of pore that forms preferentially depends on the type of ion channel and the hydration and electrostatic profile of the VSDs. The graphs in Fig. 2 b summarize the results obtained for all channels (different types of pores are indicated by different markers as shown in the figure legend). The horizontal bars in Fig. 2 b indicate the length of each simulation. The markers show the time of the first ion passage through a given pore (orange color for Na, green color for Cl, circles for lipid pores, triangles for VSD pores). Note that unlike lipid pores, which start conducting both Na and Cl ions practically simultaneously, VSD pores usually start conducting one type of ions preferentially. More detailed description of individual simulations is given in the following sections. For all simulations, the reader can also find additional results in Figs. S1–S4, including the number of ions that passed each pore, the progression of the pore radius, the change in the number of protein residues in helical structure, and the change in the protein’s solvent-accessible surface area.

Figure 2.

Summary of the simulation results. (a) A schematic representation of the types of ion-conductive transmembrane pathways induced by an electric field that were observed in the simulations. (b) Graphs show the time of the first Na⁺ and Cl⁻ ion passages through a given pore (see legend) in simulations for all channels. Black dots and black stars show the time at which a lipid pore and a VSD pore, respectively, became stabilized by lipid headgroups (i.e., the time when at least two lipid headgroups were found within 0.5 nm from the middle of the membrane). If a VSD pore became stabilized by lipid headgroups, such pore was called a “complex pore.” The horizontal bars correspond to the simulation length. The text next to each horizontal bar gives the index of the VSD in which the VSD pore or complex pore was formed. The data presented in this figure are also tabulated in Table S2. The scheme on the bottom right shows how ions redistribute around the cell membrane upon exposure to an electric field; on the side facing the positive electrode (anode), the membrane becomes hyperpolarized, whereas on the opposite side, it becomes depolarized. To see this figure in color, go online.

Electroporation of the NavMs channel

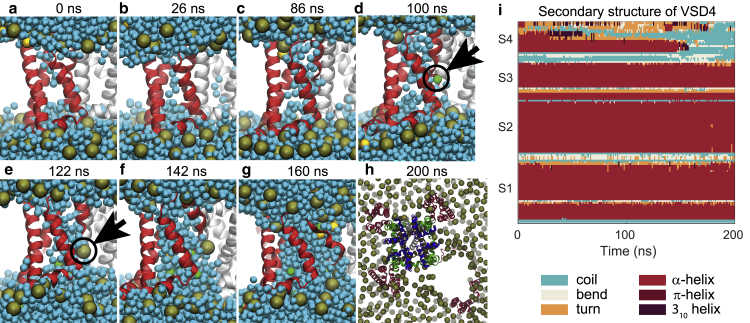
We first performed a simulation of NavMs channel under a hyperpolarizing TMV of −1.5 V. The VSDs of NavMs were already hydrated in the absence of an external electric field (Fig. 3 a). After the onset of the electric field, more water molecules entered the VSDs (Fig. 3 b). In one of these domains, denoted as VSD4, the S3 helix moved away from S1, S2, and S4, which further promoted hydration of the domain’s interior (Fig. 3 c). Compared to the other helices, S3 is weakly connected to the rest of the voltage sensor. First, it is a short helix, which limits the number of interactions it can form, and second, it has only one salt-bridge interaction with S4, unlike, for instance, S2, which has two such salt bridges; we anticipate that this weak connection resulted in the S3 helix being detached first under an excessive electric field. Shortly after S3 moved, at ∼90 ns, VSD4 was crossed by the first Cl⁻ ion (Fig. 3 d), which was followed by the passage of the first Na⁺ ion at ∼130 ns. We will further refer to such conductive pathway as the “VSD pore.” During the simulation, this VSD pore expanded and eventually became stabilized by lipid headgroups that migrated toward the middle of the membrane (Fig. 3, e–g). Following previous suggestions in the literature (49,50), we will refer to such lipid-stabilized structure as the “complex pore.” With expansion of the complex pore, the S4 helix lost its secondary structure, and VSD4 began to unfold, as shown in Fig. 3, h–i (and Fig. S1; Videos S1 and S2). In this simulation, another VSD pore was formed in VSD1 at ∼120 ns, which allowed the passage of a single Cl⁻ ion.

Figure 3.

Formation of a complex pore in VSD4 of NavMs channel. (a) VSD was hydrated already in the absence of electric field. (b and c) Upon electric field application, more water molecules entered the VSD. (d) The first Cl⁻ ion passed through the VSD at ∼90 ns after the onset of the electric field. (e and f) More water and ions entered the VSD, and this VSD pore became stabilized by lipid headgroups forming the so-called complex pore. (g) As the complex pore expanded, the VSD began to unfold from the channel. (h) Unfolded VSD viewed from the extracellular side. In (a)–(h) the VSD is colored in red, water in cyan, lipid phosphorus atoms in gold, and sodium and chloride ions in yellow and green, respectively. Black arrows mark the first Cl ion within VSD and the first lipid headgroup moving into the pore. (i) Disruption of the VSD’s secondary structure. To see this figure in color, go online.

Video S1. Complex Pore in NavMs - Side View

Side view of the formation of a complex pore in VSD4 of NavMs at hyperpolarizing TMV. Snapshots were taken from the entire trajectory (0-200 ns). The VSDs are represented as red ribbons, the rest of the protein is represented as cyan ribbons. Water molecules are represented as transparent volume, whereas phosphorus atoms of lipid headgroups, Na+ ions, and Cl- ions, are shown as gold, yellow, and green spheres, respectively.

Video S2. Complex Pore in NavMs - Top View

Formation of a complex pore in VSD4 of NavMs at hyperpolarizing TMV viewed from the extracellular medium. Water and ions are omitted from representation.

To verify that these results are reproducible, we performed a second 200-ns-long simulation under the same conditions. Again, we observed formation of a VSD pore followed by its expansion into a complex pore, but this time in VSD3, with the first passage of a Cl⁻ ion occurring at ∼110 ns. Subsequently, a second complex pore was formed in VSD4, suggesting that multiple such pores can be formed in the same voltage-gated ion channel (Fig. S9). The NavMs has four identical VSDs; therefore, it is expected that pores can be formed randomly in any of them with equal probability.

We further performed simulations under a depolarizing TMV of 1.5 V. In this case, we also observed formation of VSD pores, but they did not expand into complex ones, even though we prolonged the simulations to 400 ns. In the first out of two simulations, VSD pores were formed in VSD2 and VSD4. In the second simulation, a single Na⁺ and a single Cl⁻ ion passed through VSD2, confirming that the formation of complex pores is more difficult under depolarizing compared to hyperpolarizing TMV.

In all simulations, we also observed passage of Na⁺ through the central pore of the channel (Fig. 4; see also results from control simulations in Supporting Materials and Methods, Section S4.3; Fig. S8). The structure of NavMs was presumed to be in an open state (20), although in simulations, we observed that the channel pore became fully hydrated and conductive only upon application of a strong (beyond physiological values) electric field. Furthermore, the pore stopped conducting as soon as we either lowered the electric field by 50% or completely turned it off, although in both cases, the channel pore still became fully hydrated occasionally, similarly as already shown in Fig. 4 a at 2 ns. By counting the number of Na⁺ ions that passed through the channel pore within ∼150 ns at ±1.5 V, we estimated its conductance to be ∼17 and ∼2 pS in the two simulations under hyperpolarizing TMV and ∼17 and ∼15 pS in the two simulations under depolarizing TMV (all at 27°C) (Table S2). The estimated conductance appears lower than the experimental value (33 pS at 22°C) (51). Overall, we speculate that the channel structure that we used in our simulations does not correspond to a fully open state and that the passage of Na⁺ ions was only enabled by the high electric field, which promoted the hydration of the hydrophobic gate along the channel pore.

Figure 4.

Passage of Na⁺ ions through the central pore of the NavMs channel. (a) Before electric-field application, the bottom half of the pore is dehydrated. After the application, a stable water bridge is formed in the bottom half of the channel pore, and the number of water molecules hydrating the bottom half gradually increases, allowing the transport of Na⁺ ions. (b) The cumulative sum of the number of ions that passed through the channel pore in simulations under hyperpolarizing (blue shades) and depolarizing TMV (red shades). To see this figure in color, go online.

Electroporation of the NavPaS channel

To verify that the formation of VSD pores and complex pores is not observable only in NavMs, we studied also the eukaryotic NavPaS channel. The same as for NavMs, we performed two simulations for NavPaS under hyperpolarizing and two under depolarizing TMV. In the first simulation under a hyperpolarizing field, VSD pores were formed in VSD1 and VSD2 at ∼233 ns and ∼249 ns, respectively. Whereas the pore in VSD1 did not expand considerably and mainly enabled the transport of Cl⁻ ions, that in VSD2 expanded into a complex pore that led to unfolding of the VSD from the channel, similarly as in NavMs complex pores (Fig. 5 a; Videos S3 and S4). In the second simulation under hyperpolarizing TMV, a VSD pore was formed in VSD2 at ∼120 ns, which further expanded into a complex pore. However, the complex pore did not continue to expand within the VSD. Instead, the pore expanded into the bilayer, as shown in Fig. 5 b. This limited the number of residues that lost their helical secondary structure (Fig. S2). In the first simulation under depolarizing TMV, a VSD pore was formed in VSD1 at ∼80 ns. In addition, at ∼190 ns a lipid pore was formed in the lipid bilayer surrounding the channel, as illustrated in Fig. 5 c. In the second simulation, a VSD pore was again formed in VSD1 and also in VSD2, but only in VSD2 did the pore expand into a complex one, similarly as in Fig. 5 a. Importantly, unlike NavMs, NavPaS has four different VSDs; therefore, differences in their perturbation are expected. Ion passage through the central pore was not observed in any of the simulations. It should be noted that the functional state of the NavPaS structure is unclear because it was not possible to electrophysiologically characterize this channel (21).

Figure 5.

Formation of pores in the NavPaS system. (a) Formation of a complex pore in VSD2. Expansion of the pore continues to unfold the VSD. (b) Formation of a complex pore initiates in the VSD and then expands into the bilayer. (c) Formation of a lipid pore close to, but not associated with, the protein. Top row shows the side view of the VSD. Bottom row shows the extracellular view of the protein. Representation of atoms is the same as in Figs. 1 and 3. To see this figure in color, go online.

Video S3. Complex Pore in NavPaS - Side View

Side view of the formation of a complex pore in VSD2 of NavPaS at hyperpolarizing TMV. Snapshots were taken between 200 ns and 370 ns of the trajectory.

Video S4. Complex Pore in NavPaS - Top View

Formation of a complex pore in VSD2 of NavPaS at hyperpolarizing TMV viewed from the extracellular medium. Water and ions are omitted from representation.

Electroporation of the HCN1 channel

In addition to Nav channels, we performed simulations on HCN1. The VSDs of HCN1 turned out to be much less prone to poration than those of NavMs and NavPaS (Figs. 2 and S3). In one out of two simulations performed under hyperpolarizing TMV, we observed the passage of two Na⁺ ions through VSD4 at ∼497 and ∼525 ns. However, in both simulations, we also observed formation of a lipid pore in the lipid bilayer surrounding the protein, suggesting that formation of pores within the identical VSDs is energetically less favorable than that of lipid pores (Videos S5 and S6). In the single simulation performed at depolarizing TMV, we observed no pores within the entire 600 ns run. The structure of this channel is expected to be in the closed state, and in none of the simulations did we observe passage of ions through the channel pore.

Video S5. Lipid Pore in HCN1 - Side View

Side view of the formation of a lipid pore in HCN1 at hyperpolarizing TMV. Snapshots were taken between 100 ns and 230 ns of the trajectory.

Video S6. Lipid Pore in HCN1 - Top View

Formation of a lipid pore in HCN1 at hyperpolarizing TMV viewed from the extracellular medium. Water and ions are omitted from representation.

VSD pores and complex pores form more easily in VSDs that are more hydrated and are electrostatically more favorable for the entry of ions

The results presented above showed that it is possible to observe conduction of ions through one or more VSDs in all three channels. However, not all VSDs are equally likely to be perturbed by the electric field (Fig. 2). Considering all simulations performed, we observed ionic conduction through all of the identical VSDs of NavMs. In addition, in NavMs we observed the expansion of VSD pores into complex ones in all VSDs (see also the control simulations reported in Tables S4 and S5). In NavPaS, which has four different VSDs, we observed ionic conduction only through VSD1 and VSD2. Moreover, VSD2 formed a complex pore, whereas VSD1 did not. In HCN1, formation of a lipid pore was more favorable compared to a VSD pore, as we could only observe the passage of two sodium ions through VSD4 in one out of the three simulations, whereas a lipid pore was formed in two of these simulations. Overall, these differences suggest that there should be some features of the VSD that make it more prone to porate. We thus hypothesized that VSD pores and complex pores are formed more easily in VSDs that are more hydrated. This hypothesis is based on previous MD simulations of pure lipid bilayers showing the crucial role of water molecules in formation of lipid pores (52), as well as on the observation that in a lipid bilayer, a pore is formed more easily if this bilayer is pre-embedded with water molecules (53).

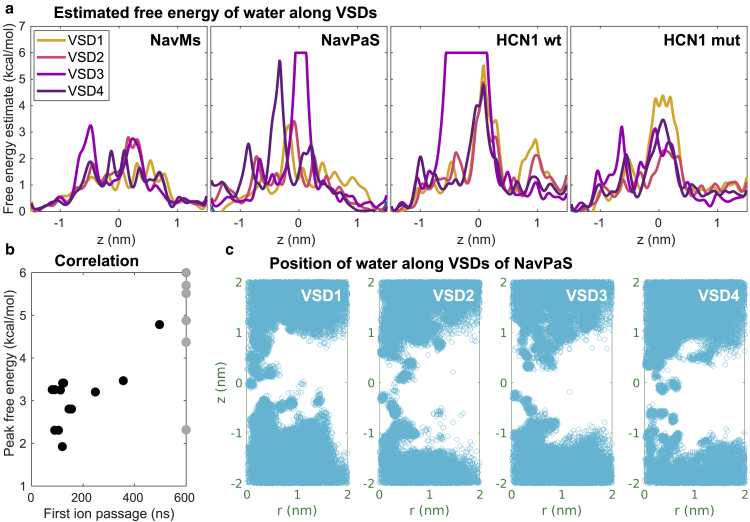
To investigate the hydration profile of individual VSDs, we estimated the free energy of water molecules as a function of their position along the VSDs by analyzing the probability distribution of these molecules in the absence of an external electric field (Fig. 6 a). The free energy profiles indeed show the lowest barriers in the VSDs in which we observed formation of VSD pores and complex pores, i.e., in the VSDs of NavMs and in VSD1 and VSD2 of NavPaS. The water probability distribution in the two other VSDs of NavPaS and the four VSDs of HCN1 has hydrophobic gaps, resulting in considerably higher free energy barriers (see also two-dimensional images showing the position of water molecules in Fig. 6 c; Supporting Materials and Methods, Section S5). Furthermore, for all VSDs from all the channels, we plotted the height of the free energy barrier versus the time of the first ion passage (either Na⁺ or Cl⁻) through the VSD. The graph in Fig. 6 b shows that there is a positive correlation between these two variables, confirming that hydration of the VSD is an important feature that contributes to VSD’s propensity for poration. To corroborate this hypothesis further, we considered a mutant’s HCN1 VSD that contained three mutations of nonpolar into polar residues (54). The mutations increased the hydration of the VSDs and decreased the free energy barrier for water molecules, as shown in Fig. 6 a. We then performed simulations of the mutant HCN1 under hyperpolarizing TMV. In one out of two simulations, a VSD pore was formed at ∼250 ns after the onset of the electric field, followed by its transformation into a complex pore; this observation indicates that the VSDs of the mutant HCN1 can be more easily porated compared with the wild-type channel and goes in line with our hypothesis (Fig. S4; Table S2).

Figure 6.

Hydration of VSDs. (a) Free energy profiles estimated from probabilities of water distribution along the VSD principal axis (z) of NavMs, NavPaS, wild-type HCN1, and mutant HCN1, averaged over 200 ns. Note that the free energy barriers are cut at 6 kcal/mol. (b) Correlation between the height of the free energy barrier and the time of the first ion passage (either Na⁺ or Cl⁻) through a VSD. Ion passage times are taken from all simulations reported in Table S2. Gray dots represent VSDs that were not porated in any of the simulations. The outlier at (600 ns, 2.3 kcal/mol) corresponds to VSD2 of HCN1 mutant; note that we performed only two simulations for this channel. (c) Positions of water molecules in each VSD of NavPaS projected along the VSD radius (r) and the VSD principal axis (z). The VSDs’ center of mass is located at (0,0). Blue circles show all positions extracted from 200 frames of the last 200 ns of the equilibration trajectory. To see this figure in color, go online.

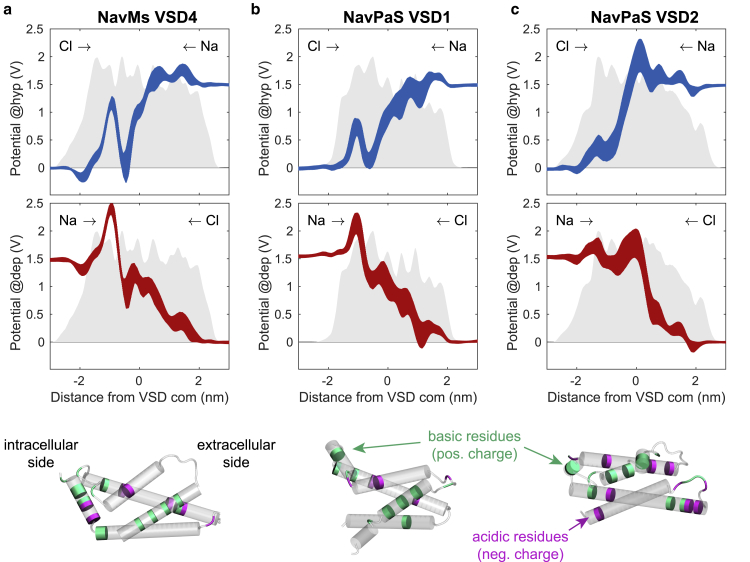
The electrostatic potential inside the VSD is another candidate feature that contributes to VSDs’ propensity for poration. The simulations showed that in NavMs, complex pores could only be formed under hyperpolarizing TMV. In NavPaS, we observed formation of a complex pore in VSD2 regardless of the TMV polarity, whereas in VSD1 we only observed formation of a VSD pore. Moreover, the pore in VSD1 was considerably more selective for Cl⁻ ions under depolarizing TMV. We hypothesized that the observed asymmetry in pore formation and conduction is due to the asymmetric distribution of charges along the VSDs. Fig. 7 compares the electrostatic potential profiles along one of the VSDs of NavMs (all four VSDs show a similar profile; Fig. S19) and VSD1 and VSD2 of NavPaS. Note that the electrostatic potential was determined under an applied electric field before poration. The NavMs VSD has a high positive peak at the extracellular side, which attracts Cl⁻ ions but repels Na⁺. The transport of ions is thus impeded under depolarizing TMV, for which we observed formation of VSD pores, but not complex pores. In VSD2 of NavPaS, in which a complex pore was formed under both hyperpolarizing and depolarizing TMV, the electrostatic profile is similar at either side of the membrane. In VSD1 of NavPaS, the electrostatic potential also shows a positive peak at the extracellular side. Accordingly, we observed selective conduction of Cl⁻ ions through this VSD under depolarizing TMV, allowing passage of 9 Cl⁻ ions compared with only 1 Na⁺ ion (see Table S2). Interestingly, the height of the peaks for VSD1 and VSD2 are similar, yet complex pores were formed only in VSD2. This suggests that there are additional features of the VSDs that influence pore formation such as, for instance, the salt-bridge connections. VSD2 has fewer salt-bridge connections between S1–S4 helices than VSD1 (3 vs. 4; see Table S7), which could be the reason why it unfolds more easily.

Figure 7.

Electrostatic profiles along different VSDs under hyperpolarizing (blue lines) and depolarizing TMV (red lines). (a) VSD4 of NavMs. (b) VSD1 of NavPaS. (c) VSD2 of NavPaS. Corresponding profiles in the absence of applied electric field are given in Fig. S18. The line thickness corresponds to standard deviation of 10 1D profiles. The gray area at the back of each graph shows the mass density profile of the VSD. Images below graphs show the position of charged residues on each VSD: positively charged ARG, HIS, and LYS are colored green, negatively charged residues ASP and GLU are colored magenta. Intracellular side is on the left. To see this figure in color, go online.

Complex pores can conduct ions preferentially in one direction

To investigate further the asymmetric ion conduction through complex pores, we performed additional simulations of NavMs and NavPaS with these pores under a 3× lower electric field, i.e., resulting in TMV ≈ E_z L_z = 0.5 V (55). We reduced the electric field to prevent the complex pores from further expansion, and we characterized ionic transport through such stabilized pores (53,54). As expected, the conduction of ions through NavMs complex pore was considerably larger under hyperpolarizing TMV, especially for Cl⁻ ions, whereas the conduction through the NavPaS complex pore (in VSD2) was less dependent on TMV polarity (Fig. S20). More specifically, within 100 ns of the simulation, the NavMs complex pore was crossed by 37 Na⁺ and 195 Cl⁻ ions under hyperpolarization and by 20 Na⁺ and 52 Cl⁻ ions under depolarization. The NavPaS complex pore was crossed by 104 Na⁺ and 276 Cl⁻ ions under hyperpolarization and by 99 Na⁺ and 189 Cl⁻ ions under depolarization. Both complex pores were less conductive to Na⁺ compared to Cl⁻ ions. A similar preference for Cl⁻ ions has been observed in lipid pores, in which this selectivity could be explained by lower bulk mobility of Na⁺ ions and their binding to lipid headgroups, which also affects the electrostatic environment inside the pore and induces an electroosmotic flow in the direction of Cl⁻ ion movement (56).

The size of complex pores depends on the TMV

When maintaining the TMV at 1.5 V, complex pores continue to expand in size. However, the size of the pores can be stabilized by reducing the applied electric field (and thereby the TMV). This is similar to what has been observed before for pores in pure lipid bilayers (44,57). Fig. 8 shows the progression of the radius of example complex pores in NavMs and NavPaS. The pores were created at a TMV of ±1.5 V, and then the simulation was continued either at a TMV of ±1.5 V or at a lower electric field, resulting in TMV of ±1.0 V or ±0.5 V. The behavior of both NavMs and NavPaS complex pores was similar. For a TMV of ±1.5 V, the pore radius continued to rapidly increase. For a TMV of ±1.0 V, the pore radius also continued to increase but at a slower rate. For a TMV of ±0.5 V, the pore radius somewhat decreased and became stabilized. Note that complex pores are lined both by transmembrane helices and lipid headgroups and have an irregular shape. The pore radius, determined here as the radius of the largest sphere than can be pushed through the pore, is thus a simplified representation of the pore size.

Complex pores are more stable than lipid pores

Pores created by electric fields in pure 1-palmytoyl-2-oleoyl-phosphatidylcholine bilayers have been reported to close on average within ∼50 ns (38). To investigate the postpulse stability of complex pores, we conducted a 1-μs-long simulation of the NavMs complex pore, presented in Fig. 3, in the absence of an electric field. Fig. 9 a shows the configuration of the pore at 0, 100, and 1000 ns after switching off the electric field. The pore reduced in size but remained stabilized by lipid headgroups even after 1000 ns. Ions were able to enter and pass through the pore by diffusion (Fig. 9 b). We further tested the stability of complex pores presented in Fig. 8. These pores also remained opened and stabilized by lipid headgroups at the end of the 400-ns-long simulation (Supporting Materials and Methods, Section S8). However, we expect that the time for which a complex pore remains open depends on the size that it reached during the electric-field exposure and the extent by which it deformed the VSD. We observed that in a NavMs complex pore, which barely met our criterion for a complex pore and became stabilized by only two lipids, the lipids returned to their default orientation ∼200 ns after turning off the electric field (Fig. S22). Nevertheless, in none of the abovementioned simulations did we observe complete recovery of the VSD’s secondary structure; all simulations suggested that formation of complex pores leads to persistent perturbation of the VSD structure, especially the S4 helix (Figs. S21–S23).

Salt-bridge reorganization in VSDs

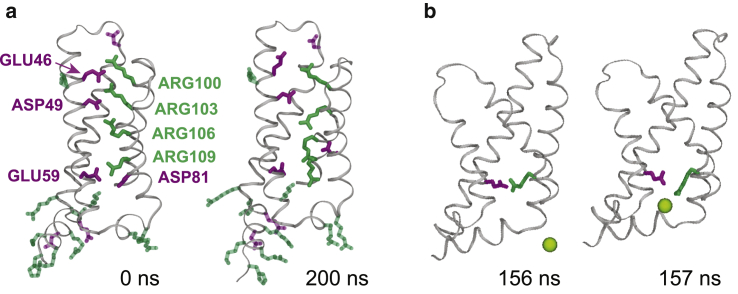
The ability of VSDs to respond to changes in TMV is granted by positively charged residues of the S4 segment. Being embedded into a low dielectric medium, these residues are primary elements to sense an applied electric field. Inside a VSD, they interact with negative counterparts coming from the remaining S1–S3 segments through salt bridges. Upon electric-field application, the S4 residues move along its direction, causing the disruption of existing salt bridges and formation of new ones (58, 59, 60). In our simulations, application of the electric field modified the salt-bridge connections within the investigated VSD: some existing salt bridges were broken, and new salt bridges were formed. An example is depicted in Fig. 10 a and Video S7, which show how salt bridges were perturbed in VSD2 of the NavMs channel under hyperpolarizing TMV (note that VSD2 was not porated in this simulation). Before application of the electric field, there were four connections formed by positively charged arginine residues on the S4 helix and negatively charged residues on the S1–S3 helices (Fig. 10 a). Upon an electric-field application, all these salt bridges were broken, and ARG106 shifted such that it formed a new connection with ASP81. After turning off the electric field, this new connection, ARG106-ASP81, remained stable for at least 1 μs (last time tested). Two other connections, ARG103-ASP49 and ARG109-ASP81, that existed before the electric-field application were reformed (Figs. S24–S27). Similar breakage and formation of salt bridges was also observed in other NavMs VSDs and in other channels, as shown in Tables S6–S8. It is interesting to note that the entry of ions into the VSDs was not necessary for the breakage of salt bridges, but it could facilitate this breakage, as shown in Fig. 10 b.

Figure 10.

Reorganization of salt bridges in VSDs. (a) An example from the first simulation of NavMs under hyperpolarizing TMV showing positively charged (green) and negatively charged (magenta) residues in VSD2. All four salt-bridge connections, ARG103-ASP49, ARG106-ASP49, ARG109-GLU59, and ARG109-ASP81, broke during the pulse, and one new connection was formed: ARG106-ASP81. (b) An example showing how a Cl⁻ ion facilitates breakage of a salt bridge between ARG109 and GLU59 in VSD4 of NavMs. Other residues are omitted from representation for clarity. Frames were taken from the second simulation under hyperpolarizing TMV. To see this figure in color, go online.

Video S7. Salt-Bridge Reorganization in VSD2 of NavMs at Hyperpolarizing TMV

The first and second half of the movie correspond to, respectively, 200 ns during and 200 ns after electric field application. Positively charged ARG, HIS, and LYS are colored green, negatively charged residues ASP and GLU are colored magenta.

Comparison with the charge imbalance method

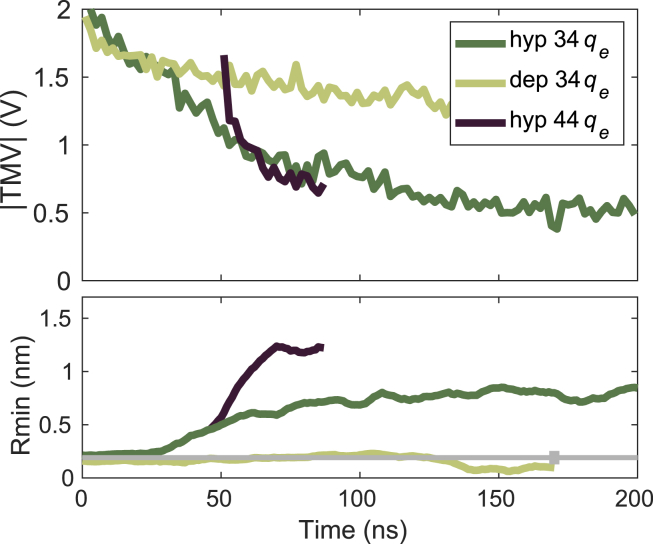
Finally, we performed additional simulations for the NavMs system, in which we mimicked electroporation conditions by establishing a charge imbalance across the membrane. With these simulations we observed similar sets of events as in simulations with the external electric-field method: both under hyperpolarizing and depolarizing TMV, firstly Na⁺ ions started to pass through the central channel pore, and then a VSD pore formed (Fig. S11). Under hyperpolarizing TMV, the VSD pore formed in VSD1 at 29 ns and then expanded into a complex pore. Under depolarizing TMV, the VSD pore formed in VSD3 at 104 ns, whereas this pore was not able to expand into a complex pore within the ∼200-ns-long simulation. However, we observed an important difference between the charge imbalance and external electric-field simulations. In charge imbalance, the TMV kept dropping though the simulation, even though the charge imbalance was kept constant. This is due to redistribution of ions during simulation (some of the ions move into the central channel pore or VSD pore or complex pores) and thus contribute differently to the TMV than at the beginning of the simulation. Under hyperpolarizing conditions, the TMV dropped in absolute value from ∼2 to ∼0.5 V (Fig. 11). The complex pore thus did not continue to expand, but its size became stabilized at a radius of ∼0.8 nm. We tested whether we could increase the pore size by increasing the charge imbalance once a complex pore is formed. Indeed, the pore radius expanded to ∼1.2 nm, but at the same time, the TMV dropped to ∼0.6 V. Under hyperpolarizing conditions, the TMV also kept dropping throughout the simulation from ∼2 to ∼1.3 V, although only a VSD pore was formed in this simulation.

Figure 11.

Charge imbalance simulations. Two main simulations were performed, in which the charge imbalance was 34q_e (q_e is the elementary charge), such that it resulted in hyperpolarizing or depolarizing TMV. For hyperpolarizing TMV a short additional simulation was performed in which the charge imbalance was increased to 44q_e after a complex pore was formed under 34q_e. Graphs show the absolute value of the TMV and the pore radius in all three simulations. Note that a complex pore formed under hyperpolarizing TMV and a VSD pore formed under depolarizing TMV. The gray horizontal line shows the average radius of a pathway within a VSD in the absence of an electric field. To see this figure in color, go online.

Discussion

Formation of complex pores is one explanation for the decrease in ionic current through VGICs observed experimentally

Electrophysiological measurements showed that electroporative submicrosecond electric pulses can cause a decrease in ionic currents through Nav and Cav channels during action potentials in different excitable cells, whereby this decrease was suggested to involve electroconformational changes of the channels (6, 7, 8). Our simulations showed that electric fields can induce the formation of VSD pores that can expand into lipid-stabilized complex pores, leading to unfolding of the VSD from the channel. We expect that such unfolded VSDs become dysfunctional and unable to regulate the opening and closure of the channel pore. A dysfunctional ion channel cannot respond to changes in TMV anymore, which in electrophysiological measurements can indeed be detected as reduced current during action potentials. The complex pores (and the channel pore, if the channel got stuck in an intermediate open state) can only contribute to the “leak” current, which would be interpreted as the current flowing through lipid pores or other permeable defects caused by pulsed electric field. Overall, our simulations offer a mechanism that can potentially explain the experimentally measured decrease in ion channels’ currents.

Our simulations also revealed that, depending on the hydration and electrostatic properties, some VSDs can be more easily porated than others. This offers a possible explanation of why some channels appear to be affected at weaker electric fields than others (8). Furthermore, our simulations showed that some VSDs are more easily porated at hyperpolarizing (or depolarizing) TMV, which offers a possible mechanism of how the decrease in channel conductance depends on the polarity of the TMV (9). Because different species express channels with different sequences, we anticipate that the electric-field-mediated effects on ion channels should to some extent be species and also cell-type specific.

VSD-associated complex pores: a type of long-lived metastable pores?

The mechanisms by which cell membranes remain permeable for seconds or minutes after application of electric pulses are still being discussed (4). Lipid pores do not seem to be stable long enough to account for this long-lived permeability as suggested based on their average lifetime: several microseconds as measured experimentally on pure lipid bilayers (61,62) or a few tens to hundreds of nanoseconds in the absence of external electric fields as estimated using MD (38,63). It has been proposed that lipid pores could evolve into metastable pores involving both lipids and membrane proteins (49,50). The complex pores observed in our simulations are indeed stabilized by lipid headgroups and VSD helices and can have a long lifetime: after turning off the electric field, we could not observe the pore closure within a 1-μs-long simulation. This is longer than reported for closure of lipid pores in MD simulations (38,63). Although we cannot infer from our simulations whether such complex pores could remain open for seconds or minutes after the pulse, it seems reasonable to anticipate that if a VSD unfolds to a major extent, it would not spontaneously refold back, thus leaving a long-lived permeable defect in the membrane until protein internalization by cell’s quality control machinery (64). Recent electrophysiological measurements on wild-type HEK cells and HEK cells expressing Cav1.3 channels indeed showed about two-fold greater increase in the postpulse membrane conductance of Cav-expressing cells after treatment with submicrosecond pulses (65). Interestingly, despite the overall increase in the membrane conductance, the voltage-dependent Ca²⁺ current through Cav channels became decreased after exposure. These experimental results support our predictions that VGICs can act as (additional) sites of poration, whereas at the same time, such porated channels become dysfunctional and unable to respond to changes in TMV. It is further noteworthy that formation and ionic conduction of complex pores can be asymmetric with respect to TMV polarity. Such or similar protein-associated complex pores could therefore contribute to the not-well-understood mechanism of asymmetric cell membrane electropermeabilization, whereby exposure to electric pulses makes the membrane more extensively permeabilized either on anodic (hyperpolarized) or cathodic (depolarized) side (66, 67, 68).

Although our simulations mimicked exposure to high-intensity submicrosecond electric pulses, we expect that similar perturbation of VGICs could also occur during exposure to longer, more conventional microsecond or millisecond pulses with lower intensity. In one simulation of the mutant HCN1 channel under a two-fold lower TMV of ∼0.7 V (this simulation was initially intended for a different study (54)), we observed formation of a complex pore at ∼4 μs after the onset of the electric field (Fig. S28). Thus, we expect that VSD pores and complex pores can form also at lower TMV, just at a lower rate, similarly as observed for lipid pores (38).

Activation of Nav channels by nanosecond pulsed electric fields

Depolarization of the membrane of excitable cells by external electric fields is known to trigger action potentials and is used for various purposes, for example, artificial pacemaking, heart defibrillation, deep brain stimulation, and functional electrical stimulation. Stimulation of peripheral nerves is also an expected, though undesired, side effect in electroporation-based treatments that utilize microsecond- or millisecond-long pulses (69). High-intensity pulses with nano- and picosecond duration can activate VGICs and trigger action potentials as well (15,70,71). However, it remains unclear whether such short pulses are sufficiently long to activate VGICs by moving the VSDs during the pulse or whether the activation is caused by postpulse membrane depolarization resulting from ionic leakage across permeabilized membrane that disrupts the transmembrane ionic gradients. Stimulation of excitable cells by nanosecond pulses has been characterized by optical monitoring as the increase of intracellular Ca²⁺ and has been observed in bovine chromaffin cells exposed to a 5 ns, 50 kV/cm pulse (16); adult rat cardiomyocytes exposed to 4 ns, 20–80 kV/cm pulses (15); and rat embryonic cardiomyocytes exposed to a 10 ns, ≥36 kV/cm pulse (17). The first study (16) suggested that Ca²⁺ entered the cells through Cav channels, which were activated indirectly by postpulse membrane depolarization. The second study (15) also suggested that Nav and Cav channels became activated by postpulse membrane depolarization. Finally, the third study (17) reported that a Cav-mediated increase in intracellular Ca²⁺ could be observed below the threshold for detectable membrane electropermeabilization (63 kV/cm). More recently, action potential generation in response to a 200 ns, ≥1.9 kV/cm pulse has been monitored in E18 rat hippocampal neurons by voltage-sensitive fluorescent dye (11). This study reported that action potentials could only be triggered above the electropermeabilization threshold; however, it was possible that Nav channels were activated directly by the electric field. Direct activation of Nav channels by 12 ns pulses, not mediated by electropermeabilization, was also suggested in experiments on a peripheral nerve (12).

Activation of a VGIC involves the movement of S4 helix, during which the positively charged residues on S4 break existing connections and form new ones with negatively charged residues on S1–S3 helices. Our analysis revealed that a high TMV, which can build on the membrane during application of electroporative pulses, can induce breakage and formation of salt bridges in the VSD on a nanosecond timescale. However, this occurs quite randomly in different VSDs of the channel and mainly involves formation of just one new salt bridge. An additional in-depth study is required to confirm or exclude the possibility that the TMV induced by high-intensity nanosecond pulses can activate VGICs.

Comment on the difference between the external electric-field and charge imbalance methods

Our results showed that in contrast to external electric-field method, in the charge imbalance method, the TMV keeps dropping throughout the simulation because of the formation and expansion of pores. However, neither of the two simulation methods models a realistic time course of TMV on a cell membrane. When exposing a cell to an electric field in experiments, the TMV that establishes itself on the membrane is controlled on a larger scale by the charging and discharging process of the entire cell membrane. More specifically, the TMV in experiments is governed by the capacitance and conductance of the entire cell membrane, the geometry of the cell, and the conductivity and dielectric permittivity of the extracellular and intracellular solutions (72). Thus, the TMV does not change much by formation of a single pore (although formation of numerous pores over a large cell membrane area does influence the membrane conductance considerably and affects the induced TMV). The time course of TMV during exposure to electroporative pulses with microsecond duration and nanosecond duration has been predicted by models (73,74) and measured experimentally using voltage-sensitive fluorescent membrane dyes (41,66), although the measurements for nanosecond pulses have been challenging because of uncertain calibration of the voltage-sensitive dye (41). With further progress in experimental measurements, it will be interesting in the future to simulate different possible realistic time courses of TMV in MD simulations.

Conclusions

We performed MD simulations of three different VGICs under conditions mimicking exposure to pulsed electric fields. The following conclusions can be drawn from our results. Pulsed electric fields create conductive pores in the VSDs of VGICs, which can evolve into complex pores stabilized by lipid headgroups accompanied by unfolding of the VSD from the channel. VSDs are more or less prone to poration, depending on their hydration and electrostatic profile: the more hydrated the VSD is and the more electrostatically favorable for the entry of ions, the more easily it porates. Poration of VSDs is one explanation for the decreased conductance of Nav and Cav channels observed in experiments. The differences in poration of different VSDs could explain why some channels are affected at lower pulse amplitude than others. Moreover, formation of VSD pores and complex pores, as well as their ionic conduction, can depend on the polarity of the TMV. Hence, such pores could participate in the not completely understood asymmetric electropermeabilization of the cell membranes with respect to its anodic and cathodic side. We speculate that VSD-associated complex pores that lead to unfolding of the VSD from the protein could act as long-lived permeable defects, allowing enhanced transport of species during the seconds- or minutes-long cell membrane resealing.

Our study opens several new research directions. First, we hope that our results will stimulate further experimental investigations of electroporation-mediated membrane protein perturbation by methods such as NMR or Förster resonance energy transfer. Furthermore, it will be interesting to investigate whether our findings are translatable to other membrane proteins. Our conclusions are mainly built on analyses of protein hydration and electrostatic profiles, which can be straightforwardly performed on other membrane proteins. In this regard, a recent MD study on a human aquaporin has revealed the formation of a transient electric-field-induced pore through this protein; unlike the complex pores observed in our simulations, this pore closed within ∼20 ns after turning off the electric field (75,76). In our work, we additionally reported conduction of ions through the central channel pore in the NavMs structure, which was presumably solved in an open state. Another possible research direction, therefore, would be to investigate electroporation of the different functional states of this and other channels. Finally, an interesting observation from our study is that in some cases, particularly in HCN1, lipid pores formed in addition to, or instead of, VSD pores. It is known that different lipids are differently suspectable for electroporation; for example, formation of lipid pores is facilitated in lipids with shorter tails or in peroxidized lipids (77,78). Therefore, it will be interesting to investigate how the lipid environment affects poration of VGICs and other membrane proteins in upcoming studies.

Author Contributions

L.R., M.A.K., I.T., and L.D. designed the research. L.R. performed simulations and analyzed data. L.R., M.A.K., I.T., and L.D. interpreted the results. L.R. wrote the manuscript. M.K., L.D., and I.T. revised the manuscript.

Editor: Vasanthi Jayaraman.