The Impact of Recessive Deleterious Variation on Signals of Adaptive Introgression in Human Populations

Abstract

Admixture with archaic hominins has altered the landscape of genomic variation in modern human populations. Several gene regions have been identified previously as candidates of adaptive introgression (AI) that facilitated human adaptation to specific environments. However, simulation-based studies have suggested that population genetic processes other than adaptive mutations, such as heterosis from recessive deleterious variants private to populations before admixture, can also lead to patterns in genomic data that resemble AI. The extent to which the presence of deleterious variants affect the false-positive rate and the power of current methods to detect AI has not been fully assessed. Here, we used extensive simulations under parameters relevant for human evolution to show that recessive deleterious mutations can increase the false positive rates of tests for AI compared to models without deleterious variants, especially when the recombination rates are low. We next examined candidates of AI in modern humans identified from previous studies, and show that 24 out of 26 candidate regions remain significant, even when deleterious variants are included in the null model. However, two AI candidate genes, HYAL2 and HLA, are particularly susceptible to high false positive signals of AI due to recessive deleterious mutations. These genes are located in regions of the human genome with high exon density together with low recombination rate, factors that we show increase the rate of false-positives due to recessive deleterious mutations. Although the combination of such parameters is rare in the human genome, caution is warranted in such regions, as well as in other species with more compact genomes and/or lower recombination rates. In sum, our results suggest that recessive deleterious mutations cannot account for the signals of AI in most, but not all, of the top candidates for AI in humans, suggesting they may be genuine signals of adaptation.

GENE flow between populations can rapidly increase the genetic variation in the recipient group by introducing new variants from a different population. If some of this genetic variation increases an organism’s ability to survive or reproduce in a specific environment, it can be considered adaptive. Adaptive introgression (AI) has been found to facilitate adaptation to local environments in a wide range of taxa, from plants to animals (Song et al. 2011; Racimo et al. 2015; Payseur and Rieseberg 2016; Burgarella et al. 2019). In modern humans, introgression with archaic hominins, including Neanderthals (Prüfer et al. 2013, 2017) and Denisovans (Reich et al. 2010; Meyer et al. 2012), has changed the genomic diversity of, and supplied adaptive alleles to, most populations outside of Africa. Previous studies have identified at least 30 candidate genomic regions in modern humans that were putatively adaptively introgressed (Abi-Rached et al. 2011; Mendez et al. 2012; Ding et al. 2013; SIGMA Type 2 Diabetes Consortium et al. 2014; Vernot and Akey 2014; Gittelman et al. 2016; Sankararaman et al. 2016; Mallick et al. 2016; Racimo et al. 2016, 2017; Enard and Petrov 2018)—among which one of the most well-known examples is a Denisovan-like haplotype at the EPAS1 gene that facilitated adaptation to high altitude in the Tibetan population (Huerta-Sánchez et al. 2014; Huerta-Sánchez and Casey 2015). As of today, the putative AI tracts in modern humans can be traced back to Neanderthals (Vernot and Akey 2014; Gittelman et al. 2016; Browning et al. 2018; Enard and Petrov 2018), Denisovans (Huerta-Sánchez et al. 2014; Racimo et al. 2016), unknown archaic groups (Plagnol and Wall 2006; Durvasula and Sankararaman 2019), or a mix of more than one population (Racimo et al. 2015; Browning et al. 2018).

The detection of AI relies mostly on independently looking for signatures of introgression (Plagnol and Wall 2006; Green et al. 2010; Durand et al. 2011; Martin et al. 2014; Browning et al. 2018) and signatures of positive selection (Tajima 1989; Fay and Wu 2000; Sabeti et al. 2002, 2007; Voight et al. 2006; Grossman et al. 2010). Additionally, a number of allele frequency-based summary statistics have been shown to be particularly powerful at directly inferring AI without needing to apply separate tests for introgression and selection at genomic regions. These statistics include: the number of uniquely shared alleles between donor and recipient populations (U statistic), the quantile distribution of derived alleles in the recipient population (Q statistic), and the sequence divergence ratio (RD) (Racimo et al. 2017). Racimo et al. (2017) further demonstrated the robustness of these statistics to several factors that may confound the detection of AI, including incomplete lineage sorting and ancestral population structure.

While there is tremendous interest in identifying candidate regions for AI, most mutations that occur in genomes are likely either neutral or deleterious (Lynch et al. 1999; Eyre-Walker and Keightley 2007; Lynch 2010; Lohmueller 2014). Deleterious mutations continue to accumulate in the distinct populations after they split from each other (Henn et al. 2016). These deleterious mutations can also affect the genomic landscape in the recipient population after introgression. The genetic load (i.e., reduction in population fitness due to deleterious variants) of archaic hominins is usually higher than that of modern humans due to the former’s small effective population size (Prüfer et al. 2013). Thus, most introgressed archaic ancestry is ultimately purged from the modern human gene pool (Harris and Nielsen 2016; Juric et al. 2016). Conversely, a higher frequency of archaic variants and longer introgressed tracts are the typical signatures indicating AI. However, recent studies suggest that other population genetic processes can also generate long introgressed tracts at high frequencies in a recipient population. For example, if the recipient population harbors many recessive deleterious mutations that are not shared with the donor (Whitlock et al. 2000; Bierne et al. 2002; Agrawal and Whitlock 2011; Harris and Nielsen 2016; Kim et al. 2018), after introgression admixed individuals will have higher heterozygosity at those sites and the deleterious effect will be reduced (Figure 1). As such, an initial heterosis effect occurs, since admixed individuals have higher fitness compared to unadmixed individuals due to the masking of recessive deleterious variants. The neutral markers nearby the recessive deleterious variants would also increase in frequency (Ingvarsson and Whitlock 2000; Bierne et al. 2002), leading to an overall increase of introgressed ancestry in the admixed population (Harris and Nielsen 2016), resembling what is expected from AI (Racimo et al. 2015, 2017).

Figure 1.

The heterosis effect from an increase in heterozygosity due to admixture. A red or yellow star represents a mutation that is deleterious and recessive (h = 0). Each individual in the pre-admixed populations is homozygous for recessive deleterious variants at two distinct sites. If the two populations admix in equally, all mutations that were private to the original populations and were previously homozygous are now heterozygous in the F1 population.

As an example of this, Harris and Nielsen (Harris and Nielsen 2016) simulated a modern human–Neanderthal admixture, and suggested that the heterosis effect from recessive deleterious variants can increase the Neanderthal ancestry in modern humans by up to 3%. Kim et al. (2018) showed that low recombination rate, high exon densities, and small recipient population size can all amplify the effect of deleterious variants leading to an increase in introgressed ancestry. However, both Harris and Nielsen (2016) and Kim et al. (2018) illustrated the confounding effect of deleterious variants on AI by directly tracking the introgressed ancestry from simulations. Although straightforward and convenient in simulation studies, introgressed ancestry is difficult to measure precisely in empirical data. Thus, it remains unclear whether other summary statistics aimed to detect AI are affected by the presence of deleterious variants.

Our present work aims to systematically explore the behavior of the summary statistics for detecting AI in the presence of recessive deleterious variants in realistic human demographic models. By performing extensive simulations under different evolutionary parameters (demography, recombination rate, and genic structure), we show that null models assuming neutrality, without accounting for the heterosis effect caused by recessive deleterious mutations, lead to increased false positive rates for most statistics.

By examining the currently known AI candidate regions in modern humans, we next show that most of the human AI candidate genes cannot be explained by deleterious variants, suggesting they may be genuine targets of AI. However, we also show that at least several candidate genes previously identified as being under AI [HYAL2 (Ding et al. 2013) and the HLA gene cluster (Abi-Rached et al. 2011)] may alternatively be false-positives due to the presence of deleterious variants. We further show that the greater exon density and low recombination rate are the main factors contributing to the high false positive rates in the two genes. Greater exon density generates a higher density of recessive deleterious mutations, leading to a higher probability of heterosis upon admixture (Kim et al. 2018). A low recombination rate maintains haplotypes at a given genomic region in a population. The combination of the two factors maximizes the heterosis effect due to deleterious mutations upon admixture. We discuss implications of these results for detecting AI in different regions of the genome and different species.

Materials and Methods

Simulations and measurement of AI

We used the software SLiM (version 3.2.0) (Haller and Messer 2018) throughout this work for the simulations. We obtained 200 simulation replicates under each of the different demographic models of admixture. Each of the models consists of three populations: an ancestral population at equilibrium that splits into two subpopulations (pD for “donor population” and pO for “outgroup”), and one of the subpopulations subsequently splits again after a period of time (pO, and pR for “recipient population”). After the pO–pR split, a pulse of admixture (lasting one generation) occurs from pD to pR and the admixture proportion is 10%. Figure 2 shows an illustration of the two demographic models used in this study: (1) Model_0 (Figure 2A) represents a demography where the recipient population size is 10 times smaller than the donor population size throughout the simulation, and the pulse of admixture occurs at 10,000 generations ago; and (2) Model_h (Figure 2B) represents a more realistic human demography with a single pulse of archaic admixture introduced to the non-African population (Reich et al. 2010; Gravel et al. 2011; Sankararaman et al. 2012; Prüfer et al. 2013, 2017) 1610 generations ago. Here the recipient population (pR) represents a non-African population, the outgroup population (pO) represents Africans, and the donor population (pD) represents an archaic group such as Neanderthals or Denisovans.

Figure 2.

Simulated demographic models. Going forward in time, after a burn-in period of 10*N generations (100k generations for Model_0 and 73k for Model_h), the ancestral population diverged into two subpopulations, the donor population (pD) and the ancestral population of pO and the recipient population (pR). The second population split results in pR and pO. Some time after the split of pO and pR, a single pulse of admixture occurred such that 10% of the ancestry of pR came from pD. Beneficial mutations are denoted by the yellow star.

Kim et al. (2018) reported that a long-term population contraction can greatly influence the dynamics of introgression, and that a prolonged bottleneck in the recipient population leads to a drastic increase of introgressed ancestry when the deleterious mutations are recessive. Thus, we use Model_0 as a general model to examine the robustness of the summary statistics when the heterosis effect from recessive deleterious variants is maximized. In contrast, Model_h serves as a comparison to evaluate the behavior of the summary statistics under a realistic demography for human populations.

We introduced mutations in the simulations that could have one of four different effects on fitness: (1) “Neutral”: all mutations being neutral (s = 0); (2) “Deleterious”: recessive deleterious mutations present in the populations, drawn from a gamma distribution of fitness effect (DFE) with a shape parameter of 0.186 and average selection coefficient of −0.01315 (see Kim et al. 2017), as well as a 2.31:1 ratio (Huber et al. 2017) of nonsynonymous to synonymous mutations; (3) “Mild-Pos”: the Deleterious model with an adaptive mutation with milder strength of positive selection (s = 0.01) introduced in pD (donor population) after the initial pD–pO split; (4) “Strong-Pos”: the Deleterious model with an adaptive mutation with stronger strength of positive selection (s = 0.1) introduced in pD after the initial split.

All simulated genomic regions have a length of 5 Mb, with genic structure from the modern human genome build GRCh37/hg19. We used the exon ranges defined by the GENCODE v.14 annotations (Harrow et al. 2012) and the sex-averaged recombination map by Kong et al. (2010) averaged over a 10-kb scale. The per base pair mutation rate was fixed at 1.5*10⁻⁸. For comparison purposes, we also applied a uniform recombination rates at 10⁻⁸ and 10⁻⁹ per base pair per generation as specified below. We also scaled the simulation parameters by a scaling factor of c (c = 5) to increase computational efficiency. The population size thus was rescaled to N/c, all generation times to t/c, selection coefficient to s*c, mutation rate to μ*c, and the recombination rate also at r*c {approximation from 0.5 [1−(1−2^r)^c] for small r and small c}. Other evolutionary parameters remain the same before and after rescaling. For each simulation, we sampled 100 chromosomes from the recipient, donor and outgroup population. Unless otherwise stated, deleterious mutations are recessive (dominance coefficient h=0).

To explore a potential extreme case of how recessive deleterious mutations could influence the false positive rate, for each of the models described above with different fitness effect, we simulated a 5 Mb region with the genic structure of a window in the human genome (Harrow et al. 2012) that has the highest density of exons (chr11:62.3–67.3 Mb; referred to as “Chr11max”; Figure S1; Figure 3, Figure 4, and Figure 6). To explore the effect of recessive deleterious mutations on putatively adaptively introgressed regions in humans, we identified the genomic coordinates using the original studies that identified the AI candidate genes (Table S1), and extracted their flanking regions upstream and downstream of the gene region to a total length of 5 Mb, with the gene region positioned in the center.

Figure 3.

U50 statistics under Model_0. (A–D) show the distributions of U50 statistic in 50-kb windows across the 5-Mb region on Chr11. U50 is the number of sites with an archaic allele that has frequency >50% in the recipient population. For each 50-kb window (the x-axis), we plot the interquartile distributions of U50 over 200 simulation replicates in boxes, with whiskers extending to all data points. Mutations are (A) neutral, (B) recessive and deleterious with selection effects drawn from a gamma DFE, (C) same as (B) with a single mildly beneficial (s = 0.01) mutation, and (D) same as (B) with a single highly beneficial (s = 0.1) mutation. Recombination was simulated at a uniform rate of 1e−9 per site. The adaptive mutations in (C and D) are placed in a window in the middle of the region (2.5 Mb), indicated by the green solid line. We simulated under the demography described by Model_0 (see Figure 2).

Figure 4.

Distributions, true positive rate (TPR), and false positive rate (FPR) of the U50 and RD Statistics. (A) The U50 statistic. (B) The RD statistic. The left panels show the distribution of U50 and divergence ratio (RD) statistics using values obtained from all windows, and the critical values (blue dotted line) used to compute the FPR and TPR on the right panels. The right panels show the FPR (under the neutral and deleterious models) and the TPRs (under the models with positive selection) for each 50-kb window in a region of 5 Mb. For the simulations, red, orange, blue and black represent Strong-Pos, Mild-Pos, Neutral, and Deleterious, respectively. The light blue lines in the midpanels illustrate the exons where new mutations can arise, and the green solid line represents the window where the adaptive mutation occurred. The simulations were run under Model_0 using the genic structure of the Chr11Max region, using a uniform low recombination rate of 1e–9.

Figure 6.

Genomic factors that contribute to high FPRs in the outlier regions. (A) The relationship between the exon density and mean recombination rate in 5-Mb sliding windows across the human genome (step size 100 kb). (B) The relationship between background selection strength (measured by the B-statistic), and the strength of selection in protein-coding regions (measured by dN/dS ratio), on 5-Mb sliding windows (step size 100 kb) across the human genome (hg19). A low value of the B-statistic indicates stronger selection on linked variants, and a low value of the dN/dS ratio indicates more constrained regions. The contour lines show the quantile of the gray points. The blue points highlight the regions of AI candidate genes mentioned in the main text, including the outliers (HYAL2, HLA), and the typical ones (EPAS1, BNC2). The black point represents the “Chr11max” region mentioned in earlier sections. The dashed lines denote the mean values of the respective axes.

Computing the mean exon density, recombination rate, and B-statistic across the human genome

To tabulate exon density across the genome, we scanned the 22 autosomes of the human genome using a sliding window of 5 Mb with step size of 100 kb, and counted the number of exons per 5-Mb window. For each window, we calculated “exon density” as the total number of exons per window, the mean recombination rate (Kong et al. 2010), the mean of the B-statistic (McVicker et al. 2009) that captures the strength of background selection, and the mean of dN/dS ratio computed for all genes within the 5 Mb windows over primate phylogeny (Enard et al. 2016).

Summary statistics for detecting adaptive introgression

For each simulation replicate, we computed the summary statistics for detecting adaptive introgression for nonoverlapping 50 kb windows throughout the simulated segment. A full list of the AI summary statistics used in our study can be found in Table 1. We also directly tracked the Introgressed ancestry in the recipient population that originated from the donor population using the tree sequence file generated from SLiM, and reconstructed the information using pyslim (Kelleher et al. 2018) and msprime (Kelleher et al. 2016) modules in Python3, which was referred to as “introgressed ancestry” or pI (Kim et al. 2018). Therefore, the introgressed ancestry calculated from this study is the true proportion of ancestry.

Table 1. Summary statistics informative about AI examined in this study.

Statistic	Definition	Reference
pI	Ancestry in the recipient population introgressed from the donor population. This measurement is directly tracked in simulations using tree sequences.	Kelleher et al. (2016), Kim et al. (2018)
RD	Average ratio of sequence divergence between an individual from the recipient and an individual from the donor population, and the divergence between an individual from the outgroup and an individual from the donor population	Racimo et al. (2017)
D	Patterson’s D statistic, which measures the excess allele sharing between the recipient and donor population than between the recipient and an outgroup population that is unadmixed.	Green et al. (2010)
fD	A statistic that measures the excess allele sharing while controlling for local variation in ancestry in the recipient population	Martin et al. (2015)
U20/U50/U80	Number of uniquely shared alleles between the recipient and donor population that are of frequency <1% in the outgroup, 100% in the donor, and more than 20/50/80% in the recipient population	Racimo et al. (2017)
Q90/Q95	90/95% quantile of the distribution of derived allele frequencies in the recipient population, that are of frequency below 1% in the outgroup and 100% in the donor population.	Racimo et al. (2017)
Heterozygosity	Expected heterozygosity in the recipient population measured by the mean of 2*p*(1-p), with p being the frequency of any given allele in the recipient population	Crow et al. (1970)

For the other summary statistics that capture the signature of adaptive introgression, we used a custom Python script to extract the sampled haplotype matrices that are in MS style from the SLiM output (100 haplotype samples per population), and filled in the nonsegregating ancestral alleles to match the size of the haplotype matrices from the donor, recipient, and outgroup populations respectively. We calculated the summary statistics at nonoverlapping 50-kb windows using the same Python script pipeline for each simulation replicate.

For each statistic, we defined the critical value as the most extreme 5% quantile value in the distribution of Neutral simulations, grouping all windows and replicates together. For the Deleterious simulations, the false positive rate (FPR) is defined as the proportion of simulations per 50-kb window exceeding the critical values. Similarly, for the Mild- and Strong-Pos simulations, the true positive rate (TPR) is defined as the proportion of simulations per-window exceeding the critical value. For the D statistic (Green et al. 2010; Durand et al. 2011), since the critical value from the Neutral model can reach its highest possible value (D = 1), we calculate the FPR as the proportion of simulations per window that equals the critical value.

Summary statistics for non-African modern human populations

We calculated a variety of AI summary statistics using modern human genome variation data from Phase 3 of The 1000 Genomes Project Consortium et al. (2015). To illustrate the signals of AI captured by the summary statistics from previous studies, we used all individuals from seven representative populations from Eurasia and the Americas as recipient populations (for archaic introgression). Specifically, we used Western Europeans (CEU), British (GBR), Finnish (FIN), Italians (TSI), Han Chinese (CHB), Indians (GIH), and Peruvians (PEL). We also used Yorubans (YRI) as the unadmixed outgroup population. For the donor population, we used the unphased, high-quality whole genome sequences from the Altai Neanderthal (Prüfer et al. 2013) and/or the Altai Denisovan (Meyer et al. 2012), depending on which archaic group was identified as the AI source (Column 4 in Table S1). We referred to the coordinates of AI candidate genes listed in Table S1 to identify each 5 Mb region centered on the candidate gene, and extracted the corresponding genomic sequences from the modern populations and their respective donor populations. We additionally removed sites in the archaic genomes that have potential quality issues (quality score <40 and/or mapping quality <30). If a previously identified AI gene was found to be associated with more than one archaic group, we used only the Altai Neanderthal sequence for these cases. As we did on the simulations, the summary statistics were calculated at nonoverlapping 50-kb windows in the empirical data.

To compute the FPR due to deleterious mutations, we use the neutral simulations (i.e., no deleterious mutations) to define the critical values for each test statistic. We then use the simulations with recessive deleterious mutations as the test datasets to examine the FPR (see Figure 5). These simulations used the recombination rate and exon structure in the 5-Mb region around each candidate AI gene and assumed the demography described by Model_h. Again, the FPR represents the proportion of simulations for a given statistic in a 50-kb window in a candidate gene that are as extreme as, or more extreme than, the 5% neutral critical value. Here, we also computed P-values for each of these empirical AI candidate regions under two null models. The first null model assumed all mutations are neutral, while the second included fully recessive deleterious mutations. We then defined the critical values for each test statistic using these simulations. We computed P-values for each 50-kb window within the candidate region by examining where the empirical summary statistics computed from the 1000 Genomes Project data fell within simulated distributions (see Figure 7).

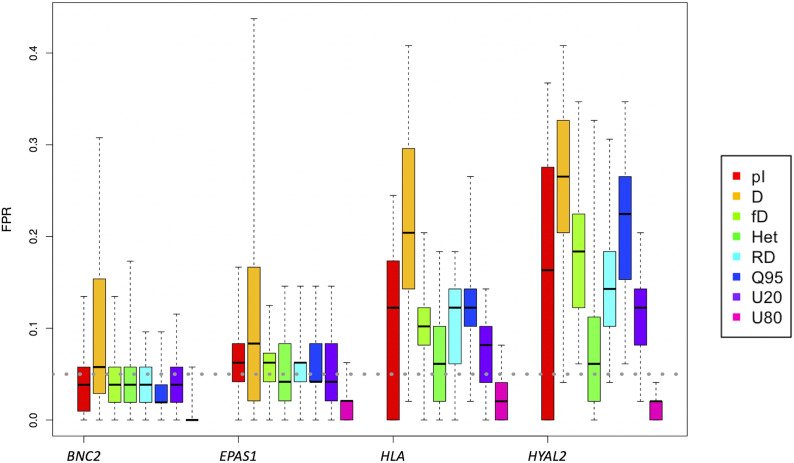
Figure 5.

False positive rates (FPR) for summary statistics from human AI candidate regions. FPRs for several summary statistics are computed by simulating data under the Deleterious mutation model, using critical values determined from the neutral model. All simulations assume Model_h and the recombination rates and exon density of these regions of the genome. The HLA and HYAL2-like regions result in the highest FPRs, while the EPAS1 and BNC2-like regions have similar FPRs as the other regions simulated.

Figure 7.

The difference in the number of significant hits in null models with and without deleterious regions within a 500-kb region surrounding HYAL2 and HLA genes. Each point represents the difference in the number of hits (y-axis: number of windows significant under a neutral model – number of windows significant under the deleterious null model) for the statistics shown on the x-axis. The positive values, highlighted in the gray-shaded area and colored by population, imply the deleterious null model is more conservative for a given statistic. If an AI candidate region shows points above zero for most of the summary statistics, such candidate region is likely prone to false positives due to the heterosis effect, and the validity of adaptive introgression on this region requires further investigation.

Data availability

The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article. All scripts necessary for reproducing the simulations presented in this work are available at: https://github.com/xzhang-popgen/HeterosisAIScripts/. Supplemental materials, including additional methods, Figures S1–S16 and Table S1, are available online through FigShare. Supplemental material available at figshare: https://doi.org/10.25386/genetics.12404324.

Results

Recessive deleterious variants affect summary statistics used to detect AI

We first tested how the presence of recessive deleterious variants affects the distribution of the AI summary statistics listed in Table 1. To maximize the heterosis effect, here we simulated the genic structure of the “Chr11Max” genomic region with a uniformly low recombination rate (r = 1e−9) under the Model_0 demography.

Figure 3 shows the distribution of one of the summary statistics, U50 in nonoverlapping 50-kb windows. U50 captures the number of high-frequency introgressed-derived alleles in the recipient population. Under the scenario where all mutations are neutral, we expect the dynamics of introgressed-derived alleles to be influenced simply by gene flow and other subsequent neutral processes. With a small pulse of admixture, only a small fraction of the introgressed alleles is expected to drift to high frequencies, which is reflected by the low to zero U50 allele count in the distribution of U50 under the Neutral simulations (Figure 3A). However, in the presence of recessive deleterious variants, the count of U50 alleles becomes elevated in all genomic windows (Figure 3B). This pattern is illustrated by the substantially increased mean and variance in the distribution, in contrast to the Neutral comparison (Figure 3B). In cases of AI where a beneficial mutation is introduced in the donor population prior to admixture (Figure 3, C and D), a notable increase of the mean and variance of U50 is also observed. Therefore, the signatures of AI and the heterosis effect due to deleterious mutations are similar, but AI leads to a more pronounced peak at the beneficial mutation. Additionally, an adaptive mutation elevates the range of summary statistics in the flanking region, and the length of the region under its influence positively correlates with the strength of selection. However, when the elevation in U50 is due to recessive deleterious mutations, there is a slight, but consistent, upward shift across the entire region.

We next examined the distribution of other summary statistics under the four fitness scenarios (Figure S2), and observed similar patterns as for U50. These findings indicate that, consistent with what Kim et al. (2018) observed for introgressed ancestry, deleterious variations can generate similar patterns as AI in the absence of beneficial alleles and local adaptation.

To better understand the spatial patterns of variation across the simulated region, we visualized the haplotypes (Supplemental Methods; Marnetto and Huerta-Sánchez 2017) in a 100-kb window in the middle of the segment containing the adaptive mutation when applicable (Figure S3). The haplotypes left by recessive deleterious mutations (Figure S3A) and true adaptive mutations (Figure S3B) differ in structure. Interestingly, both scenarios lead to higher haplotype homozygosity in the recipient population. However, in the AI scenario (Figure S3B), the haplotypes from the donor and recipient populations are more like each other (i.e., the number of differences between the donor haplotype and the introgressed haplotype is smaller, shown in the right panels of Figure S3) than under the scenario with recessive deleterious mutations.

Deleterious mutations increase the FPR for AI detection

To quantify the extent to which deleterious mutations can give false evidence of AI, we used the neutral distribution of summary statistics in each 50-kb window across the large 5-Mb segment to define the critical values for a test of AI. We define the critical value as the most extreme 5% quantile value grouping all windows from neutral simulations together.

For the recessive deleterious model, we obtain the proportion of simulations (200 replicates) per window that exceeds the critical value under the neutral model, and define this proportion as the FPR, as no true adaptive mutations are present. Similarly, we define the TPR for the mild- and strong–positive selection models as the per-window proportion of simulations exceeding the critical value, where the critical value is again defined from the neutral model. Figure 4 shows the neutral critical value and the true/false positive rates in U50 and RD statistics under the simulation setting described in the section above. The TPR/FPR distribution for other summary statistics can be found in Figure S4. The neutral model simulations have FPRs ∼5%, by definition. In contrast, the recessive deleterious simulations show elevated FPRs in most windows for both statistics (8.62–34.48% for RD; 3.45–22.41% for U50). The high FPRs are not negligible, as the identification of AI in empirical data relies on looking for outliers in summary statistics when the presence and location of the adaptive mutation is unknown. Deleterious variation is also more common in human genomes than adaptive variation (Lynch et al. 1999; Eyre-Walker and Keightley 2007; Lynch 2010; Lohmueller 2014), which may further compound this effect.

To further understand how demographic history and recombination rate influence the FPR/TPR of the tests for AI, we simulated the “Chr11Max” 5 Mb segment (see Simulations and measurements of adaptive introgression in Materials and Methods) using the human demographic model (Model_h), and realistic estimates of recombination rate in this region (referred to as r = hg19 in Table 2). We summarized the FPRs and TPRs of a subset of statistics (pI, RD, U50, Q95) under these scenarios in Table 2 (also see Figures S5–S7). We observed that simulations with low recombination rate showed higher mean FPRs using these statistics. Moreover, the standard deviation (SD) of the statistics increases when the realistic recombination rates are applied (average recombination rate higher than 1e−9).

Table 2. Summary of the FPR and TPR under different models.

Simulation Scenario	Statistics	Mean of FPR in Deleterious Model	SD of FPR in Deleterious Model	Focal Window TPR in Mild-Pos Model	Focal Window TPR in Strong-Pos Model
Model_0; Chr11Max; r = 1e-9	pI	0.354	0.047	0.900	1.000
	RD	0.204	0.048	0.521	0.569
	U50	0.117	0.037	0.438	0.432
	Q95	0.437	0.051	0.875	1.000
Model 0, Chr11Max; r = hg19	pI	0.229	0.086	0.885	1.000
	RD	0.134	0.061	0.577	0.648
	U50	0.081	0.046	0.365	0.444
	Q95	0.121	0.034	0.637	0.752
Model_h; Chr11Max; r = hg19	pI	0.087	0.108	0.967	1.000
	RD	0.098	0.117	1.000	0.654
	U50	0.097	0.036	0.767	0.500
	Q95	0.099	0.120	1.000	0.933

For the deleterious model, we computed the false positive rates (FPRs) in 50-kb nonoverlapping windows using the most extreme 5% value from the neutral distribution as the critical value, and show the mean FPR in the third column. For the AI models (Mild-Pos and Strong Pos), we computed the TPRs using the same neutral cutoff value in all windows, and show the TPR in the window that contains the adaptive mutation (“Focal TPR”). Note that a properly calibrated null model should have a FPR of 0.05.

On average, the TPRs are close to, or higher than, the FPRs in corresponding windows, and they are especially distinguishable from the neutral and deleterious models with a distinct peak in the focal windows containing the adaptive mutation (Figure 4). This shows that the summary statistics have high statistical power in general at detecting a true AI signal, as they reject the null hypothesis more often for true positives (density plots in Figure 4). It should be noted that the power varies across statistics, and correlates positively with the FPR. For example, the power of pI can be up to 100% in AI models, but its mean FPR in the deleterious models is also high (Table 2).

Altogether, recessive deleterious variants contribute to a higher FPR for AI detection in all summary statistics examined. Some statistics appear to be more vulnerable than others, with pI, RD, U stats, and Q stats being most affected (Figure S2 and Figure S4). Low recombination rates amplify the heterosis effect that mimics the AI signature, while the modern human demography (Model_h) results in fewer false positives than Model_0 in general, which has a relatively long-term contraction in the recipient population (Figures S5 and S6).

Deleterious mutations have a limited effect on top candidates for AI in humans

Next, we sought to systematically assess whether the patterns of AI summary statistics caused by recessive deleterious variants could lead to false detection of AI when we simulate under the genic structure observed for previously identified AI candidate regions in humans. This is an important consideration because these regions were detected as unusual either in comparison to the rest of the genome or under demographic models that assumed all mutations were neutral. Thus, it remains unclear whether deleterious variation could provide an alternate mechanism for the observed patterns.

We extracted the recombination rates and genic structure of the 5 Mb sequences surrounding 26 previously identified AI regions (Abi-Rached et al. 2011; Mendez et al. 2012, 2013; Ding et al. 2013; Huerta-Sánchez et al. 2014; Sankararaman et al. 2014; SIGMA Type 2 Diabetes Consortium et al. 2014; Vernot and Akey 2014; Deschamps et al. 2016; Gittelman et al. 2016; Racimo et al. 2016, 2017; Browning et al. 2018) (Table S1). For each candidate region, using its recombination rate and exon density, we ran 200 simulation replicates under the human demography described by Model_h. We simulated under two models (the Neutral and Deleterious models) to compute the FPRs in the AI candidate gene regions.

Overall, we find that most statistics do not have extremely elevated FPRs across most of the gene regions in the presence of deleterious mutations (Figure S7). The D statistic, however, is a notable exception, showing a higher FPR across all candidates. This is rather unsurprising because, although the D statistic is powerful at detecting genome-wide excess of shared derived alleles between groups (a metric indicating admixture), studies have shown its limitations and reduced reliability for inferring local ancestry using small genomic regions (Martin et al. 2014). The fD statistic, on the other hand, is powerful at detecting introgression at localized loci, and does not show unusually high FPR for all candidate regions.

Notably, with the exception of two simulated regions (representing the regions of HLA and HYAL2, Figure 5), we find that the FPR is well-controlled in the other 24 simulated AI candidate regions (Figure S7). Here, we show the FPRs for the EPAS1 and the BNC2-like regions (Figure 5) since these two regions have similar recombination rates, exon density and FPRs as the other AI regions considered here. Other than the D statistic discussed above, the rest of the summary statistics show an average of FPR around or <5%. In particular, the Q and U statistics appear to be the most robust against false positives from deleterious mutations. In contrast, HLA-A, HLA-B, and HLA-C genes (referred to as “HLA” in this work), and a segment on chromosome 3 that contains HYAL2 gene show elevated FPRs on nearly all statistics.

High exon density and low recombination rate can lead to deleterious mutations mimicking AI in humans

To understand why the HYAL2 and HLA genes exhibit higher FPRs in the presence of recessive deleterious variants, we evaluated several possible factors that could contribute to the false positives, including: (1) recent human population growth, (2) the mean recombination rate, (3) the density of exons where deleterious mutations occur, and (4) the strength of natural selection in these genes.

We first simulated genomic regions with the structure of the four genes shown in Figure 5 under four different scenarios of population size change (Figure S9). We find that outlier regions, such as HYAL2 and HLA, continue to have high FPRs across the different growth scenarios. Growth (e.g., “Growth 2” and “Growth 4” in Figure S9 where the population size at the end generation is >70-fold larger than the initial size) slightly intensifies the already high FPRs in these two genes (Figure S10), which can be explained by an increase in the efficacy of selection when the effective population size is large (Fisher 1923; Wright 1931). The other two simulated regions (representing the BNC2 and EPAS1 regions) do not exhibit increased FPRs in the presence of population growth.

We next explored how changes in recombination rate impact the FPRs for the summary statistics used to detect AI. By using a uniformly low or high recombination rate in the simulations under Model_h (Figure S11), we observed that a high recombination rate can substantially reduce the FPRs to nominal levels (∼0.05) on all statistics in all genes. Conversely, a uniformly low recombination rate led to high FPRs in the two outlier regions (HYAL2 and HLA), while the FPRs do not necessarily increase in most statistics in other regions like BNC2 and EPAS1.

Motivated by this finding that the recombination rate can influence the FPR in HYAL2 and HLA regions as well as prior work suggesting that low recombination rate and high exon density can lead to deleterious mutations mimicking signals of AI (Kim et al. 2018), we performed a more detailed analysis as to whether the combination of exon density and recombination rate can explain the elevated FPRs in the HYAL2 and HLA regions. We computed the mean recombination rates and exon densities for sliding 5-Mb windows across the human genome (see Materials and Methods), and found that that HYAL2 and HLA regions are indeed outliers. These two genes have both high exon density and low recombination rate compared to most of the other regions of the genome (Figure 6A).

It is also possible that the high FPR in HLA and HYAL2 could be due to mutations in these genes being unusually deleterious compared to mutations in the other candidate AI regions. To test for this, we considered two summary statistics that quantify the amount of selection in local regions of the genome. Specifically, we examined the degree of background selection measured by the B-statistic inferred across the human genome (McVicker et al. 2009), and, second, we used the dN/dS ratio computed across primate species including humans (Enard et al. 2016) as a proxy for the degree of selective constraint (i.e., selection coefficients at nonsynonymous mutations) in these genes. We found that HLA and HYAL2 have low B-values (McVicker et al. 2009) relative to other 5-Mb regions of the genome (Figure 6B and Figure S14), suggesting that these genes are experiencing more linked selection than the rest of the genome. However, HYAL2 and HLA have dN/dS ratios that are well within the genome-wide distribution (Figure 6B), suggesting that the strength of selection is not the main factor inflating the FPRs in these regions. Since the B-values are influenced by the combined effects of the density of functional elements in which deleterious mutations occur, recombination rate, and the selective effects of coding and noncoding regions, the fact that HLA and HYAL2 are outliers on this metric confirms our conclusion that the high exon density, together with low recombination rate, are the major factors influencing false-positive inferences of AI due to recessive deleterious mutations.

A null model with deleterious variation reduces the number of statistically significant AI candidates

Lastly, we asked whether the empirical values of the summary statistics at the 5-Mb regions surrounding the AI loci studied are statistically significant under a null model assuming mutations are neutral or a model assuming mutations are neutral or recessive and deleterious. We used the Altai Neanderthal (Prüfer et al. 2013) or Denisovan (Meyer et al. 2012) as the donor population, Yorubans (YRI) as the outgroup (nonadmixed) population and a non-African population from the 1000 Genomes Project dataset (The 1000 Genomes Project Consortium et al. 2015) as the recipient population (see Materials and Methods). We computed their p-values using the distributions from the simulations under two different (Neutral or Deleterious) null models. Given that our deleterious null model assumes all deleterious mutations are recessive (h = 0), it maximizes the impact of false positives due to deleterious mutations. Under this model, if the values of the summary statistics in the regions surrounding the candidate genes are statistically significant, then the AI signals cannot be explained by the heterosis effect.

We calculated the critical values for all summary statistics using the most extreme 5% tail values under the two null models, and computed the P-values of the empirical data points for the statistics. Among the four genes we use as examples (Figure S15), the “outlier” genes (HLA region and HYAL2) on average have higher P-values under the deleterious null models than under the neutral null models. This trend is reflected by the points falling mostly above the diagonal in Figure S15. The higher P-values when we use the Deleterious null model indicate that this model is more conservative at AI inference. Note that, for the two “typical” AI genes, the P-values fall along the diagonal (Figure S15), suggesting that a null model with and without deleterious mutations yield similar results.

To summarize the difference between the two null models, we computed the number of 50-kb windows that fell in the extreme 5% tail of the Neutral or Deleterious null distribution. We calculated the difference between the number of windows that are significant under the Neutral null model and the number of windows that failed to reach significance under the Deleterious null model, computed within a 500-kb core region that encompasses each AI candidate gene (Figure 7 and Figure S16). Promisingly, we find that most of the candidate regions (24/26) show similar P-values on most, if not all, of the statistics, regardless of whether a null model with deleterious mutations or neutral mutations is used. This observation further confirms the conclusion from an earlier section, that the recessive deleterious variants have a limited impact on the detection of the majority of modern human adaptive introgression candidates. However, two genes (HLA and HYAL2) do exhibit a reduced signature of AI under a deleterious null model. As shown in the previous section, these two genes have low recombination and high exon density which are two factors that enhance the effect of heterosis. Therefore, these regions may not be adaptively introgressed, in contrast to previous findings (Ding et al. 2013; Vernot and Akey 2014; Racimo et al. 2017; Browning et al. 2018).

Discussion

Our work represents one of the first comprehensive efforts to consider the influence of negative selection in the detection of AI in humans. We systematically examined whether recessive deleterious variants carried by populations prior to admixture can affect the robustness of signals in summary statistics that have been shown to be informative about AI.

Through these simulations, we found that the presence of recessive deleterious mutations alone is sufficient to significantly increase the mean and variance of AI summary statistics in at least some genomic regions. These shifts in the distribution of statistics (Figure 3) lead to a higher probability of falsely identifying “AI candidates” when using a neutral demographic model to define the critical value for the AI summary statistics. However, most of the previously identified top AI candidates in humans are unaffected, due to the fact that their signals of AI are too strong to be accounted for by deleterious mutations and/or that the exon density and recombination rates of these regions decrease the chance that recessive deleterious mutations can generate false-positive signals. However, recessive deleterious mutations may still impede the detection of weaker signals of AI or for genes within a specific genomic context. In fact, by examining population genomic data, we show that such effects from recessive deleterious variants can result in spurious signals of AI in two candidate genes (HLA and HYAL2) in humans.

We tested which individual genomic and/or evolutionary parameters can explain why certain genes like HLA and HYAL2 are more susceptible to false-positives in humans, compared to the other candidates. We found that these two genes have a high exon density and low recombination rate when compared to the rest of the genome (Figure 6). High exon density effectively creates a larger mutational target, which leads to the accumulation of more deleterious mutations in a given genomic region. Low recombination rate lowers the probability of crossing over, so linked recessive deleterious variants are more likely to remain linked on a given haplotype. Effectively, both high exon density and low recombination rate maximize the heterosis effect because admixture with a distantly related population will bring in haplotypes carrying nondeleterious alleles at these positions. Therefore, the introgressed ancestry at these regions will increase in the recipient population despite carrying a different set of deleterious variants, leading to the elevation of FPRs in the AI summary statistics. This process acts in a similar manner as AI, except that no beneficial mutations are involved. Fortunately for human geneticists, the density of exons in the human genome is rather low, mitigating the effect of recessive deleterious mutations on generating false positive signals of AI for most (24/26) of the previously identified top candidates.

Other genomic factors, like the density of noncoding functional elements as well as the strength on natural selection acting on deleterious mutations could, in principle, affect the FPR in certain genomic regions. To quantify the importance of these factors, we examined the distributions of B-statistics and dN/dS ratios. The B-statistic measures the strength of background selection due to linked variants (Hudson and Kaplan 1995; Charlesworth 2012), and its value is computed by combining information from the distribution of exons, noncoding variants, recombination rate, and selection coefficient (McVicker et al. 2009). Notably, HYAL2 exhibits a strikingly low B-statistic when compared to the rest of the genome and HLA also has a below-average B-statistic, suggesting these genes experience more linked selection. To test whether the low B-statistics in these genes is driven by mutations in these genes being highly deleterious, rather than their high exon density and their low recombination rate, we examined the distribution of dN/dS ratios. Neither gene has unusually low dN/dS values, implying that the selection coefficients for nonsynonymous mutations in these genes are not more deleterious than these in most other genes. Taken together, these results argue that exon density and recombination rate are the important factors driving the elevated FPR for AI in these regions of the genome.

We also show that the demographic history of human populations, including a change in the recipient population size, does not play a major role in affecting the FPR of tests for AI. However, the near-exponential population growth in the recent history of modern humans may have increased the FPR in genes that are already susceptible to false-positive results due to deleterious mutations. This is consistent with the findings of Kim et al. (2018) where they showed that a recovery of population size after a bottleneck in the recipient population can exaggerate the heterosis effect. This is likely due to the fact that a large effective population size restricts the extent of genetic drift, leading to a more prominent effect of natural selection, including the complementation of deleterious alleles via the heterosis effect.

Our modeling approach makes a number of assumptions. For instance, we mainly considered the extreme case where deleterious variants are completely recessive (h = 0). The reason for this is that we set out to determine whether deleterious variants are a concern for AI signals when this effect is maximized. Kim et al. (2018) already studied the effect from additive variants and observed little effect on introgressed ancestry. In empirical genomic data, the distribution of dominance should be in between the two extremes (Lynch et al. 1999; Whitlock et al. 2000; Eyre-Walker and Keightley 2007; Lynch 2010; Agrawal and Whitlock 2011; Harris and Nielsen 2016; Kim et al. 2018). A current challenge is that the empirical values of dominance coefficients for deleterious mutations in humans remain unknown. We show in our simulations (Figure S13) that the genomic regions with elevated FPRs maintain this behavior under models with a wide range of dominance coefficients, including when the mutations are partially recessive (hs relationship (Henn et al. 2016)). It is promising that, even when the heterosis effect acts in its most extreme manner (assuming h = 0), the signature of AI in the top candidate regions persists. Other values of h would be unlikely to affect the conclusion that 24/26 candidates are robust to confounding by deleterious mutations.

Another simplifying assumption made in most of simulations with genuine AI is that the positive selection on the archaic variant began immediately after introgression. To explore whether the time of positive selection affects the distribution of AI statistics on HLA and HYAL2, we performed additional simulations of these regions when there is a gap between the timing of introgression and positive selection [Standing Archaic Variation (SAV); Supplemental Methods; Jagoda et al. 2017]. We observe that the AI summary statistics from this model, which in effect resemble a weaker positive selection signal, are even less distinguishable from the Deleterious model than the Mild-Pos model (Figure S8).

Even though the signals in most of the top AI candidate genes in humans are unaffected by deleterious variation, there are several reasons why deleterious mutations should still be considered in null models for detecting AI. First, the combination of evolutionary parameters (low recombination rate and high exon density) that leads to an elevation of false-positives may occur much more commonly in other study systems. Moreover, even for modern humans, the demography used in simulations is an approximation of the modern Eurasian population history, which may not represent the true evolutionary history of all non-African populations. For example, when more than one introgression event occurs [e.g., Denisovan introgression in Asia (Browning et al. 2018; Jacobs et al. 2019)], and when the ancestral modern human populations were small, the heterosis effect from deleterious variants could have a different impact under a complex demography. And finally, subtle signals of true AI might not be as distinct from the signals left by deleterious mutations. For instance, a model where selection does not act immediately after introgression may lead to a weaker signature of adaptive introgression. We recommend caution in interpreting these weaker signals, especially in regions of the genome with low recombination rate and high exon density.

Future work to try to distinguish true AI from false-positives due to deleterious mutations in regions of the genome with low recombination rate and high exon density could use the spatial pattern of summary statistics across a genomic region. Indeed, Figure 3 shows that genuine AI leads to a more peaked elevation of U50 at the adaptive mutation compared to recessive deleterious mutations. However, these plots show the distribution over 200 simulation replicates. By visualizing the distribution of statistics values in randomly selected single replicates of simulations (Figure S12), an elevated statistical “peak” value, which is a typical signature of AI, can be generated at a random region of the genome by recessive deleterious mutations only. Thus, the spatial pattern may not be a complete solution in any particular region of the genome with low recombination rate and high exon density.

Although heterosis upon admixture effectively reduces the deleterious effect of recessive variants, its mechanism and biological consequences are essentially different from adaptive introgression, which we expect to produce phenotypic variation in biologically meaningful genes under a given environment. It is thus important to distinguish the signals generated by the heterosis effect on recessive deleterious mutations from legitimate adaptive introgression. Therefore, improving null models to better distinguish between these two processes is important, especially when studying organisms that have compact genomic structures, and/or distinct demographic events that may accelerate the dynamics of the heterosis effect after introgression.