Uncovering axes of variation among single-cell cancer specimens

Abstract

While several tools have been developed to map axes of variation among individual cells, no analogous approaches exist for identifying axes of variation among multicellular biospecimens profiled at single-cell resolution. For this purpose, we developed ‘phenotypic earth mover’s distance’ (PhEMD). PhEMD is a general method for embedding a ‘manifold of manifolds’, in which each datapoint in the higher-level manifold (of biospecimens) represents a collection of points that span a lower-level manifold (of cells). We apply PhEMD to a newly generated drug-screen dataset and demonstrate that PhEMD uncovers axes of cell subpopulational variation among a large set of perturbation conditions. Moreover, we show that PhEMD can be used to infer the phenotypes of biospecimens not directly profiled. Applied to clinical datasets, PhEMD generates a map of the patient-state space that highlights sources of patient-to-patient variation. PhEMD is scalable, compatible with leading batch-effect correction techniques and generalizable to multiple experimental designs.

Single-cell experimental designs are becoming increasingly complex, with data now often collected across numerous experimental conditions to characterize libraries of drugs, pools of CRISPR knockdowns or groups of patients undergoing clinical trials^1–7. The challenge in these experiments is to characterize the ways in which not only individual cells but also multicellular experimental conditions vary. Comparing single-cell experimental conditions (for example, distinct perturbation conditions or patient samples) is challenging, as each condition is itself high-dimensional and comprises a heterogeneous population of cells with each cell characterized by many gene measurements (Supplementary Notes 1 and 2). To address this problem, we propose PhEMD, a ‘manifold of manifolds’ approach to understanding the state space of experimental conditions. PhEMD first leverages the observation that the structure of a single-cell experimental condition (multicellular biospecimen) can be well represented as a low-dimensional manifold (that is, cell-state embedding) using techniques such as PHATE⁸ or diffusion maps⁹. In this first-level manifold, individual datapoints represent cells, and distances between cells represent cell-to-cell dissimilarity. PhEMD models the cellular state space of each experimental condition as a ‘low-level’ manifold and then models the experimental condition state space as a ‘higher-level’ manifold. The ultimate goal of PhEMD is to generate this higher-level manifold, in which each datapoint represents a distinct experimental condition and distances between points represent biospecimen-to-biospecimen dissimilarity. We explore the properties of this final higher-level manifold in depth and show that it can be visualized and clustered to reveal the key axes of variation among a large set of experimental conditions. We also show that such embeddings can be extended with additional data sources to impute experimental conditions not directly measured with single-cell technologies.

To demonstrate the utility of PhEMD, we apply it to a newly generated, large perturbation screen performed on breast cancer cells undergoing TGF-β-induced epithelial-to-mesenchymal transition (EMT), measured at single-cell resolution with mass cytometry. EMT is a process that is thought to play a role in cancer metastasis, whereby polarized epithelial cells within a local tumor undergo specific biochemical changes that result in cells with increased migratory capacity, invasiveness and other characteristics consistent with the mesenchymal phenotype¹⁰. In our experiment, each perturbation condition consists of cells from the Py2T breast cancer cell line stimulated simultaneously with TGF-β (to undergo EMT) and a unique kinase inhibitor, with the ultimate goal being to compare the effects of different inhibitors on our model EMT system. We use PhEMD to embed the space of the kinase inhibitors to reveal the main axes of variation among all inhibitors. We further validate these drug-effect findings by showing that they are consistent with the drug-effect findings of a previously published study that profiled the drug-target binding specificities of several of the same drugs as ours. To highlight the generalizability of the PhEMD embedding approach, we perform analogous analyses on three additional single-cell datasets: one generated dataset with known ground-truth structure, one collection of 17 melanoma samples and a collection of 75 clear-cell renal cell carcinoma samples. Collectively, our varied analyses demonstrate PhEMD’s wide applicability to various single-cell experiments.

Results

Overview of PhEMD

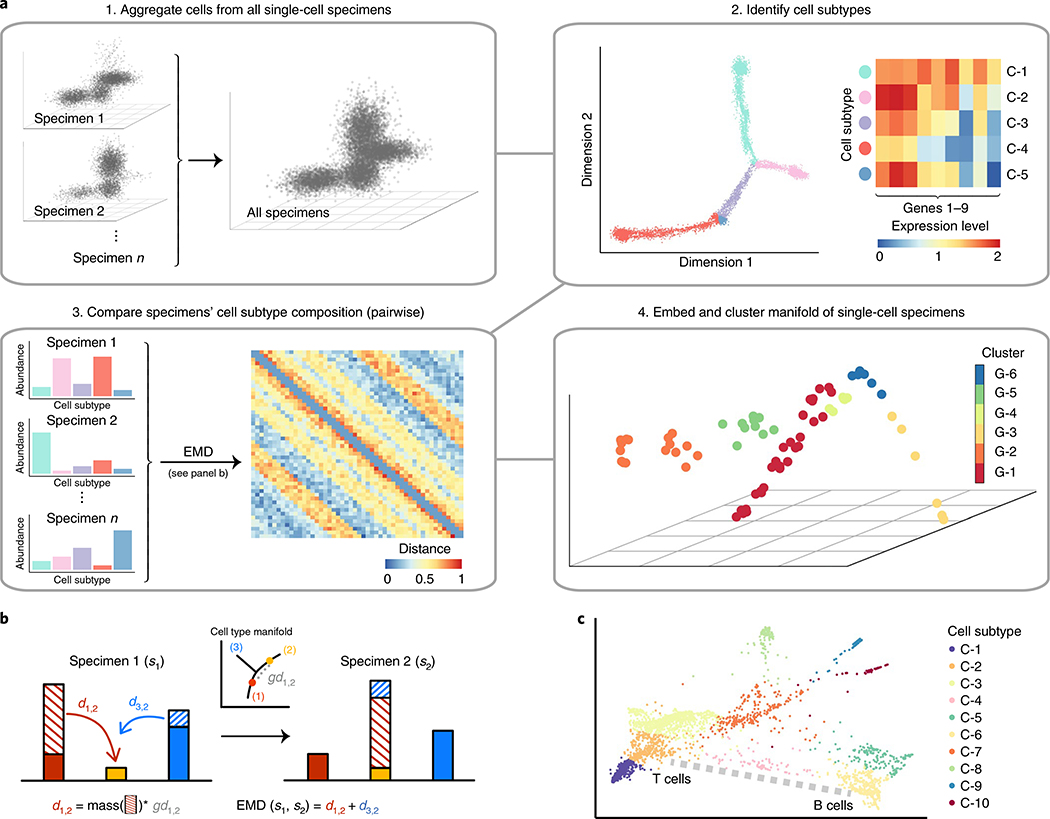
PhEMD is a method for embedding a ‘manifold of manifolds’, that is, a set of datapoints in which each datapoint itself represents a collection of points that comprise a manifold. In the setting of analyzing single-cell data, each datapoint in the ‘manifold of manifolds’ represents an experimental condition (that is, single-cell specimen), which itself comprises a heterogeneous mixture of cells that span a cell-state manifold. PhEMD first embeds each biospecimen as a manifold and then derives a pairwise distance between the manifolds. Deriving a ‘higher-level’ embedding then involves using these pairwise specimen-to-specimen distances to find a coordinate system (that is, axes of variability) such that each point represents a specimen, and the distance between the points represents the dissimilarity between specimens. PhEMD derives such an embedding using the following general steps (Fig. 1):

Fig. 1 |. The PhEMD approach.

a, Flow diagram outlining the sequential steps performed in the PhEMD analysis pipeline. b, Schematic of the EMD computation, which accounts for both the differences in heights of matching bins and the intrinsic similarity of bins (that is, cell subtypes). d, distance. c, Visual representation of ‘ground distance’ (dissimilarity) between cell subtypes. The ground distance between subtypes C-2 and C-6 can be conceptualized as the length of the dotted path drawn in gray.

1. Compute a distance between each pair of datasets (that is, experimental conditions) as follows:

   1. Embed points within each dataset using PHATE⁸
   2. Cluster datapoints using spectral clustering
   3. Represent each dataset as a vector of relative cluster proportions
   4. Compute the distance between two datasets using earth mover’s distance (EMD)¹¹ (Supplementary Note 2)

2. Take the distance matrix derived from the previous step and compute a diffusion map embedding of the data¹²

When specifically applied to single-cell data, PhEMD leverages PHATE and spectral clustering to define cell subtypes, EMD to compute pairwise distances between biospecimens (based on their cell-subtype relative abundances) and the diffusion map approach to generate a final low-dimensional embedding of biospecimens. Pseudocode and additional details on the PhEMD algorithm can be found in Methods.

PhEMD recovers the correct cell-state and biological-specimen embeddings for single-cell data with known ground-truth structure

PhEMD was applied to simulated single-cell data with known ground-truth structure to determine whether PhEMD could accurately model both the cellular heterogeneity within each specimen and the specimen-to-specimen heterogeneity based on cell-subtype relative abundances. The simulated cells lay on a continuous branched trajectory, wherein progression along a branch represented concurrent changes in gene expression in select differentially expressed genes¹³. The distribution of cell density across branches was varied between specimens to simulate a heterogeneous multi-specimen dataset. PhEMD correctly recovered the branched cell-state manifold structure using PHATE (Supplementary Fig. 1a,b). The specimen-to-specimen EMD-based comparison and resulting embedding were also found to be accurate (Supplementary Note 3 and Supplementary Fig. 1c,d). A critical component of deriving the correct single-cell specimen embedding was computing accurate specimen-to-specimen distances. Two existing methods for doing so were cellAlign¹⁴ and sc-UniFrac¹⁵, although they imposed limiting assumptions or faced scalability issues that were addressed in our implementation of EMD (Supplementary Note 4 and Supplementary Fig. 2).

Effect of drug perturbations on the EMT landscape in breast cancer

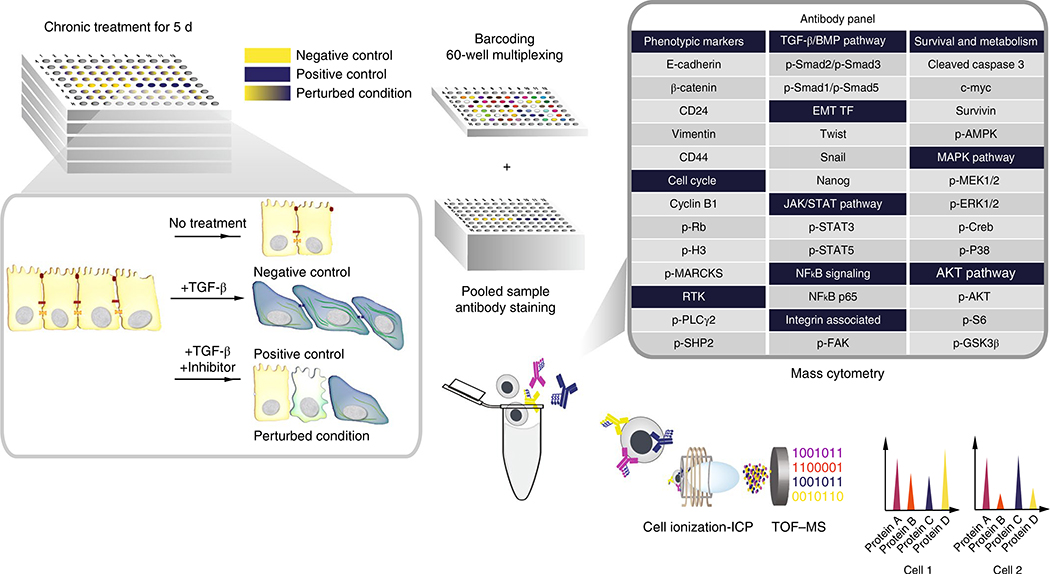
To study key regulators of EMT in breast cancer, we performed a drug screen consisting of 300 inhibition and control conditions, collectively inhibiting over 100 unique protein targets in murine breast cancer cells undergoing TGF-β-induced EMT (Fig. 2 and Supplementary Table 1). These specimens collectively contained over 1.7 × 10⁶ cells measured in a total of five mass cytometry runs. Time-of-flight mass cytometry (CyTOF) was used on day 5 of cell culture to measure the concurrent expression of 31 protein markers in each cell (Supplementary Table 2), and PhEMD was used to model both the cell-state transition process and the perturbation-effect manifold. Batch correction was performed using canonical correlation analysis (CCA)¹⁶ before modeling the cell-state and single-cell specimen embeddings to analyze all experimental conditions across all plates simultaneously.

Fig. 2 |. Experimental design for measuring perturbation effects of small-molecule inhibitors on EMT.

Perturbation and control conditions for TGF-β-induced EMT. Time of flight–mass spectrometry (TOF-MS) was used to characterize the cellular composition of each EMT experimental condition. ICP, inductively coupled plasma.

Cell-subtype definition via manifold clustering

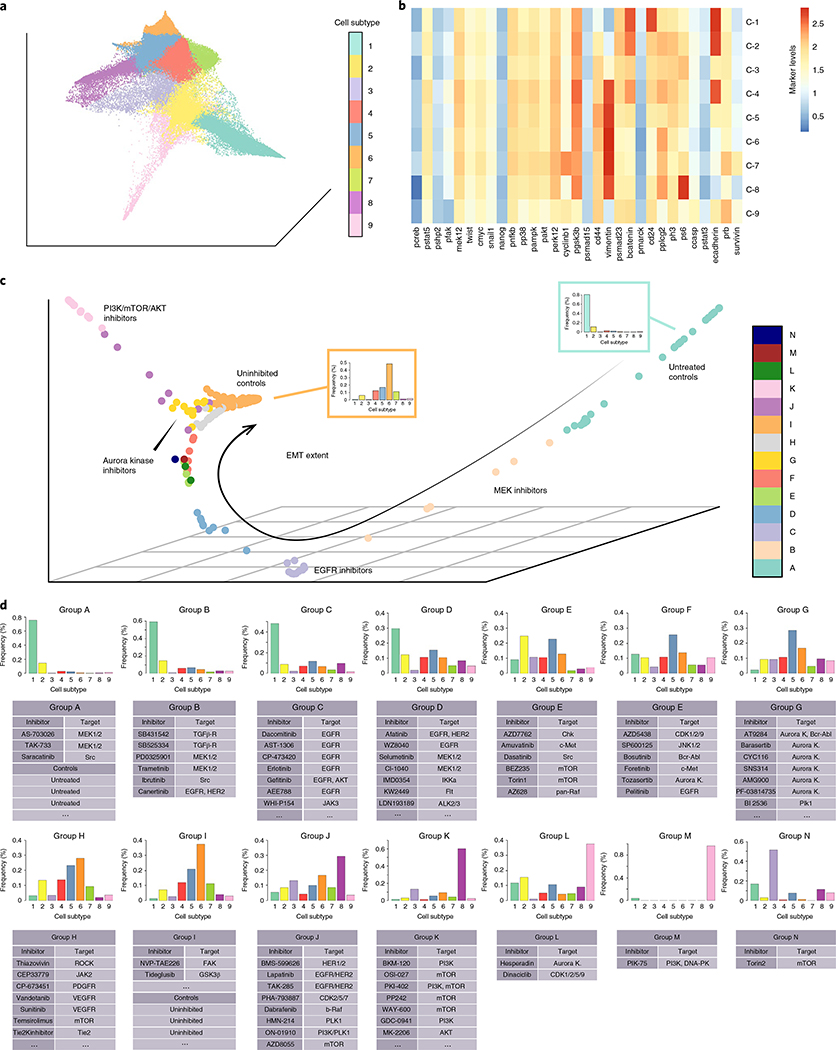
By design, all cells undergoing EMT were derived from the same homogeneous epithelial cell population. Thus, a continuous manifold with potentially branched structure (as modeled by PHATE) was ideal to model the cell-state space. CCA successfully corrected for batch effect in the full dataset (Supplementary Fig. 3 and Supplementary Note 5), and PHATE identified nine cell subtypes across all unperturbed and perturbed EMT conditions (Fig. 3a,b). These included the starting epithelial subtype (C-1), main mesenchymal subtype (C-6) and transitional subtypes on the major EMT axis (C-2 to C-5), with gene expression patterns consistent with known epithelial, mesenchymal and ‘hybrid’ EMT cell phenotypes (Supplementary Note 6)^17–26.

Fig. 3 |. Axes of variation among EMT perturbation conditions.

a, PHATE embedding of cells from all 300 experimental conditions, colored by cell subtype. b, Heatmap representing log₂ protein expression levels for each cell subpopulation representing its respective cell subtype. c, Diffusion map embedding of control and drug-inhibited conditions, colored by clusters determined by hierarchical clustering. d, Individual inhibitors assigned to each inhibitor group. Histograms represent bin-wise mean of relative frequency of each cell subtype for all inhibitors in a given group. The full list of inhibitors in each group can be found in Supplementary Table 3.

In addition to modeling the main EMT trajectory that one would expect to recover in our experiment, the PHATE cell-state embedding identified additional cell subtypes mapped to regions off of the main EMT axis. C-7 and C-8 were mesenchymal cell subtypes mapped close to C-5, the predominant mesenchymal subtype (Fig. 3a,b). C-9 formed a branch off of the main EMT trajectory and demonstrated high E-cadherin and cleaved caspase-3 expression, consistent with an epithelial subpopulation undergoing apoptosis. By using PHATE, which applied no previous assumptions on the intrinsic geometry of the cell-state embedding, we were able to uncover a more complex, continuous model of EMT than has been previously reported.

Constructing and clustering the EMD-based drug-inhibitor manifold

After modeling the EMT cell-state space with PHATE, PhEMD mapped the experimental variable (that is, multicellular biospecimen) state space as a low-dimensional embedding (Fig. 3c). Hierarchical clustering revealed clusters of inhibitors with similar net effects on EMT. Moreover, ‘uninhibited’ controls (TGF-β applied in absence of any inhibitor) and ‘untreated’ controls (neither TGF-β nor inhibitor applied) were included to distinguish inhibitors with notable effects on EMT.

The final embedding of drug inhibitors highlighted the variable extent of EMT that had occurred in the different inhibition conditions (Fig. 3c,d). This diffusion map embedding was low-dimensional with an intrinsic dimensionality of 2.4 (Supplementary Fig. 4), implying relatively few axes of variation that could be appropriately visualized in three dimensions. Fourteen inhibitor clusters (Clusters A–N) were identified (Supplementary Table 3). Cluster A included the untreated controls and the TGF-β-receptor inhibitor condition, each of which consisted almost entirely of epithelial cells (C-1). These were experimental conditions in which EMT was effectively not induced. On the other hand, Cluster I included all uninhibited control conditions and inhibitors ineffective at modulating EMT; inhibitors in this cluster were found to have mostly mesenchymal (C-6) cells. Clusters B to H included inhibitors that had generally decreasing strength with respect to halting EMT (Fig. 3c,d). The inhibitors in Clusters J and K formed a prominent trajectory off the main EMT-extent trajectory in the inhibitor embedding (Fig. 3c). Clusters J and K were enriched in cell subtype C-8, with Cluster K inhibitors inducing cell populations that almost entirely consisted of C-8 cells.

All of the Cluster K inhibitors targeted PI3K, Akt, or mTOR protein kinases: three members of a well-characterized pathway. Compared to the predominant mesenchymal subtype observed in the uninhibited controls (C-6), C-8 comprised cells with similarly high expression of vimentin and CD44 and markedly higher expression of phospho-S6 (Fig. 3). This expression profile was consistent with an alternative-mesenchymal EMT subtype. Examining the cell yield of these inhibitors compared to the respective uninhibited control conditions in their respective batches, we found that the cell yield of the Cluster K inhibitors was on average 60% lower than the TGF-β-only controls (Supplementary Table 4). Based on these findings and a previous report that high expression of phospho-S6 was associated with resistance to PI3K inhibitors²⁷, the C-8 subtype is likely a mesenchymal cell population relatively resistant to inhibition of the PI3K-Akt-mTOR axis.

In general, small-molecule inhibitors that had the same molecular target tended to cluster together, consistent with the intuitive notion that drugs with similar mechanisms of action likely have similar net effects on a given cell population (for example, Cluster C and Cluster G). However, several inhibitors with the same reported primary target generated different resulting single-cell profiles and were clustered into different inhibitor clusters. This phenomenon may be due to differences in inhibitor potency and differences in off-target effects.

An analysis of 60 inhibition and control conditions measured in the same mass cytometry run (and hence not requiring batch normalization) was performed to assess whether applying PhEMD to batch-normalized and single-batch expression data would yield consistent results (Supplementary Note 7, Supplementary Fig. 5 and Supplementary Tables 3 and 5). Three replicates involving independent cell culture experiments measured in distinct mass cytometry runs were analyzed to demonstrate reproducibility of results (Supplementary Fig. 6 and Supplementary Table 5). Consistent results were observed across all single-batch and multibatch analyses, demonstrating PhEMD’s reproducibility and robustness to batch-normalized data (Fig. 3 and Supplementary Figs. 5 and 6).

Imputing the effects of inhibitors based on a small measured dictionary

In the final PhEMD embedding of the abovementioned drug-screen experiment, single-cell biospecimens were distributed along a branched, continuous manifold with varying density. For example, the embedding space containing Cluster I inhibitors was characterized by high point density, while the embedding space containing Cluster B points was more sparsely populated (Fig. 3c). The high-density regions suggested that perhaps not every inhibition condition needed to have been measured to capture the geometry of the drug-inhibition state space. Applying a previously published sampling technique to the PhEMD drug-screen embedding²⁸, we found that 34 landmark points could fully capture the EMT perturbation state space (Supplementary Fig. 7); the phenotypes of the remaining experimental conditions could be inferred in relation to these 34 (Supplementary Note 8). This finding highlighted a potential opportunity for reducing the cost of future single-cell drug-screen experiments, as it suggested that only a small fraction (11%) of all inhibitors may need to be experimentally measured using expensive single-cell profiling techniques to learn the full range of perturbation effects.

Validating the PhEMD embedding using external information on similarities between small-molecule inhibitors

We sought to validate our PhEMD drug-screen embedding by comparing the drug–drug similarities learned from our experiment (in the context of effects on EMT) to drug–drug similarities based on known drug-target binding specificities from a previous experiment²⁹. Since the previous experiment and ours measured an overlapping set of inhibitors, they could be conceptualized as two complementary ‘views’ of the same shared inhibitors. We hypothesized that for the inhibitors shared between the two experiments, one view of the data might inform the other. Intuitively, this would support the notion that drugs with more similar protein targets action may tend to have more similar effects on EMT (and vice versa). Our approach to assessing this hypothesis was twofold: (1) we used a measure of inhibitor–inhibitor similarity, derived from the drug-target specificity data, to extend our PhEMD embedding and predict the effects of unmeasured inhibitors on our model EMT system, and (2) we used our PhEMD embedding to predict the drug-target specificity of inhibitors shared between the two drug-screen experiments.

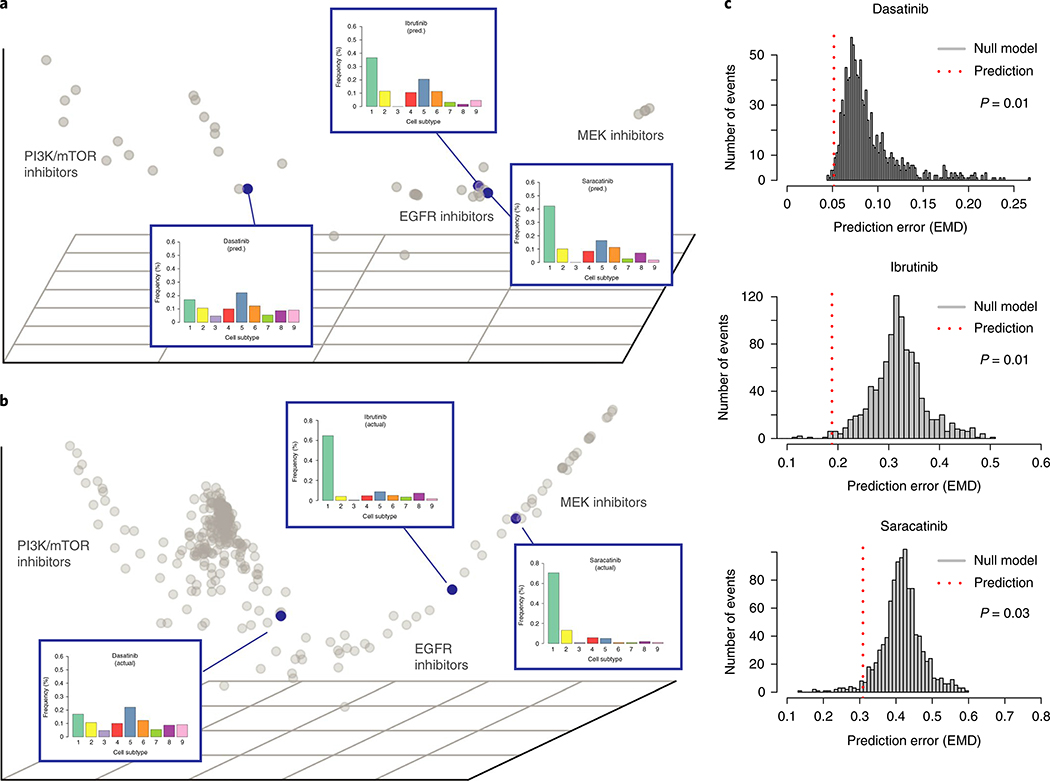
Leveraging Nystrom extension^30–32, a method of extending a diffusion map embedding to include new points based on partial affinity to existing points, we accurately predicted the effects of three unmeasured inhibitors on EMT using drug-target specificity data (P < 0.05, Fig. 4a–c and Supplementary Note 9). We also performed leave-out-out cross validation on all 39 inhibitors in our CyTOF experiment with known drug-target specificity data and found that single-cell profile predictions leveraging our imputed PhEMD embedding were significantly more accurate than a null model (P = 0.005). Altogether, these findings suggested that PhEMD offered information that could be integrated with additional data sources and data types to support not only comparison of biospecimens directly measured but also prediction of single-cell phenotypes for additional, unmeasured specimens.

Fig. 4 |. Nyström extension predicts single-cell profiles of unmeasured EMT perturbation conditions.

a, Nystrom extension embedding showing predicted effect of three selected inhibitors (dasatinib, ibrutinib, saracatinib) on EMT relatively to other measured inhibitors. b, PhEMD diffusion map embedding showing measured effects of three selected inhibitors on EMT. c, Histogram showing distribution of prediction error for null model (n = 1,000 independent permutations). Dotted red line represents prediction error for actual prediction (that is, alternative model). P values were computed using a one-sided permutation test.

We then sought to assess whether the reverse was true—whether the learned relationships between inhibitors from our EMT perturbation experiment could be used to predict drug-target binding specificities. For this prediction task, we used the 39 inhibitors present in both the drug-target profiling experiment and ours, and those that had at least one protein target identified by their experiment. Our predictive model that incorporated PhEMD results into the prediction was significantly more accurate than the null model (P = 6.57 × 10⁻⁵; Supplementary Fig. 8). This suggested that while the two experiments measured two distinct sets of inhibitor features, the inhibitor–inhibitor relationships learned from both experiments were consistent.

PhEMD highlights manifold structure of tumor specimens in CyTOF and single-cell RNA-sequencing experiments

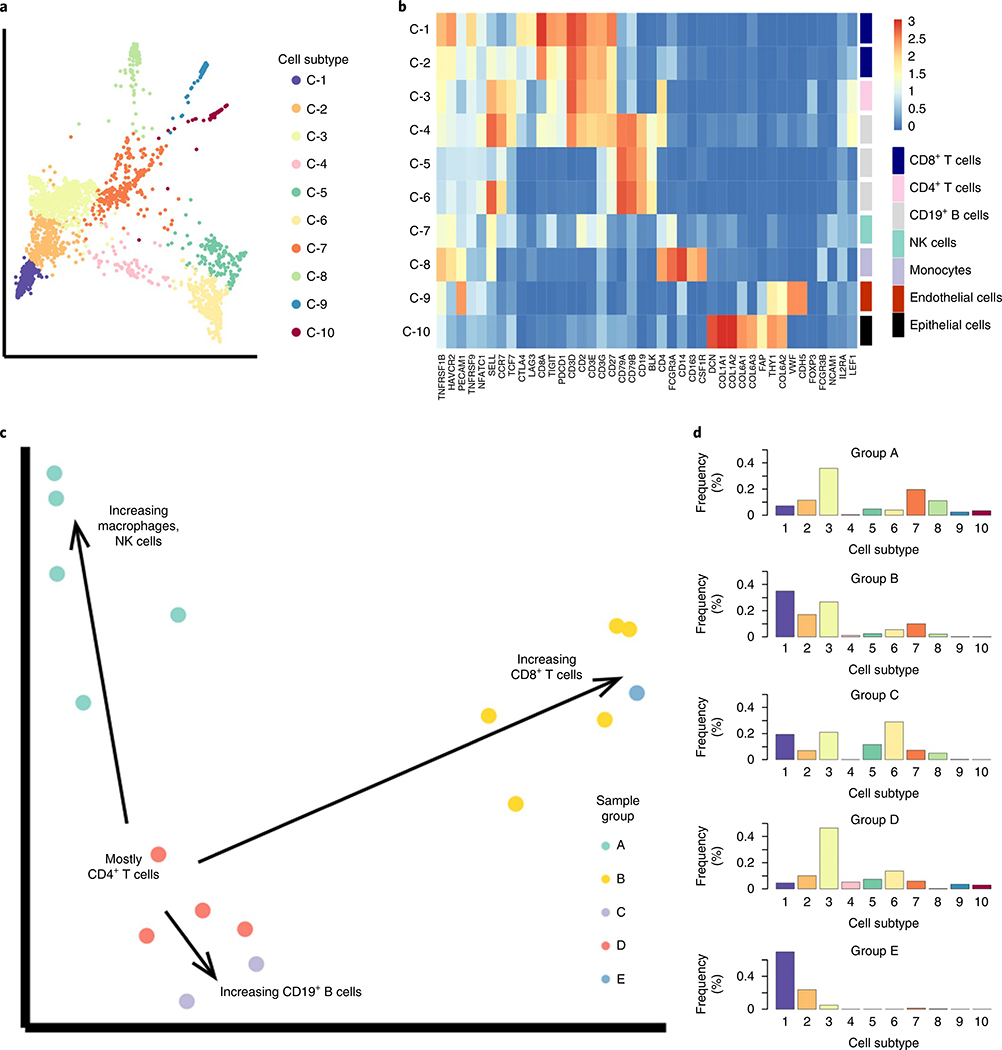
To demonstrate an additional application of the PhEMD analytical approach, we used PhEMD to characterize the specimen-to-specimen heterogeneity in immune cell profiles of multiple tumor specimens. We first applied PhEMD to a single-cell RNA-sequencing dataset consisting of the ‘healthy’ (nonmalignant) cells of 17 melanoma biopsies². The cell-state embedding identified a total of ten cell subtypes with gene expression profiles consistent with previously reported subpopulations of B cells, T cells, endothelial cells, epithelial cells, natural killer (NK) cells and monocytes (Fig. 5a,b)². When comparing patient specimens, PhEMD identified the specimen ‘Mel75’ as having a unique immune cell profile characterized by the greatest proportion of exhausted CD8⁺ cells. These cell-state and tumor-comparison findings corroborated previously published results on the immune cell subtypes and interspecimen heterogeneity present in this cohort². In addition to confirming previous findings, this analysis yielded an embedding that revealed the manifold structure of the single-cell specimen state space. With respect to a reference group of biospecimens (Group D) that consisted mostly of CD4⁺ T cells and were mapped to one part of the manifold, three axes of variation emerged that corresponded to increasing relative proportions of B cells (C-5, C-6), macrophages (C-7) and exhausted CD8⁺ T cells (C-1) (Fig. 5c,d and Supplementary Table 6). While it was well-understood that a set of individual cells, such as those undergoing differentiation, may demonstrate manifold structure^33,34, our PhEMD embedding suggested that a set of patients with a shared phenotype (for example, melanoma) may also lie on a continuous manifold³⁵.

Fig. 5 |. PheMD applied to single-cell RNa-seq data of 17 melanoma samples (nontumor cells only) highlights heterogeneous immune profiles among different patients.

a, PHATE cell-state embedding colored by cell subtype. b, Heatmap showing mean rNA expression values of each cluster, colored by a log₂ scale. c, Diffusion map embedding of samples (colored by group assignment) revealing multiple trajectories that represent increasing relative frequency of selected cell populations. d, Summary histograms, each representing the bin-wise mean relative frequency of cell subtypes for all samples assigned to a given group. The sample IDs (as assigned in the original dataset published by Chevrier et al.³) of all samples in each inhibitor group can be found in Supplementary Table 6.

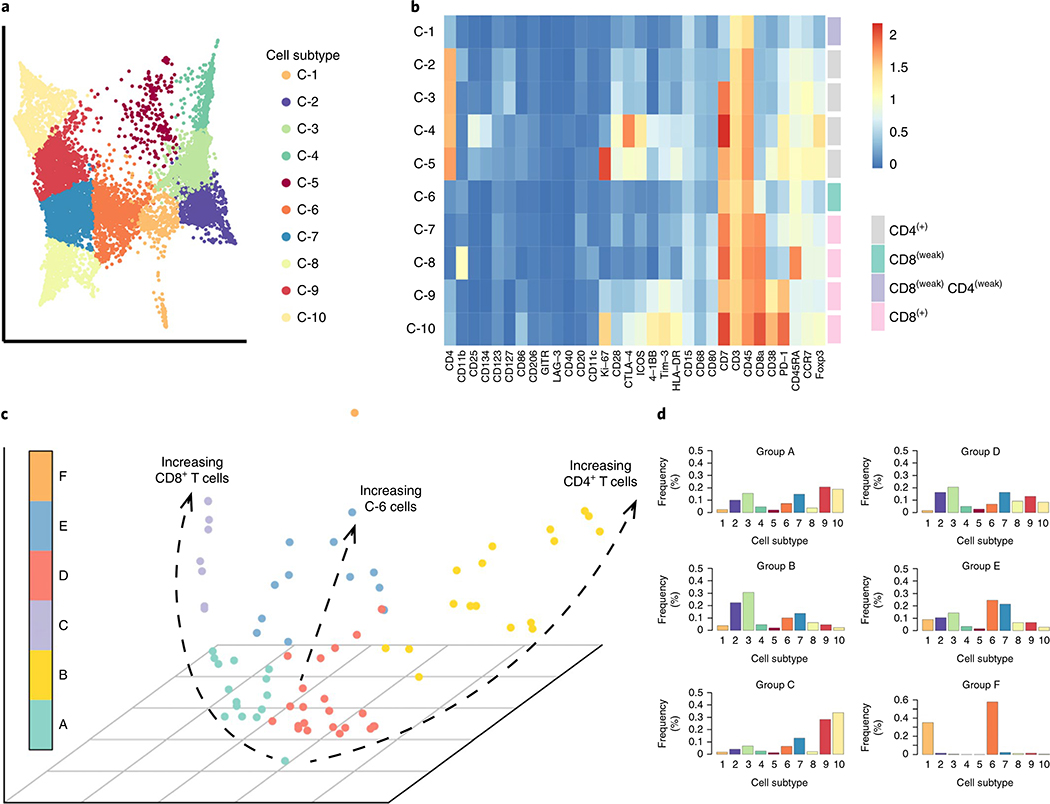
To further explore this concept, we applied PhEMD to a mass cytometry dataset containing the T cell infiltrates of 75 clear cell renal cell carcinoma (ccRCC) specimens³. At the cellular level, our analysis recapitulated previous findings of important T-cell subpopulations present, including prominent CD8⁺ PD1⁺ CD38⁺ Tim-3⁺ exhausted T-cell (C-9, C-10) and CD4⁺ regulatory T-cell (C-4) populations (Fig. 6a,b). We then modeled the diversity in immune cell signatures as a tumor-specimen embedding that could be used to characterize specimen-to-specimen variation (Fig. 6c). A group of tumor specimens (Cluster B) mapping to one end of the PhEMD embedding was characterized by a marked predominance of CD4⁺ T cells (C-2, C-3), and progression toward the other end of the tumor-space manifold represented a relative decrease in CD4⁺ T cells and marked relative increase in CD8⁺ PD1⁺ exhausted T cells (C-9, C-10) (Fig. 6c and Supplementary Table 7). This finding was supported by the initial report of substantial interpatient variability in T-cell profiles especially related to CD8⁺ cells³. The detection of a subset of patients with exhausted T cell enrichment may be of particular clinical interest, as immunotherapy agents that combat T-cell exhaustion have become a mainstay of advanced-stage ccRCC treatment, but patients continue to have highly variable treatment responses^36,37. Future single-cell tumor-profiling experiments assessing treatment response may be able to use PhEMD as a tool to identify subgroups of patients that might especially benefit from PD-1 or PD-L1 inhibitor immunotherapy.

Fig. 6 |. PheMD applied to mass cytometry data of 75 ccRCC samples gated for t cells.

a, PHATE embedding of T cell manifold colored by cell subtype. b, Heatmap showing mean protein expression values of each cell-subtype cluster, colored by a log₂ scale. c, Diffusion map embedding of all tumors colored by tumor subgroup, defined by hierarchical clustering. The main axes of intersample variability are highlighted as dotted-black trajectories. d, Summary histograms, each representing the bin-wise mean relative frequency of cell subtypes for all samples assigned to a given group. The sample IDs (as assigned in the original publication of these data²) of all samples in each inhibitor group can be found in Supplementary Table 7.

Discussion

Here, we have demonstrated the successful mapping of single-cell experimental conditions using our proposed PhEMD embedding technique. We extensively studied the Py2T murine breast cancer cell line treated with TGF-β and perturbed with over 200 kinase inhibitors, measured using mass cytometry. In this experiment, PhEMD revealed the structure of the kinase inhibitor space based on each drug’s effect on the Py2T cell populations undergoing EMT. The final embedding of inhibitors was found to have low-dimensional structure, with drugs mapping to one of three main axes. We have shown that the embedding produced by PhEMD is useful in several ways:

1. Visualizing the experimental variable (that is, single-cell specimen) state space

2. Identifying clusters of similar experimental variable settings (for example, similar drugs with respect to their measured effects on a given cell population)

3. Characterizing axes of variability among specimens in terms of biologically interpretable differences in the types and abundances of cell subpopulations present

4. Extending the experimental variable state space through inference of unmeasured experimental settings based on similarity to existing (measured) settings

PhEMD can enable a new pattern of searching for effective therapeutic agents by identifying a small subset drugs that collectively capture the network geometry of a larger drug set. We demonstrated this application by computing a dictionary of 34 experimental conditions and showing that these experimental conditions were sufficient to capture the network geometry of the 300-specimen state space. This finding has the potential to reduce experimental burden in future drug discovery efforts. For example, one can first apply PhEMD to measurements obtained using one profiling technique (for example, mass cytometry) to identify a small set of dictionary specimens from a large set of candidates and then investigate this smaller set further using complementary technologies that may be more limited in scale (for example, single-cell RNA-sequencing).

The PhEMD embedding can be integrated with additional data sources and data types for even larger and richer analyses. By using drug-target specificity data from a complementary inhibitor profiling experiment along with data imputation approaches, we were able to accurately predict the effects of inhibitors not directly measured in our experiment on TGF-β-induced breast cancer EMT. This approach is useful for analyzing drug-screen experiments, as it enables an initial mapping of a modest set of drugs (‘dictionary points’) measured with single-cell resolution to be extended to include additional drugs. This application is not limited to perturbation screen data and can be useful for imputing the phenotypes of specimens (of any type) that are not directly measured using single-cell profiling. For example, examining a cohort of patients in which only some patients were biopsied and genomically profiled, one could potentially incorporate a nongenomic-based measure of patient-to-patient similarity (for example, based on clinicopathologic features) to predict the single-cell-based phenotypes of all patients in the cohort.

We explored the applicability of PhEMD to other experimental designs besides drug screens by applying it to single-cell data from two clinical tumor-biopsy cohorts. These analyses revealed that PhEMD can uncover manifold structure in the tumor-specimen space that is biologically meaningful based on the observed proportions of the specimens’ cell subpopulations. When applied to the melanoma and ccRCC datasets, PhEMD revealed ‘trajectories’ of patients, with the most notable axis in both datasets consisting of patients with an increasing proportion of exhausted CD8⁺ T cells. It is possible that the abundance of tumor-infiltrating, exhausted T cells may predict response to immunotherapy, although additional studies are needed to assess this. The PhEMD method may be useful for developing personalized cancer treatment regimens involving immunotherapy.

This study is not without limitations. Our approach specifically compares cell-subtype relative abundances among biospecimens, which entails normalizing each biospecimen by its total cell count. In this setting, since relative abundances by definition sum to one for each biospecimen, the EMD is a true metric and is robust across all pairwise comparisons of biospecimens. Comparing cell-subtype relative abundances rather than absolute abundances is also often preferable from a biological perspective, as biospecimens (for example, biopsy samples) may demonstrate variation in cell yield that is a technical artifact of little biological interest. Nevertheless, there exist experimental scenarios in which cell yield is of biological importance. In future work, we aim to incorporate cell yield into specimen-to-specimen comparisons and into the final biospecimen embedding. Another area of active investigation is exploring alternative methods of embedding the cell-subtype and biospecimen-state space. In the presented experiments, PHATE was used to model the cell-subtype space and diffusion maps were used to generate the biospecimen-state space. Future work may assess the use of other methods that are potentially applicable for these tasks.

In the present study, PhEMD was used to characterize mass cytometry and single-cell RNA-sequencing data, although PhEMD may be applied to data generated by other single-cell profiling platforms as well. Many experimental designs may benefit from PhEMD—for example, comparisons of specimens pre- and post-treatment (or receiving different treatments), time-series analyses of cells undergoing transition processes and organization of heterogeneous-yet-related specimens for the purpose of disease subtyping. Additionally, applying PhEMD to large-scale functional genomics (for example, single-cell CRISPR) screens may yield embeddings that reveal complex relationships between genes. We have demonstrated in our analysis of over 1.7 × 10⁶ cells across 300 specimens and five mass cytometry runs that PhEMD is highly scalable and robust to batch effect. PhEMD offers the efficiency, flexibility and model interpretability necessary to analyze single-cell experiments of increasingly large scale and complexity.

Methods

The PhEMD analytical approach

In single-cell data, each cell is characterized by a set of features, such as protein or transcript expression levels of genes. The purpose of measuring these expression-based features for each cell (for example, via single-cell RNA-seq or mass cytometry) is to answer biological questions especially related to the cell subpopulations present in a biospecimen. In particular, the features may be used for defining phenotypes of cells^1,38, resolving cellular dynamics using transition-process modeling^39–41 and studying signaling networks^42,43. In sum, the features are shared, quantitative characteristics of cells that may be used to organize a set of cells into a data geometry. An analogy can be made when attempting to compare single-cell specimens rather than individual cells. A biospecimen is a collection of cells. To compare single-cell biospecimens for the purpose of organizing a set of cell collections (for example, different patient specimens or perturbation conditions), one must first determine useful features for a cell collection. Previous studies have shown that cell subtypes are highly useful features that are shared across all specimens and can be quantitatively measured. Moreover, they can be used to represent single-cell specimens efficiently for downstream analyses (Supplementary Note 2). Just as transcript counts can be measured for selected genes in a single cell, so can cell counts be measured for selected cell subtypes in a cell collection.

We use PHATE for the task of defining cell subtypes⁸. PHATE is a diffusion-based single-cell dimensionality reduction technique that both identifies unique cell subpopulations and relates them to one another on a low-dimensional manifold. Of note, PHATE preserves an information theoretic distance between points (that is, cells) in the diffusion space to derive a stable low-dimensional embedding that reveals local, global, continual and discrete nonlinear structures in single-cell data. By applying PHATE to an aggregate of cells in a single-cell experiment, we can represent a biospecimen as the relative frequency of cells in each cell subtype. This representation of single-cell specimens is consistent with the ‘signatures-and-weights’ representation of multidimensional distributions, first formalized by Rubner et al.¹¹, that was found to yield optimal data representation efficiency in other computer vision applications. In our case, a ‘signature’ can be thought of as a distinct cell subtype (for example, memory B cells or CD8⁺ effector T cells), and the corresponding ‘weight’ represents the proportion of cells in a given specimen assigned to the cell subtype. However, comparing single-cell specimens represented as such is still a nontrivial task. Many studies represent single-cell specimens as their cell subtype composition and use known class labels (for example, normal lung versus lung adenocarcinoma) to group specimens and perform class-based comparisons (for example, identifying cell subtypes enriched in a disease state)^4,5. However, this approach is limited to comparing a few predefined classes of specimens and does not reveal insights into intra-class heterogeneity. Other studies organize a set of many single-cell specimens based on their relative frequency of one or a few important cell subtypes^6,38,44. However, this approach requires a priori knowledge of the most important cell subtypes and does not provide a complete view of specimen-to-specimen dissimilarity, especially in the context of high intra-specimen cellular heterogeneity.

We posit that the ideal metric for comparing specimens should take into account both the difference in weights of matching bins (for example, number of CD8⁺ T cells) for all bins and the dissimilarity of the bins themselves (for example, intrinsic dissimilarity between CD8⁺ and CD4⁺ T cells). EMD is a nonparametric metric that can capture both of these concepts to yield a final singular measure of distance, or dissimilarity, between two specimens¹¹. EMD can be conceptualized as the minimal amount of ‘effort’ needed to move mass (for example, cells) between bins of one histogram so that its shape matches that of the other histogram (that is, all matching bins of two histograms have the same counts). Mathematically, EMD is defined by the following optimization problem:

$$\mathrm{EMD}(P,Q)=\frac{{\sum }_{i=1}^m{\sum }_{j=1}^n{f}_{ij}{d}_{ij}}{{\sum }_{i=1}^m{\sum }_{j=1}^n{f}_{ij}}$$ (1)

such that ${\sum }_{i=1}^m{\sum }_{j=1}^n{f}_{ij}{d}_{ij}$ is minimized subject to the following constraints:

1. f_ij ≥0 for all 1≤ I ≤ m,1≤ j ≤ n

2. ${\sum }_{j=1}^n{f}_{ij}=w_{p_i}\text{for}\text{all}1\le i\le m$

3. ${\sum }_{i=1}^m{f}_{ij}=w_{q_j}\text{for}\text{all}1\le j\le n$

Definition 1. EMD as an optimization problem. $P=(p_1,w_{p_1}),\dots ,(p_m,w_{p_m})$, where p_i represents histogram bin i in the initial starting signature P and $w_{p_i}$ represents the amount of ‘mass’ present in the bin. Similarly, $Q=(q_1,w_{q_1}),\dots ,(q_n,w_{q_n})$, where q_j represents histogram bin j in the final signature Q and $w_{q_i}$ represents the amount of ‘mass’ present in the bin. $f_{i_j}$ represents the ‘flow’ of mass from bin p_i to bin q_j. $d_{i_j}$ represents the ‘ground distance’ between bins p_i and q_j. Constraint 1 ensures that P and Q are the starting and final signatures, respectively. Constraints 2 and 3 ensure that no more mass is moved from any bin p_i than is present initially.

EMD has been used in various applications including image retrieval^11,45, visual tracking⁴⁶ and melodic similarity musical analysis⁴⁷—all tasks that require accurate comparison of multidimensional distributions (analogous to comparing single-cell specimens). Additionally, a previous study demonstrated proof-of-concept that EMD can be used effectively to differentiate flow cytometry specimens of phenotypically distinct individuals⁴⁸. By design, EMD is a distance measure between probability distributions that is particularly invariant to small shifts in data (that is, noise or technical variability) across specimens^11,48. EMD also gives a ‘complete’ measure of overall dissimilarity between two specimens, largely attributable to the fact that it takes into account both the difference in height of corresponding histogram bins between specimens (for example, number of CD8⁺ cells) and the concept that certain bins (for example, cell subtypes) have a smaller ‘ground distance’ (that is, are more similar) than others. Including ground distance between bins in the EMD computation allows us to incorporate the idea that it requires more ‘effort’ to move mass to a faraway bin than to a nearby bin (that is, it requires more effort to convert cells to a more dissimilar cell signature than to a more similar cell signature). In our application, we define the ground distance between two cell subtypes as the manifold distance between the cluster centroids of the two cell subpopulations representing the subtypes (Supplementary Note 2).

Leveraging these features of EMD, we developed PhEMD as an approach to simultaneously relating a large set of single-cell specimens (Fig. 1a). PhEMD first aggregates cells from all biospecimens and applies a single-cell embedding technique (for example, PHATE) to model the cell-state space. PHATE simultaneously identifies all cell subtypes and relates them in a low-dimensional manifold. After constructing the cell-state manifold, PhEMD represents each specimen to be compared as a frequency histogram capturing relative abundance of each cell subtype. In the event that subsampling is performed when constructing the cell-state manifold, cells are assigned to a subtype using a nearest-neighbor approach (Supplementary Note 10). PhEMD then uses EMD, incorporating manifold distance as ground distance between bins, to compare two relative abundance histograms and derive a single value representing the dissimilarity between two single-cell specimens. PhEMD computes EMD pairwise for each pair of specimens to generate a distance matrix representing specimen-to-specimen dissimilarity. Finally, using this distance matrix, PhEMD generates a low-dimensional embedding of single-cell specimens using diffusion maps to highlight specimen-to-specimen relationships in the context of overall network structure⁴⁹. Diffusion maps are useful in this case as they learn a nonlinear mapping of samples from high- to low-dimensional space, capture both local and global structure, and have intrinsic denoising properties. PhEMD identifies and visualizes clusters of similar samples based on the compositional similarity of their respective cell populations.

Pseudocode for the PhEMD algorithm is shown in Algorithm 1.

Algorithm 1.

Pseudocode for the PhEMD analytical approach

1: procedure PHEMD(multispecimen.data)

2: ▹Map first-level manifold (e.g., cell-state embedding)

3: data.all←aggregateData all specimens(multispecimen.data)

4: first.level.embedding←embedDatapoints(data.all)

5: first.level.clusts←clusterPoints(first.level.embedding)

6: cluster.ground.dists←computeGroundDists(first.level.embedding; first.level.clusts)

7:

8: ▹Map higher-level manifold (e.g., single-cell specimen embedding)

9: specimen.clus.prop←GetClusterProportions(data.all; first.level.embedding; first.level.clusts)

10: for each pair of specimens si; sj do

11: Dists[i; j]←EMD(cluster.ground.dists; specimen.clus.prop[i]; specimen.clus.prop[j])

12: specimen.embedding←DiffusionMap(Dists)

13: specimen.clusters←ClusterSpecimens(Dists)

Py2T cell culture and stimulation

Py2T cells were obtained from the laboratory of G. Christofori, University of Basel, Switzerland⁵⁰. Cells were tested for mycoplasma contamination on arrival and regularly during culturing and before being used for experiments. Cells were cultured at 37 °C in DMEM (Sigma Aldrich), supplemented with 10% FBS, 2 mM l-glutamine, 100 U ml⁻¹ penicillin and 100 μg ml⁻¹ streptomycin, at 5% CO₂. For cell passaging, cells were incubated with TrypLE Select 10X (Life Technologies) in PBS in a 1:5 ratio (v/v) for 10 min at 37 °C.

Human recombinant TGF-β₁ was purchased from Cell Signaling Technologies as lyophilized powder and was reconstituted in PBS containing 0.1% carrier protein, according to the manufacturer’s protocol to 400 ng ml⁻¹. The stock solution was kept at −20 °C until use. For daily treatment, TGF-β₁ stock was diluted into medium to 40 ng ml⁻¹ working concentration. Following small-molecule inhibitor treatment, 10 μl of TGF-β₁ was added to the cells for a final concentration of 4 ng ml⁻¹. As a control, PBS containing carrier protein diluted with growth medium was used.

Small-molecule inhibitors

A library of 234 small-molecule kinase inhibitors was purchased from Selleckchem (Supplementary Table 1). Small-molecule inhibitors were distributed within the 60 inner wells of five separate 96-well format deep well blocks with exception of wells within row E, which contained DMSO. Stock solutions of 2 mM small-molecule inhibitor in DMSO were kept at −80 °C until used. For daily treatment, the stock solution was equilibrated at room temperature for 1 h and then 5 μl of stock solution was added 995 μl of medium. Small-molecule inhibitor (or DMSO) was added to cells once per day, immediately after the cell growth media change and before application of TGF-β₁. Small-molecule inhibitor treatment was performed by adding 10 μl of pre-diluted reagent to the cells in 80 μl of cell growth medium; this resulted in a final concentration of 1 μM of small-molecule inhibitor and 0.1% DMSO.

Chronic kinase inhibition screen

For the chronic inhibition experiment, Py2T cells were seeded in 96-well plates (Techno Plastic Products AG) with a seeding density of 1,800 cells per well in 80 μl of growth cell media. Only the 60 inner wells were used for analysis. To acquire sufficient sample size, five 96-well plates were used for single condition. After seeding, cells were allowed to recover for 36 h to reach 50% confluence. Cells were treated simultaneously with TGF-β₁ or vehicle (PBS) and small-molecule inhibitor or vehicle (DMSO) for 5 d, and medium was changed daily. All pipetting procedures were performed at room temperature using a Biomek FX Laboratory Automation Workstation (Beckman Coulter) supplied with 96-well pipetting pod.

In addition to experimental conditions treated with small-molecule inhibitors, at least five ‘uninhibited’ control conditions and five ‘untreated’ control conditions were included on each 96-well plate. Uninhibited control conditions were those in which TGF-β was applied to induce EMT in absence of any inhibitor. Untreated control conditions were those in which neither TGF-β nor inhibitor was applied and no EMT was induced.

Cell collection

The cell collection protocol was performed using a Biomek FX Laboratory Automation Workstation. The cell growth medium was removed using the multiple aspiration pipetting technique, and cells were washed twice with 37 °C PBS. Dissociation reagent TrypLE Select 10X (Life Technologies) was diluted into PBS at a 1:5 ratio (v/v) was added to the cells and incubated for 10 min at 37 °C. Cells were detached from plates. Five identically treated 96-well plates were combined into a single deep well block and were fixed for 10 min with paraformaldehyde (PFA) at the final concentration of 1.6% v/v. PFA was blocked with the addition of 600 μl of 10% BSA in cell staining media (CSM). The cells were centrifuged for 5 min at 1,040g, at 4 °C. The supernatant was removed and the cells were resuspended in 300 μl of −20 °C MeOH. Samples were then transferred onto dry ice and to −80 °C storage.

Metal-labeled antibodies

Antibodies were obtained in carrier/protein free buffer and labeled with isotopically pure metals (Trace Sciences) using MaxPAR antibody conjugation kit (Fluidigm) according to the manufacturer’s standard protocol. After determining the percent yield by measurement of absorbance at 280 nm, the metal-labeled antibodies were diluted in Candor PBS Antibody Stabilization solution (Candor Bioscience GmbH) for long-term storage at 4 °C. Antibodies used in this study are listed in Supplementary Table 2.

Mass-tag cellular barcoding and antibody staining

Cell samples in methanol were washed three times with CSM (PBS with 0.5% BSA, 0.02% NaN₃) and once with PBS at 4 °C. The cells were then resuspended at 1 × 10⁶ cells ml⁻¹ in PBS containing barcoding reagents (¹⁰²Pd, ¹⁰⁴Pd, ¹⁰⁵Pd, ¹⁰⁶Pd, ¹⁰⁸Pd and ¹¹⁰Pd; Fluidigm) were conjugated to bromoacetamidobenzyl-EDTA (BABE, Dojindo) and two indium isotopes (¹¹³In and ¹¹⁵In, Fluidigm) were conjugated to 1,4,7,10-tetraazacyclododecane-1,4,7-tris-acetic acid 10-maleimide ethylacetamide (mDOTA, Mycrocyclics) following standard procedures^51,52. Cells and barcoding reagent were incubated for 30 min at room temperature. Barcoded cells were then washed three times with CSM, pooled and stained with the metal-conjugated antibody mix (Supplementary Table 2) at room temperature for 1 h. Unbound antibodies were removed by washing cells three times with CSM and once with PBS. For cellular DNA staining, an iridium-containing intercalator (Fluidigm) was diluted to 250 nM in PBS containing 1.6% PFA, added to the cells at 4 °C, and incubated overnight. Before measurement, the intercalator solution was removed and cells were washed with CSM, PBS and doubly distilled H₂O. After the last wash step, cells were resuspended in MilliQ H₂O to 1 × 10⁶ cells ml⁻¹ and filtered through a 40-μm strainer.

Mass cytometry data processing

EQ Four Element Calibration Beads (Fluidigm) were added to the cell suspension in a 1:10 ratio (v/v). Samples were measured on a CyTOF1 system (DVS Sciences). The manufacturer’s standard operation procedures were used for acquisition at a cell rate of ~300 cells s⁻¹ as described previously⁵³. After the acquisition, all .fcs files from the same barcoded sample were concatenated using the Cytobank concatenation tool.

Data were then normalized⁵⁴ and bead events were removed. Cell doublet removal and de-barcoding of cells into their corresponding wells was done using a doublet-free filtering scheme and single-cell deconvolution algorithm⁵¹. Subsequently, data were processed using Cytobank (http://www.cytobank.org/). Additional gating on the DNA channels (¹⁹¹Ir and ¹⁹³Ir) was used to remove remaining doublets, debris and contaminating particles. Final events of interest were exported as .csv files.

In-depth analysis of breast cancer EMT cell-state space and drug-inhibitor manifold from a single mass cytometry run

CyTOF measurements of cells undergoing unperturbed and perturbed EMT were generated and processed as described above. Data were then pooled from all experimental conditions, taking an equal random subsample from each condition to generate the cell-state embedding. Cell-state definitions and relationships were modeled with PHATE. Subsequently, all cells from all experimental conditions were assigned a cell subtype using a nearest-neighbor approach (Supplementary Note 10).

Next, the cell-subtype composition of each inhibition condition (that is, relative frequencies of each cell subtype that sum to one for each sample) was determined. Using this cell subtype frequency-based representation of inhibition conditions, EMD was computed pairwise between single-cell samples. Euclidean distances between cluster centroids in the PHATE space (which approximate diffusion-based potential distances derived from the expression data native dimensions⁸) were used as a measure of intrinsic dissimilarity between cell subtypes for the EMD ground-distance matrix. EMD in this case represented the minimum ‘effort’ required to transform one inhibition condition to another (conceptually equivalent to the total ‘effort’ needed to move cells from relatively ‘overweight’ parts of the branched, continuous, EMT cell-state manifold to relatively ‘underweight’ parts). The EMD between every pair of inhibition conditions was computed to construct a network of drug inhibition conditions, represented as an EMD-based distance matrix. The resulting distance matrix was embedded using the diffusion map approach (as implemented in the ‘destiny’ Bioconductor R package⁹) and partitioned using hierarchical clustering (applied to the untransformed distance matrix) to highlight inhibitors with notable effects on EMT or similar effects to one another.

Integrating batch-effect correction to compare 300 EMT inhibition and control conditions measured in five experimental runs

CyTOF measurements of cells undergoing unperturbed and perturbed EMT were generated and processed as described in the above sections. Markers shared across all batches (n = 31) were used for downstream analyses. Data were pooled from all experimental conditions on a per-batch basis. Expression values were then linearly scaled for each gene to ensure all values were positive and in the same range across batches. After this initial normalization, an equal random subsample of cells from each batch (20,000 × 5) was used as the input for canonical correlation analysis (CCA)¹⁶. CCA mapped expression data from each batch into an aligned, eight-dimensional space shared by all batches. The cell-state manifold and cell-subtype definitions were modeled by applying the PHATE dimensionality reduction and clustering method⁸ to the eight dimensions of the CCA-aligned space as input.

All cells from all experimental conditions were assigned a cell subtype using a nearest-neighbor approach (Supplementary Note 10). Next, the cell-subtype composition of each inhibition condition (that is, relative frequencies of each cell subtype that sum to one for each sample) was determined. Using this cell subtype-based representation of inhibition conditions, EMD was computed pairwise between single-cell samples. The ground distance (that is, intrinsic dissimilarity) between cell subtypes was defined as the Euclidean distance between their respective centroids in the three-dimensional PHATE space. The resulting sample-to-sample distance matrix was embedded using the ‘destiny’ Bioconductor R package⁹ and partitioned using hierarchical clustering (applied to the untransformed distance matrix) to identify 13 clusters of inhibitors with similar effects on EMT.

Intrinsic dimensionality analysis of the EMT perturbation state space

To assess the intrinsic dimensionality of the EMT perturbation state space, we applied the bias-corrected maximum likelihood estimator approach⁵⁵. We computed the sample-to-sample distance matrix for the 300 samples as described above and estimated intrinsic dimensionality of this embedding using the ‘ider’ R package⁵⁶. Intrinsic dimensionality was estimated over a range of values for (k-nearest neighbors (knn) parameter k from 1 to 100. The final value of intrinsic dimensionality was determined by examining the stable estimated value across a range of sufficiently large values for k (defined as >30).

Imputing the effects of inhibitions based on a small measured dictionary

To assess whether the network geometry of all 300 inhibition and control conditions could be captured using a smaller subset of conditions, we applied a previously published sampling technique for identifying landmark points of an embedding²⁸. The technique, called incompletely pivoted QR-based (ICPQR) dimensionality reduction, learns a concise embedding of a large collection of data points by identifying a subset of ‘landmark points’ that collectively capture the geometry of the full collection of samples. The fundamental concept is that these N landmark points comprise an N-dimensional subspace and that all other existing and new points can be mapped in relation to these. ICPQR identifies the concise ‘landmark point’ dictionary based on known pairwise distances between samples (for example, our EMD-based distance matrix of sample-to-sample distances). The ICPQR procedure was applied as follows: first, the PhEMD distance matrix containing pairwise distances between our 300 experimental conditions was converted to an affinity matrix using a Gaussian kernel (σ=2) and Markov-normalized to obtain probabilities. The (ICPQR) dimensionality reduction technique was then applied to this affinity matrix, using a μ distortion parameter of 0.01, to identify 34 landmark points. To assess whether the 34 landmark points adequately captured the geometry of the full collection of 300 samples, the landmark points identified were then used to impute the geometric coordinates of the remaining (nonlandmark) points using the out-of-sample extension technique associated with ICPQR²⁸. The result was a 34-dimensional embedding of all 300 samples. We computed a 300 × 300 distance matrix based on the pairwise Euclidean distances between samples in this 34-dimensional space and then embedded using the ‘destiny’ Bioconductor R package⁹.

Incorporating drug-target binding specificity data to extend the PhEMD embedding and predict the effects of unmeasured inhibitors on TGF-β-induced breast cancer EMT

We hypothesized that we could predict the influence of additional inhibitors on TGF-β-induced EMT based on knowledge of inhibitor–inhibitor similarity from another data source. To test this, we obtained drug-target specificity data from a previously published experiment²⁹ for a set of 39 inhibitors that overlapped between our experiment and theirs. We then selected saracatinib, ibrutinib and dasatinib as three nonspecific Src inhibitors whose drug-target specificity data were known and whose effects on EMT we wanted to predict. Next, we generated a PhEMD embedding based on our CyTOF experimental results (not including the three selected inhibitors). To predict the effects of the three inhibitors on EMT relatively to other inhibitors in our experiment, we performed Nystrom extension on the diffusion map embedding. All 39 inhibitors that were found to have an effect on EMT in our experiment and that had known drug-target specificity profiles were included in the Nystrom extension. Pairwise distances between each ‘extended’ point and each existing point in the original diffusion map were required for Nystrom extension. These distances were based on the similarity of drug-target specificity profiles between the two inhibitors, defined as (1 − cosine similarity)²⁰ × 4 for all pairs of inhibitors with known drug-target specificity profiles. The remaining pairwise distances were imputed based on known PhEMD-based inhibitor–inhibitor dissimilarity and known pairwise drug-target specificity-based dissimilarity using the MAGIC imputation algorithm⁵⁷.

We observed a global shift in embedding coordinates between the original diffusion map (based on PhEMD distances) and the Nystrom extension points (based on normalized cosine similarity using drug-target specificity data). This was likely due to a difference in scale between PhEMD-based distances and cosine similarity-based distances. Nonetheless, we were able to use the Nystrom extension points alone to predict the effect of the three selected inhibitors on EMT. First, we visualized the Nystrom extension embedding to show the predicted relation of the three inhibitors to other inhibitors with known (measured) effects on EMT. Next, we used partial least squares regression (‘pls’ R package) to predict the cell-subtype relative frequencies that would result from applying the inhibitors to breast cancer cells undergoing TGF-β-induced EMT. Nystrom extension embedding coordinates were used as the input variables for the regression model. To validate our findings, we measured the three selected inhibitors directly using CyTOF and included them along with the rest of the inhibitors in the PhEMD analysis pipeline. We compared the actual to the predicted cell-subtype relative frequencies and the actual to the predicted embedding coordinates relative to other similar, ‘nearby’ inhibitors. To assess prediction accuracy, we compared our prediction error to the prediction error of the null hypothesis modeled by first randomizing the PhEMD-based and drug-target specificity-based distance matrices and then generating a predictive model in the same way as in the alternative model. Prediction error was defined as the EMD between the predicted and actual (measured) cell-subtype relative frequency distributions. The null hypothesis was modeled as a distribution of EMDs generated by randomizing the PhEMD-based and drug-target specificity-based distance matrices 1,000 times and subsequently imputing cell-subtype frequencies. P values were computed by performing a permutation test comparing our prediction error to that of the empirical null distribution (n = 1,000) and applying a one-sided significance test at a significance level of 0.05.

To more comprehensively assess PhEMD as a predictive tool, we performed leave-one-out cross validation on the 39 inhibitors with known (measured) cell-subtype relative frequencies and drug-target specificity data. For each inhibitor, we constructed a PhEMD embedding based on known measurements of the 39 others and performed a Nystrom extension to impute the relationship between the inhibitor and the measured ones. We then constructed a partial least squares regression model using the same input variables as above to predict the cell-subtype relative frequencies of the inhibitor. Prediction error was defined the same as above (that is, EMD between predicted and actual cell-subtype relative frequency distributions). The null model was also defined in the same way as above by randomizing the PhEMD and distance matrices 100 times for the prediction of each inhibitor. To determine whether our alternative model was effective, we assessed whether the prediction errors in the alternative model (n = 39) were lower than the EMDs in the null model (n = 3,900) using a one-sided Mann–Whitney U-test.

Predicting drug-target binding specificities based on PhEMD results from EMT perturbation experiment

We hypothesized that if the PhEMD embedding were meaningful, it would have predictive power. To test this, we used the PhEMD embedding of inhibitors to predict the inhibitors’ drug-target binding specificities. The drug-target binding specificity data were obtained from a previously published study that used a chemical proteomic approach to identify the protein targets of many clinical kinase inhibitors²⁹. We chose to predict the profiles of 39 inhibitors that were present in both the drug-target binding specificity experiment and ours, and that had at least one protein target identified by the binding specificity experiment. Next, we computed a 39-by-39 knn kernel (k = 3) using the PhEMD inhibitor–inhibitor distances and then row-normalized the resulting matrix to one to turn it into a Markov operator. We then performed a leave-one-out cross validation, in which we set one of the inhibitor target values (that is, drug-target binding specificity profiles) in the Klaeger et al. data to be unknown. Note that a drug-target binding specificity profile was represented as a vector of length 270, which represented the binding specificity between the drug and each of 270 potential protein targets. We predicted the drug-target binding specificity values using the MAGIC imputation method⁵⁷ with the PhEMD Markov operator as input and a diffusion parameter t of 2. We computed leave-one-out predictions for each of the 39 inhibitors. To quantify the performance of our predictive model, we computed Pearson correlation between the original ground-truth (experimentally measured) target values and the predicted values. To determine the accuracy of our predictions, we compared our results to a null model, in which we randomized the PhEMD matrix 1,000 times and each time ran the prediction using this randomized matrix. Prediction accuracy (Pearson correlations) of our alternative model (n = 39 predictions, one per inhibitor) was compared to that of the null model (n = 39,000 predictions, 1,000 per inhibitor) using a one-sided Mann–Whitney U-test.

Generation and analysis of dataset with known ground-truth branching structure

To evaluate the accuracy of the PhEMD analytical approach, high-dimensional single-cell data (‘Synthetic Dataset A’) were generated using Splatter, a previously published tool designed to simulate single-cell expression data¹³. The basic tree structure represented in Supplementary Fig. 1a was generating using the following Splatter parameters: nGenes=100, de.prob=0.5, path. from=c(0,0,0,3,3,5,5,7,7,7). Each single-cell sample consisted of 2,000 cells sampled from this cell-state manifold at varying degrees of cellular density spread across the cell-state space. For Samples A-I, cellular density was concentrated in cell subtypes C-1 to C-9 (constituting the main axis), with 55% of Sample A consisting of C-1 and C-2 cells and 55% of Sample I consisting of C-8 and C-9 cells. Samples B-H consisted of progressively fewer cells in the starting cell states (that is, C-1 and C-2) and progressively more cells in the terminal cell states (that is, C-8 and C-9). Samples X, Y and Z were enriched for cells in C-10, C-13 and C-14, respectively. Samples J-M consisted predominantly of C-11 cells and Samples N-Q consisted predominantly of C-12 cells at increasing degrees of cell-type enrichment.

We applied PhEMD to the library-size normalized Splatter data as outlined in Fig. 1. First, the tree structure was modeled by PHATE based on cells aggregated from all biological samples. Then, the relative frequency of cells across different cell subtypes was computed for each sample. EMD was computed pairwise for all cells using PHATE distances as a measure of ground distance between cell subtypes. A final diffusion map embedding of biological samples was generated using the ‘destiny’ Bioconductor R package (Fig. 3).

Analysis of melanoma single-cell RNA-sequencing dataset

Data from a previous single-cell RNA-sequencing experiment were downloaded from the NCBI Gene Expression Omnibus website, accession number GSE72056 (ref. ²). These data contained read-count expression values that were log TPM-normalized values. Two of the 19 samples were excluded from analysis due to low cell yield of immune cells. Initial feature selection was performed by selecting 44 features found in the initial publication characterization of this dataset to distinguish between key cell types². The PHATE model of the cell-state space was constructed using default parameters to identify ten cell subtypes. The remaining PhEMD analysis pipeline was completed as described in In-depth analysis of breast cancer EMT cell-state space and drug-inhibitor manifold from a single mass cytometry run; a final embedding of biopsy samples was generated using the ‘destiny’ Bioconductor R package and partitioned using hierarchical clustering.

Analysis of clear cell renal cell carcinoma dataset

CyTOF data from a recent publication characterizing the immune landscape of clear cell renal cell carcinoma were downloaded from https://premium.cytobank.org/cytobank/projects/875 (ref. ³). Cell data were filtered and normalized using the method described in Methods section ‘Mass cytometry data processing’. The PHATE model of the cell-state space was constructed with a diffusion parameter ‘t’ of 40 to identify 10 cell subtypes. The remaining PhEMD analysis pipeline was completed as described in In-depth analysis of breast cancer EMT cell-state space and drug-inhibitor manifold from a single mass cytometry run.

Statistical methods

Statistical tests were performed as detailed in the above subsections. Differences in group medians were assessed using a Mann–Whitney U-test. Benchmarking of prediction accuracy (point estimate) against a null distribution was performed using a permutation (that is, randomization) test. All statistical comparisons were performed at a two-sided significance level of 0.05 unless otherwise stated.

Reporting Summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Data availability

The mass cytometry data that support the findings of this study are available at https://community.cytobank.org/cytobank/projects/1296. Source data for Figs. 3–6 are provided with the paper. Any additional data supporting the findings of this study are available from the corresponding author upon request.

Code availability

PhEMD takes as input a list of N matrices representing N single-cell specimens. An R implementation of PhEMD is publicly available as a Bioconductor R package (package name: ‘phemd’) and can alternatively be downloaded from https://github.com/wschen/phemd. Note that the cell-state space for all analyses presented in this manuscript was modeled using the PHATE method⁸. However, alternative approaches are viable and we have provided support for PHATE, Monocle2 (ref. ⁴¹) and Louvain community detection (as implemented in the Seurat software package)¹⁶ for this purpose in the R package.