Summary
In the root, meristem and elongation zone lengths remain stable, despite growth and division of cells. To gain insight into zone stability, we imaged individual Arabidopsis thaliana roots through a horizontal microscope and used image analysis to obtain velocity profiles. For a root, velocity profiles obtained every 5 min over 3 h coincided closely, implying that zonation is regulated tightly. However, the position of the elongation zone saltated, by on average 17 μm every 5 min. Saltation was apparently driven by material elements growing faster and then slower, while moving through the growth zone. When the shoot was excised, after about 90 min, growth zone dynamics resembled those of intact roots, except that the position of the elongation zone moved, on average, rootward, by several hundred microns in 24 h. We hypothesize that mechanisms determining elongation zone position receive input from the shoot.
Subject Areas: Biological Sciences, Plant Biology, Plant Development
Graphical Abstract
Highlights
-
•
For Arabidopsis thaliana roots, the distribution of elongation is stable over several hours
-
•
The position of the elongation zone saltates (moving ±17 μm on average over 5 min)
-
•
After shoot excision, saltation continues with a net movement toward the tip
-
•
The elongation zone may be sited by a feedback mechanism, with input from the shoot
Biological Sciences; Plant Biology; Plant Development
Introduction
The region at the tip of the plant root where growth occurs is divided into functional zones. The zones generally distinguished are cap, meristem, elongation zone, and maturation zone. At the extremity of the root, the cap protects the meristem, senses gravity, and deposits material—and even cells—that influence the structure of the soil and the behavior of surrounding organisms. The meristem contains cells that divide continuously, generating the cells that make up the root. The elongation zone contains cells that do not divide and instead elongate rapidly, about 10 times faster than meristem cells. Finally, shootward of the elongation zone comes the maturation zone, where cells neither elongate nor divide but take on their mature functions. Here, we use shootward to mean toward the shoot tip and rootward to mean toward the root tip (Baskin et al., 2010).
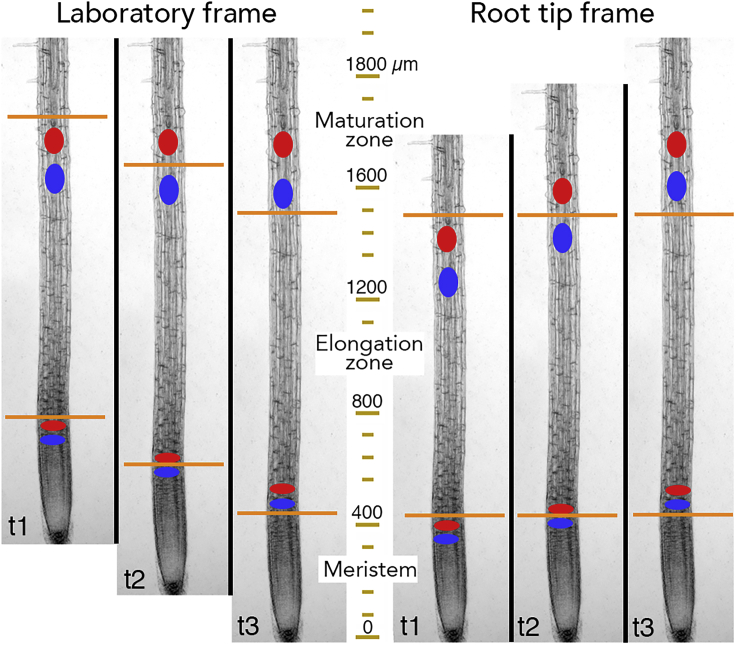
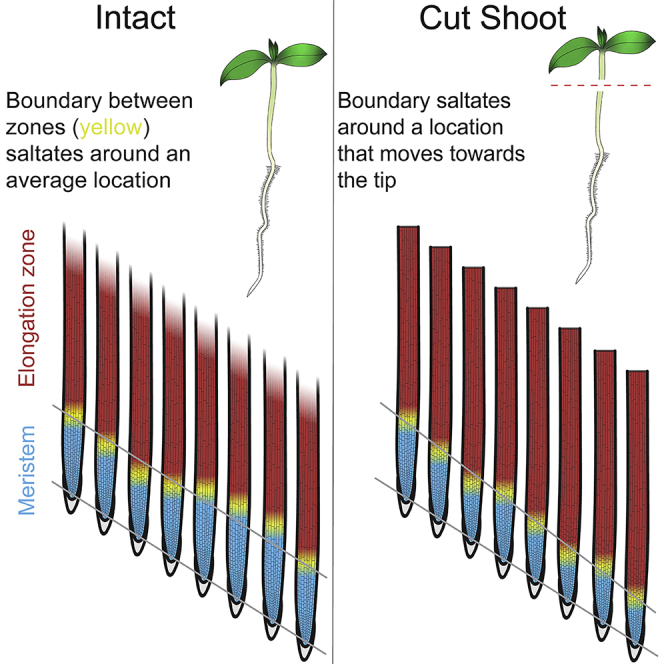
Although these functional zones are a basic attribute of roots, the zones are often perceived as static entities. Seeing the root's zonation as static arises perhaps because of the discrete functions of the zones or because an image shows the root at only a single time point, divided into zones like countries on a map. Nevertheless, because root cells are growing, the zones are dynamic. On its own, the growth of cells would enlarge meristem and elongation zone indefinitely. To the contrary, as the root grows, these zones often maintain a constant length and when they do change length, the change is finite. Thus the positions of the boundaries between the zones must be adjusted continually, usually moving in step with growth (Figure 1, left). As the boundaries keep pace with the root tip, a cell in the meristem, say, will soon find itself in the elongation zone, and soon after that, in the maturation zone.
Figure 1.
Root Growth Dynamics at Steady State
In the laboratory frame (left), where growth pushes the tip downward, the boundaries (orange lines) between zones move, keeping pace with the root tip. In this frame, the boundaries pass by cells (blue and red ovals) and by the spatial coordinates (mustard-colored scale). In the root-tip frame (right), where growth apparently pushes material upward, the boundaries remain at the same coordinates and are traversed by cells. The tip (in fact, the quiescent center) is assigned x = 0. Reference values (microns) on the scale are approximate.
A boundary sweeping across cells is unusual. Developmental boundaries usually block cell passage, and, in fact, interactions between cells on either side of the boundary are used to reinforce distinct cell identities. For example, the leaf blade is divided into abaxial and adaxial zones, a differentiation maintained in part by cells in each domain interacting antagonistically where they meet at the leaf margin. In the root, even while the boundaries move across fields of cells, the specialization of each zone remains intact. We have a limited understanding of how zones of stable identity are maintained despite the boundaries moving over cells.
In general, we might account for dynamic boundaries by invoking two kinds of mechanism. The first is cell-autonomous. This view endows a cell with a behavioral program (divide for some period, elongate for some period, then mature), and the relatively coherent behavior of myriad cells in the root emerges from programs being run in strict synchrony. The second is non-cell-autonomous, where extrinsic signals impinge on cells at the boundary and modify behavior. In distinguishing these views, we note that cell autonomy has been considered to underlie certain root growth behaviors (Band et al., 2012; Cole et al., 2014; Pavelescu et al., 2018) but in contrast to generate discontinuous growth patterns that are contrary to observations of root anatomy (De Vos et al., 2014). These mechanisms are not exclusive, and indeed both probably are operating to delimit boundaries effectively.
To gain insight into how roots maintain a stable zonation, we sought to characterize boundary movement during growth. To do so, we took advantage of the fact that the boundaries are evident in kinematic analysis. Kinematics revolve around velocity, namely the rate and direction of movement (Silk and Erickson, 1979; Gandar, 1983; Silk, 1984). Because a root grows predominantly axially, kinematics are simplified by reporting velocity in the direction parallel to the root's long axis only and by averaging points over the root's cross section. This generates a one-dimensional velocity profile, plotting speed as a function of distance from the tip. In general, the velocity profile falls gradually from a maximum at the very tip, and then falls steeply, before finally reaching zero. The gradual region corresponds to the meristem, the steep region to the elongation zone, and the region with zero velocity to the maturation zone. Thus, the velocity profile reveals the boundaries between these zones as defined by their growth.
To an observer, velocity is greatest at the root tip and falls to zero at the maturation zone, where there is no growth and hence no motion; we will refer to this observational viewpoint as the laboratory frame. To simplify calculations, an alternative frame of reference is used for kinematic analysis, namely, the root tip frame (Silk, 1984). In this frame, the tip of the root is the origin (position and velocity both equal zero), and velocity rises to reach a plateau in non-growing regions. For a root growing at steady state, in the laboratory frame the boundaries move at the same rate as the root tip and traverse cells; whereas in the root-tip frame, the boundaries are motionless and cells move across the boundary from one zone to the next (Figure 1).
We used Arabidopsis thaliana, because the thin roots of these species facilitate high-resolution imaging and kinematic analysis (Beemster and Baskin, 1998), and imaged the same root for 3 h, obtaining a velocity profile every 5 min. Here, we show that growth dynamics over 3 h are remarkably stable. However, the rootward boundary of the elongation zone saltates toward and away from the tip. Overall, the saltations span approximately 75 μm, with an average step in 5 min of 17 μm. When the shoot is removed, the root continues to grow but shootward steps are modestly suppressed, and thus the position where rapid elongation rate is attained moves steadily rootward, halving the length of the meristem in 24 h. These results suggest that the boundary between meristem and elongation zone is sited in part by an extrinsic signal, originating from the shoot.
Results
Root Growth Dynamics Vary Significantly over Time
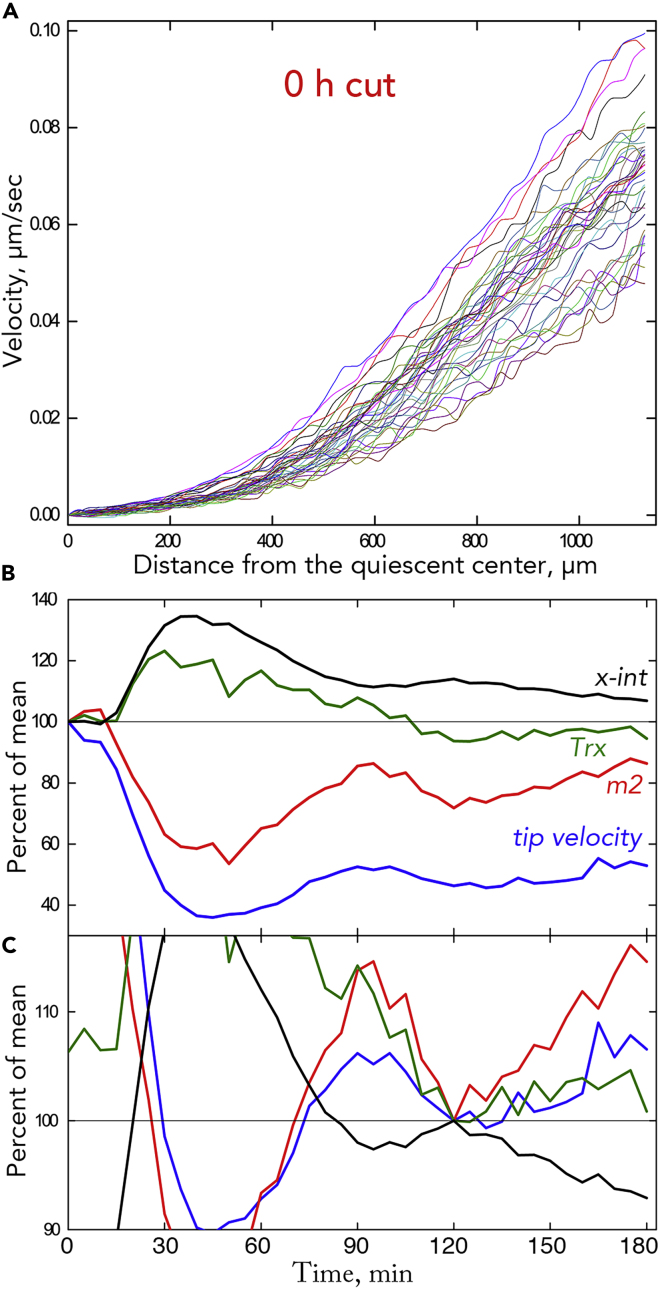
To characterize root growth dynamics, we imaged a root for 3 h so that a velocity profile could be obtained every 5 min. Roots were imaged through a horizontal microscope and grew inside the agar medium, an enclosure that enhances image quality and suppresses lateral movement of the root (see Figure S4). Images spanned meristem and elongation zone but excluded the maturation zone, because including it would have decreased resolution. From a pair of images separated by 30 s, the velocity profile was obtained by Stripflow software (Yang et al., 2017; Baskin and Zelinsky, 2019). At each pixel along the midline of the root image, starting at the quiescent center, Stripflow estimates the motion in the two images of a strip-like region of interest, as wide as the root and 40 pixels (∼20 μm) long, centered at that midline pixel; the component of motion tangent to the midline is taken as velocity.
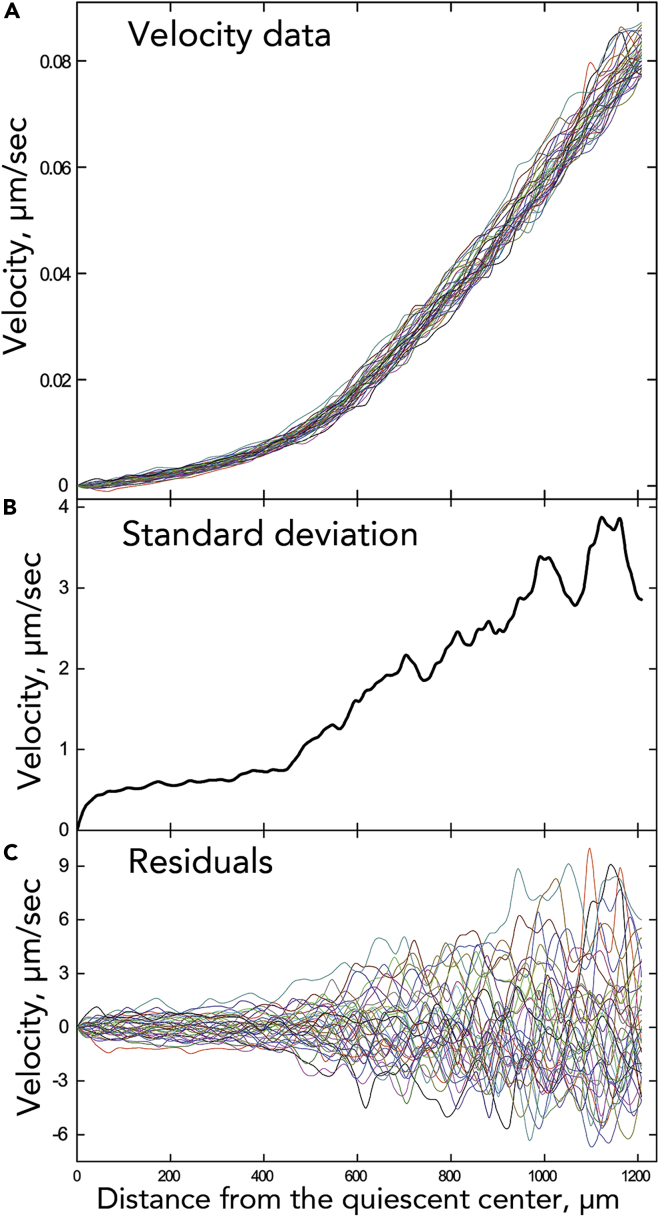
In general, the velocity profiles for a root coincided closely (Figure 2A). The alignment appeared closest in the rootward 0.5 mm or so, corresponding to the meristem along with any adjacent transition zone. For this study, a total of 35 control roots were imaged, and all showed velocity profiles that were well aligned over the 3 h (Figure S1). This study includes roots imaged in the United Kingdom (Nottingham) and in the United States (Amherst) with similar results. To illustrate the alignment, we averaged all 37 velocity profiles for a single root and plotted the standard deviation around that average (Figure 2B) and the residuals (Figure 2C). Both types of plot have a transition between regions of low and high variability (at around x = 475 μm in the example shown), with the sharpness of the transition underscoring the congruence among the underlying velocity profiles.
Figure 2.
Velocity Profiles for One Root
(A) 37 velocity profiles, one every 5 min over 3 h. For other roots, see Figure S1.
(B) Standard deviation versus position of the 37 velocity values shown in (A).
(C) Difference between the raw datum and the mean (i.e., the residual) versus position for the 37 profiles shown in (A).
To characterize the temporal variation within a set of velocity profiles, we used principal-component analysis. Strikingly, the first component score explained more than 60% of the variation in the data whereas the second explained less than 8% (Figure 3A). Because of its dominance, we focus here on principal component 1. The first component score, but neither the second nor the third, underwent pronounced temporal fluctuations (Figures 3B and S2). These fluctuations appeared broad and somewhat sinusoidal for the roots imaged in Nottingham but narrower and less regular for those imaged in Amherst (Figure S2). To determine how likely this temporal variation would have happened by chance, we carried out a runs test, which tests for serial correlation in a sequence of values against a null hypothesis stating that the sequence is random (Bradley, 1968). For the roots imaged in Nottingham, the time-dependent variation in the first principal component was significant in 11 of the 12 roots imaged, and for roots imaged in Amherst, the variation was significant in 17 of the 23 roots imaged (Figure 3C). Thus for most roots, velocity profiles over time deviate from perfect superposition not only because of noise but also because of some non-random (i.e., time-dependent) behavior.
Figure 3.
Principal-Component Analysis
(A) Amount of the total variance explained by each of the first 37 components. Open circles plot mean ± standard deviation (when larger than the symbol) for the 35 intact roots.
(B) Plot of the first three component scores versus time for a single root. For other roots, see Figure S2.
(C) Outcome of runs test for non-randomness of the first three components. Roots 1–12 are from Nottingham.
The First Principal-Component Score Relates to the Position of the Elongation Zone
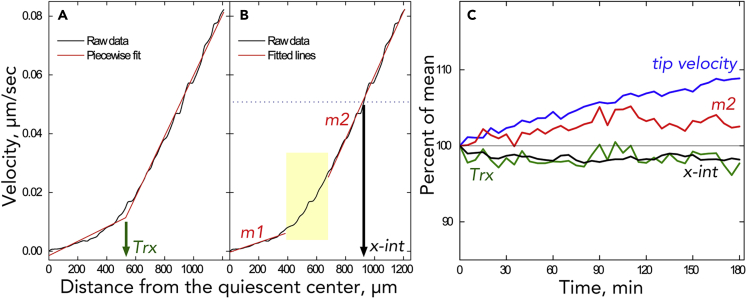
Principal-component analysis has the advantage of acting on the data directly, without any modification; however, it has the disadvantage that the components elaborated are purely mathematical. To relate the principal component to root growth, we parameterized the velocity profile. The first parameter is tip velocity (i.e., the rate at which the tip moves), measured directly by Stripflow. The second parameter, Trx, was obtained as the x-coordinate of the intersection of the best-fit pair of lines to the velocity profile (Figure 4A). Trx represents, roughly, the transition between meristem and elongation zone. Then, lines were fitted to the data on either side of Trx, except that a 300-μm interval, centered on Trx, was excluded because the velocity profile within this region is non-linear (Figure 4B). Also excluded was the shootward region of the data in any instances where the profile curved downward due to the velocity plateau (see, e.g., Figure 7D). The next two parameters were the slopes of these lines (m1 for the presumptive meristem, m2 for the elongation zone). The slopes have units of 1/time and estimate elemental elongation rate. This rate is how fast length increases without regard to absolute length and represents the speed of the elongation process itself (a process sometimes called cell elongation, despite the process being sub-cellular). Strictly speaking, elemental elongation rate applies to an infinitesimal increment of length; by fitting a line to a segment of the velocity profile, we are approximating elemental elongation rate over that region as constant, equal to the line's slope. The final parameter, x-int, was obtained as the x axis coordinate of the point where the line fitted to the profile in the elongation zone for m2 intersects a horizontal line at a value of y chosen for that root to bisect the average fitted interval (Figure 4B). In terms of root growth, x-int represents the relative position of the zone of elongation (i.e., a larger value indicates that the elongation zone is farther from the tip).
Figure 4.
Parameterization of the Velocity Profile
(A) The parameter Trx is found as the x-coordinate of the intersection of the two best-fitted regression lines (red) to the raw data (black, velocity profile) for a single time point.
(B) The slopes m1 and m2 are found by centering a 300-μm window at Trx and then fitting lines to the data on either side (red). Finally, x-int is found from the x coordinate of the intersection of the velocity profile with a reference velocity (horizontal blue dotted line). The reference is obtained for a given root as the y coordinate of the midpoint of the average regression interval used to find m2.
(C) Parameter time courses.
Parameters for each root were averaged over time, expressed as a percentage of the mean, and then translated horizontally so that each curve would start at 100. The tip velocity parameter is measured directly by Stripflow along with the velocity profile. The time course for m1 is omitted for clarity. Sample size = 35. Parameters (including m1) are plotted as absolute values in Figures S10 and S11.
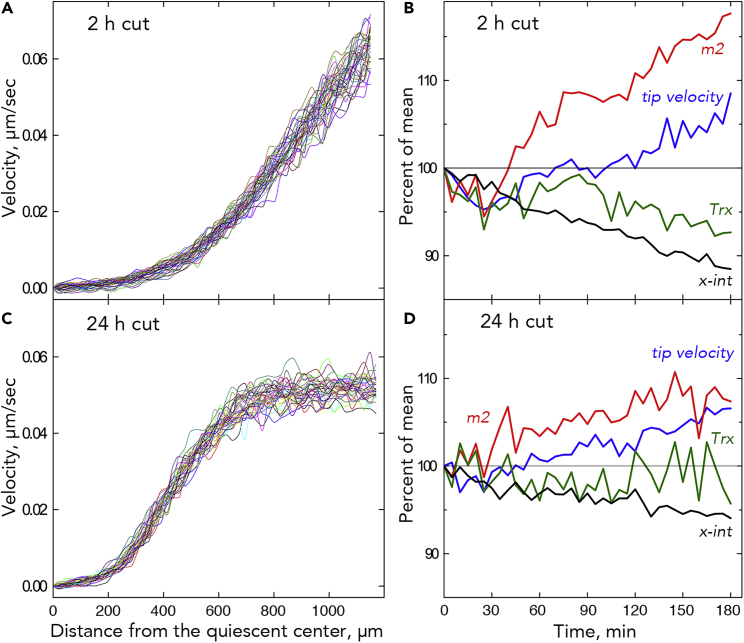
Figure 7.
Shoot Removal
(A) All 37 velocity profiles for a root following shoot removal, with imaging started 2 h after removing the shoot (“2-h cut”). All replicate roots shown in Figure S5.
(B) Parameter time courses for the 2-h cut roots, plotted as for Figure 4. Sample size = 17.
(C) All 37 velocity profiles for a root following shoot removal, with imaging started 24 h after removing the shoot (“24-h cut”). All replicate roots shown in Figure S7.
(D) Parameter time courses for the 24-h cut roots, plotted as for Figure 4. Sample size = 12. Absolute parameter values are plotted in Figures S10 and S11.
When the parameters at each time are averaged over the roots in the dataset, their temporal stability is clear (Figure 4C). Stability was also seen for growth rate in meristem (m1), but this parameter is less accurately measured and is omitted from Figure 4C (see Figure S12). Only tip velocity changed by more than 5% over the 3 h, increasing steadily. Roots of A. thaliana are known to grow faster over time (Beemster and Baskin, 1998), although that study reported a rate of increase about half as fast as seen here. Both Trx and the x-intercept were strikingly constant over the 3 h. Although the absolute values of the parameters on average show that roots imaged at Amherst were growing slightly faster and with slightly larger elemental growth rate in the elongation zone (m2) than those in Nottingham, the data from the two laboratories are otherwise similar (Table 1).
Table 1.
Average Root-Growth Parameters
| Treatment | Tip Velocity μm/min |
m1 %/h |
Trx μm |
m2 %/h |
x-int μm |
|---|---|---|---|---|---|
| Intact Plants | |||||
| Nottingham | 8.3 ± 2 | 5.7 ± 0.9 | 40 ± 4.6 | 553 ± 51 | 915 ± 44 |
| Amherst | 5.5 ± 1.1 | 5.6 ± 0.6 | 34 ± 4.3 | 532 ± 42 | 979 ± 90 |
| All | 7.3 ± 2.2 | 5.7 ± 0.8 | 38 ± 5.3 | 548 ± 51 | 957 ± 82 |
| Shoot Removed | |||||
| 0 h | 4.9 ± 1 | 4.3 ± 0.8 | 31 ± 2.7 | 474 ± 73 | 1,028 ± 92 |
| 2 h | 4.7 ± 0.8 | 3.1 ± 0.7 | 32 ± 3.2 | 540 ± 65 | 888 ± 76 |
| 24 h | 3.6 ± 0.8 | 4.6 ± 1 | 37 ± 3.2 | 273 ± 63 | 503 ± 82 |
Data are mean ± SD, with n = 12 (Nottingham), 23 (Amherst), 35 (All), 17 (2 h), 12 (24 h), and 12 (0 h). For shoot removed, the times given are the times between shoot removal and the start of imaging, except for 0 h where approximately 2 min elapsed between cutting and imaging onset
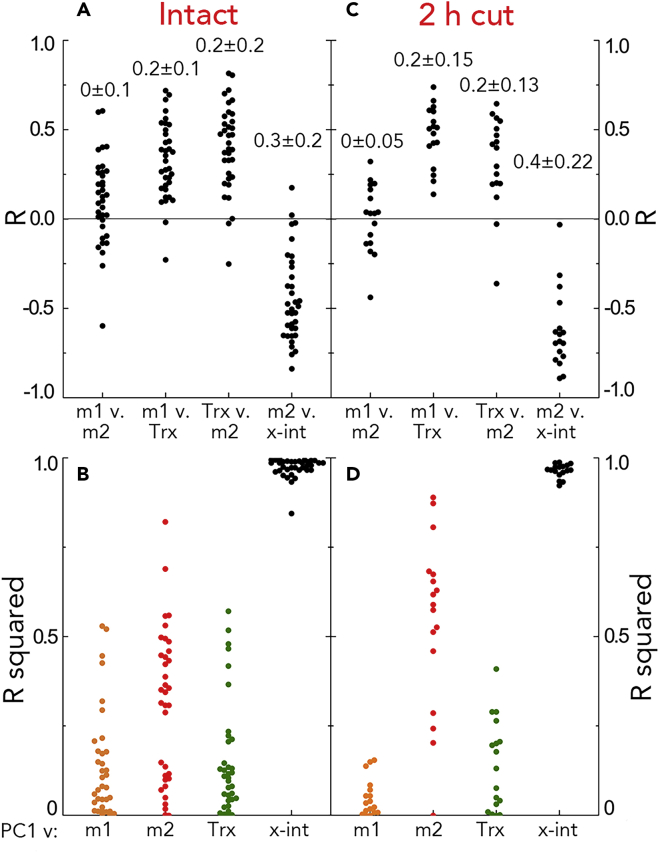
These parameters were chosen to represent distinct elements of the velocity profile. To examine to what extent the parameters are independent, we calculated the correlation coefficient between various pairs (Figure 5A). The parameters were correlated modestly, although average R2 values were rather low. The reasons for the modest correlations are not clear, but we feel that such a level of dependence will not influence our conclusions unduly.
Figure 5.
Correlations among Key Parameters
(A and C) Values of the correlation coefficient (R) for the indicated parameter pairs for intact (A) and 2-h cut (C) roots. Numbers above the symbols give mean ± SD of the R2 value.
(B and D) Squares of the correlation coefficient (R2) for the indicated parameters versus the first principal component for intact (B) and 2-h cut (D). Each symbol represents a root. Comparable data for 24-h cut are shown in Figure S7.
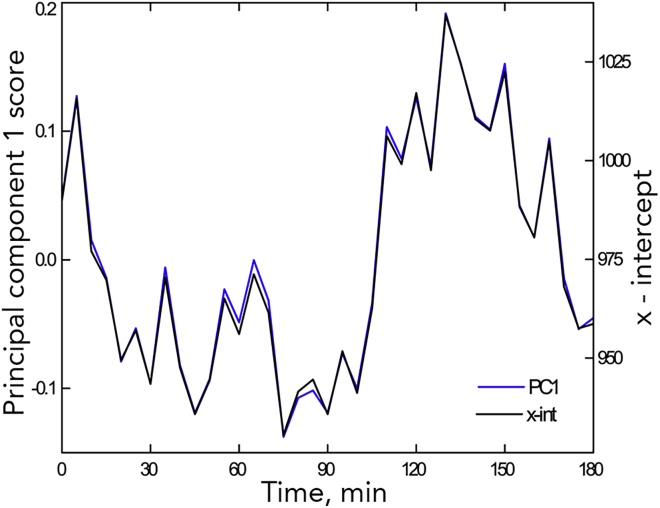
Next, we calculated the correlation between these parameters and the first principal-component score. Here, because the sign of the component is arbitrary, we present the values for the squared coefficient only (Figure 5B). The first principal-component score was correlated weakly to m1, m2, and Trx, but strongly to the x-intercept. To illustrate the strength of this correlation, we plot x-int together with the score versus time (Figure 6 and S3). The strict similarity extends even to roots where the temporal variation in the first component was not significant in the runs test. Evidently, the time-dependent variation demonstrated for the first principal component is captured substantially by x-int. Insofar as x-int reflects the position of the elongation zone, these results indicate that the localization of that zone saltates.
Figure 6.
Comparison of the Time Course for Principal Component 1 Score and x-int for a Single Intact Root
Data for all intact roots shown in Figure S3.
Shoot Removal Provokes the x-Intercept to Move Rootward
To characterize the time-dependent variation further, we perturbed root growth by removing the shoot. Because in our system the roots grow inside the agar, removing the shoot is convenient compared with imposing salt or nutrient stress. Also, because the growth medium for all experiments contains sucrose, an energy source remains present. Without a shoot, the primary root grew surprisingly well for several days (Figure S4). To allow transients to diminish, we waited for 2 h before starting the 3-h image acquisition. As for intact plants, roots without a shoot had velocity profiles over time that coincided closely (Figure 7A). In a few examples, the growth zone appeared to be shortened, evidenced by the velocity nearing a plateau (Figure S5). Also similar to intact plants, the parameters were correlated to each other to only a limited extent, whereas the first principal-component score was again strikingly correlated to the x-intercept (Figures 5C and 5D).
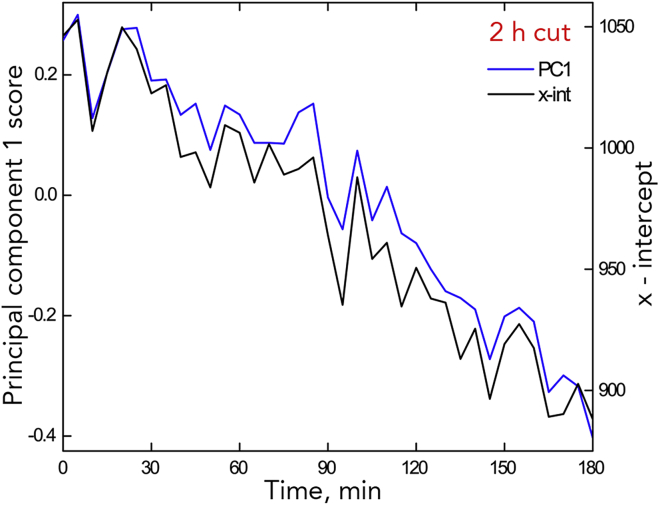
However, differences from intact plants appear when considering the parameters averaged at each time point (Figure 7B). While tip velocity increased across most of the interval, similar to the increase for intact plants (Figure 4), the elongation zone slope (m2) increased more steeply and the x-intercept, and to a lesser extent Trx, decreased steadily (Figure 7B). Furthermore, removing the shoot altered the behavior of the first principal-component score and likewise the x-intercept: the saltations became unbalanced, moving the x-intercept on-average rootward (Figures 8 and S6). On average, over the 3-h interval, the x-intercept moved closer to the tip by about 100 μm.
Figure 8.
Comparison of the Time Course for Principal Component 1 and x-int for a Single 2-h Cut Root
Data for all 2-h cut roots shown in Figure S5.
To extend these results, after removing the shoot, we waited 24 h before starting the 3-h image acquisition. Again, the 37 velocity profiles closely coincided; only now the profiles for nearly all the roots reached an evident plateau, indicating that the complete growth zone had become small enough to be spanned by the ∼1.2-mm image field (Figures 7C and S7). The shorter growth zone gave rise to a reduced tip velocity (Table 1). Based on parameterizing the velocity profiles and on principal-component analysis, the root's behavior at 24 h after excision resembled a noisier version of the behavior at 2 h (Figures 7D, S8, and S9). In particular, although its progress was noisy and diminished, the x-intercept continued a net rootward movement. By 24 h after shoot removal, the elongation zone slope (m2) had recovered its pre-excision value, whereas Trx had moved about 250 μm toward the tip (Table 1). Strongly decreased Trx a day after excision is consistent with previous observations of the A. thaliana root having a shorter apparent meristem 2 days following shoot excision (Grieneisen et al., 2007; Mähönen et al., 2014).
Evidently, removing the shoot converts a stable back-and-forth saltation of the x-intercept to a net movement toward the tip. To determine how soon this new pattern was established, we began the 3-h image acquisition as soon as possible after shoot excision, in practice about 2 min. Note that for the following data, time zero is the time of the first image, not the time of cutting. With this treatment, the velocity profiles diverged (Figures 9A and S10). About 15 min after removing the shoot, the measured parameters changed profoundly but transiently; by 45 min after cutting, tip velocity and elongation zone slope fell to about half of their time zero value, similar to results for tobacco (Nagel et al., 2006), whereas both Trx and x-intercept increased by around 25% (Figure 9B). By ∼90 min, all these parameters returned to near their pre-cut values, with only tip velocity failing to recover. We normalized parameter values to their value at 120 min and plotted them on the same scale as used previously (Figure 9C). After 120 min, the parameters changed steadily and in a way that resembled what was seen for roots imaged starting 2 h after shoot removal. The similarity between the third hour of the roots imaged immediately after shoot removal and the first hour of those imaged starting 2 h afterward is apparent from plotting absolute values of the parameters (Figure S11).
Figure 9.
Growth Dynamics with Imaging Started Immediately after Shoot Removal (“Zero-Hour Cut”)
(A) All 37 velocity profiles.
(B) Parameter time courses, plotted as in Figure 4, but with the scale reduced to accommodate the large changes. Sample size = 12. Parameters are plotted as absolute values in Figures S10 and S11.
(C) Same data as in (B), but shown on a scale similar to that of Figure 4 and translated so that the curves all equal 100% at 120 min.
Along with causing the x-intercept to move rootward, removing the shoot also decreased the elemental elongation rate of the meristem (m1) (Table 1; Figure S12). This rate was particularly low 4 to 5 h after shoot removal but had not recovered fully by 24 h. It would be interesting to determine whether this was accompanied by an increased duration of the cell cycle. In general, rates of division and elongation in the meristem are tightly coupled, keeping average cell length constant (Green, 1976), but we know little about how this is regulated.
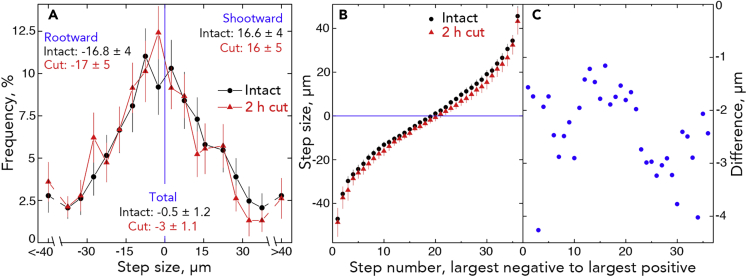
To gain further insight into the movement of the x-intercept, we plotted the distribution of the amount moved (“step size”) in 5 min (i.e., between each time point) for intact plants and those imaged 2 h after shoot removal (Figure 10A). The distribution for intact plants was symmetrical with the majority of steps being 10 μm or less. The mean was slightly negative (rootward), implying there might have been a slight net rootward displacement of the x-intercept, too small to have shown up in the average plots. The shape of the distribution differed from that of a Gaussian curve, a deviation implying that the underlying process is out of equilibrium, consistent with a non-random temporal process (Wang et al., 2012). Removing the shoot changed the distribution subtly. First, shoulders appeared at −30 and +20 μm. Second, the frequency of the smallest rootward step size was increased, whereas the frequency of most shootward step sizes was reduced. We also examined the cumulative distribution of steps by sorting steps for each root from the largest negative to the largest positive step (Figures 10B and 10C). For all step-size ranks, the steps of cut roots were a few microns more negative than those of intact roots, a difference that if anything was slightly larger for shootward (i.e., positive) steps. Taken together, these data show that, with the shoot removed, balanced saltation of the elongation zone continued, but the balance point moved slowly (10–30 μm/h) rootward.
Figure 10.
Analysis of x-int Steps for Intact and 2-h Cut Seedlings
The step size is the difference between successive (i.e., every 5 min) values.
(A) Frequency distribution. Symbols plot mean for each root ±95% confidence interval. Numerical values show mean ± SD for all steps in the treatment.
(B and C) Cumulative distributions. For each root, steps were sorted from largest negative to largest positive and then averaged over each rank (i.e., the smallest steps were averaged, then the next smallest, and so on). (B) Average step size of each rank ±95% confidence interval. (C) The difference (2-h cut minus intact) for the data in (B). Total roots: n = 35 for intact, 17 for 2-h cut; total steps: n = 1,269 for intact, n = 612 for 2-h cut.
Temporal Analysis Shows Material Elements Grow Faster and Then Slower
The above analysis is spatial (sometimes called Eulerian); a contrasting approach is temporal (or Lagrangian) (Silk, 2006). A spatial reference is converted to a temporal one by means of a time-position trajectory (Figure 11A). To make the trajectory, a particle is placed at an arbitrary position (say, 400 μm from the tip) and allowed to move for 5 min at the velocity known for that position from the first velocity profile. The particle arrives at a new position, and the next 5 min of movement is taken from the second velocity profile, and so on, until the last velocity profile. The positions reached by the particle at each time point give rise to the trajectory. In Figure 11A, three trajectories are shown: from roughly 400 to 490 μm, from 490 to 670 μm, and from 670 to 1,100 μm. Together, the three trajectories span the transition region and most of the imaged elongation zone. Although each trajectory represents 3 h, the trajectories are increasingly longer in space because velocity increases with position.
Figure 11.
Temporal Analysis for the Root of an Intact Seedling
(A) Position trajectories. The end of the black trajectory is at the position where the red one starts; the end of the red trajectory is where the blue one starts.
(B) Elemental elongation rate as a function of time for the three trajectories. Plots for all intact roots in Figure S12.
(C) Elemental elongation rate as a function of position for the three trajectories. Plots for all intact roots in Figure S13.
With trajectories built, we followed elemental elongation rate for a material element as it moved through the root (Figures 11B, 11C, and S13). The material element represents an infinitesimally thin band of root, but one may imagine these plots as following a cell. When viewed with respect to time, elemental elongation rate increased gradually, particularly for the lower two trajectories, but here and there the rate fluctuated (Figure 11B). A fluctuation could happen in a single trajectory, or in two or all three synchronously (Figure S13). When viewed with respect to position, the fluctuations happened throughout the studied region (Figures 11C and S14). Notably in these fluctuations, local growth rate not only increased but also decreased. Growth rate decreases are surprising, insofar as growth rate from meristem to elongation zone is generally considered to increase monotonically. As discussed in the following section, these transients probably account for the saltatory movement of the x-intercept.
Discussion
We sought to understand root zonation by characterizing growth dynamics. We found in general that growth dynamics are reasonably stable on a minutes-to-hours scale, implying the existence of tight regulation. Stable growth dynamics are consistent with previous observations (e.g., Chavarría-Krauser et al., 2008; Shih et al., 2014), at least as assessed by eye. However, we also discovered significant temporal variation. The variation was significant statistically for the principal-component 1 score, notable because principal-component analysis reflects the data directly. Because the first component explains a majority of the variation in the dataset and is correlated tightly to x-int, we conclude that x-int likewise varies significantly over time. We did not carry out a runs test on x-int because of the strength of its correlation to the first component score. This x-intercept saltates toward and away from the root tip, a fluctuation implying that zonation is regulated in part by a feedback mechanism. Consistently, we discovered that removing the shoot alters the balance of x-intercept movement, resulting in the elongation zone moving toward the root tip. We hypothesize that the shoot supplies one or more signals to a feedback mechanism shaping the growth zone.
Variations on the Theme
Our experiments began at the University of Nottingham, where principal-component 1 varied over time with sufficient regularity that we could fit a sine function to the data and determine an average period of around 90 min (also found with auto-correlation analysis). Experiments continued at the University of Massachusetts, where principal-component 1 varied over time, but with less regularity (Figure S2). At Amherst, to obtain smoother kinetics, we varied a variety of factors, both biological (e.g., size of Petri dish, growth chamber model, seed batch) and technical (e.g., microscope camera, optics, light source), to no avail. That none of these things altered the results appreciably gives us confidence that they are robust; however, the reason for the qualitative differences between the two settings remains unknown.
A 90 min period is similar to periods reported previously for various kinds of rhythmic growth phenomena, including organ growth rate (Baskin, 2015). These rhythms are sometimes called ultradian to contrast them from the longer and more commonly studied circadian rhythms. Therefore, we checked to what extent principal-component 1 is correlated to tip velocity (Figure S15). For all the treatments studied, squared correlation coefficients were spread rather evenly from zero to 1. Thus, in our system, displacement of the root tip is rhythmic in the ultradian range sometimes but not always; moreover, movement of the x-intercept is only occasionally associated tightly with root tip velocity.
The Movement of the x-Intercept
What is the meaning of this x-intercept and its movement? The x-intercept is one of several parameters used here in representing the velocity profile as two linear regions (with slope m1 and m2) that flank a curved (and un-parameterized) transition region. These slopes represent elemental elongation rate. As shown previously, the velocity profile within the elongation zone is fitted by a line surprisingly well, meaning that it is reasonable to assume that the zone elongates at a constant rate throughout much of its length (van der Weele et al., 2003). The x-intercept represents the position of this line along the x axis. When x-int decreases, the elongation zone has expanded to become closer to the root tip; conversely, when x-int increases, the elongation zone has receded to become farther away from the tip. We conceptualize changes in the x-intercept as movement of the elongation zone's rootward boundary, although we recognize that the boundary is gradual. Because the elongation zone was too large to image in its entirety, we do not know if rootward and shootward boundaries move independently, although we suspect they do.
What could cause the rootward boundary of the elongation zone to translate back and forth along the x axis? The intercept's position will be affected by changes in the slope of the line (m2); but, around the midpoint of the regression interval, these changes should be too small to shift the intercept's position by the tens of microns often recorded. Also minor, compared with the magnitude of x-intercept movement, is the imprecision associated with defining the origin of each velocity profile (i.e., x = 0), an uncertainty that we estimate to be about plus-or-minus 1 μm. Given that the value of the x-intercept depends on the length of the meristem (plus associated transition zone), were that region to rapidly increase in length then that would move the x-intercept shootward. However, the growth rates measured for that region are too slow to account for all but the smallest shootward steps.
Instead, the most tenable explanation for the back-and-forth movement is increases and decreases in elemental growth rate around the rootward flank of the elongation zone. A rootward step indicates that additional material has joined the zone of elongation, an accretion that shortens the distance between the root tip and rapidly elongating material; conversely, a shootward step indicates that a band of material at the rootward edge has slowed its elongation, a loss that increases the amount of slowly growing material between the tip and the elongation zone. This explanation motivated the temporal analysis, which in fact found the predicted growth rate transients (Figures 11B and 11C). Evidently, growth is prone to speed up and slow down as it ramps up to its eventual maximum.
Are these growth rate transients related to mechanisms that position the rootward boundary of the zone of elongation? Positioning the boundary and growth rate transients might be independent phenomena. Alternatively, the mechanism siting the boundary might home in on the desired position by using feedback from external signals, prompting first a growth rate increase and then a decrease. In this view, the loss of information from the shoot would alter the poise between these opposing impulses. We favor the mechanistic link because the growth rate transients are large and the two processes are spatially congruent.
Role of the Shoot in the Growth Dynamics of the Root
When the shoot is removed, growth changes in two phases. In the first, which lasts less than 2 h, nearly every feature of growth dynamics changes. In the second phase, which lasts for at least a day, growth dynamics resemble those of intact plants, except that the position of the elongation zone moves steadily rootward. In both phases, the responses presumably happen because the roots lose something provided by shoot, but for each phase the missing material might be distinct.
Based on its speed, the first phase could be triggered by the abrupt release of tension in the xylem and the consequent upward surge in water potential. Within minutes, removing the shoot changes turgor pressure in cortical cells (Zimmermann et al., 1992; Rygol et al., 1993) and decreases aquaporin expression and hydraulic conductivity (Vandeleur et al., 2014; Meng et al., 2016). What's more, following excision, aquaporins and conductivity decrease even when the phloem has been stopped beforehand by girdling (Vandeleur et al., 2014) but stay constant when xylem cells at the cut root stump are connected to a pump and put in tension (Meng et al., 2016). Nevertheless, factors that govern water transport from the root to the shoot (summed up in root hydraulic conductivity) probably are distinct from those governing growth at the root tip. Indeed, root tip velocity decreases rapidly (similar to the kinetics seen here) when A. thaliana leaves are wounded carefully to keep the xylem intact; and the velocity decreases even more when such wounds are laced with bacteria (Schmidt et al., 2010). These results imply that the initial rapid changes in root growth are not necessarily explained directly by lost xylem tension.
About 2 h after shoot removal, growth parameters become stable, but the balanced back-and-forth movement of the x-intercept changes to favor a net movement toward the root tip, a movement that continues for at least a day and shortens the apparent meristem. Likewise, the elongation zone becomes shorter, as seen by velocity profiles at 24 h after shoot removal, reaching a plateau within the microscope's field of view (Figures 7C and S7). Evidently, without a shoot, both boundaries of the elongation zone move rootward. Although the changes during the second phase could be a root-based response to lost xylem tension, we hypothesize that the position of the boundaries is influenced by a signal transmitted from the shoot.
What is the signal? One possibility is sucrose, which reaches the root through the phloem and in addition to being a substrate often acts as a signal (Ruan, 2014). In our experiments, sucrose (1%) is present in the medium; when the sucrose is omitted, shoot removal stops root growth entirely within an hour or two, suggesting that sucrose is taken up by shootless roots (MacGregor et al., 2008). However, sucrose entering the root via the epidermis might send a distinct signal compared with sucrose unloaded from the phloem.
Instead, the signal might be auxin, a compound known to influence almost every aspect of plant physiology. Oscillations in auxin signaling drive the formation of lateral roots (De Smet et al., 2007; Moreno-Risueno et al., 2010; Xuan et al., 2015), although their period is 4 h or more, longer than the ∼1.5 h seen here. We sought to determine whether auxin could mimic the presence of a shoot and maintain balanced movement of the x-intercept. Applying auxin to the cut stump and assaying root elongation over several days, we reasoned that an excessive concentration would inhibit growth strongly, whereas a suitable concentration would be at the threshold for inhibition. Contrary to our reasoning and in contrast to previous results (e.g., Reed et al., 1998; Fu and Harberd, 2003), the auxin did nothing to root growth, regardless of concentration and of whether auxin was applied in agar or lanolin or onto cut or intact plants (at the root-shoot junction). Likewise, auxin added to the stump failed to decrease fluorescence at the root tip from the DII-Venus reporter. Auxin has been reported to need the phloem to move effectively from shoot to root (Bishopp et al., 2011) and sometimes moves to a limited extent in intact plants (Chen et al., 2014). Be that as it may, we were unable to test auxin involvement experimentally.
Another candidate signal is cytokinin, because this hormone regulates the size of the meristem (Takatsuka and Umeda, 2014; Gu et al., 2018); however, cytokinin typically represses the size of the meristem, as seen, for example, by exogenous cytokinin shrinking the meristem (Beemster and Baskin, 2000) and by loss of cytokinin responsiveness enlarging it (Dello Ioio et al., 2008, 2012). What's more, meristem size is unchanged when cytokinin reaching the root is limited by a cytokinin oxidase expressed specifically in the phloem (Bishopp et al., 2011). Apparently, the cytokinin used for sizing the meristem is internal to the root.
Besides auxin, hormones that positively regulate the size of the meristem include gibberellin and brassinosteroid (Band et al., 2012; Wei and Li, 2016). Loss of either could be expected to shorten the meristem. However, in addition, both these hormones positively regulate elemental (“cell”) elongation rate. Insofar as roots without shoots recover their elemental elongation rate (as indicated by m2) to precut levels (Table 1; Figure S11), neither of these hormones are straightforward candidates.
The final possibility to consider is signals carried by ions such as action potentials or calcium waves (Choi et al., 2017; Toyota et al., 2018). Although wounding generates such signals avidly, the implication here is that the signal is present continuously in intact plants, adjusting the position where constant elemental elongation rate is attained. Discovering the signal that propagates stably through the plant to convey information influencing root growth dynamics stands as a challenge for the future.
Limitations of the Study
As discussed in the previous section, we identify three limitations. (1) The velocity profiles contain high-frequency noise and we do not know whether the noise originates from technology (e.g., vibrations) or biology (e.g., cytoplasmic streaming). (2) The shootward boundary of the elongation zone was not imaged, and we do not know whether this boundary moves together with, or independently of, the rootward boundary. (3) The rootward boundary of the elongation zone is positioned with input from the shoot, but we do not know the nature of this input.
Resource Availability
Lead Contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Tobias Baskin, baskin@umass.edu.
Materials Availability
This study generated no new materials.
Data and Code Availability
Stripflow is available here: https://github.com/TobiasBaskin/Stripflow-release. The data and other code supporting the current study have not been deposited in a public repository because they are idiosyncratic and unwieldy, but are available from the corresponding author on request.
Methods
All methods can be found in the accompanying Transparent Methods supplemental file.
Acknowledgments
TIB was supported in part by the European Commission under the Marie Curie International Incoming Fellowship Program; however, the contents of this publication do not reflect the views of the European Commission. We thank Dr. Adam Saffer (Yale University) for insightful comments on the manuscript.
Author Contributions
Conceptualization, T.I.B.; Software, D.B., S.P., and D.M.W.; Formal Analysis, S.P.; Investigation, T.I.B., E.Z., X.Y., and M.E.; Resources, D.M.W. and M.J.B.; Writing – Original Draft, T.I.B.; Writing – Review and Editing, T.I.B., E.Z., S.P., and M.J.B.; Supervision, T.I.B. and M.J.B.; Funding Acquisition, T.I.B.
Declaration of Interests
The authors declare no competing interests.
Published: July 24, 2020
Footnotes
Supplemental Information can be found online at https://doi.org/10.1016/j.isci.2020.101309.
Supplemental Information
References
- Band L.R., Úbeda-Tomás S., Dyson R.J., Middleton A.M., Hodgman T.C., Owen M.R., Jensen O.E., Bennett M.J., King J.R. Growth-induced hormone dilution can explain the dynamics of plant root cell elongation. Proc. Natl. Acad. Sci. U S A. 2012;109:7577–7582. doi: 10.1073/pnas.1113632109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baskin T.I. Ultradian growth oscillations in organ: Physiological signal or noise? In: Mancuso S., Shabala S., editors. Rhythms in Plants. Springer; 2015. pp. 3–17. [Google Scholar]
- Baskin T.I., Peret B., Baluška F., Benfey P.N., Bennett M., Forde B.G., Gilroy S., Helariutta Y., Hepler P.K., Leyser O. Shootward and rootward: peak terminology for plant polarity. Trends Plant Sci. 2010;15:593–594. doi: 10.1016/j.tplants.2010.08.006. [DOI] [PubMed] [Google Scholar]
- Baskin T.I., Zelinsky E. Kinematic characterization of root growth by means of Stripflow. In: Cvrčková F., Žárský V., editors. Plant Cell Morphogenesis: Methods and Protocols. Second Edition. Humana Press; 2019. pp. 291–305. [DOI] [PubMed] [Google Scholar]
- Beemster G.T.S., Baskin T.I. Analysis of cell division and elongation underlying the developmental acceleration of root growth in Arabidopsis thaliana. Plant Physiol. 1998;116:1515–1526. doi: 10.1104/pp.116.4.1515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beemster G.T.S., Baskin T.I. STUNTED PLANT 1 mediates effects of cytokinin, but not of auxin, on cell division and expansion in the root of arabidopsis. Plant Physiol. 2000;124:1718–1727. doi: 10.1104/pp.124.4.1718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bishopp A., Lehesranta S., Vatén A., Help H., El-Showk S., Scheres B., Helariutta K., Mähönen A.P., Sakakibara H., Helariutta Y. Phloem-transported cytokinin regulates polar auxin transport and maintains vascular pattern in the root meristem. Curr. Biol. 2011;21:927–932. doi: 10.1016/j.cub.2011.04.049. [DOI] [PubMed] [Google Scholar]
- Bradley J.V. Prentice-Hall; 1968. Distribution-Free Statistical Tests, Chapter 12. [Google Scholar]
- Chavarría-Krauser A., Nagel K.A., Palme K., Schurr U., Walter A., Scharr H. Spatio-temporal quantification of differential growth processes in root growth zones based on a novel combination of image sequence processing and refined concepts describing curvature production. New Phytol. 2008;177:811–821. doi: 10.1111/j.1469-8137.2007.02299.x. [DOI] [PubMed] [Google Scholar]
- Chen Q., Dai X., De-Paoli H., Cheng Y., Takebayashi Y., Kasahara H., Kamiya Y., Zhao Y. Auxin overproduction in shoots cannot rescue auxin deficiencies in arabidopsis roots. Plant Cell Physiol. 2014;55:1072–1079. doi: 10.1093/pcp/pcu039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi W.G., Miller G., Wallace I., Harper J., Mittler R., Gilroy S. Orchestrating rapid long-distance signaling in plants with calcium, ROS, and electrical signals. Plant J. 2017;90:698–707. doi: 10.1111/tpj.13492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole R.A., McInally S.A., Fowler J.E. Developmentally distinct activities of the exocyst enable rapid cell elongation and determine meristem size during primary root growth in arabidopsis. BMC Plant Biol. 2014;14:386. doi: 10.1186/s12870-014-0386-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Smet I., Tetsumura T., De Rybel B., Frei dit Frey N., Laplaze L., Casimiro I., Swarup R., Naudts M., Vanneste S., Audenaert D. Auxin-dependent regulation of lateral root positioning in the basal meristem of arabidopsis. Development. 2007;134:681–690. doi: 10.1242/dev.02753. [DOI] [PubMed] [Google Scholar]
- De Vos D., Vissenberg K., Broeckhove J., Beemster G.T.S. Putting theory to the test: which regulatory mechanisms can drive realistic growth of a root. PLoS Comput. Biol. 2014;10:e1003910. doi: 10.1371/journal.pcbi.1003910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dello Ioio R., Galinha C., Fletcher A.G., Grigg S.P., Molnar A., Willemsen V., Scheres B., Sabatini S., Baulcombe D., Maini P.K., Tsiantis M. A PHABULOSA/cytokinin feedback loop controls root growth in arabidopsis. Curr. Biol. 2012;22:1699–1704. doi: 10.1016/j.cub.2012.07.005. [DOI] [PubMed] [Google Scholar]
- Dello Ioio R., Nakamura K., Moubayidin L., Perilli S., Taniguchi M., Morita M.T., Aoyama T., Costantino P., Sabatini S. A genetic framework for the control of cell division and differentiation in the root meristem. Science. 2008;322:1380–1384. doi: 10.1126/science.1164147. [DOI] [PubMed] [Google Scholar]
- Fu X., Harberd N.P. Auxin promotes arabidopsis root growth by modulating gibberellin response. Nature. 2003;421:740–743. doi: 10.1038/nature01387. [DOI] [PubMed] [Google Scholar]
- Gandar P.W. Growth in root apices. I. The kinematic description of growth. Bot. Gaz. 1983;144:1–10. [Google Scholar]
- Green P.B. Growth and cell pattern formation on an axis: Critique of concepts, terminology, and modes of study. Bot. Gaz. 1976;137:187–202. [Google Scholar]
- Grieneisen V.A., Xu J., Marée A.F.M., Hogeweg P., Scheres B. Auxin transport is sufficient to generate a maximum and gradient guiding root growth. Nature. 2007;449:1008–1013. doi: 10.1038/nature06215. [DOI] [PubMed] [Google Scholar]
- Gu J., Li Z., Mao Y., Struik P.C., Zhang H., Liu L., Wang Z., Yang J. Roles of nitrogen and cytokinin signals in root and shoot communications in maximizing of plant productivity and their agronomic applications. Plant Sci. 2018;274:320–331. doi: 10.1016/j.plantsci.2018.06.010. [DOI] [PubMed] [Google Scholar]
- MacGregor D.R., Deak K.I., Ingram P.A., Malamy J.E. Root system architecture in arabidopsis grown in culture is regulated by sucrose uptake in the aerial tissues. Plant Cell. 2008;20:2643–2660. doi: 10.1105/tpc.107.055475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mähönen A.P., ten Tusscher K., Siligato R., Smetana O., Díaz-Triviño S., Salojärvi J., Wachsman G., Prasad K., Heidstra R., Scheres B. PLETHORA gradient formation mechanism separates auxin responses. Nature. 2014;515:125–129. doi: 10.1038/nature13663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meng D., Walsh M., Fricke W. Rapid changes in root hydraulic conductivity and aquaporin expression in rice (Oryza sativa L.) in response to shoot removal - xylem tension as a possible signal. Ann. Bot. 2016;118:809–819. doi: 10.1093/aob/mcw150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moreno-Risueno M.A., Van Norman J.M., Moreno A., Zhang J., Ahnert S.E., Benfey P.N. Oscillating gene expression determines competence for periodic arabidopsis root branching. Science. 2010;329:1306–1311. doi: 10.1126/science.1191937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagel K.A., Schurr U., Walter A. Dynamics of root growth stimulation in Nicotiana tabacum in increasing light intensity. Plant Cell Environ. 2006;29:1936–1945. doi: 10.1111/j.1365-3040.2006.01569.x. [DOI] [PubMed] [Google Scholar]
- Pavelescu I., Vilarrasa-Blasi J., Planas-Riverola A., González-García M.P., Caño-Delgado A.I., Ibañes M. A Sizer model for cell differentiation in Arabidopsis thaliana root growth. Mol. Syst. Biol. 2018;14:e7687. doi: 10.15252/msb.20177687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reed R.C., Brady S.R., Muday G.K. Inhibition of auxin movement from the shoot into the root inhibits lateral root development in arabidopsis. Plant Physiol. 1998;118:1369–1378. doi: 10.1104/pp.118.4.1369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruan Y.L. Sucrose metabolism: Gateway to diverse carbon use and sugar signaling. Ann. Rev. Plant Biol. 2014;65:33–67. doi: 10.1146/annurev-arplant-050213-040251. [DOI] [PubMed] [Google Scholar]
- Rygol J., Pritchard J., Zhu J.J., Tomos A.D., Zimmermann U. Transpiration induces radial turgor pressure gradients in wheat and maize roots. Plant Physiol. 1993;103:493–500. doi: 10.1104/pp.103.2.493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt L., Hummel G.M., Schöttner M., Schurr U., Walter A. Jasmonic acid does not mediate root growth responses to wounding in Arabidopsis thaliana. Plant Cell Environ. 2010;33:104–116. doi: 10.1111/j.1365-3040.2009.02062.x. [DOI] [PubMed] [Google Scholar]
- Shih H.W., Miller N.D., Dai C., Spalding E.P., Monshausen G.B. The receptor-like kinase FERONIA is required for mechanical signal transduction in arabidopsis seedlings. Curr. Biol. 2014;24:1887–1892. doi: 10.1016/j.cub.2014.06.064. [DOI] [PubMed] [Google Scholar]
- Silk W.K. Quantitative descriptions of development. Ann. Rev. Plant Physiol. 1984;35:479–518. [Google Scholar]
- Silk W.K. Moving with the flow: what transport laws reveal about cell division and expansion. J. Plant Res. 2006;119:23–29. doi: 10.1007/s10265-005-0248-9. [DOI] [PubMed] [Google Scholar]
- Silk W.K., Erickson R.O. Kinematics of plant growth. J. Theor. Biol. 1979;76:481–501. doi: 10.1016/0022-5193(79)90014-6. [DOI] [PubMed] [Google Scholar]
- Takatsuka H., Umeda M. Hormonal control of cell division and elongation along differentiation trajectories in roots. J. Exp. Bot. 2014;65:2633–2643. doi: 10.1093/jxb/ert485. [DOI] [PubMed] [Google Scholar]
- Toyota M., Spencer D., Sawai-Toyota S., Jiaqi W., Zhang T., Koo A.J., Howe G.A., Gilroy S. Glutamate triggers long-distance, calcium-based plant defense signaling. Science. 2018;361:1112–1115. doi: 10.1126/science.aat7744. [DOI] [PubMed] [Google Scholar]
- van der Weele C.M., Jiang H.S., Palaniappan K.K., Ivanov V.B., Palaniappan K., Baskin T.I. A new algorithm for computational image analysis of deformable motion at high spatial and temporal resolution applied to root growth. Roughly uniform elongation in the meristem and also, after an abrupt acceleration, in the elongation zone. Plant Physiol. 2003;132:1138–1148. doi: 10.1104/pp.103.021345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vandeleur R.K., Sullivan W., Athman A., Jordans C., Gilliham M., Kaiser B.N., Tyerman S.D. Rapid shoot-to-root signalling regulates root hydraulic conductance via aquaporins. Plant Cell Environ. 2014;37:520–538. doi: 10.1111/pce.12175. [DOI] [PubMed] [Google Scholar]
- Wang B., Kuo J., Bae S.C., Granick S. When Brownian diffusion is not Gaussian. Nat. Mat. 2012;11:481–485. doi: 10.1038/nmat3308. [DOI] [PubMed] [Google Scholar]
- Wei Z., Li J. Brassinosteroids regulate root growth, development, and symbiosis. Mol. Plant. 2016;9:86–100. doi: 10.1016/j.molp.2015.12.003. [DOI] [PubMed] [Google Scholar]
- Xuan W., Audenaert D., Parizot B., Möller B.K., Njo M.F., De Rybel B., De Rop G., Van Isterdael G., Mähönen A.P., Vanneste S., Beeckman T. Root cap-derived auxin pre-patterns the longitudinal axis of the arabidopsis root. Curr. Biol. 2015;25:1381–1388. doi: 10.1016/j.cub.2015.03.046. [DOI] [PubMed] [Google Scholar]
- Yang X., Dong G., Palaniappan K., Mi G., Baskin T.I. Temperature-compensated cell production rate and elongation zone length in the root of Arabidopsis thaliana. Plant Cell Environ. 2017;40:264–276. doi: 10.1111/pce.12855. [DOI] [PubMed] [Google Scholar]
- Zimmermann U., Rygol J., Balling A., Klöck G., Metzler A., Haase A. Radial turgor and osmotic pressure profiles in intact and excised roots of Aster tripolium: pressure probe measurements and nuclear magnetic resonance-imaging analysis. Plant Physiol. 1992;99:186–196. doi: 10.1104/pp.99.1.186. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Stripflow is available here: https://github.com/TobiasBaskin/Stripflow-release. The data and other code supporting the current study have not been deposited in a public repository because they are idiosyncratic and unwieldy, but are available from the corresponding author on request.