Abstract
The evolution of “informatics” technologies has the potential to generate massive databases, but the extent to which personalized medicine may be effectuated depends on the extent to which these rich databases may be utilized to advance understanding of the disease molecular profiles and ultimately integrated for treatment selection, necessitating robust methodology for dimension reduction. Yet, statistical methods proposed to address challenges arising with the high-dimensionality of omics-type data predominately rely on linear models and emphasize associations deriving from prognostic biomarkers. Existing methods are often limited for discovering predictive biomarkers that interact with treatment and fail to elucidate the predictive power of their resultant selection rules. In this article, we present a Bayesian predictive method for personalized treatment selection that is devised to integrate both the treatment predictive and disease prognostic characteristics of a particular patient’s disease. The method appropriately characterizes the structural constraints inherent to prognostic and predictive biomarkers, and hence properly utilizes these complementary sources of information for treatment selection. The methodology is illustrated through a case study of lower grade glioma. Theoretical considerations are explored to demonstrate the manner in which treatment selection is impacted by prognostic features. Additionally, simulations based on an actual leukemia study are provided to ascertain the method’s performance with respect to selection rules derived from competing methods.
Keywords: Bayesian analysis, high-dimensional data, nonexchangeable, personalized medicine, predictive probability, unsupervised clustering
1. Introduction
Human diseases can be intrinsically heterogeneous with respect to their pathogenesis among patient populations and in some contexts vary in composition among multiple locations within a patient. Owing to pharmacogenetic diversities, a particular therapeutic strategy may yield very different outcomes among patients with similar diagnoses (Spear et al., 2001). In the oncology setting, wherein the majority of definitive comparisons in phase III fail to demonstrate the hypothesized extent of benefit for new treatment strategies for solid tumors (Amiri-Kordestani and Fojo, 2012), it is widely accepted that the relative utility of a given therapy is determined by the confluence of a patient’s particular clinical prognosis as well as the tumor’s particular molecular composition. In fact, drug development strategies devised to characterize cohort-averaged treatment benefits have largely failed in oncology with only 34% of confirmatory phase III trials yielding a significant result from 2003 to 2010 (Sutter and Lamotta, 2011).
Personalized medicine endeavors to understand the mechanisms of pharmacogenetics and ultimately achieve conformality between therapeutic interventions and the individuals being treated. With advancements in the understanding of molecular cancer biology, several treatment strategies that target specific biomarkers, such as crizotinib for non-small-cell lung cancer characterized by an anaplastic lymphoma kinase gene rearrangement, have been discovered and translated into clinical practice (Kelloff and Sigman, 2012). Early successes of molecularly targeted interventions have to some extent effectuated personalized medicine. The successes are limited, however, when one considers the tremendous amount of resources heretofore dedicated to precision medicine endeavors (Kuner, 2013).
Inherent to the realization of personalized medicine is the understanding of both predictive and prognostic markers (Simon, 2010; Ma et al., 2015). The difference between the two is that prognostic biomarkers determine how likely patients will achieve therapeutic responses regardless of the types of treatment, while predictive biomarkers determine who are likely/unlikely to benefit from a particular class of treatment regimes. Statistically, prognostic biomarkers are often identified as significant main effects, whereas predictive biomarkers are identified as significant interaction effects between a candidate biomarker and the treatment (Ternes et al., 2017). As depicted in Figure 1, studies have proposed quantitative biomarkers arising from clinical, genomic and recently imaging sources (Yip and Aerts, 2016). For examples, several genomic-based biomarkers have been proposed for a variety of tumors types (Ballman, 2015), and radiomic-based imaging features have been shown to characterize degrees of prognostication for patients with lung cancer (Aerts et al., 2014). While the evolution of “informatics” technology has the potential to generate massive databases for quantitative-based interrogations (Kelloff and Sigman, 2012) of many informatics sources, the extent to which personalized medicine may be effectuated depends on the extent to which these rich databases may be utilized to advance understanding of the disease molecular profiles and ultimately integrated for treatment selection.
Figure 1.

Precision medicine in oncology relies on biomarkers deriving from a diverse array of sources. Treatment decisions may be based on clinical characteristics of the patient and tumor (such as histopathology and cytopathology), genomic-variants (such as somatic mutations), or imaging features that describe a tumor tissue’s density, morphology, or texture.
While several statistical methods have been proposed to address challenges arising with the high-dimensionality of omics-type data, these methods associate the clinical outcomes with genomic features, usually measured on a relatively limited number of patients (Witten and Tibshirani, 2009; Archer and Williams, 2012). These methods, while useful for identifying associations deriving from prognostic biomarkers, are often limited for discovering predictive biomarkers that interact with treatment and fail to elucidate the predictive power of the resultant biomarkers. Ma et al. (2015) provide a survey of statistical methods for establishing personalized treatment selection rules that are currently available in the statistical literature. Conventional approaches should be considered limited, however, as they often rely of assumptions of statistical exchangeability among patients within biomarker defined subgroups or rely on linear models despite the presence of large numbers of potentially correlated inputs and interaction terms. Recently, Bayesian approaches that predict the personalized treatment utility for a given individual’s tumor on the basis of measures of inter-patient molecular similarity (Ma et al., 2016, 2017) have been established using predictive biomarkers stemming from multi-gene signatures. In both empirical and case studies, the Bayesian predictive methods were shown to effectively leverage a large set of tumor features and substantially outperformed competing methods based on penalized regression (Archer and Williams, 2012; Geng et al., 2015).
In this article, we propose a Bayesian predictive framework for personalized treatment selection that is devised to leverage both predictive and prognostic biomarkers. Given a genomic signature and a set of prognostic markers, usally selected in previous lab, clinical, and/or in silico studies, the methodology endeavors to formulate and test an optimal, individualized rule for treatment selection. Following the power prior predictive probability modeling framework and adopting the Bayesian discriminant analysis approach with prognostic biomarkers, the proposed method appropriately characterizes the structural constraints inherent to prognostic and predictive biomarkers, and hence properly utilizes these complementary sources of information for treatment selection (Lavine and West, 1992; Ma et al., 2016). Specifically, we build upon Ma et al. (2016) and propose a framework that, in addition to predictive markers, accounts for prognostic determinants to predict the extent to which a given patient is likely to attain a level of clinical response. Predictive markers are utilized to extend the prediction beyond prognostication, and adjust the outcome probability measures for each candidate therapy in relation to the molecular similarities and clinical endpoints of previously treated patients. In this article, we study the effect of prognostic markers on treatment selection, both theoretically and empirically, and evaluate the overall performances of the proposed treatment selection approach that includes both predictive and prognostic markers.
The article is organized as follows. Section 2 describes the methodology as well as explores theoretical aspects of the Bayesian predictive method for personalized treatment selection. We demonstrate and compare the method’s performance via simulation in Section 3, and report results arising from a case study of lower grade glioma in Section 4. Finally we conclude in Section 5.
2. Bayesian predictive methodology for treatment selection
Inherently a problem of outcome prediction, approaches to treatment selection can be enhanced through strategies that integrate prognostic with predictive characteristics of a candidate patient/disease. While intrinsic to the generalized linear model, the belief that prognostic features convey no additional information for treatment selection is actually a specific manifestation of the linear predictor. As we demonstrate in this section, this premise fails for broader classes of modeling strategies based on predictive probability. We formalize the integrative treatment selection strategy in three parts. Given a discrete set of ordered response-levels describing a spectrum of possible clinical outcomes, Section 2.1 derives “baseline” predictive probability measures on the basis of the prognostic determinants of a particular patient’s disease profile. Section 2.2 integrates the predictive features to adjust the baseline probability measures to reflect current knowledge pertaining to the effectiveness of each treatment option for the specific disease characteristics exhibited by the candidate patient. Section 2.3 provides rational to further elucidate the manner in which considerations of prognostic effects may alter treatment decisions derived from predictive features alone.
2.1. Baseline probability measures derived from prognostic determinants
Assume the existence of a training data set of n patients, (yi, Zi) where i = 1, … , n, for which yi denotes a random variable for the ith patient’s outcome (or response) and Zi characterizes a d–dimensional vector of prognostic features. Our strategy for treatment selection assumes that the effectiveness of any treatment can be described by the probability of K ordered response-levels characterizing the range of possible clinical outcomes for the particular disease understudy. An assumption that is common to oncology where outcomes often characterize varying levels of treatment response in terms of the extent of “residual disease” (local as well as distant migration) after a pre-specified, clinically relevant post-therapy follow-up duration. Letting yi assume a specific response-level, k, we use P(yi = k|πk) = πk with π = {πk : k = 0, … , K − 1} to denote the probability of observing the K response-levels for the ith patient. We start from the Bayesian discriminant analysis model (Lavine and West, 1992), that can be written as the following normal-mixture model:
The joint density function for the training data can be written as
| (1) |
Under the assumption that (μ, Σ) is a priori independent of π, the posterior distribution can be represented up to proportionality as
| (2) |
Let i★ index a future, heretofore untreated patient with pre-treatment characteristics . The outcome prediction for a future patient on the basis of pre-therapy prognostic determinants is intrinsically an evaluation of the following predictive probability measure
| (3) |
where represents the predictive distribution for obtained from a general model with parameters θk = (μk, Σk) that determine its conditional distribution under response-level k and characterizes the posterior probability of response-level k. Note that is specified conditionally on Y as .
Following the work of (Lavine and West, 1992), we use conjugate priors for the parameters of μ, Σ and π, with Dirichlet(α) as the prior for π, where α = {αk : k = 0, 1, … , K − 1}. Using nk to denote the number of patients that contribute to response-level k, the posterior distribution of p(π|Y, Z) is Dirichlet with . In addition, we assume that μk, Σk are mutually independent over K response groups with conjugate priors of normal-inverse Wishart and hyperparameters (μ0k, Λ0k/k0k;ν0k, Λ0k). The joint prior density of and μk|Σk ~ N(μ0k, Λ0k/k0k) is given as
| (4) |
The posterior pf p(μk, Σk|Y, Z) is normal-inverse Wishart, such that , , , , and , where .
Note that for any given values of the outcome variable, it can be shown that follows the multivariate Student-t distribution of , which is used to calculate the predictive density of and can be calculated in closed-form as the expected value of a Dirichlet distribution.
2.2. Treatment selection integrating predictive biomarkers
Heretofore, the normal-mixture modeling strategy delineates patient subgroups on the basis of their response and assumes that patients in the same response subtypes are statistically exchangeable. Yet, underlying the precision medicine paradigm, is the assumption of personalized treatment utility. We develop a selection strategy that uses predictive biomarkers to determine the extent to which any two patients should be considered exchangeable and adjusts the baseline response probability measures accordingly.
Assuming that J candidate therapies have been evaluated in the training dataset with their relative effectiveness determined by l predictive covariates denoted by Xl×n. The predictive covariates can be incorporated in our framework as defined by the following hierarchical model (one for each treatment):
This Section mostly concern with the definition of a power prior that is a function of the predictive covariates, and with the resulting predictive distribution that will be used for treatment selection. Under each candidate treatment for j = 1, 2, … , J,, the resulting predictive probabilities are
| (5) |
where . Evaluations of equation (5) depend on the predictive distribution of prognostic features as described in Section 2.1, as well as the predictive probability of achieving response-level k under treatment assignment j, . While various approaches could be used to formulate , we utilize the recently developed Bayesian predictive modeling approach of Ma et al. (2016), which treats similarity measures obtained from cluster analysis of the high-dimensional predictive features as measures of partial exchangeability. The methodology, which was developed in a clinical oncology context, was formulated on the assumption that the extent to which a result for any previously treated patient should influence the prediction of future success for a new patient should depend upon the extent to which their tumors (or disease characteristics more generally) exhibit similarity on the basis of current knowledge.
Using the consensus clustering method with the input of , one can obtain a (symmetric) similarity matrix, S, characterizing the extent of pairwise similarities between any two patients (Monti et al., 2003). We use 0 ≤ S(i★, i) ≤ 1 to denote the specific pairwise similarity metric between new patient i★ and the ith patient. Then assume that S(i★, i) determines the degree of influence imposed by ith patient in estimating the effectiveness of the treatment received for the new patient, which can be achieved via a power prior model (Ma et al., 2016, 2017; Ibrahim et al., 2003). Let nj represent the number of previous treated patients receiving treatment j. The posterior predictive distribution of response , X based on the predictive features can be formulated with a power prior model as
| (6) |
where πj = {πj,k : k = 0, 1, 2, … , K − 1 represents model parameters under treatment j, and the power prior is . Thus, each previously treated patient’s contribution to inform the outcome prediction for the new patient i★ under treatment j is modulated by raising their likelihood contribution to the power of S(i★, i) for i = 1, 2, … , nj. Assuming a Dirichlet prior distribution with hyperparameters αj = {αj,k : k = 0, 1, 2, … , K − 1} for model parameter θj, yields the following predictive probability of response-level k under treatment j
| (7) |
where . Note that derivation of equation (7) is identical to equation (3) in Ma et al. (2016). Thus, the predictive probability of (5) can be evaluated using (7) and the density of described in Section 2.1.
Given binary outcomes, equation (5) can be used directly for treatment selection, i.e., recommend the treatment j with highest value of , assuming that outcome 1 offers better clinical utility than outcome 0. To facilitate treatment selection for multinomial ordinal outcomes, one can elicit response utility weights and evaluate its expectation for each candidate therapy (Ma et al., 2016). Using ωk to denote the utility assigned to response-level k, the mean “predictive utility” of treatment j for patient i★ is
| (8) |
Our Bayesian approach to treatment selection assigns patient i★ to the treatment with the largest value of (8), which may be considered as “optimal” among the available therapies given the current information. In general, wk is chosen as 0 = ω0 ≤ ωk ≤ ωK−1 = 100 to reflect the importance of clinical relevance for each level of the ordinal responses. Section 4.2 provides additional discussion pertaining to the specification of utility weights.
2.3. Impact of predictive and prognostic determinants on treatment selection
In our framework, both prognostic and predictive markers contribute to determining the treatment selection; in contrast, alternative approaches based on linear regression models assume that prognostic features have no impact on the treatment selection process (Ma et al., 2015). While intrinsic to the generalized linear model, this premise fails for broader classes of modeling strategies based on predictive probability. Specifically, in our modeling framework the optimal treatment is determined with the utility quantity calculated from (5), which is a weighted probability of with the weight of for k = 0, 1, 2 … , K − 1 To understand how prognostic features may alter the treatment selection, consider the case of two candidate therapies A = (1, 2). Let represent the predictive probability of observing outcome k for treatment j. When there is no prognostic features incorporated, the mean utility can be calculated as ϕ = ω1pj1 + ⋯ + 100pj(K −1) (i★ is dropped for simplicity), whereas the mean utility difference is ϕ1 – ϕ2 = ω1(p11 − p21) + ω2(p12 − p22) + ⋯ + 100(p1(K − 1) – p2(K − 1)) such that treatment 1 is considered to be optimal if this is greater than 0. When both the prognostic and predictive features are incorporated it follows that
| (9) |
where , and . Similarly treatment 1 is considered as optimal if . Since may differ from the sign of (ϕ – ϕ2), a treatment selection decision could be reversed upon leveraging the prognostic determinants.
In fact, the sign of depends on multiple quantities, ωk, pjk and dk. An analytical form of its relationship with the sign of (ϕ1 − ϕ2) is mathematically difficult to generalize, especially when K is large. To provide insight, in this section we consider fixed values of ωk, pjk in the case where K equals 3. Let (p10, p11, p12) equal to (0.2,0.5,0.3), (p20, p21, p22) equal to (0.2,0.7,0.1) and (ω0, ω1, ω2) equal to (0,40,100), respectively. The difference in mean utility when using only predictive features is ϕ1 − ϕ2 = ω1(p11 − p21)+w2(p12 − p22) = 12, hence treatment 1 is considered as optimal. With both prognostic and predicative features, the difference of the expected utility is , where C1 = d0p10 + d1p11 + d2p12 and C2 = d0p20 + d1p21 + d2p22 Noting that , which indicates that treatment 2 is optimal in our example. Note that, the conditions of and indicate that the probability of observing the outcome of tends to 0 given the data. Practically, in this scenario the treatment with higher probability of observing the outcome of would be considered as optimal, which results from selection based on but not ϕ1 − ϕ2.
Section S.1 of the supplementary materials provides more details as well demonstrates the scenarios under which the treatment selection is unaltered by the prognostic factors, such as in the setting for binary outcomes and for specific combinations of pjks and dks in the context of ordinal-valued clinical outcomes. It is worth noting that our framework incorporates those proposed by Ma et al. (2016) as special cases when , where treatment selections are determined by predictive covariates only.
3. Simulation study
We evaluated performance via simulation studies based on gene expression data from a leukemia study (Golub et al., 1999) with outcome generation based on an ordinal continuation-ratio logistic model and outcome prediction based on a leave-one-out cross-validated (LOOCV) strategy, i.e. we do not simulate from our model. We considered the Bayesian predictive strategy integrating predictive with prognostic features based on (8), referred to hereafter as BPP, as well as implementation of the Bayesian approach based on the predictive features only, or BPO, which neglects to incorporate prognostic characteristics into the selection rule. While in principle, similarity measures obtained from any clustering method could be utilized, we implemented the Bayesian predictive approaches using three: hierarchical (HC), k-means (KM) and partitioning around medoids (PAM), with R package ConsensusClusterPlus (Wilkerson and Hayes, 2010).
The Bayesian approaches were compared with selection rules based on linear models with estimation using the L1 penalized continuation ratio model (or Lasso) and ridge regression (Archer and Williams, 2012). Specifically, using LOOCV separate Lasso/ridge models were fitted for each treatment based on the training set to estimate the regression coefficients. We refer to these approaches as Lasso and Ridge, respectively. As a frequentist analog to (8), an optimal treatment was then selected for each simulated future patient to yield the highest treatment utility given the estimated response probability vector and response utilities, ω. Additionally, we evaluated performance for joint fits of the aforementioned penalized regression models, with main effects along with treatment-covariate interactions to characterize predictive effects. These approaches are denoted LassoInt and RidgeInt, respectively. Because the simulation studies compare performance for treatment selection given that each feature has been predefined as either predictive or prognostic, estimation with the penalized regression models included both main effects and interaction terms for all predictive features. Of note, the clustering methods necessitate the specification of ranks. Because an optimal rank is unknown in practice, ranks were selected using a nested LOOCV analyses for each simulated patient based on the training data. A similar step was necessary to effectuate model selection for penalized regression approaches, which we implemented based on Akaike’s information criterion (Friedman et al., 2010).
3.1. Simulation design
Patient-level prognostic and predictive features.
Our simulation study was devised to emulate the dependence structure observed in a well-known dataset of leukemia containing gene expression levels for a total of 5,000 genes across 38 patients (Golub et al., 1999). To obtain a comparable sample size to that used in our case study presented in Section 4 (where n = 158) we expanded the dataset to yield a total of 152 simulated patients each with 92 features. We selected the first 90 features as predictive, and reserved the remaining 2 as prognostic. More details are provided in Section S.2.
Performance evaluation.
Our simulation study considered two treatments and three levels of the ordinal-valued response variable (i.e., K = 3). The optimal treatment for each simulated patient is determined as the inner product of their true ordinal response probability (ORP) and the response-level utility weights, ω. To reflect the cancer context, wherein tumor response is often characterized by progression, partial response, and complete response, ω was fixed at ω = (0, 40, 100). We compare methods based on three performance metrics:
MOT: 0 ≤ MOT ≤ n, where n is the total number of patients evaluated. This metric counts the number of patients misassigned to their optimal treatment. The smaller the better.
%ΔMTUg, (%Δg, in short): −1 ≤ %Δg ≤ 1. This metric represent the relative gain in treatment utility, respect to the other treatment (it is defined only for the case of two alternative treatments). An optimal treatment assignment rule g will achieve %Δg, = 1.
NPC: 0 ≤ NPC ≤ n. This metric counts the number of patients for which the model correctly predicted their simulated outcome. The larger the better.
Both MOT and NPC have a straightforward interpretation. The construction of % MTUΔg, requires few steps:
We denote the mean treatment utility of treatment j for patient i by MTU(j, i) and denote its difference by DMTU(i) such that negative (positive) values indicate that treatment 1 (treatment 2) offers enhanced effectiveness for patient i.
For any simulation scenario we can determine the maximum possible gain in mean treatment utility that could be achieved upon selecting treatments for all n patients as the summed magnitudes of relative differences, .
Given assignments obtained from selection rule g, let jg(i) assume value 1 if the optimal treatment was recommended for patient i and assume value −1 otherwise. The total gain in mean treatment utility of selection method g can be defined as .
To ensure an uniform criteria for methods comparison across simulation scenarios with varying ΔMTUopt, we compared selection rules on the basis of their achieved proportion of the maximum possible gain in total mean treatment utility, or %ΔMTUg = ΔMTUg/ΔMTUopt.
We want to remark that intrinsic to personalized medicine is the assumption that the extent to which a particular patient benefits from a given therapeutic strategy is heterogenous. In the context of our simulation study, this extent of benefit is determined explicitly for each patient by DMTU(i). Tracking the true “utility” of each simulated assignment in relation to the extent of differential benefit offers an improved metric for methods comparison. %ΔMTUg attains value 1 if selection rule g recommends the optimal treatment for all patients and −1 if all patients are recommended to non-optimal treatments. Thus, in our simulation study improved method performance is indicated by smaller values of MOT as well as larger values of %ΔMTUg and NPC.
Simulation scenarios.
The influence on the ORPs contributed by prognostic effects was specified to be moderate in scenario 1 and stronger in scenario 2; whereas identical predictive effects were utilized for both scenarios. This yields larger variability in scenario 2 in the extent of benefit among patients with identical optimal treatments. The average DMTU is smaller, however, for many patients in scenario 2 when compared to scenario 1, as stronger prognostic effects impact the magnitude DMTU, while not necessarily altering the direction of benefit. Additional sensitivity analyses were conducted with respect to the prognostic features. Initially, both scenarios were evaluated using the prognostic covariates with power transformations. We further implement the simulation studies using prognostic covariates (1) of original scale as well as (2) by random sampling from independent normal distributions with mean and variance estimated from the original data. We refer to these scenarios as 1O, 1N, 2O, and 2N, respectively. Simulation study (1) is designed to test the behavior of the proposed approach in settings where the prognostic features are clearly not Normally distributed. Prior specification used independent Dirichlet(1/3, 1/3, 1/3) for πj; and assumed hyperparameters of ν0k = d + 1, k0k = 1, μ0k = 0 and the identity matrix for Λ0k. Further details pertaining to the simulation design are provided in Section S.2 of the supplementary materials.
3.2. Simulation results
Ordinal-valued responses for each patient were randomly generated to produce 100 replicate data sets for methods comparison. Tables 1–3 provide means and standard deviations (SD) of the performance metrics of NPC, MOT, and %ΔMTUg by method; while Figure 2 describes their distributions.
Table 1.
Simulation results for scenarios 1 and 2. The table provides means values and standard deviations (SD) obtained for the summary measures of %Δg = %ΔMTUg, MOT, and NPC. Results are based on 100 duplicated data sets.
| Method | Scenario 1 | Scenario 2 | ||||
|---|---|---|---|---|---|---|
| MOT(SD) | %Δg (SD) | NPC(SD) | MOT(SD) | %Δg (SD) | NPC(SD) | |
| Naive | ||||||
| 45.0 | 0.284 | 72.7 (8.5) | 45.0 | 0.278 | 62.7 (10.8) | |
| HC-BPP | 6.0 (3.1) | 0.932 (0.04) | 79.5 (8.1) | 9.0 (8.5) | 0.867 (0.13) | 84.5 (8.3) |
| KM-BPP | 10.0 (7.5) | 0.876 (0.11) | 76.6 (8.1) | 20.0 (10.7) | 0.723 (0.17) | 80.1 (9.4) |
| PAM-BPP | 15.0 (3.3) | 0.802 (0.05) | 77.8 (8.3) | 23.0 (9.9) | 0.669 (0.15) | 78.3 (9.8) |
| HC-BPO | 6.0 (2.7) | 0.934 (0.03) | 79.4 (8.1) | 9.0 (6.6) | 0.863 (0.12) | 74.2 (8.8) |
| KM-BPO | 10.0 (7.5) | 0.871 (0.11) | 76.6 (8.2) | 20.0 (10.2) | 0.692 (0.17) | 74.1 (7.4) |
| PAM-BPO | 15.0 (3.1) | 0.800 (0.05) | 77.9 (8.2) | 21.0 (9.1) | 0.719 (0.14) | 73.7 (7.6) |
| LASSO | 44.0 (9.3) | 0.462 (0.12) | 69.6 (8.3) | 47.0 (9.1) | 0.466 (0.12) | 98.8 (10.0) |
| Ridge | 15.0 (7.1) | 0.801 (0.11) | 78.0 (7.1) | 28.0 (6.0) | 0.578 (0.10) | 76.1 (6.5) |
| LassoINT | 36.0 (9.4) | 0.556 (0.12) | 67.1 (8.0) | 44.0 (10.9) | 0.440 (0.16) | 104.5 (9.3) |
| RidgeINT | 17.0 (7.2) | 0.790 (0.09) | 70.3 (5.1) | 36.0 (9.4) | 0.434 (0.17) | 76.9 (6.4) |
Table 3.
Simulation results for scenario 2 with prognostic covariates considered on their original scales (2O) as well as generated from independent normal distributions (2N). The table provides means values and standard deviations (SD) obtained for the summary measures of %Δg = %ΔMTUg, MOT, and NPC. Results are based on 100 duplicated data sets.
| Method | Scenario 2O | Scenario 2N | ||||
|---|---|---|---|---|---|---|
| MOT(SD) | %Δg (SD) | NPC(SD) | MOT(SD) | %Δg (SD) | NPC(SD) | |
| HC-BPP | 10.0 (6.2) | 0.840 (0.10) | 84.4 (6.8) | 9.0 (6.3) | 0.860 (0.12) | 73.6 (6.2) |
| KM-BPP | 20.0 (9.8) | 0.707 (0.16) | 83.2 (7.0) | 21.0 (9.8) | 0.678 (0.16) | 72.5 (7.0) |
| PAM-BPP | 22.0 (8.7) | 0.689 (0.13) | 79.9 (8.1) | 20.0 (8.8) | 0.725 (0.14) | 70.2 (7.3) |
| LASSO | 49.0 (8.7) | 0.412 (0.14) | 85.1 (8.6) | 53.0 (6.4) | 0.261 (0.09) | 62.3 (7.0) |
| Ridge | 27.0 (6.0) | 0.591 (0.10) | 73.8 (6.4) | 25.0 (5.9) | 0.620 (0.10) | 68.0 (7.3) |
| LassoINT | 46.0 (10.0) | 0.408 (0.14) | 89.4 (8.8) | 49.0 (7.9) | 0.322 (0.11) | 61.8 (6.9) |
| RidgeINT | 38.0 (8.8) | 0.431 (0.15) | 75.4 (5.9) | 31.0 (8.4) | 0.517 (0.14) | 65.1 (5.5) |
Figure 2.
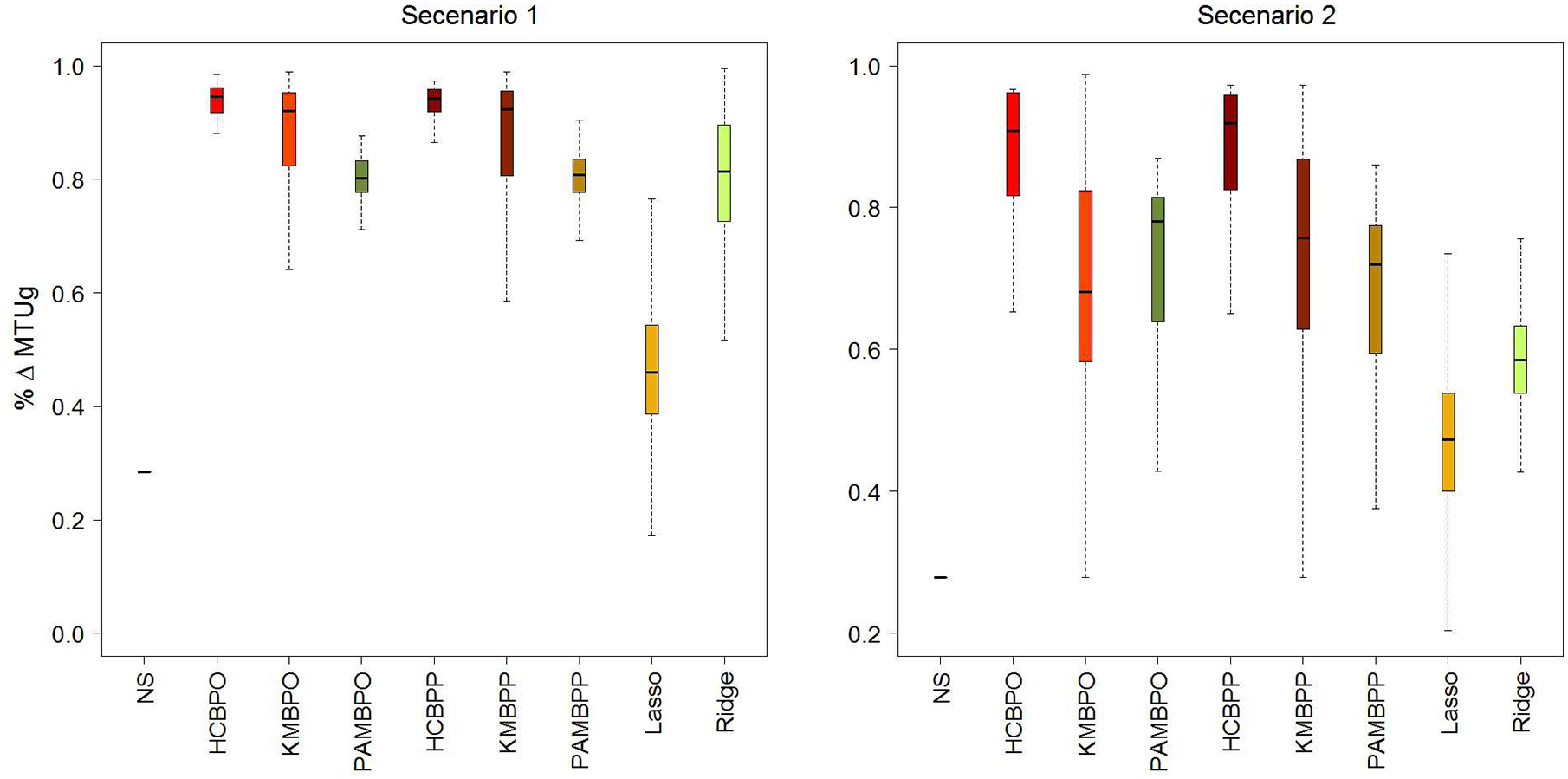


Simulation results for scenarios 1 and 2. The boxplot depicts the distributions of mean values obtained for the summary measures of %ΔMTUg, MOT, and NPC.
In tables 1–4,“HC” stands for hierarchical clustering, “KM” for k-means, “PAM” for partitioning around medoids, “BPP” for the proposed Bayesian prediction approach that integrate predictive with prognostic features, and “BPO” for the proposed Bayesian prediction approach that based only on predictive features. The “Naive” approach (“NS”, in Figure 2) assumes that all patients are statistically exchangeable.
Table 4.
Results obtained from treatment selection using patients observed in the glioma case study.
| Method | NPC | ESM |
|---|---|---|
| HC-BPP | 64 | 0.132 |
| KM-BPP | 69 | 0.090 |
| PAM-BPP | 72 | 0.085 |
| HC-BPO | 58 | 0.114 |
| KM-BPO | 61 | 0.090 |
| PAM-BPO | 65 | 0.102 |
| LASSO | 73 | 0.071 |
| Ridge | 77 | 0.060 |
| LassoINT | 73 | 0.061 |
| RidgeINT | 76 | 0.068 |
On the basis of these results, we have several observations. The proposed Bayesian predictive methods with clustering algorithms of HC and KM were found to outperform penalized regression based approaches for treatment selection in both simulation scenarios 1 and 2 (Table 1). Bayesian selection with PAM was comparable to ridge regression in scenario 1, but outperformed both ridge and LASSO in the presence of stronger prognostic effects in scenario 2. Treatment selection was least effective when based on the linear predictor facilitated by LASSO. Moreover, in the simulation scenarios Bayesian approaches integrating predictive with prognostic features provided similar results for treatment selection based on (MOT and %Δg) to those obtained from selection based on predictive features alone.
By way of contrast, performance for outcome prediction, as measured by NPC, varied between two simulation scenarios (Table 1). In scenario 1, mean NPC was comparable, with lower values for LASSO, LassoInt and RidgeINT methods. In scenario 2, however, each integrative Bayesian model (BPP) outperformed the corresponding predictive only (BPO) for NPC correctly predicting the outcomes of 78.3 to 84.5 patients (out of 152 total patients) on average for BPP versus 73.7 to 74.2 for BPO. Moreover, LASSO outperformed the others correctly predicted outcomes 98.8 (SD=10.0) patients out of 152 on average, while yielding a low proportion of mean assignment utility (only 47%). This suggests that the contributions of predictive features to the linear predictor utilized for treatment assignment were attenuated in presence of strong prognostic effects when LASSO was used for treatment selection. Figure 2 depicts the entire distributions of these summary measures by selection method. For the sake of completeness, we also evaluated selection rules using a naive approach which assumed that all patients were statistical exchangeable and thereby failing to account for inter-patient prognostic and predictive diversities. Not surprisingly, on the basis of all performance measures, this approach yielded the worst performance for treatment selection yielding assignments that achieved only 28% of the total mean utility on average.
To elucidate sensitivity to distributional heterogeneity, the simulation studies were repeated using un-transformed prognostic covariates on their original scales (scenario 1O and 2O), as well as generated from independent normal distributions (scenarios 1N and 2N). Results were impacted only slightly for scenarios 1O and 1N when compared to scenario 1. With the presence of strong prognostic effects in scenario 2, however, the results for penalized regression were impacted by the covariate distributions. Treatment selection based on ridge regression performed similarly in scenarios 2 and 2O. Modest improvement was observed with Gaussian distribution in scenario 2N for selection rules based on ridge. Performance for LASSO was comparable in scenario 2O, but diminished in scenario 2N with considerable reductions in %ΔMTUg and NPC from 0.466 and 98.8 to 0.261 and 62.3, respectively. These findings suggest that selection rules based on the proposed Bayesian predictive methods are less sensitive to distributional assumptions pertaining to the prognostic features.
Overall, the proposed integrative Bayesian predictive methods yielded selection rules that outperformed those obtained from penalized regression with BPP combined with hierarchical clustering attaining the highest values of %ΔMTUg ranging from (0.860 – 0.935) indicating that the resultant assignment rules achieved 86% to 94% of the total possible assignment mean utilities, on average. Among the integrative Bayesian predictive approaches, BPP with partitioning around medoids yielded the lowest mean values of %ΔMTUg ranging from 67% to 80% on average. For comparison, the best performance for LASSO derived selection rules achieved only 57% of total mean utility, on average. Moreover, performance for LASSO was reduced to as low as 26% in scenario 2N. Ridge regression performed better, yielding selection rules that attained as high as 81% of total mean utility in scenario 1O and as low as 43% on average in scenario 2O. Lastly, selection rules derived from LassoINT were generally comparable or better than those from LASSO, while results from RidgeINT were worse than or comparable to those from ridge regression.
Insofar we considered two prognostic and ninety predictive variables for our empirical study. To investigate the scale of our approach with relatively large number of prognostic variables, we extended simulation scenario 2 to scenario 2.1 with the 2 features and 8 noise random variables, and scenario 2.2 with the 2 features and 6 random noise variables. These noise variables were generated from normal distribution and were not used to generate the outcome variables. Our approach performed well and results from these scenarios are comparable to those from scenario 2, except that the NPC are relatively small, Supplementary Table S1. In our experience, this is common for high dimensional data with some noise variables, and hence data are often pre-processed to improve model accuracy in predicting the outcomes (Yu and Liu, 2003). More details in this regard are provided in Section 4.3.
4. A case study of lower grade glioma
4.1. TCGA data
Methods for treatment selection were also compared through application to a publicly available data of lower grade glioma (LGG) from the TCGA data portal using both clinical and level 3 protein expression data from https://tcga-data.nci.nih.gov/tcga/tcgaHome2.jsp. Baseline and follow-up information was collected for 411 patients. Exclusions included 18 patients with missing values of treatments and 68 patients who failed to contribute protein expression information. Among the remaining 325 patients, 196 received molecularly targeted therapies, 211 received adjuvant radiotherapy, and 79 received “conventional” cytotoxic therapies that involved neither targeted nor radiotherapy regimens. Our case study considered treatment selection of standard (neither targeted nor radiotherapy, n=79) versus advanced treatments (targeted or radiotherapy, n=246). Using the RECIST criteria (http://www.recist.com/), tumor response was categorized using the four standard ordinal-levels of progressive disease (PD), stable disease (SD), partial response (PR) and complete response (CR). Among those receiving standard therapy, only 9 patients achieved PR. Therefore, we combined PR and SD to formulate a new category of responders, which we abbreviate as PS, yielding three ordinal-levels of the outcome: CR, PS, and PD.
4.2. Matching and utility weight specification
To account for potential select bias, we matched patients on the basis of the baseline covariates of tumor grade, gender, age and initial year of pathological diagnosis (IYPD). Specifically, 79 pairs of patients were produced using the R package of MatchIt (default settings) (Ho et al., 2011); the resultant standardized mean differences were 0.000, −0.050, 0.051, and 0.162 for tumor grade, gender, age and IYPD, respectively. Reasonably satisfactory matches were obtained, as all final standardized mean differences were below than the suggested cut-off value of 0.25 (Imai et al., 2008).
Adopting utility based criterion for treatment selection with ordinal outcomes, weights were specified for each level of the ordinal responses to account for their relative clinical importance using the arbitrary domain of 0 to 100. Without loss of generality, weights 0 and 100 (ω0 = 0 and ωK−1 = 100) can be assigned to least and most favorable response levels, respectively. Following the recommendations of Ma et al. (2016), specification of a weight for the intermediate response-level, PS, considered the relative benefit in terms of long-term overall survival duration in data analysis using Cox regression. A 120-day landmark analysis was used since most responses were observed after two, eight-week treatment cycles (Anderson et al., 2008). More specifically, for response level PS we estimated the relative risk (with CR as the reference) of 10-year overall survival as 2.46 when adjusted for age, gender, tumor grade and IYPD. Thus, the utility weight for PS was defined as (1/2.46)100 ≃ 41. Note that the TCGA data set includes the short-term clinical outcome of tumor responses as well the overall survival data, and the elicited utility weight for PS reflects its relative importance in terms of long term benefits. The same procedure may be followed using historical data that are obtained from similar populations. Alternatively, we may provide physicians the weights of 0 and 100 for the least and most favorable response levels, respectively, and ask them to specify the weights for the intermediate response outcomes. More details of weight elicitation can be found in Ma et al. (2016).
4.3. Prognostic and predictive features
To identify potential prognostic/predictive features among the 173 protein expressions were measured in the LGG data, we fitted univariate logistic regression models with covariates of a protein, treatment, and their interaction (R package of MASS (Venables and Ripley, 2002)). A protein was considered as a potential predictive (prognostic) feature given a p-value, obtained from Wald’s test, was < 0.1 for the interaction (main) effect. With this criteria, we selected 23 proteins as potential predictive features and 5 as potential prognostic features. Two prognostic covariates, ACVRL1-R-C and HSP70-R-C, were utilized in the application given that they yielded the highest accuracy rate (78/158) in discriminant analysis using the 79 pairs of matched data with binary outcomes of PD/SD/PR as 0 and CR as 1. It is worthy noting that, to remove noise variables and enhance model performance, data pre-processing is commonly applied in high dimensional settings. We here describe a straightforward approach to pre-select some features for data analysis, and more advanced approaches can be found in (Yu and Liu, 2003) and its references.
4.4. Summary measures
While summary measure NPC can be calculated same way as in simulation studies, given that the true optimal treatments are unknown in the case study precluding MOT and %ΔMTUg as measures of performance. Another summary, described in detail by (Ma et al., 2016) and (Kang et al., 2014), was adopted, however. For a binary outcome variable Y = {0, 1}, we can define the treatment contrast as Δ(X) = P(Y = 1|A = 1, X) − P (Y = 1|A = 0, X). The relative increase in the population response rate attributable to a proposed treatment allocation method when compared with randomly allocation can be ascertained through
Several authors have demonstrated estimation of this measure from data (Kang et al., 2014; Song and Pepe, 2004), which we refer to hereafter as ESM or empirical summary measure. For example, P(Y = 1|A), as the overall response rate under the randomization strategy, can be estimated as the sample proportion of responders. Similarly, P(Y = 1|A = 1, Δ(X) > 0) can be estimated with the subgroup of n1 patients who would be assigned treatment 1. The weight, P(Δ(X) > 0), can be estimated as n1/n. While, treatment assignments were obtained for each patient in consideration of the ordinal tumor response-levels (CR, PS, and PD) of patients in the training set, in order to use ESM for methods comparison we evaluated the resultant assignments with the summary measure based on binary outcomes of constructed as responders (CR) and non-responders (PS and PD).
4.5. Results
Table 4 reports NPC and ESM summary measures computed from assignments obtained from LOOCV. The Bayesian assignment strategies outperformed the penalized regression approaches of ridge and LASSO in terms of the ESM. For example, HC-BPP attained an ESM of 0.132 representing a 37% increase in the response rate when compared to randomized assignment with a response rate of 58/158 ≈ 0.361; while ESM for ridge regression was 0.06 reflecting an increase of only 17%. The penalized regression methods tended to perform better for outcome prediction, however, while the Bayesian strategy using only predictive features yielded lower NPC on average. These results are quite consistent with those obtained from our simulation study of scenario 2, where prognostic features have strong coefficient effect.
5. Discussion
The concept of personalizing clinical care, while a topic of recent emphasis, isn’t entirely new. Evaluations of individual-level characteristics have long been used to inform treatment selection (Byar and Corle, 1977). Recent advances in informatics technologies, however, have provided access to enormous databases of clinical, imaging and genomic features yielding inputs that facilitate interrogation of therapeutic options at multiple levels and in the presence of diverse types of molecular and clinic information. Thus, the current environment offers the potential to alter one-fits-all clinical paradigms to effectuate more precise, personalized therapeutic strategies.
In this article, we described a Bayesian power prior predictive modeling framework for integrating prognostic and predictive features for treatment selection, which is more suitable in the development of personalized medicine using training data. The method assumes that patients are nonexchangeable within each subgroup determined by normal-mixture models. Given the focus on treatment selection rather than inference on model parameters, conjugate priors were assumed for model parameters which resulted in a closed form expressions for computing the predictive probability measures and thereby avoided sampling techniques. We evaluated the proposed method via empirical studies and compared them with penalized regression approaches. In all scenarios, the proposed methods outperformed the penalized regression approaches with respect to treatment selection as well as yielded robust results when the distribution of the prognostic feature were not correctly specified. Compared to the methods by (Ma et al., 2016), the proposed methods demonstrated improved prognostic values in predicting clinical outcomes. The utility of the proposed methods was further illustrated with an actual study of lower grade glioma using protein expression data, yet the method may be easily applied to various types of genomic or imaging features.
From a modeling perspective, the proposed methodology can be extended in several directions. For example we assumed that π and (μ, Σ) are independent a priori. This common assumption (Lavine and West, 1992) ensure interpretability and closed form inference. More flexible modeling approaches may be suitable and better fit the data at hand; in our analyses the proposed model worked well and we did not observed any lack of fit or any other poor performances indicator. A more flexible modeling strategy may be achieved following, for example, some Bayesian nonparametrics techniques, such as the probit-stick breaking (Rodriguez and Dunson, 2011) or the product partition model with covariates (Mueller et al., 2011); in this case, the flexibility-computational cost trade-off needs to be evaluated.
However, it is important to note that we did not attempt to develop prognostic/predictive biomarkers but rather use established molecular features for personalized treatment selection. Moreover, while we found that the proposed method performed well in a variety of scenarios, the quality and reliability of the inputted features will always determine the effectiveness of any treatment selection approach. Our empirical evaluations suggested that the selection method was robust to the distributional forms of the prognostic features. In our previous work (Ma et al., 2016), we investigated the sensitivity to the inclusion of additional sets of predictive features: we considered the performance for treatment selection rules among 38 patients formulated with the top 100 and 200 varied features (the maximum minus the minimum level of observed gene expression) and observed comparable results.
For the case study, we implemented univariate analyses to select a reasonable number of prognostic/predictive features. Specifically, we considered features with statistically significant main effects as prognostic markers and those with significant interaction effects as predictive. This strategy for identifying prognostic and predictive markers is commonly employed in practice (Witten and Tibshirani, 2009; Werft et al., 2012; Jenkins et al., 2011; Zhao and Zeng, 2013). Alternatively we may investigate signatures that have been reported in the literature from different studies. For example, (Ma et al., 2017) investigated several literature-reported genomic signatures for patients with lung squamous cell carcinoma, and they found that a 13-gene signature developed by (Kaufman et al., 2014) performed well for treatment selection. Thus, the approach is encouraging given that results obtained from these signatures are generally robust due to the external cross validation process.
While the potential benefits of such biomarker-guided therapy are seemingly substantial, discovery of prognostic and predictive markers from signal in the presence of many noise covariates remains a challenge (Food and Drug Administration, 2013). Retrospective reviews in oncology are difficult because treatment assignments often depend on prognostic characteristics of the treated patients. The result of this is highly biased treatment comparisons. Our modeling strategy is devised to acknowledge that prognostic and predictive determinants conjointly inform expectations of future response and thus impact treatment selection. Several aspects of the feature inputs, such as process or inter-observer reproducibility, need to be considered carefully before using the proposed methods for personalized selection with large scale genomic, imaging and clinical data. A checklist criteria has been developed by the US National Cancer Institute which addresses issues of specimens, assays, clinical trial design (McShane et al., 2013). In our case study, we matched patients with tumor grade, gender, age and initial year of pathological diagnosis. Although this matching seeks to reduce the potential impact of selection bias, the proposed method is perhaps most clinically useful when implemented with training data obtained from randomized clinical study. In addition, our methods rely on a heuristic measure of similarity obtained from clustering methods that often consider only one type of data source (Wilkerson and Hayes, 2010). An integrative clustering analysis of multiple data sources (e.g., protein, gene expression) may provide a more comprehensive understanding of nature of disease heterogeneity (such as (Lock and Dunson, 2013)). Given the potential for enhancing the accuracy and robustness of results for treatment selection, which we plan to pursue methodology for treatment selection with integrative clustering as a future endeavor.
Moreover, a patient’s experience upon receiving a particular therapeutic strategy is often a complex synthesis of measures that describe both the extent of induced-harm as well as clinical benefit. Thus, patient response is often difficult to characterize in many cancer settings, especially for multi-modal treatment strategies (see e.g. Hobbs et al., 2016). As a consequence, most methods for treatment selection implicitly assume that all patients should be treated with one of the therapeutic regimes under study (Ma et al., 2015; Geng et al., 2015). Yet, its important to note that future advances in statistical methods that facilitate formal prediction of harm-versus-benefit trade-offs may further elucidate sub-populations for which the absence of further clinical intervention provides the best option. This goal can be achieved only if prognostic features are integrated into the treatment selection process.
Supplementary Material
Table 2.
Simulation results for scenario 1 with prognostic covariates considered on their original scales (1O) as well as generated from independent normal distributions (1N). The table provides means values and standard deviations (SD) obtained for the summary measures of %Δg = %ΔMTUg, MOT, and NPC. Results are based on 100 duplicated data sets.
| Method | Scenario 1O | Scenario 1N | ||||
|---|---|---|---|---|---|---|
| MOT(SD) | %Δg (SD) | NPC(SD) | MOT(SD) | %Δg (SD) | NPC(SD) | |
| HC-BPP | 7.0 (2.5) | 0.929 (0.03) | 76.4 (8.6) | 6.0 (2.6) | 0.935 (0.03) | 78.5 (8.0) |
| KM-BPP | 11.0 (6.9) | 0.870 (0.10) | 74.4 (9.5) | 10.0 (7.0) | 0.866 (0.10) | 74.6 (8.5) |
| PAM-BPP | 15.0 (4.2) | 0.796 (0.06) | 75.2 (8.3) | 15.0 (3.5) | 0.794 (0.05) | 76.3 (8.3) |
| LASSO | 44.0 (8.6) | 0.450 (0.11) | 67.6 (8.3) | 44.0 (8.7) | 0.433 (0.10) | 65.1 (7.9) |
| Ridge | 15.0 (6.9) | 0.806 (0.10) | 77.9 (7.2) | 15.0 (6.8) | 0.797 (0.11) | 76.7 (7.3) |
| LassoINT | 35.0 (10.0) | 0.570 (0.13) | 65.2 (8.2) | 38.0 (11.0) | 0.526 (0.14) | 61.5 (7.0) |
| RidgeINT | 18.0 (7.2) | 0.782 (0.09) | 69.4 (5.3) | 17.0 (6.8) | 0.798 (0.10) | 68.1 (6.0) |
Acknowledgements
The second and third authors were partially supported by the NIH/NCI Cancer Center Support Grant (P30 CA016672), and the third author was also partially supported by the NIH/NCI P50 CA070907-16A1 grant. The authors thank LeeAnn Chastain for editing assistance.
Footnotes
Conflict of Interest The authors have declared no conflict of interest.
References
- Aerts HJ, Velazquez ER, Leijenaar RT, Parmar C, Grossmann P, Cavalho S, Bussink J, Monshouwer R, Haibe-Kains B, Rietveld D, et al. (2014). Decoding tumour phenotype by noninvasive imaging using a quantitative radiomics approach. Nature communications 5, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amiri-Kordestani L and Fojo T (2012). Why do phase iii clinical trials in oncology fail so often? Journal of the National Cancer Institute 104, 568–569. [DOI] [PubMed] [Google Scholar]
- Anderson JR, Cain KC, and Gelber RD (2008). Analysis of survival by tumor response and other comparisons of time-to-event by outcome variables. Journal of Clinical Oncology 26, 3913–3915. [DOI] [PubMed] [Google Scholar]
- Archer K and Williams A (2012). L1 penalized continuation ratio models for ordinal response prediction using high-dimensional datasets. Statistics in Medicine 31, 1464–1474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ballman KV (2015). Biomarker: predictive or prognostic? Journal of Clinical Oncology pages JCO–2015. [DOI] [PubMed] [Google Scholar]
- Byar DP and Corle DK (1977). Selecting optimal treatment in clinical trials using covariate information. Journal of chronic diseases 30, 445–459. [DOI] [PubMed] [Google Scholar]
- Food and Drug Administration (2013). Paving the Way for Personalized Medicine: FDA’s Role in a New Era of Medical Product Development. http://www.fda.gov/downloads/ScienceResearch/SpecialTopics/PersonalizedMedicine.
- Friedman J, Hastie T, and Tibshirani R (2010). Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software 33, 1–22. [PMC free article] [PubMed] [Google Scholar]
- Geng Y, Zhang HH, and Lu W (2015). On optimal treatment regimes selection for mean survival time. Statistics in medicine 34, 1169–1184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, Mesirov JP, Coller H, Loh ML, Downing JR, Caligiuri MA, et al. (1999). Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science 286, 531–537. [DOI] [PubMed] [Google Scholar]
- Ho DE, Imai K, King G, and Stuart EA (2011). MatchIt: Nonparametric preprocessing for parametric causal inference. Journal of Statistical Software 42, 1–28. [Google Scholar]
- Hobbs BP, Thall PF, and Lin SH (2016). Bayesian group sequential clinical trial design using total toxicity burden and progression-free survival. Journal of the Royal Statistical Society: Series C (Applied Statistics) 65, 273–297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ibrahim JG, Chen M-H, and Sinha D (2003). On optimality properties of the power prior. Journal of the American Statistical Association 98, 204–213. [Google Scholar]
- Imai K, King G, and Stuart EA (2008). Misunderstandings between experimentalists and observation-alists about causal inference. Journal of the Royal Statistical Society: Series A (Statistics in Society) 171, 481–502. [Google Scholar]
- Jenkins M, Flynn A, Smart T, Harbron C, Sabin T, Ratnayake J, Delmar P, Herath A, Jarvis P, and Matcham J (2011). A statistician’s perspective on biomarkers in drug development. Pharmaceutical statistics 10, 494–507. [DOI] [PubMed] [Google Scholar]
- Kang C, Janes H, and Huang Y (2014). Combining biomarkers to optimize patient treatment recommendations. Biometrics 70, 695–707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufman JM, Amann JM, Park K, Arasada RR, Li H, Shyr Y, and Carbone DP (2014). Lkb1 loss induces characteristic patterns of gene expression in human tumors associated with nrf2 activation and attenuation of pi3k-akt. Journal of Thoracic Oncology 9, 794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelloff GJ and Sigman CC (2012). Cancer biorkers: selecting the right drug for the right patient. Nature Reviews Drug Discovery 11, 201–214. [DOI] [PubMed] [Google Scholar]
- Kuner R (2013). Lung cancer gene signatures and clinical perspectives. Microarrays 2, 318–339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavine M and West M (1992). A bayesian method for classification and discrimination. Canadian Journal of Statistics 20, 451–461. [Google Scholar]
- Lock EF and Dunson DB (2013). Bayesian consensus clustering. Bioinformatics pages 1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma J, Hobbs BP, and Stingo FC (2015). Statistical methods for establishing personalized treatment rules in oncology. BioMed Research International 2015, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma J, Hobbs BP, and Stingo FC (2017). Integrating genomic signatures for treatment selection with bayesian predictive failure time models. Statistical Methods in Medical Research page In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma J, Stingo FC, and Hobbs BP (2016). Bayesian predictive modeling for genomic based personalized treatment selection. Biometrics 72, 575–583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McShane LM, Cavenagh MM, Lively TG, Eberhard DA, Bigbee WL, Williams PM, Mesirov JP, Polley M-YC, Kim KY, Tricoli JV, et al. (2013). Criteria for the use of omics-based predictors in clinical trials. Nature 502, 317–320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monti S, Tamayo P, Mesirov J, and Golub T (2003). Consensus clustering: a resampling-based method for class discovery and visualization of gene expression microarray data. Machine Learning 52, 91–118. [Google Scholar]
- Mueller P, Quintana F, and Rosner GL (2011). A product partition model with regression on covariates. Journal of Computational and Graphical Statistics 20, 260–278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez A and Dunson D (2011). Nonparametric bayesian models through probit stick-breaking processes. Bayesian Analysis 6, 145–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon R (2010). Clinical trial designs for evaluating the medical utility of prognostic and predictive biomarkers in oncology. Personalized medicine 7, 33–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song X and Pepe MS (2004). Evaluating markers for selecting a patient’s treatment. Biometrics 60,874–883. [DOI] [PubMed] [Google Scholar]
- Spear B, Heath-Chiozzi M, and Huff J (2001). Clinical application of pharmacogenetics. Trends in molecular medicine 7, 201. [DOI] [PubMed] [Google Scholar]
- Sutter S and Lamotta L (2011). Cancer drugs have worst phase iii track record. Internal Medicine News Digital Network. [Google Scholar]
- Ternes N, Rotolo F, Heinze G, and Michiels S (2017). Identification of biomarker-by-treatment interactions in randomized clinical trials with survival outcomes and high-dimensional spaces. Biometrical Journal 59, 685–701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venables WN and Ripley BD (2002). Modern Applied Statistics with S. Springer, New York, fourth edition ISBN 0-387-95457-0. [Google Scholar]
- Werft W, Benner A, and Kopp-Schneider A (2012). On the identification of predictive biomarkers: Detecting treatment-by-gene interaction in high-dimensional data. Computational Statistics & Data Analysis 56, 1275–1286. [Google Scholar]
- Wilkerson MD and Hayes DN (2010). Consensusclusterplus: a class discovery tool with confidence assessments and item tracking. Bioinformatics 26, 1572–1573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witten DM and Tibshirani R (2009). Survival analysis with high-dimensional covariates. Statistical Methods in Medical Research pages 1–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yip SS and Aerts HJ (2016). Applications and limitations of radiomics. Physics in Medicine & Biology 61, R150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu L and Liu H (2003). Feature selection for high-dimensional data: A fast correlation-based filter solution. In Proceedings of the 20th international conference on machine learning (ICML-03), pages 856–863. [Google Scholar]
- Zhao Y and Zeng D (2013). Recent development on statistical methods for personalized medicine discovery. Frontiers of medicine 7, 102–110. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


