Modeling heterogeneous tumor growth dynamics and cell-cell interactions at single-cell and cell-population resolution

Abstract

Cancer is a complex, dynamic disease that despite recent advances remains mostly incurable. Inter- and intratumoral heterogeneity are generally considered major drivers of therapy resistance, metastasis, and treatment failure. Recent advances in high-throughput experimentation have produced a wealth of data on tumor heterogeneity and researchers are increasingly turning to mathematical modeling to aid in the interpretation of these complex datasets. In this mini-review, we discuss three important classes of approaches for modeling cellular dynamics within heterogeneous tumors: agent-based models, population dynamics, and multiscale models. An important new focus, for which we provide an example, is the role of intratumoral cell-cell interactions.

Graphical Abstract

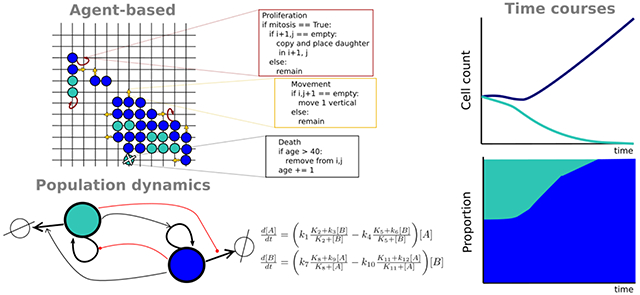
Introduction

Tumors are comprised of a heterogeneous mix of cell subpopulations with common traits and heritable phenotypes [1,2] (e.g., morphological, proliferative, tumorigenic, transcriptional) that compete for resources and interact with each other and with non-cancer cells in complex ways [3,4]. Tumor heterogeneity has been implicated as a source of therapeutic resistance and treatment failure and is seen both across tumors (among patients and between primary and metastatic sites within patients) and within individual tumors [1,2]. Factors contributing to intertumoral heterogeneity include genomic and epigenomic alterations, intrinsic differences between individuals, cell type of origin, and microenvironmental differences across anatomical (primary and secondary) sites. Intratumoral heterogeneity (Fig. 1) is driven by a complex mix of genomic instability, cellular plasticity, regional differences in the microenvironment (e.g., oxygen availability), cell-cell interactions, and intrinsic fluctuations in cell fate and gene expression.

Fig 1. Three sources of intratumoral heterogeneity.

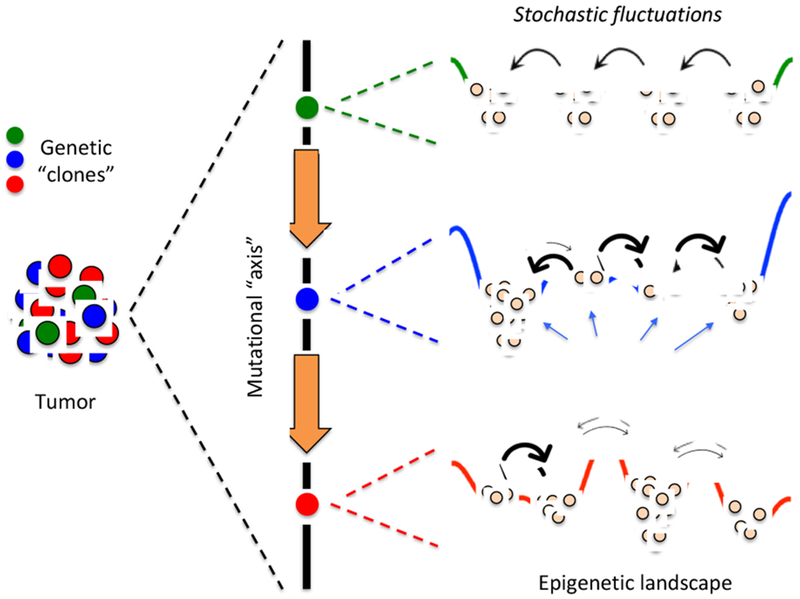
Genetic clones are cells with common origin but genetically diversified by mutations that either pre-exist or are acquired during the course of therapy [1,2]. Each genetic clone can be envisioned as existing along a “mutational axis” and having an associated “epigenetic landscape,” i.e., a quasi-potential energy surface where local minima, or “basins of attraction,” correspond to cellular subtypes [5]. From a molecular perspective, the epigenetic landscape is the consequence of the complex biochemical interaction networks that underlie cell fate decisions [6,7]. Thus, gene expression noise [8], and other sources of intrinsic (e.g., fluctuations in the production and contents of secreted factors) and extrinsic stochasticity can drive transitions between subtypes (thick arrows represent fast transitions, and vice versa). Altogether, at any point in time the subtype composition of a tumor will depend on the genetic clones present within the tumor, the topographies (depths of basins and heights of barriers) of the associated epigenetic landscapes, and the magnitudes of intracellular fluctuations within individual cells.

The complex nature of tumor heterogeneity can be understood within the framework of “epigenetic landscapes,” first proposed by Waddington [5] as a conceptual tool for understanding cellular differentiation during development. More recently, it has been applied to tumors, where “stem-like” cells have the capacity to differentiate into multiple phenotypes and seed tumor growth. Viewing tumor heterogeneity through the lens of epigenetic landscapes may serve as a means for better understanding tumor dynamics and therapy response [2]. Borrowing ideas from physical chemistry, an epigenetic landscape is a quasi-potential energy surface where local minima, or “basins of attraction,” correspond to cellular phenotypes [6,7]. The genetic state of a cell sets the topography of the landscape and genetic mutations can modify it, for example by changing the depths of the basins (Fig. 1). Cells can transition amongst these phenotypes at rates dependent on the heights of the barriers separating basins (Fig. 1). Fluctuations in intrinsic (e.g., gene expression [8]) and/or extrinsic (e.g., secreted factors [9], intracellular protein concentrations [10], oxygen production [11]) processes may serve as sources of noise that drive these transitions. This combination of epigenetic landscape heterogeneity and intrinsic/extrinsic stochasticity, together with genomic diversity (either acquired during normal tumor progression or over the course of therapy) results in a highly heterogeneous tumor (Fig. 1). This view of tumor heterogeneity is consistent with both known genetic clonality of tumors [12] as well as a growing body of literature on non-genetic (epigenetic) inheritance in cancer cells. The latter includes the cancer stem cell (CSC) hypothesis, which posits that phenotypically distinct tumorigenic subpopulations sit atop a hierarchy of non-tumorigenic progeny [13], as well as reports of stem-like cancer cells that are not organized in a classical hierarchy but are metastable and can reversibly shift phenotypes [14,15•]. Notably, stem cells are known to function within niches and interactions between stem-like and niche-like cells may govern tumor dynamics in an analogous manner to their tissue of origin. These cell-cell interactions may influence switching between epigenetic basins as well in response to tumor therapy.

In light of this confluence of genetic, epigenetic, and stochastic factors that underlie tumor heterogeneity, it is no surprise that durable anticancer therapies remain elusive. To tackle this complexity, a systems biology approach is required and has been steadily growing in popularity [16]. By combining high-throughput experimentation, ‘Big Data’ analysis, and mathematical modeling with in vitro and in vivo validation experiments, cancer systems biologists aim to disentangle the complex web of interactions, feedbacks, and dysregulated control mechanisms that has stymied clinical progress [1,2]. Mathematical models are essential to this endeavor because they can predict behaviors outside the range of the experimental conditions on which they are based and can explore the effects of drug dosing, scheduling, and changes in the microenvironment on tumor response [17]. Moreover, mathematical models can explicitly account for both inter- and intratumoral heterogeneity by varying model structure and parameter values. Intertumoral heterogeneity, for example, can be captured by creating variants of a model with different cellular and/or molecular species or by varying the values of rate parameters to account for genetic or microenvironmental differences across individuals or disease sites. Intratumoral heterogeneity can be accounted for by including multiple cell subtypes, interactions through physical contact and/or secreted factors, and by including spatial inhomogeneity of biological factors, such as oxygen, over the computational domain. Below, we provide a brief review of recent approaches for modeling tumor heterogeneity, followed by a short example from our own work.

Mathematical formalisms for modeling tumor growth

Agent-based models

At the resolution of single cells, agent-based models (ABMs) aim to capture complex and emergent behaviors of cell populations through simple and intuitive rules [18]. ABMs are particularly useful when detailed mechanisms of cell behavior are not known but there is a qualitative understanding of the conditions under which certain cellular behaviors are observed. The simplest type of ABM is the cellular automaton (CA) [19•], in which cells are organized in a regular grid and can take on one of a finite number of discrete states. Rules are defined that change the cell state based on its current value and those of its neighbors and updates can be performed synchronously or asynchronously (i.e., stochastically). Modern ABMs extend the basic CA by permitting cells to have multiple properties (e.g., age, phenotypic state, mutation), with discrete or continuous state values, and allowing rules to be either deterministic (occurring if a certain condition is met) or probabilistic (occurring with some probability if the condition is met) [20•]. An example of a rule governing cell death based on the age of a cell and its phenotypic state is (ccl.northwestern.edu/netlogo/models/Tumor)

if (not stem?) and (not metastatic?) and (age > 20)

   [die]

if (not stem?) and metastatic? and (age > 4)

   [die]

ABMs can also be on-lattice (i.e., grid-based) or off-lattice. On-lattice models are often used to model cell movement within a tumor microenvironment [21–26]. Off-lattice models can be beneficial for modeling cells as clusters or functional units, such as colon crypts [19•,27•–29]. ABMs can also be non-spatial, where the cell state is informed by its environment and the states of other cells but not by location or distance from other cells [30–32]. ABMs can be implemented in custom computer code or using one of numerous publicly available software packages (e.g., [33–36]).

Examples of ABMs applied in cancer include Enderling & Hahnfeldt [21], who constructed an on-lattice ABM of CSCs and non-CSCs, including crowding effects, and predicted that low proliferative capacity and a high rate of spontaneous cell death—which might be expected to keep tumor growth and metastasis in check—actually leads to a less densely seeded tumor where CSCs have the physical space to divide, produce progeny, and eventually escape and seed metastasis. Stichel et al. [27] developed an off-lattice ABM that includes displacement of cells in response to external forces from neighboring cells (e.g., repulsive forces at close cell-cell distances) and a vector-valued velocity term based on these forces. The model was able to reproduce diverse in vitro cell speed dynamics and migratory behaviors, such as straight cell fronts and the formation of cellular bridges.

Population dynamics models

In contrast to ABMs, population dynamics models do not track individual cells over time but rather the size of the cell population [37•]. The classic model of population growth is

$$\text{Cell}\stackrel{k}{\to }2\text{Cell},$$

which, if one assumes continuous and deterministic dynamics, gives the exponential growth equation

$$N(t)=N(0)e^{\mathit{kt}},$$ (1)

where N(t) is the cell count at time t and the growth rate constant k can be positive or negative. Since its inception, numerous extensions to the exponential growth model have been proposed, including adding an upper limit on the population size (“carrying capacity”) to account for nutrient consumption (e.g., logistic and Monod kinetics) [38] and reducing growth rates at small population sizes to account for the positive effects of cell-cell interactions on growth (e.g., the Allee effect) [39]. Models explicitly accounting for progression through the cell cycle, the apoptotic program, and entry into quiescence/senescence have also been developed [40,41]. Spatial heterogeneity can be accounted for by including cell diffusion and migration over either a continuous or discrete domain [42] and the inherent randomness of cell fate decisions can be modeled using stochastic methods, such as the chemical Master Equation or the Gillespie algorithm [43]. A variety of tools are available for constructing and simulating population dynamics models, including environments such as Matlab and Python and numerous general-purpose software packages (e.g., [44–50]).

In cancer, heterogeneous tumor growth and drug-response dynamics can be modeled by including multiple cell subpopulations that compete and interact [51]: clonal competition can be modeled by varying growth rates across subpopulations [52–54•]; genetic mutations can be included by allowing for spontaneous creation of new subpopulations with pre-specified growth rates [55•]; epigenetic states can be accounted for by allowing cells to reversibly transition between subpopulations [14,22,31,52,54•,56,57]; and cell-cell communication can be incorporated by including density-dependent growth rates [58–61] or by modeling (explicitly or implicitly) the secretion of factors that modify the growth dynamics of other cells [62–66]. As an example, Gupta et al. [14] constructed a population dynamics model describing phenotypic transitions among luminal, basal, and stem-like subpopulations in two breast cancer cell lines and recapitulated the experimental observation that isolated subpopulations recover the cell-state proportions of the parental cell line over time. Based on this, they predicted that after cessation of CSC-targeted therapies, surviving non-CSCs would transition back into CSCs and restart tumor growth, thereby reversing any therapeutic gains. In a subsequent study, Zhou et al. [52] extended this model to include subpopulation-specific growth rates and derived analytical expressions for the temporal dynamics of cell-state proportions as well as the conditions necessary for distinct subpopulations to coexist. Below, we present a similar model of subpopulation dynamics in tumors with the added feature of subtype interactions mediated by secreted factors (see “Example: modeling subtype interactions in small cell lung cancer”).

Multiscale models

Biological processes span multiple scales, from genes to proteins to cells to tissues to organisms [67•]. However, most mathematical models of biological processes operate at only a single scale and either ignore processes at other scales or try to incorporate their effects in some approximate way. Multiscale models attempt to address this shortcoming by explicitly modeling processes at different spatial and/or temporal scales and connecting these models through some type of information exchange interface [67•–71]. In multiscale tumor models, the “cell level” model can either be an ABM or a population dynamics model, which can be coupled to, e.g., a reaction-diffusion model governing background concentrations of bioactive species (e.g., oxygen, nutrients, extracellular matrix) [72–78] or a kinetic or Boolean model describing the intracellular biochemical networks driving cell fate (e.g., progression through the cell cycle, apoptosis) [19•,79]. Typically, simulations are performed by running a short simulation (possibly a single step) of a model at one scale, passing information generated from that simulation to another model at a different scale, running a short simulation of that model with updated initial and/or boundary conditions, and repeating. While in the majority of cases multiscale models are constructed by composing single-scale models in well-established modeling tools and linking them together with specialty purpose code [80], there is a rapidly growing list of general-purpose software packages for multiscale modeling [81–86]. These represent a community-wide effort to develop easy-to-use platforms that facilitate calibration, validation, reproducibility, and exchange of multiscale models using methods firmly rooted in formal mathematical theory [80].

As an example, Yan et al. [87•] used a multiscale hybrid discrete-continuum model to investigate vascular-tumor signaling in glioblastoma (GBM). The continuum (spatial population dynamics) model includes various GBM cells (stem, progenitor, terminally differentiated, dead), host tissue, and human primary endothelial cells, as well as nutrients and signaling molecules. Angiogenesis is modeled via a discrete, off-lattice ABM: blood vessels sprout, grow, and branch at rates dependent on tumor density and background concentrations of vascular endothelial growth factor (VEGF) and other signaling molecules. The vasculature also produces a factor that maintains the pool of GBM stem cells by increasing their proliferation rate and self-renewal capability. Central to the model is a positive feedback loop whereby nutrient-poor tumor cells produce VEGF, inducing vasculature growth, which increases GBM stem cell growth and leads to even more VEGF production. Using the model, the authors confirmed the experimental observation that anti-angiogenesis treatments have a negative effect of inducing the growth of invasive “fingers” that eventually develop into multifocal tumors. Blocking vasculature-secreted factors, however, disrupts growth and reduces tumor size without increasing invasiveness, as also seen experimentally [88,89].

Example: modeling subtype interactions in small cell lung cancer

SCLC is an aggressive and highly metastatic neuroendocrine (NE) carcinoma [90,91•] for which the standard of care (etoposide + cis-platinum and radiation), until very recently [92], had not changed in over 30 years. SCLC is characterized by loss-of-function mutations in TP53 and RBI and is often described as a homogeneous-looking cancer, with “small blue round cells” and minimal presence of non-tumor cells. Indeed, genomic analyses indicate that, on average, primary SCLC tumors are composed of ~84% tumor cells [93]. However, over time it has become clear that SCLC tumors are actually highly heterogeneous, with various cell subtypes coexisting, some of which may provide the trophic support that non-cancer cells often provide in other cancer types [94•,95].

Due to the challenges of acquiring human SCLC samples, heterogeneity in SCLC has been primarily studied in animal models [96]. A study using a genetically engineered mouse model of SCLC, with induced loss of p53, Rb, and p130 tumor suppressor genes in lung epithelial cells, demonstrated that in that model the most abundant tumor cells are NE self-renewing “tumor propagating cells” (TPCs), characterized by CD24^high, CD44^low, and EpCAM^high surface expression [15•]. A non-NE population with high expression of Hes1 and lacking NE markers but active in the Notch signaling pathway was also identified [94•]. This subtype was shown to have increased resistance to chemotherapy in comparison to NE cells (TPCs), suggesting a possible role in chemoresistance. A third population, also non-NE, with high levels of CD44 and characterized by expression of mesenchymal markers, such as vimentin, has also been reported [97]. Furthermore, in vitro co-culture experiments of NE and Hes1⁺ non-NE cells show that NE cell growth is enhanced in the presence of non-NE cells [94•,97]. In vivo experiments have been reported showing that mice injected with an admixture of NE and CD44⁺ non-NE cells develop metastases but mice injected with only a single subpopulation do not [97]. Taken together, these data suggest that TPCs, Hes1⁺, and CD44⁺ cell subtypes form an SCLC tumor ecosystem that supports growth, metastasis, and treatment evasion.

Improving our understanding of the dynamics of SCLC tumors and the interactions between cell subtypes through mathematical modeling could lead to improved treatment options in the future [98]. Therefore, we present here a population dynamics model of the SCLC tumor ecosystem as an illustrative example of the model building and analysis process. We begin by enumerating a list of biological rules (Table 1) that encompass, to the best of our ability, all that is presently known about SCLC tumor heterogeneity and subtype interactions. Notably, these rules, which form the basis of our model, derive from the experimental results described above [15•,94•,97] and are primarily qualitative in nature. This is an important point as most biological data, especially in the early stages of a research project, are not quantitative [99]. As we shall show, it is nevertheless possible to construct a predictive mathematical model based on these data that can provide valuable insight and guide future, more quantitative experiments. These follow-up experiments can, in turn, provide the necessary data to perform more advanced modeling tasks, such as parameter estimation and identifiability analysis [100], which can significantly improve the scope and quality of the model predictions. This iterative process of model construction, experimentation, and refinement lies at the heart of the systems biology approach [16,17].

Table 1.

Biological rules used to construct the SCLC population dynamics model.

Index	Description and Reference(s)
1	Tumor-propagating cells (TPCs) divide approximately once per day in culture [15•].
2	TPCs have a 20-30% apoptosis rate in culture and a 0-5% apoptosis rate in vivo [15•].
3	TPCs can differentiate into other cell types, e.g., Hes1+/Notch-active cells and CD44+ cells (and possibly other subtypes as well) [94•].
4	Hes1+ cells have a lower division rate than TPCs [94•].
5	Hes1+ cells support the growth of the TPC population by both enhancing cell division and reducing apoptosis [94•].
6	There is evidence that TPCs inhibit proliferation of Hes1+ populations in vitro (30-50% reduction as assessed by BrdU incorporation) [94•].
7	Role of CD44+ cells is unclear but they may be pro-metastatic and promote invasion by secretion of fibroblast growth factor, which activates ERK1/2 signaling in TPCs [93,97].
8	In vivo tumors are comprised of approximately 50% TPCs, 25% Hes1+ cells, 5% CD44+ cells, and 20% unknown cell types [15•,94•].
9	Interactions among cell types may involve secretion of soluble factors [94•,97].

With these biological rules in hand (Table 1), we next synthesize this knowledge into a simple diagram (Fig. 2A) that illustrates the basic biological processes we aim to model, namely, division, death, differentiation, and inhibition/enhancement of division and death via cell-cell interactions. We then translate this diagram into mathematical form by writing down eight kinetic equations representing division and death of each subtype and differentiation of TPCs into Hes1⁺ and CD44⁺ subtypes (Table 2). For five of these processes (Hes1⁺ death, CD44⁺ division/death, TPC differentiation), we currently have no information regarding any potential mediating factors (Table 1). Therefore, we make the simplest possible assumption, that the rates of these processes are directly proportional to the population sizes of the subtypes (known as the “law of mass action”). For the other three processes (Hes1⁺ division, TPC division/death), experimental data suggest that the rates are dependent on cell-cell interactions (Table 1). We assume these interactions to be mediated by secreted factors according to the following simple reaction motif,

$$\begin{array}{ccc}\hfill A\stackrel{k_x}{\to }A+x\hfill & \hfill B+x\stackrel{k_f}{\to }{B}^{\ast }+x\hfill & \hfill B\stackrel{k_{\text{fate}}}{\to }2B\text{or}\varnothing \hfill \\ \hfill x\stackrel{k_{-x}}{\to }\varnothing \hfill & \hfill B^{\ast }\stackrel{k_r}{\to }B\hfill & \hfill B^{\ast }\stackrel{k_r}{\to }B\text{or}\varnothing \hfill \end{array}$$

where A and B are cell types, A secretes a factor x that interacts with B and converts it into an “active” form B* that has an increased or decreased rate of division or death, and ∅ represents cell death. Assuming that the concentration of x is stable, i.e., its rates of production and degradation are equal (known as the “quasi steady state assumption”), and that the rates of interconversion between B and B* are equal (known as the “partial equilibrium assumption”), we can derive an analytical expression for the rate of the cell fate (division or death) of cell type B as a function of the population size of cell type A,

$$v_{\text{fate}}=\left(\frac{k_{\text{fate}}{K}_D{K}_x^{\mathrm{eq}}+k_{\text{fate}}^{\ast }[A]}{K_D{K}_x^{\mathrm{eq}}+[A]}\right)\cdot {[B]}_T,$$ (2)

where K_D ≡ k_r/k_f, $K_x^{\mathrm{eq}}\equiv k_{-x}∕k_x$, and [B]_T ≡ [B] + [B*] is the total amount of B. Note that Eq. (2) models an increase in the rate of division or death by the diffusible factor x if $k_{\text{fate}}^{\ast }>k_{\text{fate}}$, reduction in the rate if $k_{\text{fate}}^{\ast }<k_{\text{fate}}$, and reduces to v_fate = k_fate[B]_T (mass-action kinetics) if $k_{\text{fate}}^{\ast }=k_{\text{fate}}$ (i.e., if x has no effect). Reactions 1–3 in Table 2 have rate expressions of this form, with the parameters k_fate, $k_{\text{fate}}^{\ast }$, and $K_D{K}_x^{\mathrm{eq}}$ written as numbered parameters k_i or K_i, and [B]_T = [TPC] or [Hes1⁺].

Fig. 2. Population dynamics model of subtype interactions in SCLC.

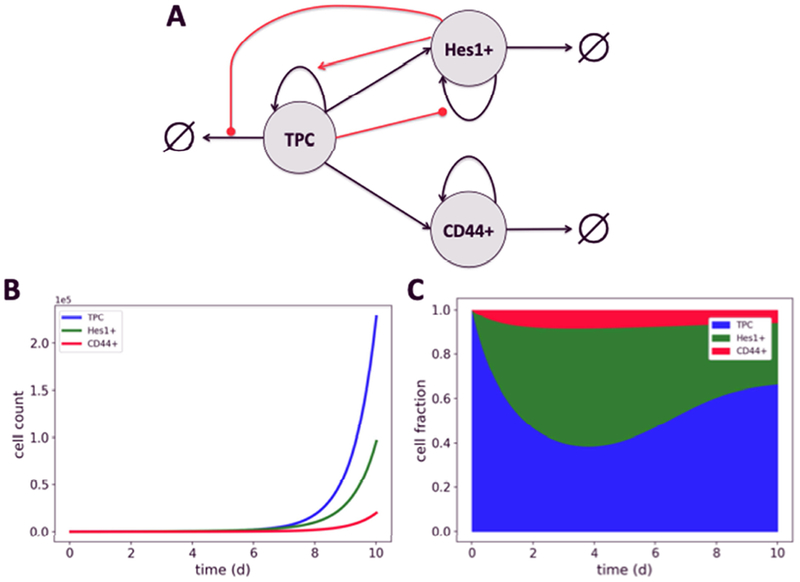
(A) Schematic representation. Black arrows represent cell fates (division, death, differentiation); red arrows/circles represent enhancement/inhibition of cell fate by secreted factors; ∅ represents cell death. (B,C) Simulated time courses of cell counts and fractions. ODE simulations were performed in PySB [49] with initial conditions [TPC]₀ = 100, [Hes1+]₀ = 0, [CD44+]₀ = 0 and the following parameter values (see Table 2): k₁ = 1; K₂ = 1000; k₃ = 2; k₄ = 0.2; K₅ =1000; k₆ = 0.1; k₇ = 0.5; K₈ = 1000; k₉ = 0.25; k₁₀ = 0.2; k₁₁ = 0.3; k₁₂ = 0.2; k₁₃ = 0.5; k₁₄ = 0.1. These values were chosen to produce subtype proportions similar to those seen in vivo (Table 2, Rule 8; excluding the 20% unknown cell types).

Table 2. Kinetic formulation of the SCLC population dynamics model.

[X] is the population of cell type X; ∅ represents cell death.

Index	Reaction	Rate expression	Description
1	TPC → 2 TPC	$\left(\frac{k_1{K}_2+k_3[{\mathrm{Hes}1}^{+}]}{K_2+[{\mathrm{Hes}1}^{+}]}\right)\cdot [\mathrm{TPC}]$	TPC cell division (k3 > k1) (Hes1+ promotes growth)
2	TPC → ∅	$\left(\frac{k_4{K}_5+k_6[{\mathrm{Hes}1}^{+}]}{K_5+[{\mathrm{Hes}1}^{+}]}\right)\cdot [\mathrm{TPC}]$	TPC cell death (k6 < k4) (Hes1+ inhibits apoptosis)
3	Hes1+ → 2 Hes1+	$\left(\frac{k_7{K}_8+k_9[\mathrm{TPC}]}{K_8+[\mathrm{TPC}]}\right)\cdot [{\mathrm{Hes}1}^{+}]$	Hes1+ cell division (k9 < k7) (TPC inhibits growth)
4	Hes1+ → ∅	k10[Hes1+]	Hes1+ cell death
5	CD44+ → 2 CD44+	k11[CD44+]	CD44+ cell division
6	CD44+ → ∅	k12[CD44+]	CD44+ cell death
7	TPC → Hes1+	k13[TPC]	TPC differentiation into Hes1+
8	TPC → CD44+	k14[TPC]	TPC differentiation into CD44+

It is important to emphasize that the model in Table 2 is certainly not the only possible mathematical interpretation of the diagram in Fig. 2A. It is simply our first attempt at codifying our knowledge of SCLC subtype interactions and dynamics in mathematical form. Over time, we expect to include additional interactions, cell types, and processes as experimental observations are made that cannot be captured by this preliminary model. A common approach when the details of a biological process are not well known is to construct numerous “candidate” models and then systematically eliminate unlikely candidates using various “model selection” metrics, such as Akaike or Bayesian information criteria [101]. Thus, rather than a single model, we expect to construct a compendium of SCLC tumor models that will grow and change over time. Numerous software tools and environments exist to facilitate such efforts (e.g., [49,102–105]). One such tool is PySB [49], a “rule-based” modeling platform [106,107] written in Python that includes an easy-to-use modeling language and a variety of deterministic and stochastic simulators [46,50,108,109] and analysis tools [110]. We constructed the model in Table 2 in PySB (available at github.com/lh64/CurrOpinSysBiol_2019) and used it to automatically generate the following set of coupled ordinary differential equations,

$$\frac{d[\mathrm{TPC}]}{\mathit{dt}}=\left(\frac{k_1{K}_2+k_3[{\mathrm{Hes}1}^{+}]}{K_2+[{\mathrm{Hes}1}^{+}]}-\frac{k_4{K}_5+k_6[{\mathrm{Hes}1}^{+}]}{K_5+[{\mathrm{Hes}1}^{+}]}-k_{13}-k_{14}\right)[\mathrm{TPC}],$$ (3)

$$\frac{d[{\mathrm{Hes}1}^{+}]}{\mathit{dt}}=\left(\frac{k_7{K}_8+k_9[\mathrm{TPC}]}{K_8+[\mathrm{TPC}]}-k_{10}\right)[{\mathrm{Hes}1}^{+}]+k_{13}[\mathrm{TPC}],$$ (4)

$$\frac{d[{\mathrm{CD}44}^{+}]}{\mathit{dt}}=(k_{11}-k_{12})[{\mathrm{CD}44}^{+}]+k_{14}[\mathrm{TPC}].$$ (5)

These equations were then numerically integrated using algorithms available in the Python package SciPy [108].

Since our experimental data is qualitative (Table 1), for our preliminary simulation analysis (Fig. 2B,C) we decided to manually choose parameter values using the experimental observations as a guide (see caption to Fig. 2 for values). For example, the division rate for TPCs unaffected by secreted factors (k₁ in Table 2) was set to 1/day, consistent with experimental observations (Table 1, Rule 1). The division rate for unaffected Hes1⁺ cells (k₇ in Table 2) was then set to 0.5/day based on the observation that they divide at a lower rate than TPCs (Table 1, Rule 4). Initial values for all other rate parameters were chosen based on similar reasoning. All parameter values were then manually varied until values were found that produced steady-state subtype proportions similar to those seen in in vivo mouse tumors (Table 1, Rule 8; Fig. 2C). Of note is that the rate of differentiation from TPCs to Hes1⁺ cells (k₁₃ in Table 2) had to be set to a value five times larger than that for TPCs to CD44⁺ cells (k₁₄ in Table 2) because modulating the division and death rates of the subtypes alone could not achieve the desired subtype proportions.

This result is a simple illustration of the non-trivial relationships that often exist between parameter values and model outputs in systems biology models [111]. An obvious next step in the model analysis process would be to quantify these relationships through a “sensitivity analysis” [112] that would identify parameters (or sets of parameters) that act as “control points” for modulating model behavior. These could then be tested experimentally to either validate or refute the current version of the model and suggest possible refinements. As mentioned above, these validation experiments may be quantitative. In such cases, one could then move beyond sensitivity analysis and perform a formal “parameter estimation” [113], which would allow for quantitative model predictions that could be further tested experimentally. Modern parameter estimation algorithms utilize Monte Carlo (or similar) techniques to generate “ensembles” of parameter sets that provide similar fits to experimental data [110,111,114]. Model predictions are then generated by sampling over the ensemble, producing a predictive “envelope” (e.g., [54]) that hopefully is not excessively broad (if it is, further experiments could be designed to reduce the breadth of the envelope [115]). We do not go into this level of sophistication here as our goal is simply to demonstrate how a preliminary model can be built and analyzed but we will employ these techniques in the future as the model grows in complexity and additional experimental data is collected.

Finally, even though our model is based on qualitative observations and static measurements of the compositions of in vivo mouse tumors, the population dynamics formalism that we use allows us to explore and speculate on the temporal dynamics of tumor growth. In Fig. 2B,C, we show time courses for a 10 day in silico experiment starting with a pure population of 100 TPCs. Interestingly, we see that while the total cell count grows continuously throughout the simulation (because the current model lacks a carrying capacity; Fig. 2B), the cell-state proportions stabilize around Day 10 (Fig. 2C). This is consistent with prior theoretical work [14,52], which was experimentally validated [14], showing that phenotypic state transitions can lead to stable steady-state proportions in heterogeneous cell populations. However, our simulation also shows pronounced non-linear dynamics prior to Day 10, with the Hes1⁺ proportion peaking around Day 4 (Fig. 2C). This is a direct result of modeling cell-cell interactions (which were not considered in [14,52]) between the TPC and Hes1⁺ subtypes (Fig. 2A and Table 2). Thus, these non-linear dynamics represent a prediction of the model that could be tested experimentally: if observed it would provide support for the underlying assumptions of our model and verify the importance of cell-cell interactions in SCLC tumor dynamics.

Conclusion

Significant progress has been made in recent years in cancer therapy, including the development of new chemotherapies, targeted agents, and immunotherapies. However, cancer morbidity remains stubbornly high, in large part due to inter- and intratumoral heterogeneity. To overcome this challenge, an integrative systems approach involving experimentation, bioinformatics, and mathematical modeling is beginning to take root and produce results [16]. ABMs, population dynamics, and multiscale models are central to this effort as they provide a window onto the underlying mechanisms of therapy resistance [17]. Going forward, a major goal in the field will be to develop patient-specific tumor models, parameterized by clinical data and spanning genetic, cellular, and tissue scales, which can act as in silico platforms for testing and designing personalized anticancer therapies. The promise of this approach is a significant improvement in clinical outcomes and quality of life for millions worldwide suffering from this deadly disease.

Highlights.

• Tumors are highly heterogenous, composed of multiple interacting cell types

• Cell-cell interactions can be modeled at the single cell and cell population levels

• Modeling approaches include agent-based, population dynamics, and multiscale models

• Small cell lung cancer is a highly heterogeneous and aggressive tumor

• A small cell lung cancer cell-cell interaction model predicts non-linear dynamics