Impact of gradient imperfections on bone water quantification with UTE MRI.

Abstract

Purpose

The impact of gradient imperfections on UTE images, and UTE image-derived bone water quantification, was investigated at 3 T field strength.

Methods

The effects of simple gradient time delays and eddy currents on UTE images, and of gradient error corrections were studied with simulation and phantom experiments. The k-space trajectory was mapped with a 2D sequence with phase encoding on both spatial axes by measuring the phase of the signal in small time increments during ramp-up of the read gradient. In vivo 3D UTE images were reconstructed with and without gradient error compensation to determine the bias in bone water quantification. Finally, imaging was performed on two equally configured Siemens TIM Trio systems to investigate the impact of such gradient imperfections on inter-scanner measurement bias.

Results

Compared to values derived from UTE images with full gradient error compensation, total bone water was found to deviate substantially with no (up to 17%), or partial (delay-only) compensation (up to10.8%). Bound water, obtained with inversion recovery-prepared UTE, was somewhat less susceptible to gradient errors (up to 2.2% for both correction strategies). Inter-scanner comparison indicated a statistically significant bias between measurements from the two MR systems for both total and bound water, which either vanished or was substantially reduced following gradient error correction.

Conclusion

Gradient imperfections impose spatially dependent artifacts on UTE images, which compromise not only bone water quantification accuracy but also inter-scanner measurement agreement if left uncompensated.

1 |. Introduction

A number of studies in recent years have provided evidence that quantitative imaging of bone water with ultra- short echo time (UTE) or zero echo time (ZTE) radial MRI is feasible (1–3). Using similar technology, mineral phosphorus has been imaged by ³¹P MRI in bone specimens (2,4,5) and also in vivo in humans (6,7). Collagen, the main component of the bone matrix, is not directly visible by in vivo MRI due to its extremely short T₂* (tens of microseconds), however, the protons on water molecules bound to the matrix (bound water, or BW) are detectable (8–11) and scale linearly with matrix density. Pore space in cortical bone can also be indirectly evaluated by capturing the signal from water residing within the pores (pore water, PW) (8–11). Further, since phosphorus is a primary constituent of bone mineral (nonstoichiometric calcium hydroxyapatite), quantitative ³¹P MRI can assess mineral density (6,7,12). More recently, attempts have been made to quantify both bone water and bone mineral with a single integrated protocol in vivo in human subjects (13).

One potential problem with short-TE MRI techniques is caused by the radial acquisition scheme, which is more susceptible to gradient imperfections than their Cartesian counterpart (14–20). Hardware related time delays and eddy current-induced waveform distortions (21) result in k-space trajectories deviating from their prescribed paths. In Cartesian scanning, k-space trajectory deviations are consistent between phase steps and will only lead to an undetectable linear phase shifts in magnitude images. In radial sequences the k-space trajectory error can vary with view angle, and this inconsistent k-space encoding may result in artifacts in magnitude images. Furthermore, since each view passes through the central k-space region and determines overall image contrast, signal intensity measurements could be adversely affected yielding inaccurate values. Importantly, the gradient imperfections are scanner hardware-dependent, but once quantified, the gradient trajectory errors can be accounted for in the reconstruction code.

A number of techniques have been proposed to address this problem in UTE. Some are dedicated to time delay correction only (22), while others attempt to compensate for the full distortion of the gradient waveform (14,20,23–25). For the latter, one of the ways to correct for gradient waveform distortions is by directly measuring the true gradient trajectory. Trajectory measurements could be extracted from either the phase of the acquired image or by determining the location of the zeroth moment following the application of additional gradients (14,20,23,26,27). Another way to determine gradient distortions relies on the measurement of the frequency response of the gradient system, treating the gradient hardware as a system fully described by a gradient system transfer function (24,25,28). However, to the best of the authors’ knowledge, except for the work by Latta et al. (29) comparing relative proton density in brain white matter from images with and without trajectory correction, there has been no systematic investigation of how UTE image and image-based quantification are affected by gradient imperfections, and particularly, how such errors impact inter-scanner agreement.

This work is designed to evaluate the impact of gradient imperfections and consequential k-space trajectory mis-mapping on UTE image-based bone water quantification. Toward this end, simulation and phantom experiments were first performed to demonstrate image artifacts in the presence of different extents of k-space trajectory shifts as well as the spatial dependence of the resulting artifacts. Bone water densities were then quantified and the results compared between human subject UTE images obtained without correction, with time delay-only correction, and with full trajectory correction. Finally, bone water densities obtained from two different MRI scanners were compared to evaluate the effect of image corrections on inter-scanner agreement.

2 |. Methods

2.1 |. Theory

Ignoring relaxation, the signal collected in an MRI experiment can be represented as

$$s\left(\mathit{k}\right)=\int \rho (\mathit{r})e^{-i2\pi \mathit{k}\cdot \mathit{r}}d\mathit{r}$$ [1]

with ρ(r) being the position-dependent spin density, and $\mathit{k}(t)=\frac{\gamma }{2\pi }\int \mathit{G}(t)dt$, the time-dependent spatial frequency vector. The argument of the exponential in Equation 1 denotes the instantaneous phase φ(t) = 2πk(t)r of the k space signal at position r. After appropriate re-gridding (as required, for instance, in radial encoding) the image typically is reconstructed as the inverse Fourier transform of the k-space (Equation 2):

$$\rho \left(\mathit{r}\right)=\int s(\mathit{k})e^{i2\pi \mathit{k}\cdot \mathit{r}}d\mathit{k}$$ [2]

However, a realistic reconstruction requires accurate knowledge of the k-space trajectory, which is susceptible to inaccuracies in the gradient waveform G(t). Due to hardware imperfections such as time delays and effects of eddy currents, the actual gradient G′(t) ≠ G(t), i.e. the encoding gradient deviates from the prescribed waveform, and as a result, image quality is compromised by the mis-mapping of k-space data points.

In the following sections we illustrate the problem with actual data and describe a method for gradient waveform correction in UTE imaging, with a particular focus on quantification of bone water.

2.2 |. Gradient delay, k-space trajectory measurement and UTE image correction

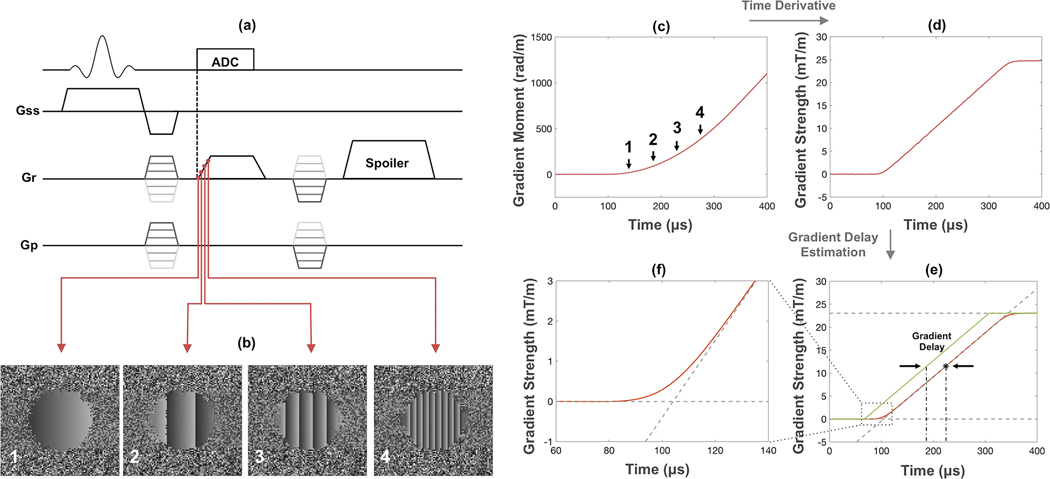
The k-space trajectory was measured using a phase mapping technique described earlier for spiral imaging (26,27), recently modified for radial UTE acquisitions (23). The technique was originally proposed to map x- and y-trajectories for 2D UTE, and was extended in this work for measurement along all three principal axes (Figure 1a). First, a 2D slice (5-mm thick) parallel to the targeted gradient direction was excited and phase-encoded along both directions, followed by a ramp-readout that is to be used for the UTE sequence. The two phase-encodings generate a series of 2D images, each corresponding to a single time-point along the readout gradient direction. The readout gradient causes the phase to be shifted during gradient ramp-up (Figure 1b). The slope of the phase φ(r,t) = 2π k(t)r, at any given location r in these phase maps corresponds to the instantaneous k-space location, which is proportional to the zeroth gradient moment (Figure 1c). The true gradient waveform is simply the time derivative of the gradient moment (Figure 1d). This measured k-space trajectory embodies the effects of both hardware-related time delay and eddy current-induced waveform distortions. To determine the time delay, the mid-point of the linear portion of the ramp on the measured gradient is compared to the mid-point of ramp on a nominally trapezoidal gradient (Figure 1e). The measured trajectory or gradient delay can thus be used for either full trajectory correction or delay-only correction during image reconstruction. For full correction, trajectories along three principal axes are measured as described above, while the ones along oblique directions are represented as linear combinations of them. This is because the gradient system can be regarded as linear time invariant (30). The image is subsequently generated by re-gridding reconstruction. For delay-only correction, trajectories of principal axes are calculated from the assumed trapezoidal gradient waveform, but with measured delays incorporated. The oblique trajectories are obtained in the same way as in full trajectory correction. For the most accurate measurements of k-space trajectories and gradient delays, scan parameters such as FOV, dwell time and gradient ramp times should be matched to those of the actual UTE imaging sequence.

Figure 1.

(a) Trajectory mapping sequence based on the technique proposed in [23]. (b) Phase maps acquired during ramp-up of the readout gradient. (c) Zeroth moment of the readout gradient (k-space trajectory) obtained by linear fitting of the phase during gradient ramping. (d) Time derivative of the gradient moment yields the true gradient waveform. (e) Gradient delay determined by comparing the mid-point of the measured gradient ramp with that of the ideal gradient (green line). (f) Actual gradient waveform deviates from nominal trapezoid due to eddy currents.

2.3 |. Simulation experiments

Two sets of simulation experiments were performed. The first was to demonstrate the overall effect of various k-space shifts on the UTE image. Trajectories along the principal axes were calculated based on ideal trapezoidal gradient waveforms. Delays of −6 μs to +6 μs (hardware delays typically observed on clinical scanners (16,22)) were then introduced in 2-μs increments. To clearly demonstrate the effects of varying timing delays on the resulting artifacts, the delays were applied along only a single direction (x-axis). A more realistic scenario was simulated in the second experiment, where full trajectories measured from the scanner were used. Assumed scan parameters were: FOV = (250 mm)², dwell time = 4μs, ramp time = 240μs; 158 points along each FID were needed to reconstruct an image of matrix size 256×256. Two types of phantoms were considered: (1) a single large cylindrical object (110 mm diameter, resembling the standard Siemens cylinder phantom) placed at the FOV center, and (2) five smaller cylindrical objects (18 mm diameter) placed in a row along the x-axis, to investigate the spatial dependence of image artifacts. Density compensation and gridding throughout this work were performed using the fast iterative algorithm provided by Zwart, et al (31) (website: http://ismrm.org/mri_unbound), as the method was shown to be highly accurate and computationally efficient and is applicable for arbitrary k-space trajectories. The gridded data was subsequently Fourier transformed into image space, and normalized by a de-apodizing filter computed by similarly processing a delta function in k-space.

2.4 |. Phantom imaging experiments

Phantom experiments were performed on a Siemens 3 T Trio system (Siemens Medical Solutions, Erlangen, Germany) using a three-dimensional (3D) UTE sequence. The standard Siemens cylindrical phantom (3.75 g NiSO₄·6H₂O + 5 g NaCl per 1000 g H₂O) was imaged with a birdcage calf coil (Rapid Biomedical, Rimpar, Germany) custom-made for ³¹P and ¹H bone imaging of human subjects. In addition, five test-tubes of doped water (18 mm diameter, 20% H₂O/80% D₂O, doped with 27 mmol/L of MnCl₂ to achieve a H₂O concentration of 11 mol/L, proton T₁ = 4.5 ms, T₂* = 327 μs) that served as ¹H density calibration samples in an earlier in vivo bone water quantification study (13) were imaged with a wider vendor supplied 12-channel Siemens head coil to evaluate the spatial dependence of gradient-waveform related artifacts. Scan parameters were identical as the in vivo UTE protocol in the previous study (13) and are as follows: FOV = (250 mm)³, TR = 10ms, flip angle = 16°, TE = 50μs, and 50,000 FIDs were collected with a dwell time of 4μs. Following data acquisition, images were reconstructed to matrix size of 256×256×256, yielding an isotropic spatial resolution of (0.98 mm)³, in three ways: 1) no correction, 2) correction for gradient delay only (delay correction), and 3) full trajectory correction, which includes the effects of delays and higher order errors due to eddy currents. In addition, the same series of delays used in the simulations were intentionally introduced into the full trajectory corrected k-space data to demonstrate the influence of varying delays on actual experimental data. All resultant images were compared with simulations. Finally, since the T₂* value of the calibration samples is too short to be detected with Cartesian sequences, five additional test-tubes doped with ~1mM gadolinium and arranged similarly to the calibration samples were scanned with a conventional gradient echo sequence for comparison.

2.5 |. In vivo imaging experiments

To investigate the impact of gradient imperfections on bone water quantification, data acquired from a previous study in ten healthy subjects ranging in age from 29 to 65 years (13) were corrected with the newly measured gradient delay and measured full k-space trajectories. The left mid-tibia of each subject was co-imaged with one ¹H calibration sample as mentioned above. Total bone water and bound water were imaged with ¹H UTE and ¹H rapid inversion recovery-prepared UTE (IR-rUTE), respectively. Scan protocol for UTE were the same as those for the phantom experiment above, while for IR-rUTE the following parameters were used (13): seven FIDs with varying flip angles were acquired with dwell time of 4μs near the soft tissue null point following each inversion; TE of each FID = 50μs; TR between each UTE readout = 2ms; TI = 65ms; TR between inversion pulses = 194ms; and total of 12,000 FIDs were collected to shorten scan time which is prolonged due to the IR preparation. Images were reconstructed to 256×256×256 isotropic matrix size. Following reconstruction, the tibial cortex was segmented out (inset of Figure 5) with a semi-automatic algorithm that detects the endosteal and periosteal boundaries of the cortex by taking derivatives along radial directions from the center of medullary cavity (13). The pixel intensities within the mid-tibia cortex were compared to that within the calibration sample, after accounting for the different relaxation times, to determine bone water concentration:

$${\rho }_{bone}={\rho }_{ref}\frac{I_{bone}{F}_{ref}}{I_{ref}{F}_{bone}}{e}^{-TE\left(\frac{1}{T_{2,ref}^{\mathrm{*}}}-\frac{1}{T_{2,bone}^{\mathrm{*}}}\right)}$$ [3]

where ρ_ref and ρ_bone are water proton densities in reference sample and cortical bone, respectively, and I_ref and I_bone are the corresponding image intensities. F_ref and F_bone represent the analytically determined fractions of magnetization available for signal detection when the duration of the RF pulse is comparable to T₂* and are derived elsewhere (13). Similar relaxation values as used previously based on population averages were also utilized in this work (13): T_1,TW = 250ms, T_2,TW* = 750μs, T_1,BW = 145ms, and T_2,BW* = 390μs (TW: total water, BW: bound water). For comparison, the different bone water pools were quantified from images without correction, with delay correction only and with full k-space trajectory correction.

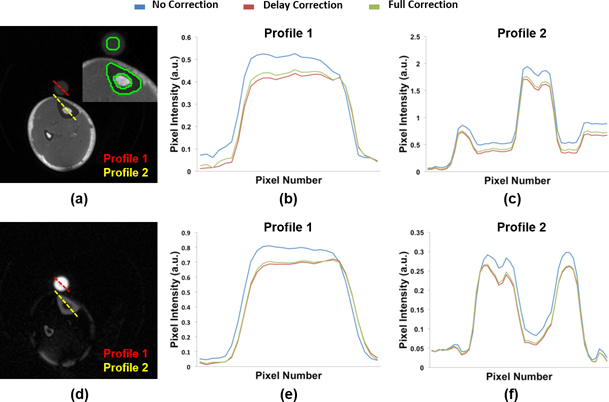
Figure 5.

Axial view of 3D (a) UTE and (d) IR-rUTE images of the calf of a healthy subject acquired with dual-frequency calf coil. (b, c, e, f) Profiles as indicated in the cross-sectional images to illustrate effect of different reconstruction methods. The inset in the UTE image shows the placement of ROI’s for bone water quantification.

To investigate the impact of gradient imperfections on inter-scanner quantification agreement, the above procedure was performed on two Siemens Trio systems on five individual subjects (one female, four males (one of which also participated in the previous ten-subject study), aged: 37±5 y/o). The agreement in bone water densities obtained from the two scanners was compared with and without gradient correction via Bland-Altman analysis.

3 |. Results

3.1 |. Effects of simple k-space shift on UTE image

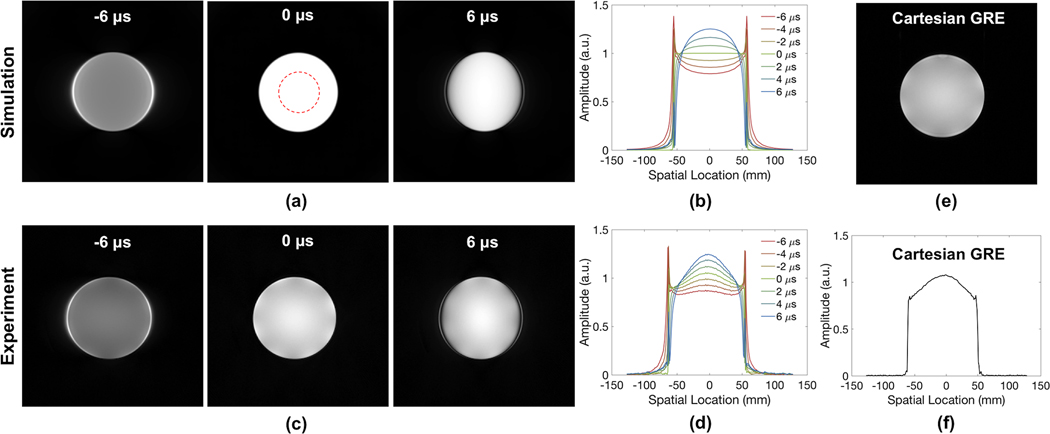
Simulated and experimentally acquired UTE images of a standard Siemens cylindrical phantom after introduction of gradient delays are shown in Figure 2. Most prominent are the edge effects, best seen in the profiles (b, d). Intensity distortions worsen with increasing timing errors. Overall, there is close agreement between simulation and experiments except for some additional intensity modulation on the experimentally acquired images (best visible on the profiles in Figures 2b and d), likely caused by dielectric effects (32,33), and perhaps a small contribution from varying proximity to the coil elements. Similar effects could be observed in a standard gradient echo image of the phantom and its profile as well (Figures 2e and f). Results from the five doped phantoms in Figure 3 also reveal the high spatial dependency of these artifacts—the farther away an object is located from the FOV center, the more severe the distortion. The elevated intensities observed for off-center samples on the experimental images are likely due to greater coil sensitivity at these locations, as similar variations are observed in the gradient echo results shown in Figures 3e and 3f.

Figure 2.

(a) Simulated and (c) experimentally acquired UTE images of a standard Siemens phantom in the presence of gradient delays up to ±6 μs along x-direction (left-right) and their horizontal cross-sectional profiles (b, d). Compared to the profile of simulated images, the slight unevenness of the signal intensity is likely due to dielectric effects. For comparison, a gradient echo image of the phantom and its profile are shown in (e) and (f), respectively.

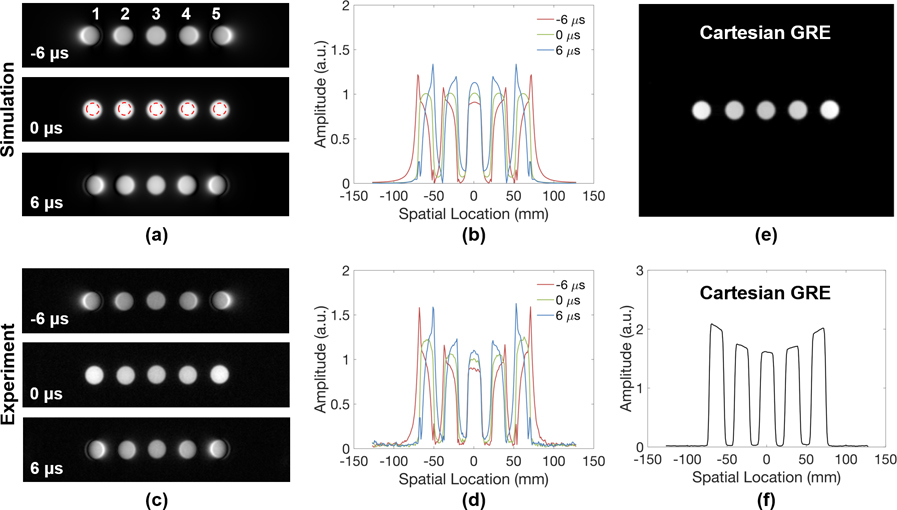
Figure 3.

(a) Simulated and (c) experimentally acquired UTE images of five doped samples used for bone water calibration in the presence of different amounts of gradient delays along x-direction (left-right) and (b, d) their respective horizontal cross-sectional profiles. Gradient delays cause distortions in image profile, as well as leakage of signal into neighboring pixels, particularly in objects located further from FOV center. Greater signal intensities observed for the outer samples of the sample array images are due to increasing coil sensitivity nearer to the head coil elements. For comparison, a gradient echo image and the profiles of five gadolinium-doped vials positioned in a similar fashion are shown in (e) and (f).

To quantitatively determine the impact of such timing errors on image contrast, average intensities within the ROIs indicated in Figure 2a and 3a (red dashed circles) were compared among images with and without gradient delay for each phantom. Fractional differences in intensity are summarized in Table 1. Close agreement is observed between the simulation and experimental data for both large and small phantoms. Interestingly, although intensity increases with positive gradient delay and decreases with negative delay for the inner samples, a net signal loss always occurs for the outer samples as a result of greater image distortions farther away from the FOV center.

Table 1.

Percent deviation in average intensity measured from ROIs in Figure 2a and Figure 3a as a function of gradient delay.

Phantom	Large		Small
Delay (μs)	Simulation	Experiment	Simulation					Experiment
			1*	2	3	4	5	1	2	3	4	5
−6	−20.2	−16.6	−24.0	−13.7	−9.5	−13.7	−28.7	−29.1	−15.0	−9.7	−16.2	−28.6
−4	−13.8	−11.2	−12.0	−8.3	−6.5	−8.3	−15.6	−16.0	−9.2	−6.6	−10.3	−15.1
−2	−7.0	−5.4	−3.6	−3.6	−3.6	−3.6	−5.4	−5.5	−3.9	−3.1	−4.4	−5.0
0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
2	7.4	6.1	−2.4	2.4	3.6	2.4	0.6	0.0	2.4	3.1	2.9	−0.8
4	15.0	11.8	−10.8	4.2	7.1	4.2	−5.4	−5.5	3.4	5.6	3.9	−7.1
6	22.8	16.6	−25.7	3.6	10.7	3.6	−17.4	−15.6	3.4	7.7	3.9	−18.1

^*Sample number as indicated in Figure 3.

3.2 |. Effects of gradient imperfections on phantom UTE images

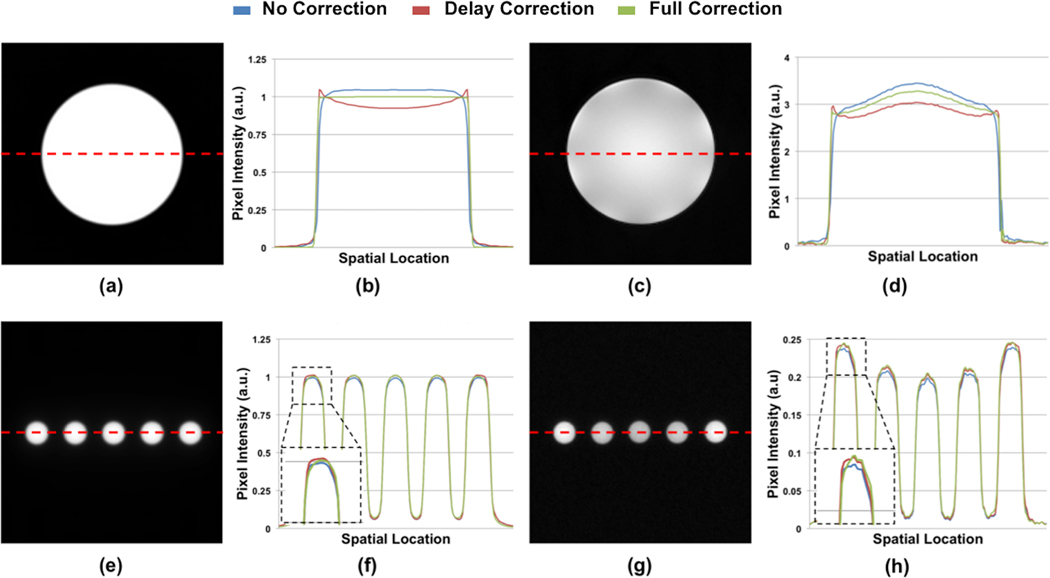
The gradient delays measured with the various combinations of coils and scanners used in this study are summarized in Table 2. Figure 4 illustrates simulated and experimentally acquired UTE images following correction of time delay only as well as after full trajectory correction. For the Siemens phantom, there appears to be some over-compensation for when only time delay correction is applied. For the calibration samples, on the other hand, the differences between delay correction and full trajectory correction appear somewhat more subtle.

Table 2.

Gradient delays (μs) measured from two Siemens 3 T Trio scanners with two different coils.

Scanner	1		2
Coil	Rapid	Siemens	Rapid
X Gradient	2.2	0	2.8
Y Gradient	1.0	−1.3	1.5
Z Gradient	1.0	−0.5	3.9

Figure 4.

(a, e) Simulated and (c, g) experimentally acquired UTE images of Siemens phantom and calibration samples. (b, d, f, h) Profiles (as indicated by the red dashed line) taken from images reconstructed with no correction, with gradient delay correction only, and with full trajectory correction are compared.

3.3 |. Effects of gradient imperfections on in vivo UTE images

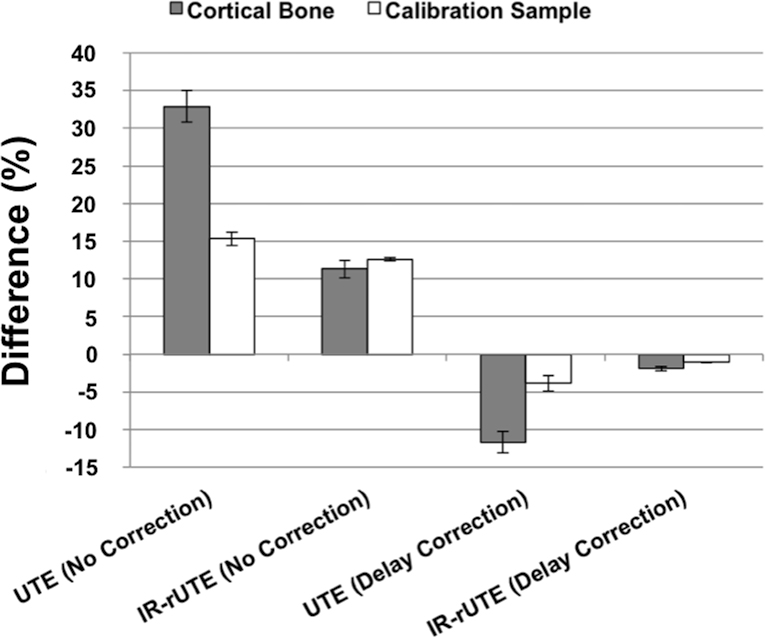
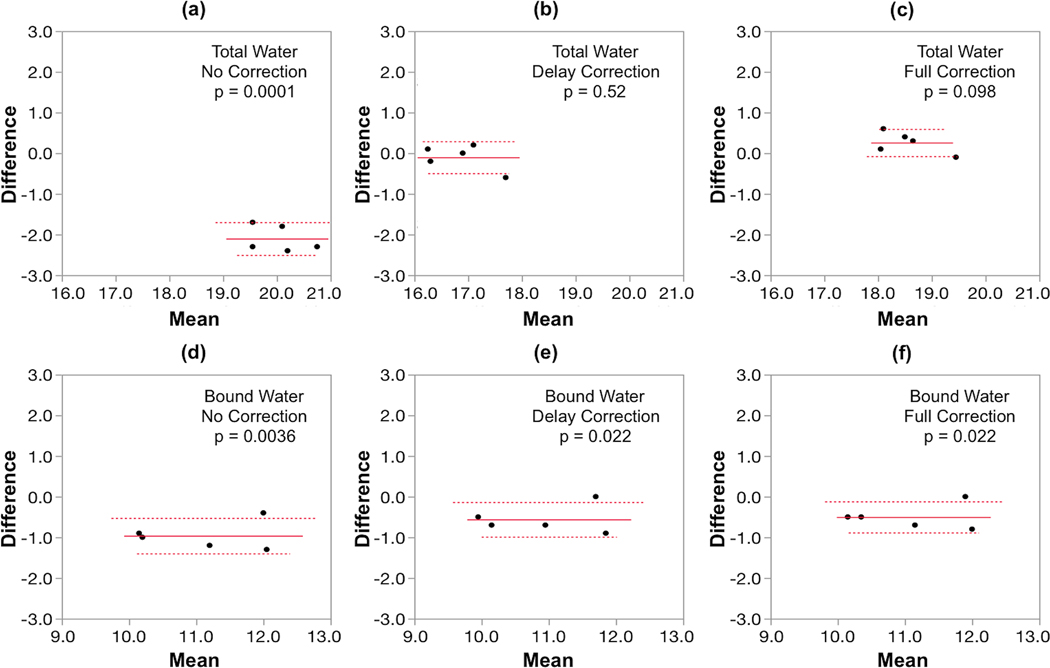
Figure 5 displays the UTE and IR-rUTE images of a healthy subject and compares the cross-sectional profiles with and without gradient imperfection compensation. As before, although the shapes of profiles are improved after accounting for gradient errors, a slight ‘over-compensation’ was observed for delay-only correction. The data on the ten subjects from an earlier work are presented in Table 3 and Figure 6. Table 3 lists the percent differences in bone water derived from images with no correction and delay-only correction relative to that derived from images with full correction. Figure 6 shows the fractional differences in average pixel intensities for cortical bone and calibration sample between gradient correction and no correction, demonstrating the substantial effects gradient imperfections exert on relative signal intensities. Figure 7 shows Bland-Altman plots from the five subjects scanned on two different scanners indicating the reduction in inter-scanner bias of bone water quantitative metrics for both total bone water obtained with UTE and bound water, obtained with inversion-recovery preparation to suppress pore and tissue water (IR-rUTE). The data demonstrate the elimination of bias for total water measurement and a significant reduction for bound water measurement.

Table 3.

Percent deviations in bone water densities quantified from in vivo UTE images with no correction and delay-only correction versus those with full trajectory correction.

	Total Water		Bound Water		Pore Water
Subject	Uncorrected	Delay Corrected	Uncorrected	Delay Corrected	Uncorrected	Delay Corrected
1	15.6	−10.4	0.0	−0.9	48.3	−30.0
2	16.6	−10.8	0.0	−1.9	52.0	−32.0
3	16.9	−10.1	1.7	−0.9	46.7	−28.3
4	13.9	−7.3	−2.2	−2.2	38.6	−17.5
5	15.7	−9.4	−1.0	0.0	34.8	−19.1
6	16.4	−8.5	−1.0	0.0	40.0	−20.0
7	16.2	−7.9	0.0	0.0	39.0	−19.5
8	17.0	−9.1	0.9	−0.9	49.2	−27.1
9	13.7	−7.7	2.1	−1.0	28.6	−15.5
10	14.1	−8.6	0.0	−0.9	43.6	−25.5

Figure 6.

Percent difference in the average pixel intensity within cortical bone or calibration sample between full, and either partial or no correction. The difference is largest without soft-tissue suppression (UTE), but smaller when mobile bone water and soft-tissue water and fat are suppressed (IR-rUTE), and negligible for the latter sequence after correction. This figure indicates that the differences in computed bone water densities are primarily due to differences in measured signal from cortical bone regions, as opposed to those from the calibration samples.

Figure 7.

Bland-Altman plots comparing bone water metrics between scanners 1 and 2, both equally configured Siemens Trio Systems, with the x- and y-axes indicating the mean of measurements from the two scanners and inter-scanner differences, respectively. Note the tight distributions of values within the five young test subjects (mean age 37±5 years) but large inter-scanner disparity without correction for total bone water (panel a) and to a lesser extent bound water (panel d). After delay correction the bias vanishes for total water (panel b) and is much reduced for bound water (panel e). The results are similar for dual correction (panels c and f, respectively).

4 |. Discussion

Reconstructing non-Cartesian MRI data requires re-sampling (or re-gridding) collected data points onto a Cartesian grid before Fourier transformation. However, the k-space value at each time point during readout may deviate from the nominal value due to the effects of time delays and gradient distortions (19,21,30,34). For quantification, UTE is more sensitive to eddy current effects compared to full-echo radial schemes since the central k-space region, which is directly impacted by these errors, dominates image contrast. For example, Takizawa, et al [21], have shown that even in the absence of timing delays, the residual higher order gradient distortions lead to significant image degradation in UTE images, while artifacts are unnoticeable in full-echo radial images.

The gradient distortion problem is not unique to UTE-based bone water quantification. Rather, it should affect any UTE-based applications. However, the problem is likely exacerbated for bone water quantification since bone water density is only about 20% that of soft tissues, and the inherently low signal in cortical bone makes it more susceptible to potential signal contamination from neighboring soft tissue as a result of gradient imperfections.

Without destructive testing, true bone water content remains unknown. Thus, it is uncertain whether the values derived with full gradient trajectory correction are more accurate than those with delay-only or without any correction. However, given that it is known that higher order gradient errors exist and that we could measure and compensate for these deviations, it is reasonable to assume that full corrections will likely yield the best estimates. Furthermore, as Table 1 shows, the patterns of signal intensity deviations from the phantom experiments in which the gradient trajectories were first fully compensated and various delays subsequently applied closely resemble those of simulated phantoms for which the ground truth is known. These results lend further support to the supposition that full trajectory correction likely yields the best estimates for actual bone water content.

At first glance, Figures 4 and 5 seem to indicate that delay-only correction may be sufficient since the differences appear small. While the profiles of full and delay-only correction may seem similar, quantitatively, the differences are non-negligible. In the cortical bone regions of the UTE images (the two “valleys” abutting the high signal marrow region in Figure 5c), the signal intensities in delay-only images are lower than those of full-correction by approximately 12% as indicated in Figure 6. As Equation 3 shows, bone water concentration is directly proportional to the measured bone water signal while inversely proportional to the signal in the calibration sample, and together total bone water in the delay-only correction is lower by about 9% on average compared to that of full correction due to these offsets (Table 3). Also, while there was good inter-scanner agreement with either delay-only or full trajectory correction, comparison of Figure 7b and 7c indicates a shift in the mean value of water content, again reflecting the ~9% difference shown in Table 3.

As Table 3 shows, deviations for pore water is much larger than those of total or bound water. While total and bound water are derived via Equation 3 using measured signal from UTE and IR-rUTE images, pore water is computed by subtracting bound from total water. According to the table, the bias in bound water is relatively small, often negligible. Thus, any bias in total water will yield about the same absolute bias in pore water. However, since pore water density is typically a fraction of that of bound water (about one-fourth according to refs. 1,13), the percent deviation in pore water will become magnified since the same absolute bias is divided by a much smaller value. For this reason, a substantially larger deviation is observed for pore water than for total or bound water.

For total water, a statistically significant difference exists between total water measured from the two MR systems (p = 0.0001), which however, vanishes after accounting for the gradient errors. For bound water, on the other hand, the difference after correction, although still marginally significant, is reduced. This observation suggests that the quantification of total water may be more sensitive to k-space trajectory errors than bound water, a conclusion inferred by Table 3 as well. This phenomenon may be due to signal contamination from surrounding soft tissue in the absence of long-T₂ suppression. In UTE images, the signal from soft tissues (such as muscle and bone marrow) may be interfering with the signal from cortical bone in the presence of gradient errors due to signal leakage (Figure 3). In IR-rUTE images, on the other hand, soft tissues signal are suppressed and signal contamination should therefore be less of an issue. In fact, this may explain why signal from the calibration sample, which is mostly surrounded by air, is less affected by gradient errors than cortical bone in the absence of long-T₂ suppression (UTE), while they are similarly affected when soft-tissue signal is suppressed (IR-rUTE) (Figure 6). These effects lead to greater deviations for total water than for bound water (Table 3).

There seems to be a slight gradient overcompensation when time-delay only correction is applied. This, at least in part, may be due to the fact that the timing delay in our work is determined from the midpoint of the rising gradient ramp. In Figure 1f where the two dashed lines meet, the zeroeth moment at that point should be zero for an ideal trapezoidal waveform since the gradient has not yet begun to rise. However, when the time delay correction is applied based on the midpoint of the ramp of an ideal trapezoid, the actual rise in gradient amplitude from zero will have begun earlier than expected (as shown in Fig. 1f). This will lead to an effective shift of the gradient to the left (towards earlier time) and cause overcompensation for time delay.

One interesting observation from our study is depicted in Table 2 which shows that using different receive coils yielded different measured gradient errors. There are two possible explanations for this observation. First, since many modern receivers (including the two coils we have used) have built-in electronics, such as preamplifiers, small differences in their performance could potentially yield slightly different timing delays. In addition, differences in the layout of the conductive coil elements, e.g. size, number and location of rungs, could lead to slight differences in eddy currents that are generated by the imaging gradients. While it is also possible that the measurement of the gradient distortions could itself be influenced by the receive coils, such differentiation is beyond the scope of this paper and may warrant further investigation.

While Table 2 indicates that both absolute gradient errors and inter-scanner differences in gradient delays could be small, Table 3 shows that even such small gradient inaccuracies could cause substantial quantification errors. It seems likely that MR equipment vendors have in recent years fine-tuned their instruments to minimize these timing errors and eddy currents effects, in particular since full-echo and UTE radial sequences have become more popular and these pulse sequences have been provided by the vendors as either product or “works-in-progress” sequences. Even so, our results show that additional gradient compensation could further improve measurement accuracy.

The difference in k-space signal between an object at FOV center and the same object offset from the center is a linear phase shift according to the Fourier shift theorem, with objects that are further displaced accruing larger phase shifts. Thus, the phase of the received signal will vary more rapidly from one k-space point to the next with increasing distance from the FOV center. Consequently, similar errors in k-space mapping will cause different levels of phase errors, with larger errors occurring for further displaced objects. This phenomenon is demonstrated in the point-spread-function (PSF) simulations shown in Supporting Information Figure S1, showing increasing levels of artifacts, namely, broadening peak and signal leakage into adjacent spatial regions, with increasing distance of a point object from the FOV center. K-space signal of a point object at FOV center is a constant, and thus no error will result from k-space mis-mappings. However, with increasing distance from FOV center, phase of the signal changes more rapidly in k-space, and errors in k-space mapping will lead to greater phase errors, leading to increasing levels of artifacts. The profiles of the five samples shown in Figure 3 results from the convolution of an undistorted profile with the PSFs shown in Figure S1. This is of importance to quantification because the positioning of a subject and the calibration sample may vary from scan to scan. The measured signal intensity within the tibial cortex and the sample may be affected to different extents depending on their spatial locations within the FOV in the absence of a correction. In addition, the distorted intensity profile of an uncorrected image (Figure 3) may also make quantification sensitive to ROI placement. Accounting for these gradient imperfections is expected to improve not only intra-subject test-retest repeatability, but also augment the sensitivity to differentiate bone water concentrations among subjects.

Several trajectory correction methods able to handle both time delay and eddy current (14,19,20,23–25) have been proposed for UTE. The phase mapping technique originally designed for spiral imaging (26,27), and recently modified for radial UTE acquisitions (23), was chosen for the current study because it is simple to implement, it does not rely on any models where assumptions might have been made, and it directly measures the trajectory of the exact gradient waveform used for UTE imaging.

Although the current study focuses on bone water quantification, the conclusions are equally applicable to evaluation of bone mineral. Both UTE and ZTE have previously been explored as an alternative to CT for bone mineral interrogation via ³¹P MRI (2,6,7,13). Similar artifacts were observed during our ZTE experiments (not shown here). Although neither gradient delay nor eddy current-induced gradient waveform distortion matter in ZTE, potential problems may occur due to timing errors in other hardware components such as the frequency demodulation unit (17).

5 |. Conclusions

In conclusion, the present study shows that gradient imperfections due to hardware-related timing delays and eddy current-induced waveform distortions compromise not only UTE image quality but, more importantly, bone water quantification. Correcting for these gradient system imperfections effectively alleviates image artifacts and may substantially improve in vivo bone water quantification inter-scanner concordance.

Supplementary Material

figure S1

Supporting Information Figure S1. Point-spread-functions as a function of distance from FOV center at gradient delays of −6, 0, and +6 μs. The locations of these point objects were matched to those of the five small samples shown in Figure 3.